3.9: Resolver ecuaciones usando números enteros; La propiedad de división de igualdad (Parte 1)
- Page ID
- 114205
- Determinar si un entero es una solución de una ecuación
- Resolver ecuaciones con números enteros usando las Propiedades de Suma y Resta de Igualdad
- Modelar la División Propiedad de Igualdad
- Resolver ecuaciones usando la Propiedad de División de Igualdad
- Traducir a una ecuación y resolver
Antes de comenzar, toma este cuestionario de preparación.
- Evaluar\(x + 4\) cuándo\(x = −4\). Si te perdiste este problema, revisa el Ejemplo 3.2.9.
- Resolver:\(y − 6 = 10\). Si te perdiste este problema, revisa el Ejemplo 2.3.6.
- Traducir en una expresión algebraica\(5\) menor que\(x\). Si te perdiste este problema, revisa la Tabla 1.3.1.
Determinar si un número es una solución de una ecuación
En Resolver ecuaciones con las propiedades de resta y suma de igualdad, vimos que una solución de una ecuación es un valor de una variable que hace una declaración verdadera cuando se sustituye en esa ecuación. En esa sección, encontramos soluciones que eran números enteros. Ahora que hemos trabajado con enteros, encontraremos soluciones enteras a ecuaciones.
Los pasos que tomamos para determinar si un número es una solución a una ecuación son los mismos si la solución es un número entero o un entero.
Paso 1. Sustituir el número por la variable en la ecuación.
Paso 2. Simplifica las expresiones en ambos lados de la ecuación.
Paso 3. Determinar si la ecuación resultante es verdadera.
- Si es cierto, el número es una solución.
- Si no es cierto, el número no es una solución.
Determinar si cada uno de los siguientes es una solución de\(2x − 5 = −13\):
- \(x = 4\)
- \(x = −4\)
- \(x = −9\)
Solución
| a) Sustituir 4 por x en la ecuación para determinar si es verdadera. | 2x − 5 = −13 |
| Sustituto\(\textcolor{red}{4}\) por x. | \(2(\textcolor{red}{4}) - 5 \stackrel{?}{=} -13\) |
| Multiplicar. | \(8 - 5 \stackrel{?}{=} -13\) |
| Restar. | \(3 \neq -13\) |
Dado que\(x = 4\) no da como resultado una ecuación verdadera, no\(4\) es una solución a la ecuación.
| b) Sustituir -4 por x en la ecuación para determinar si es verdadera. | 2x − 5 = −13 |
| Sustituto\(\textcolor{red}{-4}\) por x. | \(2(\textcolor{red}{-4}) - 5 \stackrel{?}{=} -13\) |
| Multiplicar. | \(-8 - 5 \stackrel{?}{=} -13\) |
| Restar. | \(-13 = -13 \; \checkmark\) |
Dado que\(x = −4\) da como resultado una ecuación verdadera,\(−4\) es una solución a la ecuación.
| b) Sustituir -9 por x en la ecuación para determinar si es verdadera. | 2x − 5 = −13 |
| Sustituto\(\textcolor{red}{-9}\) por x. | \(2(\textcolor{red}{-9}) - 5 \stackrel{?}{=} -13\) |
| Multiplicar. | \(-18 - 5 \stackrel{?}{=} -13\) |
| Restar. | \(-23 \neq -13\) |
Dado que\(x = −9\) no da como resultado una ecuación verdadera, no\(−9\) es una solución a la ecuación.
Determinar si cada uno de los siguientes es una solución de\(2x − 8 = −14\):
- \(x = −11\)
- \(x = 11\)
- \(x = −3\)
- Contestar a
-
no
- Respuesta b
-
no
- Respuesta c
-
si
Determinar si cada uno de los siguientes es una solución de\(2y + 3 = −11\):
- \(y = 4\)
- \(y = −4\)
- \(y = −7\)
- Contestar a
-
no
- Respuesta b
-
no
- Respuesta c
-
si
Resolver ecuaciones con números enteros usando las propiedades de suma y resta de igualdad
En Resolver ecuaciones con las propiedades de resta y suma de igualdad, resolvimos ecuaciones similares a las dos que se muestran aquí usando las propiedades de resta y suma de igualdad. Ahora podemos volver a usarlos con enteros.
\[\begin{split} x + 4 & = 12 \qquad \qquad \qquad y - 5 = 9 \\ x + 4 \textcolor{red}{-4} & = 12 \textcolor{red}{-4} \qquad \; \; y - 5 \textcolor{red}{+5} = 9 \textcolor{red}{+5} \\ x & = 8 \qquad \qquad \qquad \qquad \; y = 14 \end{split} \nonumber \]
Cuando sumas o restas la misma cantidad de ambos lados de una ecuación, todavía tienes igualdad.
| Resta Propiedad de Igualdad | Adición Propiedad de Igualdad |
|---|---|
| Para cualquier número a, b, c, si a = b entonces a − c = b − c. | Para cualquier número a, b, c, si a = b entonces a + c = b + c. |
Resolver:\(y + 9 = 5\).
Solución
| Resta 9 de cada lado para deshacer la suma. | \(y + 9 \textcolor{red}{-9} = 5 \textcolor{red}{-9}\) |
| Simplificar. | \(y = -4\) |
Verifique el resultado sustituyéndolo\(−4\) en la ecuación original.
| Sustituir −4 por y | \(-4 + 9 \stackrel{?}{=} 5\) |
| \(5 = 5 \; \checkmark\) |
Dado\(y = −4\) que hace\(y + 9 = 5\) una verdadera afirmación, encontramos la solución a esta ecuación
Resolver:\(y + 11 = 7\)
- Contestar
-
\(-4\)
Resolver:\(y + 15 = −4\)
- Contestar
-
\(-19\)
Resolver:\(a − 6 = −8\)
Solución
| Agrega 6 a cada lado para deshacer la resta. | \(a - 6 \textcolor{red}{+6} = -8 \textcolor{red}{+6}\) |
| Simplificar. | \(a = -2\) |
| Verifique el resultado sustituyendo −2 en la ecuación original. | \(a - 6 = -8\) |
| Sustituir −2 por a. | \(-2 - 6 \stackrel{?}{=} -8\) |
| \(-8 = -8 \; \checkmark\) |
La solución a\(a − 6 = −8\) es\(−2\). Ya\(a = −2\) que hace\(a − 6 = −8\) una verdadera afirmación, encontramos la solución a esta ecuación.
Resolver:\(a − 2 = −8\)
- Contestar
-
\(-6\)
Resolver:\(n − 4 = −8\)
- Contestar
-
\(-4\)
Modelar la División Propiedad de Igualdad
Todas las ecuaciones que hemos resuelto hasta ahora han sido de la forma\(x + a = b\) o\(x − a = b\). Pudimos aislar la variable sumando o restando el término constante. Ahora veremos cómo resolver ecuaciones que involucren división. Modelaremos una ecuación con sobres y contadores en la Figura\(\PageIndex{1}\).
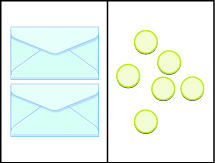
Figura\(\PageIndex{1}\)
Aquí, hay dos sobres idénticos que contienen el mismo número de contadores. Recuerda, el lado izquierdo del espacio de trabajo debe ser igual al lado derecho, pero los contadores del lado izquierdo están “ocultos” en los sobres. Entonces, ¿cuántos contadores hay en cada sobre?
Para determinar el número, separe los contadores del lado derecho en\(2\) grupos del mismo tamaño. Entonces\(6\) contadores divididos en\(2\) grupos significa que debe haber\(3\) contadores en cada grupo (ya que\(6 ÷ 2 = 3\)).
¿Qué ecuación modela la situación mostrada en la Figura\(\PageIndex{2}\)? Hay dos sobres, y cada uno contiene\(x\) contadores. En conjunto, los dos sobres deben contener un total de\(6\) contadores. Entonces la ecuación que modela la situación es\(2x = 6\).
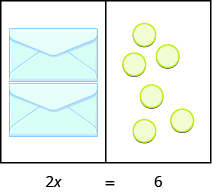
Figura\(\PageIndex{2}\)
Podemos dividir ambos lados de la ecuación por\(2\) como hicimos con los sobres y los contadores.
\[\begin{split} \dfrac{2x}{\textcolor{red}{2}} & = \dfrac{6}{\textcolor{red}{2}} \\ x & = 3 \end{split} \nonumber \]
Encontramos que cada sobre contiene\(3\) contadores. ¿Esto comprueba? Sabemos\(2 • 3 = 6\), entonces funciona. Tres contadores en cada uno de dos sobres hace igual a seis. La figura\(\PageIndex{3}\) muestra otro ejemplo.
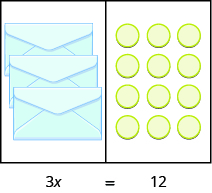
Figura\(\PageIndex{3}\)
Ahora tenemos sobres y\(12\) mostradores\(3\) idénticos. ¿Cuántos contadores hay en cada sobre? Tenemos que separar los\(12\) contadores en\(3\) grupos. Ya que\(12 ÷ 3 = 4\), debe haber\(4\) contadores en cada sobre. Ver Figura\(\PageIndex{4}\).
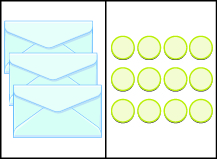
Figura\(\PageIndex{4}\)
La ecuación que modela la situación es\(3x = 12\). Podemos dividir ambos lados de la ecuación por\(3\).
\[\begin{split} \dfrac{3x}{\textcolor{red}{3}} & = \dfrac{12}{\textcolor{red}{3}} \\ x & = 4 \end{split} \nonumber \]
¿Esto comprueba? Lo hace porque\(3 • 4 = 12\).
Escribir una ecuación modelada por los sobres y contadores, y luego resolverla.
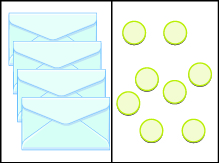
Solución
Hay\(4\) sobres, o valores\(4\) desconocidos, a la izquierda que coinciden con los\(8\) contadores de la derecha. Llamemos a la cantidad desconocida en los sobres\(x\).
| Escribe la ecuación. | \(4x = 8\) |
| Divide ambos lados por 4. | \(\dfrac{4x}{\textcolor{red}{4}} = \dfrac{8}{\textcolor{red}{4}}\) |
| Simplificar. | \(x = 2\) |
Hay\(2\) mostradores en cada sobre.
Escribe la ecuación modelada por los sobres y contadores. Entonces resolverlo.
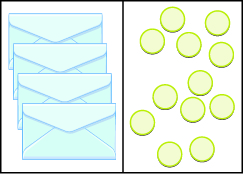
- Contestar
-
\(4x=12\);\(x=3\)
Escribe la ecuación modelada por los sobres y contadores. Entonces resolverlo.
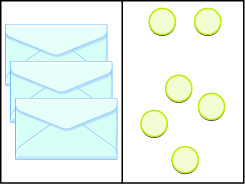
- Contestar
-
\(3x=6\);\(x=2\)
Resolver ecuaciones usando la propiedad de división de igualdad
Los ejemplos anteriores llevan a la División Propiedad de la Igualdad. Cuando divides ambos lados de una ecuación por cualquier número distinto de cero, aún tienes igualdad.
Para cualquier número\(a, b, c\)\(c ≠ 0\), y
\[\text{If } a = b \text{ then } \dfrac{a}{c} = \dfrac{b}{c} \ldotp\]
Resolver:\(7x = −49\).
Solución
Para aislarnos\(x\), necesitamos deshacer la multiplicación.
| Divide cada lado por 7. | \(\dfrac{7x}{\textcolor{red}{7}} = \dfrac{-49}{\textcolor{red}{7}}\) |
| Simplificar | \(x = -7\) |
Consulta la solución.
| Sustituye −7 por x. | \(7(-7) \stackrel{?}{=} -49\) |
| \(-49 = -49 \; \checkmark\) |
Por lo tanto,\(−7\) es la solución a la ecuación.
Resolver:\(8a = 56\)
- Contestar
-
\(7\)
Resolver:\(11n = 121\)
- Contestar
-
\(11\)
Resolver:\(−3y = 63\).
Solución
Para aislarnos\(y\), necesitamos deshacer la multiplicación.
| Divide cada lado por −3. | \(\dfrac{-3y}{\textcolor{red}{-3}} = \dfrac{63}{\textcolor{red}{-3}}\) |
| Simplificar. | \(y = -21\) |
Consulta la solución.
| Sustituir −21 por y. | \(-3(-21) \stackrel{?}{=} 63\) |
| \(63 = 63 \; \checkmark\) |
Dado que esta es una afirmación verdadera,\(y = −21\) es la solución a la ecuación.
Resolver:\(−8p = 96\)
- Contestar
-
\(-12\)
Resolver:\(−12m = 108\)
- Contestar
-
\(-9\)


