Saltar al contenido principal
LibreTexts Español

4.9: Suma y resta fracciones con diferentes denominadores (Parte 2)

  1. Última actualización
  2. Guardar como PDF
  • Page ID
    114258

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

    Identificar y usar operaciones de fracciones

    A estas alturas en este capítulo, ya has practicado multiplicar, dividir, sumar y restar fracciones. En la siguiente tabla se resumen estas cuatro operaciones de fracción. Recuerda: Se necesita un denominador común para sumar o restar fracciones, pero no para multiplicar o dividir fracciones.

    Resumen de Operaciones de Fracción

    Multiplicación de fracciones: Multiplicar los numeradores y multiplicar los denominadores.

    \[\dfrac{a}{b} \cdot \dfrac{c}{d} = \dfrac{ac}{bd}\]

    División de fracciones: Multiplicar la primera fracción por el recíproco de la segunda.

    \[\dfrac{a}{b} \div \dfrac{c}{d} = \dfrac{a}{b} \cdot \dfrac{d}{c}\]

    Adición de fracciones: Suma los numeradores y coloca la suma sobre el denominador común. Si las fracciones tienen diferentes denominadores, primero conviértelos a formas equivalentes con la LCD.

    \[\dfrac{a}{c} + \dfrac{b}{c} = \dfrac{a + b}{c}\]

    Resta de fracciones: Restar los numeradores y colocar la diferencia sobre el denominador común. Si las fracciones tienen diferentes denominadores, primero conviértelos a formas equivalentes con la LCD.

    \[\dfrac{a}{c} - \dfrac{a}{c} = \dfrac{a - b}{c}\]

    Ejemplo\(\PageIndex{11}\): simplify

    Simplificar:

    1. \(− \dfrac{1}{4} + \dfrac{1}{6}\)
    2. \(− \dfrac{1}{4} \div \dfrac{1}{6}\)

    Solución

    Primero nos preguntamos: “¿Cuál es la operación?”

    1. La operación es suma. ¿Las fracciones tienen un denominador común? No.
    Encuentra la pantalla LCD.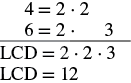
    Reescribe cada fracción como una fracción equivalente con la pantalla LCD. \(- \dfrac{1 \cdot \textcolor{red}{3}}{4 \cdot \textcolor{red}{3}} + \dfrac{1 \cdot \textcolor{red}{2}}{6 \cdot \textcolor{red}{2}} \)
    Simplificar los numeradores y denominadores. \(- \dfrac{3}{12} + \dfrac{2}{12} \)
    Agrega los numeradores y coloca la suma sobre el denominador común. \(- \dfrac{1}{12} \)
    Comprueba si se puede simplificar la respuesta. No puede.  
    1. La operación es división. No necesitamos un denominador común.
    Para dividir fracciones, multiplique la primera fracción por el recíproco de la segunda. \(- \dfrac{1}{4} \cdot \dfrac{6}{1}\)
    Multiplicar. \(- \dfrac{6}{4}\)
    Simplificar. \(- \dfrac{3}{2} \)
    Ejercicio\(\PageIndex{21}\)

    Simplificar:

    1. \(− \dfrac{3}{4} - \dfrac{1}{6}\)
    2. \(− \dfrac{3}{4} \cdot \dfrac{1}{6}\)
    Contestar a

    \(-\dfrac{11}{12}\)

    Respuesta b

    \(-\dfrac{1}{8}\)

    Ejercicio\(\PageIndex{22}\)

    Simplificar:

    1. \(\dfrac{5}{6} \div \left(- \dfrac{1}{4}\right)\)
    2. \(\dfrac{5}{6} - \left(- \dfrac{1}{4}\right)\)
    Contestar a

    \(-\dfrac{10}{3}\)

    Respuesta b

    \(\dfrac{13}{12}\)

    Ejemplo\(\PageIndex{12}\): simplify

    Simplificar:

    1. \(\dfrac{5x}{6} - \dfrac{3}{10}\)
    2. \(\dfrac{5x}{6} \cdot \dfrac{3}{10}\)

    Solución

    1. La operación es resta. Las fracciones no tienen un denominador común.
    Reescribe cada fracción como una fracción equivalente con la pantalla LCD, 30. \(\dfrac{5x \cdot \textcolor{red}{5}}{6 \cdot \textcolor{red}{5}} - \dfrac{3 \cdot \textcolor{red}{3}}{10 \cdot \textcolor{red}{3}} \)
      \(\dfrac{25x}{30} - \dfrac{9}{30} \)
    Restar los numeradores y colocar la diferencia sobre el denominador común. \(\dfrac{25x - 9}{30} \)
    1. La operación es multiplicación; sin necesidad de un denominador común.
    Para multiplicar fracciones, multiplicar los numeradores y multiplicar los denominadores. \(\dfrac{5x \cdot 3}{ 6 \cdot 10} \)
    Reescribir, mostrando factores comunes. \(\dfrac{\cancel{5} \cdot x \cdot \cancel{3}}{2 \cdot \cancel{3} \cdot 2 \cdot \cancel{5}} \)
    Elimine los factores comunes para simplificar. \(\dfrac{x}{4} \)
    Ejercicio\(\PageIndex{23}\)

    Simplificar:

    1. \(\dfrac{3a}{4} - \dfrac{8}{9}\)
    2. \(\dfrac{3a}{4} \cdot \dfrac{8}{9}\)
    Contestar a

    \(\dfrac{27a-32}{36}\)

    Respuesta b

    \(\dfrac{2a}{3}\)

    Ejercicio\(\PageIndex{24}\)

    Simplificar:

    1. \(\dfrac{4k}{5} + \dfrac{5}{6}\)
    2. \(\dfrac{4k}{5} \div \dfrac{5}{6}\)
    Contestar a

    \(\dfrac{24k+25}{30}\)

    Respuesta b

    \(\dfrac{24k}{25}\)

    Utilice el orden de operaciones para simplificar fracciones complejas

    En Multiplicar y dividir números mixtos y fracciones complejas, vimos que una fracción compleja es una fracción en la que el numerador o denominador contiene una fracción. Simplificamos fracciones complejas reescribiéndolas como problemas de división. Por ejemplo,

    \[\dfrac{\dfrac{3}{4}}{\dfrac{5}{8}} = \dfrac{3}{4} \div \dfrac{5}{8} \nonumber \]

    Ahora veremos fracciones complejas en las que se puede simplificar el numerador o denominador. Para seguir el orden de las operaciones, primero simplificamos el numerador y el denominador por separado. Entonces dividimos el numerador por el denominador.

    CÓMO: Simplificar fracciones complejas

    Paso 1. Simplifica el numerador.

    Paso 2. Simplifica el denominador.

    Paso 3. Divide el numerador por el denominador.

    Paso 4. Simplificar si es posible.

    Ejemplo\(\PageIndex{13}\): simplify

    Simplificar:\(\dfrac{\left(\dfrac{1}{2}\right)^{2}}{4 + 3^{2}}\).

    Solución

    Simplifica el numerador. \(\dfrac{\dfrac{1}{4}}{4 + 3^{2}}\)
    Simplifica el término con el exponente en el denominador. \(\dfrac{\dfrac{1}{4}}{4 + 9} \)
    Agregar los términos en el denominador. \(\dfrac{\dfrac{1}{4}}{13} \)
    Divide el numerador por el denominador. \(\dfrac{1}{4} \div 13 \)
    Reescribir como multiplicación por el recíproco. \(\dfrac{1}{4} \cdot \dfrac{1}{13} \)
    Multiplicar. \(\dfrac{1}{52}\)
    Ejercicio\(\PageIndex{25}\)

    Simplificar:\(\dfrac{\left(\dfrac{1}{3}\right)^{2}}{2^{3} + 2}\).

    Contestar

    \(\dfrac{1}{90}\)

    Ejercicio\(\PageIndex{26}\)

    Simplificar:\(\dfrac{1 + 4^{2}}{\left(\dfrac{1}{4}\right)^{2}}\).

    Contestar

    \(272\)

    Ejemplo\(\PageIndex{14}\): simplify

    Simplificar:\(\dfrac{\dfrac{1}{2} + \dfrac{2}{3}}{\dfrac{3}{4} - \dfrac{1}{6}}\).

    Solución

    Reescribe el numerador con la LCD de 6 y denominador con LCD de 12. \(\dfrac{\dfrac{3}{6} + \dfrac{4}{6}}{\dfrac{9}{12} - \dfrac{2}{12}} \)
    Añadir en el numerador. Restar en el denominador. \(\dfrac{\dfrac{7}{6}}{\dfrac{7}{12}} \)
    Divide el numerador por el denominador. \(\dfrac{7}{6} \div \dfrac{7}{12}\)
    Reescribir como multiplicación por el recíproco. \(\dfrac{7}{6} \cdot \dfrac{12}{7} \)
    Reescribir, mostrando factores comunes. \(\dfrac{\cancel{7} \cdot \cancel{6} \cdot 2}{\cancel{6} \cancel{7} \cdot 1} \)
    Simplificar. \(2 \)
    Ejercicio\(\PageIndex{27}\)

    Simplificar:\(\dfrac{\dfrac{1}{3} + \dfrac{1}{2}}{\dfrac{3}{4} - \dfrac{1}{3}}\).

    Contestar

    \(2\)

    Ejercicio\(\PageIndex{28}\)

    Simplificar:\(\dfrac{\dfrac{2}{3} - \dfrac{1}{2}}{\dfrac{1}{4} + \dfrac{1}{3}}\).

    Contestar

    \(\dfrac{2}{7}\)

    Evaluar expresiones variables con fracciones

    Hemos evaluado expresiones antes, pero ahora también podemos evaluar expresiones con fracciones. Recuerde, para evaluar una expresión, sustituimos el valor de la variable en la expresión y luego simplificamos.

    Ejemplo\(\PageIndex{15}\): evaluate

    Evaluar\(x + \dfrac{1}{3}\) cuándo

    1. \(x = - \dfrac{1}{3}\)
    2. \(x = - \dfrac{3}{4}\)

    Solución

    1. Evaluar\(x + \dfrac{1}{3}\) cuándo\(x = − \dfrac{1}{3}\),\(− \dfrac{1}{3}\) sustituir\(x\) en la expresión.
    Sustituto\(\textcolor{red}{- \dfrac{1}{3}}\) por x. \(\textcolor{red}{- \dfrac{1}{3}} + \dfrac{1}{3} \)
    Simplificar. \(0 \)
    1. Evaluar\(x + \dfrac{1}{3}\) cuándo\(x = − \dfrac{3}{4}\),\(− \dfrac{3}{4}\) sustituimos\(x\) en la expresión.
    Sustituto\(\textcolor{red}{- \dfrac{3}{4}}\) por x. \(\textcolor{red}{- \dfrac{1}{3}} + \dfrac{1}{3}\)
    Reescribe como fracciones equivalentes con la pantalla LCD, 12. \(- \dfrac{3 \cdot 3}{4 \cdot 3} + \dfrac{1 \cdot 4}{3 \cdot 4} \)
    Simplificar los numeradores y denominadores. \(- \dfrac{9}{12} + \dfrac{4}{12} \)
    Agregar. \(- \dfrac{5}{12} \)
    Ejercicio\(\PageIndex{29}\)

    Evaluar\(x + \dfrac{3}{4}\) cuando:

    1. \(x = - \dfrac{7}{4}\)
    2. \(x = - \dfrac{5}{4}\)
    Contestar a

    \(-1\)

    Respuesta b

    \(-\dfrac{1}{2}\)

    Ejercicio\(\PageIndex{30}\)

    Evaluar\(y + \dfrac{1}{2}\) cuando:

    1. \(y = \dfrac{2}{3}\)
    2. \(y = - \dfrac{3}{4}\)
    Contestar a

    \(\dfrac{7}{6}\)

    Respuesta b

    \(-\dfrac{1}{4}\)

    Ejemplo\(\PageIndex{16}\): evaluate

    Evaluar\(y − \dfrac{5}{6}\) cuándo\(y = - \dfrac{2}{3}\).

    Solución

    Nosotros\(− \dfrac{2}{3}\) sustituimos\(y\) en la expresión.

    Sustituto\(\textcolor{red}{- \dfrac{2}{3}}\) de y. \(\textcolor{red}{- \dfrac{2}{3}} - \dfrac{5}{6}\)
    Reescribir como fracciones equivalentes con la pantalla LCD, 6. \(- \dfrac{4}{6} - \dfrac{5}{6} \)
    Restar. \(- \dfrac{9}{6} \)
    Simplificar. \(- \dfrac{3}{2} \)
    Ejercicio\(\PageIndex{31}\)

    Evaluar\(y − \dfrac{1}{2}\) cuándo\(y = - \dfrac{1}{4}\).

    Contestar

    \(-\dfrac{3}{4}\)

    Ejercicio\(\PageIndex{32}\)

    Evaluar\(x − \dfrac{3}{8}\) cuándo\(x = - \dfrac{5}{2}\).

    Contestar

    \(-\dfrac{23}{8}\)

    Ejemplo\(\PageIndex{17}\):

    Evaluar\(2x^2y\) cuándo\(x = \dfrac{1}{4}\) y\(y = − \dfrac{2}{3}\).

    Solución

    Sustituir los valores en la expresión. En\(2x^2y\), el exponente aplica sólo a\(x\).

    Sustituye\(\textcolor{red}{\dfrac{1}{4}}\) por x y\(\textcolor{blue}{- \dfrac{2}{3}}\) por y. \(2 \left(\textcolor{red}{\dfrac{1}{4}}\right)^{2} \left(\textcolor{blue}{- \dfrac{2}{3}}\right) \)
    Simplifique primero los exponentes. \(2 \left(\dfrac{1}{16}\right) \left(- \dfrac{2}{3}\right)\)
    Multiplicar. El producto será negativo. \(- \dfrac{2}{1} \cdot \dfrac{1}{16} \cdot \dfrac{2}{3} \)
    Simplificar. \(- \dfrac{4}{48} \)
    Eliminar los factores comunes. \(- \dfrac{1 \cdot \cancel{4}}{\cancel{4} \cdot 12} \)
    Simplificar. \(- \dfrac{1}{12} \)
    Ejercicio\(\PageIndex{33}\)

    Evaluar:\(3ab^2\) cuándo\(a = − \dfrac{2}{3}\) y\(b = − \dfrac{1}{2}\).

    Contestar

    \(-\dfrac{1}{2}\)

    Ejercicio\(\PageIndex{34}\)

    Evaluar:\(4c^3d\) cuándo\(c = − \dfrac{1}{2}\) y\(d = − \dfrac{4}{3}\).

    Contestar

    \(\dfrac{2}{3}\)

    Ejemplo\(\PageIndex{18}\): evaluate

    Evaluar:\(\dfrac{p + q}{r}\) cuándo\(p = −4\),\(q = −2\), y\(r = 8\).

    Solución

    Sustituimos los valores en la expresión y simplificamos.

    Sustituto\(\textcolor{red}{-4}\) por p,\(\textcolor{blue}{-2}\) por q y\(\textcolor{magenta}{8}\) por r. \(\dfrac{\textcolor{red}{-4} + \textcolor{blue}{(-2)}}{\textcolor{magenta}{8}} \)
    Agregue primero en el numerador. \(- \dfrac{6}{8}\)
    Simplificar. \(- \dfrac{3}{4}\)
    Ejercicio\(\PageIndex{35}\)

    Evaluar:\(\dfrac{a + b}{c}\) cuándo\(a = −8\),\(b = −7\), y\(c = 6\).

    Contestar

    \(-\dfrac{5}{2}\)

    Ejercicio\(\PageIndex{36}\)

    Evaluar:\(\dfrac{x + y}{z}\) cuándo\(x = 9\),\(y = −18\), y\(z =- 6\).

    Contestar

    \(\dfrac{3}{2}\)

    La práctica hace la perfección

    Encuentre el Mínimo Denominador Común (LCD)

    En los siguientes ejercicios, encuentra el mínimo denominador común (LCD) para cada conjunto de fracciones.

    1. \(\dfrac{2}{3}\)y\(\dfrac{3}{4}\)
    2. \(\dfrac{3}{4}\)y\(\dfrac{2}{5}\)
    3. \(\dfrac{7}{12}\)y\(\dfrac{5}{8}\)
    4. \(\dfrac{9}{16}\)y\(\dfrac{7}{12}\)
    5. \(\dfrac{13}{30}\)y\(\dfrac{25}{42}\)
    6. \(\dfrac{23}{30}\)y\(\dfrac{5}{48}\)
    7. \(\dfrac{21}{35}\)y\(\dfrac{39}{56}\)
    8. \(\dfrac{18}{35}\)y\(\dfrac{33}{49}\)
    9. \(\dfrac{2}{3}, \dfrac{1}{6}\)y\(\dfrac{3}{4}\)
    10. \(\dfrac{2}{3}, \dfrac{1}{4}\)y\(\dfrac{3}{5}\)

    Convertir fracciones a fracciones equivalentes con la pantalla LCD

    En los siguientes ejercicios, convierta a fracciones equivalentes usando la pantalla LCD.

    1. \(\dfrac{1}{3}\)y\(\dfrac{1}{4}\), LCD = 12
    2. \(\dfrac{1}{4}\)y\(\dfrac{1}{5}\), LCD = 20
    3. \(\dfrac{5}{12}\)y\(\dfrac{7}{8}\), LCD = 24
    4. \(\dfrac{7}{12}\)y\(\dfrac{5}{8}\), LCD = 24
    5. \(\dfrac{13}{16}\)y\(- \dfrac{11}{12}\), LCD = 48
    6. \(\dfrac{11}{16}\)y\(- \dfrac{5}{12}\), LCD = 48
    7. \(\dfrac{1}{3}, \dfrac{5}{6}\), y\(\dfrac{3}{4}\), LCD = 12
    8. \(\dfrac{1}{3}, \dfrac{3}{4}\)y\(\dfrac{3}{5}\), LCD = 60

    Sumar y restar fracciones con diferentes denominadores

    En los siguientes ejercicios, sumar o restar. Escribe el resultado en forma simplificada.

    1. \(\dfrac{1}{3} + \dfrac{1}{5}\)
    2. \(\dfrac{1}{4} + \dfrac{1}{5}\)
    3. \(\dfrac{1}{2} + \dfrac{1}{7}\)
    4. \(\dfrac{1}{3} + \dfrac{1}{8}\)
    5. \(\dfrac{1}{3} - \left(- \dfrac{1}{9}\right)\)
    6. \(\dfrac{1}{4} - \left(- \dfrac{1}{8}\right)\)
    7. \(\dfrac{1}{5} - \left(- \dfrac{1}{10}\right)\)
    8. \(\dfrac{1}{2} - \left(- \dfrac{1}{6}\right)\)
    9. \(\dfrac{2}{3} + \dfrac{3}{4}\)
    10. \(\dfrac{3}{4} + \dfrac{2}{5}\)
    11. \(\dfrac{7}{12} + \dfrac{5}{8}\)
    12. \(\dfrac{5}{12} + \dfrac{3}{8}\)
    13. \(\dfrac{7}{12} - \dfrac{9}{16}\)
    14. \(\dfrac{7}{16} - \dfrac{5}{12}\)
    15. \(\dfrac{11}{12} - \dfrac{3}{8}\)
    16. \(\dfrac{5}{8} - \dfrac{7}{12}\)
    17. \(\dfrac{2}{3} - \dfrac{3}{8}\)
    18. \(\dfrac{5}{6} - \dfrac{3}{4}\)
    19. \(− \dfrac{11}{30} + \dfrac{27}{40}\)
    20. \(− \dfrac{9}{20} + \dfrac{17}{30}\)
    21. \(− \dfrac{13}{30} + \dfrac{25}{42}\)
    22. \(− \dfrac{23}{30} + \dfrac{5}{48}\)
    23. \(− \dfrac{39}{56} - \dfrac{22}{35}\)
    24. \(− \dfrac{33}{49} - \dfrac{18}{35}\)
    25. \(- \dfrac{2}{3} - \left(- \dfrac{3}{4}\right)\)
    26. \(- \dfrac{3}{4} - \left(- \dfrac{4}{5}\right)\)
    27. \(- \dfrac{9}{16} - \left(- \dfrac{4}{5}\right)\)
    28. \(- \dfrac{7}{20} - \left(- \dfrac{5}{8}\right)\)
    29. 1 +\(\dfrac{7}{8}\)
    30. 1 +\(\dfrac{5}{6}\)
    31. 1 −\(\dfrac{5}{9}\)
    32. 1 −\(\dfrac{3}{10}\)
    33. \(\dfrac{x}{3} + \dfrac{1}{4}\)
    34. \(\dfrac{y}{2} + \dfrac{2}{3}\)
    35. \(\dfrac{y}{4} - \dfrac{3}{5}\)
    36. \(\dfrac{x}{5} - \dfrac{1}{4}\)

    Identificar y usar operaciones de fracciones

    En los siguientes ejercicios, realizar las operaciones indicadas. Escribe tus respuestas en forma simplificada.

    1. a\(\dfrac{3}{4} + \dfrac{1}{6}\)) b\(\dfrac{3}{4} \div \dfrac{1}{6}\)
    2. a\(\dfrac{2}{3} + \dfrac{1}{6}\)) b\(\dfrac{2}{3} \div \dfrac{1}{6}\)
    3. a\(- \dfrac{2}{5} - \dfrac{1}{8}\)) b\(- \dfrac{2}{5} \cdot \dfrac{1}{8}\)
    4. a\(- \dfrac{4}{5} - \dfrac{1}{8}\)) b\(- \dfrac{4}{5} \cdot \dfrac{1}{8}\)
    5. a\(\dfrac{5n}{6} \div \dfrac{8}{15}\)) b\(\dfrac{5n}{6} - \dfrac{8}{15}\)
    6. a\(\dfrac{3a}{8} \div \dfrac{7}{12}\)) b\(\dfrac{3a}{8} - \dfrac{7}{12}\)
    7. a\(\dfrac{9}{10} \cdot \left(− \dfrac{11d}{12}\right)\)) b\(\dfrac{9}{10} + \left(− \dfrac{11d}{12}\right)\)
    8. a\(\dfrac{4}{15} \cdot \left(− \dfrac{5}{q}\right)\)) b\(\dfrac{4}{15} + \left(− \dfrac{5}{q}\right)\)
    9. \(- \dfrac{3}{8} \div \left(- \dfrac{3}{10}\right)\)
    10. \(- \dfrac{5}{12} \div \left(- \dfrac{5}{9}\right)\)
    11. \(- \dfrac{3}{8} + \dfrac{5}{12}\)
    12. \(- \dfrac{1}{8} + \dfrac{7}{12}\)
    13. \(\dfrac{5}{6} − \dfrac{1}{9}\)
    14. \(\dfrac{5}{9} − \dfrac{1}{6}\)
    15. \(\dfrac{3}{8} \cdot \left(− \dfrac{10}{21}\right)\)
    16. \(\dfrac{7}{12} \cdot \left(− \dfrac{8}{35}\right)\)
    17. \(− \dfrac{7}{15} - \dfrac{y}{4}\)
    18. \(− \dfrac{3}{8} - \dfrac{x}{11}\)
    19. \(\dfrac{11}{12a} \cdot \dfrac{9a}{16}\)
    20. \(\dfrac{10y}{13} \cdot \dfrac{8}{15y}\)

    Utilice el orden de operaciones para simplificar fracciones complejas

    En los siguientes ejercicios, simplifique.

    1. \(\dfrac{\left(\dfrac{1}{5} \right)^{2}}{2 + 3^{2}}\)
    2. \(\dfrac{\left(\dfrac{1}{3} \right)^{2}}{5 + 2^{2}}\)
    3. \(\dfrac{2^{3} + 4^{2}}{\left(\dfrac{2}{3}\right)^{2}}\)
    4. \(\dfrac{3^{3} - 3^{2}}{\left(\dfrac{3}{4}\right)^{2}}\)
    5. \(\dfrac{\left(\dfrac{3}{5} \right)^{2}}{\left(\dfrac{3}{7}\right)^{2}}\)
    6. \(\dfrac{\left(\dfrac{3}{4} \right)^{2}}{\left(\dfrac{5}{8}\right)^{2}}\)
    7. \(\dfrac{2}{\dfrac{1}{3} + \dfrac{1}{5}}\)
    8. \(\dfrac{5}{\dfrac{1}{4} + \dfrac{1}{3}}\)
    9. \(\dfrac{\dfrac{2}{3} + \dfrac{1}{2}}{\dfrac{3}{4} - \dfrac{2}{3}}\)
    10. \(\dfrac{\dfrac{3}{4} + \dfrac{1}{2}}{\dfrac{5}{6} - \dfrac{2}{3}}\)
    11. \(\dfrac{\dfrac{7}{8} - \dfrac{2}{3}}{\dfrac{1}{2} + \dfrac{3}{8}}\)
    12. \(\dfrac{\dfrac{3}{4} - \dfrac{3}{5}}{\dfrac{1}{4} + \dfrac{2}{5}}\)

    Práctica Mixta

    En los siguientes ejercicios, simplifique.

    1. \(\dfrac{1}{2} + \dfrac{2}{3} \cdot \dfrac{5}{12}\)
    2. \(\dfrac{1}{3} + \dfrac{2}{5} \cdot \dfrac{3}{4}\)
    3. 1 −\(\dfrac{3}{5} \div \dfrac{1}{10}\)
    4. 1 −\(\dfrac{5}{6} \div \dfrac{1}{12}\)
    5. \(\dfrac{2}{3} + \dfrac{1}{6} + \dfrac{3}{4}\)
    6. \(\dfrac{2}{3} + \dfrac{1}{4} + \dfrac{3}{5}\)
    7. \(\dfrac{3}{8} - \dfrac{1}{6} + \dfrac{3}{4}\)
    8. \(\dfrac{2}{5} + \dfrac{5}{8} - \dfrac{3}{4}\)
    9. 12\(\left(\dfrac{9}{20} − \dfrac{4}{15}\right)\)
    10. 8\(\left(\dfrac{15}{16} − \dfrac{5}{6}\right)\)
    11. \(\dfrac{\dfrac{5}{8} + \dfrac{1}{6}}{\dfrac{19}{24}}\)
    12. \(\dfrac{\dfrac{1}{6} + \dfrac{3}{10}}{\dfrac{14}{30}}\)
    13. \(\left(\dfrac{5}{9} + \dfrac{1}{6}\right) \div \left(\dfrac{2}{3} − \dfrac{1}{2}\right)\)
    14. \(\left(\dfrac{3}{4} + \dfrac{1}{6}\right) \div \left(\dfrac{5}{8} − \dfrac{1}{3}\right)\)

    En los siguientes ejercicios, evaluar la expresión dada. Exprese sus respuestas de forma simplificada, utilizando fracciones impropias si es necesario.

    1. x +\(\dfrac{1}{2}\) cuando
      1. x =\(− \dfrac{1}{8}\)
      2. x =\(− \dfrac{1}{2}\)
    2. x +\(\dfrac{2}{3}\) cuando
      1. x =\(− \dfrac{1}{6}\)
      2. x =\(− \dfrac{5}{3}\)
    3. x +\(\left(− \dfrac{5}{6}\right)\) cuando
      1. x =\(\dfrac{1}{3}\)
      2. x =\(− \dfrac{1}{6}\)
    4. x +\(\left(− \dfrac{11}{12}\right)\) cuando
      1. x =\(\dfrac{11}{12}\)
      2. x =\(\dfrac{3}{4}\)
    5. x −\(\dfrac{2}{5}\) cuando
      1. x =\(\dfrac{3}{5}\)
      2. x =\(- \dfrac{3}{5}\)
    6. x −\(\dfrac{1}{3}\) cuando
      1. x =\(\dfrac{2}{3}\)
      2. x =\(- \dfrac{2}{3}\)
    7. \(\dfrac{7}{10}\)− w cuando
      1. w =\(\dfrac{1}{2}\)
      2. w =\(- \dfrac{1}{2}\)
    8. \(\dfrac{5}{12}\)− w cuando
      1. w =\(\dfrac{1}{4}\)
      2. w =\(- \dfrac{1}{4}\)
    9. 4p 2 q cuando p =\(- \dfrac{1}{2}\) y q =\(\dfrac{5}{9}\)
    10. 5m 2 n cuando m =\(- \dfrac{2}{5}\) y n =\(\dfrac{1}{3}\)
    11. 2x 2 y 3 cuando x =\(- \dfrac{2}{3}\) e y =\(- \dfrac{1}{2}\)
    12. 8u 2 v 3 cuando u =\(- \dfrac{3}{4}\) y v =\(- \dfrac{1}{2}\)
    13. \(\dfrac{u + v}{w}\)cuando u = −4, v = −8, w = 2
    14. \(\dfrac{m + n}{p}\)cuando m = −6, n = −2, p = 4
    15. \(\dfrac{a + b}{a - b}\)cuando a = −3, b = 8
    16. \(\dfrac{r - s}{r + s}\)cuando r = 10, s = −5

    Matemáticas cotidianas

    1. Decorar a Laronda es hacer fundas para los cojines de su sofá. Para cada funda de almohada, necesita\(\dfrac{3}{16}\) yarda de tela estampada y\(\dfrac{3}{8}\) yarda de tela sólida. ¿Cuál es la cantidad total de tela que Laronda necesita para cada funda de almohada?
    2. Hornear Vanessa es hornear galletas con chispas de chocolate y galletas de avena. Ella necesita\(1 \dfrac{1}{4}\) tazas de azúcar para las galletas con chispas de chocolate, y\(1 \dfrac{1}{8}\) tazas para las galletas de avena ¿Cuánto azúcar necesita en conjunto?

    Ejercicios de escritura

    1. Explique por qué es necesario tener un denominador común para sumar o restar fracciones.
    2. Explica cómo encontrar el LCD de dos fracciones.

    Autocomprobación

    (a) Después de completar los ejercicios, utilice esta lista de verificación para evaluar su dominio de los objetivos de esta sección.

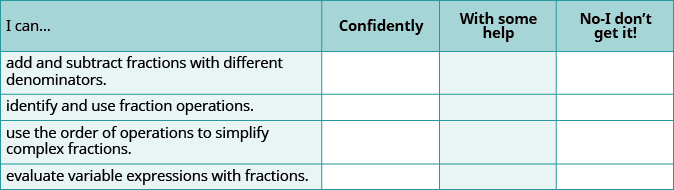
    (b) Después de mirar la lista de verificación, ¿cree que está bien preparado para la siguiente sección? ¿Por qué o por qué no?

    Colaboradores y Atribuciones

    This page titled 4.9: Suma y resta fracciones con diferentes denominadores (Parte 2) is shared under a not declared license and was authored, remixed, and/or curated by OpenStax.