4.10: Suma y resta números mixtos (Parte 1)

Última actualización
Guardar como PDF

Page ID: 114249

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

$ \newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$

( \newcommand{\kernel}{\mathrm{null}\,}\) $ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\id}{\mathrm{id}}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\kernel}{\mathrm{null}\,}$

$ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$

$ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$

$ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\AA}{\unicode[.8,0]{x212B}}$

$ \newcommand{\vectorA}[1]{\vec{#1}} % arrow$

$ \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow$

$ \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vectorC}[1]{\textbf{#1}} $

$ \newcommand{\vectorD}[1]{\overrightarrow{#1}} $

$ \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} $

$ \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} $

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

$\newcommand{\avec}{\mathbf a}$ $\newcommand{\bvec}{\mathbf b}$ $\newcommand{\cvec}{\mathbf c}$ $\newcommand{\dvec}{\mathbf d}$ $\newcommand{\dtil}{\widetilde{\mathbf d}}$ $\newcommand{\evec}{\mathbf e}$ $\newcommand{\fvec}{\mathbf f}$ $\newcommand{\nvec}{\mathbf n}$ $\newcommand{\pvec}{\mathbf p}$ $\newcommand{\qvec}{\mathbf q}$ $\newcommand{\svec}{\mathbf s}$ $\newcommand{\tvec}{\mathbf t}$ $\newcommand{\uvec}{\mathbf u}$ $\newcommand{\vvec}{\mathbf v}$ $\newcommand{\wvec}{\mathbf w}$ $\newcommand{\xvec}{\mathbf x}$ $\newcommand{\yvec}{\mathbf y}$ $\newcommand{\zvec}{\mathbf z}$ $\newcommand{\rvec}{\mathbf r}$ $\newcommand{\mvec}{\mathbf m}$ $\newcommand{\zerovec}{\mathbf 0}$ $\newcommand{\onevec}{\mathbf 1}$ $\newcommand{\real}{\mathbb R}$ $\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}$ $\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}$ $\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}$ $\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}$ $\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$ $\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$ $\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$ $\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$ $\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}$ $\newcommand{\laspan}[1]{\text{Span}\{#1\}}$ $\newcommand{\bcal}{\cal B}$ $\newcommand{\ccal}{\cal C}$ $\newcommand{\scal}{\cal S}$ $\newcommand{\wcal}{\cal W}$ $\newcommand{\ecal}{\cal E}$ $\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}$ $\newcommand{\gray}[1]{\color{gray}{#1}}$ $\newcommand{\lgray}[1]{\color{lightgray}{#1}}$ $\newcommand{\rank}{\operatorname{rank}}$ $\newcommand{\row}{\text{Row}}$ $\newcommand{\col}{\text{Col}}$ $\renewcommand{\row}{\text{Row}}$ $\newcommand{\nul}{\text{Nul}}$ $\newcommand{\var}{\text{Var}}$ $\newcommand{\corr}{\text{corr}}$ $\newcommand{\len}[1]{\left|#1\right|}$ $\newcommand{\bbar}{\overline{\bvec}}$ $\newcommand{\bhat}{\widehat{\bvec}}$ $\newcommand{\bperp}{\bvec^\perp}$ $\newcommand{\xhat}{\widehat{\xvec}}$ $\newcommand{\vhat}{\widehat{\vvec}}$ $\newcommand{\uhat}{\widehat{\uvec}}$ $\newcommand{\what}{\widehat{\wvec}}$ $\newcommand{\Sighat}{\widehat{\Sigma}}$ $\newcommand{\lt}{<}$ $\newcommand{\gt}{>}$ $\newcommand{\amp}{&}$ $\definecolor{fillinmathshade}{gray}{0.9}$

Objetivos de aprendizaje

Modelo de adición de números mixtos con un denominador común
Sumar números mixtos con un denominador común
Modelo de resta de números mixtos
Restar números mixtos con un denominador común
Sumar y restar números mixtos con diferentes denominadores

¡prepárate!

Antes de comenzar, toma este cuestionario de preparación.

Dibuja figura a modelo$\dfrac{7}{3}$. Si te perdiste este problema, revisa el Ejemplo 4.1.6.
Cambiar$\dfrac{11}{4}$ a un número mixto. Si te perdiste este problema, revisa el Ejemplo 4.1.9.
Cambiar$3 \dfrac{1}{2}$ a una fracción impropia. Si te perdiste este problema, revisa el Ejemplo 4.1.11.

Adición Modelo de Números Mixtos con un Denominador Común

Hasta el momento, hemos sumado y restado fracciones propias e impropias, pero no números mixtos. Empecemos pensando en sumar números mixtos usando dinero.

Si Ron tiene$1$ dólar y$1$ trimestre, tiene$1 \dfrac{1}{4}$ dólares. Si Don tiene$2$ dólares y$1$ trimestre, tiene$2 \dfrac{1}{4}$ dólares. ¿Y si Ron y Don juntaran su dinero? Tendrían$3$ dólares y$2$ trimestres. Suman los dólares y suman los trimestres. Esto hace$3 \dfrac{2}{4}$ dólares. Porque dos trimestres es medio dólar, tendrían dólares$3$ y medio, o$3 \dfrac{1}{2}$ dólares.

\[\begin{split} & 1 \dfrac{1}{4} \\ + & 2 \dfrac{1}{4} \\ \hline \\ & 3 \dfrac{2}{4} = 3 \dfrac{1}{2} \end{split} \nonumber \]

Cuando agregaste los dólares y luego agregaste los trimestres, estabas sumando los números enteros y luego sumando las fracciones.

\[1 \dfrac{1}{4} + 2 \dfrac{1}{4} \nonumber \]

Podemos usar círculos de fracciones para modelar este mismo ejemplo:

Empezar con$1 \dfrac{1}{4}$.	una$\dfrac{1}{4}$ pieza entera y una	$1 \dfrac{1}{4}$
Agrega$2 \dfrac{1}{4}$ más.	dos enteros y una$\dfrac{1}{4}$ pieza	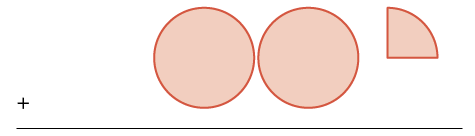$\begin{split}+ & 2 \dfrac{1}{4} \\ & \hline \end{split}$
La suma es:	tres enteros y dos$\dfrac{1}{4}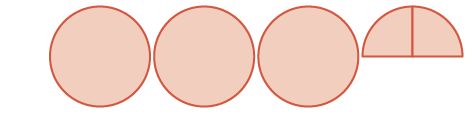$	$3 \dfrac{2}{4} = 3 \dfrac{1}{2}$

Ejemplo$\PageIndex{1}$: model

Modelar$2 \dfrac{1}{3} + 1 \dfrac{2}{3}$ y dar la suma.

Solución

Utilizaremos círculos de fracciones, círculos enteros para los números enteros y$\dfrac{1}{3}$ piezas para las fracciones.

dos enteros y uno$\dfrac{1}{3}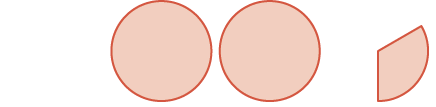$		$2 \dfrac{1}{3}$
más uno entero y dos$\dfrac{1}{3}$ s		$\begin{split}+ & 1 \dfrac{2}{3} \\ & \hline \end{split}$
suma es tres enteros y tres$\dfrac{1}{3}$ s		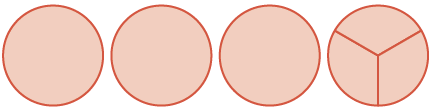$3 \dfrac{3}{3} = 4$

Esto es lo mismo que$4$ los enteros. Entonces,$2 \dfrac{1}{3} + 1 \dfrac{2}{3} = 4$.

Ejercicio$\PageIndex{1}$

Utilice un modelo para agregar lo siguiente. Haz un dibujo para ilustrar tu modelo. $1 \dfrac{2}{5} + 3 \dfrac{3}{5}$

Contestar

$5$

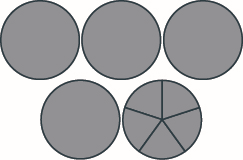
$Ex 4.6.1.png$

Ejercicio$\PageIndex{2}$

Utilice un modelo para agregar lo siguiente. Haz un dibujo para ilustrar tu modelo. $2 \dfrac{1}{6} + 2 \dfrac{5}{6}$

Contestar

$5$

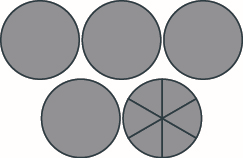
$Ex 4.6.2.png$

Ejemplo$\PageIndex{2}$: model

Modele$1 \dfrac{3}{5} + 2 \dfrac{3}{5}$ y dé la suma como un número mixto.

Solución

Utilizaremos círculos de fracciones, círculos enteros para los números enteros y$\dfrac{1}{5}$ piezas para las fracciones.

uno entero y tres$\dfrac{1}{5}$ s		$1 \dfrac{3}{5}$
más dos enteros y tres$\dfrac{1}{5}$ s		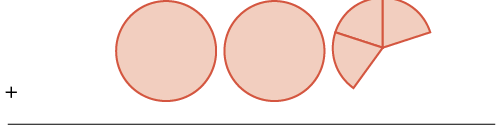$\begin{split}+ & 2 \dfrac{3}{5} \\ & \hline \end{split}$
suma es tres enteros y seis$\dfrac{1}{5}$ s		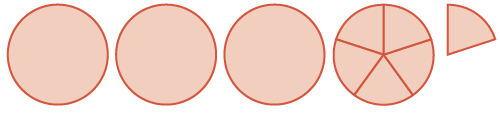$3 \dfrac{6}{5} = 4 \dfrac{1}{5}$

Sumando los círculos enteros y las quintas piezas, obtuvimos una suma de$3 \dfrac{6}{5}$. Podemos ver que$\dfrac{6}{5}$ es equivalente a$1 \dfrac{1}{5}$, así que agregamos eso a la$3$ para obtener$4 \dfrac{1}{5}$.

Ejercicio$\PageIndex{3}$

Modele, y dé la suma como un número mixto. Haz un dibujo para ilustrar tu modelo. $2 \dfrac{5}{6} + 1 \dfrac{5}{6}$

Contestar

$4\dfrac{2}{3}$

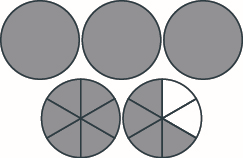
$Ex 4.6.3.png$

Ejercicio$\PageIndex{4}$

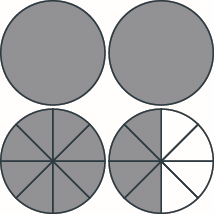
Modele, y dé la suma como un número mixto. Haz un dibujo para ilustrar tu modelo. $1 \dfrac{5}{8} + 1 \dfrac{7}{8}$

Contestar

$3\dfrac{1}{2}$

$Ex 4.6.4.png$

Agregar números mixtos

Modelar con círculos de fracciones ayuda a ilustrar el proceso para sumar números mixtos: Agregamos los números enteros y sumamos las fracciones, y luego simplificamos el resultado, si es posible.

CÓMO: AGREGAR NÚMEROS MIXTOS CON UN

Paso 1. Sumar los números enteros.

Paso 2. Añadir las fracciones.

Paso 3. Simplificar, si es posible.

Ejemplo$\PageIndex{3}$: add

Agregar:$3 \dfrac{4}{9} + 2 \dfrac{2}{9}$.

Solución

Sumar los números enteros.	$\begin{split} & \textcolor{red}{3} \dfrac{4}{9} \\ + & \textcolor{red}{2} \dfrac{2}{9} \\ \hline \\ & \textcolor{red}{5} \end{split}$
Añadir las fracciones.	$\begin{split} & 3 \textcolor{red}{\dfrac{4}{9}} \\ + & 2 \textcolor{red}{\dfrac{2}{9}} \\ \hline \\ & 5 \textcolor{red}{\dfrac{6}{9}} \end{split}$
Simplifica la fracción.	$\begin{split} & 3 \dfrac{4}{9} \\ + & 2 \dfrac{2}{9} \\ \hline \\ & \textcolor{red}{5 \dfrac{6}{9}} = 5 \dfrac{2}{3} \end{split}$

Ejercicio$\PageIndex{5}$

Encuentra la suma:$4 \dfrac{4}{7} + 1 \dfrac{2}{7}$.

Contestar: $5\dfrac{6}{7}$

Ejercicio$\PageIndex{6}$

Encuentra la suma:$2 \dfrac{3}{11} + 5 \dfrac{6}{11}$.

Contestar: $7\dfrac{9}{11}$

En Ejemplo$\PageIndex{3}$, la suma de las fracciones fue una fracción propia. Ahora trabajaremos a través de un ejemplo donde la suma es una fracción impropia.

Ejemplo$\PageIndex{4}$: add

Encuentra la suma:$9 \dfrac{5}{9} + 5 \dfrac{7}{9}$.

Solución

Sumar los números enteros y luego sumar las fracciones.	$\begin{split} & 9 \dfrac{5}{9} \\ + & 5 \dfrac{7}{9} \\ \hline \\ & 14 \dfrac{12}{9} \end{split}$
Reescribir$\dfrac{12}{9}$ como una fracción impropia.	$14 + 1 \dfrac{3}{9}$
Agregar.	$15 \dfrac{3}{9}$
Simplificar.	$15 \dfrac{1}{3}$

Ejercicio$\PageIndex{7}$

Encuentra la suma:$8 \dfrac{7}{8} + 7 \dfrac{5}{8}$.

Contestar: $16\dfrac{1}{2}$

Ejercicio$\PageIndex{8}$

Encuentra la suma:$6 \dfrac{7}{9} + 8 \dfrac{5}{9}$.

Contestar: $15\dfrac{1}{3}$

Un método alternativo para sumar números mixtos es convertir los números mixtos en fracciones impropias y luego sumar las fracciones impropias. Este método generalmente se escribe horizontalmente.

Ejemplo$\PageIndex{5}$: add

Sumar convirtiendo los números mixtos a fracciones impropias:$3 \dfrac{7}{8} + 4 \dfrac{3}{8}$.

Solución

Convertir a fracciones impropias.	$\dfrac{31}{8} + \dfrac{35}{8}$
Añadir las fracciones.	$\dfrac{31 + 35}{8}$
Simplifica el numerador.	$\dfrac{66}{8}$
Reescribir como un número mixto.	$8 \dfrac{2}{8}$
Simplifica la fracción.	$8 \dfrac{1}{4}$

Dado que el problema se dio en forma de número mixto, escribiremos la suma como un número mixto.

Ejercicio$\PageIndex{9}$

Encuentra la suma convirtiendo los números mixtos a fracciones impropias:$5 \dfrac{5}{9} + 3 \dfrac{7}{9}$

Contestar: $9\dfrac{1}{3}$

Ejercicio$\PageIndex{10}$

Encuentra la suma convirtiendo los números mixtos a fracciones impropias:$3 \dfrac{7}{10} + 2 \dfrac{9}{10}$

Contestar: $6\dfrac{3}{5}$

Tabla$\PageIndex{1}$ compara los dos métodos de adición, utilizando la expresión$3 \dfrac{2}{5} + 6 \dfrac{4}{5}$ como ejemplo. ¿Cuál es la manera que prefieres?

Mesa$\PageIndex{1}$
Números Mixtos	Fracciones impropias
$\begin{split} & 3 \dfrac{2}{5} \\ + & 6 \dfrac{4}{5} \\ \hline \\ & 9 \dfrac{6}{5} \end{split}$	$3 \dfrac{2}{5} + 6 \dfrac{4}{5}$
$9 + \dfrac{6}{5}$	$\dfrac{17}{5} + \dfrac{34}{5}$
$9 + 1 \dfrac{1}{5}$	$\dfrac{51}{5}$
$10 \dfrac{1}{5}$	$10 \dfrac{1}{5}$

Modelo de resta de números mixtos

Volvamos a pensar en pizzas para modelar la resta de números mixtos con un denominador común. Supongamos que acabas de hornear una pizza entera y quieres darle a tu hermano la mitad de la pizza. ¿Qué le tienes que hacer a la pizza para darle la mitad? Hay que cortarlo en al menos dos pedazos. Entonces le puedes dar la mitad.

Usaremos círculos de fracciones (¡pizzas!) para ayudarnos a visualizar el proceso. Empezar con un todo.

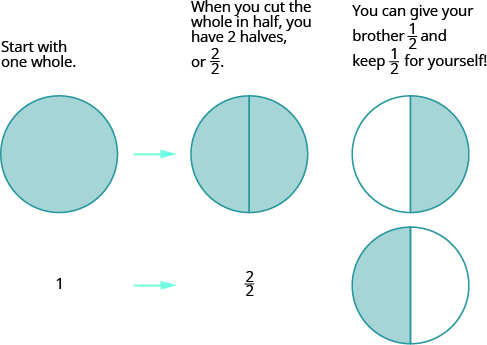
$Se muestra un círculo sombreado. Debajo se encuentra un 1. Hay flechas que apuntan a un círculo sombreado dividido en 2 partes iguales. Debajo se encuentra 2 sobre 2. Junto a esto hay dos círculos, cada uno dividido en 2 partes iguales. El círculo superior tiene la mitad derecha sombreada y el círculo inferior tiene la mitad izquierda sombreada.$

Figura$\PageIndex{1}$

Álgebraicamente, escribirías:

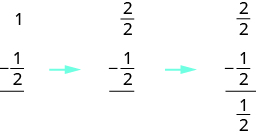
$A la izquierda, dice 1 menos 1 mitad. Hay una flecha apuntando a 2 sobre 2 menos 1 sobre 2. Hay otra flecha apuntando a 2 sobre 2 menos 1 sobre 2 es igual a 1 sobre 2.$

Ejemplo$\PageIndex{6}$: subtract

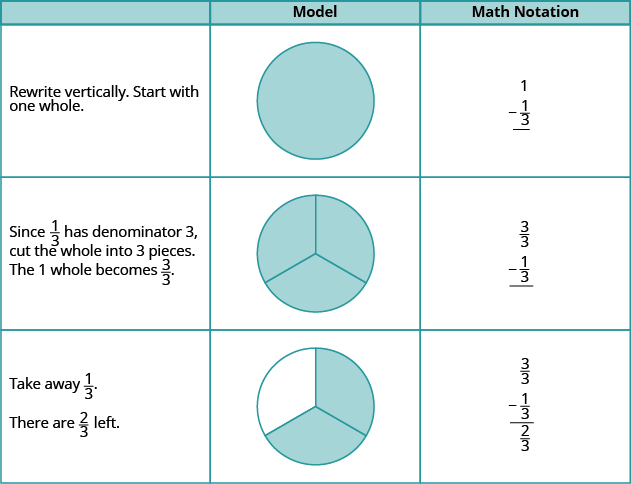
Utilice un modelo para restar:$1 − \dfrac{1}{3}$.

Solución

$Hay una mesa con cinco filas y tres columnas. La primera columna no está etiquetada. La segunda columna está etiquetada como “Modelo”. La tercera columna está etiquetada como “Notación matemática”. En la primera columna, la primera fila dice: “Reescribe verticalmente. Empezar con un todo”. La siguiente fila dice: “Ya que un tercio tiene denominador 3, corta el conjunto en 3 pedazos. El todo 1 se convierte en 3 tercios”. La siguiente fila dice: “Llévate un tercio”. La última fila dice: “Quedan dos tercios”. En la columna “Modelo”, hay una imagen de un círculo sombreado. Debajo de eso hay una imagen de un círculo sombreado dividido en 3 piezas iguales. Debajo de eso hay una imagen de un círculo dividido en 3 piezas iguales con 2 piezas sombreadas. En la columna “Notación matemática”, la primera fila muestra 1 menos 1 tercio. La siguiente fila dice 3 tercios menos 1 tercio. La última fila dice 3 tercios menos 1 tercio es 2 tercios.$

Ejercicio$\PageIndex{11}$

Utilice un modelo para restar:$1 − \dfrac{1}{4}$.

Contestar: $\dfrac{3}{4}$

Ejercicio$\PageIndex{12}$

Utilice un modelo para restar:$1 − \dfrac{1}{5}$.

Contestar: $\dfrac{4}{5}$

¿Y si empezamos con más de un todo? Vamos a averiguarlo.

Ejemplo$\PageIndex{7}$: subtract

Utilice un modelo para restar:$2 − \dfrac{3}{4}$.

Solución

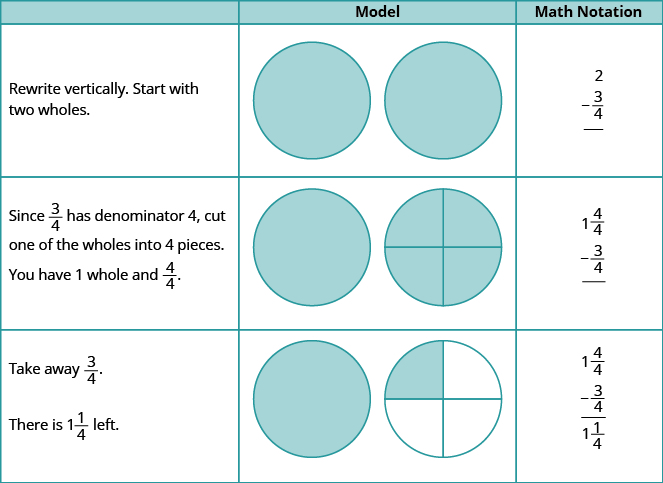
$Hay una mesa con cuatro filas y tres columnas. La primera columna no está etiquetada. La segunda columna está etiquetada como “Modelo”. La tercera columna está etiquetada como “Notación matemática”. En la primera columna, la primera fila dice: “Reescribe verticalmente. Comienza con dos enteros”. La siguiente fila dice: “Dado que las tres cuartas partes tienen denominador 4, corta uno de los enteros en 4 pedazos. Tienes uno entero y 4 cuartas partes”. La siguiente fila dice: “Llévate las tres cuartas partes”. La última fila dice: “Quedan 1 y 1 cuarto”. En la columna “Modelo”, hay una imagen de dos círculos sombreados. Debajo de eso hay una imagen de dos círculos sombreados. Uno de los círculos se divide en 4 piezas iguales. Debajo de eso hay una imagen de un círculo sombreado completo y un círculo dividido en 4 piezas iguales con 1 pieza sombreada. En la columna “Notación matemática”, la primera fila muestra 2 menos 3 cuartos. La siguiente fila dice 1 y 4 cuartos menos 3 cuartos. La última fila dice 1 y 4 cuartos menos 3 cuartos equivale a 1 y 1 cuarto.$

Ejercicio$\PageIndex{13}$

Utilice un modelo para restar:$2 − \dfrac{1}{5}$.

Contestar: $\dfrac{9}{5}$

Ejercicio$\PageIndex{14}$

Utilice un modelo para restar:$2 − \dfrac{1}{3}$.

Contestar: $\dfrac{5}{3}$

En el siguiente ejemplo, restaremos más de un todo.

Ejemplo$\PageIndex{8}$: subtract

Utilice un modelo para restar:$2 − 1 \dfrac{2}{5}$.

Solución

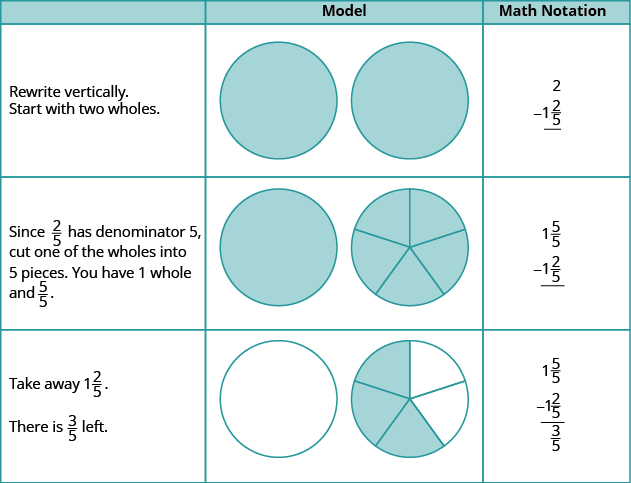
$Hay una mesa con cinco filas y tres columnas. La primera columna no está etiquetada. La segunda columna está etiquetada como “Modelo”. La tercera columna está etiquetada como “Notación matemática”. En la primera columna, la primera fila dice: “Reescribe verticalmente. Comienza con dos enteros”. La siguiente fila dice: “Como dos quintas partes tiene denominador 5, corta uno de los enteros en 5 pedazos. Tienes uno entero y 5 quintos”. La siguiente fila dice: “Llévate 1 y dos quintos”. La última fila dice: “Quedan 3 quintas partes”. En la columna “Modelo”, hay una imagen de dos círculos sombreados. Debajo de eso hay una imagen de dos círculos sombreados. Uno de los círculos se divide en 5 piezas iguales. Debajo de eso hay una imagen de un círculo completo sin sombra y un círculo dividido en 5 piezas iguales con 3 piezas sombreadas. En la columna “Notación matemática”, la primera fila muestra 2 menos 1 y 2 quintos. La siguiente fila dice 1 y 5 quintos menos 1 y 2 quintos. La última fila dice 1 y 5 quintos menos 1 y 2 quintos equivale a 3 quintos.$

Ejercicio$\PageIndex{15}$

Utilice un modelo para restar:$2 − 1 \dfrac{1}{3}$.

Contestar: $\dfrac{2}{3}$

Ejercicio$\PageIndex{16}$

Utilice un modelo para restar:$2 − 1 \dfrac{1}{4}$.

Contestar: $\dfrac{3}{4}$

¿Y si comienzas con un número mixto y necesitas restar una fracción? Piensa en esta situación: Necesitas poner tres cuartos en un parquímetro, pero solo tienes una$\$1$ factura y un cuarto. ¿Qué podrías hacer? Podrías cambiar el billete de dólar a$4$ trimestres. El valor de los$4$ cuartos es el mismo que el billete de un dólar, pero los$4$ cuartos son más útiles para el parquímetro. Ahora, en lugar de tener una$\$1$ factura y un cuarto, tienes$5$ cuartos y puedes poner$3$ cuartos en el medidor.

Esto modela lo que sucede cuando restamos una fracción de un número mixto. Le restamos tres cuartas partes de un dólar y un cuarto.

También podemos modelar esto usando círculos de fracciones, al igual que hicimos para la adición de números mixtos.

Ejemplo$\PageIndex{9}$: subtract

Utilice un modelo para restar:$1 \dfrac{1}{4} − \dfrac{3}{4}$

Solución

Reescribir verticalmente. Empezar con un todo y un cuarto.		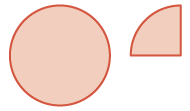$\begin{split} & \textcolor{red}{1 \dfrac{1}{4}} \\ - & \dfrac{3}{4} \\ \hline \end{split}$
Dado que las fracciones tienen denominador 4, corta el conjunto en 4 pedazos. Ahora tienes$\dfrac{4}{4}$ y$\dfrac{1}{4}$ cual es$\dfrac{5}{4}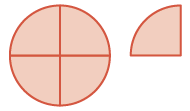$.		$\begin{split} & \textcolor{red}{\dfrac{5}{4}} \\ - & \dfrac{3}{4} \\ \hline \end{split}$
Para llevar$\dfrac{3}{4}$. Ahí$\dfrac{1}{2}$ queda.		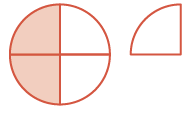$\begin{split} & \dfrac{5}{4}\\\textcolor{red}{- & \dfrac}3}{4}}\\ \hline \\ & \dfrac{2}{4} = \dfrac{1}{2} \end{split}$

Ejercicio$\PageIndex{17}$

Utilice un modelo para restar. Haz un dibujo para ilustrar tu modelo. $1 \dfrac{1}{3} − \dfrac{2}{3}$

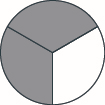
Contestar: $Ex 4.6.17.png$

Ejercicio$\PageIndex{18}$

Utilice un modelo para restar. Haz un dibujo para ilustrar tu modelo. $1 \dfrac{1}{5} − \dfrac{4}{5}$

Contestar: $Ex 4.6.18.png$

Colaboradores y Atribuciones

Template:ContribOpenStaxPreAlgebra

Empezar con\(1 \dfrac{1}{4}\).	una\(\dfrac{1}{4}\) pieza entera y una	\(1 \dfrac{1}{4}\)
Agrega\(2 \dfrac{1}{4}\) más.	dos enteros y una\(\dfrac{1}{4}\) pieza	\(\begin{split}+ & 2 \dfrac{1}{4} \\ & \hline \end{split}\)
La suma es:	tres enteros y dos\(\dfrac{1}{4}\)	\(3 \dfrac{2}{4} = 3 \dfrac{1}{2}\)

dos enteros y uno\(\dfrac{1}{3}\)		\(2 \dfrac{1}{3}\)
más uno entero y dos\(\dfrac{1}{3}\) s		\(\begin{split}+ & 1 \dfrac{2}{3} \\ & \hline \end{split}\)
suma es tres enteros y tres\(\dfrac{1}{3}\) s		\(3 \dfrac{3}{3} = 4\)

uno entero y tres\(\dfrac{1}{5}\) s		\(1 \dfrac{3}{5}\)
más dos enteros y tres\(\dfrac{1}{5}\) s		\(\begin{split}+ & 2 \dfrac{3}{5} \\ & \hline \end{split}\)
suma es tres enteros y seis\(\dfrac{1}{5}\) s		\(3 \dfrac{6}{5} = 4 \dfrac{1}{5}\)

Sumar los números enteros y luego sumar las fracciones.	\(\begin{split} & 9 \dfrac{5}{9} \\ + & 5 \dfrac{7}{9} \\ \hline \\ & 14 \dfrac{12}{9} \end{split}\)
Reescribir\(\dfrac{12}{9}\) como una fracción impropia.	\(14 + 1 \dfrac{3}{9}\)
Agregar.	\(15 \dfrac{3}{9}\)
Simplificar.	\(15 \dfrac{1}{3}\)

Números Mixtos	Fracciones impropias
\(\begin{split} & 3 \dfrac{2}{5} \\ + & 6 \dfrac{4}{5} \\ \hline \\ & 9 \dfrac{6}{5} \end{split}\)	\(3 \dfrac{2}{5} + 6 \dfrac{4}{5}\)
\(9 + \dfrac{6}{5}\)	\(\dfrac{17}{5} + \dfrac{34}{5}\)
\(9 + 1 \dfrac{1}{5}\)	\(\dfrac{51}{5}\)
\(10 \dfrac{1}{5}\)	\(10 \dfrac{1}{5}\)

Search

Text Color

Text Size

Margin Size

Font Type

Ejemplo\(\PageIndex{1}\): model

Ejercicio\(\PageIndex{1}\)

Ejercicio\(\PageIndex{2}\)

Ejemplo\(\PageIndex{2}\): model

Ejercicio\(\PageIndex{3}\)

Ejercicio\(\PageIndex{4}\)

CÓMO: AGREGAR NÚMEROS MIXTOS CON UN

Ejemplo\(\PageIndex{3}\): add

Ejercicio\(\PageIndex{5}\)

Ejercicio\(\PageIndex{6}\)

Ejemplo\(\PageIndex{4}\): add

Ejercicio\(\PageIndex{7}\)

Ejercicio\(\PageIndex{8}\)

Ejemplo\(\PageIndex{5}\): add

Ejercicio\(\PageIndex{9}\)

Ejercicio\(\PageIndex{10}\)

Ejemplo\(\PageIndex{6}\): subtract

Ejercicio\(\PageIndex{11}\)

Ejercicio\(\PageIndex{12}\)

Ejemplo\(\PageIndex{7}\): subtract

Ejercicio\(\PageIndex{13}\)

Ejercicio\(\PageIndex{14}\)

Ejemplo\(\PageIndex{8}\): subtract

Ejercicio\(\PageIndex{15}\)

Ejercicio\(\PageIndex{16}\)

Ejemplo\(\PageIndex{9}\): subtract

Ejercicio\(\PageIndex{17}\)

Ejercicio\(\PageIndex{18}\)

Sumar los números enteros.	\(\begin{split} & \textcolor{red}{3} \dfrac{4}{9} \\ + & \textcolor{red}{2} \dfrac{2}{9} \\ \hline \\ & \textcolor{red}{5} \end{split}\)
Añadir las fracciones.	\(\begin{split} & 3 \textcolor{red}{\dfrac{4}{9}} \\ + & 2 \textcolor{red}{\dfrac{2}{9}} \\ \hline \\ & 5 \textcolor{red}{\dfrac{6}{9}} \end{split}\)
Simplifica la fracción.	\(\begin{split} & 3 \dfrac{4}{9} \\ + & 2 \dfrac{2}{9} \\ \hline \\ & \textcolor{red}{5 \dfrac{6}{9}} = 5 \dfrac{2}{3} \end{split}\)

Convertir a fracciones impropias.	\(\dfrac{31}{8} + \dfrac{35}{8}\)
Añadir las fracciones.	\(\dfrac{31 + 35}{8}\)
Simplifica el numerador.	\(\dfrac{66}{8}\)
Reescribir como un número mixto.	\(8 \dfrac{2}{8}\)
Simplifica la fracción.	\(8 \dfrac{1}{4}\)

Reescribir verticalmente. Empezar con un todo y un cuarto.		\(\begin{split} & \textcolor{red}{1 \dfrac{1}{4}} \\ - & \dfrac{3}{4} \\ \hline \end{split}\)
Dado que las fracciones tienen denominador 4, corta el conjunto en 4 pedazos. Ahora tienes\(\dfrac{4}{4}\) y\(\dfrac{1}{4}\) cual es\(\dfrac{5}{4}\).		\(\begin{split} & \textcolor{red}{\dfrac{5}{4}} \\ - & \dfrac{3}{4} \\ \hline \end{split}\)
Para llevar\(\dfrac{3}{4}\). Ahí\(\dfrac{1}{2}\) queda.		\(\begin{split} & \dfrac{5}{4}\\\textcolor{red}{- & \dfrac}3}{4}}\\ \hline \\ & \dfrac{2}{4} = \dfrac{1}{2} \end{split}\)