Saltar al contenido principal
LibreTexts Español

6.2: Resolver Aplicaciones Generales de Porcentaje

  1. Última actualización
  2. Guardar como PDF
  • Page ID
    114309

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

    Objetivos de aprendizaje
    • Traducir y resolver ecuaciones porcentuales básicas
    • Resolver aplicaciones de porcentaje
    • Encuentra incremento porcentual y disminución porcentual
    ¡prepárate!

    Antes de comenzar, toma este cuestionario de preparación.

    1. Traducir y resolver:\(\dfrac{3}{4}\) de x es 24. Si te perdiste este problema, revisa el Ejemplo 4.13.11.
    2. Simplificar: (4.5) (2.38). Si te perdiste este problema, revisa el Ejemplo 5.3.5.
    3. Resolver: 3.5 = 0.7n. Si te perdiste este problema, revisa el Ejemplo 5.7.4.

    Traducir y resolver ecuaciones básicas de porcentaje

    Resolveremos ecuaciones porcentuales usando los métodos que usamos para resolver ecuaciones con fracciones o decimales. En el pasado, es posible que hayas resuelto problemas porcentuales configurándolos como proporciones. Ese era el mejor método disponible cuando no contabas con las herramientas del álgebra. Ahora como estudiante de preálgebra, puedes traducir oraciones de palabras en ecuaciones algebraicas, y luego resolver las ecuaciones.

    Veremos una aplicación común de porcentaje, propinas a un servidor en un restaurante, para ver cómo configurar una aplicación básica de porcentaje.

    Cuando Aolani y sus amigas cenaron en un restaurante, la cuenta llegó a 80 dólares. Querían dejar una propina del 20%. ¿Qué cantidad sería la propina? Para resolver esto, queremos encontrar qué cantidad es 20% de $80. A los 80 dólares se le llama la base. El monto de la propina sería de 0.20 (80), o $16 Ver Figura\(\PageIndex{1}\). Para encontrar el monto de la propina, multiplicamos el porcentaje por la base.

    La figura muestra una copia de cliente de un recibo de restaurante con el monto de la factura, $80, y el monto de la propina, $16. Hay un grupo de facturas por un total de 16 dólares.

    Figura\(\PageIndex{1}\) - Una propina del 20% por una factura de restaurante de $80 sale a $16.

    En los siguientes ejemplos, encontraremos la cantidad. Debemos estar seguros de cambiar el porcentaje dado a un decimal cuando traduzcamos las palabras en una ecuación.

    Ejemplo\(\PageIndex{1}\):

    ¿Qué número es 35% de 90?

    Solución

    Traducir al álgebra. Dejar n = el número.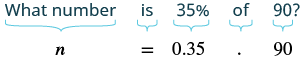
    Multiplicar. n = 31.5

    31.5 es 35% de 90

    Ejercicio\(\PageIndex{1}\):

    ¿Qué número es 45% de 80?

    Contestar

    36

    Ejercicio\(\PageIndex{2}\):

    ¿Qué número es 55% de 60?

    Contestar
    33
    Ejemplo\(\PageIndex{2}\):

    ¿125% de 28 es qué número?

    Solución

    Traducir al álgebra. Dejar a = el número.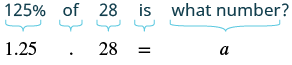
    Multiplicar. 35 = a

    125% de 28 es 35

    Recuerda que un porcentaje superior al 100 es un número mayor que 1. Encontramos que el 125% de 28 es 35, que es mayor que 28.

    Ejercicio\(\PageIndex{3}\):

    ¿150% de 78 es qué número?

    Contestar
    117
    Ejercicio\(\PageIndex{4}\):

    175% de 72 es ¿qué número?

    Contestar
    126

    En los siguientes ejemplos, se nos pide encontrar la base.

    Ejemplo\(\PageIndex{3}\):

    Traducir y resolver: ¿36 es 75% de qué número?

    Solución

    Traducir. Sea b = el número.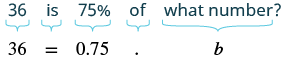
    Divide ambos lados por 0.75. $$\ dfrac {36} {0.75} =\ dfrac {0.75b} {0.75} $$
    Simplificar. 48 = b

    36 es 75% de 48

    Ejercicio\(\PageIndex{5}\):

    ¿17 es 25% de qué número?

    Contestar
    68
    Ejercicio\(\PageIndex{6}\):

    40 es 62.5% de qué número?

    Contestar
    64
    Ejemplo\(\PageIndex{4}\):

    ¿6.5% de qué número es $1.17?

    Solución

    Traducir. Sea b = el número.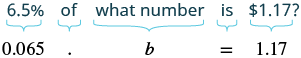
    Divide ambos lados por 0.065. $$\ dfrac {0.065n} {0.065} =\ dfrac {1.17} {0.065} $$
    Simplificar. n = 18

    6.5% de $18 es $1.17.

    Ejercicio\(\PageIndex{7}\):

    ¿7.5% de qué número es $1.95?

    Contestar
    $26
    Ejercicio\(\PageIndex{8}\):

    ¿8.5% de qué número es $3.06?

    Contestar
    $36

    En los siguientes ejemplos, vamos a resolver para el porcentaje.

    Ejemplo\(\PageIndex{5}\):

    ¿Cuál por ciento de 36 es 9?

    Solución

    Traducir al álgebra. Dejar p = el porcentaje.
    Dividir por 36. $$\ dfrac {36p} {36} =\ dfrac {9} {36} $$
    Simplificar. $$p =\ dfrac {1} {4} $$
    Convertir a forma decimal. p = 0.25
    Convertir a porcentaje. p = 25%

    25% de 36 es 9.

    Ejercicio\(\PageIndex{9}\):

    ¿Cuál por ciento de 76 es 57?

    Contestar
    75%
    Ejercicio\(\PageIndex{10}\):

    ¿Cuál por ciento de 120 es 96?

    Contestar
    80%
    Ejemplo\(\PageIndex{6}\):

    ¿144 es qué porcentaje de 96?

    Solución

    Traducir al álgebra. Dejar p = el porcentaje.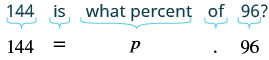
    Dividir por 96. $$\ dfrac {144} {96} =\ dfrac {96p} {96} $$
    Simplificar. 1.5 = p
    Convertir a porcentaje. 150% = p

    144 es 150% de 96.

    Ejercicio\(\PageIndex{11}\):

    ¿110 es qué porcentaje de 88?

    Contestar
    125%
    Ejercicio\(\PageIndex{12}\):

    ¿126 es qué porcentaje de 72?

    Contestar
    175%

    Resolver Aplicaciones de Porcentaje

    Muchas aplicaciones de porcentaje ocurren en nuestra vida diaria, como propinas, impuestos a las ventas, descuentos e intereses. Para resolver estas aplicaciones traduciremos a una ecuación básica de porcentaje, igual que las que resolvimos en los ejemplos anteriores en esta sección. Una vez que traduces la oración en una ecuación porcentual, ya sabes cómo resolverla.

    Actualizaremos la estrategia que usamos en nuestras aplicaciones anteriores para incluir ecuaciones ahora. Observe que vamos a traducir una oración en una ecuación.

    CÓMO: RESOLVER UNA APLICACIÓN
    • Paso 1. Identifica lo que te piden encontrar y elige una variable para representarlo.
    • Paso 2. Escribe una frase que dé la información para encontrarla.
    • Paso 3. Traducir la oración en una ecuación.
    • Paso 4. Resolver la ecuación usando buenas técnicas de álgebra.
    • Paso 5. Comprueba la respuesta en el problema y asegúrate de que tenga sentido.
    • Paso 6. Escribe una oración completa que responda a la pregunta.

    Ahora que tenemos la estrategia a la que hacer referencia, y hemos practicado resolver ecuaciones básicas de porcentaje, estamos listos para resolver aplicaciones porcentuales. Asegúrese de preguntarse si su respuesta final tiene sentido, ya que muchas de las aplicaciones que resolveremos involucran situaciones cotidianas, puede confiar en su propia experiencia.

    Ejemplo\(\PageIndex{7}\):

    Dezohn y su novia disfrutaron de una cena en un restaurante, y la factura era de 68,50 dólares. Quieren dejar una propina del 18%. Si la propina será del 18% del total de la factura, ¿cuánto debería ser la propina?

    Solución

    ¿Qué se le pide que encuentre? la cantidad de la propina
    Elija una variable para representarla. Dejar t = cantidad de propina.
    Escribe una frase que dé la información para encontrarla. La propina es del 18% del total de la factura.
    Traducir la oración en una ecuación.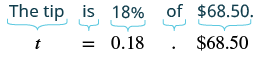
    Multiplicar. t = 12.33
    Cheque. ¿Esta respuesta es razonable? Si aproximamos la factura a 70 dólares y el porcentaje a 20%, tendríamos una propina de 14 dólares. Entonces una propina de 12.33 dólares parece razonable.
    Escribe una oración completa que responda a la pregunta. La pareja debe dejar una propina de 12.33 dólares.
    Ejercicio\(\PageIndex{13}\):

    Cierra y su hermana disfrutaron de una cena especial en un restaurante, y la factura fue de 81.50 dólares. Si quiere dejar el 18% de la factura total como propina, ¿cuánto debería dejar?

    Contestar
    $14.67
    Ejercicio\(\PageIndex{14}\):

    Kimngoc almorzó en su restaurante favorito. Ella quiere dejar como propina el 15% del total de la factura. Si su factura era de 14.40 dólares, ¿cuánto dejará para la propina?

    Contestar
    $2.16
    Ejemplo\(\PageIndex{8}\):

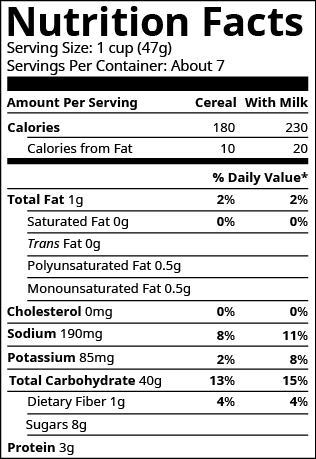
    La etiqueta del cereal para el desayuno de Masao decía que una porción de cereal aporta 85 miligramos (mg) de potasio, que es 2% de la cantidad diaria recomendada. ¿Cuál es la cantidad diaria total recomendada de potasio?

    Las cifras muestran los datos nutricionales del cereal.

    Solución

    ¿Qué se le pide que encuentre? la cantidad total de potasio recomendada
    Elija una variable para representarla. Dejar a = cantidad total de potasio.
    Escribe una frase que dé la información para encontrarla. 85 mg es 2% de la cantidad total.
    Traducir la oración en una ecuación.
    Divide ambos lados por 0.02. $$\ dfrac {85} {0.02} =\ dfrac {0.02a} {0.02} $$
    Simplificar. 4,250 =a
    Consulta: ¿Esta respuesta es razonable? Sí. 2% es un porcentaje pequeño y 85 es una pequeña parte de 4,250.
    Escribe una oración completa que responda a la pregunta. La cantidad de potasio que se recomienda es de 4250 mg.
    Ejercicio\(\PageIndex{15}\):

    Una porción de cereal cuadrado de trigo tiene 7 gramos de fibra, que es 29% de la cantidad diaria recomendada. ¿Cuál es la cantidad diaria total recomendada de fibra?

    Contestar
    24.1 gramos
    Ejercicio\(\PageIndex{16}\):

    Una porción de cereal de arroz tiene 190 mg de sodio, que es 8% de la cantidad diaria recomendada. ¿Cuál es la cantidad diaria total recomendada de sodio?

    Contestar
    2,375 mg
    Ejemplo\(\PageIndex{9}\):

    Mitzi recibió unos brownies gourmet como regalo. El envoltorio decía que cada brownie era de 480 calorías, y tenía 240 calorías de grasa. ¿Qué porcentaje del total de calorías en cada brownie proviene de la grasa?

    Solución

    ¿Qué se le pide que encuentre? el porcentaje del total de calorías de la grasa
    Elija una variable para representarla. Dejar p = por ciento de grasa.
    Escribe una frase que dé la información para encontrarla. ¿Cuál por ciento de 480 es 240?
    Traducir la oración en una ecuación.
    Divide ambos lados por 480. $$\ dfrac {p\ cdot 480} {480} =\ dfrac {240} {480} $$
    Simplificar. p = 0.5
    Convertir a forma porcentual. p = 50%
    Cheque. ¿Esta respuesta es razonable? Sí. 240 es la mitad de 480, así que el 50% tiene sentido.
    Escribe una oración completa que responda a la pregunta. Del total de calorías en cada brownie, el 50% es grasa.
    Ejercicio\(\PageIndex{17}\):

    Verónica planea hacer muffins a partir de una mezcla. El paquete dice que cada muffin será de 230 calorías y 60 calorías serán de grasa. ¿Qué porcentaje del total de calorías proviene de la grasa? (Redondear al porcentaje entero más cercano.)

    Contestar
    26%
    Ejercicio\(\PageIndex{18}\):

    El mix de brownie que Ricardo planea usar dice que cada brownie será de 190 calorías, y 70 calorías son de grasa. ¿Qué porcentaje de las calorías totales provienen de la grasa?

    Contestar
    37%

    Encuentre aumento porcentual y disminución porcentual

    La gente en los medios suele hablar de cuánto ha aumentado o disminuido una cantidad a lo largo de un cierto período de tiempo. Suelen expresar este incremento o disminución como porcentaje.

    Para encontrar el incremento porcentual, primero encontramos la cantidad de incremento, que es la diferencia entre la nueva cantidad y la cantidad original. Entonces encontramos qué porcentaje es la cantidad de incremento de la cantidad original.

    cómo: encontrar incremento porcentual

    Paso 1. Encuentra la cantidad de incremento.

    • aumento = nueva cantidad − importe original

    Paso 2. Encuentra el incremento porcentual como porcentaje de la cantidad original.

    Ejemplo\(\PageIndex{10}\):

    En 2011, el gobernador de California propuso aumentar las tarifas de los colegios comunitarios de 26 dólares por unidad a 36 dólares por unidad. Encuentra el incremento porcentual. (Redondear a la décima más cercana de un porcentaje.)

    Solución

    ¿Qué se le pide que encuentre? el incremento porcentual
    Elija una variable para representarla. Dejar p = por ciento.
    Encuentra la cantidad de incremento.
    Encuentra el incremento porcentual. El incremento es ¿qué porcentaje de la cantidad original?
    Traducir a una ecuación.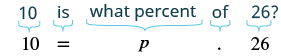
    Divide ambos lados por 26. $$\ dfrac {10} {26} =\ dfrac {26p} {26} $$
    Redondear a la milésima más cercana. 0.384 = p
    Convertir a forma porcentual. 38.4% = p
    Escribe una oración completa. Las nuevas comisiones representan un incremento del 38.4% respecto a las antiguas.
    Ejercicio\(\PageIndex{19}\):

    En 2011, el IRS incrementó el costo de kilometraje deducible a 55.5 centavos de 51 centavos. Encuentra el incremento porcentual. (Redondear a la décima más cercana de un porcentaje.)

    Contestar
    8.8%
    Ejercicio\(\PageIndex{20}\):

    En 1995, la tarifa estándar de autobús en Chicago era de 1,50 dólares. En 2008, la tarifa estándar del autobús era de $2.25. Encuentra el incremento porcentual. (Redondear a la décima más cercana de un porcentaje.)

    Contestar
    50%

    Encontrar la disminución porcentual es muy similar a encontrar el incremento porcentual, pero ahora el monto de disminución es la diferencia entre el monto original y el monto final. Entonces encontramos qué porcentaje es el monto de disminución de la cantidad original.

    CÓMO: ENCONTRAR LA DISminución

    Paso 1. Encuentra la cantidad de disminución.

    • decremento = cantidad original − nueva cantidad

    Paso 2. Encuentra el porcentaje de disminución como porcentaje de la cantidad original.

    Ejemplo\(\PageIndex{11}\):

    El precio promedio de un galón de gas en una ciudad en junio de 2014 fue de $3.71. El precio promedio en esa ciudad en julio fue de $3.64. Encuentra la disminución porcentual.

    Solución

    El precio promedio de un galón de gas en una ciudad en junio de 2014 fue de $3.71. El precio promedio en esa ciudad en julio fue de $3.64. Encuentra la disminución porcentual.

    ¿Qué se le pide que encuentre? la disminución porcentual
    Elija una variable para representarla. Dejar p = por ciento.
    Encuentra la cantidad de disminución.
    Encuentra el porcentaje de disminución. La disminución es ¿qué porcentaje de la cantidad original?
    Traducir a una ecuación.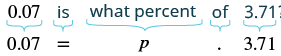
    Divide ambos lados por 3.71. $$\ dfrac {0.07} {3.71} =\ dfrac {3.71p} {3.71} $$
    Redondear a la milésima más cercana. 0.019 = p
    Convertir a forma porcentual. 1.9% = p
    Escribe una oración completa. El precio del gas disminuyó 1.9%.
    Ejercicio\(\PageIndex{21}\):

    La población de una ciudad era de alrededor de 672 mil en 2010. Se proyecta que la población de la ciudad sea de alrededor de 630,000 en 2020. Encuentra la disminución porcentual. (Redondear a la décima más cercana de un porcentaje.)

    Contestar
    6.3%
    Ejercicio\(\PageIndex{22}\):

    El año pasado el salario de Sheila era de 42 mil dólares. Por días de licencia, este año su salario era de 37.800 dólares. Encuentra la disminución porcentual. (Redondear a la décima más cercana de un porcentaje.)

    Contestar
    10%
    Acceder a recursos adicionales en línea

    Porcentaje de aumento y porcentaje de disminución de visualización

    La práctica hace la perfección

    Traducir y resolver ecuaciones básicas de porcentaje

    En los siguientes ejercicios, traduzca y resuelva.

    1. ¿Qué número es 45% de 120?
    2. ¿Qué número es 65% de 100?
    3. ¿Qué número es 24% de 112?
    4. ¿Qué número es 36% de 124?
    5. ¿250% de 65 es qué número?
    6. ¿150% de 90 es qué número?
    7. ¿800% de 2,250 es qué número?
    8. ¿600% de 1,740 es qué número?
    9. ¿28 es 25% de qué número?
    10. ¿36 es 25% de qué número?
    11. ¿81 es 75% de qué número?
    12. ¿93 es 75% de qué número?
    13. ¿8.2% de qué número es $2.87?
    14. ¿6.4% de qué número es $2.88?
    15. ¿11.5% de qué número es $108.10?
    16. ¿12.3% de qué número es $92.25?
    17. ¿Cuál por ciento de 260 es 78?
    18. ¿Cuál por ciento de 215 es 86?
    19. ¿Cuál por ciento de 1,500 es 540?
    20. ¿Cuál por ciento de 1,800 es 846?
    21. ¿30 es qué porcentaje de 20?
    22. ¿50 es qué porcentaje de 40?
    23. 840 es ¿qué porcentaje de 480?
    24. 790 es ¿qué porcentaje de 395?

    Resolver aplicaciones de porcentajes

    En los siguientes ejercicios, resolver las aplicaciones de porcentajes.

    1. Ginebra atendió a sus padres a cenar en su restaurante favorito. El proyecto de ley era de 74.25 dólares. Ella quiere dejar como propina el 16% del total de la factura. ¿Cuánto debería ser la propina?
    2. Cuando Hiro y sus compañeros de trabajo almorzaron en un restaurante la factura era de 90.50 dólares. Quieren dejar como propina el 18% del total de la factura. ¿Cuánto debería ser la propina?
    3. Trong tiene 12% de cada cheque de pago automáticamente depositado en su cuenta de ahorros. Su último sueldo fue de 2.165 dólares. ¿Cuánto dinero se depositó en la cuenta de ahorros de Trong?
    4. Cherise deposita 8% de cada cheque de pago en su cuenta de retiro. Su último sueldo fue de 1.485 dólares. ¿Cuánto depositó Cherise en su cuenta de retiro?
    5. Una porción de avena tiene 8 gramos de fibra, que es 33% de la cantidad diaria recomendada. ¿Cuál es la cantidad diaria total recomendada de fibra?
    6. Una porción de trail mix tiene 67 gramos de carbohidratos, que es 22% de la cantidad diaria recomendada. ¿Cuál es la cantidad diaria total recomendada de carbohidratos?
    7. Una hamburguesa con queso y tocino en un popular restaurante de comida rápida contiene 2,070 miligramos (mg) de sodio, que es 86% de la cantidad diaria recomendada. ¿Cuál es la cantidad diaria total recomendada de sodio?
    8. Una ensalada de pollo a la parrilla en un popular restaurante de comida rápida contiene 650 miligramos (mg) de sodio, que es 27% de la cantidad diaria recomendada. ¿Cuál es la cantidad diaria total recomendada de sodio?
    9. La hoja informativa de nutrición en un restaurante de comida rápida dice que el sándwich de pescado tiene 380 calorías, y 171 calorías son de grasa. ¿Qué porcentaje del total de calorías proviene de la grasa?
    10. La hoja informativa de nutrición en un restaurante de comida rápida dice que una pequeña porción de nuggets de pollo tiene 190 calorías, y 114 calorías son de grasa. ¿Qué porcentaje del total de calorías proviene de la grasa?
    11. A Emma le pagan 3.000 dólares mensuales. Ella paga $750 mensuales por renta. ¿Qué porcentaje de su paga mensual va a la renta?
    12. A Hoyuelo se le pagan $3,200 mensuales. Ella paga $960 mensuales por renta. ¿Qué porcentaje de su paga mensual va a la renta?

    Encuentre aumento porcentual y disminución porcentual

    En los siguientes ejercicios, encuentra el incremento porcentual o disminución porcentual.

    1. Tamanika obtuvo un aumento en su paga por hora, de 15.50 dólares a 17.55 dólares. Encuentra el incremento porcentual.
    2. Ayodele obtuvo un aumento en su paga por hora, de 24.50 dólares a 25.48 dólares. Encuentra el incremento porcentual.
    3. Las cuotas anuales de los estudiantes en la Universidad de California aumentaron de aproximadamente $4,000 en 2000 a aproximadamente $9,000 en 2014. Encuentra el incremento porcentual.
    4. El precio de una acción de una acción subió de $12.50 a $50. Encuentra el incremento porcentual.
    5. Según la revista Time (7/19/2011) el consumo mundial anual de mariscos aumentó de 22 libras por persona en 1960 a 38 libras por persona en la actualidad. Encuentra el incremento porcentual. (Redondear a la décima más cercana de un porcentaje.)
    6. En un mes, el precio medio de la vivienda en el Noreste subió de 225,400 dólares a $241,500. Encuentra el incremento porcentual. (Redondear a la décima más cercana de un porcentaje.)
    7. Una tienda de abarrotes redujo el precio de una barra de pan de $2.80 a $2.73. Encuentra la disminución porcentual.
    8. El precio de una acción de una acción cayó de 8.75 dólares a 8.54 dólares. Encuentra la disminución porcentual.
    9. El salario de Hernando fue de 49,500 dólares el año pasado. Este año su salario se redujo a $44.055. Encuentra la disminución porcentual.
    10. De 2000 a 2010, la población de Detroit cayó de alrededor de 951,000 a aproximadamente 714,000. Encuentra la disminución porcentual. (Redondear a la décima más cercana de un porcentaje.)
    11. En un mes, el precio medio de la vivienda en Occidente cayó de $203,400 a $192,300. Encuentra la disminución porcentual. (Redondear a la décima más cercana de un porcentaje.)
    12. Las ventas de videojuegos y consolas cayeron de $1,150 millones a $1,030 millones en un año. Encuentra la disminución porcentual. (Redondear a la décima más cercana de un porcentaje.)

    Matemáticas cotidianas

    1. Propinas En el carrito de café del campus, un café mediano cuesta $1.65. MaryAnne trae $2.00 con ella cuando compra una taza de café y deja el cambio como propina. ¿Qué porcentaje de propina deja?
    2. Cargos atrasados Alison se retrasaba pagando la factura de su tarjeta de crédito de 249 dólares. A ella se le cobró una tasa de retraso del 5%. ¿Cuál era el monto del cargo por demora?

    Ejercicios de escritura

    1. Sin resolver el problema “44 es 80% de qué número”, piensa en cuál podría ser la solución. ¿Debería ser un número mayor que 44 o menor que 44? Explica tu razonamiento.
    2. Sin resolver el problema “¿Qué es 20% de 300?” pensar en cuál podría ser la solución. ¿Debería tratarse de un número que sea mayor a 300 o menor a 300? Explica tu razonamiento.
    3. Después de regresar de vacaciones, Alex dijo que debería haber empacado un 50% menos de pantalones cortos y un 200% más de camisas. Explica lo que Alex quiso decir.
    4. Debido a la construcción de carreteras en una ciudad, se aconsejó a los viajeros que planificaran su viaje el lunes por la mañana para tomar el 150% de su tiempo habitual de viaje. Explique lo que esto significa.

    Autocomprobación

    (a) Después de completar los ejercicios, utilice esta lista de verificación para evaluar su dominio de los objetivos de esta sección.

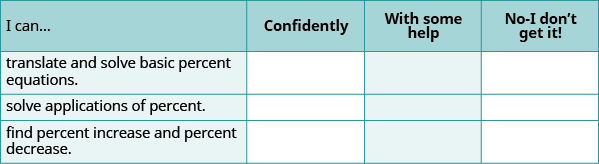
    (b) Después de revisar esta lista de verificación, ¿qué hará para tener confianza en todos los objetivos?

    Colaboradores y Atribuciones

    This page titled 6.2: Resolver Aplicaciones Generales de Porcentaje is shared under a not declared license and was authored, remixed, and/or curated by OpenStax.