7.4: Propiedad distributiva
- Page ID
- 114180
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)- Simplificar expresiones usando la propiedad distributiva
- Evaluar expresiones usando la propiedad distributiva
Antes de comenzar, toma este cuestionario de preparación.
- Multiplicar: 3 (0.25). Si te perdiste este problema, revisa el Ejemplo 5.3.5
- Simplificar: 10 − (−2) (3). Si te perdiste este problema, revisa el Ejemplo 3.7.5.
- Combinar términos similares: 9y + 17 + 3y − 2. Si te perdiste este problema, revisa el Ejemplo 2.3.10.
Simplificar expresiones mediante la propiedad distributiva
Supongamos que tres amigos van al cine. Cada uno necesita $9.25; es decir, 9 dólares y 1 trimestre. ¿Cuánto dinero necesitan todos juntos? Se puede pensar en los dólares por separado de los trimestres.
Necesitan 3 veces $9, entonces $27, y 3 veces 1 trimestre, entonces 75 centavos. En total, necesitan 27.75 dólares. Si piensas en hacer las matemáticas de esta manera, estás usando la Propiedad Distributiva.
Si a, b, c son números reales, entonces a (b + c) = ab + ac.
De vuelta a nuestros amigos en el cine, podríamos mostrar los pasos matemáticos que tomamos para encontrar la cantidad total de dinero que necesitan así:
\[\begin{split} 3(9&.25) \\ 3(9 &+ 0.25) \\ 3(9) &+ 3(0.25) \\ 27 &+ 0.75 \\ 27&.75 \end{split}\]
En álgebra, utilizamos la Propiedad Distributiva para eliminar paréntesis a medida que simplificamos las expresiones. Por ejemplo, si se nos pide simplificar la expresión 3 (x + 4), el orden de las operaciones dice trabajar primero entre paréntesis. Pero no podemos agregar x y 4, ya que no son como términos. Entonces usamos la Propiedad Distributiva, como se muestra en Ejemplo\(\PageIndex{1}\).
Simplificar: 3 (x + 4).
Solución
| Distribuir. | 3 • x + 3 • 4 |
| Multiplicar. | 3x + 12 |
Simplificar: 4 (x + 2).
- Contestar
-
\(4x+8\)
Simplificar: 6 (x + 7).
- Contestar
-
6x + 42
A algunos estudiantes les resulta útil dibujar flechas para recordarles cómo usar la Propiedad Distributiva. Entonces el primer paso en el Ejemplo 7.17 se vería así:
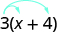
\[3 \cdot x + 3 \cdot 4\]
Simplificar: 6 (5y + 1).
Solución
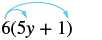
| Distribuir. | $$6\ cdot 5y + 6\ cdot 1$$ |
| Multiplicar. | $30y + 6$$ |
Simplificar: 9 (3y + 8).
- Contestar
-
27 años + 72
Simplificar: 5 (5w + 9).
- Contestar
-
25w + 45
La propiedad distributiva se puede utilizar para simplificar expresiones que se ven ligeramente diferentes de a (b + c). Aquí hay otras dos formas.
Si a, b, c son números reales, entonces\[a(b + c) = ab + ac$$Other forms$$a(b − c) = ab − ac$$$$(b + c)a = ba + ca\]
Simplificar: 2 (x − 3).
Solución
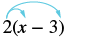
| Distribuir. | $$2\ cdot x + 2\ cdot 3$$ |
| Multiplicar. | $2x - 6$$ |
Simplificar: 7 (x − 6).
- Contestar
-
7x - 42
Simplificar: 8 (x − 5).
- Contestar
-
8x - 40
¿Recuerdas cómo multiplicar una fracción por un número entero? Tendremos que hacerlo en los siguientes dos ejemplos.
Simplificar:\(\dfrac{3}{4}\) (n + 12).
Solución
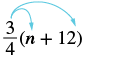
| Distribuir. | $$\ dfrac {3} {4}\ cdot n +\ dfrac {3} {4}\ cdot 12$$ |
| Multiplicar. | $$\ dfrac {3} {4} n + 9$$ |
Simplificar:\(\dfrac{2}{5}\) (p + 10).
- Contestar
-
\(\frac{2}{5}p + 4 \)
Simplificar:\(\dfrac{3}{7}\) (u + 21).
- Contestar
-
\(\frac{3}{7}u +9 \)
Simplificar:\(8 \left(\dfrac{3}{8}x + \dfrac{1}{4}\right)\).
Solución
| Distribuir. | $$8\ cdot\ dfrac {3} {8} x + 8\ cdot\ dfrac {1} {4} $$ |
| Multiplicar. | $$3x + 2$$ |
Simplificar:\(6 \left(\dfrac{5}{6}y + \dfrac{1}{2}\right)\).
- Contestar
-
5y + 3
Simplificar:\(12 \left(\dfrac{1}{3}n + \dfrac{3}{4}\right)\).
- Contestar
-
4n + 9
Usar la Propiedad Distributiva como se muestra en el siguiente ejemplo será muy útil cuando resolvamos aplicaciones de dinero más adelante.
Simplificar: 100 (0.3 + 0.25q).
Solución
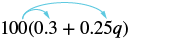
| Distribuir. | $$100 (0.3) + 100 (0.25q) $$ |
| Multiplicar. | $$30 + 25q$$ |
Simplificar: 100 (0.7 + 0.15p).
- Contestar
-
70 + 15p
Simplificar: 100 (0.04 + 0.35d).
- Contestar
-
4 + 35d
En el siguiente ejemplo vamos a multiplicar por una variable. Tendremos que hacer esto en un capítulo posterior.
Simplificar:\(m(n − 4)\).
Solución
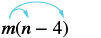
| Distribuir. | $$m\ cdot n - m\ cdot 4$$ |
| Multiplicar. | $$mn - 4m$$ |
Observe que escribimos m • 4 como 4m. Esto lo podemos hacer por la Propiedad Conmutativa de la Multiplicación. Cuando un término es producto de un número y una variable, escribimos primero el número.
Simplificar: r (s − 2).
- Contestar
-
rs - 2r
Simplificar: y (z − 8).
- Contestar
-
yz - 8 años
En el siguiente ejemplo se utilizará la forma 'al revés' de la Propiedad Distributiva, (b + c) a = ba + ca.
Simplificar: (x + 8) p.
Solución
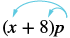
| Distribuir. | $$px + 8p$$ |
Simplificar: (x + 2) p.
- Contestar
-
xp + 2p
Simplificar: (y + 4) q.
- Contestar
-
yq + 4q
Cuando distribuyes un número negativo, debes tener mucho cuidado para que las señales sean correctas.
Simplificar: −2 (4y + 1).
Solución
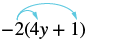
| Distribuir. | $$-2\ cdot 4y + (-2)\ cdot 1$$ |
| Simplificar. | $$-8y - 2$$ |
Simplificar: −3 (6m + 5).
- Contestar
-
-18m - 15
Simplificar: −6 (8n + 11).
- Contestar
-
-48n - 66
Simplificar: −11 (4 − 3a).
Solución
| Distribuir. | $$-11\ cdot 4 - (-11)\ cdot 3a$$ |
| Multiplicar. | $$-44 - (-33a) $$ |
| Simplificar. | $$-44 + 33a$$ |
También podrías escribir el resultado como 33a − 44. ¿Sabes por qué?
Simplificar: −5 (2 − 3a).
- Contestar
-
-10 + 15a
Simplificar: −7 (8 − 15y).
- Contestar
-
-56 + 105 años
En el siguiente ejemplo, mostraremos cómo usar la Propiedad Distributiva para encontrar lo contrario de una expresión. Recuerde, −a = −1 • a.
Simplificar: − (y + 5).
Solución
| Multiplicar por −1 resulta en lo contrario. | $$-1 (y + 5) $$ |
| Distribuir. | $$-1\ cdot y + (-1)\ cdot 5$$ |
| Simplificar. | $$-y + (-5) $$ |
| Simplificar. | $$-y -5$$ |
Simplificar: − (z − 11).
- Contestar
-
-z + 11
Simplificar: − (x − 4).
- Contestar
-
-x + 4
A veces necesitamos usar la Propiedad Distributiva como parte del orden de operaciones. Empieza por mirar los paréntesis. Si no se puede simplificar la expresión dentro de los paréntesis, el siguiente paso sería multiplicar usando la propiedad distributiva, que elimina los paréntesis. Los siguientes dos ejemplos ilustrarán esto.
Simplificar: 8 − 2 (x + 3).
Solución
| Distribuir. | $$8 - 2\ cdot x - 2\ cdot 3$$ |
| Multiplicar. | $$8 - 2x - 6$$ |
| Combina términos similares. | $$-2x + 2$$ |
Simplificar: 9 − 3 (x + 2).
- Contestar
-
-3x + 3
Simplificar: 7x − 5 (x + 4).
- Contestar
-
2x - 20
Simplificar: 4 (x − 8) − (x + 3).
Solución
| Distribuir. | $$4x - 32 - x - 3$$ |
| Combina términos similares. | $$3x - 35$$ |
Simplificar: 6 (x − 9) − (x + 12).
- Contestar
-
5x - 66
Simplificar: 8 (x − 1) − (x + 5).
- Contestar
-
7x - 13
Evaluar expresiones usando la propiedad distributiva
Algunos estudiantes necesitan estar convencidos de que la Propiedad Distributiva siempre funciona. En los ejemplos siguientes, practicaremos evaluar algunas de las expresiones de ejemplos anteriores; en la parte (a), evaluaremos el formulario con paréntesis, y en la parte (b) evaluaremos la forma que obtuvimos después de distribuir. Si evaluamos ambas expresiones correctamente, esto demostrará que efectivamente son iguales.
Cuando y = 10 evaluar: (a) 6 (5y + 1) (b) 6 • 5y + 6 • 1.
Solución
(a) 6 (5y + 1)
| Sustituto\(\textcolor{red}{10}\) de y. | $$6 (5\ cdot\ textcolor {rojo} {10} + 1) $$ |
| Simplificar entre paréntesis. | $6 (51) $$ |
| Multiplicar. | $306$$ |
(b) 6 • 5 años + 6 • 1
| Sustituto\(\textcolor{red}{10}\) de y. | $$6\ cdot 5\ cdot\ textcolor {rojo} {10} + 6\ cdot 1$$ |
| Simplificar. | $$300 + 6$$ |
| Agregar. | $306$$ |
Fíjate, las respuestas son las mismas. Cuando y = 10, 6 (5y + 1) = 6 • 5y + 6 • 1. Pruébalo tú mismo por un valor diferente de y.
Evalúe cuando w = 3: (a) 5 (5w + 9) (b) 5 • 5w + 5 • 9.
- Contestar a
-
\(120\)
- Respuesta b
-
\(120\)
Evaluar cuando y = 2: (a) 9 (3y + 8) (b) 9 • 3y + 9 • 8.
- Contestar a
-
\(126\)
- Respuesta b
-
\(126\)
Cuando y = 3, evalúe (a) −2 (4y + 1) (b) −2 • 4y + (−2) • 1.
Solución
(a) −2 (4y + 1)
| Sustituto\(\textcolor{red}{3}\) de y. | $$-2 (4\ cdot\ textcolor {rojo} {3} + 1) $$ |
| Simplificar entre paréntesis. | $$-2 (13) $$ |
| Multiplicar. | $$-26$$ |
(b) −2 • 4y + (−2) • 1
| Sustituto\(\textcolor{red}{3}\) de y. | $$-2\ cdot 4\ cdot\ textcolor {rojo} {3} + (-2)\ cdot 1$$ |
| Multiplicar. | $$-24 - 2$$ |
| Restar. | $$-26$$ |
| Las respuestas son las mismas cuando y = 3. | $$-2 (4y + 1) = -8y - 2$$ |
Evalúe cuando n = −2: (a) −6 (8n + 11) (b) −6 • 8n + (−6) • 11.
- Contestar a
-
\(30\)
- Respuesta b
-
\(30\)
Evalúe cuando m = −1: (a) −3 (6m + 5) (b) −3 • 6m + (−3) • 5.
- Contestar a
-
\(3\)
- Respuesta b
-
\(3\)
Cuando y = 35 evalúe (a) − (y + 5) y (b) −y − 5 para mostrar que − (y + 5) = −y − 5.
Solución
(a) − (y + 5)
| Sustituto\(\textcolor{red}{35}\) de y. | $$- (\ textcolor {rojo} {35} + 5) $$ |
| Añadir entre paréntesis. | $$- (40) $$ |
| Simplificar. | $$-40$$ |
(b) −y − 5
| Sustituto\(\textcolor{red}{35}\) de y. | $$-\ textcolor {rojo} {35} - 5$$ |
| Simplificar. | $$-40$$ |
| Las respuestas son las mismas cuando y = 35, demostrando que | $$- (y + 5) = -y - 5$$ |
Evalúe cuando x = 36: (a) − (x − 4) (b) −x + 4 para mostrar que − (x − 4) = − x + 4.
- Responder a
-
\(-32\)
- Respuesta b
-
\(-32\)
Evalúe cuando z = 55: (a) − (z − 10) (b) −z + 10 para mostrar que − (z − 10) = − z + 10.
- Responder a
-
\(-45\)
- Respuesta b
-
\(-45\)
La práctica hace la perfección
Simplificar expresiones mediante la propiedad distributiva
En los siguientes ejercicios, simplificar el uso de la propiedad distributiva.
- 4 (x + 8)
- 3 (a + 9)
- 8 (4 años + 9)
- 9 (3w + 7)
- 6 (c − 13)
- 7 (y − 13)
- 7 (3p − 8)
- 5 (7u − 4)
- \(\dfrac{1}{2}\)(n + 8)
- \(\dfrac{1}{3}\)(u + 9)
- \(\dfrac{1}{4}\)(3q + 12)
- \(\dfrac{1}{5}\)(4m + 20)
- \(9 \left(\dfrac{5}{9} y − \dfrac{1}{3}\right)\)
- \(10 \left(\dfrac{3}{10} x − \dfrac{2}{5}\right)\)
- \(12 \left(\dfrac{1}{4} + \dfrac{2}{3} r\right)\)
- \(12 \left(\dfrac{1}{6} + \dfrac{3}{4} s\right)\)
- r (s − 18)
- u (v − 10)
- (y + 4) p
- (a + 7) x
- −2 (y + 13)
- −3 (a + 11)
- −7 (4p + 1)
- −9 (9a+4)
- −3 (x − 6)
- −4 (q − 7)
- −9 (3a − 7)
- −6 (7x − 8)
- − (r + 7)
- − (q + 11)
- − (3x − 7)
- − (5p − 4)
- 5 + 9 (n − 6)
- 12 + 8 (u − 1)
- 16 − 3 (y + 8)
- 18 − 4 (x + 2)
- 4 − 11 (3c − 2)
- 9 − 6 (7n − 5)
- 22 − (a + 3)
- 8 − (r − 7)
- −12 − (u + 10)
- −4 − (c − 10)
- (5m − 3) − (m + 7)
- (4y − 1) − (y − 2)
- 5 (2n + 9) + 12 (n − 3)
- 9 (5u + 8) + 2 (u − 6)
- 9 (8x − 3) − (−2)
- 4 (6x − 1) − (−8)
- 14 (c − 1) − 8 (c − 6)
- 11 (n − 7) − 5 (n − 1)
- 6 (7 años + 8) − (30 años − 15)
- 7 (3n + 9) − (4n − 13)
Evaluar expresiones usando la propiedad distributiva
En los siguientes ejercicios, evalúe ambas expresiones para el valor dado.
- Si v = −2, evalúe
- 6 (4v + 7)
- 6 · 4v + 6 · 7
- Si u = −1, evalúe
- 8 (5u + 12)
- 8 · 5u + 8 · 12
- Si n =\(\dfrac{2}{3}\), evaluar
- \(3 \left(n + \dfrac{5}{6}\right)\)
- 3 • n + 3 •\(\dfrac{5}{6}\)
- Si y = 3 4, evaluar
- 4 y + 3 8
- 4 • y + 4 •\(\dfrac{3}{8}\)
- Si y =\(\dfrac{7}{12}\), evaluar
- −3 (4 años + 15)
- 3 • 4 años + (−3) • 15
- Si p =\(\dfrac{23}{30}\), evaluar
- −6 (5p + 11)
- −6 • 5p + (−6) • 11
- Si m = 0.4, evaluar
- −10 (3m − 0.9)
- −10 • 3m − (−10) (0.9)
- Si n = 0.75, evaluar
- −100 (5n + 1.5)
- −100 • 5n + (−100) (1.5)
- Si y = −25, evaluar
- − (y − 25)
- −y + 25
- Si w = −80, evalúe
- − (w − 80)
- −w + 80
- Si p = 0.19, evaluar
- − (p + 0.72)
- −p − 0.72
- Si q = 0.55, evaluar
- − (q + 0.48)
- −q − 0.48
Matemáticas cotidianas
- Comprando por estuche Joe puede comprar su té helado favorito en una tienda de conveniencia por $1.99 por botella. En la tienda de abarrotes, puede comprar una caja de 12 botellas por 23.88 dólares.
- Utilice la propiedad distributiva para encontrar el costo de 12 botellas compradas individualmente en la tienda de conveniencia. (Pista: observe que $1.99 es $2 − $0.01.)
- ¿Es una ganga comprar el té helado en la tienda de abarrotes por el caso?
- Compra en paquete múltiple El champú de Adele se vende por $3.97 por botella en la farmacia. En la tienda del almacén, el mismo shampoo se vende como un paquete de 3 por $10.49.
- Muestra cómo puedes usar la propiedad distributiva para encontrar el costo de 3 botellas compradas individualmente en la farmacia.
- ¿Cuánto ahorraría Adele comprando el paquete de 3 en la tienda del almacén?
Ejercicios de escritura
- Simplifique el\(8 \left(x − \dfrac{1}{4}\right)\) uso de la propiedad distributiva y explique cada paso.
- Explica cómo puedes multiplicar 4 ($5.97) sin papel o una calculadora pensando en $5.97 como 6 − 0.03 y luego usando la propiedad distributiva.
Autocomprobación
(a) Después de completar los ejercicios, utilice esta lista de verificación para evaluar su dominio de los objetivos de esta sección.
(b) ¿Qué te dice esta lista de verificación sobre tu dominio de esta sección? ¿Qué pasos tomarás para mejorar?