7.6: Sistemas de Medición (Parte 1)
- Page ID
- 114166
- Hacer conversiones de unidades en el sistema estadounidense
- Usar unidades de medida mixtas en el sistema de EE. UU.
- Hacer conversiones de unidades en el sistema métrico
- Utilizar unidades de medida mixtas en el sistema métrico
- Convertir entre Estados Unidos y los sistemas métricos de medición
- Convertir entre temperaturas Fahrenheit y Celsius
Antes de comenzar, toma este cuestionario de preparación.
- Multiplicar: 4.29 (1000). Si te perdiste este problema, revisa el Ejemplo 5.3.8.
- Simplificar:\(\dfrac{30}{54}\). Si te perdiste este problema, revisa el Ejemplo 4.3.2.
- Multiplicar:\(\dfrac{7}{15} \cdot \dfrac{25}{28}\). Si te perdiste este problema, revisa el Ejemplo 4.3.9.
En esta sección veremos cómo convertir entre diferentes tipos de unidades, como pies a millas o kilogramos a libras. La idea básica en todas las conversiones unitarias será utilizar una forma de 1, la identidad multiplicativa, para cambiar las unidades pero no el valor de una cantidad.
Hacer conversiones de unidades en el sistema estadounidense
Existen dos sistemas de medición de uso común en todo el mundo. La mayoría de los países utilizan el sistema métrico. Estados Unidos utiliza un sistema de medición diferente, generalmente llamado sistema estadounidense. Primero veremos el sistema estadounidense.
El sistema de medición estadounidense utiliza unidades de pulgada, pie, yarda y milla para medir la longitud y libra y tonelada para medir el peso. Para la capacidad, las unidades utilizadas son taza, pinta, cuarto de galón y galones. Tanto el sistema estadounidense como el sistema métrico miden el tiempo en segundos, minutos u horas.
Las equivalencias entre las unidades básicas del sistema de medición de Estados Unidos se listan en la Tabla\(\PageIndex{1}\). El cuadro también muestra, entre paréntesis, las abreviaturas comunes para cada medición.
| Unidades del Sistema de Estados Unidos | |
|---|---|
| Largo | Volumen |
|
1 pie (ft) = 12 pulgadas (pulg.) 1 yarda (yd) = 3 pies (ft) 1 milla (mi) = 5280 pies (ft) |
3 cucharaditas (t) = 1 cucharada (T) 16 Cucharadas (T) = 1 taza (C) 1 taza (C) = 8 onzas líquidas (fl oz) 1 pinta (pt) = 2 tazas (C) 1 cuarto (qt) = 2 pintas (pt) 1 galón (gal) = 4 cuartos (qt) |
| Peso | Tiempo |
|
1 libra (lb) = 16 onzas (oz) 1 tonelada = 2000 libras (lb) |
1 minuto (min) = 60 segundos (s) 1 hora (h) = 60 minutos (min) 1 día = 24 horas (h) 1 semana (semana) = 7 días 1 año (año) = 365 días |
En muchas aplicaciones de la vida real, necesitamos convertir entre unidades de medida. Utilizaremos la propiedad de identidad de la multiplicación para hacer estas conversiones. Replantaremos aquí la Identidad Propiedad de Multiplicación para una fácil referencia.
Para cualquier número real a,
\[a \cdot 1 = a \qquad 1 \cdot a = a\]
Para usar la propiedad de identidad de multiplicación, escribimos 1 en una forma que nos ayudará a convertir las unidades. Por ejemplo, supongamos que queremos convertir pulgadas a pies. Sabemos que 1 pie es igual a 12 pulgadas, por lo que podemos escribir 1 como la fracción\(\dfrac{1\; ft}{12\; in}\). Cuando multiplicamos por esta fracción, no cambiamos el valor sino simplemente cambiamos las unidades. Pero\(\dfrac{12\; in}{1\; ft}\) también equivale a 1. ¿Cómo decidimos si multiplicar por\(\dfrac{1\; ft}{12\; in}\) o\(\dfrac{12\; in}{1\; ft}\)? Elegimos la fracción que hará que las unidades que queremos convertir se dividan. Por ejemplo, supongamos que queríamos convertir 60 pulgadas a pies. Si elegimos la fracción que tiene pulgadas en el denominador, podemos eliminar las pulgadas.
\[60\; \cancel{in} \cdot \dfrac{1\; ft}{12\; \cancel{in}} = 5\; ft\]
Por otro lado, si quisiéramos convertir 5 pies a pulgadas, elegiríamos la fracción que tiene pies en el denominador.
\[5\; \cancel{ft} \cdot \dfrac{12\; in}{1\; \cancel{ft}} = 60\; in\]
Tratamos las palabras unitarias como factores y “dividimos” unidades comunes como hacemos factores comunes.
Paso 1. Multiplique la medida a convertir por 1; escriba 1 como una fracción relacionando las unidades dadas y las unidades necesarias.
Paso 2. Multiplicar.
Paso 3. Simplifica la fracción, realizando las operaciones indicadas y eliminando las unidades comunes.
Mary Anne mide 66 pulgadas de alto. ¿Cuál es su estatura en pies?
Solución
| Convierte 66 pulgadas en pies. | |
| Multiplique la medida a convertir por 1. | 66 pulgadas • 1 |
| Escribir 1 como fracción relacionando las unidades dadas y las unidades necesarias. | $66\; pulgadas\ cdot\ dfrac {1\; pie} {12\; pulgadas} $$ |
| Multiplicar. | $$\ dfrac {66\; pulgadas\;\ cdot 1\; pie} {12\; pulgadas} $$ |
| Simplifica la fracción. | $$\ dfrac {66\;\ cancel {pulgadas}\;\ cdot 1\; pie} {12\;\ cancel {pulgadas}} =\ dfrac {66\; pies} {12} $$ |
| 5.5 pies |
Observe que cuando simplificamos la fracción, primero dividimos las pulgadas. Mary Anne mide 5.5 pies de altura.
Lexie mide 30 pulgadas de alto. Convierte su estatura a pies.
- Contestar
-
2.5 pies
Rene compró una manguera que mide 18 yardas de largo. Convierte la longitud a pies.
- Contestar
-
54 pies
Cuando usamos la Propiedad Identidad de Multiplicación para convertir unidades, necesitamos asegurarnos de que las unidades de las que queremos cambiar se dividirán. Normalmente esto significa que queremos que la fracción de conversión tenga esas unidades en el denominador.
Ndula, un elefante en el San Diego Safari Park, pesa casi 3.2 toneladas. Convierte su peso en libras.

Figura\(\PageIndex{1}\) (crédito: Guldo Da Rozze, Flickr)
Solución
Convertiremos 3.2 toneladas en libras, utilizando las equivalencias de la Tabla\(\PageIndex{1}\). Utilizaremos la Propiedad Identidad de la Multiplicación, escribiendo 1 como la fracción\(\dfrac{2000\; pounds}{1\; ton}\)
| Multiplique la medida a convertir por 1. | 3.2 toneladas • 1 |
| Escribe 1 como fracción relativa toneladas y libras. | $$3.2\; toneladas\;\ cdot\ dfrac {2000\; lbs} {1\; toneladas} $$ |
| Simplificar. | $$\ dfrac {3.2\;\ cancel {toneladas}\;\ cdot 2000\; lbs} {1\;\ cancel {toneladas}} $$ |
| Multiplicar. | 6400 lbs |
.Ndula pesa casi 6,400 libras.
El SUV de Arnold pesa alrededor de 4.3 toneladas. Convierte el peso a libras.
- Contestar
-
8600 libras
Un crucero pesa 51,000 toneladas. Convierte el peso a libras.
- Contestar
-
102,000,000 libras
A veces para convertir de una unidad a otra, es posible que necesitemos usar varias otras unidades intermedias, por lo que necesitaremos multiplicar varias fracciones.
Julieta va con su familia a su casa de verano. Ella estará fuera por 9 semanas. Convertir el tiempo a minutos.
Solución
Para convertir semanas en minutos, convertiremos semanas en días, días en horas y luego horas en minutos. Para ello, multiplicaremos por factores de conversión de 1.
| Escribe 1 como\(\dfrac{7\; days}{1\; week}, \dfrac{24\; hours}{1\; day}, \dfrac{60\; minutes}{1\; hour}\). | $$\ dfrac {9\; wk} {1}\ cdot\ dfrac {7\; días} {1\; semana}\ cdot\ dfrac {24\; hr} {1\; día}\ cdot\ dfrac {60\; min} {1\; hr} $$ |
| Cancelar unidades comunes. | $$\ dfrac {9\;\ cancel {wk}} {1}\ cdot\ dfrac {7\;\ cancel {\ textcolor {azul} {días}}} {1\;\ cancel {semana}}\ cdot\ dfrac {24\;\ cancel {\ textcolor {rojo} {hr}}} {1\;\ cancel {\ textcolor {azul} día}}}\ cdot\ dfrac {60\; min} {1\;\ cancel {\ textcolor {rojo} {hr}}} $$ |
| Multiplicar. | $$\ dfrac {9\ cdot 7\ cdot 24\ cdot\ cdot 60\; min} {1\ cdot 1\ cdot 1\ cdot 1} = 90.720\; min$$ |
Julieta estará fuera por 90,720 minutos.
La distancia entre la Tierra y la Luna es de unas 250.000 millas. Convierte esta longitud en yardas.
- Contestar
-
440,000,000 yardas
Un equipo de astronautas pasa 15 semanas en el espacio. Convertir el tiempo a minutos.
- Contestar
-
151,200 minutos
¿Cuántas onzas líquidas hay en 1 galón de leche?

Figura\(\PageIndex{2}\) (crédito: www.bluewaikiki.com, Flickr)
Solución
Usa los factores de conversión para obtener las unidades correctas: convierte galones en cuartos, cuartos en pintas, pintas en tazas y tazas en onzas líquidas.
| Multiplique la medida a convertir por 1. | $$\ dfrac {1\; gal} {1}\ cdot\ dfrac {4\; qt} {1\; gal}\ cdot\ dfrac {2\; pt} {1\; qt}\ cdot\ dfrac {2\; C} {1\; pt}\ cdot\ dfrac {8\; fl\; oz} {1\; C} $$ |
| Simplificar. | $$\ dfrac {1\;\ cancel {gal}} {1}\ cdot\ dfrac {4\;\ cancel {qt}} {1\;\ cancel {gal}}\ cdot\ dfrac {2\;\ cancel {pt}} {1\;\ cancel {qt}}\ cdot\ dfrac {2\;\ cancel {C}} {1\;\ cancelar {pt}}\ cdot\ dfrac {8\; fl\; oz} {1\;\ cancel {C}} $$ |
| Multiplicar. | $$\ dfrac {1\ cdot 4\ cdot 2\ cdot 2\ cdot 8\; fl\; oz} {1\ cdot 1\ cdot 1\ cdot 1\ cdot 1\ cdot 1} $$ |
| Simplificar. | 128 onzas líquidas |
Hay 128 onzas líquidas en un galón.
¿Cuántas tazas hay en 1 galón?
- Contestar
-
16 tazas
¿Cuántas cucharaditas hay en 1 taza?
- Contestar
-
48 cucharaditas
Utilizar Unidades Mixtas de Medida en el Sistema de Estados Unidos
Realizar operaciones aritméticas en mediciones con unidades mixtas de medidas requiere cuidado. Asegúrese de sumar o restar como unidades.
Charlie compró tres filetes para una barbacoa. Sus pesos eran 14 onzas, 1 libra 2 onzas y 1 libra 6 onzas. ¿Cuántas libras totales de bistec compró?

Figura\(\PageIndex{3}\) (crédito: Helen Penjam, Flickr)
Solución
Añadiremos los pesos de los filetes para encontrar el peso total de los filetes.
| Agrega las onzas. Después agrega las libras. | $$\ begin {split} 14\; &onzas\\ 1\; libra\ quad 2\; &onzas\\ +\; 1\; libra\ cuádruple 6\; &onzas\\\ hline 2\; libras\ cuádruple 22\; &onzas\ end {split} $$ |
| Convierte 22 onzas en libras y onzas. | $$22\; onzas = 1\; libra,\; 6\; onzas$$ |
| Agrega las libras. | 2 libras + 1 libra, 6 onzas = 3 libras, 6 onzas |
Charlie compró 3 libras 6 onzas de bistec.
Laura dio a luz trillizos que pesaban 3 libras 12 onzas, 3 libras 3 onzas y 2 libras 9 onzas. ¿Cuál fue el peso total al nacer de los tres bebés?
- Contestar
-
9 lbs. 8 oz
Seymour cortó dos piezas de moldura de corona para su habitación familiar que eran 8 pies 7 pulgadas y 12 pies 11 pulgadas. ¿Cuál fue la longitud total de la moldura?
- Contestar
-
21 pies y 6 pulg.
Anthony compró cuatro tablones de madera que eran cada uno de 6 pies y 4 pulgadas de largo. Si los cuatro tablones se colocan de extremo a extremo, ¿cuál es la longitud total de la madera?

Solución
Multiplicaremos la longitud de una tabla por 4 para encontrar la longitud total.
| Multiplica las pulgadas y luego los pies. | $$\ begin {split} 6\; pies\ quad 4\; pulgadas&\\\ veces\ qquad 4&\\ hline 24\; pies\ quad 16\; pulgadas&\ end {split} $$ |
| Convierte 16 pulgadas a pies. | 24 pies + 1 pie 4 pulgadas |
| Agrega los pies. | 25 pies 4 pulgadas |
Anthony compró 25 pies 4 pulgadas de madera.
Henri quiere triplicar su receta de salsa de espagueti, que exige 1 libra y 8 onzas de pavo molido. ¿Cuántas libras de pavo molido necesitará?
- Contestar
-
4 lbs. 8 oz.
Joellen quiere duplicar una solución de 5 galones 3 cuartos. ¿Cuántos galones de solución tendrá en total?
- Contestar
-
11 gal. 2 qts.
Hacer conversiones de unidades en el sistema métrico
En el sistema métrico, las unidades están relacionadas por potencias de 10. Las palabras de raíz de sus nombres reflejan esta relación. Por ejemplo, la unidad básica para medir la longitud es un metro. Un kilómetro es de 1000 metros; el prefijo kilo- significa mil. Un centímetro es\(\dfrac{1}{100}\) de metro, porque el prefijo centi- significa una centésima (igual que un centavo es\(\dfrac{1}{100}\) de un dólar).
Las equivalencias de las medidas en el sistema métrico se muestran en la Tabla\(\PageIndex{2}\). Las abreviaturas comunes para cada medición se dan entre paréntesis.
| Mediciones Métricas | ||
|---|---|---|
| Largo | Masa | Volumen/Capacidad |
|
1 kilómetro (km) = 1000 m 1 hectómetro (hm) = 100 m 1 dekameter (presa) = 10 m 1 metro (m) = 1 m 1 decímetro (dm) = 0.1 m 1 centímetro (cm) = 0.01 m 1 milímetro (mm) = 0.001 m |
1 kilogramo (kg) = 1000 g 1 hectogramo (hg) = 100 g 1 dekagrama (dag) = 10 g 1 gramo (g) = 1 g 1 decigramo (dg) = 0.1 g 1 centigramo (cg) = 0.01 g 1 miligramo (mg) = 0.001 g |
1 kiloliter (kL) = 1000 L 1 hectolitro (hL) = 100 L 1 dekaliter (dAL) = 10 L 1 litro (L) = 1 L 1 decilitro (dL) = 0.1 L 1 centilitro (cL) = 0.01 L 1 mililitro (mL) = 0.001 L |
|
1 metro = 100 centímetros 1 metro = 1000 milímetros |
1 gramo = 100 centigramos 1 gramo = 1000 miligramos |
1 litro = 100 centilitros 1 litro = 1000 mililitros |
Para realizar conversiones en el sistema métrico, utilizaremos la misma técnica que hicimos en el sistema estadounidense. Usando la propiedad de identidad de multiplicación, multiplicaremos por un factor de conversión de uno para llegar a las unidades correctas.
¿Alguna vez has corrido una carrera de 5 k o 10 k? Las longitudes de esas carreras se miden en kilómetros. El sistema métrico se usa comúnmente en Estados Unidos cuando se habla de la duración de una carrera.
Nick corrió una carrera de 10 kilómetros. ¿Cuántos metros corrió?

Figura\(\PageIndex{4}\) (crédito: William Warby, Flickr)
Solución
Convertiremos kilómetros a metros utilizando la Propiedad Identidad de Multiplicación y las equivalencias en la Tabla 7.63.
| Multiplique la medida a convertir por 1. | $$10\;\ textcolor {rojo} {km}\;\ cdot 1$$ |
| Escribe 1 como fracción relativa kilómetros y metros. | $$10\;\ textcolor {rojo} {km}\;\ cdot\ dfrac {1000\; m} {1\;\ textcolor {rojo} {km}} $$ |
| Simplificar. | $$\ dfrac {10\;\ cancel {\ textcolor {rojo} {km}}\;\ cdot 1000\; m} {1\;\ cancel {\ textcolor {rojo} {km}}} $$ |
| Multiplicar. | $10,000\; m$$ |
Nick corrió 10 mil metros.
Sandy completó su primera carrera de 5 km. ¿Cuántos metros corrió?
- Contestar
-
5000 m
Herman compró una alfombra de 2.5 metros de largo. ¿Cuántos centímetros es la longitud?
- Contestar
-
250 cm
El bebé recién nacido de Eleanor pesaba 3200 gramos. ¿Cuántos kilogramos pesó el bebé?
Solución
Vamos a convertir gramos a kilogramos.
| Multiplique la medida a convertir por 1. | $$3200\;\ textcolor {rojo} {g}\;\ cdot 1$$ |
| Escribe 1 como fracción relativa kilogramos y gramos. | $$3200\;\ textcolor {rojo} {g}\;\ cdot\ dfrac {1\; kg} {1000\;\ textcolor {rojo} {g}} $$ |
| Simplificar. | $$3200\;\ cancel {\ textcolor {rojo} {g}}\;\ cdot\ dfrac {1\; kg} {1000\;\ cancel {\ textcolor {rojo} {g}}} $$ |
| Multiplicar. | $$\ dfrac {3200\; kilogramos} {1000} $$ |
| Dividir. | $3.2\; kilogramos$$ |
El bebé pesaba 3.2 kilogramos.
El bebé recién nacido de Kari pesaba 2800 gramos. ¿Cuántos kilogramos pesó el bebé?
- Contestar
-
2.8 kilogramos
Anderson recibió un paquete que estaba marcado con 45004500 gramos. ¿Cuántos kilogramos pesó este paquete?
- Contestar
-
4.5 kilogramos
Dado que el sistema métrico se basa en múltiplos de diez, las conversiones implican multiplicar por múltiplos de diez. En Operaciones decimales aprendimos a simplificar estos cálculos simplemente moviendo el decimal. Para multiplicar por 10, 100 o 1000, movemos el decimal a la derecha 1, 2 o 3 lugares, respectivamente. Para multiplicar por 0.1, 0.01 o 0.001 movemos el decimal a la izquierda 1, 2 o 3 lugares respectivamente. Podemos aplicar este patrón cuando hacemos conversiones de medición en el sistema métrico.
En el Ejemplo 7.51, cambiamos 3200 gramos a kilogramos multiplicando por 1 1000 (o 0.001). Esto es lo mismo que mover los decimales 3 lugares hacia la izquierda.
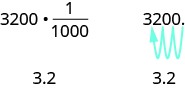
Convertir: (a) 350 litros a kilolitros (b) 4.1 litros a mililitros.
Solución
(a) Convertiremos litros a kilolitros. En el Cuadro 7.63, vemos que 1 kilolitro = 1000 litros.
| Multiplicar por 1, escribiendo 1 como una fracción que relaciona litros con kilolitros. | $$350\; L\;\ cdot\ dfrac {1\; kL} {1000\; L} $$ |
| Simplificar. | $$350\;\ cancel {L}\;\ cdot\ dfrac {1\; kL} {1000\;\ cancel {L}} $$ |
| Mueve las 3 unidades decimales hacia la izquierda. | 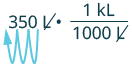 |
0.35 kL
(b) Convertiremos litros a mililitros. En el Cuadro 7.63, vemos que 1 litro = 1000 mililitros.
| Multiplique por 1, escribiendo 1 como una fracción que relaciona mililitros con litros. | $4.1\; L\;\ cdot\ dfrac {1000\; mL} {1\; L} $$ |
| Simplificar. | $4.1\;\ cancel {L}\;\ cdot\ dfrac {1000\; mL} {1\;\ cancel {L}} $$ |
| Mueve las 3 unidades decimales hacia la izquierda. |  |
4100 mL
Convertir: (a) 7.25 L a kL (b) 6.3 L a mL.
- Contestar a
-
0.00725 kL
- Respuesta b
-
6300 mL
Convertir: (a) 350 hL a L (b) 4.1 L a cL.
- Contestar a
-
35,000 L
- Respuesta b
-
410 cL


