7.S: Las propiedades de los números reales (Resumen)
- Page ID
- 114182
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)
Términos Clave
| Identidad Aditiva | La identidad aditiva es 0. Cuando se agrega cero a cualquier número, no cambia el valor. |
| Inversa Aditiva | Lo contrario de un número es su inversa aditiva. La inversa aditiva de a es −a. |
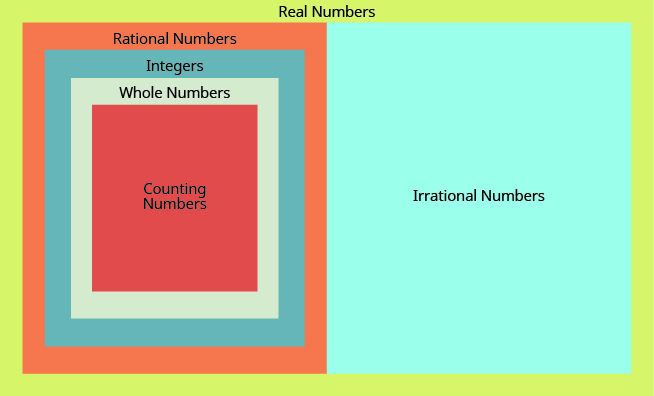
| Número irracional | Un número que no se puede escribir como la relación de dos enteros. Su forma decimal no se detiene y no se repite. |
| Identidad Multiplicativa | La identidad multiplicativa es 1. Cuando se multiplica cualquier número, no cambia el valor. |
| Inverso Multiplicativo | El recíproco de un número es su inverso multiplicativo. El inverso multiplicativo de a es\(\dfrac{1}{a}\). |
| Número racional | Un número que se puede escribir en la forma\(\dfrac{p}{q}\), donde p y q son enteros y q ≠ 0. Su forma decimal se detiene o se repite. |
| Número real | Un número que es racional o irracional. |
Conceptos clave
7.1 - Números racionales e irracionales
- Números reales
7.2 - Propiedades conmutativas y asociativas
- Propiedades conmutativas
- Propiedad conmutativa de la suma: Si a, b son números reales, entonces a + b = b + a
- Propiedad conmutativa de la multiplicación: Si a, b son números reales, entonces a • b = b • a
- Propiedades asociativas
- Propiedad asociativa de la suma: Si a, b, c son números reales entonces (a + b) + c = a + (b + c)
- Propiedad asociativa de la multiplicación: Si a, b, c son números reales entonces (a • b) • c = a • (b • c)
7.3 - Propiedad Distributiva
- Propiedad Distributiva:
- Si a, b, c son números reales entonces
- a (b + c) = ab + ac
- (b + c) a = ba + ca
- a (b - c) = ab - ac
- Si a, b, c son números reales entonces
7.4 - Propiedades de Identidad, Inversa y Cero
- Propiedades de Identidad
- Identidad Propiedad de Adición: Para cualquier número real a: a + 0 = a, 0 + a = a
- 0 es la identidad aditiva
- Identidad Propiedad de Multiplicación: Para cualquier número real a: a • 1 = a, 1 • a = a
- 1 es la identidad multiplicativa
- Identidad Propiedad de Adición: Para cualquier número real a: a + 0 = a, 0 + a = a
- Propiedades inversas
- Propiedad inversa de suma: Para cualquier número real a: a + (- a) = 0
- - a es la inversa aditiva de a
- Propiedad inversa de multiplicación: Para cualquier número real a: (a ≠ 0) a •\(\dfrac{1}{a}\) = 1
- \(\dfrac{1}{a}\)es la inversa multiplicativa de un
- Propiedad inversa de suma: Para cualquier número real a: a + (- a) = 0
- Inmuebles de Zero
- Multiplicación por Cero: Para cualquier número real a, a • 0 = 0, 0 • a = 0
- El producto de cualquier número y 0 es 0.
- División de Cero: Para cualquier número real a\(\frac{0}{a} = 0\),\(0 \div a = 0\)
- Cero dividido por cualquier número real, excepto él mismo, es cero.
- División por Cero: Para cualquier número real a,\(\dfrac{a}{0}\) es indefinido y a ÷ 0 es indefinido.
- La división por cero no está definida.
- Multiplicación por Cero: Para cualquier número real a, a • 0 = 0, 0 • a = 0


