9.1: Usar una estrategia de resolución de problemas (Parte 1)
- Page ID
- 114176
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)- Abordar los problemas de la palabra con actitud positiva
- Usar una estrategia de resolución de problemas para problemas de palabras
- Resolver problemas numéricos
Antes de comenzar, toma este cuestionario de preparación.
- Traducir “6 menos que dos veces x” en una expresión algebraica. Si te perdiste este problema, revisa el Ejemplo 2.4.13.
- Resolver:\(\dfrac{2}{3}\) x = 24. Si te perdiste este problema, revisa el Ejemplo 8.3.4.
- Resolver: 3x + 8 = 14. Si te perdiste este problema, revisa el Ejemplo 8.4.1.
Abordar problemas de palabras con una actitud positiva
El mundo está lleno de problemas de palabras. ¿Cuánto dinero necesito para llenar el auto con gasolina? ¿Cuánto debo darle propina al servidor en un restaurante? ¿Cuántos calcetines debo empacar para vacaciones? ¿Qué tan grande necesito comprar un pavo para la cena de Acción de Gracias, y a qué hora necesito ponerlo en el horno? Si mi hermana y yo le compramos un regalo a nuestra madre, ¿cuánto pagará cada uno de nosotros?
Ahora que podemos resolver ecuaciones, estamos listos para aplicar nuestras nuevas habilidades a los problemas verbales. ¿Conoces a alguien que haya tenido experiencias negativas en el pasado con problemas verbales? ¿Alguna vez has tenido pensamientos como el alumno en Figura\(\PageIndex{1}\)?
Figura\(\PageIndex{1}\) - Los pensamientos negativos sobre los problemas verbales pueden ser barreras para el éxito.
Cuando sentimos que no tenemos control, y seguimos repitiendo pensamientos negativos, establecemos barreras para el éxito. Necesitamos calmar nuestros miedos y cambiar nuestros sentimientos negativos.
Comienza con una nueva pizarra y comienza a pensar pensamientos positivos como el alumno en Figura\(\PageIndex{2}\). Lee los pensamientos positivos y dilos en voz alta.
Figura\(\PageIndex{2}\) - Cuando se trata de problemas verbales, una actitud positiva es un gran paso hacia el éxito.
Si tomamos el control y creemos que podemos tener éxito, podremos dominar los problemas verbales.
Piensa en algo que puedas hacer ahora pero que no podrías hacer hace tres años. Ya sea conducir un automóvil, hacer snowboard, cocinar una comida gourmet o hablar un nuevo idioma, has podido aprender y dominar una nueva habilidad. Los problemas de palabras no son diferentes. Incluso si has luchado con problemas de palabras en el pasado, ¡has adquirido muchas habilidades matemáticas nuevas que te ayudarán a tener éxito ahora!
Usar una estrategia de resolución de problemas para problemas de palabras
En capítulos anteriores, tradujo frases de palabras a expresiones algebraicas, utilizando algún vocabulario y símbolos matemáticos básicos. Desde entonces has aumentado tu vocabulario matemático a medida que aprendiste más procedimientos algebraicos, y has tenido más práctica traduciendo de palabras a álgebra.
También ha traducido oraciones de palabras a ecuaciones algebraicas y resuelto algunos problemas de palabras. Los problemas de palabras aplicaron la matemática a situaciones cotidianas. Había que replantear la situación en una oración, asignar una variable, y luego escribir una ecuación para resolver. Este método funciona siempre y cuando la situación te sea familiar y las matemáticas no sean demasiado complicadas.
Ahora desarrollaremos una estrategia que puedas usar para resolver cualquier problema de palabras. Esta estrategia te ayudará a tener éxito con problemas de palabras. Demostraremos la estrategia a medida que resolvamos el siguiente problema.
Pete compró una playera a la venta por 18 dólares, que es la mitad del precio original. ¿Cuál era el precio original de la playera?
Solución
Paso 1. Lee el problema. Asegúrate de entender todas las palabras e ideas. Es posible que tengas que leer el problema dos o más veces. Si hay palabras que no entiendes, búscalas en un diccionario o en Internet.
- En este problema, ¿entiende lo que se está discutiendo? ¿Entiendes cada palabra?
Paso 2. Identifica lo que buscas. ¡Es difícil encontrar algo si no estás seguro de qué es! ¡Vuelve a leer el problema y busca palabras que te digan lo que estás buscando!
- En este problema, las palabras “cuál era el precio original de la camisa” te dicen que lo que buscas: el precio original de la camisa.
Paso 3. Nombra lo que buscas. Elija una variable para representar esa cantidad. Puedes usar cualquier letra para la variable, pero puede ser útil elegir una que te ayude a recordar lo que representa.
- Dejar p = el precio original de la camisa.
Paso 4. Traducir en una ecuación. Puede ayudar reafirmar primero el problema en una frase, con toda la información importante. Después traduzca la oración en una ecuación.
Paso 5. Resolver la ecuación usando buenas técnicas de álgebra. Incluso si conoces la respuesta de inmediato, usar álgebra te preparará mejor para resolver problemas que no tienen respuestas obvias.
| Escribe la ecuación. | \(18 = \dfrac{1}{2} p\) |
| Multiplica ambos lados por 2. | \(\textcolor{red}{2} \cdot 18 = \textcolor{red}{2} \cdot \dfrac{1}{2} p\) |
| Simplificar. | \(36 = p\) |
Paso 6. Comprueba la respuesta en el problema y asegúrate de que tenga sentido.
- Encontramos que p = 36, lo que significa que el precio original fue de 36 dólares. ¿Tiene sentido 36 dólares en el problema? Sí, porque 18 es la mitad de 36, y la playera estaba a la venta a la mitad del precio original.
Paso 7. Contesta la pregunta con una oración completa.
- El problema preguntaba “¿Cuál era el precio original de la playera?” La respuesta a la pregunta es: “El precio original de la playera era de 36 dólares”.
Si esto fuera un ejercicio de tarea, nuestro trabajo podría verse así:
| Dejar p = el precio original. | 18 es la mitad del precio original. $$\ begin {split} 18 &=\ dfrac {1} {2} p\\ 2\ cdot 18 &= 2\ cdot\ dfrac {1} {2} p\\ 36 &= p\ end {split} $$ |
|
Comprobar: ¿Es $36 un precio razonable por una playera? Sí. ¿18 es la mitad de 36? Sí. |
El precio original de la playera era de 36 dólares. |
Joaquin compró una librería a la venta por 120 dólares, que era dos tercios del precio original. ¿Cuál era el precio original de la librería?
- Responder
-
$180
Dos quintas partes de las personas en el comedor del centro senior son hombres. Si hay 16 hombres, ¿cuál es el número total de personas en el comedor?
- Responder
-
40
Enumeramos los pasos que tomamos para resolver el ejemplo anterior.
- Paso 1. Lee el problema de la palabra. Asegúrate de entender todas las palabras e ideas. Es posible que tengas que leer el problema dos o más veces. Si hay palabras que no entiendes, búscalas en un diccionario o en internet.
- Paso 2. Identifica lo que buscas.
- Paso 3. Nombra lo que buscas. Elija una variable para representar esa cantidad.
- Paso 4. Traducir en una ecuación. Puede ser útil volver a plantear primero el problema en una oración antes de traducirlo.
- Paso 5. Resolver la ecuación usando buenas técnicas de álgebra.
- Paso 6. Consulta la respuesta en el problema. Asegúrate de que tenga sentido.
- Paso 7. Contesta la pregunta con una oración completa.
Usemos este enfoque con otro ejemplo.
Yash trajo manzanas y plátanos a un picnic. El número de manzanas fue de tres más del doble del número de plátanos. Yash trajo 11 manzanas al picnic. ¿Cuántos plátanos trajo?
Solución
| Paso 1. Lee el problema. | |
| Paso 2. Identifica lo que buscas. | ¿Cuántos plátanos trajo? |
| Paso 3. Nombra lo que buscas. Elija una variable para representar el número de plátanos. | Let b = número de plátanos |
| Paso 4. Traducir. Reafirmar el problema en una frase con toda la información importante. Traducir en una ecuación. |
|
| Paso 5. Resuelve la ecuación. | $11 = 3b + 3$$ |
| Restar 3 de cada lado. | \(11 \textcolor{red}{-3} = 2b + 3 \textcolor{red}{-3}\) |
| Simplificar. | \(8 = 2b\) |
| Divide cada lado por 2. | \(\dfrac{8}{\textcolor{red}{2}} = \dfrac{2b}{\textcolor{red}{2}}\) |
| Simplificar. | \(4 = b\) |
| Paso 6. Consulta: Primero, ¿nuestra respuesta es razonable? Sí, llevar cuatro plátanos a un picnic parece razonable. El problema dice que el número de manzanas era tres más del doble que el número de plátanos. Si hay cuatro plátanos, ¿eso hace once manzanas? Dos veces 4 plátanos es 8. Tres más de 8 es 11. | |
| Paso 7. Contesta la pregunta. | Yash trajo 4 plátanos al picnic. |
Guillermo compró libros de texto y cuadernos en la librería. El número de libros de texto fue 3 más que el número de cuadernos. Compró 5 libros de texto. ¿Cuántos cuadernos compró?
- Responder
-
2
Gerry trabajó esta semana con rompecabezas de Sudoku y crucigramas. El número de rompecabezas de Sudoku que completó es siete más que el número de crucigramas. Completó 14 acertijos de Sudoku. ¿Cuántos crucigramas completó?
- Responder
-
7
En Solve Sales Tax, Commission y Discount Applications aprendimos a traducir y resolver ecuaciones básicas de porcentaje y las usamos para resolver solicitudes de impuestos sobre ventas y comisiones. En el siguiente ejemplo, aplicaremos nuestra Estrategia de Resolución de Problemas a más aplicaciones de porcentaje.
La prima del seguro de auto de Nga aumentó 60 dólares, lo que representó 8% del costo original. ¿Cuál era el costo original de la prima?
Solución
| Paso 1. Lee el problema. Recuerda, si hay palabras que no entiendes, búscalas. | |
| Paso 2. Identifica lo que buscas. | el costo original de la prima |
| Paso 3. Nombre. Elija una variable para representar el costo original de la prima. | Let c = el costo original |
| Paso 4. Traducir. Reafirmar como una sola oración. Traducir en una ecuación. |  |
| Paso 5. Resuelve la ecuación. | $60 = 0.08c$$ |
| Divide ambos lados por 0.08. | $$\ dfrac {60} {\ textcolor {rojo} {0.08}} =\ dfrac {0.08c} {\ textcolor {rojo} {0.08}} $$ |
| Simplificar. | $$c = 750$$ |
| Paso 6. Consulta: ¿Nuestra respuesta es razonable? Sí, una prima de $750 en el seguro de auto es razonable. Ahora vamos a revisar nuestro álgebra. ¿El 8% de 750 es igual a 60? | $$\ begin {split} 750 &= c\\ 0.08 (750) &= 60\\ 60 &= 60\;\ marca de verificación\ end {split} $$ |
| Paso 7. Contesta la pregunta. | El costo original de la prima de Nga era de 750 dólares. |
La renta de Pilar aumentó 4%. El incremento fue de 38 dólares. ¿Cuál era el monto original de la renta de Pilar?
- Responder
-
$950
Steve ahorra 12% de su sueldo cada mes. Si ahorró 504 dólares el mes pasado, ¿cuánto le costó su sueldo?
- Responder
-
$4200
Resolver problemas de números
Ahora traduciremos y resolveremos problemas de números. En problemas numéricos, se le dan algunas pistas sobre uno o más números, y usa estas pistas para construir una ecuación. Los problemas numéricos no suelen surgir en el día a día, pero proporcionan una buena introducción a la práctica de la Estrategia de Resolución de Problemas. Recuerda buscar palabras clave como diferencia, de, y y.
La diferencia de un número y seis es de 13. Encuentra el número.
Solución
| Paso 1. Lee el problema. ¿Entiendes todas las palabras? | |
| Paso 2. Identifica lo que buscas. | el número |
| Paso 3. Nombre. Elija una variable para representar el número. | Let n = el número |
| Paso 4. Traducir. Reafirmar como una sola oración. Traducir en una ecuación. |  |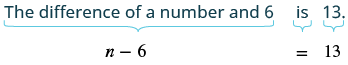
| Paso 5. Resuelve la ecuación. Agrega 6 a ambos lados. Simplificar. | $$\ begin {split} n - 6 &= 13\\ n -\ textcolor {rojo} {+6} &= 13\ textcolor {rojo} {+6}\\ n &= 19\ end {split} $$ |
| Paso 6. Consulta: La diferencia de 19 y 6 es 13. Comproba. | |
| Paso 7. Contesta la pregunta. | El número es 19. |
La diferencia de un número y ocho es de 17. Encuentra el número.
- Responder
-
25
La diferencia de un número y once es −7. Encuentra el número.
- Responder
-
4
La suma de dos veces por número y siete es 15. Encuentra el número.
Solución
| Paso 1. Lee el problema. | |
| Paso 2. Identifica lo que buscas. | el número |
| Paso 3. Nombre. Elija una variable para representar el número. | Let n = el número |
| Paso 4. Traducir. Reformular el problema como una sola oración. Traducir en una ecuación. |  |
| Paso 5. Resuelve la ecuación. | $$2n + 7 = 15$$ |
| Restar 7 de cada lado y simplificar. | $$2n = 8$$ |
| Divide cada lado por 2 y simplifica. | $$n = 4$$ |
| Paso 6. Cheque: ¿la suma de dos veces 4 y 7 es igual a 15? | $$\ begin {split} 2\ cdot 4 + 7 &= 15\\ 8 + 7 &= 15\\ 15 &= 15\;\ marca de verificación\ end {split} $$ |
| Paso 7. Contesta la pregunta. | El número es 4. |
La suma de cuatro veces un número y dos es 14. Encuentra el número.
- Responder
-
3
La suma de tres veces un número y siete es 25. Encuentra el número.
- Responder
-
6