Saltar al contenido principal
LibreTexts Español

9.8: Resolver aplicaciones de geometría: círculos y figuras irregulares

  1. Última actualización
  2. Guardar como PDF
  • Page ID
    114158

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

    Objetivos de aprendizaje
    • Usa las propiedades de los círculos
    • Encuentra el área de figuras irregulares
    ¡prepárate!

    Antes de comenzar, toma este cuestionario de preparación.

    1. Evalúa x 2 cuando x = 5. Si te perdiste este problema, revisa el Ejemplo 2.3.3.
    2. Usando 3.14 para\(\pi\), aproximar la (a) circunferencia y (b) el área de un círculo con radio de 8 pulgadas. Si te perdiste este problema, revisa el Ejemplo 5.6.12.
    3. Simplifica\(\dfrac{22}{7}\) (0.25) 2 y redondea a la milésima más cercana. Si te perdiste este problema, revisa el Ejemplo 5.5.9.

    En esta sección, continuaremos trabajando con aplicaciones de geometría. Añadiremos varias fórmulas nuevas a nuestra colección de fórmulas. Para ayudarte mientras haces los ejemplos y ejercicios de esta sección, aquí te mostraremos la Estrategia de Resolución de Problemas para Aplicaciones de Geometría.

    Estrategia de resolución de problemas para aplicaciones de geometría

    Paso 1. Lee el problema y asegúrate de entender todas las palabras e ideas. Dibuja la figura y etiquétala con la información dada.

    Paso 2. Identifica lo que buscas.

    Paso 3. Nombra lo que buscas. Elija una variable para representar esa cantidad

    Paso 4. Traducir en una ecuación escribiendo la fórmula o modelo apropiado para la situación. Sustituir en la información dada.

    Paso 5. Resolver la ecuación usando buenas técnicas de álgebra.

    Paso 6. Comprueba la respuesta en el problema y asegúrate de que tenga sentido.

    Paso 7. Contesta la pregunta con una oración completa.

    Utilizar las propiedades de los círculos

    ¿Recuerdas las propiedades de los círculos de Decimales y Fracciones? Los mostraremos aquí nuevamente para referirnos ya que los usamos para resolver aplicaciones.

    Definición: Propiedades de los Círculos

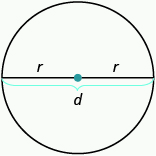
    Se muestra una imagen de un círculo. Hay una línea dibujada a través de la parte más ancha en el centro del círculo con un punto rojo que indica el centro del círculo. La línea está etiquetada d. Los dos segmentos desde el centro del círculo hasta el exterior del círculo están etiquetados cada uno r.

    • r es la longitud del radio
    • d es la longitud del diámetro
    • d = 2r
    • Circunferencia es el perímetro de un círculo. La fórmula para la circunferencia es C = 2\(\pi\) r
    • La fórmula para el área de un círculo es A =\(\pi\) r 2

    Recuerda, que aproximamos\(\pi\) con 3.14 o\(\dfrac{22}{7}\) dependiendo de si el radio del círculo se da como decimal o fracción. Si usa la\(\pi\) clave de su calculadora para hacer los cálculos en esta sección, sus respuestas serán ligeramente diferentes de las respuestas mostradas. Eso se debe a que la\(\pi\) clave utiliza más de dos decimales.

    Ejemplo\(\PageIndex{1}\):

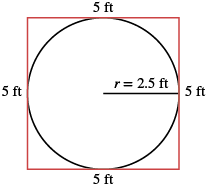
    Una caja de arena circular tiene un radio de 2.5 pies. Encuentra la (a) circunferencia y (b) área de la caja de arena.

    Solución

    a)

    Paso 1. Lee el problema. Dibuja la figura y etiquétala con la información dada. 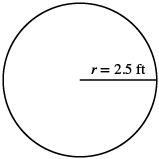CNX_BMath_Figure_09_05_029_img-01.png
    Paso 2. Identifica lo que buscas. la circunferencia del círculo
    Paso 3. Nombre. Elija una variable para representarla. Let c = circunferencia del círculo
    Paso 4. Traducir. Escriba la fórmula apropiada. Sustituto. $$\ begin {split} C &= 2\ pi r\\ C &= 2\ pi (2.5)\ end {split} $$
    Paso 5. Resuelve la ecuación. $$\ begin {split} C &\ approx 2 (3.14) (2.5)\\ C &\ approx 15\; ft\ end {split} $$
    Paso 6. Cheque. ¿Tiene sentido esta respuesta?

    Sí. Si dibujamos un cuadrado alrededor del círculo, sus lados serían 5 pies (el doble del radio), por lo que su perímetro sería de 20 pies. Esto es un poco más que la circunferencia del círculo, 15.7 pies.

    CNX_BMath_Figure_09_05_029_img-02.png
    Paso 7. Contesta la pregunta. La circunferencia de la caja de arena es de 15.7 pies.

    b)

    Paso 1. Lee el problema. Dibuja la figura y etiquétala con la información dada. CNX_BMath_Figure_09_05_029_img-01.png
    Paso 2. Identifica lo que buscas. el área del círculo
    Paso 3. Nombre. Elija una variable para representarla. Let A = el área del círculo
    Paso 4. Traducir. Escriba la fórmula apropiada. Sustituto. $$\ begin {split} A &=\ pi r^ {2}\\ A &=\ pi (2.5) ^ {2}\ end {split} $$
    Paso 5. Resuelve la ecuación. $$\ begin {split} A &\ approx (3.14) (2.5) ^ {2}\\ A &\ aproximadamente 19.625\; sq.\; ft\ end {split} $$
    Paso 6. Cheque. ¿Tiene sentido esta respuesta? Sí. Si dibujamos un cuadrado alrededor del círculo, sus lados serían de 5 pies, como se muestra en la parte (a). Entonces el área de la plaza sería de 25 pies cuadrados. Esto es un poco más que el área del círculo, 19.625 pies cuadrados.
    Paso 7. Contesta la pregunta. El área del círculo es de 19.625 pies cuadrados.
    Ejercicio\(\PageIndex{1}\):

    Un espejo circular tiene un radio de 5 pulgadas. Encuentra la (a) circunferencia y (b) área del espejo.

    Contestar a

    31.4 in.

    Respuesta b

    78.5 pulg.

    Ejercicio\(\PageIndex{2}\):

    Un spa circular tiene un radio de 4.5 pies. Encontrar la (a) circunferencia y (b) área del spa.

    Contestar a

    28.26 ft

    Respuesta b

    63.585 pies cuadrados

    Normalmente vemos la fórmula para circunferencia en términos del radio r del círculo:

    \[C = 2 \pi r\]

    Pero como el diámetro de un círculo es dos veces el radio, podríamos escribir la fórmula para la circunferencia en términos de d.

    \[\begin{split} C &= 2 \pi r \\ Using\; the\; commutative\; property,\; we\; get \qquad C &= \pi \cdot 2r \\ Then\; substituting\; d = 2r \qquad C &= \pi \cdot d \\ So \qquad C &= \pi d \end{split}\]

    Utilizaremos esta forma de la circunferencia cuando nos den la longitud del diámetro en lugar del radio.

    Ejemplo\(\PageIndex{2}\):

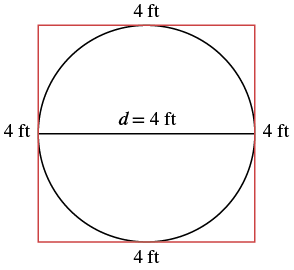
    Una mesa circular tiene un diámetro de cuatro pies. ¿Cuál es la circunferencia de la mesa?

    Solución

    Paso 1. Lee el problema. Dibuja la figura y etiquétala con la información dada. 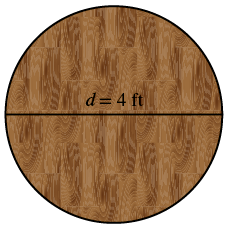CNX_BMath_Figure_09_05_032_img-01.png
    Paso 2. Identifica lo que buscas. la circunferencia de la mesa
    Paso 3. Nombre. Elija una variable para representarla. Let c = la circunferencia de la tabla
    Paso 4. Traducir. Escribir la fórmula apropiada para la situación. Sustituto. $$\ begin {split} C &=\ pi d\\ C &=\ pi (4)\ end {split} $$
    Paso 5. Resuelve la ecuación, usando 3.14 para\(\pi\). $$\ begin {split} C &\ approx (3.14) (4)\\ C &\ approx 12.56\; ft\ end {split} $$
    Paso 6. Cheque.

    Si ponemos un cuadrado alrededor del círculo, su lado sería 4. El perímetro sería de 16. Tiene sentido que la circunferencia del círculo, 12.56, sea un poco menos de 16.

    CNX_BMath_Figure_09_05_032_img-02.png
    Paso 7. Contesta la pregunta. El diámetro de la mesa es de 12.56 pies cuadrados.
    Ejercicio\(\PageIndex{3}\):

    Encuentra la circunferencia de una hoguera circular cuyo diámetro es de 5.5 pies.

    Responder

    17.27 ft

    Ejercicio\(\PageIndex{4}\):

    Si el diámetro de un trampolín circular es de 12 pies, ¿cuál es su circunferencia?

    Responder

    37.68 pies

    Ejemplo\(\PageIndex{3}\):

    Encuentra el diámetro de un círculo con una circunferencia de 47.1 centímetros.

    Solución

    Paso 1. Lee el problema. Dibuja la figura y etiquétala con la información dada. 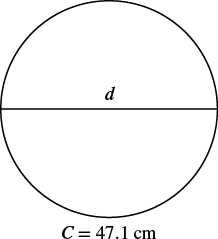CNX_BMath_Figure_09_05_033_img-01.png
    Paso 2. Identifica lo que buscas. el diámetro del círculo
    Paso 3. Nombre. Elija una variable para representarla. Let d = el diámetro del círculo
    Paso 4. Traducir. Escribe la fórmula. Sustituir, usando 3.14 para aproximar\(\pi\). $$\ begin {split} C &=\ pi d\\ 47.1 &\ approx 3.14d\ end {split} $$
    Paso 5. Resolver. $$\ begin {split}\ dfrac {47.11} {3.14} &\ approx\ dfrac {3.14d} {3.14}\\ 15 &\ d aprox\ end {split} $$
    Paso 6. Cheque. $$\ begin {split} 47.1 &\ stackrel {?} {=} (3.14) (15)\\ 47.1 &= 47.1\;\ marca de verificación\ end {split} $$
    Paso 7. Contesta la pregunta. El diámetro del círculo es de aproximadamente 15 centímetros.
    Ejercicio\(\PageIndex{5}\):

    Encuentra el diámetro de un círculo con circunferencia de 94.2 centímetros.

    Responder

    30 cm

    Ejercicio\(\PageIndex{6}\):

    Encuentra el diámetro de un círculo con circunferencia de 345.4 pies.

    Responder

    110 pies

    Encuentra el Área de Cifras Irregulares

    Hasta el momento, hemos encontrado área para rectángulos, triángulos, trapecios y círculos. Una figura irregular es una figura que no es una forma geométrica estándar. Su área no se puede calcular utilizando ninguna de las fórmulas de área estándar. Pero algunas figuras irregulares están conformadas por dos o más formas geométricas estándar. Para encontrar el área de una de estas figuras irregulares, podemos dividirla en figuras cuyas fórmulas conocemos y luego agregar las áreas de las figuras.

    Ejemplo\(\PageIndex{4}\):

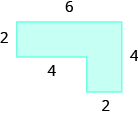
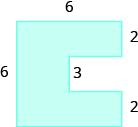
    Encuentra el área de la región sombreada.

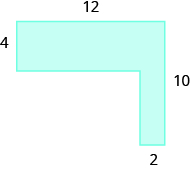
    Se muestra una imagen de un rectángulo horizontal adjunto y un rectángulo vertical. La parte superior está etiquetada con 12, el lado del rectángulo horizontal está etiquetada con 4. El lado está etiquetado con 10, el ancho del rectángulo vertical está etiquetado con 2.

    Solución

    La cifra dada es irregular, pero podemos dividirla en dos rectángulos. El área de la región sombreada será la suma de las áreas de ambos rectángulos.

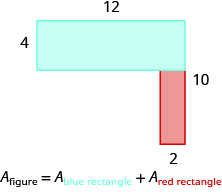
    Se muestra una imagen de un rectángulo horizontal adjunto y un rectángulo vertical. La parte superior está etiquetada con 12, el lado del rectángulo horizontal está etiquetada con 4. El lado está etiquetado con 10, el ancho del rectángulo vertical está etiquetado con 2.

    El rectángulo azul tiene una anchura de 12 y una longitud de 4. El rectángulo rojo tiene un ancho de 2, pero su longitud no está etiquetada. El lado derecho de la figura es la longitud del rectángulo rojo más la longitud del rectángulo azul. Dado que el lado derecho del rectángulo azul tiene 4 unidades de largo, la longitud del rectángulo rojo debe ser de 6 unidades.

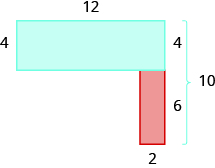
    Se muestra una imagen de un rectángulo horizontal azul unido a un rectángulo vertical rojo. La parte superior está etiquetada con 12, el lado del rectángulo azul está etiquetada con 4. Todo el lado está etiquetado con 10, la porción azul está etiquetada con 4 y la porción roja está etiquetada con 6. El ancho del rectángulo rojo está etiquetado como 2.

    \[\begin{split} A_{figure} &= A_{\textcolor{blue}{rectangle}} + A_{\textcolor{red}{rectangle}} \\ A_{figure} &= \textcolor{blue}{bh} + \textcolor{red}{bh} \\ A_{figure} &= \textcolor{blue}{12 \cdot 4} + \textcolor{red}{2 \cdot 6} \\ A_{figure} &= \textcolor{blue}{48} + \textcolor{red}{12} \\ A_{figure} &= 60 \end{split}\]

    El área de la figura es de 60 unidades cuadradas.

    ¿Hay otra manera de dividir esta figura en dos rectángulos? Pruébalo y asegúrate de obtener la misma área.

    Ejercicio\(\PageIndex{7}\):

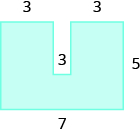
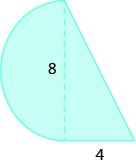
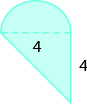
    Encuentra el área de cada región sombreada:

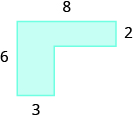
    Se muestra una forma geométrica azul. Parece un rectángulo horizontal unido a un rectángulo vertical. La parte superior está etiquetada como 8, el ancho del rectángulo horizontal se etiqueta como 2. El lado está etiquetado como 6, el ancho del rectángulo vertical se etiqueta como 3.

    Responder

    28 unidades sq.

    Ejercicio\(\PageIndex{8}\):

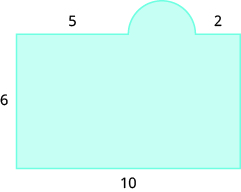
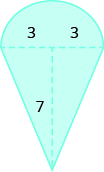
    Encuentra el área de cada región sombreada:

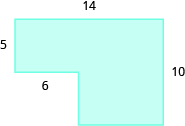
    Se muestra una forma geométrica azul. Parece un rectángulo horizontal unido a un rectángulo vertical. La parte superior está etiquetada como 14, el ancho del rectángulo horizontal se etiqueta como 5. El lado está etiquetado como 10, el ancho del espacio faltante se etiqueta como 6.

    Responder

    110 unidades sq.

    Ejemplo\(\PageIndex{5}\):

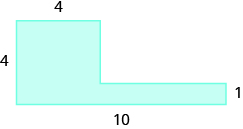
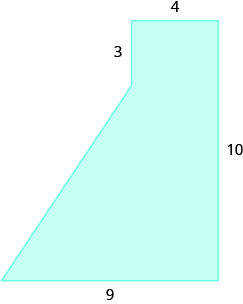
    Encuentra el área de la región sombreada.

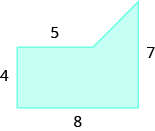
    Se muestra una forma geométrica azul. Parece un rectángulo con un triángulo unido a la parte superior en el lado derecho. El lado izquierdo está etiquetado con 4, el superior 5, el inferior 8, el lado derecho 7.

    Solución

    Podemos romper esta figura irregular en un triángulo y un rectángulo. El área de la figura será la suma de las áreas de triángulo y rectángulo.

    El rectángulo tiene una longitud de 8 unidades y un ancho de 4 unidades.

    Necesitamos encontrar la base y la altura del triángulo.

    Dado que ambos lados del rectángulo son 4, el lado vertical del triángulo es 3, que es 7 − 4. La longitud del rectángulo es 8, por lo que la base del triángulo será 3, que es 8 − 4.

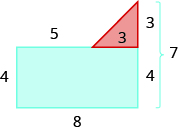
    Se muestra una forma geométrica. Se trata de un rectángulo azul con un triángulo rojo unido a la parte superior en el lado derecho. El lado izquierdo está etiquetado con 4, el superior 5, el inferior 8, el lado derecho 7. El lado derecho del rectángulo está etiquetado como 4. El lado derecho y la parte inferior del triángulo están etiquetados 3.

    Ahora podemos agregar las áreas para encontrar el área de la figura irregular.

    \[\begin{split} A_{figure} &= A_{\textcolor{blue}{rectangle}} + A_{\textcolor{red}{triangle}} \\ A_{figure} &= \textcolor{blue}{lw} + \dfrac{1}{2} \textcolor{red}{bh} \\ A_{figure} &= \textcolor{blue}{8 \cdot 4} + \dfrac{1}{2} \cdot \textcolor{red}{3 \cdot 3} \\ A_{figure} &= \textcolor{blue}{32} + \textcolor{red}{4.5} \\ A_{figure} &= 3.65\; sq.\; units \end{split}\]

    El área de la figura es de 36.5 unidades cuadradas.

    Ejercicio\(\PageIndex{9}\):

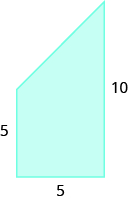
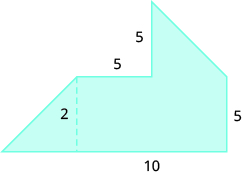
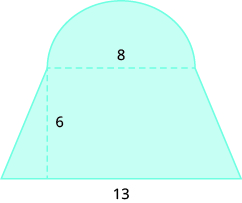
    Encuentra el área de cada región sombreada.

    Se muestra una forma geométrica azul. Parece un rectángulo con un triángulo unido al lado inferior derecho. La base del rectángulo está etiquetada con 8, la altura del rectángulo está etiquetada con 4. La distancia desde la parte superior del rectángulo hasta donde comienza el triángulo está etiquetada con 3, la parte superior del triángulo está etiquetada con 3.

    Responder

    36.5 unidades cuadrados

    Ejercicio\(\PageIndex{10}\):

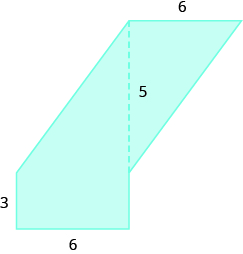
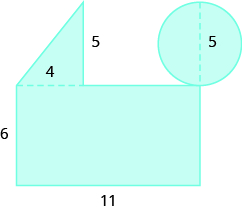
    Encuentra el área de cada región sombreada.

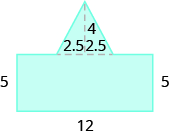
    Se muestra una forma geométrica azul. Parece un rectángulo con un triángulo equilátero unido a la parte superior. La base del rectángulo está etiquetada con 12, cada lado está etiquetada con 5. La base del triángulo se divide en dos piezas, cada una etiquetada 2.5.

    Responder

    70 unidades sq.

    Ejemplo\(\PageIndex{6}\):

    Una pista de secundaria tiene forma de rectángulo con un semicírculo (medio círculo) en cada extremo. El rectángulo tiene longitud 105 metros y ancho 68 metros. Encuentra el área encerrada por la pista. Redondea tu respuesta a la centésima más cercana.

    Se muestra una pista, en forma de rectángulo con un semicírculo unido a cada lado.

    Solución

    Romperemos la figura en un rectángulo y dos semicírculos. El área de la figura será la suma de las áreas del rectángulo y los semicírculos.

    Se muestra una forma geométrica azul. Parece un rectángulo con un semicírculo unido a cada lado. La base del rectángulo está etiquetada con 105 m. La altura del rectángulo y el diámetro del círculo de la izquierda está etiquetada con 68 m.

    El rectángulo tiene una longitud de 105 m y un ancho de 68 m. Los semicírculos tienen un diámetro de 68 m, por lo que cada uno tiene un radio de 34 m.

    \[\begin{split} A_{figure} &= A_{\textcolor{blue}{rectangle}} + A_{\textcolor{red}{semicircles}} \\ A_{figure} &= \textcolor{blue}{bh} + \textcolor{red}{2\left(\dfrac{1}{2} \pi \cdot r^{2} \right)} \\ A_{figure} &\approx \textcolor{blue}{105 \cdot 68} + \textcolor{red}{2 \left(\dfrac{1}{2} \cdot 3.14 \cdot 34^{2}\right)} \\ A_{figure} &\approx \textcolor{blue}{7140} + \textcolor{red}{3629.84} \\ A_{figure} &\approx 10,769.84\; square\; meters \end{split}\]

    Ejercicio\(\PageIndex{11}\):

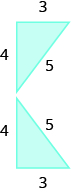
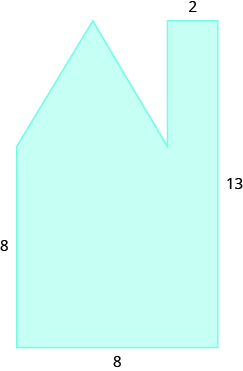
    Encuentra la zona:

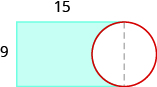
    Se muestra una forma. Es un rectángulo azul con una porción del rectángulo que falta. Hay un círculo rojo de la misma altura que el rectángulo unido al lado faltante del rectángulo. La parte superior del rectángulo está etiquetada con 15, la altura está etiquetada con 9.

    Responder

    103.2 unidades

    Ejercicio\(\PageIndex{12}\):

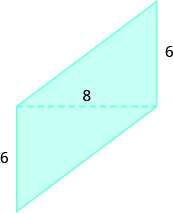
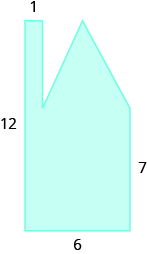
    Encuentra la zona:

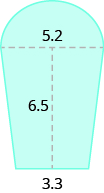
    Se muestra una forma geométrica azul. Parece ser dos trapecios con un semicírculo en la parte superior. La base del semicírculo está etiquetada 5.2. La altura de los trapecios está etiquetada 6.5. La base combinada de los trapecios está etiquetada 3.3.

    Responder

    38.24 unidades cuadrados

    Acceder a recursos adicionales en línea

    Circunferencia de un círculo

    Área de un círculo

    Área de un polígono en forma de L

    Área de un polígono en forma de L con decimales

    Perímetro que involucra un rectángulo y un círculo

    Área que involucra un rectángulo y un círculo

    La práctica hace la perfección

    Utilizar las propiedades de los círculos

    En los siguientes ejercicios, resuelve usando las propiedades de los círculos.

    1. La tapa de un cubo de pintura es un círculo con radio de 7 pulgadas. Encuentra la (a) circunferencia y (b) área de la tapa.
    2. Una pizza extra grande es un círculo con radio de 8 pulgadas. Encuentra la (a) circunferencia y (b) área de la pizza.
    3. Un aspersor de granja extiende el agua en un círculo con un radio de 8.5 pies. Encuentra la (a) circunferencia y (b) área del círculo regado.
    4. Una alfombra circular tiene un radio de 3.5 pies. Encuentra la (a) circunferencia y (b) área de la alfombra.
    5. Una piscina reflectante tiene la forma de un círculo con un diámetro de 20 pies. ¿Cuál es la circunferencia de la piscina?
    6. Un plato giratorio es un círculo con diámetro de 10 pulgadas. ¿Cuál es la circunferencia del tocadiscos?
    7. Una sierra circular tiene un diámetro de 12 pulgadas. ¿Cuál es la circunferencia de la sierra?
    8. Una moneda redonda tiene un diámetro de 3 centímetros. ¿Cuál es la circunferencia de la moneda?
    9. Una parrilla de barbacoa es un círculo con un diámetro de 2.2 pies. ¿Cuál es la circunferencia de la parrilla?
    10. La parte superior de una lata para pastel es un círculo con un diámetro de 9.5 pulgadas. ¿Cuál es la circunferencia de la parte superior?
    11. Un círculo tiene una circunferencia de 163.28 pulgadas. Encuentra el diámetro.
    12. Un círculo tiene una circunferencia de 59.66 pies. Encuentra el diámetro.
    13. Un círculo tiene una circunferencia de 17.27 metros. Encuentra el diámetro.
    14. Un círculo tiene una circunferencia de 80.07 centímetros. Encuentra el diámetro.

    En los siguientes ejercicios, encuentra el radio del círculo con circunferencia dada.

    1. Un círculo tiene una circunferencia de 150.72 pies.
    2. Un círculo tiene una circunferencia de 251.2 centímetros.
    3. Un círculo tiene una circunferencia de 40.82 millas.
    4. Un círculo tiene una circunferencia de 78.5 pulgadas.

    Encuentra el Área de Cifras Irregulares

    En los siguientes ejercicios, encuentra el área de la figura irregular. Redondea tus respuestas a la centésima más cercana.

    1. Se muestra una forma geométrica. Es un rectángulo horizontal unido a un rectángulo vertical. La parte superior está etiquetada con 6, la altura del rectángulo horizontal está etiquetada con 2, la distancia desde el borde del rectángulo horizontal hasta el inicio del rectángulo vertical es 4, la base del rectángulo vertical es 2, el lado derecho de la forma es 4.
    2. Se muestra una forma geométrica. Es una forma de L. La base está etiquetada con 10, el lado derecho 1, el lado superior e izquierdo están etiquetados cada uno con 4.
    3. Se muestra una forma geométrica. Es una forma de U lateral. La parte superior está etiquetada con 6, el lado izquierdo está etiquetada con 6. Una pieza horizontal interior está etiquetada con 3. Cada una de las piezas verticales de la derecha está etiquetada 2.
    4. Se muestra una forma geométrica. Es una forma de U. La base está etiquetada con 7. El lado derecho está etiquetado como 5. Las dos líneas horizontales en la parte superior y la vertical en el interior están todas etiquetadas con 3.
    5. Se muestra una forma geométrica. Se trata de un rectángulo con un triángulo unido al lado inferior izquierdo. La parte superior está etiquetada con 4. El lado derecho está etiquetado como 10. La base está etiquetada con 9. La línea vertical desde la parte superior del triángulo hasta la parte superior del rectángulo está etiquetada con 3.
    6. Se muestra un trapecio. Las bases están etiquetadas 5 y 10, la altura es 5.
    7. Se muestran dos triángulos. Parecen ser triángulos rectos. Las bases están etiquetadas 3, las alturas 4, y los lados más largos 5.
    8. Se muestra una forma geométrica. Parece estar compuesta por dos triángulos. La base compartida de ambos triángulos es 8, las alturas están etiquetadas con 6.
    9. Se muestra una forma geométrica. Se compone de dos trapecios. La base está etiquetada con 10. La altura de un trapecio es 2. Los lados horizontal y vertical están todos etiquetados como 5.
    10. Se muestra una forma geométrica. Se trata de un trapecio unido a un triángulo. La base del triángulo está etiquetada con 6, la altura está etiquetada con 5. La altura del trapecio es 6, una base es 3.
    11. Se muestra una forma geométrica. Se trata de un rectángulo con un triángulo y otro rectángulo unido. El lado izquierdo está etiquetado con 8, el inferior es 8, el lado derecho es 13 y el ancho del rectángulo más pequeño es 2.
    12. Se muestra una forma geométrica. Se trata de un rectángulo con un triángulo y otro rectángulo unido. El lado izquierdo está etiquetado 12, el lado derecho 7, la base 6. El ancho del rectángulo más pequeño está etiquetado como 1.
    13. Se muestra una forma geométrica. Es un rectángulo unido a un semicírculo. La base del rectángulo está etiquetada con 5, la altura es 7.
    14. Se muestra una forma geométrica. Es un rectángulo unido a un semicírculo. La base del rectángulo está etiquetada con 10, la altura es 6. La porción del rectángulo a la izquierda del semicírculo está etiquetada con 5, la porción de la derecha está etiquetada con 2.
    15. Se muestra una forma geométrica. Un triángulo está unido a un semicírculo. La base del triángulo está etiquetada con 4. La altura del triángulo y el diámetro del círculo son 8.
    16. Se muestra una forma geométrica. Un triángulo está unido a un semicírculo. La altura del triángulo está etiquetada con 4. La base del triángulo, también el diámetro del semicírculo, está etiquetada con 4.
    17. Se muestra una forma geométrica. Es un rectángulo unido a un semicírculo. La base del rectángulo está etiquetada con 5, la altura es 7.
    18. Se muestra una forma geométrica. Se muestra un trapecio con un semicírculo unido a la parte superior. El diámetro del círculo, que también es la parte superior del trapecio, está etiquetado como 8. La altura del trapecio es de 6. El fondo del trapecio es 13.
    19. Se muestra una forma geométrica. Se trata de un rectángulo con un triángulo unido a la parte superior en el lado izquierdo y un círculo unido a la esquina superior derecha. El diámetro del círculo está etiquetado como 5. La altura del triángulo está etiquetada con 5, la base está etiquetada con 4. La altura del rectángulo está etiquetada con 6, la base 11.
    20. Se muestra una forma geométrica. Es un trapecio con un triángulo unido a la parte superior, y un círculo unido al triángulo. El diámetro del círculo es 4. La altura del triángulo es 5, la base del triángulo, que también es la parte superior del trapecio, es 6. El fondo del trapecio es 9. La altura del trapecio es de 7.

    En los siguientes ejercicios, resuelve.

    1. Un parque de la ciudad cubre una cuadra más partes de cuatro cuadras más, como se muestra. El bloque es un cuadrado con lados de 250 pies de largo, y los triángulos son triángulos rectos isósceles. Encuentra la zona del parque.

    Se muestra un cuadrado con cuatro triángulos saliendo de cada lado.

    1. Se realizará una caja de regalo a partir de una pieza rectangular de cartón de 12 pulgadas por 20 pulgadas, con cuadrados recortados en las esquinas de los lados, como se muestra. Los lados de los cuadrados son de 3 pulgadas. Encuentra el área del cartón después de cortar las esquinas.

    Se muestra un rectángulo. Cada esquina tiene un cuadrado sombreado gris. Hay líneas punteadas dibujadas a través del lado de cada cuadrado unido al siguiente cuadrado.

    1. Perry necesita poner un césped nuevo. Su lote es un rectángulo con una longitud de 120 pies y un ancho de 100 pies. La casa es rectangular y mide 50 pies por 40 pies. Su entrada es rectangular y mide 20 pies por 30 pies, como se muestra. Encuentra el área del césped de Perry.

    Se muestra un lote rectangular. En ella se encuentra una casa con forma de rectángulo unida a un camino de entrada rectangular.

    1. Denise planea poner una cubierta en su patio trasero. La cubierta será un rectángulo de 20 pies por 12 pies con un semicírculo de 6 pies de diámetro, como se muestra a continuación. Encuentra el área de la cubierta.

    Se muestra una imagen de una baraja. Tiene forma de rectángulo con un semicírculo unido a la parte superior del lado izquierdo.

    Matemáticas cotidianas

    1. Área de un Sobremesa Yuki compró una mesa de cocina de hoja abatible. La parte rectangular de la mesa es un rectángulo de 1 pie por 3 pies con un semicírculo en cada extremo, como se muestra. (a) Encontrar el área de la mesa con una hoja hacia arriba. b) Encontrar el área de la mesa con ambas hojas arriba.

    Se muestra una imagen de una tabla. Hay una porción rectangular unida a una porción semicircular. Hay otra hoja semicircular doblada hacia abajo en el otro lado del rectángulo.

    1. Pintura Leora quiere pintar la guardería en su casa. El vivero es un rectángulo de 8 pies por 10 pies, y el techo mide 8 pies de altura. Hay una puerta de 3 pies por 6.5 pies en una pared, una puerta de armario de 3 pies por 6.5 pies en otra pared y una ventana de 4 pies por 3.5 pies en la tercera pared. La cuarta pared no tiene puertas ni ventanas. Si solo va a pintar las cuatro paredes, y no el techo o las puertas, ¿cuántos pies cuadrados necesitará pintar?

    Ejercicios de escritura

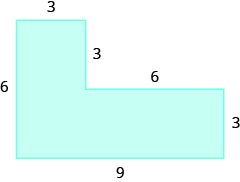
    1. Describe dos formas diferentes de encontrar el área de esta figura, y luego muestra tu trabajo para asegurarte de que ambas formas den la misma área.

    Se muestra una forma geométrica. Es un rectángulo vertical unido a un rectángulo horizontal. El ancho del rectángulo vertical es 3, el lado izquierdo está etiquetado con 6, el fondo está etiquetado con 9 y el ancho del rectángulo horizontal está etiquetado con 3. La parte superior del rectángulo horizontal está etiquetada con 6, y la distancia desde la parte superior de ese rectángulo hasta la parte superior del otro rectángulo está etiquetada con 3.

    1. Un círculo tiene un diámetro de 14 pies. Encuentra el área del círculo (a) usando 3.14 para\(\pi\) (b) usando\(\dfrac{22}{7}\) for\(\pi\). c) ¿Qué cálculo preferir? ¿Por qué?

    Autocomprobación

    (a) Después de completar los ejercicios, utilice esta lista de verificación para evaluar su dominio de los objetivos de esta sección.

    CNX_BMath_Figure_AppB_055.jpg

    (b) Después de mirar la lista de verificación, ¿cree que está bien preparado para la siguiente sección? ¿Por qué o por qué no?

    Colaboradores y Atribuciones

    This page titled 9.8: Resolver aplicaciones de geometría: círculos y figuras irregulares is shared under a not declared license and was authored, remixed, and/or curated by OpenStax.