9.10: Aplicaciones de Resolver Geometría- Volumen y Área de Superficie (Parte 2)
- Page ID
- 114191
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Encuentra el volumen y la superficie de las esferas
Una esfera es la forma de una básquetbol, como un círculo tridimensional. Al igual que un círculo, el tamaño de una esfera está determinado por su radio, que es la distancia desde el centro de la esfera hasta cualquier punto de su superficie. Las fórmulas para el volumen y la superficie de una esfera se dan a continuación.
Mostrar de dónde vienen estas fórmulas, como hicimos para un sólido rectangular, está más allá del alcance de este curso. Nos aproximaremos\(\pi\) con 3.14.
Para una esfera con radio r:
Una esfera tiene un radio de 6 pulgadas. Encontrar su (a) volumen y (b) superficie.
Solución
El paso 1 es el mismo tanto para (a) como para (b), así que lo mostraremos solo una vez.
| Paso 1. Lee el problema. Dibuja la figura y etiquétalo con la información dada. |  |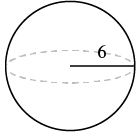
(a)
| Paso 2. Identifica lo que buscas. | el volumen de la esfera |
| Paso 3. Nombre. Elija una variable para representarla. | let V = volumen |
| Paso 4. Traducir. Escriba la fórmula apropiada. | $$V =\ dfrac {4} {3}\ pi r^ {3}\ tag {9.6.12} $$ |
| Paso 5. Resolver. | $$\ begin {split} V &\ approx\ dfrac {4} {3} (3.14) 6^ {3}\ V &\ aprox 904.32\; cúbicas\; pulgadas\ final {split} $$ |
| Paso 6. Cheque. | Vuelva a verificar sus matemáticas en una calculadora. |
| Paso 7. Contesta la pregunta. | El volumen es de aproximadamente 904.32 pulgadas cúbicas. |
b)
| Paso 2. Identifica lo que buscas. | la superficie del cubo |
| Paso 3. Nombre. Elija una variable para representarla. | let S = superficie |
| Paso 4. Traducir. Escriba la fórmula apropiada. | $$S = 4\ pi r^ {2}\ tag {9.6.13} $$ |
| Paso 5. Resolver. | $$\ begin {split} S &\ approx 4 (3.14) 6^ {2}\\ S &\ aproximadamente 452.16\; sq.\; pulgadas\ final {split} $$ |
| Paso 6. Cheque. | Vuelva a verificar sus matemáticas en una calculadora. |
| Paso 7. Contesta la pregunta. | El área de superficie es de aproximadamente 452.16 pulgadas cuadradas. |
Encuentra el (a) volumen y (b) superficie de una esfera con radio de 3 centímetros.
- Contestar a
-
113.04 cu. cm
- Respuesta b
-
113.04 cm cuadrados
Encontrar el (a) volumen y (b) área de superficie de cada esfera con un radio de 1 pie
- Contestar a
-
4.19 pies cúbicos
- Respuesta b
-
12.56 pies cuadrados
Un globo de la Tierra tiene la forma de una esfera con un radio de 14 centímetros. Encontrar su (a) volumen y (b) superficie. Redondear la respuesta a la centésima más cercana.
| Paso 1. Lee el problema. Dibuja la figura y etiquétalo con la información dada. |  |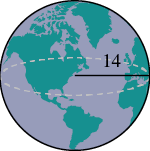
(a)
| Paso 2. Identifica lo que buscas. | el volumen de la esfera |
| Paso 3. Nombre. Elija una variable para representarla. | let V = volumen |
| Paso 4. Traducir. Escriba la fórmula apropiada. Sustituto. (Use 3.14 para\(\pi\)) | $$\ begin {split} V &=\ dfrac {4} {3}\ pi r^ {3}\\ V &\ approx\ dfrac {4} {3} (3.14) 14^ {3}\ end {split} $$ |
| Paso 5. Resolver. | $$V\ aprox 11,488.21\ tag {9.6.14} $$ |
| Paso 6. Cheque. | Te dejamos que compruebes tus cálculos. |
| Paso 7. Contesta la pregunta. | El volumen es de aproximadamente 11,488.21 pulgadas cúbicas. |
b)
| Paso 2. Identifica lo que buscas. | la superficie de la esfera |
| Paso 3. Nombre. Elija una variable para representarla. | let S = superficie |
| Paso 4. Traducir. Escriba la fórmula apropiada. | $$\ begin {split} S &= 4\ pi r^ {2}\\ S &\ approx 4 (3.14) 14^ {2}\ end {split} $$ |
| Paso 5. Resolver. | $$S\ approx 2461.76\ tag {9.6.15} $$ |
| Paso 6. Cheque. | Te dejamos que compruebes tus cálculos. |
| Paso 7. Contesta la pregunta. | La superficie es de aproximadamente 2461.76 pulgadas cuadradas. |
Una pelota de playa tiene la forma de una esfera con un radio de 9 pulgadas. Encontrar su (a) volumen y (b) superficie.
- Contestar a
-
3052.08 cu. en
- Respuesta b
-
1017.36 pulg.
Una estatua romana representa a Atlas sosteniendo un globo con un radio de 1.5 pies. Encuentra el (a) volumen y (b) superficie del globo.
- Contestar a
-
14.13 pies cúbicos
- Respuesta b
-
28.26 pies cuadrados
Encontrar el volumen y el área de superficie de un cilindro
Si alguna vez has visto una lata de refresco, ya sabes cómo se ve un cilindro. Un cilindro es una figura sólida con dos círculos paralelos del mismo tamaño en la parte superior e inferior. La parte superior e inferior de un cilindro se llaman las bases. La altura h de un cilindro es la distancia entre las dos bases. Para todos los cilindros con los que trabajaremos aquí, los lados y la altura, h, serán perpendiculares a las bases.
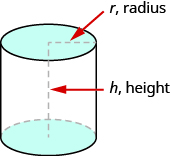
Figura\(\PageIndex{5}\) - Un cilindro tiene dos bases circulares de igual tamaño. La altura es la distancia entre las bases.
Los sólidos rectangulares y los cilindros son algo similares porque ambos tienen dos bases y una altura. La fórmula para el volumen de un sólido rectangular, V = Bh, también se puede utilizar para encontrar el volumen de un cilindro.
Para el sólido rectangular, el área de la base, B, es el área de la base rectangular, largo × ancho. Para un cilindro, el área de la base, B, es el área de su base circular,\(\pi\) r 2. La figura\(\PageIndex{6}\) compara cómo se utiliza la fórmula V = Bh para sólidos rectangulares y cilindros.
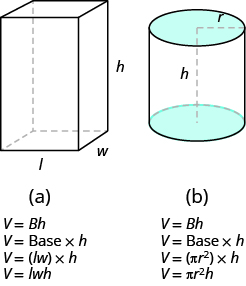
Figura\(\PageIndex{6}\) - Ver cómo un cilindro es similar a un sólido rectangular puede facilitar la comprensión de la fórmula para el volumen de un cilindro.
Para entender la fórmula para la superficie de un cilindro, piense en una lata de verduras. Tiene tres superficies: la parte superior, la inferior y la pieza que forma los lados de la lata. Si cortas cuidadosamente la etiqueta del costado de la lata y la desenrollas, verás que es un rectángulo. Ver Figura\(\PageIndex{7}\).
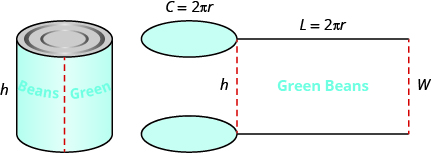
Figura\(\PageIndex{7}\) - Al cortar y desenrollar la etiqueta de una lata de verduras, podemos ver que la superficie de un cilindro es un rectángulo. La longitud del rectángulo es la circunferencia de la base del cilindro, y el ancho es la altura del cilindro.
La distancia alrededor del borde de la lata es la circunferencia de la base del cilindro y también es la longitud L de la etiqueta rectangular. La altura del cilindro es el ancho W de la etiqueta rectangular. Así que el área de la etiqueta se puede representar como
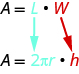
Para encontrar la superficie total del cilindro, agregamos las áreas de los dos círculos al área del rectángulo.
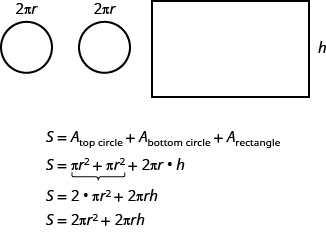
La superficie de un cilindro con radio r y altura h, es
\[S = 2 \pi r^{2} + 2 \pi rh \tag{9.6.16}\]
Para un cilindro con radio r y altura h:
Un cilindro tiene altura 5 centímetros y radio 3 centímetros. Encontrar el (a) volumen y (b) área de superficie.
Solución
| Paso 1. Lee el problema. Dibuja la figura y etiquétalo con la información dada. |  |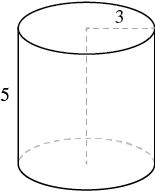
(a)
| Paso 2. Identifica lo que buscas. | el volumen del cilindro |
| Paso 3. Nombre. Elija una variable para representarla. | let V = volumen |
| Paso 4. Traducir. Escriba la fórmula apropiada. Sustituto. (Use 3.14 para\(\pi\)) | $$\ begin {split} V &=\ pi r^ {2} h\\ V &\ aprox (3.14) 3^ {2}\ cdot 5\ end {split} $$ |
| Paso 5. Resolver. | $$V\ aprox 141.3\ tag {9.6.17} $$ |
| Paso 6. Cheque. | Te dejamos que compruebes tus cálculos. |
| Paso 7. Contesta la pregunta. | El volumen es de aproximadamente 141.3 pulgadas cúbicas. |
b)
| Paso 2. Identifica lo que buscas. | la superficie del cilindro |
| Paso 3. Nombre. Elija una variable para representarla. | let S = superficie |
| Paso 4. Traducir. Escriba la fórmula apropiada. | $$\ begin {split} S &= 2\ pi r^ {2} + 2\ pi rh\\ S &\ aprox 2 (3.14) 3^ {2} + 2 (3.14) (3) 5\ end {split} $$ |
| Paso 5. Resolver. | $$S\ approx 150.72\ tag {9.6.18} $$ |
| Paso 6. Cheque. | Te dejamos que compruebes tus cálculos. |
| Paso 7. Contesta la pregunta. | El área de superficie es de aproximadamente 150.72 pulgadas cuadradas. |
Encuentra el (a) volumen y (b) superficie del cilindro con radio 4 cm y altura 7 cm.
- Contestar a
-
351.68 cu. cm
- Respuesta b
-
276.32 pies cuadrados
Encuentre el (a) volumen y (b) área de superficie del cilindro con un radio dado de 2 pies y una altura de 8 pies.
- Contestar a
-
100.48 pies cúbicos
- Respuesta b
-
125.6 pies cuadrados
Encontrar el (a) volumen y (b) superficie de una lata de refresco. El radio de la base es de 4 centímetros y la altura es de 13 centímetros. Supongamos que la lata tiene exactamente la forma de un cilindro.
Solución
| Paso 1. Lee el problema. Dibuja la figura y etiquétalo con la información dada. |  |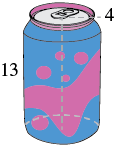
(a)
| Paso 2. Identifica lo que buscas. | el volumen del cilindro |
| Paso 3. Nombre. Elija una variable para representarla. | let V = volumen |
| Paso 4. Traducir. Escriba la fórmula apropiada. Sustituto. (Use 3.14 para\(\pi\)) | $$\ begin {split} V &=\ pi r^ {2} h\\ V &\ aprox (3.14) 4^ {2}\ cdot 13\ end {split} $$ |
| Paso 5. Resolver. | $$V\ aprox 653.12\ tag {9.6.19} $$ |
| Paso 6. Cheque. | Te lo dejamos a ti para que lo compruebes. |
| Paso 7. Contesta la pregunta. | El volumen es de aproximadamente 653.12 centímetros cúbicos. |
b)
| Paso 2. Identifica lo que buscas. | la superficie del cilindro |
| Paso 3. Nombre. Elija una variable para representarla. | let S = superficie |
| Paso 4. Traducir. Escriba la fórmula apropiada. | $$\ begin {split} S &= 2\ pi r^ {2} + 2\ pi rh\\ S &\ aprox 2 (3.14) 4^ {2} + 2 (3.14) (4) 13\ end {split} $$ |
| Paso 5. Resolver. | $$S\ approx 427.04\ tag {9.6.20} $$ |
| Paso 6. Cheque. | Te dejamos que compruebes tus cálculos. |
| Paso 7. Contesta la pregunta. | La superficie es de aproximadamente 427.04 centímetros cuadrados. |
Encuentra el (a) volumen y (b) superficie de una lata de pintura con radio 8 centímetros y altura 19 centímetros. Supongamos que la lata tiene exactamente la forma de un cilindro.
- Contestar a
-
3,818.24 cm cu. cm
- Respuesta b
-
1,356.48 cm cuadrados
Encuentre el (a) volumen y (b) área de superficie de un tambor cilíndrico con radio 2.7 pies y altura 4 pies. Supongamos que el tambor tiene la forma exacta de un cilindro.
- Contestar a
-
91.5624 pies cúbicos
- Respuesta b
-
113.6052 pies cuadrados
Encuentra el Volumen de Conos
La primera imagen que muchos de nosotros tenemos cuando escuchamos la palabra 'cono' es un cono de helado. Hay muchas otras aplicaciones de los conos (pero la mayoría no son tan sabrosos como los conos de helado). En esta sección, veremos cómo encontrar el volumen de un cono.
En geometría, un cono es una figura sólida con una base circular y un vértice. La altura de un cono es la distancia entre su base y el vértice.Los conos que veremos en esta sección siempre tendrán la altura perpendicular a la base. Ver Figura\(\PageIndex{8}\).
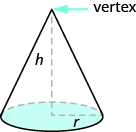
Figura\(\PageIndex{8}\) - La altura de un cono es la distancia entre su base y el vértice.
Anteriormente en esta sección, vimos que el volumen de un cilindro es de V =\(\pi\) r 2 h Podemos pensar en un cono como parte de un cilindro. La figura\(\PageIndex{9}\) muestra un cono colocado dentro de un cilindro con la misma altura y la misma base. Si comparamos el volumen del cono y el cilindro, podemos ver que el volumen del cono es menor que el del cilindro.
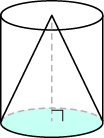
Figura\(\PageIndex{9}\) - El volumen de un cono es menor que el volumen de un cilindro con la misma base y altura.
De hecho, el volumen de un cono es exactamente un tercio del volumen de un cilindro con la misma base y altura. El volumen de un cono es
\[V = \dfrac{1}{3} \textcolor{blue}{B} h \tag{9.6.21}\]
Dado que la base de un cono es un círculo, podemos sustituir la fórmula de área de un círculo,\(\pi\) r 2, por B para obtener la fórmula para volumen de un cono.
\[V = \dfrac{1}{3} \textcolor{blue}{\pi r^{2}} h \tag{9.6.22}\]
En este libro, solo encontraremos el volumen de un cono, y no su superficie.
Para un cono con radio r y altura h.
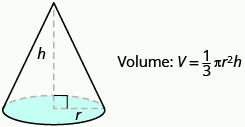
Encuentra el volumen de un cono con altura 6 pulgadas y radio de su base 2 pulgadas.
Solución
| Paso 1. Lee el problema. Dibuja la figura y etiquétalo con la información dada. |  |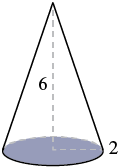
| Paso 2. Identifica lo que buscas. | el volumen del cono |
| Paso 3. Nombre. Elija una variable para representarla. | let V = volumen |
| Paso 4. Traducir. Escriba la fórmula apropiada. Sustituto. (Use 3.14 para\(\pi\)) | $$\ begin {split} V &=\ dfrac {1} {3}\ pi r^ {2} h\\ V &\ approx\ dfrac {1} {3} (3.14) (2) ^ {2} (6)\ end {split} $$ |
| Paso 5. Resolver. | $$V\ aprox. 25.12\ tag {9.6.23} $$ |
| Paso 6. Cheque. | Te dejamos que compruebes tus cálculos. |
| Paso 7. Contesta la pregunta. | El volumen es de aproximadamente 25.12 pulgadas cúbicas. |
Encuentra el volumen de un cono con altura 7 pulgadas y radio 3 pulgadas
- Contestar
-
65.94 cu. in.
Encuentra el volumen de un cono con altura 9 centímetros y radio 5 centímetros
- Contestar
-
235.5 cu. cm
El gastro pub favorito de Marty sirve papas fritas en una envoltura de papel con forma de cono. ¿Cuál es el volumen de una envoltura cónica que mide 8 pulgadas de alto y 5 pulgadas de diámetro? Redondear la respuesta a la centésima más cercana.
Solución
| Paso 1. Lee el problema. Dibuja la figura y etiquétalo con la información dada. |  |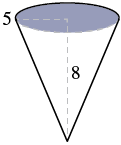
| Paso 2. Identifica lo que buscas. | el volumen del cono |
| Paso 3. Nombre. Elija una variable para representarla. | let V = volumen |
| Paso 4. Traducir. Escriba la fórmula apropiada. Sustituto. (Use 3.14 para\(\pi\), y observe que nos dieron la distancia a través del círculo, que es su diámetro. El radio es de 2.5 pulgadas.) | $$\ begin {split} V &=\ dfrac {1} {3}\ pi r^ {2} h\\ V &\ approx\ dfrac {1} {3} (3.14) (2.5) ^ {2} (8)\ end {split} $$ |
| Paso 5. Resolver. | $$V\ aprox 52.33\ tag {9.6.24} $$ |
| Paso 6. Cheque. | Te dejamos que compruebes tus cálculos. |
| Paso 7. Contesta la pregunta. | El volumen de la envoltura es de aproximadamente 52.33 pulgadas cúbicas. |
¿Cuántas pulgadas cúbicas de dulces caben en una piñata en forma de cono que mide 18 pulgadas de largo y 12 pulgadas en su base? Redondear la respuesta a la centésima más cercana.
- Contestar
-
678.24 cu. in.
¿Cuál es el volumen de un sombrero de fiesta en forma de cono que mide 10 pulgadas de alto y 7 pulgadas de ancho en la base? Redondear la respuesta a la centésima más cercana.
- Contestar
-
128.2 cu. in.
Resumen de fórmulas de geometría
En las siguientes gráficas se resumen todas las fórmulas que se tratan en este capítulo.
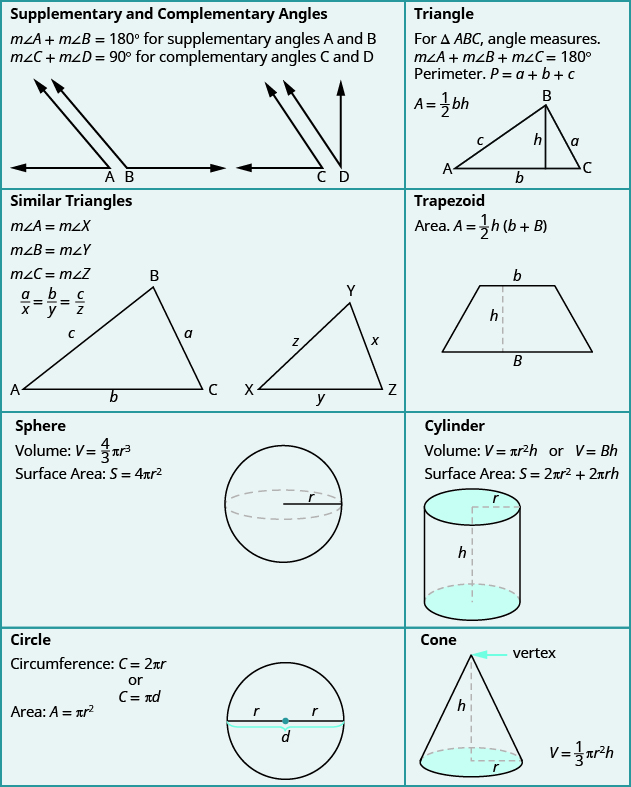
La práctica hace la perfección
Buscar volumen y área de superficie de sólidos rectangulares
En los siguientes ejercicios, encuentra (a) el volumen y (b) la superficie del sólido rectangular con las dimensiones dadas.
- largo 2 metros, ancho 1.5 metros, alto 3 metros
- largo 5 pies, ancho 8 pies, alto 2.5 pies
- largo 3.5 yardas, ancho 2.1 yardas, alto 2.4 yardas
- largo 8.8 centímetros, ancho 6.5 centímetros, alto 4.2 centímetros
En los siguientes ejercicios, resuelve.
- Camioneta para mudanzas Una camioneta móvil rectangular tiene una longitud de 16 pies, un ancho de 8 pies y una altura de 8 pies. Encontrar su (a) volumen y (b) superficie.
- Caja para regalo Una caja de regalo rectangular tiene 26 pulgadas de largo, 16 pulgadas de ancho y 4 pulgadas de alto. Encontrar su (a) volumen y (b) superficie.
- Caja Una caja rectangular tiene longitud 21.3 cm, ancho 24.2 cm y alto 6.5 cm. Encontrar su (a) volumen y (b) superficie.
- Contenedor de envío Un contenedor de envío rectangular tiene una longitud de 22.8 pies, un ancho de 8.5 pies y una altura de 8.2 pies. Encontrar su (a) volumen y (b) superficie.
En los siguientes ejercicios, encuentra (a) el volumen y (b) la superficie del cubo con la longitud lateral dada.
- 5 centímetros
- 6 pulgadas
- 10.4 pies
- 12.5 metros
En los siguientes ejercicios, resuelve.
- Centro de ciencias Cada lado del cubo en el Discovery Science Center en Santa Ana mide 64 pies de largo. Encontrar su (a) volumen y (b) superficie.
- Museo Un museo en forma de cubo tiene lados de 45 metros de largo. Encontrar su (a) volumen y (b) superficie.
- Base de estatua La base de una estatua es un cubo con lados de 2.8 metros de largo. Encontrar su (a) volumen y (b) superficie.
- Caja de pañuelos Una caja de pañuelos es un cubo con lados de 4.5 pulgadas de largo. Encontrar su (a) volumen y (b) superficie.
Encuentra el volumen y la superficie de las esferas
En los siguientes ejercicios, encuentra (a) el volumen y (b) la superficie de la esfera con el radio dado. Respuestas redondas a la centésima más cercana.
- 3 centímetros
- 9 pulgadas
- 7.5 pies
- 2.1 yardas
En los siguientes ejercicios, resuelve. Respuestas redondas a la centésima más cercana.
- Balón de ejercicio Una pelota de ejercicio tiene un radio de 15 pulgadas. Encontrar su (a) volumen y (b) superficie.
- Paseo en globo El Great Park Balloon es una gran esfera naranja con un radio de 36 pies. Encontrar su (a) volumen y (b) superficie.
- Pelota de golf Una pelota de golf tiene un radio de 4.5 centímetros. Encontrar su (a) volumen y (b) superficie.
- Béisbol Un beisbol tiene un radio de 2.9 pulgadas. Encontrar su (a) volumen y (b) superficie.
Encontrar el volumen y el área de superficie de un cilindro
En los siguientes ejercicios, encuentra (a) el volumen y (b) la superficie del cilindro con el radio y la altura dados. Respuestas redondas a la centésima más cercana.
- radio 3 pies, altura 9 pies
- radio 5 centímetros, altura 15 centímetros
- radio 1.5 metros, altura 4.2 metros
- radio 1.3 yardas, altura 2.8 yardas
En los siguientes ejercicios, resuelve. Respuestas redondas a la centésima más cercana.
- Lata de café Una lata de café tiene un radio de 5 cm y una altura de 13 cm. Encontrar su (a) volumen y (b) superficie.
- Paquete de refrigerios Un paquete de galletas para refrigerios tiene la forma de un cilindro con radio de 4 cm y altura de 3 cm. Encontrar su (a) volumen y (b) superficie.
- Poste de peluquería Un poste cilíndrico de peluquería tiene un diámetro de 6 pulgadas y una altura de 24 pulgadas. Encontrar su (a) volumen y (b) superficie.
- Arquitectura Una columna cilíndrica tiene un diámetro de 8 pies y una altura de 28 pies. Encontrar su (a) volumen y (b) superficie.
Encuentra el Volumen de Conos
En los siguientes ejercicios, encuentra el volumen del cono con las dimensiones dadas. Respuestas redondas a la centésima más cercana.
- altura 9 pies y radio 2 pies
- altura 8 pulgadas y radio 6 pulgadas
- altura 12.4 centímetros y radio 5 cm
- altura 15.2 metros y radio 4 metros
En los siguientes ejercicios, resuelve. Respuestas redondas a la centésima más cercana.
- Tipi ¿Cuál es el volumen de una tienda tipi en forma de cono que mide 10 pies de alto y 10 pies de ancho en la base?
- Taza de palomitas de maíz ¿Cuál es el volumen de una taza de palomitas de maíz en forma de cono que mide 8 pulgadas de alto y 6 pulgadas de ancho en la base?
- Silo ¿Cuál es el volumen de un silo en forma de cono que mide 50 pies de alto y 70 pies de ancho en la base?
- Pila de arena ¿Cuál es el volumen de una pila de arena en forma de cono que mide 12 metros de altura y 30 metros de ancho en la base?
Matemáticas cotidianas
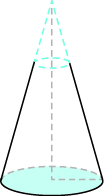
- Poste farola El poste de una farola tiene forma de cono truncado, como se muestra en la imagen de abajo. Es un cono grande menos un cono superior más pequeño. El cono grande mide 30 pies de alto con un radio de base de 1 pie. El cono más pequeño mide 10 pies de alto con un radio de base de 0.5 pies. Al décimo más cercano, (a) encuentra el volumen del cono grande. (b) encontrar el volumen del cono pequeño. (c) encontrar el volumen del poste restando el volumen del cono pequeño del volumen del cono grande.
- Conos de helado Un cono de helado regular mide 4 pulgadas de alto y tiene un diámetro de 2.5 pulgadas. Un cono de gofre mide 7 pulgadas de alto y tiene un diámetro de 3.25 pulgadas. A la centésima más cercana, (a) encuentra el volumen del cono de helado regular. (b) encontrar el volumen del cono de gofre. (c) ¿cuánto más helado cabe en el cono de gofre en comparación con el cono regular?
Ejercicios de escritura
- Las fórmulas para el volumen de un cilindro y un cono son similares. Explica cómo puedes recordar qué fórmula va con qué forma.
- ¿Cuál tiene un volumen mayor, un cubo de lados de 8 pies o una esfera con un diámetro de 8 pies? Explica tu razonamiento.
Autocomprobación
(a) Después de completar los ejercicios, utilice esta lista de verificación para evaluar su dominio de los objetivos de esta sección.
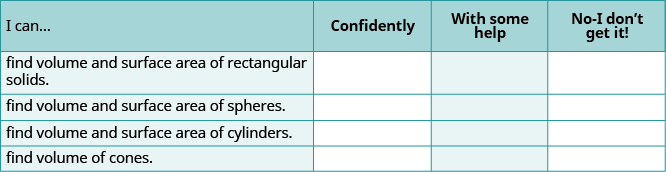
(b) Después de revisar esta lista de verificación, ¿qué hará para confiar en todos los objetivos?