10.9: Exponentes enteros y notación científica (Parte 2)
- Page ID
- 114281
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Convertir de notación decimal a notación científica
¿Recuerdas trabajar con valor posicional para números enteros y decimales? Nuestro sistema de números se basa en potencias de 10. Usamos decenas, cientos, miles, y así sucesivamente. Nuestros números decimales también se basan en potencias de diez, décimas, centésimas, milésimas, etc.
Considera los números 4000 y 0.004. Sabemos que 4000 significa 4 × 1000 y 0.004 significa 4 ×\(\dfrac{1}{1000}\). Si escribimos el 1000 como una potencia de diez en forma exponencial, podemos reescribir estos números de esta manera:
\[\begin{split} &4000 \qquad \qquad 0.004 \\ &4 \times 1000 \qquad 4 \times \dfrac{1}{1000} \\ &4 \times 10^{3} \qquad \; \; 4 \times \dfrac{1}{10^{3}} \\ &\qquad \qquad \quad \; \; \; 4 \times 10^{-3} \end{split}\]
Cuando un número se escribe como producto de dos números, donde el primer factor es un número mayor o igual a uno pero menor que 10, y el segundo factor es una potencia de 10 escrita en forma exponencial, se dice que está en notación científica.
Un número se expresa en notación científica cuando es de la forma a × 10 n donde a ≥ 1 y a < 10 y n es un número entero.
Es costumbre en la notación científica usar × como signo de multiplicación, aunque evitemos usar este signo en otra parte del álgebra.
La notación científica es una forma útil de escribir números muy grandes o muy pequeños. Se utiliza a menudo en las ciencias para facilitar los cálculos.
Si miramos lo que pasó con el punto decimal, podemos ver un método para convertir fácilmente de la notación decimal a la notación científica.
En ambos casos, el decimal se movió 3 lugares para obtener el primer factor, 4, por sí mismo.
- La potencia de 10 es positiva cuando el número es mayor a 1:4000 = 4 × 10 3.
- La potencia de 10 es negativa cuando el número está entre 0 y 1:0.004 = 4 × 10 −3.
Escribir 37,000 en notación científica.
Solución
| Paso 1: Mueve el punto decimal para que el primer factor sea mayor o igual a 1 pero menor que 10. |  |
| Paso 2: Contar el número de decimales, n, que se movió el punto decimal. |
3.70000 4 lugares |
| Paso 3: Escribe el número como un producto con una potencia de 10. | 3.7×10 4 |
|
Si el número original es:
|
|
| Paso 4: Verificar.10 4 es 10,000 y 10,000 veces 3.7 serán 37 mil. | 37.000 = 3.7×10 4 |
Escribir en notación científica: 96,000.
- Responder
-
9.6 × 10 4
Escribir en notación científica: 48,300.
- Responder
-
4.83 × 10 4
Paso 1. Mueva el punto decimal para que el primer factor sea mayor o igual a 1 pero menor que 10.
Paso 2. Contar el número de decimales, n, que se movió el punto decimal.
Paso 3. Escribe el número como un producto con una potencia de 10.
Si el número original es:
- mayor que 1, la potencia de 10 será de 10 n.
- entre 0 y 1, la potencia de 10 será de 10 −n.
Paso 4. Cheque.
Escribir en notación científica: 0.0052.
Solución
| Mueve el punto decimal para obtener 5.2, un número entre 1 y 10. |  |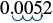
| Contar el número de decimales que se movió el punto. | 3 lugares |
| Escribir como un producto con una potencia de 10. | 5.2 × 10 −3 |
| Consulta tu respuesta: | $$\ begin {split} 5.2 &\ times 10^ {-3}\\ 5.2 &\ veces\ dfrac {1} {10^ {3}}\\ 5.2 &\ veces\ dfrac {1} {1000}\\ 5.2 &\ veces 0.001\\ 0. &0052\ fin {split} $$ |
| 0.0052 = 5.2 × 10 −3 |
Escribir en notación científica: 0.0078.
- Responder
-
7.8 × 10 -3
Escribir en notación científica: 0.0129.
- Responder
-
1.29 × 10 -2
Convertir Notación Científica a Forma Decimal
¿Cómo podemos convertir de notación científica a forma decimal? Veamos dos números escritos en notación científica y veamos.
\[\begin{split} &9.12 \times 10^{4} \qquad \qquad 9.12 \times 10^{-4} \\ &9.12 \times 10,000 \qquad 9.12 \times 0.0001 \\ &91,200 \qquad \qquad \quad 0.000912 \end{split}\]
Si miramos la ubicación del punto decimal, podemos ver un método fácil para convertir un número de notación científica a forma decimal.
En ambos casos el punto decimal se movió 4 lugares. Cuando el exponente era positivo, el decimal se movía hacia la derecha. Cuando el exponente era negativo, el punto decimal se movía hacia la izquierda.
Convertir a forma decimal: 6.2 × 10 3.
Solución
| Paso 1: Determinar el exponente, n, sobre el factor 10. | 6.2 × 10 3 |
| Paso 2: Mueva el punto decimal n lugares, agregando ceros si es necesario. |  |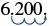
|
6,200 |
| Paso 3: Comprueba si tu respuesta tiene sentido. | |
| 10 3 es 1000 y 1000 veces 6.2 serán 6,200. | 6.2 × 10 3 = 6,200 |
Convertir a forma decimal: 1.3 × 10 3.
- Responder
-
1,300
Convertir a forma decimal: 9.25 × 10 4.
- Responder
-
92,500
Paso 1. Determinar el exponente, n, sobre el factor 10.
Paso 2. Mueva los decimales n lugares, agregando ceros si es necesario.
- Si el exponente es positivo, mueva el punto decimal n lugares hacia la derecha.
- Si el exponente es negativo, mueva el punto decimal |n| lugares hacia la izquierda.
Paso 3. Cheque.
Convertir a forma decimal: 8.9 × 10 −2.
Solución
| Determinar el exponente n, sobre el factor 10. | El exponente es −2. |
| Mueve el punto decimal 2 lugares hacia la izquierda. |  |
| Agregue ceros según sea necesario para los marcadores de posición. | 0.089 |
| 8.9 × 10 −2 = 0.089 | |
| El Cheque se te deja a ti. |
Convertir a forma decimal: 1.2 × 10 −4.
- Responder
-
0.00012
Convertir a forma decimal: 7.5 × 10 −2.
- Responder
-
0.075
Multiplicar y dividir usando notación científica
Utilizamos las Propiedades de los Exponentes para multiplicar y dividir números en notación científica.
Multiplicar. Escribe las respuestas en forma decimal: (4 × 10 5) (2 × 10 −7).
Solución
| Utilice la Propiedad Conmutativa para reorganizar los factores. | 4 • 2 • 10 5 • 10 −7 |
| Multiplica 4 por 2 y usa la Propiedad del Producto para multiplicar 10 5 por 10 −7. | 8 × 10 −2 |
| Cambiar a forma decimal moviendo los decimales dos lugares a la izquierda. | 0.08 |
Multiplicar. Escribe las respuestas en forma decimal: (3 × 10 6) (2 × 10 −8).
- Responder
-
0.06
Multiplicar. Escribe las respuestas en forma decimal: (3 × 10 −2) (3 × 10 −1).
- Responder
-
0.009
Dividir. Escribir respuestas en forma decimal:\(\dfrac{9 \times 10^{3}}{3 \times 10^{−2}}\).
Solución
| Separar los factores. | $$\ dfrac {9} {3}\ veces\ dfrac {10^ {3}} {10^ {-2}} $$ |
| Divide 9 por 3 y usa la Propiedad Cociente para dividir 10 3 por 10 −2. | 3 × 10 5 |
| Cambie a la forma decimal moviendo los cinco lugares decimales a la derecha. | 300,000 |
Dividir. Escribe las respuestas en decimal para m:\dfrac {8\ times 10^ {4}} {2\ times 10^ {-1}}.
- Responder
-
400,000
Dividir. Escribe las respuestas en decimal para m:\dfrac {8\ times 10^ {2}} {4\ times 10^ {-2}}.
- Responder
-
20,000
La práctica hace la perfección
Usar la definición de un exponente negativo
En los siguientes ejercicios, simplifique.
- 5 −3
- 8 −2
- 3 −4
- 2 −5
- 7 −1
- 10 −1
- 2 −3 + 2 −2
- 3 −2 + 3 −1
- 3 −1 + 4 −1
- 10 −1 + 2 −1
- 10 0 − 10 −1 + 10 −2
- 2 0 − 2 −1 + 2 −2
- (a) (−6) −2 (b) −6 −2
- (a) (−8) −2 (b) −8 −2
- (a) (−10) −4 (b) −10 −4
- (a) (−4) −6 (b) −4 −6
- (a) 5 • 2 −1 (b) (5 • 2) −1
- (a) 10 • 3 −1 (b) (10 • 3) −1
- (a) 4 • 10 −3 (b) (4 • 10) −3
- (a) 3 • 5 −2 (b) (3 • 5) −2
- n −4
- p −3
- c −10
- m −5
- (a) 4x −1 (b) (4x) −1 (c) (−4x) −1
- (a) 3q −1 (b) (3q) −1 (c) (−3q) −1
- (a) 6m −1 (b) (6m) −1 (c) (−6m) −1
- (a) 10k −1 (b) (10k) −1 (c) (−10k) −1
Simplificar expresiones con exponentes enteros
En los siguientes ejercicios, simplifique.
- p −4 • p 8
- r −2 • r 5
- n −10 • n 2
- q −8 • q 3
- k −3 • k −2
- z −6 • z −2
- a • a −4
- m • m −2
- p 5 • p −2 • p −4
- x 4 • x −2 • x −3
- a 3 b −3
- u 2 v −2
- (x 5 y −1) (x −10 y −3)
- (a 3 b −3) (a −5 b −1)
- (uv −2) (u −5 v −4)
- (pq −4) (p −6 q −3)
- (−2r −3 s 9) (6r 4 s −5)
- (−3p −5 q 8) (7p 2 q −3)
- (−6m −8 n −5) (−9m 4 n 2)
- (−8a −5 b −4) (−4a 2 b 3)
- (a 3) −3
- (q 10) −10
- (n 2) −1
- (x 4) −1
- (y −5) 4
- (p −3) 2
- (q −5) −2
- (m −2) −3
- (4y −3) 2
- (3q −5) 2
- (10p −2) −5
- (2n −3) −6
- u 9 u −2
- b 5 b −3
- x −6 x 4
- m 5 m −2
- q 3 q 12
- r 6 r 9
- n −4 n −10
- p −3 p −6
Convertir de notación decimal a notación científica
En los siguientes ejercicios, escriba cada número en notación científica.
- 45,000
- 280.000
- 8,750,000
- 1,290,000
- 0.036
- 0.041
- 0.00000924
- 0.0000103
- La población de Estados Unidos al 4 de julio de 2010 era de casi 310 mil millones.
- La población del mundo al 4 de julio de 2010 era de más de 6 mil 850 millones.
- El ancho promedio de un cabello humano es de 0.0018 centímetros.
- La probabilidad de ganar la lotería Megamillions 2010 es de aproximadamente 0.0000000057.
Convertir Notación Científica a Forma Decimal
En los siguientes ejercicios, convierte cada número a forma decimal.
- 4.1 × 10 2
- 8.3 × 10 2
- 5.5 × 10 8
- 1.6 × 10 10
- 3.5 × 10 −2
- 2.8 × 10 −2
- 1.93 × 10−5
- 6.15 × 10−8
- En 2010, el número de usuarios de Facebook cada día que cambiaban su estado a 'comprometidos' era de 2 × 10 4.
- Al inicio de 2012, el presupuesto federal estadounidense tenía un déficit de más de 1.5 × 10 13 dólares.
- La concentración de dióxido de carbono en la atmósfera es 3.9 × 10 −4.
- El ancho de un protón es de 1 × 10 −5 del ancho de un átomo.
Multiplicar y dividir usando notación científica
En los siguientes ejercicios, multiplica o divide y escribe tu respuesta en forma decimal.
- (2 × 10 5) (2 × 10 −9)
- (3 × 10 2) (1 × 10 −5)
- (1.6 × 10 −2) (5.2 × 10 −6)
- (2.1 × 10 −4) (3.5 × 10 −2)
- \(\dfrac{6 \times 10^{4}}{3 \times 10^{−2}}\)
- \(\dfrac{8 \times 10^{6}}{4 \times 10^{−1}}\)
- \(\dfrac{7 \times 10^{-2}}{1 \times 10^{−8}}\)
- \(\dfrac{5 \times 10^{-3}}{1 \times 10^{−10}}\)
Matemáticas cotidianas
- Calorías En mayo de 2010 los Fabricantes de Alimentos y Bebidas se comprometieron a reducir sus productos en 1.5 billones de calorías para finales de 2015.
- Escribe 1.5 billones en notación decimal.
- Escribe 1.5 billones en notación científica.
- Duración de un año La diferencia entre el año calendario y el año astronómico es de 0.000125 días.
- Escribe este número en notación científica.
- ¿Cuántos años tarda la diferencia en llegar a ser 1 día?
- Visualización de la calculadora Muchas calculadoras muestran automáticamente las respuestas en notación científica si hay más dígitos de los que caben en la pantalla de la calculadora. Para encontrar la probabilidad de obtener una mano particular de 5 cartas de una baraja de cartas, Mario dividió 1 por 2,598,960 y vio la respuesta 3.848 × 10 −7. Escribe el número en notación decimal.
- Visualización de la calculadora Muchas calculadoras muestran automáticamente las respuestas en notación científica si hay más dígitos de los que caben en la pantalla de la calculadora. Para encontrar la cantidad de formas en que Barbara podría hacer un collage con 6 de sus 50 fotografías favoritas, multiplicó 50 • 49 • 48 • 47 • 46 • 45. Su calculadora dio la respuesta 1.1441304 × 10 10. Escribe el número en notación decimal.
Ejercicios de escritura
- (a) Explicar el significado del exponente en la expresión 2 3. (b) Explicar el significado del exponente en la expresión 2 −3.
- Cuando conviertes un número de notación decimal a notación científica, ¿cómo sabes si el exponente será positivo o negativo?
Autocomprobación
(a) Después de completar los ejercicios, utilice esta lista de verificación para evaluar su dominio de los objetivos de esta sección.
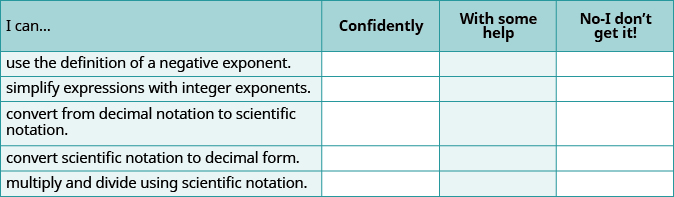
(b) Después de mirar la lista de verificación, ¿cree que está bien preparado para la siguiente sección? ¿Por qué o por qué no?