Saltar al contenido principal
LibreTexts Español

11.1: Usar el Sistema de Coordenadas Rectangulares (Parte 1)

  1. Última actualización
  2. Guardar como PDF
  • Page ID
    114231

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

    Objetivos de aprendizaje
    • Trazar puntos en un sistema de coordenadas rectangulares
    • Identificar puntos en una gráfica
    • Verificar soluciones a una ecuación en dos variables
    • Completar una tabla de soluciones a una ecuación lineal
    • Encontrar soluciones a ecuaciones lineales en dos variables
    ¡prepárate!

    Antes de comenzar, toma este cuestionario de preparación.

    1. Evaluar: x + 3 cuando x = −1. Si te perdiste este problema, revisa el Ejemplo 3.4.10.
    2. Evaluar: 2x − 5y cuando x = 3, y = −2. Si te perdiste este problema, revisa Ejemplo 3.8.106.
    3. Resolver para y: 40 − 4y = 20. Si te perdiste este problema, revisa el Ejemplo 8.4.1.

    Trazar puntos en un sistema de coordenadas rectangulares

    Muchos mapas, como el Mapa del Campus que se muestra en la Figura\(\PageIndex{1}\), utilizan un sistema de cuadrícula para identificar ubicaciones. ¿Ves los números 1, 2, 3 y 4 en la parte superior e inferior del mapa y las letras A, B, C y D a lo largo de los lados? Cada ubicación en el mapa puede ser identificada por un número y una letra.

    Por ejemplo, el Centro Estudiantil se encuentra en la sección 2B. Se encuentra en la sección de cuadrícula por encima del número 2 y junto a la letra B. ¿En qué sección de cuadrícula se encuentra el Estadio? El Estadio se encuentra en la sección 4D.

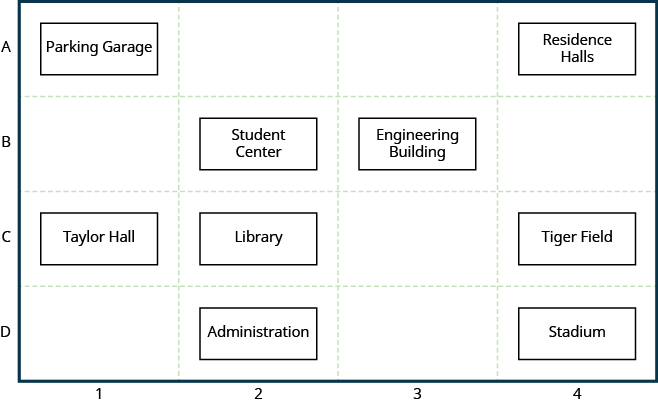
    La figura muestra una cuadrícula etiquetada que representa el Mapa del Campus. Las columnas están etiquetadas del 1 al 4 y las filas están etiquetadas de la A a la D. En la posición A-1 se encuentra el título Garaje de Estacionamiento. En la posición A-4 hay un rectángulo etiquetado como Residencias. En la posición B-2 hay un rectángulo etiquetado como Centro Estudiantil. En la posición B-3 hay un rectángulo etiquetado como Edificio de Ingeniería. En la posición C-1 hay un rectángulo etiquetado como Taylor Hall. En la posición C-2 hay un rectángulo etiquetado Biblioteca. En la posición C-4 hay un rectángulo etiquetado como Campo de Tigre. En la posición D-4 hay un rectángulo etiquetado como Estadio.

    Figura\(\PageIndex{1}\)

    Ejemplo\(\PageIndex{1}\):

    Utilice el mapa de la Figura\(\PageIndex{1}\). (a) Encuentra la sección de cuadrícula de las Residencias. (b) ¿Qué se encuentra en la sección de cuadrícula 4C?

    Solución

    (a) Lea el número debajo de las Residencias Residenciales, 4, y la letra al costado, A. Así que las Residencias Residenciales están en la cuadrícula sección 4A.

    (b) Encuentra 4 en la parte inferior del mapa y C a lo largo del costado. Mira debajo del 4 y al lado del C. Tiger Field está en la cuadrícula sección 4C.

    Ejercicio\(\PageIndex{1}\):

    Utilice el mapa de la Figura\(\PageIndex{1}\). (a) Encuentra la sección de cuadrícula de Taylor Hall. b) ¿Qué se encuentra en la fracción 3B?

    Responder a

    1C

    Respuesta b

    Edificio de Ingeniería

    Ejercicio\(\PageIndex{1}\):

    Utilice el mapa de la Figura\(\PageIndex{1}\). (a) Encuentra la sección de rejilla del Garaje de Estacionamiento. b) ¿Qué se encuentra en la sección 2C?

    Responder a

    1A

    Respuesta b

    Biblioteca

    Así como los mapas utilizan un sistema de cuadrícula para identificar ubicaciones, un sistema de cuadrícula se usa en álgebra para mostrar una relación entre dos variables en un sistema de coordenadas rectangular. Para crear un sistema de coordenadas rectangulares, comience con una recta numérica horizontal. Muestre tanto los números positivos como los negativos como lo hizo antes, usando una cómoda unidad de escala. Esta línea numérica horizontal se llama eje x.

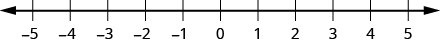
    La figura muestra una línea numérica con valores enteros etiquetados de -5 a 5.

    Ahora, haga una recta numérica vertical que pase por el eje x en 0. Ponga los números positivos por encima de 0 y los negativos por debajo de 0. Ver Figura\(\PageIndex{2}\). Esta línea vertical se llama eje y.

    Las líneas verticales de la rejilla pasan a través de los enteros marcados en el eje x. Las líneas horizontales de la cuadrícula pasan a través de los enteros marcados en el eje y. La rejilla resultante es el sistema de coordenadas rectangulares.

    El sistema de coordenadas rectangulares también se llama plano x-y, plano de coordenadas o sistema de coordenadas cartesianas (ya que fue desarrollado por un matemático llamado René Descartes).

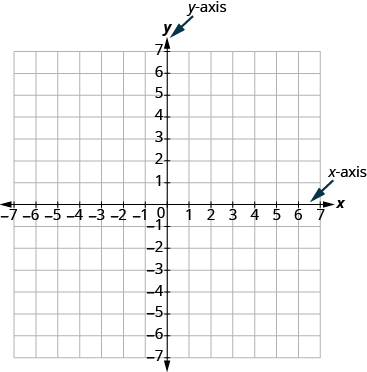
    La gráfica muestra el plano de la coordenada x y. Los ejes x e y van cada uno de -7 a 7. Una flecha apunta al eje horizontal con la etiqueta “eje x”. Una flecha apunta al eje vertical con la etiqueta “eje y”. Una flecha apunta a la intersección de los ejes con la etiqueta “origen”.

    Figura\(\PageIndex{2}\) - El sistema de coordenadas rectangulares.

    El eje x y el eje y forman el sistema de coordenadas rectangulares. Estos ejes dividen un plano en cuatro áreas, llamadas cuadrantes. Los cuadrantes se identifican por números romanos, comenzando en la parte superior derecha y avanzando en sentido antihorario. Ver Figura\(\PageIndex{3}\).

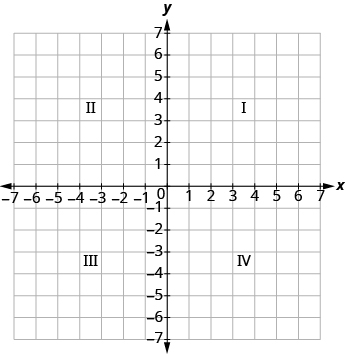
    La gráfica muestra el plano de la coordenada x y. Los ejes x e y van cada uno de -7 a 7. La parte superior derecha del plano está etiquetada como “I”, la parte superior izquierda del plano está etiquetada como “II”, la parte inferior izquierda del plano está etiquetada como “III” y la parte inferior derecha del plano está etiquetada como “IV”

    Figura\(\PageIndex{3}\) - Los cuatro cuadrantes del sistema de coordenadas rectangulares.

    En el sistema de coordenadas rectangulares, cada punto está representado por un par ordenado. El primer número del par ordenado es la coordenada x del punto, y el segundo número es la coordenada y del punto.

    Definición: Par ordenado

    Un par ordenado, (x, y) da las coordenadas de un punto en un sistema de coordenadas rectangular. El primer número es la coordenada x. El segundo número es la coordenada y.

    El par ordenado x y se etiqueta con la primera coordenada x etiquetada como “coordenada x” y la segunda coordenada y etiquetada como “coordenada y”

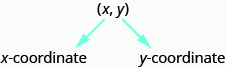
    Entonces, ¿cómo las coordenadas de un punto te ayudan a localizar un punto en el plano x-y?

    Intentemos localizar el punto (2, 5). En este par ordenado, la coordenada x es 2 y la coordenada y es 5.

    Comenzamos por ubicar el valor x, 2, en el eje x. Luego dibujamos ligeramente una línea vertical a través de x = 2, como se muestra en la Figura\(\PageIndex{4}\)

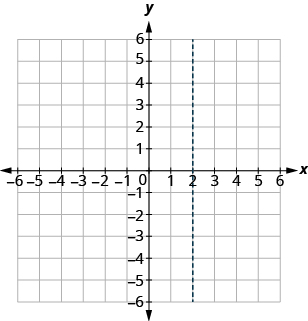
    La gráfica muestra el plano de la coordenada x y. Los ejes x e y van cada uno de -6 a 6. Hay una línea punteada vertical que pasa por 2 en el eje x.

    Figura\(\PageIndex{4}\)

    Ahora localizamos el valor y, 5, en el eje y y esbozamos una línea horizontal a través de y = 5. El punto donde se encuentran estas dos líneas es el punto con coordenadas (2, 5). Trazamos el punto ahí, como se muestra en la Figura\(\PageIndex{5}\).

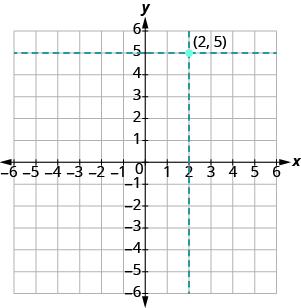
    La gráfica muestra el plano de la coordenada x y. Los ejes x e y van cada uno de -6 a 6. Una flecha comienza en el origen y se extiende hacia la derecha hasta el número 2 en el eje x. Una flecha comienza al final de la primera flecha en 2 en el eje x y va verticalmente 5 unidades a un punto etiquetado como “2, 5” entre paréntesis.

    Figura\(\PageIndex{5}\)

    Ejemplo\(\PageIndex{2}\):

    Parcela (1, 3) y (3, 1) en el mismo sistema de coordenadas rectangulares.

    Solución

    Los valores de coordenadas son los mismos para ambos puntos, pero los valores x e y se invierten. Empecemos por el punto (1, 3). La coordenada x es 1 así que encuentra 1 en el eje x y dibuja una línea vertical a través de x = 1. La coordenada y es 3 por lo que encontramos 3 en el eje y y esbozamos una línea horizontal a través de y = 3. Donde las dos líneas se encuentran, trazamos el punto (1, 3).

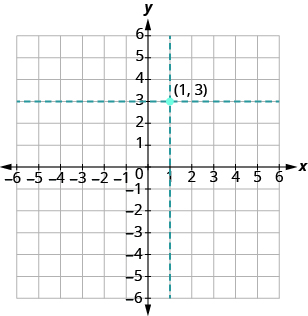
    La gráfica muestra el plano de la coordenada x y. Los ejes x e y van cada uno de -6 a 6. Una línea punteada horizontal pasa por 3 en el eje y. Una línea punteada vertical pasa por 1 en el eje x. Las líneas punteadas se cruzan en un punto etiquetado como “par ordenado 1, 3”.

    Para trazar el punto (3, 1), comenzamos por ubicar 3 en el eje x y bosquejar una línea vertical a través de x = 3. Después encontramos 1 en el eje y y bosquejamos una línea horizontal a través de y = 1. Donde las dos líneas se encuentran, trazamos el punto (3, 1).

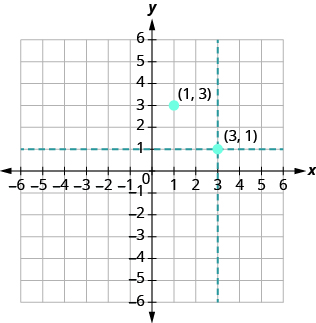
    La gráfica muestra el plano de la coordenada x y. Los ejes x e y van cada uno de -6 a 6. Una línea punteada horizontal pasa por 1 en el eje y. Una línea punteada vertical pasa por 3 en el eje x. La línea punteada se cruza en un punto etiquetado como “par ordenado 3, 1".

    Observe que el orden de las coordenadas sí importa, entonces, (1, 3) no es el mismo punto que (3, 1).

    Ejercicio\(\PageIndex{3}\):

    Trazar cada punto en el mismo sistema de coordenadas rectangulares: (2, 5), (5, 2).

    Responder

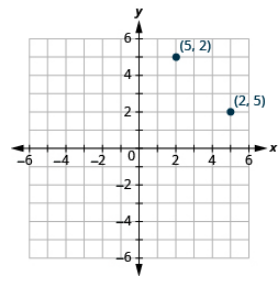
    Esta gráfica de respuesta muestra el plano de coordenadas x y. Los ejes x e y van cada uno de -6 a 6. Hay dos puntos etiquetados: el primero es par ordenado (5, 2), y el segundo es (2, 5)

    Ejercicio\(\PageIndex{4}\):

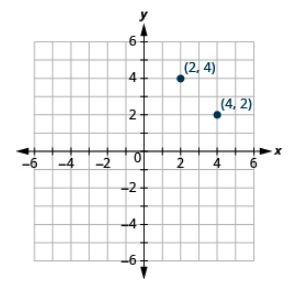
    Trazar cada punto en el mismo sistema de coordenadas rectangulares: (4, 2), (2, 4).

    Responder
    Esta gráfica de respuesta muestra el plano de coordenadas x y. Los ejes x e y van cada uno de -6 a 6. Hay dos puntos etiquetados: el primero es par ordenado (2, 4), y el segundo es (4, 2)
    Ejemplo\(\PageIndex{3}\):

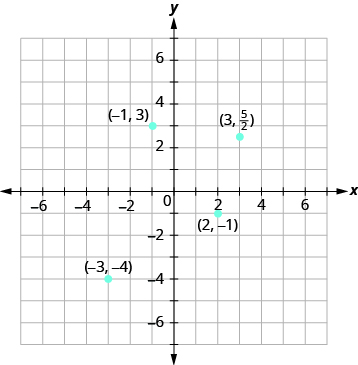
    Trazar cada punto en el sistema de coordenadas rectangulares e identificar el cuadrante en el que se encuentra el punto: (a) (−1, 3) (b) (−3, −4) (c) (2, −3) (d)\(\left(3, \dfrac{5}{2}\right)\)

    Solución

    El primer número del par de coordenadas es la coordenada x y el segundo número es la coordenada y.

    1. Dado que x = −1, y = 3, el punto (−1, 3) está en el Cuadrante II.
    2. Dado que x = −3, y = −4, el punto (−3, −4) está en el Cuadrante III.
    3. Dado que x = 2, y = −1, el punto (2, −1) está en el Cuadrante lV.
    4. Ya que x = 3, y =\(\dfrac{5}{2}\), el punto\(\left(3, \dfrac{5}{2}\right)\) está en el Cuadrante I. Puede ser útil escribir\(\dfrac{5}{2}\) como el número mixto,\(2 \dfrac{1}{2}\), o decimal, 2.5. Entonces sabemos que el punto está a medio camino entre 2 y 3 en el eje y.

    La gráfica muestra el plano de la coordenada x y. Los ejes x e y van cada uno de -7 a 7. El punto “par ordenado 3, 5 sobre 2” está etiquetado como “par ordenado “3,5 sobre 2”. El punto “par ordenado -1, 3” se etiqueta como “par ordenado -1, 3”. El punto “par ordenado -3, -4” está etiquetado como “par ordenado -3, -4”. El punto “par ordenado 2, -1” se etiqueta como “par ordenado 2, -1”.

    Ejercicio\(\PageIndex{5}\):

    Trazar cada punto en el sistema de coordenadas rectangulares e identificar el cuadrante en el que se encuentra el punto: (a) (−2, 1) (b) (−3, −1) (c) (4, −4) (d)\(\left(-4, \dfrac{3}{2}\right)\)

    Responder
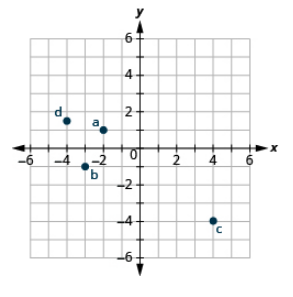
    La gráfica muestra el plano de la coordenada x y. Los ejes x e y van cada uno de -6 a 6. El punto “par ordenado -2, 1” está etiquetado como “a”. El punto “par ordenado -3, 1” se etiqueta con “b”. El punto “par ordenado 4, -4 está etiquetado como “c”. El punto “par ordenado -4, 3/2” está etiquetado como “d”.
    Ejercicio\(\PageIndex{6}\):

    Trazar cada punto en el sistema de coordenadas rectangulares e identificar el cuadrante en el que se encuentra el punto: (a) (−4, 1) (b) (−2, 3) (c) (2, −5) (d)\(\left(-3, \dfrac{5}{2}\right)\)

    Responder
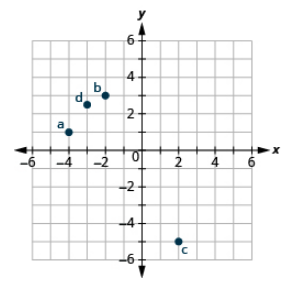
    Esta imagen es una gráfica de respuestas y muestra el plano de coordenadas x y. Los ejes x e y van cada uno de -6 a 6. El punto “par ordenado -4, 1” está etiquetado como “a”. El punto “par ordenado -2, 3” está etiquetado como “b”. El punto “par ordenado 2, -5” está etiquetado como “c”. El punto “par ordenado -3, 5/2” se etiqueta con “d”.

    ¿Cómo afectan las señales a la ubicación de los puntos?

    Ejemplo\(\PageIndex{4}\):

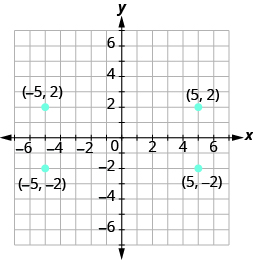
    Trazar cada punto: (a) (−5, 2) (b) (−5, −2) (c) (5, 2) (d) (5, −2)

    Solución

    Al ubicar la coordenada x y la coordenada y, debemos tener cuidado con las señales.

    La gráfica muestra el plano de la coordenada x y. Los ejes x e y van cada uno de -7 a 7. El punto “par ordenado 5, 2” está etiquetado como “par ordenado 5, 2”. El punto “par ordenado -5, 2” está etiquetado como “par ordenado -5, 2”. El punto “par ordenado -5, -2” está etiquetado como “par ordenado -5, -2”. El punto “par ordenado 5, -2” está etiquetado como “par ordenado 5, -2”.

    Ejercicio\(\PageIndex{7}\):

    Trazar cada punto: (a) (4, −3) (b) (4, 3) (c) (−4, −3) (d) (−4, 3)

    Responder
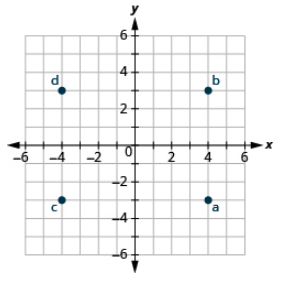
    Esta imagen es una gráfica de respuestas y muestra el plano de coordenadas x y. Los ejes x e y van cada uno de -6 a 6. El punto “par ordenado 4, -3” está etiquetado como “a”. El punto “par ordenado 4, 3” está etiquetado como “b”. El punto “par ordenado -4, -3” está etiquetado como “c”. El punto “par ordenado -4, 3” está etiquetado como “d”.
    Ejercicio\(\PageIndex{8}\):

    Trazar cada punto: (a) (−1, 4) (b) (1, 4) (c) (1, −4) (d) (−1, −4)

    Responder
    Esta imagen es una gráfica de respuestas y muestra el plano de coordenadas x y. Los ejes x e y van cada uno de -6 a 6. El punto “par ordenado -1, -4” está etiquetado como “a”. El punto “par ordenado 1, 4” está etiquetado como “b”. El punto “par ordenado 1, -4” está etiquetado como “c”. El punto “par ordenado -1, -4” se etiqueta con “d”.

    Es posible que hayas notado algunos patrones al graficar los puntos en los dos ejemplos anteriores.

    Por cada punto del Cuadrante IV, ¿qué nota de los signos de las coordenadas?

    ¿Y las señales de las coordenadas de los puntos en el tercer cuadrante? ¿El segundo cuadrante? ¿El primer cuadrante?

    ¿Se puede decir con solo mirar las coordenadas en qué cuadrante se encuentra el punto (−2, 5)? ¿En qué cuadrante se encuentra (2, −5)?

    ...

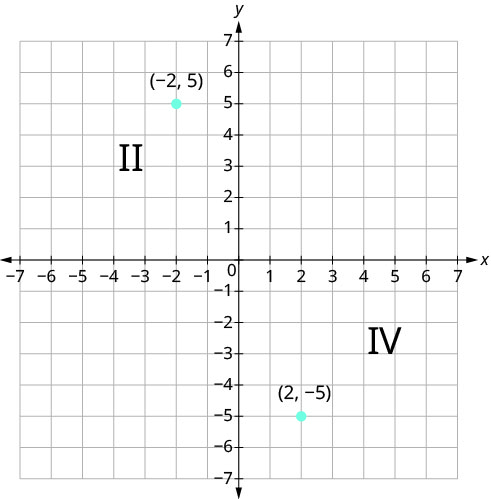
    Podemos resumir los patrones de signos de los cuadrantes de la siguiente manera. Ver también la Figura\(\PageIndex{6}\).

    Mesa\(\PageIndex{1}\)
    Cuadrante I Cuadrante II Cuadrante III Cuadrante IV
    (x, y) (x, y) (x, y) (x, y)
    (+, +) (-, +) (-, -) (+, -)

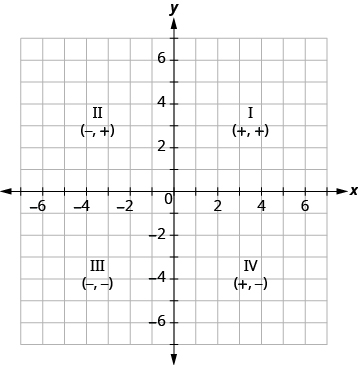
    La gráfica muestra el plano de la coordenada x y. Los ejes x e y van cada uno de -7 a 7. La parte superior derecha del avión está etiquetada como “I” y “par ordenado +, +”, la parte superior izquierda del avión está etiquetada como “II” y “par ordenado -, +”, la parte inferior izquierda del plano está etiquetada como “III” “par ordenado -, -” y la parte inferior derecha del plano está etiquetada como “IV” y “par ordenado +, -”.

    Figura\(\PageIndex{6}\)

    ¿Y si una coordenada es cero? ¿Dónde se encuentra el punto (0, 4)? ¿Dónde se encuentra el punto (−2, 0)? El punto (0, 4) está en el eje y y el punto (− 2, 0) está en el eje x.

    Definición: Puntos en los Ejes

    Los puntos con una coordenada y igual a 0 están en el eje x y tienen coordenadas (a, 0).

    Los puntos con una coordenada x igual a 0 están en el eje y, y tienen coordenadas (0, b).

    ¿Cuál es el par ordenado del punto donde se cruzan los ejes? En ese punto ambas coordenadas son cero, por lo que su par ordenado es (0, 0). El punto tiene un nombre especial. Se le llama el origen.

    Definición: el origen

    Al punto (0, 0) se le llama origen. Es el punto donde se cruzan el eje x y el eje y.

    Ejemplo\(\PageIndex{5}\):

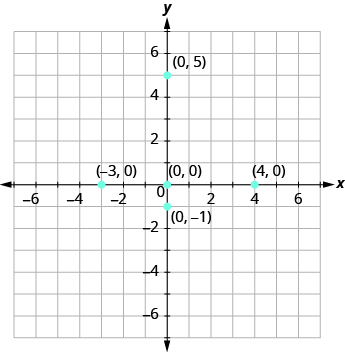
    Trazar cada punto en una cuadrícula de coordenadas: (a) (0, 5) (b) (4, 0) (c) (−3, 0) (d) (0, 0) (e) (0, −1)

    Solución

    1. Dado que x = 0, el punto cuyas coordenadas son (0, 5) está en el eje y.
    2. Desde y = 0, el punto cuyas coordenadas son (4, 0) está en el eje x.
    3. Dado que y = 0, el punto cuyas coordenadas son (−3, 0) está en el eje x.
    4. Dado que x = 0 e y = 0, el punto cuyas coordenadas son (0, 0) es el origen.
    5. Dado que x = 0, el punto cuyas coordenadas son (0, −1) está en el eje y.

    La gráfica muestra el plano de la coordenada x y. Los ejes x e y van cada uno de -7 a 7. El punto “par ordenado 0, 0” se etiqueta “0, 0” entre paréntesis. El punto “par ordenado 4, 0” se etiqueta “4, 0” entre paréntesis. El punto “par ordenado 0, 5” se etiqueta “0, 5” entre paréntesis. El punto “par ordenado 0, -1” se etiqueta “0, -1” entre paréntesis.

    Ejercicio\(\PageIndex{9}\):

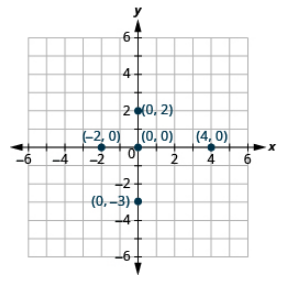
    Trazar cada punto en una cuadrícula de coordenadas: (a) (4, 0) (b) (−2, 0) (c) (0, 0) (d) (0, 2) (e) (0, −3)

    Responder
    Esta imagen es una gráfica de respuestas y muestra el plano de coordenadas x y. Los ejes x e y van cada uno de -6 a 6. Se traza el punto para el par ordenado 4, 0. Se traza el punto para el par ordenado -2, 0. Se traza el punto para el par ordenado 0,0. Se traza el punto para el par ordenado 0, 2. Se traza el punto para el par ordenado 0, -3.
    Ejercicio\(\PageIndex{10}\):

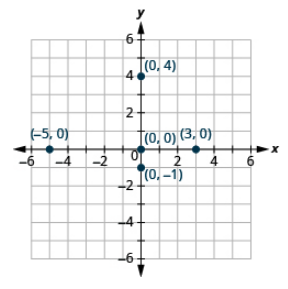
    Trazar cada punto en una cuadrícula de coordenadas: (a) (−5, 0) (b) (3, 0) (c) (0, 0) (d) (0, −1) (e) (0, 4)

    Responder
    Esta imagen es una gráfica de respuestas y muestra el plano de coordenadas x y. Los ejes x e y van cada uno de -6 a 6. Se traza el punto para el par ordenado -5, 0. Se traza el punto para el par ordenado 3, 0. Se traza el punto para el par ordenado 0,0. Se traza el punto para el par ordenado 0, -1. Se traza el punto para el par ordenado 0,4.

    Identificar puntos en una gráfica

    En álgebra, ser capaz de identificar las coordenadas de un punto mostrado en una gráfica es tan importante como poder trazar puntos. Para identificar la coordenada x de un punto en una gráfica, lea el número en el eje x directamente encima o debajo del punto. Para identificar la coordenada y de un punto, lea el número en el eje y directamente a la izquierda o derecha del punto. Recuerda, escribir el par ordenado usando el orden correcto (x, y).

    Ejemplo\(\PageIndex{6}\):

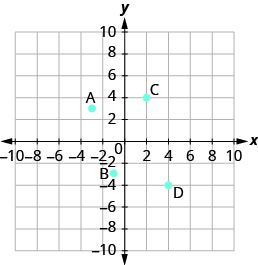
    Nombra el par ordenado de cada punto mostrado:

    La gráfica muestra el plano de la coordenada x y. Los ejes x e y van cada uno de -7 a 7. El punto “par ordenado 2, 4” está etiquetado C. El punto “par ordenado -3, 3” está etiquetado A. El punto “par ordenado -1, -3” está etiquetado B. El punto “par ordenado 4, -4” está etiquetado como D.

    Solución

    El punto A está por encima de −3 en el eje x, por lo que la coordenada x del punto es −3. El punto está a la izquierda de 3 en el eje y, por lo que la coordenada y del punto es 3. Las coordenadas del punto son (−3, 3).

    El punto B está por debajo de −1 en el eje x, por lo que la coordenada x del punto es −1. El punto está a la izquierda de −3 en el eje y, por lo que la coordenada y del punto es −3. Las coordenadas del punto son (−1, −3).

    El punto C está por encima de 2 en el eje x, por lo que la coordenada x del punto es 2. El punto está a la derecha de 4 en el eje y, por lo que la coordenada y del punto es 4. Las coordenadas del punto son (2, 4).

    El punto D está por debajo de 4 en el eje x -, por lo que la coordenada x del punto es 4. El punto está a la derecha de −4 en el eje y, por lo que la coordenada y del punto es −4. Las coordenadas del punto son (4, −4)

    Ejercicio\(\PageIndex{11}\):

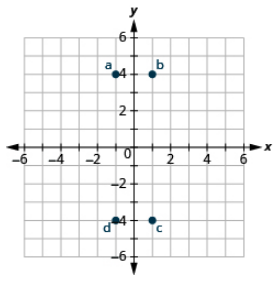
    Nombra el par ordenado de cada punto mostrado:

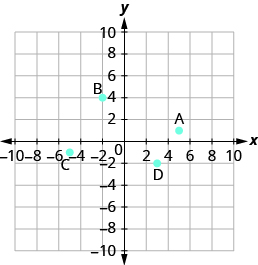
    La gráfica muestra el plano de la coordenada x y. Los ejes x e y van cada uno de -7 a 7. El punto “par ordenado 5, 1” está etiquetado A. El punto “par ordenado -2, 4” está etiquetado B. El punto “par ordenado -5, -1” está etiquetado C. El punto “par ordenado 3, -2” está etiquetado como D.

    Responder
    A: (5,1), B: (−2,4), C: (−5, −1), D: (3, −2)
    Ejercicio\(\PageIndex{12}\):

    Nombra el par ordenado de cada punto mostrado:

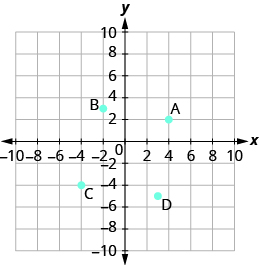
    La gráfica muestra el plano de la coordenada x y. Los ejes x e y van cada uno de -7 a 7. El punto “par ordenado 4, 2” está etiquetado A. El punto “par ordenado -2, 3” está etiquetado B. El punto “par ordenado -4, -4” está etiquetado C. El punto “par ordenado 3, -5” está etiquetado como D.

    Responder
    A: (4,2), B: (−2,3), C: (−4, −4), D: (3, −5)
    Ejemplo\(\PageIndex{7}\):

    Nombra el par ordenado de cada punto mostrado:

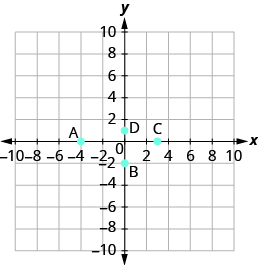
    La gráfica muestra el plano de la coordenada x y. Los ejes x e y van cada uno de -7 a 7. El punto “par ordenado 3, 0” está etiquetado C. El punto “par ordenado 0, 1” está etiquetado D. El punto “par ordenado -4, 0” está etiquetado A. El punto “par ordenado 0, -2” está etiquetado como B.

    Solución

    El punto A está en el eje x en x = − 4. Las coordenadas del punto A son (− 4, 0).
    El punto B está en el eje y en y = − 2. Las coordenadas del punto B son (0, − 2).
    El punto C está en el eje x en x = 3. Las coordenadas del punto C son (3, 0).
    El punto D está en el eje y en y = 1. Las coordenadas del punto D son (0, 1).
    Ejercicio\(\PageIndex{13}\):

    Nombra el par ordenado de cada punto mostrado:

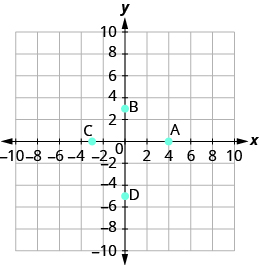
    La gráfica muestra el plano de la coordenada x y. Los ejes x e y van cada uno de -7 a 7. El punto “par ordenado 4, 0” está etiquetado A. El punto “par ordenado 0, 3” está etiquetado B. El punto “par ordenado -3, 0” está etiquetado C. El punto “par ordenado 0, -5” está etiquetado como D.

    Responder
    A: (4,0), B: (0,3), C: (−3,0), D: (0, −5)
    Ejercicio\(\PageIndex{14}\):

    Nombra el par ordenado de cada punto mostrado:

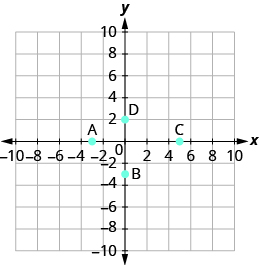
    La gráfica muestra el plano de la coordenada x y. Los ejes x e y van cada uno de -7 a 7. El punto “par ordenado 5, 0” está etiquetado C. El punto “par ordenado 0, 2” está etiquetado D. El punto “par ordenado -3, 0” está etiquetado A. El punto “par ordenado 0, -3” está etiquetado como B.

    Responder
    A: (−3,0), B: (0, −3), C: (5,0), D: (0,2)

    Colaboradores y Atribuciones

    This page titled 11.1: Usar el Sistema de Coordenadas Rectangulares (Parte 1) is shared under a not declared license and was authored, remixed, and/or curated by OpenStax.