11.2: Usar el Sistema de Coordenadas Rectangulares (Parte 2)
- Page ID
- 114228
Verificar soluciones a una ecuación en dos variables
Todas las ecuaciones que resolvimos hasta ahora han sido ecuaciones con una variable. En casi todos los casos, cuando resolvimos la ecuación obtuvimos exactamente una solución. El proceso de resolver una ecuación terminó con una declaración como x = 4. Luego comprobamos la solución sustituyendo de nuevo a la ecuación.
Aquí hay un ejemplo de una ecuación lineal en una variable, y su única solución.
\[\begin{split} 3x + 5 &= 17 \\ 3x &= 12 \\ x &= 4 \end{split}\]
Pero las ecuaciones pueden tener más de una variable. Las ecuaciones con dos variables se pueden escribir en la forma general Ax + By = C. Una ecuación de esta forma se denomina ecuación lineal en dos variables.
Una ecuación de la forma Ax + By = C, donde A y B no son ambos cero, se denomina ecuación lineal en dos variables.
Observe que la palabra “línea” está en lineal.
Aquí hay un ejemplo de una ecuación lineal en dos variables, x e y:
\[\begin{split} \textcolor{red}{A} x + \textcolor{blue}{B} y &= \textcolor{green}{C} \\ x + \textcolor{blue}{4} y &= \textcolor{green}{8} \\ \textcolor{red}{A = 1},\; \textcolor{blue}{B = 4},\; &\textcolor{green}{C = 8} \end{split}\]
¿Y = −5x + 1 es una ecuación lineal? No parece estar en la forma Ax + By = C. Pero podríamos reescribirlo en esta forma.
| $$y = -5x + 1$$ | |
| Agrega 5x a ambos lados. | $$y + 5x = -5x + 1 + 5x$$ |
| Simplificar. | $$y + 5x = 1$$ |
| Usa la Propiedad Conmutativa para ponerla en Ax + By = C. | $$\ begin {split}\ textcolor {rojo} {A} x +\ textcolor {azul} {B} y &= C\\ 5 +\ quad y &= 1\ end {split} $$ |
Al reescribir y = −5x + 1 como 5x + y = 1, podemos ver que es una ecuación lineal en dos variables porque se puede escribir en la forma Ax + By = C.
Las ecuaciones lineales en dos variables tienen infinitamente muchas soluciones. Por cada número que se sustituye por x, hay un valor y correspondiente. Este par de valores es una solución a la ecuación lineal y está representado por el par ordenado (x, y). Cuando sustituimos estos valores de x e y en la ecuación, el resultado es una declaración verdadera porque el valor del lado izquierdo es igual al valor del lado derecho.
Un par ordenado (x, y) es una solución a la ecuación lineal Ax + By = C, si la ecuación es una declaración verdadera cuando los valores x e y del par ordenado se sustituyen en la ecuación.
Determinar qué pares ordenados son soluciones de la ecuación x + 4y = 8: (a) (0, 2) (b) (2, −4) (c) (−4, 3)
Solución
Sustituir los valores x e y de cada par ordenado en la ecuación y determinar si el resultado es una declaración verdadera.
| (a) (0, 2) | b) (2, −4) | (c) (−4, 3) |
| $$\ begin {split} x =\ textcolor {azul} {0},\; y &=\ textcolor {rojo} {2}\\ x + 4y &= 8\\\ textcolor {azul} {0} + 4\ cdot\ textcolor {rojo} {2} &\ stackrel {?} {=} 8\\ 0 + 8 &\ stackrel {?} {=} 8\\ 8 &= 8\;\ marca de verificación\ final {dividir} $$ | $$\ begin {split} x =\ textcolor {azul} {2},\; y &=\ textcolor {rojo} {-4}\\ x + 4y &= 8\\\ textcolor {azul} {2} + 4 (\ textcolor {rojo} {-4}) &\ stackrel {?} {=} 8\\ 2 + (-16) &\ stackrel {?} {=} 8\\ -14 &\ neq 8\ final {dividir} $$ | $$\ begin {split} x =\ textcolor {azul} {-4},\; y &=\ textcolor {rojo} {3}\\ x + 4y &= 8\\\ textcolor {azul} {-4} + 4\ cdot\ textcolor {rojo} {3} &\ stackrel {?} {=} 8\\ -4 + 12 &\ stackrel {?} {=} 8\\ 8 &= 8\;\ marca de verificación\ final {dividir} $$ |
| (0, 2) es una solución. | (2, −4) no es una solución. | (−4, 3) es una solución. |
Determinar qué pares ordenados son soluciones a la ecuación dada: 2x + 3y = 6
(a) (3, 0) (b) (2, 0) (c) (6, −2)
- Contestar
-
a), c)
Determinar qué pares ordenados son soluciones a la ecuación dada: 4x − y = 8
(a) (0, 8) (b) (2, 0) (c) (1, −4)
- Contestar
-
b), c)
Determinar qué pares ordenados son soluciones de la ecuación. y = 5x − 1: (a) (0, −1) (b) (1, 4) (c) (−2, −7)
Solución
Sustituya los valores x e y de cada par ordenado en la ecuación y determine si da como resultado una declaración verdadera.
| (a) (0, -1) | b) (1, 4) | (c) (−2, -7) |
| $$\ begin {split} x &=\ textcolor {azul} {0},\; y =\ textcolor {rojo} {-1}\\ y &= 5x - 1\\\ textcolor {rojo} {-1} &\ stackrel {?} {=} 5 (\ textcolor {azul} {0}) - 1\\ -1 &\ stackrel {?} {=} 0 - 1\\ -1 &= -1\;\ marca de verificación\ end {split} $$ | $$\ begin {split} x &=\ textcolor {azul} {1},\; y =\ textcolor {rojo} {4}\\ y &= 5x - 1\\\ textcolor {rojo} {4} &\ stackrel {?} {=} 5 (\ textcolor {azul} {1}) - 1\\ 4 &\ stackrel {?} {=} 5 - 1\\ 4 &= 4\;\ marca de verificación\ end {split} $$ | $$\ begin {split} x &=\ textcolor {azul} {-2},\; y =\ textcolor {rojo} {-7}\\ y &= 5x - 1\\\ textcolor {rojo} {-7} &\ stackrel {?} {=} 5 (\ textcolor {azul} {-2}) - 1\\ -7 &\ stackrel {?} {=} -10 - 1\\ -7 &\ neq -11\ end {split} $$ |
| (0, -1) es una solución. | (1, 4) es una solución. | (−2, -7) no es una solución. |
Determinar qué pares ordenados son soluciones de la ecuación dada: y = 4x − 3
(a) (0, 3) (b) (1, 1) (c) (1, 1)
- Contestar
-
b)
Determinar qué pares ordenados son soluciones de la ecuación dada: y = −2x + 6
(a) (0, 6) (b) (1, 4) (c) (−2, −2)
- Contestar
-
a), b)
Completar una Tabla de Soluciones a una Ecuación Lineal
En los ejemplos anteriores, sustituimos los valores x e y de un par ordenado dado para determinar si era o no una solución a una ecuación lineal. Pero, ¿cómo encontramos los pares ordenados si no se dan? Una forma es elegir un valor para x y luego resolver la ecuación para y, o bien, elegir un valor para y y luego resolver para x.
Empezaremos por mirar las soluciones a la ecuación y = 5x − 1 que encontramos en Ejemplo\(\PageIndex{1}\). Podemos resumir esta información en una tabla de soluciones.
| y = 5x − 1 | ||
|---|---|---|
| x | y | (x, y) |
| 0 | -1 | (0, -1) |
| 1 | 4 | (1, 4) |
Para encontrar una tercera solución, dejaremos x = 2 y resolveremos para y.
| $$y = 5x − 1$$ | |
| Sustituto x =\(\textcolor{blue}{2}\). | $$y = 5 (\ textcolor {azul} {2}) - 1$$ |
| Multiplicar. | $$y = 10 − 1$$ |
| Simplificar. | $$y = 9$$ |
El par ordenado es una solución a y = 5x - 1. Lo agregaremos a la mesa.
| y = 5x − 1 | ||
|---|---|---|
| x | y | (x, y) |
| 0 | -1 | (0, -1) |
| 1 | 4 | (1, 4) |
| 2 | 9 | (2, 9) |
Podemos encontrar más soluciones a la ecuación sustituyendo cualquier valor de x o cualquier valor de y y resolviendo la ecuación resultante para obtener otro par ordenado que sea una solución. Hay un número infinito de soluciones para esta ecuación.
Completa la tabla para encontrar tres soluciones a la ecuación y = 4x − 2:
| y = 4x - 2 | ||
|---|---|---|
| x | y | (x, y) |
| 0 | ||
| -1 | ||
| 2 | ||
Solución
Sustituye x = 0, x = −1 y x = 2 en y = 4x − 2.
| x =\(\textcolor{blue}{0}\) | x =\(\textcolor{blue}{-1}\) | x =\(\textcolor{blue}{2}\) |
| y = 4x − 2 | y = 4x − 2 | y = 4x − 2 |
| y = 4 •\(\textcolor{blue}{0}\) − 2 | y = 4 (\(\textcolor{blue}{-1}\)) − 2 | y = 4 •\(\textcolor{blue}{2}\) − 2 |
| y = 0 − 2 | y = −4 − 2 | y = 8 − 2 |
| y = −2 | y = −6 | y = 6 |
| (0, −2) | (−1, −6) | (2, 6) |
Los resultados se resumen en la tabla.
| y = 4x - 2 | ||
|---|---|---|
| x | y | (x, y) |
| 0 | -2 | (0, -2) |
| -1 | -6 | (-1, -6) |
| 2 | 6 | (2, 6) |
Complete la tabla para encontrar tres soluciones a la ecuación: y = 3x − 1.
| y = 3x − 1 | ||
|---|---|---|
| x | y | (x, y) |
| 0 | ||
| -1 | ||
| 2 | ||
- Contestar
-
y = 3x − 1 x y (x, y) 0 -1 (0, -1) -1 -4 (-1, -4) 2 5 (2, 5)
Completa la tabla para encontrar tres soluciones a la ecuación: y = 6x + 1.
| y = 6x + 1 | ||
|---|---|---|
| x | y | (x, y) |
| 0 | ||
| 1 | ||
| -2 | ||
- Contestar
-
y = 6x + 1 x y (x, y) 0 1 (0, 1) -1 7 (1, 7) 2 -11 (-2, -11)
Completa la tabla para encontrar tres soluciones a la ecuación 5x − 4y = 20:
| 5x − 4 años = 20 | ||
|---|---|---|
| x | y | (x, y) |
| 0 | ||
| 0 | ||
| 5 | ||
Solución
| $$\ begin {split} x &=\ textcolor {azul} {0}\\ 5x - 4y &= 20\\ 5\ cdot\ textcolor {azul} {0} - 4y &= 20\\\ textcolor {azul} {0} - 4y &= 20\\ -4y &= 20\\ y &= -5\\ (0,\; &-5)\ end {split} $$ | $$\ begin {split} y &=\ textcolor {rojo} {0}\\ 5x - 4y &= 20\\ 5x - 4\ cdot\ textcolor {rojo} {0} &= 20\\ 5x - 0 &= 20\\ 5x &= 20\\ x &= 4\\ (&4,\; 0)\ end {split} $$ | $$\ begin {split} y &=\ textcolor {rojo} {5}\\ 5x - 4y &= 20\\ 5x - 4\ cdot\ textcolor {rojo} {5} &= 20\\ 5x - 20 &= 20\\ 5x &= 40\\ x &= 8\\ (&8,\; 5)\ end {split} $$ |
Los resultados se resumen en la tabla.
| 5x − 4 años = 20 | ||
|---|---|---|
| x | y | (x, y) |
| 0 | -5 | (0, -5) |
| 4 | 0 | (-4, 0) |
| 8 | 5 | (8, 5) |
Completa la tabla para encontrar tres soluciones a la ecuación: 2x − 5y = 20.
| 2x - 5 años = 20 | ||
|---|---|---|
| x | y | (x, y) |
| 0 | ||
| 0 | ||
| -5 | ||
- Contestar
-
2x - 5 años = 20 x y (x, y) 0 -4 (0, -4) 10 0 (10, 0) -5 -6 (-5, -6)
Completa la tabla para encontrar tres soluciones a la ecuación: 3x − 4y = 12.
| 3x - 4 años = 12 | ||
| x | y | (x, y) |
| 0 | ||
| 0 | ||
| -4 | ||
- Contestar
-
3x - 4 años = 12 x y (x, y) 0 -3 (0, -3) 4 0 (4, 0) -4 -6 (-4, -6)
Encuentre soluciones a ecuaciones lineales en dos variables
Para encontrar una solución a una ecuación lineal, podemos elegir cualquier número que queramos sustituir en la ecuación ya sea para x o y. Podríamos elegir 1, 100, 1,000 o cualquier otro valor que queramos. Pero es una buena idea elegir un número con el que sea fácil trabajar. Normalmente elegiremos 0 como uno de nuestros valores.
Encuentra una solución a la ecuación 3x + 2y = 6.
Solución
| Paso 1: Elija cualquier valor para una de las variables de la ecuación. |
Podemos sustituir cualquier valor que queramos por x o cualquier valor por y. Escojamos x = 0. ¿Cuál es el valor de y si x = 0? |
|
| Paso 2: Sustituir ese valor en la ecuación. Resolver para la otra variable. |
Sustituye 0 por x. Simplificar. Divide ambos lados por 2. |
$$\ begin {split} 3x + 2y &= 6\\ 3\ cdot\ textcolor {azul} {0} + 2y &= 6\\ 0 + 2y &= 6\\ 2y &= 6\\ y &= 3\ end {split} $$ |
| Paso 3: Escribe la solución como un par ordenado. | Entonces, cuando x = 0, y = 3. | Esta solución está representada por el par ordenado (0, 3). |
| Paso 4: Comprobar. |
Sustituye x =\(\textcolor{blue}{0}\), y =\(\textcolor{red}{3}\) en la ecuación 3x + 2y = 6. ¿El resultado es una ecuación verdadera? ¡Sí! |
$$\ begin {split} 3x + 2y &= 6\\ 3\ cdot\ textcolor {azul} {0} + 2\ cdot\ textcolor {rojo} {3} &\ stackrel {?} {=} 6\\ 0 + 6 &\ stackrel {?} {=} 6\\ 6 &= 6\;\ marca de verificación\ final {dividir} $$ |
Encuentra una solución a la ecuación: 4x + 3y = 12.
- Contestar
-
Las respuestas variarán
Encuentra una solución a la ecuación: 2x + 4y = 8.
- Contestar
-
Las respuestas variarán
Dijimos que las ecuaciones lineales en dos variables tienen infinitamente muchas soluciones, y acabamos de encontrar una de ellas. Busquemos algunas otras soluciones a la ecuación 3x + 2y = 6.
Encuentra tres soluciones más a la ecuación 3x + 2y = 6.
Solución
Para encontrar soluciones a 3x + 2y = 6, elija un valor para x o y. Recuerde, podemos elegir cualquier valor que queramos para x o y. Aquí elegimos 1 para x, y 0 y −3 para y.
| Sustitúyelo en la ecuación. | $$\ begin {split} y &=\ textcolor {rojo} {0}\\ 3x + 2y &= 6\\ 3x + 2 (\ textcolor {rojo} {0}) &= 6\ end {split} $$ | $$\ begin {split} x &=\ textcolor {azul} {1}\\ 3x + 2y &= 6\\ 3 (\ textcolor {azul} {1}) + 2y &= 6\ end {split} $$ | $$\ begin {split} y &=\ textcolor {rojo} {-3}\\ 3x + 2y &= 6\\ 3x + 2 (\ textcolor {rojo} {-3}) &= 6\ end {split} $$ |
| Simplificar. Resolver. | $$\ start {split} 3x + 0 &= 6\\ 3x &= 6\ end {split} $$ | $$\ begin {split} 3 + 2y &= 6\\ 2y &= 3\ end {split} $$ | $$\ begin {split} 3x - 6 &= 6\\ 3x &= 12\ end {split} $$ |
| x = 2 | y =\(\dfrac{3}{2}\) | x = 4 | |
| Escribe el par ordenado. | (2, 0) | (1,\(\dfrac{3}{2}\)) | (4, −3) |
Consulta tus respuestas.
| (2, 0) | (1,\(\dfrac{3}{2}\)) | (4, −3) |
| $$\ begin {split} 3x + 2y &= 6\\ 3\ cdot\ textcolor {azul} {2} + 2\ cdot\ textcolor {rojo} {0} &\ stackrel {?} {=} 6\\ 6 + 0 &\ stackrel {?} {=} 6\\ 6 &= 6\;\ marca de verificación\ final {dividir} $$ | $$\ begin {split} 3x + 2y &= 6\\ 3\ cdot\ textcolor {azul} {1} + 2\ cdot\ textcolor {rojo} {\ dfrac {3} {2}} &\ stackrel {?} {=} 6\\ 3 + 3 &\ stackrel {?} {=} 6\\ 6 &= 6\;\ marca de verificación\ final {dividir} $$ | $$\ begin {split} 3x + 2y &= 6\\ 3\ cdot\ textcolor {azul} {4} + 2\ cdot (\ textcolor {rojo} {-3}) &\ stackrel {?} {=} 6\\ 12 + (-6) &\ stackrel {?} {=} 6\\ 6 &= 6\;\ marca de verificación\ final {dividir} $$ |
Entonces (2, 0), (1,\(\dfrac{3}{2}\)) y (4, −3) son todas soluciones a la ecuación 3x + 2y = 6. En el ejemplo anterior, encontramos que (0, 3) es una solución, también. Podemos enumerar estas soluciones en una tabla.
| 3x + 2 años = 6 | ||
|---|---|---|
| x | y | (x, y) |
| 0 | 3 | (0, 3) |
| 2 | 0 | (2, 0) |
| 1 | \(\dfrac{3}{2}\) | (1,\(\dfrac{3}{2}\)) |
| 4 | -3 | (4, -3) |
Encuentra tres soluciones a la ecuación: 2x + 3y = 6.
- Contestar
-
Las respuestas variarán
Encuentra tres soluciones a la ecuación: 4x + 2y = 8.
- Contestar
-
Las respuestas variarán
Busquemos algunas soluciones a otra ecuación ahora.
Encuentra tres soluciones a la ecuación x − 4y = 8.
Solución
| Elija un valor para x o y. | x =\(\textcolor{blue}{0}\) | y =\(\textcolor{red}{0}\) | y =\(\textcolor{red}{3}\) |
| Sustitúyelo en la ecuación. | $$\ textcolor {azul} {0} - 4y = 8$$ | $$x - 4\ cdot\ textcolor {rojo} {0} = 8$$ | $$x - 4\ cdot\ textcolor {rojo} {3} = 8$$ |
| Resolver. | $$\ begin {split} -4y &= 8\\ y &= -2\ end {split} $$ | $$\ begin {split} x - 0 &= 8\\ x &= 8\ end {split} $$ | $$\ start {split} x - 12 &= 8\\ x &= 20\ end {split} $$ |
| Escribe el par ordenado. | (0, −2) | (8, 0) | (20, 3) |
Entonces (0, −2), (8, 0) y (20, 3) son tres soluciones a la ecuación x − 4y = 8.
| x − 4y = 8 | ||
|---|---|---|
| x | y | (x, y) |
| 0 | -2 | (0, -2) |
| 8 | 0 | (8, 0) |
| 20 | 3 | (20, 3) |
Recuerde, hay un número infinito de soluciones para cada ecuación lineal. Cualquier punto que encuentres es una solución si hace que la ecuación sea verdadera.
Encuentra tres soluciones a la ecuación: 4x + y = 8.
- Contestar
-
Las respuestas variarán
Encuentra tres soluciones a la ecuación: x + 5y = 10.
- Contestar
-
Las respuestas variarán
La práctica hace la perfección
Trazar puntos en un sistema de coordenadas rectangulares
En los siguientes ejercicios, trazar cada punto en una cuadrícula de coordenadas.
- (3, 2)
- (4, 1)
- (1, 5)
- (3, 4)
- (4, 1), (1, 4)
- (3, 2), (2, 3)
- (3, 4), (4, 3)
En los siguientes ejercicios, trazar cada punto en una cuadrícula de coordenadas e identificar el cuadrante en el que se encuentra el punto.
- (a) (−4, 2) (b) (−1, −2) (c) (3, −5) (d)\(\left(2, \dfrac{5}{2}\right)\)
- (a) (−2, −3) (b) (3, −3) (c) (−4, 1) (d)\(\left(1, \dfrac{3}{2}\right)\)
- (a) (−1, 1) (b) (−2, −1) (c) (1, −4) (d)\(\left(3, \dfrac{7}{2}\right)\)
- (a) (3, -2) (b) (−3, 2) (c) (-3, −2) (d) (3, 2)
- (a) (4, -1) (b) (−4, 1) (c) (-4, -1) (d) (4, 1)
- (a) (−2, 0) (b) (−3, 0) (c) (0, 4) (d) (0, 2)
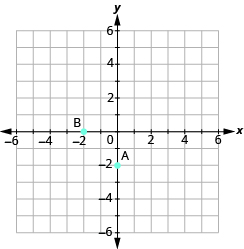
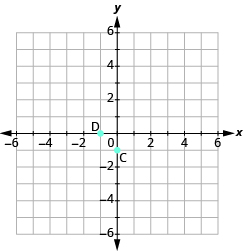
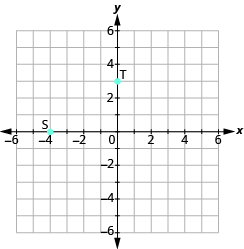
Identificar puntos en una gráfica
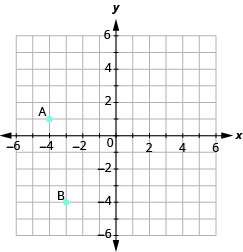
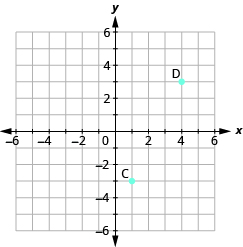
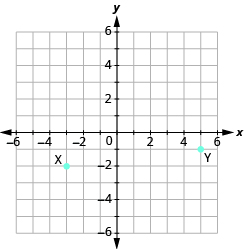
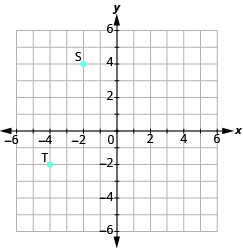
En los siguientes ejercicios, nombra el par ordenado de cada punto mostrado.
Verificar soluciones a una ecuación en dos variables
En los siguientes ejercicios, determinar qué pares ordenados son soluciones a la ecuación dada.
- 2x + y = 6
- (1, 4)
- (3, 0)
- (2, 3)
- x + 3y = 9
- (0, 3)
- (6, 1)
- (-3, -3)
- 4x − 2y = 8
- (3, 2)
- (1, 4)
- (0, -4)
- 3x − 2 años = 12
- (4, 0)
- (2, -3)
- (1, 6)
- y = 4x + 3
- (4, 3)
- (-1, -1)
- (\(\dfrac{1}{2}\), 5)
- y = 2x − 5
- (0, -5)
- (2, 1)
- (\(\dfrac{1}{2}\), -4)
- y =\(\dfrac{1}{2}\) x − 1
- (2, 0)
- (-6, -4)
- (-4, -1)
- y =\(\dfrac{1}{3}\) x + 1
- (-3, 0)
- (9, 4)
- (-6, -1)
Encuentre soluciones a ecuaciones lineales en dos variables
En los siguientes ejercicios, complete la tabla para encontrar soluciones a cada ecuación lineal.
y = 2x − 4
| x | y | (x, y) |
|---|---|---|
| -1 | ||
| 0 | ||
| 2 |
- y = 3x − 1
| x | y | (x, y) |
|---|---|---|
| -1 | ||
| 0 | ||
| 2 |
- y = − x + 5
| x | y | (x, y) |
|---|---|---|
| -2 | ||
| 0 | ||
| 3 |
- y =\(\dfrac{1}{3}\) x + 1
| x | y | (x, y) |
|---|---|---|
| 0 | ||
| 3 | ||
| 6 |
- y =\(− \dfrac{3}{2}\) x − 2
| x | y | (x, y) |
|---|---|---|
| -2 | ||
| 0 | ||
| 2 |
- x + 2y = 8
| x | y | (x, y) |
|---|---|---|
| 0 | ||
| 4 | ||
| 0 |
Matemáticas cotidianas
- Peso de un bebé Mackenzie registró el peso de su bebé cada dos meses. La edad del bebé, en meses, y el peso, en libras, se enumeran en la tabla, y se muestran como un par ordenado en la tercera columna.
- Trazar los puntos en una rejilla de coordenadas.
- ¿Por qué solo se necesita Quadrant I?
| Edad | Peso | (x, y) |
|---|---|---|
| 0 | 7 | (0, 7) |
| 2 | 11 | (2, 11) |
| 4 | 15 | (4, 15) |
| 6 | 16 | (6, 16) |
| 8 | 19 | (8, 19) |
| 10 | 20 | (10, 20) |
| 12 | 21 | (12, 21) |
- Peso de un niño Latresha registró la estatura y el peso de su hijo cada año. Su estatura, en pulgadas, y su peso, en libras, se enumeran en la tabla, y se muestran como un par ordenado en la tercera columna.
- Trazar los puntos en una rejilla de coordenadas.
- ¿Por qué solo se necesita Quadrant I?
| Altura | Peso | (x, y) |
| 28 | 22 | (28, 22) |
| 31 | 27 | (31, 27) |
| 33 | 33 | (33, 33) |
| 37 | 35 | (37, 35) |
| 40 | 41 | (40, 41) |
| 42 | 45 | (42, 45) |
Ejercicios de escritura
- ¿Alguna vez ha utilizado un mapa con un sistema de coordenadas rectangulares? Describe el mapa y cómo lo usaste.
- ¿Cómo se determina si un par ordenado es una solución a una ecuación dada?
Autocomprobación
(a) Después de completar los ejercicios, utilice esta lista de verificación para evaluar su dominio de los objetivos de esta sección.
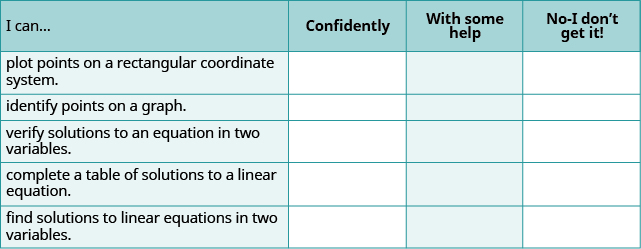
(b) Si la mayoría de sus cheques fueron:
... con confianza. ¡Felicidades! Has logrado los objetivos en esta sección. Reflexiona sobre las habilidades de estudio que usaste para que puedas seguir usándolas. ¿Qué hiciste para confiar en tu capacidad para hacer estas cosas? Ser específico.
... con alguna ayuda. Esto debe abordarse rápidamente porque los temas que no dominas se convierten en baches en tu camino hacia el éxito. En matemáticas, cada tema se basa en trabajos anteriores. Es importante asegurarse de tener una base sólida antes de seguir adelante. ¿A quién puedes pedir ayuda? Tus compañeros de clase e instructor son buenos recursos. ¿Hay algún lugar en el campus donde estén disponibles los tutores de matemáticas? ¿Se pueden mejorar tus habilidades de estudio?
... no, ¡no lo comprendo! Esta es una señal de advertencia y no debes ignorarla. Deberías obtener ayuda de inmediato o te sentirás abrumado rápidamente. Consulte a su instructor lo antes posible para discutir su situación. Juntos pueden idear un plan para obtener la ayuda que necesita.