Inicio
Matemáticas
Pre-Álgebra
Libro: Preálgebra (OpenStax)
11: Gráficas
11.8: Comprender la pendiente de una línea (Parte 2)

11.8: Comprender la pendiente de una línea (Parte 2)

Última actualización
Guardar como PDF

Page ID: 114239

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

$ \newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$

( \newcommand{\kernel}{\mathrm{null}\,}\) $ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\id}{\mathrm{id}}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\kernel}{\mathrm{null}\,}$

$ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$

$ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$

$ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\AA}{\unicode[.8,0]{x212B}}$

$ \newcommand{\vectorA}[1]{\vec{#1}} % arrow$

$ \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow$

$ \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vectorC}[1]{\textbf{#1}} $

$ \newcommand{\vectorD}[1]{\overrightarrow{#1}} $

$ \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} $

$ \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} $

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

$\newcommand{\avec}{\mathbf a}$ $\newcommand{\bvec}{\mathbf b}$ $\newcommand{\cvec}{\mathbf c}$ $\newcommand{\dvec}{\mathbf d}$ $\newcommand{\dtil}{\widetilde{\mathbf d}}$ $\newcommand{\evec}{\mathbf e}$ $\newcommand{\fvec}{\mathbf f}$ $\newcommand{\nvec}{\mathbf n}$ $\newcommand{\pvec}{\mathbf p}$ $\newcommand{\qvec}{\mathbf q}$ $\newcommand{\svec}{\mathbf s}$ $\newcommand{\tvec}{\mathbf t}$ $\newcommand{\uvec}{\mathbf u}$ $\newcommand{\vvec}{\mathbf v}$ $\newcommand{\wvec}{\mathbf w}$ $\newcommand{\xvec}{\mathbf x}$ $\newcommand{\yvec}{\mathbf y}$ $\newcommand{\zvec}{\mathbf z}$ $\newcommand{\rvec}{\mathbf r}$ $\newcommand{\mvec}{\mathbf m}$ $\newcommand{\zerovec}{\mathbf 0}$ $\newcommand{\onevec}{\mathbf 1}$ $\newcommand{\real}{\mathbb R}$ $\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}$ $\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}$ $\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}$ $\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}$ $\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$ $\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$ $\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$ $\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$ $\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}$ $\newcommand{\laspan}[1]{\text{Span}\{#1\}}$ $\newcommand{\bcal}{\cal B}$ $\newcommand{\ccal}{\cal C}$ $\newcommand{\scal}{\cal S}$ $\newcommand{\wcal}{\cal W}$ $\newcommand{\ecal}{\cal E}$ $\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}$ $\newcommand{\gray}[1]{\color{gray}{#1}}$ $\newcommand{\lgray}[1]{\color{lightgray}{#1}}$ $\newcommand{\rank}{\operatorname{rank}}$ $\newcommand{\row}{\text{Row}}$ $\newcommand{\col}{\text{Col}}$ $\renewcommand{\row}{\text{Row}}$ $\newcommand{\nul}{\text{Nul}}$ $\newcommand{\var}{\text{Var}}$ $\newcommand{\corr}{\text{corr}}$ $\newcommand{\len}[1]{\left|#1\right|}$ $\newcommand{\bbar}{\overline{\bvec}}$ $\newcommand{\bhat}{\widehat{\bvec}}$ $\newcommand{\bperp}{\bvec^\perp}$ $\newcommand{\xhat}{\widehat{\xvec}}$ $\newcommand{\vhat}{\widehat{\vvec}}$ $\newcommand{\uhat}{\widehat{\uvec}}$ $\newcommand{\what}{\widehat{\wvec}}$ $\newcommand{\Sighat}{\widehat{\Sigma}}$ $\newcommand{\lt}{<}$ $\newcommand{\gt}{>}$ $\newcommand{\amp}{&}$ $\definecolor{fillinmathshade}{gray}{0.9}$

Graficar una línea dado un punto y la pendiente

En este capítulo, graficamos líneas trazando puntos, usando intercepciones y reconociendo líneas horizontales y verticales.

Otro método que podemos utilizar para graficar líneas es el método punto-pendiente. En ocasiones, se nos dará un punto y la pendiente de la línea, en lugar de su ecuación. Cuando esto sucede, utilizamos la definición de pendiente para dibujar la gráfica de la línea.

Ejemplo$\PageIndex{11}$:

Grafica la línea que pasa por el punto (1, −1) cuya pendiente es m =$\dfrac{3}{4}$.

Solución

Trazar el punto dado, (1, −1).

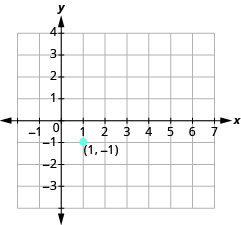
$La gráfica muestra el plano de coordenadas x y. El eje x va de -1 a 7. El eje y va de -3 a 4. Un punto etiquetado se dibuja en “par ordenado 1, -1”.$

Utilice la fórmula de pendiente m =$\dfrac{rise}{run}$ para identificar la subida y la carrera.

\[\begin{split} m &= \dfrac{3}{4} \\ \dfrac{rise}{run} &= \dfrac{3}{4} \\ rise &= 3 \\ run &= 4 \end{split}\]

Partiendo del punto que trazamos, cuenta la subida y corre para marcar el segundo punto. Contamos 3 unidades arriba y 4 unidades a la derecha.

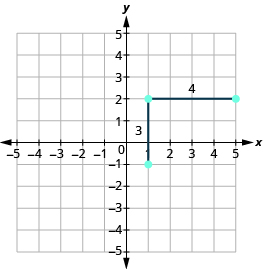
$La gráfica muestra el plano de coordenadas x y. Ambos ejes van de -5 a 5. Se dibujan dos segmentos de línea. Un segmento de línea vertical conecta los puntos “par ordenado 1, -1” y “par de orden “1, 2”. Está etiquetado como “3”. Un segmento de línea horizontal inicia en la parte superior del segmento de línea vertical y va hacia la derecha, conectando los puntos “par ordenado 1, 2” y “par ordenado 5, 2”. Está etiquetado como “4”.$

Después conectamos los puntos con una línea y dibujamos flechas en los extremos para mostrar que continúa.

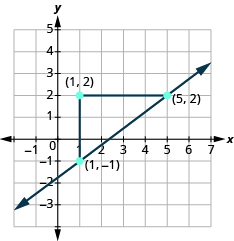
$La gráfica muestra el plano de coordenadas x y. El eje x va de -3 a 5. El eje y va de -1 a 7. Dos puntos sin etiquetar se dibujan en “par ordenado 1, -1” y “par ordenado 5, 2". Una línea pasa por los puntos. Dos segmentos de línea forman un triángulo con la línea. Una línea vertical conecta “par ordenado 1, -1” y “par ordenado 1, 2”. Un segmento de línea horizontal conecta “par ordenado 1, 2" y “par ordenado 5, 2".$

Podemos verificar nuestra línea comenzando en cualquier punto y contando hasta 3 y a la derecha 4. Deberíamos llegar a otro punto de la línea.

Ejercicio$\PageIndex{21}$:

Grafica la línea que pasa por el punto con la pendiente dada:

(2, −2), m =$\dfrac{4}{3}$

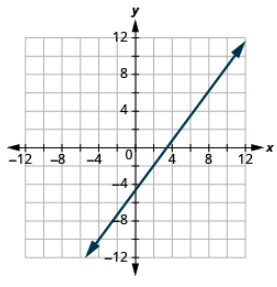
Contestar: $La gráfica muestra el plano de coordenadas x y. El eje x va de -12 a 12. El eje y va de -12 a 12. Una línea pasa por los puntos “par ordenado -2, 3” y “par ordenado 8, 6”.$

Ejercicio$\PageIndex{22}$:

Grafica la línea que pasa por el punto con la pendiente dada:

(−2, 3), m =$\dfrac{1}{4}$

Contestar: $La gráfica muestra el plano de coordenadas x y. El eje x va de -12 a 12. El eje y va de -12 a 12. Una línea pasa por los puntos “par ordenado -2, 3” y “par ordenado 2, 4”.$

CÓMO: GRAPAR UNA LÍNEA DADO UN PUNTO Y UNA TOL

Paso 1. Trazar el punto dado.

Paso 2. Utilice la fórmula de pendiente para identificar la subida y la carrera.

Paso 3. Comenzando en el punto dado, cuente la subida y corra para marcar el segundo punto.

Paso 4. Conecta los puntos con una línea.

Ejemplo$\PageIndex{12}$:

Grafica la línea con y -intercept (0, 2) y pendiente m =$− \dfrac{2}{3}$.

Solución

Trazar el punto dado, la intercepción y (0, 2).

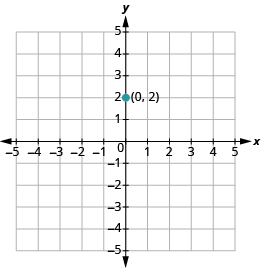
$La gráfica muestra el plano de coordenadas x y. El eje x va de -1 a 4. El eje y va de -1 a 3. El punto “par ordenado 0, 2” está etiquetado.$

Utilice la fórmula de pendiente m = carrera de subida para identificar la subida y la carrera.

\[\begin{split} m &= − \dfrac{2}{3} \\ \dfrac{rise}{run} &= \dfrac{−2}{3} \\ rise &= –2 \\ run &= 3 \end{split}\]

A partir de (0, 2), contar la subida y la carrera y marcar el segundo punto.

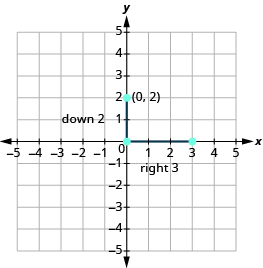
$La gráfica muestra el plano de coordenadas x y. Ambos ejes van de -5 a 5. Un segmento de línea vertical conecta puntos en “par ordenado 0, 2” y “par ordenado 0, 0” y se etiqueta “abajo 2”. Un segmento de línea horizontal conecta “par ordenado 0, 0" y “par ordenado 0, 3" y está etiquetado como “derecha 3".$

Conecta los puntos con una línea.

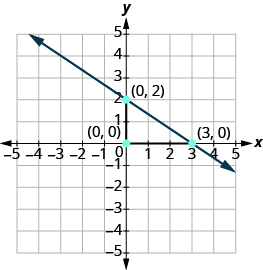
$La gráfica muestra el plano de coordenadas x y. Ambos ejes van de -5 a 5. Dos puntos etiquetados se dibujan en “par ordenado 0, 2” y “par ordenado 3, 0”. Una línea pasa por los puntos. Dos segmentos de línea forman un triángulo con la línea. Una línea vertical conecta “par ordenado 0, 2” y “par ordenado 0, 0”. Un segmento de línea horizontal conecta “par ordenado 0, 0” y “par ordenado 3, 0”.$

Ejercicio$\PageIndex{23}$:

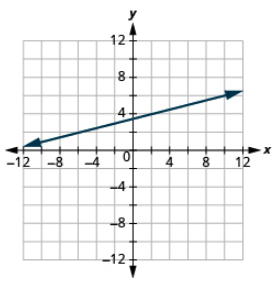
Grafica la línea con la intercepción y pendiente dadas:

intercepción en Y 4, m =$− \dfrac{5}{2}$

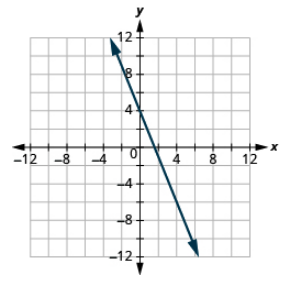
Contestar: $La gráfica muestra el plano de coordenadas x y. El eje x va de -12 a 12. El eje y va de -12 a 12. Una línea pasa por los puntos “par ordenado 0, 4” y “par ordenado 4, -6”.$

Ejercicio$\PageIndex{24}$:

Grafica la línea con la intercepción y pendiente dadas:

intercepción x-3, m =$− \dfrac{3}{4}$

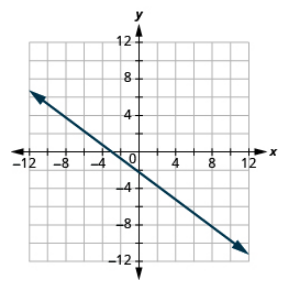
Contestar: $La gráfica muestra el plano de coordenadas x y. El eje x va de -12 a 12. El eje y va de -12 a 12. Una línea pasa por los puntos “par ordenado -3, 0” y “par ordenado 8, -8”.$

Ejemplo$\PageIndex{13}$:

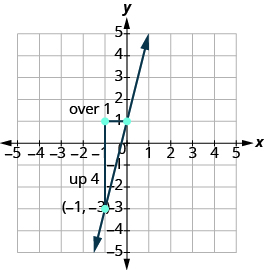
Grafique la línea que pasa por el punto (−1, −3) cuya pendiente es m = 4.

Solución

Trazar el punto dado.

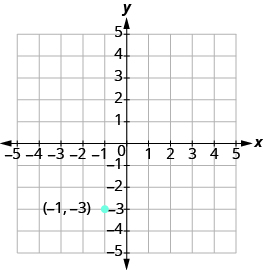
$La gráfica muestra el plano de coordenadas x y. Ambos ejes van de -5 a 5. Se etiqueta el punto “par ordenado -1, -3”.$

Identificar la subida y la carrera.	$$m = 4\ tag {11.4.44} $$
Escribe 4 como una fracción.	$$\ dfrac {rise} {run} =\ dfrac {4} {1}\ tag {11.4.45} $$
	subida = 4, corrida = 1

Cuenta la subida y corre.

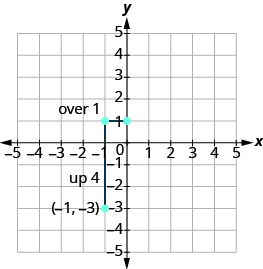
$La gráfica muestra el plano de coordenadas x y. Ambos ejes van de -5 a 5. El eje y va de -4 a 2. Un segmento de línea vertical conecta puntos en “par ordenado -1, -3” y “par ordenado -1, 1” y se etiqueta “arriba 4”. Un segmento de línea horizontal conecta “par ordenado -1, 1" y “par ordenado 0, 1" y está etiquetado como “sobre 1".$

Marcar el segundo punto. Conecta los dos puntos con una línea.

$La gráfica muestra el plano de coordenadas x y. Ambos ejes van de -5 a 5. Dos puntos etiquetados se dibujan en “par ordenado -1, -3” y “par ordenado -1, 1". Una línea pasa por los puntos. Dos segmentos de línea forman un triángulo con la línea. Una línea vertical conecta “par ordenado -1, -3” y “par ordenado -1, 1”. Se etiqueta “arriba 4” Un segmento de línea horizontal conecta “par ordenado -1, 1” y “par ordenado 0, 1". Está etiquetado como “más de 1”$

Ejercicio$\PageIndex{25}$:

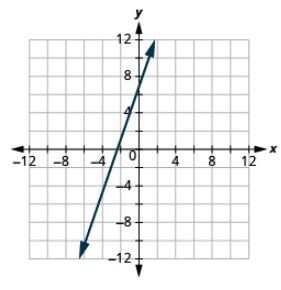
Grafica la línea con la intercepción y pendiente dadas: (−2, 1), m = 3.

Contestar: $La gráfica muestra el plano de coordenadas x y. El eje x va de -7 a 7. El eje y va de -7 a 7. Una línea pasa por los puntos “par ordenado -2, 1” y “par ordenado 0, 7”.$

Ejercicio$\PageIndex{26}$:

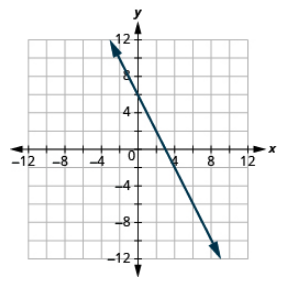
Grafica la línea con la intercepción y pendiente dadas: (4, −2), m = −2.

Contestar: $La gráfica muestra el plano de coordenadas x y. El eje x va de -7 a 7. El eje y va de -7 a 7. Una línea pasa por los puntos “par ordenado 0, 6” y “par ordenado 0, 3”.$

Resolver aplicaciones de pendientes

Al inicio de esta sección, dijimos que hay muchas aplicaciones de talud en el mundo real. Echemos un vistazo a algunos ahora.

Ejemplo$\PageIndex{14}$:

La inclinación del techo de un edificio es la pendiente de la cubierta. Conocer el terreno de juego es importante en climas donde hay fuertes nevadas. Si el techo es demasiado plano, el peso de la nieve puede hacer que se derrumbe. ¿Cuál es la pendiente de la cubierta que se muestra?

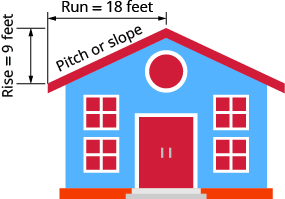
$Esta figura muestra una casa con techo inclinado. El techo en la mitad del edificio está etiquetado como “paso del techo”. Hay un segmento de línea con flechas en cada extremo que mide la longitud vertical de la cubierta y está etiquetado como “subida = 9 pies”. Hay un segmento de línea con flechas en cada extremo midiendo la longitud horizontal de la raíz y está etiquetado como “run = 18 pies”.$

Solución

Utilice la fórmula de pendiente.	$$m =\ dfrac {rise} {run}\ tag {11.4.46} $$
Sustituir los valores por subida y corrida.	$$m =\ dfrac {9\; ft} {18\; ft}\ tag {11.4.47} $$
Simplificar.	$$m =\ dfrac {1} {2}\ tag {11.4.48} $$
	La pendiente de la cubierta es$\dfrac{1}{2}$.

Ejercicio$\PageIndex{27}$:

Encuentra la pendiente dada subida y corre: Un techo con una subida = 14 y corrida = 24.

Contestar: $\frac{7}{12}$

Ejercicio$\PageIndex{28}$:

Encuentra la pendiente dada subida y corre: Un techo con una subida = 15 y corrida = 36.

Contestar: $\frac{5}{12}$

¿Alguna vez has pensado en que las tuberías de aguas residuales van de tu casa a la calle? Su pendiente es un factor importante en la forma en que quitan los desechos de tu casa.

Ejemplo$\PageIndex{15}$:

Las tuberías de aguas residuales deben inclinarse hacia abajo$\dfrac{1}{4}$ pulgadas por pie para drenar adecuadamente. ¿Cuál es la pendiente requerida?

$Esta figura muestra un triángulo rectángulo. La pata corta es vertical y está etiquetada con “1 sobre 4 pulgadas”. La pierna larga etiquetada como “1 pie”.$

Solución

Utilice la fórmula de pendiente.	$$m =\ dfrac {rise} {run} =\ dfrac {-\ dfrac {1} {4}\; in.} {1\; ft}\ tag {11.4.49} $$
Convierte 1 pie a 12 pulgadas.	$$m =\ dfrac {-\ dfrac {1} {4}\; in.} {12\; in}\ tag {11.4.50} $$
Simplificar.	$$m = -\ dfrac {1} {48}\ tag {11.4.51} $$
	La pendiente de la tubería es$− \dfrac{1}{48}$.

Ejercicio$\PageIndex{29}$:

Encuentra la pendiente de la tubería: La tubería se incline hacia abajo$\dfrac{1}{3}$ pulgadas por pie.

Contestar: $-\frac{1}{36}$

Ejercicio$\PageIndex{30}$:

Encuentra la pendiente de la tubería: La tubería desciende$\dfrac{3}{4}$ pulgadas por yarda.

Contestar: $-\frac{1}{48}$

Acceder a recursos adicionales en línea

Determinar pendiente positiva a partir de una gráfica

Determinar pendiente negativa a partir de una gráfica

Determinar pendiente a partir de dos puntos

La práctica hace la perfección

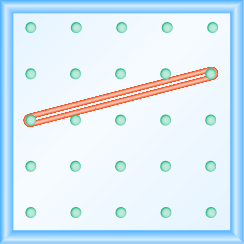
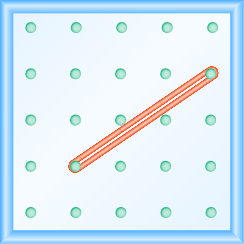
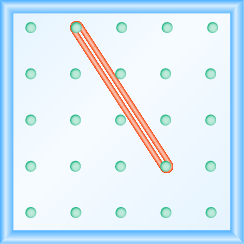
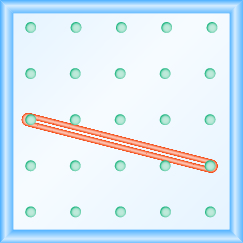
Uso de geoplacas para modelar taludes

En los siguientes ejercicios, encuentra la pendiente modelada en cada geobordo.

$La figura muestra una cuadrícula de puntos uniformemente espaciados. Hay 5 filas y 5 columnas. Hay un bucle estilo banda elástica que conecta el punto en la columna 1 fila 3 y el punto en la columna 5 fila 2.$
$La figura muestra una cuadrícula de puntos uniformemente espaciados. Hay 5 filas y 5 columnas. Hay un bucle estilo banda elástica que conecta el punto en la columna 2 fila 4 y el punto en la columna 5 fila 2.$
$La figura muestra una cuadrícula de puntos uniformemente espaciados. Hay 5 filas y 5 columnas. Hay un bucle estilo banda elástica que conecta el punto en la columna 2 fila 1 y el punto en la columna 4 fila 4.$
$La figura muestra una cuadrícula de puntos uniformemente espaciados. Hay 5 filas y 5 columnas. Hay un bucle estilo banda elástica que conecta el punto en la columna 2 fila 1 y el punto en la columna 4 fila 4.$

En los siguientes ejercicios, modele cada pendiente. Haz un dibujo para mostrar tus resultados.

$\dfrac{2}{3}$
$\dfrac{3}{4}$
$\dfrac{1}{4}$
$\dfrac{4}{3}$
$- \dfrac{1}{2}$
$- \dfrac{3}{4}$
$- \dfrac{2}{3}$
$- \dfrac{3}{2}$

Encuentra la Pendiente de una Línea a partir de su Gráfica

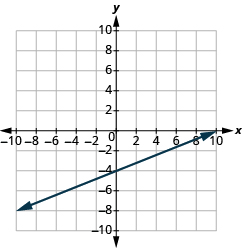
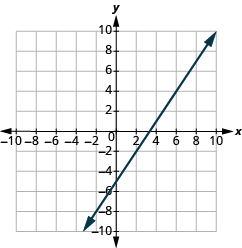
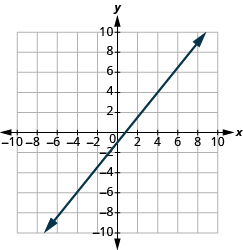
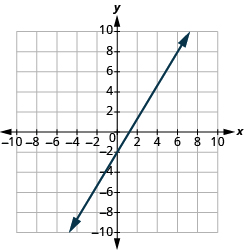
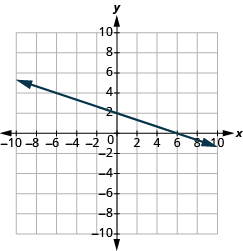
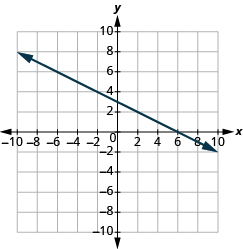
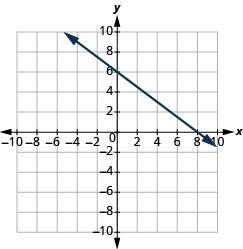
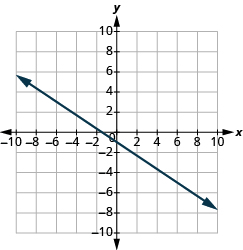
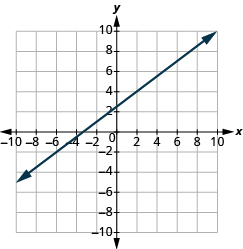
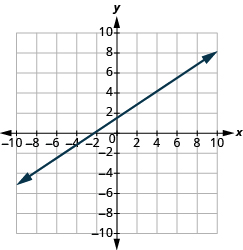
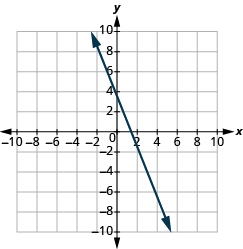
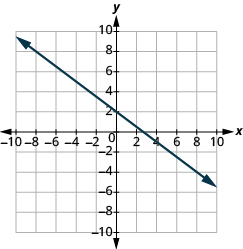
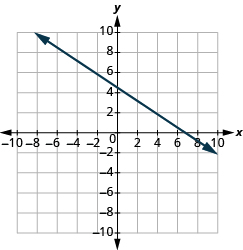
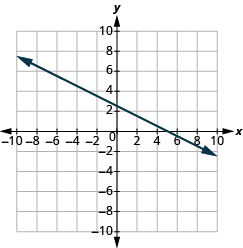
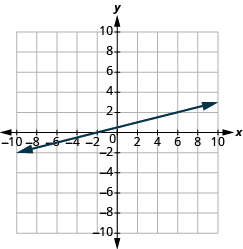
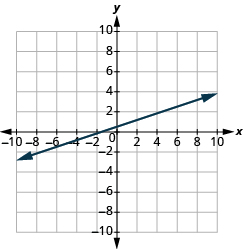
En los siguientes ejercicios, encuentra la pendiente de cada línea mostrada.

$La gráfica muestra el plano de coordenadas x y. El eje x va de -10 a 10. El eje y va de -10 a 10. Una línea pasa por los puntos “par ordenado 0, -4” y “par ordenado 10, 0”.$
$La gráfica muestra el plano de coordenadas x y. El eje x va de -10 a 10. El eje y va de -10 a 10. Una línea pasa por los puntos “par ordenado 0, -5” y “par ordenado 3, 0”.$
$La gráfica muestra el plano de coordenadas x y. El eje x va de -12 a 12. El eje y va de -12 a 12. Una línea pasa por los puntos “par ordenado 0, -1” y “par ordenado 1, 0”.$
$La gráfica muestra el plano de coordenadas x y. El eje x va de -10 a 10. El eje y va de -10 a 10. Una línea pasa por los puntos “par ordenado 0, 3” y “par ordenado 6, 0”.$
$La gráfica muestra el plano de coordenadas x y. El eje x va de -10 a 10. El eje y va de -10 a 10. Una línea pasa por los puntos “par ordenado 0, 2” y “par ordenado 6, 0”.$
$La gráfica muestra el plano de coordenadas x y. El eje x va de -10 a 10. El eje y va de -10 a 10. Una línea pasa por los puntos “par ordenado 0, 2” y “par ordenado 6, 0”.$
$La gráfica muestra el plano de coordenadas x y. El eje x va de -10 a 10. El eje y va de -10 a 10. Una línea pasa por los puntos “par ordenado 0, 6” y “par ordenado 8, 0”.$
$La gráfica muestra el plano de coordenadas x y. El eje x va de -10 a 10. El eje y va de -10 a 10. Una línea pasa por los puntos “par ordenado -1, 0” y “par ordenado 0, -1”.$
$La gráfica muestra el plano de coordenadas x y. El eje x va de -10 a 10. El eje y va de -10 a 10. Una línea pasa por los puntos “par ordenado -4, 0” y “par ordenado -4, 6”.$
$La gráfica muestra el plano de coordenadas x y. El eje x va de -10 a 10. El eje y va de -10 a 10. Una línea pasa por los puntos “par ordenado -2, 0” y “par ordenado 4, 4”.$
$La gráfica muestra el plano de coordenadas x y. El eje x va de -10 a 10. Una línea pasa por los puntos “par ordenado 0, 4” y “par ordenado 4, -6”.$
$La gráfica muestra el plano de coordenadas x y. El eje x va de -10 a 10. Una línea pasa por los puntos “par ordenado 0, 4” y “par ordenado 4, -6”.$
$La gráfica muestra el plano de coordenadas x y. El eje x va de -10 a 10. Una línea pasa por los puntos “par ordenado 1, 4” y “par ordenado 7, 0”.$
$La gráfica muestra el plano de coordenadas x y. El eje x va de -10 a 10. Una línea pasa por los puntos “par ordenado 0, 3” y “par ordenado 7, 0”.$
$La gráfica muestra el plano de coordenadas x y. El eje x va de -10 a 10. Una línea pasa por los puntos “par ordenado 2, 0” y “par ordenado 10, 4”.$
$La gráfica muestra el plano de coordenadas x y. El eje x va de -10 a 10. Una línea pasa por los puntos “par ordenado 6, 2” y “par ordenado 0, -3”.$

Encuentra la Pendiente de Líneas Horizontales y Verticales

En los siguientes ejercicios, encuentra la pendiente de cada línea.

y = 3
y = 1
x = 4
x = 2
y = −2
y = −3
x = −5
x = −4

Usa la Fórmula de Talud para encontrar la Talud de una Línea entre Dos Puntos

En los siguientes ejercicios, usa la fórmula de pendiente para encontrar la pendiente de la línea entre cada par de puntos.

(1, 4), (3, 9)
(2, 3), (5, 7)
(0, 3), (4, 6)
(0, 1), (5, 4)
(2, 5), (4, 0)
(3, 6), (8, 0)
(−3, 3), (2, −5)
(−2, 4), (3, −1)
(−1, −2), (2, 5)
(−2, −1), (6, 5)
(4, −5), (1, −2)
(3, −6), (2, −2)

Graficar una línea dado un punto y la pendiente

En los siguientes ejercicios, grafica la línea dada un punto y la pendiente.

(1, −2); m =$\dfrac{3}{4}$
(1, −1); m =$\dfrac{1}{2}$
(2, 5); m =$− \dfrac{1}{3}$
(1, 4); m =$− \dfrac{1}{2}$
(−3, 4); m =$− \dfrac{3}{2}$
(−2, 5); m =$− \dfrac{5}{4}$
. (−1, −4); m =$\dfrac{4}{3}$
(−3, −5); m =$\dfrac{3}{2}$
(0, 3); m =$− \dfrac{2}{5}$
(0, 5); m =$− \dfrac{4}{3}$
(−2, 0); m =$−\dfrac{3}{4}$
(−1, 0); m =$\dfrac{1}{5}$
(−3, 3); m = 2
(−4, 2); m = 4
(1, 5); m = −3
(2, 3); m = −1

Resolver aplicaciones de pendientes

En los siguientes ejercicios, resuelve estas aplicaciones de taludes.

Pendiente de un techo Una manera bastante fácil de determinar la pendiente es tomar un nivel de 12 pulgadas y colocarlo en un extremo de la superficie del techo. Luego toma una cinta métrica o regla, y mide desde el otro extremo del nivel hasta la superficie del techo. Puede utilizar estas medidas para calcular la pendiente de la cubierta. ¿Cuál es la pendiente del techo en esta imagen?

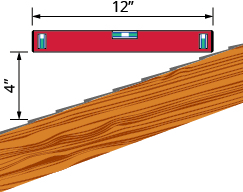
$La figura muestra una tabla de madera en diagonal que representa una rebanada de vista lateral de un techo inclinado. Un segmento de línea vertical con flechas en ambos extremos mide el cambio vertical de altura de la cubierta y está etiquetado como “4 pulgadas”. Una herramienta nivelada está en posición horizontal por encima del tablero y encima de ella hay un segmento de línea con flechas en ambos extremos etiquetadas como “12 pulgadas”.$

¿Cuál es la pendiente de la cubierta que se muestra?

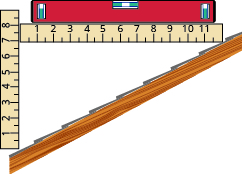
$La figura muestra una vista lateral diagonal de un techo inclinado. Una regla en posición vertical se encuentra en la parte inferior del segmento de cubierta y muestra las etiquetas de unidad 1 a 8 y se extiende una unidad más. Una segunda regla comienza en la etiqueta “7” de la regla vertical y se extiende horizontalmente hasta que golpea el techo ascendente. La regla horizontal tiene etiquetas unitarias 1 a 11 y se extiende una unidad más.$

Grado vial Una carretera local tiene una pendiente del 6%. El grado de una carretera es su pendiente expresada como porcentaje.
1. Encuentra la pendiente de la carretera como una fracción y luego simplifica la fracción.
2. ¿Qué subida y carrera reflejaría esta pendiente o pendiente?
Grado de autopista Una carretera local se eleva 2 pies por cada 50 pies de carretera.
1. ¿Cuál es la pendiente de la autopista?
2. El grado de una carretera es su pendiente expresada como porcentaje. ¿Cuál es el grado de esta autopista?

Matemáticas cotidianas

Rampa para sillas de ruedas Las reglas para rampas para sillas de ruedas requieren un aumento máximo de 1 pulgada para una carrera de 12 pulgadas
1. ¿Cuánto tiempo debe ser la rampa para acomodar una elevación de 24 pulgadas a la puerta?
2. Dibuja un modelo de esta rampa.
Rampa para silla de ruedas Una elevación de 1 pulgada para una carrera de 16 pulgadas facilita que el piloto de silla de ruedas ascienda por la rampa.
1. ¿Cuánto tiempo debe ser la rampa para acomodar fácilmente una elevación de 24 pulgadas a la puerta?
2. Dibuja un modelo de esta rampa.

Ejercicios de escritura

¿Qué te dice el letrero de la pendiente de una línea?
¿En qué se$\dfrac{1}{2}$ diferencia la gráfica de una línea con pendiente m = de la gráfica de una línea con pendiente m = 2?
¿Por qué no está definida la pendiente de una línea vertical?
Explica cómo puedes graficar una línea dado un punto y su pendiente.

Autocomprobación

(a) Después de completar los ejercicios, utilice esta lista de verificación para evaluar su dominio de los objetivos de esta sección.

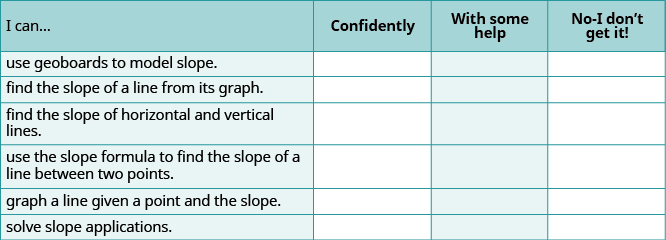
$CNX_BMath_Figure_AppB_069.jpg$

b) En una escala del 1 al 10, ¿cómo calificaría su dominio de esta sección a la luz de sus respuestas en la lista de verificación? ¿Cómo se puede mejorar esto?

Colaboradores y Atribuciones

Template:ContribOpenStaxPreAlgebra

Search

Text Color

Text Size

Margin Size

Font Type

Ejemplo\(\PageIndex{11}\):

Ejercicio\(\PageIndex{21}\):

Ejercicio\(\PageIndex{22}\):

CÓMO: GRAPAR UNA LÍNEA DADO UN PUNTO Y UNA TOL

Ejemplo\(\PageIndex{12}\):

Ejercicio\(\PageIndex{23}\):

Ejercicio\(\PageIndex{24}\):

Ejemplo\(\PageIndex{13}\):

Ejercicio\(\PageIndex{25}\):

Ejercicio\(\PageIndex{26}\):

Ejemplo\(\PageIndex{14}\):

Ejercicio\(\PageIndex{27}\):

Ejercicio\(\PageIndex{28}\):

Ejemplo\(\PageIndex{15}\):

Ejercicio\(\PageIndex{29}\):

Ejercicio\(\PageIndex{30}\):

Acceder a recursos adicionales en línea