1.3: Introducción a las funciones

Uno de los conceptos centrales en Álgebra Universitaria es la función. Hay muchas formas de describir una función y comenzamos definiendo una función como un tipo especial de relación.

Definición 1.6

Se dice que una relación en la que cada\(x\) coordenada coincide con una sola\(y\) coordenada se describe\(y\) como una función de\(x\).

Ejemplo 1.3.1

¿Cuál de las siguientes relaciones describen\(y\) como una función de\(x\)?

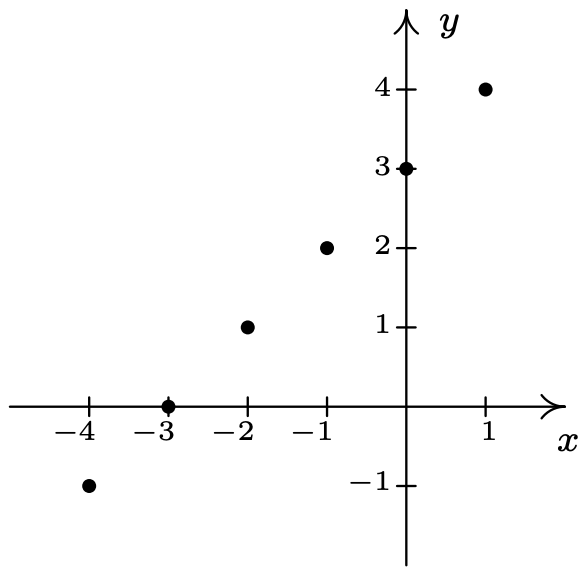
1. \(R_{1} = \{ (-2,1), (1,3), (1,4), (3,-1) \}\)
2. \(R_{2} = \{ (-2,1), (1,3), (2,3), (3,-1) \}\)

Solución

Un escaneo rápido de los puntos en\(R_{1}\) revela que la\(x\) coordenada\(1\) -se empareja con dos\(y\) coordenadas diferentes: a saber,\(3\) y\(4\). De ahí que en\(R_{1}\), no\(y\) es una función de\(x\). Por otro lado, cada\(x\) coordenada en\(R_{2}\) ocurre solo una vez, lo que significa que cada\(x\) coordenada tiene solo una\(y\) coordenada correspondiente. Entonces,\(R_{2}\) representa\(y\) como una función de\(x\).

Obsérvese que en el ejemplo anterior, la relación\(R_{2}\) contenía dos puntos diferentes con las mismas\(y\) coordenadas, a saber\((1,3)\) y\((2,3)\). Recuerda, para poder decir\(y\) es una función de\(x\), solo necesitamos asegurarnos de que no se use la misma\(x\) coordenada en más de un punto. ¹

Para ver qué significa geométricamente el concepto de función, graficamos\(R_{1}\) y\(R_{2}\) en el plano.

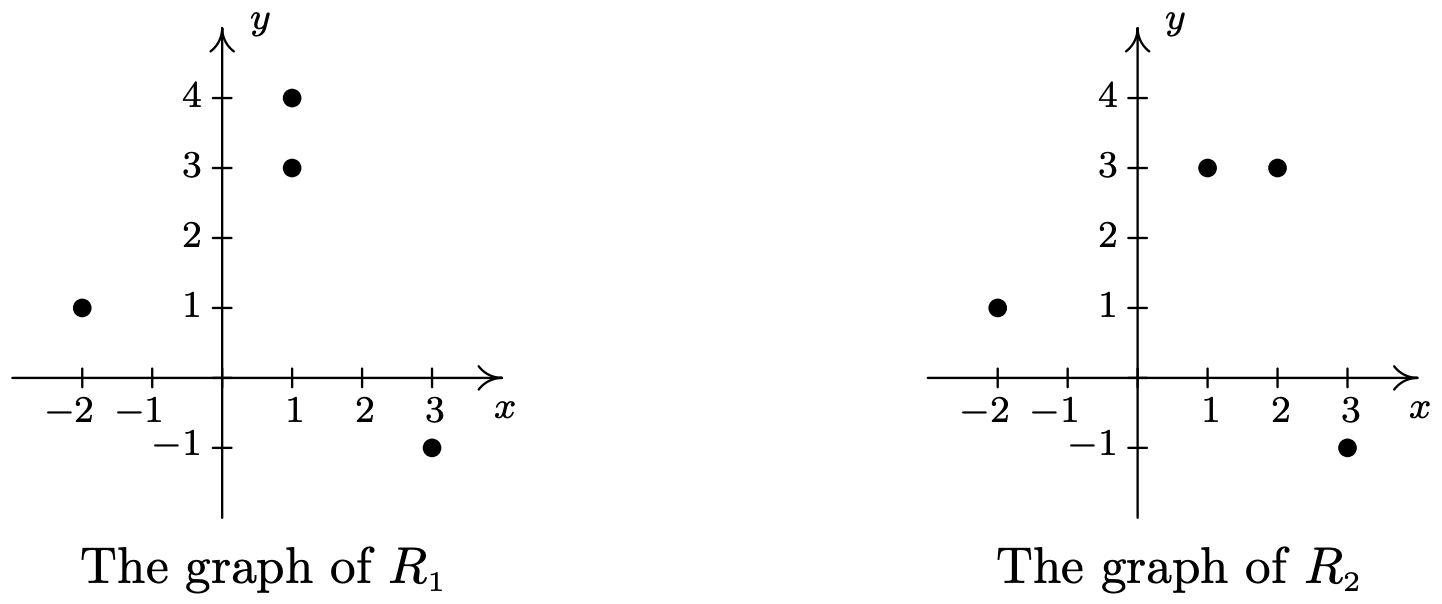
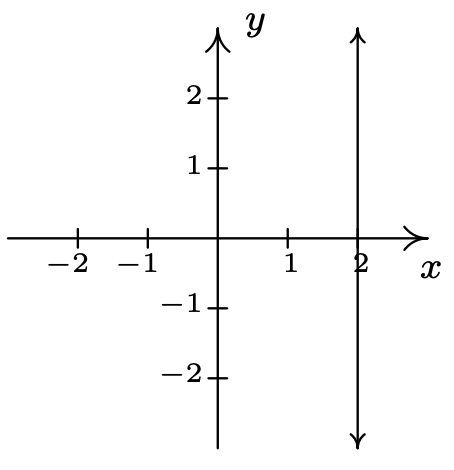
El hecho de que la\(x\) coordenada\(1\) se empareja con dos\(y\) coordenadas diferentes en se\(R_{1}\) presenta gráficamente como los puntos\((1,3)\) y se\((1,4)\) encuentra en la misma línea vertical,\(x=1\). Si volvemos nuestra atención a la gráfica de\(R_{2}\), vemos que no hay dos puntos de la relación que se encuentran en la misma línea vertical. Podemos generalizar esta idea de la siguiente manera

Definición 1.1. La prueba de línea vertical

Un conjunto de puntos en el plano representa\(y\) como una función de\(x\) si y sólo si no hay dos puntos en la misma línea vertical.

Vale la pena tomarse un tiempo para meditar en la Prueba de Línea Vertical; comprobará para ver qué tan bien entiendes el concepto de 'función' así como el concepto de 'gráfico'.

Ejemplo 1.3.2

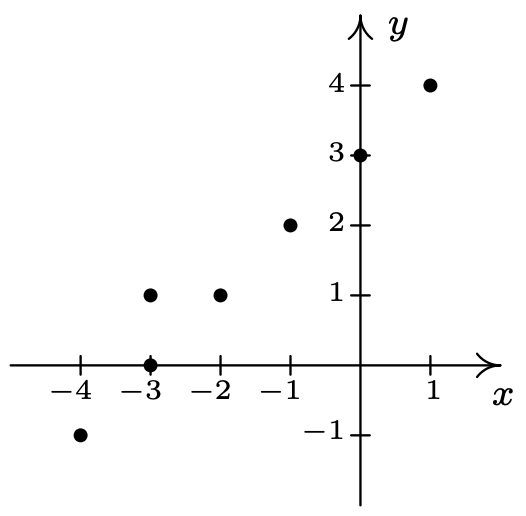
Utilice la Prueba de Línea Vertical para determinar cuál de las siguientes relaciones describe\(y\) como una función de\(x\).

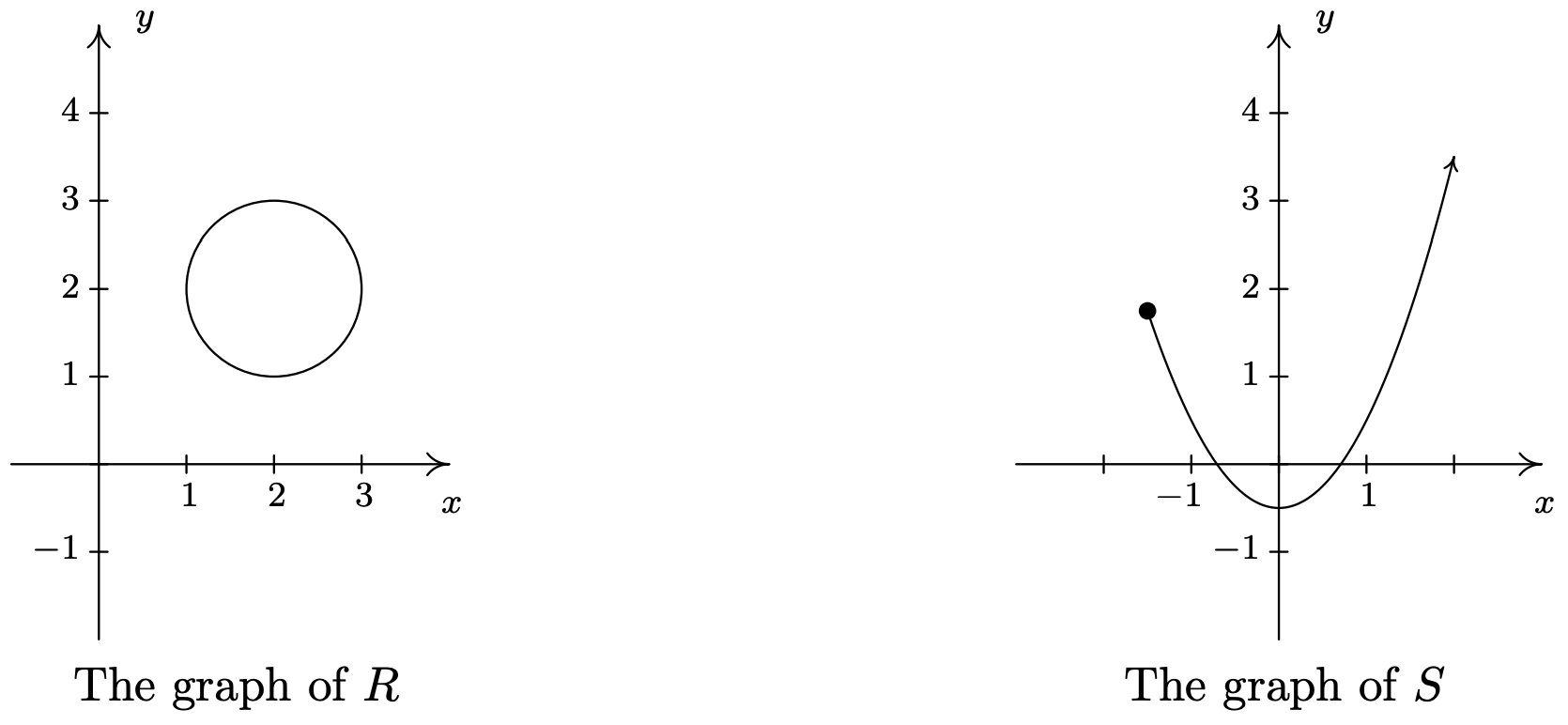
Solución

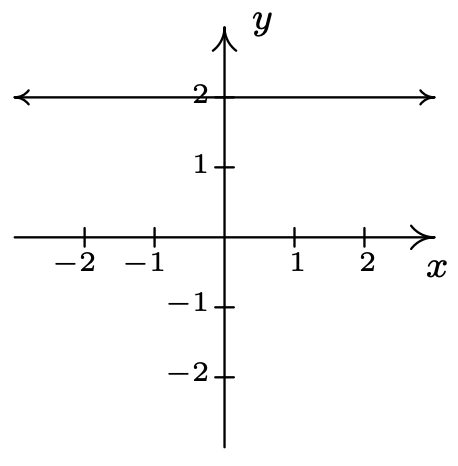
Mirando la gráfica de\(R\), podemos imaginar fácilmente una línea vertical cruzando la gráfica más de una vez. Por lo tanto,\(R\) no representa\(y\) como una función de\(x\). Sin embargo, en la gráfica de\(S\), cada línea vertical cruza la gráfica\(y\) como máximo una vez, por lo que\(S\) representa en función de\(x\).

En la prueba anterior, decimos que la gráfica de la relación\(R\) falla la Prueba de Línea Vertical, mientras que la gráfica de\(S\) pasa la Prueba de Línea Vertical. Tenga en cuenta que en la gráfica de\(R\) hay infinitamente muchas líneas verticales que cruzan la gráfica más de una vez. No obstante, para fallar la Prueba de Línea Vertical, todo lo que necesitas es una línea vertical que se ajuste a la factura, como lo ilustra el siguiente ejemplo.

Ejemplo 1.3.3

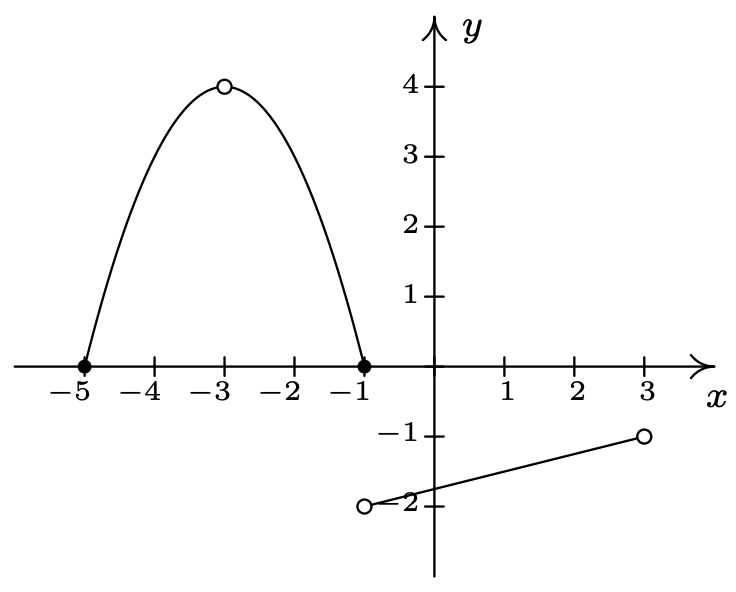
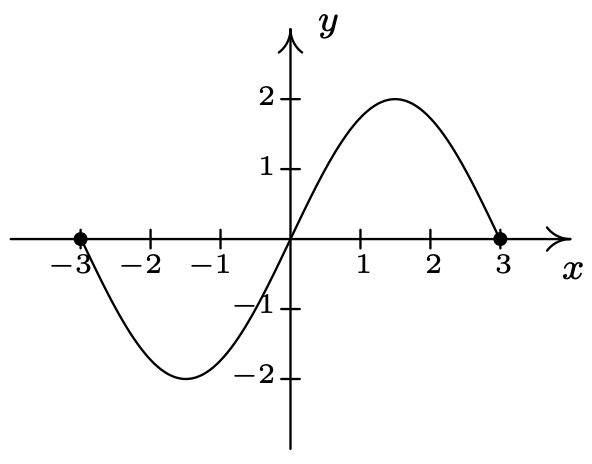
Utilice la Prueba de Línea Vertical para determinar cuál de las siguientes relaciones describe\(y\) como una función de\(x\).

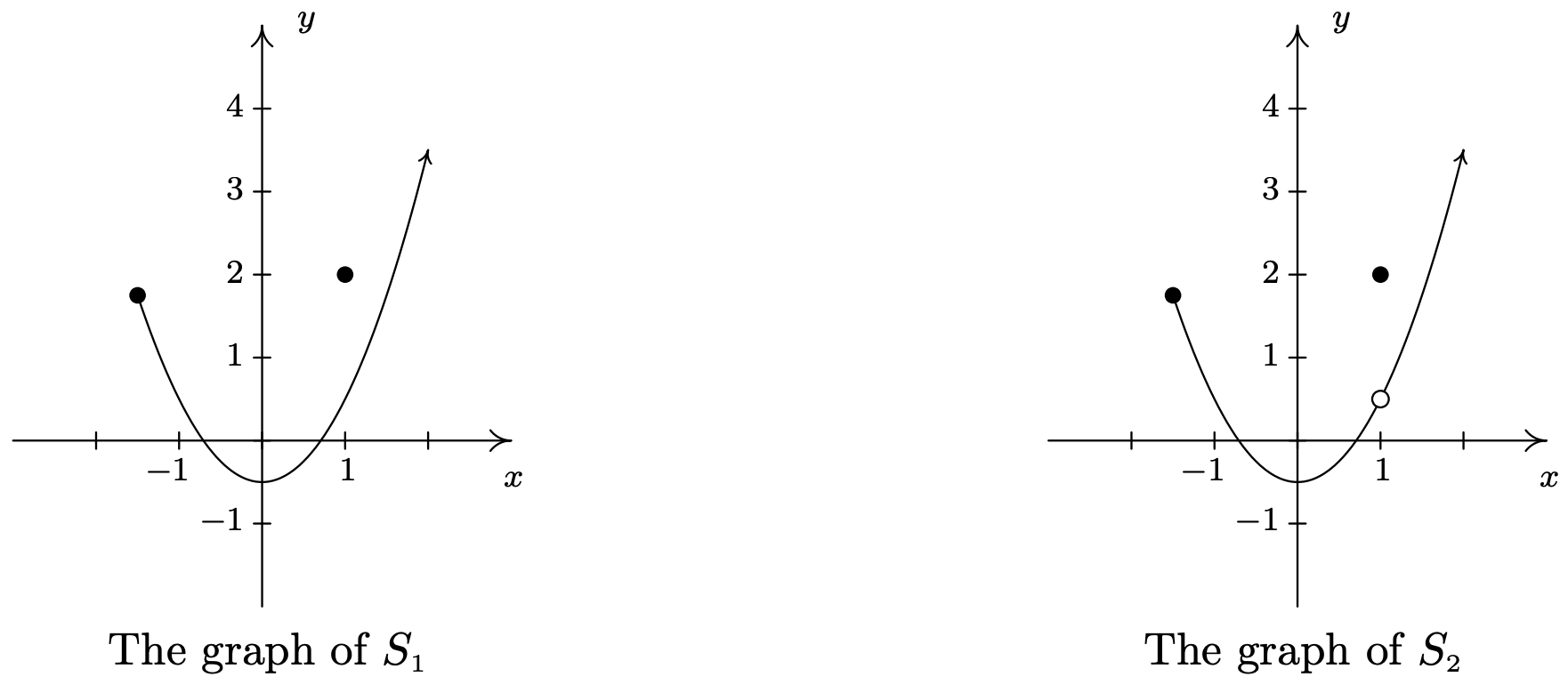
Solución

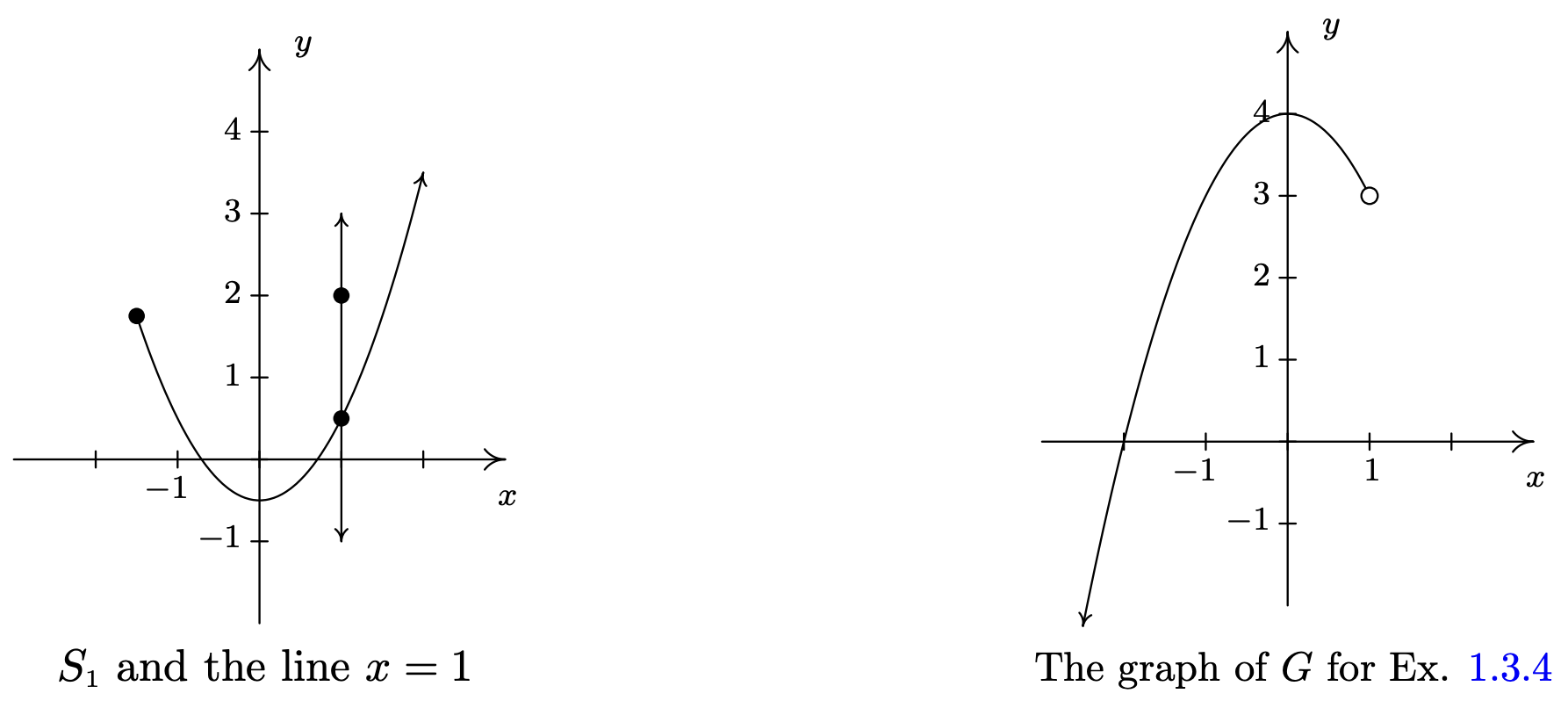
Ambos\(S_{1}\) y\(S_{2}\) son ligeras modificaciones a la relación\(S\) en el ejemplo anterior cuya gráfica determinamos pasó la Prueba de Línea Vertical. En ambos\(S_{1}\) y\(S_{2}\), es la adición del punto\((1,2)\) lo que amenaza con causar problemas. En\(S_{1}\), hay un punto en la curva con\(x\) -coordenada 1 justo debajo\((1,2)\), lo que significa que ambos\((1,2)\) y este punto en la curva se encuentran en la línea vertical\(x=1\). (Ver la imagen de abajo y la izquierda.) De ahí que la gráfica de\(S_{1}\) falle la Prueba de Línea Vertical, por lo que no\(y\) es una función de\(x\) aquí. No obstante, en\(S_{2}\) aviso que se ha omitido el punto con\(x\) -coordenada 1 en la curva, dejando ahí un 'círculo abierto'. De ahí que la línea vertical\(x=1\) cruce la gráfica de\(S_{2}\) sólo en el punto\((1,2)\). En efecto, cualquier línea vertical cruzará la gráfica como máximo una vez, por lo que tenemos que la gráfica de\(S_{2}\) pasa la Prueba de Línea Vertical. Así se describe\(y\) como una función de\(x\).

Supongamos que una relación\(F\) describe\(y\) como una función de\(x\). A los conjuntos de\(y\) coordenadas\(x\) - y -se les dan nombres especiales que definimos a continuación.

Definición 1.7

Supongamos que\(F\) es una relación que describe\(y\) como una función de\(x\).

• El conjunto de las\(x\) -coordenadas de los puntos en\(F\) se llama el dominio de\(F\).
• El conjunto de las\(y\) coordenadas -de los puntos en\(F\) se llama el rango de\(F\).

Demostramos encontrar el dominio y el rango de funciones que se nos han dado ya sea gráficamente o mediante el método roster en el siguiente ejemplo.

Ejemplo 1.3.4

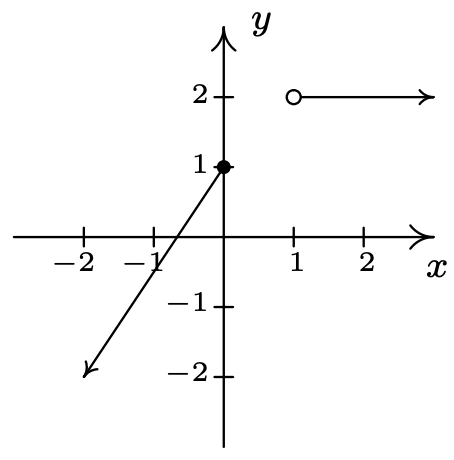
Encuentra el dominio y rango de la función\(F = \{ (-3, 2), (0, 1), (4, 2), (5, 2) \}\) y de la función\(G\) cuya gráfica se da arriba a la derecha.

Solución

El dominio de\(F\) es el conjunto de las\(x\) -coordenadas de los puntos en\(F\), es decir,\(\{ -3, 0, 4, 5 \}\) y el rango de\(F\) es el conjunto de las\(y\) -coordenadas, a saber\(\{ 1,2 \}.\)

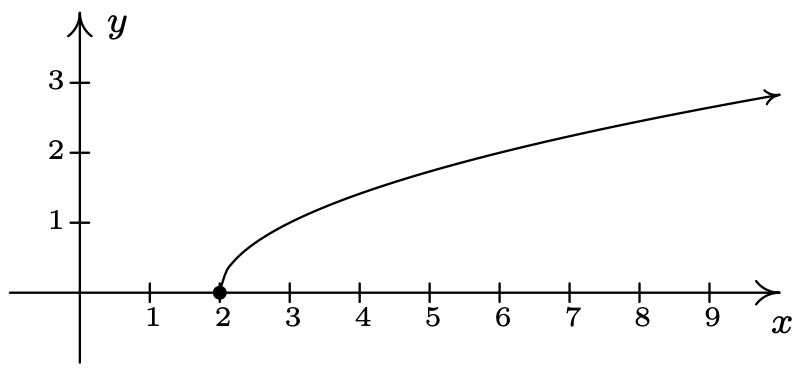
Para determinar el dominio y rango de\(G\), necesitamos determinar cuáles\(x\) y\(y\) valores ocurren como coordenadas de puntos en la gráfica dada. Para encontrar el dominio, puede ser útil imaginar colapsar la curva al\(x\) eje y determinar la porción del\(x\) eje que se cubre. A esto se le llama proyectar la curva hacia el\(x\) eje. Antes de comenzar a proyectar, debemos prestar atención a dos anotaciones sutiles en la gráfica: la punta de flecha en la esquina inferior izquierda de la gráfica indica que la gráfica sigue curvándose hacia abajo hacia la izquierda para siempre más; y el círculo abierto en\((1,3)\) indica que el punto\((1,3)\) no está en la gráfica, pero todos los puntos de la curva que conducen a ese punto lo son.

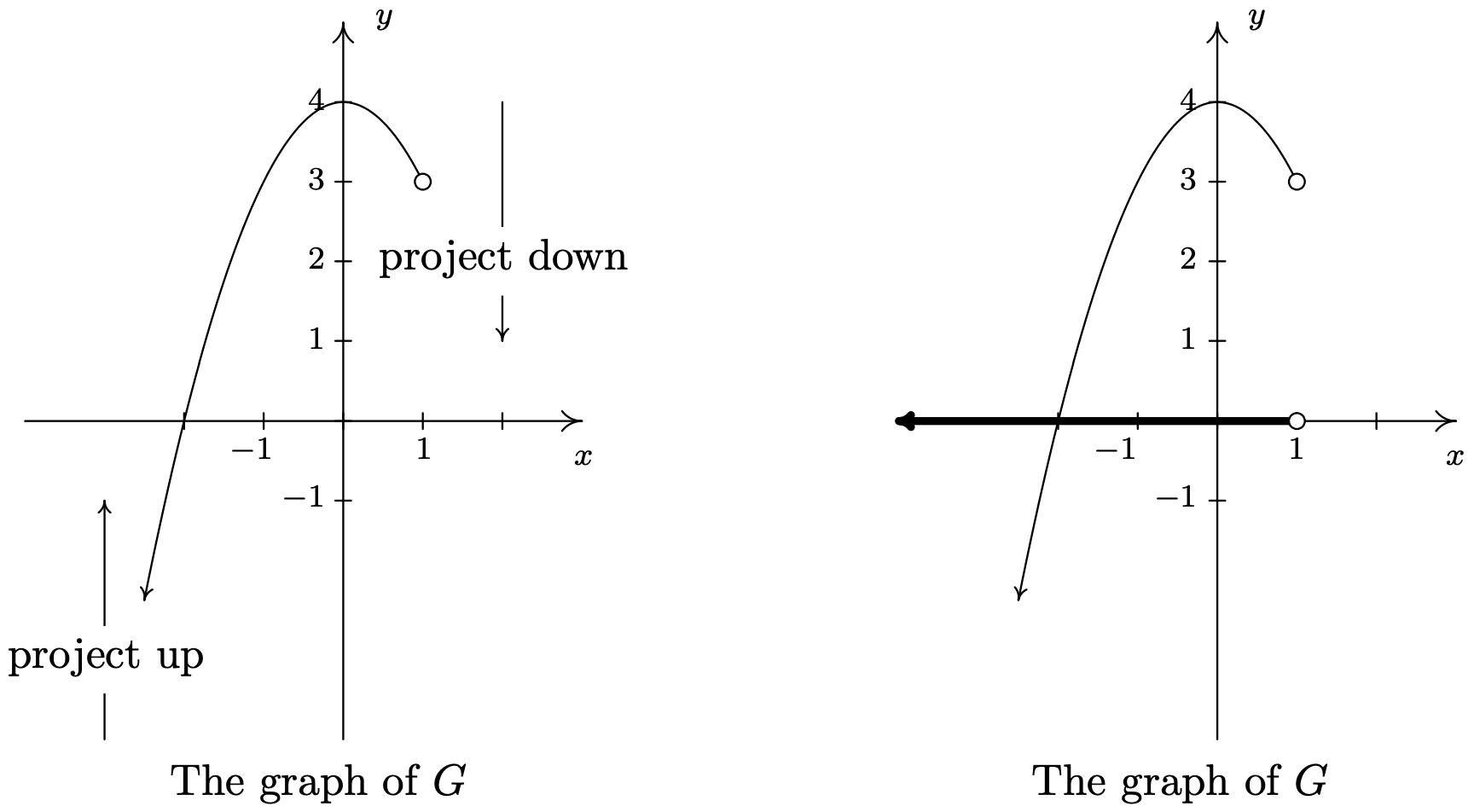
Vemos de la figura que si proyectamos la gráfica de\(G\) al\(x\) eje -eje, obtenemos todos los números reales menores que\(1\). Usando la notación de intervalos, escribimos el dominio de\(G\) as\((-\infty, 1)\). Para determinar el rango de\(G\), proyectamos la curva al\(y\) eje -de la siguiente manera:

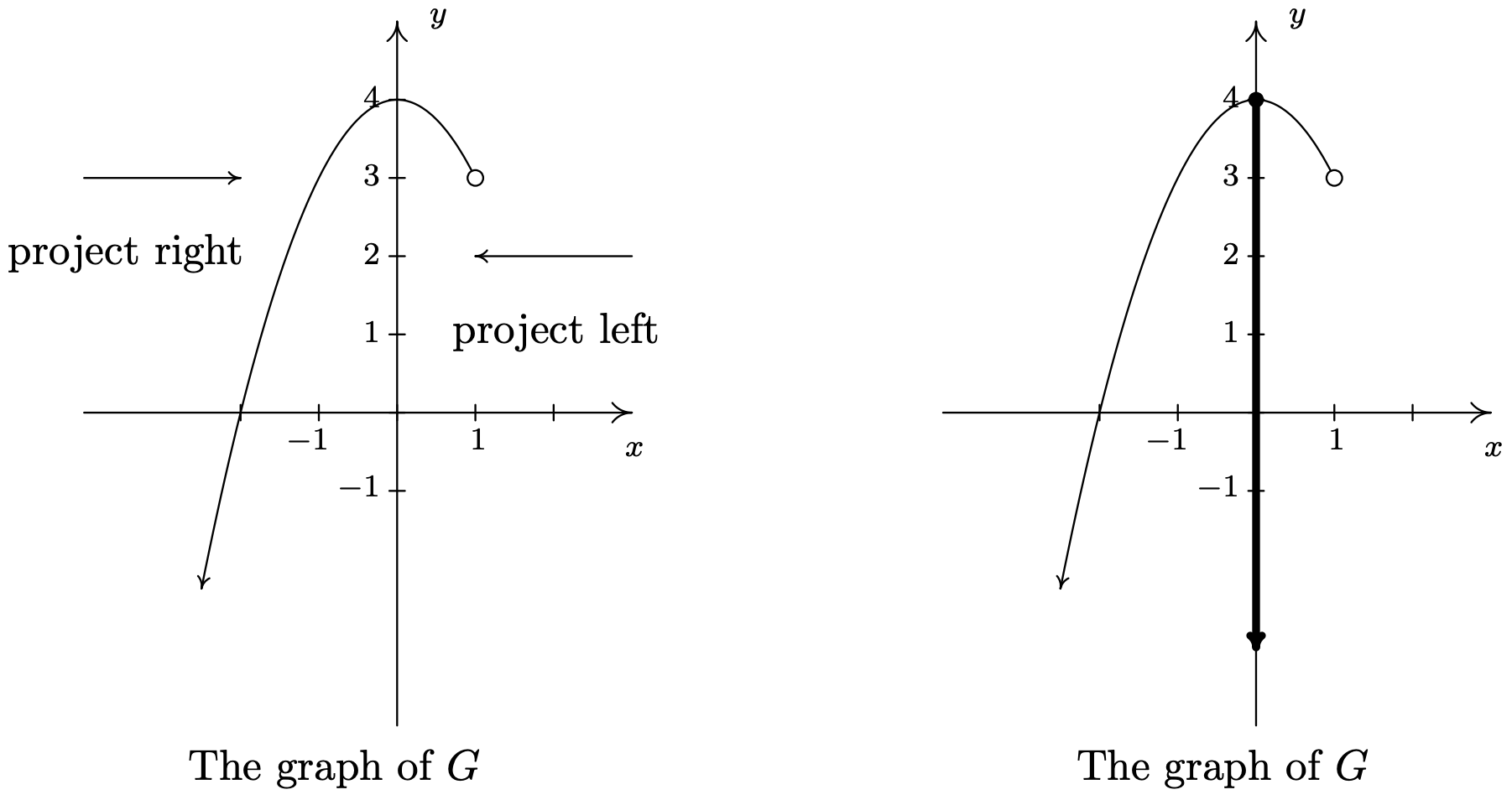
Tenga en cuenta que a pesar de que hay un círculo abierto en\((1,3)\), todavía incluimos el\(y\) valor de\(3\) en nuestro rango, ya que el punto\((-1,3)\) está en la gráfica de\(G\). Vemos que el rango de\(G\) es todos los números reales menores o iguales a\(4\), o, en notación de intervalos,\((-\infty, 4]\).

Todas las funciones son relaciones, pero no todas las relaciones son funciones. Así, las ecuaciones que describieron las relaciones en la Sección 1.2 pueden o no describir\(y\) como una función de\(x\). La representación algebraica de funciones es posiblemente la forma más importante de verlas por lo que necesitamos un proceso para determinar si una ecuación de una relación representa o no una función. (Retrasamos la discusión de encontrar el dominio de una función dada algebraicamente hasta la Sección 1.4.)

Ejemplo 1.3.5

Determinar qué ecuaciones representan\(y\) en función de\(x\).

1. \(x^3 + y^2 = 1\)
2. \(x^2 + y^3 = 1\)
3. \(x^2y = 1 - 3y\)

Solución

Para cada una de estas ecuaciones, resolvemos\(y\) y determinamos si cada elección de\(x\) determinará solo un valor correspondiente de\(y\).

1. \[\begin{array}{rclr} x^3 + y^2 & = & 1 & \\ y^2 & = & 1 - x^3 & \\ \sqrt{y^2} & = & \sqrt{1 - x^3} & \mbox{extract square roots} \\ y & = & \pm \sqrt{1 - x^3} & \\ \end{array}\]
2. \[\begin{array}{rclr} x^2 + y^3 & = & 1 & \\ y^3 & = & 1 - x^2 & \\ \sqrt[3]{y^3} & = & \sqrt[3]{1 - x^2} & \\ y & = & \sqrt[3]{1 - x^2} & \\ \end{array}\]
3. \[\begin{array}{rclr} x^2y & = & 1 - 3y & \\ x^2y + 3y & = & 1 & \\ y \left(x^2 + 3\right) & = & 1 & \mbox{factor} \\ y & = & \dfrac{1}{x^2 + 3} & \\ \end{array}\]

Para cada elección de\(x\), sólo hay un valor para\(y\), por lo que esta ecuación describe\(y\) como una función de\(x\).

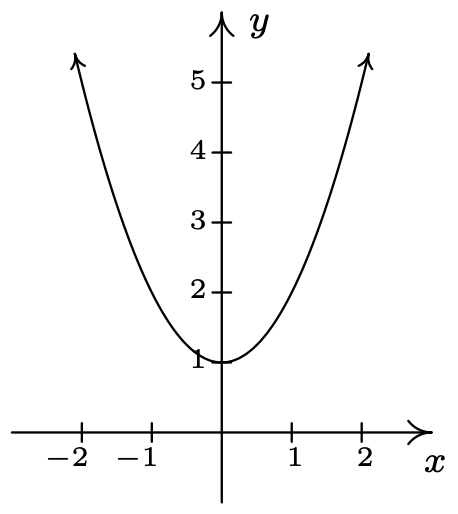
Podríamos intentar usar nuestra calculadora gráfica para verificar nuestras respuestas al ejemplo anterior, pero inmediatamente nos encontramos con problemas. El menú “Y=” de la calculadora requiere que la ecuación sea de la forma '\(y\)= alguna expresión de\(x\)'. Si quisiéramos verificar que la primera ecuación del Ejemplo 1.3.5 no representa\(y\) como una función de\(x\), necesitaríamos ingresar dos expresiones separadas en la calculadora: una para la raíz cuadrada positiva y otra para la raíz cuadrada negativa que encontramos al resolver la ecuación para\(y\). Como se predijo, la gráfica resultante que se muestra a continuación falla claramente la Prueba de Línea Vertical, por lo que la ecuación no representa\(y\) en función de\(x\).

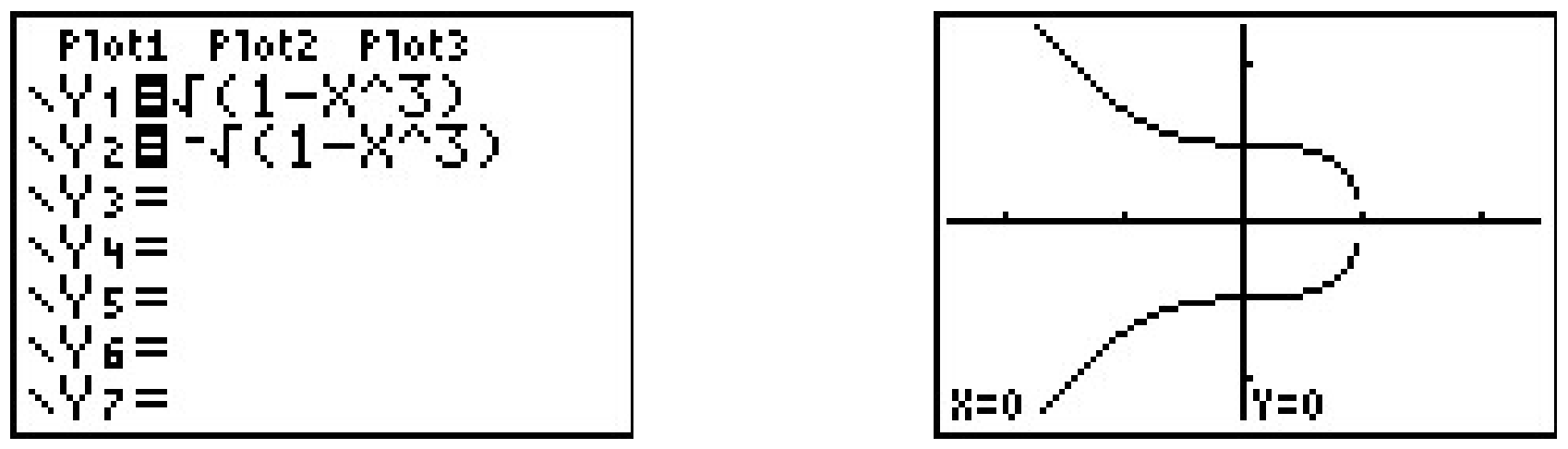
Así, para poder usar la calculadora para mostrar que\(x^3 + y^2 = 1\) no representa\(y\) como una función de\(x\) necesitábamos saber analíticamente que no\(y\) era una función de\(x\) para que pudiéramos usar la calculadora correctamente. Hay utilidades gráficas más avanzadas que pueden hacer gráficas de funciones implícitas, pero necesitas conocer aún más Álgebra para que funcionen correctamente. ¿Entiende el punto que estamos tratando de hacer aquí? Creemos que es lo mejor para ti aprender la forma analítica de hacer las cosas para que siempre seas más inteligente que tu calculadora.

1.3.1 Ejercicios

En los Ejercicios 1-12, determinar si la relación representa\(y\) o no en función de\(x\). Encontrar el dominio y rango de aquellas relaciones que son funciones.

1. {\((-3, 9)\),\(\;(-2, 4)\),\(\;(-1, 1)\),\(\;(0, 0)\),\(\;(1, 1)\),\(\;(2, 4)\),\(\;(3, 9)\}\)
2. \(\left\{ (-3,0), (1,6), (2, -3), (4,2), (-5,6), (4, -9), (6,2) \right\}\)
3. \(\left\{ (-3,0), (-7,6), (5,5), (6,4), (4,9), (3,0) \right\}\)
4. \(\left\{ (1,2), (4,4), (9,6), (16,8), (25,10), (36, 12), \ldots \right\}\)
5. {(\(x, y) \, | \, x\)es un entero impar, y\(y\) es un entero par}
6. {\((x, 1) \, | \, x\)es un número irracional}
7. {\((1, 0)\),\(\;(2, 1)\),\(\;(4, 2)\),,\(\;(8, 3)\),\(\;(16, 4)\),\(\;(32, 5), \;\)...}
8. {\(\ldots, \; (-3, 9)\),\(\;(-2, 4)\),\(\;(-1, 1)\),,\(\;(0, 0)\),\(\;(1, 1)\),\(\;(2, 4)\),\(\;(3, 9), \;\)...}
9. \(\{ (-2, y) \, | \, -3 < y < 4\}\)
10. \(\{ (x,3) \, | \, -2 \leq x < 4\}\)
11. \(\ \left\{\left(x, x^{2}\right) \mid x \text { is a real number }\right\}\)
12. \(\ \left\{\left(x^{2}, x\right) \mid x \text { is a real number }\right\}\)

En los Ejercicios 13-32, determinar si la relación representa\(y\) o no en función de\(x\). Encontrar el dominio y rango de aquellas relaciones que son funciones.

13. 
14. 
15. 
16. 
17. 
18. 
19. 
20. 
21. 
22. 
23. 
24. 
25. 
26. 
27. 
28. 
29. 
30. 
31. 
32. 

En los Ejercicios 33-37, determinar si la ecuación representa\(y\) o no en función de\(x\).

33. \(y = x^{3} - x\)
34. \(y = \sqrt{x - 2}\)
35. \(x^{3}y = -4\)
36. \(x^{2} - y^{2} = 1\)
37. \(y = \dfrac{x}{x^{2} - 9}\)
38. \(x = -6\)
39. \(x = y^2 + 4\)
40. \(y = x^2 + 4\)
41. \(x^2 + y^2 = 4\)
42. \(y = \sqrt{4-x^2}\)
43. \(x^2 - y^2 = 4\)
44. \(x^3 + y^3 = 4\)
45. \(2x + 3y = 4\)
46. \(2xy = 4\)
47. \(x^2 = y^2\)
48. Explique por qué la población\(P\) de Sasquatch en un área determinada es función del tiempo\(t\). ¿Cuál sería el alcance de esta función?
49. Explica por qué la relación entre tus compañeros de clase y sus direcciones de correo electrónico puede no ser una función. ¿Y los números de teléfono y los números de Seguro Social?

El proceso dado en el Ejemplo 1.3.5 para determinar si una ecuación de una relación representa\(y\) como una función de\(x\) desgloses si no podemos resolver la ecuación para\(y\) en términos de\(x\). Sin embargo, eso no nos impide probar que una ecuación no logra representar\(y\) en función de\(x\). Lo que realmente necesitamos son dos puntos con la misma\(x\) -coordenada y diferentes\(y\) -coordenadas que ambos satisfagan la ecuación para que la gráfica de la relación falle la Prueba de Línea Vertical 1.1. Discuta con tus compañeros de clase cómo podrías encontrar esos puntos para las relaciones dadas en los Ejercicios 50-53.

50. \(x^{3} + y^{3} - 3xy = 0\)
51. \(x^{4} = x^{2} + y^{2}\)
52. \(y^{2} = x^{3} + 3x^{2}\)
53. \((x^{2} + y^{2})^{2} = x^{3} + y^{3}\)

1.3.2 Respuestas

1. 
   Dominio de función = {\(-3\),\(-2\),\(-1\),\(0\),\(1\),\(2\),\(3\)}
   rango = {\(0\),,\(1\),\(4\),\(9\)}

2. No es una función

3. 
   Dominio de función =\(\left\{ -7, -3, 3, 4, 5, 6 \right\}\)
   rango =\(\left\{ 0,4,5,6,9 \right\}\)

4. 
   Dominio de función =\ (\\ {1,4,9,16,25,36,\ ldots\}
   =\ {x\ mid x\ text {es un cuadrado perfecto}\}\)
   range=\ (\\ {2,4,6,8,10,12,\ ldots\}
   =\ {y\ mid y\ text {es un entero par positivo}\}\)

5. No es una función

6. 
   Dominio de función=\(\ \{x \mid x \text { is irrational }\}\)
   rango = {\(1\)}

7. 
   Dominio de función =\(\ \left\{x \mid x=2^{n} \text { for some whole number } n\right\}\)
   rango =\(\ \{y \mid y \text { is any whole number }\}\)

8. 
   Dominio de función =\(\ \{x \mid x \text { is any integer }\}\)
   rango =\(\ \left\{y \mid y=n^{2} \text { for some integer } n\right\}\)

9. No es una función

10. 
    Dominio de función =\([-2, 4)\), rango = {\(3\)}

11. 
    Dominio de función =\((-\infty, \infty)\)
    rango =\([0,\infty)\)

12. No es una función

13. 
    Dominio de función = {\(-4\),\(-3\),\(-2\),\(-1\),\(0\),\(1\)}
    rango = {\(-1\),,\(0\),\(1\),\(2\),\(3\),\(4\)}

14. No es una función

15. 
    Dominio de función =\((-\infty, \infty)\)
    rango =\([1, \infty)\)

16. No es una función

17. 
    Dominio de función =\([2, \infty)\)
    rango =\([0, \infty)\)

18. 
    Dominio de función =\((-\infty, \infty)\)
    rango =\((0, 4]\)

19. No es una función

20. 
    Dominio de función =\([-5,-3) \cup(-3, 3)\)
    rango =\((-2, -1) \cup [0, 4)\)

21. 
    Dominio de función =\([-2, \infty)\)
    rango =\([-3, \infty)\)

22. No es una función

23. 
    Dominio de función =\([-5,4)\)
    rango =\([-4,4)\)

24. 
    Dominio de función =\([0,3) \cup (3,6]\)
    rango =\((-4,-1] \cup [0,4]\)

25. 
    Dominio de función =\((-\infty, \infty)\)
    rango =\((-\infty, 4]\)

26. 
    Dominio de función =\((-\infty, \infty)\)
    rango =\((-\infty, 4]\)

27. 
    Dominio de función =\([-2, \infty)\)
    rango =\((-\infty, 3]\)

28. 
    Dominio de función =\((-\infty, \infty)\)
    rango =\((-\infty, \infty)\)

29. 
    Dominio de función =\((-\infty, 0] \cup (1, \infty)\)
    rango =\((-\infty, 1] \cup \{ 2\}\)

30. 
    Dominio de función =\([-3,3]\)
    rango =\([-2,2]\)

31. No es una función

32. 
    Dominio de función =\((-\infty, \infty)\)
    rango =\(\{2\}\)

33. Función
34. Función
35. Función
36. No es una función
37. Función
38. No es una función
39. No es una función
40. Función
41. No es una función
42. Función
43. No es una función
44. Función
45. Función
46. Función
47. No es una función

---

Referencia

¹ Tendremos ocasión más adelante en el texto de preocuparnos por el concepto de\(\ x\) ser una función de\(\ y\). En este caso,\(\ R_{1}\) representa x en función de\(\ y\);\(\ R_{2}\) no.