2.1: Funciones lineales
- Page ID
- 119482
Comenzamos ahora el estudio de familias de funciones. Nuestra primera familia, las funciones lineales, son viejos amigos como pronto veremos. Recuerde de Geometría que dos puntos distintos en el plano determinan una línea única que contiene esos puntos, como se indica a continuación.
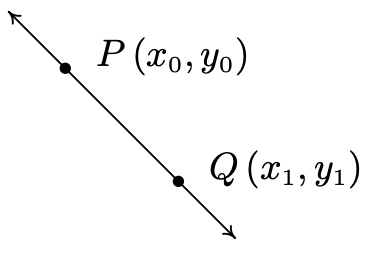
Para dar una idea de la 'inclinación' de la línea, recordamos que podemos calcular la pendiente de la línea usando la fórmula a continuación.
La pendiente\(\ m\) de la línea que contiene los puntos\(\ P\left(x_{0}, y_{0}\right)\) y\(\ Q\left(x_{1}, y_{1}\right)\) es:
\(\ m=\frac{y_{1}-y_{0}}{x_{1}-x_{0}},\)
siempre\(\ x_{1} \neq x_{0}\).
Un par de notas sobre la Ecuación 2.1 están en orden. Primero, no preguntes por qué usamos la letra\(\ ‘m’\) para representar pendiente. Hay muchas explicaciones por ahí, pero al parecer nadie sabe con certeza. 1 En segundo lugar, la estipulación\(\ x_{1} \neq x_{0}\) asegura que no estamos tratando de dividir por cero. Se invita al lector a hacer una pausa para pensar en lo que está sucediendo geométricamente; el lector ansioso puede saltarse al siguiente ejemplo.
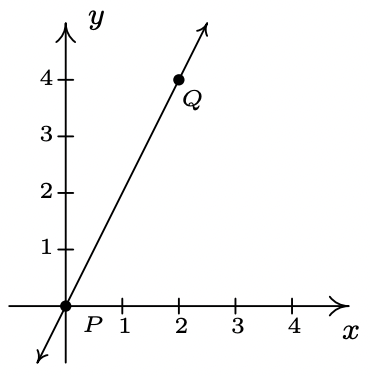
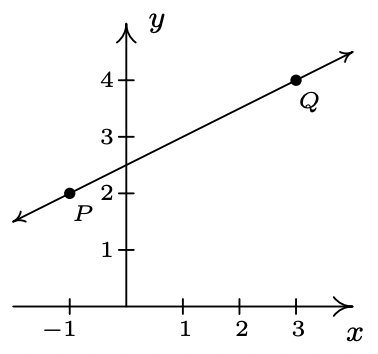
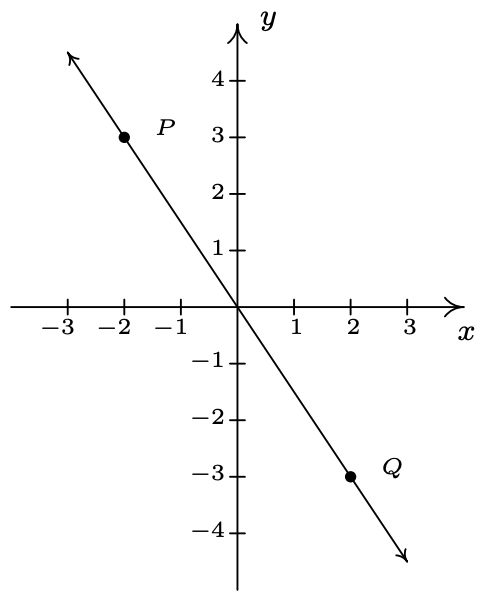
Encuentra la pendiente de la línea que contiene los siguientes pares de puntos, si existe. Trazar cada par de puntos y la línea que los contiene.
- \(\ P(0,0), Q(2,4)\)
- \(\ P(-1,2), Q(3,4)\)
- \(\ P(-2,3), Q(2,-3)\)
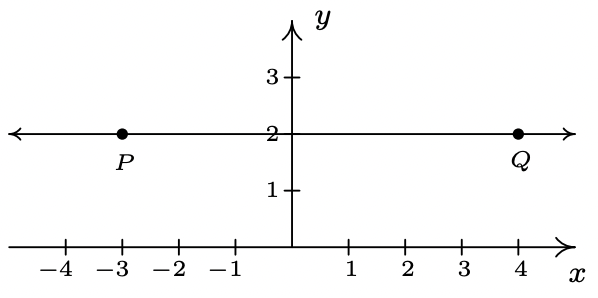
- \(\ P(-3,2), Q(4,2)\)
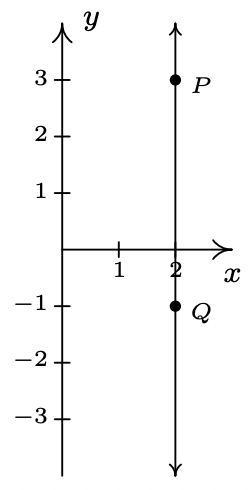
- \(\ P(2,3), Q(2,-1)\)
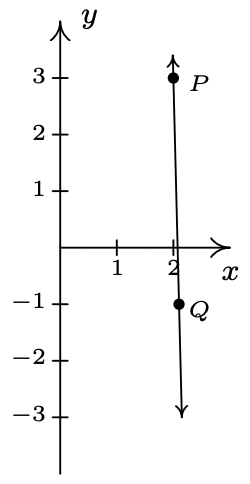
- \(\ P(2,3), Q(2.1,-1)\)
Solución
En cada uno de estos ejemplos, aplicamos la fórmula de pendiente, Ecuación 2.1.
- \(\ m=\frac{4-0}{2-0}=\frac{4}{2}=2\)
- \(\ m=\frac{4-2}{3-(-1)}=\frac{2}{4}=\frac{1}{2}\)
- \(\ m=\frac{-3-3}{2-(-2)}=\frac{-6}{4}=-\frac{3}{2}\)
- \(\ m=\frac{2-2}{4-(-3)}=\frac{0}{7}=0\)
- \(\ m=\frac{-1-3}{2-2}=\frac{-4}{0}\), que no está definido
- \(\ m=\frac{-1-3}{2.1-2}=\frac{-4}{0.1}=-40\)
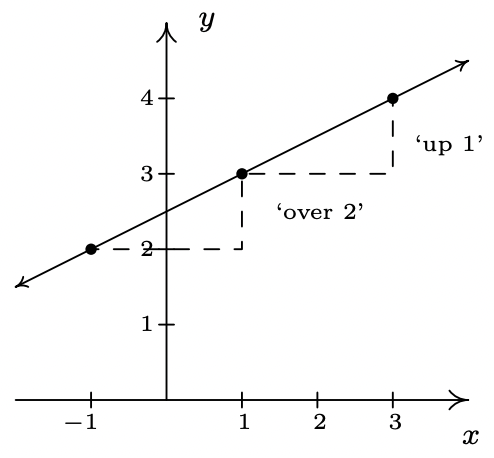
Algunos comentarios sobre el Ejemplo 2.1.1 están en orden. Primero, por razones que pronto quedarán claras, si la pendiente es positiva entonces se dice que la línea resultante va en aumento. Si es negativo, decimos que la línea está disminuyendo. Una pendiente de 0 da como resultado una línea horizontal que decimos que es constante, y una pendiente indefinida da como resultado una línea vertical. 2 En segundo lugar, cuanto mayor sea la pendiente en valor absoluto, más pronunciada será la línea. Tal vez recuerdes de Álgebra Intermedia que la pendiente puede describirse como la relación\(\ \frac{\text { ‘rise’ }}{\text { run }}\). Por ejemplo, en la segunda parte del Ejemplo 2.1.1, encontramos que la pendiente era 1 2. Podemos interpretar esto como una subida de 1 unidad hacia arriba por cada 2 unidades a la derecha que viajemos a lo largo de la línea, como se muestra a continuación.
Usando notación más formal, dado puntos\(\ \left(x_{0}, y_{0}\right)\) y\(\ \left(x_{1}, y_{1}\right)\), usamos la letra griega delta\(\ \text{‘}\Delta\text{’}\) para escribir\(\ \Delta y=y_{1}-y_{0}\) y\(\ \Delta x=x_{1}-x_{0}\). En la mayoría de los círculos científicos, el símbolo\(\ \Delta\) significa 'cambio'. De ahí que podamos escribir
\(\ m=\frac{\Delta y}{\Delta x},\)
que describe la pendiente como la tasa de cambio de\(\ y\) con respecto a\(\ x\). Las tasas de cambio abundan en el 'mundo real', como ilustra el siguiente ejemplo.
Supongamos que se tomaron dos lecturas de temperatura separadas en la estación de guardabosques en la cima del monte. Sasquatch: a las 6 AM la temperatura era\(\ 24^{\circ} \mathrm{F}\) y a las 10 AM lo era\(\ 32^{\circ} \mathrm{F}\).
- Encuentra la pendiente de la línea que contiene los puntos (6, 24) y (10, 32).
- Interpreta tu respuesta a la primera parte en términos de temperatura y tiempo.
- Predecir la temperatura al mediodía.
Solución
- Para la pendiente, tenemos\(\ m=\frac{32-24}{10-6}=\frac{8}{4}=2\).
- Dado que los valores en el numerador corresponden a las temperaturas en\(\ { }^{\circ} \mathrm{F}\), y los valores en el denominador corresponden al tiempo en horas, podemos interpretar la pendiente como\(\ 2=\frac{2}{1}=\frac{2^{\circ} \mathrm{F}}{1 \text { hour }}\), o\(\ 2^{\circ} \mathrm{F}\) por hora. Dado que la pendiente es positiva, sabemos que esto corresponde a una línea creciente. De ahí que la temperatura esté aumentando a un ritmo de\(\ 2^{\circ} \mathrm{F}\) por hora.
- El mediodía es dos horas después de las 10 AM. Suponiendo un incremento de temperatura\(\ 2^{\circ} \mathrm{F}\) por hora, en dos horas la temperatura debería subir\(\ 4^{\circ} \mathrm{F}\). Dado que la temperatura a las 10 AM es\(\ 32^{\circ} \mathrm{F}\), esperaríamos que la temperatura al mediodía sea\(\ 32+4=36^{\circ} \mathrm{F}\).
Ahora bien puede suceder que en el escenario anterior, al mediodía la temperatura sea sólo\(\ 33^{\circ} \mathrm{F}\). Esto no quiere decir que nuestros cálculos sean incorrectos, más bien, significa que el cambio de temperatura a lo largo del día no es una constante\(\ 2^{\circ} \mathrm{F}\) por hora. Como se discute en la Sección 1.4.1, los modelos matemáticos son justamente eso: modelos. Las predicciones que obtenemos de los modelos pueden ser matemáticamente precisas, pero pueden no parecerse a lo que sucede en el mundo real.
En la Sección 1.2, se discutieron las ecuaciones de líneas verticales y horizontales. Utilizando el concepto de pendiente, podemos desarrollar ecuaciones para las otras variedades de líneas. Supongamos que una línea tiene una pendiente de m y contiene el punto\(\ \left(x_{0}, y_{0}\right)\). Supongamos que\(\ (x, y)\) es otro punto en la línea, como se indica a continuación.
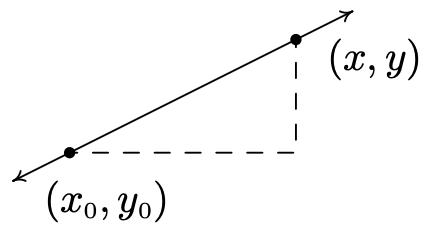
Ecuación 2.1 rendimientos
\ (\\ comenzar {alineado}
m &=\ frac {y-y_ {0}} {x-x_ {0}}\\
m\ izquierda (x-x_ {0}\ derecha) &=y-y_ {0}\
y-y_ {0} &=m\ izquierda (x-x_ {0}\ derecha)
\ final {alineado}\)
Acabamos de derivar la forma punto-pendiente de una línea. 3
La forma punto-pendiente de la línea con pendiente\(\ m\) que contiene el punto\(\ \left(x_{0}, y_{0}\right)\) es la ecuación\(\ y-y_{0}=m\left(x-x_{0}\right)\).
Escribe la ecuación de la línea que contiene los puntos (−1, 3) y (2, 1).
Solución
Para usar la Ecuación 2.2 necesitamos encontrar la pendiente de la línea en cuestión así que usamos la Ecuación 2.1 para obtener\(\ m=\frac{\Delta y}{\Delta x}=\frac{1-3}{2-(-1)}=-\frac{2}{3}\). Tenemos muchas opciones para elegir por un punto\(\ \left(x_{0}, y_{0}\right)\). Usaremos (−1, 3) y dejaremos que el lector compruebe que usando (2, 1) resulta en la misma ecuación. Sustituyendo en la forma punto-pendiente de la línea, obtenemos
\ (\\ comenzar {alineado}
y-y_ {0} &=m\ izquierda (x-x_ {0}\ derecha)\\
y-3 &=-\ frac {2} {3} (x- (-1))\\
y-3 &=-\ frac {2} {3} (x+1)\
y-3 &=-\ frac {2} {3} x-\ frac {2} {3}\\
y &=-\ frac {2} {3} x+\ frac {7} {3}.
\ end {alineado}\)
Podemos verificar nuestra respuesta mostrando que tanto (−1, 3) como (2, 1) están en la gráfica de\(\ y=-\frac{2}{3} x+\frac{7}{3}\) algebraicamente, como hicimos en la Sección 1.2.1.
Al simplificar la ecuación de la línea en el ejemplo anterior, producimos otra forma de línea, la forma pendiente-intersección. Esta es la\(\ y = mx + b\) forma familiar que probablemente hayas visto en Álgebra Intermedia. El 'intercepto' en 'pendiente-intercepción' viene del hecho de que si nos fijamos\(\ x = 0\), obtenemos\(\ y = b\). En otras palabras, la intercepción y de la línea\(\ y = mx + b\) es\(\ (0, b)\).
La forma pendiente-intercepción de la línea con pendiente\(\ m\) e intercepción y\(\ (0, b)\) es la ecuación\(\ y = mx + b\).
Tenga en cuenta que si tenemos pendiente\(\ m = 0\), obtenemos la ecuación\(\ y = b\) que coincide con nuestra fórmula para una línea horizontal dada en la Sección 1.2. La fórmula dada en la Ecuación 2.3 se puede utilizar para describir todas las líneas excepto las verticales. Todas las líneas excepto las verticales son funciones (¿Por qué es esto?) así que finalmente hemos llegado a un buen punto para introducir funciones lineales.
Una función lineal es una función de la forma
\(\ f(x)=m x+b,\)
donde\(\ m\) y b son números reales con\(\ m \neq 0\). El dominio de una función lineal es\(\ (-\infty, \infty)\).
Para el caso\(\ m = 0\), obtenemos\(\ f(x) = b\). A estos se les da su propia clasificación.
Una función constante es una función de la forma
\(\ f(x)=b,\)
donde\(\ b\) está el número real. El dominio de una función constante es\(\ (-\infty, \infty)\).
Recordemos que para graficar una función,\(\ f\), graficamos la ecuación\(\ y = f(x)\). De ahí que la gráfica de una función lineal es una línea con pendiente\(\ m\) e intersección y\(\ (0, b)\); la gráfica de una función constante es una línea horizontal (una línea con pendiente\(\ m = 0\)) y una intersección en y de\(\ (0, b)\). Ahora piensa de nuevo a la Sección 1.6.1, específicamente a la Definición 1.10 relativa a las funciones crecientes, decrecientes y constantes. Una línea con pendiente positiva se llamó línea creciente porque una función lineal con\(\ m > 0\) es una función creciente. De igual manera, una línea con pendiente negativa se denominó línea decreciente porque una función lineal con\(\ m < 0\) es una función decreciente. Y las líneas horizontales se llamaban constantes porque, bueno, esperamos que ya hayas hecho la conexión.
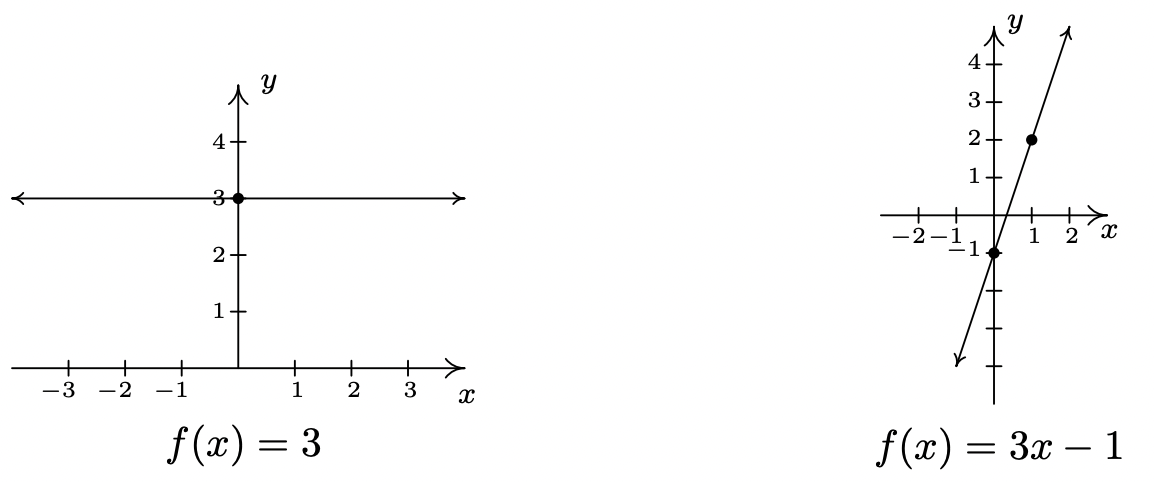
Grafica las siguientes funciones. Identificar la pendiente y la intercepción en y.
- \(\ f(x) = 3\)
- \(\ f(x) = 3x − 1\)
- \(\ f(x)=\frac{3-2 x}{4}\)
- \(\ f(x)=\frac{x^{2}-4}{x-2}\)
Solución
- Para graficar\(\ f(x) = 3\), graficamos\(\ y = 3\). Se trata de una línea horizontal (\(\ m = 0\)) a través de (0, 3).
- La gráfica de\(\ f(x) = 3x − 1\) es la gráfica de la línea\(\ y = 3x − 1\). Comparación de esta ecuación con los rendimientos de la Ecuación 2.3\(\ m = 3\) y\(\ b = −1\). Por lo tanto, nuestra pendiente es 3 y nuestra intercepción y es (0, −1). Para conseguir otro punto en la línea, podemos trazar\(\ (1, f(1)) = (1, 2)\).
- A primera vista, la función\(\ f(x)=\frac{3-2 x}{4}\) no se ajusta a la forma en la Definición 2.1 pero después de algunos reordenamientos obtenemos\(\ f(x)=\frac{3-2 x}{4}=\frac{3}{4}-\frac{2 x}{4}=-\frac{1}{2} x+\frac{3}{4}\). Identificamos\(\ m=-\frac{1}{2}\) y\(\ b=\frac{3}{4}\). De ahí que nuestra gráfica sea una línea con una pendiente de\(\ -\frac{1}{2}\) y una intercepción y de\(\ \left(0, \frac{3}{4}\right)\). Trazando un punto adicional, podemos optar\(\ (1, f(1))\) por obtener\(\ \left(1, \frac{1}{4}\right)\).
- Si simplificamos la expresión para\(\ f\), obtenemos
\(\ f(x)=\frac{x^{2}-4}{x-2}=\frac{\cancel{(x-2)}(x+2)}{\cancel{(x-2)}}=x+2\).
Si fuéramos a declarar\(\ f(x) = x + 2\), estaríamos cometiendo un pecado de omisión. Recuerda, para encontrar el dominio de una función, ¡lo hacemos antes de simplificar! En este caso,\(\ f\) tiene grandes problemas cuando\(\ x = 2\), y como tal, el dominio de\(\ f\) es\(\ (-\infty, 2) \cup(2, \infty)\). Para indicarlo, escribimos\(\ f(x) = x + 2\),\(\ x \neq 2\). Entonces, excepto en\(\ x = 2\), graficamos la línea\(\ y = x + 2\). La pendiente\(\ m = 1\) y la intercepción y es (0, 2). Un segundo punto en la gráfica es\(\ (1, f(1)) = (1, 3)\). Como nuestra función f no está definida en\(\ x = 2\), ponemos un círculo abierto en el punto que estaría en la línea\(\ y = x + 2\) cuando\(\ x = 2\), es decir (2, 4).
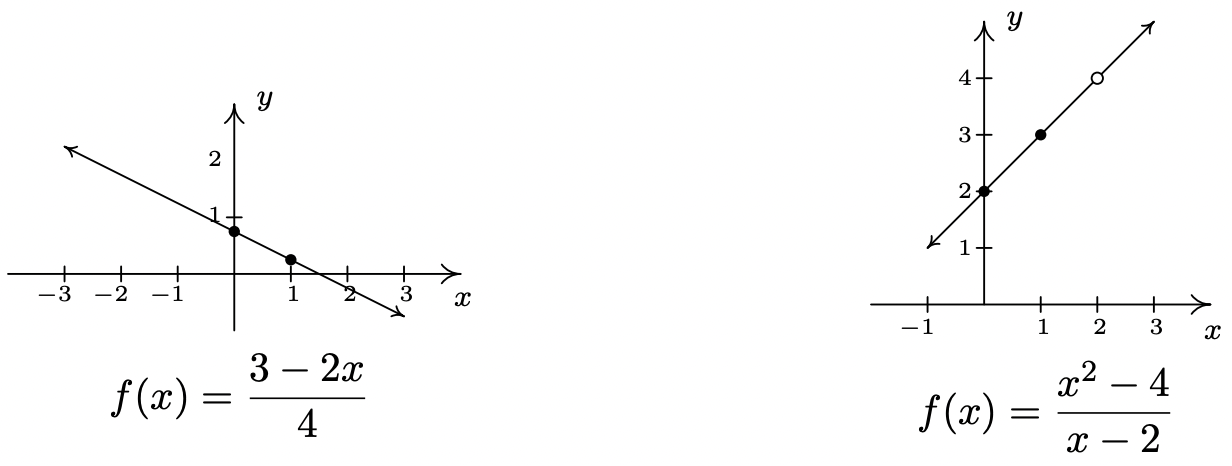
Las dos últimas funciones del ejemplo anterior muestran parte de la dificultad de definir una función lineal usando la frase 'de la forma' como en la Definición 2.1, ya que algunas manipulaciones algebraicas pueden ser necesarias para reescribir una función dada para que coincida con 'la forma'. Tenga en cuenta que los dominios de funciones lineales y constantes son todos números reales\(\ (-\infty, \infty)\), por lo que si bien se\(\ f(x)=\frac{x^{2}-4}{x-2}\) simplifican a una fórmula\(\ f(x) = x + 2\), no\(\ f\) se considera una función lineal ya que su dominio excluye\(\ x = 2\). Sin embargo, consideraríamos
\(\ f(x)=\frac{2 x^{2}+2}{x^{2}+1}\)
ser una función constante ya que su dominio es todo números reales (¿Puede decirnos por qué?) y
\(\ f(x)=\frac{2 x^{2}+2}{x^{2}+1}=\frac{2\cancel{\left(x^{2}+1\right)}}{\cancel{\left(x^{2}+1\right)}}=2\)
El siguiente ejemplo utiliza funciones lineales para modelar alguna relación económica básica
El costo\(\ C\), en dólares, para producir\(\ x\) PortaBoy 4 sistemas de juegos para un minorista local es dado por\(\ C(x) = 80x + 150\) for\(\ x ≥ 0\).
- Encontrar e interpretar\(\ C(10)\).
- ¿Cuántos PortaBoys se pueden producir por $15,000?
- Explicar la significación de la restricción sobre el dominio,\(\ x ≥ 0\).
- Encontrar e interpretar\(\ C(0)\).
- Encuentra e interpreta la pendiente de la gráfica de\(\ y = C(x)\).
Solución
- Para encontrar\(\ C(10)\), reemplazamos cada ocurrencia de\(\ x\) con 10 en la fórmula\(\ C(x)\) para obtener\(\ C(10) = 80(10) + 150 = 950\). Dado que\(\ x\) representa el número de PortaBoys producidos, y\(\ C(x)\) representa el costo, en dólares,\(\ C(10) = 950\) significa que cuesta $950 producir 10 PortaBoys para el minorista local.
- Para saber cuántos PortaBoys se pueden producir por $15,000, resolvemos\(\ C(x) = 15000\), o\(\ 80x + 150 = 15000\). Resolviendo, obtenemos\(\ x=\frac{14850}{80}=185.625\). Dado que solo podemos producir una cantidad entera de PortaBoys, podemos producir 185 PortaBoys por $15,000.
- La restricción\(\ x ≥ 0\) es el dominio aplicado, como se discute en la Sección 1.4.1. En este contexto,\(\ x\) representa el número de PortaBoys producidos. No tiene sentido producir una cantidad negativa de sistemas de juego. 5
- Nos encontramos\(\ C(0) = 80(0) + 150 = 150\). Esto significa que cuesta $150 producir 0 PortaBoys. Como se menciona en la página 82, este es el costo fijo, o de puesta en marcha de esta empresa.
- Si tuviéramos que graficar\(\ y = C(x)\), estaríamos graficando la porción de la línea\(\ y = 80x + 150\) para\(\ x ≥ 0\). Reconocemos la pendiente,\(\ m = 80\). Como cualquier pendiente, podemos interpretar esto como una tasa de cambio. Aquí,\(\ C(x)\) está el costo en dólares, mientras que\(\ x\) mide el número de portaboys por lo
\(\ m=\frac{\Delta y}{\Delta x}=\frac{\Delta C}{\Delta x}=80=\frac{80}{1}=\frac{\$ 80}{1 \text { PortaBoy }}.\)
En otras palabras, el costo está aumentando a una tasa de 80 dólares por PortaBoy producido. A esto se le suele llamar el costo variable para esta empresa.
El siguiente ejemplo nos pide encontrar una función lineal para modelar un problema económico relacionado.
El minorista local en el Ejemplo 2.1.5 ha determinado que el número\(\ x\) de sistemas de juegos PortaBoy vendidos en una semana está relacionado con el precio\(\ p\) en dólares de cada sistema. Cuando el precio era de 220 dólares, se vendieron 20 sistemas de juego en una semana. Cuando los sistemas salieron a la venta la semana siguiente, se vendieron 40 sistemas a 190 dólares la pieza.
- Encuentra una función lineal que se ajuste a estos datos. Utilizar las ventas semanales\(\ x\) como variable independiente y el precio\(\ p\) como variable dependiente.
- Encuentre un dominio aplicado adecuado.
- Interpretar la pendiente.
- Si el minorista quiere vender 150 PortaBoys la próxima semana, ¿cuál debería ser el precio?
- ¿Cuáles serían las ventas semanales si el precio se fijara en $150 por sistema?
Solución
- Recordamos de la Sección 1.4 el significado de variable 'independiente' y 'dependiente'. Ya que\(\ x\) va a ser la variable independiente, y\(\ p\) la variable dependiente, tratamos\(\ x\) como la variable de entrada y\(\ p\) como la variable de salida. De ahí que estemos buscando una función de la forma\(\ p(x) = mx+b\). Para determinar\(\ m\) y\(\ b\), utilizamos el hecho de que se vendieron 20 PortaBoys durante la semana cuando el precio era de 220 dólares y se vendieron 40 unidades cuando el precio era de 190 dólares. Usando la notación de funciones, estos dos hechos se pueden traducir como\(\ p(20) = 220\) y\(\ p(40) = 190\). Ya que\(\ m\) representa la tasa de cambio de\(\ p\) con respecto a\(\ x\), tenemos
\(\ m=\frac{\Delta p}{\Delta x}=\frac{190-220}{40-20}=\frac{-30}{20}=-1.5.\)
Ahora lo hemos determinado\(\ p(x) = −1.5x+b\). Para determinar\(\ b\), podemos volver a utilizar nuestros datos dados. Usando\(\ p(20) = 220\), sustituimos\(\ x = 20\) en\(\ p(x) = 1.5x + b\) y establecemos el resultado igual a 220:\(\ −1.5(20) + b = 220\). Resolviendo, obtenemos\(\ b = 250\). De ahí, obtenemos\(\ p(x) = −1.5x + 250\). Podemos comprobar nuestra fórmula por computación\(\ p(20)\) y\(\ p(40)\) para ver si obtenemos 220 y 190, respectivamente. Puede recordar de la página 82 que la función\(\ p(x)\) se llama la función precio-demanda (o simplemente demanda) para esta empresa.
- Para determinar el dominio aplicado, observamos las limitaciones físicas del problema. Ciertamente, no podemos vender un número negativo de PortaBoys, entonces\(\ x ≥ 0\). No obstante, también observamos que la pendiente de esta función lineal es negativa, y como tal, el precio va disminuyendo a medida que se venden más unidades. Por lo tanto, otra restricción en el precio es\(\ p(x) ≥ 0\). Resolviendo\(\ −1.5x + 250 ≥ 0\) resultados en\(\ −1.5x ≥ −250\) o\(\ x \leq \frac{500}{3}=166 . \overline{6}\). Dado que\(\ x\) representa el número de PortaBoys vendidos en una semana, redondeamos a 166. En consecuencia, un dominio aplicado razonable para\(\ p\) es [0, 166].
- La pendiente\(\ m = −1.5\), una vez más, representa la tasa de cambio del precio de un sistema con respecto a las ventas semanales de PortaBoys. Dado que la pendiente es negativa, tenemos que el precio está disminuyendo a una tasa de $1.50 por portaboY vendido. (Dicho de otra manera, se puede vender un portaboy más por cada caída de $1.50 en el precio.)
- Para determinar el precio que moverá 150 PortaBoys, encontramos\(\ p(150) = −1.5(150)+250 = 25\). Es decir, el precio tendría que ser de 25 dólares.
- Si el precio de un PortaBook se fijó en $150, tenemos\(\ p(x) = 150\), o,\(\ −1.5x+250 = 150\). Resolviendo, obtenemos\(\ −1.5x = −100\) o\(\ x=66 . \overline{6}\). Esto significa que podrías vender 66 PortaBoys a la semana si el precio fuera $150 por sistema.
No todos los fenómenos del mundo real se pueden modelar usando funciones lineales. Sin embargo, es posible utilizar el concepto de pendiente para ayudar a analizar funciones no lineales usando lo siguiente.
Let\(\ f\) Ser una función definida en el intervalo\(\ [a, b]\). La tasa promedio de cambio de\(\ f\) más\(\ [a, b]\) se define como:
\(\ \frac{\Delta f}{\Delta x}=\frac{f(b)-f(a)}{b-a}\)
Geométricamente, si tenemos la gráfica de\(\ y = f(x)\), la tasa promedio de cambio sobre\(\ [a, b]\) es la pendiente de la línea que conecta\(\ (a, f(a))\) y\(\ (b, f(b))\). A esto se le llama la línea secante a través de estos puntos. Por esa razón, algunos libros de texto utilizan la notación\(\ m_{\mathrm{sec}}\) para la tasa promedio de cambio de una función. Tenga en cuenta que para una función lineal\(\ m=m_{\mathrm{sec}}\), o en otras palabras, su tasa de cambio a lo largo de un intervalo es la misma que su tasa de cambio promedio.
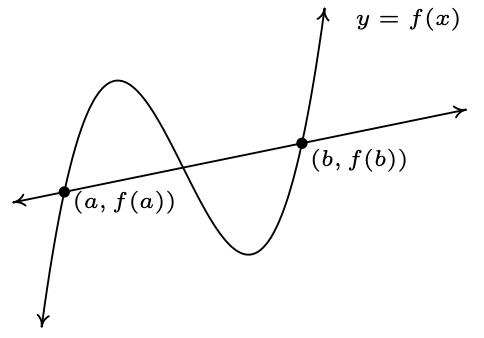 La gráfica de\(\ y = f(x)\) y su línea secante a través\(\ (a, f(a))\) y\(\ (b, f(b))\)
La gráfica de\(\ y = f(x)\) y su línea secante a través\(\ (a, f(a))\) y\(\ (b, f(b))\)El lector interesado puede cuestionar el adjetivo 'promedio' en la frase 'tasa promedio de cambio'. En la figura anterior, podemos ver que la función cambia salvajemente\(\ [a, b]\), sin embargo, la pendiente de la línea secante solo captura una instantánea de la acción en\(\ a\) y\(\ b\). Esta situación es totalmente análoga a la velocidad promedio en un viaje. Supongamos que te toma 2 horas recorrer 100 millas. Su velocidad promedio es de\(\ \frac{100 \text { miles }}{2 \text { hours }}=50\) millas por hora. Sin embargo, es totalmente posible que al inicio de su viaje, viajara 25 millas por hora, luego aceleró hasta 65 millas por hora, y así sucesivamente. La tasa promedio de cambio es similar a tu velocidad promedio en el viaje. Tu velocímetro mide tu velocidad en cualquier instante a lo largo del viaje, tu ritmo de cambio instantáneo, y este es uno de los temas centrales del Cálculo. 6
Al interpretar las tasas de cambio, las interpretamos de la misma manera que hicimos pendientes. En el contexto de las funciones, puede ser útil pensar en la tasa promedio de cambio como:
\(\ \frac{\text { change in outputs }}{\text { change in inputs }}\)
Recordemos de la página 82, los ingresos por vender\(\ x\) unidades a un precio\(\ p\) por unidad vienen dados por la fórmula\(\ R = xp\). Supongamos que estamos en el escenario de los Ejemplos 2.1.5 y 2.1.6.
- Encuentre y simplifique una expresión para los ingresos\(\ R(x)\) semanales en función de las ventas semanales\(\ x\).
- Encontrar e interpretar la tasa promedio de cambio de\(\ R(x)\) durante el intervalo\(\ [0, 50]\).
- Encuentra e interpreta la tasa promedio de cambio de\(\ R(x)\) como\(\ x\) cambios de 50 a 100 y compárela con tu resultado en la parte 2.
- Encuentre e interprete la tasa promedio de cambio de los ingresos semanales a medida que las ventas semanales aumentan de 100 portaboys a 150 portaboys.
Solución
- Ya que\(\ R = xp\), sustituimos\(\ p(x) = −1.5x+ 250\) del Ejemplo 2.1.6 para obtener\(\ R(x)=x(-1.5x +250)=-1.5 x^{2}+250 x\). Ya que determinamos que la función precio-demanda\(\ p(x)\) está restringida a\(\ 0 ≤ x ≤ 166\),\(\ R(x)\) se restringe a estos valores de x también.
- Usando la Definición 2.3, obtenemos que la tasa promedio de cambio es
\(\ \frac{\Delta R}{\Delta x}=\frac{R(50)-R(0)}{50-0}=\frac{8750-0}{50-0}=175.\)
Interpretando esta pendiente como lo hemos hecho en situaciones similares, concluimos que por cada PortaBoy adicional vendido durante una semana determinada, los ingresos semanales aumentan 175 dólares.
- La redacción de esta parte es ligeramente diferente a la de la Definición 2.3, pero su significado es encontrar la tasa promedio de cambio de\(\ R\) sobre el intervalo [50, 100]. Para encontrar esta tasa de cambio, calculamos
\(\ \frac{\Delta R}{\Delta x}=\frac{R(100)-R(50)}{100-50}=\frac{10000-8750}{50}=25.\)
Es decir, por cada portaBoy adicional vendido, los ingresos aumentan en 25 dólares. Tenga en cuenta que si bien los ingresos siguen aumentando al vender más sistemas de juegos, no estamos obteniendo tanto aumento como lo hicimos en la parte 2 de este ejemplo. (¿Se te ocurre por qué sucedería esto?)
- Al traducir el inglés a las matemáticas, se nos está pidiendo encontrar la tasa promedio de cambio de\(\ R\) sobre el intervalo [100, 150]. Encontramos
\(\ \frac{\Delta R}{\Delta x}=\frac{R(150)-R(100)}{150-100}=\frac{3750-10000}{50}=-125.\)
Esto significa que estamos perdiendo $125 dólares de ingresos semanales por cada PortaBoy adicional vendido. (¿Puedes pensar por qué esto es posible?)
Cerramos esta sección con una nueva mirada a los cocientes de diferencia que se introdujeron por primera vez en la Sección 1.4. Si queremos calcular la tasa promedio de cambio de una función a\(\ f\) lo largo del intervalo\(\ [x, x + h]\), entonces tendríamos
\(\ \frac{\Delta f}{\Delta x}=\frac{f(x+h)-f(x)}{(x+h)-x}=\frac{f(x+h)-f(x)}{h}\)
Como hemos indicado, la tasa de cambio de una función (promedio o no) es de gran importancia en Cálculo. 7 Además, tenemos la interpretación geométrica de los cocientes de diferencia que se le prometió en la página 81; un cociente diferencial arroja la pendiente de una línea secante.
2.1.1 Ejercicios
En los Ejercicios 1 - 10, encuentra tanto la forma punto-pendiente como la forma pendiente-intersección de la línea con la pendiente dada que pasa por el punto dado.
- \(\ m = 3, P(3, −1)\)
- \(\ m = −2, P(−5, 8)\)
- \(\ m = −1, P(−7, −1)\)
- \(\ m=\frac{2}{3}, \quad P(-2,1)\)
- \(\ m=-\frac{1}{5}, \quad P(10,4)\)
- \(\ m=\frac{1}{7}, \quad P(-1,4)\)
- \(\ m = 0, P(3, 117)\)
- \(\ m=-\sqrt{2}, \quad P(0,-3)\)
- \(\ m=-5, \quad P(\sqrt{3}, 2 \sqrt{3})\)
- \(\ m = 678, P(−1, −12)\)
En los Ejercicios 11 - 20, encuentra la forma pendiente-intercepción de la línea que pasa por los puntos dados.
- \(\ P(0, 0), Q(−3, 5)\)
- \(\ P(−1, −2), Q(3, −2)\)
- \(\ P(5, 0), Q(0, −8)\)
- \(\ P(3, −5), Q(7, 4)\)
- \(\ P(−1, 5), Q(7, 5)\)
- \(\ P(4, −8), Q(5, −8)\)
- \(\ P\left(\frac{1}{2}, \frac{3}{4}\right), Q\left(\frac{5}{2},-\frac{7}{4}\right)\)
- \(\ P\left(\frac{2}{3}, \frac{7}{2}\right), Q\left(-\frac{1}{3}, \frac{3}{2}\right)\)
- \(\ P(\sqrt{2},-\sqrt{2}), Q(-\sqrt{2}, \sqrt{2})\)
- \(\ P(-\sqrt{3},-1), Q(\sqrt{3}, 1)\)
En Ejercicios 21 - 26, grafica la función. Encuentra la pendiente, la intercepción y y la intercepción x, si existe alguna.
- \(\ f(x)=2 x-1\)
- \(\ f(x)=3-x\)
- \(\ f(x)=3\)
- \(\ f(x)=0\)
- \(\ f(x)=\frac{2}{3} x+\frac{1}{3}\)
- \(\ f(x)=\frac{1-x}{2}\)
- Encuentra todos los puntos de la línea\(\ y = 2x + 1\) que están a 4 unidades del punto (-1, 3).
- Jeff puede caminar cómodamente a 3 millas por hora. Encuentra una función lineal\(\ d\) que represente la distancia total que Jeff puede caminar en\(\ t\) horas, asumiendo que no toma ningún descanso.
- Carl puede rellenar 6 sobres por minuto. Encuentra una función lineal\(\ E\) que represente el número total de sobres que Carl puede rellenar después de t horas, asumiendo que no toma ningún descanso.
- Una empresa de paisajismo cobra $45 por yarda cúbica de mantillo más un cargo de entrega de $20. Encuentre una función lineal que compute el costo total\(\ C\) (en dólares) para entregar yardas\(\ x\) cúbicas de mucho.
- Un plomero cobra $50 por una llamada de servicio más $80 por hora. Si no pasa más de 8 horas diarias en cualquier sitio, encuentre una función lineal que represente sus cargos diarios totales\(\ C\) (en dólares) en función del tiempo\(\ t\) (en horas) que pasa en una ubicación determinada.
- A una vendedora se le pagan $200 semanales más 5% de comisión por sus ventas semanales de\(\ x\) dólares. Encuentra una función lineal que represente su salario semanal total,\(\ W\) (en dólares) en términos de\(\ x\). ¿Cuáles deben ser sus ventas semanales para que gane 475.00 dólares por semana?
- 33. Un editor bajo demanda cobra $22.50 para imprimir un libro de 600 páginas y $15.50 para imprimir un libro de 400 páginas. Encuentre una función lineal que modele el costo de un libro\(\ C\) en función del número de páginas\(\ p\). Interpretar la pendiente de la función lineal y encontrar e interpretar\(\ C(0)\).
- The Topology Taxi Company cobra $2.50 por el primer quinto de milla y $0.45 por cada quinto adicional de milla. Encuentre una función lineal que modele la tarifa\(\ F\) del taxi en función del número de millas recorridas,\(\ m\). Interpretar la pendiente de la función lineal y encontrar e interpretar\(\ F(0)\).
- El agua se congela a\(\ 0^{\circ}\) Celsius y\(\ 32^{\circ}\) Fahrenheit y hierve a\(\ 100^{\circ} \mathrm{C}\) y\(\ 212^{\circ} \mathrm{F}\).
- Encuentra una función lineal\(\ F\) que exprese la temperatura en la escala Fahrenheit en términos de grados Celsius. Utilice esta función para\(\ 20^{\circ} \mathrm{C}\) convertir a Fahrenheit.
- Encuentra una función lineal\(\ C\) que exprese la temperatura en la escala Celsius en términos de grados Fahrenheit. Utilice esta función para\(\ 110^{\circ} \mathrm{F}\) convertir a Celsius.
- ¿Hay una temperatura n tal que\(\ F(n) = C(n)\)?
- Cuenta la leyenda que un toro Sasquatch en rutina aullará aproximadamente 9 veces por hora cuando esté\(\ 40^{\circ} \mathrm{F}\) afuera y sólo 5 veces por hora si es\(\ 70^{\circ} \mathrm{F}\). Suponiendo que el número de aullidos por hora\(\ N\),, puede ser representado por una función lineal de temperatura Fahrenheit, encontrar el número de aullidos por hora que hará cuando sólo esté\(\ 20^{\circ} \mathrm{F}\) afuera. ¿Cuál es el dominio aplicado de esta función? ¿Por qué?
- Las fuerzas económicas más allá del control de nadie han cambiado la función de costo para PortaBoys a\(\ C(x) = 105x + 175\). Ejemplo de retrabajo 2.1.5 con esta nueva función de costo.
- En respuesta a las fuerzas económicas del Ejercicio 37 anterior, el minorista local fija el precio de venta de un PortaCoin en 250 dólares. Notablemente, se vendieron 30 unidades cada semana. Cuando los sistemas salieron a la venta por 220 dólares, se vendieron 40 unidades semanales. Retrabajar los Ejemplos 2.1.6 y 2.1.7 con estos nuevos datos. ¿Qué dificultades te encuentras?
- Una pizzería local ofrece pizzas medianas de dos topping entregadas por $6.00 por pizza más un cargo de entrega de $1.50 por pedido. Los fines de semana, la tienda ejecuta un especial de 'día de juego': si se piden seis o más pizzas medianas de dos topping, cuestan $5.50 cada una sin cargo por envío. Escriba una función lineal definida por partes que calcule el costo\(\ C\) (en dólares) de pizzas\(\ p\) medianas de dos topping entregadas durante un fin de semana.
- Un restaurante ofrece un buffet que cuesta $15 por persona. Para fiestas de 10 o más personas, se aplica un descuento grupal, y el costo es de $12.50 por persona. Escriba una función lineal definida por partes que calcule la factura total\(\ T\) de una fiesta de\(\ n\) personas que elijan el buffet.
- Un plan móvil cobra una tarifa base mensual de $10 por los primeros 500 minutos de tiempo de emisión más un cargo de 15¢ por cada minuto adicional. Escriba una función lineal definida por partes que calcule el costo mensual\(\ C\) (en dólares) para usar\(\ m\) minutos de tiempo de aire.
CONSEJO: Es posible que desee volver a visitar el Ejercicio 74 en la Sección 1.4
- La tienda de mascotas local cobra 12¢ por grillo hasta 100 grillos, y 10¢ por grillo a partir de entonces. Escribir una función lineal definida por partes que calcule el precio\(\ P\), en dólares, de comprar\(\ c\) grillos.
- La sección transversal de una piscina está debajo. Escriba una función lineal definida por partes que describa la profundidad de la piscina,\(\ D\) (en pies) como una función de:
- la distancia (en pies) desde el borde del extremo poco profundo de la piscina, d.
- la distancia (en pies) desde el borde del extremo profundo de la piscina,\(\ s\).
- Grafique cada una de las funciones en (a) y (b). Discuta con sus compañeros de clase cómo transformar uno en otro y cómo se relacionan con el diagrama de la piscina.
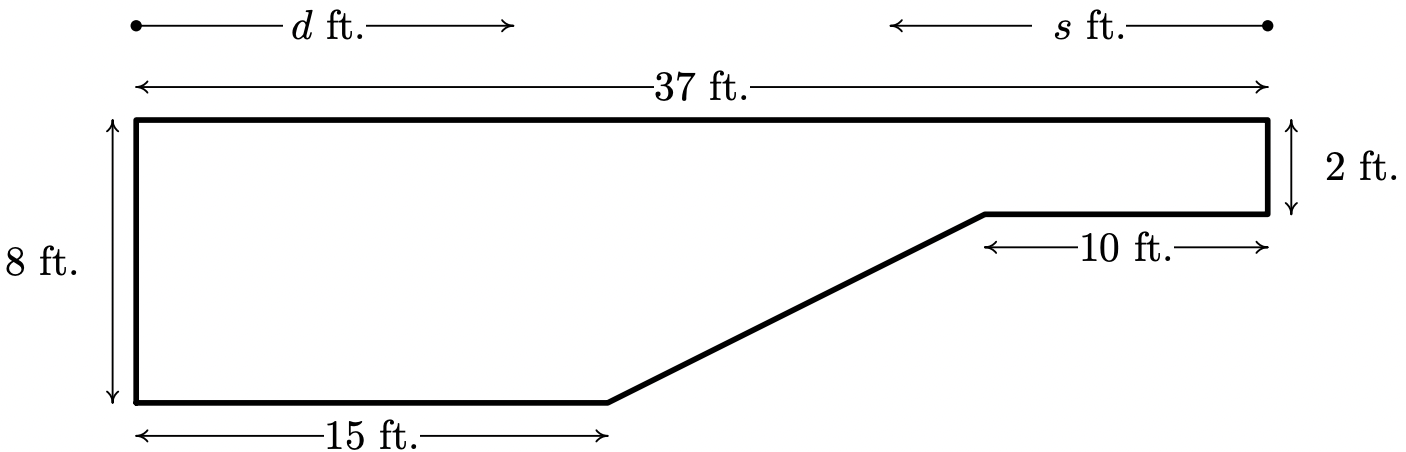
En Ejercicios 44 - 49, compute la tasa promedio de cambio de la función durante el intervalo especificado.
- \(\ f(x)=x^{3},[-1,2]\)
- \(\ f(x)=\frac{1}{x},[1,5]\)
- \(\ f(x)=\sqrt{x},[0,16]\)
- \(\ f(x)=x^{2},[-3,3]\)
- \(\ f(x)=\frac{x+4}{x-3},[5,7]\)
- \(\ f(x)=3 x^{2}+2 x-7,[-4,2]\)
En Ejercicios 50 - 53, computa la tasa promedio de cambio de la función dada a lo largo del intervalo\(\ [x, x + h]\). Aquí asumimos que\(\ [x, x + h]\) está en el dominio de la función.
- \(\ f(x)=x^{3}\)
- \(\ f(x)=\frac{1}{x}\)
- \(\ f(x)=\frac{x+4}{x-3}\)
- \(\ f(x)=3 x^{2}+2 x-7\)
- La altura de un objeto caído del techo de un edificio de ocho pisos está modelada por:\(\ h(t)=-16 t^{2}+64,0 \leq t \leq 2\). Aquí,\(\ h\) es la altura del objeto del suelo en pies,\(\ t\) segundos después de que el objeto se haya caído. Encontrar e interpretar la tasa promedio de cambio de\(\ h\) sobre el intervalo [0, 2].
- Utilizando datos de Bureau of Transportation Statistics, la economía promedio de combustible\(\ F\) en millas por galón para los turismos en Estados Unidos puede ser modelada por\(\ F(t)=-0.0076 t^{2}+0.45 t+16\)\(\ 0 ≤ t ≤ 28\),, donde\(\ t\) es el número de años desde 1980. Encontrar e interpretar la tasa promedio de cambio de\(\ F\) sobre el intervalo [0, 28].
- La temperatura\(\ T\) en grados Fahrenheit\(\ t\) horas después de las 6 AM viene dada por:
\(\ T(t)=-\frac{1}{2} t^{2}+8 t+32, \quad 0 \leq t \leq 12\)
- Encontrar e interpretar\(\ T(4)\),\(\ T(8)\) y\(\ T(12)\).
- Encontrar e interpretar la tasa promedio de cambio de\(\ T\) sobre el intervalo [4, 8].
- Encontrar e interpretar la tasa promedio de cambio de\(\ T\) de\(\ t = 8\) a\(\ t = 12\).
- Encuentra e interpreta la tasa promedio de cambio de temperatura entre las 10 AM y las 6 PM.
- Supongamos que\(\ C(x)=x^{2}-10 x+27\) representa los costos, en cientos, para producir\(\ x\) mil bolígrafos. Encuentre e interprete la tasa promedio de cambio a medida que aumenta la producción de 3000 a 5000 plumas.
- Con la ayuda de tus compañeros de clase encuentra varios otros ejemplos “del mundo real” de tasas de cambio que se utilizan para describir fenómenos no lineales.
(Líneas paralelas) Recuerde del álgebra intermedia que las líneas paralelas tienen la misma pendiente. (Tenga en cuenta que dos líneas verticales también son paralelas entre sí aunque tengan una pendiente indefinida). En los Ejercicios 59 - 64, se le da una línea y un punto que no está en esa línea. Encuentra la línea paralela a la línea dada que pasa por el punto dado.
- \(\ y = 3x + 2, P(0, 0) \)
- \(\ y = −6x + 5, P(3, 2)\)
- \(\ y=\frac{2}{3} x-7, P(6,0)\)
- \(\ y=\frac{4-x}{3}, P(1,-1)\)
- \(\ y = 6, P(3, −2)\)
- \(\ x = 1, P(−5, 0)\)
(Líneas perpendiculares) Recuerde del álgebra intermedia que dos líneas no verticales son perpendiculares si y solo si tienen pendientes recíprocas negativas. Es decir, si una línea tiene pendiente\(\ m_{1}\) y la otra tiene pendiente\(\ m_{2}\) entonces\(\ m_{1} \cdot m_{2}=-1\). (Se le guiará a través de un comprobante de este resultado en el Ejercicio 71.) Tenga en cuenta que una línea horizontal es perpendicular a una línea vertical y viceversa, por lo que asumimos\(\ m_{1} \neq 0\) y\(\ m_{2} \neq 0\). En los Ejercicios 65 - 70, se le da una línea y un punto que no está en esa línea. Encuentra la línea perpendicular a la línea dada que pasa por el punto dado.
- \(\ y=\frac{1}{3} x+2, P(0,0)\)
- \(\ y=-6 x+5, P(3,2)\)
- \(\ y=\frac{2}{3} x-7, P(6,0)\)
- \(\ y=\frac{4-x}{3}, P(1,-1)\)
- \(\ y = 6, P(3, −2)\)
- \(\ x = 1, P(−5, 0)\)
- Ahora probaremos que\(\ y=m_{1} x+b_{1}\) es perpendicular a\(\ y=m_{2} x+b_{2}\) si y sólo si\(\ m_{1} \cdot m_{2}=-1\). Para hacernos la vida más fácil asumiremos que\(\ m_{1}>0\) y\(\ m_{2}<0\). También podemos “mover” las líneas para que su punto de intersección sea el origen sin estropear las cosas, así que asumiremos\(\ b_{1}=b_{2}=0\). (Tómese un momento con sus compañeros de clase para discutir por qué está bien esto). Graficando las líneas y trazando los puntos\(\ O(0, 0)\),\(\ P\left(1, m_{1}\right)\) y nos\(\ Q\left(1, m_{2}\right)\) da la siguiente configuración.
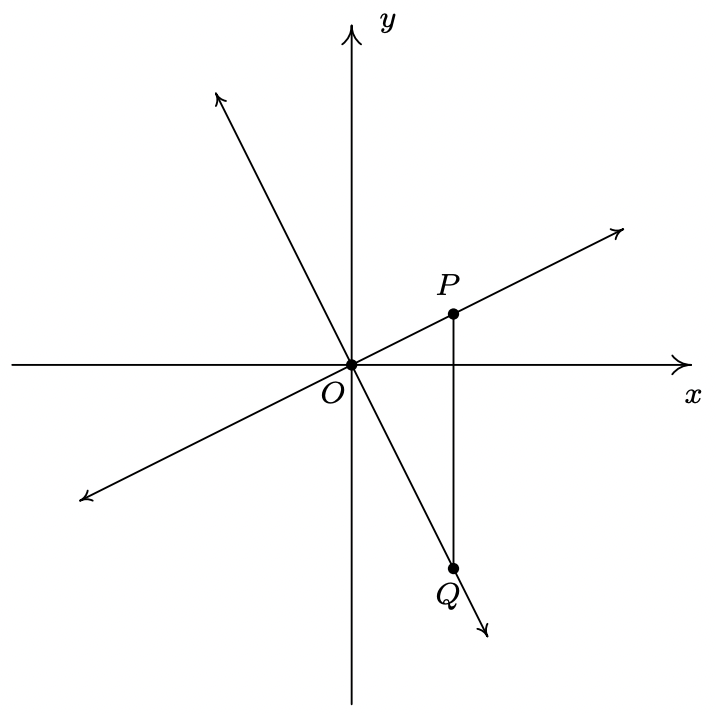
La línea\(\ y=m_{1} x\) será perpendicular a la línea\(\ y=m_{2} x\) si y sólo si\(\ \triangle O P Q\) es un triángulo rectángulo. Dejar\(\ d_{1}\) ser la distancia de\(\ O\) a\(\ P\), dejar\(\ d_{2}\) ser la distancia de\(\ O\) a\(\ Q\) y dejar\(\ d_{3}\) ser la distancia de\(\ P\) a\(\ Q\). Usa el Teorema de Pitágoras para mostrar que\(\ \triangle O P Q\) es un triángulo rectángulo si y solo si\(\ m_{1} \cdot m_{2}=-1\) mostrando\(\ d_{1}^{2}+d_{2}^{2}=d_{3}^{2}\) si y solo si\(\ m_{1} \cdot m_{2}=-1\).
- Mostrar que si\(\ a \neq b\), la línea que contiene los puntos\(\ (a, b)\) y\(\ (b, a)\) es perpendicular a la línea\(\ y = x\). (Acoplado con el resultado del Ejemplo 1.1.7 en la página 13, ahora hemos mostrado que la línea\(\ y = x\) es una bisectriz perpendicular del segmento de línea que conecta\(\ (a, b)\) y\(\ (b, a)\). Esto significa que los puntos\(\ (a, b)\) y\(\ (b, a)\) son simétricos alrededor de la línea\(\ y = x\). Volveremos a examinar esta simetría en la sección 5.2.)
- La función definida por\(\ I(x) = x\) se llama Función de Identidad.
- Discuta con tus compañeros de clase por qué este nombre tiene sentido.
- Mostrar que la forma punto-pendiente de una línea (Ecuación 2.2) se puede obtener a partir del\(\ I\) uso de una secuencia de las transformaciones definidas en la Sección 1.7.
2.1.2 Respuestas
- \ (\\ comenzar {alineado}
&y+1 = 3 (x-3)\\
&y=3 x-10
\ final {alineado}\) - \ (\\ comenzar {alineado}
&y-8=-2 (x+5)\\
&y=-2 x-2
\ final {alineado}\) - \ (\\ comenzar {alineado}
&y+1 =- (x+7)\\
&y=-x-8
\ final {alineado}\) - \ (\\ comenzar {alineado}
&y-1=\ frac {2} {3} (x+2)\\
&y=\ frac {2} {3} x+\ frac {7} {3}
\ end {alineado}\) - \ (\\ comenzar {alineado}
&y-4=-\ frac {1} {5} (x-10)\\
&y=-\ frac {1} {5} x+6
\ final {alineado}\) - \ (\\ comenzar {alineado}
&y-4=\ frac {1} {7} (x+1)\\
&y=\ frac {1} {7} x+\ frac {29} {7}
\ end {alineado}\) - \ (\\ comenzar {alineado}
&y-117=0\\
&y=117
\ final {alineado}\) - \ (\\ comenzar {alineado}
&y+3 =-\ sqrt {2} (x-0)\\
&y=-\ sqrt {2} x-3
\ final {alineado}\) - \ (\\ comenzar {alineado}
&y-2\ sqrt {3} =-5 (x-\ sqrt {3})\\
&y=-5 x+7\ sqrt {3}
\ end {alineado}\) - \ (\\ comenzar {alineado}
&y+12=678 (x+1)\\
&y=678 x+666
\ final {alineado}\) - \(\ y=-\frac{5}{3} x\)
- \(\ y = −2\)
- \(\ y=\frac{8}{5} x-8\)
- \(\ y=\frac{9}{4} x-\frac{47}{4}\)
- \(\ y = 5\)
- \(\ y = −8\)
- \(\ y=-\frac{5}{4} x+\frac{11}{8}\)
- \(\ y=2 x+\frac{13}{6}\)
- \(\ y = −x\)
- \(\ y=\frac{\sqrt{3}}{3} x\)
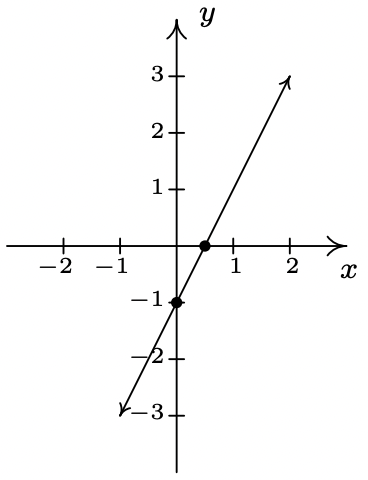
- \(\ f(x) = 2x − 1\)
pendiente:\(\ m = 2\)
intercepción en Y: (0, −1)
X-intercepción:\(\ \left(\frac{1}{2}, 0\right)\)
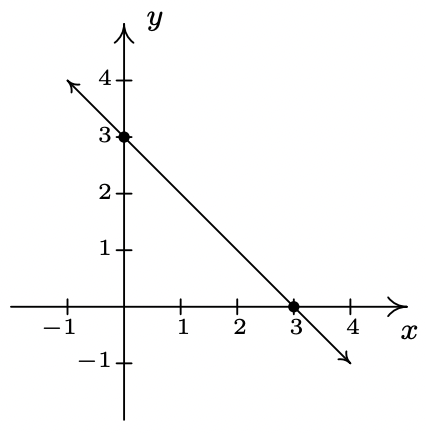
- \(\ f(x) = 3 − x\)
pendiente:\(\ m = − 1\)
intercepción en Y: (0, 3)
intercepción x: (3, 0)
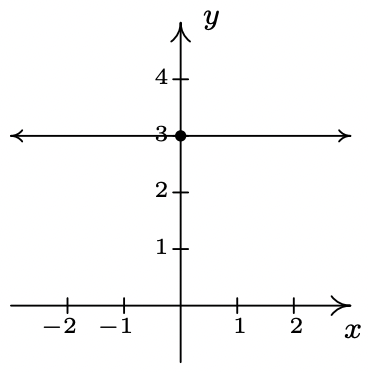
- \(\ f(x) = 3\)
pendiente:\(\ m = 0\)
intercepción en Y: (0, 3)
x-intercept: ninguno
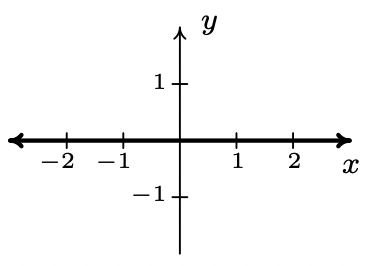
- f (x) = 0
pendiente:\(\ m = 0\)
intercepción en Y: (0, 0)
x-intercept:\(\ \{(x, 0)| x\) es un número real\(\ \}\)
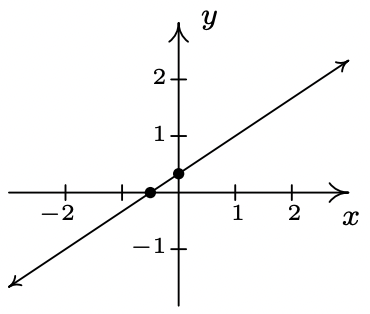
- \(\ f(x)=\frac{2}{3} x+\frac{1}{3}\)
pendiente:\(\ m=\frac{2}{3}\)
intercepción en Y:\(\ \left(0, \frac{1}{3}\right)\)
X-intercepción:\(\ \left(-\frac{1}{2}, 0\right)\)
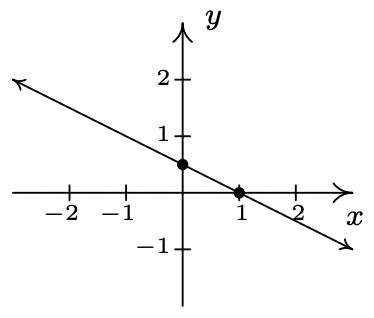
- \(\ f(x)=\frac{1-x}{2}\)
pendiente:\(\ m=-\frac{1}{2}\)
intercepción en Y:\(\ \left(0, \frac{1}{2}\right)\)
X-intercepción:\(\ (1,0)\)
- \(\ (-1,-1) \text { and }\left(\frac{11}{5}, \frac{27}{5}\right)\)
- \(\ d(t)=3 t, t \geq 0\)
- \(\ E(t)=360 t, t \geq 0\)
- \(\ C(x)=45 x+20, x \geq 0\)
- \(\ C(t)=80 t+50,0 \leq t \leq 8\)
- \(\ W(x)=200+.05 x, x \geq 0\)Ella debe hacer $5500 en ventas semanales
- \(\ C(p)=0.035 p+1.5\)La pendiente 0.035 significa que cuesta 3.5¢ por página. \(\ C(0) = 1.5\)significa que hay un costo fijo, o inicial, de $1.50 para hacer cada libro.
- \(\ F(m) = 2.25m+ 2.05\)La pendiente 2.25 significa que cuesta $2.25 adicionales por cada milla más allá de las primeras 0.2 millas. \(\ F(0) = 2.05\), por lo que según el modelo, costaría $2.05 por un viaje de 0 millas. ¿Esto realmente sucedería alguna vez? Depende del chofer y del pasajero, suponemos.
-
- \(\ F(C)=\frac{9}{5} C+32\)
- \(\ C(F)=\frac{5}{9}(F-32)=\frac{5}{9} F-\frac{160}{9}\)
- \(\ F(−40) = −40 = C(−40)\)
- \(\ N(T)=-\frac{2}{15} T+\frac{43}{3} \text { and } N(20)=\frac{35}{3} \approx 12 \text { howls per hour }\)
Tener un número negativo de aullidos no tiene sentido y ya que\(\ N(107.5) = 0\) podemos poner un límite superior de\(\ 107.5^{\circ} \mathrm{F}\) sobre el dominio. El límite inferior es más complicado porque no hay nada más que sentido común para continuar. A medida que hace más frío, aúlla con más frecuencia. En algún momento o hará tanto frío que se congela hasta morir o está aullando sin parar. Entonces vamos a decir que puede soportar temperaturas no inferiores a las de\(\ -60^{\circ} \mathrm{F}\) tal manera que el dominio aplicado es [−60, 107.5].
- \ (\ C (p) =\ left\ {\ begin {array} {rll}
6 p+1.5 &\ text {if} & 1\ leq p\ leq 5\\
5.5 p &\ text {if} & p\ geq 6
\ end {array}\ right.\) - \ (\ T (n) =\ izquierda\ {\ begin {array} {rll}
15 n &\ text {if} & 1\ leq n\ leq 9\\
12.5 n &\ text {if} & n\ geq 10
\ end {array}\ right.\) - \ (\ C (m) =\ left\ {\ begin {array} {rll}
10 &\ text {if} & 0\ leq m\ leq 500\\
10+0.15 (m-500) &\ text {if} & m>500
\ end {array}\ right.\) - \ (\ P (c) =\ left\ {\ begin {array} {rll}
0.12 c &\ text {if} & 1\ leq c\ leq 100\\
12+0.1 (c-100) &\ text {if} & c>100
\ end {array}\ right.\) -
- \ (\ D (d) =\ left\ {\ begin {array} {rll}
8 &\ text {if} & 0\ leq d\ leq 15\\
-\ frac {1} {2} {2} d+\ frac {31} {2} &\ text {if} & 15\ leq d\ leq 27\
2 &\ text {if} & 27\ leq d\ q 37
\ end {array}\ derecho.\) - \ (\ D (s) =\ izquierda\ {\ begin {array} {rll}
2 &\ text {if} & 0\ leq s\ leq 10\\
\ frac {1} {2} s-3 &\ text {if} & 10\ leq s\ leq s\ leq 22\\
8 &\ text {if} & 22\ leq s\ leq 37
\ end {array}\ derecho.\) 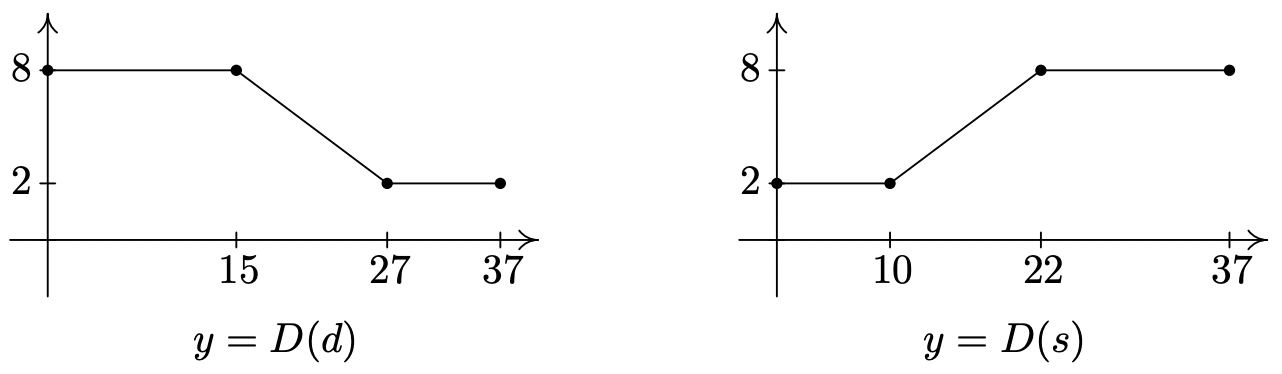
- \ (\ D (d) =\ left\ {\ begin {array} {rll}
- \(\ \frac{2^{3}-(-1)^{3}}{2-(-1)}=3\)
- \(\ \frac{\frac{1}{5}-\frac{1}{1}}{5-1}=-\frac{1}{5}\)
- \(\ \frac{\sqrt{16}-\sqrt{0}}{16-0}=\frac{1}{4}\)
- \(\ \frac{3^{2}-(-3)^{2}}{3-(-3)}=0\)
- \(\ \frac{\frac{7+4}{7-3}-\frac{5+4}{5-3}}{7-5}=-\frac{7}{8}\)
- \(\ \frac{\left(3(2)^{2}+2(2)-7\right)-\left(3(-4)^{2}+2(-4)-7\right)}{2-(-4)}=-4\)
- \(\ 3 x^{2}+3 x h+h^{2}\)
- \(\ \frac{-1}{x(x+h)}\)
- \(\ \frac{-7}{(x-3)(x+h-3)}\)
- \(\ 6 x+3 h+2\)
- La tasa promedio de cambio es\(\ \frac{h(2)-h(0)}{2-0}=-32\). Durante los dos primeros segundos posteriores a su caída, el objeto ha caído a una velocidad promedio de 32 pies por segundo. (Esto se llama la velocidad promedio del objeto.)
- La tasa promedio de cambio es\(\ \frac{F(28)-F(0)}{28-0}=0.2372\). Durante los años de 1980 a 2008, la economía promedio de combustible de los turismos en Estados Unidos aumentó, en promedio, a una tasa de 0.2372 millas por galón al año.
-
- \(\ T(4) = 56\), así que a las 10 AM (4 horas después de las 6 AM), lo es\(\ 56^{\circ} \mathrm{F}\). \(\ T(8) = 64\), así que a las 2 PM (8 horas después de las 6 AM), lo es\(\ 64^{\circ} \mathrm{F}\). \(\ T(12) = 56\), así que a las 6 PM (12 horas después de las 6 AM), lo es\(\ 56^{\circ} \mathrm{F}\).
- La tasa promedio de cambio es\(\ \frac{T(8)-T(4)}{8-4}=2\). Entre las 10 AM y las 2 PM, la temperatura aumenta, en promedio, a un ritmo de\(\ 2^{\circ} \mathrm{F}\) por hora.
- La tasa promedio de cambio es\(\ \frac{T(12)-T(8)}{12-8}=-2\). Entre las 2 PM y las 6 PM, la temperatura disminuye, en promedio, a una tasa\(\ 2^{\circ} \mathrm{F}\) por hora.
- La tasa promedio de cambio es\(\ \frac{T(12)-T(4)}{12-4}=0\). Entre las 10 AM y las 6 PM, la temperatura, en promedio, se mantiene constante.
- La tasa promedio de cambio es\(\ \frac{C(5)-C(3)}{5-3}=-2\). A medida que aumenta la producción de 3000 a 5000 plumas, el costo disminuye a una tasa promedio de $200 por cada 1000 plumas producidas (20¢ por pluma).
- \(\ y = 3x\)
- \(\ y = −6x + 20\)
- \(\ y=\frac{2}{3} x-4\)
- \(\ y=-\frac{1}{3} x-\frac{2}{3}\)
- \(\ y = −2\)
- \(\ x = −5\)
- \(\ y = −3x\)
- \(\ y=\frac{1}{6} x+\frac{3}{2}\)
- \(\ y=-\frac{3}{2} x+9\)
- \(\ y = 3x − 4\)
- \(\ x = 3\)
- \(\ y = 0\)
Referencia
1 Consulte www.mathforum.org o www.mathworld.wolfram.com para discusiones sobre este tema.
2 Algunos autores utilizan el desafortunado nombre 'sin pendiente' cuando una pendiente es indefinida. Es fácil confundir las nociones de 'sin pendiente' con 'pendiente de 0'. Por esta razón, describiremos las pendientes de las líneas verticales como 'indefinidas'.
3 También podemos entender esta ecuación en términos de aplicar transformaciones a la función\(\ I(x) = x\). Ver los Ejercicios.
4 La similitud de este nombre con PortaJohn es deliberada.
5 En realidad, tampoco tiene sentido producir una parte fraccionaria de un sistema de juego, como vimos en la parte anterior de este ejemplo. Este absurdo, sin embargo, nos parece bastante perdonable en algunos libros de texto pero no a nosotros.
6 Aquí vamos otra vez...
7 Entonces no te estamos torturando con estos por nada.


