2.2: Funciones de Valor Absoluto

Última actualización
Guardar como PDF

Page ID: 119486

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

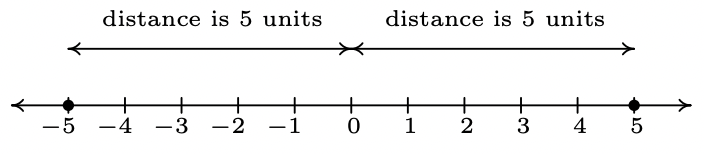
Hay algunas formas de describir lo que se entiende por el valor absoluto$|x|$ de un número real$x$. Es posible que te hayan enseñado que$|x|$ es la distancia desde el número real$x$ hasta$0$ en la línea numérica. Entonces, por ejemplo,$|5| = 5$ y$|-5| = 5$, ya que cada uno es$5$ unidades de$0$ en la recta numérica.

$Screen Shot 2022-03-15 en 4.08.25 PM.png$

Otra forma de definir el valor absoluto es mediante la ecuación$|x| = \sqrt{x^2}$. Usando esta definición, tenemos$|5| = \sqrt{(5)^2} = \sqrt{25} = 5$ y$|-5| = \sqrt{(-5)^2} = \sqrt{25} = 5$. El largo y corto de ambos procedimientos es que$|x|$ toma números reales negativos y los asigna a sus homólogos positivos mientras deja solos los números positivos. Esta última descripción es la que adoptaremos, y se resume en la siguiente definición.

Definición 2.4

El valor absoluto de un número real$x$, denotado$|x|$, viene dado por

$|x| = \left\{ \begin{array}{rcl} -x, & \mbox{if} & x < 0 \\ x, & \mbox{if} & x \geq 0 \\ \end{array} \right.$

En la Definición 2.4, definimos$|x|$ usando una función definida por partes. (Ver página en la Sección 1.4.) Para comprobar que esta definición concuerda con lo que antes entendíamos como valor absoluto, tenga en cuenta que ya que$5 \geq 0$, para encontrar$|5|$ utilizamos la regla$|x| = x$, así$|5|=5$. De igual manera$-5 < 0$, ya que, utilizamos la regla$|x| = -x$, para que$|-5| = -(-5) = 5$. Este es uno de los momentos en los que es mejor interpretar la expresión '$-x$' como 'lo opuesto de$x$ 'en contraposición a$x$ 'negativa'. Antes de comenzar a estudiar las funciones de valor absoluto, nos recordamos las propiedades del valor absoluto.

Teorema 2.1. Propiedades de Valor Absoluto

Dejar$a$,$b$ y$x$ ser números reales y dejar$n$ ser un entero. ^a Entonces

Regla del producto:$|ab|= |a||b|$
Regla de potencia:$\left| a^{n} \right| = |a|^{n}$ siempre que$a^{n}$ se defina
Regla del cociente:$\left| \dfrac{a}{b} \right| = \dfrac{|a|}{|b|}$, siempre y cuando$b \neq 0$

Propiedades de Igualdad:

$|x| = 0$si y sólo si$x = 0$.
Para$c > 0$,$|x| = c$ si y solo si$x = c$ o$-x = c$.
Para$c < 0$, no$|x| = c$ tiene solución.

^a Consulta la página 2 si no recuerdas qué es un entero.

Las pruebas de las Reglas de Producto y Cociente en el Teorema 2.1 se reducen a verificar cuatro casos: cuando ambos$a$ y$b$ son positivos; cuando ambos son negativos; cuando uno es positivo y el otro es negativo; y cuando uno o ambos son cero.

Por ejemplo, supongamos que deseamos demostrarlo$|ab| = |a||b|$. Tenemos que demostrar que esta ecuación es cierta para todos los números reales$a$ y$b$. Si$a$ y ambos$b$ son positivos, entonces también lo es$ab$. De ahí,$|a| = a$,$|b| = b$ y$|ab| = ab$. De ahí que la ecuación$|ab| = |a||b|$ sea la misma$ab = ab$ que la que es verdadera. Si ambos$a$ y$b$ son negativos, entonces$ab$ es positivo. De ahí,$|a| = -a$,$|b| = -b$ y$|ab| = ab$. La ecuación$|ab| = |a||b|$ se convierte$ab = (-a)(-b)$, lo cual es cierto. Supongamos que$a$ es positivo y$b$ es negativo. Entonces$ab$ es negativo, y tenemos$|ab| = -ab$,$|a| = a$ y$|b| = -b$. La ecuación$|ab| = |a||b|$ reduce a$-ab = a(-b)$ lo que es cierto. Un argumento simétrico muestra que la ecuación se$|ab| = |a||b|$ mantiene cuando$a$ es negativa y$b$ positiva. Finalmente, si alguno$a$ o$b$ (o ambos) son cero, entonces ambos lados de$|ab| = |a||b|$ son cero, así que la ecuación se mantiene en este caso, también. Toda esta retórica ha demostrado que la ecuación es$|ab| = |a||b|$ cierta en todos los casos.

La prueba de la Regla del Cociente es muy similar, con la excepción de que$b \neq 0$. La Regla de Poder se puede mostrar mediante la aplicación repetida de la Regla del Producto. Las 'Propiedades de Equidad' pueden probarse utilizando la Definición 2.4 y observando los casos cuando$x\geq 0$, en cuyo caso$|x| = x$, o cuándo$x<0$, en qué caso$|x| = -x$. Por ejemplo, si$c>0$, y$|x| = c$, entonces si$x \geq 0$, tenemos$x = |x| = c$. Si, por otro lado,$x < 0$, entonces$-x = |x| = c$, así$x = -c$. Las propiedades restantes se demuestran de manera similar y se dejan para los Ejercicios. Nuestro primer ejemplo revisa cómo resolver ecuaciones básicas que involucran valor absoluto usando las propiedades enumeradas en el Teorema 2.1.

Ejemplo 2.2.1

$|3x-1| = 6$
$3 - |x+5| = 1$
$3|2x+1| - 5 = 0$
$4 - |5x+3| = 5$
$|x| = x^2-6$
$|x-2| + 1 = x$

Solución

La ecuación$|3x-1| = 6$ es de la forma$|x| = c$ para$c>0$, así que por las Propiedades de Igualdad,$|3x-1| = 6$ es equivalente a$3x-1=6$ o$3x-1 = -6$. Resolviendo lo primero, llegamos a$x = \frac{7}{3}$, y resolviendo lo segundo, obtenemos$x = -\frac{5}{3}$. Podemos verificar ambas soluciones sustituyéndolas en la ecuación original y mostrando que la aritmética funciona.
Para usar las Propiedades de Igualdad para resolver$3 - |x+5| = 1$, primero aislamos el valor absoluto.
$\begin{array}{rclr} 3 - |x+5| & = & 1 & \\ -|x+5| & = & -2 & \text{subtract $3$} \\ |x+5| & = & 2 & \text{divide by $-1$} \\ \end{array}$
Al igual que en el ejemplo anterior, primero aislamos el valor absoluto en la ecuación$3|2x+1| - 5 = 0$ y obtenemos$|2x+1| = \frac{5}{3}$. Usando las Propiedades de Igualdad, tenemos$2x+1 = \frac{5}{3}$ o$2x+1 = -\frac{5}{3}$. Resolver lo primero da$x = \frac{1}{3}$ y resolver el segundo da$x = -\frac{4}{3}$. Como es habitual, podemos sustituir ambas respuestas en la ecuación original para verificar.
Al aislar el valor absoluto en la ecuación$4 - |5x+3| = 5$, obtenemos$|5x+3| = -1$. En este punto, sabemos que no puede haber ninguna solución real, ya que, por definición, el valor absoluto de cualquier cosa nunca es negativo. Ya terminamos.
La ecuación nos$|x| = x^2-6$ presenta cierta dificultad, ya que$x$ aparece tanto dentro como fuera del valor absoluto. Además, hay valores$x$ para los cuales$x^2-6$ es positivo, negativo y cero, por lo que no podemos usar las Propiedades de Igualdad sin el riesgo de introducir soluciones extrañas, o peor aún, perder soluciones. Por esta razón, dividimos ecuaciones como esta en casos reescribiendo el término en valores absolutos,$|x|$, usando la Definición 2.4. Para$x < 0$,$|x| = -x$, así para$x < 0$, la ecuación$|x| = x^2-6$ es equivalente a$-x = x^2-6$. Reorganizar esto nos da$x^2+x-6 = 0$, o$(x+3)(x-2) = 0$. Obtenemos$x = -3$ o$x=2$. Ya que solo$x=-3$ satisface$x<0$, esta es la respuesta que guardamos. Para$x \geq 0$,$|x| = x$, así$|x| = x^2-6$ se convierte la ecuación$x = x^2-6$. A partir de esto, obtenemos$x^2-x-6 =0$ o$(x-3)(x+2) = 0$. Nuestras soluciones son$x=3$ o$x = -2$, y como solo$x=3$ satisface$x \geq 0$, esta es la que guardamos. De ahí que nuestras dos soluciones$|x| = x^2-6$ sean$x=-3$ y$x=3$.
Para resolver$|x-2| + 1 = x$, primero aislamos el valor absoluto y obtenemos$|x-2| = x-1$. Como vemos$x$ tanto dentro como fuera del valor absoluto, rompemos la ecuación en casos. El término con valores absolutos aquí es$|x-2|$, por lo que reemplazamos$x$ '' con la cantidad '$(x-2)$' en la Definición 2.4 para obtener
$|x-2| = \left\{ \begin{array}{rcl} -(x-2), & \mbox{if} & (x-2) < 0 \\ (x-2), & \mbox{if} & (x-2) \geq 0 \\ \end{array} \right.$

Entonces, para$x<2$,$|x-2| = -x+2$ y nuestra ecuación$|x-2| = x-1$ se convierte$-x+2 = x-1$, lo que da$x = \frac{3}{2}$. Ya que esta solución satisface$x < 2$, la conservamos. A continuación, para$x \geq 2$,$|x-2| = x-2$, así$|x-2| = x-1$ se convierte la ecuación$x-2 = x-1$. Aquí, la ecuación se reduce a$-2 = -1$, lo que significa que aquí no tenemos soluciones. De ahí que nuestra única solución sea$x = \frac{3}{2}$.

A continuación, volvemos nuestra atención a graficar funciones de valor absoluto. Nuestra estrategia en el siguiente ejemplo es hacer un uso liberal de la Definición 2.4 junto con lo que sabemos sobre graficar funciones lineales (de la Sección 2.1) y funciones definidas por partes (de la Sección 1.4).

Ejemplo 2.2.2

Grafica cada una de las siguientes funciones.

$f(x) = |x|$
$g(x) = |x-3|$
$h(x) = |x| -3$
$i(x) = 4 - 2|3x+1|$

Encuentra los ceros de cada función y las$x$ - y$y$ -intercepciones de cada gráfica, si existe alguna. A partir de la gráfica, determinar el dominio y el rango de cada función, enumerar los intervalos en los que la función es creciente, decreciente o constante, y encontrar los extremos relativos y absolutos, si existen.

Solución

Para encontrar los ceros de$f$, nos fijamos$f(x)= 0$. Obtenemos$|x|=0$, que, por Teorema 2.1 nos da$x=0$. Ya que los ceros de$f$ son las$x$ -coordenadas de las$x$ -intercepciones de la gráfica de$y=f(x)$, obtenemos$(0,0)$ como nuestra única$x$ -intercepción. Para encontrar la$y$ -intercepción, establecemos$x=0$, y encontramos$y = f(0) = 0$, así que esa$(0,0)$ es nuestra$y$ -intercepción también. ¹ Usando la Definición 2.4, obtenemos
$\ f(x) = |x| = \left\{ \begin{array}{rcl} -x, & \mbox{if} & x < 0 \\ x, & \mbox{if} & x \geq 0 \\ \end{array} \right.$

De ahí$x < 0$, para, estamos graficando la línea$y = -x$; para$x \geq 0$, tenemos la línea$y = x$. Procediendo como hicimos en la Sección 1.6, obtenemos

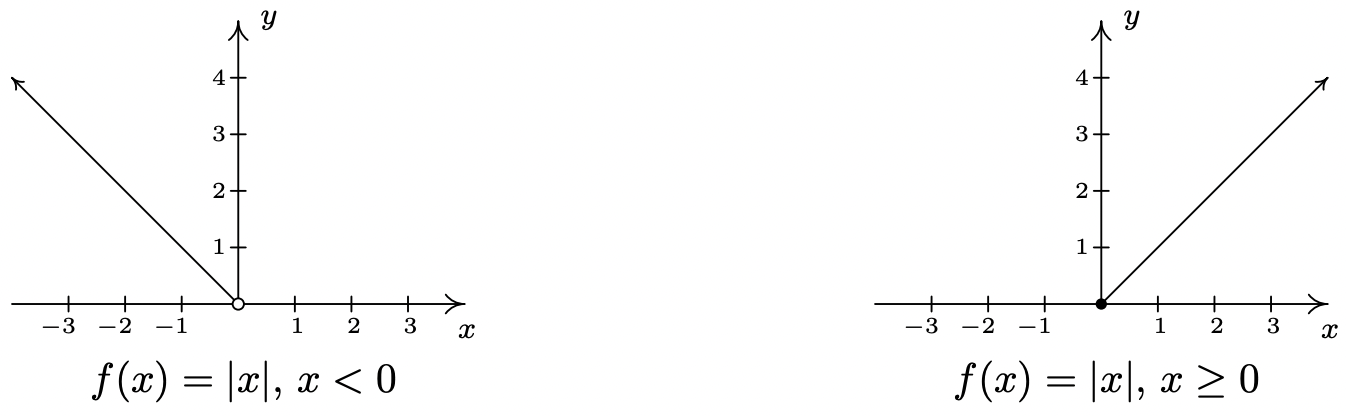
$Screen Shot 2022-03-15 a las 4.37.17 PM.png$

Observe que tenemos un 'círculo abierto' en$(0,0)$ en la gráfica cuando$x<0$. Como hemos visto antes, esto se debe a que los puntos en$y = -x$ aproximación$(0,0)$ como los$x$ -valores se acercan$0$. Dado que$x$ se requiere que sea estrictamente inferior a cero en este tramo, el círculo abierto se dibuja en el origen. No obstante, observe que cuando$x \geq 0$, lleguemos a rellenar el punto en$(0,0)$, que efectivamente 'tapona' el agujero indicado por el círculo abierto. Así conseguimos,

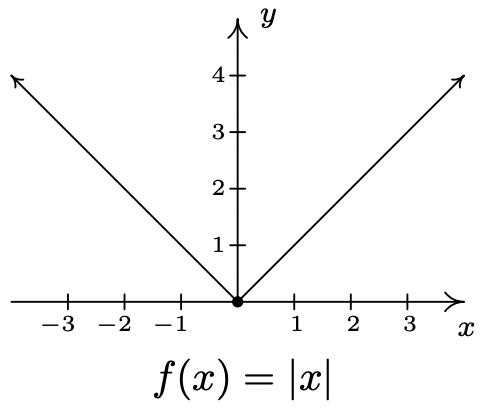
$Screen Shot 2022-03-15 en 4.38.11 PM.png$

Al proyectar la gráfica al$x$ eje -eje, vemos que el dominio es$(-\infty, \infty)$. Proyectar al$y$ eje -nos da el rango$[0,\infty)$. La función está aumentando$[0,\infty)$ y disminuyendo en$(-\infty,0]$. El valor mínimo relativo de$f$ es el mismo que el mínimo absoluto, es decir,$0$ que ocurre en$(0,0)$. No hay valor máximo relativo de$f$. Tampoco hay valor máximo absoluto de$f$, ya que$y$ los valores en la gráfica se extienden infinitamente hacia arriba.
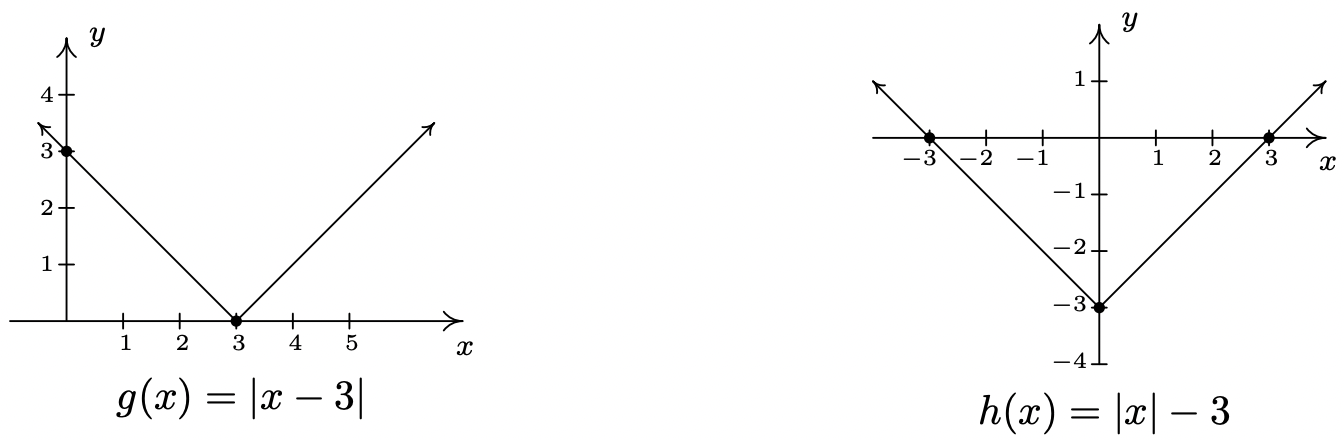
Para encontrar los ceros de$g$, nos fijamos$g(x) = |x-3|=0$. Por Teorema 2.1, obtenemos$x-3=0$ así que$x=3$. De ahí que la$x$ -intercepción sea$(3,0)$. Para encontrar nuestra$y$ -intercepción, nos fijamos$x=0$ así que$y = g(0) = |0-3| = 3$, que cede$(0,3)$ como nuestra$y$ -intercepción. Para graficar$g(x) = |x-3|$, usamos la Definición 2.4 para reescribir$g$ como
$\ g(x) = |x-3| = \left\{ \begin{array}{rcl} -(x-3), & \mbox{if} & (x-3) < 0 \\ (x-3), & \mbox{if} & (x -3) \geq 0 \\ \end{array} \right.$

Simplificando, obtenemos

$\ g(x) =\left\{ \begin{array}{rcl} -x+3, & \mbox{if} & x<3 \\ x-3, & \mbox{if} & x \geq 3 \\ \end{array} \right.$

Como antes, el círculo abierto que introducimos a$(3,0)$ partir de la gráfica de$y = -x+3$ es llenado por el punto$(3,0)$ de la línea$y = x-3$. Determinamos el dominio como$(-\infty, \infty)$ y el rango as$[0,\infty)$. La función$g$ está aumentando$[3,\infty)$ y disminuyendo en$(-\infty,3]$. El valor mínimo relativo y absoluto de$g$ es el$0$ que se produce en$(3,0)$. Como antes, no hay valor máximo relativo o absoluto de$g$.
Ajuste$h(x) = 0$ para buscar ceros da$|x|-3=0$. Al igual que en el Ejemplo 2.2.1, aislamos el valor absoluto para obtener$|x| = 3$ así que$x =3$ o$x=-3$. Como resultado, tenemos un par de$x$ -intercepciones:$(-3,0)$ y$(3,0)$. $x=0$El ajuste da$y = h(0) = |0|-3 = -3$, así que nuestra$y$ -intercepción es$(0,-3)$. Como antes, reescribimos el valor absoluto en$h$ para obtener
$\ h(x) =\left\{ \begin{array}{rcl} -x-3, & \mbox{if} & x<0 \\ x-3, & \mbox{if} & x \geq 0 \\ \end{array} \right.$

Una vez más, el círculo abierto en$(0,-3)$ de una pieza de la gráfica de$h$ es llenado por el punto$(0,-3)$ de la otra pieza de$h$. A partir de la gráfica, determinamos el dominio de$h$ is$(-\infty, \infty)$ y el rango es$[-3,\infty)$. On$[0,\infty)$,$h$ está aumentando; en$(-\infty,0]$ él está disminuyendo. El mínimo relativo se produce en el punto$(0,-3)$ de la gráfica, y vemos$-3$ es tanto el valor mínimo relativo como absoluto de$h$. Además, no$h$ tiene valor máximo relativo o absoluto.

$Screen Shot 2022-03-15 a las 4.42.18 PM.png$
Como antes, nos pusimos$i(x)=0$ a encontrar los ceros de$i$ y obtener$4 - 2|3x+1|=0$. Aislar el término valor absoluto da$|3x+1|=2$, así que cualquiera$3x+1 = 2$ o$3x+1=-2$. Obtenemos$x=\frac{1}{3}$ o$x=-1$, entonces nuestras$x$ -intercepciones son$\left(\frac{1}{3},0\right)$ y$(-1,0)$. Sustituyendo$x=0$ da$y = i(0) = 4-2|3(0)+1| = 2$, por una$y$ -intercepción de$(0,2)$. Reescribiendo la fórmula para$i(x)$ sin valores absolutos dar
$\ i(x) =\left\{ \begin{array}{rcl} 4-2(-(3x+1)), & \mbox{if} & (3x+1) <0 \\ 4-2(3x+1), & \mbox{if} & (3x+1) \geq 0 \\ \end{array} \right. = \left\{ \begin{array}{rcl} 6x+6, & \mbox{if} & x < -\frac{1}{3} \\[2pt] -6x+2, & \mbox{if} & x \geq - \frac{1}{3} \\ \end{array} \right.$

El análisis habitual cerca del lugar problemático$x=-\frac{1}{3}$ da la 'esquina' de esta gráfica es$\left( -\frac{1}{3}, 4\right)$, y obtenemos la forma distintiva$\vee$ '':

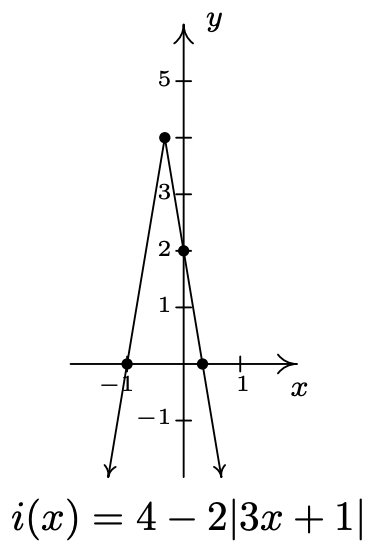
$Screen Shot 2022-03-15 en 4.43.40 PM.png$

El dominio de$i$ es$(-\infty, \infty)$ mientras el rango es$(-\infty, 4]$. La función$i$ está aumentando$\left(-\infty, -\frac{1}{3}\right]$ y disminuyendo en$\left[ -\frac{1}{3}, \infty\right)$. El máximo relativo ocurre en el punto$\left(-\frac{1}{3}, 4\right)$ y el valor máximo relativo y absoluto de$i$ es$4$. Dado que la gráfica de$i$ se extiende hacia abajo para siempre más, no existe un valor mínimo absoluto. Como podemos ver en la gráfica, tampoco hay mínimo relativo.

Tenga en cuenta que todas las funciones del ejemplo anterior llevan la forma característica$\vee$ '' de la gráfica de$y=|x|$. Podríamos haber graficado las funciones$g$,$h$ y$i$ en el Ejemplo 2.2.2 comenzando con la gráfica$f(x)=|x|$ y aplicando transformaciones como en la Sección 1.7 como ilustra nuestro siguiente ejemplo.

Ejemplo 2.2.3

Grafique las siguientes funciones comenzando con la gráfica de$f(x) = |x|$ y usando transformaciones.

$g(x) = |x-3|$
$h(x) = |x| - 3$
$i(x) = 4-2|3x+1|$

Solución

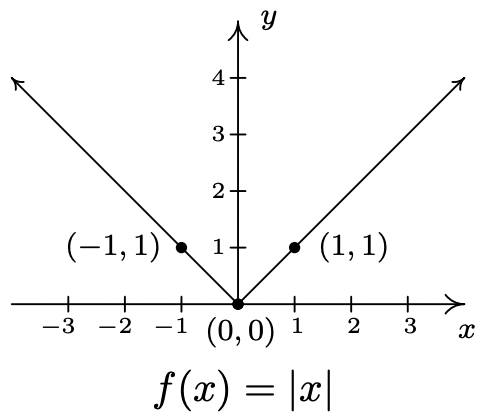
Comenzamos por graficar$f(x) = |x|$ y etiquetar tres puntos,$(-1,1)$,$(0,0)$ y$(1,1)$.

$Screen Shot 2022-03-15 en 4.53.29 PM.png$

Ya que$g(x) = |x-3| = f(x-3)$, Teorema 1.7 nos dice que sumemos$3$ a cada uno de los$x$ -valores de los puntos en la gráfica de$y=f(x)$ para obtener la gráfica de$y=g(x)$. Esto desplaza la gráfica de$y=f(x)$ a las$3$ unidades correctas y mueve el punto$(-1,1)$ hacia$(2,1)$,$(0,0)$ hacia$(3,0)$ y$(1,1)$ hacia$(4,1)$. Conectando estos puntos de la manera clásica$\vee$ '' produce la gráfica de$y = g(x)$.
$Screen Shot 2022-03-15 en 4.54.47 PM.png$
Para$h(x) = |x| - 3 = f(x) -3$, Teorema 1.7 nos dice restar$3$ de cada uno de los$y$ -valores de los puntos en la gráfica de$y=f(x)$ para obtener la gráfica de$y = h(x)$. Esto desplaza la gráfica de$3$ unidades$y=f(x)$ descendentes y se mueve$(-1,1)$ hacia$(-1,-2)$,$(0,0)$ hacia$(0,-3)$ y$(1,1)$ hacia$(1,-2)$. Conectando estos puntos con la forma$\vee$ '' produce nuestra gráfica de$y=h(x)$.
$Screen Shot 2022-03-15 en 4.56.23 PM.png$
Reescribimos$i(x) = 4-2|3x+1| = 4-2f(3x+1) = -2f(3x+1) + 4$ y aplicamos el Teorema 1.7. Primero, nos ocupamos de los cambios en el 'interior' del valor absoluto. En lugar de$|x|$, tenemos$|3x+1|$, entonces, de acuerdo con el Teorema 1.7, primero restamos$1$ de cada uno de los$x$ -valores de puntos en la gráfica de$y = f(x)$, luego dividimos cada uno de esos nuevos valores por$3$. Esto afecta a una$1$ unidad de desplazamiento horizontal a la izquierda seguida de un encogimiento horizontal por un factor de$3$. Estas transformaciones se mueven$(-1,1)$ hacia$\left(-\frac{2}{3}, 1 \right)$,$(0,0)$ hacia$\left(-\frac{1}{3}, 0 \right)$ y$(1,1)$ hacia$\left(0,1\right)$. A continuación, nos ocupamos de lo que sucede 'fuera de' el valor absoluto. El teorema 1.7 nos instruye a multiplicar primero cada$y$ -valor de estos nuevos puntos por$-2$ luego sumar$4$. Geométricamente, esto corresponde a un estiramiento vertical por un factor de$2$, una reflexión a través del$x$ eje y finalmente, un desplazamiento vertical hacia arriba$4$ unidades. Estas transformaciones se mueven$\left(-\frac{2}{3}, 1 \right)$$\left(-\frac{1}{3}, 0 \right)$ hacia$\left(-\frac{2}{3}, 2 \right)$$\left(-\frac{1}{3}, 4 \right)$, hacia y$\left(0,1\right)$ hacia$\left(0, 2\right)$. Conectando estos puntos con la forma '$\vee$' habitual produce nuestra gráfica de$y = i(x)$.
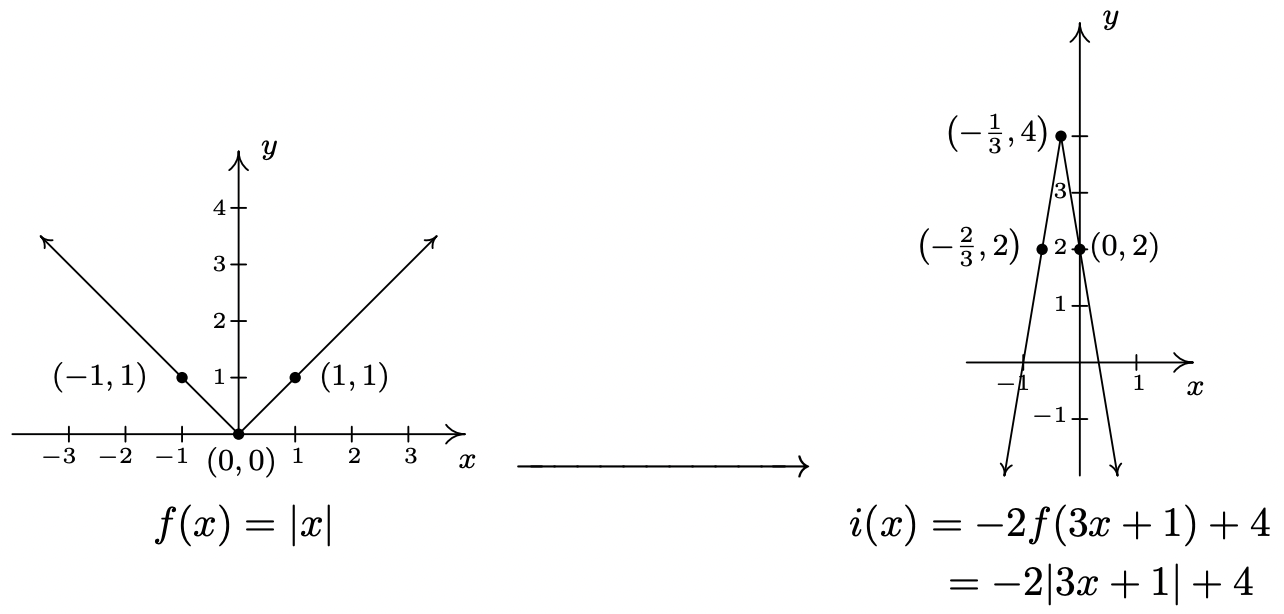
$Screen Shot 2022-03-15 en 5.03.29 PM.png$

Si bien los métodos de la Sección 1.7 se pueden usar para graficar una familia completa de funciones de valor absoluto, no todas las funciones que involucran valores absolutos poseen la forma característica$\vee$ ''. Como ilustra el siguiente ejemplo, muchas veces no hay sustituto para apelar directamente a la definición.

Ejemplo 2.2.4

Grafica cada una de las siguientes funciones. Encuentra los ceros de cada función y las$x$ - y$y$ -intercepciones de cada gráfica, si existe alguna. A partir de la gráfica, determinar el dominio y el rango de cada función, enumerar los intervalos en los que la función es creciente, decreciente o constante, y encontrar los extremos relativos y absolutos, si existen.

$f(x) = \dfrac{|x|}{x}$
$g(x) = |x+2| - |x-3|+1$

Solución

Primero señalamos que, debido a la fracción en la fórmula de$f(x)$,$x \neq 0$. Así es el dominio$(-\infty, 0) \cup (0, \infty)$. Para encontrar los ceros de$f$, nos fijamos$f(x) = \frac{|x|}{x} = 0$. Esta última ecuación implica$|x|=0$, lo que, a partir del Teorema 2.1, implica$x=0$. Sin embargo, no$x=0$ está en el dominio de$f$, lo que significa que, de hecho, no tenemos$x$ -intercepciones. Tampoco tenemos$y$ -intercepciones, ya que$f(0)$ es indefinido. Reescribir el valor absoluto en la función da
$\(f(x) =\left\{ \begin{array}{rcl} \dfrac{-x}{x}, & \mbox{if} & x <0 \\ [10pt] \dfrac{x}{x}, & \mbox{if} & x > 0 \\ \end{array} \right. = \left\{ \begin{array}{rcl} -1, & \mbox{if} & x < 0 \\ 1, & \mbox{if} & x >0 \\ \end{array} \right.$

Para graficar esta función, graficamos dos líneas horizontales:$y = -1$ for$x < 0$ y$y = 1$ for$x > 0$. Tenemos círculos abiertos en$(0,-1)$ y$(0,1)$ (¿Puedes explicar por qué?) así conseguimos

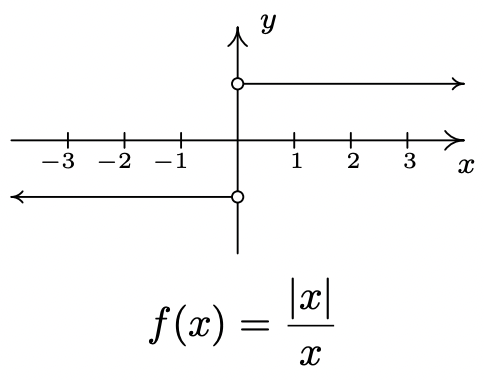
$Screen Shot 2022-03-15 a las 5.10.00 PM.png$

Como encontramos anteriormente, el dominio es$(-\infty, 0)\cup(0,\infty)$. El rango consta de solo dos$y$ -valores:$\{-1,1\}$. La función$f$ es constante en$(-\infty,0)$ y$(0,\infty)$. El valor mínimo local de$f$ es el valor mínimo absoluto de$f$, es decir$-1$; los valores máximos locales y máximos absolutos para que$f$ también$-$ coincidan ambos son$1$. Cada punto en la gráfica de$f$ es simultáneamente un máximo relativo y un mínimo relativo. (¿Recuerdas por qué a la luz de la Definición 1.11? Esto se exploró en los Ejercicios de la Sección 1.6.2.)
Para encontrar los ceros de$g$, nos fijamos$g(x) = 0$. El resultado es$|x+2|-|x-3| +1 = 0$. Intentar aislar el término de valor absoluto se complica por el hecho de que existen dos términos con valores absolutos. En este caso, es más fácil proceder usando casos reescribiendo la función$g$ con dos aplicaciones separadas de Definición 2.4 para eliminar cada instancia de los valores absolutos, uno a la vez. En la primera vuelta conseguimos
$\ g(x) =\left\{ \begin{array}{rcl} -(x+2) - |x-3|+1, & \mbox{if} & (x+2) <0 \\ (x+2) - |x-3|+1, & \mbox{if} & (x+2) \geq 0 \\ \end{array} \right. = \left\{ \begin{array}{rcl} -x-1 - |x-3|, & \mbox{if} & x<-2 \\ x+3-|x-3|, & \mbox{if} & x \geq -2 \\ \end{array} \right.$

Dado que

$\ |x-3| =\left\{ \begin{array}{rcl} -(x-3), & \mbox{if} & (x-3) <0 \\ x-3, & \mbox{if} & (x-3) \geq 0 \\ \end{array} \right. = \left\{ \begin{array}{rcl} -x+3, & \mbox{if} & x<3 \\ x-3, & \mbox{if} & x \geq 3 \\ \end{array} \right.,$

necesitamos romper el dominio nuevamente en$x=3$. Tenga en cuenta que si$x < -2$$x < 3$, entonces, así reemplazamos$|x-3|$ con$-x+3$ para esa parte del dominio, también. Nuestra revisión completa de la forma de$g$ rendimientos

$\ g(x) = \left\{ \begin{array}{rcl} -x-1 - (-x+3), & \mbox{if} & x<-2 \\ x+3-(-x+3), & \mbox{if} & x \geq -2 \, \mbox{ and } \, x < 3 \\ x+3 - (x-3), & \mbox{if} & x \geq 3 \\ \end{array} \right. \;\; = \;\; \left\{ \begin{array}{rcl} -4, & \mbox{if} & x<-2 \\ 2x, & \mbox{if} & -2 \leq x < 3 \\ 6, & \mbox{if} & x \geq 3 \\ \end{array} \right.$

Para resolver$g(x)=0$, vemos que la única pieza que contiene una variable es$g(x) = 2x$ para$-2 \leq x < 3$. Resolver$2x=0$ da$x=0$. Ya que$x=0$ está en el intervalo$[-2,3)$, mantenemos esta solución y tenemos$(0,0)$ como nuestra única$x$ -intercepción. En consecuencia, la$y$ -intercepción también lo es$(0,0)$. Para graficar$g$, comenzamos con$x < -2$ y graficamos la línea horizontal$y=-4$ con un círculo abierto en$(-2,-4)$. Para$-2 \leq x < 3$, graficamos la línea$y=2x$ y el punto$(-2,-4)$ parchea el agujero dejado por la pieza anterior. Un círculo abierto en$(3,6)$ completa la gráfica de esta parte. Finalmente, graficamos la línea horizontal$y=6$ para$x \geq 3$, y el punto$(3,6)$ rellena el círculo abierto dejado por la parte anterior de la gráfica. La gráfica terminada es

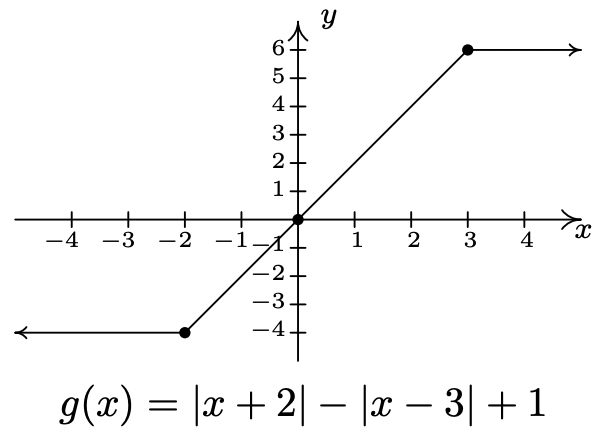
$Screen Shot 2022-03-15 a las 5.14.32 PM.png$

El dominio de$g$ es todos los números reales,$(-\infty, \infty)$, y el rango de$g$ es todos los números reales entre$-4$ e$6$ inclusivos,$[-4,6]$. La función es cada vez mayor$[-2,3]$ y constante en$(-\infty, -2]$ y$[3,\infty)$. El valor mínimo relativo de$f$ es el$-4$ que coincide con el mínimo absoluto. Los valores máximos relativos y absolutos también coinciden en$6$. Cada punto en la gráfica de$y=g(x)$ for$x<-2$ y$x> 3$ produce tanto un mínimo relativo como un máximo relativo. El punto$(-2,-4)$, sin embargo, da solo un mínimo relativo y el punto solo$(3,6)$ rinde un máximo relativo. (Recordemos los Ejercicios en la Sección 1.6.2 que trataban de funciones constantes.)

Muchas de las aplicaciones que los autores conocen que involucran valores absolutos también involucran desigualdades de valor absoluto. Por esa razón, guardamos nuestra discusión de las solicitudes para la Sección 2.4.

2.2.1 Ejercicios

En los Ejercicios 1 - 15, resuelve la ecuación.

$|x| = 6$[solveabsvalequfirst]
$|3x-1| = 10$
$|4-x| = 7$
$4 - |x| = 3$
$2|5x+1| - 3 = 0$
$|7x-1| + 2 = 0$
$\dfrac{5 - |x|}{2} = 1$
$\frac{2}{3} |5-2x| - \frac{1}{2} = 5$
$|x| = x + 3$
$|2x-1| = x+1$
$4 - |x| = 2x+1$
$|x-4| = x-5$
$|x| = x^2$
$|x| = 12 - x^2$
$|x^2 - 1| = 3$

Demostrar que si$\ |f(x)|=|g(x)|$ entonces cualquiera$\ f(x)=g(x)$ o$\ f(x)=-g(x)$. Usa ese resultado para resolver las ecuaciones en los Ejercicios 16 - 21.

$\ |3 x-2|=|2 x+7|$
$\ |3 x+1|=|4 x|$
$\ |1-2 x|=|x+1|$
$\ |4-x|-|x+2|=0$
$\ |2-5 x|=5|x+1|$
$\ 3|x-1|=2|x+1|$

En Ejercicios 22 - 33, grafica la función. Encuentra los ceros de cada función y las intercepciones x e y de cada gráfica, si existe alguna. A partir de la gráfica, determinar el dominio y el rango de cada función, enumerar los intervalos en los que la función es creciente, decreciente o constante, y encontrar los extremos relativos y absolutos, si existen.

$\ f(x)=|x+4|$
$\ f(x)=|x|+4$
$\ f(x)=|4 x|$
$\ f(x)=-3|x|$
$\ f(x)=3|x+4|-4$
$\ f(x)=\frac{1}{3}|2 x-1|$
$\ f(x)=\frac{|x+4|}{x+4}$
$\ f(x)=\frac{|2-x|}{2-x}$
$\ f(x)=x+|x|-3$
$\ f(x)=|x+2|-x$
$\ f(x)=|x+2|-|x|$
$\ f(x)=|x+4|+|x-2|$
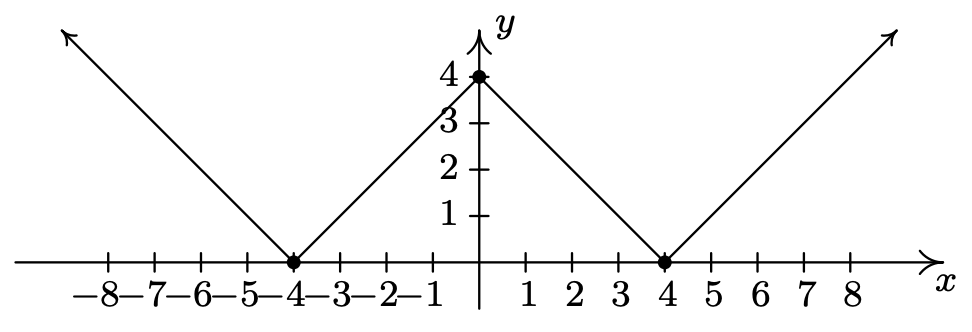
Con la ayuda de tus compañeros de clase, encuentra una función de valor absoluto cuya gráfica se da a continuación.
$Screen Shot 2022-03-25 a las 5.29.35 PM.png$
Con la ayuda de tus compañeros, prueba la segunda, tercera y quinta parte del Teorema 2.1.
Demostrar La Desigualdad Triángulo: Para todos los números reales$\ a$ y$\ b$,$\ |a+b| \leq|a|+|b|$.

RESPUESTAS

$x = -6$o$x=6$
$x = -3$o$x= \frac{11}{3}$
$x = -3$o$x= 11$
$x = -1$o$x= 1$
$x=-\frac{1}{2}$o$x= \frac{1}{10}$
sin solución
$x=-3$o$x= 3$
$x = -\frac{13}{8}$o$x= \frac{53}{8}$
$x=-\frac{3}{2}$
$x=0$o$x= 2$
$x=1$
sin solución
$x=-1$,$x= 0$ o$x= 1$
$x=-3$o$x=3$
$x=-2$o$x=2$
$x = -1$o$x = 9$
$x = -\frac{1}{7}$o$x = 1$
$x = 0$o$x = 2$
$x=1$
$x = -\frac{3}{10}$
$x = \frac{1}{5}$o$x = 5$
$f(x) = |x + 4|$
$f(-4) = 0$
$x$-interceptar$(-4, 0)$
$y$ -interceptar$(-\infty, \infty)$
Rango de$(0, 4)$
dominio$[0, \infty)$
decreciente$(-\infty, -4]$
al aumentar en $[-4, \infty)$
Min. relativo y absoluto a$(-4,0)$
No máximo relativo o absoluto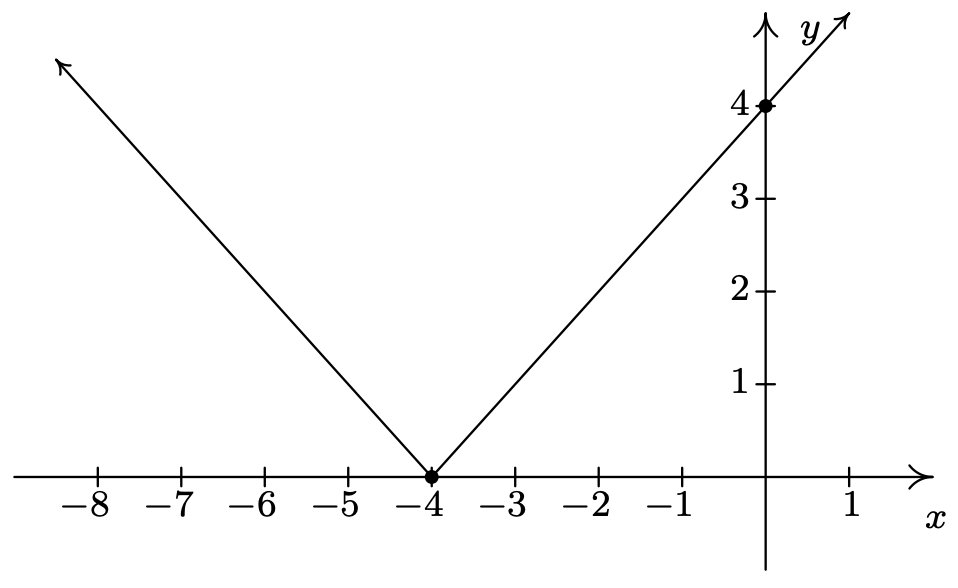
$Screen Shot 2022-03-25 a las 5.35.15 PM.png$
$\ f(x)=|x|+4$
Sin ceros
No$x$ -intercepta
$y$ -interceptar$(-\infty, \infty)$
Rango de$(0, 4)$
dominio$[4, \infty)$
Disminución$(-\infty, 0]$
al aumentar en $[0, \infty)$
Mínimo relativo y absoluto en$(0, 4)$
Sin máximo relativo o absoluto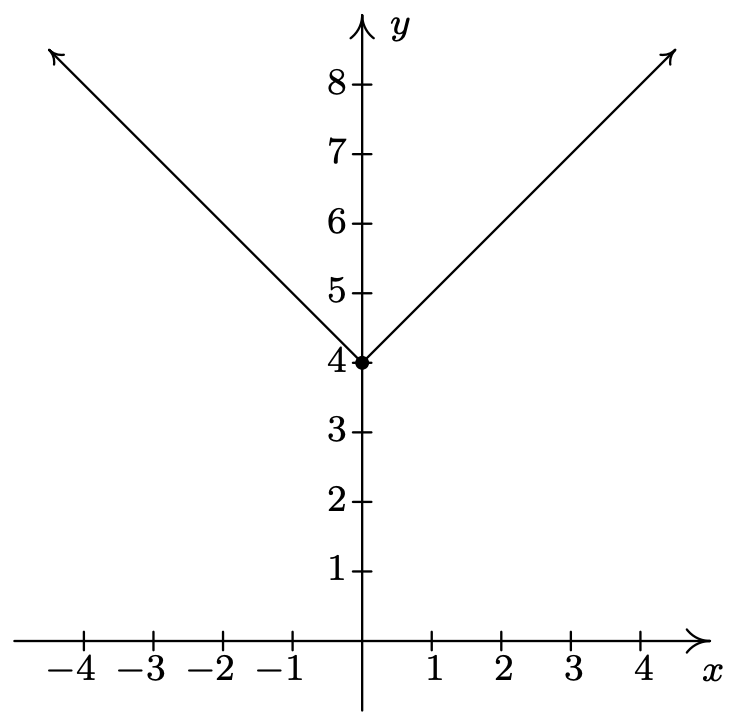

$Screen Shot 2022-03-25 a las 5.36.32 PM.png$
$\ f(x)=|4 x|$
$f(0) = 0$
$x$-interceptar$(0, 0)$
$y$ -interceptar$(-\infty, \infty)$
Rango de$(0, 0)$
dominio$[0, \infty)$
decreciente$(-\infty, 0]$
al aumentar en $[0, \infty)$
Mínimo relativo y absoluto en$(0, 0)$
Sin máximo relativo o absoluto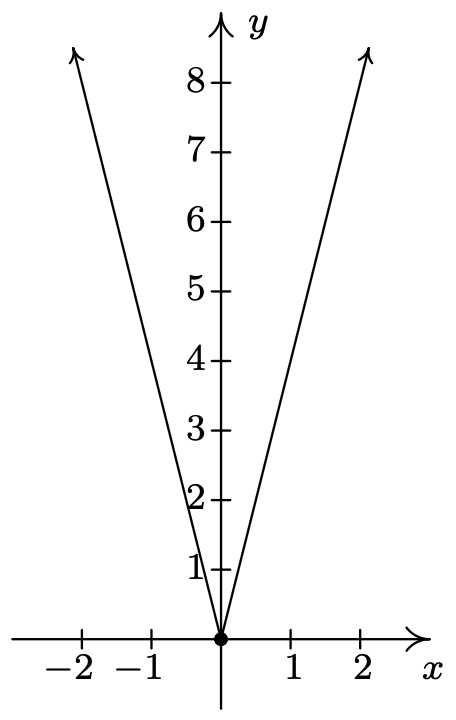

$Screen Shot 2022-03-25 a las 5.38.57 PM.png$
$f(x) = -3|x|$
$f(0) = 0$
$x$-interceptar$(0, 0)$
$y$ -interceptar$(-\infty, \infty)$
Rango de$(0, 0)$
dominio$(-\infty, 0]$
Aumentando$(-\infty, 0]$
al disminuir en $[0, \infty)$
Máximo relativo y absoluto en$(0, 0)$
Sin mínimo relativo o absoluto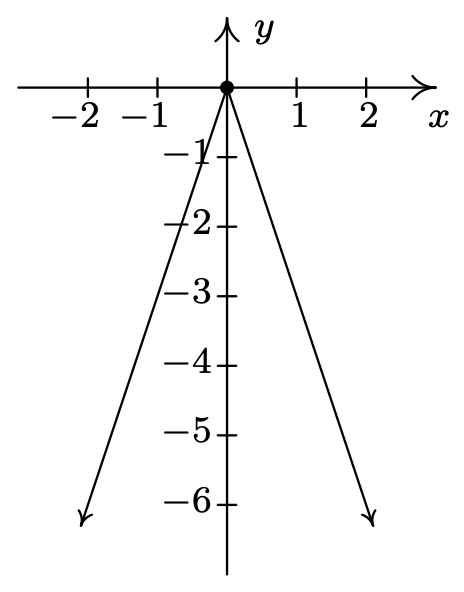

$Screen Shot 2022-03-25 a las 5.41.45 PM.png$
$f(x) = 3|x + 4| - 4$
$f\left(-\frac{16}{3}\right) = 0$,$f\left(-\frac{8}{3}\right) = 0$
$x$ -intercepta$\left(-\frac{16}{3}, 0\right)$,$\left(-\frac{8}{3}, 0\right)$
$y$ -interceptar$(-\infty, \infty)$
Rango de$(0, 8)$
dominio$[-4, \infty)$
Disminución en$(-\infty, -4]$
Aumentando en Min.$[-4, \infty)$
relativo y absoluto a$(-4,-4)$
Sin máximo relativo o absoluto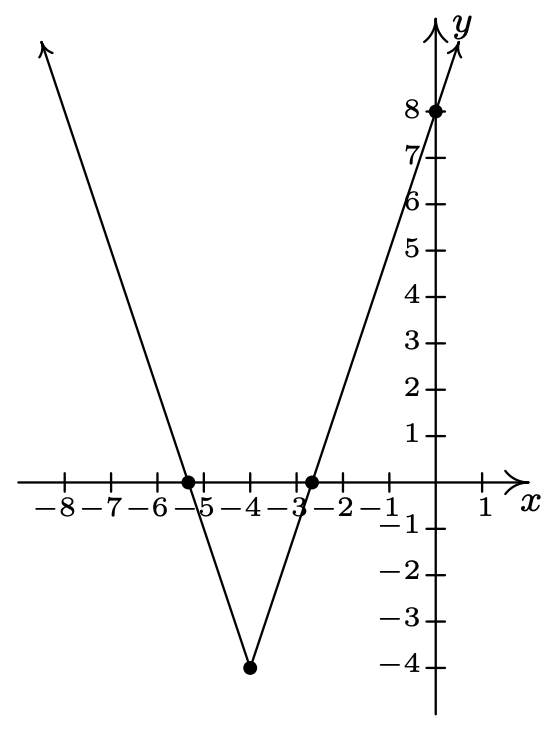

$Screen Shot 2022-03-25 a las 5.43.35 PM.png$
$f(x) = \frac{1}{3}|2x - 1|$
$f\left(\frac{1}{2}\right) = 0$
$x$-intercepta$\left(\frac{1}{2}, 0\right)$
$y$ -interceptar$(-\infty, \infty)$
Rango de$\left(0, \frac{1}{3}\right)$
dominio$[0, \infty)$
decreciente$\left(-\infty, \frac{1}{2}\right]$
al aumentar en $\left[\frac{1}{2}, \infty\right)$
Min. relativo y absoluto a$\left(\frac{1}{2},0\right)$
No máximo relativo o absoluto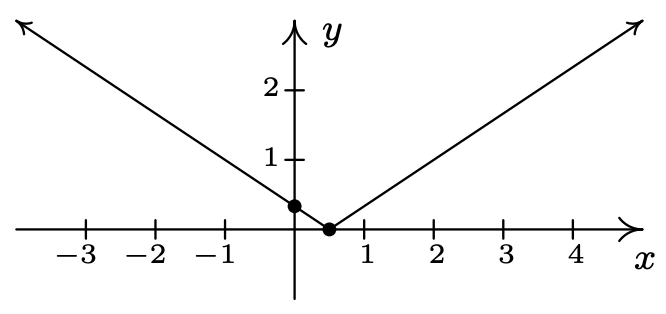

$Screen Shot 2022-03-25 a las 5.46.28 PM.png$
z$f(x) = \dfrac{|x + 4|}{x + 4}$
Sin ceros
No$x$ -interceptar
$y$ -interceptar Constante de$(-\infty, -4) \cup (-4, \infty)$
rango de$(0, 1)$
dominio en$\{-1, 1\}$
$(-\infty, -4)$
Constante encendido$(-4, \infty)$
Mínimo absoluto en cada punto$(x, -1)$ donde Máximo$x < -4$
absoluto en cada punto$(x, 1)$ donde Máximo$x > -4$
relativo Y mínimo en cada punto de la gráfica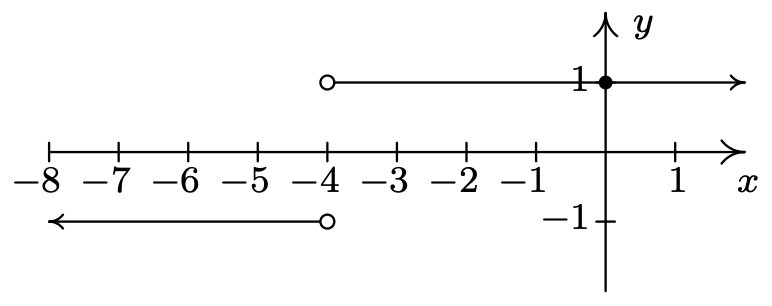

$Screen Shot 2022-03-25 a las 5.49.15 PM.png$
$f(x) = \dfrac{|2 - x|}{2 - x}$
Sin ceros
No$x$ -interceptar
$y$ -interceptar Constante de$(-\infty, 2) \cup (2, \infty)$
rango de$(0, 1)$
dominio en$\{-1, 1\}$
$(-\infty, 2)$
Constante encendido$(2, \infty)$
Mínimo absoluto en cada punto$(x, -1)$ donde Máximo$x > 2$
absoluto en cada punto$(x, 1)$ donde Máximo$x < 2$
relativo Y mínimo en cada punto de la gráfica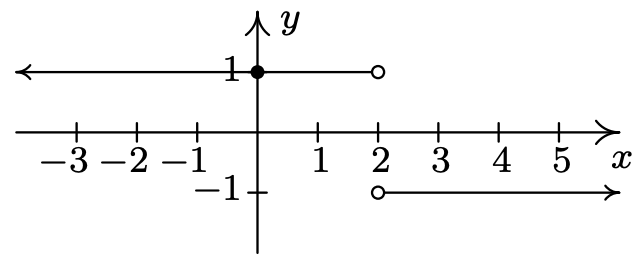

$Screen Shot 2022-03-25 a las 5.57.26 PM.png$
Volver a escribir$f(x) = x+|x| - 3$ como
${\displaystyle f(x) = \left\{ \begin{array}{rcl} -3 & \mbox{ if } & x < 0\\ 2x -3 & \mbox{ if } & x \geq 0 \\ \end{array} \right. }$
$f\left(\frac{3}{2}\right) = 0$
$x$ -interceptar$\left(\frac{3}{2}, 0\right)$
$y$ -interceptar$(-\infty, \infty)$
rango de$(0,-3)$
dominio$[-3, \infty)$
aumentando en $[0,\infty)$
Constante en Mínimo$(-\infty, 0]$
absoluto en cada punto$(x,-3)$ donde$x \leq 0$
Ningún máximo absoluto Mínimo
relativo en cada punto$(x, -3)$ donde Máximo$x \leq 0$
relativo en cada punto$(x, -3)$ donde$x < 0$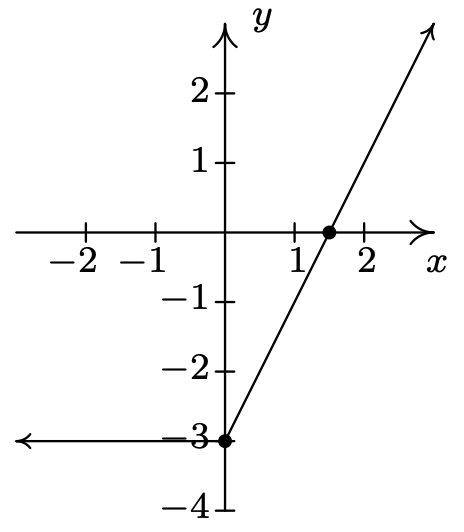

$Screen Shot 2022-03-25 en 5.58.29 PM.png$
Reescribir$f(x) = |x+2| - x$ como
${\displaystyle f(x) = \left\{ \begin{array}{rcl} -2x-2 & \mbox{ if } & x < -2\\ 2 & \mbox{ if } & x \geq -2 \\ \end{array} \right. }$
Sin ceros
No$x$ -intercepta
$y$ -interceptar$(-\infty, \infty)$
Rango de$(0,2)$
dominio$[2, \infty)$
Disminución en$(-\infty, -2]$
Constante en Mínimo$[-2,\infty)$
absoluto en cada punto$(x,2)$ donde$x \geq -2$
Ningún máximo absoluto Mínimo
relativo en cada punto$(x, 2)$ donde Máximo$x \geq -2$
relativo en cada punto $(x, 2)$donde$x > -2$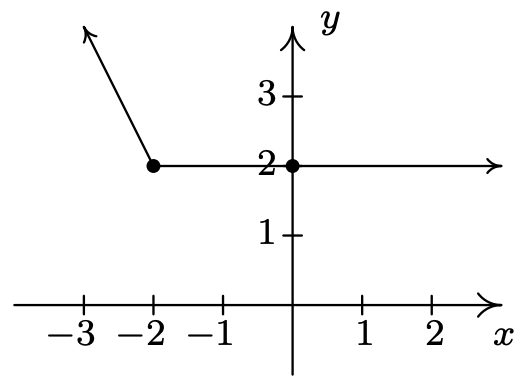

$Screen Shot 2022-03-25 a las 5.59.18 PM.png$
Volver a escribir$f(x) = |x+2|-|x|$ como
${\displaystyle f(x) = \left\{ \begin{array}{rcl} -2 & \mbox{ if } & x < -2\\ 2x+2 & \mbox{ if } & -2 \leq x < 0 \\ 2 & \mbox{ if } & x \geq 0 \\ \end{array} \right. }$
$f\left(-1\right) = 0$
$x$ -interceptar$\left(-1, 0\right)$
$y$ -interceptar$(-\infty, \infty)$
rango de$(0,2)$
dominio$[-2,2]$
aumentando en $[-2,0]$
Constante en$(-\infty, -2]$
Constante en Mínimo$[0,\infty)$
absoluto en cada punto$(x,-2)$ donde Máximo$x \leq -2$
absoluto en cada punto$(x,2)$ donde Mínimo$x \geq 0$
relativo en cada punto$(x, -2)$ donde$x \leq -2$ y en cada punto$(x,2)$ donde Máximo$x>0$
relativo en cada punto$(x, -2)$ donde$x < -2$ y en cada punto$(x,2)$ donde$x \geq 0$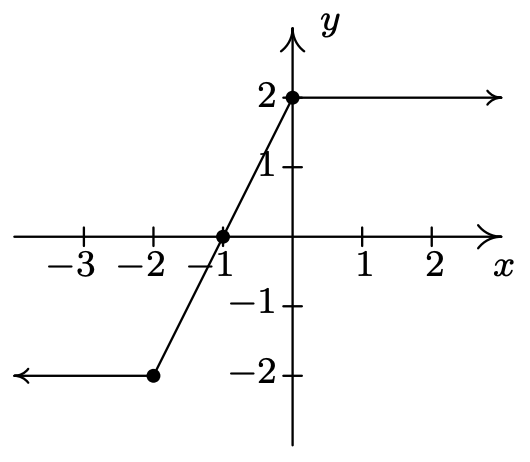

$Screen Shot 2022-03-25 a 6.02.56 PM.png$
Reescribir$f(x) = |x + 4| + |x - 2|$ como
${\displaystyle f(x) = \left\{ \begin{array}{rcl} -2x - 2 & \mbox{ if } & x < -4\\ 6 & \mbox{ if } & -4 \leq x < 2\\ 2x + 2 & \mbox{ if } & x \geq 2 \end{array} \right. }$
Sin ceros
Sin$x$ -interceptar
$y$ -interceptar$(-\infty, \infty)$
Rango de$(0, 6)$
dominio$[6, \infty)$
Disminución en$(-\infty, -4]$
Constante al$[-4, 2]$
Incrementar en Mínimo$[2, \infty)$
Absoluto en cada punto$(x, 6)$ donde$-4 \leq x \leq 2$
Ningún máximo absoluto Mínimo
relativo en cada punto$(x, 6)$ donde$-4 \leq x \leq 2$
Máximo relativo en cada punto$(x, 6)$ donde$-4 < x < 2$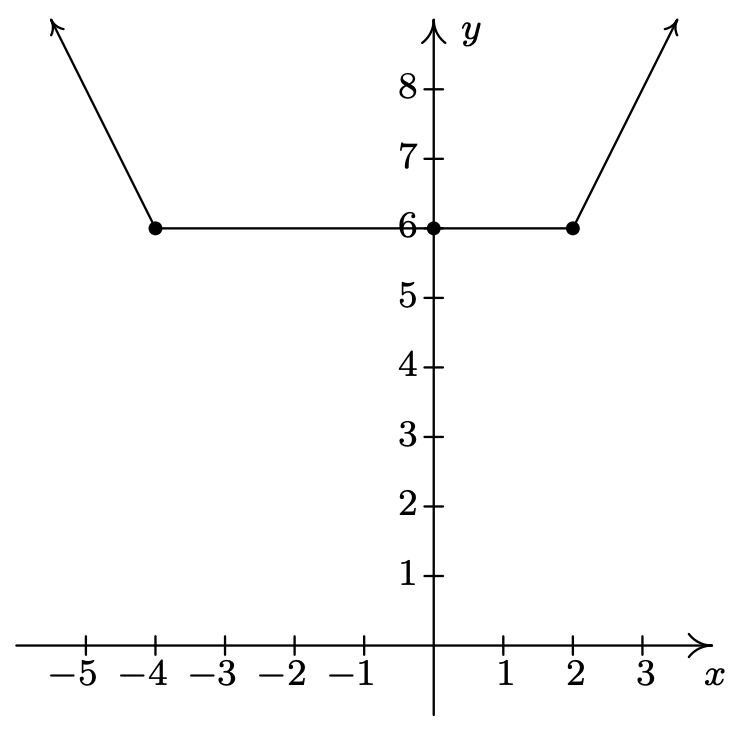

$Screen Shot 2022-03-25 a las 6.04.00 PM.png$

$f(x) = ||x| - 4|$

Referencia

¹ En realidad, ya que las funciones pueden tener como máximo una intercepción y (¿sabes por qué?) , tan pronto como encontramos (0, 0) como la intercepción x, supimos que esta era también la intercepción y.