2.3: Funciones cuadráticas

Tal vez recuerdes estudiar ecuaciones cuadráticas en Álgebra Intermedia. En esta sección, revisamos esas ecuaciones en el contexto de nuestra siguiente familia de funciones: las funciones cuadráticas.

Definición 2.5.

Una función cuadrática es una función de la forma

\(f(x) = ax^2 + bx + c,\)

donde\(a\),\(b\) y\(c\) son números reales con\(a \neq 0\). El dominio de una función cuadrática es\((-\infty, \infty)\).

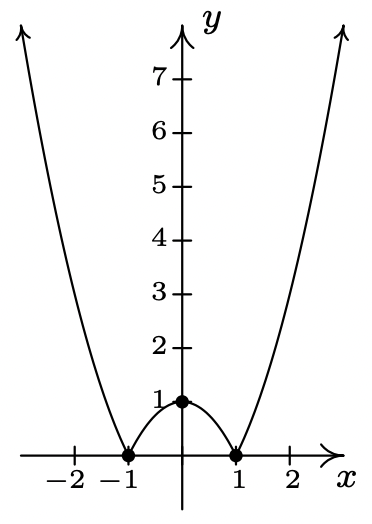
La función cuadrática más básica es\(f(x) = x^2\), cuya gráfica aparece a continuación. Su forma debe parecer familiar a partir del Álgebra Intermedio — se llama parábola. Al punto\((0,0)\) se le llama el vértice de la parábola. En este caso, el vértice es un mínimo relativo y también es el donde se\(f\) puede encontrar el valor mínimo absoluto de.

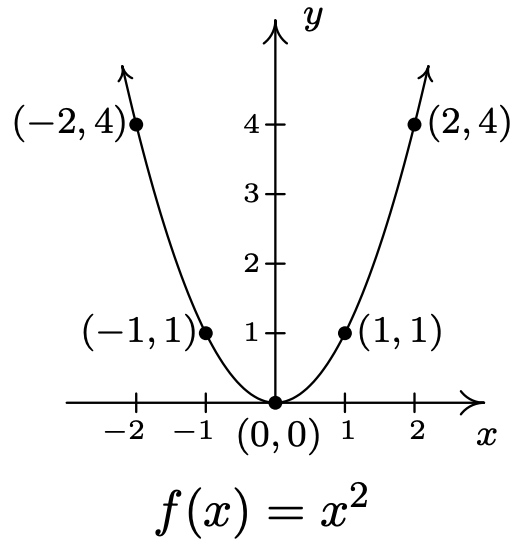
Al igual que muchas de las funciones de valor absoluto en la Sección 2.2, conocer la gráfica de nos\(f(x) = x^2\) permite graficar toda una familia de funciones cuadráticas usando transformaciones.

Ejemplo 2.3.1

Grafique las siguientes funciones comenzando con la gráfica de\(f(x) = x^2\) y usando transformaciones. Encuentra el vértice, indica el rango y encuentra las\(y\) intercepciones\(x\) - y -si existen.

1. \(g(x) = (x+2)^2 - 3\)
2. \(h(x) = -2(x-3)^2+1\)

Solución.

1. Ya que\(g(x) = (x+2)^2 - 3 = f(x+2) - 3\), el Teorema 1.7 nos instruye a restar primero\(2\) de cada uno de los\(x\) -valores de los puntos en\(y=f(x)\). Esto desplaza la gráfica de las\(2\) unidades\(y = f(x)\) a la izquierda y se mueve\((-2,4)\) a\((-4,4)\),\((-1,1)\) a\((-3,1)\),\((0,0)\) a\((-2,0)\),\((1,1)\) a\((-1,1)\) y\((2,4)\) hacia\((0,4)\). A continuación, restamos\(3\) de cada uno de los\(y\) -valores de estos nuevos puntos. Esto mueve la gráfica hacia abajo\(3\) unidades y se mueve\((-4,4)\) a\((-4,1)\),\((-3,1)\) a\((-3,-2)\),\((-2,0)\) a\((-2,3)\),\((-1,1)\) a\((-1,-2)\) y\((0,4)\) hacia\((0,1)\). Conectamos los puntos de manera parabólica para conseguir

   

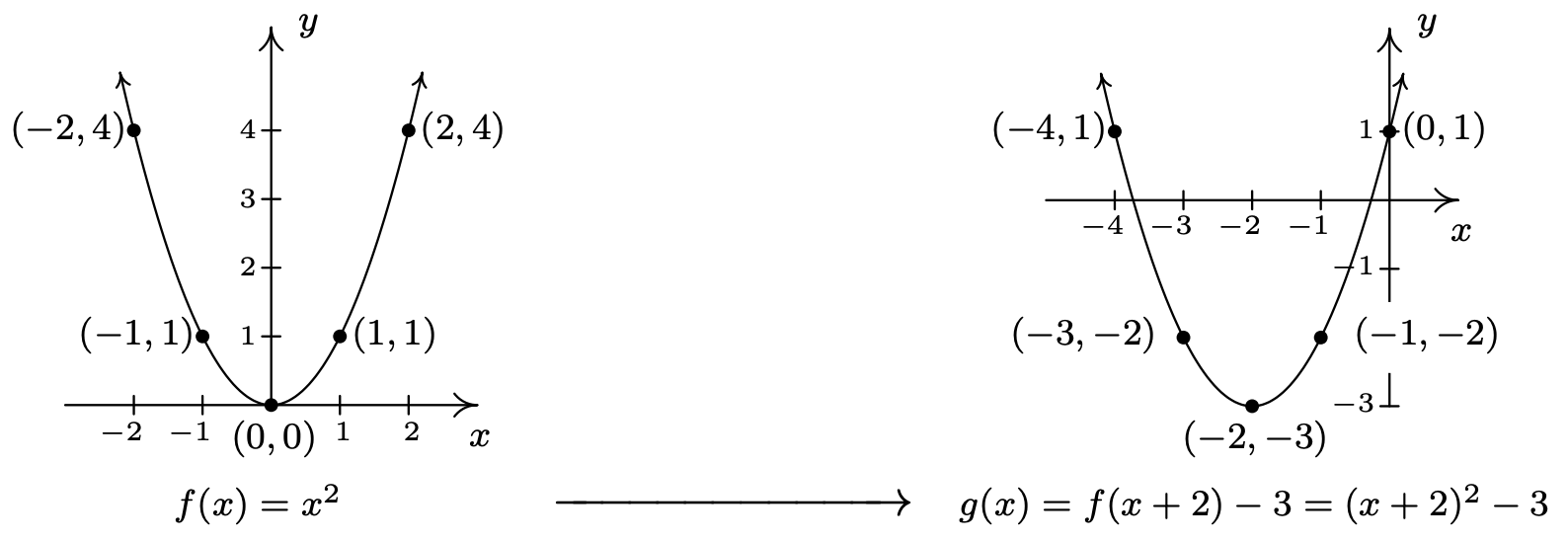
   De la gráfica, vemos que el vértice se ha movido de\((0,0)\) en la gráfica de\(y = f(x)\) a\((-2,-3)\) en la gráfica de\(y = g(x)\). Esto establece\([-3, \infty)\) como el rango de\(g\). Vemos que la gráfica de\(y=g(x)\) cruza el\(x\) -eje dos veces, por lo que esperamos dos\(x\) -intercepciones. Para encontrarlos, nos fijamos\(y = g(x) = 0\) y resolvemos. Hacerlo arroja la ecuación\((x+2)^2 - 3 = 0\), o\((x+2)^2 = 3\). La extracción de raíces cuadradas da\(x + 2 = \pm \sqrt{3}\), o\(x = -2 \pm \sqrt{3}\). Nuestras\(x\) -intercepciones son\((-2-\sqrt{3}, 0) \approx (-3.73, 0)\) y\((-2+\sqrt{3}, 0) \approx (-0.27, 0)\). El\(y\) -intercepto de la gráfica,\((0,1)\) fue uno de los puntos que trazamos originalmente, así que ya terminamos.

2. Siguiendo el Teorema 1.7 una vez más\(h(x) = -2(x-3)^2+1 = -2f(x-3)+1\), para graficar, primero comenzamos sumando\(3\) a cada uno de los\(x\) -valores de los puntos en la gráfica de\(y=f(x)\). Esto efectúa un desplazamiento horizontal a la derecha de\(3\) las unidades y se mueve\((-2,4)\)\((-1,1)\) a\((1,4)\)\((2,1)\),\((0,0)\) a\((3,0)\),\((1,1)\) a, a\((4,1)\) y\((2,4)\) a\((5,4)\). A continuación, multiplicamos cada uno de nuestros\(y\) -valores primero por\(-2\) y luego agregamos\(1\) a ese resultado. Geométricamente, se trata de un estiramiento vertical por un factor de\(2\), seguido de una reflexión alrededor del\(x\) eje, seguido de una\(1\) unidad de desplazamiento vertical hacia arriba. Esto pasa\((1,4)\) a\((1,-7)\),\((2,1)\) a\((2,-1)\),\((3,0)\) a\((3,1)\),\((4,1)\) a\((4,-1)\) y\((5,4)\) a\((5,-7)\).

   

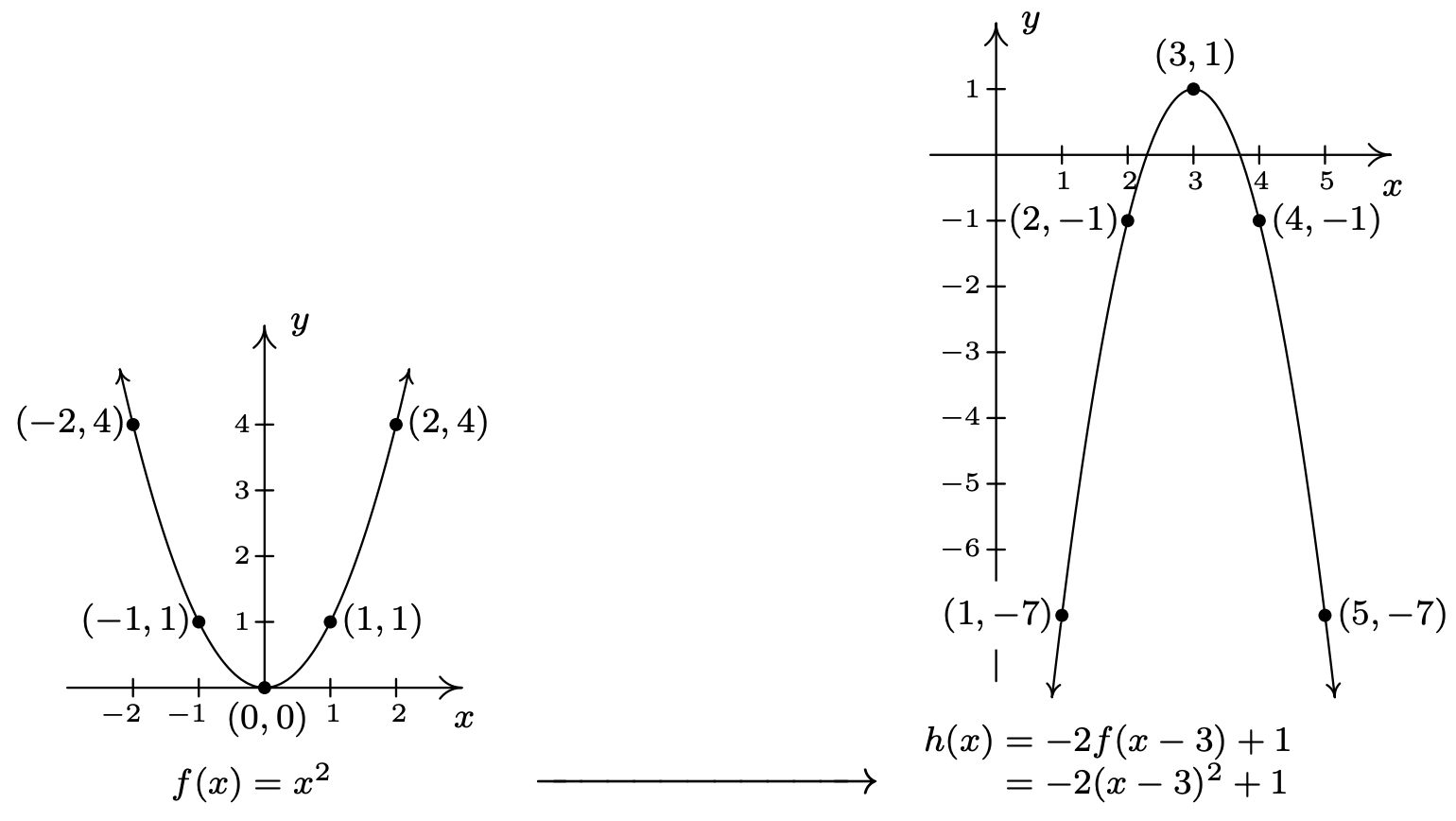
   El vértice es el\((3,1)\) que hace que el rango de\(h\)\((-\infty, 1]\). A partir de nuestra gráfica, sabemos que hay dos\(x\) -intercepciones, así que establecemos\(y = h(x) = 0\) y resolvemos. Obtenemos\(-2(x-3)^2+1 = 0\) lo que da\((x-3)^2 = \frac{1}{2}\). Extrayendo raíces cuadradas ¹ da\(x - 3 = \pm \frac{\sqrt{2}}{2}\), de modo que cuando agregamos\(3\) a cada lado, ² obtenemos\(x = \frac{6 \pm \sqrt{2}}{2}\). De ahí, nuestras\(x\) -intercepciones son\(\left(\frac{6 - \sqrt{2}}{2}, 0 \right) \approx (2.29, 0)\) y\(\left(\frac{6 + \sqrt{2}}{2}, 0 \right) \approx (3.71, 0)\). Aunque nuestro gráfico no lo muestra, hay una\(y\) -intercepción que se puede encontrar configurando\(x=0\). Con\(h(0) = -2(0-3)^2+1 = -17\), tenemos que nuestra\(y\) -intercepción es\((0,-17)\).

Algunos comentarios sobre el Ejemplo 2.3.1 están en orden. Primero tenga en cuenta que ni la fórmula dada para\(g(x)\) ni la dada para\(h(x)\) coinciden con la forma dada en la Definición 2.5. Podríamos, por supuesto, convertir ambos\(g(x)\) y\(h(x)\) en esa forma expandiéndonos y recopilando términos similares. Haciéndolo, encontramos\(g(x) = (x+2)^2 - 3 = x^2 + 4x+1\) y\(h(x) = -2(x-3)^2+1 = -2x^2+12x-17\). Si bien estas fórmulas 'simplificadas' para\(g(x)\) y\(h(x)\) satisfacen la Definición 2.5, no se prestan a graficar fácilmente. Por esa razón, a la forma de\(g\) y\(h\) presentada en el Ejemplo 2.3.2 se le da un nombre especial, el cual enumeramos a continuación, junto con el formulario presentado en la Definición 2.5.

Definición 2.6

Forma Estándar y General de las Funciones Cuadráticas: Supongamos que\(f\) es una función cuadrática.

• La forma general de la función cuadrática\(f\) es\(f(x) = ax^2+bx+c\), dónde\(a\),\(b\) y\(c\) son números reales con\(a \neq 0\).
• La forma estándar de la función cuadrática\(f\) es\(f(x) = a(x-h)^2 + k\), dónde\(a\),\(h\) y\(k\) son números reales con\(a\neq 0\).

Es importante señalar en esta etapa que no tenemos garantías de que cada función cuadrática pueda escribirse en forma estándar. Esto es realmente cierto, y lo demostramos más adelante en la exposición, pero por ahora celebramos las ventajas de la forma estándar, comenzando por el siguiente teorema.

Teorema 2.2

Fórmula de vértice para cuadráticas en forma estándar: Para la función cuadrática\(f(x) = a(x-h)^2 + k\), donde\(a\),\(h\) y\(k\) son números reales con\(a\neq 0\), el vértice de la gráfica de\(y = f(x)\) es\((h,k)\).

Podemos verificar fácilmente la fórmula dada Teorema 2.2 con las dos funciones dadas en el Ejemplo 2.3.1. Después de una (leve) reescritura,\(g(x) = (x+2)^2 - 3 = (x-(-2))^2+(-3)\), e identificamos\(h=-2\) y\(k=-3\). Bastante seguro, encontramos que el vértice de la gráfica\(y=g(x)\) de ser\((-2,-3)\). Para\(h(x) = -2(x-3)^{2}+1\), no se necesita reescribir. Podemos identificar directamente\(h=3\) y\(k=1\) y, efectivamente, encontramos el vértice de la gráfica de\(y=h(x)\) ser\((3,1)\).

Para ver por qué la fórmula en Teorema 2.2 produce el vértice, considere la gráfica de la ecuación\(y = a(x-h)^2 + k\). Cuando sustituimos\(x=h\), obtenemos\(y=k\), así\((h,k)\) está en la gráfica. Si\(x \neq h\), entonces\(x-h \neq 0\) así\((x-h)^2\) es un número positivo. Si\(a>0\), entonces\(a(x-h)^2\) es positivo, así\(y = a(x-h)^2 + k\) es siempre un número mayor que\(k\). Esto quiere decir que cuando\(a>0\),\((h,k)\) es el punto más bajo de la gráfica y así la parábola debe abrirse hacia arriba, haciendo\((h,k)\) el vértice. Un argumento similar muestra que si\(a<0\),\((h,k)\) es el punto más alto de la gráfica, entonces la parábola se abre hacia abajo, y también\((h,k)\) es el vértice en este caso.

Alternativamente, podemos aplicar la maquinaria en la Sección 1.7. Dado que el vértice de\(y = x^2\) es\((0,0)\), podemos determinar el vértice de\(y = a(x-h)^2+k\) determinando el destino final de a\((0,0)\) medida que se mueve a través de cada transformación. Para obtener la fórmula\(f(x)= a(x-h)^2+k\), comenzamos con\(g(x)=x^2\) y primero definimos\(g_{1}(x) = a g(x) = ax^2\). Esto se traduce en una escala vertical y/o reflexión. ³ Ya que multiplicamos la salida por\(a\), multiplicamos las\(y\) coordenadas -en la gráfica de\(g\) por\(a\), así el punto\((0,0)\) permanece\((0,0)\) y sigue siendo el vértice. A continuación, definimos\(g_{2}(x) = g_{1}(x-h) = a(x-h)^2\). Esto induce un desplazamiento horizontal a la derecha o a la izquierda.\(h\) Las unidades ⁴ mueven el vértice, en cualquier caso, a\((h,0)\). Finalmente,\(f(x) = g_{2}(x)+k = a(x-h)^2+k\) que efectúa un desplazamiento vertical hacia arriba o hacia abajo\(k\) unidades ⁵ dando como resultado que el vértice se mueva de\((h,0)\) a\((h,k)\).

Además de verificar el Teorema 2.2, los argumentos en los dos párrafos anteriores también nos han mostrado el papel del número\(a\) en las gráficas de funciones cuadráticas. La gráfica de\(y = a(x-h)^2 + k\) es una parábola 'abriendo hacia arriba' si\(a > 0\), y 'abriendo hacia abajo' si\(a < 0\). Además, la simetría que disfruta la gráfica de\(y = x^2\) alrededor del\(y\) eje se traduce en una simetría alrededor de la línea vertical\(x=h\) que es la línea vertical a través del vértice. ⁶ Esta línea se denomina eje de simetría de la parábola y se discontinua en las figuras siguientes.

Gráficas de\(y=a(x-h)^2+k\).

Sin duda, la forma estándar de una función cuadrática, aunada a la maquinaria en la Sección 1.7, nos permite enumerar los atributos de las gráficas de dichas funciones de manera rápida y elegante. Lo que queda por mostrar, sin embargo, es el hecho de que cada función cuadrática puede escribirse en forma estándar. Para convertir una función cuadrática dada en forma general en forma estándar, empleamos el antiguo rito de 'Completar la plaza'. Recordamos al lector cómo se hace esto en nuestro siguiente ejemplo.

Ejemplo 2.3.2

Convierta las siguientes funciones de forma general a forma estándar. Encuentra el vértice, el eje de simetría y cualquier\(x\) - o\(y\) -intercepción. Grafica cada función y determina su rango.

1. \(f(x) = x^2-4x+3\).
2. \(g(x) = 6-x-x^2\)

Solución.

1. Para convertir de forma general a forma estándar, completamos el cuadrado. ⁷ Primero, verificamos que el coeficiente de\(x^2\) es\(1\). A continuación, encontramos el coeficiente de\(x\), en este caso\(-4\), y tomamos la mitad del mismo para conseguir\(\frac{1}{2}(-4) = -2\). Esto nos dice que nuestra cantidad cuadrada perfecta objetivo es\((x-2)^2\). Para obtener una expresión equivalente a\((x-2)^2\), necesitamos\((-2)^2 = 4\) sumar al\(x^2-4x\) para crear un trinomio cuadrado perfecto, pero para mantener el equilibrio, también debemos restarlo. Recopilamos los términos que crean el cuadrado perfecto y reunimos los términos constantes restantes. Poniéndolo todo junto, obtenemos

   \(\begin{array}{rclr} f(x) & = & x^2-4x+3 & \text{(Compute $\frac{1}{2} (-4) = -2$.)} \\[4pt] & = & \left(x^2 - 4x + \underline{4} - \underline{4}\right) + 3 & \text{(Add and subtract $(-2)^2 = 4$ to $(x^2+4x)$.)}\\[4pt] & = & \left(x^2 - 4x + 4\right) - 4 + 3 & \text{(Group the perfect square trinomial.)}\\[4pt] & = & (x-2)^2 - 1 & \text{(Factor the perfect square trinomial.)} \\ \end{array}\)

   Por supuesto, siempre podemos comprobar nuestra respuesta multiplicando\(f(x) = (x-2)^2 -1\) para ver que se simplifica a\(f(x) = x^2 - 4x - 1\). En la forma\(f(x) = (x-2)^2-1\), encontramos fácilmente que el vértice es el\((2,-1)\) que hace el eje de simetría\(x = 2\). Para encontrar las\(x\) -intercepciones, nos fijamos\(y = f(x) = 0\). Tenemos muchas opciones para elegir, ya que tenemos dos fórmulas para\(f(x)\). Ya que reconocemos\(f(x) = x^2-4x+3\) ser fácilmente factorizables, ⁸ procedemos a resolver\(x^2-4x+3 = 0\). Factoring da\((x-3)(x-1) = 0\) para que\(x = 3\) o\(x=1\). Los\(x\) -interceptos son entonces\((1,0)\) y\((3,0)\). Para encontrar la\(y\) -intercepción, nos fijamos\(x=0\). Una vez más, la forma general\(f(x) = x^2-4x+3\) es más fácil de trabajar aquí, y la encontramos\(y = f(0) = 3\). De ahí que la\(y\) -intercepción sea\((0,3)\). Con el vértice, eje de simetría y las intercepciones, obtenemos una gráfica bastante buena sin necesidad de trazar puntos adicionales. Vemos que el rango de\(f\) es\([-1,\infty)\) y estamos hechos.

2. Para comenzar, reescribimos\(g(x) = 6-x-x^2 = -x^2-x+6\) y notamos que el coeficiente de\(x^2\) es\(-1\), no\(1\). Esto significa que nuestro primer paso es factorizar el tanto\((-1)\) de\(x^2\) los\(x\) términos como. Seguidamente seguimos la receta completa del cuadrado como arriba. \(\begin{array}{rclr} g(x) & = & -x^2-x+6 & \\ & = & (-1)\left(x^2 + x \right) + 6 & \text{(Factor the coefficient of $x^2$ from $x^2$ and $x$.)} \\[4pt] & = & (-1)\left(x^2 + x + \underline{\frac{1}{4}} - \underline{\frac{1}{4}} \right) + 6 & \\[4pt] & = & (-1)\left(x^2 + x + \frac{1}{4}\right) + (-1)\left(-\frac{1}{4}\right) + 6 & \text{(Group the perfect square trinomial.)}\\[4pt] & = & -\left(x +\frac{1}{2}\right)^2 + \frac{25}{4} & \\ \end{array}\)

De\(\ g(x)=-\left(x+\frac{1}{2}\right)^{2}+\frac{25}{4}\), obtenemos que el vértice sea\(\ \left(-\frac{1}{2}, \frac{25}{4}\right)\) y el eje de simetría sea\(\ x=-\frac{1}{2}\). Para obtener las intercepciones x, optamos por establecer la fórmula dada\(\ g(x)=6-x-x^{2}=0\). Resolviendo, obtenemos\(\ x = −3\) y\(x = 2\), así las intercepciones x son (−3, 0) y (2, 0). \(x = 0\)Ajustando, encontramos g (0) = 6, por lo que la intercepción y es (0, 6). Trazar estos puntos nos da la gráfica a continuación. Vemos que el rango de\(\ g\) es\(\ \left(-\infty, \frac{25}{4}\right]\).

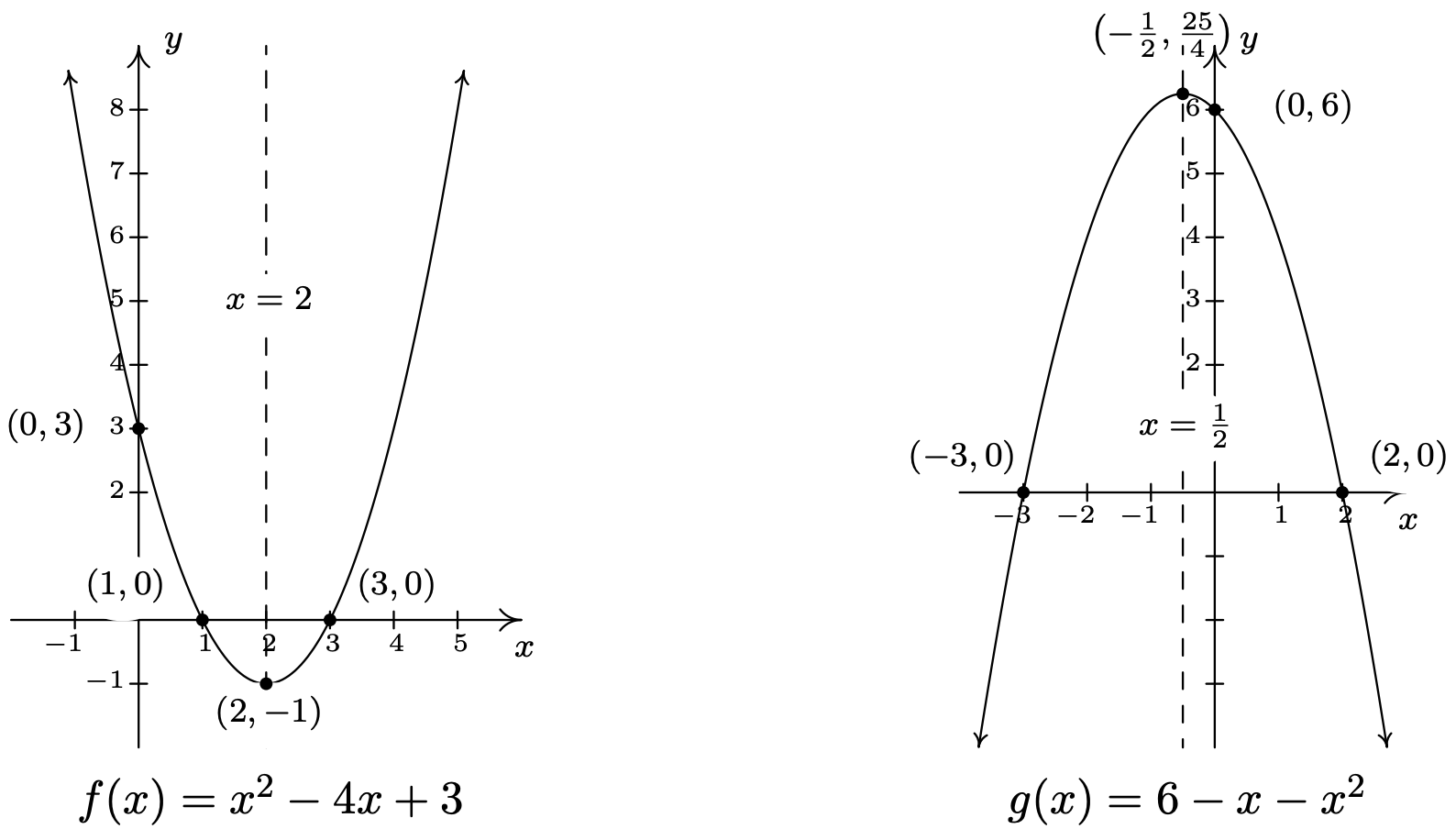
Con el Ejemplo 2.3.2 fresco en nuestras mentes, ahora estamos en condiciones de demostrar que cada función cuadrática se puede escribir en forma estándar. Comenzamos con\(f(x) = ax^2+bx+c\)\(a \neq 0\), asumimos y completamos la plaza en completa generalidad.

\(\ \begin{aligned} f(x) &=a x^{2}+b x+c \\ &\left.=a\left(x^{2}+\frac{b}{a} x\right)+c \quad \quad \text { (Factor out coefficient of } x^{2} \text { from } x^{2} \text { and } x .\right) \\ &=a\left(x^{2}+\frac{b}{a} x+\frac{b^{2}}{\frac{4 a^{2}}{2}}-\frac{b^{2}}{4 a^{2}}\right)+c \\ &=a\left(x^{2}+\frac{b}{a} x+\frac{b^{2}}{4 a^{2}}\right)-a\left(\frac{b^{2}}{4 a^{2}}\right)+c \quad \quad \text { (Group the perfect square trinomial.) } \\ &=a\left(x+\frac{b}{2 a}\right)^{2}+\frac{4 a c-b^{2}}{4 a} \quad \text { (Factor and get a common denominator.) } \end{aligned}\)

Comparando esta última expresión con la forma estándar, nos identificamos\((x-h)\) con\(\left(x+\frac{b}{2a}\right)\) para que\(h = -\frac{b}{2a}\). En lugar de memorizar el valor\(k = \frac{4ac - b^2}{4a}\), vemos eso\(f\left(-\frac{b}{2a}\right) = \frac{4ac - b^2}{4a}\). Como tal, hemos derivado una fórmula de vértice para la forma general. Resumimos ambas fórmulas de vértices en el recuadro en la parte superior de la página siguiente.

Ecuación 2.4

Fórmulas de vértice para funciones cuadráticas: Supongamos\(a\)\(b\)\(c\),,,\(h\) y\(k\) son números reales con\(a \neq 0\). [vérticofquadráticasfunciones]

• Si\(f(x) = a(x-h)^2 + k\), el vértice de la gráfica de\(y=f(x)\) es el punto\((h,k)\).
• Si\(f(x) = ax^2+bx+c\), el vértice de la gráfica de\(y=f(x)\) es el punto\(\left(-\dfrac{b}{2a}, f\left(-\dfrac{b}{2a}\right)\right)\).

Hay dos resultados más que se pueden obtener de la forma cuadrada completa de la forma general de una función cuadrática,

\[f(x) = ax^2 + bx + c = a\left(x+\dfrac{b}{2a}\right)^2 + \dfrac{4ac - b^2}{4a}\]

Hemos visto que el número\(a\) en la forma estándar de una función cuadrática determina si la parábola se abre hacia arriba (si\(a>0\)) o hacia abajo (si\(a < 0\)). Vemos aquí que este número no\(a\) es otro que el coeficiente de\(x^2\) en la forma general de la función cuadrática. Es decir, es el coeficiente de\(x^2\) solo el que determina este comportamiento —resultado que se generaliza en la Sección 3.1. El segundo tesoro es un redescubrimiento de la fórmula cuadrática.

Ecuación 2.5

La fórmula cuadrática: Si\(a\),\(b\) y\(c\) son números reales con\(a \neq 0\), entonces las soluciones a\(ax^2 + bx + c = 0\)

\(x = \dfrac{-b \pm \sqrt{b^2-4ac}}{2a}.\)

Asumiendo las condiciones de la Ecuación 2.5, las soluciones a\(ax^2+bx+c = 0\) son precisamente los ceros de\(f(x) = ax^2 + bx + c\). Desde

\(f(x) = ax^2+bx+c = a\left(x+\dfrac{b}{2a}\right)^2 + \dfrac{4ac - b^2}{4a}\)

la ecuación\(ax^2 + bx + c = 0\) es equivalente a

\(a\left(x+\dfrac{b}{2a}\right)^2 + \dfrac{4ac - b^2}{4a} = 0.\)

Resolver da

\(\begin{array}{rclr} a\left(x+\dfrac{b}{2a}\right)^2 + \dfrac{4ac - b^2}{4a} & = & 0 & \\[15pt] a\left(x+\dfrac{b}{2a}\right)^2 & = & - \dfrac{4ac - b^2}{4a} & \\[15pt] \dfrac{1}{a} \left[a\left(x+\dfrac{b}{2a}\right)^2\right] & = & \dfrac{1}{a} \left(\dfrac{b^2-4ac}{4a}\right) & \\[15pt] \left(x+\dfrac{b}{2a}\right)^2 & = & \dfrac{b^2-4ac}{4a^2} & \\[15pt] x+\dfrac{b}{2a} & = & \pm \sqrt{\dfrac{b^2-4ac}{4a^2}} & \mbox{extract square roots} \\[15pt] x+\dfrac{b}{2a} & = & \pm \dfrac{\sqrt{b^2-4ac}}{2a} & \\[15pt] x & = & -\dfrac{b}{2a} \pm \dfrac{\sqrt{b^2-4ac}}{2a} \\[15pt] x & = & \dfrac{-b \pm \sqrt{b^2-4ac}}{2a} & \end{array}\)

En nuestras discusiones de dominio, se nos advirtió contra tener números negativos debajo de la raíz cuadrada. Dado que\(\sqrt{b^{2} - 4ac}\) eso forma parte de la Fórmula Cuadrática, habrá que prestar especial atención al radicando\(b^{2} - 4ac\). Resulta que la cantidad\(b^2-4ac\) juega un papel crítico en la determinación de la naturaleza de las soluciones a una ecuación cuadrática. Se le da un nombre especial.

Definición 2.7

Si\(\ a\),\(\ b\) y\(\ c\) son números reales con\(\ a \neq 0\), entonces el discriminante de la ecuación cuadrática\(\ a x^{2}+b x+c=0\) es la cantidad\(\ b^{2}-4 a c\).

El discriminante 'discrimina' entre los tipos de soluciones que obtenemos de una ecuación cuadrática. Estos casos, y su relación con el discriminante, se resumen a continuación.

Teorema 2.3. Tricotomía discriminante

Dejar\(a\),\(b\) y\(c\) ser números reales con\(a \neq 0\).

• Si\(b^2 - 4ac < 0\), la ecuación no\(ax^2 + bx + c = 0\) tiene soluciones reales.
• Si\(b^2 - 4ac = 0\), la ecuación\(ax^2 + bx + c = 0\) tiene exactamente una solución real.
• Si\(b^2 - 4ac > 0\), la ecuación\(ax^2 + bx + c = 0\) tiene exactamente dos soluciones reales.

La prueba del Teorema 2.3 deriva de la posición del discriminante en la ecuación cuadrática, y se deja como un buen ejercicio mental para el lector. El siguiente ejemplo explota los frutos de todo nuestro trabajo en esta sección hasta el momento.

Ejemplo 2.3.3

Recordemos que el beneficio (definido en Resumen de Funciones Económicas Comunes) para un producto se define por la ecuación\(\mbox{Profit} = \mbox{Revenue} - \mbox{Cost}\), o\(P(x) = R(x) - C(x)\). En el Ejemplo 2.1.7 se encontró que los ingresos semanales, en dólares, realizados al vender\(x\) PortaBoy Game Systems estaban\(R(x) = -1.5x^2+250x\) con la restricción (arrastrada de la función precio-demanda) que\(0 \leq x \leq 166\). El costo, en dólares, para producir\(x\) PortaBoy Game Systems se da en el Ejemplo 2.1.5 en\(C(x) = 80x + 150\) cuanto a\(x \geq 0\).

1. Determinar la función de ganancia semanal\(P(x)\).
2. Gráfica\(y = P(x)\). Incluir las\(y\) intercepciones\(x\) - y -así como el vértice y el eje de simetría.
3. Interpretar los ceros de\(P\).
4. Interpretar el vértice de la gráfica de\(y = P(x)\).
5. Recordemos que la ecuación semanal precio-demanda para PortaBoys es\(p(x) = -1.5x+250\), dónde\(p(x)\) está el precio por PortaBoy, en dólares, y\(x\) es la venta semanal. ¿Cuál debe ser el precio por sistema para maximizar las ganancias?

Solución.

1. Para encontrar la función de ganancia\(P(x)\), restamos\(P(x) = R(x) - C(x) = \left(-1.5x^2+250x\right) - \left(80x + 150\right) = -1.5x^2+170x-150.\) Dado que la función de ingresos es válida cuando\(0 \leq x \leq 166\), también\(P\) se restringe a estos valores.
2. Para encontrar las\(x\) -intercepciones, establecemos\(P(x) = 0\) y resolvemos\(-1.5x^2+170x-150=0\). El mero pensamiento de tratar de factorizar el lado izquierdo de esta ecuación podría ocasionar graves daños psicológicos, por lo que recurrimos a la fórmula cuadrática, Ecuación 2.5. Identificar\(a = -1.5\)\(b=170\), y\(c=-150\), obtenemos

   \( \begin{array}{rclr} x & = & \dfrac{-b \pm \sqrt{b^2-4ac}}{2a} & \\ & = & \dfrac{-170 \pm \sqrt{170^2 - 4(-1.5)(-150)}}{2(-1.5)} & \\ & = & \dfrac{-170 \pm \sqrt{28000}}{-3} & \\ & = & \dfrac{170 \pm 20 \sqrt{70}}{3} & \\ \end{array}\)

   Obtenemos dos\(x\) -intercepciones:\(\left( \frac{170 - 20 \sqrt{70}}{3},0\right)\) y\(\left( \frac{170 + 20 \sqrt{70}}{3},0\right)\). Para encontrar la\(y\) -intercepción, nos fijamos\(x=0\) y encontramos\(y=P(0)=-150\) para una\(y\) -intercepción de\((0,-150)\). Para encontrar el vértice, utilizamos el hecho de que\(P(x)=-1.5x^2+170x-150\) está en la forma general de una función cuadrática y apelamos a la Ecuación 2.4. Sustituyendo\(a = -1.5\) y\(b=170\), obtenemos\(x = -\frac{170}{2(-1.5)} = \frac{170}{3}\). Para encontrar la\(y\) coordenada -del vértice, calculamos\(P\left( \frac{170}{3} \right) = \frac{14000}{3}\) y encontramos que nuestro vértice es\(\left(\frac{170}{3}, \frac{14000}{3}\right)\). El eje de simetría es la línea vertical que pasa por el vértice por lo que es la línea\(x=\frac{170}{3}\). Para esbozar una gráfica razonable, aproximamos las\(x\) -intercepciones,\((0.89,0)\) y\((112.44,0)\), y el vértice,\((56.67,4666.67)\). (Tenga en cuenta que para que las\(x\) -intercepciones y el vértice se mostraran en la misma imagen, tuvimos que escalar el\(x\) eje -de manera diferente al\(y\) eje -eje. Esto da como resultado que la\(x\) intercepción de la izquierda y la\(y\) intercepción estén incómodamente cerca una de la otra y del origen en la imagen.)

   

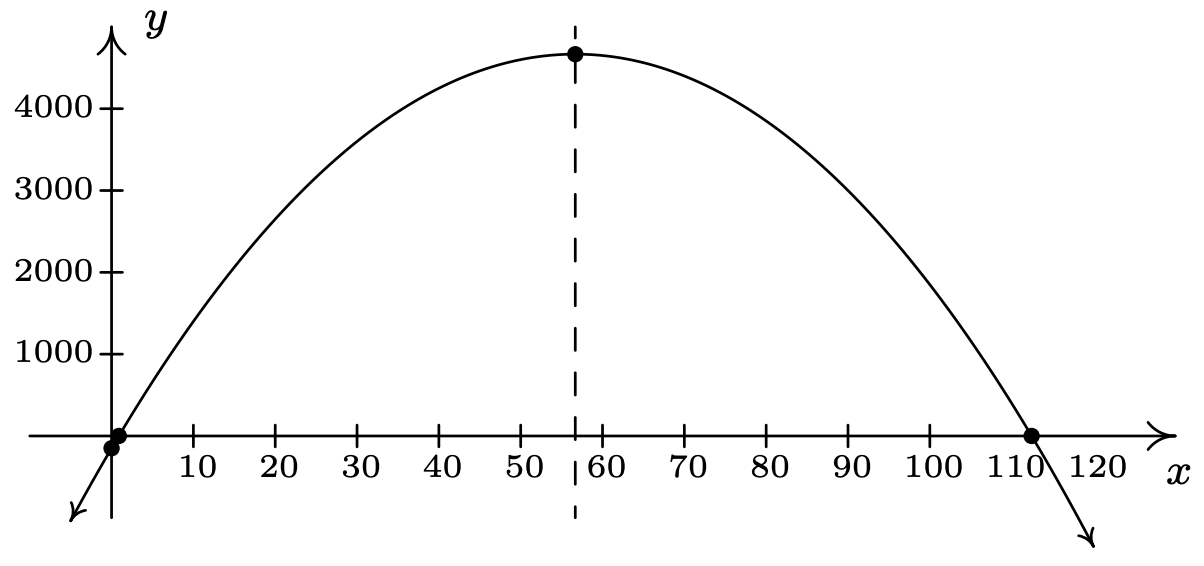
3. Los ceros de\(P\) son las soluciones a\(P(x)=0\), que hemos encontrado que son aproximadamente\(0.89\) y\(112.44\). Como vimos en el Ejemplo 1.5.3, estos son los puntos de 'equilibrio' de la función de ganancia, donde se vende suficiente producto para recuperar el costo gastado para hacer el producto. Más importante aún, vemos en la gráfica que mientras\(x\) esté entre\(0.89\) y\(112.44\), la gráfica\(y=P(x)\) está por encima del\(x\) eje -eje, es decir\(y = P(x) > 0\) ahí. Esto quiere decir que para estos valores de\(x\), se está obteniendo un beneficio. Dado que\(x\) representa las ventas semanales de Portaboy Game Systems, redondeamos los ceros a enteros positivos y tenemos eso siempre y cuando\(1\), pero no más que los sistemas de\(112\) juego se vendan semanalmente, el minorista obtendrá ganancias.
4. De la gráfica, vemos que el valor máximo de\(P\) ocurre en el vértice, que es aproximadamente\((56.67,4666.67)\). Como anteriormente,\(x\) representa las ventas semanales de los sistemas PortaBoy, por lo que no podemos vender sistemas de\(56.67\) juegos. Comparando\(P(56) = 4666\) y\(P(57)=4666.5\), concluimos que obtendremos un beneficio máximo de\(\$ 4666.50\) si vendemos sistemas de\(57\) juego.
5. En la parte anterior, encontramos que necesitamos vender\(57\) PortaBoys por semana para maximizar las ganancias. Para encontrar el precio por portaboy, sustituimos\(x=57\) en la función precio-demanda para obtener\(p(57) = -1.5(57)+250 = 164.5\). El precio debe fijarse en\(\$164.50\).

Nuestro siguiente ejemplo es otra aplicación clásica de funciones cuadráticas.

Ejemplo 2.3.4

Para sorpresa y deleite de Donnie, hereda una gran parcela de tierra en el condado de Ashtabula de uno de sus (e) extraños (d) parientes. Finalmente es el momento adecuado para que persiga su sueño de cultivar alpaca. Desea construir un pasto rectangular, y estima que tiene suficiente dinero para 200 pies lineales de material de cercado. Si hace el pasto adyacente a un arroyo (por lo que no se requiere cercas en ese lado), ¿cuáles son las dimensiones del pasto que maximizan el área? ¿Cuál es el área máxima? Si una alpaca promedio necesita 25 pies cuadrados de área de pastoreo, ¿cuántas alpacas puede mantener Donnie en su pasto?

Solución. Siempre es útil esbozar la situación del problema, así que lo hacemos a continuación.

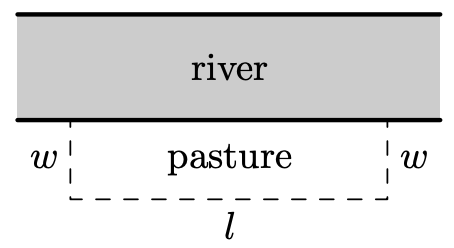
Tenemos la tarea de encontrar las dimensiones de los pastos que darían una superficie máxima. Dejamos\(w\) denotar el ancho del pasto y dejamos\(l\) denotar la longitud del pasto. Ya que las unidades que nos dan en el enunciado del problema son pies, asumimos\(w\) y\(l\) se miden en pies. El área del pasto, que llamaremos\(A\), está relacionada con\(w\) y\(l\) por la ecuación\(A = wl\). Desde\(w\) y ambos\(l\) se miden en pies,\(A\) tiene unidades de\(\text{feet}^2\), o pies cuadrados. Se nos da la cantidad total de cercas disponibles es\(200\) pies, lo que significa\(w + l + w = 200\), o,\(l+2w = 200\). Ahora tenemos dos ecuaciones,\(A = wl\) y\(l+2w = 200\). Para poder utilizar las herramientas que se nos dan en esta sección para maximizar\(A\), necesitamos usar la información dada para escribir\(A\) en función de una sola variable, ya sea\(w\) o\(l\). Aquí es donde usamos la ecuación\(l+2w = 200\). Resolviendo para\(l\), encontramos\(l = 200-2w\), y sustituimos esto en nuestra ecuación por\(A\). Obtenemos\(A = wl = w(200-2w) = 200w-2w^2\). Ahora tenemos\(A\) como función de\(w\),\(A(w) = 200w-2w^2 = -2w^2+200w\).

Antes de ir más lejos, necesitamos encontrar el dominio aplicado de\(A\) para que sepamos qué valores tienen\(w\) sentido en esta situación problemática. ⁹ Dado que\(w\) representa el ancho del pasto,\(w > 0\). De igual manera,\(l\) representa la longitud del pasto, así\(l = 200-2w > 0\). Resolviendo esta última desigualdad, encontramos\(w < 100\). De ahí que sea\(A(w) = -2w^2 + 200w\) para la función que deseamos maximizar\(0 < w < 100\). Ya que\(A\) es una función cuadrática (de\(w\)), sabemos que la gráfica de\(y = A(w)\) es una parábola. Ya que el coeficiente de\(w^2\) es\(-2\), sabemos que esta parábola se abre hacia abajo. Esto quiere decir que hay un valor máximo por encontrar, y sabemos que ocurre en el vértice. Usando la fórmula de vértice, encontramos\(w = -\frac{200}{2(-2)} = 50\), y\(A(50) = -2(50)^2 + 200(50) = 5000\). Ya que se\(w=50\) encuentra en el dominio aplicado\(0 < w < 100\),, tenemos que el área del pasto se maximiza cuando el ancho es\(50\) pies. Para encontrar la longitud, usamos\(l = 200-2w\) y encontramos\(l = 200-2(50) = 100\), por lo que la longitud del pasto es\(100\) pies. El área máxima es\(A(50) = 5000\), o pies\(5000\) cuadrados. Si una alpaca promedio requiere 25 pies cuadrados de pasto, Donnie puede elevar alpaca\(\frac{5000}{25} = 200\) promedio.

Concluimos esta sección con la gráfica de una función de valor absoluto más complicada.

Ejemplo 2.3.5

Gráfica\(f(x) = |x^2 - x - 6|\).

Solución

Usando la definición de valor absoluto, Definición 2.4, tenemos

\(f(x) = \left\{ \begin{array}{rcl} -\left(x^2 - x - 6\right), & \mbox{if} & x^2 - x - 6 < 0 \\ x^2 - x - 6, & \mbox{if} & x^2 - x - 6 \geq 0 \\ \end{array} \right.\)

El problema es que aún tenemos que desarrollar técnicas analíticas para resolver desigualdades no lineales como\(x^2 - x - 6 < 0\). No tendrás que esperar mucho; este es uno de los temas principales de la Sección 2.4. Sin embargo, podemos atacar este problema gráficamente. Para ello, graficamos\(y = g(x) = x^2 - x-6\) usando las intercepciones y el vértice. Para encontrar las\(x\) -intercepciones, resolvemos\(x^2 - x - 6 = 0\). Factoring da\((x-3)(x+2)=0\) así\(x=-2\) o\(x=3\). De ahí,\((-2,0)\) y\((3,0)\) son\(x\) -intercepciones. La\(y\) -intercepción\((0,-6)\) se encuentra por ajuste\(x=0\). Para trazar el vértice, encontramos\(x = -\frac{b}{2a} = -\frac{-1}{2(1)} = \frac{1}{2}\), y\(y = \left(\frac{1}{2}\right)^2 - \left(\frac{1}{2}\right)-6 = -\frac{25}{4} = -6.25\). Trazando, obtenemos la parábola que se ve abajo a la izquierda. Para obtener puntos en la gráfica de\(y = f(x) = |x^2-x-6|\), podemos tomar puntos en la gráfica de\(g(x) = x^2-x-6\) y aplicar el valor absoluto a cada uno de los\(y\) valores en la parábola. Vemos de la gráfica de\(g\) eso para\(x \leq -2\) o\(x \geq 3\), los\(y\) valores en la parábola son mayores o iguales a cero (ya que la gráfica está sobre o por encima del\(x\) eje -eje), por lo que el valor absoluto deja estas porciones de la gráfica solas. Para\(x\) entre\(-2\) y\(3\), sin embargo, los\(y\) valores en la parábola son negativos. Por ejemplo, el punto\((0,-6)\) on\(y = x^2-x-6\) daría como resultado el punto\((0,|-6|) = (0,-(-6))= (0,6)\) en la gráfica de\(f(x) = |x^2-x-6|\). Procediendo de esta manera para todos los puntos con\(x\) -coordenadas entre\(-2\) y\(3\) resultados en la gráfica que se ve a continuación a la derecha.

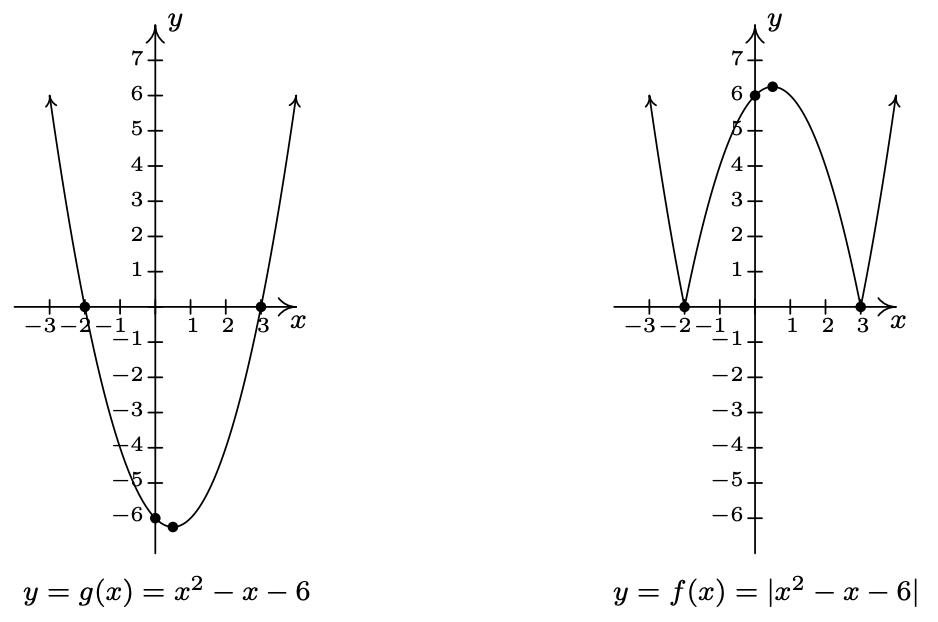
Si damos un paso atrás y miramos las gráficas de\(g\) y\(f\) en el último ejemplo, notamos que para obtener la gráfica de a\(f\) partir de la gráfica de\(g\), reflejamos una porción de la gráfica de\(g\) alrededor del\(x\) eje -eje. Podemos ver esto analíticamente sustituyendo\(g(x) = x^2-x-6\) en la fórmula para\(f(x)\) y recordando el Teorema 1.4 de la Sección 1.7.

\(f(x) = \left\{ \begin{array}{rcl} -g(x), & \mbox{if} & g(x) < 0 \\ g(x), & \mbox{if} & g(x) \geq 0 \\ \end{array} \right.\)

La función\(f\) se define de manera que cuando\(g(x)\) es negativa (es decir, cuando su gráfica está por debajo del\(x\) eje -), la gráfica de\(f\) es su refección a través del\(x\) eje -eje. Esta es una plantilla general para graficar funciones del formulario\(f(x) = |g(x)|\). Desde esta perspectiva, la gráfica de se\(f(x) = |x|\) puede obtener reflejando la porción de la línea\(g(x) =x\) que está por debajo del\(x\) eje -detrás sobre el\(x\) -eje creando la forma característica\(\vee\) ''.

2.3.1 Ejercicios

En los Ejercicios 1-9, grafica la función cuadrática. Encuentra las\(x\) - y\(y\) -intercepciones de cada gráfica, si existe alguna. Si se da en forma general, conviértalo en forma estándar; si se da en forma estándar, conviértalo en forma general. Encuentre el dominio y el rango de la función y enumere los intervalos en los que la función está aumentando o disminuyendo. Identificar el vértice y el eje de simetría y determinar si el vértice produce un máximo o mínimo relativo y absoluto.

1. \(f(x) = x^{2} + 2\)
2. \(f(x) = -(x + 2)^{2}\)
3. \(f(x) = x^{2} - 2x - 8\)
4. \(f(x) = -2(x + 1)^{2} + 4\)
5. \(f(x) = 2x^2 - 4x - 1\)
6. \(f(x) = -3x^{2} + 4x - 7\)
7. \(f(x) = x^2 + x + 1\)
8. \(f(x) = -3x^2+5x+4\)
9. ¹⁰\(f(x) = x^{2} - \dfrac{1}{100} x - 1\)

En los Ejercicios 10-14, se dan las funciones costo y precio-demanda para diferentes escenarios. Para cada escenario,

• Encuentra la función de ganancia\(P(x)\).
• Encuentre el número de artículos que deben venderse para maximizar las ganancias.
• Encuentra el beneficio máximo.
• Encuentra el precio a cobrar por artículo para maximizar las ganancias.
• Encuentra e interpreta puntos de equilibrio.

10. El costo, en dólares, de producir camisetas\(x\) “Prefiero ser un Sasquatch” es\(C(x) = 2x+26\),\(x \geq 0\) y la función precio-demanda, en dólares por camisa, es\(p(x) = 30 - 2x\),\(0 \leq x \leq 15\). [maxprofitfirst]
11. El costo, en dólares, para producir\(x\) botellas de\(100 \%\) All-Natural Certified Free-Trade Organic Sasquatch Tonic es\(C(x) = 10x+100\),\(x \geq 0\) y la función precio-demanda, en dólares por botella, es\(p(x) = 35 - x\),\(0 \leq x \leq 35\).
12. El costo, en centavos, para producir\(x\) tazas de Mountain Thunder Lemonade en el Puesto de Limonada Junior es\(C(x) = 18x + 240\),\(x \geq 0\) y la función precio-demanda, en centavos por taza, es\(p(x) = 90-3x\),\(0 \leq x \leq 30\).
13. El costo diario, en dólares, para producir\(x\) Sasquatch Berry Pies es\(C(x) = 3x + 36\),\(x \geq 0\) y la función precio-demanda, en dólares por pastel, es\(p(x) = 12-0.5x\),\(0 \leq x \leq 24\).
14. El costo mensual, en cientos de dólares, para producir scooters eléctricos a\(x\) medida es\(C(x) = 20x + 1000\),\(x \geq 0\) y la función precio-demanda, en cientos de dólares por scooter, es\(p(x) = 140-2x\),\(0 \leq x \leq 70\). [maxprofitlast]
15. La International Silver Strings Submarine Band realiza una venta de pasteles cada año para financiar su viaje a la Convención Nacional Sasquatch. Se ha determinado que el costo en dólares de hornear\(x\) galletas es\(C(x) = 0.1x + 25\) y que la función de demanda de sus galletas es\(p = 10 - .01x.\) ¿Cuántas galletas deben hornear para maximizar su ganancia?
16. Utilizando datos de Bureau of Transportation Statistics, la economía promedio de combustible\(\ F\) en millas por galón para los turismos en Estados Unidos puede ser modelada por\(\ F(t)=-0.0076 t^{2}+0.45 t+16\)\(\ 0 \leq t \leq 28\),, donde\(\ t\) es el número de años desde 1980. Encuentra e interpreta las coordenadas del vértice de la gráfica de\(\ y = F(t)\).
17. La temperatura\(T\), en grados Fahrenheit,\(t\) horas después de las 6 AM viene dada por:\[T(t) = -\frac{1}{2} t^2 + 8t+32, \quad 0 \leq t \leq 12\]
18. Supongamos que\(C(x) = x^2-10x+27\) representa los costos, en cientos, para producir\(x\) mil bolígrafos. ¿Cuántas plumas se deben producir para minimizar el costo? ¿Cuál es este costo mínimo?
19. [fixedperimetermaxareagarden] Skippy desea plantar un huerto a lo largo de un lado de su casa. En su cochera, encontró 32 pies lineales de esgrima. Dado que un lado del jardín bordeará la casa, Skippy no necesita cercas a lo largo de ese lado. ¿Cuáles son las dimensiones del jardín que maximizarán el área del jardín? ¿Cuál es la superficie máxima del jardín?
20. En la situación del Ejemplo 2.3.4, Donnie tiene la pesadilla de que uno de sus rebaños de alpaca cayó al río y se ahogó. Para evitar esto, quiere alejar su pasto rectangular del río. Esto significa que los cuatro lados del pasto requieren cercas. Si la cantidad total de cercas disponibles sigue siendo de 200 pies lineales, ¿qué dimensiones maximizan ahora el área del pasto? ¿Cuál es el área máxima? Asumiendo que una alpaca promedio requiere 25 pies cuadrados de pasto, ¿cuántas alpaca puede criar ahora?
21. ¿Cuál es el área rectangular más grande que uno puede encerrar con 14 pulgadas de cuerda?
22. La altura de un objeto caído del techo de un edificio de ocho pisos está modelada por\(h(t) = -16t^2 + 64\),\(0 \leq t \leq 2\). Aquí,\(h\) es la altura del objeto del suelo, en pies,\(t\) segundos después de que el objeto se haya caído. ¿Cuánto tiempo antes de que el objeto golpee el suelo?
23. La altura\(h\) en pies de un cohete modelo sobre el suelo\(t\) segundos después del despegue viene dada por\(h(t) = -5t^2+100t\), para\(0 \leq t \leq 20\). ¿Cuándo alcanza el cohete su altura máxima sobre el suelo? ¿Cuál es su altura máxima?
24. Jason, el amigo de Carl, participa en los Juegos Highland. En un evento, el lanzamiento del martillo, la altura\(h\) en pies del martillo sobre el suelo\(t\) segundos después de que Jason lo deja ir está modelada por\(h(t) = -16t^2 + 22.08t + 6\). ¿Cuál es la altura máxima del martillo? ¿Cuál es el tiempo total del martillo en el aire? Redondee sus respuestas a dos decimales.
25. Asumiendo que no hay resistencia al aire o fuerzas distintas de la gravedad de la Tierra, la altura sobre el suelo en el momento\(t\) de la caída de un objeto viene dada por\(s(t) = -4.9t^{2} + v_0t + s_0\) dónde\(s\)\(t\) está en metros,\(v_0\) es en segundos, es la velocidad inicial del objeto en metros por segundo y\(s_0\) es su posición inicial en metros. [whatgoesup]
    1. ¿Cuál es el dominio aplicado de esta función?
    2. Discuta con tus compañeros de clase lo que cada uno de\(v_0 > 0, \; v_0 = 0\) y\(v_0 < 0\) significaría.
    3. Llegar a un escenario en el que\(s_0 < 0\).
    4. Digamos que se utiliza un tirachinas para disparar una canica directamente desde el suelo\((s_0 = 0)\) con una velocidad inicial de 15 metros por segundo. ¿Cuál es la altura máxima del mármol sobre el suelo? ¿A qué hora golpeará el suelo?
    5. Ahora dispara el mármol desde lo alto de una torre que mide 25 metros de altura. ¿Cuándo golpea el suelo?
    6. ¿Cuál sería la función de altura si en lugar de disparar la canica desde la torre, la dispararas directamente hacia ABAJO desde lo alto de la torre?
26. Las dos torres de un puente colgante están a 400 pies de distancia. El cable parabólico ¹¹ unido a las cimas de las torres se encuentra a 10 pies por encima del punto en la cubierta del puente que se encuentra a medio camino entre las torres. Si las torres son de 100 pies de altura, encuentra la altura del cable directamente encima de un punto de la cubierta del puente que está a 50 pies a la derecha de la torre izquierda.
27. Gráfica\(f(x) = |1 - x^{2}|\)
28. Encuentra todos los puntos de la línea\(y=1-x\) que son\(2\) unidades de\((1,-1)\).
29. \(L\)Déjese ser la línea\(y = 2x+1\). Encuentra una función\(D(x)\) que mida la distancia al cuadrado de un punto\(L\) a\((0,0)\). Usa esto para encontrar el punto\(L\) más cercano a\((0,0)\).
30. Con la ayuda de tus compañeros de clase, demuestra que si una función cuadrática\(f(x) = ax^{2} + bx + c\) tiene dos ceros reales entonces la\(x\) coordenada -del vértice es el punto medio de los ceros.

En los Ejercicios 31-36, resuelve la ecuación cuadrática para la variable indicada.

31. \(x^{2} - 10y^{2} = 0\)para\(x\)
32. \(y^{2} - 4y = x^{2} - 4\)para\(x\)
33. \(x^{2} - mx = 1\)para\(x\)
34. \(y^{2} - 3y = 4x\)para\(y\)
35. \(y^{2} - 4y = x^{2} - 4\)para\(y\)
36. \(-gt^{2} + v_0t + s_0 = 0\)para\(t\) (Asumir\(g \neq 0\).)

2.3.2 Respuestas

1. \(f(x) = x^{2} + 2\)(¡esto es ambas formas!)
   No\(x\) -intercepta
   \(y\) -interceptar\((0, 2)\)
   Dominio:\((-\infty, \infty)\)
   Rango:\([2, \infty)\)
   Disminuir\((-\infty, 0]\)
   al aumentar en el\([0, \infty)\)
   vértice\((0, 2)\) es a mínimo
   Eje de simetría\(x = 0\)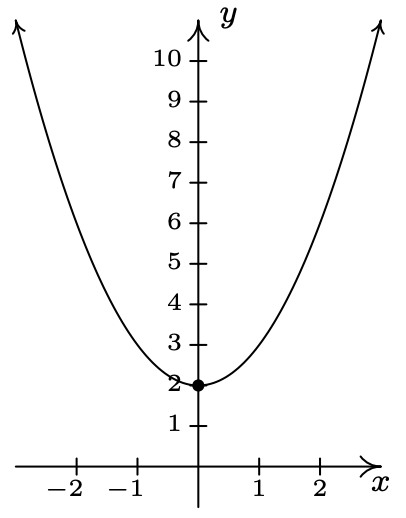

   

2. \(f(x) = -(x + 2)^{2} = -x^2-4x-4\)
   \(x\)-interceptar\((-2, 0)\)
   \(y\) -interceptar\((0, -4)\)
   Dominio:\((-\infty, \infty)\)
   Rango:\((-\infty, 0]\)
   Aumentando al\((-\infty, -2]\)
   disminuir en\([-2, \infty)\)
   El vértice\((-2, 0)\) es un
   eje máximo de simetría\(x = -2\)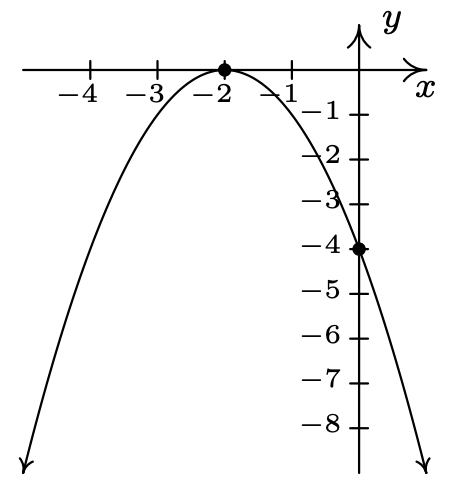

   

3. \(f(x) = x^{2} - 2x - 8 = (x - 1)^{2} - 9\)
   \(x\)-intercepta\((-2, 0)\) y\((4, 0)\)
   \(y\) -intercepta\((0, -8)\)
   Dominio:\((-\infty, \infty)\)
   Rango:\([-9, \infty)\)
   Disminuyendo al\((-\infty, 1]\)
   Incrementar en\([1, \infty)\)
   El vértice\((1, -9)\) es un
   eje mínimo de simetría\(x = 1\)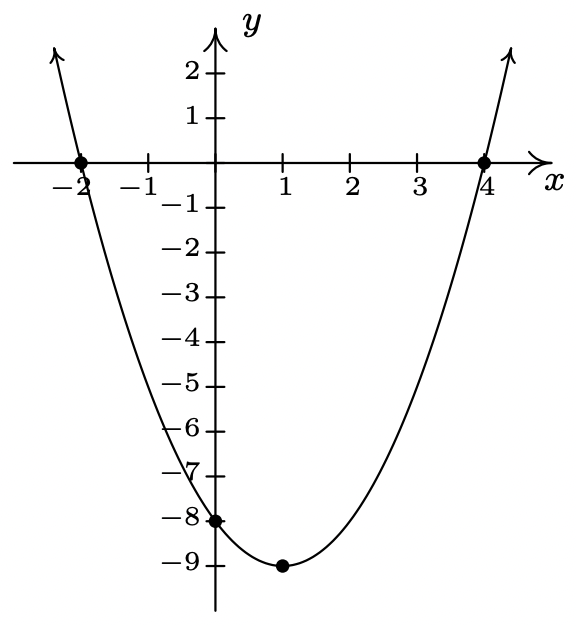

   

4. \(f(x) = -2(x + 1)^{2} + 4 = -2x^2-4x+2\)
   \(x\)-intercepta\((-1 - \sqrt{2}, 0)\) y\((-1 + \sqrt{2}, 0)\)
   \(y\) -intercepta\((0, 2)\)
   Dominio:\((-\infty, \infty)\)
   Rango:\((-\infty, 4]\)
   Aumentando al\((-\infty, -1]\)
   disminuir en \([-1, \infty)\)
   El vértice\((-1, 4)\) es un
   eje máximo de simetría\(x = -1\)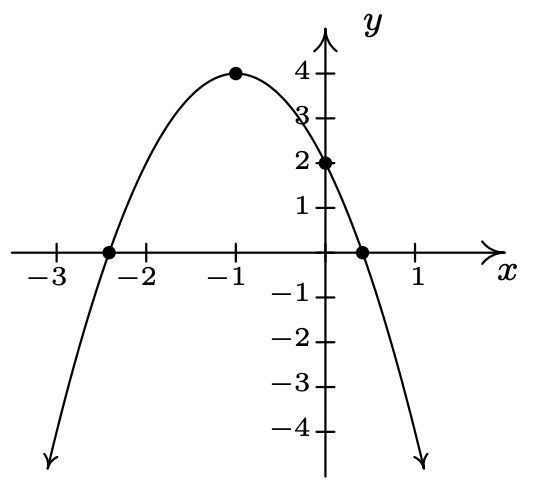

   

5. \(f(x) = 2x^2-4x-1 = 2(x-1)^2-3\)
   \(x\)-intercepta\(\left(\frac{2-\sqrt{6}}{2}, 0\right)\) y\(\left(\frac{2+\sqrt{6}}{2}, 0\right)\)
   \(y\) -intercepta\((0, -1)\)
   Dominio:\((-\infty, \infty)\)
   Rango:\([-3, \infty)\)
   Aumentando al\([1,\infty)\)
   disminuir en \((-\infty,1]\)
   El vértice\((1, -3)\) es un
   eje mínimo de simetría\(x = 1\)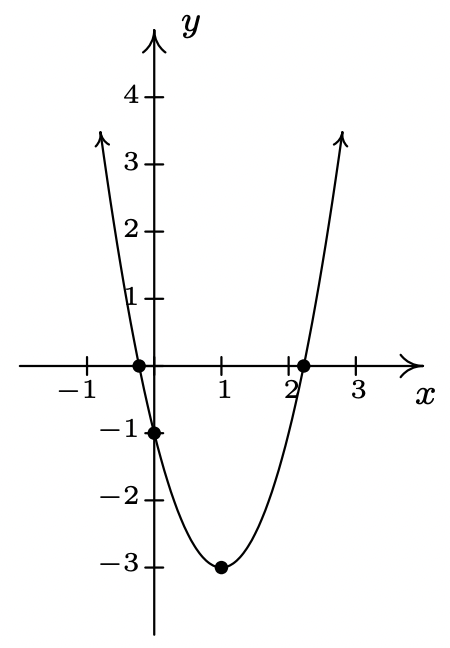

   

6. \(f(x) = -3x^{2} + 4x - 7 = -3\left(x - \frac{2}{3} \right)^{2} - \frac{17}{3}\)
   No\(x\) -intercepta
   \(y\) -intercepción\((0, -7)\)
   Dominio:\((-\infty, \infty)\)
   Rango:\(\left(-\infty, -\frac{17}{3}\right]\)
   Aumentando al\(\left(-\infty, \frac{2}{3}\right]\)
   disminuir en el\(\left[\frac{2}{3}, \infty\right)\)
   vértice \(\left(\frac{2}{3}, -\frac{17}{3}\right)\)es un
   eje máximo de simetría\(x = \frac{2}{3}\)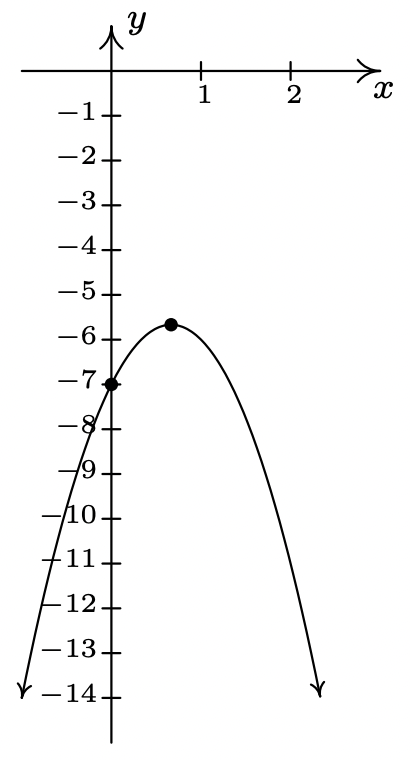

   

7. \(f(x) = x^2+x+1 = \left(x + \frac{1}{2}\right)^{2} + \frac{3}{4}\)
   No\(x\) -intercepta
   \(y\) -intercepción\((0, 1)\)
   Dominio:\((-\infty, \infty)\)
   Rango:\(\left[ \frac{3}{4}, \infty\right)\)
   Aumentando al\(\left[-\frac{1}{2}, \infty\right)\)
   disminuir en el\(\left(-\infty, -\frac{1}{2}\right]\)
   vértice \(\left(-\frac{1}{2}, \frac{3}{4}\right)\)es un mínimo
   Eje de simetría\(x = -\frac{1}{2}\)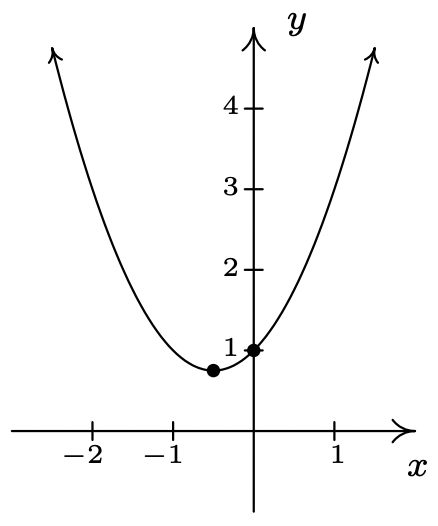

   

8. \(f(x) = -3x^2+5x+4 = -3\left(x-\frac{5}{6}\right)^2 + \frac{73}{12}\)
   \(x\)-intercepta\(\left(\frac{5 - \sqrt{73}}{6}, 0\right)\) y\(\left(\frac{5+\sqrt{73}}{6}, 0\right)\)
   \(y\) -intercepta\((0, 4)\)
   Dominio:\((-\infty, \infty)\)
   Rango:\(\left(-\infty, \frac{73}{12} \right]\)
   Aumentando al\(\left(-\infty, \frac{5}{6}\right]\)
   disminuir en \(\left[ \frac{5}{6}, \infty\right)\)
   El vértice\(\left(\frac{5}{6}, \frac{73}{12} \right)\) es un
   eje máximo de simetría\(x = \frac{5}{6}\)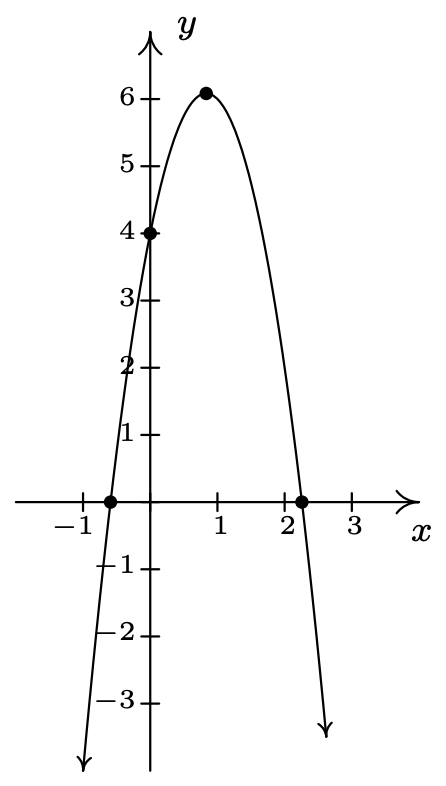

   

9. \(f(x) = x^{2} - \frac{1}{100} x - 1 = \left(x - \frac{1}{200}\right)^{2} - \frac{40001}{40000}\)
   \(x\)-intercepta\(\left(\frac{1 + \sqrt{40001}}{200}\right)\) y\(\left(\frac{1 - \sqrt{40001}}{200}\right)\)
   \(y\) -intercepta\((0, -1)\)
   Dominio:\((-\infty, \infty)\)
   Rango:\(\left[-\frac{40001}{40000}, \infty \right)\)
   Disminuyendo al\(\left(-\infty, \frac{1}{200}\right]\)
   Incrementar en\(\left[\frac{1}{200}, \infty \right)\)
   El vértice\(\left(\frac{1}{200}, -\frac{40001}{40000}\right)\) es un mínimo de ¹²
   ejes de simetría\(x = \frac{1}{200}\)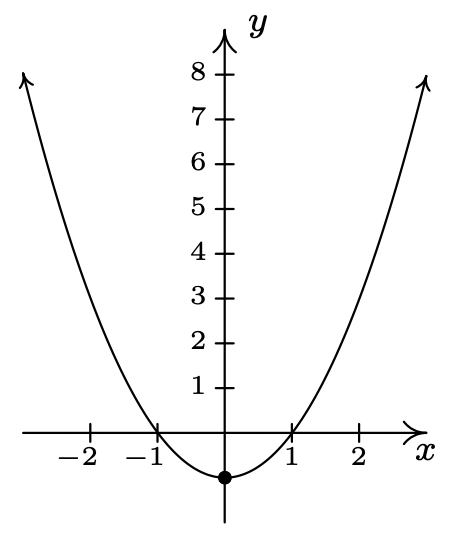

   

10. • \(P(x) = -2x^2+28x-26\), para\(0 \leq x \leq 15\).
    • \(7\)Las playeras deben fabricarse y venderse para maximizar las ganancias.
    • El beneficio máximo es\(\$72\).
    • El precio por camiseta debe establecerse en\(\$16\) para maximizar las ganancias.
    • Los puntos de quiebre son\(x=1\) y\(x=13\), por lo tanto, para obtener ganancias, se necesitan fabricar y vender entre 1 y 13 playeras.
11. • \(P(x) = -x^2+25x-100\), para\(0 \leq x \leq 35\)
    • Dado que el vértice se produce en\(x=12.5\), y es imposible hacer o vender\(12.5\) botellas de tónico, el máximo beneficio se produce cuando se elaboran y venden cualquiera\(12\) o\(13\) botellas de tónico.
    • El beneficio máximo es\(\$56\).
    • El precio por botella puede ser\(\$23\) (para vender 12 botellas) o\(\$22\) (para vender 13 botellas.) Ambos resultarán en el beneficio máximo.
    • Los puntos de equilibrio son\(x=5\) y\(x=20\), así que para obtener ganancias, se necesitan fabricar y vender entre 5 y 20 botellas de tónico.
12. • \(P(x) = -3x^2+72x-240\), para\(0 \leq x \leq 30\)
    • \(12\)Se necesitan hacer y vender tazas de limonada para maximizar las ganancias.
    • El beneficio máximo es\(192\) o\(\$1.92\).
    • El precio por taza debe establecerse en\(54\) por taza para maximizar las ganancias.
    • Los puntos de equilibrio son\(x=4\) y\(x=20\), así que para obtener ganancias, se necesitan hacer y vender entre 4 y 20 tazas de limonada.
13. • \(P(x) = -0.5 x^2+9x-36\), para\(0 \leq x \leq 24\)
    • \(9\)las tartas deben elaborarse y venderse para maximizar el beneficio diario.
    • El beneficio máximo diario es\(\$4.50\).
    • El precio por pastel debe establecerse en\(\$7.50\) para maximizar las ganancias.
    • Los puntos de equilibrio son\(x=6\) y\(x=12\), por lo tanto, para obtener ganancias, se necesitan hacer y vender diariamente entre 6 y 12 tartas.
14. • \(P(x) = -2x^2+120x-1000\), para\(0 \leq x \leq 70\)
    • \(30\)Los scooters deben fabricarse y venderse para maximizar las ganancias.
    • El beneficio mensual máximo es de\(800\) cien dólares, o\(\$80,\!000\).
    • El precio por scooter debe fijarse en\(80\) cien dólares, o\(\$8000\) por scooter.
    • Los puntos de equilibrio son\(x=10\) y\(x=50\), por lo tanto, para obtener ganancias, se necesitan hacer y vender mensualmente entre 10 y 50 scooters.
15. 495 cookies
16. El vértice es (aproximadamente)\((29.60, 22.66)\), lo que corresponde a una economía máxima de combustible de 22.66 millas por galón, alcanzada en algún momento entre 2009 y 2010 (29 — 30 años después de 1980). Desafortunadamente, el modelo sólo es válido hasta 2008 (28 años después de 1908.) Entonces, en este punto, estamos utilizando el modelo para predecir la máxima economía de combustible.
17. \(64^{\circ}\)a las 2 PM (8 horas después de las 6 AM.)
18. Se deben producir 5000 plumas por un costo de\(\$200\).
19. 8 pies por 16 pies; el área máxima es de 128 pies cuadrados.
20. 50 pies por 50 pies; el área máxima es de 2500 pies; puede levantar 100 alpacas promedio.
21. El rectángulo más grande tiene área de pulgadas\(12.25\) cuadradas.
22. \(2\)segundos.
23. El cohete alcanza su altura máxima de\(500\) pies\(10\) segundos después del despegue.
24. El martillo alcanza una altura máxima de aproximadamente\(13.62\) pies. El martillo está en el aire aproximadamente\(1.61\) segundos.
25. 1. El dominio aplicado es\([0, \infty)\).
    2. La función de altura es este caso es\(s(t) = -4.9t^{2} + 15t\). El vértice de esta parábola es aproximadamente por\((1.53, 11.48)\) lo que la altura máxima alcanzada por el mármol es de\(11.48\) metros. Vuelve a golpear el suelo cuando\(t \approx 3.06\) segundos.
    3. La función de altura revisada es la\(s(t) = -4.9t^{2} + 15t + 25\) que tiene ceros en\(t \approx -1.20\) y\(t \approx 4.26\). Ignoramos el valor negativo y afirmamos que el mármol golpeará el suelo después de\(4.26\) segundos.
    4. Derribar significa que la velocidad inicial es negativa por lo que las funciones de altura se vuelven\(s(t) = -4.9t^{2} - 15t + 25\).
26. Hacer el vértice de la parábola\((0, 10)\) para que esté el punto en la parte superior de la torre izquierda donde se conecta el cable\((-200, 100)\) y el punto en la parte superior de la torre de la derecha esté\((200, 100)\). Entonces la parábola viene dada por\(p(x) = \frac{9}{4000}x^{2} + 10\). Pie de\(50\) pie a la derecha de la torre izquierda significa que estás parado en\(x= -150\) y\(p(-150) = 60.625\). Por lo que el cable está a 60.625 pies sobre la cubierta del puente ahí.
27. \(y = |1 -x^{2}|\)

    

28. \(\left(\dfrac{3 - \sqrt{7}}{2}, \dfrac{-1 + \sqrt{7}}{2} \right)\),\(\left(\dfrac{3 + \sqrt{7}}{2}, \dfrac{-1 - \sqrt{7}}{2} \right)\)
29. \(D(x) = x^2 + (2x+1)^2 = 5x^2+4x+1\),\(D\) se minimiza cuando\(x=-\frac{2}{5}\), por lo que el punto\(y=2x+1\) más cercano a\((0,0)\) es\(\left(-\frac{2}{5}, \frac{1}{5}\right)\)

31. \(x = \pm y\sqrt{10}\)
32. \(x = \pm (y - 2)\)
33. \(x = \dfrac{m \pm \sqrt{m^{2} + 4}}{2}\)
34. \(y = \dfrac{3 \pm \sqrt{16x + 9}}{2}\)
35. \(y = 2 \pm x\)
36. \(t = \dfrac{v_0 \pm \sqrt{v_0^{2} + 4gs_0}}{2g}\)

---

Referencia

¡¹ y racionalizando a los denominadores!

¡² y consigue denominadores comunes!

³ Solo una escala si\(\ a>0\). Si\(\ a < 0\), hay una reflexión involucrada.

⁴ Derecha si\(\ h > 0\), izquierda si\(\ h < 0\).

⁵ Arriba si\(\ k > 0\), abajo si\(\ k < 0\).

⁶ ¡Debes usar transformaciones para verificar esto!

⁷ Si olvidas por qué hacemos lo que hacemos para completar el cuadrado, estrella\(\ a(x-h)^{2}+k\), multiplicarlo, paso a paso, y luego revertir el proceso.

⁸ La experiencia da sus frutos, ¡aquí!

⁹ Donnie estaría muy molesto si, por ejemplo, le dijéramos que el ancho del pasto tiene que ser de −50 pies

¹⁰ Ya hemos visto la gráfica de esta función. Se utilizó como ejemplo en la Sección 1.6 para mostrar cómo la calculadora gráfica puede ser engañosa.

¹² Necesitarás usar tu calculadora para acercar lo suficiente como para ver que el vértice no es la intercepción y.