2.4: Desigualdades con valor absoluto y funciones cuadráticas

Última actualización
Guardar como PDF

Page ID: 119483

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

En esta sección, no sólo desarrollamos técnicas para resolver diversas clases de desigualdades analíticamente, también las observamos gráficamente. El primer ejemplo motiva las ideas centrales.

Ejemplo 2.4.1

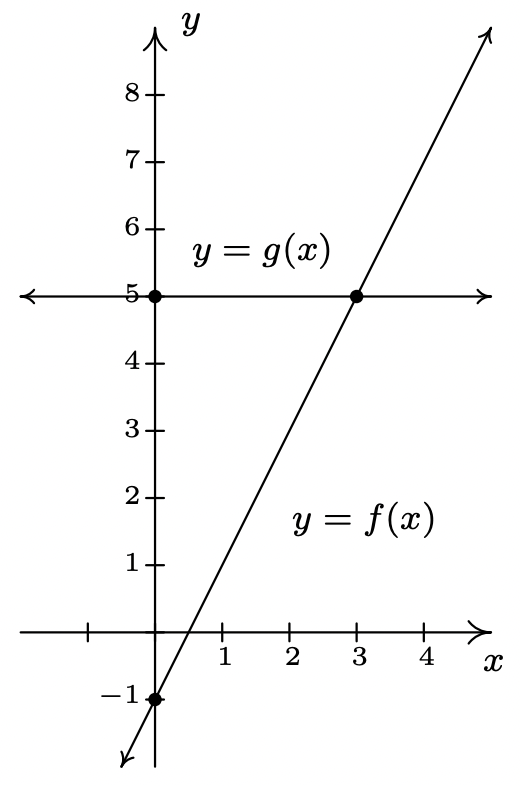
Dejar$f(x) = 2x-1$ y$g(x)=5$.

Resolver$f(x) = g(x)$.
Resolver$f(x) < g(x)$.
Resolver$f(x) > g(x)$.
$y=f(x)$Grafique y$y=g(x)$ en el mismo conjunto de ejes e interprete sus soluciones a las partes 1 a 3 anteriores.

Solución

Para resolver$f(x) = g(x)$, reemplazamos$f(x)$ con$2x-1$ y$g(x)$ con$5$ para obtener$2x-1 = 5$. Resolviendo para$x$, obtenemos$x=3$.
La desigualdad$f(x) < g(x)$ es equivalente a$2x-1 < 5$. Resolviendo da$x < 3$ o$(-\infty, 3)$.
Para encontrar dónde$f(x) > g(x)$, resolvemos$2x-1 > 5$. Obtenemos$x > 3$, o$(3, \infty)$.
Para graficar$y=f(x)$$y = 2x-1$, graficamos, que es una línea con una$y$ intersección de$(0,-1)$ y una pendiente de$2$. La gráfica de$y=g(x)$ es$y=5$ que es una línea horizontal a través$(0,5)$.
$Screen Shot 2022-03-26 a las 5.55.43 PM.png$

Para ver la conexión entre la gráfica y el Álgebra, recordamos el Principio de Gráfica Fundamental para Funciones en la Sección 1.6: el punto$(a,b)$ está en la gráfica de$f$ si y solo si$f(a)=b$. Es decir, un punto genérico en la gráfica de$y=f(x)$ es$(x,f(x))$, y un punto genérico en la gráfica de$y=g(x)$ es$(x,g(x))$. Cuando buscamos soluciones a$f(x)=g(x)$, estamos buscando$x$ valores cuyos$y$ valores en las gráficas de$f$ y$g$ sean los mismos. En la parte 1, encontramos$x=3$ es la solución a$f(x)=g(x)$. Bastante seguro,$f(3) = 5$ y$g(3) = 5$ para que el punto$(3,5)$ esté en ambas gráficas. En otras palabras, las gráficas de$f$ y se$g$ cruzan en$(3,5)$. En la parte 2, nos fijamos$f(x) < g(x)$ y resolvimos encontrar$x < 3$. Para$x < 3$, el punto$(x,f(x))$ está por debajo$(x,g(x))$ ya que los$y$ valores en la gráfica de$f$ son menores que los$y$ valores en la gráfica de$g$ ahí. Análogamente, en la parte 3, resolvimos$f(x) > g(x)$ y encontramos$x > 3$. Para$x > 3$, tenga en cuenta que la gráfica de$f$ está por encima de la gráfica de$g$, ya que$y$ los valores en la gráfica de$f$ son mayores que los$y$ valores en la gráfica de$g$ para esos valores de$x$.
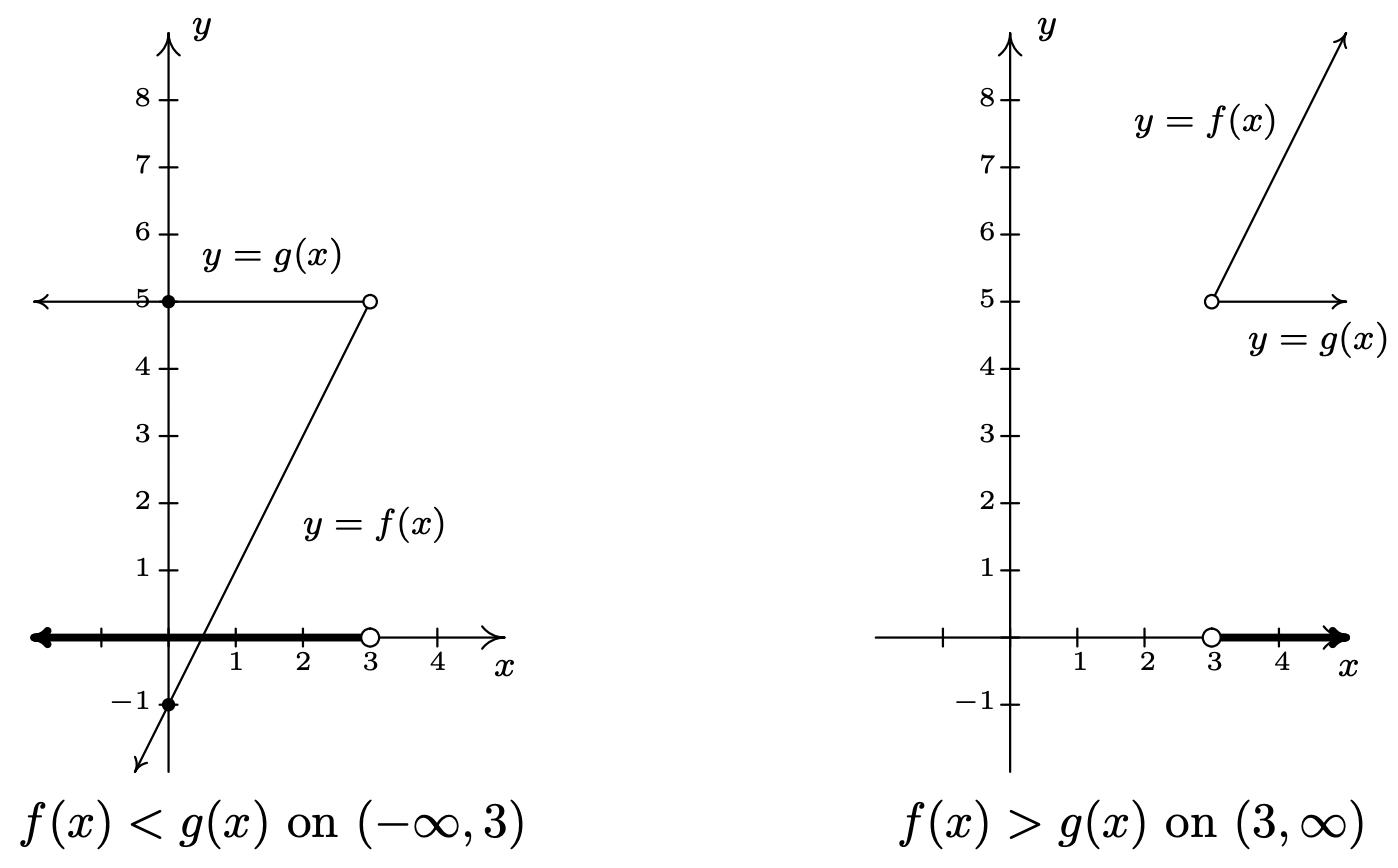
$Screen Shot 2022-03-26 en 5.57.41 PM.png$

El ejemplo anterior demuestra lo siguiente, que es consecuencia del Principio Fundamental de Gráfica para Funciones.

Interpretación gráfica de ecuaciones y desigualdades

Supongamos$f$ y$g$ son funciones.

Las soluciones a$f(x)=g(x)$ son los$x$ valores donde las gráficas de$y=f(x)$ y se$y=g(x)$ cruzan.
La solución a$f(x) < g(x)$ es el conjunto de$x$ valores donde la gráfica de$y=f(x)$ está debajo de la gráfica de$y=g(x)$.
La solución a$f(x) > g(x)$ es el conjunto de$x$ valores donde se encuentra la gráfica de$y=f(x)$ arriba de la gráfica de$y=g(x)$.

El siguiente ejemplo da vuelta a las tablas y proporciona las gráficas de dos funciones y pide soluciones a ecuaciones y desigualdades.

Ejemplo 2.4.2

Las gráficas de$f$ y$g$ están a continuación. (La gráfica de$y=g(x)$ está en negrita.) Utilice estas gráficas para responder a las siguientes preguntas.

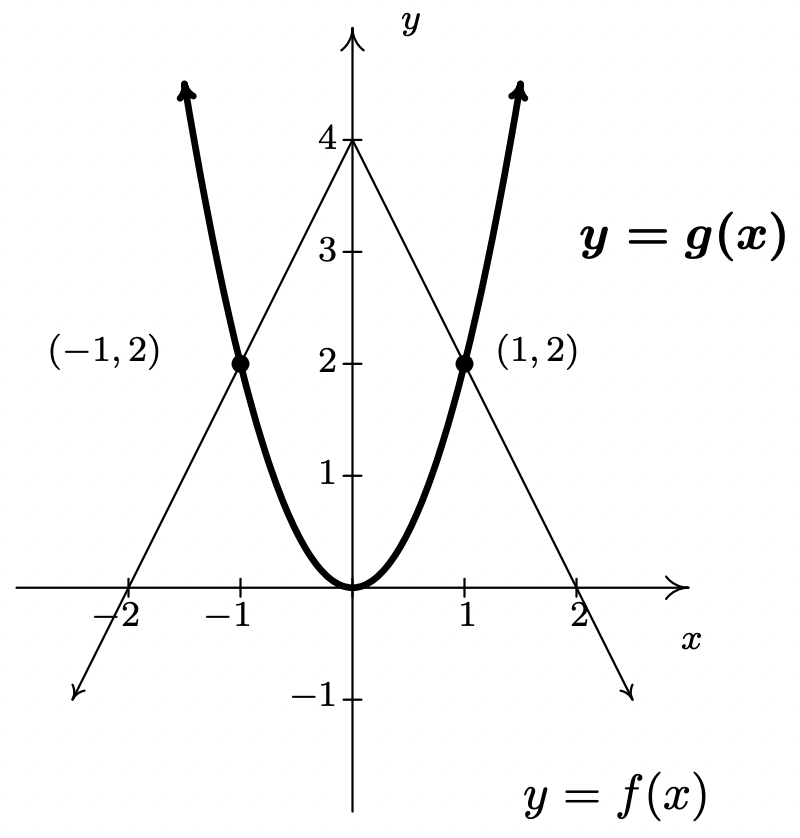
$Screen Shot 2022-03-26 en 6.03.54 PM.png$

Resolver$f(x) = g(x)$.
Resolver$f(x) < g(x)$.
Resolver$f(x) \geq g(x)$.

Solución

Para resolver$f(x)=g(x)$, buscamos dónde se cruzan las gráficas$f$ y se$g$ cruzan. Estos parecen estar en los puntos$(-1,2)$ y$(1,2)$, por lo que nuestras soluciones$f(x) = g(x)$ son$x = -1$ y$x=1$.
Para resolver$f(x) < g(x)$, buscamos dónde$f$ está la gráfica de debajo de la gráfica de$g$. Esto parece suceder para los$x$ valores menores que$-1$ y mayores que$1$. Nuestra solución es$(-\infty, -1) \cup (1,\infty)$.
Para resolver$f(x) \geq g(x)$, buscamos soluciones$f(x)=g(x)$ tanto para como$f(x) > g(x)$. Resolvimos la ecuación anterior y encontramos$x = \pm 1$. Para resolver$f(x) > g(x)$, buscamos dónde$f$ está la gráfica de encima de la gráfica de$g$. Esto parece suceder entre$x=-1$ y$x=1$, en el intervalo$(-1,1)$. De ahí que nuestra solución$f(x) \geq g(x)$ sea$[-1,1]$.

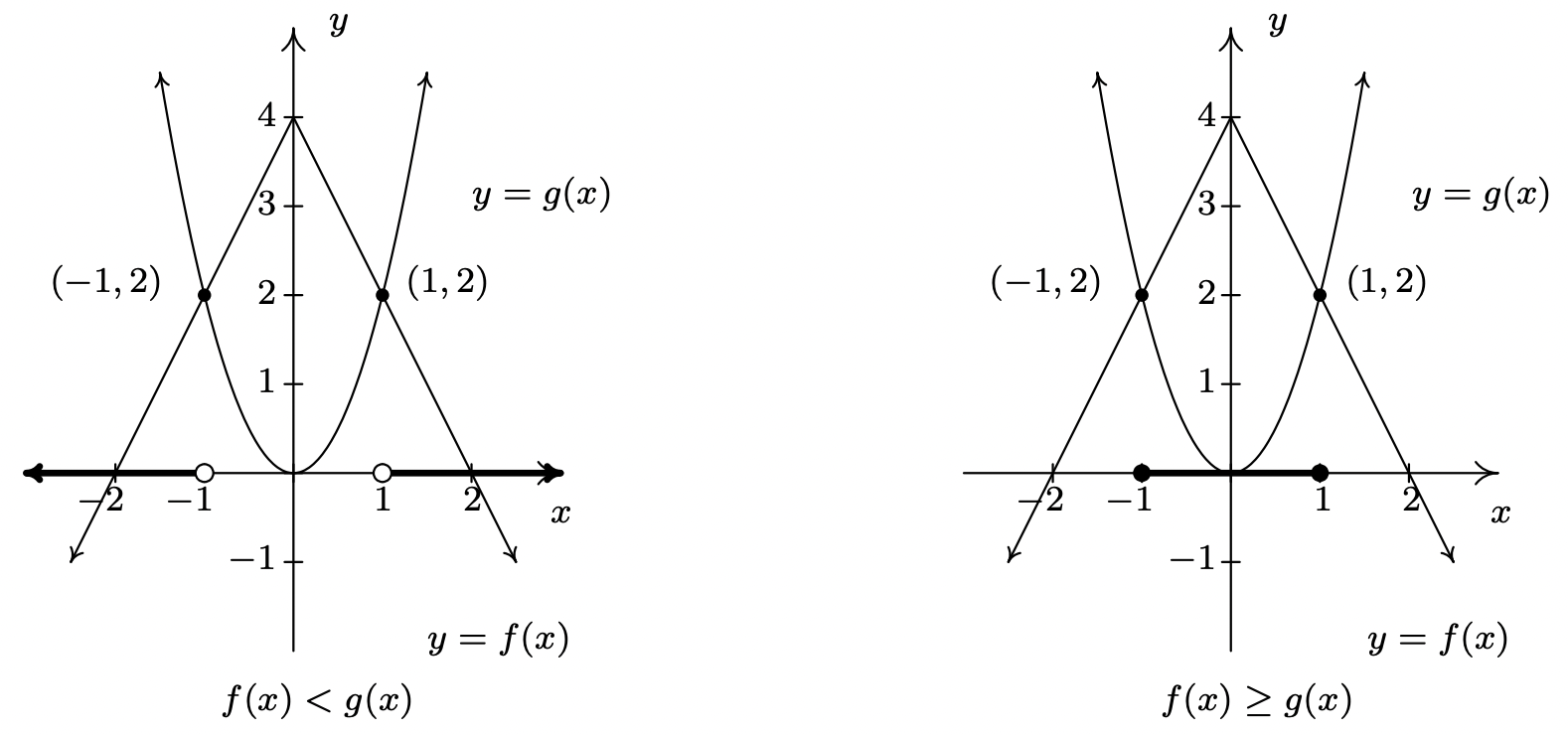
$Screen Shot 2022-03-26 a las 6.06.12 PM.png$

Ahora volvemos nuestra atención a la solución de desigualdades que involucran el valor absoluto. Tenemos el siguiente teorema de Álgebra Intermedia para ayudarnos.

Teorema 2.4. Desigualdades que involucran el valor absoluto

$c$Déjese ser un número real.

Para$c > 0$,$|x| < c$ es equivalente a$-c<x<c$.
Para$c > 0$,$|x| \leq c$ es equivalente a$-c \leq x \leq c$.
Para$c \leq 0$, no$|x| < c$ tiene solución, y para$c < 0$, no$|x| \leq c$ tiene solución.
Para$c \geq 0$,$|x| > c$ es equivalente a$x<-c$ o$x>c$.
Para$c \geq 0$,$|x| \geq c$ es equivalente a$x \leq -c$ o$x \geq c$.
Para$c < 0$,$|x| > c$ y$|x| \geq c$ son ciertos para todos los números reales.

Al igual que con el Teorema 2.1 en la Sección 2.2, podríamos argumentar el Teorema 2.4 usando casos. No obstante, a la luz de lo que hemos desarrollado en esta sección, podemos entender gráficamente estas afirmaciones. Por ejemplo, si$c > 0$, la gráfica de$y=c$ es una línea horizontal que se encuentra por encima del$x$ eje -pasante$(0,c)$. Para resolver$|x| < c$, estamos buscando$x$ los valores donde la gráfica de$y=|x|$ está debajo de la gráfica de$y=c$. Sabemos que las gráficas se cruzan cuando$|x|=c$, que, a partir de la Sección 2.2, sabemos que sucede cuando$x=c$ o$x=-c$. Graficando, obtenemos

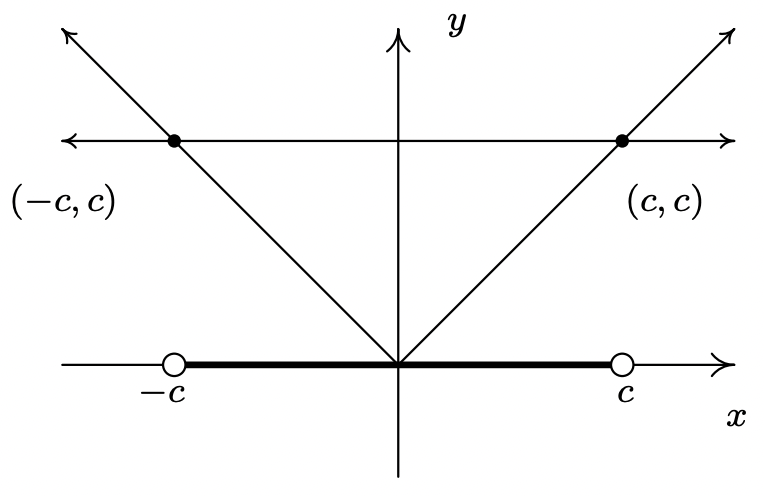
$Screen Shot 2022-03-26 a las 6.12.36 PM.png$

Vemos que la gráfica de$y=|x|$ está abajo$y=c$ para$x$ entre$-c$ y$c$, y por lo tanto obtenemos$|x| < c$ es equivalente a$-c < x < c$. Las otras propiedades del Teorema 2.4 se pueden mostrar de manera similar.

Ejemplo 2.4.3

Resuelve analíticamente las siguientes desigualdades; revisa tus respuestas gráficamente.

$|x-1| \geq 3$
$4 - 3|2x+1| > -2$
$2 < |x-1| \leq 5$
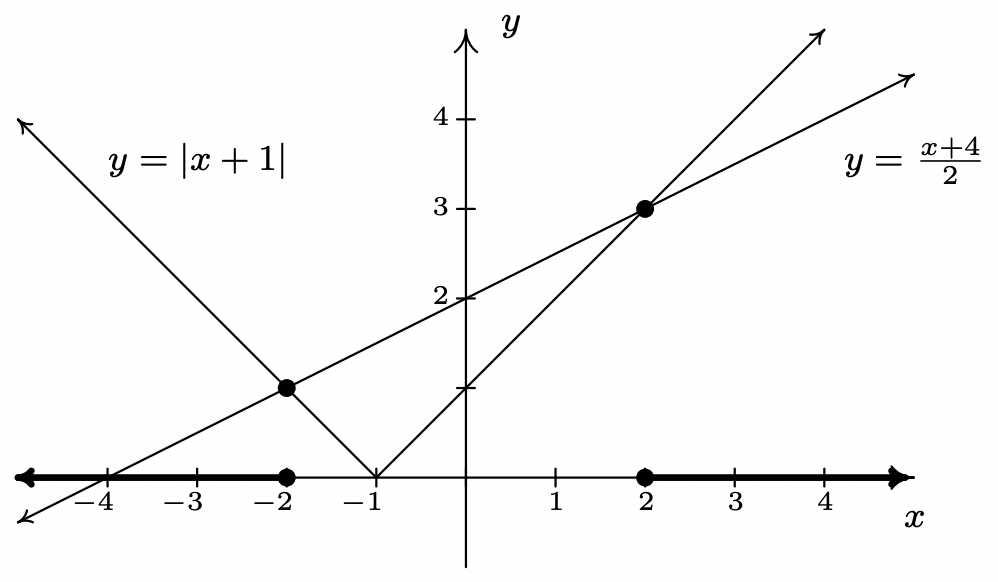
$|x+1|\geq \dfrac{x+4}{2}$

Solución

Del Teorema 2.4,$|x-1|\geq3$ es equivalente a$x-1 \leq -3$ o$x-1 \geq 3$. Resolviendo, obtenemos$x \leq -2$ o$x \geq 4$, que, en notación de intervalos es$(-\infty,-2] \cup [4,\infty)$. Gráficamente, tenemos
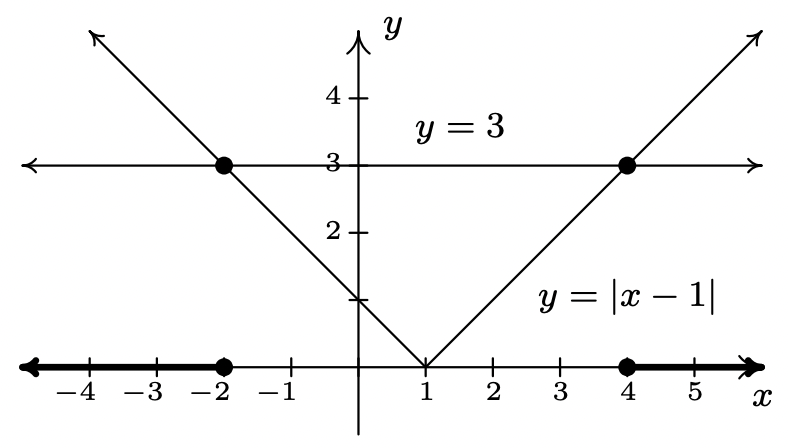
$Screen Shot 2022-03-26 a las 6.17.56 PM.png$

Vemos que la gráfica de$y=|x-1|$ está por encima de la línea horizontal$y=3$ para$x < -2$ y de$x > 4$ ahí ahí es donde$|x-1| > 3$. Los dos gráficos se cruzan cuando$x=-2$ y$x=4$, así tenemos confirmación gráfica de nuestra solución analítica.
Para resolver$4 - 3|2x+1| > -2$ analíticamente, primero aislamos el valor absoluto antes de aplicar el Teorema 2.4. Para ello, obtenemos$-3|2x+1|>-6$ o$|2x+1|<2$. Reescribiendo, ahora tenemos$-2 < 2x+1 < 2$ así que$-\frac{3}{2} < x < \frac{1}{2}$. En notación de intervalos, escribimos$\left(-\frac{3}{2}, \frac{1}{2}\right)$. Gráficamente vemos que la gráfica de$y=4-3|2x+1|$ está arriba$y=-2$ para$x$ valores entre$-\frac{3}{2}$ y$\frac{1}{2}$.
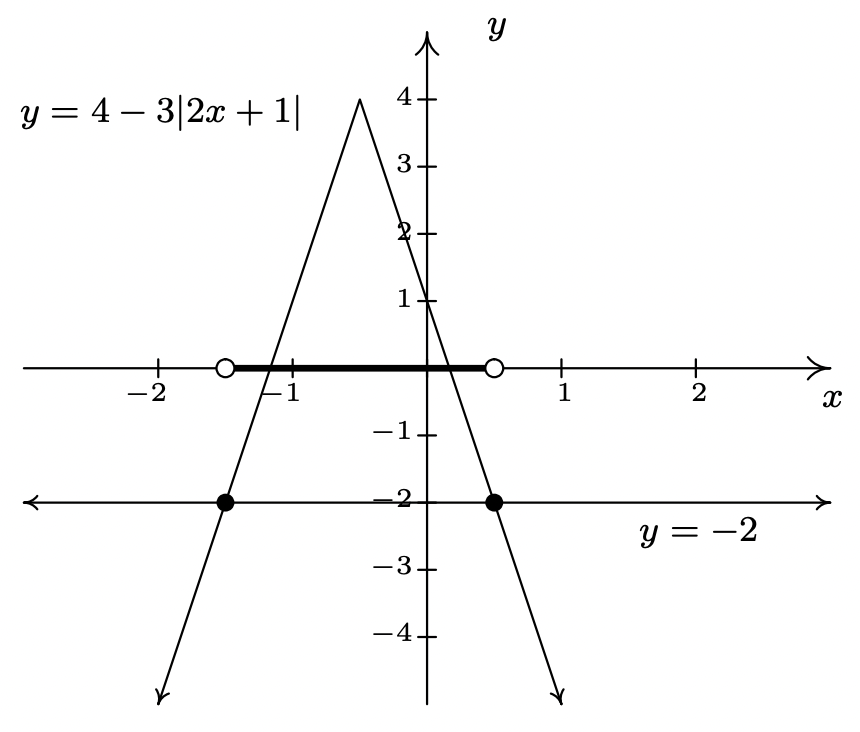
$Screen Shot 2022-03-26 a las 6.21.23 PM.png$
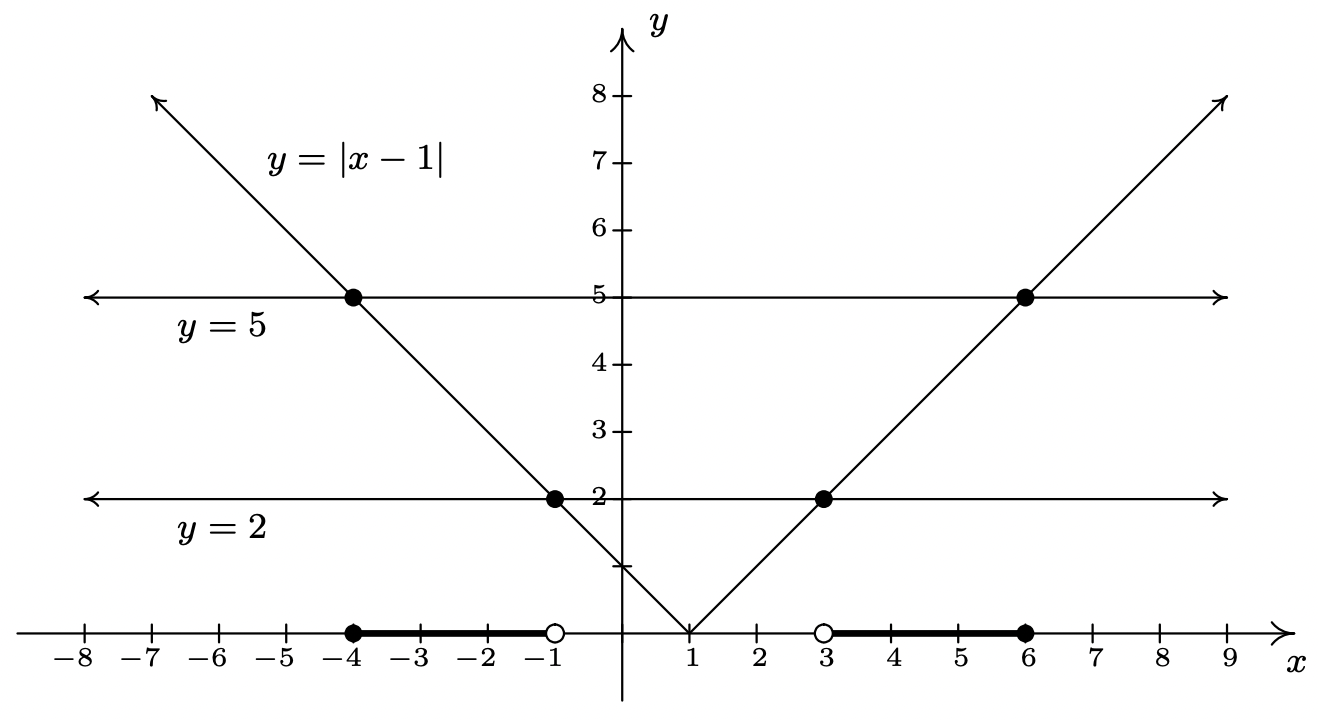
Reescribir la desigualdad compuesta$2 < |x-1| \leq 5$ como '$2 < |x-1|$y$|x-1| \leq 5$' nos permite resolver cada pieza usando el Teorema 2.4. La primera desigualdad,$2 < |x-1|$ puede ser reescrita como$|x-1|>2$ tal$x-1 < -2$ o$x-1 > 2$. Obtenemos$x<-1$ o$x>3$. Nuestra solución a la primera desigualdad es entonces$(-\infty, -1) \cup (3, \infty)$. Para$|x-1| \leq 5$, combinamos resultados en Teoremas 2.1 y 2.4 para obtener$-5 \leq x-1 \leq 5$ así que$-4 \leq x \leq 6$, o$[-4,6]$. Nuestra solución$2 < |x-1| \leq 5$ está compuesta por valores de los$x$ cuales satisfacen ambas partes de la desigualdad, por lo que tomamos la intersección ¹ de$(-\infty, -1) \cup (3, \infty)$ y$[-4,6]$ para obtener$[-4,-1) \cup (3,6]$. Gráficamente, vemos que la gráfica de$y=|x-1|$ está 'entre' las líneas horizontales$y=2$ y$y=5$ para$x$ valores entre$-4$ y así$-1$ como aquellos entre$3$ y$6$. Incluyendo los$x$ valores donde$y=|x-1|$ e$y=5$ intersectamos, obtenemos
$Screen Shot 2022-03-26 a las 6.39.33 PM.png$
Tenemos que tener especial precaución a la hora de resolver$|x+1|\geq \frac{x+4}{2}$. Como vimos en el Ejemplo 2.2.1 en la Sección 2.2, cuando las variables están tanto dentro como fuera del valor absoluto, suele ser mejor referirse a la definición de valor absoluto, Definición 2.4, para eliminar los valores absolutos y proceder de ahí. Para ello, tenemos$|x+1| = -(x+1)$ si$x < -1$ y$|x+1| = x+1$ si$x \geq -1$. Rompemos la desigualdad en casos, siendo el primer caso cuándo$x<-1$. Para estos valores de$x$, nuestra desigualdad se vuelve$-(x+1) \geq \frac{x+4}{2}$. Resolviendo, obtenemos$-2x-2 \geq x+4$, así que eso$-3x \geq 6$, lo que significa$x \leq -2$. Dado que todas estas soluciones entran en la categoría$x < -1$, las mantenemos todas. Para el segundo caso, asumimos$x \geq -1$. Nuestra desigualdad se convierte$x+1 \geq \frac{x+4}{2}$, que da$2x+2 \geq x+4$ o$x \geq 2$. Dado que todos estos valores de$x$ son mayores o iguales a$-1$, aceptamos todas estas soluciones también. Nuestra respuesta final es$(-\infty, -2] \cup [2,\infty)$.
$Screen Shot 2022-03-26 a las 6.45.21 PM.png$

Ahora volvemos nuestra atención a las desigualdades cuadráticas. En el último ejemplo de la Sección 2.3, necesitábamos determinar la solución a$x^2 - x -6 < 0$. Ahora volveremos a visitar este problema utilizando algunas de las técnicas desarrolladas en esta sección no sólo para reforzar nuestra solución en la Sección 2.3, sino también para ayudar a formular un procedimiento analítico general para resolver todas las desigualdades cuadráticas. Si consideramos$f(x) = x^2-x-6$ y$g(x)=0$, entonces resolver$x^2 - x -6 < 0$ corresponde gráficamente a encontrar los valores de$x$ para los cuales la gráfica de$y=f(x)=x^2-x-6$ (la parábola) está por debajo de la gráfica de$y=g(x)=0$ (el$x$ eje -). Hemos proporcionado de nuevo la gráfica para referencia.

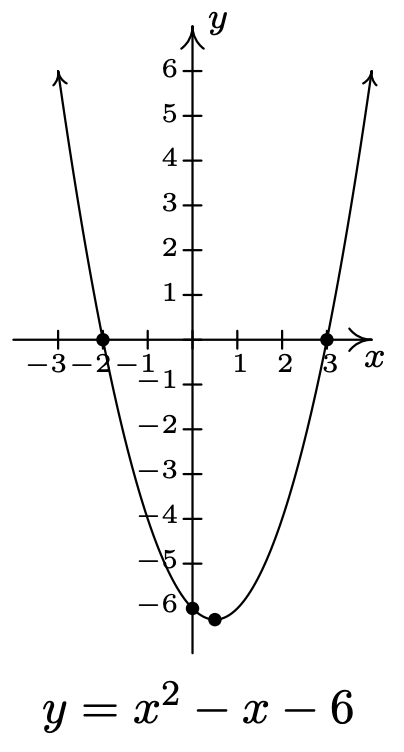
$Screen Shot 2022-03-26 a las 6.49.42 PM.png$

Podemos ver que la gráfica de$f$ sí cae por debajo del$x$ -eje entre sus dos$x$ -intercepciones. Los ceros de$f$ son$x=-2$ y$x=3$ en este caso y dividen el dominio (el$x$ -eje) en tres intervalos:$(-\infty, -2)$,$(-2,3)$ y$(3, \infty)$. Por cada número en$(-\infty, -2)$, la gráfica de$f$ está por encima del$x$ eje -; en otras palabras,$f(x) > 0$ para todos$x$ en$(-\infty, -2)$. De igual manera,$f(x) < 0$ para todos$x$ en$(-2,3)$, y$f(x) > 0$ para todos$x$ en$(3, \infty)$. Podemos representar esquemáticamente esto con el diagrama de signos a continuación.

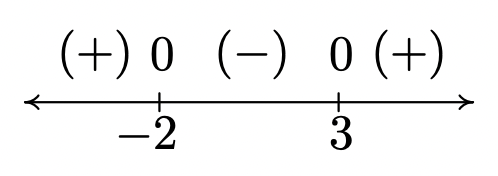
$Screen Shot 2022-03-26 a las 6.50.57 PM.png$

Aquí,$(+)$ lo anterior una porción de la línea numérica indica$f(x) > 0$ para esos valores de$x$; la$(-)$ indica$f(x) < 0$ ahí. Los números etiquetados en la recta numérica son los ceros de$f$, así que colocamos$0$ encima de ellos. Vemos de inmediato que la solución a$f(x) < 0$ es$(-2,3)$.

Nuestro siguiente objetivo es establecer un procedimiento mediante el cual podamos generar el diagrama de signos sin graficar la función. Una propiedad importante ² de las funciones cuadráticas es que si la función es positiva en un punto y negativa en otro, la función debe tener al menos un cero en el medio. Gráficamente, esto significa que una parábola no puede estar por encima del$x$ eje en un punto y por debajo del$x$ eje en otro punto sin cruzar el$x$ eje. Esto nos permite determinar el signo de todos los valores de función en un intervalo dado probando la función en un solo valor en el intervalo. Esto nos da lo siguiente.

Pasos para resolver una desigualdad cuadrática

Reescribir la desigualdad, si es necesario, como una función cuadrática$f(x)$ en un lado de la desigualdad y$0$ por el otro.
Encuentra los ceros de$f$ y colócalos en la línea numérica con el número$0$ encima de ellos.
Elija un número real, llamado valor de prueba, en cada uno de los intervalos determinados en el paso 2.
Determine el signo de$f(x)$ para cada valor de prueba en el paso 3, y escriba ese signo por encima del intervalo correspondiente.
Elija los intervalos que correspondan al signo correcto para resolver la desigualdad.

Ejemplo 2.4.4

Resuelve las siguientes desigualdades analíticamente usando diagramas de signos. Verifica tu respuesta gráficamente.

$2x^2 \leq 3-x$
$x^2 - 2x > 1$
$x^2+1 \leq 2x$
$2x-x^2 \geq |x-1|-1$

Solución

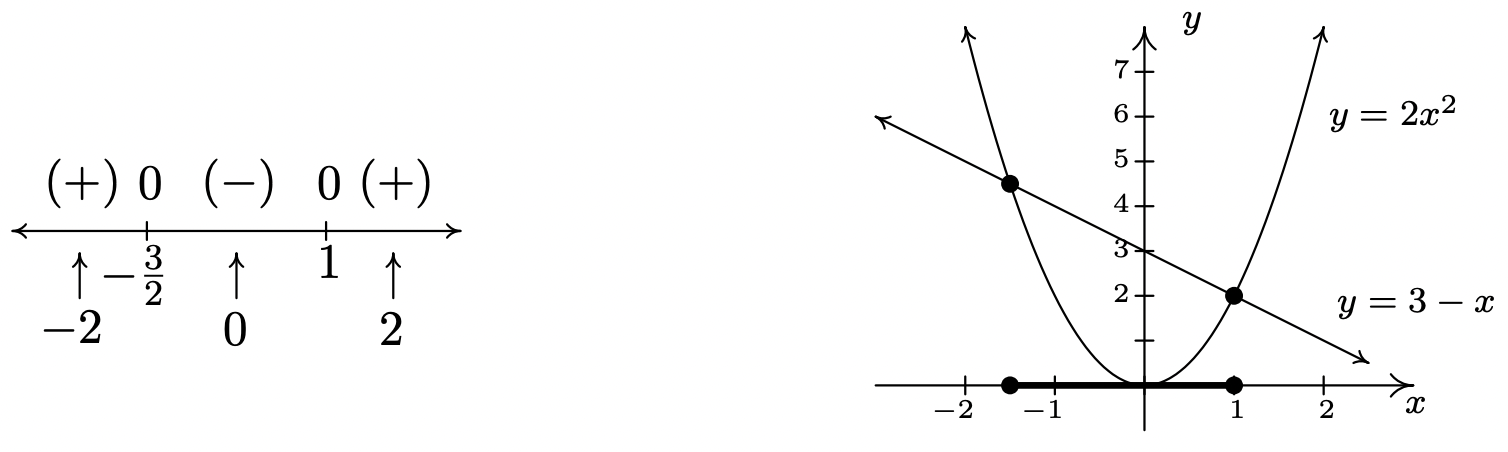
Para resolver$2x^2 \leq 3-x$, primero nos ponemos$0$ en un lado de la desigualdad que rinde$2x^2+x-3 \leq 0$. Encontramos los ceros de$f(x) = 2x^2 + x - 3$ resolviendo$2x^2 + x - 3 = 0$ para$x$. Factoring da$(2x+3)(x-1)=0$, así$x = -\frac{3}{2}$ o$x = 1$. Colocamos estos valores en la recta numérica con$0$ encima de ellos y elegimos valores de prueba en los intervalos$\left(-\infty, -\frac{3}{2}\right)$,$\left(-\frac{3}{2},1\right)$ y$(1,\infty)$. Para el intervalo$\left(-\infty, -\frac{3}{2}\right)$, elegimos ³$x=-2$; para$\left(-\frac{3}{2},1\right)$, elegimos$x=0$; y para$(1,\infty)$,$x=2$. Evaluar la función en los tres valores de prueba nos da$f(-2) = 3 > 0$, así que colocamos$(+)$ arriba$\left(-\infty, -\frac{3}{2}\right)$;$f(0)=-3 < 0$, así$(-)$ va por encima del intervalo$\left(-\frac{3}{2},1\right)$; y,$f(2) = 7$, que significa que$(+)$ se coloca arriba$(1,\infty)$. Ya que estamos resolviendo$2x^2+x-3 \leq 0$, buscamos soluciones para así$2x^2+x-3 < 0$ como soluciones para$2x^2+x-3 =0$. Para$2x^2+x-3 < 0$, necesitamos los intervalos que tenemos a$(-)$. Comprobando el diagrama de señales, vemos que esto es$\left(-\frac{3}{2},1\right)$. Sabemos$2x^2+x-3 =0$ cuándo$x=-\frac{3}{2}$ y$x=1$, así que nuestra respuesta final es$\left[-\frac{3}{2},1\right]$.
Para verificar nuestra solución gráficamente, nos referimos a la desigualdad original,$2x^2 \leq 3-x$. Dejamos$g(x) = 2x^2$ y$h(x)=3-x$. Estamos buscando$x$ los valores donde la gráfica de$g$ está por debajo de la de$h$ (la solución a$g(x) < h(x)$) así como los puntos de intersección (las soluciones a$g(x)=h(x)$). Las gráficas de$g$ y$h$ se dan a la derecha con el gráfico de signos a la izquierda.

$Screen Shot 2022-03-26 en 7.08.16 PM.png$
Una vez más, reescribimos$x^2-2x > 1$ como$x^2-2x-1>0$ e identificamos$f(x)=x^2-2x-1$. Cuando vamos a buscar los ceros de$f$, nos encontramos, para nuestro disgustado, que lo cuadrático$x^2-2x-1$ no factoriza muy bien. De ahí que recurrimos a la fórmula cuadrática para resolver$x^2-2x-1=0$, y llegar a$x=1 \pm \sqrt{2}$. Como antes, estos ceros dividen la recta numérica en tres pedazos. Para ayudarnos a decidir sobre los valores de prueba, aproximamos$1 - \sqrt{2} \approx -0.4$ y$1 + \sqrt{2} \approx 2.4$. Elegimos$x=-1$,$x=0$ y$x=3$ como nuestros valores de prueba y encontramos$f(-1)= 2$, cual es$(+)$;$f(0)=-1$ cual es$(-)$; y$f(3)=2$ cual es$(+)$ otra vez. Nuestra solución para$x^2-2x-1>0$ es donde tenemos$(+)$, entonces, en notación de intervalos$\left(-\infty, 1-\sqrt{2}\right) \cup \left(1+\sqrt{2},\infty\right)$. Para comprobar la desigualdad$x^2 - 2x > 1$ gráficamente, establecemos$g(x) = x^2-2x$ y$h(x)=1$. Estamos buscando$x$ los valores donde la gráfica de$g$ está por encima de la gráfica de$h$. Como antes presentamos las gráficas a la derecha y la gráfica de signos a la izquierda.
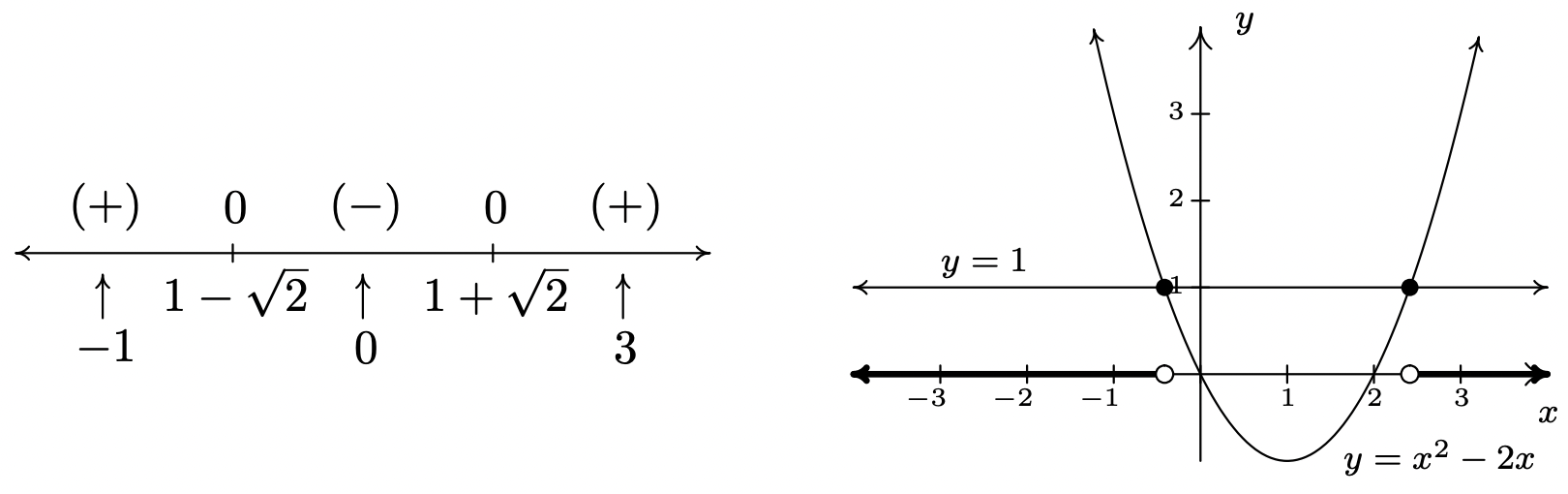
$Screen Shot 2022-03-26 a las 7.09.58 PM.png$
$Screen Shot 2022-03-27 a las 6.12.11 PM.png$
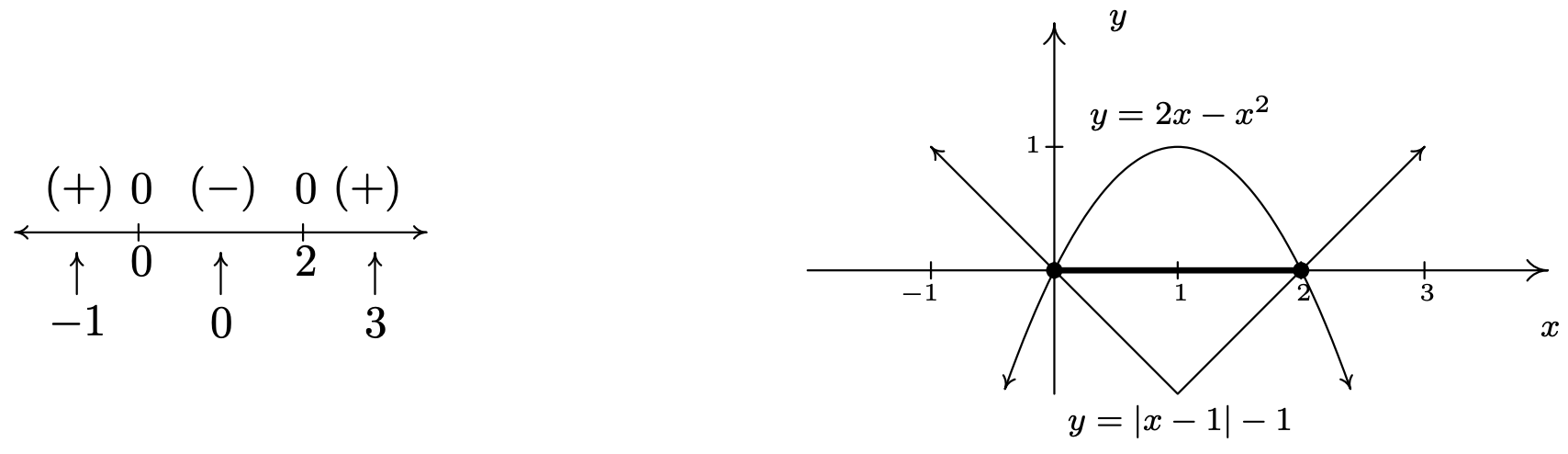
Para resolver nuestra última desigualdad,$2x-x^2 \geq |x-1|-1$, reescribimos el valor absoluto usando casos. Para$x < 1$,$|x-1| = -(x-1) = 1-x$, así conseguimos$2x-x^2 \geq 1-x-1$, o$x^2-3x \leq 0$. Encontrar los ceros de$f(x) = x^2-3x$, obtenemos$x=0$ y$x=3$. No obstante, sólo nos preocupa la porción de la línea numérica donde$x < 1$, por lo que el único cero que nos ocupa es$x=0$. Esto divide el intervalo$x<1$ en dos intervalos:$(-\infty, 0)$ y$(0,1)$. Elegimos$x=-1$ y$x=\frac{1}{2}$ como nuestros valores de prueba. Nos encontramos$f(-1) = 4$ y$f\left(\frac{1}{2}\right) = -\frac{5}{4}$. De ahí que nuestra solución a$x^2-3x \leq 0$ for$x < 1$ es$[0,1)$. A continuación, dirigimos nuestra atención al caso$x \geq 1$. Aquí,$|x-1| = x-1$, así nuestra desigualdad original se convierte$2x-x^2 \geq x-1-1$, o$x^2-x-2 \leq 0$. Ajuste$g(x) = x^2-x-2$, nos encontramos con los ceros de$g$ ser$x=-1$ y$x=2$. De estos, sólo$x=2$ se encuentra en la región$x \geq 1$, por lo que ignoramos$x=-1$. Nuestros intervalos de prueba son ahora$[1,2)$ y$(2,\infty)$. Elegimos$x=1$ y$x=3$ como nuestros valores de prueba y encontramos$g(1) = -2$ y$g(3) = 4$. De ahí que nuestra solución para$g(x) = x^2-x-2 \leq 0$, en esta región es$[1,2)$.
$Screen Shot 2022-03-27 a las 6.13.48 PM.png$

Combinando estos en un diagrama de signos, tenemos que nuestra solución es$[0,2]$. Gráficamente$2x-x^2 \geq |x-1|-1$, para verificar, establecemos$h(x) = 2x-x^2$$i(x) = |x-1|-1$ y buscamos los$x$ valores donde la gráfica de$h$ está por encima de la gráfica de$i$ (la solución de$h(x) > i(x)$) así como las$x$ -coordenadas de los puntos de intersección de ambas gráficas (donde$h(x)=i(x)$). El gráfico de signos combinados se da a la izquierda y los gráficos a la derecha.

$Screen Shot 2022-03-27 a las 6.15.26 PM.png$

Una de las aplicaciones clásicas de las desigualdades es la noción de tolerancias. ⁵ Recordemos que para números reales$x$ y$c$, la cantidad$|x-c|$ puede interpretarse como la distancia de$x$ a$c$. Resolver desigualdades de la forma$|x-c| \leq d$ para entonces$d \geq 0$ puede interpretarse como encontrar todos los números$x$ que se encuentran dentro de$d$ unidades de$c$. Podemos pensar en el número$d$ como una 'tolerancia' y nuestras soluciones$x$ como estar dentro de una tolerancia aceptada de$c$. Utilizamos este principio en el siguiente ejemplo.

Ejemplo 2.4.5

El área$A$ (en pulgadas cuadradas) de una pieza cuadrada de tablero de partículas que mide$x$ pulgadas en cada lado es$A(x) = x^2$. Supongamos que un fabricante necesita producir una pieza cuadrada de tablero de partículas$24$$24$ pulgada por pulgada como parte de un kit de escritorio de oficina en casa. ¿Qué tan cerca se necesita cortar el lado de la pieza de tablero de partículas a$24$ pulgadas para garantizar que el área de la pieza esté dentro de una tolerancia de pulgadas$0.25$ cuadradas del área objetivo de pulgadas$576$ cuadradas?

Solución

Matemáticamente, expresamos el deseo de que el área$A(x)$ esté dentro de pulgadas$0.25$ cuadradas de$576$ as$|A - 576| \leq 0.25$. Ya que$A(x) = x^2$, obtenemos$|x^2 - 576| \leq 0.25$, que es equivalente a$-0.25 \leq x^2 - 576 \leq 0.25$. Una forma de proceder en este punto es resolver las dos desigualdades$-0.25 \leq x^2 - 576$ e$x^2 - 576 \leq 0.25$ individualmente usando diagramas de signos y luego tomando la intersección de los conjuntos de soluciones. Si bien de esta manera (eventualmente) conducirá a la respuesta correcta, aprovechamos esta oportunidad para mostrar la creciente propiedad de la raíz cuadrada: si$0 \leq a \leq b$, entonces$\sqrt{a} \leq \sqrt{b}$. Para utilizar esta propiedad, procedemos de la siguiente manera

\[\begin{array}{rclr} -0.25 \leq & x^2 - 576 & \leq 0.25 & \\ 575.75 \leq & x^2 & \leq 576.25 & \text{(add $576$ across the inequalities.)} \\ \sqrt{575.75} \leq & \sqrt{x^2} & \leq \sqrt{576.25} & \text{(take square roots.)} \\ \sqrt{575.75} \leq & |x| & \leq \sqrt{576.25} & \text{($\sqrt{x^2} = |x|$)} \\ \end{array}\]

Por Teorema 2.4, encontramos la solución$\sqrt{575.75} \leq |x|$ para ser$\left(-\infty, -\sqrt{575.75} \, \right] \cup \left[\sqrt{575.75}, \infty \right)$ y la solución$|x| \leq \sqrt{576.25}$ para ser$\left[-\sqrt{576.25}, \sqrt{576.25} \, \right]$. Para resolver$\sqrt{575.75} \leq |x| \leq \sqrt{576.25}$, nos cruzamos estos dos conjuntos para obtener$[-\sqrt{576.25}, -\sqrt{575.75}] \cup [\sqrt{575.75},\sqrt{576.25}]$. Ya que$x$ representa una longitud, descartamos las respuestas negativas y obtenemos$[\sqrt{575.75},\sqrt{576.25}]$. Esto significa que el lado de la pieza de tablero de partículas debe cortarse entre$\sqrt{575.75} \approx 23.995$ y$\sqrt{576.25} \approx 24.005$ pulgadas, una tolerancia de (aproximadamente)$0.005$ pulgadas de la longitud objetivo de$24$ pulgadas.

Nuestro último ejemplo en la sección demuestra cómo se pueden utilizar las desigualdades para describir regiones en el plano, como vimos anteriormente en la Sección 1.2.

Ejemplo 2.4.6

Esbozar las siguientes relaciones.

$R = \{ (x,y) : y > |x| \}$
$S = \{ (x,y) : y \leq 2-x^2 \}$
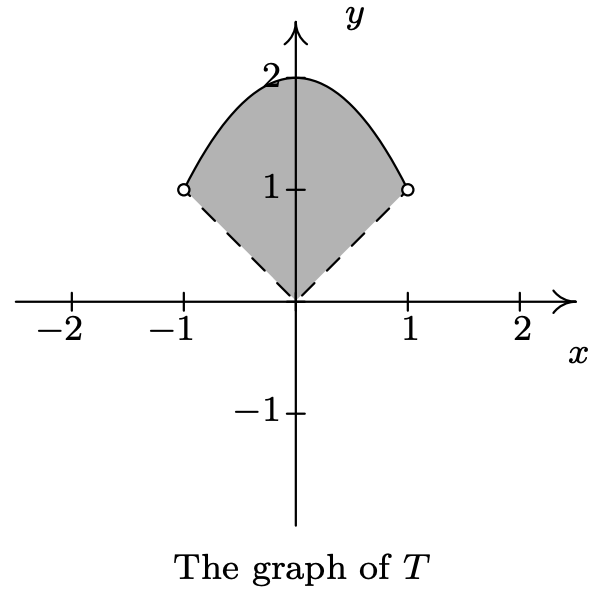
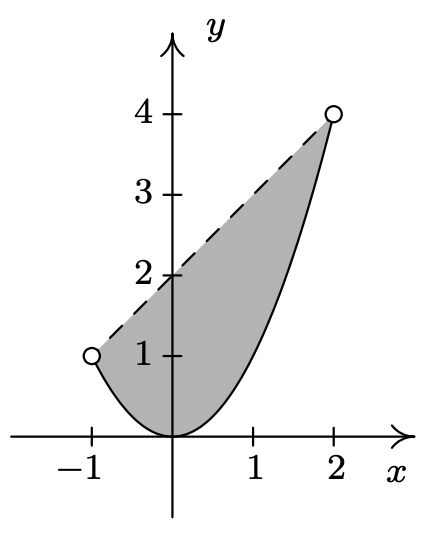
$T = \{ (x,y) : |x| < y \leq 2-x^2 \}$

Solución

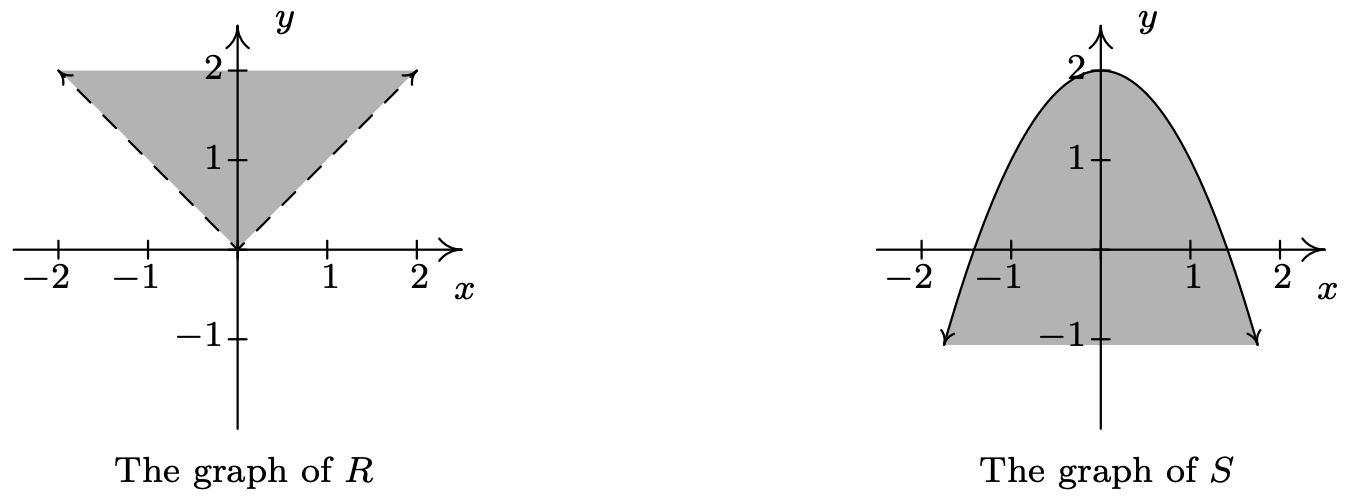
La relación$R$ consiste en todos los puntos$(x,y)$ cuya$y$ -coordenada es mayor que$|x|$. Si graficamos$y=|x|$, entonces queremos todos los puntos en el plano por encima de los puntos de la gráfica. Punteando la gráfica de$y=|x|$ como hemos hecho antes para indicar que los puntos en la gráfica en sí no están en la relación, obtenemos la región sombreada de abajo a la izquierda.
Para que un punto esté adentro$S$, su$y$ coordenada debe ser menor o igual que la$y$ coordenada en la parábola$y=2-x^2$. Este es el conjunto de todos los puntos abajo o en la parábola$y=2-x^2$.
$Screen Shot 2022-03-27 a las 6.30.32 PM.png$
Finalmente, la relación$T$ toma los puntos cuyas$y$ coordenadas satisfacen tanto las condiciones dadas en como$R$ las de$S$. Así sombreamos la región entre$y=|x|$ y$y=2-x^2$, manteniendo esos puntos en la parábola, pero no los puntos puestos$y=|x|$. Para obtener una gráfica precisa, necesitamos encontrar dónde se cruzan estas dos gráficas, así que establecemos$|x| = 2-x^2$. Procediendo como antes, rompiendo esta ecuación en casos, obtenemos$x=-1,1$. Graficando rendimientos
$Screen Shot 2022-03-27 a las 6.31.27 PM.png$

2.4.1. Ejercicios

En los Ejercicios 1-32, resolver la desigualdad. Escribe tu respuesta usando notación de intervalos.

$|3x - 5| \leq 4$
$|7x + 2| > 10$
$|2x+1| - 5 < 0$
$|2-x| - 4 \geq -3$
$|3x+5| + 2 < 1$
$2|7-x| +4 > 1$
$2 \leq |4-x| < 7$
$1 < |2x - 9| \leq 3$
$|x + 3| \geq |6x + 9|$
$|x-3| - |2x+1| < 0$
$|1-2x| \geq x + 5$
$x + 5 < |x+5|$
$x \geq |x+1|$
$|2x + 1| \leq 6-x$
$x + |2x-3| < 2$
$|3-x| \geq x-5$
$x^{2} + 2x - 3 \geq 0$
$16x^2+8x+1 > 0$
$x^2+9 < 6x$
$9x^2 + 16 \geq 24x$
$x^2+4 \leq 4x$
$x^{2} + 1 < 0$
$3x^{2} \leq 11x + 4$
$x > x^{2}$
$2x^2-4x-1 > 0$
$5x+4 \leq 3x^2$
$2 \leq |x^{2} - 9| < 9$
$x^{2} \leq |4x - 3|$
$x^{2} + x + 1 \geq 0$
$x^2 \geq |x|$
$x |x+5| \geq -6$
$x |x-3| < 2$
El beneficio, en dólares, que se obtiene al vender$x$ botellas de Tónico Sasquatch Orgánico Certificado$100 \%$ All-Natural Certified Free-Trade es dado por$P(x) = -x^2+25x-100$, para$0 \leq x \leq 35$. ¿Cuántas botellas de tónico deben venderse para obtener al menos$\$50$ en ganancias?
Supongamos$C(x) = x^2-10x+27$,$x \geq 0$ representa los costos, en cientos de dólares, para producir$x$ mil bolígrafos. Encuentre el número de bolígrafos que se pueden producir para no más de$\$1100$.
La temperatura$T$, en grados Fahrenheit,$t$ horas después de las 6 AM es dada por$T(t) = -\frac{1}{2} t^2 + 8t+32$, para$0 \leq t \leq 12$. ¿Cuándo es más cálido que$42^{\circ}$ Fahrenheit?
La altura$h$ en pies de un cohete modelo sobre el suelo$t$ segundos después del despegue viene dada por$h(t) = -5t^2+100t$, para$0 \leq t \leq 20$. ¿Cuándo está el cohete al menos a$250$ pies del suelo? Redondee su respuesta a dos decimales.
Si se usa un tirachinas para disparar una canica directamente al aire desde 2 metros sobre el suelo con una velocidad inicial de 30 metros por segundo, ¿para qué valores de tiempo el mármol$t$ estará a más de 35 metros sobre el suelo? (Consulte el Ejercicio 25 en la Sección 2.3 para obtener asistencia si es necesario.) Redondee sus respuestas a dos decimales.
¿Qué valores de temperatura en grados Celsius son equivalentes al rango de temperatura$50^{\circ}F$ a$95^{\circ}F$? (Consulte el Ejercicio 35 en la Sección 2.1 para obtener asistencia si es necesario.)

En los Ejercicios 39-42, escribir y resolver una desigualdad que involucre valores absolutos para el enunciado dado.

Encuentra todos los números reales$x$ para que$x$ esté dentro de$4$ unidades de$2$.
Encuentra todos los números reales$x$ para que$3x$ esté dentro de$2$ unidades de$-1$.
Encuentra todos los números reales$x$ para que$x^2$ esté dentro de la$1$ unidad de$3$.
Encuentra todos los números reales$x$ para que$x^2$ esté al menos a$7$ unidades de distancia de$4$.
El área$S$ de superficie de un cubo con longitud de borde$x$ viene dada por$S(x) = 6x^{2}$ for$x > 0$. Supongamos que se supone que los cubos que fabrica su empresa tienen una superficie de exactamente 42 centímetros cuadrados, pero las máquinas que posee son viejas y no siempre pueden hacer un cubo con la superficie precisa deseada. Escribe una desigualdad usando valor absoluto que diga que el área de superficie de un cubo dado no está a más de 3 centímetros cuadrados de distancia (alto o bajo) del objetivo de 42 centímetros cuadrados. Resuelve la desigualdad y escribe tu respuesta usando notación de intervalos.
Supongamos que$f$ es una función,$L$ es un número real y$\varepsilon$ es un número positivo. Discuta con sus compañeros de clase qué$|f(x) - L| < \varepsilon$ significa la desigualdad algebraica y gráficamente. ⁶

En Ejercicios 45 - 50, bosquejar la gráfica de la relación.

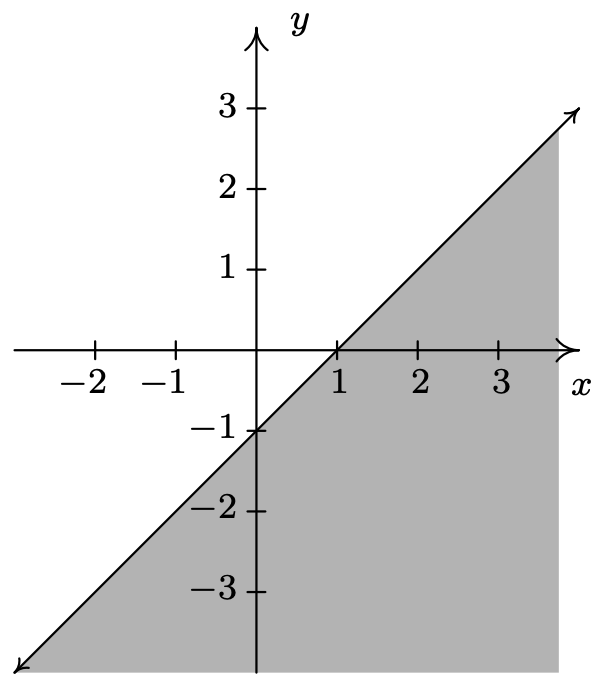
$R = \left\{ (x,y) : y \leq x-1 \right\}$
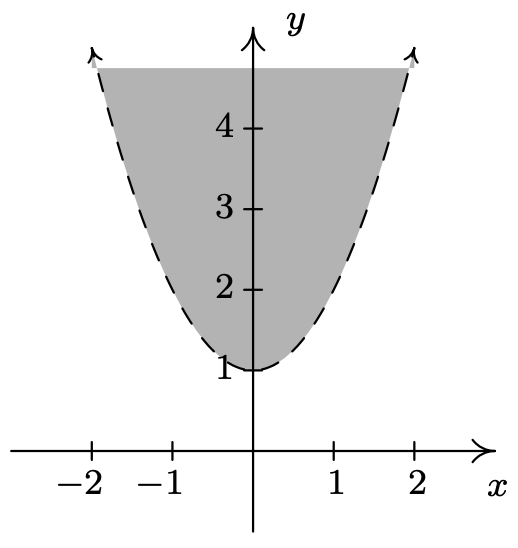
$R = \left\{ (x,y) : y > x^2 +1 \right\}$
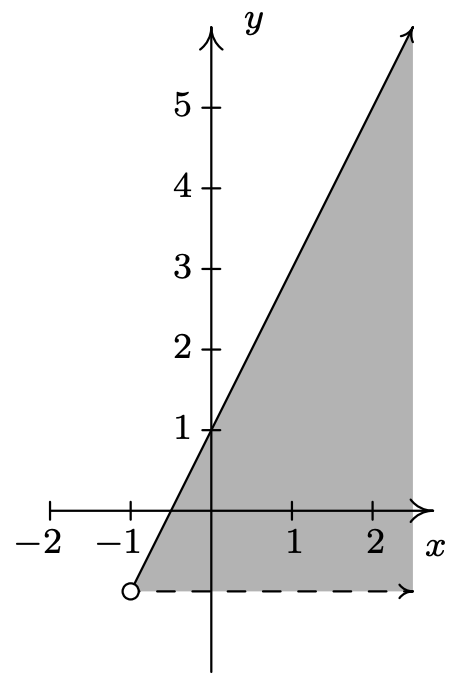
$R = \left\{ (x,y) : -1 < y \leq 2x + 1 \right\}$
$R = \left\{ (x,y) : x^2 \leq y < x+2 \right\}$
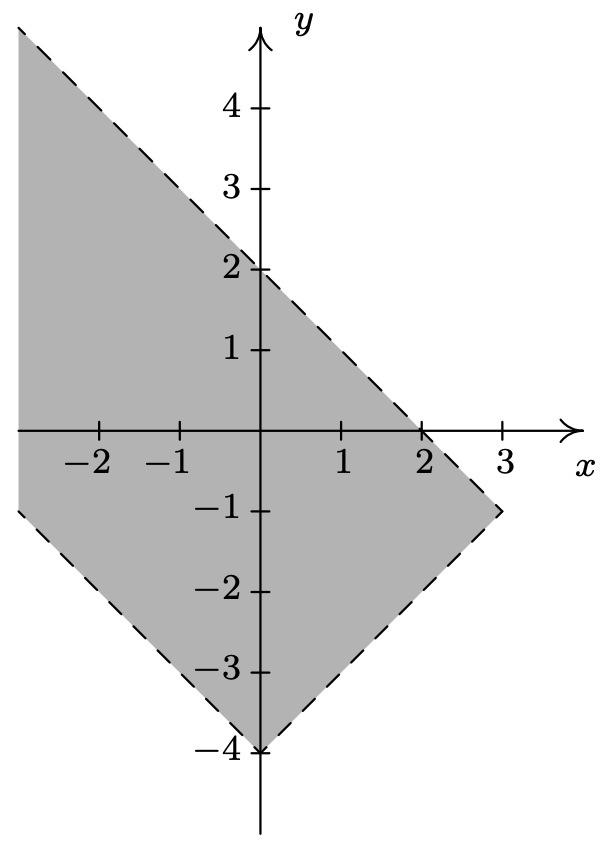
$R = \left\{ (x,y) : |x|-4 < y < 2-x \right\}$
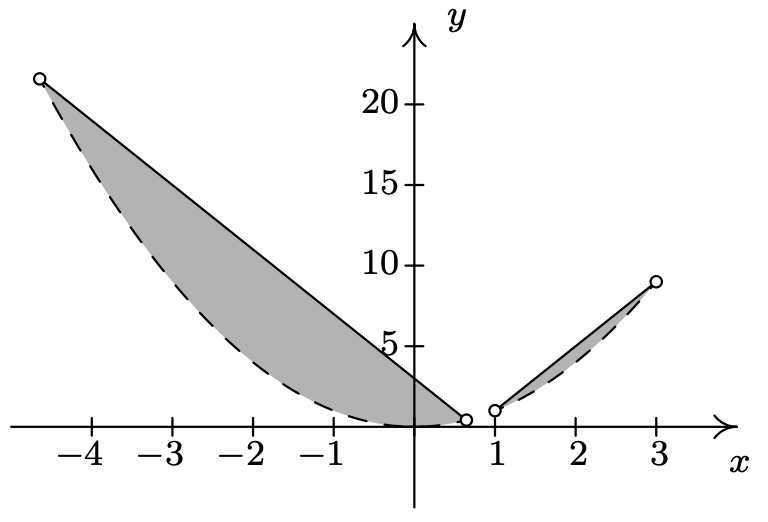
$R = \left\{ (x,y) : x^{2} < y \leq |4x - 3| \right\}$[sketchregionineqlast]
Demostrar la segunda, tercera y cuarta partes del Teorema 2.4.

2.4.2 Respuestas

$\left[\frac{1}{3}, 3\right]$
$\left(-\infty, -\frac{12}{7} \right) \cup \left(\frac{8}{7}, \infty\right)$
$(-3,2)$
$(-\infty,1] \cup [3,\infty)$
Sin solución
$(-\infty, \infty)$
$(-3,2] \cup [6,11)$
$[3, 4) \cup (5, 6]$
$\left[-\frac{12}{7}, -\frac{6}{5}\right]$
$(-\infty, -4) \cup \left( \frac{2}{3}, \infty\right)$
$\left(-\infty, -\frac{4}{3} \right] \cup [6, \infty)$
$(-\infty, -5)$
Sin Solución.
$\left[ -7, \frac{5}{3}\right]$
$\left( 1, \frac{5}{3} \right)$
$(-\infty, \infty)$
$(-\infty, -3] \cup [1, \infty)$
$\left(-\infty, -\frac{1}{4}\right) \cup \left(-\frac{1}{4}, \infty \right)$
Sin solución
$(-\infty, \infty)$
$\left\{2 \right\}$
Sin solución
$\left[-\frac{1}{3}, 4 \right]$
$(0, 1)$
$\left(-\infty, 1-\frac{\sqrt{6}}{2} \right) \cup \left(1+\frac{\sqrt{6}}{2}, \infty \right)$
$\left(-\infty, \frac{5 - \sqrt{73}}{6} \right] \cup \left[\frac{5 + \sqrt{73}}{6}, \infty \right)$
$\left(-3\sqrt{2}, -\sqrt{11} \right] \cup \left[-\sqrt{7}, 0 \right) \cup \left(0, \sqrt{7} \right] \cup \left[\sqrt{11}, 3\sqrt{2} \right)$
$\left[-2-\sqrt{7}, -2+\sqrt{7} \right] \cup [1, 3]$
$(-\infty, \infty)$
$(-\infty, -1] \cup \left\{ 0 \right\} \cup [1,\infty)$
$[-6,-3] \cup [-2, \infty)$
$(-\infty, 1) \cup \left(2, \frac{3+\sqrt{17}}{2}\right)$
$P(x) \geq 50$encendido$[10,15]$. Esto significa que en cualquier lugar entre 10 y 15 botellas de tónico deben venderse para obtener al menos$\$50$ ganancias.
$C(x) \leq 11$encendido$[2,8]$. Esto significa que se pueden producir entre 2000 y 8000 plumas y el costo no excederá$\$1100$.
$T(t) > 42$el$(8-2\sqrt{11}, 8+2\sqrt{11}) \approx (1.37, 14.63)$, que corresponde entre las 7:22 AM (1.37 horas después de las 6 AM) a las 8:38 PM (14.63 horas después de las 6 AM.) No obstante, dado que el modelo es válido solo para$t$,$0 \leq t \leq 12$, restringimos nuestra respuesta y encontramos que es más cálido que$42^{\circ}$ Fahrenheit de 7:22 AM a 6 PM.
$h(t) \geq 250$encendido$[10-5\sqrt{2}, 10+5\sqrt{2}] \approx [2.93, 17.07]$. Esto significa que el cohete se encuentra al menos a 250 pies del suelo entre 2.93 y 17.07 segundos después del despegue.
$s(t) = -4.9t^2 + 30t + 2$. $s(t) > 35$en (aproximadamente)$(1.44, 4.68)$. Esto significa que entre 1.44 y 4.68 segundos después de que se lanza al aire, el mármol está a más de 35 pies del suelo.
De nuestro trabajo anterior$C(F) = \frac{5}{9}(F - 32)$ así$50 \leq F \leq 95$ se vuelve$10 \leq C \leq 35$.
$|x-2| \leq 4$,$[-2,6]$
$|3x+1| \leq 2$,$\left[-1, \frac{1}{3}\right]$
$|x^2-3| \leq 1$,$[-2, -\sqrt{2} \,] \cup [\sqrt{2}, 2]$
$|x^2 -4| \geq 7$,$(-\infty, -\sqrt{11} \,] \cup [\sqrt{11}, \infty)$
Resolver$|S(x) - 42| \leq 3$ y desatender las soluciones negativas rinde$\left[\sqrt{\frac{13}{2}}, \sqrt{\frac{15}{2}}\right] \approx [2.550, 2.739]$. La longitud del borde debe estar dentro$2.550$ y$2.739$ centímetros.

$~$
$Screen Shot 2022-03-27 a las 6.54.57 PM.png$
$~$
$Screen Shot 2022-03-27 a las 6.56.42 PM.png$
$~$
$Screen Shot 2022-03-27 a las 6.59.06 PM.png$
$~$
$Screen Shot 2022-03-27 a las 7.00.05 PM.png$
$~$
$Screen Shot 2022-03-27 a las 7.00.42 PM.png$
$~$
$Screen Shot 2022-03-27 en 7.02.26 PM.png$

Referencia

¹ Véase Definición 1.2 en la Sección 1.1.1.

² Le daremos un nombre a esta propiedad en el Capítulo 3 y luego volveremos a visitar este concepto.

³ Tenemos que elegir algo en cada intervalo. Si no le gustan nuestras opciones, no dude en elegir diferentes números. Obtendrás el mismo gráfico de señales.

⁴ En este caso, decimos que la línea$\ y=2 x$ es tangente a$\ y=x^{2}+1$ at (1, 2). Encontrar líneas tangentes a funciones arbitrarias es un problema fundamental resuelto, en general, con Cálculo.

⁵ El concepto subyacente de Cálculo puede formularse en términos de tolerancias, por lo que bien merece su atención

⁶ Entender este tipo de desigualdad es realmente importante en Cálculo.