4.1: Introducción a las funciones racionales

Última actualización
Guardar como PDF

Page ID: 119515

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

Si sumamos, restamos o multiplicamos funciones polinómicas de acuerdo con las reglas aritméticas de función definidas en la Sección 1.5, produciremos otra función polinómica. Si, por otro lado, dividimos dos funciones polinómicas, el resultado puede no ser un polinomio. En este capítulo estudiamos las funciones racionales - funciones que son proporciones de polinomios.

Definición 4.1.

Una función racional es una función que es la relación de funciones polinómicas. Dicho de otra manera,$r$ es una función racional si es de la forma

$r(x) = \dfrac{p(x)}{q(x)},$

donde$p$ y$q$ son funciones polinomiales. ^a

^a De acuerdo con esta definición, todas las funciones polinómicas son también funciones racionales. (Tomar$q(x) = 1)$.

Como recordamos de la Sección 1.4, tenemos problemas de dominio cada vez que el denominador de una fracción es cero. En el siguiente ejemplo, revisamos este concepto así como algunas de las aritméticas de expresiones racionales.

Ejemplo 4.1.1

Encuentra el dominio de las siguientes funciones racionales. Escríbelos en la forma$\frac{p(x)}{q(x)}$ para funciones polinómicas$p$ y$q$ y simplifique.

$f(x) = \dfrac{2x-1}{x+1}$
$g(x) = 2 - \dfrac{3}{x+1}$
$h(x) = \dfrac{2x^2-1}{x^2-1} - \dfrac{3x-2}{x^2-1}$
$r(x) = \dfrac{2x^2-1}{x^2-1} \div \dfrac{3x-2}{x^2-1}$

Solución

Para encontrar el dominio de$f$, procedemos como hicimos en la Sección 1.4: encontramos los ceros del denominador y los excluimos del dominio. Establecer$x+1=0$ resultados en$x=-1$. De ahí que nuestro dominio sea$(-\infty, -1) \cup (-1,\infty)$. La expresión ya$f(x)$ está en la forma solicitada y cuando comprobamos factores comunes entre el numerador y denominador no encontramos ninguno, entonces ya terminamos.
Procediendo como antes, determinamos el dominio de$g$ resolviendo$x+1=0$. Como antes, encontramos el dominio de$g$ es$(-\infty, -1) \cup (-1,\infty)$. Para escribir$g(x)$ en el formulario solicitado, necesitamos obtener un denominador común
$\begin{array}{rclclcl} g(x) & = & 2 - \dfrac{3}{x+1} & = & \dfrac{2}{1} - \dfrac{3}{x+1} & = & \dfrac{(2)(x+1)}{(1)(x+1)} - \dfrac{3}{x+1} \\ [.15in] & = & \dfrac{(2x+2) - 3}{x+1} & = & \dfrac{2x-1}{x+1} & & \\ \end{array}$

Esta fórmula ahora está completamente simplificada.
Los denominadores en la fórmula para$h(x)$ son ambos$x^2-1$ cuyos ceros son$x = \pm 1$. En consecuencia, el dominio de$h$ es$(-\infty, -1) \cup (-1,1) \cup (1, \infty)$. Ahora procedemos a simplificar$h(x)$. Como tenemos el mismo denominador en ambos términos, restamos los numeradores. Luego factorizamos el numerador y denominador resultantes, y cancelamos el factor común.
$\begin{array}{rclcl} h(x) & = & \dfrac{2x^2-1}{x^2-1} - \dfrac{3x-2}{x^2-1} & = & \dfrac{\left(2x^2-1\right) - \left(3x-2\right)}{x^2-1} \\ [.15in] & = & \dfrac{2x^2-1 - 3x+2}{x^2-1} & = & \dfrac{2x^2 - 3x+1}{x^2-1} \\ [.15in] & = & \dfrac{(2x-1)(x-1)}{(x+1)(x-1)} & = & \dfrac{(2x-1)\cancel{(x-1)}}{(x+1)\cancel{(x-1)}} \\ [.15in] & = & \dfrac{2x-1}{x+1} & & \\ \end{array}$
Para encontrar el dominio de$r$, puede ayudar a reescribir temporalmente$r(x)$ como
$r(x) = \dfrac{\dfrac{2x^2-1}{x^2-1} }{\dfrac{3x-2}{x^2-1}\vphantom{\left(\dfrac{X}{X}\right)}}$

Tenemos que poner a todos los denominadores iguales a cero lo que significa que tenemos que resolver no sólo$x^2-1= 0$, sino también$\frac{3x-2}{x^2-1}=0$. Encontramos$x = \pm 1$ para el primero y$x= \frac{2}{3}$ para el segundo. Nuestro dominio es$(-\infty, -1) \cup \left(-1,\frac{2}{3}\right) \cup \left(\frac{2}{3},1\right) \cup (1, \infty)$. Simplificamos$r(x)$ reescribiendo la división como multiplicación por lo recíproco y luego cancelando el factor común

$\begin{array}{rclclcl} r(x) & = & \dfrac{2x^2-1}{x^2-1} \div \dfrac{3x-2}{x^2-1} & = & \dfrac{2x^2-1}{x^2-1} \cdot \dfrac{x^2-1}{3x-2} & = & \dfrac{\left(2x^2-1\right)\left(x^2-1\right)}{\left(x^2-1\right)(3x-2)} \\ [.15in] & = & \dfrac{\left(2x^2-1\right)\cancel{\left(x^2-1\right)}}{\cancel{\left(x^2-1\right)}(3x-2)} & = & \dfrac{2x^2-1}{3x-2} & & \\ \end{array}$

Algunos comentarios sobre el Ejemplo 4.1.1 están en orden. Tenga en cuenta que las expresiones para$f(x)$,$g(x)$ y$h(x)$ funcionan para ser las mismas. Sin embargo, sólo dos de estas funciones son realmente iguales. Recordemos que las funciones son en última instancia conjuntos de pares ordenados, ¹ así que para que dos funciones sean iguales, necesitan, entre otras cosas, tener el mismo dominio. Desde$f(x) = g(x)$ y$f$ y$g$ tienen el mismo dominio, son funciones iguales. A pesar de que la fórmula$h(x)$ es la misma que$f(x)$, el dominio de$h$ es diferente al dominio de$f$, y por lo tanto son funciones diferentes.

Ahora volvemos nuestra atención a las gráficas de las funciones racionales. Considere la función$f(x) = \frac{2x-1}{x+1}$ del Ejemplo 4.1.1. Usando una calculadora gráfica, obtenemos

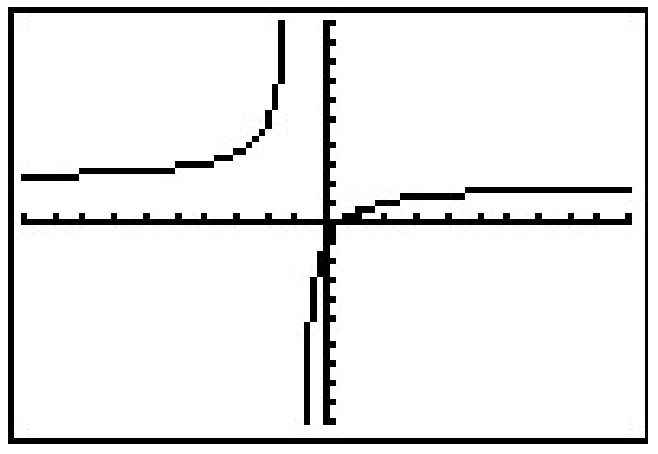
$Screen Shot 2022-03-31 en 3.11.43 PM.png$

Dos comportamientos de la gráfica son dignos de mayor discusión. Primero, tenga en cuenta que la gráfica parece 'romperse' en$x=-1$. Sabemos por nuestro último ejemplo que no$x=-1$ está en el dominio de$f$ qué medio$f(-1)$ está indefinido. Cuando hacemos una tabla de valores para estudiar el comportamiento de$f$ cerca$x=-1$ vemos que podemos llegar 'cerca'$x=-1$ desde dos direcciones. Podemos elegir valores un poco menos que$-1$, por ejemplo$x=-1.1$,$x=-1.01$,$x=-1.001$, y así sucesivamente. Se dice que estos valores 'se acercan$-1$ desde la izquierda'. De igual manera, se dice que los valores$x=-0.9$$x=-0.99$$x=-0.999$,,, etc., 'se acercan$-1$ desde la derecha'. Si hacemos dos tablas, encontramos que los resultados numéricos confirman lo que vemos gráficamente.

$\begin{array}{|r||c|c|} \hline x & f(x) & (x,f(x)) \\ \hline -1.1 & 32 & (-1.1, 32) \\ \hline -1.01 & 302 & (-1.01, 302) \\ \hline -1.001 & 3002 & ( -1.001, 3002) \\ \hline -1.0001 & 30002 & ( -1.001, 30002) \\ \hline \end{array}$

$\begin{array}{|r||c|c|} \hline x & f(x) & (x,f(x)) \\ \hline -0.9 & -28 & ( -0.9 , -28) \\ \hline -0.99 & -298 & ( -0.99, -298) \\ \hline -0.999 & -2998& (-0.999,-2998) \\ \hline -0.9999 & -29998& (-0.9999,-29998) \\ \hline \end{array}$

A medida que los$x$ valores se acercan$-1$ desde la izquierda, los valores de las funciones se convierten en números positivos cada vez mayores. ² Esto lo expresamos simbólicamente declarando como$x \rightarrow -1^{-}$,$f(x) \rightarrow \infty$. Del mismo modo, utilizando notación análoga, concluimos de la tabla que como$x \rightarrow -1^{+}$,$f(x) \rightarrow -\infty$. Para este tipo de comportamiento ilimitado, decimos que la gráfica de$y=f(x)$ tiene una asíntota vertical de$x = -1$. En términos generales, esto significa que cerca$x=-1$, la gráfica se parece mucho a la línea vertical$x=-1$.

La otra característica digna de mención sobre la gráfica de$y=f(x)$ es que parece 'nivelar' en los lados izquierdo y derecho de la pantalla. Esta es una declaración sobre el comportamiento final de la función. Como se discutió en la Sección 3.1, el comportamiento final de una función es su comportamiento ya que$x$ alcanza valores negativos mayores de ³ y mayores sin límite$x \rightarrow -\infty$, y como$x$ se vuelve grande sin límite,$x \rightarrow \infty$. Haciendo tablas de valores, encontramos

$\begin{array}{|r||c|c|} \hline x & f(x) & (x,f(x)) \\ \hline -10 & \approx 2.3333 & \approx (-10, 2.3333) \\ \hline -100 & \approx 2.0303 & \approx (-100, 2.0303) \\ \hline -1000 & \approx 2.0030 & \approx ( -1000, 2.0030) \\ \hline -10000 & \approx 2.0003 & \approx ( -10000, 2.0003) \\ \hline \end{array}$

$\begin{array}{|r||c|c|} \hline x & f(x) & (x,f(x)) \\ \hline 10 & \approx 1.7273 & \approx (10, 1.7273) \\ \hline 100 & \approx 1.9703 & \approx (100, 1.9703) \\ \hline 1000 & \approx 1.9970 & \approx ( 1000, 1.9970) \\ \hline 10000 & \approx 1.9997 & \approx ( 10000, 1.9997) \\ \hline \end{array}$

De las mesas, vemos eso como$x \rightarrow -\infty$,$f(x) \rightarrow 2^{+}$ y como$x \rightarrow \infty$,$f(x) \rightarrow 2^{-}$. Aquí el '$+$' significa 'desde arriba' y el '$-$' significa 'desde abajo'. En este caso, decimos que la gráfica de$y=f(x)$ tiene una asíntota horizontal de$y=2$. Esto significa que el comportamiento final de$f$ se asemeja a la línea horizontal$y=2$, lo que explica el comportamiento de 'nivelación' que vemos en la gráfica de la calculadora. Formalizamos los conceptos de asíntotas verticales y horizontales en las siguientes definiciones.

Definición 4.2.

La línea$x=c$ se denomina asíntota vertical de la gráfica de una función$y=f(x)$ si como$x \rightarrow c^{-}$ o como$x \rightarrow c^{+}$, ya sea$f(x) \rightarrow \infty$ o$f(x) \rightarrow -\infty$.

Definición 4.3.

La línea$y=c$ se denomina asíntota horizontal de la gráfica de una función$y=f(x)$ si como$x \rightarrow -\infty$ o como$x \rightarrow \infty$,$f(x) \rightarrow c$.

Tenga en cuenta que en la Definición 4.3, escribimos$f(x) \rightarrow c$ (no$f(x) \rightarrow c^{+}$ o$f(x) \rightarrow c^{-}$) porque no nos preocupa desde qué dirección los valores se$f(x)$ acercan al valor$c$, siempre y cuando lo hagan. ⁴

En nuestra discusión siguiente Ejemplo 4.1.1, determinamos que, a pesar de que la fórmula para$h(x)$ reducir a la misma fórmula que$f(x)$, las funciones$f$ y$h$ son diferentes, ya que$x=1$ está en el dominio de$f$, pero no$x=1$ está en el dominio de$h$. Si graficamos$h(x)=\frac{2x^2-1}{x^2-1} - \frac{3x-2}{x^2-1}$ usando una calculadora gráfica, nos sorprende encontrar que la gráfica se ve idéntica a la gráfica de$y=f(x)$. Hay una asíntota vertical en$x=-1$, pero cerca$x=1$, todo parece estar bien. Las tablas de valores proporcionan evidencia numérica que sustenta la observación gráfica.

$\begin{array}{|r||c|c|} \hline x & h(x) & (x,h(x)) \\ \hline 0.9 & \approx 0.4210 & \approx (0.9, 0.4210) \\ \hline 0.99 & \approx 0.4925 & \approx (0.99, 0.4925) \\ \hline 0.999 & \approx 0.4992 & \approx (0.999, 0.4992) \\ \hline 0.9999 & \approx 0.4999 & \approx (0.9999, 0.4999) \\ \hline \end{array}$

$\begin{array}{|r||c|c|} \hline x & h(x) & (x,h(x)) \\ \hline 1.1 & \approx 0.5714 & \approx (1.1, 0.5714) \\ \hline 1.01 & \approx 0.5075 & \approx (1.01, 0.5075) \\ \hline 1.001 & \approx 0.5007 & \approx (1.001, 0.5007) \\ \hline 1.0001 & \approx 0.5001 & \approx (1.0001, 0.5001) \\ \hline \end{array}$

Eso lo vemos como$x \rightarrow 1^{-}$,$h(x) \rightarrow 0.5^{-}$ y como$x \rightarrow 1^{+}$,$h(x) \rightarrow 0.5^{+}$. Es decir, los puntos en la gráfica de$y=h(x)$ se acercan$(1,0.5)$, pero como no$x=1$ está en el dominio de$h$, sería inexacto rellenar un punto en$(1,0.5)$. Como hemos hecho en secciones pasadas cuando ocurre algo así, ⁵ ponemos un círculo abierto (también llamado agujero en este caso ⁶) en$(1,0.5)$. A continuación se muestra una gráfica detallada de$y=h(x)$, con las asíntotas verticales y horizontales como líneas discontinuas.

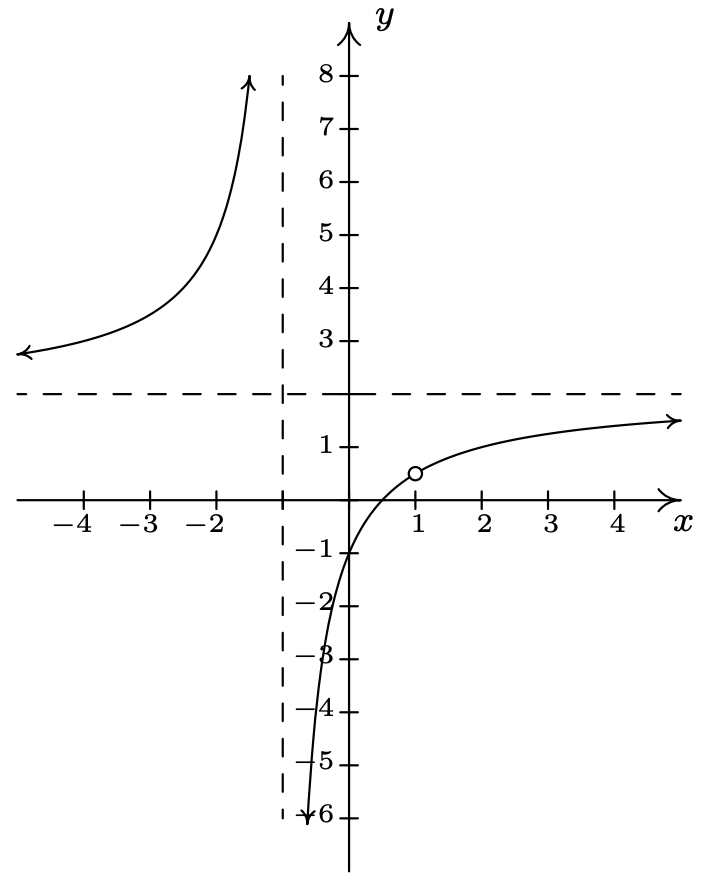
$Screen Shot 2022-03-31 en 3.31.31 PM.png$

Ni$x=-1$ tampoco$x=1$ están en el dominio de$h$, sin embargo el comportamiento de la gráfica de$y=h(x)$ es drásticamente diferente cerca de estos$x$ -valores. El motivo de esto radica en el segundo al último paso cuando simplificamos la fórmula para$h(x)$ en el Ejemplo 4.1.1, donde tuvimos$h(x) = \frac{(2x-1)(x-1)}{(x+1)(x-1)}$. La razón no$x=-1$ está en el dominio de$h$ es porque el factor$(x+1)$ aparece en el denominador de$h(x)$; de igual manera, no$x=1$ está en el dominio de$h$ por el factor$(x-1)$ en el denominador de$h(x)$. La mayor diferencia entre estos dos factores es que se$(x-1)$ cancela con un factor en el numerador mientras que$(x+1)$ no. Hablando en voz baja, el problema causado por$(x-1)$ en el denominador se cancela mientras el factor$(x+1)$ queda por causar travesuras. Es por ello que la gráfica de$y=h(x)$ tiene una asíntota vertical en$x=-1$ pero sólo un agujero en$x=1$. Estas observaciones son generalizadas y resumidas en el teorema a continuación, cuya prueba se encuentra en Cálculo.

Teorema 4.1. Ubicación de asíntotas verticales y agujeros

^a Supongamos$r$ es una función racional que puede escribirse como$r(x) = \frac{p(x)}{q(x)}$ donde$p$ y no$q$ tener ceros comunes. ^b$c$ Sea un número real que no esté en el dominio de$r$.

Si$q(c) \neq 0$, entonces la gráfica de$y=r(x)$ tiene un agujero en$\left(c, \frac{p(c)}{q(c)}\right)$.
Si$q(c) = 0$, entonces la línea$x=c$ es una asíntota vertical de la gráfica de$y=r(x)$.

^a O, 'Cómo distinguir tu asíntota desde un agujero en la gráfica. '

^b En otras palabras,$r(x)$ está en términos más bajos.

En inglés, el Teorema 4.1 dice que si no$x=c$ está en el dominio de$r$ sino, cuando simplificamos$r(x)$, ya no hace el denominador$0$, entonces tenemos un agujero en$x=c$. De lo contrario, la línea$x=c$ es una asíntota vertical de la gráfica de$y=r(x)$.

Ejemplo 4.1.2

Encuentra las asíntotas verticales de, y/o agujeros en, las gráficas de las siguientes funciones racionales. Verifica tus respuestas usando una calculadora gráfica y describe el comportamiento de la gráfica cerca de ellas usando la notación adecuada.

$f(x) = \dfrac{2x}{x^2-3}$
$g(x) = \dfrac{x^2-x-6}{x^2-9}$
$h(x) = \dfrac{x^2-x-6}{x^2+9}$
$r(x) = \dfrac{x^2-x-6}{x^2+4x+4}$

Solución

Para usar el Teorema 4.1, primero encontramos todos los números reales que no están en el dominio de$f$. Para ello, resolvemos$x^2 - 3 = 0$ y obtenemos$x = \pm \sqrt{3}$. Dado que la expresión$f(x)$ está en términos más bajos, no hay cancelación posible, y concluimos que las líneas$x = -\sqrt{3}$ y$x=\sqrt{3}$ son asíntotas verticales a la gráfica de$y=f(x)$. El calculador verifica esta afirmación, y a partir de la gráfica, vemos que como$x \rightarrow -\sqrt{3}^{\, -}$$f(x) \rightarrow -\infty$,$x\rightarrow -\sqrt{3}^{\, +}$, como$f(x) \rightarrow \infty$, como$x \rightarrow \sqrt{3}^{\, -}$$f(x) \rightarrow -\infty$, y finalmente como$x\rightarrow \sqrt{3}^{\, +}$,$f(x) \rightarrow \infty$.
Resolver$x^2 - 9 = 0$ da$x = \pm 3$. En términos más bajos$g(x) = \frac{x^2-x-6}{x^2-9} = \frac{(x-3)(x+2)}{(x-3)(x+3)} = \frac{x+2}{x+3}$. Ya que$x=-3$ sigue causando problemas en el denominador, sabemos que la línea$x=-3$ es una asíntota vertical de la gráfica de$y=g(x)$. Como ya$x=3$ no produce una$0$ en el denominador, tenemos un agujero en$x=3$. Para encontrar la$y$ coordenada -del agujero, sustituimos$x=3$ en$\frac{x+2}{x+3}$ y encontramos que el agujero está en$\left(3, \frac{5}{6}\right)$. Cuando graficamos$y=g(x)$ usando una calculadora, vemos claramente la asíntota vertical en$x=-3$, pero todo parece tranquilo cerca$x=3$. De ahí$x \rightarrow -3^{-}$, como$g(x) \rightarrow \infty$, como$x \rightarrow -3^{+}$$g(x) \rightarrow -\infty$, como$x \rightarrow 3^{-}$, como$g(x) \rightarrow \frac{5}{6}^{-}$, y como$x \rightarrow 3^{+}$,$g(x) \rightarrow \frac{5}{6}^{+}$.
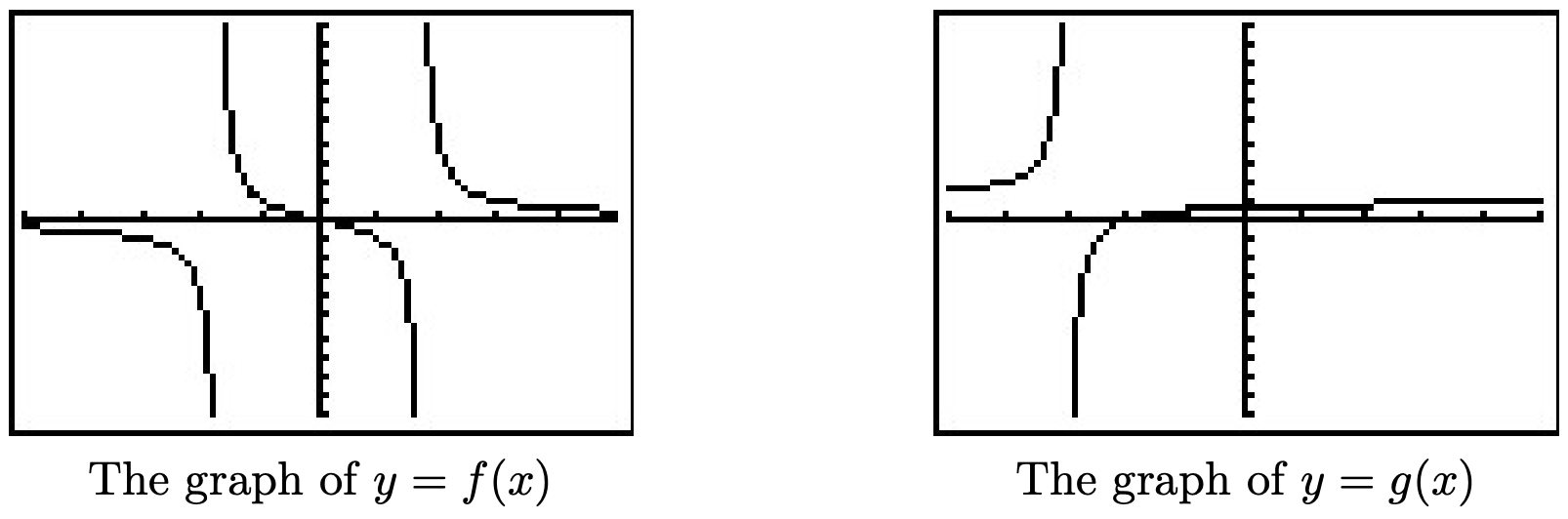
$Screen Shot 2022-03-31 en 3.51.09 PM.png$
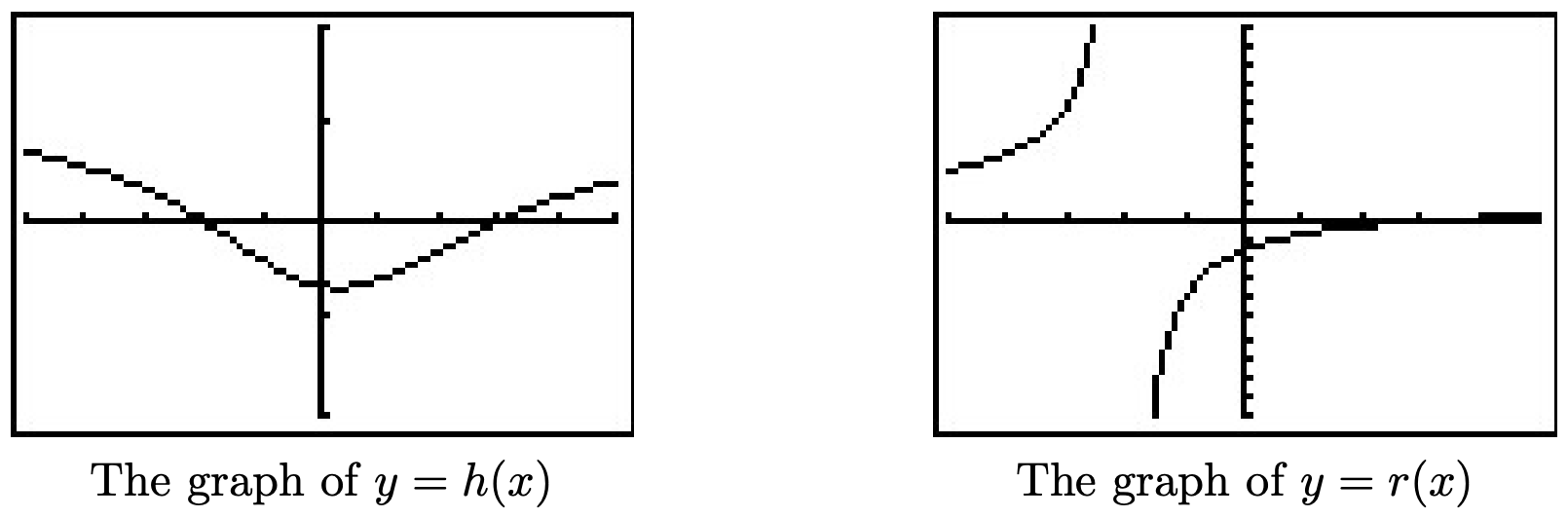
El dominio de$h$ es todo números reales, ya que no$x^2+9 = 0$ tiene soluciones reales. En consecuencia, la gráfica de$y=h(x)$ está desprovista tanto de asíntotas verticales como de agujeros.
El ajuste nos$x^2+4x+4 = 0$ da$x=-2$ como el único número real de preocupación. Simplificando, vemos$r(x) = \frac{x^2-x-6}{x^2+4x+4} = \frac{(x-3)(x+2)}{(x+2)^2} = \frac{x-3}{x+2}$. Dado que$x=-2$ continúa produciendo una$0$ en el denominador de la función reducida, sabemos que$x=-2$ es una asíntota vertical a la gráfica. La calculadora lo confirma, y, además, lo vemos como$x\rightarrow -2^{-}$,$r(x) \rightarrow \infty$ y como$x \rightarrow -2^{+}$,$r(x) \rightarrow -\infty$.
$Screen Shot 2022-03-31 en 3.53.12 PM.png$

Nuestro siguiente ejemplo nos da una interpretación física de una asíntota vertical. Este tipo de modelo surge de una familia de ecuaciones llamadas alegremente ecuaciones de 'fin del mundo'. ⁷

Ejemplo 4.1.3

Un modelo matemático para la población$P$, en miles, de una determinada especie de bacteria,$t$ días después de su introducción a un ambiente es dado por$P(t) = \frac{100}{(5-t)^{2}}$,$0 \leq t < 5$.

Encontrar e interpretar$P(0)$.
¿Cuándo llegará la población$100,\!000$?
Determinar el comportamiento de$P$ as$t \rightarrow 5^{-}$. Interpretar este resultado gráficamente y dentro del contexto del problema.

Solución

Sustituir$t=0$ da$P(0) = \frac{100}{(5-0)^2} = 4$, lo que significa que$4000$ las bacterias se introducen inicialmente en el ambiente.
Para encontrar cuándo llega la población$100,\! 000$, primero hay que recordar que$P(t)$ se mide en miles. En otras palabras,$100,\! 000$ las bacterias corresponden a$P(t) = 100$. Sustituir por$P(t)$ da la ecuación$\frac{100}{(5-t)^2} = 100$. Despejando denominadores y dividiendo por$100$ da$(5-t)^2=1$, que, después de extraer raíces cuadradas, produce$t = 4$ o$t=6$. De estas dos soluciones, sólo$t=4$ en nuestro dominio, por lo que esta es la solución que guardamos. De ahí que la población de bacterias tarden$4$ días en llegar$100,\! 000$.
Para determinar el comportamiento de$P$ as$t \rightarrow 5^{-}$, podemos hacer una tabla
$\begin{array}{|r||c|} \hline t & P(t) \\ \hline 4.9 & 10000 \\ \hline 4.99 & 1000000 \\ \hline 4.999 & 100000000 \\ \hline 4.9999 & 10000000000 \\ \hline \end{array}$

En otras palabras, como$t \rightarrow 5^{-}$,$P(t) \rightarrow \infty$. Gráficamente, la línea$t=5$ es una asíntota vertical de la gráfica de$y=P(t)$. Físicamente, esto significa que la población de bacterias está aumentando sin ataduras ya que nos acercamos a los 5 días, lo que en realidad no puede suceder. Por ello,$t=5$ se llama el 'día del juicio final' para esta población. No hay forma de que cualquier ambiente pueda soportar infinitamente muchas bacterias, así que poco antes$t = 5$ el ambiente colapsaría.

Ahora que hemos investigado a fondo las asíntotas verticales, podemos dirigir nuestra atención hacia las asíntotas horizontales. El siguiente teorema nos dice cuándo esperar asíntotas horizontales.

Teorema 4.2. Ubicación de asíntotas horizontales

Supongamos que$r$ es una función racional$p$ y$r(x) = \frac{p(x)}{q(x)}$, donde y$q$ son funciones polinómicas con coeficientes iniciales$a$ y$b$, respectivamente.

^{Si el grado de$p(x)$ es el mismo que el grado de$q(x)$, entonces$y=\frac{a}{b}$ es la asíntota horizontal de la gráfica de$y=r(x)$.}
Si el grado de$p(x)$ es menor que el grado de$q(x)$, entonces$y=0$ es la asíntota horizontal de la gráfica de$y=r(x)$.
Si el grado de$p(x)$ es mayor que el grado de$q(x)$, entonces la gráfica de no$y=r(x)$ tiene asíntotas horizontales.

^a El uso del artículo definido se justificará momentáneamente.

Al igual que el Teorema 4.1 , el Teorema 4.2 se prueba usando Cálculo. Sin embargo, podemos entender la idea detrás de esto usando nuestro ejemplo$f(x) = \frac{2x-1}{x+1}$. Si interpretamos$f(x)$ como un problema de división$(2x-1) \div (x+1)$,, encontramos que el cociente es$2$ con un resto de$-3$. Usando lo que sabemos sobre la división polinómica, específicamente el Teorema 3.4, obtenemos$2x-1 = 2(x+1) -3$. Dividiendo ambos lados por$(x+1)$ da$\frac{2x-1}{x+1} = 2 - \frac{3}{x+1}$. (Tal vez recuerdes esto como la fórmula para$g(x)$ en el Ejemplo 4.1.1.) A medida que$x$ queda sin límites en cualquier dirección, la cantidad$\frac{3}{x+1}$ se acerca cada vez más para$0$ que los valores de cada vez$f(x)$ se acerquen más a ⁸ a$2$. En símbolos, como$x \rightarrow \pm \infty$,$f(x) \rightarrow 2$, y tenemos el resultado. ⁹ Observe que la gráfica se acerca al mismo$y$ valor que$x \rightarrow -\infty$ o$x \rightarrow \infty$. Esto quiere decir que la gráfica sólo puede tener asíntota horizontal si va a tener una. Así fuimos justificados en el uso de 'la' en el teorema anterior.

Alternativamente, podemos usar lo que sabemos sobre el comportamiento final de los polinomios para ayudarnos a entender este teorema. A partir del Teorema 3.2, sabemos que el comportamiento final de un polinomio está determinado por su término principal. Aplicando esto al numerador y denominador de$f(x)$, obtenemos eso como$x \rightarrow \pm \infty$,$f(x) = \frac{2x-1}{x+1} \approx \frac{2x}{x} = 2$. Este último enfoque es útil en Cálculo, y, de hecho, se hace riguroso allí. (Tenga esto en cuenta para lo que resta de este párrafo.) Aplicando este razonamiento al caso general, supongamos$r(x) = \frac{p(x)}{q(x)}$ dónde$a$ está el coeficiente principal de$p(x)$ y$b$ es el coeficiente principal de$q(x)$. Como$x \rightarrow \pm \infty$,$r(x) \approx \frac{ax^n}{bx^m}$, donde$n$ y$m$ son los grados de$p(x)$ y$q(x)$, respectivamente. Si el grado de$p(x)$ y el grado de$q(x)$ son los mismos, entonces entonces eso$r(x) \approx \frac{a}{b}$,$n=m$ lo que significa$y=\frac{a}{b}$ es la asíntota horizontal en este caso. Si el grado de$p(x)$ es menor que el grado de$q(x)$, entonces$n < m$, también lo$m-n$ es un número positivo, y por lo tanto,$r(x) \approx \frac{a}{bx^{m-n}} \rightarrow 0$ como$x \rightarrow \pm \infty$. Si el grado de$p(x)$ es mayor que el grado de$q(x)$, entonces$n > m$, y por lo tanto$n-m$ es un número positivo y$r(x) \approx \frac{ax^{n-m}}{ b}$, que se vuelve ilimitado como$x \rightarrow \pm \infty$. Como dijimos antes, si una función racional tiene una asíntota horizontal, entonces sólo tendrá una. (Esto no es cierto para otros tipos de funciones que veremos en capítulos posteriores.)

Ejemplo 4.1.4

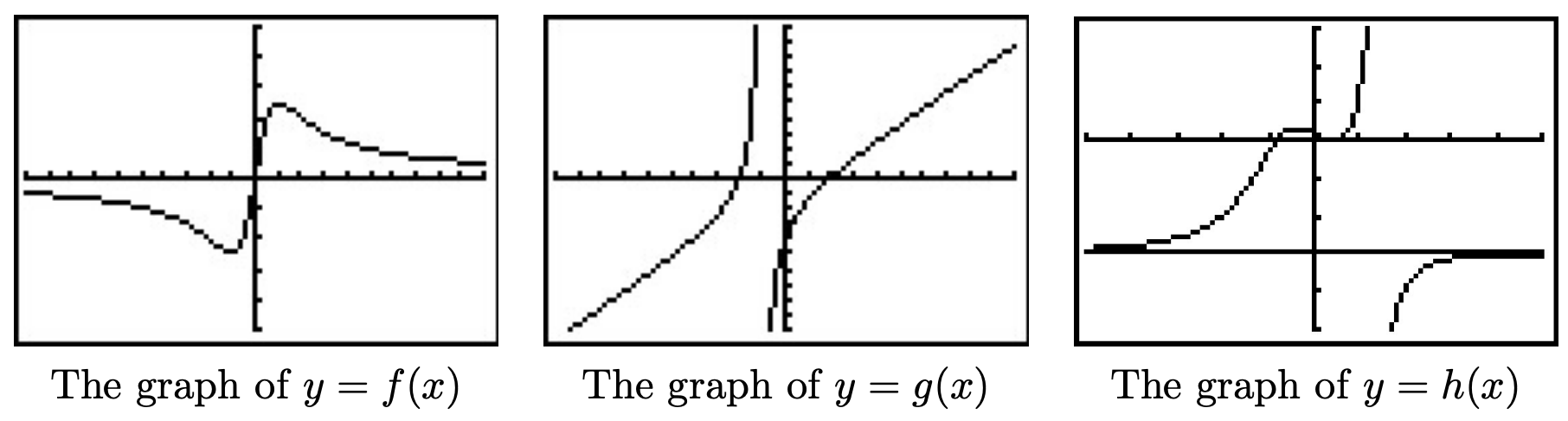
Enumerar las asíntotas horizontales, en su caso, de las gráficas de las siguientes funciones. Verifica tus respuestas usando una calculadora gráfica y describe el comportamiento de la gráfica cerca de ellas usando la notación adecuada.

$f(x) = \dfrac{5x}{x^2+1}$
$g(x) = \dfrac{x^2-4}{x+1}$
$h(x) = \dfrac{6x^3-3x+1}{5-2x^3}$

Solución.

El numerador de$f(x)$ es$5x$, que tiene grado$1$. El denominador de$f(x)$ es$x^2+1$, que tiene grado$2$. Aplicando el Teorema 4.2,$y=0$ es la asíntota horizontal. Efectivamente, vemos por la gráfica que como$x \rightarrow - \infty$,$f(x) \rightarrow 0^{-}$ y como$x \rightarrow \infty$,$f(x) \rightarrow 0^{+}$.
El numerador de$g(x)$,$x^2-4$, tiene grado$2$, pero el grado del denominador,$x+1$, tiene grado$1$. Por Teorema 4.2, no hay asíntota horizontal. De la gráfica, vemos que la gráfica de$y=g(x)$ no parece nivelarse a un valor constante, por lo que no hay asíntota horizontal. ¹⁰
Los grados del numerador y denominador de$h(x)$ son ambos tres, así que el Teorema 4.2 nos dice que$y = \frac{6}{-2} = -3$ es la asíntota horizontal. Vemos por la gráfica de la calculadora que como$x \rightarrow -\infty$,$h(x) \rightarrow -3^{+}$, y como$x \rightarrow \infty$,$h(x) \rightarrow -3^{-}$.

$Screen Shot 2022-03-31 en 4.57.56 PM.png$

Nuestro siguiente ejemplo de la sección nos da una aplicación real de una asíntota horizontal. ¹¹

Ejemplo 4.1.5

El número de estudiantes$N$ en la universidad local que han tenido la gripe$t$ meses después de que comience el semestre puede ser modelado por la fórmula$N(t) = 500 - \frac{450}{1+3t}$ para$t \geq 0$.

Encontrar e interpretar$N(0)$.
¿Cuánto tiempo pasará hasta que$300$ los estudiantes hayan tenido la gripe?
Determinar el comportamiento de$N$ as$t \rightarrow \infty$. Interpretar este resultado gráficamente y dentro del contexto del problema.

Solución

$N(0) = 500 - \frac{450}{1+3(0)} = 50$. Esto quiere decir que al inicio del semestre,$50$ los alumnos han tenido la gripe.
Nos pusimos$N(t) = 300$ a conseguir$500 - \frac{450}{1+3t} = 300$ y resolver. Aislar la fracción da$\frac{450}{1+3t} = 200$. Los denominadores de compensación da$450 = 200(1+3t)$. Por último, conseguimos$t = \frac{5}{12}$. Esto significa que tardarán$\frac{5}{12}$ meses, o alrededor de 13 días, para que$300$ los estudiantes hayan tenido la gripe.
Para determinar el comportamiento de$N$ as$t\rightarrow \infty$, podemos usar una tabla.
$\begin{array}{|r||c|} \hline t & N(t) \\ \hline 10 & \approx 485.48 \\ \hline 100& \approx 498.50 \\ \hline 1000 & \approx 499.85 \\ \hline 10000 & \approx 499.98 \\ \hline \end{array}$

La tabla sugiere que como$t \rightarrow \infty$,$N(t) \rightarrow 500$. (Más específicamente,$500^{-}$.) Esto significa que con el paso del tiempo, solo un total de 500 estudiantes habrán tenido alguna vez la gripe.

Cerramos esta sección con una discusión de la tercera (¡y final!) tipo de asíntota que puede asociarse con las gráficas de funciones racionales. Volvamos a la función$g(x) = \frac{x^2-4}{x+1}$ en el Ejemplo 4.1.4. Realizando división larga, ¹² obtenemos$g(x) = \frac{x^2-4}{x+1} = x-1 - \frac{3}{x+1}$. Desde el término$\frac{3}{x+1} \rightarrow 0$ as$x \rightarrow \pm \infty$, es lógico razonar que como$x$ se vuelve ilimitado, los valores de la función$g(x) = x-1 - \frac{3}{x+1} \approx x-1$. Geométricamente, esto significa que la gráfica de$y=g(x)$ debe parecerse a la línea$y = x-1$ como$x \rightarrow \pm \infty$. Vemos que esto se desarrolla tanto numéricamente como gráficamente a continuación.

$\begin{array}{|r||c|c|} \hline x & g(x) & x-1 \\ \hline -10 & \approx -10.6667 & -11 \\ \hline -100 & \approx -100.9697 & -101 \\ \hline -1000 & \approx -1000.9970& -1001 \\ \hline -10000 & \approx -10000.9997 & -10001 \\ \hline \end{array}$

$\begin{array}{|r||c|c|} \hline x & g(x) & x-1 \\ \hline 10 & \approx 8.7273 & 9 \\\hline 100 & \approx 98.9703 & 99 \\ \hline 1000 & \approx 998.9970 & 999 \\ \hline 10000 & \approx 9998.9997 & 9999 \\ \hline \end{array}$
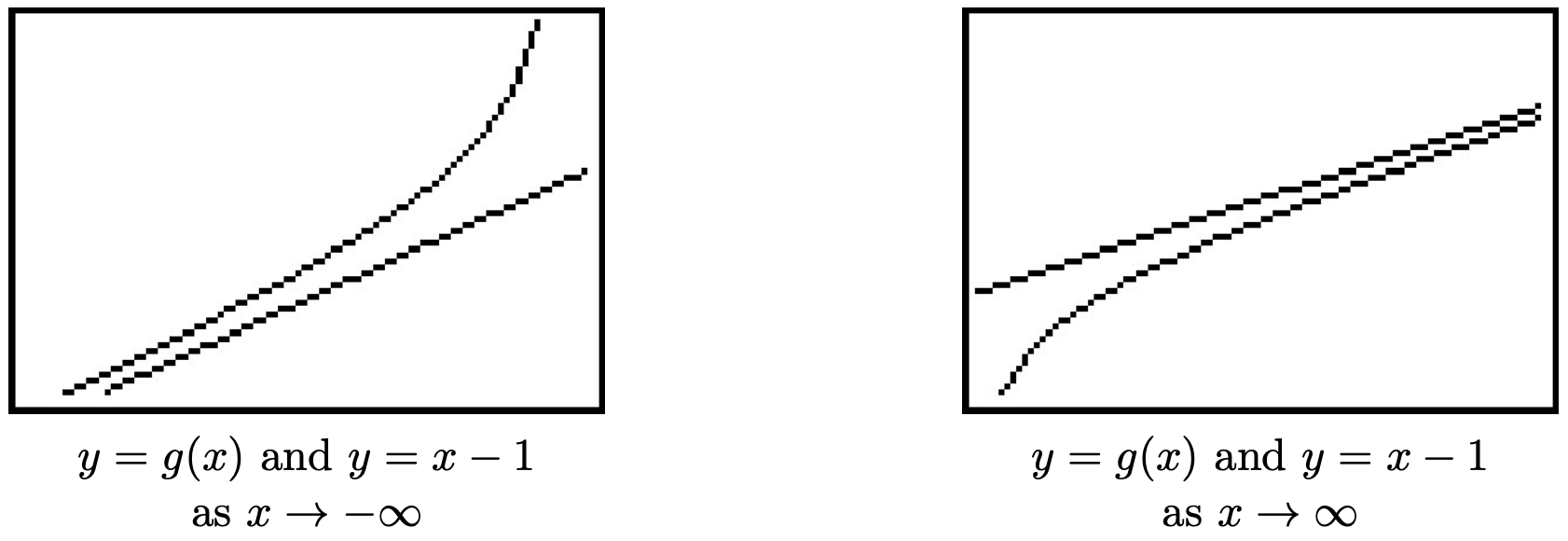
$Screen Shot 2022-03-31 a las 9.41.55 PM.png$

La forma en que simbolizamos la relación entre el comportamiento final de$y=g(x)$ con el de la línea$y=x-1$ es escribir 'as$x \rightarrow \pm \infty$, '$g(x) \rightarrow x-1$. En este caso, decimos que la línea$y=x-1$ es una asíntota inclinada ¹³ a la gráfica de$y=g(x)$. Informalmente, la gráfica de una función racional tiene una asíntota inclinada si, como$x \rightarrow \infty$ o como$x \rightarrow -\infty$, la gráfica se asemeja a una línea no horizontal o “inclinada”. Formalmente, definimos una asíntota inclinada de la siguiente manera.

Definición 4.4.

La línea$y = mx+b$ donde$m \neq 0$ se llama asíntota inclinada de la gráfica de una función$y=f(x)$ si como$x \rightarrow -\infty$ o como$x \rightarrow \infty$,$f(x) \rightarrow mx+b$.

Algunas observaciones están en orden. Primero, tenga en cuenta que la estipulación$m \neq 0$ en la Definición 4.4 es lo que hace que la asíntota 'oblicua' sea 'inclinada' a diferencia del caso cuando$m=0$ en cuyo caso tendríamos una asíntota horizontal. En segundo lugar, si bien hemos motivado lo que quiero decir intuitivamente por la notación '$f(x) \rightarrow mx+b$,' como tantas ideas en esta sección, la definición formal requiere Cálculo. Otra forma de expresar este sentimiento, sin embargo, es reformular$f(x) \rightarrow mx+b$ '' como '$f(x) - (mx+b) \rightarrow 0$. Es decir, la gráfica de$y=f(x)$ tiene la asíntota inclinada$y = mx+b$ si y sólo si la gráfica de$y = f(x) - (mx+b)$ tiene una asíntota horizontal$y=0$.

Nuestra siguiente tarea es determinar las condiciones bajo las cuales la gráfica de una función racional tiene una asíntota inclinada, y si lo hace, cómo encontrarla. En el caso de$g(x) = \frac{x^2-4}{x+1}$, el grado del numerador$x^2-4$ es$2$, que es exactamente uno más que el grado si su denominador$x+1$ que es$1$. Esto da como resultado un polinomio de cociente lineal, y es este polinomio cociente el que es la asíntota inclinada. Generalizar esta situación nos da el siguiente teorema. ¹⁴

Teorema 4.3. Determminación de asíntotas inclinadas

Supongamos que$r$ es una función racional y$r(x) = \frac{p(x)}{q(x)}$, donde el grado de$p$ es exactamente uno más que el grado de$q$. Entonces la gráfica de$y=r(x)$ tiene la asíntota inclinada$y=L(x)$ donde$L(x)$ está el cociente obtenido dividiendo$p(x)$ por$q(x)$.

De la misma manera que el Teorema 4.2 nos da una manera fácil de ver si la gráfica de una función racional$r(x) = \frac{p(x)}{q(x)}$ tiene una asíntota horizontal comparando los grados del numerador y denominador, el Teorema 4.3 nos da una manera fácil de verificar si hay asíntotas inclinadas. A diferencia del Teorema 4.2, que nos da una manera rápida de encontrar las asíntotas horizontales (si las hay), el Teorema 4.3 no nos da tal 'atención'. Si existe una asíntota inclinada, no tenemos más remedio que usar la división larga para encontrarla. ¹⁵

Ejemplo 4.1.6

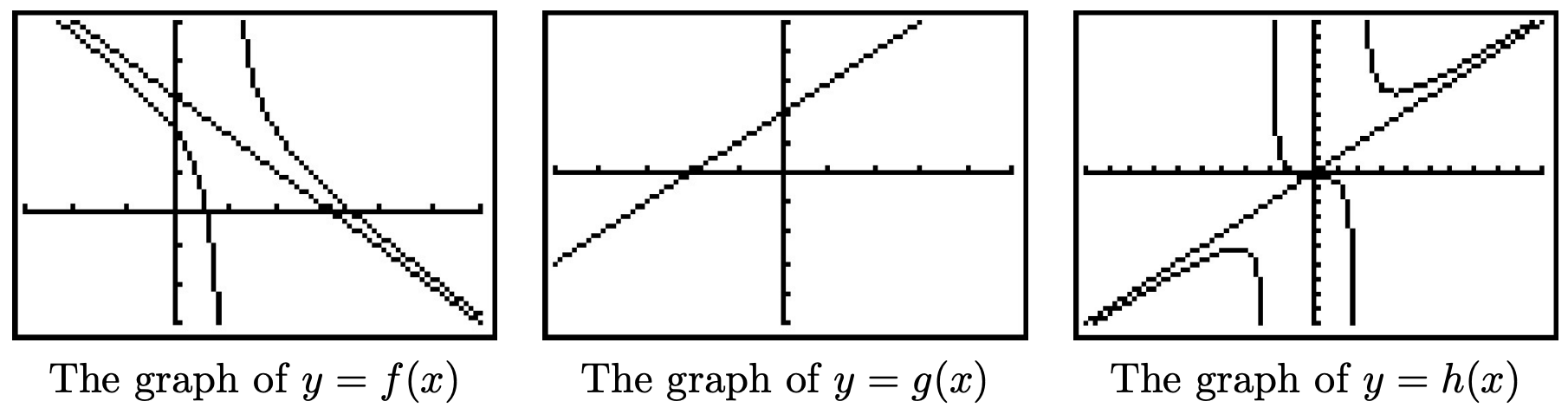
Encuentra las asíntotas inclinadas de las gráficas de las siguientes funciones si existen. Verifica tus respuestas usando una calculadora gráfica y describe el comportamiento de la gráfica cerca de ellas usando la notación adecuada.

$f(x) = \dfrac{x^2-4x+2}{1-x}$
[sacancel]$g(x) = \dfrac{x^2-4}{x-2}$
$h(x) = \dfrac{x^3+1}{x^2-4}$

Solución.

El grado del numerador es$2$ y el grado del denominador es$1$, por lo que el Teorema 4.3 nos garantiza una asíntota inclinada. Para encontrarlo,$1-x = -x+1$ dividimos en$x^2-4x+2$ y obtenemos un cociente de$-x+3$, así es nuestra asíntota inclinada$y=-x+3$. Esto lo confirmamos gráficamente, y vemos que como$x \rightarrow -\infty$, la gráfica de$y=f(x)$ se acerca a la asíntota desde abajo, y como$x \rightarrow \infty$, la gráfica de$y=f(x)$ se acerca a la asíntota desde arriba. ¹⁶
Al igual que con el ejemplo anterior, el grado del numerador$g(x) = \frac{x^2-4}{x-2}$ es$2$ y el grado del denominador es$1$, por lo que se aplica el Teorema 4.3. En este caso,
$g(x) = \frac{x^2-4}{x-2} = \frac{(x+2)(x-2)}{(x-2)} = \frac{(x+2) \cancel{(x-2)}}{\cancelto{1}{(x-2)}} = x+2, \quad x \neq 2$

así tenemos que la asíntota inclinada$y=x+2$ es idéntica a la gráfica de$y=g(x)$ except at$x=2$ (donde esta última tiene un 'agujero' en$(2,4)$.) La calculadora respalda esta afirmación. ¹⁷
Pues$h(x) = \frac{x^3+1}{x^2-4}$, el grado del numerador es$3$ y el grado del denominador$2$ lo es otra vez, se nos garantiza la existencia de una asíntota inclinada. La división larga$\left(x^3+1 \right) \div \left(x^2-4\right)$ da un cociente de justo$x$, así que nuestra asíntota inclinada es la línea$y=x$. La calculadora lo confirma, y encontramos que como$x \rightarrow -\infty$, la gráfica de$y=h(x)$ se acerca a la asíntota desde abajo, y as$x \rightarrow \infty$, la gráfica de$y=h(x)$ se acerca a la asíntota desde arriba.

$Screen Shot 2022-03-31 a las 10.03.33 PM.png$

El lector puede estar un poco decepcionado con los autores en este punto debido a que en los Ejemplos 4.1.2, 4.1.4 y 4.1.6, se utilizó la calculadora para determinar el comportamiento de la función cerca de las asíntotas. Rectificamos eso en la siguiente sección donde, con insoportante detalle, demostramos la utilidad del 'sentido número' para revelar este comportamiento analíticamente.

4.1.1 Ejercicios

En los Ejercicios 1 - 18, para la función racional dada$f$:

Encuentra el dominio de$f$.
Identificar cualquier asíntota vertical de la gráfica de$y = f(x)$.
Identificar cualquier agujero en la gráfica.
Encuentra la asíntota horizontal, si existe.
Encuentra la asíntota inclinada, si existe.
Grafique la función usando una utilidad gráfica y describa el comportamiento cerca de las asíntotas.

$f(x) = \dfrac{x}{3x - 6}$
$f(x) = \dfrac{3 + 7x}{5 - 2x}$
$f(x) = \dfrac{x}{x^{2} + x - 12}$
$f(x) = \dfrac{x}{x^{2} + 1}$
$f(x) = \dfrac{x + 7}{(x + 3)^{2}}$
$f(x) = \dfrac{x^{3} + 1}{x^{2} - 1}$
$f(x) = \dfrac{4x}{x^2+4}$
$f(x) = \dfrac{4x}{x^2-4}$
$f(x) = \dfrac{x^2-x-12}{x^2+x-6}$
$f(x) = \dfrac{3x^2-5x-2}{x^2-9}$
$f(x) = \dfrac{x^3+2x^2+x}{x^2-x-2}$
$f(x) = \dfrac{x^{3} - 3x + 1}{x^{2} + 1}$
$f(x) = \dfrac{2x^{2} + 5x - 3}{3x + 2}$
$f(x) = \dfrac{-x^{3} + 4x}{x^{2} - 9}$
$f(x) = \dfrac{-5x^{4} - 3x^{3} + x^{2} - 10}{x^{3} - 3x^{2} + 3x - 1}$
$f(x) = \dfrac{x^3}{1-x}$
$f(x) = \dfrac{18-2x^2}{x^2-9}$
$f(x) = \dfrac{x^3-4x^2-4x-5}{x^2+x+1}$[alltheasiplast]
El costo$C$ en dólares para eliminar$p$% de las especies invasoras de peces Ippizuti del estanque Sasquatch viene dado por\[C(p) = \frac{1770p}{100 - p}, \quad 0 \leq p < 100 \nonumber\]
1. Encontrar e interpretar$C(25)$ y$C(95)$.
2. ¿Qué significa la asíntota vertical en$x = 100$ el contexto del problema?
3. ¿Qué porcentaje del pez Ippizuti puedes quitar por $40000?
En el Ejercicio 71 de la Sección 1.4, la población de Sasquatch en el Condado de Portage fue modelada por la función\[P(t) = \frac{150t}{t + 15},\nonumber\] donde$t = 0$ representa el año 1803. Encuentra la asíntota horizontal de la gráfica de$y = P(t)$ y explica lo que significa.
Recordemos del Ejemplo 1.5.3 que el costo$C$ (en dólares) para hacer reproductores multimedia$x$ DoPi es$C(x) = 100x+2000$,$x \geq 0$.
1. Encuentra una fórmula para el costo promedio$\overline{C}(x)$. Recordar:$\overline{C}(x) = \frac{C(x)}{x}$.
2. Encontrar e interpretar$\overline{C}(1)$ y$\overline{C}(100)$.
3. ¿Cuántos DOPI se necesitan producir para que el costo promedio por DOPI sea$\$ 200$?
4. Interpretar el comportamiento de$\overline{C}(x)$ as$x \rightarrow 0^{+}$. (CONSEJO: Es posible que desee encontrar el costo fijo$C(0)$ para ayudar en su interpretación.)
5. Interpretar el comportamiento de$\overline{C}(x)$ as$x \rightarrow \infty$. (CONSEJO: Es posible que desee encontrar el costo variable (definido en el Ejemplo 2.1.5 en la Sección 2.1) para ayudar en su interpretación.)

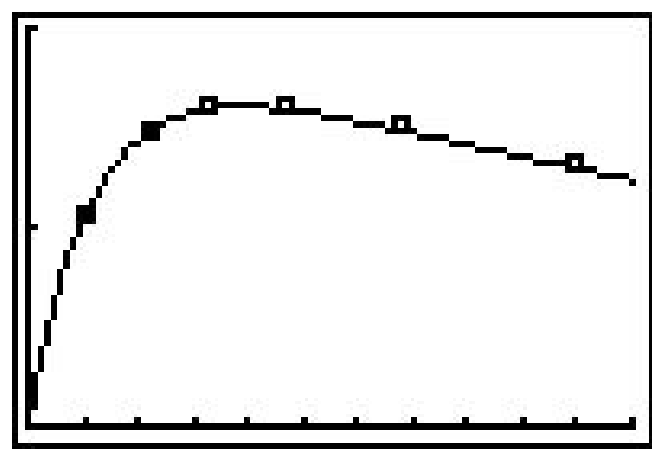
En el Ejercicio 35 de la Sección 3.1, ajustamos algunos modelos polinómicos a los siguientes datos del circuito eléctrico. (El circuito fue construido con una resistencia variable. Para cada uno de los siguientes valores de resistencia (medidos en kilo-ohmios,$k \Omega$), la potencia correspondiente a la carga (medida en milivatios,$mW$) se da en la siguiente tabla). ¹⁸

Resistencia: ($k \Omega$)	1.012	2.199	3.275	4.676	6.805	9.975
\ (k\ Omega\))” style="text-align:left;” class="LT-MATH-80777">Potencia: ($mW$)	1.063	1.496	1.610	1.613	1.505	1.314

Usando algunas leyes fundamentales del análisis de circuitos mezcladas con una dosis saludable de álgebra, podemos derivar la fórmula real que relaciona el poder con la resistencia. Para este circuito, es$P(x) = \frac{25x}{(x + 3.9)^2}$, donde$x$ está el valor de resistencia,$x \geq 0$.

Grafica los datos junto con la función$y = P(x)$ en tu calculadora.
Usa tu calculadora para aproximar la potencia máxima que se puede entregar a la carga. ¿Cuál es el valor de resistencia correspondiente?
Encontrar e interpretar el comportamiento final de$P(x)$ as$x \rightarrow \infty$.

En su ahora famosa disertación de 1919 La ecuación de la curva de aprendizaje, Louis Leon Thurstone presenta una función racional que modela el número de palabras que una persona puede escribir en cuatro minutos en función del número de páginas de práctica que se haya completado. (Este trabajo, que ahora es de dominio público y se puede encontrar aquí, es de una época pasada cuando los estudiantes de las escuelas de negocios tomaron clases de mecanografía sobre máquinas de escribir manuales). Usando su notación original y lenguaje original, tenemos$Y = \frac{L(X + P)}{(X + P) + R}$ donde$L$ está el límite de práctica previsto en términos de unidades de velocidad,$X$ es páginas escritas,$Y$ es velocidad de escritura en términos de palabras en cuatro minutos,$P$ es equivalente práctica previa en términos de páginas y $R$es la tasa de aprendizaje. En la Figura 5 del papel, grafica un diagrama de dispersión y la curva$Y = \frac{216(X + 19)}{X + 148}$. Discuta esta ecuación con tus compañeros de clase. ¿Cómo actualizarías la notación? Explique qué significa la asíntota horizontal de la gráfica. Deberías tomarte un tiempo para mirar el papel original. Salta los cálculos que aún no entiendes y trata de tener una idea de la hora y el lugar en que se realizó el estudio.

4.1.2 Respuestas

$f(x) = \dfrac{x}{3x - 6}$
Dominio: asíntota$(-\infty, 2) \cup (2, \infty)$
vertical:$x = 2$
As$x \rightarrow 2^{-}, f(x) \rightarrow -\infty$
As$x \rightarrow 2^{+}, f(x) \rightarrow \infty$
Sin agujeros en la gráfica Asintota
horizontal:$y = \frac{1}{3}$
As$x \rightarrow -\infty, f(x) \rightarrow \frac{1}{3}^{-}$
Como$x \rightarrow \infty, f(x) \rightarrow \frac{1}{3}^{+}$
$f(x) = \dfrac{3 + 7x}{5 - 2x}$
Dominio: asíntota$(-\infty, \frac{5}{2}) \cup (\frac{5}{2}, \infty)$
vertical:$x = \frac{5}{2}$
As$x \rightarrow \frac{5}{2}^{-}, f(x) \rightarrow \infty$
As$x \rightarrow \frac{5}{2}^{+}, f(x) \rightarrow -\infty$
Sin agujeros en la gráfica Asintota
horizontal:$y = -\frac{7}{2}$
As$x \rightarrow -\infty, f(x) \rightarrow -\frac{7}{2}^{+}$
Como$x \rightarrow \infty, f(x) \rightarrow -\frac{7}{2}^{-}$
$f(x) = \dfrac{x}{x^{2} + x - 12} = \dfrac{x}{(x + 4)(x - 3)}$
Dominio: asíntotas$(-\infty, -4) \cup (-4, 3) \cup (3, \infty)$
verticales: As$x = -4, x = 3$
As$x \rightarrow -4^{-}, f(x) \rightarrow -\infty$
As$x \rightarrow -4^{+}, f(x) \rightarrow \infty$
As$x \rightarrow 3^{-}, f(x) \rightarrow -\infty$
As$x \rightarrow 3^{+}, f(x) \rightarrow \infty$
Sin agujeros en la gráfica
Asíntota horizontal:$y = 0$
As$x \rightarrow -\infty, f(x) \rightarrow 0^{-}$
As$x \rightarrow \infty, f(x) \rightarrow 0^{+}$
$f(x) = \dfrac{x}{x^{2} + 1}$
Dominio:$(-\infty, \infty)$
Sin asíntotas verticales
Sin agujeros en la gráfica Asintota
horizontal:$y = 0$
As$x \rightarrow -\infty, f(x) \rightarrow 0^{-}$
As$x \rightarrow \infty, f(x) \rightarrow 0^{+}$
$f(x) = \dfrac{x + 7}{(x + 3)^{2}}$
Dominio: Asintota$(-\infty, -3) \cup (-3, \infty)$
vertical:$x = -3$
As$x \rightarrow -3^{-}, f(x) \rightarrow \infty$
As$x \rightarrow -3^{+}, f(x) \rightarrow \infty$
Sin agujeros en la gráfica
Asintota horizontal:$y = 0$
¹⁹As$x \rightarrow -\infty, f(x) \rightarrow 0^{-}$
As$x \rightarrow \infty, f(x) \rightarrow 0^{+}$
$f(x) = \dfrac{x^{3} + 1}{x^{2} - 1} = \dfrac{x^{2} - x+ 1}{x-1}$
Dominio: asíntota$(-\infty, -1) \cup (-1, 1) \cup (1, \infty)$
vertical:$x = 1$
$x \rightarrow 1^{-}, f(x) \rightarrow -\infty$
Como$x \rightarrow 1^{+}, f(x) \rightarrow \infty$
agujero en asíntota$(-1, -\frac{3}{2})$
inclinada:$y=x$
As$x \rightarrow -\infty$, la gráfica es abajo$y=x$
As$x \rightarrow \infty$, el gráfico está arriba$y=x$
$f(x) = \dfrac{4x}{x^{2} + 4}$
Dominio:$(-\infty, \infty)$
Sin asíntotas verticales
Sin agujeros en la gráfica Asintota
horizontal:$y = 0$
As$x \rightarrow -\infty, f(x) \rightarrow 0^{-}$
As$x \rightarrow \infty, f(x) \rightarrow 0^{+}$
$f(x) = \dfrac{4x}{x^{2} -4} = \dfrac{4x}{(x + 2)(x - 2)}$
Dominio: asíntotas$(-\infty, -2) \cup (-2, 2) \cup (2, \infty)$
verticales: As$x = -2, x = 2$
As$x \rightarrow -2^{-}, f(x) \rightarrow -\infty$
As$x \rightarrow -2^{+}, f(x) \rightarrow \infty$
As$x \rightarrow 2^{-}, f(x) \rightarrow -\infty$
As$x \rightarrow 2^{+}, f(x) \rightarrow \infty$
Sin agujeros en la gráfica
Asíntota horizontal:$y = 0$
As$x \rightarrow -\infty, f(x) \rightarrow 0^{-}$
As$x \rightarrow \infty, f(x) \rightarrow 0^{+}$
$f(x) = \dfrac{x^2-x-12}{x^{2} +x - 6} = \dfrac{x-4}{x - 2}$
Dominio: asíntota$(-\infty, -3) \cup (-3, 2) \cup (2, \infty)$
vertical:$x = 2$
$x \rightarrow 2^{-}, f(x) \rightarrow \infty$
Como$x \rightarrow 2^{+}, f(x) \rightarrow -\infty$
agujero en asíntota$\left(-3, \frac{7}{5} \right)$
horizontal:$y = 1$
Como$x \rightarrow -\infty, f(x) \rightarrow 1^{+}$
Como$x \rightarrow \infty, f(x) \rightarrow 1^{-}$
$f(x) = \dfrac{3x^2-5x-2}{x^{2} -9} = \dfrac{(3x+1)(x-2)}{(x + 3)(x - 3)}$
Dominio: asíntotas$(-\infty, -3) \cup (-3, 3) \cup (3, \infty)$
verticales: As$x = -3, x = 3$
As$x \rightarrow -3^{-}, f(x) \rightarrow \infty$
As$x \rightarrow -3^{+}, f(x) \rightarrow -\infty$
As$x \rightarrow 3^{-}, f(x) \rightarrow -\infty$
As$x \rightarrow 3^{+}, f(x) \rightarrow \infty$
Sin agujeros en la gráfica
Asíntota horizontal:$y = 3$
As$x \rightarrow -\infty, f(x) \rightarrow 3^{+}$
As$x \rightarrow \infty, f(x) \rightarrow 3^{-}$
$f(x) = \dfrac{x^3+2x^2+x}{x^{2} -x-2} = \dfrac{x(x+1)}{x - 2}$
Dominio: asíntota$(-\infty, -1) \cup (-1, 2) \cup (2, \infty)$
vertical:$x = 2$
$x \rightarrow 2^{-}, f(x) \rightarrow -\infty$
Como$x \rightarrow 2^{+}, f(x) \rightarrow \infty$
agujero en asíntota$(-1,0)$
inclinada:$y=x+3$
As$x \rightarrow -\infty$, la gráfica es abajo$y=x+3$
As$x \rightarrow \infty$, el gráfico está arriba$y=x+3$
$f(x) = \dfrac{x^3-3x+1}{x^2+1}$
Dominio:$(-\infty, \infty)$
Sin asíntotas verticales
Sin agujeros en la gráfica Asintota
inclinada:$y=x$
As$x \rightarrow -\infty$, la gráfica está arriba$y=x$
As$x \rightarrow \infty$, la gráfica está abajo $y=x$
$f(x) = \dfrac{2x^{2} + 5x - 3}{3x + 2}$
Dominio: asíntota$\left(-\infty, -\frac{2}{3}\right) \cup \left(-\frac{2}{3}, \infty\right)$
vertical:$x = -\frac{2}{3}$
$x \rightarrow -\frac{2}{3}^{-}, f(x) \rightarrow \infty$
As$x \rightarrow -\frac{2}{3}^{+}, f(x) \rightarrow -\infty$
As Sin agujeros en la gráfica Asintota
inclinada:$y = \frac{2}{3}x + \frac{11}{9}$
As$x \rightarrow -\infty$, la gráfica es arriba$y = \frac{2}{3}x + \frac{11}{9}$
As$x \rightarrow \infty$, la gráfica está abajo$y = \frac{2}{3}x + \frac{11}{9}$
$f(x) = \dfrac{-x^{3} + 4x}{x^{2} - 9} = \dfrac{-x^{3} + 4x}{(x-3)(x+3)}$
Dominio: asíntotas$(-\infty, -3) \cup (-3, 3) \cup (3, \infty)$
verticales:$x = -3$, As$x=3$
As$x \rightarrow -3^{-}, f(x) \rightarrow \infty$
As$x \rightarrow -3^{+}, f(x) \rightarrow -\infty$
As$x \rightarrow 3^{-}, f(x) \rightarrow \infty$
As$x \rightarrow 3^{+}, f(x) \rightarrow -\infty$
Sin agujeros en la gráfica
Asintota inclinada:$y=-x$
As$x \rightarrow -\infty$, la gráfica está arriba$y=-x$
As$x \rightarrow \infty$, la gráfica está abajo$y=-x$
$f(x) = \dfrac{-5x^{4} - 3x^{3} + x^{2} - 10}{x^{3} - 3x^{2} + 3x - 1} \\ \phantom{f(x)} = \dfrac{-5x^{4} - 3x^{3} + x^{2} - 10}{(x-1)^3}$
Dominio: asíntotas$(-\infty, 1) \cup (1, \infty)$
verticales:$x = 1$
As$x \rightarrow 1^{-}, f(x) \rightarrow \infty$
As$x \rightarrow 1^{+}, f(x) \rightarrow -\infty$
Sin agujeros en la gráfica Asintota
inclinada:$y=-5x-18$
As$x \rightarrow -\infty$, la gráfica es arriba$y=-5x-18$
As$x \rightarrow \infty$, la gráfica está abajo$y=-5x-18$
$f(x) = \dfrac{x^3}{1-x}$
Dominio: asíntota$(-\infty, 1) \cup (1, \infty)$
vertical:$x=1$
$x \rightarrow 1^{-}, f(x) \rightarrow \infty$
As$x \rightarrow 1^{+}, f(x) \rightarrow -\infty$
As Sin agujeros en la gráfica
Sin asíntota horizontal o inclinada
As$x \rightarrow -\infty$,$f(x) \rightarrow -\infty$
Como$x \rightarrow \infty$,$f(x) \rightarrow -\infty$
$f(x) = \dfrac{18-2x^2}{x^2-9} = -2$
Dominio:$(-\infty, -3) \cup (-3,3) \cup (3, \infty)$
Sin asíntotas verticales
Agujeros en la gráfica en$(-3,-2)$ y asíntota$(3,-2)$
Horizontal$y = -2$
As$x \rightarrow \pm \infty$,$f(x) = -2$
$f(x) = \dfrac{x^3-4x^2-4x-5}{x^2+x+1} = x-5$
Dominio:$(-\infty, \infty)$
Sin asíntotas verticales
Sin agujeros en la gráfica Asintota
inclinada:$y = x-5$
$f(x) = x-5$ en todas partes.
1. $C(25) = 590$significa que cuesta 590 dólares eliminar el 25% de los peces y y$C(95)= 33630$ significa que costaría $33630 retirar el 95% de los peces del estanque.
2. La asíntota vertical en$x = 100$ significa que a medida que intentamos sacar el 100% de los peces del estanque, el costo aumenta sin ataduras; es decir, es imposible eliminar todos los peces.
3. Por $40000 podrías eliminar alrededor del 95.76% del pescado.
La asíntota horizontal de la gráfica de$P(t) = \frac{150t}{t + 15}$ es$y = 150$ y significa que el modelo predice que la población de Sasquatch en el condado de Portage nunca superará los 150.
1. $\overline{C}(x) = \frac{100x+2000}{x}$,$x > 0$.
2. $\overline{C}(1) = 2100$y$\overline{C}(100) = 120$. Cuando solo se produce$1$ DoPi, el costo por DOPi es$\$2100$, pero cuando$100$ se producen DOPI, el costo por DOPi es$\$120$.
3. $\overline{C}(x) = 200$cuando$x = 20$. Entonces, para obtener el costo por DOPI$\$200$,$20$ es necesario producir DOPI.
4. Como$x \rightarrow 0^{+}$,$\overline{C}(x) \rightarrow \infty$. Esto significa que a medida que se producen cada vez menos DOPI, el costo por DOPI queda sin límites. En esta situación, hay un costo fijo de$\$2000$ ($C(0) = 2000$), estamos tratando de repartir eso$\$2000$ sobre cada vez menos DOPI.
5. Como$x \rightarrow \infty$,$\overline{C}(x) \rightarrow 100^{+}$. Esto significa que a medida que se producen más y más DOPI, se acerca el costo por DOPI$\$100$, pero siempre es un poco más que$\$100$. Dado que$\$100$ es el costo variable por doPi ($C(x) = \underline{100}x+2000$), significa que no importa cuántos DOPI se produzcan, el costo promedio por doPi siempre será un poco mayor que el costo variable para producir un DOPI. Al igual que antes, podemos atribuir esto al costo$\$2000$ fijo, que influye en el costo promedio por DOPI sin importar cuántos DOPI se produzcan.
1. $Screen Shot 2022-03-31 a las 10.33.19 PM.png$
2. La potencia máxima es aproximadamente$1.603 \; mW$ la que corresponde a$3.9 \; k\Omega$.
3. Como$x \rightarrow \infty, \; P(x) \rightarrow 0^{+}$ lo que significa que a medida que la resistencia aumenta sin ataduras, la potencia disminuye a cero.

Referencia

¹ Deberías revisar las Secciones 1.2 y 1.3 si esta declaración te tomó desprevenido.

² Necesitaríamos Cálculo para confirmarlo analíticamente.

³ Aquí, la palabra 'mayor' significa mayor en valor absoluto.

⁴ Como veremos en el siguiente apartado, las gráficas de funciones racionales pueden, de hecho, cruzar sus asíntotas horizontales. Si esto sucede, sin embargo, lo hace solo un número finito de veces, y así para cada elección de$x \rightarrow-\infty$ y$x \rightarrow \infty$,$f(x)$ se acercará ya sea$c$ desde abajo (en el caso$f(x) \rightarrow c^{-}$) o arriba (en el caso)$f(x) \rightarrow c^{+}$. Dejamos$f(x) \rightarrow c$ genéricos en nuestra definición, sin embargo, para permitir que este concepto se aplique a especímenes menos domesticados en el zoológico Precálculo, como el Ejercicio 50 en la Sección 10.5.

⁵ Por ejemplo, graficar funciones definidas por partes en la Sección 1.6.

⁶ En Cálculo, veremos cómo estos 'agujeros' pueden ser 'tapados' al embarcarse en un estudio más avanzado de continuidad.

⁷ Estas funciones surgen en Ecuaciones Diferenciales. El desafortunado nombre tendrá sentido en breve.

⁸ Como se ve en las tablas inmediatamente anteriores Definición 4.2.

⁹ Más específicamente, como$x \rightarrow-\infty$,$f(x) \rightarrow 2^{+}$, y como$x \rightarrow \infty$,$f(x) \rightarrow 2^{-}$.

¹⁰ ¡Siéntate apretado! En breve revisaremos esta función y su comportamiento final.

¹¹ Aunque la población de abajo se modela con mayor precisión con las funciones del Capítulo 6, la aproximamos (¡usando Cálculo, por supuesto!) utilizando una función racional.

¹² Ver las observaciones siguientes Teorema 4.2.

¹³ También se llama asíntota 'oblicua' en algunos textos, ostensiblemente de clase superior (y más caros).

¹⁴ Una vez más, este teorema se le trae cortesía del Teorema 3.4 y Cálculo.

¹⁵ Eso está bien, sin embargo. En la siguiente sección, usaremos la división larga para analizar el comportamiento final y ¡merece la pena el esfuerzo!

¹⁶ Tenga en cuenta que a propósito estamos evitando la notación como 'as$x \rightarrow \infty, f(x) \rightarrow(-x+3)^{+}$. Si bien es posible definir estas nociones formalmente con Cálculo, no es estándar hacerlo. Además, con la introducción del símbolo '!' en la siguiente sección, los autores sienten que ya estamos en suficientes problemas.

¹⁷ Si bien la palabra 'asíntota' tiene la connotación de 'acercarse pero no igualar', las Definiciones 4.3 y 4.4 invitan al mismo tipo de patologías que vimos con las Definiciones 1.11 en la Sección 1.6.

¹⁸ Los autores desean agradecer a Don Anthan y Ken White, de Lakeland Community College, por idear este problema y generar el conjunto de datos que lo acompaña.

¹⁹ Esto es difícil de ver en la calculadora, pero créeme, la gráfica está debajo del$x$ eje -a la izquierda de$x = −7$.