4.3: Desigualdades racionales y aplicaciones

En esta sección, resolvemos ecuaciones y desigualdades que involucran funciones racionales y exploramos problemas de aplicación asociados. Nuestro primer ejemplo muestra la diferencia crítica en el procedimiento entre resolver una ecuación racional y una desigualdad racional.

Ejemplo 4.3.1

1. Resolver\(\dfrac{x^3-2x+1}{x-1} = \dfrac{1}{2}x-1\).
2. Resolver\(\dfrac{x^3-2x+1}{x-1} \geq \dfrac{1}{2}x-1\).
3. Usa tu calculadora para verificar gráficamente tus respuestas a 1 y 2.

Solución.

1. Para resolver la ecuación, aclaramos los denominadores

   \[\begin{array}{rclr} \dfrac{x^3-2x+1}{x-1} & = & \dfrac{1}{2}x-1 & \\[4pt] \left(\dfrac{x^3-2x+1}{x-1}\right) \cdot 2(x-1) & = & \left( \dfrac{1}{2}x-1 \right) \cdot 2(x-1) & \\[4pt] 2x^3 - 4x + 2 & = & x^2-3x+2 & \mbox{expand} \\ 2x^3 -x^2 - x & = & 0 & \\ x(2x+1)(x-1) & = & 0 & \mbox{factor}\\ x & = & -\frac{1}{2}, \, 0, \, 1 & \\ \end{array}\nonumber\]

   Dado que limpiamos los denominadores, necesitamos verificar si hay soluciones extrañas. Efectivamente, vemos que\(x=1\) no satisface la ecuación original y hay que desechar. Nuestras soluciones son\(x=-\frac{1}{2}\) y\(x=0\).

2. Para resolver la desigualdad, puede ser tentador comenzar como hicimos con la ecuación\(-\) a saber multiplicando ambos lados por la cantidad\((x-1)\). El problema es que, dependiendo de\(x\),\((x-1)\) puede ser positivo (lo que no afecta la desigualdad) o\((x-1)\) podría ser negativo (lo que revertiría la desigualdad). En lugar de trabajar por casos, recogemos todos los términos de un lado de la desigualdad con\(0\) el otro y hacemos un diagrama de signos utilizando la técnica dada en la página 321 en la Sección 4.2.

   \[\begin{array}{rclr} \dfrac{x^3-2x+1}{x-1} & \geq & \dfrac{1}{2}x-1 & \\[4pt] \dfrac{x^3-2x+1}{x-1} - \dfrac{1}{2} x + 1& \geq & 0& \\[4pt] \dfrac{2\left(x^3-2x+1\right)-x(x-1)+1(2(x-1))}{2(x-1)} & \geq & 0 & \mbox{get a common denominator} \\[4pt] \dfrac{2x^3-x^2-x}{2x-2} & \geq & 0 & \mbox{expand} \\ \end{array}\nonumber\]

   Viendo el lado izquierdo como una función racional\(r(x)\) hacemos un diagrama de signos. El único valor excluido del dominio de\(r\) es\(x=1\) cuál es la solución a\(2x-2=0\). Los ceros de\(r\) son las soluciones a\(2x^3-x^2-x=0\), que ya hemos encontrado que son\(x=0\),\(x=-\frac{1}{2}\) y\(x=1\), este último fue descontado como cero porque no está en el dominio. Al elegir los valores de prueba en cada intervalo de prueba, construimos el diagrama de signos a continuación.

   

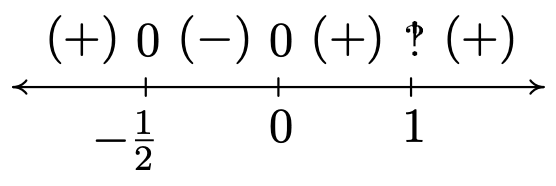
   Nos interesa dónde\(r(x) \geq 0\). Nos encontramos\(r(x) > 0\), o\((+)\), en los intervalos\(\left(-\infty, -\frac{1}{2}\right)\),\((0,1)\) y\((1, \infty)\). A estos intervalos le sumamos los ceros de\(r\),\(-\frac{1}{2}\) y\(0\), para obtener nuestra solución final:\(\left( - \infty, -\frac{1}{2} \right] \cup [0,1) \cup (1, \infty)\).

3. Geométricamente, si establecemos\(f(x) = \frac{x^3-2x+1}{x-1}\) y\(g(x) = \frac{1}{2} x -1\), las soluciones a\(f(x)=g(x)\) son las\(x\) -coordenadas de los puntos donde las gráficas de\(y=f(x)\) y se\(y=g(x)\) cruzan. La solución a\(f(x) \geq g(x)\) representa no sólo dónde se encuentran las gráficas, sino los intervalos sobre los cuales la gráfica de\(y=f(x)\) está por encima de (\(>\)) la gráfica de\(g(x)\). Obtenemos las gráficas a continuación.

   

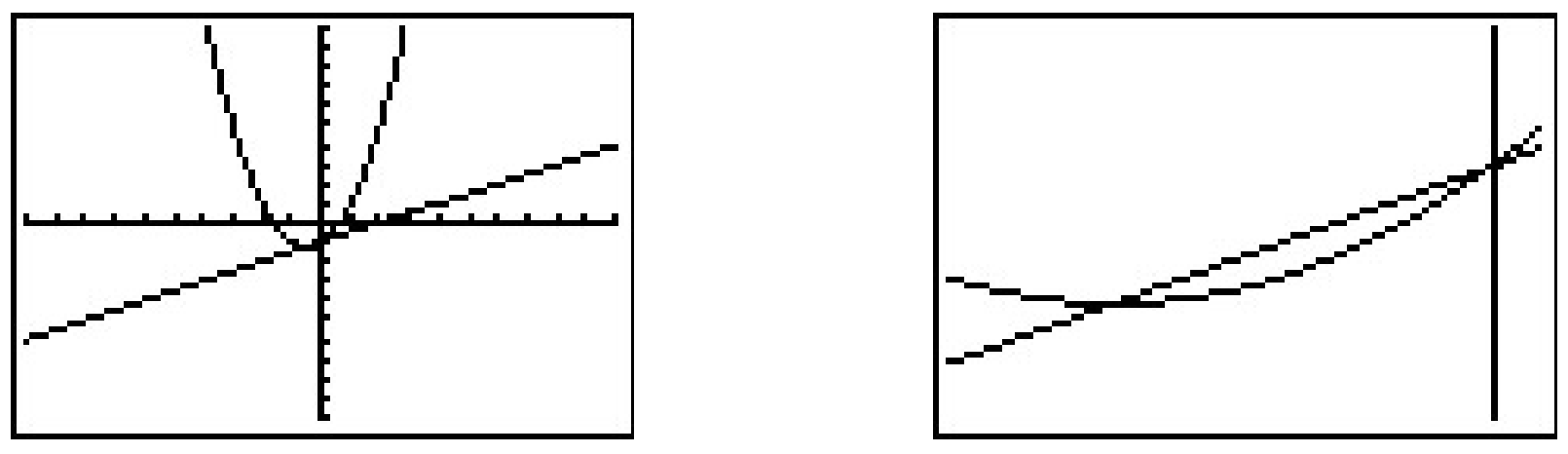
   El comando 'Intersectar' confirma que las gráficas se cruzan cuando\(x=-\frac{1}{2}\) y\(x=0\). Es claro a partir de la calculadora que la gráfica de\(y=f(x)\) está por encima de la gráfica de\(y=g(x)\) on así\(\left(-\infty, -\frac{1}{2}\right)\) como on\((0,\infty)\). Según la calculadora, nuestra solución es entonces la\(\left(-\infty, -\frac{1}{2}\right] \cup [0, \infty)\) que casi coincide con la respuesta que encontramos analíticamente. Tenemos que recordar que no\(f\) está definido en\(x=1\), y, aunque no se muestre en la calculadora, hay un hoyo ¹ en la gráfica de\(y=f(x)\) cuándo\(x=1\) es por eso\(x=1\) que no forma parte de nuestra respuesta final.

A continuación, exploramos cómo se pueden utilizar las ecuaciones racionales para resolver algunos problemas clásicos que involucran tasas.

Ejemplo 4.3.2

Carl decide explorar el río Meander, la ubicación de varios avistamientos recientes de Sasquatch. Desde el campamento, canoas río abajo cinco millas para ver un supuesto nido de Sasquatch. Al no encontrar nada, inmediatamente se da la vuelta, vuelve a recorrer su ruta (esta vez viajando río arriba), y regresa al campamento 3 horas después de que se fue. Si Carl canoas a razón de 6 millas por hora en agua sin gas, ¿qué tan rápido fluía ese día el río Meander?

Solución

Se nos da información sobre distancias, tarifas (velocidades) y tiempos. El principio básico que relaciona estas cantidades es:\[\text{distance} = \text{rate} \cdot \text{time}\nonumber\] La primera observación a hacer, sin embargo, es que la distancia, la tasa y el tiempo que se nos dan no son 'compatibles': la distancia dada es la distancia para solo una parte del viaje, la tasa dada es la velocidad que Carl puede canoa en aguas tranquilas, no en un fluyendo río, y el tiempo dado es la duración de todo el viaje. En definitiva, estamos tras la velocidad del río, así que llamemos a eso\(R\) medido en millas por hora para que sea consistente con la otra tasa que se nos ha dado. Para comenzar, dividamos el viaje en sus dos partes: el viaje inicial aguas abajo y el viaje de regreso aguas arriba. Para el viaje río abajo, lo único que sabemos es que la distancia recorrida son\(5\) millas.

\[\begin{array}{rcl} \text{distance downstream} & = & \text{rate traveling downstream} \cdot \text{time traveling downstream} \\ 5 \, \text{miles} & = & \text{rate traveling downstream} \cdot \text{time traveling downstream} \\ \end{array}\nonumber\]

Dado que el viaje de regreso río arriba siguió la misma ruta que el viaje río abajo, sabemos que la distancia recorrida río arriba también es de 5 millas.

\[\begin{array}{rcl} \text{distance upstream} & = & \text{rate traveling upstream} \cdot \text{time traveling upstream} \\ 5 \, \text{miles} & = & \text{rate traveling upstream} \cdot \text{time traveling upstream} \\ \end{array}\nonumber\]

Nos dicen que Carl puede hacer canoa a razón de\(6\) millas por hora en agua sin gas. ¿Cómo figura esto en las tarifas que viajan aguas arriba y aguas abajo? La velocidad que recorre la canoa en el río es una combinación de la velocidad a la que Carl puede propulsar la canoa en aguas tranquilas, 6 millas por hora, y la velocidad del río, que estamos llamando\(R\). Al viajar río abajo, el río está ayudando a Carl a lo largo, así que agregamos estas dos velocidades:

\[\begin{array}{rcl} \text{rate traveling downstream} & = & \text{rate Carl propels the canoe} + \text{speed of the river} \\ & = & 6 \frac{\text{miles}}{\text{hour}} + R \frac{\text{miles}}{\text{hour}} \\ \end{array}\nonumber\]

Entonces nuestra velocidad aguas abajo es\((6+R) \frac{\text{miles}}{\text{hour}}\). Sustituyendo esto en nuestra ecuación de “distancia-velocidad-tiempo” para la parte aguas abajo del viaje, obtenemos:

\[\begin{array}{rcl} 5 \, \text{miles} & = & \text{rate traveling downstream} \cdot \text{time traveling downstream} \\ 5 \, \text{miles} & = & (6+R) \frac{\text{miles}}{\text{hour}} \cdot \text{time traveling downstream} \\ \end{array}\nonumber\]

Al viajar río arriba, Carl trabaja contra la corriente. Dado que la canoa logra viajar río arriba, la velocidad que Carl puede canoa en aguas tranquilas es mayor que la velocidad del río, por lo que restamos la velocidad del río de la velocidad de canoa de Carl para obtener:

\[\begin{array}{rcl} \text{rate traveling upstream} & = & \text{rate Carl propels the canoe} - \text{river speed} \\ & = & 6 \frac{\text{miles}}{\text{hour}} - R \frac{\text{miles}}{\text{hour}} \\ \end{array}\nonumber\]

Procediendo como antes, obtenemos

\[\begin{array}{rcl} 5 \, \text{miles} & = & \text{rate traveling upstream} \cdot \text{time traveling upstream} \\ 5 \, \text{miles} & = & (6 - R) \frac{\text{miles}}{\text{hour}} \cdot \text{time traveling upstream} \\ \end{array}\nonumber\]

El último dato que nos dio es que el viaje total duró\(3\) horas. Si dejamos\(t_{\text{down}}\) denotar el tiempo del viaje aguas abajo y\(t_{\text{up}}\) el tiempo del viaje aguas arriba, tenemos:\(t_{\text{down}} + t_{\text{up}} = 3 \, \text{hours}\). Sustituyendo\(t_{\text{down}}\) y\(t_{\text{up}}\) en las ecuaciones de 'distancia-rate-tiempo', obtenemos (suprimiendo las unidades) tres ecuaciones en tres incógnitas: ²\[\left\{\begin{array}{lrcl} E1 & (6+R) \, t_{\text{down}} & = & 5 \\ E2 & (6-R) \, t_{\text{up}} & = & 5 \\ E3 & t_{\text{down}} + t_{\text{up}} & = & 3 \end{array} \right.\nonumber\]

Como en última instancia estamos después\(R\), necesitamos usar estas tres ecuaciones para obtener al menos una ecuación que involucre solo\(R\). Para ello, resolvemos\(E1\)\(t_{\text{down}}\) por dividir ambos lados ³ por la cantidad\((6+R)\) a obtener\(t_{\text{down}} = \frac{5}{6+R}\). De igual manera, resolvemos\(E2\) para\(t_{\text{up}}\) y obtenemos\(t_{\text{up}} = \frac{5}{6-R}\). Sustituyendo estos en\(E3\), obtenemos: ⁴ Denominadores de\[\dfrac{5}{6+R} + \dfrac{5}{6 - R} = 3.\nonumber\] compensación, obtenemos\(5(6-R) + 5(6+R) = 3(6+R)(6-R)\) lo que reduce a\(R^2 = 16\). Encontramos\(R = \pm 4\), y ya que\(R\) representa la velocidad del río, elegimos\(R = 4\). El día en cuestión, el río Meandro fluye a una velocidad de\(4\) millas por hora.

Una de las lecciones importantes que hay que aprender del Ejemplo 4.3.2 es que las velocidades, y más generalmente, las tasas, son aditivas. Como vemos en nuestro siguiente ejemplo, el concepto de tasa y sus principios asociados pueden aplicarse a una amplia variedad de problemas, no solo escenarios de 'distancia-tarifa-tiempo'.

Ejemplo 4.3.3

Trabajando solo, Taylor puede desyerbar el jardín en 4 horas. Si Carl ayuda, pueden desyerbar el jardín en 3 horas. ¿Cuánto tiempo tardaría Carl en desyerbar el jardín por su cuenta?

Solución

La relación clave entre el trabajo y el tiempo que utilizamos en este problema es:\[\text{amount of work done} = \text{rate of work} \cdot \text{time spent working}\nonumber\]

Nos dicen que, trabajando solo, Taylor puede desyerbar el jardín en 4 horas. En el caso de Taylor entonces:\[\begin{array}{rcl} \text{amount of work Taylor does} & = & \text{rate of Taylor working} \cdot \text{time Taylor spent working} \\ 1 \, \text{garden} & = & (\text{rate of Taylor working}) \cdot (4 \, \text{hours}) \\ \end{array}\nonumber\]

Entonces tenemos que la tasa que trabaja Taylor es\(\frac{1 \, \text{garden}}{ 4 \, \text{hours}} = \frac{1}{4} \frac{\text{garden}}{\text{hour}}\). También nos dicen que al trabajar juntos, Taylor y Carl pueden desyerbar el jardín en tan solo 3 horas. Contamos con:

\[\begin{array}{rcl} \text{amount of work done together} & = & \text{rate of working together} \cdot \text{time spent working together} \\ 1 \, \text{garden} & = & (\text{rate of working together}) \cdot (3 \, \text{hours}) \\ \end{array}\nonumber\]

A partir de esto, encontramos que la tasa de Taylor y Carl trabajando juntos es\(\frac{1 \, \text{garden}}{3 \, \text{hours}} = \frac{1}{3} \frac{\text{garden}}{\text{hour}}\). Se nos pide que averiguaremos cuánto tiempo tardaría Carl en desyerbar el jardín por su cuenta. Llamemos a esto desconocido\(t\), medido en horas para ser congruente con las otras veces que nos dieron en el problema. Entonces:

\[\begin{array}{rcl} \text{amount of work Carl does} & = & \text{rate of Carl working} \cdot \text{time Carl spent working} \\ 1 \, \text{garden} & = & (\text{rate of Carl working}) \cdot (t \, \text{hours}) \\ \end{array}\nonumber\]

Para poder encontrar\(t\), necesitamos encontrar la tasa de Carl trabajando, así que llamemos a esta cantidad\(R\), con unidades\(\frac{\text{garden}}{\text{hour}}\). Utilizando el hecho de que las tarifas son aditivas, tenemos:

\[\begin{array}{rcl} \text{rate working together} & = & \text{rate of Taylor working} + \text{rate of Carl working} \\[4pt] \frac{1}{3} \frac{\text{garden}}{\text{hour}} & = & \frac{1}{4} \frac{\text{garden}}{\text{hour}} + R \frac{\text{garden}}{\text{hour}} \\ \end{array}\nonumber\]

para que\(R = \frac{1}{12} \frac{\text{garden}}{\text{hour}}\). Sustituyendo esto en nuestra ecuación de “trabajo-rate-tiempo” para Carl, obtenemos:

\[\begin{array}{rcl} 1 \, \text{garden} & = & (\text{rate of Carl working}) \cdot (t \, \text{hours}) \\[4pt] 1 \, \text{garden} & = & \left(\frac{1}{12} \frac{\text{garden}}{\text{hour}} \right) \cdot (t \, \text{hours}) \\ \end{array}\nonumber\]

Resolviendo\(1 = \frac{1}{12} t\), obtenemos\(t = 12\), así que Carl tarda 12 horas en desyerbar el jardín por su cuenta. ⁵

Como es común con los 'problemas de palabra' como los Ejemplos 4.3.2 y 4.3.3, no hay atajo a la respuesta. Animamos al lector a pensar cuidadosamente y aplicar los principios básicos de tasa a cada uno (¡potencialmente diferente!) situación. Es tiempo bien empleado. También fomentamos el seguimiento de las unidades, especialmente en las primeras etapas del problema. Esto no sólo promueve la uniformidad en las unidades, también sirve como un medio rápido para verificar si una ecuación tiene sentido. ⁶

Nuestro siguiente ejemplo trata sobre la función de costo promedio, introducida por primera vez en la página 82, aplicada a los sistemas PortaBoy Game del Ejemplo 2.1.5 en la Sección 2.1.

Ejemplo 4.3.4

Dada una función de costo\(C(x)\), que devuelve el costo total de producir\(x\) artículos, recuerde que la función de costo promedio,\(\overline{C}(x) = \frac{C(x)}{x}\) calcula el costo por artículo cuando se producen\(x\) los artículos. Supongamos que el costo\(C\), en dólares, para producir sistemas de juegos\(x\) PortaBoy para un minorista local es\(C(x) = 80x + 150\),\(x \geq 0\).

1. Encuentre una expresión para la función de costo promedio\(\overline{C}(x)\).
2. Resolver\(\overline{C}(x) < 100\) e interpretar.
3. Determinar el comportamiento de\(\overline{C}(x)\) as\(x \rightarrow \infty\) e interpretar.

Solución.

1. De\(\overline{C}(x) = \frac{C(x)}{x}\), obtenemos\(\overline{C}(x) = \frac{80x+150}{x}\). El dominio de\(C\) es\(x \geq 0\), pero como\(x=0\) causa problemas para\(\overline{C}(x)\), conseguimos que nuestro dominio sea\(x>0\), o\((0, \infty)\).
2. Resolver\(\overline{C}(x) < 100\) significa que resolvemos\(\frac{80x+150}{x} < 100\). Se procede como en el ejemplo anterior.

   \[\begin{array}{rclr} \dfrac{80x+150}{x} & < & 100 & \\[4pt] \dfrac{80x+150}{x} - 100 & < & 0 & \\[4pt] \dfrac{80x + 150 - 100x}{x} & < & 0 & \mbox{common denominator} \\[4pt] \dfrac{150 - 20x}{x} & < & 0 & \\ \end{array}\nonumber\]

   Si tomamos el lado izquierdo para ser una función racional\(r(x)\), hay que tener en cuenta que el dominio aplicado del problema es\(x > 0\). Esto significa que consideramos solo la mitad positiva de la línea numérica para nuestro diagrama de signos. On\((0, \infty)\),\(r\) se define en todas partes así que solo necesitamos buscar ceros de\(r\). Ajuste\(r(x)=0\) da\(150-20x =0\), así que eso\(x = \frac{15}{2}= 7.5\). Los intervalos de prueba en nuestro dominio son\((0, 7.5)\) y\((7.5, \infty)\). Nos encontramos\(r(x) < 0\) en\((7.5, \infty)\).

   

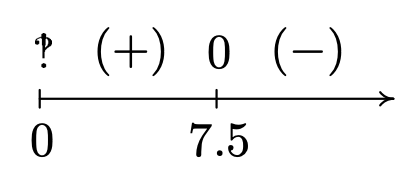
   En el contexto del problema,\(x\) representa el número de sistemas de juegos PortaBoy producidos y\(\overline{C}(x)\) es el costo promedio para producir cada sistema. Resolver\(\overline{C}(x) < 100\) significa que estamos tratando de encontrar cuántos sistemas necesitamos producir para que el costo promedio sea menor que\(\$100\) por sistema. Nuestra solución, nos\((7.5, \infty)\) dice que necesitamos producir más que\(7.5\) sistemas para lograrlo. Como no tiene sentido producir medio sistema, nuestra respuesta final es\([8, \infty)\).

3. Cuando aplicamos el Teorema 4.2 a\(\overline{C}(x)\) encontramos que\(y=80\) es una asíntota horizontal a la gráfica de\(y=\overline{C}(x)\). Para determinar con mayor precisión el comportamiento de\(\overline{C}(x)\) as\(x \rightarrow \infty\), primero usamos la división larga ⁷ y reescribimos\(\overline{C}(x) = 80+\frac{150}{x}\). Como\(x \rightarrow \infty\),\(\frac{150}{x} \rightarrow 0^{+}\), lo que significa\(\overline{C}(x) \approx 80+\text { very small }(+)\). Así, el costo promedio por sistema se está acercando a\(\$ 80\) por sistema. Si nos fijamos\(\overline{C}(x) = 80\), obtenemos\(\frac{150}{x} = 0\), lo cual es imposible, entonces concluimos que\(\overline{C}(x) > 80\) para todos\(x > 0\). Esto significa que el costo promedio por sistema siempre es mayor que\(\$ 80\) por sistema, pero el costo promedio se acerca a esta cantidad a medida que se producen más y más sistemas. Mirando hacia atrás en el Ejemplo 2.1.5, nos damos cuenta\(\$ 80\) es el costo variable por sistema\(-\) el costo por sistema por encima y más allá del costo inicial fijo de\(\$150\). Otra forma de interpretar nuestra respuesta es que “infinitamente” se necesitarían producir muchos sistemas para efectivamente 'eliminar' el costo fijo.

Nuestro siguiente ejemplo es otro problema clásico de 'caja sin top'.

Ejemplo 4.3.5

Se va a construir una caja con base cuadrada y sin tapa para que tenga un volumen de centímetros\(1000\) cúbicos. Dejar\(x\) denotar el ancho de la caja, en centímetros como se ve a continuación.

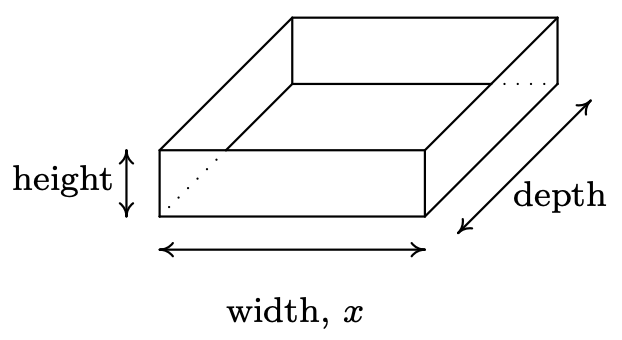
1. Exprese la altura\(h\) en centímetros en función del ancho\(x\) e indique el dominio aplicado.
2. Resolver\(h(x) \geq x\) e interpretar.
3. Encontrar e interpretar el comportamiento de\(h(x)\) como\(x \rightarrow 0^{+}\) y como\(x \rightarrow \infty\).
4. Exprese el área\(S\) de superficie de la caja como una función\(x\) y estado del dominio aplicado.
5. Use una calculadora para aproximar (a dos decimales) las dimensiones de la caja que minimizan el área de superficie.

Solución.

1. Nos dicen que el volumen de la caja es de centímetros\(1000\) cúbicos y eso\(x\) representa el ancho, en centímetros. De la geometría, sabemos\(\mbox{Volume} = \mbox{width} \times \mbox{height} \times \mbox{depth}\). Dado que la base de la caja es un cuadrado, el ancho y la profundidad son ambos\(x\) centímetros. Usando\(h\) para la altura, tenemos\(1000 = x^2h\), así que eso\(h = \frac{1000}{x^2}\). Usando notación de funciones, ⁸ En\(h(x) = \frac{1000}{x^2}\) cuanto al dominio aplicado, para que haya una caja en absoluto,\(x > 0\), y dado que cada elección de este tipo\(x\) devolverá un número positivo para la altura no\(h\) tenemos otras restricciones y concluimos que nuestro dominio es \((0, \infty)\).
2. Para resolverlo\(h(x) \geq x\), procedemos como antes y recogemos todos los términos distintos de cero en un lado de la desigualdad para usar un diagrama de signos.

   \[\begin{array}{rclr} h(x) & \geq & x & \\[4pt] \dfrac{1000}{x^2} & \geq & x & \\[4pt] \dfrac{1000}{x^2} - x & \geq & 0 \\[4pt] \dfrac{1000-x^3}{x^2} & \geq & 0 & \mbox{common denominator} \\[10pt] \end{array}\nonumber\]

   Consideramos el lado izquierdo de la desigualdad como nuestra función racional\(r(x)\). Vemos\(r\) es indefinido en\(x=0\), pero, como en el ejemplo anterior, el dominio aplicado del problema es\(x > 0\), por lo que estamos considerando sólo el comportamiento de\(r\) on\((0, \infty)\). El único cero de\(r\) viene cuando\(1000-x^3 = 0\), que es\(x=10\). Escogiendo valores de prueba en los intervalos\((0,10)\) y\((10, \infty)\) da el siguiente diagrama.

   

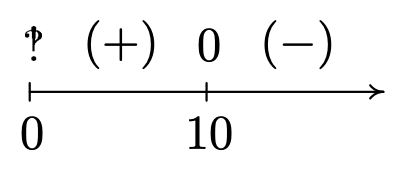
   Vemos\(r(x) > 0\) en\((0,10)\), y desde\(r(x) = 0\) en\(x=10\), nuestra solución es\((0,10]\). En el contexto del problema,\(h\) representa la altura de la caja mientras que\(x\) representa el ancho (y profundidad) de la caja. Resolver\(h(x) \geq x\) equivale a encontrar los valores de los\(x\) cuales resultan en un cuadro donde la altura es al menos tan grande como el ancho (y, en este caso, la profundidad). Nuestra respuesta nos dice que el ancho de la caja puede ser como máximo\(10\) centímetros para que esto suceda.

3. Como\(x \rightarrow 0^{+}\),\(h(x) = \frac{1000}{x^2} \rightarrow \infty\). Esto significa que cuanto menor sea el ancho\(x\) (y, en este caso, la profundidad), mayor debe ser la altura\(h\) para mantener un volumen de centímetros\(1000\) cúbicos. Como\(x \rightarrow \infty\), encontramos\(h(x) \rightarrow 0^{+}\), lo que significa que para mantener un volumen de centímetros\(1000\) cúbicos, el ancho y la profundidad deben hacerse más grandes a medida que la altura se hace más pequeña.
4. Dado que la caja no tiene parte superior, el área de superficie se puede encontrar agregando el área de cada uno de los lados al área de la base. La base es un cuadrado de dimensiones\(x\) por\(x\), y cada lado tiene dimensiones\(x\) por\(h\). Obtenemos la superficie,\(S = x^2+4xh\). Para obtener\(S\) en función de\(x\), sustituimos\(h = \frac{1000}{x^2}\) para obtener\(S = x^2+4x \left( \frac{1000}{x^2}\right)\). De ahí que, en función de\(x\),\(S(x) = x^2 + \frac{4000}{x}\). El dominio de\(S\) es el mismo que\(h\), es decir\((0, \infty)\), por las mismas razones que antes.
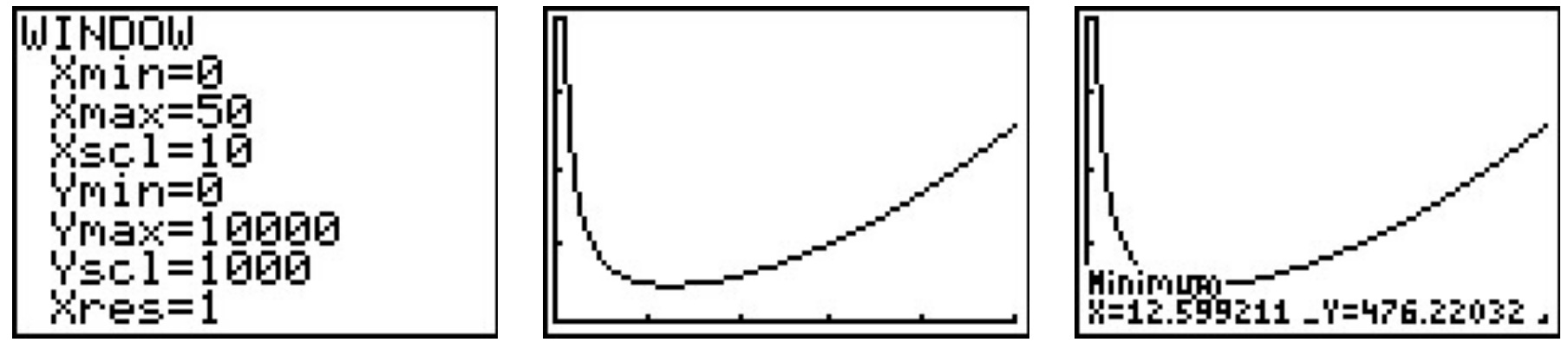
5. Un primer intento de la gráfica de\(y=S(x)\) en la calculadora puede llevar a la frustración. Es muy probable que la primera ventana elegida para ver la gráfica sugiera que\(y=S(x)\) tenga el\(x\) eje -como asíntota horizontal. De la fórmula\(S(x) = x^2 + \frac{4000}{x}\), sin embargo, obtenemos\(S(x) \approx x^2\) como\(x \rightarrow \infty\), entonces\(S(x) \rightarrow \infty\). Reajustando la ventana, encontramos que\(S\) posee un mínimo relativo en\(x \approx 12.60\). Por lo que podemos decir, ⁹ este es el único extremo relativo, por lo que también es el mínimo absoluto. Esto significa que el ancho y la profundidad de la caja deben medir cada uno aproximadamente\(12.60\) centímetros. Para determinar la altura, encontramos\(h(12.60) \approx 6.30\), por lo que la altura de la caja debe ser aproximadamente\(6.30\) centímetros.

4.3.1 Variación

En muchos casos en las ciencias, las funciones racionales se encuentran como resultado de leyes naturales fundamentales que suelen ser el resultado de asumir ciertas relaciones básicas entre variables. Estas relaciones básicas se resumen en la siguiente definición.

Definición 4.5

Supongamos\(x\),\(y\) y\(z\) son cantidades variables. Nosotros decimos

• \(y\)varía directamente con (o es directamente proporcional a)\(x\) si hay una constante\(k\) tal que\(y=kx\).
• \(y\)varía inversamente con (o es inversamente proporcional a)\(x\) si hay una constante\(k\) tal que\(y=\frac{k}{x}\).
• \(z\)varía conjuntamente con (o es conjuntamente proporcional a)\(x\) y\(y\) si hay una constante\(k\) tal que\(z = kxy\).

La constante\(k\) en las definiciones anteriores se llama la constante de proporcionalidad.

Ejemplo 4.3.6

Traduzca lo siguiente en ecuaciones matemáticas usando la Definición 4.5.

1. Ley de Hooke: La fuerza\(F\) ejercida sobre un muelle es directamente proporcional a la extensión\(x\) del resorte.
2. Ley de Boyle: A temperatura constante, la presión\(P\) de un gas ideal es inversamente proporcional a su volumen\(V\).
3. El volumen\(V\) de un cono circular derecho varía conjuntamente con la altura\(h\) del cono y el cuadrado del radio\(r\) de la base.
4. Ley de Ohm: La corriente\(I\) a través de un conductor entre dos puntos es directamente proporcional al voltaje\(V\) entre los dos puntos e inversamente proporcional a la resistencia\(R\) entre los dos puntos.
5. Ley de la Gravitación Universal de Newton: Supongamos que dos objetos, uno de masa\(m\) y otro de masa\(M\), están posicionados de manera que la distancia entre sus centros de masa sea\(r\). La fuerza gravitacional\(F\) ejercida sobre los dos objetos varía directamente con el producto de las dos masas e inversamente con el cuadrado de la distancia entre sus centros de masa.

Solución.

1. Aplicando la definición de variación directa, obtenemos\(F = k x\) por alguna constante\(k\).
2. Ya que\(P\) y\(V\) son inversamente proporcionales, escribimos\(P = \frac{k}{V}\).
3. Aquí hay un poco de ambigüedad. Es claro que el volumen y la altura del cono están representados por las cantidades\(V\) y\(h\), respectivamente, pero ¿\(r\)representa el radio de la base o el cuadrado del radio de la base? Es el primero. Por lo general, si se especifica una operación algebraica (como la cuadratura), se pretende que se exprese en la fórmula. Aplicamos la Definición 4.5 para obtener\(V = k h r^{2}\).
4. A pesar de que el problema no usa la frase 'varía conjuntamente', está implícito por el hecho de que la corriente\(I\) está relacionada con dos cantidades diferentes. Ya que\(I\) varía directamente con\(V\) pero inversamente con\(R\), escribimos\(I = \frac{k V}{R}\).
5. Escribimos el producto de las masas\(mM\) y el cuadrado de la distancia como\(r^2\). Tenemos que\(F\) varía directamente con\(mM\) e inversamente con\(r^2\), entonces\(F = \frac{kmM}{r^2}\).

En muchas de las fórmulas del ejemplo anterior, se relacionan más de dos cantidades variables. En la práctica, sin embargo, generalmente todas las cantidades menos dos se mantienen constantes en un experimento y los datos recopilados se utilizan para relacionar solo dos de las variables. Comparar solo dos cantidades variables nos permite ver la relación entre ellas como funcional, como ilustra el siguiente ejemplo.

Ejemplo 4.3.7

Según este sitio web se dan a continuación los datos reales relativos al volumen\(V\) de un gas y su presión\(P\) utilizada por Boyle y su asistente en 1662 para verificar la ley de gas que lleva su nombre.

\[\begin{array}{|c||c|c|c|c|c|c|c|c|c|c|c|c|c|} \hline V & 48 & 46 & 44 & 42 & 40 & 38 & 36 & 34 & 32 & 30 & 28 & 26 & 24 \\ \hline P & 29.13 & 30.56 & 31.94 & 33.5 & 35.31 & 37 & 39.31 & 41.63 & 44.19 & 47.06 & 50.31 & 54.31 & 58.81 \\ \hline \end{array}\nonumber\]

\[\begin{array}{|c||c||c|c|c|c|c|c|c|c|c|c|c|c|} \hline V & 23 & 22 & 21 & 20 & 19 & 18 & 17 & 16 & 15 & 14 & 13 & 12 \\ \hline P & 61.31 & 64.06 & 67.06 & 70.69 & 74.13 & 77.88 & 82.75 & 87.88 & 93.06 & 100.44 & 107.81 & 117.56 \\ \hline \end{array}\nonumber\]

1. Usa tu calculadora para generar un diagrama de dispersión para estos datos usando\(V\) como variable independiente y\(P\) como variable dependiente. ¿Aparece de la gráfica que\(P\) es inversamente proporcional a\(V\)? Explique.
2. Suponiendo que\(P\) y\(V\) sí varían inversamente, utilizar los datos para aproximar la constante de proporcionalidad.
3. Usa tu calculadora para determinar una 'Regresión de Potencia' para estos datos ¹⁰ y utilízala verifica tus resultados en 1 y 2.

Solución.

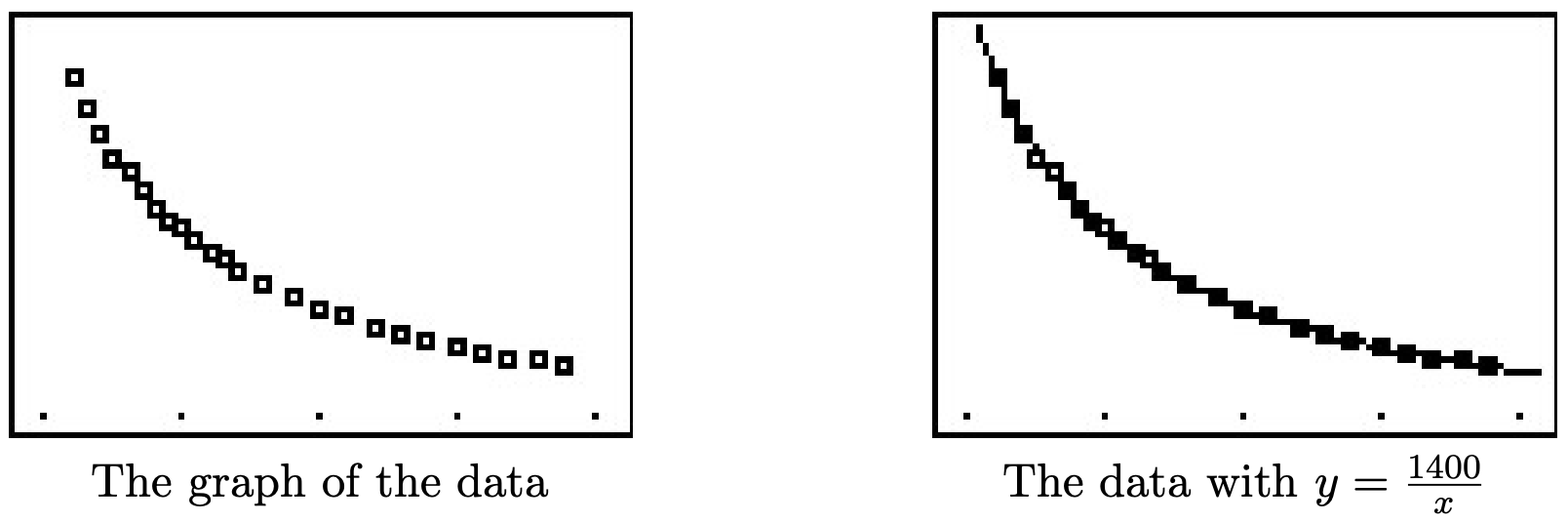
1. Si\(P\) realmente varía inversamente con\(V\), entonces\(P = \frac{k}{V}\) para alguna constante\(k\). A partir de la gráfica de datos, los puntos parecen estar a lo largo de una curva como\(y = \frac{k}{x}\).
2. Para determinar la constante de proporcionalidad, observamos que de\(P = \frac{k}{V}\), obtenemos\(k = PV\). Multiplicando cada uno de los números de volumen por cada uno de los números de presión, ¹¹ producimos un número que siempre es aproximadamente\(1400\). Eso sospechamos\(P = \frac{1400}{V}\). Graficar\(y = \frac{1400}{x}\) junto con los datos nos da una buena razón para creer nuestras hipótesis que\(P\) y, de hecho,\(V\) están inversamente relacionadas.

   

3. Después de realizar una 'regresión de potencia', la calculadora ajusta los datos a la curva\(y = ax^b\) donde\(a \approx 1400\) y\(b \approx -1\) con un coeficiente de correlación el cual está casi perfecto. ¹² En otras palabras,\(y = 1400 x^{-1}\) o\(y = \frac{1400}{x}\), como adivinamos.

   

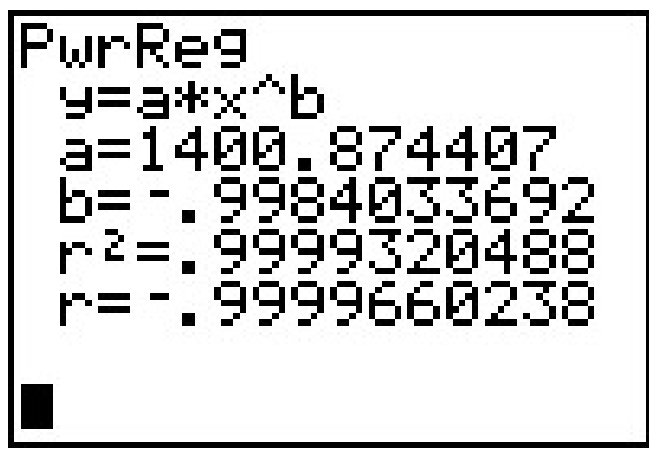
4.3.2 Ejercicios

En los Ejercicios 1 - 6, resuelve la ecuación racional. Asegúrese de verificar si hay soluciones extrañas.

1. \(\dfrac{x}{5x + 4} = 3\)
2. \(\dfrac{3x - 1}{x^{2} + 1} = 1\)
3. \(\dfrac{1}{x + 3} + \dfrac{1}{x - 3} = \dfrac{x^{2} - 3}{x^{2} - 9}\)
4. \(\dfrac{2x + 17}{x + 1} = x + 5\)
5. \(\dfrac{x^{2} - 2x + 1}{x^{3} + x^{2} - 2x} = 1\)
6. \(\dfrac{-x^{3} + 4x}{x^{2} - 9} = 4x\)

En los Ejercicios 7 - 20, resolver la desigualdad racional. Exprese su respuesta usando notación de intervalos.

7. \(\dfrac{1}{x + 2} \geq 0\)
8. \(\dfrac{x - 3}{x + 2} \leq 0\)
9. \(\dfrac{x}{x^{2} - 1} > 0\)
10. \(\dfrac{4x}{x^2+4} \geq 0\)
11. \(\dfrac{x^2-x-12}{x^2+x-6} > 0\)
12. \(\dfrac{3x^2-5x-2}{x^2-9} < 0\)
13. \(\dfrac{x^3+2x^2+x}{x^2-x-2} \geq 0\)
14. \(\dfrac{x^{2} + 5x + 6}{x^{2} - 1} > 0\)
15. \(\dfrac{3x - 1}{x^{2} + 1} \leq 1\)
16. \(\dfrac{2x + 17}{x + 1} > x + 5\)
17. \(\dfrac{-x^{3} + 4x}{x^{2} - 9} \geq 4x\)
18. \(\dfrac{1}{x^{2} + 1} < 0\)
19. \(\dfrac{x^4-4x^3+x^2-2x-15}{x^3-4x^2} \geq x\)
20. \(\dfrac{5x^3-12x^2+9x+10}{x^2-1}\geq 3x-1\)
21. Carl y Mike inician una carrera de 3 millas al mismo tiempo. Si Mike corrió la carrera a 6 millas por hora y termina la carrera 10 minutos antes que Carl, ¿qué tan rápido corre Carl?
22. Un día, Donnie observa que el viento sopla a 6 millas por hora. Una golondrina en vacío que anida cerca de la casa de Donnie vuela tres cuartos de milla por la carretera (en la dirección del viento), se da la vuelta y regresa exactamente 4 minutos después. ¿Cuál es la velocidad del aire de la golondrina en vacío? (Aquí, 'velocidad aerodinámica' es la velocidad que la golondrina puede volar en aire quieto).
23. Para eliminar el agua de un sótano inundado, se utilizan dos bombas, cada una con una calificación de 40 galones por minuto. Después de media hora, la única bomba se quema, y la segunda bomba termina de retirar el agua media hora después. ¿Cuántos galones de agua se retiraron del sótano?
24. Un grifo puede llenar un fregadero en 5 minutos mientras que un desagüe vaciará el mismo fregadero en 8 minutos. Si el grifo está encendido y el desagüe se deja abierto, ¿cuánto tiempo tardará en llenar el fregadero?
25. Trabajando juntos, Daniel y Donnie pueden limpiar la pluma de llama en 45 minutos. Por su cuenta, Daniel puede limpiar la pluma en una hora. ¿Cuánto tiempo le toma a Donnie limpiar el bolígrafo de llama por su cuenta?
26. En el Ejercicio 32, la función\(C(x) = .03x^{3} - 4.5x^{2} + 225x + 250\), for\(x \geq 0\) se utilizó para modelar el costo (en dólares) para producir sistemas de juego\(x\) PortaBoy. Usando esta función de costo, encuentre el número de PortaBoys que se deben producir para minimizar el costo promedio\(\overline{C}\). Redondee su respuesta al número más cercano de sistemas.
27. Supongamos que estamos en la misma situación que el Ejemplo 4.3.5. Si el volumen de la caja va a ser centímetros\(500\) cúbicos, use su calculadora para encontrar las dimensiones de la caja que minimicen el área de superficie. ¿Cuál es la superficie mínima? Redondee sus respuestas a dos decimales.
28. La caja para el nuevo cereal de temática Sasquatch, 'Crypt-Os', es tener un volumen de pulgadas\(140\) cúbicas. Por razones estéticas, la altura de la caja necesita ser\(1.62\) multiplicada por el ancho de la base de la caja. ¹³ Encuentre las dimensiones de la caja que minimizarán el área de superficie de la caja. ¿Cuál es la superficie mínima? Redondee sus respuestas a dos decimales.
29. Sally es vecina de Skippy del Ejercicio 19 en la Sección 2.3. Sally también quiere plantar un huerto a un costado de su casa. Ella no tiene ningún cercado, pero quiere mantener el tamaño del jardín a 100 pies cuadrados. ¿Cuáles son las dimensiones del jardín que minimizarán la cantidad de cercas que necesita comprar? ¿Cuál es la cantidad mínima de esgrima que necesita para comprar? Redondee sus respuestas al pie más cercano. (Nota: Dado que un lado del jardín bordeará la casa, Sally no necesita cercas a lo largo de ese lado).
30. Otro problema clásico: Una lata está hecha en forma de cilindro circular derecho y es para sostener una pinta. (Para productos secos, una pinta es igual a pulgadas\(33.6\) cúbicas). ¹⁴
    1. Encuentra una expresión para el volumen\(V\) de la lata en términos de la altura\(h\) y el radio base\(r\).
    2. Encuentre una expresión para el área\(S\) de superficie de la lata en términos de la altura\(h\) y el radio base\(r\). (Sugerencia: La parte superior e inferior de la lata son círculos de radio\(r\) y el lado de la lata es realmente solo un rectángulo que se ha doblado en un cilindro).
    3. Utilizando el hecho de que\(V = 33.6\), escribir\(S\) en función de\(r\) y exponer su dominio aplicado.
    4. Utilice su calculadora gráfica para encontrar las dimensiones de la lata que tiene un área de superficie mínima.
31. Un tambor cilíndrico derecho es para contener 7.35 pies cúbicos de líquido. Encuentre las dimensiones (radio de la base y altura) del tambor lo que minimizaría el área de superficie. ¿Cuál es la superficie mínima? Redondee sus respuestas a dos decimales.
32. En el Ejercicio 71 de la Sección 1.4, la población de Sasquatch en el Condado de Portage fue modelada por la función\(P(t) = \frac{150t}{t + 15}\), donde\(t = 0\) representa el año 1803. ¿Cuándo había menos de 100 Sasquatch en el condado de Portage?

En los Ejercicios 33 - 38, traduzca lo siguiente en ecuaciones matemáticas.

33. A una presión constante, la temperatura\(T\) de un gas ideal es directamente proporcional a su volumen\(V\). (Esta es la Ley de Carlos)
34. La frecuencia de una onda\(f\) es inversamente proporcional a la longitud de onda de la onda\(\lambda\).
35. La densidad\(d\) de un material es directamente proporcional a la masa del objeto\(m\) e inversamente proporcional a su volumen\(V\).
36. El cuadrado del periodo orbital de un planeta\(P\) es directamente proporcional al cubo del semieje mayor de su órbita\(a\). (Esta es la Tercera Ley del Movimiento Planetario de Kepler)
37. El arrastre de un objeto que viaja a través de un fluido\(D\) varía conjuntamente con la densidad del fluido\(\rho\) y el cuadrado de la velocidad del objeto\(\nu\).
38. Supongamos que dos cargas puntuales eléctricas, una con carga\(q\) y otra con carga\(Q\), se colocan\(r\) unidades separadas. La fuerza electrostática\(F\) ejercida sobre las cargas varía directamente con el producto de las dos cargas e inversamente con el cuadrado de la distancia entre las cargas. (Esta es la Ley de Coulomb)
39. Según esta página web, la frecuencia\(f\) de una cuerda vibratoria viene dada por\(f = \dfrac{1}{2L} \sqrt{\dfrac{T}{\mu}}\) dónde\(T\) está la tensión,\(\mu\) es la masa lineal ¹⁵ de la cuerda y\(L\) es la longitud de la parte vibrante de la cuerda. Expresar esta relación utilizando el lenguaje de la variación.
40. De acuerdo con los Centros para el Control y la Prevención de Enfermedades www.cdc.gov, el Índice de Masa Corporal de una persona\(B\) es directamente proporcional a su peso\(W\) en libras e inversamente proporcional al cuadrado de su estatura\(h\) en pulgadas.
    1. Expresar esta relación como una ecuación matemática.
    2. Si una persona que tenía\(5\) pies,\(10\) pulgadas de alto pesaba 235 libras tenía un Índice de Masa Corporal de 33.7, ¿cuál es el valor de la constante de proporcionalidad?
    3. Reescribe la ecuación matemática que se encuentra en la parte 40a para incluir el valor de la constante que se encuentra en la parte 40b y luego encuentra tu Índice de Masa Corporal.
41. Sabemos que la circunferencia de un círculo varía directamente con su radio con\(2\pi\) como la constante de proporcionalidad. (Es decir, sabemos\(C = 2\pi r.\)) Con la ayuda de tus compañeros, haz una lista de otras relaciones geométricas básicas que pueden verse como variaciones.

4.3.3 Respuestas

1. \(x = -\frac{6}{7}\)
2. \(x = 1, \; x = 2\)
3. \(x = -1\)
4. \(x = -6, \; x = 2\)
5. Sin solución
6. \(x = 0, \; x = \pm 2\sqrt{2}\)
7. \((-2, \infty)\)
8. \((-2, 3]\)
9. \((-1, 0) \cup (1, \infty)\)
10. \([0, \infty)\)
11. \((-\infty, -3) \cup (-3,2) \cup (4, \infty)\)
12. \(\left(-3, -\frac{1}{3} \right) \cup (2,3)\)
13. \((-1,0] \cup (2, \infty)\)
14. \((-\infty, -3) \cup (-2, -1) \cup (1, \infty)\)
15. \((-\infty, 1] \cup [2, \infty)\)
16. \((-\infty, -6) \cup (-1, 2)\)
17. \((-\infty, -3) \cup \left[-2\sqrt{2}, 0\right] \cup \left[2\sqrt{2}, 3\right)\)
18. Sin solución
19. \([-3,0) \cup (0,4) \cup [5, \infty)\)
20. \(\left(-1,-\frac{1}{2}\right] \cup (1, \infty)\)
21. 4.5 millas por hora
22. 24 millas por hora
23. 3600 galones
24. \(\frac{40}{3} \approx 13.33\)minutos
25. 3 horas
26. El mínimo absoluto de\(y=\overline{C}(x)\) ocurre en\(\approx (75.73, 59.57)\). Dado que\(x\) representa el número de sistemas de juego, comprobamos\(\overline{C}(75) \approx 59.58\) y\(\overline{C}(76) \approx 59.57\). De ahí que para minimizar el costo promedio,\(76\) los sistemas deben producirse a un costo promedio de\(\$59.57\) por sistema.
27. El ancho (y profundidad) debe ser\(10.00\) centímetros, la altura debe ser\(5.00\) centímetros. La superficie mínima es de centímetros\(300.00\) cuadrados.
28. El ancho de la base de la caja debe ser\(\approx 4.12\) pulgadas, la altura de la caja debe ser\(\approx 6.67\) pulgadas, y la profundidad de la base de la caja debe ser\(\approx 5.09\) pulgadas; área de superficie mínima pulgadas\(\approx 164.91\) cuadradas.
29. Las dimensiones son\(\approx 7\) pies a\(\approx 14\) pies; cantidad mínima de vallas requeridas\(\approx 28\) pies.
30. 1. \(V = \pi r^{2}h\)
    2. \(S = 2 \pi r^{2} + 2\pi r h\)
    3. \(S(r) = 2\pi r^{2} + \frac{67.2}{r}, \;\)Dominio\(r > 0\)
    4. \(r \approx 1.749\,\)en. y\(h \approx 3.498\,\) en.
31. El radio del tambor debe ser\(\approx 1.05\) pies y la altura del tambor debe ser\(\approx 2.12\) pies. La superficie mínima del tambor es de pies\(\approx 20.93\) cúbicos.
32. \(P(t) < 100\)on\((-15, 30)\), y la porción de esto que se encuentra en el dominio aplicado es\([0,30)\). Ya que\(t=0\) corresponde al año 1803, desde 1803 hasta finales de 1832, hubo menos de 100 Sasquatch en el condado de Portage.
33. \(T = k V\)
34. ¹⁶\(f = \dfrac{k}{\lambda}\)
35. \(d = \dfrac{k m}{V}\)
36. \(P^2 = k a^3\)
37. ¹⁷\(D = k \rho \nu^2\)
38. ¹⁸\(F = \dfrac{kqQ}{r^2}\)
39. Reescribiendo\(f = \dfrac{1}{2L} \sqrt{\dfrac{T}{\mu}}\) como\(f = \dfrac{\frac{1}{2} \sqrt{T}}{L \sqrt{\mu}}\) vemos que la frecuencia\(f\) varía directamente con la raíz cuadrada de la tensión y varía inversamente con la longitud y la raíz cuadrada de la masa lineal.
40. 1. \(B = \dfrac{kW}{h^{2}}\)
    2. ¹⁹\(k = 702.68\)
    3. \(B = \dfrac{702.68W}{h^{2}}\)

---

Referencia

¹ No hay asíntota en\(x = 1\) ya que la gráfica se comporta bien cerca\(x = 1\). Según el Teorema 4.1, debe haber un agujero ahí.

² A esto se le llama un sistema de ecuaciones. Sin duda, ya has tenido experiencia con estas cosas antes, y estudiaremos los sistemas con mayor detalle en el Capítulo 8.

³ Si bien solemos desalentar dividir ambos lados de una ecuación por una expresión variable, lo sabemos\((6+R) \neq 0\) ya que de lo contrario no podríamos multiplicarla por\(t_{\text {down }}\) y obtener 5.

⁴ Se anima al lector a verificar que las unidades en esta ecuación son las mismas en ambos lados. Para empezar, las unidades en el '3' son 'horas'.

⁵ Carl preferiría pasar su tiempo escribiendo textos matemáticos de código abierto que jardinería de todos modos.

⁶ En otras palabras, ¡asegúrate de no intentar agregar manzanas a las naranjas!

⁷ En este caso, la división larga equivale a división término por término.

⁸ Es decir,\(h(x)\) significa '\(h\)de\(x\)', no '\(h\)veces\(x\)' aquí.

⁹ sin Cálculo, es decir...

¹⁰ Hablaremos más de esto en los próximos capítulos.

¹¹ Puedes usar decirle a la calculadora para hacer esta aritmética en las listas y ahorrarte algo de tiempo.

¹² Revisaremos este ejemplo una vez que hayamos desarrollado logaritmos en el Capítulo 6 para ver cómo podemos realmente 'linealizar' estos datos y hacer una regresión lineal para obtener el mismo resultado.

¹³ 1.62 es una aproximación cruda de la llamada 'Relación Dorada'\(\phi=\frac{1+\sqrt{5}}{2}\).

¹⁴ Según www.dictionary.com, hay diferentes valores dados para esta conversión. Nos quedaremos con 33.6in ³ para este problema.

¹⁵ También conocida como la densidad lineal. Es simplemente una medida de masa por unidad de longitud.

¹⁶ El carácter λ es la letra griega minúscula 'lambda'.

¹⁷ Los caracteres\(\rho\) y\(\nu\) son las letras griegas minúsculas 'rho' y 'nu, respectivamente.

¹⁸ Obsérvese la similitud con esta fórmula y la Ley de la Gravitación Universal de Newton como se discute en el Ejemplo 5.

¹⁹ El CDC utiliza 703.