5.1: Composición de la función

Antes de embarcarnos en otras aventuras con funciones, necesitamos tomarnos un tiempo para reunir nuestros pensamientos y obtener alguna perspectiva. El Capítulo 1 nos introdujo por primera vez a las funciones en la Sección 1.3. En ese momento, las funciones eran tipos específicos de relaciones - conjuntos de puntos en el plano que pasaron la Prueba de Línea Vertical, Teorema 1.1. En la Sección 1.4, desarrollamos la idea de que las funciones son procesos -reglas que hacen coincidir entradas con salidas- y esto dio lugar a los conceptos de dominio y rango. Hablamos sobre cómo las funciones podrían combinarse en la Sección 1.5 utilizando las cuatro operaciones aritméticas básicas, analizamos con más detalle sus gráficas en la Sección 1.6 y estudiamos cómo se comportaban sus gráficas bajo ciertas clases de transformaciones en la Sección 1.7. En el Capítulo 2, analizamos más de cerca tres familias de funciones: funciones lineales (Sección 2.1), funciones de valor absoluto ¹ (Sección 2.2) y funciones cuadráticas (Sección 2.3). Las funciones lineales y cuadráticas fueron casos especiales de funciones polinómicas, las cuales estudiamos en generalidad en el Capítulo 3. El capítulo 3 culminó con el Teorema Real de Factorización, Teorema 3.16, que dice que todas las funciones polinómicas con coeficientes reales pueden ser pensadas como productos de funciones lineales y cuadráticas. Nuestro siguiente paso fue ampliar nuestro campo de estudio ² a funciones racionales en el Capítulo 4. Al ser cocientes de polinomios, en última instancia podemos ver esta familia de funciones como una construcción de funciones lineales y cuadráticas también. Entonces, en cierto sentido, los Capítulos 2, 3 y 4 pueden ser pensados como un estudio exhaustivo de las funciones lineales y cuadráticas de ³ y sus combinaciones aritméticas como se describe en la Sección 1.5. Ahora queremos estudiar otras funciones algebraicas, tales como\(f(x) = \sqrt{x}\) y\(g(x) = x^{2/3}\), y el propósito de las dos primeras secciones de este capítulo es ver cómo este tipo de funciones surgen de funciones polinómicas y racionales. Para ello, primero estudiamos una nueva forma de combinar funciones como se definen a continuación.

Definición 5.1.

Supongamos\(f\) y\(g\) son dos funciones. El compuesto de\(g\) con\(f\), denotado\(g \circ f\), se define por la fórmula\((g \circ f) (x) = g(f(x))\), siempre que\(x\) sea un elemento del dominio de\(f\) y\(f(x)\) es un elemento del dominio de\(g\).

La cantidad también\(g \circ f\) se lee '\(g\)compuesta con\(f\)' o, más simplemente '\(g\)de'\(f\). ' En su nivel más básico, la Definición 5.1 nos dice obtener la fórmula para\(\left(g \circ f\right)(x)\), reemplazamos cada ocurrencia de\(x\) en la fórmula para\(g(x)\) con la fórmula que tenemos para\(f(x)\). Si damos un paso atrás y miramos esto desde una perspectiva procedimental, de 'entradas y salidas', la Definición 5.1 nos dice que la salida de\(g \circ f\) se encuentra tomando la salida de\(f\),\(f(x)\), y luego haciendo que la entrada a\(g\). El resultado,\(g(f(x))\), es la salida de\(g \circ f\). Desde esta perspectiva, vemos\(g \circ f\) como un proceso de dos pasos tomando una entrada\(x\) y primero aplicando el procedimiento\(f\) luego aplicando el procedimiento\(g\). Abstractamente, tenemos

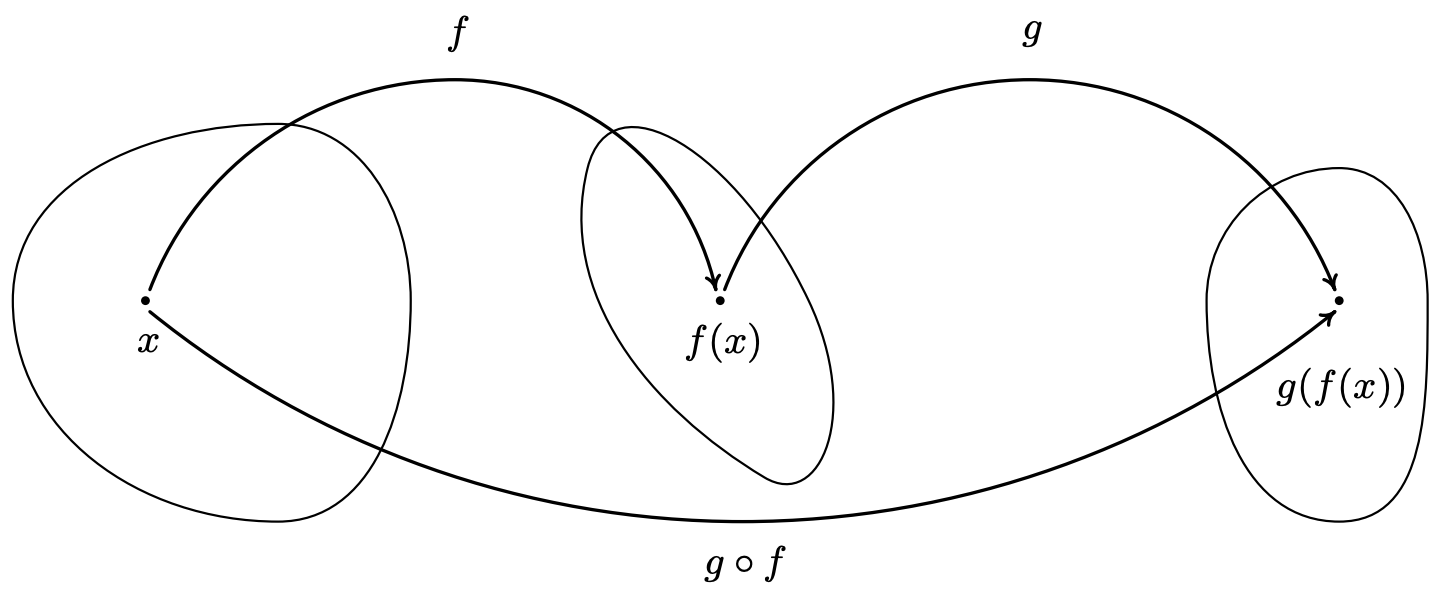
En la expresión\(g(f(x))\), la función a menudo\(f\) se llama la función 'inside' mientras que a menudo\(g\) se llama la función 'outside'. Hay dos formas de evaluar las funciones compuestas -'adentro out' y 'outside in'- dependiendo de qué función reemplacemos primero con su fórmula. Ambas formas se demuestran en el siguiente ejemplo.

Ejemplo 5.1.1

Vamos\(f(x) = x^2-4x\),\(g(x) = 2-\sqrt{x+3}\), y\(h(x) = \dfrac{2x}{x+1}\).

En los números 1 - 3, encuentra el valor de función indicado.

1. \((g \circ f)(1)\)
2. \((f \circ g)(1)\)
3. \((g \circ g)(6)\)

En los números 4 - 10, encuentre y simplifique las funciones compuestas indicadas. Declarar el dominio de cada uno.

4. \((g \circ f)(x)\)
5. \((f \circ g)(x)\)
6. \((g \circ h)(x)\)
7. \((h \circ g)(x)\)
8. \((h \circ h)(x)\)
9. \((h \circ (g \circ f))(x)\)
10. \(((h \circ g) \circ f)(x)\)

Solución.

1. Usando la Definición 5.1,\((g \circ f)(1) = g(f(1))\). Nos encontramos\(f(1) = -3\), así\[(g \circ f)(1) = g(f(1)) = g(-3) = 2\nonumber\]
2. Como antes, usamos la Definición 5.1 para escribir\((f \circ g)(1) = f(g(1))\). Nos encontramos\(g(1) = 0\), así\[(f \circ g)(1) = f(g(1)) = f(0) = 0\nonumber\]
3. Una vez más, nos dice la Definición 5.1\((g \circ g)(6) = g(g(6))\). Es decir, evaluamos\(g\) en\(6\), luego enchufamos ese resultado nuevamente en\(g\). Dado que\(g(6) = -1\),\[(g \circ g)(6) = g(g(6)) = g(-1) = 2-\sqrt{2}\nonumber\]
4. Por definición,\((g \circ f)(x) = g(f(x))\). Ahora ilustramos dos formas de abordar este problema.
   • adentro hacia afuera: Insertamos la expresión\(f(x)\) en\(g\) primero para obtener\[(g \circ f)(x) = g(f(x)) = g\left(x^2-4x\right) = 2 - \sqrt{\left(x^2-4x\right)+3} = 2 - \sqrt{x^2-4x+3}\nonumber\] Por lo tanto,\((g \circ f)(x) = 2 - \sqrt{x^2-4x+3}\).
   • afuera en: Utilizamos la fórmula para\(g\) primero para obtener\[(g \circ f)(x) = g(f(x)) = 2 - \sqrt{f(x)+3} = 2 - \sqrt{\left(x^2-4x\right)+3} = 2 - \sqrt{x^2-4x+3}\nonumber\] Obtenemos la misma respuesta que antes,\((g \circ f)(x) = 2 - \sqrt{x^2-4x+3}\).

   Para encontrar el dominio de\(g \circ f\), necesitamos encontrar los elementos en el dominio de\(f\) cuyas salidas\(f(x)\) están en el dominio de\(g\). Esto lo logramos siguiendo la regla establecida en la Sección 1.4, es decir, encontramos el dominio antes de simplificar. Para ello, examinamos\((g \circ f)(x) = 2 - \sqrt{\left(x^2-4x\right)+3}\). Para mantener feliz a la raíz cuadrada, resolvemos la desigualdad\(x^2-4x+3 \geq 0\) creando un diagrama de signos. Si lo dejamos\(r(x) = x^2-4x+3\), encontramos los ceros de\(r\) ser\(x = 1\) y\(x = 3\). Obtenemos

   

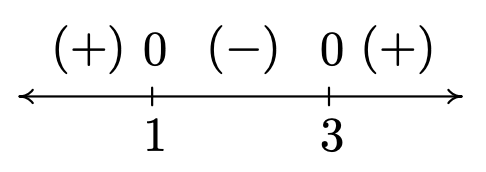
   Nuestra solución a\(x^2-4x+3 \geq 0\), y por lo tanto el dominio de\(g \circ f\), es\((-\infty, 1] \cup [3,\infty)\).

5. Para encontrar\((f \circ g)(x)\), nos encontramos\(f(g(x))\).
   • adentro hacia afuera: Insertamos la expresión\(g(x)\) en\(f\) primero para obtener

     \ (\ begin {alineado}
     (f\ circ g) (x) &=f (g (x)) =f (2-\ sqrt {x+3})\\
     & =( 2-\ sqrt {x+3}) ^ {2} -4 (2-\ sqrt {x+3})\\
     &=4-4\ sqrt {x+3} + (\ sqrt {x+3}) {2} -8+4\ sqrt {x+3}\\
     &=4+x+3-8\\
     &=x-1
     \ end {alineado}\)

   • afuera adentro: Utilizamos la fórmula para\(f(x)\) primero para obtener

     \ (\ begin {alineado}
     (f\ circ g) (x) &=f (g (x)) =( g (x)) ^ {2} -4 (g (x))\\
     & =( 2-\ sqrt {x+3}) ^ {2} -4 (2-\ sqrt {x+3})\\
     &=x-1\ quad\ quad\ quad\ quad\ quad\ quad\ text {mismo álgebra que antes}
     \ end {alineado}\)

   Así conseguimos\((f \circ g)(x) = x-1\). Para encontrar el dominio de\((f \circ g)\), miramos al paso antes de hacer alguna simplificación y encontrar\((f \circ g)(x) = \left(2-\sqrt{x+3}\right)^2 - 4\left(2-\sqrt{x+3}\right)\). Para mantener feliz a la raíz cuadrada, establecemos\(x+3 \geq 0\) y encontramos nuestro dominio para ser\([-3, \infty)\).

6. Para encontrar\((g \circ h)(x)\), calculamos\(g(h(x))\).
   • adentro hacia afuera: Insertamos la expresión\(h(x)\) en\(g\) primero para obtener

     \ (\ comenzar {alineado}
     (g\ circ h) (x) &=g (h (x)) =g\ izquierda (\ frac {2 x} {x+1}\ derecha)\\
     &=2-\ sqrt {\ izquierda (\ frac {2 x} {x+1}\ derecha) +3}\\
     &=2-\ sqrt {\ frac {2 x} {x+1} +\ frac {3 (x+1)} {x+1}}\ cuádruple\ cuádruple\ cuádruple\ cuádruple\ texto {
     obtener común denominadores}\\
     &=2-\ sqrt {\ frac {5 x+3} {x+1}}
     \ end {alineado}\)

   • afuera adentro: Utilizamos la fórmula para\(g(x)\) primero para obtener

     \ (\ comenzar {alineado}
     (g\ circ h) (x) &=g (h (x)) =2-\ sqrt {h (x) +3}\\
     &=2-\ sqrt {\ izquierda (\ frac {2 x} {x+1}\ derecha) +3}\\
     &=2-\ sqrt {\ frac {5 x+3} {x+1}}\ cuádruple\ quad\ quad\ quad\ text {
     obtener denominadores comunes como antes}
     \ end {alineado}\)

   Para encontrar el dominio de\((g \circ h)\), miramos al paso antes de comenzar a simplificar:\[(g \circ h)(x) = 2 - \sqrt{\left(\frac{2x}{x+1}\right)+3}\nonumber\] Para evitar la división por cero, necesitamos\(x \neq -1\). Para mantener feliz al radical, necesitamos resolver\[\frac{2x}{x+1} +3 = \frac{5x+3}{x+1}\geq 0\nonumber\] Definir\(r(x) = \frac{5x+3}{x+1}\), vemos\(r\) es indefinido en\(x=-1\) y\(r(x) = 0\) en\(x = -\frac{3}{5}\). Obtenemos

   

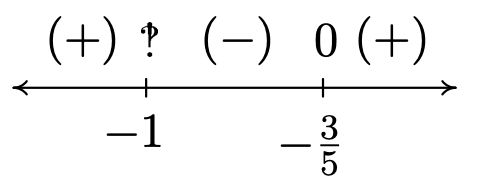
   Nuestro dominio es\((-\infty, -1) \cup \left[-\frac{3}{5}, \infty\right)\).

7. Nos encontramos\((h \circ g)(x)\) por encontrar\(h(g(x))\).
   • adentro hacia afuera: Insertamos la expresión\(g(x)\) en\(h\) primero para obtener

     \ (\ begin {alineado}
     (h\ circ g) (x) &=h (g (x)) =h (2-\ sqrt {x+3})\\
     &=\ frac {2 (2-\ sqrt {x+3})} {(2-\ sqrt {x+3}) +1}\\
     &=\ frac {4-2\ sqrt {x+3}} {-\ sqrt {x+3}}
     \ fin {alineado}\)

   • afuera adentro: Utilizamos la fórmula para\(h(x)\) primero para obtener

     \ [\ begin {alineado}
     (h\ circ g) (x) &=h (g (x)) =\ frac {2 (g (x))} {(g (x)) +1}\\
     &=\ frac {2 (2-\ sqrt {x+3})} {(2-\ sqrt {x+3}) +1}\\
     &=\ frac {4-2\ sqrt {x+3}} {3-\ sqrt {x+3}}
     \ final {alineado}\ nonumber\]

   Para encontrar el dominio de\(h \circ g\), miramos al paso antes de cualquier simplificación:\[(h \circ g)(x) = \frac{2 \left(2-\sqrt{x+3} \right)}{\left(2-\sqrt{x+3}\right)+1}\nonumber\] Para mantener feliz a la raíz cuadrada, requerimos\(x+3 \geq 0\) o\(x \geq -3\). Establecer el denominador igual a cero da\(\left(2-\sqrt{x+3}\right)+1=0\) o\(\sqrt{x+3} = 3\). Al cuadrar ambos lados nos da\(x+3=9\), o\(x=6\). Desde\(x=6\) cheques en la ecuación original,\(\left(2-\sqrt{x+3}\right)+1=0\), sabemos que\(x=6\) es el único cero del denominador. De ahí que el dominio de\(h \circ g\) es\([-3,6) \cup (6, \infty)\).

8. Para encontrar\((h \circ h)(x)\), sustituimos la función\(h\) en sí misma,\(h(h(x))\).
   • adentro hacia afuera: Insertamos la expresión\(h(x)\) en\(h\) para obtener

     \ (\ begin {alineada}
     (h\ circ h) (x) &=h (h (x)) =h\ izquierda (\ frac {2x} {x+1}\ derecha)\\
     &=\ frac {2\ izquierda (\ frac {2 x} {x+1}\ derecha)} {\ izquierda (\ frac {2 x} {x+1}\ derecha) +1}\
     &=\ frac {\ frac {4 x} {x+1}} {\ frac {2 x} {x+1} +1}\ cdot\ frac {(x+1)} {(x+1)}\\
     &=\ frac {\ frac {4 x} {x+1}\ cdot (x+1)} {\ izquierda (\ frac {2 x} {x+1}\ derecha)\ cdot (x+1) +1\ cdot (x+1)}\\
     &=\ frac {\ frac {4 x} {\ cancelto {1} {(x+1)}} i\ cancelar {(+1)}} {\ frac {2 x} {\ cancelto {1} {(x+1)}}\ cdot\ cancel {(x+1)} +x+1}\\
     &=\ frac {4 x} {3 x+1}
     \ end { alineado}\)

   • afuera adentro: Este enfoque rinde

     \ (\ begin {alineado}
     (h\ circ h) (x) &=h (h (x)) =\ frac {2 (h (x))} {h (x) +1}\\
     &=\ frac {2\ izquierda (\ frac {2 x} {x+1}\ derecha)} {\ izquierda (\ frac {2 x} {x+1}\ derecha) +1}\\
     &=\ frac {4 x} {3 x+1}\ quad\ quad\ quad\ quad\ quad\ text {mismo álgebra que antes}
     \ end {alineado}\)

   Para encontrar el dominio de\(h \circ h\), analizamos\[(h \circ h)(x) = \dfrac{2\left(\dfrac{2x}{x+1}\right)}{\left(\dfrac{2x}{x+1}\right)+1}\nonumber\] Para mantener\(x+1\) feliz el denominador, necesitamos\(x \neq -1\). Establecer el denominador\[\frac{2x}{x+1}+1 = 0\nonumber\] da\(x = -\frac{1}{3}\). Nuestro dominio es\((-\infty, -1) \cup \left(-1, -\frac{1}{3}\right) \cup \left(-\frac{1}{3}, \infty\right)\).

9. La expresión\((h \circ (g \circ f))(x)\) indica que primero encontramos el compuesto,\(g \circ f\) y componemos la función\(h\) con el resultado. Sabemos por el número 1 que\((g \circ f)(x) = 2 - \sqrt{x^2-4x+3}\). Ahora procedemos como de costumbre.
   • adentro hacia afuera: Insertamos la expresión\((g \circ f)(x)\) en\(h\) primero para obtener

     \ (\ begin {alineado}
     (h\ circ (g\ circ f)) (x) &=h ((g\ circ f) (x)) =h\ izquierda (2-\ sqrt {x^ {2} -4 x+3}\ derecha)\\
     &=\ frac {2\ izquierda (2-\ sqrt {x^ {2} -4 x+3}\ derecha)} {izquierda (2-\ sqrt {x^ {2} -4 x+3}\ derecha) +1}\\
     &=\ frac {4-2\ sqrt {x^ {2} -4 x+3}} {3-\ sqrt {x^ {2} -4 x +3}}
     \ final {alineado}\)

   • afuera adentro: Utilizamos la fórmula para\(h(x)\) primero para obtener

     \ (\ begin {alineado}
     (h\ circ (g\ circ f)) (x) &=h ((g\ circ f) (x)) =\ frac {2 ((g\ circ f) (x))} {((g\ circ f) (x)) +1}\\
     &=\ frac {2\ izquierda (2-\ sqrt {x^ {2} -4 x+3}\ derecha)} {\ izquierda (2-\ sqrt {x^ {2} -4 x+3}\ derecha) +1}\\
     &=\ frac {4-2\ sqrt {x^ {2} -4 x+3}} {3-\ sqrt {x^ {2} -4 x+3}}
     \ final {alineado}\)

   Para encontrar el dominio de\((h \circ (g \circ f))\), nos fijamos en el paso antes de empezar a simplificar,\[(h \circ (g \circ f))(x) = \frac{2 \left(2 - \sqrt{x^2-4x+3}\right)}{\left(2 - \sqrt{x^2-4x+3}\right)+1}\nonumber\] Para la raíz cuadrada, necesitamos\(x^2-4x+3 \geq 0\), que determinamos en el número 1 para ser\((-\infty, 1] \cup [3,\infty)\). A continuación, establecemos el denominador a cero y resolvemos:\(\left(2 - \sqrt{x^2-4x+3}\right)+1 = 0\). Obtenemos\(\sqrt{x^2-4x+3} = 3\), y, después de cuadrar ambos lados, tenemos\(x^2-4x+3 = 9\). Para resolver\(x^2-4x-6 = 0\), usamos la fórmula cuadrática y obtenemos\(x = 2 \pm \sqrt{10}\). Se anima al lector a verificar que ambos números satisfacen la ecuación original,\(\left(2 - \sqrt{x^2-4x+3}\right)+1 = 0\). De ahí que debemos excluir estos números del dominio de\(h \circ (g \circ f)\). Nuestro dominio final para\(h \circ (f \circ g)\) es\((-\infty, 2 -\sqrt{10}) \cup (2 - \sqrt{10}, 1] \cup \left[3, 2 + \sqrt{10}\right) \cup \left(2+\sqrt{10}, \infty\right)\).

10. La expresión\(((h \circ g) \circ f)(x)\) indica que primero encontramos el compuesto\(h \circ g\) y luego lo componemos con\(f\). Del número 4, tenemos\[(h \circ g)(x) = \frac{4-2\sqrt{x+3}}{3-\sqrt{x+3}}\nonumber\] Ahora procedemos como antes.
    • adentro hacia afuera: Insertamos la expresión\(f(x)\) en\(h \circ g\) primero para obtener

      \ (\ begin {alineado}
      ((h\ circ g)\ circ f) (x) & =( h\ circ g) (f (x)) =( h\ circ g)\ izquierda (x^ {2} -4 x\ derecha)\\
      &=\ frac {4-2\ sqrt {\ izquierda (x^ {2} -4 x\ derecha) +3}} {3-\ sqrt {\ sqrt (x^ {2} -4 x\ derecha) +3} {3-\ sqrt {\ izquierda (x^ {2} -4 x\ derecha) +3}}\\
      &=\ frac {4-2\ sqrt {x^ {2} -4 x+3}} {3-\ sqrt {x^ {2} -4 x+ 3}}
      \ final {alineado}\)

    • afuera adentro: Utilizamos la fórmula para\((h \circ g)(x)\) primero para obtener

      \ (\ begin {alineado}
      ((h\ circ g)\ circ f) (x) & =( h\ circ g) (f (x)) =\ frac {4-2\ sqrt {(f (x)) +3}} {3-\ sqrt {f (x)) +3}}\\
      &=\ frac {4-2\ sqrt {\ izquierda (x^ {} -4 x\ derecha) +3}} {3-\ sqrt {\ izquierda (x^ {2} -4 x\ derecha) +3}}\\
      &=\ frac {4-2\ sqrt {x^ {2} -4 x+3}} {3-\ sqrt {x^ {2} -4 x+3}}
      \ final {alineado}\)

    Observamos que la fórmula para\(((h \circ g) \circ f)(x)\) antes de simplificación es idéntica a la de\((h \circ (g \circ f))(x)\) antes la simplificamos. De ahí que las dos funciones tengan el mismo dominio,\(h \circ (f \circ g)\) es\((-\infty, 2 -\sqrt{10}) \cup (2 - \sqrt{10}, 1] \cup \left[3, 2 + \sqrt{10}\right) \cup \left(2+\sqrt{10}, \infty\right)\).

Debe quedar claro a partir del Ejemplo 5.1.1 que, en general, cuando se componen dos funciones, como\(f\) y\(g\) por encima, el orden importa. ⁴ Se encontró que las funciones\(f \circ g\) y\(g \circ f\) eran diferentes como fueron\(g \circ h\) y\(h \circ g\). Pensar en las funciones como procesos, esto no es tan sorprendente. Si pensamos en un proceso como ponernos los calcetines, y el otro como ponernos los zapatos, el orden en que hagamos estas dos tareas sí importa. ⁵ También tenga en cuenta la importancia de encontrar el dominio de la función compuesta antes de simplificar. Por ejemplo, el dominio de\(f \circ g\) es muy diferente de lo que indicaría su fórmula simplificada. Componer una función consigo misma, como en el caso de encontrar\((g\circ g)(6)\) y\((h \circ h)(x)\), puede parecer extraño. Mirando esto desde una perspectiva procesal, sin embargo, esto simplemente indica realizar una tarea\(h\) y luego volverla a hacer, como configurar la lavadora para que haga un 'enjuague doble'. Componer una función consigo misma se llama 'iterar' la función, y fácilmente podríamos gastar todo un curso en eso. Los dos últimos problemas del Ejemplo 5.1.1 sirven para demostrar la propiedad asociativa de las funciones. Es decir, al componer tres (o más) funciones, siempre y cuando mantengamos el orden igual, no importa qué dos funciones compongamos primero. Esta propiedad así como otra propiedad importante se enumeran en el teorema a continuación.

Teorema 5.1. Propiedades de la composición de la función

Supongamos\(f\)\(g\),, y\(h\) son funciones.

• \(h \circ (g \circ f) = (h \circ g) \circ f\), siempre que se definan las funciones compuestas.
• Si\(I\) se define como\(I(x) = x\) para todos los números reales\(x\), entonces\(I \circ f = f \circ I =f\).

Por repetidas aplicaciones de la Definición 5.1, encontramos\((h \circ (g \circ f))(x) = h((g \circ f)(x)) = h(g(f(x)))\). De igual manera,\(((h \circ g) \circ f)(x) = (h \circ g)(f(x)) = h(g(f(x)))\). Esto establece que las fórmulas para las dos funciones son las mismas. Dejamos al lector pensar por qué los dominios de estas dos funciones son idénticos, también. Estos dos hechos establecen la igualdad\(h \circ (g \circ f) = (h \circ g) \circ f\). Una consecuencia de la asociatividad de la composición de funciones es que no hay necesidad de paréntesis cuando escribimos\(h \circ g \circ f\). La segunda propiedad también se puede verificar usando la Definición 5.1. Recordemos que la función\(I(x) = x\) se denomina función de identidad y se introdujo en el Ejercicio 73 en la Sección 2.1. Si componemos la función\(I\) con una función\(f\), entonces tenemos\((I \circ f)(x) = I(f(x)) = f(x)\), y un cálculo similar muestra\((f\circ I)(x) = f(x)\). Esto establece que tenemos una identidad para la composición de funciones mucho de la misma manera que el número real\(1\) es una identidad para la multiplicación de números reales. Es decir, al igual que para cualquier número real\(x\)\(1 \cdot x = x \cdot 1 = x\),, tenemos para cualquier función\(f\),\(I \circ f = f \circ I =f\). Veremos que el concepto de identidad adquiere gran trascendencia en el siguiente apartado. En la naturaleza, la composición de funciones se utiliza a menudo para relacionar dos cantidades que pueden no estar directamente relacionadas, pero que tienen una variable en común, como se ilustra en nuestro siguiente ejemplo.

Ejemplo 5.1.2

El área superficial\(S\) de una esfera es función de su radio\(r\) y viene dada por la fórmula\(S(r) = 4 \pi r^2\). Supongamos que la esfera se está inflando para que el radio de la esfera aumente según la fórmula\(r(t) = 3t^2\), donde\(t\) se mide en segundos,\(t \geq 0\), y\(r\) se mide en pulgadas. Encontrar e interpretar\((S \circ r)(t)\).

Solución

Si miramos las funciones\(S(r)\) e\(r(t)\) individualmente, vemos que la primera da la superficie de una esfera de un radio dado mientras que la segunda da el radio en un momento dado. Entonces, dado un tiempo específico,\(t\), podríamos encontrar el radio en ese momento,\(r(t)\) y alimentarlo\(S(r)\) para encontrar el área de superficie en ese momento. De esto vemos que la superficie\(S\) es en última instancia una función del tiempo\(t\) y nos encontramos\((S \circ r)(t) = S(r(t)) = 4 \pi (r(t))^2 = 4 \pi \left(3t^2\right)^2 = 36 \pi t^{4}\). Esta fórmula nos permite calcular el área de superficie directamente dado el tiempo sin pasar por el 'hombre medio'\(r\).

Una habilidad útil en Cálculo es poder tomar una función complicada y descomponerla en una composición de funciones más fáciles que ilustra nuestro último ejemplo.

Ejemplo 5.1.3

Escribe cada una de las siguientes funciones como una composición de dos o más funciones (no identitarias). Comprueba tu respuesta realizando la composición de la función.

1. \(F(x) = |3x-1|\)
2. \(G(x) = \dfrac{2}{x^2+1}\)
3. \(H(x) = \dfrac{\sqrt{x}+1}{\sqrt{x}-1}\)

Solución. Existen muchos enfoques para este tipo de problemas, y mostramos una metodología diferente en cada una de las soluciones a continuación.

1. Nuestro objetivo es expresar la función\(F\) como\(F = g \circ f\) para funciones\(g\) y\(f\). De la Definición 5.1, sabemos\(F(x) = g(f(x))\), y podemos pensar que es la función 'interior' y\(g\) como la función 'externa'.\(f(x)\) Mirando\(F(x) = |3x-1|\) desde una perspectiva 'interior versus exterior', podemos pensar en\(3x-1\) estar dentro de los símbolos de valor absoluto. Tomando esta señal, definimos\(f(x) = 3x-1\). En este punto, tenemos\(F(x) = |f(x)|\). ¿Cuál es la función externa? La función que toma el valor absoluto de su entrada,\(g(x) = |x|\). Bastante seguro\((g \circ f)(x) = g(f(x)) = |f(x)| = |3x-1| = F(x)\),, así que terminamos.
2. Atacamos la deconstrucción\(G\) desde un enfoque operativo. Dada una entrada\(x\), el primer paso es cuadrar\(x\), luego agregar\(1\), luego dividir el resultado en\(2\). Asignaremos a cada uno de estos pasos una función para escribir\(G\) como un compuesto de tres funciones:\(f\),\(g\) y\(h\). Nuestra primera función,\(f\), es la función que cuadra su entrada,\(f(x) = x^2\). La siguiente función es la función que se suma\(1\) a su entrada,\(g(x) = x+1\). Nuestra última función toma su entrada y la divide en\(2\),\(h(x) = \frac{2}{x}\). El reclamo es ese\(G = h \circ g \circ f\). Encontramos\[(h \circ g \circ f)(x) = h(g(f(x))) = h(g\left(x^2\right)) = h\left(x^2+1\right)= \frac{2}{x^2+1} = G(x),\nonumber\] así que terminamos.
3. Si miramos\(H(x) = \frac{\sqrt{x}+1}{\sqrt{x}-1}\) con miras hacia construir una función complicada a partir de funciones más simples, vemos que la expresión\(\sqrt{x}\) es una pieza simple de la función más grande. Si definimos\(f(x) = \sqrt{x}\), tenemos\(H(x) = \frac{f(x)+1}{f(x)-1}\). Si queremos descomponernos\(H = g \circ f\), entonces podemos obtener la fórmula para\(g(x)\) mirar a qué se le está haciendo\(f(x)\). Tomamos\(g(x) = \frac{x+1}{x-1}\), así\[(g \circ f)(x) = g(f(x)) = \frac{f(x)+1}{f(x)-1} = \frac{\sqrt{x}+1}{\sqrt{x}-1} = H(x),\nonumber\] como se requiera.

5.1.1 Ejercicios

En los Ejercicios 1 - 12, usa el par de funciones dado para encontrar los siguientes valores si existen.

• \((g\circ f)(0)\)
• \((f\circ g)(-1)\)
• \((f \circ f)(2)\)
• \((g\circ f)(-3)\)
• \((f\circ g)\left(\frac{1}{2}\right)\)
• \((f \circ f)(-2)\)

1. \(f(x) = x^2\),\(g(x) = 2x+1\)
2. \(f(x) = 4-x\),\(g(x) = 1-x^2\)
3. \(f(x) = 4-3x\),\(g(x) = |x|\)
4. \(f(x) = |x-1|\),\(g(x) = x^2-5\)
5. \(f(x) = 4x+5\),\(g(x) = \sqrt{x}\)
6. \(f(x) = \sqrt{3-x}\),\(g(x) = x^2+1\)
7. \(f(x) = 6-x-x^2\),\(g(x) = x\sqrt{x+10}\)
8. \(f(x) = \sqrt[3]{x+1}\),\(g(x) = 4x^2-x\)
9. \(f(x) = \dfrac{3}{1-x}\),\(g(x) = \dfrac{4x}{x^2+1}\)
10. \(f(x) = \dfrac{x}{x+5}\),\(g(x) = \dfrac{2}{7-x^2}\)
11. \(f(x) = \dfrac{2x}{5-x^2}\),\(g(x) = \sqrt{4x+1}\)
12. \(f(x) =\sqrt{2x+5}\),\(g(x) = \dfrac{10x}{x^2+1}\)

En los Ejercicios 13 - 24, utilice el par de funciones dado para encontrar y simplificar expresiones para las siguientes funciones y establecer el dominio de cada una usando notación de intervalo.

• \((g \circ f)(x)\)
• \((f \circ g)(x)\)
• \((f \circ f)(x)\)

13. \(f(x) = 2x+3\),\(g(x) = x^2-9\)
14. \(f(x) = x^2 -x+1\),\(g(x) = 3x-5\)
15. \(f(x) = x^2-4\),\(g(x) = |x|\)
16. \(f(x) = 3x-5\),\(g(x) = \sqrt{x}\)
17. \(f(x) = |x+1|\),\(g(x) = \sqrt{x}\)
18. \(f(x) = 3-x^2\),\(g(x) = \sqrt{x+1}\)
19. \(f(x) = |x|\),\(g(x) = \sqrt{4-x}\)
20. \(f(x) = x^2-x-1\),\(g(x) = \sqrt{x-5}\)
21. \(f(x) = 3x-1\),\(g(x) = \dfrac{1}{x+3}\)
22. \(f(x) = \dfrac{3x}{x-1}\),\(g(x) =\dfrac{x}{x-3}\)
23. \(f(x) = \dfrac{x}{2x+1}\),\(g(x) = \dfrac{2x+1}{x}\)
24. \(f(x) = \dfrac{2x}{x^2-4}\),\(g(x) =\sqrt{1-x}\)

En Ejercicios 25 - 30, utilice\(f(x) = -2x\),\(g(x) = \sqrt{x}\) y\(h(x) = |x|\) para encontrar y simplificar expresiones para las siguientes funciones y establecer el dominio de cada una usando notación de intervalo.

25. \((h\circ g \circ f)(x)\)
26. \((h\circ f \circ g)(x)\)
27. \((g\circ f \circ h)(x)\)
28. \((g\circ h \circ f)(x)\)
29. \((f\circ h \circ g)(x)\)
30. \((f\circ g \circ h)(x)\)

En los Ejercicios 31 - 40, escriba la función dada como una composición de dos o más funciones no identitarias. (Hay varias respuestas correctas, así que verifica tu respuesta usando la composición de funciones).

31. \(p(x) = (2x+3)^3\)
32. \(P(x) = \left(x^2-x+1\right)^5\)
33. \(h(x) = \sqrt{2x-1}\)
34. \(H(x) = |7-3x|\)
35. \(r(x) = \dfrac{2}{5x+1}\)
36. \(R(x) = \dfrac{7}{x^2-1}\)
37. \(q(x) = \dfrac{|x|+1}{|x|-1}\)
38. \(Q(x) = \dfrac{2x^3+1}{x^3-1}\)
39. \(v(x) = \dfrac{2x+1}{3-4x}\)
40. \(w(x) = \dfrac{x^2}{x^4+1}\)
41. Escribir la función\(F(x) = \sqrt{\dfrac{x^{3} + 6}{x^{3} - 9}}\) como una composición de tres o más funciones no identitarias.
42. Dejar\(g(x) = -x, \, h(x) = x + 2, \, j(x) = 3x\) y\(k(x) = x - 4\). ¿En qué orden se deben componer estas funciones\(f(x) = \sqrt{x}\) para crear\(F(x) = 3\sqrt{-x + 2} - 4\)?
43. ¿En qué funciones lineales podrían utilizarse para\(f(x) = x^{3}\) transformarse\(F(x) = -\frac{1}{2}(2x - 7)^{3} + 1\)? ¿Cuál es el orden adecuado de composición?

En Ejercicios 44 - 55, let\(f\) be the function defined by\[f = \{(-3, 4), (-2, 2), (-1, 0), (0, 1), (1, 3), (2, 4), (3, -1)\}\nonumber\] and let\(g\) be the function defined\[g = \{(-3, -2), (-2, 0), (-1, -4), (0, 0), (1, -3), (2, 1), (3, 2)\}\nonumber\]. Encuentra el valor si existe.

44. \((f \circ g)(3)\)
45. \(f(g(-1))\)
46. \((f \circ f)(0)\)
47. \((f \circ g)(-3)\)
48. \((g \circ f)(3)\)
49. \(g(f(-3))\)
50. \((g \circ g)(-2)\)
51. \((g \circ f)(-2)\)
52. \(g(f(g(0)))\)
53. \(f(f(f(-1)))\)
54. \(f(f(f(f(f(1)))))\)
55. \(\underbrace{(g \circ g \circ \cdots \circ g)}_{n \text { times }}(0)\)

En Ejercicios 56 - 61, utilice las gráficas de\(y=f(x)\) y\(y=g(x)\) siguientes para encontrar el valor de la función.

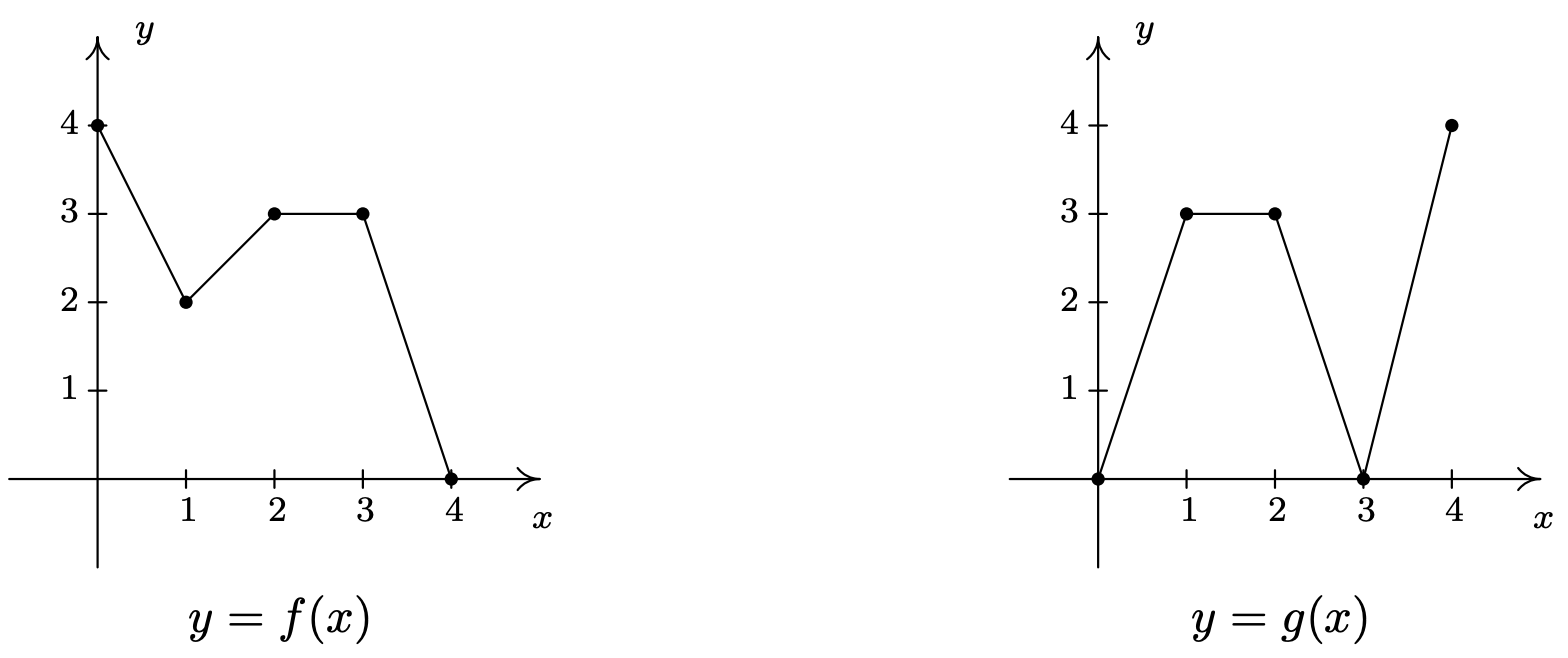
56. \((g\circ f)(1)\)
57. \((f \circ g)(3)\)
58. \((g\circ f)(2)\)
59. \((f\circ g)(0)\)
60. \((f\circ f)(1)\)
61. \((g \circ g)(1)\)
62. El volumen\(V\) de un cubo es una función de su longitud lateral\(x\). Supongamos que también\(x = t + 1\) es una función del tiempo\(t\), donde\(x\) se mide en pulgadas y\(t\) se mide en minutos. Encuentra una fórmula para\(V\) como una función de\(t\).
63. Supongamos que un vendedor local cobra\(\$2\) por hot dog y que el número de hot dogs vendidos por hora\(x\) viene dado por\(x(t) = -4t^2+20t+92\), donde\(t\) esta el numero de horas desde\(10\) AM,\(0 \leq t \leq 4\).
    1. Encuentre una expresión para los ingresos por hora\(R\) en función de\(x\).
    2. Encuentre y simplifique\(\left(R \circ x\right)(t)\). ¿Qué representa esto?
    3. ¿Cuál es el ingreso por hora al mediodía?
64. Discuta con sus compañeros de clase cómo los procesos del “mundo real”, como llenar formularios federales de impuestos sobre la renta o calcular la calificación final de su curso, podrían verse como un uso de la composición de funciones. Encontrar un proceso para el cual la composición consigo misma (iteración) tenga sentido.

RESPUESTAS

1. Para\(f(x) = x^2\) y\(g(x) = 2x+1\),
   • \((g\circ f)(0) = 1\)
   • \((f\circ g)(-1) = 1\)
   • \((f \circ f)(2) = 16\)
   • \((g\circ f)(-3) = 19\)
   • \((f\circ g)\left(\frac{1}{2}\right) = 4\)
   • \((f \circ f)(-2) = 16\)
2. Para\(f(x) = 4-x\) y\(g(x) = 1-x^2\),
   • \((g\circ f)(0) = -15\)
   • \((f\circ g)(-1) = 4\)
   • \((f \circ f)(2) = 2\)
   • \((g\circ f)(-3) = -48\)
   • \((f\circ g)\left(\frac{1}{2}\right) = \frac{13}{4}\)
   • \((f \circ f)(-2) = -2\)
3. Para\(f(x) = 4-3x\) y\(g(x) = |x|\),
   • \((g\circ f)(0) = 4\)
   • \((f\circ g)(-1) = 1\)
   • \((f \circ f)(2) = 10\)
   • \((g\circ f)(-3) = 13\)
   • \((f\circ g)\left(\frac{1}{2}\right) = \frac{5}{2}\)
   • \((f \circ f)(-2) = -26\)
4. Para\(f(x) = |x-1|\) y\(g(x) = x^2-5\),
   • \((g\circ f)(0) = -4\)
   • \((f\circ g)(-1) = 5\)
   • \((f \circ f)(2) = 0\)
   • \((g\circ f)(-3) = 11\)
   • \((f\circ g)\left(\frac{1}{2}\right) = \frac{23}{4}\)
   • \((f \circ f)(-2) = 2\)
5. Para\(f(x) = 4x+5\) y\(g(x) = \sqrt{x}\),
   • \((g\circ f)(0) = \sqrt{5}\)
   • \((f\circ g)(-1)\)no es real
   • \((f \circ f)(2) = 57\)
   • \((g\circ f)(-3)\)no es real
   • \((f\circ g)\left(\frac{1}{2}\right) = 5+2\sqrt{2}\)
   • \((f \circ f)(-2) = -7\)
6. Para\(f(x) = \sqrt{3-x}\) y\(g(x) = x^2+1\),
   • \((g\circ f)(0) = 4\)
   • \((f\circ g)(-1) = 1\)
   • \((f \circ f)(2) = \sqrt{2}\)
   • \((g\circ f)(-3) = 7\)
   • \((f\circ g)\left(\frac{1}{2}\right) = \frac{\sqrt{7}}{2}\)
   • \((f \circ f)(-2) = \sqrt{3 - \sqrt{5}}\)
7. Para\(f(x) = 6-x-x^2\) y\(g(x) = x\sqrt{x+10}\),
   • \((g\circ f)(0) = 24\)
   • \((f\circ g)(-1) = 0\)
   • \((f \circ f)(2) = 6\)
   • \((g\circ f)(-3) = 0\)
   • \((f\circ g)\left(\frac{1}{2}\right) = \frac{27-2\sqrt{42}}{8}\)
   • \((f \circ f)(-2) = -14\)
8. Para\(f(x) = \sqrt[3]{x+1}\) y\(g(x) = 4x^2-x\),
   • \((g\circ f)(0) = 3\)
   • \((f\circ g)(-1) = \sqrt[3]{6}\)
   • \((f \circ f)(2) = \sqrt[3]{\sqrt[3]{3}+1}\)
   • \((g\circ f)(-3) = 4\sqrt[3]{4}+\sqrt[3]{2}\)
   • \((f\circ g)\left(\frac{1}{2}\right) = \frac{\sqrt[3]{12}}{2}\)
   • \((f \circ f)(-2) = 0\)
9. Para\(f(x) = \frac{3}{1-x}\) y\(g(x) = \frac{4x}{x^2+1}\),
   • \((g\circ f)(0) = \frac{6}{5}\)
   • \((f\circ g)(-1) = 1\)
   • \((f \circ f)(2) = \frac{3}{4}\)
   • \((g\circ f)(-3) = \frac{48}{25}\)
   • \((f\circ g)\left(\frac{1}{2}\right) = -5\)
   • \((f \circ f)(-2)\)está indefinido
10. Para\(f(x) = \frac{x}{x+5}\) y\(g(x) = \frac{2}{7-x^2}\),
    • \((g\circ f)(0) = \frac{2}{7}\)
    • \((f\circ g)(-1) = \frac{1}{16}\)
    • \((f \circ f)(2) = \frac{2}{37}\)
    • \((g\circ f)(-3) = \frac{8}{19}\)
    • \((f\circ g)\left(\frac{1}{2}\right) = \frac{8}{143}\)
    • \((f \circ f)(-2) = -\frac{2}{13}\)
11. Para\(f(x) = \frac{2x}{5-x^2}\) y\(g(x) = \sqrt{4x+1}\),
    • \((g\circ f)(0) = 1\)
    • \((f\circ g)(-1)\)no es real
    • \((f \circ f)(2) = -\frac{8}{11}\)
    • \((g\circ f)(-3) = \sqrt{7}\)
    • \((f\circ g)\left(\frac{1}{2}\right) = \sqrt{3}\)
    • \((f \circ f)(-2) = \frac{8}{11}\)
12. Para\(f(x) =\sqrt{2x+5}\) y\(g(x) = \frac{10x}{x^2+1}\),
    • \((g\circ f)(0) = \frac{5\sqrt{5}}{3}\)
    • \((f\circ g)(-1)\)no es real
    • \((f \circ f)(2) = \sqrt{11}\)
    • \((g\circ f)(-3)\)no es real
    • \((f\circ g)\left(\frac{1}{2}\right) = \sqrt{13}\)
    • \((f \circ f)(-2) = \sqrt{7}\)
13. Para\(f(x) = 2x+3\) y\(g(x) = x^2-9\)
    • \((g \circ f)(x) = 4x^2+12x\), dominio:\((-\infty, \infty)\)
    • \((f \circ g)(x) = 2x^2-15\), dominio:\((-\infty, \infty)\)
    • \((f \circ f)(x) = 4x+9\), dominio:\((-\infty, \infty)\)
14. Para\(f(x) = x^2 -x+1\) y\(g(x) = 3x-5\)
    • \((g \circ f)(x) = 3x^2-3x-2\), dominio:\((-\infty, \infty)\)
    • \((f \circ g)(x) =9x^2-33x+31\), dominio:\((-\infty, \infty)\)
    • \((f \circ f)(x) = x^4-2x^3+2x^2-x+1\), dominio:\((-\infty, \infty)\)
15. Para\(f(x) = x^2-4\) y\(g(x) = |x|\)
    • \((g \circ f)(x) = |x^2-4|\), dominio:\((-\infty, \infty)\)
    • \((f \circ g)(x) =|x|^2-4 = x^2-4\), dominio:\((-\infty, \infty)\)
    • \((f \circ f)(x) =x^4-8x^2+12\), dominio:\((-\infty, \infty)\)
16. Para\(f(x) = 3x-5\) y\(g(x) = \sqrt{x}\)
    • \((g \circ f)(x) = \sqrt{3x-5}\), dominio:\(\left[ \frac{5}{3}, \infty \right)\)
    • \((f \circ g)(x) = 3\sqrt{x}-5\), dominio:\([0,\infty)\)
    • \((f \circ f)(x) = 9x-20\), dominio:\((-\infty, \infty)\)
17. Para\(f(x) = |x+1|\) y\(g(x) = \sqrt{x}\)
    • \((g \circ f)(x) = \sqrt{|x+1|}\), dominio:\((-\infty, \infty)\)
    • \((f \circ g)(x) = |\sqrt{x}+1| = \sqrt{x}+1\), dominio:\([0,\infty)\)
    • \((f \circ f)(x) = ||x+1|+1| = |x+1|+1\), dominio:\((-\infty, \infty)\)
18. Para\(f(x) = 3-x^2\) y\(g(x) = \sqrt{x+1}\)
    • \((g \circ f)(x) = \sqrt{4-x^2}\), dominio:\([-2,2]\)
    • \((f \circ g)(x) =2-x\), dominio:\([-1, \infty)\)
    • \((f \circ f)(x) = -x^4+6x^2-6\), dominio:\((-\infty, \infty)\)
19. Para\(f(x) = |x|\) y\(g(x) = \sqrt{4-x}\)
    • \((g \circ f)(x) = \sqrt{4-|x|}\), dominio:\([-4,4]\)
    • \((f \circ g)(x) =|\sqrt{4-x}| = \sqrt{4-x}\), dominio:\((-\infty, 4]\)
    • \((f \circ f)(x) = | |x| | = |x|\), dominio:\((-\infty, \infty)\)
20. Para\(f(x) = x^2-x-1\) y\(g(x) = \sqrt{x-5}\)
    • \((g \circ f)(x) = \sqrt{x^2-x-6}\), dominio:\((-\infty, -2] \cup [3,\infty)\)
    • \((f \circ g)(x) =x-6-\sqrt{x-5}\), dominio:\([5,\infty)\)
    • \((f \circ f)(x) =x^4-2x^3-2x^2+3x+1\), dominio:\((-\infty, \infty)\)
21. Para\(f(x) = 3x-1\) y\(g(x) = \frac{1}{x+3}\)
    • \((g \circ f)(x) = \frac{1}{3x+2}\), dominio:\(\left(-\infty, -\frac{2}{3}\right) \cup \left(-\frac{2}{3}, \infty\right)\)
    • \((f \circ g)(x) = -\frac{x}{x+3}\), dominio:\(\left(-\infty, -3\right) \cup \left(-3, \infty\right)\)
    • \((f \circ f)(x) = 9x-4\), dominio:\((-\infty, \infty)\)
22. Para\(f(x) = \frac{3x}{x-1}\) y\(g(x) =\frac{x}{x-3}\)
    • \((g \circ f)(x) =x\), dominio:\(\left(-\infty, 1\right) \cup (1, \infty)\)
    • \((f \circ g)(x) =x\), dominio:\(\left(-\infty, 3\right) \cup (3,\infty)\)
    • \((f \circ f)(x) = \frac{9x}{2x+1}\), dominio:\(\left(-\infty, -\frac{1}{2}\right) \cup \left(-\frac{1}{2}, 1 \right) \cup \left(1,\infty \right)\)
23. Para\(f(x) = \frac{x}{2x+1}\) y\(g(x) = \frac{2x+1}{x}\)
    • \((g \circ f)(x) = \frac{4x+1}{x}\), dominio:\(\left(-\infty, -\frac{1}{2}\right) \cup \left(-\frac{1}{2}, 0), \cup (0, \infty\right)\)
    • \((f \circ g)(x) = \frac{2x+1}{5x+2}\), dominio:\(\left(-\infty, -\frac{2}{5}\right) \cup \left(-\frac{2}{5}, 0\right) \cup (0,\infty)\)
    • \((f \circ f)(x) = \frac{x}{4x+1}\), dominio:\(\left(-\infty, -\frac{1}{2}\right) \cup \left(-\frac{1}{2}, -\frac{1}{4} \right) \cup \left(-\frac{1}{4},\infty\right)\)
24. Para\(f(x) = \frac{2x}{x^2-4}\) y\(g(x) =\sqrt{1-x}\)
    • \((g \circ f)(x) =\sqrt{\frac{x^2-2x-4}{x^2-4}}\), dominio:\(\left(-\infty, -2\right) \cup \left[1-\sqrt{5}, 2\right) \cup \left[1+\sqrt{5}, \infty\right)\)
    • \((f \circ g)(x) = -\frac{2\sqrt{1-x}}{x+3}\), dominio:\(\left(-\infty, -3\right) \cup \left(-3, 1\right]\)
    • \((f \circ f)(x) = \frac{4x-x^3}{x^4-9x^2+16}\), dominio:\(\left(-\infty, -\frac{1+\sqrt{17}}{2}\right) \cup \left(-\frac{1+\sqrt{17}}{2}, -2\right) \cup \left(-2, \frac{1-\sqrt{17}}{2}\right) \cup \left(\frac{1-\sqrt{17}}{2}, \frac{-1+\sqrt{17}}{2}\right) \cup \left(\frac{-1+\sqrt{17}}{2}, 2\right) \cup \left(2, \frac{1+\sqrt{17}}{2} \right) \cup \left(\frac{1+\sqrt{17}}{2}, \infty\right)\)
25. \((h\circ g \circ f)(x)= |\sqrt{-2x}|= \sqrt{-2x}\), dominio:\((-\infty, 0]\)
26. \((h\circ f \circ g)(x) = |-2\sqrt{x}|= 2\sqrt{x}\), dominio:\([0,\infty)\)
27. \((g\circ f \circ h)(x) = \sqrt{-2|x|}\), dominio:\(\{0\}\)
28. \((g\circ h \circ f)(x) = \sqrt{|-2x|} = \sqrt{2|x|}\), dominio:\((-\infty, \infty)\)
29. \((f\circ h \circ g)(x) = -2|\sqrt{x}| = -2\sqrt{x}\), dominio:\([0,\infty)\)
30. \((f\circ g \circ h)(x) = -2\sqrt{|x|}\),, dominio:\((-\infty,\infty)\)
31. Vamos\(f(x) = 2x+3\) y\(g(x) = x^3\), entonces\(p(x) = (g\circ f)(x)\).
32. Dejar\(f(x) = x^2-x+1\) y\(g(x) = x^5\),\(P(x) =(g\circ f)(x)\).
33. Vamos\(f(x) = 2x-1\) y\(g(x) = \sqrt{x}\), entonces\(h(x) = (g\circ f)(x)\).
34. Vamos\(f(x) = 7-3x\) y\(g(x) = |x|\), entonces\(H(x) = (g\circ f)(x)\).
35. Vamos\(f(x) = 5x+1\) y\(g(x) = \frac{2}{x}\), entonces\(r(x) =(g\circ f)(x)\).
36. Vamos\(f(x) = x^2-1\) y\(g(x) = \frac{7}{x}\), entonces\(R(x) =(g\circ f)(x)\).
37. Vamos\(f(x) = |x|\) y\(g(x) = \frac{x+1}{x-1}\), entonces\(q(x) =(g\circ f)(x)\).
38. Vamos\(f(x) = x^3\) y\(g(x)= \frac{2x+1}{x-1}\), entonces\(Q(x) =(g\circ f)(x)\).
39. Vamos\(f(x) =2x\) y\(g(x) = \frac{x+1}{3-2x}\), entonces\(v(x) =(g\circ f)(x)\).
40. Vamos\(f(x) = x^2\) y\(g(x) = \frac{x}{x^2+1}\), entonces\(w(x) =(g\circ f)(x)\).
41. \(F(x) = \sqrt{\frac{x^{3} + 6}{x^{3} - 9}} = (h(g(f(x)))\)dónde\(f(x) = x^{3}, \, g(x) = \frac{x + 6}{x - 9}\) y\(h(x) = \sqrt{x}\).
42. \(F(x) = 3\sqrt{-x + 2} - 4 = k(j(f(h(g(x)))))\)
43. Una posible solución es\(F(x) = -\frac{1}{2}(2x - 7)^{3} + 1 = k(j(f(h(g(x)))))\) dónde\(g(x) = 2x, \, h(x) = x - 7, \, j(x) = -\frac{1}{2}x\) y\(k(x) = x + 1\). También podrías tener\(F(x) = H(f(G(x)))\) dónde\(G(x) = 2x - 7\) y\(H(x) = -\frac{1}{2}x + 1\).
44. \((f \circ g)(3)= f(g(3)) = f(2) = 4\)
45. \(f(g(-1)) = f(-4)\)que no está definido
46. \((f \circ f)(0) = f(f(0)) = f(1) = 3\)
47. \((f \circ g)(-3) = f(g(-3)) = f(-2) = 2\)
48. \((g \circ f)(3) = g(f(3)) = g(-1) = -4\)
49. \(g(f(-3)) = g(4)\)que no está definido
50. \((g \circ g)(-2) = g(g(-2)) = g(0) = 0\)
51. \((g \circ f)(-2) = g(f(-2)) = g(2) = 1\)
52. \(g(f(g(0))) = g(f(0)) = g(1) = -3\)
53. \(f(f(f(-1))) = f(f(0)) = f(1) = 3\)
54. \(f(f(f(f(f(1))))) = f(f(f(f(3)))) =\\ f(f(f(-1))) = f(f(0)) = f(1) = 3\)
55. \(\underbrace{(g \circ g \circ \cdots \circ g)}_{n \text { times }}(0)=0\)
56. \((g\circ f)(1) = 3\)
57. \((f \circ g)(3) = 4\)
58. \((g\circ f)(2) = 0\)
59. \((f\circ g)(0) = 4\)
60. \((f\circ f)(1) = 3\)
61. \((g \circ g)(1) = 0\)
62. \(V(x) = x^{3}\)por lo\(V(x(t)) = (t + 1)^{3}\)
63. 1. \(R(x) = 2x\)
    2. \(\left(R \circ x \right)(t) = -8t^2+40t+184\),\(0 \leq t \leq 4\). Esto da los ingresos por hora en función del tiempo.
    3. El mediodía corresponde a\(t=2\), entonces\(\left(R \circ x \right)(2) = 232\). El ingreso por hora al mediodía es\(\$232\) por hora.

---

Referencia

¹ Estos fueron introducidos, como recordará, como funciones lineales definidas por partes.

² Este es un juego de palabras de matemáticas realmente malo.

³ Si ampliamos nuestro concepto de funciones para permitir coeficientes valorados complejos, el Teorema de Factorización Compleja, Teorema 3.14, nos dice que cada función que hemos estudiado hasta ahora es una combinación de funciones lineales.

⁴ Esto nos muestra que la composición de funciones no es conmutativa. Un ejemplo de una operación que realizamos en dos funciones que es conmutativa es la adición de funciones, que definimos en la Sección 1.5. Es decir, las funciones\(f + g\) y\(g + f\) son siempre iguales. ¿Cuáles de las operaciones restantes sobre funciones que hemos discutido son conmutativas?

⁵ Un ejemplo más matemático en el que el orden de dos procesos importa se puede encontrar en la Sección 1.7. De hecho, todas las transformaciones en esa sección se pueden ver en términos de componer funciones con función lineal