5.2: Funciones inversas
( \newcommand{\kernel}{\mathrm{null}\,}\)
Pensando en una función como un proceso como lo hicimos en la Sección 1.4, en esta sección buscamos otra función que pudiera revertir ese proceso. Como en la vida real, encontraremos que algunos procesos (como ponerse calcetines y zapatos) son reversibles mientras que algunos (como cocinar un bistec) no lo son. Comenzamos discutiendo una función muy básica que es reversible,f(x)=3x+4. Pensando enf como un proceso, comenzamos con una entradax y aplicamos dos pasos, como vimos en la Sección 1.4
- multiplicar por3
- agregar4
Para revertir este proceso, buscamos una funcióng que deshaga cada uno de estos pasos y tome la salida def,3x+4, y devuelva la entradax. Si pensamos en el proceso reversible de dos pasos del mundo real de primero ponerse los calcetines y luego ponerse los zapatos, para revertir el proceso, primero nos quitamos los zapatos, y luego nos quitamos los calcetines. De la misma manera, la funcióng debería deshacer el segundo paso def primero. Es decir, la funcióng debería
- restar4
- dividir por3
Siguiendo este procedimiento, obtenemosg(x)=x−43. Comprobemos para ver si la funcióng hace el trabajo. Six=5, entoncesf(5)=3(5)+4=15+4=19. Tomando la salida19 def, la sustituimos eng para obtenerg(19)=19−43=153=5, que es nuestra entrada original af. Para verificar queg hace el trabajo para todosx en el dominio def, tomamos la salida genérica def,f(x)=3x+4, y sustituimos eso eng. Es decir,g(f(x))=g(3x+4)=(3x+4)−43=3x3=x, que es nuestra aportación original af. Si examinamos cuidadosamente la aritmética a medida que simplificamosg(f(x)), en realidad vemosg primero 'deshacer' la adición de4, y luego 'deshacer' la multiplicación por3. No sólog deshacef, sino quef también deshaceg. Es decir, si tomamos la salida deg,g(x)=x−43, y ponemos eso enf, obtenemosf(g(x))=f(x−43)=3(x−43)+4=(x−4)+4=x. Utilizando el lenguaje de composición de funciones desarrollado en la Sección 5.1, los enunciadosg(f(x))=x yf(g(x))=x pueden escribirse como(g∘f)(x)=x y(f∘g)(x)=x, respectivamente. De manera abstracta, podemos visualizar la relación entref yg en el siguiente diagrama.
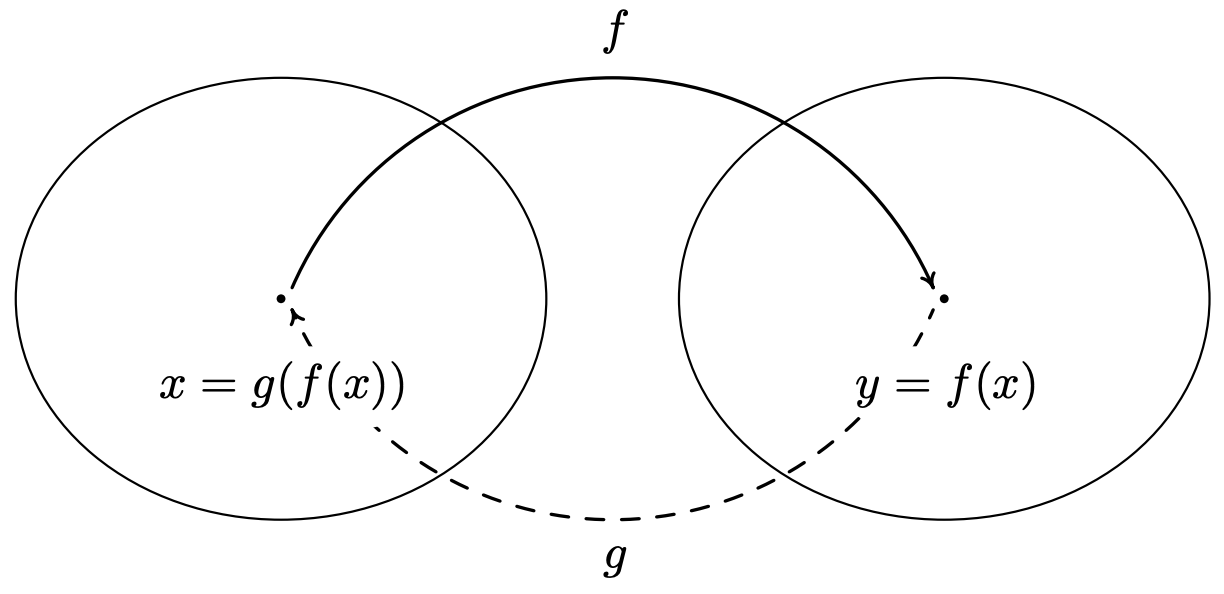
La idea principal a obtener del diagrama es queg toma las salidasf y las devuelve a sus respectivas entradas, y a la inversa,f toma salidas deg y las devuelve a sus respectivas entradas. Ahora tenemos los antecedentes suficientes para exponer la definición central de la sección.
Supongamosf yg son dos funciones tales que
- (g∘f)(x)=xpara todosx en el dominio def y
- (f∘g)(x)=xpara todosx en el dominio deg
entoncesf yg son inversos entre sí y las funcionesf yg se dice que son invertibles.
Ahora formalizamos el concepto de que las funciones inversas intercambian entradas y salidas.
Supongamosf yg son funciones inversas.
- El rango a def es el dominio deg y el dominio def es el rango deg
- f(a)=bsi y solo sig(b)=a
- (a,b)está en la gráfica def si y solo si(b,a) está en la gráfica deg
a Recordar este es el conjunto de todas las salidas de una función.
El Teorema 5.2 es una consecuencia de la Definición 5.2 y del Principio Fundamental de Gráfica para Funciones. Observamos que la tercera propiedad en el Teorema 5.2 nos dice que las gráficas de funciones inversas son reflexiones sobre la líneay=x. Para una prueba de ello, véase el Ejemplo 1.1.7 en la Sección 1.1 y el Ejercicio 72 en la Sección 2.1. Por ejemplo, trazamos las funciones inversasf(x)=3x+4 yg(x)=x−43 abajo.
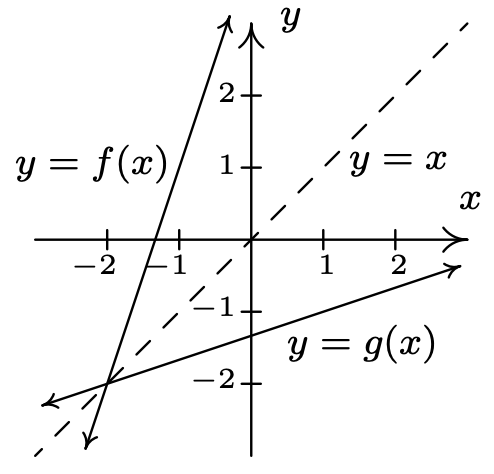
Si abstracemos un paso más, podemos expresar el sentimiento en la Definición 5.2 diciendo quef yg son inversos si y solo sig∘f=I1 yf∘g=I2 dóndeI1 está restringida la función de identidad 1 al dominio def y I2es la función de identidad restringida al dominio deg. Es decir,I1(x)=x para todosx en el dominio def yI2(x)=x para todosx en el dominio deg. Usando esta descripción de inversos junto con las propiedades de composición de funciones enumeradas en el Teorema 5.1, podemos demostrar que las inversas de función son únicas. 2 Supongamosg yh son ambos inversos de una funciónf. Por Teorema 5.2, el dominio deg es igual al dominio deh, ya que ambos son el rango def. Esto significa que la función de identidadI2 se aplica tanto al dominioh de como al dominio deg. Por lo tantoh=h∘I2=h∘(f∘g)=(h∘f)∘g=I1∘g=g, según se requiera. 3 Resumimos la discusión de los dos últimos párrafos en el siguiente teorema. 4
Supongamos quef es una función invertible.
- Hay exactamente una función inversa paraf, denotadaf−1 (lecturaf -inversa)
- La gráfica dey=f−1(x) es el reflejo de la gráfica dey=f(x) a través de la líneay=x.
La notaciónf−1 es una elección desafortunada ya que has sido programado desde Álgebra Primaria para pensar en esto como1f. Este definitivamente no es el caso ya que, por ejemplo,f(x)=3x+4 tiene como su inversaf−1(x)=x−43, que sin duda es diferente a la1f(x)=13x+4. ¿Por qué persiste esta confusa notación? Como mencionamos en la Sección 5.1, la función de identidadI es la función de composición cuál1 es el número real a la multiplicación de números reales. La elección de la notaciónf−1 alude a la propiedad quef−1∘f=I1 yf∘f−1=I2, de la misma manera que3−1⋅3=1 y3⋅3−1=1.
Volvamos nuestra atención a la funciónf(x)=x2. ¿Esf invertible? Un candidato probable para la inversa es la funcióng(x)=√x. Comprobando los rendimientos de la composición(g∘f)(x)=g(f(x))=√x2=|x|, que no es igual ax para todosx en el dominio(−∞,∞). Por ejemplo, cuandox=−2, perof(−2)=(−2)2=4g(4)=√4=2, lo que significa queg no pudo devolver la entrada−2 de su salida4. Lo queg hizo, sin embargo, es hacer coincidir la salida4 con una entrada diferente2, es decir, que satisfacef(2)=4. Este número se presenta esquemáticamente en la imagen de abajo.
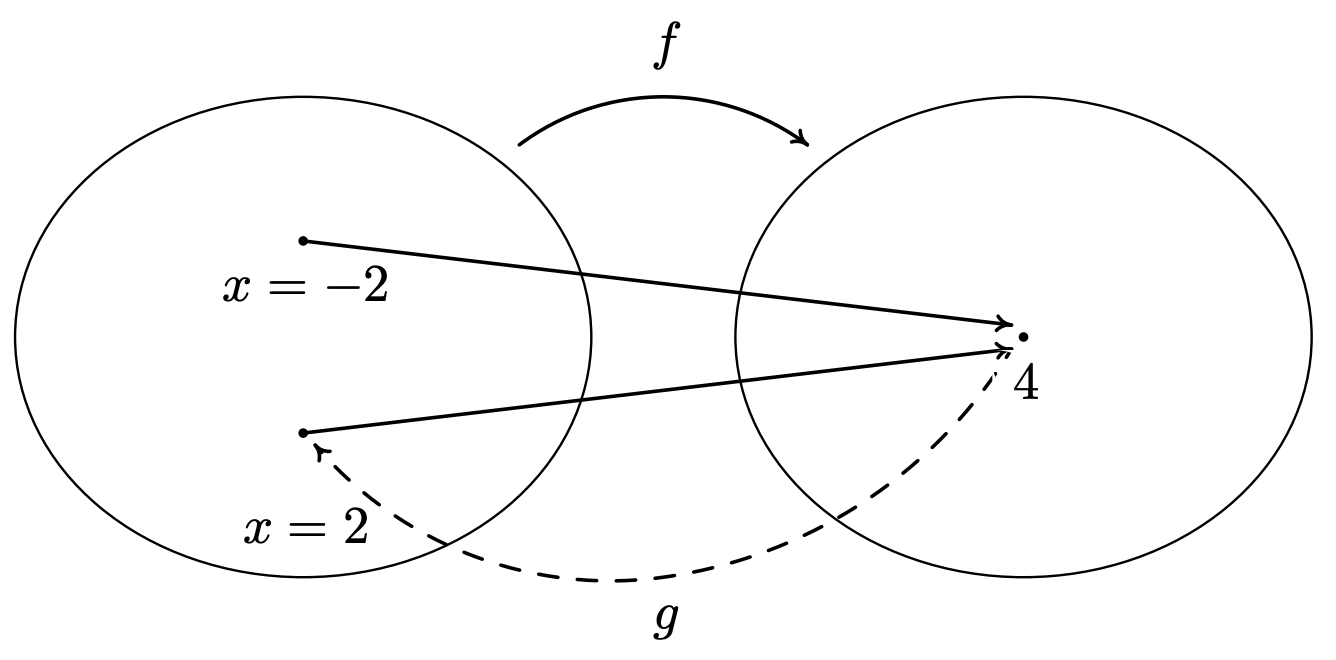
Vemos a partir del diagrama que ya que ambosf(−2) yf(2) son4, es imposible construir una función que lleve de4 vuelta a ambosx=2 yx=−2. (Por definición, una función coincide con un número real con exactamente otro número real). Desde un punto de vista gráfico, sabemos que siy=f−1(x) existe, su gráfica se puede obtener reflexionandoy=x2 sobre la líneay=x, de acuerdo con el Teorema 5.3. Hacerlo produce
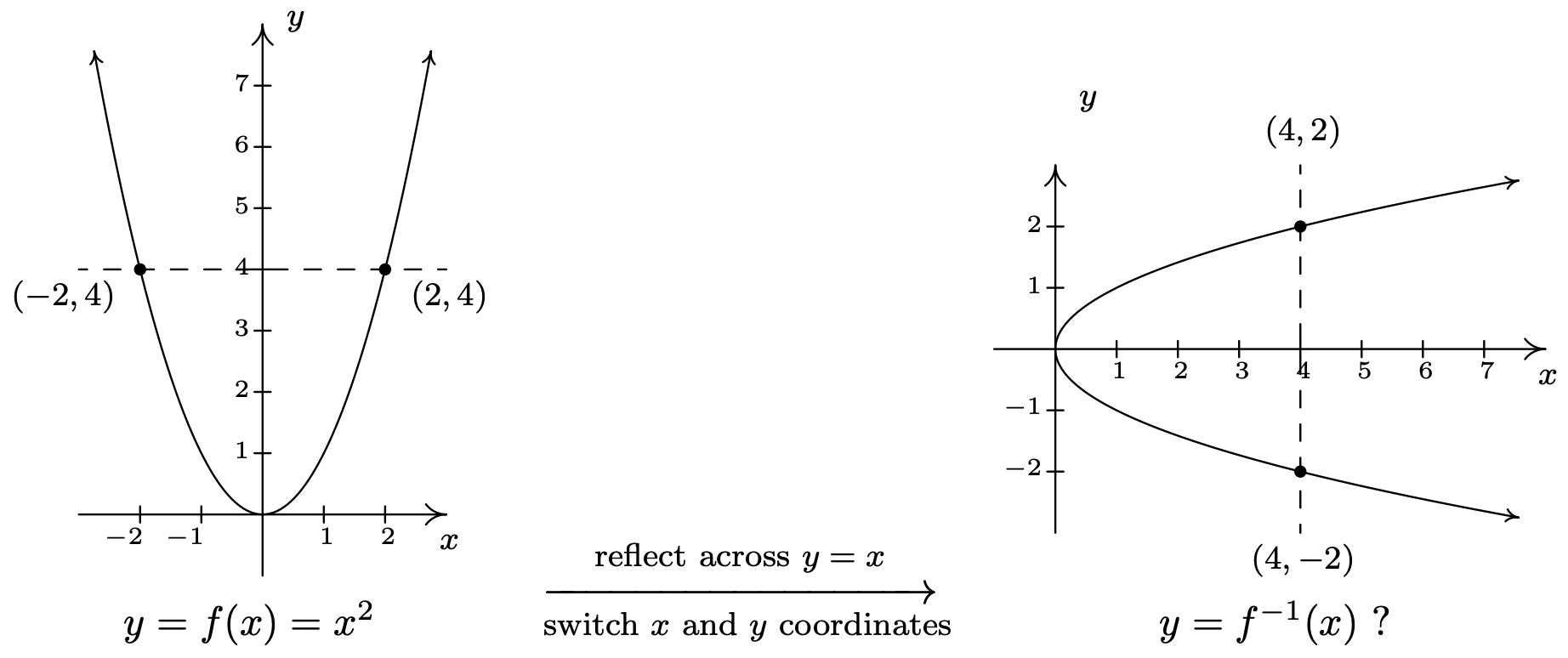
Vemos que la líneax=4 cruza la gráfica de la supuesta inversa dos veces - es decir, la gráfica falla la Prueba de Línea Vertical, Teorema 1.1, y como tal, no representay como una función dex. La línea verticalx=4 en la gráfica de la derecha corresponde a la línea horizontaly=4 en la gráfica dey=f(x). El hecho de que la línea horizontaly=4 intersecta la gráfica de dosf veces significa que dos entradas diferentes, es decirx=−2 yx=2, se emparejan con la misma salida4, que es la causa de todos los problemas. En general, para que una función tenga una inversa, diferentes entradas deben ir a diferentes salidas, o de lo contrario nos encontraremos con el mismo problema que hicimos conf(x)=x2. Le damos un nombre a esta propiedad.
Se dice que una funciónf es uno a uno sif coincide con diferentes entradas con diferentes salidas. Equivalentemente,f es uno a uno si y solo si siempre y cuando seaf(c)=f(d), entoncesc=d.
Gráficamente, detectamos funciones uno a uno usando la prueba a continuación.
Una funciónf es uno a uno si y solo si ninguna línea horizontal interseca la gráfica def más de una vez.
Decimos que la gráfica de una función pasa la Prueba de Línea Horizontal si ninguna línea horizontal cruza la gráfica más de una vez; de lo contrario, decimos que la gráfica de la función falla en la Prueba de Línea Horizontal. Hemos argumentado que sif es invertible, entoncesf debe ser uno a uno, de lo contrario la gráfica dada al reflejar la gráfica dey=f(x) alrededor de la líneay=x fallará la Prueba de Línea Vertical. Resulta que ser uno a uno también es suficiente para garantizar la invertibilidad. Para ver esto, pensamos enf como el conjunto de pares ordenados que constituyen su gráfica. Si cambiar lasy coordenadasx - y -de los puntos resulta en una función, entoncesf es invertible y hemos encontradof−1. Esto es precisamente lo que la Prueba de Línea Horizontal hace por nosotros: comprueba para ver si un conjunto de puntos describe o nox como una función dey. A continuación resumimos estos resultados.
Condiciones Equivalentes para la Invertibilidad: Supongamos quef es una función. Las siguientes declaraciones son equivalentes.
- fes invertible
- fes uno a uno
- La gráfica def pasa la Prueba de Línea Horizontal
Ponemos a trabajar este resultado en el siguiente ejemplo.
Determinar si las siguientes funciones son uno a uno de dos maneras: (a) analíticamente usando la Definición 5.3 y (b) gráficamente usando la Prueba de Línea Horizontal.
- f(x)=1−2x5
- g(x)=2x1−x
- h(x)=x2−2x+4
- F={(−1,1),(0,2),(2,1)}
Solución
-
- Para determinar sif es uno a uno analíticamente, asumimosf(c)=f(d) e intentamos deducir esoc=d.
f(c)=f(d)1−2c5=1−2d51−2c=1−2d−2c=−2dc=d✓
De ahí,f es uno a uno.
- Para verificar sif es uno a uno gráficamente, buscamos ver si la gráfica dey=f(x) pasa la Prueba de Línea Horizontal. Tenemos quef es una función lineal no constante, lo que significa que su gráfica es una línea no horizontal. Así la gráfica def pasa la Prueba de Línea Horizontal.
- Para determinar sif es uno a uno analíticamente, asumimosf(c)=f(d) e intentamos deducir esoc=d.
-
- Comenzamos con la suposición de queg(c)=g(d) e intentamos mostrarc=d.
g(c)=g(d)2c1−c=2d1−d[6pt]2c(1−d)=2d(1−c)2c−2cd=2d−2dc2c=2dc=d✓
Hemos demostrado queg es uno a uno.
- Podemos graficarg usando el procedimiento de seis pasos que se describe en la Sección 4.2. Obtenemos la única intercepción en(0,0), una asíntota verticalx=1 y una asíntota horizontal (que la gráfica nunca cruza)y=−2. Vemos a partir de eso la gráfica deg pasa la Prueba de Línea Horizontal.
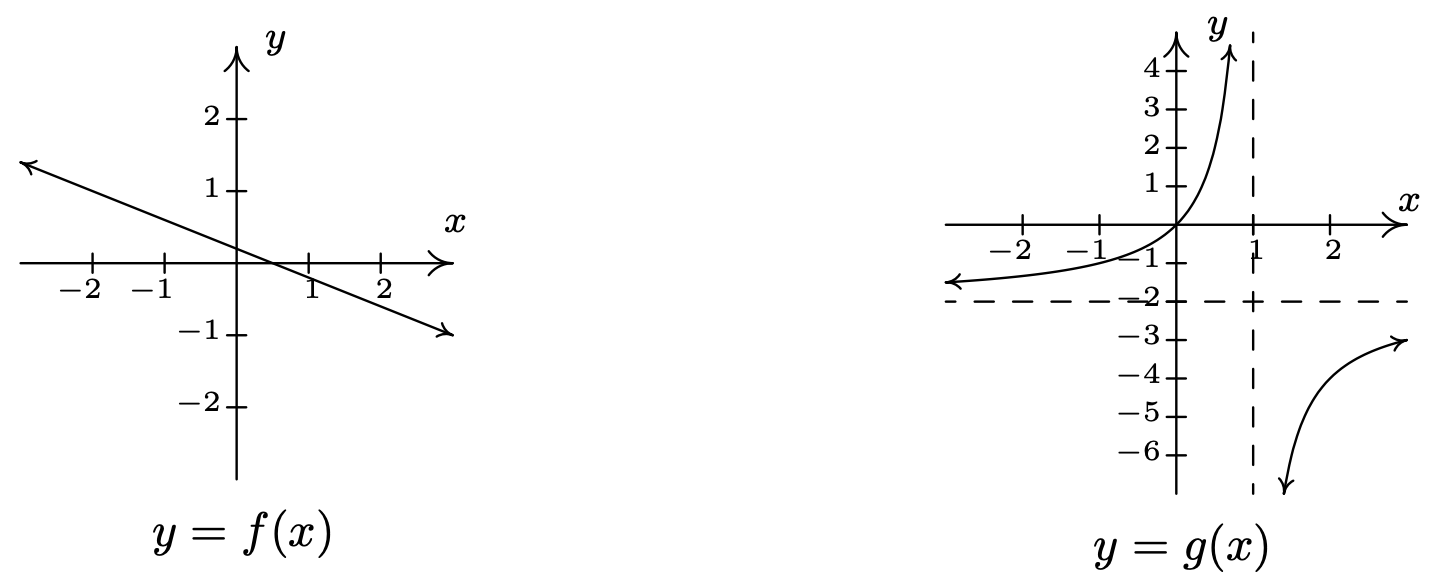
- Comenzamos con la suposición de queg(c)=g(d) e intentamos mostrarc=d.
-
- Empezamos conh(c)=h(d). A medida que nos abrimos camino a través del problema, nos encontramos con una ecuación no lineal. Movemos los términos distintos de cero hacia la izquierda, dejamos a a la0 derecha y facetamos en consecuencia.
h(c)=h(d)c2−2c+4=d2−2d+4c2−2c=d2−2dc2−d2−2c+2d=0(c+d)(c−d)−2(c−d)=0(c−d)((c+d)−2)=0factor by groupingc−d=0orc+d−2=0c=dorc=2−d
Obtenemosc=d como una posibilidad, pero también tenemos la posibilidad de quec=2−d. Esto sugiere quef puede no ser uno a uno. Tomandod=0, obtenemosc=0 oc=2. Conf(0)=4 yf(2)=4, hemos producido dos entradas diferentes con el mismo significado de salida nof es uno a uno.
- Observamos queh es una función cuadrática y graficamosy=h(x) utilizando las técnicas presentadas en la Sección 2.3. El vértice es(1,3) y la parábola se abre hacia arriba. Vemos inmediatamente de la gráfica que noh es uno a uno, ya que hay varias líneas horizontales que cruzan la gráfica más de una vez.
- Empezamos conh(c)=h(d). A medida que nos abrimos camino a través del problema, nos encontramos con una ecuación no lineal. Movemos los términos distintos de cero hacia la izquierda, dejamos a a la0 derecha y facetamos en consecuencia.
-
- La funciónF se nos da como un conjunto de pares ordenados. La condiciónF(c)=F(d) significa que las salidas de la función (lasy coordenadas -de los pares ordenados) son las mismas. Vemos que los puntos(−1,1) y(2,1) son ambos elementos deF conF(−1)=1 yF(2)=1. Ya que−1≠2, hemos establecido que noF es uno a uno.
- Gráficamente, vemos que la línea horizontaly=1 cruza la gráfica más de una vez. De ahí que la gráfica deF falle la Prueba de Línea Horizontal.
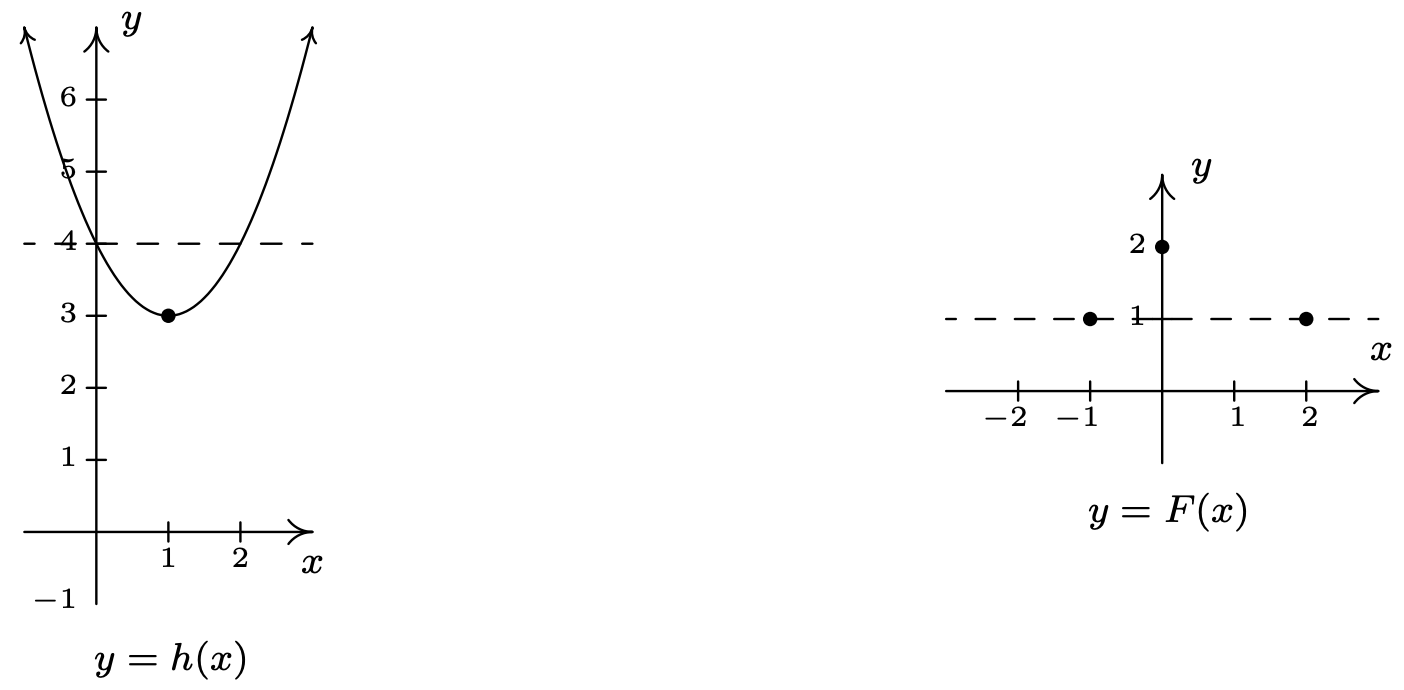
Hemos demostrado que las funcionesf yg en el Ejemplo 5.2.1 son uno-a-uno. Esto quiere decir que son invertibles, por lo que es natural preguntarse quéf−1(x) yg−1(x) sería. Porquef(x)=1−2x5, podemos pensar nuestro camino a través de lo inverso ya que solo hay una ocurrencia dex. Podemos rastrear paso a paso lo que se hacex e invertir esos pasos como lo hicimos al inicio del capítulo. La funcióng(x)=2x1−x es un poco más complicado ya quex ocurre en dos lugares. Cuando se evalúag(x) para un valor específico dex, cual es primero, el2x o el1−x? Podemos imaginar funciones más complicadas que estas por lo que necesitamos desarrollar una metodología general para atacar este problema. El teorema 5.2 nos dicey=f−1(x) que la ecuación es equivalente af(y)=x y esta es la base de nuestro algoritmo.
- Escribiry=f(x)
- Intercambiox yy
- Resolverx=f(y)y para obtenery=f−1(x)
Tenga en cuenta que podríamos haber escrito simplemente 'Resolverx=f(y) paray 'y haber terminado con él. El acto de intercambiar elx yy está ahí para recordarnos que estamos encontrando la función inversa cambiando las entradas y salidas.
Encuentra la inversa de las siguientes funciones uno a uno. Revisa tus respuestas analíticamente usando la composición de funciones y gráficamente.
- f(x)=1−2x5
- g(x)=2x1−x
Solución
- Como mencionamos anteriormente, es posible pensar nuestro camino a través de la inversa def registrando los pasos a los que aplicamosx y el orden en que los aplicamos para luego revertir esos pasos en el orden inverso. Animamos al lector a hacer esto. Nosotros, por otro lado, practicaremos el algoritmo. Escribimosy=f(x) y procedemos a cambiarx yy
y=f(x)y=1−2x5[6pt]x=1−2y5switch x and y[6pt]5x=1−2y5x−1=−2y5x−1−2=yy=−52x+12
Tenemosf−1(x)=−52x+12. Para verificar esta respuesta analíticamente, primero verificamos eso(f−1∘f)(x)=x para todosx en el dominio def, que son todos los números reales.
(f−1∘f)(x)=f−1(f(x))=−52f(x)+12[6pt]=−52(1−2x5)+12=−12(1−2x)+12[6pt]=−12+x+12=x✓
Ahora comprobamos que(f∘f−1)(x)=x para todosx en el rango de losf cuales también está todos los números reales. (Recordemos que el dominio def−1) es el rango def.)
(f∘f−1)(x)=f(f−1(x))=1−2f−1(x)5[6pt]=1−2(−52x+12)5[6pt]=1+5x−15=5x5=x✓
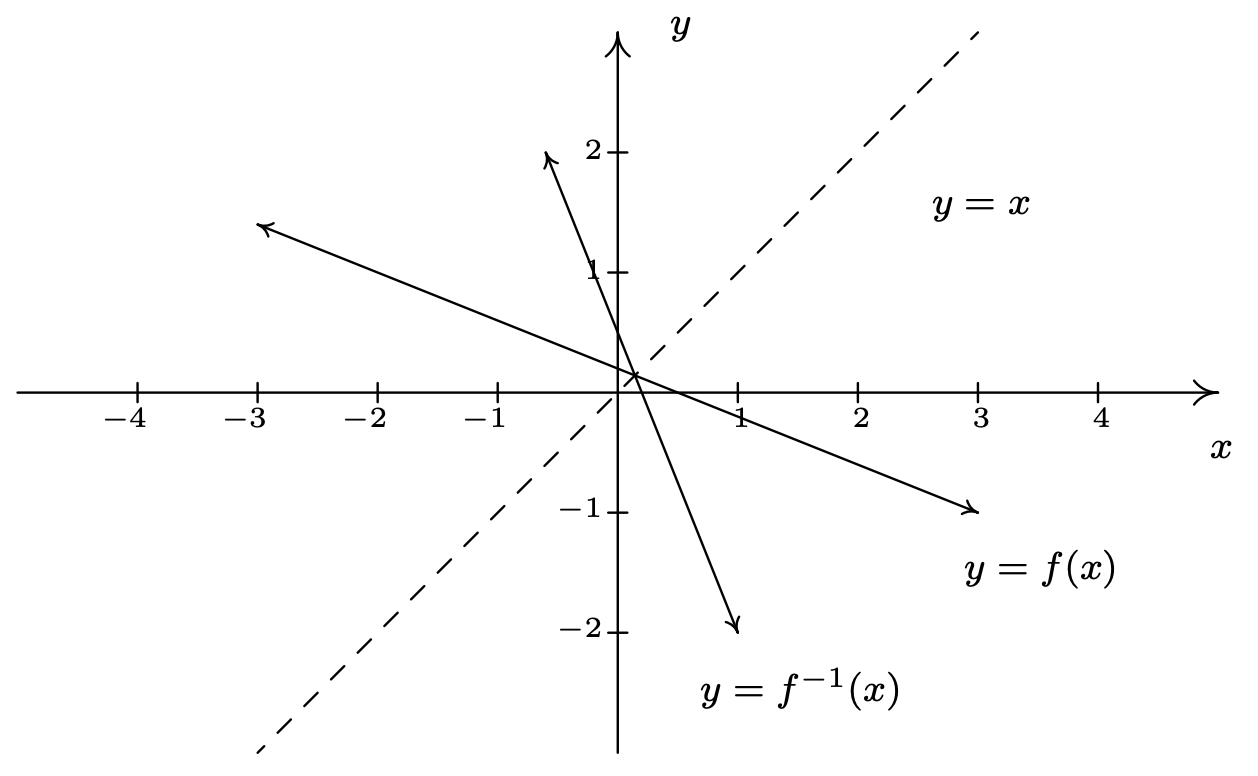
Para verificar nuestra respuesta gráficamente, graficamosy=f(x) yy=f−1(x) en el mismo conjunto de ejes. 5 Parecen ser reflejos a través de la líneay=x.
- Para encontrarg−1(x), empezamos cony=g(x). Observamos que el dominio deg es(−∞,1)∪(1,∞).
y=g(x)y=2x1−x[7pt]x=2y1−yswitch x and yx(1−y)=2yx−xy=2yx=xy+2yx=y(x+2)factor[8pt]y=xx+2
Obtenemosg−1(x)=xx+2. Para verificar esto analíticamente, primero verificamos(g−1∘g)(x)=x para todosx en el dominio deg, es decir, para todosx≠1.
\ (\ begin {alineado}
\ izquierda (g^ {-1}\ circ g\ derecha) (x) &=g^ {-1} (g (x))\\
&=g^ {-1}\ izquierda (\ frac {2 x} {1-x}\ derecha)\\
&=\ frac {\ izquierda (\ frac {2 x} {1-x}\ derecha)} {\ izquierda (\ frac {2 x} {1-x}\ derecha) +2}\\
&=\ frac {\ izquierda (\ frac {2 x} {1-x}\ derecha)} {\ izquierda (\ frac {2 x} {1-x}\ derecha) +2}\ cdot\ frac {(1-x)} {(1-x)}\ text {denominadores claros}\\
&=\ frac {2 x} {2 x+2 (1-x)}\\
&=\ frac {2 x} {2 x+2-2 x}\\
&=\ frac {2 x} {2 x}}\\
&=x\ marca de verificación
\ final {alineado}\)A continuación, verificamosg(g−1(x))=x para todosx en el rango deg. De la gráfica delg Ejemplo 5.2.1, tenemos que el rango deg es(−∞,−2)∪(−2,∞). Esto coincide con el dominio que obtenemos de la fórmulag−1(x)=xx+2, como debería.
(g∘g−1)(x)=g(g−1(x))=g(xx+2)=2(xx+2)1−(xx+2)[30pt]=2(xx+2)1−(xx+2)⋅(x+2)(x+2)clear denominators[30pt]=2x(x+2)−x=2x2=x✓
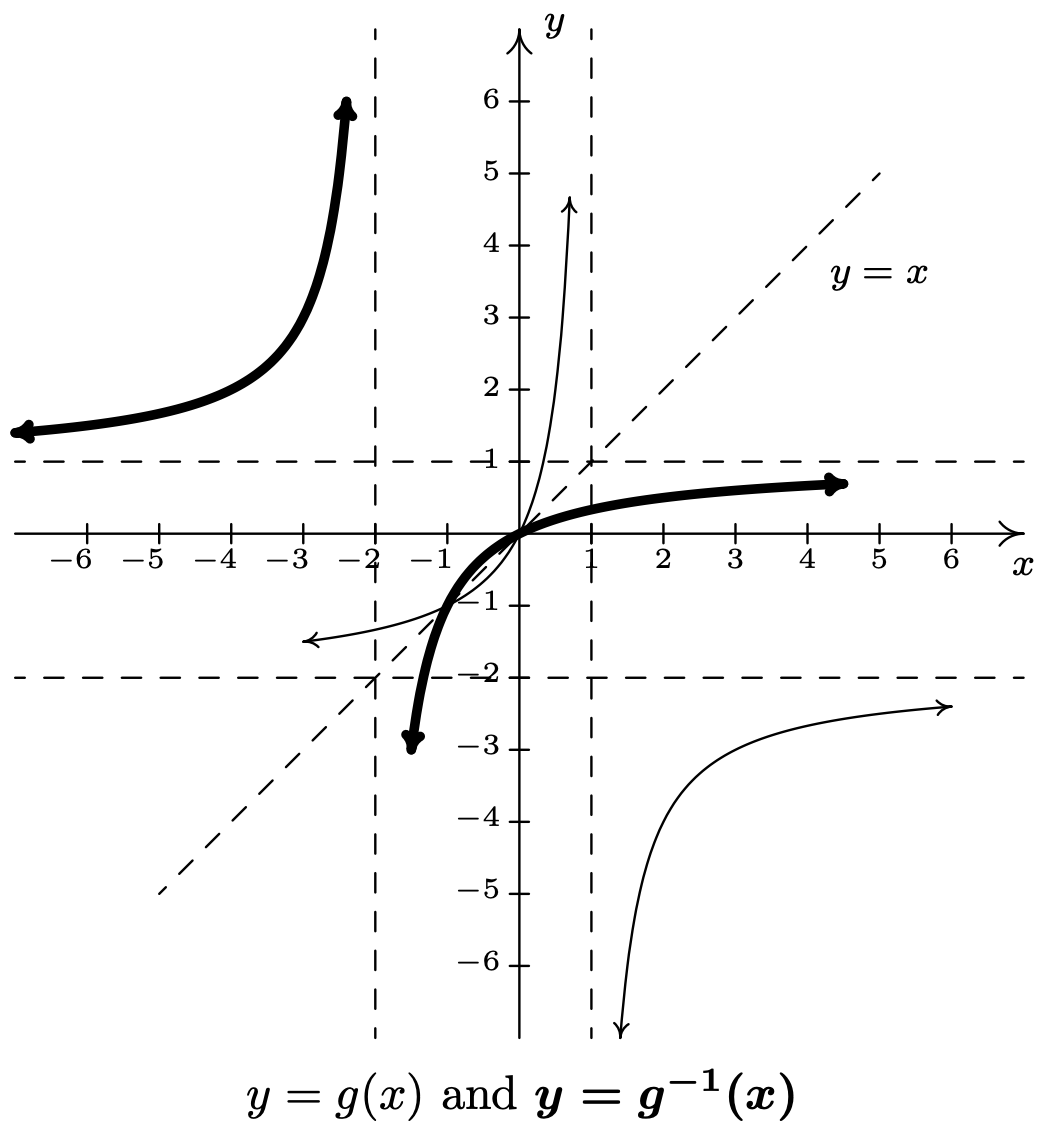
Graficary=g(x) yy=g−1(x) en el mismo conjunto de ejes está ocupado, pero podemos ver la relación simétrica si espesamos la curva paray=g−1(x). Obsérvese que la asíntota verticalx=1 de la gráfica deg corresponde a la asíntota horizontaly=1 de la gráfica deg−1, como debería yax yy se conmutan. De igual manera, la asíntota horizontaly=−2 de la gráfica deg corresponde a la asíntota verticalx=−2 de la gráfica deg−1.
Ahora volvemos af(x)=x2. Sabemos que nof es uno a uno, y por lo tanto, no es invertible. Sin embargo, si restringimos el dominio def, podemos producir una nueva funcióng que es uno a uno. Si definimosg(x)=x2x≥0,, entonces tenemos
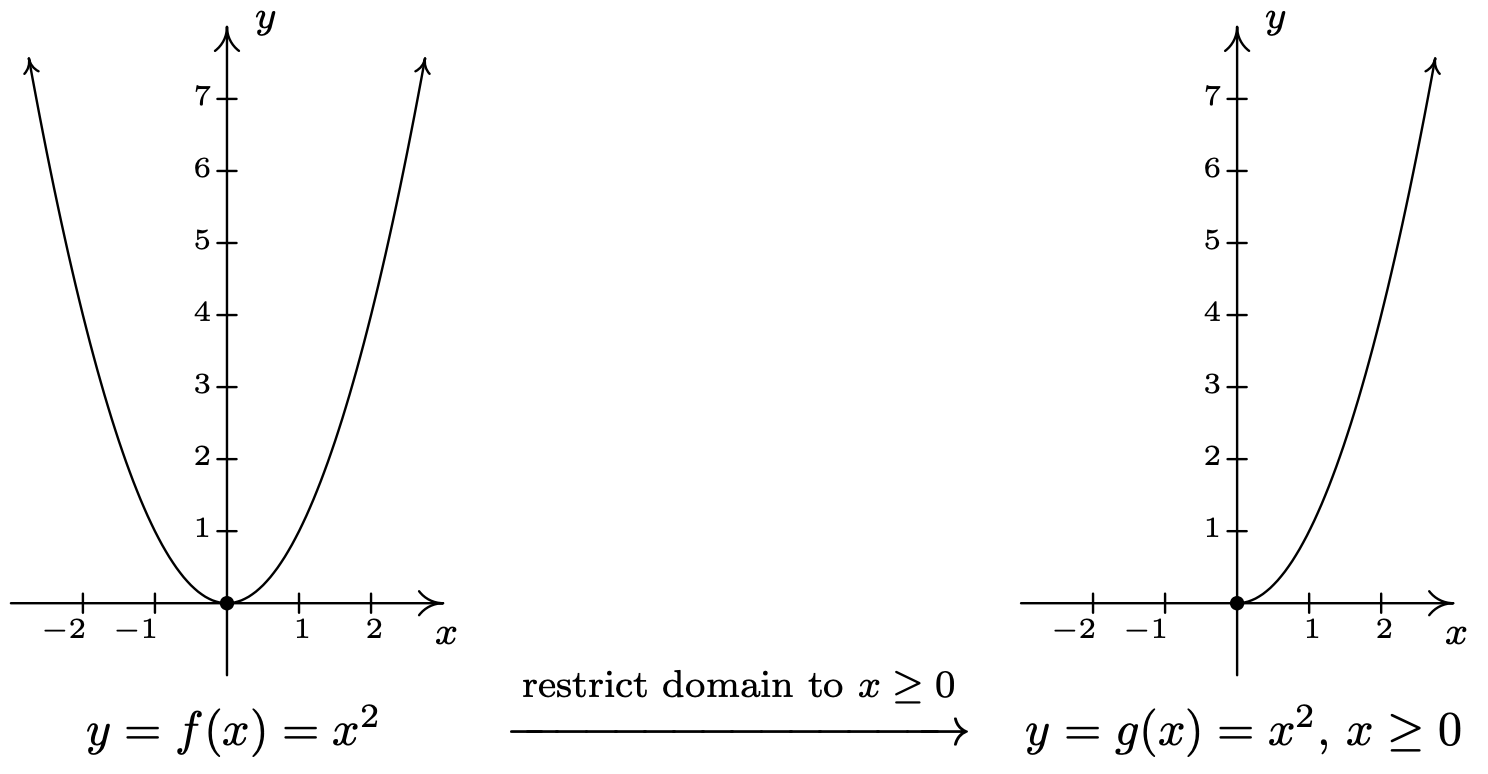
La gráfica deg pasa la Prueba de Línea Horizontal. Para encontrar una inversa deg, procedemos como de costumbre
y=g(x)y=x2,x≥0x=y2,y≥0switch x and yy=±√xy=√xsince y≥0
Obtenemosg−1(x)=√x. Al principio parece que nos encontraremos con los mismos problemas que antes, pero cuando comprobamos la composición, la restricción de dominio eng guarda el día. Obtenemos(g−1∘g)(x)=g−1(g(x))=g−1(x2)=√x2=|x|=x, ya quex≥0. Comprobación(g∘g−1)(x)=g(g−1(x))=g(√x)=(√x)2=x. Graficando 6g yg−1 en el mismo conjunto de ejes muestra que son reflejos sobre la líneay=x.
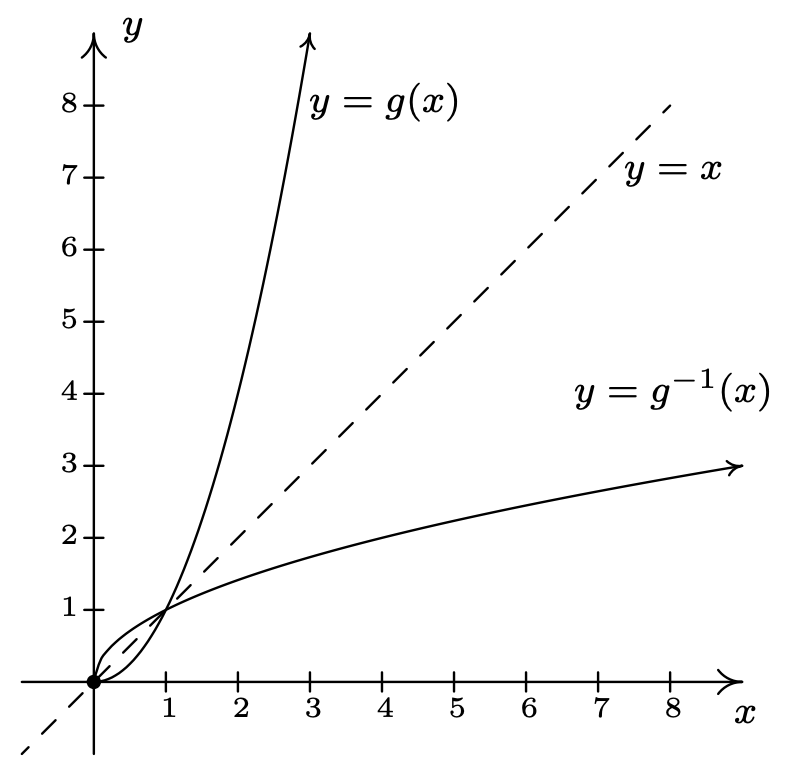
Nuestro siguiente ejemplo continúa con el tema de la restricción de dominio.
Grafica las siguientes funciones para mostrar que son uno a uno y encontrar sus inversos. Revisa tus respuestas analíticamente usando la composición de funciones y gráficamente.
- j(x)=x2−2x+4,x≤1.
- k(x)=√x+2−1
Solución.
- La funciónj es una restricción de la funciónh del Ejemplo 5.2.1. Dado que el dominio dej está restringido ax≤1, estamos seleccionando sólo la 'mitad izquierda' de la parábola. Vemos que la gráfica dej pasa la Prueba de Línea Horizontal y asíj es invertible.
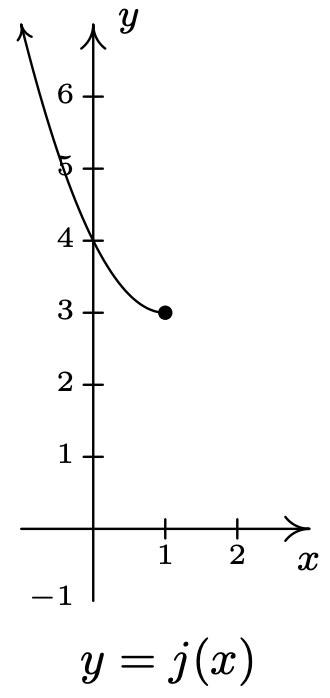
Ahora usamos nuestro algoritmo 7 para encontrarj−1(x).
y=j(x)y=x2−2x+4,x≤1x=y2−2y+4,y≤1switch x and y0=y2−2y+4−xy=2±√(−2)2−4(1)(4−x)2(1)quadratic formula, c=4−x[10pt]y=2±√4x−122[6pt]y=2±√4(x−3)2[6pt]y=2±2√x−32[6pt]y=2(1±√x−3)2[6pt]y=1±√x−3y=1−√x−3since y≤1.
Tenemosj−1(x)=1−√x−3. Cuando simplificamos(j−1∘j)(x), hay que recordar que el dominio dej esx≤1.
(j−1∘j)(x)=j−1(j(x))=j−1(x2−2x+4),x≤1=1−√(x2−2x+4)−3=1−√x2−2x+1=1−√(x−1)2=1−|x−1|=1−(−(x−1))since x≤1=x✓
Comprobandoj∘j−1, obtenemos
(j∘j−1)(x)=j(j−1(x))=j(1−√x−3)=(1−√x−3)2−2(1−√x−3)+4=1−2√x−3+(√x−3)2−2+2√x−3+4=3+x−3=x✓
Usando lo que sabemos de la Sección 1.7, graficamosy=j−1(x) yy=j(x) a continuación.
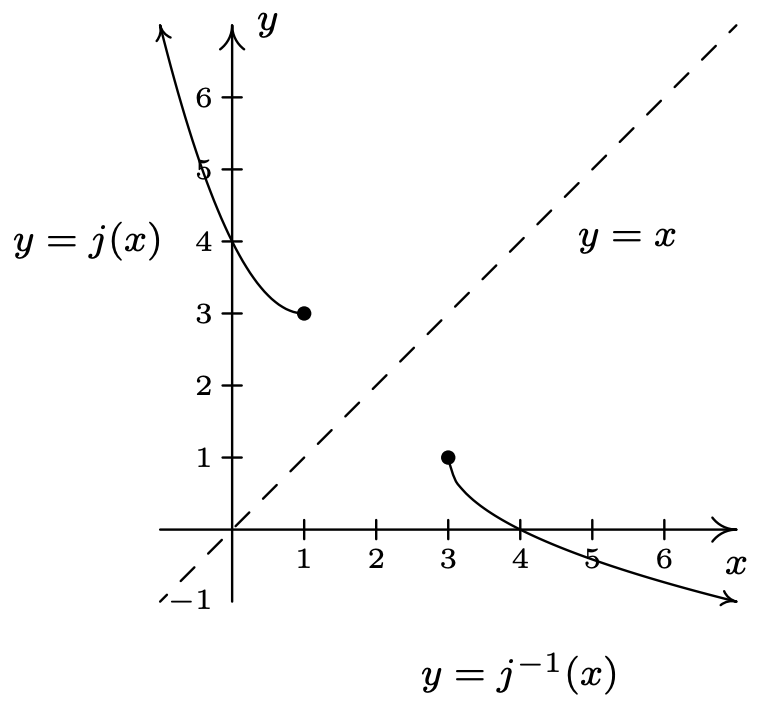
- Gráficamosy=k(x)=√x+2−1 usando lo que aprendimos en la Sección 1.7 y verk es uno a uno.
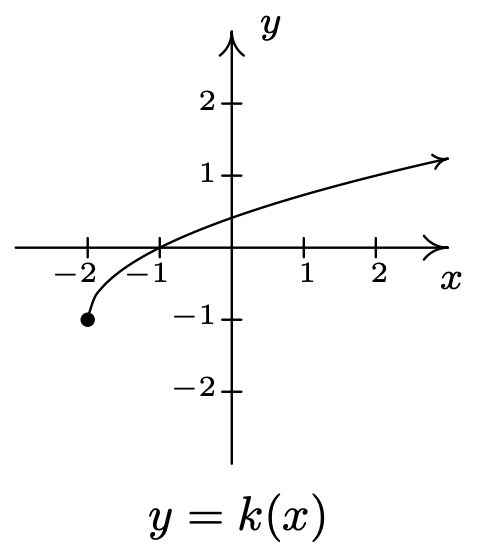
Ahora tratamos de encontrark−1.
y=k(x)y=√x+2−1x=√y+2−1switch x and yx+1=√y+2(x+1)2=(√y+2)2x2+2x+1=y+2y=x2+2x−1
Tenemosk−1(x)=x2+2x−1. Basándonos en nuestra experiencia, sabemos que algo no está del todo bien. Determinamos quek−1 es una función cuadrática, y hemos visto varias veces en esta sección que estas no son uno-a-uno a menos que sus dominios estén adecuadamente restringidos. Teorema 5.2 nos dice que el dominio dek−1 es el rango dek. De la gráfica dek, vemos que el rango es[−1,∞), lo que significa que restringimos el dominio dek−1 ax≥−1. Ahora comprobamos que esto funciona en nuestras composiciones.
(k−1∘k)(x)=k−1(k(x))=k−1(√x+2−1),x≥−2=(√x+2−1)2+2(√x+2−1)−1=(√x+2)2−2√x+2+1+2√x+2−2−1=x+2−2=x✓
y
(k∘k−1)(x)=k(x2+2x−1)x≥−1=√(x2+2x−1)+2−1=√x2+2x+1−1=√(x+1)2−1=|x+1|−1=x+1−1since x≥−1=x✓
Gráficamente, todo sale también, siempre que recordemos la restricción de dominio en losk−1 medios que tomamos la mitad derecha de la parábola.
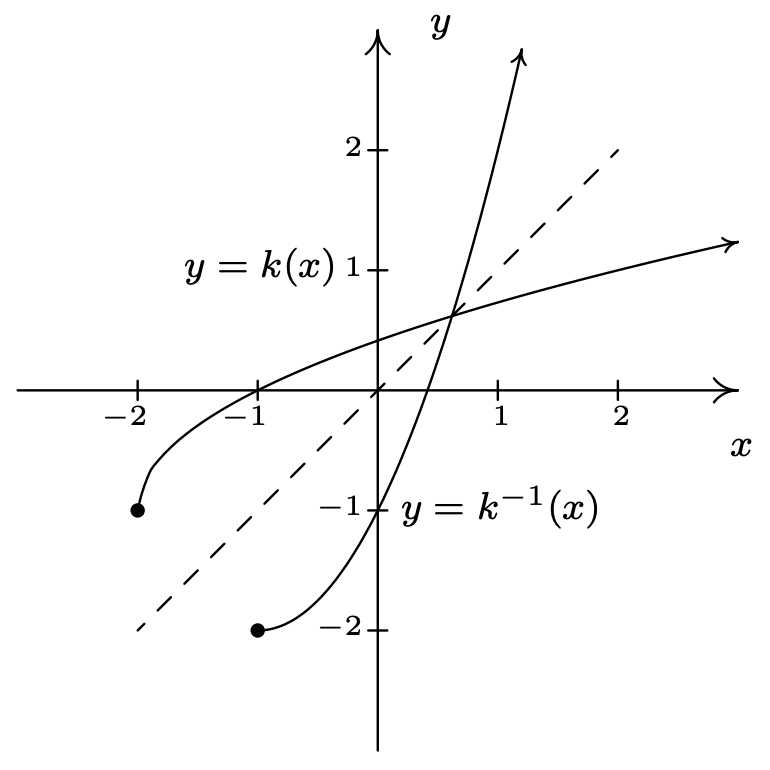
Nuestro último ejemplo de la sección da una aplicación de funciones inversas.
Recordemos de la Sección 2.1 que la ecuación precio-demanda para el sistema de juegos PortaBoy esp(x)=−1.5x+250 para0≤x≤166, dondex representa el número de sistemas que se venden semanalmente yp es el precio por sistema en dólares.
- Explica por quép es uno a uno y encuentra una fórmula parap−1(x). Declarar el dominio restringido.
- Encontrar e interpretarp−1(220).
- Recordemos de la Sección 2.3 que la ganancia semanalP, en dólares, como resultado de losx sistemas de venta viene dada porP(x)=−1.5x2+170x−150. Encontrar e interpretar(P∘p−1)(x).
- Utilice su respuesta a la parte 3 para determinar el precio por portaboy que arrojaría el máximo beneficio. Comparar con el Ejemplo 2.3.3.
Solución
- Dejamos al lector mostrar la gráfica dep(x)=−1.5x+250,0≤x≤166, es un segmento de línea de(0,250) a(166,1), y como tal pasa la Prueba de Línea Horizontal. De ahí,p es uno a uno. Encontramos la expresión parap−1(x) como de costumbre y obtenemosp−1(x)=500−2x3. El dominio dep−1 debe coincidir con el rango dep, que es[1,250], y como tal, restringimos el dominio dep−1 a1≤x≤250.
- Nos encontramosp−1(220)=500−2(220)3=20. Ya que la funciónp tomó como insumos las ventas semanales y amuebló el precio por sistema como la salida,p−1 toma el precio por sistema y devuelve las ventas semanales como su salida. De ahíp−1(220)=20 que20 los sistemas medios se venderán en una semana si el precio se fija en$220 por sistema.
- Nosotros computamos(P∘p−1)(x)=P(p−1(x))=P(500−2x3)=−1.5(500−2x3)2+170(500−2x3)−150. Después de una gran cantidad de Álgebra Primaria, obtenemos 8(P∘p−1)(x)=−23x2+220x−404503. Para entender lo que esto significa, recordemos que la función de ganancia original nosP dio el beneficio semanal en función de las ventas semanales. La función nosp−1 da las ventas semanales en función del precio. De ahí,P∘p−1 toma como insumo un precio. La funciónp−1 devuelve las ventas semanales, que a su vez se alimentaP para devolver la ganancia semanal. De ahí, nos(P∘p−1)(x) da la ganancia semanal (en dólares) en función del precio por sistemax, utilizando las ventas semanalesp−1(x) como el 'hombre intermedio'.
- Sabemos por la Sección 2.3 que la gráfica dey=(P∘p−1)(x) es una parábola que se abre hacia abajo. El beneficio máximo se realiza en el vértice. Ya que nos preocupa únicamente el precio por sistema, solo necesitamos encontrar lax coordenada del vértice. Identificandoa=−23 yb=220, obtenemos, por la Fórmula Vértice, Ecuación 2.4,x=−b2a=165. De ahí que la ganancia semanal se maximice si fijamos el precio en$165 por sistema. Comparando esto con nuestra respuesta del Ejemplo 2.3.3, hay una ligera discrepancia en la melodía de$0.50. Dejamos al lector equilibrar los libros de manera apropiada.
Ejercicios
En los Ejercicios 1 - 20, mostrar que la función dada es uno a uno y encuentra su inversa. Consulta tus respuestas algebraica y gráficamente. Verificar que el rango def es el dominio def−1 y viceversa.
- f(x)=6x−2
- f(x)=42−x
- f(x)=x−23+4
- f(x)=1−4+3x5
- f(x)=√3x−1+5
- f(x)=2−√x−5
- f(x)=3√x−1−4
- f(x)=1−2√2x+5
- f(x)=5√3x−1
- f(x)=3−3√x−2
- f(x)=x2−10x,x≥5
- f(x)=3(x+4)2−5,x≤−4
- f(x)=x2−6x+5,x≤3
- f(x)=4x2+4x+1,x<−1
- f(x)=34−x
- f(x)=x1−3x
- f(x)=2x−13x+4
- f(x)=4x+23x−6
- f(x)=−3x−2x+3
- f(x)=x−22x−1
Con la ayuda de tus compañeros de clase, encuentra los inversos de las funciones en Ejercicios 21 - 24.
- f(x)=ax+b,a≠0[genericinversefirst]
- f(x)=a√x−h+k,a≠0,x≥h
- f(x)=ax2+bx+cdondea≠0,x≥−b2a.
- f(x)=ax+bcx+d,(Ver Ejercicio 33 a continuación.)
- En el Ejemplo 1.5.3, el precio de un reproductor multimedia DoPi, en dólares por doPi, se da en función de las ventas semanalesx según la fórmulap(x)=450−15x para0≤x≤30.
- Encontrarp−1(x) y exponer su dominio.
- Encontrar e interpretarp−1(105).
- En el Ejemplo 1.5.3, determinamos que la ganancia (en dólares) obtenida de producir y venderx DOPI por semana esP(x)=−15x2+350x−2000, para0≤x≤30. Encuentra(P∘p−1)(x) y determina qué precio por DoPi produciría el máximo beneficio. ¿Cuál es el beneficio máximo? ¿Cuántos DOPI necesitan ser producidos y vendidos para lograr el máximo beneficio?
- Mostrar que la función de conversión de Fahrenheit a Celsius que se encuentra en el Ejercicio 35 en la Sección 2.1 es invertible y que su inversa es la función de conversión de Celsius a Fahrenheit.
- Analíticamente mostrar que la funciónf(x)=x3+3x+1 es uno a uno. Dado que encontrar una fórmula para su inversa está más allá del alcance de este libro de texto, use Teorema 5.2 para ayudarle a calcularf−1(1),f−1(5), yf−1(−3).
- Vamosf(x)=2xx2−1. Utilizando las técnicas de la Sección 4.2, gráficoy=f(x). Verifique quef sea uno a uno en el intervalo(−1,1). Utilice el procedimiento que se describe en la página 384 y su calculadora gráfica para encontrar la fórmula paraf−1(x). Tenga en cuenta que ya quef(0)=0, debería ser el caso quef−1(0)=0. ¿Qué sale mal cuando intentas sustituirx=0 enf−1(x)? Discuta con sus compañeros de clase cómo surgió este problema y posibles remedios.
- Con la ayuda de tus compañeros de clase, explica por qué una función que esté aumentando estrictamente o disminuyendo estrictamente en todo su dominio tendría que ser uno a uno, de ahí invertible.
- Sif es impar e invertible, demuestre que tambiénf−1 es impar.
- [fcircginverse] Dejarf yg ser funciones invertibles. Con la ayuda de tus compañeros de clase(f∘g) demuéstrense que es uno a uno, de ahí invertible, y eso(f∘g)−1(x)=(g−1∘f−1)(x).
- ¿Qué característica gráfica debef poseer una función para que sea su propia inversa?
- [whatconditions] ¿Qué condiciones debes poner a los valores dea,b,c yd en el Ejercicio 24 para garantizar que la función sea invertible?
RESPUESTAS
- f−1(x)=x+26
- f−1(x)=42−x
- f−1(x)=3x−10
- f−1(x)=−53x+13
- f−1(x)=13(x−5)2+13,x≥5
- f−1(x)=(x−2)2+5,x≤2
- f−1(x)=19(x+4)2+1,x≥−4
- f−1(x)=18(x−1)2−52,x≤1
- f−1(x)=13x5+13
- f−1(x)=−(x−3)3+2
- f−1(x)=5+√x+25
- f−1(x)=−√x+53−4
- f−1(x)=3−√x+4
- f−1(x)=−√x+12,x>1
- f−1(x)=4x−3x
- f−1(x)=x3x+1
- f−1(x)=4x+12−3x
- f−1(x)=6x+23x−4
- f−1(x)=−3x−2x+3
- f−1(x)=x−22x−1
-
- p−1(x)=450−x15. El dominio dep−1 es el rango de losp cuales es[0,450]
- p−1(105)=23. Esto significa que si el precio se establece en$105 entonces23 se venderán DOPI.
- (P∘p−1)(x)=−115x2+1103x−5000,0≤x≤450. La gráfica dey=(P∘p−1)(x) es una parábola que se abre hacia abajo con vértice(275,1253)≈(275,41.67). Esto significa que la ganancia máxima es friolera$41.67 cuando el precio por DoPi se establece en$275. A este precio, podemos producir y venderp−1(275)=11.¯6 DOPI. Como no podemos vender parte de un sistema, necesitamos ajustar el precio para vender ya11 sea DOPI o12 DOPI. Encontramosp(11)=285 yp(12)=270, lo que significa que establecemos el precio por DoPi en cualquiera$285 o$270, respectivamente. Las ganancias a estos precios son(P∘p−1)(285)=35 y(P∘p−1)(270)=40, así parece como si la ganancia máxima es$40 y se obtiene produciendo y vendiendo12 DOPI a la semana a un precio de$270 por DOPI.
- Dado esof(0)=1, tenemosf−1(1)=0. Del mismo modof−1(5)=1 yf−1(−3)=−1
Referencia
1 La función de identidad I, que fue introducida en la Sección 2.1 y mencionada en el Teorema 5.1, tiene un dominio de todos los números reales. Dado que los dominios de f y g pueden no ser todos números reales, necesitamos las restricciones enumeradas aquí.
2 En otras palabras, las funciones invertibles tienen exactamente una inversa.
3 Es un excelente ejercicio para explicar cada paso en esta cadena de igualdades.
4 En aras de una divulgación completa, los autores quisieran admitir que gran parte de la discusión de los párrafos anteriores podría haberse evitado fácilmente si hubiéramos apelado a la descripción de una función como conjunto de pares ordenados. No nos disculpamos por nuestra discusión desde el punto de vista de la composición de funciones, sin embargo, ya que expone al lector a formas más abstractas de pensar de funciones e inversas. Volveremos a revisar este concepto en el Capítulo 8.
5 Tenga en cuenta que si realiza su verificación en una calculadora para obtener funciones más sofisticadas, deberá aprovechar la función 'ZoomSquare' para obtener la perspectiva geométrica correcta.
6 Graficamosy=√x en la Sección 1.7.
7 Aquí, utilizamos la Fórmula Cuadrática para resolvery. Para 'completitud, notamos que puedes (¡y deberías!) también considere resolvery por 'completando' el cuadrado.
8 ¡Es una buena reseña para hacer esto de verdad!


