5.3: Otras funciones algebraicas
- Page ID
- 119505
Esta sección sirve de cuenca para funciones que son combinaciones de funciones polinómicas, y más generalmente, funciones racionales, con las operaciones de radicales. Es asunto de Cálculo discutir estas funciones con todo el detalle que demanden por lo que nuestro objetivo en esta sección es ayudar a apuntalar las habilidades necesarias para que el lector pueda responder a la llamada de Cálculo cuando llegue el momento. Recordamos brevemente la definición y algunas de las propiedades básicas de los radicales del Álgebra Intermedia. 1
\(x\)Sea un número real y\(n\) un número natural. a Si\(n\) es impar, la \(n^{\textbf{th}}\)raíz principal de\(x\), denotada\(\sqrt[n]{x}\) es el número real único que satisface
\[\left(\sqrt[n]{x}\right)^n = x. \nonumber\]
Si\(n\) es par,\(\sqrt[n]{x}\) se define de manera similar b proporcionado\(x \geq 0\) y\(\sqrt[n]{x} \geq 0\). El índice es el número\(n\) y el radicando es el número\(x\). Para\(n=2\), escribimos\(\sqrt{x}\) en vez de\(\sqrt[2]{x}\).
a Recordemos esto significa\(n = 1, 2, 3,\)....
b Recordar ambos\(x = −2\) y\(x = 2\) satisfacer\(x^{4}=16\), pero\(\sqrt[4]{16}=2\), no\(−2\).
Cabe remarcar que, a la luz de la Sección 5.2, podríamos definir\(f(x) = \sqrt[n]{x}\) funcionalmente como lo inverso de\(g(x) = x^n\) con la estipulación de que cuando\(n\) es par, el dominio de\(g\) se restringe al dominio de\([0, \infty)\). Por lo que sabemos\(g(x) = x^n\) de la Sección 3.1 junto con el Teorema 5.3, podemos producir las gráficas de\(f(x) = \sqrt[n]{x}\) reflejando las gráficas de\(g(x) = x^n\) a través de la línea\(y=x\). A continuación se muestran las gráficas de\(y=\sqrt{x}\),\(y=\sqrt[4]{x}\) y\(y=\sqrt[6]{x}\). El punto\((0,0)\) se indica como referencia. Los ejes están ocultos para que podamos ver la inclinación vertical cerca\(x=0\) y el aplanamiento horizontal como\(x \rightarrow \infty\).
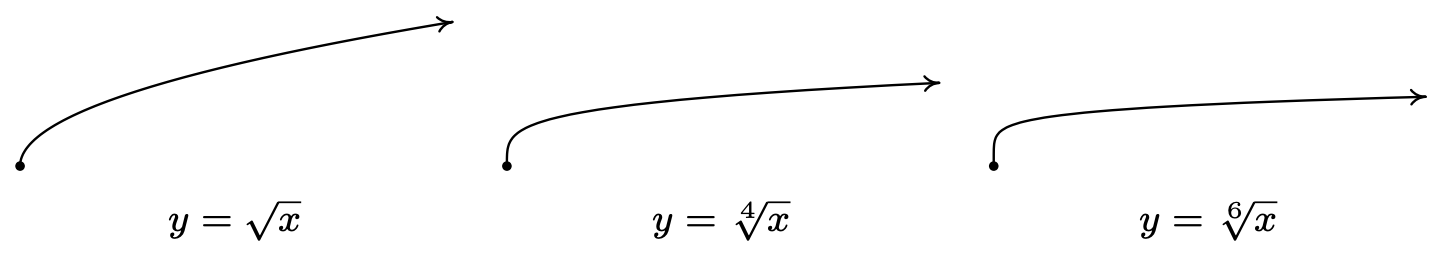
Las funciones radicales indexadas impares también siguen una tendencia predecible: empinarse cerca\(x = 0\) y aplanar como\(x \rightarrow \pm \infty\). En los ejercicios, tendrás la oportunidad de graficar algunas funciones radicales básicas utilizando las técnicas presentadas en la Sección 1.7.
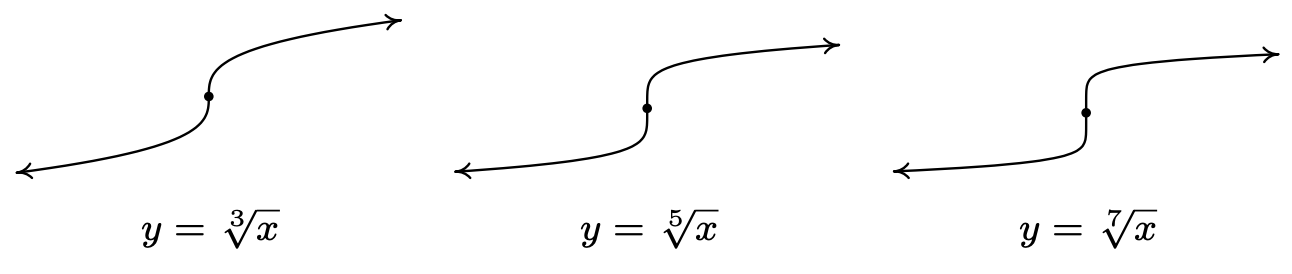
Hemos utilizado todas las siguientes propiedades en algún momento del libro de texto para el caso\(n=2\) (la raíz cuadrada), pero las enumeramos aquí en generalidad para que sean completas.
Dejar\(x\) y\(y\) ser números reales y\(m\) y\(n\) ser números naturales. Si\(\sqrt[n]{x}\),\(\sqrt[n]{y}\) son números reales, entonces
- Regla del producto:\(\sqrt[n]{xy} = \sqrt[n]{x} \, \sqrt[n]{y}\)
- Poderes de los radicales:\(\sqrt[n]{x^m} = \left(\sqrt[n]{x}\right)^m\)
- Regla del Cociente:\(\sqrt[n]{\dfrac{x}{y}} = \dfrac{\sqrt[n]{x}}{\sqrt[n]{y}}\), previsto\(y \neq 0\).
- Si\(n\) es impar,\(\sqrt[n]{x^n} = x\); si\(n\) es par,\(\sqrt[n]{x^n} = |x|\).
La prueba del Teorema 5.6 se basa en la definición de las raíces principales y propiedades de los exponentes. Para establecer la regla del producto, considere lo siguiente. Si\(n\) es impar, entonces por definición\(\sqrt[n]{xy}\) es el número real único tal que\((\sqrt[n]{xy})^{n} = xy\). Ante eso\(\left( \sqrt[n]{x} \, \sqrt[n]{y}\right)^n = \left(\sqrt[n]{x}\right)^n \left(\sqrt[n]{y}\right)^n = xy\), debe ser el caso que\(\sqrt[n]{xy} = \sqrt[n]{x} \, \sqrt[n]{y}\). Si\(n\) es par, entonces\(\sqrt[n]{xy}\) es el número real no negativo único tal que\((\sqrt[n]{xy})^{n} = xy\). También tenga en cuenta que ya\(n\) es par,\(\sqrt[n]{x}\) y también\(\sqrt[n]{y}\) son no negativos y por lo tanto también lo es\(\sqrt[n]{x}\sqrt[n]{y}\). Procediendo como arriba, nos encontramos con eso\(\sqrt[n]{xy} = \sqrt[n]{x} \, \sqrt[n]{y}\). La regla del cociente se prueba de manera similar y se deja como ejercicio. La regla de potencia resulta de la aplicación repetida de la regla del producto, siempre y cuando\(\sqrt[n]{x}\) sea un número real para empezar. 2 La última propiedad es una aplicación de la regla de poder cuando\(n\) es impar, y la ocurrencia del valor absoluto cuando\(n\) es par se debe al requisito de que\(\sqrt[n]{x} \geq 0\) en la Definición 5.4. Por ejemplo,\(\sqrt[4]{(-2)^4} = \sqrt[4]{16}= 2 = |-2|\), no\(-2\). Es esta última propiedad la que hace delicadas las composiciones de raíces y poderes. Esto es especialmente cierto cuando usamos notación exponencial para radicales. Recordemos la siguiente definición.
Dejar\(x\) ser un número real,\(m\) un entero a y\(n\) un número natural.
- \(x^{\frac{1}{n}} = \sqrt[n]{x}\)y se define siempre que\(\sqrt[n]{x}\) se define.
- \(x^{\frac{m}{n}} = \left(\sqrt[n]{x}\right)^m = \sqrt[n]{x^m}\), siempre que\(\left(\sqrt[n]{x}\right)^{m}\) se defina.
a Recordar esto significa\(m=0, \pm 1, \pm 2, \ldots\)
Los exponentes racionales definidos en la Definición 5.5 se comportan de manera muy similar a los exponentes enteros habituales del Álgebra Primaria con una excepción crítica. Considera la expresión\(\left(x^{2/3}\right)^{3/2}\). Aplicando las leyes habituales de los exponentes, estaríamos tentados a simplificar esto como\(\left(x^{2/3}\right)^{3/2} = x^{\frac{2}{3} \cdot \frac{3}{2}} = x^{1} = x\). No obstante, si sustituimos\(x=-1\) y aplicamos la Definición 5.5, encontramos\((-1)^{2/3} = \left(\sqrt[3]{-1}\right)^2 = (-1)^2 = 1\) así que\(\left((-1)^{2/3}\right)^{3/2} = 1^{3/2} = \left(\sqrt{1}\right)^3 = 1^3 = 1\). Vemos en este caso que\(\left(x^{2/3}\right)^{3/2} \neq x\). Si nos tomamos el tiempo para reescribir\(\left(x^{2/3}\right)^{3/2}\) con radicales, vemos
\[\left(x^{2/3}\right)^{3/2} = \left(\left(\sqrt[3]{x}\right)^2\right)^{3/2} = \left(\sqrt{\left(\sqrt[3]{x}\right)^2}\right)^3 =\left(\left|\sqrt[3]{x}\right|\right)^3 = \left| \left(\sqrt[3]{x}\right)^3 \right| = |x|\nonumber\]
En el análisis jugada por jugada, vemos que cuando cancelamos los\(2\)'s en multiplicar\(\frac{2}{3} \cdot \frac{3}{2}\), estábamos, de hecho, intentando cancelar un cuadrado con raíz cuadrada. El hecho de que\(\sqrt{x^2} = |x|\) y no simplemente\(x\) es la raíz 3 del problema. Puede divertir al lector saber eso\(\left(x^{3/2}\right)^{2/3} = x\), y esta verificación se deja como un ejercicio. La moraleja de la historia es que al simplificar los exponentes fraccionarios, suele ser mejor reescribirlos como radicales. 4 La última propiedad importante que vamos a exponer, y dejar a Cálculo para probar, es que las funciones radicales son continuas en sus dominios, por lo que se aplica el Teorema del Valor Intermedio, Teorema 3.1. Esto quiere decir que si tomamos combinaciones de funciones radicales con funciones polinómicas y racionales para formar lo que los autores consideran las funciones algebraicas, 5 podemos hacer diagramas de signos utilizando el procedimiento establecido en la Sección 4.2.
Supongamos que\(f\) es una función algebraica.
- Colocar cualquier valor excluido del dominio de\(f\) en la recta numérica con un ''encima de ellos.
- Encuentra los ceros de\(f\) y colócalos en la línea numérica con el número\(0\) encima de ellos.
- Elija un valor de prueba en cada uno de los intervalos determinados en los pasos 1 y 2.
- Determine el signo de\(f(x)\) para cada valor de prueba en el paso 3, y escriba ese signo por encima del intervalo correspondiente.
Nuestro siguiente ejemplo revisa bastante álgebra intermedia y demuestra algunas de las nuevas características de estas gráficas.
Para las siguientes funciones, indique sus dominios y cree diagramas de signos. Verifica tu respuesta gráficamente usando tu calculadora
- \(f(x) = 3x \sqrt[3]{2-x}\)
- \(g(x) = \sqrt{2-\sqrt[4]{x+3}}\)
- \(h(x) = \sqrt[3]{\dfrac{8x}{x+1}}\)
- \(k(x) = \dfrac{2x}{\sqrt{x^2 - 1}}\)
Solución.
- En lo que a dominio se refiere, no\(f(x)\) tiene denominadores y ni siquiera raíces, lo que significa que su dominio lo es\((-\infty, \infty)\). Para crear el diagrama de signos, encontramos los ceros de\(f\).
\[\begin{array}{rclr} f(x) & = & 0 & \\ 3x \sqrt[3]{2-x} & = & 0 \\ 3x = 0 & \mbox{or} & \sqrt[3]{2-x} = 0 & \\ x = 0 & \mbox{or} & \left(\sqrt[3]{2-x}\right)^3 = 0^3 & \\ x = 0 & \mbox{or} & 2-x = 0 & \\ x = 0 & \mbox{or} & x=2 & \\ \end{array}\nonumber\]
Los ceros\(0\) y\(2\) dividen la línea numérica real en tres intervalos de prueba. El diagrama de signos y el gráfico que lo acompaña están a continuación. Obsérvese que los intervalos en los que\(f\) se\((+)\) corresponde con donde la gráfica de\(f\) está por encima\(x\) del eje -eje, y donde la gráfica de\(f\) está por debajo\(x\) del -eje tenemos que\(f\) es\((-)\). La calculadora sugiere que algo misterioso sucede cerca\(x=2\). Al hacer zoom, la gráfica se vuelve casi vertical allí. Tendrás que esperar hasta Cálculo para entender completamente este fenómeno.
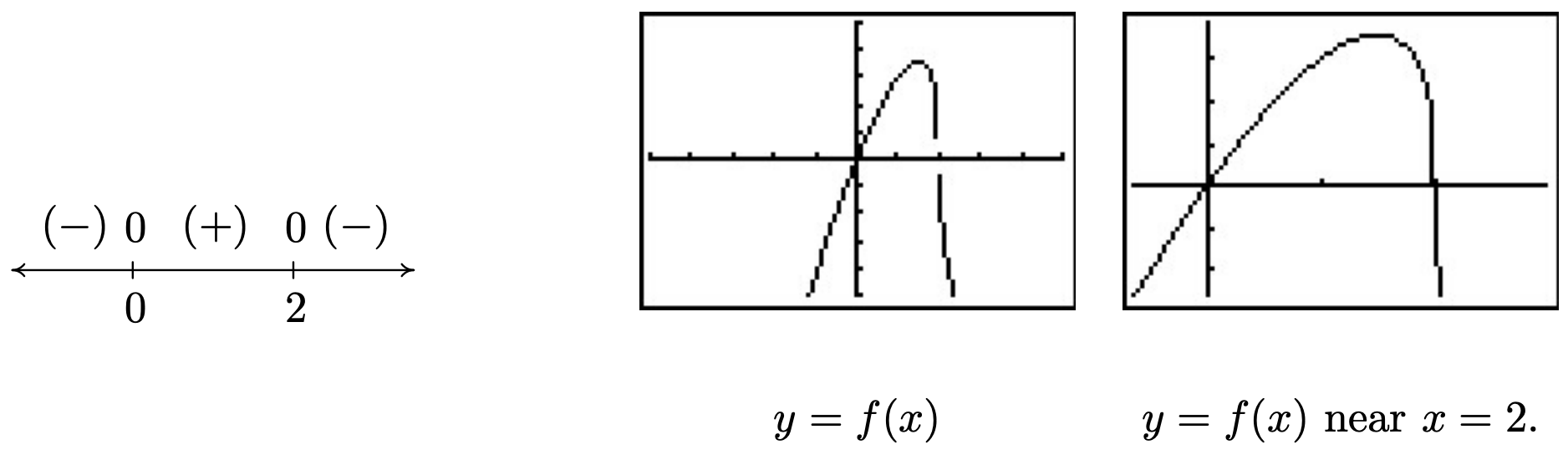
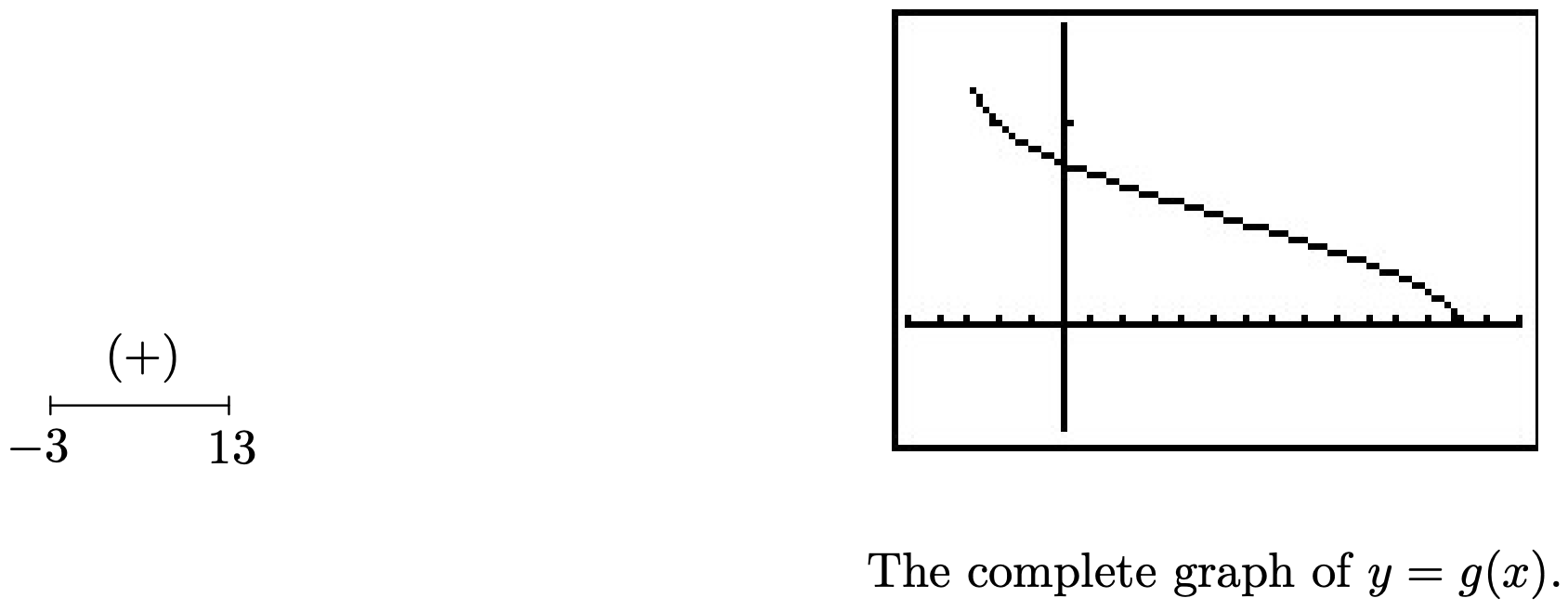
- En\(g(x) = \sqrt{2-\sqrt[4]{x+3}}\), tenemos dos radicales ambos de los cuales están incluso indexados. Para satisfacer\(\sqrt[4]{x+3}\), requerimos\(x+3 \geq 0\) o\(x \geq -3\). Para satisfacer\(\sqrt{2-\sqrt[4]{x+3}}\), necesitamos\(2-\sqrt[4]{x+3} \geq 0\). Si bien puede ser tentador escribir esto como\(2 \geq \sqrt[4]{x+3}\) y llevar ambos lados al cuarto poder, hay momentos en que esta técnica producirá resultados erróneos. 6 En su lugar, resolvemos\(2-\sqrt[4]{x+3} \geq 0\) usando un diagrama de signos. Si lo dejamos\(r(x) = 2-\sqrt[4]{x+3}\), lo sabemos\(x \geq -3\), entonces nos preocupamos solo por esta porción de la línea numérica. Para encontrar los ceros de\(r\) establecemos\(r(x) =0\) y resolvemos\(2-\sqrt[4]{x+3}=0\). Obtenemos\(\sqrt[4]{x+3} = 2\) para aquello\(\left(\sqrt[4]{x+3}\right)^4 = 2^4\) de lo que obtenemos\(x+3 = 16\) o\(x=13\). Dado que elevamos ambos lados de una ecuación a una potencia par, necesitamos verificar para ver si\(x=13\) es una solución extraña. 7 Encontramos\(x=13\) hace check desde\(2-\sqrt[4]{x+3} = 2 - \sqrt[4]{13+3} = 2 - \sqrt[4]{16} = 2 - 2 = 0\). A continuación se muestra nuestro diagrama de signos para\(r\).
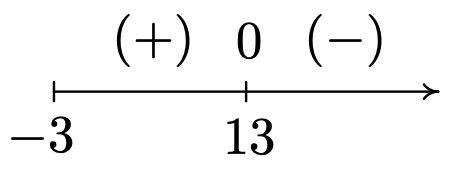
Nos encontramos\(2-\sqrt[4]{x+3} \geq 0\) encendido\([-3,13]\) así que este es el dominio de\(g\). Para encontrar un diagrama de señales para\(g\), buscamos los ceros de\(g\). \(g(x) = 0\)La configuración es equivalente a\(\sqrt{2-\sqrt[4]{x+3}}=0\). Después de cuadrar ambos lados, obtenemos\(2-\sqrt[4]{x+3} = 0\), cuya solución hemos encontrado que es\(x=13\). Ya que cuadramos ambos lados, verificamos dos veces y encontramos\(g(13)\) es, de hecho,\(0\). Nuestro diagrama de signos y gráfica de\(g\) están a continuación. Dado que el dominio de\(g\) es\([-3,13]\), lo que tenemos a continuación no es sólo una porción de la gráfica de\(g\), sino la gráfica completa. Siempre está por encima o en el\(x\) eje -eje, lo que verifica nuestro diagrama de signos.
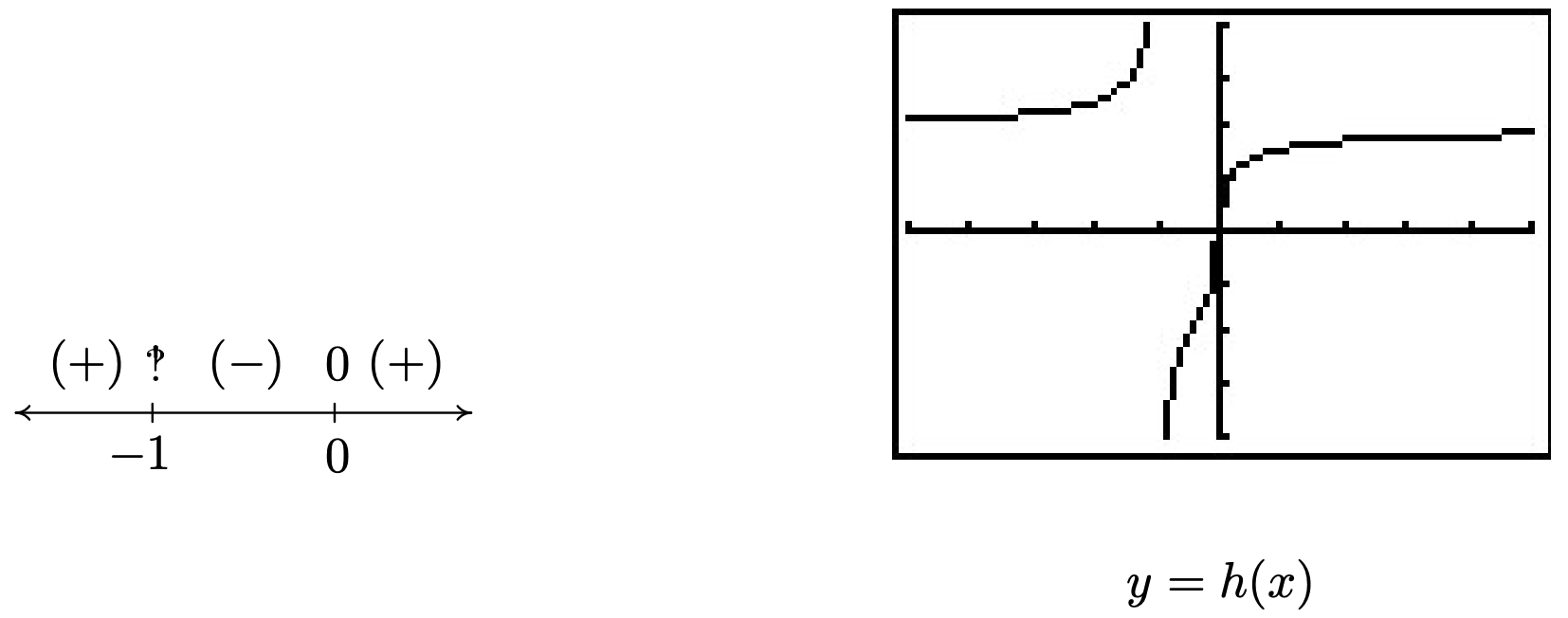
- El radical in\(h(x)\) es extraño, por lo que nuestra única preocupación es el denominador. \(x+1=0\)La configuración da\(x=-1\), entonces nuestro dominio es\((-\infty, -1) \cup (-1, \infty)\). Para encontrar los ceros de\(h\), nos fijamos\(h(x) = 0\). Para resolver\(\sqrt[3]{\frac{8x}{x+1}} = 0\), cubicamos ambos lados para conseguir\(\frac{8x}{x+1} = 0\). Obtenemos\(8x=0\), o\(x=0\). A continuación se muestra el diagrama de signos resultante y la gráfica correspondiente. De la gráfica, aparece como si fuera\(x=-1\) una asíntota vertical. La realización de un análisis\(x \rightarrow -1\) como en la Sección 4.2 lo confirma. (Dejamos los detalles al lector.) Cerca\(x=0\), tenemos una situación similar a\(x=2\) la de la gráfica del\(f\) número 1 anterior. Por último, aparece como si la gráfica de\(h\) tuviera una asíntota horizontal\(y=2\). Utilizando técnicas de la Sección 4.2, encontramos como\(x \rightarrow \pm \infty\),\(\frac{8x}{x+1} \rightarrow 8\). A partir de esto, no es de extrañar que como\(x \rightarrow \pm \infty\),\(h(x) = \sqrt[3]{\frac{8x}{x+1}} \approx \sqrt[3]{8} =2\).
- Para encontrar el dominio de\(k\), tenemos tanto una raíz pareja como un denominador que preocuparnos. Para satisfacer la raíz cuadrada,\(x^2 - 1 \geq 0\). \(r(x) = x^2-1\)Ajustando, encontramos los ceros de\(r\) ser\(x = \pm 1\), y encontramos el diagrama de signos de\(r\) ser
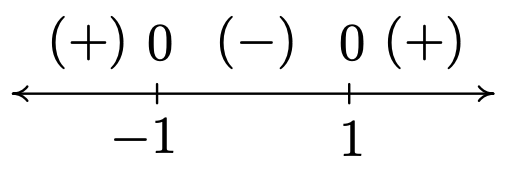
Encontramos\(x^2 - 1 \geq 0\) para\((-\infty, -1] \cup [1, \infty)\). Para mantener el denominador de\(k(x)\) lejos de cero, nos fijamos\(\sqrt{x^2-1} = 0\). Dejamos al lector verificar que las soluciones son\(x = \pm 1\), ambas de las cuales deben ser excluidas del dominio. De ahí que el dominio de\(k\) es\((-\infty, -1) \cup (1,\infty)\). Para construir el diagrama de signos para\(k\), necesitamos los ceros de\(k\). Establecer\(k(x) = 0\) resultados en\(\frac{2x}{\sqrt{x^2 - 1}}= 0\). Obtenemos\(2x =0\) o\(x=0\). Sin embargo,\(x=0\) no está en el dominio de\(k\), lo que significa que no\(k\) tiene ceros. Construimos nuestro diagrama de signos en el dominio de\(k\) abajo junto con la gráfica de\(k\). Parece que la gráfica de\(k\) tiene dos asíntotas verticales, una en\(x=-1\) y otra en\(x=1\). La brecha en la gráfica entre las asíntotas se debe a la brecha en el dominio de\(k\). En cuanto al comportamiento final, parece haber dos asíntotas horizontales,\(y = 2\) y\(y=-2\). Para ver por qué es así, pensamos en\(x\rightarrow \pm \infty\). El radicando del denominador\(x^2 - 1 \approx x^2\), y como tal,\(k(x) = \frac{2x}{\sqrt{x^2 - 1}} \approx \frac{2x}{\sqrt{x^2}} = \frac{2x}{|x|}\). Como\(x \rightarrow \infty\),\(|x| = x\) así lo tenemos\(k(x) \approx \frac{2x}{x} = 2\). Por otro lado, como\(x \rightarrow -\infty\),\(|x| = -x\), y como tal\(k(x) \approx \frac{2x}{-x} = -2\). Finalmente, aparece como si la gráfica de\(k\) pasara la Prueba de Línea Horizontal que significa que\(k\) es uno a uno y\(k^{-1}\) existe. \(k^{-1}\)La computación se deja como ejercicio.
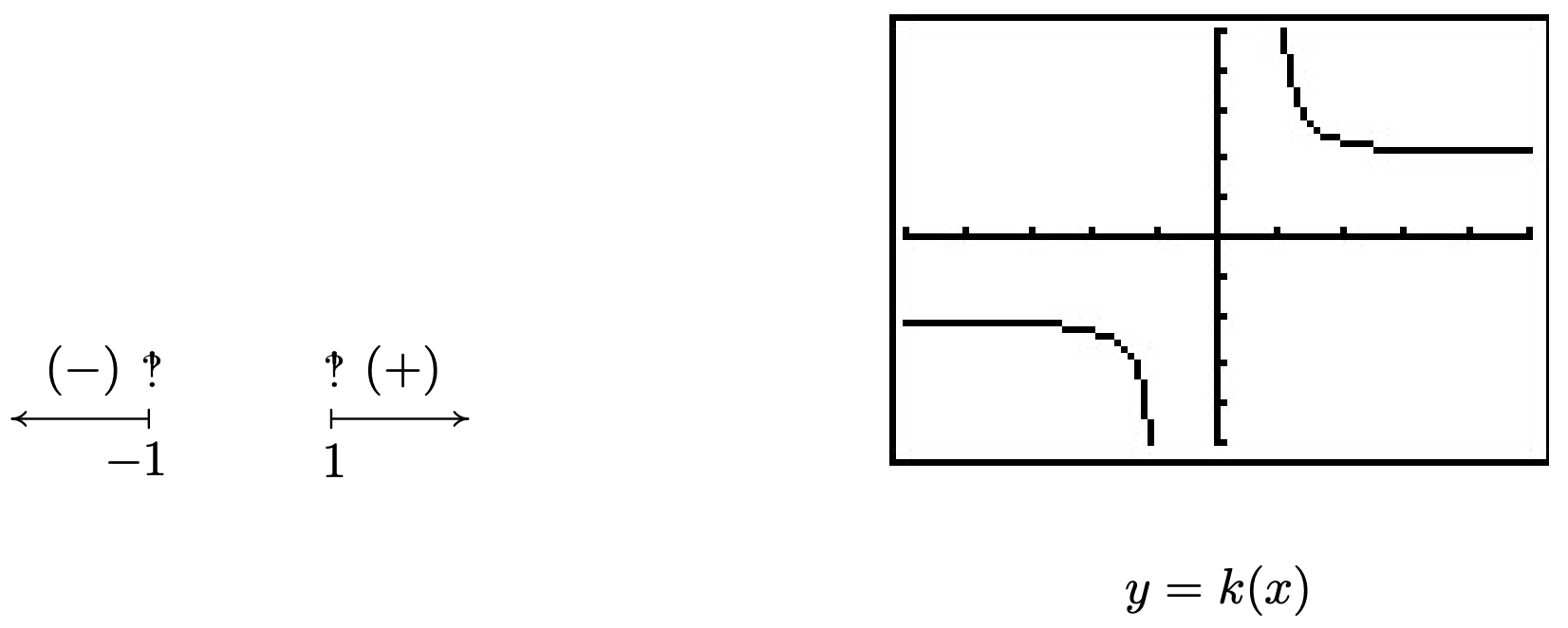
Como ilustra el ejemplo anterior, las gráficas de funciones algebraicas generales pueden tener características que hemos visto antes, como asíntotas verticales y horizontales, pero pueden ocurrir de formas nuevas y emocionantes. Por ejemplo,\(k(x) = \frac{2x}{\sqrt{x^{2} - 1}}\) tenía dos asíntotas horizontales distintas. Recordarás que las funciones racionales podrían tener como máximo una asíntota horizontal. También algunas características nuevas como 'pendiente inusual' 8 y cúspides 9 pueden aparecer en las gráficas de funciones algebraicas arbitrarias. Nuestro siguiente ejemplo primero demuestra cómo podemos usar diagramas de signos para resolver desigualdades no lineales. (No entre en pánico. La técnica es muy similar a las utilizadas en los Capítulos 2, 3 y 4.) Luego verificamos nuestras respuestas gráficamente con una calculadora y vemos algunas de las nuevas características gráficas de las funciones en esta familia extendida.
Resolver las siguientes desigualdades. Consulta tus respuestas gráficamente con una calculadora.
- \(x^{2/3} < x^{4/3} - 6\)
- \(3 (2-x)^{1/3} \leq x (2-x)^{-2/3}\)
Solución.
- Para resolver\(x^{2/3} < x^{4/3} - 6\), nos ponemos de un\(0\) lado e intentamos resolver\(x^{4/3} - x^{2/3} - 6 > 0\). Nos fijamos\(r(x) = x^{4/3} - x^{2/3} - 6\) y notamos que dado que los denominadores en los exponentes son\(3\), corresponden a las raíces cúbicas, lo que significa que el dominio de\(r\) es\((-\infty, \infty)\). Para encontrar los ceros para el diagrama de signos, establecemos\(r(x) = 0\) e intentamos resolver\(x^{4/3} - x^{2/3} - 6 = 0\). En este punto, puede no estar claro cómo proceder. Siempre podríamos intentar como último recurso convertir de nuevo a notación radical, pero en este caso podemos tomar el ejemplo del Ejemplo 3.3.4. Ya que hay tres términos, y el exponente en uno de los términos variables,\(x^{4/3}\), es exactamente el doble que el del otro,\(x^{2/3}\), tenemos a nosotros mismos un 'cuadrático en disguise' y podemos reescribir\(x^{4/3} - x^{2/3} - 6 = 0\) como\(\left(x^{2/3}\right)^2 - x^{2/3} - 6=0\). Si dejamos\(u = x^{2/3}\), entonces en términos de\(u\), obtenemos\(u^2 - u - 6 = 0\). Resolviendo para\(u\), obtenemos\(u = -2\) o\(u = 3\). Reemplazando de\(x^{2/3}\) nuevo por\(u\), obtenemos\(x^{2/3} = -2\) o\(x^{2/3} = 3\). Para evitar el problema que encontramos en la discusión que sigue a la Definición 5.5, ahora convertimos de nuevo a notación radical. Al interpretar\(x^{2/3}\) como\(\sqrt[3]{x^2}\) tenemos\(\sqrt[3]{x^2} = -2\) o\(\sqrt[3]{x^2}= 3\). Cubando ambos lados de estas ecuaciones resulta en\(x^2 = -8\), lo que admite ninguna solución real, o\(x^2 = 27\), que da\(x = \pm 3 \sqrt{3}\). Construimos un diagrama de signos y encontramos\(x^{4/3} - x^{2/3} - 6 > 0\) en\(\left(-\infty, -3 \sqrt{3}\right)\cup \left(3 \sqrt{3}, \infty\right)\). Para verificar nuestra respuesta gráficamente, establecemos\(f(x) = x^{2/3}\) y\(g(x) = x^{4/3}-6\). La solución a\(x^{2/3} < x^{4/3} - 6\) corresponde a la desigualdad\(f(x) < g(x)\), lo que significa que estamos buscando\(x\) los valores para los cuales la gráfica de\(f\) está por debajo de la gráfica de\(g\). Usando el comando 'Intersectar' confirmamos 10 que las gráficas se cruzan en\(x= \pm 3\sqrt{3}\). Vemos que la gráfica de\(f\) está por debajo de la gráfica de\(g\) (la curva más gruesa) en\(\left(-\infty, -3 \sqrt{3}\right)\cup \left(3 \sqrt{3}, \infty\right)\).
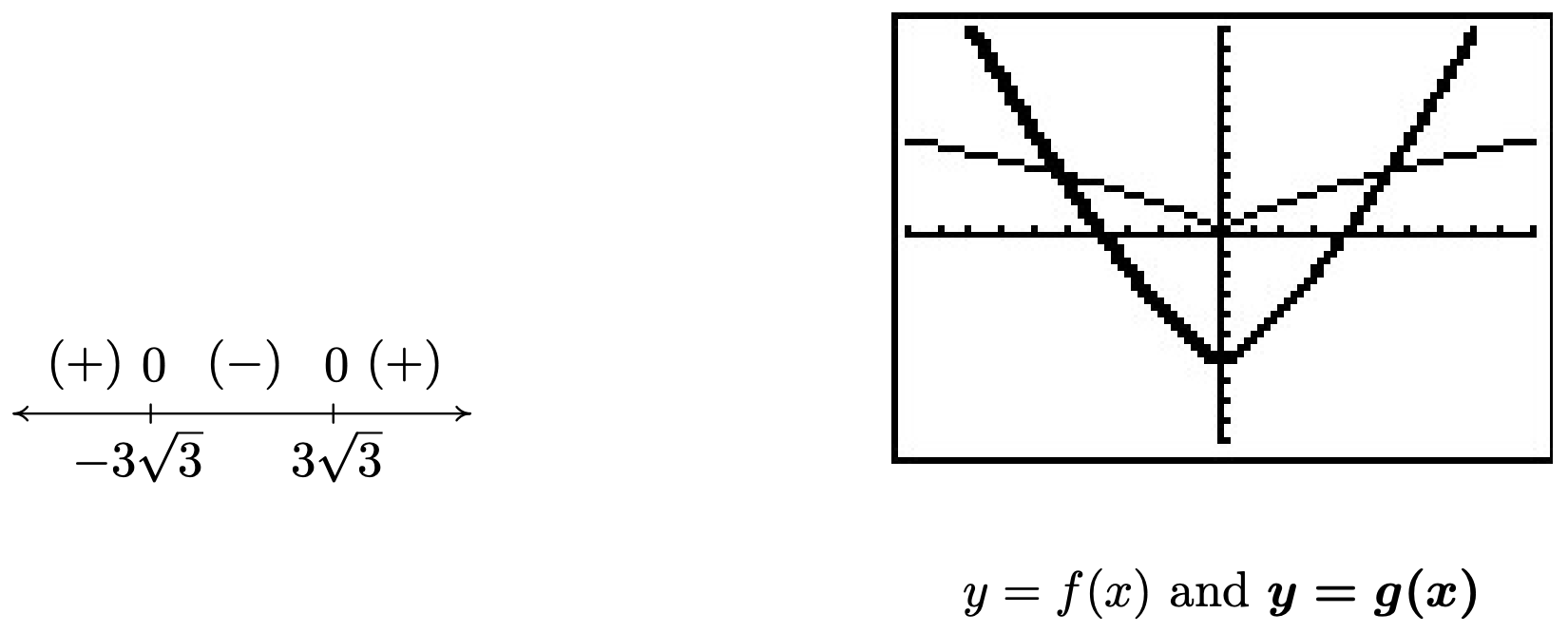
Como punto de interés, si echamos un vistazo más de cerca a las gráficas de\(f\) y\(g\) cerca\(x=0\) con los ejes apagados, vemos que a pesar de que ambos involucran raíces cúbicas, exhiben un comportamiento diferente cerca\(x=0\). La gráfica de\(f\) tiene un giro brusco, o cúspide, mientras que\(g\) no lo hace. 11
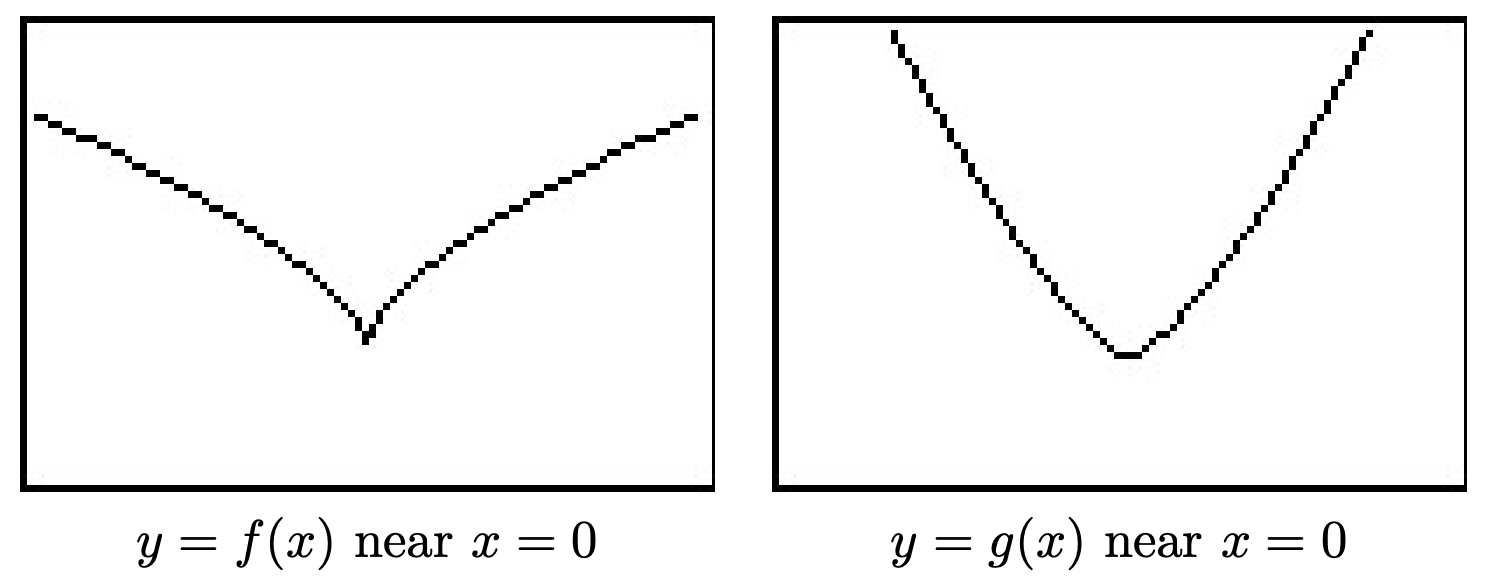
- Para resolver\(3 (2-x)^{1/3} \leq x (2-x)^{-2/3}\), reunimos todos los términos distintos de cero por un lado y obtenemos\(3 (2-x)^{1/3} - x (2-x)^{-2/3} \leq 0\). Nos fijamos\(r(x) = 3 (2-x)^{1/3} - x (2-x)^{-2/3}\). Al igual que en el número 1, los denominadores de los exponentes racionales son impares, lo que significa que no hay preocupaciones de dominio ahí. Sin embargo, el exponente negativo en el segundo término indica un denominador. Reescribiendo\(r(x)\) con exponentes positivos, obtenemos\[r(x) = 3 (2-x)^{1/3} - \frac{x}{(2-x)^{2/3}}\] Estableciendo el denominador igual a cero obtenemos\((2-x)^{2/3} = 0\), o\(\sqrt[3]{(2-x)^2} = 0\). Después de cubicar ambos lados, y posteriormente tomar raíces cuadradas, obtenemos\(2-x=0\), o\(x=2\). De ahí que el dominio de\(r\) es\((-\infty, 2) \cup (2, \infty)\). Para encontrar los ceros de\(r\), nos fijamos\(r(x) = 0\). Hay dos escuelas de pensamiento sobre cómo proceder y demostramos ambas.
- \[\begin{array}{rclr} r(x) & = & 3 (2-x)^{1/3} - x (2-x)^{-2/3} & \\[4pt] & = & (2-x)^{-2/3} \left[ 3 (2-x)^{\frac{1}{3} - \left(-\frac{2}{3}\right)} - x\right] & \\ [6pt] & = & (2-x)^{-2/3}\left[3(2-x)^{3/3} - x\right] & \\[4pt] & = & (2-x)^{-2/3}\left[3(2-x)^{1} - x\right] & \mbox{since $\sqrt[3]{u^3} = \left(\sqrt[3]{u}\right)^{3} = u$} \\[4pt] & = & (2-x)^{-2/3}\left(6-4x\right) & \\[4pt] & = & (2-x)^{-2/3}\left(6-4x\right) & \\ \end{array}\nonumber\]
Para resolver\(r(x) = 0\), establecemos\((2-x)^{-2/3}\left(6-4x\right) = 0\), o\(\frac{6-4x}{(2-x)^{2/3}} = 0\). Tenemos\(6-4x = 0\) o\(x = \frac{3}{2}\).
- Aproximación al denominador común. Reescribimos
\[\begin{array}{rclr} r(x) & = & 3 (2-x)^{1/3} - x (2-x)^{-2/3} & \\[4pt] & = & 3 (2-x)^{1/3} - \dfrac{x}{(2-x)^{2/3}} & \\ [10pt] & = & \dfrac{3 (2-x)^{1/3}(2-x)^{2/3}}{(2-x)^{2/3}} - \dfrac{x}{(2-x)^{2/3}} & \mbox{common denominator} \\ [10pt] & = & \dfrac{3 (2-x)^{\frac{1}{3} + \frac{2}{3}}}{(2-x)^{2/3}} - \dfrac{x}{(2-x)^{2/3}} & \\ [10pt] & = & \dfrac{3 (2-x)^{3/3}}{(2-x)^{2/3}} - \dfrac{x}{(2-x)^{2/3}} & \\ [10pt] & = & \dfrac{3 (2-x)^1}{(2-x)^{2/3}} - \dfrac{x}{(2-x)^{2/3}} & \mbox{since $\sqrt[3]{u^3} = \left(\sqrt[3]{u}\right)^{3} = u$} \\ [10pt] & = & \dfrac{3 (2-x) - x}{(2-x)^{2/3}} & \\ [10pt] & = & \dfrac{6-4x}{(2-x)^{2/3}} & \\ \end{array}\nonumber\]
Como antes, cuando\(r(x) = 0\) establecemos obtenemos\(x = \frac{3}{2}\).
Ahora creamos nuestro diagrama de señales y encontramos\(3 (2-x)^{1/3} - x (2-x)^{-2/3} \leq 0\) en\(\left[\frac{3}{2},2\right) \cup (2, \infty)\). Para verificar esto gráficamente, establecemos\(f(x)=3 (2-x)^{1/3}\) y\(g(x) = x (2-x)^{-2/3}\) (la curva más gruesa). Confirmamos que las gráficas se cruzan en\(x=\frac{3}{2}\) y la gráfica de\(f\) está por debajo de la gráfica de\(g\) for\(x \geq \frac{3}{2}\), con la excepción de\(x=2\) donde aparece la gráfica de\(g\) tiene una asíntota vertical.
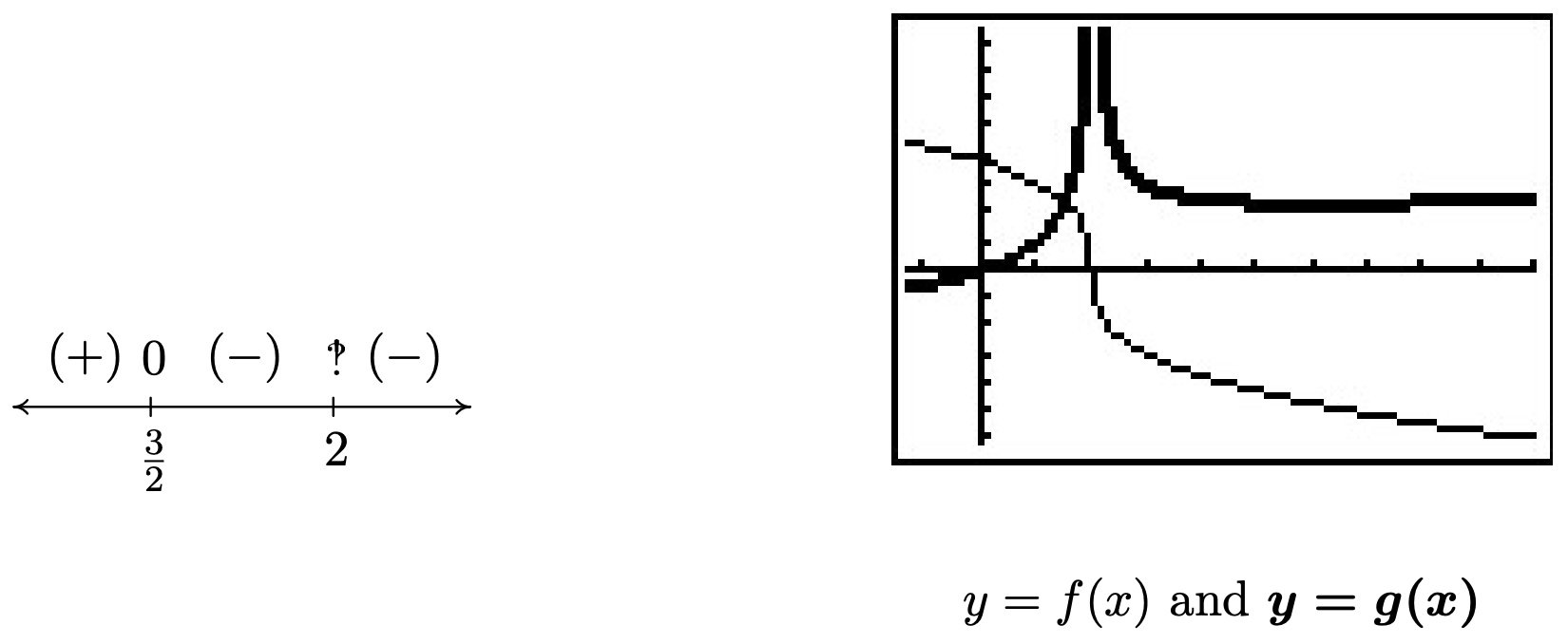
- \[\begin{array}{rclr} r(x) & = & 3 (2-x)^{1/3} - x (2-x)^{-2/3} & \\[4pt] & = & (2-x)^{-2/3} \left[ 3 (2-x)^{\frac{1}{3} - \left(-\frac{2}{3}\right)} - x\right] & \\ [6pt] & = & (2-x)^{-2/3}\left[3(2-x)^{3/3} - x\right] & \\[4pt] & = & (2-x)^{-2/3}\left[3(2-x)^{1} - x\right] & \mbox{since $\sqrt[3]{u^3} = \left(\sqrt[3]{u}\right)^{3} = u$} \\[4pt] & = & (2-x)^{-2/3}\left(6-4x\right) & \\[4pt] & = & (2-x)^{-2/3}\left(6-4x\right) & \\ \end{array}\nonumber\]
Una aplicación de funciones algebraicas se dio en el Ejemplo 1.6.6 en la Sección 1.1. Nuestro último ejemplo es una aplicación más sofisticada de la distancia.
Carl desea instalar el servicio de Internet de alta velocidad en su puesto de observación remoto Sasquatch ubicado\(30\) a millas de Route\(117\). La caja de conexiones más cercana se encuentra\(50\) a millas aguas abajo del poste, como se indica en el diagrama a continuación. Supongamos que cuesta\(\$ 15\) por milla correr el cable a lo largo de la carretera y\(\$ 20\) por milla correr el cable fuera de la carretera.
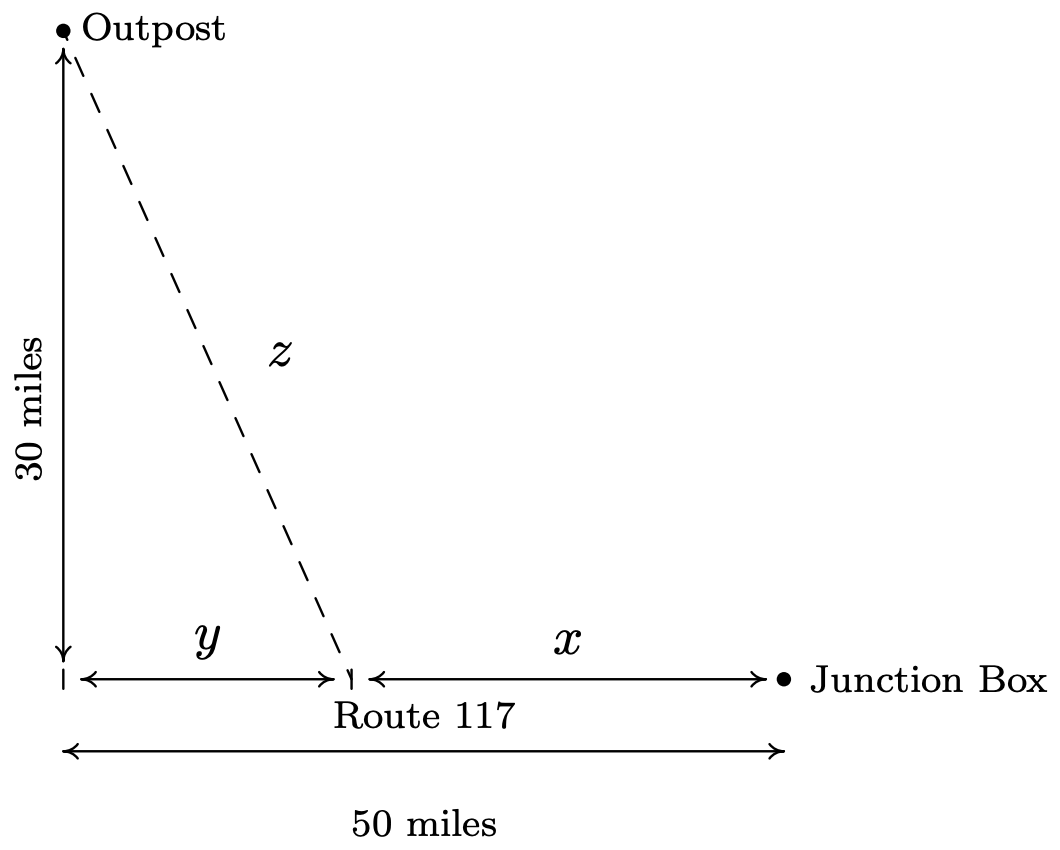
- Exprese el costo total\(C\) de conectar la Caja de Conexiones al Puesto Avanzado en función de\(x\), el número de millas por las que se recorre el cable a lo largo de la Ruta\(117\) antes de dirigirse directamente hacia el Puesto Avanzado. Determinar un dominio aplicado razonable para el problema.
- Usa tu calculadora para graficar\(y=C(x)\) sobre su dominio. ¿Cuál es el costo mínimo? ¿A qué distancia de Ruta se\(117\) debe correr el cable antes de desviarse de la carretera?
Solución.
- El costo se divide en dos partes: el costo de correr el cable a lo largo de la Ruta\(117\)\(\$15\) por milla, y el costo de correrlo fuera de la carretera\(\$20\) por milla. Dado que\(x\) representa las millas de recorrido de cable a lo largo de Route\(117\), el costo de esa porción es\(15x\). A partir del diagrama, vemos que el número de millas que el cable se corre fuera de la carretera es\(z\), por lo que el costo de esa porción es\(20z\). De ahí que el costo total sea\(C = 15x + 20z\). Nuestro siguiente objetivo es determinar\(z\) en función de\(x\). El diagrama sugiere que podemos usar el Teorema de Pitágoras para obtener\(y^2+30^2 = z^2\). Pero también vemos\(x+y = 50\) así\(y=50-x\). De ahí,\(z^2 = (50-x)^2+900\). Resolviendo para\(z\), obtenemos\(z = \pm \sqrt{(50-x)^2+900}\). Ya que\(z\) representa una distancia, elegimos\(z = \sqrt{(50-x)^2+900}\) para que nuestro costo en función de\(x\) solo esté dado por\[C(x) = 15x + 20\sqrt{(50-x)^2+900}\nonumber\] Desde el contexto del problema, tenemos\(0 \leq x \leq 50\).
- Graficando\(y=C(x)\) en una calculadora y usando la función 'Mínimo', encontramos el mínimo relativo (que también es el mínimo absoluto en este caso) a dos decimales para ser\((15.98, 1146.86)\). Aquí la\(x\) coordenada nos dice que para minimizar el costo, debemos correr\(15.98\) millas de cable por la Ruta 117 y luego desviarnos de la carretera y dirigirnos hacia el puesto avanzado. El\(y\) -coordenada nos dice que el costo mínimo, en dólares, para hacerlo es\(\$1146.86\). ¿La capacidad de transmitir en vivo Sasquatchcasts? Invaluable.
5.3.1 Ejercicios
Para cada función en los Ejercicios 1 - 10 a continuación
- Encuentra su dominio.
- Crea un diagrama de señales.
- Usa tu calculadora para ayudarte a esbozar su gráfica e identificar cualquier asíntota vertical u horizontal, 'pendiente inusual' o cúspide.
- \(f(x) = \sqrt{1 - x^{2}}\)
- \(f(x) = \sqrt{x^2-1}\)
- \(f(x) = x \sqrt{1-x^2}\)
- \(f(x) = x \sqrt{x^2-1}\)
- \(f(x) = \sqrt[4]{\dfrac{16x}{x^{2} - 9}}\)
- \(f(x) = \dfrac{5x}{\sqrt[3]{x^{3} + 8}}\)
- \(f(x) = x^{\frac{2}{3}}(x - 7)^{\frac{1}{3}}\)
- \(f(x) = x^{\frac{3}{2}}(x - 7)^{\frac{1}{3}}\)
- \(f(x) = \sqrt{x(x + 5)(x - 4)}\)
- \(f(x) = \sqrt[3]{x^{3} + 3x^{2} - 6x - 8}\)
En los Ejercicios 11 - 16, bosquejar la gráfica\(y=g(x)\) de comenzando con la gráfica de\(y = f(x)\) y utilizando las transformaciones presentadas en la Sección 1.7.
- \(f(x) = \sqrt[3]{x}\),\(g(x) = \sqrt[3]{x-1}-2\)
- \(f(x) = \sqrt[3]{x}\),\(g(x) = -2\sqrt[3]{x + 1} + 4\)
- \(f(x) = \sqrt[4]{x}\),\(g(x) = \sqrt[4]{x-1}-2\)
- \(f(x) = \sqrt[4]{x}\),\(g(x) = 3\sqrt[4]{x - 7} - 1\)
- \(f(x) = \sqrt[5]{x}\),\(g(x) = \sqrt[5]{x + 2} + 3\)
- \(f(x) = \sqrt[8]{x}\),\(g(x) = \sqrt[8]{-x} - 2\)
- \(x+1 = \sqrt{3x+7}\)
- \(2x+1 = \sqrt{3-3x}\)
- \(x + \sqrt{3x+10} = -2\)
- \(3x+\sqrt{6-9x}=2\)
- \(2x - 1 = \sqrt{x + 3}\)
- \(x^{\frac{3}{2}} = 8\)
- \(x^{\frac{2}{3}} = 4\)
- \(\sqrt{x - 2} + \sqrt{x - 5} = 3\)
- \(\sqrt{2x+1} = 3 + \sqrt{4-x}\)
- \(5 - (4-2x)^{\frac{2}{3}} = 1\)
- \(10-\sqrt{x-2} \leq 11\)
- \(\sqrt[3]{x} \leq x\)
- \(2 (x-2)^{-\frac{1}{3}} -\frac{2}{3} x(x-2)^{-\frac{4}{3}} \leq 0\)
- \(-\frac{4}{3} (x-2)^{-\frac{4}{3}} + \frac{8}{9} x (x-2)^{-\frac{7}{3}} \geq 0\)
- \(2x^{-\frac{1}{3}}(x-3)^{\frac{1}{3}} + x^{\frac{2}{3}} (x-3)^{-\frac{2}{3}} \geq 0\)
- \(\sqrt[3]{x^{3} + 3x^{2} - 6x - 8} > x + 1\)
- \(\frac{1}{3}x^{\frac{3}{4}}(x - 3)^{-\frac{2}{3}} + \frac{3}{4}x^{-\frac{1}{4}}(x - 3)^{\frac{1}{3}} < 0\)
- \(x^{-\frac{1}{3}} (x-3)^{-\frac{2}{3}} - x^{-\frac{4}{3}} (x-3)^{-\frac{5}{3}} (x^2-3x+2) \geq 0\)
- \(\frac{2}{3}(x + 4)^{\frac{3}{5}}(x - 2)^{-\frac{1}{3}} + \frac{3}{5}(x + 4)^{-\frac{2}{5}}(x - 2)^{\frac{2}{3}} \geq 0\)
- Ejemplo de retrabajo 5.3.3 para que el puesto avanzado esté a 10 millas de la ruta 117 y la caja de conexiones más cercana esté a 30 millas por la carretera para el puesto.
- El volumen\(V\) de un cono cilíndrico derecho depende del radio de su base\(r\) y su altura\(h\) y viene dado por la fórmula\(V = \frac{1}{3} \pi r^2 h\). El área superficial\(S\) de un cono cilíndrico derecho también depende de\(r\) y de\(h\) acuerdo con la fórmula\(S = \pi r \sqrt{r^2+h^2}\). Supongamos que un cono es tener un volumen de 100 centímetros cúbicos.
- Utilice la fórmula para el volumen para encontrar la altura\(h\) en función de\(r\).
- Utilice la fórmula para el área de superficie y su respuesta a 37a para encontrar el área\(S\) de superficie en función de\(r\).
- Use su calculadora para encontrar los valores de\(r\) y\(h\) cuáles minimizan el área de superficie. ¿Cuál es la superficie mínima? Redondea tus respuestas a dos decimales.
- El Servicio Meteorológico Nacional utiliza la siguiente fórmula para calcular el frío del viento:\[W = 35.74 + 0.6215 \, T_{a} - 35.75\, V^{0.16} + 0.4275 \, T_{a} \, V^{0.16}\nonumber\] donde\(W\) está la temperatura del frío del viento en\(^{\circ}\) F,\(T_{a}\) es la temperatura del aire en\(^{\circ}\) F, y\(V\) es la velocidad del viento en millas por hora. Tenga en cuenta que\(W\) se define solo para temperaturas del aire iguales o inferiores a\(50^{\circ}\) F y velocidades del viento superiores\(3\) a millas por hora.
- Supongamos que la temperatura del aire es\(42^{\circ}\) y la velocidad del viento es de\(7\) millas por hora. Encuentra la temperatura del viento frío. Redondea tu respuesta a dos decimales.
- Supongamos que la temperatura del aire es\(37^{\circ}\) F y la temperatura del frío del viento es\(30^{\circ}\) F. Encuentra la velocidad del viento. Redondea tu respuesta a dos decimales.
- Como seguimiento al Ejercicio 38, supongamos que la temperatura del aire es\(28^{\circ}\) F.
- Usa la fórmula del Ejercicio 38 para encontrar una expresión para la temperatura del frío del viento en función de la velocidad del viento,\(W(V)\).
- Resuelve\(W(V) = 0\), redondea tu respuesta a dos decimales e interpreta.
- Grafica la función\(W\) usando tu calculadora y comprueba tu respuesta a la parte 39b.
- El periodo de un péndulo en segundos viene dado por\[T = 2\pi \sqrt{\dfrac{L}{g}}\nonumber\] (para pequeños desplazamientos) donde\(L\) está la longitud del péndulo en metros y\(g = 9.8\) metros por segundo por segundo es la aceleración por gravedad. Mi reloj antiguo de escuela Seth-Thomas necesita\(T = \frac{1}{2}\) segundo y puedo ajustar la longitud del péndulo a través de una pequeña esfera en la parte inferior del bob. ¿A qué longitud debo fijar el péndulo?
- El modelo de producción Cobb-Douglas establece que el valor anual total en dólares de la producción\(P\) en una economía es una función del trabajo\(x\) (el número total de horas trabajadas en un año) y el capital\(y\) (el valor total en dólares de todas las cosas compradas para hacer cosas). Específicamente,\(P = ax^{b}y^{1 - b}\). Al fijar\(P\), creamos lo que se conoce como un 'isoquant' y luego podemos resolverlo en función de\(x\).\(y\) Supongamos que el modelo de producción Cobb-Douglas para el país de Sasquatchia es\(P = 1.23x^{0.4}y^{0.6}\).
- Dejar\(P = 300\) y resolver para\(y\) en términos de\(x\). Si\(x = 100\), ¿qué es\(y\)?
- Grafica el isocuante\(300 = 1.23x^{0.4}y^{0.6}\). ¿Qué información te da un par ordenado\((x, y)\) que hace\(P = 300\)? Con la ayuda de tus compañeros, encuentra varias combinaciones diferentes de mano de obra y capital, todas las cuales rinden\(P = 300\). Discuta cualquier patrón que pueda ver.
- Según la Teoría de la Relatividad Especial de Einstein, la masa observada\(m\) de un objeto es función de la rapidez con la que viaja el objeto. Específicamente,\[m(x) = \dfrac{m_{r}}{\sqrt{1 - \dfrac{x^{2}}{c^{2}}}}\nonumber\] donde\(m(0)=m_{r}\) está la masa del objeto en reposo,\(x\) es la velocidad del objeto y\(c\) es la velocidad de la luz.
- Encuentra el dominio aplicado de la función.
- Cómputos\(m(.1c), \, m(.5c), \, m(.9c)\) y\(m(.999c)\).
- Como\(x \rightarrow c^{-}\), ¿qué pasa con\(m(x)\)?
- ¿Qué tan lentamente debe viajar el objeto para que la masa observada no sea mayor de 100 veces su masa en reposo?
- Encuentra la inversa de\(k(x) = \dfrac{2x}{\sqrt{x^{2} - 1}}\).
- Supongamos que Fritzy the Fox, posicionado\((x,y)\) en un punto del primer cuadrante, ve a Chewbacca the Bunny en\((0,0)\). Chewbacca comienza a correr por una barda (el\(y\) eje positivo) hacia su carreta. Fritzy, por supuesto, toma persecución y ajusta constantemente su dirección para que siempre esté corriendo directamente en Chewbacca. Si la velocidad de Chewbacca es\(v_{1}\) y la de Fritzy lo es\(v_{2}\), el camino que tomará Fritzy para interceptar a Chewbacca, siempre que\(v_{2}\) sea directamente proporcional a, pero no igual a,\(v_{1}\) es modelado por
\[y = \dfrac{1}{2} \left(\dfrac{x^{1+ v_{1}/v_{2}}}{1+v_1/v_2}- \dfrac{x^{1-v_1/v_2}}{1-v_1/v_2}\right) + \dfrac{v_1 v_2}{v_2^2-v_1^2}\]
- Determinar el camino que tomará Fritzy si corre exactamente el doble de rápido que Chewbacca; es decir,\(v_{2} = 2v_{1}\). Utilice su calculadora para graficar esta ruta para\(x \geq 0\). ¿Cuál es el significado de la\(y\) -intercepción de la gráfica?
- Determina el camino que tomará Fritzy si Chewbacca corre exactamente el doble de rápido que él; es decir,\(v_{1} = 2v_{2}\). Utilice su calculadora para graficar esta ruta para\(x > 0\). Describir el comportamiento de\(y\) as\(x \rightarrow 0^{+}\) e interpretarlo físicamente.
- Con la ayuda de tus compañeros, generaliza las partes (a) y (b) a dos casos:\(v_{2} > v_{1}\) y\(v_{2} < v_{1}\). Discutiremos el caso del\(v_{1} = v_{2}\) Ejercicio 32 en la Sección 6.5.
- Verificar la Regla del Cociente para Radicales en el Teorema 5.6.
- \(\left(x^{\frac{3}{2}}\right)^{\frac{2}{3}} = x\)Demuéstralo para todos\(x \geq 0\).
- Demostrar que\(\sqrt[3]{2}\) es un número irracional mostrando primero que es un cero de\(p(x) = x^{3} - 2\) y luego mostrar no\(p\) tiene ceros racionales. (Necesitarás el Teorema de los Ceros Racionales, Teorema 3.9, para poder mostrar esta última parte.)
- Con la ayuda de tus compañeros, generaliza el Ejercicio 47 para demostrar que\(\sqrt[n]{c}\) es un número irracional para cualquier número natural\(c \geq 2\) y\(n \geq 2\) siempre que\(c \neq p^{n}\) para algún número natural\(p\).
5.3.2 Respuestas
-
\(f(x) = \sqrt{1 - x^2}\)
Dominio:\([-1, 1]\)
Sin asíntotas
Inclinación inusual en\(x = -1\) y\(x = 1\)
Sin cúspides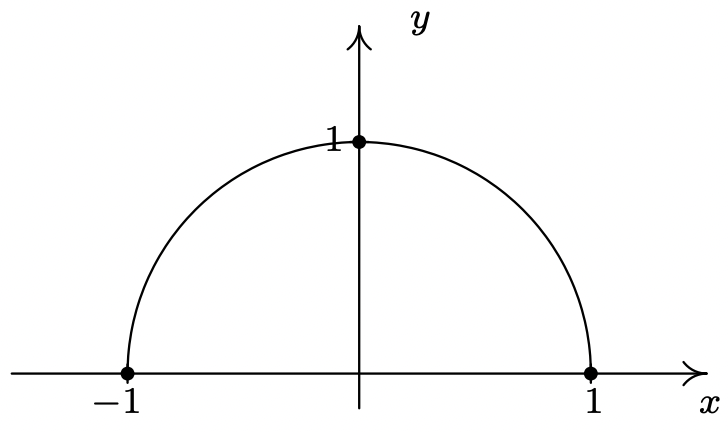
-
\(f(x) = \sqrt{x^2-1}\)
Dominio:\((-\infty, -1] \cup [1,\infty)\)
Sin asíntotas
Inclinación inusual en\(x = -1\) y\(x = 1\)
Sin cúspides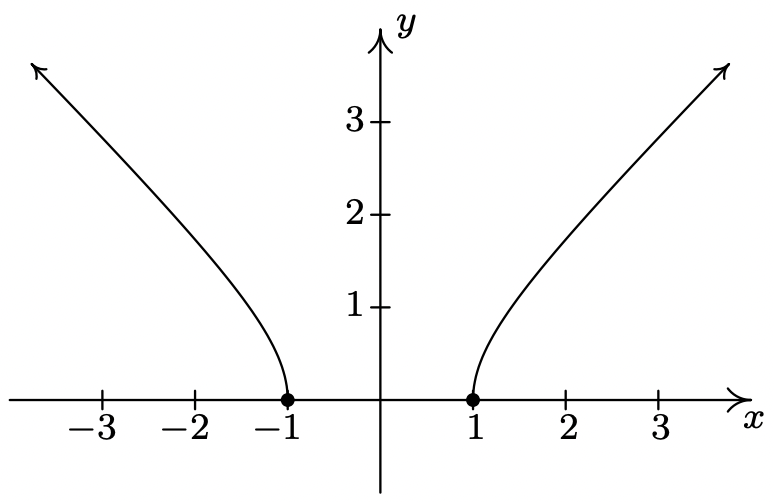
-
\(f(x) = x\sqrt{1-x^2}\)
Dominio:\([-1,1]\)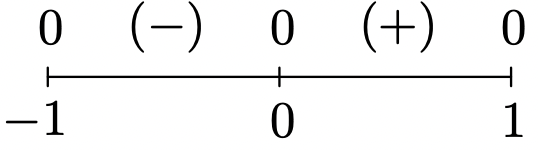
Sin asíntotas
Inpendiente inusual en\(x = -1\) y\(x = 1\)
Sin cúspides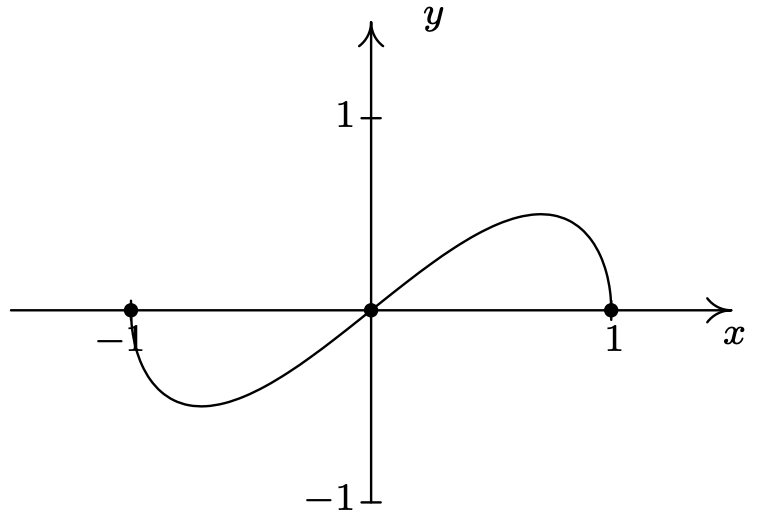
-
\(f(x) = x\sqrt{x^2-1}\)
Dominio:\((-\infty, -1] \cup [1,\infty)\)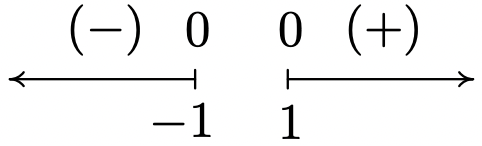
Sin asíntotas
Inpendiente inusual en\(x = -1\) y\(x = 1\)
Sin cúspides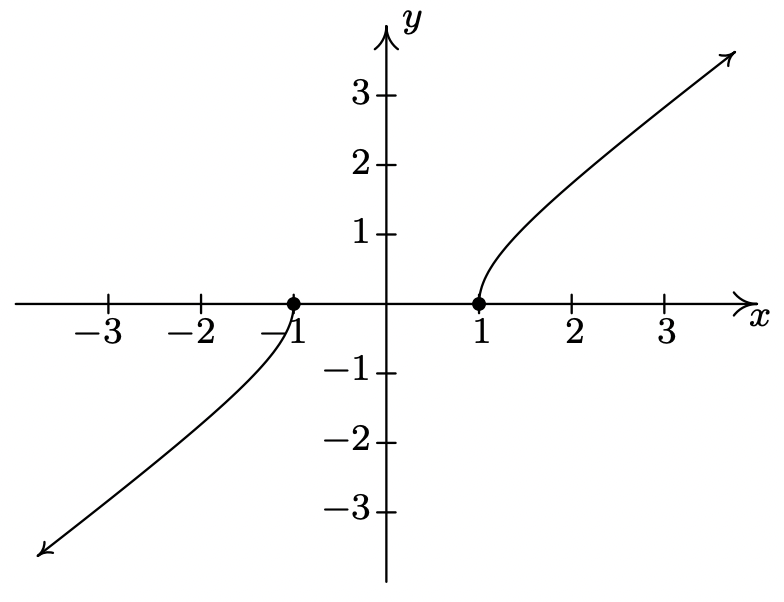
-
\(f(x) = \sqrt[4]{\dfrac{16x}{x^2 - 9}}\)
Dominio:\((-3, 0] \cup (3, \infty)\)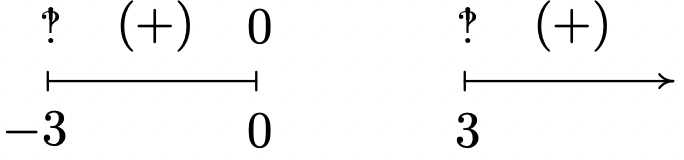
Asíntotas verticales:\(x = -3\) y asíntotas\(x = 3\)
horizontales:\(y = 0\)
Inclinación inusual en\(x = 0\)
Sin cúspides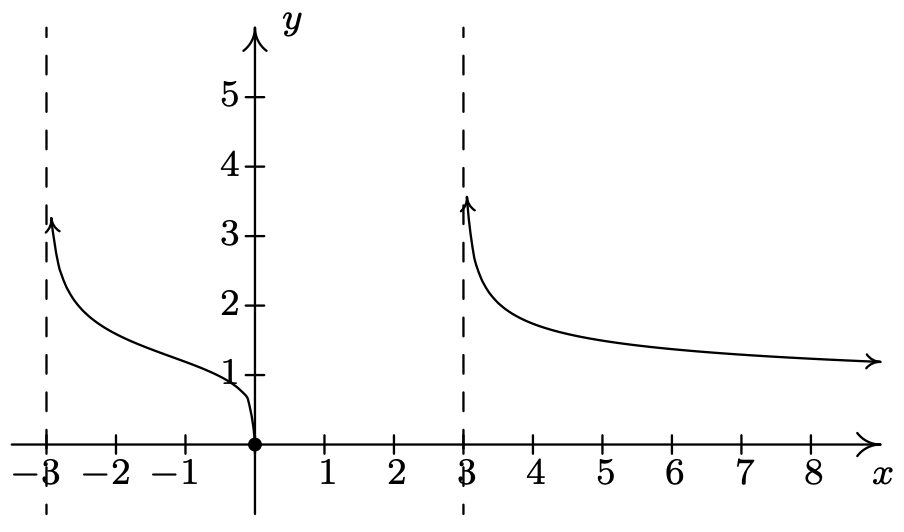
-
\(f(x) = \dfrac{5x}{\sqrt[3]{x^{3} + 8}}\)
Dominio:\((-\infty, -2) \cup (-2, \infty)\)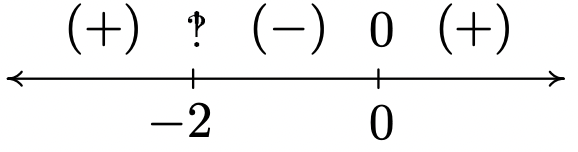
Asíntota vertical Asíntota\(x = -2\)
horizontal\(y = 5\)
Sin pendiente o cúspides inusuales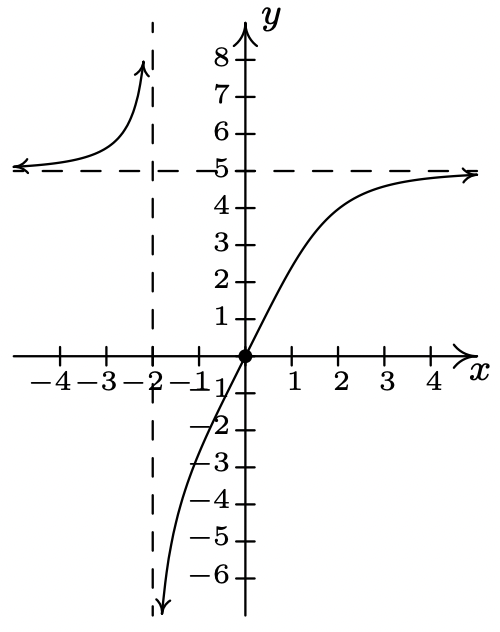
-
2\(f(x) = x^{\frac{2}{3}}(x - 7)^{\frac{1}{3}}\)
Dominio:\((-\infty, \infty)\)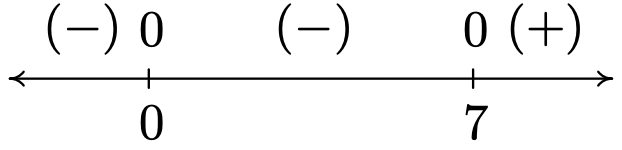
Sin asíntotas verticales u horizontales 13
Inpendiente inusual en la\(x = 7\)
Cúspide en\(x = 0\)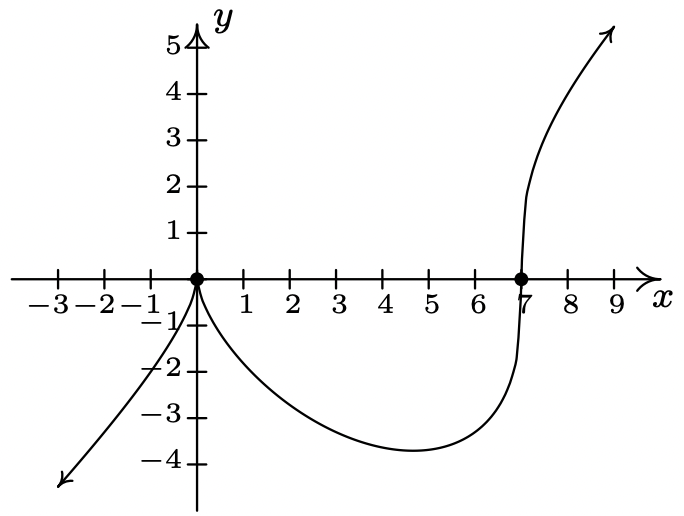
-
\(f(x) = x^{\frac{3}{2}}(x - 7)^{\frac{1}{3}}\)
Dominio:\([0, \infty)\)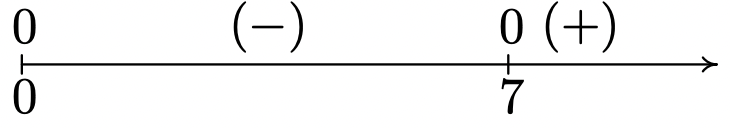
Sin asíntotas
Inclinación inusual en\(x = 7\)
Sin cúspides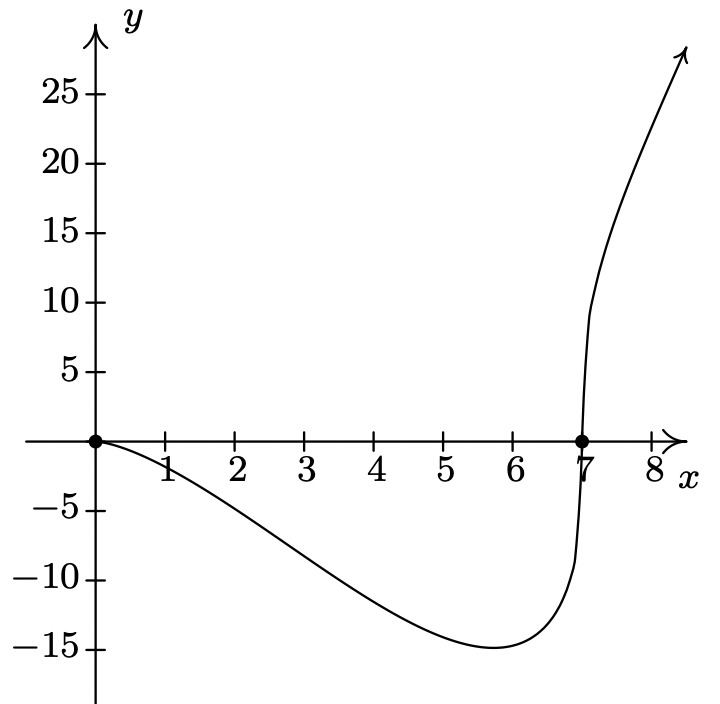
-
\(f(x) = \sqrt{x(x + 5)(x - 4)}\)
Dominio:\([-5, 0] \cup [4, \infty)\)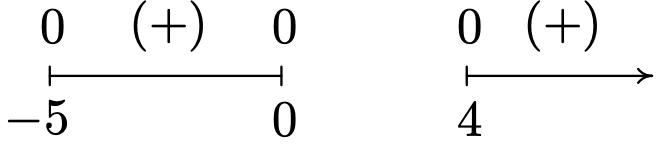
Sin asíntotas
Inpendiente inusual en\(x = -5, x = 0\) y\(x = 4\)
Sin cúspides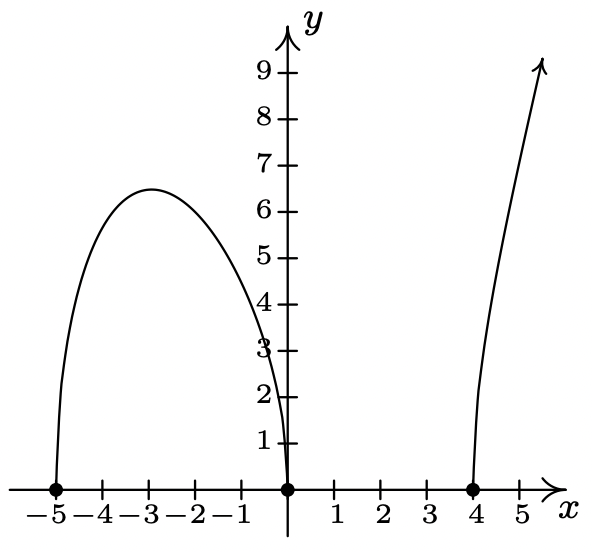
-
2\(f(x) = \sqrt[3]{x^{3} + 3x^{2} - 6x - 8}\)
Dominio:\((-\infty, \infty)\)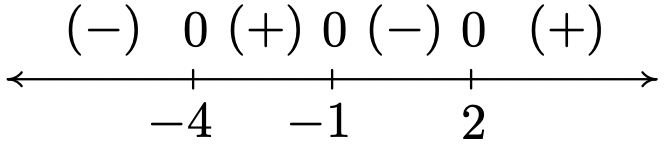
Sin asíntotas verticales u horizontales 14
Inclinación inusual en\(x = -4, x = -1\) y\(x = 2\)
Sin cúspides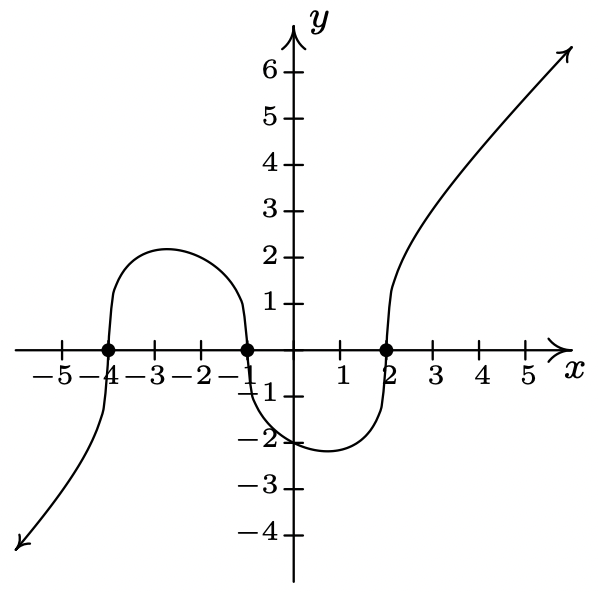
- \(g(x) = \sqrt[3]{x-1}-2\)
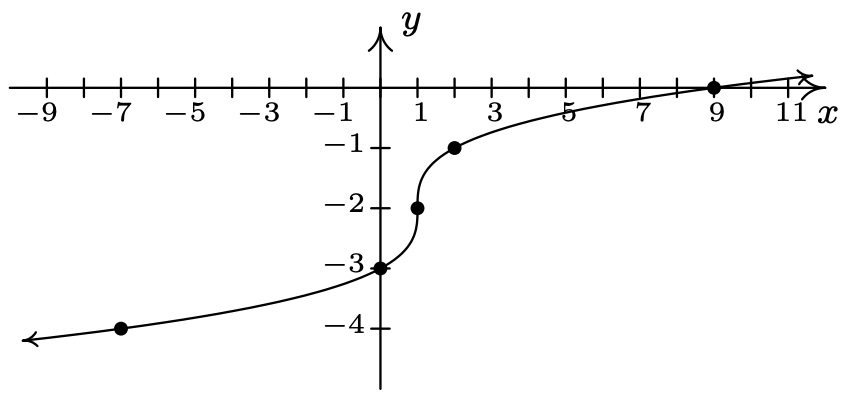
- \(g(x) = -2\sqrt[3]{x + 1} + 4\)
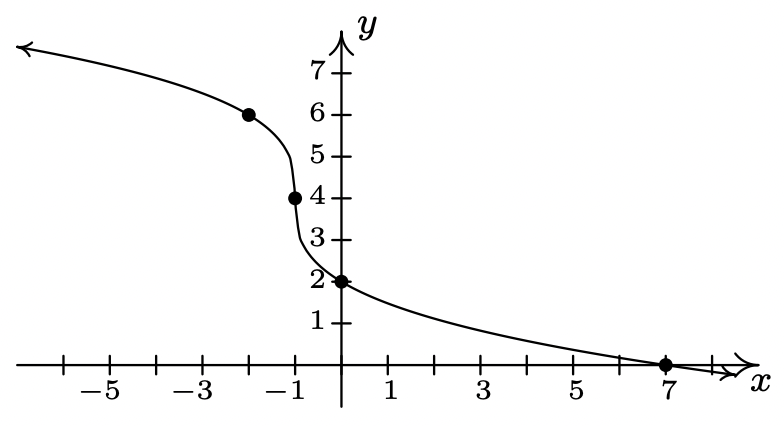
- \(g(x) = \sqrt[4]{x-1}-2\)
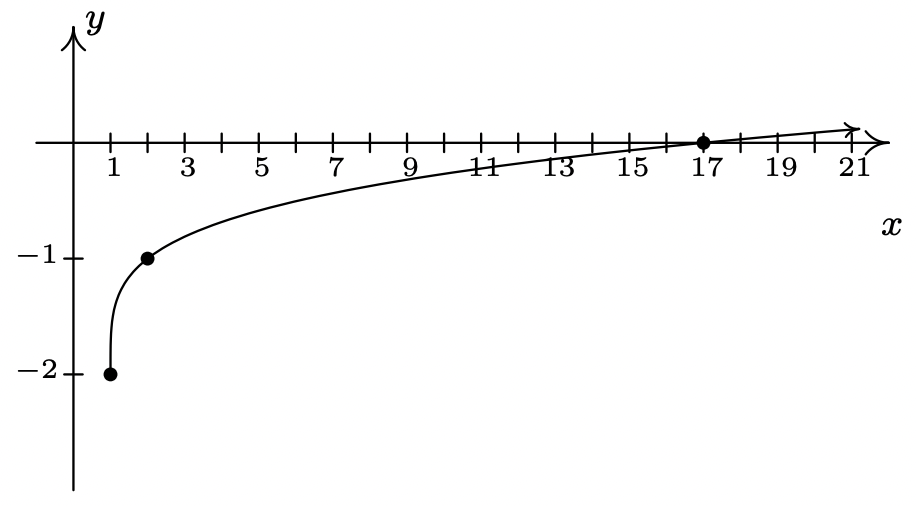
- \(g(x) = 3\sqrt[4]{x - 7} - 1\)
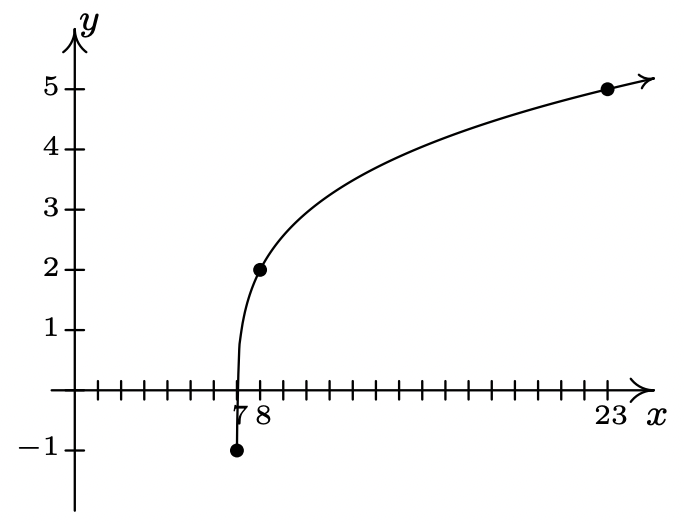
- \(g(x) = \sqrt[5]{x + 2} + 3\)
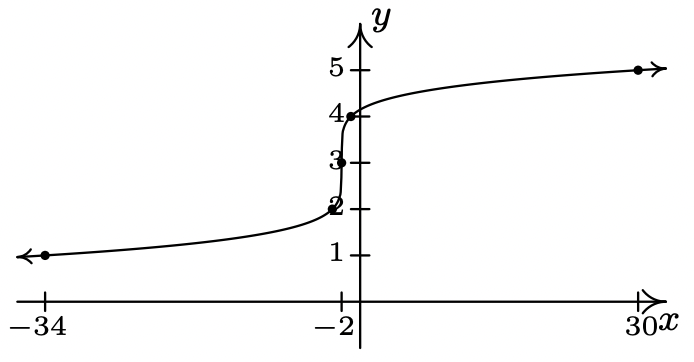
- \(g(x) = \sqrt[8]{-x} - 2\)
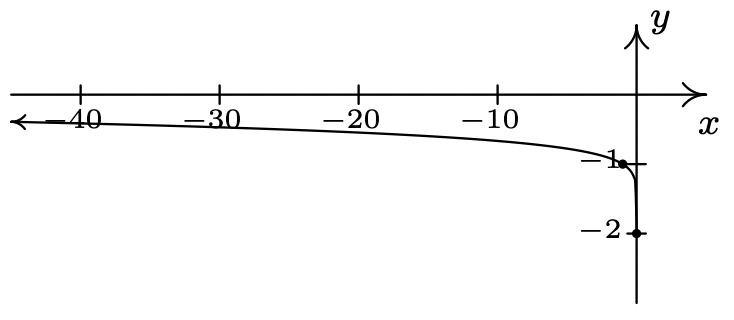
- \(x=3\)
- \(x = \frac{1}{4}\)
- \(x=-3\)
- \(x = -\frac{1}{3}, \; \frac{2}{3}\)
- \(x = \frac{5 + \sqrt{57}}{8}\)
- \(x = 4\)
- \(x = \pm 8\)
- \(x = 6\)
- \(x = 4\)
- \(x=-2, 6\)
- \([2, \infty)\)
- \([-1, 0] \cup [1, \infty)\)
- \((-\infty, 2) \cup (2,3]\)
- \((2,6]\)
- \((-\infty, 0) \cup [2,3) \cup (3, \infty)\)
- \((-\infty, -1)\)
- \(\left(0, \frac{27}{13} \right)\)
- \((-\infty, 0) \cup (0,3)\)
- \((-\infty, -4) \cup \left(-4, -\frac{22}{19}\right] \cup (2, \infty)\)
- \(C(x) = 15x+20\sqrt{100+(30-x)^2}\),\(0 \leq x \leq 30\). La calculadora da el mínimo absoluto en\(\approx (18.66, 582.29)\). Esto significa que para minimizar el costo, se deben recorrer aproximadamente 18.66 millas de cable a lo largo de la Ruta 117 antes de desviarse de la carretera y dirigirse hacia el puesto avanzado. El costo mínimo para hacer funcionar el cable es aproximadamente\(\$582.29\).
-
- \(h(r) = \frac{300}{\pi r^2}\),\(r > 0\).
- \(S(r) = \pi r \sqrt{r^2+\left(\frac{300}{\pi r^2}\right)^2} = \frac{\sqrt{\pi^2 r^6+90000}}{r}\),\(r>0\)
- La calculadora da el mínimo absoluto en el punto\(\approx (4.07, 90.23)\). Esto significa que el radio debe ser (aproximadamente) 4.07 centímetros y la altura debe ser 5.76 centímetros para dar una superficie mínima de 90.23 centímetros cuadrados.
-
- \(W \approx 37.55^{\circ}\)F.
- \(V \approx 9.84\)millas por hora.
-
- \(W(V) = 53.142 - 23.78 V^{0.16}\). Como se nos dice en el Ejercicio 38 que el frío del viento es solo efecto para velocidades de viento de más de 3 millas por hora, restringimos el dominio a\(V > 3\).
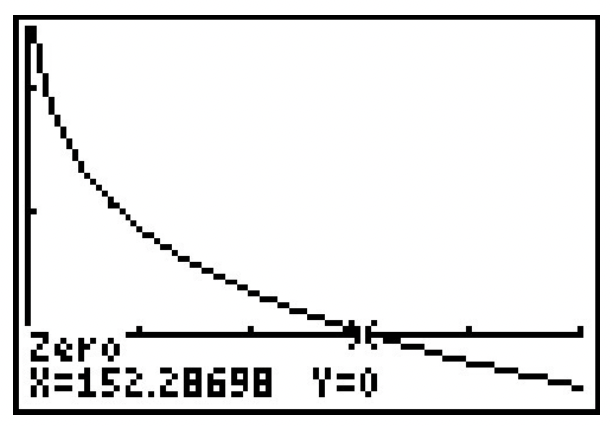
- \(W(V)=0\)cuando\(V \approx 152.29\). Esto significa que, según el modelo, para que la temperatura del frío del viento sea\(0^{\circ}\) F, la velocidad del viento necesita ser\(152.29\) millas por hora.
- A continuación se muestra la gráfica.
- \(9.8 \left(\dfrac{1}{4\pi}\right)^{2} \approx 0.062\)metros o\(6.2\) centímetros
-
- Primero reescribe el modelo como\(P = 1.23x^{\frac{2}{5}}y^{\frac{3}{5}}\). Luego\(300 = 1.23x^{\frac{2}{5}}y^{\frac{3}{5}}\) rinde\(y = \left( \dfrac{300}{1.23x^{\frac{2}{5}}} \right)^{\frac{5}{3}}\). Si\(x = 100\) entonces\(y \approx 441.93687\).
-
- \([0, c)\)
- \ (\ begin {alineado}
&m (.1 c) =\ frac {m_ {r}} {\ sqrt {.99}}\ aprox 1.005 m_ {r}\ quad m (.5 c) =\ frac {m_ {r}} {\ sqrt {.75}}\ aproximadamente 1.155 m_ {r}\\
&m (.9 c) =\ frac {m_ {r}}} {\ sqrt {.19}}\ aprox 2.294 m_ {r}\ quad m (.999 c) =\ frac {m_ {r}} {\ sqrt {.0 .001999}}\ aproximadamente 22.366 m_ {r}
\ end {alineado}\) - Como\(x \rightarrow c^{-}, \, m(x) \rightarrow \infty\)
- Si el objeto viaja no más rápido que aproximadamente\(0.99995\) veces la velocidad de la luz, entonces su masa observada no será mayor que\(100m_{r}\).
- \(k^{-1}(x) = \dfrac{x}{\sqrt{x^{2} - 4}}\)
-
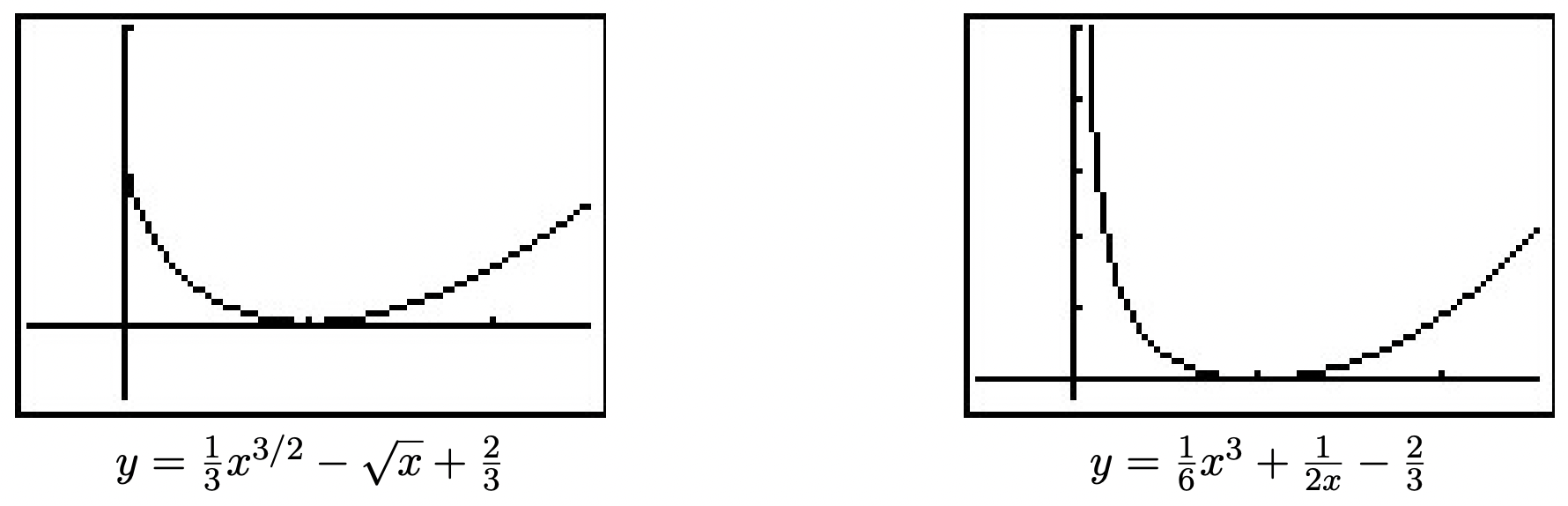
- \(y = \frac{1}{3}x^{3/2} - \sqrt{x} + \frac{2}{3}\). El punto\(\left(0,\frac{2}{3}\right)\) es cuando el camino de Fritzy cruza el camino de Chewbacca, es decir, donde Fritzy atrapa a Chewbacca.
- \(y = \frac{1}{6}x^3+\frac{1}{2x} - \frac{2}{3}\). Utilizando las técnicas del Capítulo 4, encontramos como\(x \rightarrow 0^{+}\),\(y \rightarrow \infty\) lo que significa, en este caso, la persecución de Fritzy nunca termina; nunca atrapa a Chewbacca. Esto tiene sentido ya que Chewbacca tiene ventaja y corre más rápido que Fritzy.
Referencia
1 Aunque discutimos los números imaginarios en la Sección 3.4, restringimos nuestra atención a los números reales en esta sección. Consulte el epílogo en la página 294 para más detalles.
2 De lo contrario nos encontraríamos con la misma paradoja que hicimos en la Sección 3.4.
3 ¿Te gustó ese juego de palabras?
4 En la mayoría de los demás casos, sin embargo, se prefieren los exponentes racionales.
5 Como se menciona en la Sección 2.2,\(f(x)=\sqrt{x^{2}}=|x|\) por lo que el valor absoluto también se considera una función algebraica.
6 Por ejemplo,\(-2 \geq \sqrt[4]{x+3}\), que no tiene solución o\(-2 \leq \sqrt[4]{x+3}\) 3 cuya solución es\([-3, \infty)\).
7 Recordemos, esto significa que hemos producido un candidato que no satisface la ecuación original. ¿Recuerdas cómo elevar ambos lados de una ecuación a un poder par podría causar esto?
8 El término de Cálculo adecuado para esto es 'tangente vertical', pero por ahora estaremos bien llamándolo 'pendiente inusual'.
9 Consulte la página 241 para obtener la primera referencia a esta característica.
10 O al menos confirmar a varios decimales
11 Nuevamente, presentamos esta característica en la página 241 como una característica que hace que la gráfica de una función “no sea suave”.
12 Y ejercemos especial cuidado a la hora de reducir la\(\frac{3}{3}\) potencia a 1.
13 Usando Cálculo se puede mostrar que\(y=x-\frac{7}{3}\) es una asíntota inclinada de esta gráfica.
14 Usando Cálculo se puede mostrar que\(y = x + 1\) es una asíntota inclinada de esta gráfica.

