6.1: Introducción a las funciones exponenciales y logarítmicas

De todas las funciones que estudiamos en este texto, las funciones exponenciales y logarítmicas son posiblemente las que más impactan en la vida cotidiana. ¹ Esta sección nos introduce a estas funciones mientras que el resto del capítulo explorará más a fondo sus propiedades. Hasta este punto, hemos tratado funciones que involucran términos como\(x^{2}\) o\(x^{2 / 3}\), en otras palabras, términos de la forma\(x^{p}\) donde la base del término,\(x\), varía pero el exponente de cada término,\(p\), permanece constante. En este capítulo, estudiamos funciones de la forma\(f(x)=b^{x}\) donde la base\(b\) es una constante y el exponente\(x\) es la variable. Comenzamos nuestra exploración de estas funciones con\(f(x)=2^{x}\). (Al parecer esto es una tradición. Cada libro de álgebra universitaria que hemos leído comienza con\(f(x)=2^{x}\).) Hacemos una tabla de valores, trazamos los puntos y conectamos los puntos de una manera agradable.

\ (\ begin {array} {|r||r|r|}
\ hline x & f (x) & (x, f (x))\
\ hline-3 & 2^ {-3} =\ frac {1} {8} &\ izquierda (-3,\ frac {1} {8}\ derecha)\
\ hline-2 & 2^ {-2} =\ frac {1} {4} &\ izquierda (-2,\ frac {1} {4}\ derecha)\
\ hline-1 & 2^ {-1} =\ frac {1} {2} &\ izquierda (-1,\ frac {1} {2}\ derecha)\
\ hline 0 & 2^ {0} =1 & (0,1)\\
\ hline 1 & 2^ {1} =2 & (1,2)\
\ hline 2 & 2^ {2} =4 & (2,4)\
\ hline 3 & 2^ {3} =8 & (3,8)\
\ hline
\\ {matriz}\)

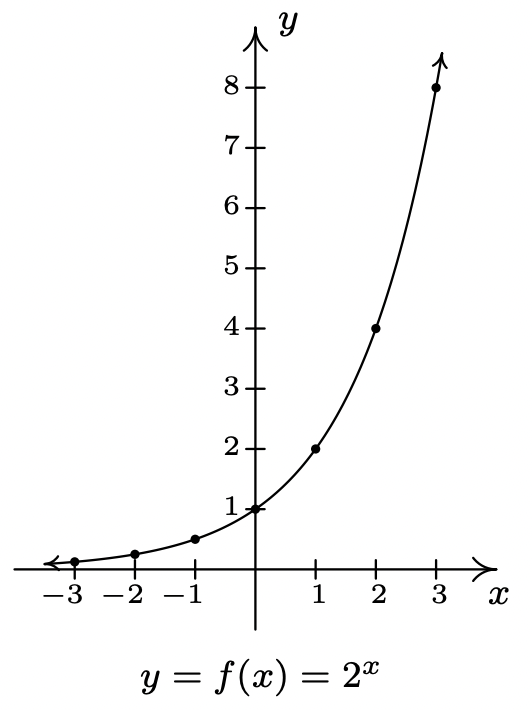
Algunos comentarios sobre la gráfica\(f(x)=2^{x}\) que hemos construido están en orden. Como\(x \rightarrow-\infty\) y alcanza valores como\(x = −100\) o\(x = −1000\), la función\(f(x)=2^{x}\) adquiere valores como\(f(-100)=2^{-100}=\frac{1}{2^{100}}\) o\(f(-1000)=2^{-1000}=\frac{1}{2^{1000}}\). En otras palabras, como\(x \rightarrow-\infty\),

\(2^{x} \approx \frac{1}{\operatorname{very~big}(+)} \approx \text { very small }(+)\)

Así como\(x \rightarrow-\infty\),\(2^{x} \rightarrow 0^{+}\). Esto se representa gráficamente usando el\(x\) eje -( la línea\(y = 0\)) como una asíntota horizontal. En el otro lado, como\(x \rightarrow \infty\), nos encontramos\(f(100)=2^{100}, f(1000)=2^{1000}\), y así sucesivamente, así\(2^{x} \rightarrow \infty\). Como resultado, nuestra gráfica sugiere el rango de\(f\) is\((0, \infty)\). El gráfico de\(f\) pasa la Prueba de Línea Horizontal que significa que\(f\) es uno a uno y por lo tanto invertible. También notamos que cuando 'conectamos los puntos de una manera agradable', hemos hecho la suposición implícita de que\(f(x)=2^{x}\) es ² continua y tiene un dominio de todos los números reales. En particular, hemos sugerido que cosas como\(2^{\sqrt{3}}\) existen como números reales. Deberíamos tomarnos un momento para discutir lo que\(2^{\sqrt{3}}\) podría significar algo así como referir al lector interesado a un sólido curso en Cálculo para una explicación más rigurosa. El número\(\sqrt{3}=1.73205 \ldots\) es un número irracional ³ y como tal, su representación decimal no se repite ni termina. Podemos, sin embargo,\(\sqrt{3}\) aproximarnos terminando decimales, y es lógico razonar ⁴ podemos usar estos para aproximar\(2^{\sqrt{3}}\). Por ejemplo, si aproximamos\(\sqrt{3}\) en 1.73, podemos aproximarnos\(2^{\sqrt{3}} \approx 2^{1.73}=2^{\frac{173}{100}}=\sqrt[100]{2^{173}}\). No es, de ninguna manera, un número agradable, pero es al menos un número que entendemos en términos de poderes y raíces. También es lógico razonar que mejores y mejores aproximaciones de\(\sqrt{3}\) rendimiento mejores y mejores aproximaciones de\(2^{\sqrt{3}}\), por lo que el valor de\(2^{\sqrt{3}}\) debe ser el resultado de esta secuencia de aproximaciones. ⁵

Supongamos que deseamos estudiar la familia de funciones\(f(x)=b^{x}\). ¿Qué bases tienen\(b\) sentido estudiar? Encontramos que nos encontramos con dificultades si\(b<0\). Por ejemplo, si\(b=-2\), entonces la función\(f(x)=(-2)^{x}\) tiene problemas, por ejemplo, at\(x=\frac{1}{2}\) ya que no\((-2)^{1 / 2}=\sqrt{-2}\) es un número real. En general, si\(x\) hay algún número racional con un denominador par, entonces no\((-2)^{x}\) está definido, por lo que debemos restringir nuestra atención a las bases\(b \geq 0\). ¿Y qué pasa\(b = 0\)? La función no\(f(x)=0^{x}\) está definida\(x \leq 0\) porque no podemos dividir por 0 y\(0^{0}\) es una forma indeterminada. Para\(x>0\),\(0^{x}=0\) entonces la función\(f(x)=0^{x}\) es la misma que la función\(f(x)=0\),\(x>0\). Sabemos todo lo que posiblemente podamos saber sobre esta función, por lo que la excluimos de nuestras investigaciones. La única otra base que excluimos es\(b = 1\), ya que la función\(f(x)=1^{x}=1\) es, una vez más, una función que ya hemos estudiado. Ahora estamos listos para nuestra definición de funciones exponenciales.

Definición 6.1

Una función de la forma\(f(x)=b^{x}\) donde\(b\) es un número real fijo,\(b>0\),\(b \neq 1\) se llama una función exponencial base b.

Dejamos al lector verificar ⁶ que si\(b>1\), entonces la función exponencial\(f(x)=b^{x}\) compartirá la misma forma básica y características que\(f(x)=2^{x}\). ¿Y si\(0<b<1\)? Considerar\(g(x)=\left(\frac{1}{2}\right)^{x}\). Ciertamente podríamos construir una tabla de valores y conectar los puntos, o podríamos dar un paso atrás y anotarlo\(g(x)=\left(\frac{1}{2}\right)^{x}=\left(2^{-1}\right)^{x}=2^{-x}=f(-x)\). Pensando en la Sección 1.7, la gráfica de\(f(-x)\) se obtiene a partir de la gráfica de\(f(x)\) reflejándola a través del\(y\) eje. Obtenemos

Vemos que el dominio y el rango de\(g\) coincidencia con el de\(f\), es decir\((-\infty, \infty)\) y\((0, \infty)\), Me gusta\(f\), también\(g\) es uno a uno. Mientras que siempre\(f\) va en aumento,\(g\) es siempre decreciente. Como resultado, como\(x \rightarrow-\infty, g(x) \rightarrow \infty\), y en el otro lado, como\(x \rightarrow \infty, g(x) \rightarrow 0^{+}\). No debería ser demasiado sorprendente que para todas las elecciones de la base\(0<b<1\), la gráfica\(y=b^{x}\) se comporte de manera similar a la gráfica de\(g\). Resumimos las propiedades básicas de las funciones exponenciales en el siguiente teorema. ⁷

Definición 6.1. Propiedades de las Funciones Exponenciales

Apoyo\(f(x)=b^{x}\).

• El dominio de\(f\) es\((-\infty, \infty)\) y el rango de\(f\) es\((0, \infty)\).
• ·\((0, 1)\) está en la gráfica de\(f\) y\(y = 0\) es una asíntota horizontal a la gráfica de\(f\).
• ·\(f\) es uno a uno, continuo y suave ^a
• Si\(b>1\):
  • \(f\)siempre va en aumento
  • Como\(x \rightarrow-\infty\),\(f(x) \rightarrow 0^{+}\)
  • Como\(x \rightarrow \infty, f(x) \rightarrow \infty\)
  • La gráfica de\(f\) se asemeja a:

    

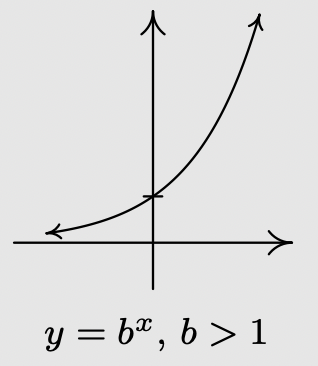
• Si\(0<b<1\):
  • \(f\)es siempre decreciente
  • Como\(x \rightarrow-\infty, f(x) \rightarrow \infty\)
  • Como\(x \rightarrow-\infty, f(x) \rightarrow \infty\)
  • Como\(x \rightarrow \infty, f(x) \rightarrow 0^{+}\)
  • La gráfica de\(f\) se asemeja a:

    

---

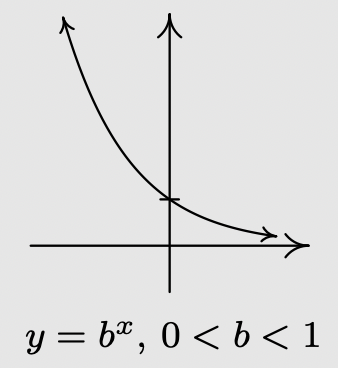
^a Recordemos que esto significa que la gráfica de no\(f\) tiene giros ni esquinas pronunciadas.

De todas las bases para funciones exponenciales, dos ocurren con mayor frecuencia en los círculos científicos. La primera, la base 10, a menudo se llama la base común. La segunda base es un número irracional,\(e \approx 2.718\), llamado la base natural. Discutiremos más formalmente los orígenes de este número en la Sección 6.5. Por ahora, basta con saber que ya que\(e>1, f(x)=e^{x}\), es una función exponencial cada vez mayor. Los siguientes ejemplos nos dan una idea de cómo se utilizan estas funciones en la naturaleza.

Ejemplo 6.1.1

El valor de un automóvil puede ser modelado por\(V(x)=25\left(\frac{4}{5}\right)^{x}\), donde\(x \geq 0\) es la edad del automóvil en años y\(V (x)\) es el valor en miles de dólares.

1. Encontrar e interpretar\(V (0)\).
2. Esbozar la gráfica del\(y = V (x)\) uso de transformaciones.
3. Encuentra e interpreta la asíntota horizontal de la gráfica que encontraste en 2.

Solución

1. Para encontrar\(V (0)\),\(x\) reemplazamos por 0 para obtener\(V(0)=25\left(\frac{4}{5}\right)^{0}=25\). Ya que\(x\) representa la edad del auto en años,\(x = 0\) corresponde a que el auto sea nuevo a estrenar. Ya que\(V (x)\) se mide en miles de dólares,\(V (0) = 25\) corresponde a un valor de $25,000. Poniéndolo todo junto, interpretamos\(V (0) = 25\) que significa que el precio de compra del auto era de $25,000.
2. Para graficar\(y=25\left(\frac{4}{5}\right)^{x}\), comenzamos con la función exponencial básica\(f(x)=\left(\frac{4}{5}\right)^{x}\). Dado que la base\(b=\frac{4}{5}\) está entre 0 y 1, la gráfica de\(y=f(x)\) es decreciente. Trazamos la intercepción y (0, 1) y otros dos puntos,\(\left(-1, \frac{5}{4}\right)\) y\(\left(1, \frac{4}{5}\right)\), y etiquetamos la asíntota horizontal\(y=0\). Para obtener\(V(x)=25\left(\frac{4}{5}\right)^{x}, x \geq 0\), multiplicamos la salida de\(f\) por 25, es decir,\(V (x) = 25f(x)\). De acuerdo con el Teorema 1.5, esto da como resultado un estiramiento vertical por un factor de 25. Multiplicamos todos los\(y\) valores de la gráfica por 25 (incluyendo el\(y\) valor de la asíntota horizontal) y obtenemos los\(\left(-1, \frac{125}{4}\right)\), (0, 25) y (1, 20). La asíntota horizontal permanece\(y = 0\). Finalmente, restringimos el dominio\([0, \infty)\) para que encaje con el dominio aplicado que se nos ha dado. Tenemos el resultado a continuación.

   

3. Vemos por la gráfica de V que su asíntota horizontal es y = 0. (Dejamos al lector verificar esto analíticamente pensando en lo que sucede a medida que tomamos poderes cada vez más grandes de\(\frac{4}{5}\).) Esto significa que a medida que el auto envejece, su valor disminuye a 0.

La función en el ejemplo anterior se suele llamar una 'curva de decaimiento'. Se utilizan funciones exponenciales crecientes para modelar 'curvas de crecimiento' y veremos varios ejemplos diferentes de los de la Sección 6.5. Por ahora, presentamos otra curva de decaimiento común que servirá de base para un mayor estudio de las funciones exponenciales. Aunque pueda parecer más complicado que el ejemplo anterior, en realidad es solo una función exponencial básica que ha sido modificada por algunas transformaciones de la Sección 1.7.

Ejemplo 6.1.2

De acuerdo con la Ley de Enfriamiento ⁸ de Newton la temperatura del café\(T\) (en grados Fahrenheit)\(t\) minutos después de que se sirve puede modelar por\(T(t)=70+90 e^{-0.1 t}\).

1. Encontrar e interpretar\(T(0)\).
2. Esbozar la gráfica del\(y = T(t)\) uso de transformaciones.
3. Encontrar e interpretar la asíntota horizontal de la gráfica.

Solución

1. Para encontrar\(T(0)\), reemplazamos cada ocurrencia de la variable independiente\(t\) con 0 para obtener\(T(0)=70+90 e^{-0.1(0)}=160\). Esto significa que el café se sirvió a 160 ^◦ F.
2. Para graficar\(y = T(t)\) usando transformaciones, comenzamos con la función básica,\(f(t)=e^{t}\). Como ya hemos comentado,\(e \approx 2.718>1\) así la gráfica de\(f\) es un exponencial creciente con\(y\) -intercept (0, 1) y asíntota horizontal\(y = 0\). Los puntos\(\left(-1, e^{-1}\right) \approx(-1,0.37)\) y también\((1, e) \approx(1,2.72)\) están en la gráfica. Dado que la fórmula\(T(t)\) parece bastante complicada, reescribimos\(T(t)\) en la forma presentada en el Teorema 1.7 y usamos ese resultado para rastrear el cambio a nuestros tres puntos y la asíntota horizontal. Tenemos

   \(T(t)=70+90 e^{-0.1 t}=90 e^{-0.1 t}+70=90 f(-0.1 t)+70\)

   La multiplicación de la entrada a\(f\)\(t\),, por −0.1 da como resultado una expansión horizontal por un factor de 10 así como una reflexión alrededor del\(y\) eje. Dividimos cada uno de los\(x\) valores de nuestros puntos por −0. (lo que equivale a multiplicarlos por −10) para obtener\(\left(10, e^{-1}\right)\),\((0, 1)\), y\((−10, e)\). Dado que ninguno de estos cambios afectó los\(y\) valores, la asíntota horizontal permanece\(y = 0\). A continuación, vemos que la salida de\(f\) se está multiplicando por 90. Esto da como resultado un estiramiento vertical por un factor de 90. Multiplicamos las\(y\) coordenadas por 90 para obtener\(\left(10,90 e^{-1}\right)\),\((0, 90)\),\((−10, 90e)\). También multiplicamos el\(y\) valor de la asíntota horizontal\(y = 0\) por 90, y permanece\(y = 0\). Finalmente, agregamos 70 a todas las\(y\) coordenadas, lo que desplaza la gráfica hacia arriba para obtener\(\left(10,90 e^{-1}+70\right) \approx(10,103.11)\)\((0, 160)\), y\((-10,90 e+70) \approx(-10,314.64)\). Agregar 70 a la asíntota horizontal la desplaza hacia arriba también a\(y = 70\). Conectamos estos tres puntos usando la misma forma en la misma dirección que en la gráfica de\(f\) y, por último pero no menos importante, restringimos el dominio para que coincida con el dominio aplicado\([0, \infty)\). El resultado está abajo.

   

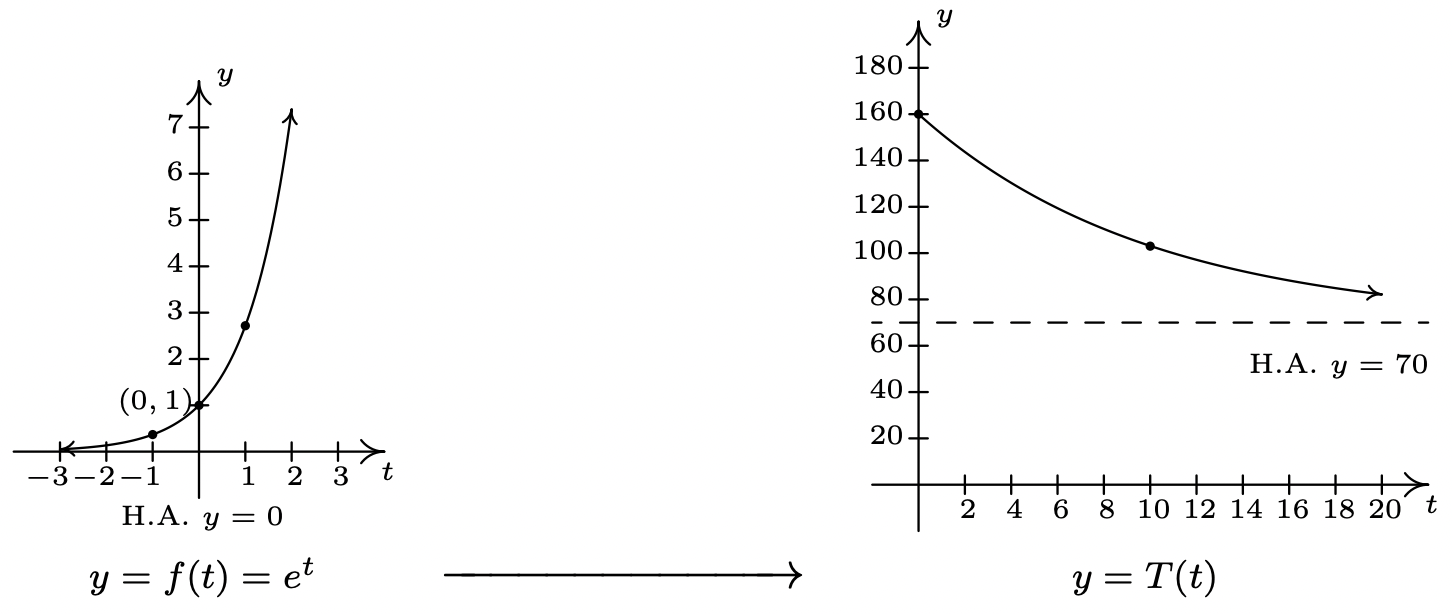
3. De la gráfica, vemos que la asíntota horizontal es\(y = 70\). Vale la pena uno o dos momentos de nuestro tiempo para ver cómo sucede esto analíticamente y revisar algunos de los 'sentidos numéricos' desarrollados en el Capítulo 4. Como\(t \rightarrow \infty\), Obtenemos\(T(t)=70+90 e^{-0.1 t} \approx 70+90 e^{\text {very big }(-)}\). Dado que\(e > 1\),

   \(e^{\text {very big }(-)}=\frac{1}{e^{\text {very big }(+)}} \approx \frac{1}{\text { very big }(+)} \approx \operatorname{very~small~}(+)\)

   Cuanto más grande\(t\) se vuelve, más pequeño\(e^{-0.1 t}\) se vuelve, entonces el término\(90 e^{-0.1 t} \approx \text { very small }(+)\). De ahí, lo\(T(t) \approx 70+\text { very small }(+)\) que significa que la gráfica se aproxima a la línea horizontal\(y = 70\) desde arriba. Esto significa que a medida que pasa el tiempo, la temperatura del café se va enfriando a\(70^{\circ} \mathrm{F}\), presumiblemente, temperatura ambiente.

Como ya hemos comentado, las gráficas de\(f(x)=b^{x}\) todos pasan la Prueba de Línea Horizontal. Así, las funciones exponenciales son invertibles. Ahora dirigimos nuestra atención a estas inversas, las funciones logarítmicas, que se llaman 'logs' para abreviar.

Definición 6.2

El inverso de la función exponencial\(f(x)=b^{x}\) se llama la función\(b\) logaritmo base, y se denota\(f^{-1}(x)=\log _{b}(x)\) Leemos\({ }^{\prime} \log _{b}(x) \text { ' }\) como 'log base\(b\) de\(x\). '

Tenemos anotaciones especiales para la base común,\(b = 10\), y la base natural,\(b = e\).

Definición 6.3

El logaritmo común de un número real\(x\) es\(\log _{10}(x)\) y suele escribirse\(\log (x)\). El logaritmo natural de un número real\(x\) es\(\log _{e}(x)\) y suele escribirse\(ln(x)\).

Dado que los registros se definen como los inversos de las funciones exponenciales, podemos usar los Teoremas 5.2 y 5.3 para decirnos sobre las funciones logarítmicas. Por ejemplo, sabemos que el dominio de una función log es el rango de una función exponencial, es decir\((0, \infty)\), y que el rango de una función log es el dominio de una función exponencial, a saber\((-\infty, \infty)\). Ya que conocemos las formas básicas de\(y=f(x)=b^{x}\) para los diferentes casos de\(b\), podemos obtener la gráfica de\(y=f^{-1}(x)=\log _{b}(x)\) reflejando la gráfica de\(f\) a través de la línea\(y = x\) como se muestra a continuación. El\(y\) -intercepto (0, 1) en la gráfica de\(f\) corresponde a un\(x\) -intercepto de (1, 0) en la gráfica de\(f^{-1}\). Las asíntotas horizontales\(y = 0\) en las gráficas de las funciones exponenciales se convierten en asíntotas verticales\(x = 0\) en las gráficas logarítmicas.

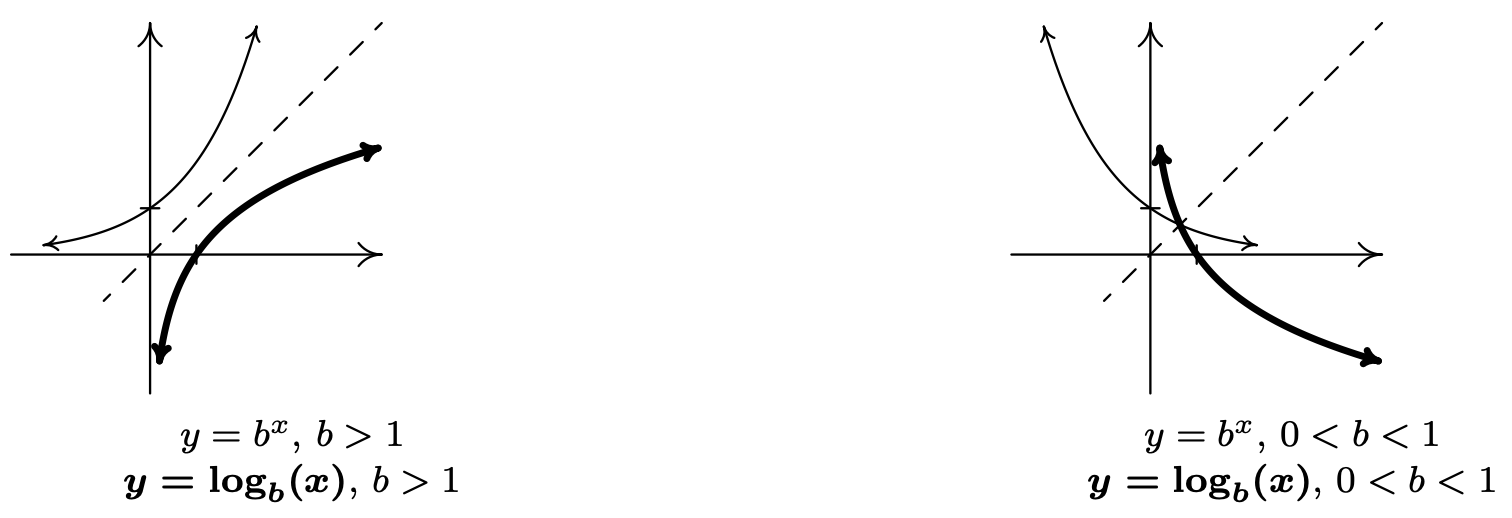
A nivel procesal, los registros deshacen los exponenciales. Considera la función\(f(x)=2^{x}\). Cuando evaluamos\(f(3)=2^{3}=8\), la entrada 3 se convierte en el exponente sobre la base 2 para producir el número real 8. La función toma\(f^{-1}(x)=\log _{2}(x)\) entonces el número 8 como su entrada y devuelve el exponente 3 como su salida. En símbolos,\(\log _{2}(8)=3\). De manera más general,\(\log _{2}(x)\) es el exponente que pones en 2 para conseguir\(x\). Así,\(\log _{2}(16)=4\), porque\(2^{4}=16\). El siguiente teorema resume las propiedades básicas de las funciones logarítmicas, todas las cuales provienen del hecho de que son inversas de funciones exponenciales.

Teorema 6.2. Propiedades de las funciones logarítmicas

Supongamos\(f(x)=\log _{b}(x)\).

• El dominio de\(f\) es\((0, \infty)\) y el rango de\(f\) es\((-\infty, \infty)\).
• (1, 0) está en la gráfica de f y\(x = 0\) es una asíntota vertical de la gráfica de\(f\).
• \(f\)es uno a uno, continuo y suave
• \(b^{a}=c\)si y sólo si\(\log _{b}(c)=a\). Es decir,\(\log _{b}(c)\) es el exponente que te pones\(b\) para obtener\(c\).
• \(\log _{b}\left(b^{x}\right)=x\)para todos\(x\) y\(b^{\log _{b}(x)}=x\) para todos\(x > 0\)
• Si\(b > 1\):
  • \(f\)siempre va en aumento
  • Como\(x \rightarrow 0^{+}, f(x) \rightarrow-\infty\)
  • Como\(x \rightarrow \infty, f(x) \rightarrow \infty\)
  • La gráfica de\(f\) se asemeja a:

    

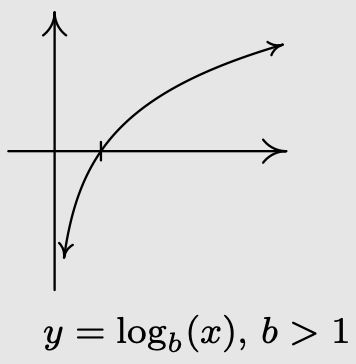
• Si\(0 < b < 1\):
  • \(f\)es siempre decreciente
  • Como\(x \rightarrow 0^{+}, f(x) \rightarrow \infty\)
  • Como\(x \rightarrow \infty, f(x) \rightarrow-\infty\)
  • La gráfica de\(f\) se asemeja a:

    

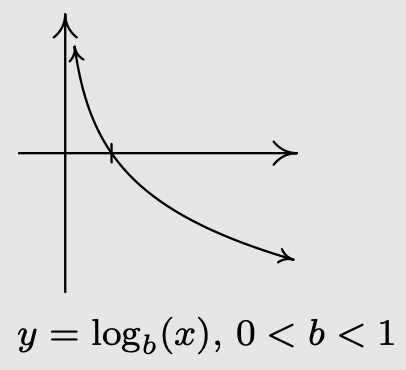
Como hemos mencionado, el Teorema 6.2 es una consecuencia de los Teoremas 5.2 y 5.3. Sin embargo, vale la pena el tiempo del lector para entender el Teorema 6.2 desde una perspectiva exponencial. Por ejemplo, sabemos que el dominio de\(g(x)=\log _{2}(x)\) es\((0, \infty)\). ¿Por qué? Porque el rango de\(f(x)=2^{x}\) es\((0, \infty)\). En cierto modo, esto lo dice todo, pero al mismo tiempo, no lo hace.Por ejemplo, si tratamos de encontrar\(\log _{2}(-1)\), estamos tratando de encontrar al exponente que ponemos en 2 para darnos −1. En otras palabras, estamos buscando\(x\) que satisfaga\(2^{x}=-1\). No existe tal número real, ya que todas las potencias de 2 son positivas. Si bien lo que hemos dicho es exactamente lo mismo que decir 'el dominio de\(g(x)=\log _{2}(x)\) es\((0, \infty)\) porque el rango de\(f(x)=2^{x}\) es\((0, \infty)\) ', sentimos que lo mejor para el estudiante es entender las afirmaciones del Teorema 6.2 a este nivel en lugar de simplemente memorizar el hechos.

Ejemplo 6.1.3

Simplifica lo siguiente.

1. \(\log _{3}(81)\)
2. \(\log _{2}\left(\frac{1}{8}\right)\)
3. \(\log _{\sqrt{5}}(25)\)
4. \(\ln \left(\sqrt[3]{e^{2}}\right)\)
5. \(\log (0.001)\)
6. \(2^{\log _{2}(8)}\)
7. \(117^{-\log _{117}(6)}\)

Solución

1. El número\(\log _{3}(81)\) es el exponente que ponemos en 3 para conseguir 81. Como tal, queremos escribir 81 como una potencia de 3. Nos encontramos\(81=3^{4}\), así que eso\(\log _{3}(81)=4\).
2. Para encontrar\(\log _{2}\left(\frac{1}{8}\right)\), necesitamos reescribir\(\frac{1}{8}\) como un poder de 2. Nos encontramos\(\frac{1}{8}=\frac{1}{2^{3}}=2^{-3}\), así\(\log _{2}\left(\frac{1}{8}\right)=-3\).
3. Para determinar\(\log _{\sqrt{5}}(25)\), necesitamos expresar 25 como un poder de\(\sqrt{5}\). Sabemos\(25=5^{2}\), y\(5=(\sqrt{5})^{2}\), así lo hemos hecho\(25=\left((\sqrt{5})^{2}\right)^{2}=(\sqrt{5})^{4}\). Obtenemos\(\log _{\sqrt{5}}(25)=4\).
4. En primer lugar, recordemos que el no\(\ln \left(\sqrt[3]{e^{2}}\right)\) significa\(\log _{e}\left(\sqrt[3]{e^{2}}\right)\), por lo que estamos buscando al exponente para ponerse\(e\) para obtener\(\sqrt[3]{e^{2}}\). Reescribiendo\(\sqrt[3]{e^{2}}=e^{2 / 3}\), encontramos\(\ln \left(\sqrt[3]{e^{2}}\right)=\ln \left(e^{2 / 3}\right)=\frac{2}{3}\).
5. Reescribiendo\(\log (0.001)\) como\(\log _{10}(0.001)\), vemos que necesitamos escribir 0.001 como una potencia de 10. Tenemos\(0.001=\frac{1}{1000}=\frac{1}{10^{3}}=10^{-3}\). De ahí,\(\log (0.001)=\log \left(10^{-3}\right)=-3\).
6. Podemos usar el Teorema 6.2 directamente para simplificar así\(2^{\log _{2}(8)}=8\). También podemos entender este problema encontrando primero\(\log _{2}(8)\). Por definición,\(\log _{2}(8)\) es el exponente que ponemos en 2 para conseguir 8. Ya que\(8=2^{3}\), tenemos\(\log _{2}(8)=3\). Ahora sustituimos para encontrar\(2^{\log _{2}(8)}=2^{3}=8\).
7. \(117^{-\log _{117}(6)}=\frac{1}{117^{\log _{117}(6)}}=\frac{1}{6}\)

Hasta este punto, las restricciones a los dominios de las funciones provenían de evitar la división por cero y mantener los números negativos por debajo de los radicales pares. Con la introducción de los registros, ahora tenemos otra restricción. Dado que el dominio de\(f(x)=\log _{b}(x)\) es\((0, \infty)\), el argumento ¹⁰ del registro debe ser estrictamente positivo.

Ejemplo 6.1.4

Encuentra el dominio de las siguientes funciones. Consulta tus respuestas gráficamente usando la calculadora.

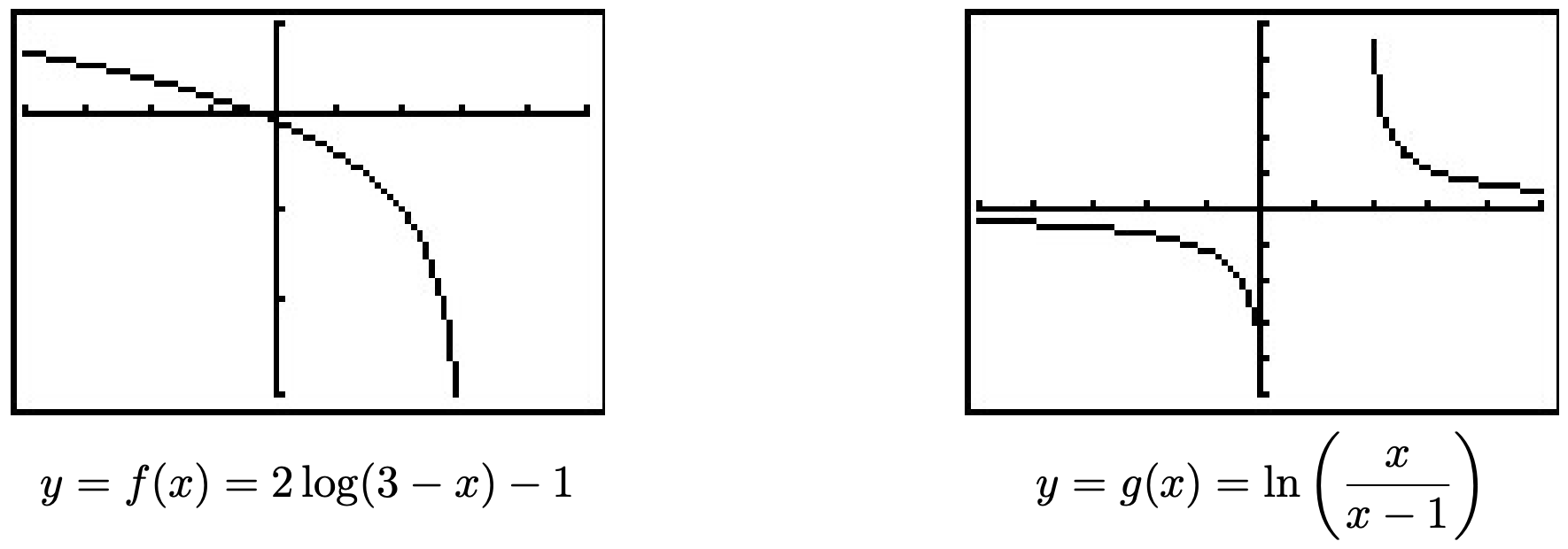
1. \(f(x)=2 \log (3-x)-1\)
2. \(g(x)=\ln \left(\frac{x}{x-1}\right)\)

Solución

1. Nos fijamos\(3-x>0\) para obtener\(x<3\), o\((-\infty, 3)\). El gráfico de la calculadora a continuación lo verifica. Tenga en cuenta que podríamos haber graficado\(f\) usando transformaciones. Tomando el ejemplo del Teorema 1.7, reescribimos\(f(x)=2 \log _{10}(-x+3)-1\) y encontramos la función principal involucrada es\(y=h(x)=\log _{10}(x)\). Seleccionamos tres puntos para rastrear,\(\left(\frac{1}{10},-1\right),(1,0) \text { and }(10,1)\), junto con la asíntota vertical\(x = 0\). Ya que\(f(x)=2 h(-x+3)-1\), el Teorema 1.7 nos dice que para obtener los destinos de estos puntos, primero restamos 3 de las\(x\) -coordenadas (desplazando la gráfica a la izquierda 3 unidades), luego dividimos (multiplicamos) por las\(x\) -coordenadas por −1 (provocando una reflexión a través del\(y\) eje). Estas transformaciones se aplican también a la asíntota\(x = 0\) vertical. Restar 3 nos da\(x = −3\) como nuestra asíntota, luego multplying por −1 nos da la asíntota vertical\(x = 3\). A continuación, multiplicamos las\(y\) coordenadas por 2 lo que resulta en un estiramiento vertical por un factor de 2, luego terminamos restando 1 de las\(y\) coordenadas -que desplaza la gráfica hacia abajo 1 unidad. Dejamos al lector realizar la aritmética indicada sobre los propios puntos y verificar la gráfica producida por la calculadora a continuación.
2. Para encontrar el dominio de\(g\), necesitamos resolver la desigualdad\(\frac{x}{x-1}>0\). Como es habitual, procedemos utilizando un diagrama de señales. Si definimos\(r(x)=\frac{x}{x-1}\), encontramos que\(r\) es indefinido en\(x = 1\) y\(r(x) = 0\) cuándo\(x = 0\). Al elegir algunos valores de prueba, generamos el diagrama de signos a continuación.

   

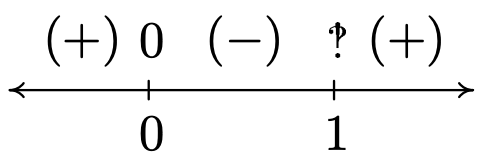
   Nos encontramos\(\frac{x}{x-1}>0\) en\((-\infty, 0) \cup(1, \infty)\) para obtener el dominio de\(g\). La gráfica de\(y=g(x)\) lo confirma. Podemos decir por la gráfica\(g\) que no es el resultado de la transformación de la Sección 1.7 que se está aplicando a la gráfica\(y=\ln (x)\), por lo que salvo un análisis más detallado usando Cálculo, la gráfica de la calculadora es lo mejor que podemos hacer. Una cosa digna de mención, sin embargo, es el comportamiento final de\(g\). El gráfico sugiere que como\(x \rightarrow \pm \infty, g(x) \rightarrow 0\). Podemos verificar esto analíticamente. Utilizando los resultados del Capítulo 4 y la continuidad, sabemos que como\(x \rightarrow \pm \infty, \frac{x}{x-1} \approx 1\). De ahí que tenga sentido eso\(g(x)=\ln \left(\frac{x}{x-1}\right) \approx \ln (1)=0\).

   

Si bien los logaritmos tienen algunas aplicaciones propias interesantes que explorarás en los ejercicios, su uso principal para nosotros será deshacer funciones exponenciales. (Así es, después de todo, como se definieron.) Nuestro último ejemplo lo solidifica y revisa todo el material de la sección.

Ejemplo 6.1.5

Vamos\(f(x)=2^{x-1}-3\).

1. \(f\)Grafique usando transformaciones y exponga el dominio y rango de\(f\).
2. Explica por qué\(f\) es invertible y encuentra una fórmula para\(f^{-1}(x)\).
3. \(f^{-1}\)Grafique usando transformaciones y exponga el dominio y rango de\(f^{-1}\).
4. Verificar\(\left(f^{-1} \circ f\right)(x)=x\) para todos\(x\) en el dominio de\(f\) y\(\left(f \circ f^{-1}\right)(x)=x\) para todos\(x\) en el dominio de\(f^{-1}\).
5. Gráfica\(f\) y\(f^{-1}\) en el mismo conjunto de ejes y comprueba la simetría alrededor de la línea\(y = x\).

Solución

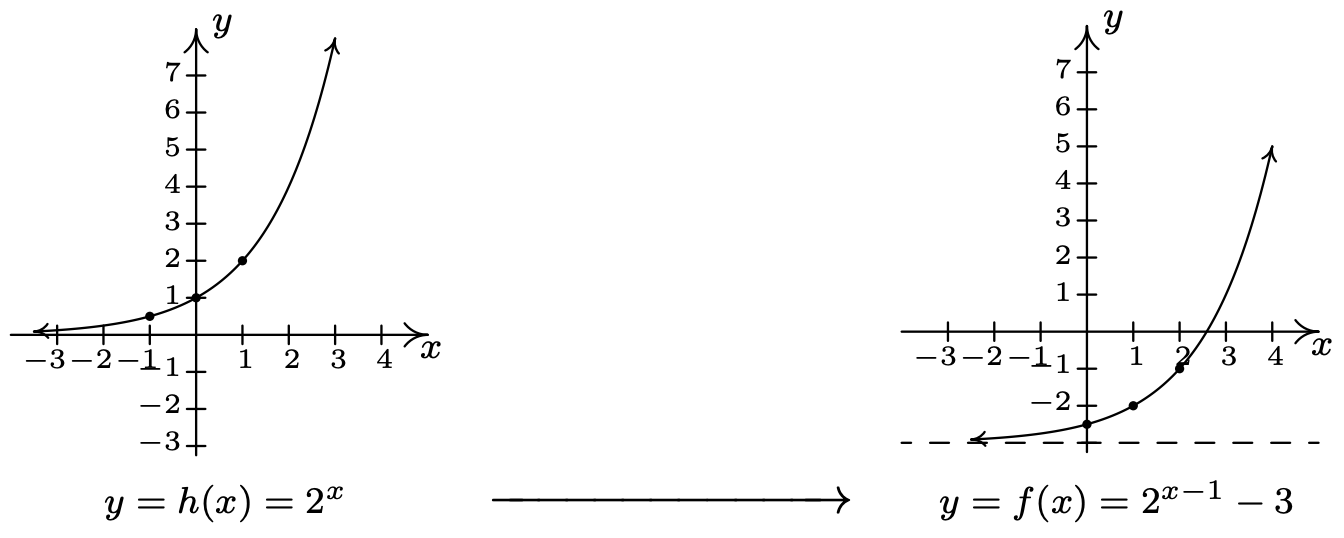
1. Si nos identificamos\(g(x)=2^{x}\), vemos\(f(x)=g(x-1)-3\). Elegimos los puntos\(\left(-1, \frac{1}{2}\right),(0,1)\) y\((1,2)\) 2) en la gráfica de\(g\) junto con el asíntopo horizontal\(y = 0\) para rastrear a través de las transformaciones. Por Teorema 1.7 primero agregamos 1 a las\(x\) -coordenadas de los puntos en la gráfica de\(g\) (desplazando\(g\) a la derecha 1 unidad) para obtener\(\left(0, \frac{1}{2}\right),(1,1) \text { and }(2,2)\). La asíntota horizontal permanece\(y = 0\). A continuación, restamos 3 de las\(y\) coordenadas, desplazando la gráfica hacia abajo 3 unidades. Obtenemos los puntos\(\left(0,-\frac{5}{2}\right),(1,-2) \text { and }(2,-1)\) con la asíntota horizontal ahora en\(y = −3\). Conectando los puntos en el orden y manera como estaban en la gráfica de\(g\), obtenemos la gráfica de abajo. Vemos que el dominio de\(f\) es el mismo que\(g\), es decir\((-\infty, \infty)\), pero que el rango de\(f\) es\((-3, \infty)\).

   

2. El gráfico de\(f\) pasa la Prueba de Línea Horizontal por lo que\(f\) es uno a uno, de ahí invertible. Para encontrar una fórmula para\(f^{-1}(x)\), normalmente establecemos\(y=f(x)\), cambiamos el\(x\) y\(y\), luego procedemos a resolver para\(y\). Hacerlo en esta situación nos lleva a la ecuación\(x=2^{y-1}-3\). Todavía tenemos que discutir cómo resolver este tipo de ecuaciones, por lo que intentaremos encontrar la fórmula para\(f^{-1}\) desde una perspectiva procesal. Si nos\(f(x)=2^{x-1}-3\) dividimos en una serie de pasos, encontramos que\(f\) toma una entrada x y aplica los pasos
   1. restar 1
   2. poner como exponente en 2
   3. restar 3

   Claramente, para deshacer restando 1, agregaremos 1, y de manera similar deshacemos restando 3 sumando 3. ¿Cómo deshacemos el segundo paso? La respuesta es que usamos el logaritmo. Por definición,\(\log _{2}(x)\) deshace la exponenciación por 2. Por lo tanto,\(f^{-1}\) debería

   1. agregar 3
   2. tomar el logaritmo base 2
   3. agregar 1

   En símbolos,\(f^{-1}(x)=\log _{2}(x+3)+1\).

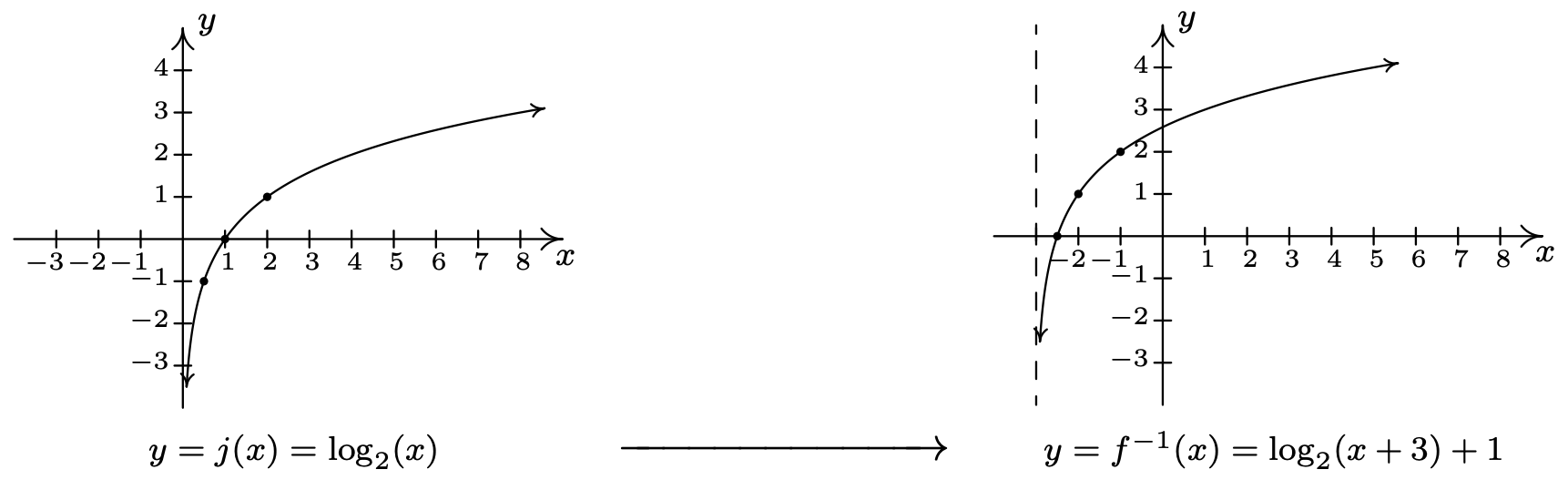
3. Para graficar\(f^{-1}(x)=\log _{2}(x+3)+1\) usando transformaciones, comenzamos con\(j(x)=\log _{2}(x)\). Rastreamos los puntos\(\left(\frac{1}{2},-1\right),(1,0) \text { and }(2,1)\) en la gráfica de\(j\) junto con la asíntota vertical\(x = 0\) a través de las transformaciones usando el Teorema 1.7. Ya que\(f^{-1}(x)=j(x+3)+1\), primero restamos 3 de cada uno de los\(x\) valores (incluyendo la asíntota vertical) para obtener\(\left(-\frac{5}{2},-1\right)\), (−2, 0) y (−1, 1) con una asíntota vertical\(x = −3\). A continuación, agregamos 1 a los\(y\) valores en la gráfica y obtenemos\(\left(-\frac{5}{2}, 0\right)\), (−2, 1) y (−1, 2). Si estás experimentando d'ej`a vu, hay una buena razón para ello pero dejamos que el lector determine la fuente de esta extraña familiaridad. Obtenemos la gráfica a continuación. El dominio de\(f^{-1}\) is\((-3, \infty)\), que coincide con el rango de\(f\), y el rango de\(f^{-1}\) es\((-\infty, \infty)\), que coincide con el dominio de\(f\).

   

4. Ahora verificamos eso\(f(x)=2^{x-1}-3\) y\(f^{-1}(x)=\log _{2}(x+3)+1\) satisfacemos el requisito de composición para inversos. Para todos los números reales\(x\),

   \ (\ begin {alineado}
   \ izquierda (f^ {-1}\ circ f\ derecha) (x) &=f^ {-1} (f (x))\\
   &=f^ {-1}\ izquierda (2^ {x-1} -3\ derecha)\\
   &=\ log _ {2}\ izquierda (\ izquierda [2^ {x-1} -3\ derecha] +3\ derecha) +1\
   &\ =\ log _ {2}\ izquierda (2^ {x-1}\ derecha) +1\\
   & =( x-1) +1\ quad\ text {Desde}\ log _ {2}\ left (2^ {u}\ right) =u\ text {para todos los números reales} u\\
   &=x\ checkmark
   \ end {alineado}\)

   Para todos los números reales\(x > −3\), tenemos ¹¹

   \ (\ begin {alineado}
   \ izquierda (f\ circ f^ {-1}\ derecha) (x) &=f\ izquierda (f^ {-1} (x)\ derecha)\\
   &=f\ izquierda (\ log _ {2} (x+3) +1\ derecha)\\
   &=2^ {\ izquierda (\ log _ {2} (x+3)\ +1 derecha) -1} -3\
   =2^ {\ log _ {2} (x+3)} -3\\
   & =( x+3) -3\ quad \ text {Desde} 2^ {\ log _ {2} (u)} =u\ text {para todos los números reales} u>0\\
   &=x\ marca de verificación
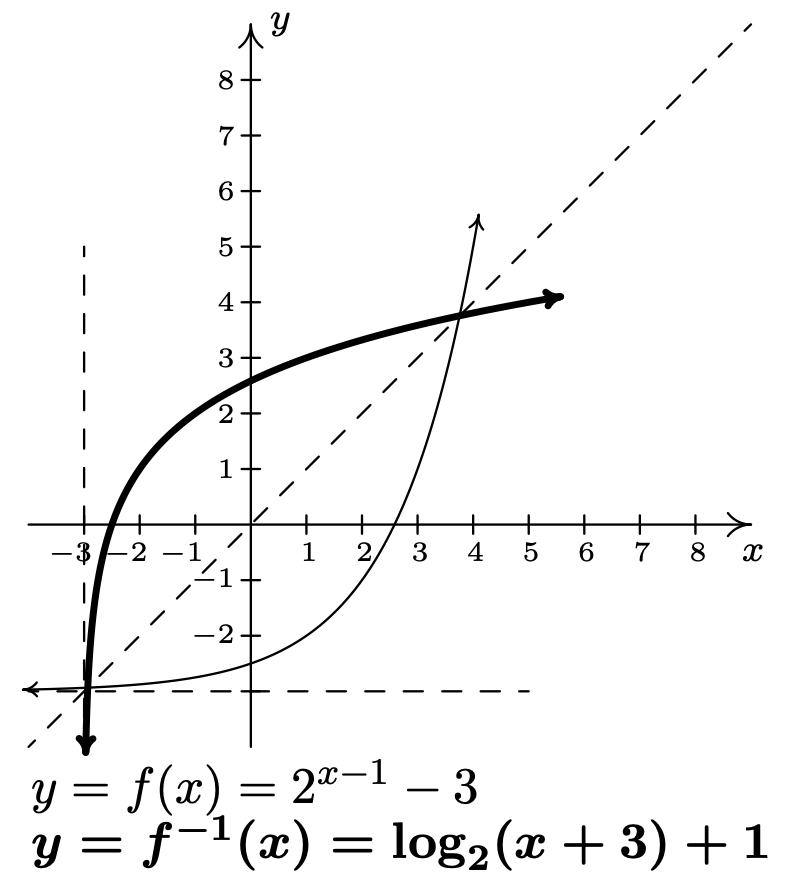
   \ end {alineado}\)

5. Por último, pero ciertamente no menos importante, graficamos\(y=f(x)\) y\(y=f^{-1}(x)\) en el mismo conjunto de ejes y vemos la simetría alrededor de la línea\(y=x\).

   

6.1.1 Ejercicios

En los Ejercicios 1 - 15, utilice la propiedad:\(b^{a}=c\) si y sólo si\(\log _{b}(c)=a\) del Teorema 6.2 para reescribir la ecuación dada en la otra forma. Es decir, reescribir las ecuaciones exponenciales como ecuaciones logarítmicas y reescribir las ecuaciones logarítmicas como ecuaciones exponenciales.

1. \(2^{3}=8\)
2. \(5^{-3}=\frac{1}{125}\)
3. \(4^{5 / 2}=32\)
4. \(\left(\frac{1}{3}\right)^{-2}=9\)
5. \(\left(\frac{4}{25}\right)^{-1 / 2}=\frac{5}{2}\)
6. \(10^{-3}=0.001\)
7. \(e^{0}=1\)
8. \(\log _{5}(25)=2\)
9. \(\log _{25}(5)=\frac{1}{2}\)
10. \(\log _{3}\left(\frac{1}{81}\right)=-4\)
11. \(\log _{\frac{4}{3}}\left(\frac{3}{4}\right)=-1\)
12. \(\log (100)=2\)
13. \(\log (0.1)=-1\)
14. \(\ln (e)=1\)
15. \(\ln \left(\frac{1}{\sqrt{e}}\right)=-\frac{1}{2}\)

En Ejercicios 16 - 42, evaluar la expresión.

16. \(\log _{3}(27)\)
17. \(\log _{6}(216)\)
18. \(\log _{2}(32)\)
19. \(\log _{6}\left(\frac{1}{36}\right)\)
20. \(\log _{8}(4)\)
21. \(\log _{36}(216)\)
22. \(\log _{\frac{1}{5}}(625)\)
23. \(\log _{\frac{1}{6}}(216)\)
24. \(\log _{36}(36)\)
25. \(\log \left(\frac{1}{1000000}\right)\)
26. \(\log (0.01)\)
27. \(\ln \left(e^{3}\right)\)
28. \(\log _{4}(8)\)
29. \(\log _{6}(1)\)
30. \(\log _{13}(\sqrt{13})\)
31. \(\log _{36}(\sqrt[4]{36})\)
32. \(7^{\log _{7}(3)}\)
33. \(36^{\log _{36}(216)}\)
34. \(\log _{36}\left(36^{216}\right)\)
35. \(\ln \left(e^{5}\right)\)
36. \(\log \left(\sqrt[9]{10^{11}}\right)\)
37. \(\log \left(\sqrt[3]{10^{5}}\right)\)
38. \(\ln \left(\frac{1}{\sqrt{e}}\right)\)
39. \(\log _{5}\left(3^{\log _{3}(5)}\right)\)
40. \(\log \left(e^{\ln (100)}\right)\)
41. \(\log _{2}\left(3^{-\log _{3}(2)}\right)\)
42. \(\ln \left(42^{6 \log (1)}\right)\)

En Ejercicios 43 - 57, encuentra el dominio de la función.

43. \(f(x)=\ln \left(x^{2}+1\right)\)
44. \(f(x)=\log _{7}(4 x+8)\)
45. \(f(x)=\ln (4 x-20)\)
46. \(f(x)=\log \left(x^{2}+9 x+18\right)\)
47. \(f(x)=\log \left(\frac{x+2}{x^{2}-1}\right)\)
48. \(f(x)=\log \left(\frac{x^{2}+9 x+18}{4 x-20}\right)\)
49. \(f(x)=\ln (7-x)+\ln (x-4)\)
50. \(f(x)=\ln (4 x-20)+\ln \left(x^{2}+9 x+18\right)\)
51. \(f(x)=\log \left(x^{2}+x+1\right)\)
52. \(f(x)=\sqrt[4]{\log _{4}(x)}\)
53. \(f(x)=\log _{9}(|x+3|-4)\)
54. \(f(x)=\ln (\sqrt{x-4}-3)\)
55. \(f(x)=\frac{1}{3-\log _{5}(x)}\)
56. \(f(x)=\frac{\sqrt{-1-x}}{\log _{\frac{1}{2}}(x)}\)
57. \(f(x)=\ln \left(-2 x^{3}-x^{2}+13 x-6\right)\)

En los Ejercicios 58 - 63, bosquejar la gráfica\(y = g(x)\) de comenzando con la gráfica de\(y = f(x)\) y usando transformaciones. Rastrea al menos tres puntos de tu elección y la asíntota horizontal a través de las transformaciones. Declarar el dominio y el rango de\(g\).

58. \(f(x)=2^{x}, g(x)=2^{x}-1\)
59. \(f(x)=\left(\frac{1}{3}\right)^{x}, g(x)=\left(\frac{1}{3}\right)^{x-1}\)
60. \(f(x)=3^{x}, g(x)=3^{-x}+2\)
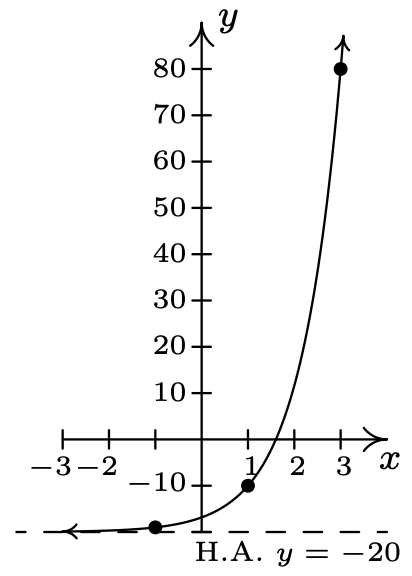
61. \(f(x)=10^{x}, g(x)=10^{\frac{x+1}{2}}-20\)
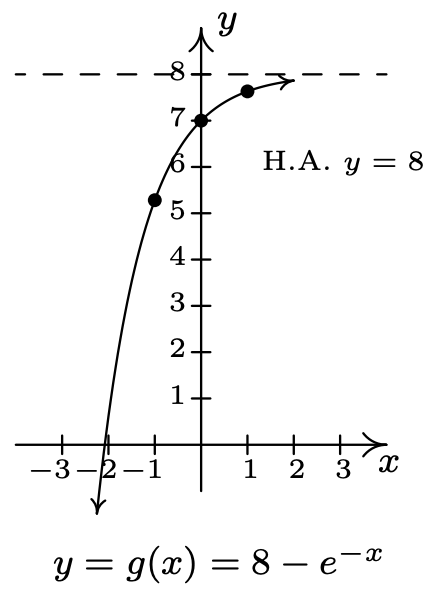
62. \(f(x)=e^{x}, g(x)=8-e^{-x}\)
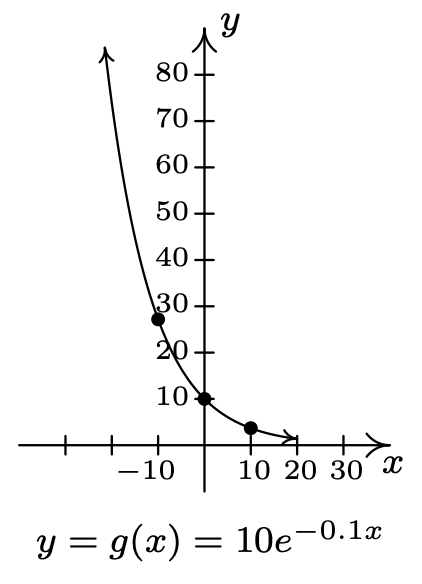
63. \(f(x)=e^{x}, g(x)=10 e^{-0.1 x}\)

En Ejercicios 64 - 69, bosquejar la gráfica\(y = g(x)\) de comenzando con la gráfica de\(y = f(x)\) y usando transformaciones. Rastrea al menos tres puntos de tu elección y la asíntota vertical a través de las transformaciones. Declarar el dominio y el rango de\(g\).

64. \(f(x)=\log _{2}(x), g(x)=\log _{2}(x+1)\)
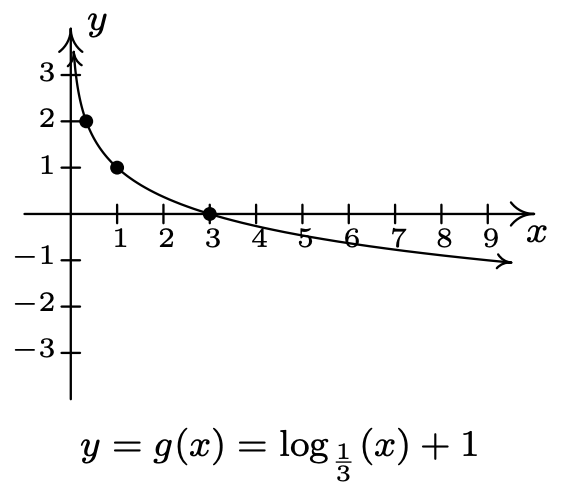
65. \(f(x)=\log _{\frac{1}{3}}(x), g(x)=\log _{\frac{1}{3}}(x)+1\)
66. \(f(x)=\log _{3}(x), g(x)=-\log _{3}(x-2)\)
67. \(f(x)=\log (x), g(x)=2 \log (x+20)-1\)
68. \(f(x)=\ln (x), g(x)=-\ln (8-x)\)
69. \(f(x)=\ln (x), g(x)=-10 \ln \left(\frac{x}{10}\right)\)
70. Verificar que cada función en Ejercicios 64 - 69 sea la inversa de la función correspondiente en Ejercicios 58 - 63. (Coinciden #58 y #64, y así sucesivamente.)

En los Ejercicios 71 - 74, encuentra la inversa de la función desde la 'perspectiva procesal' discutida en el Ejemplo 6.1.5 y grafica la función y su inversa en el mismo conjunto de ejes.

71. \(f(x)=3^{x+2}-4\)
72. \(f(x)=\log _{4}(x-1)\)
73. \(f(x)=-2^{-x}+1\)
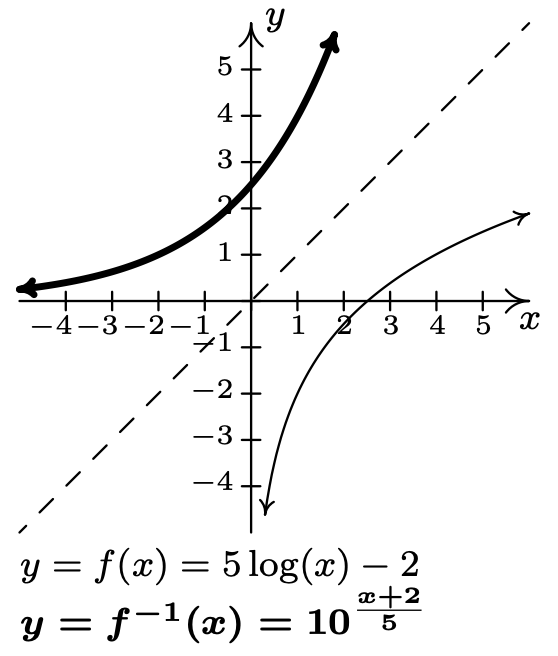
74. \(f(x)=5 \log (x)-2\)

(Escalas logarítmicas) En los Ejercicios 75 - 77, introducimos tres escalas de medición ampliamente utilizadas que involucran logaritmos comunes: la escala de Richter, la escala de decibelios y la escala de pH. Los cálculos involucrados en las tres escalas son casi idénticos, así que presta atención a las sutiles diferencias.

75. Los sismos son eventos complicados y no es nuestra intención brindar una discusión completa de la ciencia involucrada en ellos. En cambio, remitimos al lector interesado a un sólido curso de Geología ¹² o al Programa de Riesgos de Terremotos del Servicio Geológico de Estados Unidos que se encuentra aquí y presentamos solo una versión simplificada de la escala Richter. La escala de Richter mide la magnitud de un sismo comparando la amplitud de las ondas sísmicas del sismo dado con las de un “evento de magnitud 0", el cual fue elegido para ser una lectura sismógrafo de 0.001 milímetros registrada en un sismómetro a 100 kilómetros del epicentro del sismo. Específicamente, la magnitud de un sismo viene dada por

    \(M(x)=\log \left(\frac{x}{0.001}\right)\)

    donde\(x\) está la lectura del sismógrafo en milímetros del sismo registrado a 100 kilómetros del epicentro.

    1. \(M(0.001) = 0\)Demuéstralo.
    2. Computar\(M(80, 000)\).
    3. Demostrar que un sismo que registró 6.7 en la escala de Richter tuvo una lectura de sismógrafo diez veces mayor que uno que medía 5.7.
    4. Encuentra dos noticias sobre sismos recientes que dan sus magnitudes en la escala de Richter. ¿Cuántas veces mayor fue la lectura sismógrafo del sismo con mayor magnitud?
76. Si bien la escala de decibelios puede ser utilizada en muchas disciplinas, ¹³ limitaremos nuestra atención a su uso en acústica, específicamente su uso en la medición del nivel de intensidad del sonido. ¹⁴ El Nivel de Intensidad Sonora\(L\) (medido en decibelios) de una intensidad sonora\(I\) (medida en vatios por metro cuadrado) viene dado por

    \(L(I)=10 \log \left(\frac{I}{10^{-12}}\right).\)

    Al igual que la escala de Richter, esta escala se compara con\(I\) la línea base:\(10^{-12} \frac{W}{m^{2}}\) es el umbral de la audición humana.

    1. Computar\(L\left(10^{-6}\right)\).
    2. El daño a su audición puede comenzar con una exposición a corto plazo a niveles de sonido de alrededor de 115 decibelios. ¿Qué intensidad\(I\) se necesita para producir este nivel?
    3. Computar\(L(1)\). ¿Cómo se compara esto con el umbral del dolor que ronda los 140 decibelios?
77. El pH de una solución es una medida de su acidez o alcalinidad. Específicamente,\(\mathrm{pH}=-\log \left[\mathrm{H}^{+}\right]\) donde\(\left[\mathrm{H}^{+}\right]\) está la concentración de iones hidrógeno en moles por litro. Una solución con un pH menor a 7 es un ácido, una con un pH mayor a 7 es una base (alcalina) y un pH de 7 se considera neutra.
    1. La concentración de iones hidrógeno del agua pura es\(\left[\mathrm{H}^{+}\right]=10^{-7}\). Encuentra su pH.
    2. Encuentra el pH de una solución con\(\left[\mathrm{H}^{+}\right]=6.3 \times 10^{-13}\).
    3. El pH del ácido gástrico (el ácido en tu estómago) es de aproximadamente 0.7. ¿Cuál es la concentración de iones hidrógeno correspondiente?
78. Demuestre eso\(\log _{b} 1=0\) y\(\log _{b} b=1\) para cada\(b>0, b \neq 1\).
79. (Pregunta de bonificación loca) Sin usar tu calculadora, determina cuál es más grande:\(e^{\pi}\) o\(\pi^{e}\).

6.1.2 Respuestas

1. \(\log _{2}(8)=3\)
2. \(\log _{5}\left(\frac{1}{125}\right)=-3\)
3. \(\log _{4}(32)=\frac{5}{2}\)
4. \(\log _{\frac{1}{3}}(9)=-2\)
5. \(\log _{\frac{4}{25}}\left(\frac{5}{2}\right)=-\frac{1}{2}\)
6. \(\log (0.001)=-3\)
7. \(\ln (1)=0\)
8. \(5^{2}=25\)
9. \((25)^{\frac{1}{2}}=5\)
10. \(3^{-4}=\frac{1}{81}\)
11. \(\left(\frac{4}{3}\right)^{-1}=\frac{3}{4}\)
12. \(10^{2}=100\)
13. \(10^{-1}=0.1\)
14. \(e^{1}=e\)
15. \(e^{-\frac{1}{2}}=\frac{1}{\sqrt{e}}\)
16. \(\log _{3}(27)=3\)
17. \(\log _{6}(216)=3\)
18. \(\log _{2}(32)=5\)
19. \(\log _{6}\left(\frac{1}{36}\right)=-2\)
20. \(\log _{8}(4)=\frac{2}{3}\)
21. \(\log _{36}(216)=\frac{3}{2}\)
22. \(\log _{\frac{1}{5}}(625)=-4\)
23. \(\log _{\frac{1}{6}}(216)=-3\)
24. \(\log _{36}(36)=1\)
25. \(\log \frac{1}{1000000}=-6\)
26. \(\log (0.01)=-2\)
27. \(\ln \left(e^{3}\right)=3\)
28. \(\log _{4}(8)=\frac{3}{2}\)
29. \(\log _{6}(1)=0\)
30. \(\log _{13}(\sqrt{13})=\frac{1}{2}\)
31. \(\log _{36}(\sqrt[4]{36})=\frac{1}{4}\)
32. \(7^{\log _{7}(3)}=3\)
33. \(36^{\log _{36}(216)}=216\)
34. \(\log _{36}\left(36^{216}\right)=216\)
35. \(\ln \left(e^{5}\right)=5\)
36. \(\log \left(\sqrt[9]{10^{11}}\right)=\frac{11}{9}\)
37. \(\log \left(\sqrt[3]{10^{5}}\right)=\frac{5}{3}\)
38. \(\ln \left(\frac{1}{\sqrt{e}}\right)=-\frac{1}{2}\)
39. \(\log _{5}\left(3^{\log _{3} 5}\right)=1\)
40. \(\log \left(e^{\ln (100)}\right)=2\)
41. \(\log _{2}\left(3^{-\log _{3}(2)}\right)=-1\)
42. \(\ln \left(42^{6 \log (1)}\right)=0\)
43. \((-\infty, \infty)\)
44. \((-2, \infty)\)
45. \((5, \infty)\)
46. \((-\infty,-6) \cup(-3, \infty)\)
47. \((-2,-1) \cup(1, \infty)\)
48. \((-6,-3) \cup(5, \infty)\)
49. \((4,7)\)
50. \((5, \infty)\)
51. \((-\infty, \infty)\)
52. \([1, \infty)\)
53. \((-\infty,-7) \cup(1, \infty)\)
54. \((13, \infty)\)
55. \((0,125) \cup(125, \infty)\)
56. Sin dominio
57. \((-\infty,-3) \cup\left(\frac{1}{2}, 2\right)\)
58. Dominio de\(g\):\((-\infty, \infty)\)

    Rango de\(g\):\((-1, \infty)\)

    

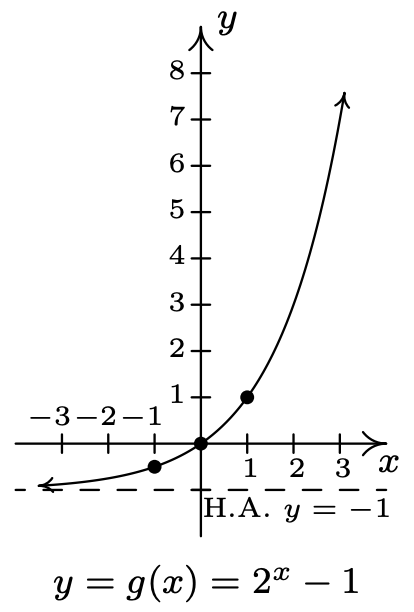
59. Dominio de\(g\):\((-\infty, \infty)\)

    Rango de g:\((0, \infty)\)

    

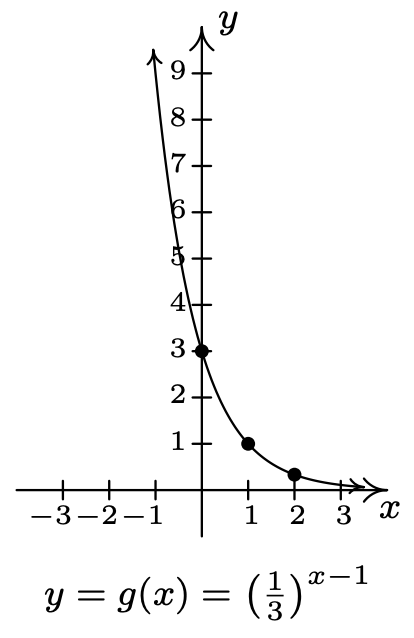
60. Dominio de\(g\):\((-\infty, \infty)\)

    Rango de\(g\):\((-20, \infty)\)

    

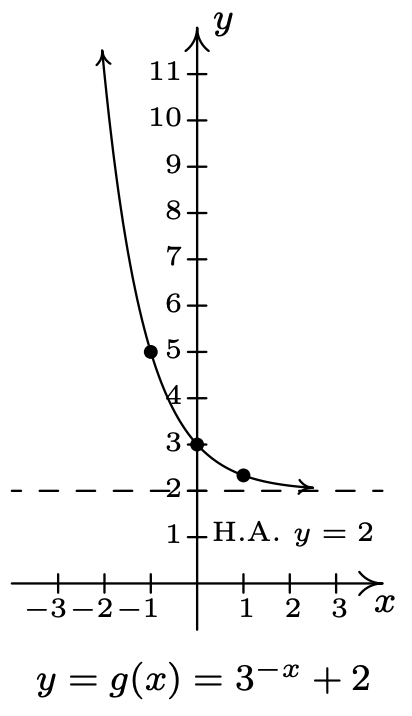
61. Dominio de\(g\):\((-\infty, \infty)\)

    Rango de\(g\):\((-\infty, 8)\)

    

62. Dominio de\(g\):\((-\infty, \infty)\)

    Rango de\(g\):\((0, \infty)\)

    

63. Dominio de\(g\):\((-1, \infty)\)

    Rango de\(g\):\((-\infty, \infty)\)

    

64. Dominio de\(g\):\((-1, \infty)\)

    Rango de\(g\):\((-\infty, \infty)\)

    

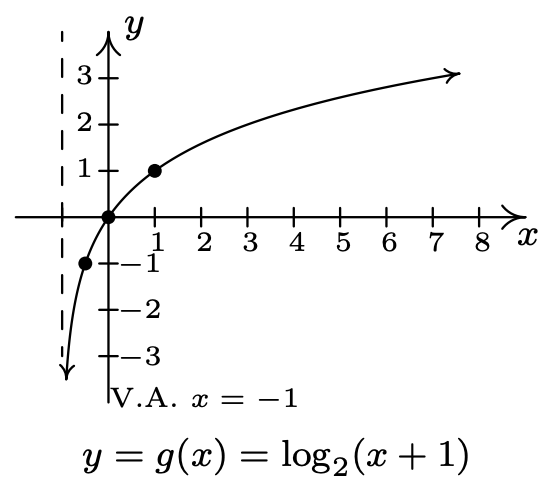
65. Dominio de\(g\):\((0, \infty)\)

    Rango de\(g\):\((-\infty, \infty)\)

    

66. Dominio de\(g\):\((2, \infty)\)

    Rango de\(g\):\((-\infty, \infty)\)

    

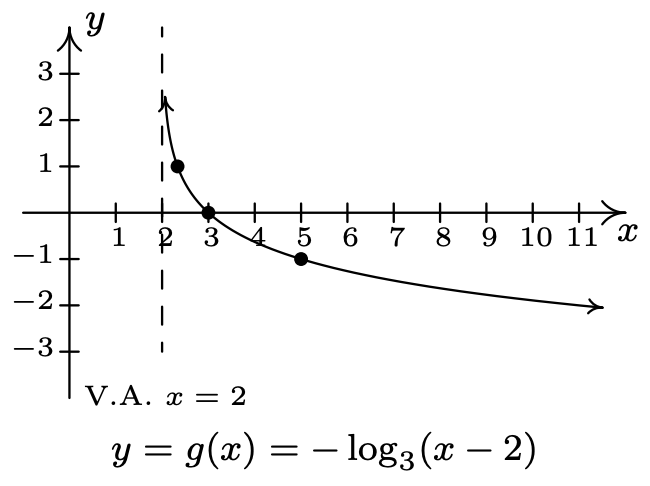
67. Dominio de\(g\):\((-20, \infty)\)

    Rango de\(g\):\((-\infty, \infty)\)

    

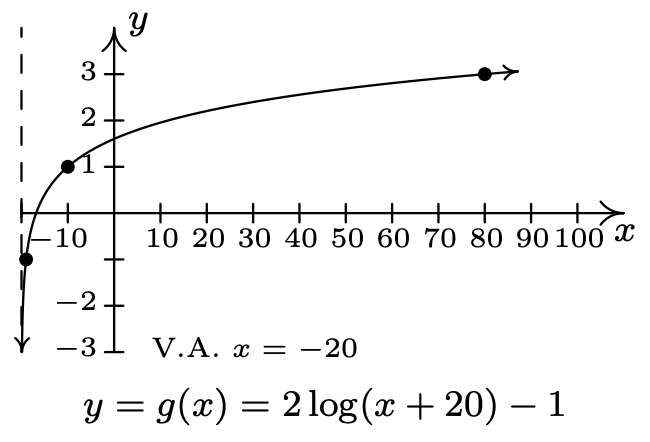
68. Dominio de\(g\):\((-\infty, 8)\)

    Rango de\(g\):\((-\infty, \infty)\)

    

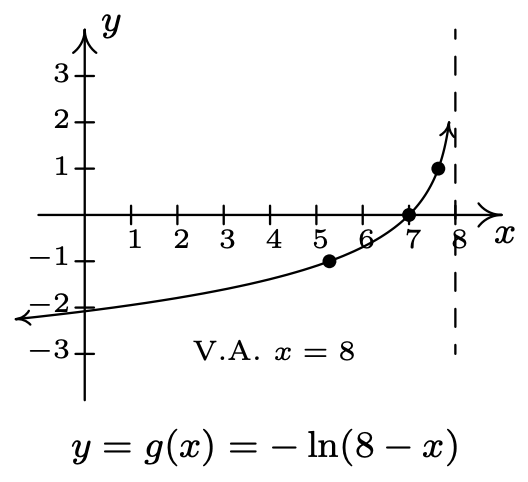
69. Dominio de\(g\):\((0, \infty)\)

    Rango de\(g\):\((-\infty, \infty)\)

    

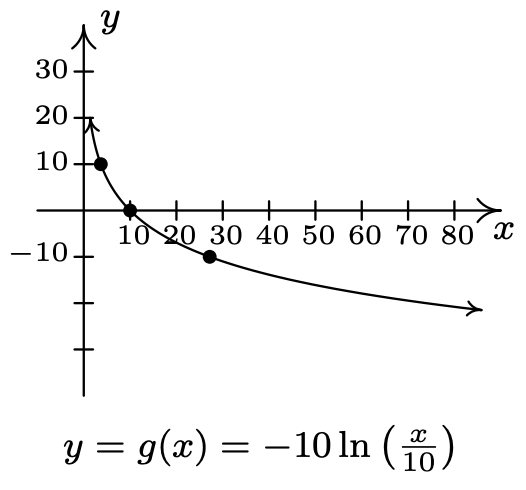
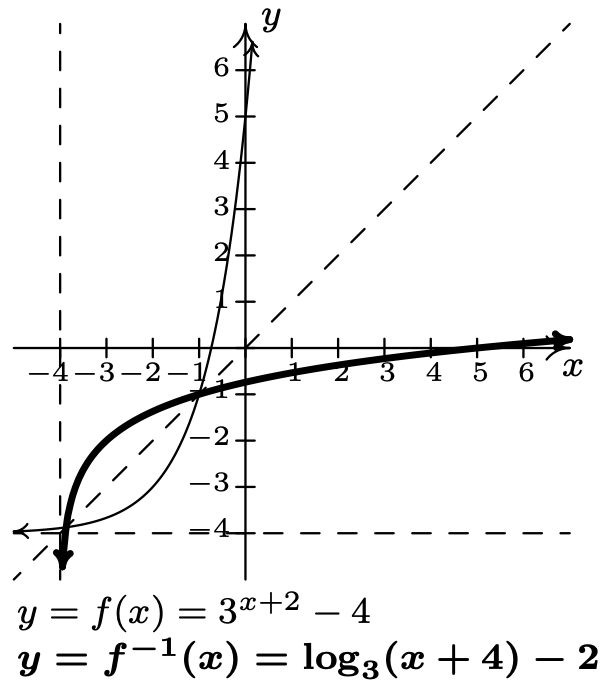
70. \(f(x)=3^{x+2}-4\)

    \(f^{-1}(x)=\log _{3}(x+4)-2\)

    

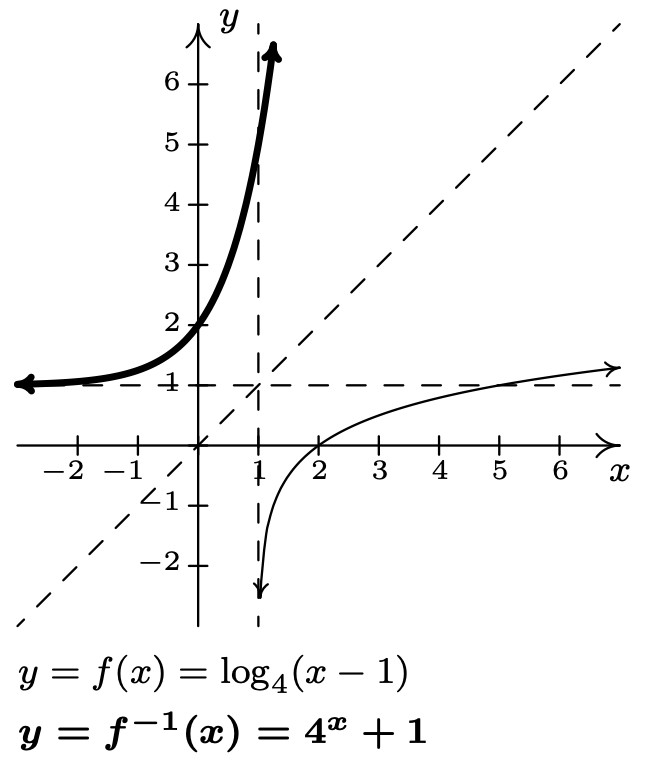
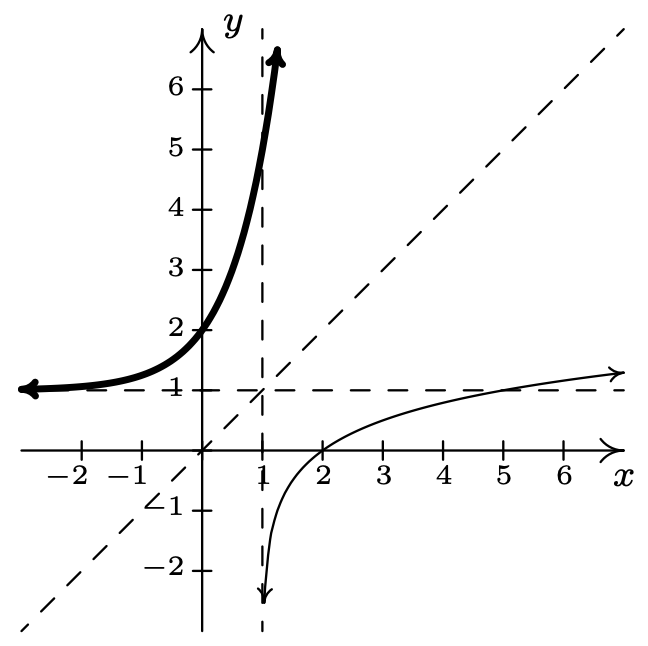
71. \(f(x)=\log _{4}(x-1)\)

    \(f^{-1}(x)=4^{x}+1\)

    

72. \(f(x)=\log _{4}(x-1)\)

    \(f^{-1}(x)=4^{x}+1\)

    

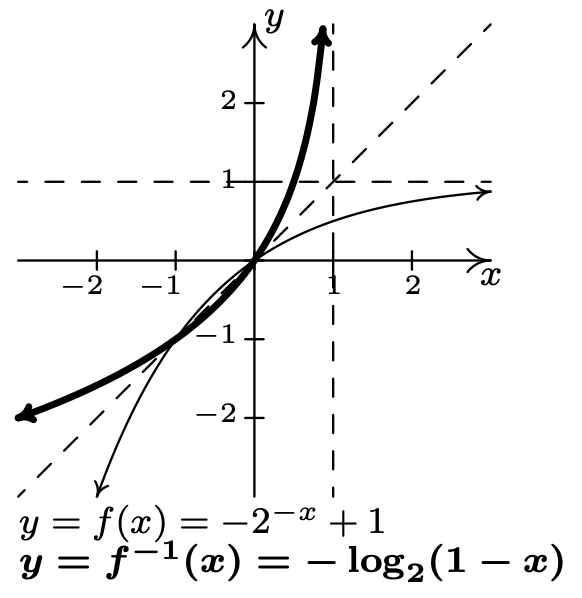
73. \(f(x)=-2^{-x}+1\)

    \(f^{-1}(x)=-\log _{2}(1-x)\)

    

74. \(f(x)=5 \log (x)-2\)

    \(f^{-1}(x)=10^{\frac{x+2}{5}}\)

    

75. 1. \(M(0.001)=\log \left(\frac{0.001}{0.001}\right)=\log (1)=0.\)
    2. \(M(80,000)=\log \left(\frac{80,000}{0.001}\right)=\log (80,000,000) \approx 7.9\)
76. 1. \(L\left(10^{-6}\right)=60\)decibelios.
    2. \(I=10^{-.5} \approx 0.316\)vatios por metro cuadrado.
    3. Desde\( L(1)=120\) decibelios y\( L(100)=140\) decibelios, un sonido con nivel de intensidad 140 decibelios tiene una intensidad 100 veces mayor que un sonido con nivel de intensidad 120 decibelios.
77. 1. El pH del agua pura es 7.
    2. Si\(\left[\mathrm{H}^{+}\right]=6.3 \times 10^{-13}\) entonces la solución tiene un pH de 12.2.
    3. \(\left[\mathrm{H}^{+}\right]=10^{-0.7} \approx .1995\)moles por litro.

---

Referencia

¹ Toma una clase de Ecuaciones Diferenciales y verás por qué.

² Recordemos que esto significa que no hay agujeros u otro tipo de roturas en la gráfica.

³ En realidad se puede probar esto considerando el polinomio\(p(x)=x^{2}-3\) y demostrando que no tiene ceros racionales aplicando el Teorema 3.9.

⁴ Aquí es donde entran en juego el Cálculo y la continuidad.

⁵ ¿Quieres más información? Busca “secuencias convergentes” en Internet.

⁶ Significado, grafica algunos ejemplos más por tu cuenta.

⁷ La prueba de la cual, como muchas cosas discutidas en el texto, requiere de Cálculo.

⁸ Lo discutiremos con mayor detalle en la Sección 6.5.

⁹ Vale la pena un momento de tu tiempo para pensar tu camino a través del por qué\(117^{\log _{117}(6)}=6\). Por definición,\(\log _{117}(6)\) es el exponente que ponemos 117 para conseguir 6. ¿Qué estamos haciendo con este exponente? Lo estamos poniendo en 117. Por definición obtenemos 6. En otras palabras, la función exponencial\(f(x)=117^{x}\) deshace la función logarítmica\(g(x)=\log _{117}(x)\).

¹⁰ Ver página 55 si has olvidado lo que significa este término

¹¹ Presta atención - ¿puedes detectar en qué paso a continuación necesitamos\(x>-3\)?

¹² Sólido como una roca, ¿quizás?

¹³ Consulte esta página web para más información.

¹⁴ A partir de la redacción de este ejercicio, la página de Wikipedia que aquí se da establece que puede no cumplir con la “pauta general de notoriedad” ni cita ninguna referencia o fuente. Esto me parece extraño porque es este mismo uso de la escala de decibelios que aparece en todos los libros de Álgebra universitaria\(I\) que han leído. Quizás esos otros libros han estado equivocados todo el tiempo y solo seguimos ciegamente la tradición.