6.3: Ecuaciones exponenciales y desigualdades

Última actualización
Guardar como PDF

Page ID: 119490

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

En esta sección desarrollaremos técnicas para resolver ecuaciones que involucren funciones exponenciales. Supongamos, por ejemplo, que queríamos resolver la ecuación$2^{x} = 128$. Después de un momento de cálculo, nos encontramos$128 = 2^{7}$, así que tenemos$2^{x} = 2^{7}$. La propiedad uno a uno de las funciones exponenciales, detallada en el Teorema 6.4, nos dice que$2^{x} = 2^{7}$ si y solo si$x=7$. Esto quiere decir que no sólo es$x=7$ una solución a$2^{x} = 2^{7}$, es la única solución. Ahora supongamos que cambiamos el problema cada vez tan ligeramente a$2^{x} = 129$. Podríamos usar una de las propiedades inversas de exponenciales y logaritmos enumerados en el Teorema 6.3 para escribir$129 = 2^{\log_{2}(129)}$. Entonces tendríamos$2^{x} = 2^{\log_{2}(129)}$, lo que significa que nuestra solución es$x = \log_{2}(129)$. Esto tiene sentido porque, después de todo, la definición de$\log_{2}(129)$ es 'el exponente que nos ponemos$2$ para obtener'$129$. De hecho podríamos haber obtenido esta solución directamente reescribiendo la ecuación$2^{x} = 129$ en su forma logarítmica$\log_{2}(129) = x$. De cualquier manera, para obtener una aproximación decimal razonable a este número, usaríamos el cambio de fórmula base, Teorema 6.7, para darnos algo más amigable con la calculadora, ¹ decir$\log_{2}(129) = \frac{\ln(129)}{\ln(2)}$. Otra forma de llegar a esta respuesta es la siguiente

\[\begin{array}{rclr} 2^{x} & = & 129 & \\ \ln\left(2^{x}\right) & = & \ln(129) & \mbox{Take the natural log of both sides.} \\ x \ln(2) & = & \ln(129) & \mbox{Power Rule} \\[4pt] x & = &\dfrac{\ln(129)}{\ln(2)} & \\ \end{array}\nonumber\]

'Tomar el tronco natural' de ambos lados es similar a cuadrar ambos lados: ya que$f(x) = \ln(x)$ es una función, siempre y cuando dos cantidades sean iguales, sus troncos naturales son iguales. ² También tenga en cuenta que tratamos$\ln(2)$ como cualquier otro número real distinto de cero y lo dividimos entre ³ para aislar la variable$x$. Resumimos a continuación las dos formas comunes de resolver ecuaciones exponenciales, motivadas por nuestros ejemplos.

Pasos para resolver una ecuación que involucra funciones exponenciales

Aísle la función exponencial.
1. Si es conveniente, exprese ambos lados con una base común e iguale los exponentes.
2. De lo contrario, toma el registro natural de ambos lados de la ecuación y usa la Regla de Poder.

Ejemplo 6.3.1.

Resuelve las siguientes ecuaciones. Verifica tu respuesta gráficamente usando una calculadora.

$2^{3x} = 16^{1-x}$
$2000 = 1000 \cdot 3^{-0.1 t}$
$9 \cdot 3^{x} = 7^{2x}$
$75 = \frac{100}{1 + 3e^{-2t}}$
$25^{x} = 5^{x} + 6$
$\frac{e^{x} - e^{-x}}{2} = 5$

Solución.

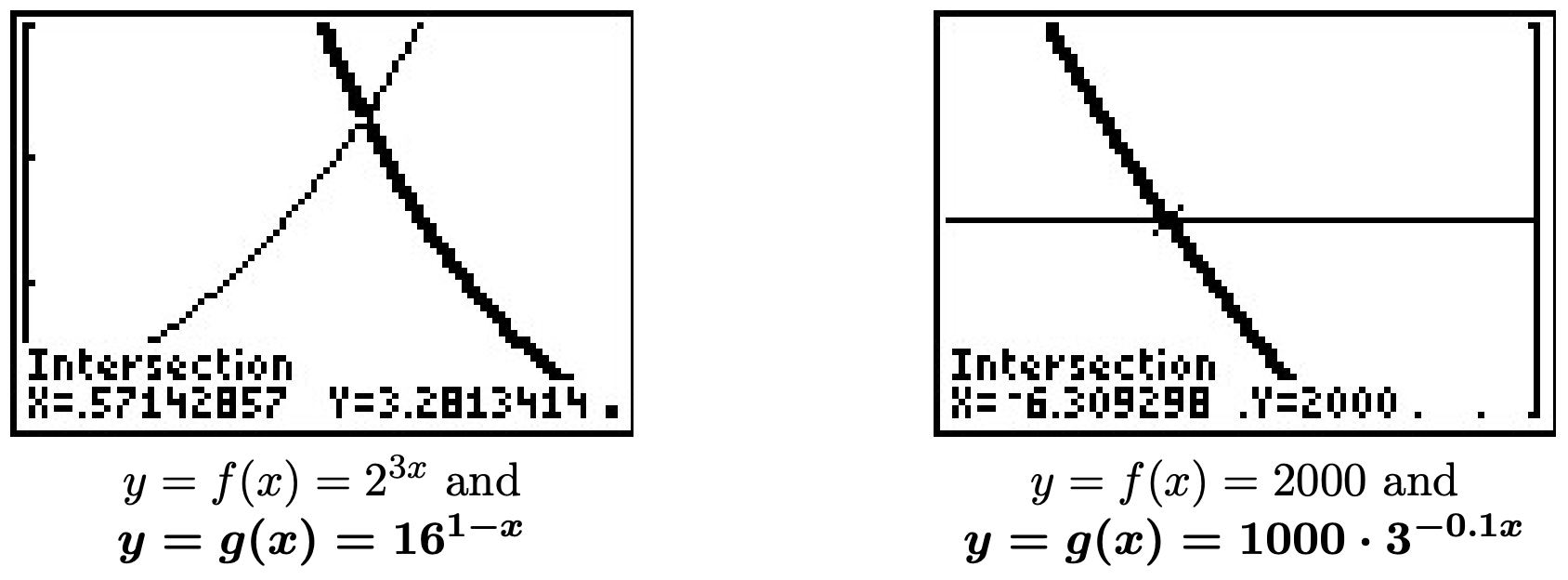
Ya que$16$ es un poder de$2$, podemos reescribir$2^{3x} = 16^{1-x}$ como$2^{3x} = \left(2^4\right)^{1-x}$. Usando propiedades de exponentes, obtenemos$2^{3x} = 2^{4(1-x)}$. Usando la propiedad uno a uno de las funciones exponenciales, obtenemos$3x = 4(1-x)$ lo que da$x=\frac{4}{7}$. Para verificar gráficamente, establecemos$f(x) = 2^{3x}$$g(x) = 16^{1-x}$ y vemos que se cruzan en$x=\frac{4}{7} \approx 0.5714$.
Comenzamos a resolver$2000 = 1000 \cdot 3^{-0.1 t}$ dividiendo ambos lados por$1000$ para aislar lo exponencial que rinde$3^{-0.1t} = 2$. Ya que es inconveniente escribir$2$ como un poder de$3$, utilizamos el registro natural para obtener$\ln\left(3^{-0.1t}\right) = \ln(2)$. Usando la Regla del Poder, obtenemos$-0.1 t \ln(3) = \ln(2)$, así que dividimos ambos lados por$-0.1 \ln(3)$ para conseguir$t = -\frac{\ln(2)}{0.1 \ln(3)} = -\frac{10\ln(2)}{\ln(3)}$. En la calculadora, graficamos$f(x) = 2000$$g(x) = 1000 \cdot 3^{-0.1 x}$ y encontramos que se cruzan en$x = -\frac{10\ln(2)}{\ln(3)} \approx -6.3093$.
$Screen Shot 2022-04-18 a las 12.49.54 AM.png$
Primero notamos que podemos reescribir la ecuación$9 \cdot 3^{x} = 7^{2x}$ como$3^2 \cdot 3^x = 7^{2x}$ para obtener$3^{x+2} = 7^{2x}$. Ya que no es conveniente expresar ambos lados como un poder de$3$ (o$7$ para el caso) utilizamos el tronco natural:$\ln\left(3^{x+2}\right) = \ln\left(7^{2x}\right)$. La regla del poder da$(x+2) \ln(3) = 2x \ln(7)$. A pesar de que esta ecuación parece muy complicada, hay que tener en cuenta eso$\ln(3)$ y$\ln(7)$ son solo constantes. La ecuación$(x+2) \ln(3) = 2x \ln(7)$ es en realidad una ecuación lineal y como tal reunimos todos los términos con$x$ en un lado, y las constantes en el otro. Luego dividimos ambos lados por el coeficiente de$x$, que obtenemos factorizando.
\[\begin{array}{rclr} (x+2) \ln(3) & = & 2x \ln(7) & \\ x \ln(3) + 2 \ln(3) & = & 2x \ln(7) & \\ 2 \ln(3) & = & 2x \ln(7) - x \ln(3) & \\ 2 \ln(3) & = & x (2 \ln(7) - \ln(3)) & \mbox{Factor.}\\ x & = & \frac{2 \ln(3)}{2\ln(7) - \ln(3)} & \\[4pt] \end{array}\nonumber\]

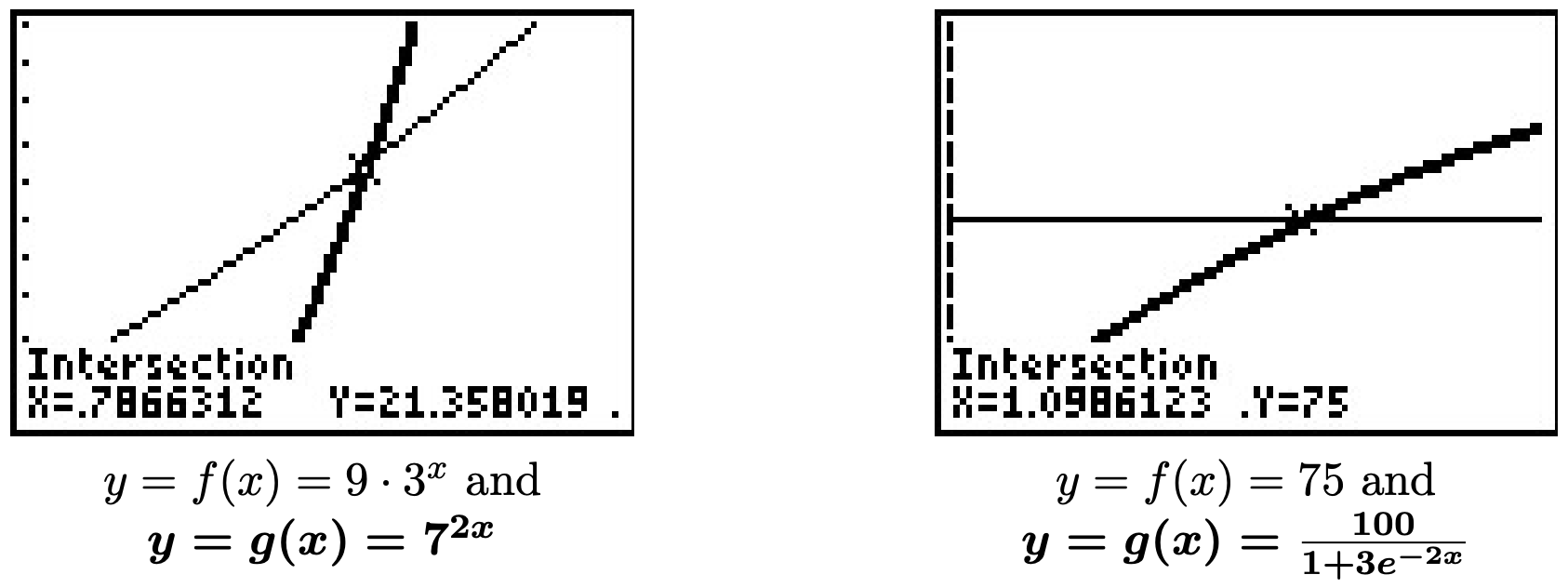
Graficando$f(x) = 9 \cdot 3^{x}$ y$g(x) = 7^{2x}$ en la calculadora, vemos que estas dos gráficas se cruzan en$x = \frac{2 \ln(3)}{2\ln(7) - \ln(3)} \approx 0.7866$.
Nuestro objetivo en la resolución$75 = \frac{100}{1 + 3e^{-2t}}$ es aislar primero lo exponencial. Para ello, despejamos denominadores y conseguimos$75\left(1 + 3e^{-2t}\right) = 100$. De esto obtenemos$75 + 225e^{-2t} =100$, lo que lleva a$225e^{-2t} = 25$, y finalmente,$e^{-2t} = \frac{1}{9}$. Tomando el tronco natural de ambos lados da$\ln\left(e^{-2t}\right) = \ln\left( \frac{1}{9} \right)$. Dado que el tronco natural es base de troncos$e$,$\ln\left(e^{-2t}\right) = -2t$. También podemos usar la Regla de Poder para escribir$\ln\left( \frac{1}{9} \right) = -\ln(9)$. Armando estos dos pasos, simplificamos$\ln\left(e^{-2t}\right) = \ln\left( \frac{1}{9} \right)$ a$-2t = -\ln(9)$. Llegamos a nuestra solución,$t = \frac{\ln(9)}{2}$ lo que simplifica a$t = \ln(3)$. (¿Puedes explicar por qué?) La calculadora confirma las gráficas de$f(x) = 75$ y se$g(x) = \frac{100}{1 + 3e^{-2x}}$ cruzan en$x = \ln(3) \approx 1.099$.
$Screen Shot 2022-04-18 en 12.53.11 AM.png$
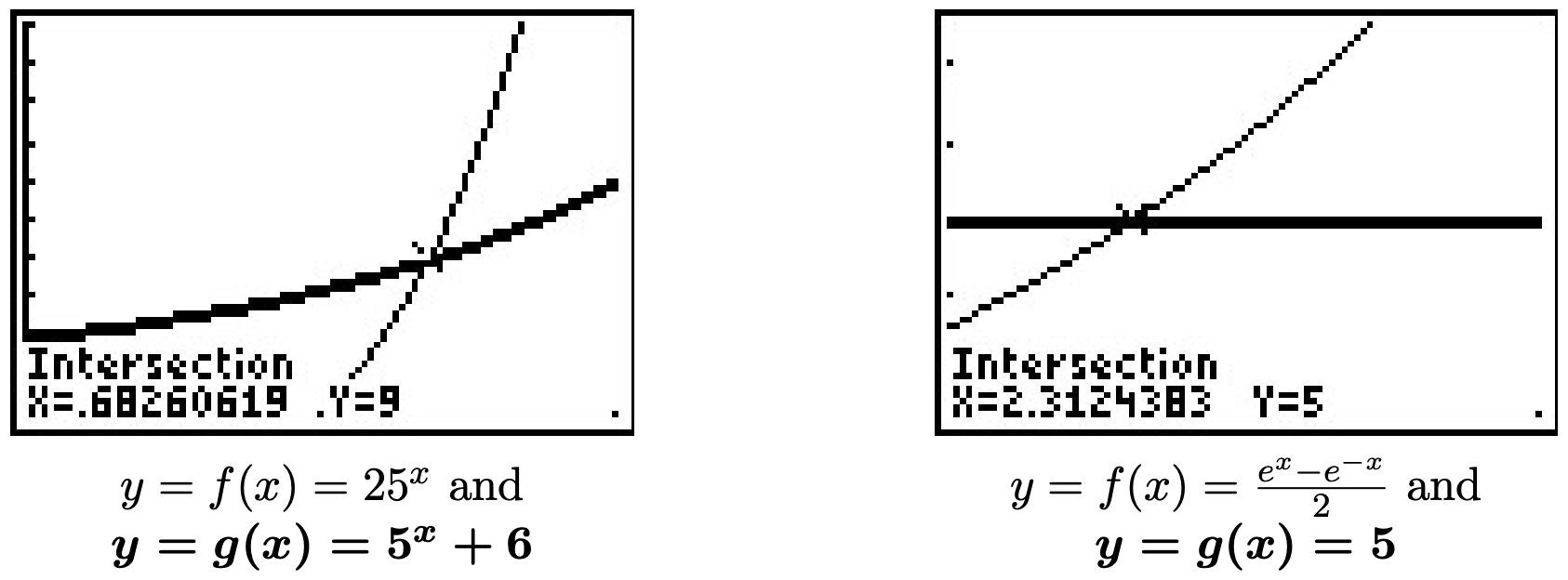
Empezamos a resolver$25^{x} = 5^{x} + 6$ reescribiendo$25 = 5^2$ para que tengamos$\left(5^2\right)^{x} = 5^{x} + 6$, o$5^{2x} = 5^{x} + 6$. A pesar de que tenemos una base común, tener dos términos en el lado derecho de la ecuación frustra nuestro plan de igualar exponentes o tomar registros. Si miramos esto el tiempo suficiente, notamos que tenemos tres términos con el exponente en un término exactamente el doble que el de otro. Para nuestra sorpresa y deleite, tenemos una 'cuadrática encubierta'. Dejando$u = 5^{x}$, tenemos$u^2 = \left(5^{x}\right)^2 = 5^{2x}$ así la ecuación$5^{2x} = 5^{x} + 6$ se convierte$u^2 = u + 6$. Resolviendo esto como$u^2 - u - 6=0$ da$u = -2$ o$u = 3$. Ya que$u = 5^{x}$, tenemos$5^{x} = -2$ o$5^{x} = 3$. Ya que no$5^{x} = -2$ tiene una solución real, (¿Por qué no?) nos enfocamos en$5^{x} = 3$. Ya que no es conveniente expresar$3$ como un poder de$5$, tomamos troncos naturales y obtenemos$\ln\left(5^{x}\right) = \ln(3)$ así que$x \ln(5) = \ln(3)$ o$x = \frac{\ln(3)}{\ln(5)}$. En la calculadora, vemos las gráficas de$f(x) = 25^{x}$ y se$g(x) = 5^{x} + 6$ cruzan en$x=\frac{\ln(3)}{\ln(5)} \approx 0.6826$.
Al principio, no está claro cómo proceder$\frac{e^{x} - e^{-x}}{2} = 5$, además de despejar el denominador para obtener$e^{x} - e^{-x} = 10$. Por supuesto, si reescribimos$e^{-x} = \frac{1}{e^{x}}$, vemos que tenemos otro denominador acechando en el problema:$e^{x} - \frac{1}{e^{x}} = 10$. Borrar este denominador nos da$e^{2x} - 1 = 10e^{x}$, y una vez más, tenemos una ecuación con tres términos donde el exponente en un término es exactamente el doble que el de otro, un 'cuadrático disfrazado'. Si lo dejamos$u = e^{x}$, entonces$u^2 = e^{2x}$ así la ecuación$e^{2x} - 1 = 10e^{x}$ puede ser vista como$u^2-1 = 10u$. Resolviendo$u^2 - 10u - 1 = 0$, obtenemos por la fórmula cuadrática$u = 5 \pm \sqrt{26}$. De esto, tenemos$e^{x} = 5 \pm \sqrt{26}$. Ya que$5 - \sqrt{26} < 0$, no obtenemos una solución real para$e^{x} = 5 - \sqrt{26}$, sino para$e^{x} = 5 + \sqrt{26}$, tomamos troncos naturales para obtener$x = \ln\left(5 + \sqrt{26}\right)$. Si graficamos$f(x) = \frac{e^{x} - e^{-x}}{2}$ y$g(x) = 5$, vemos que las gráficas se cruzan en$x = \ln\left(5 + \sqrt{26}\right) \approx 2.312$
$Screen Shot 2022-04-18 a las 12.56.25 AM.png$

Los autores serían negligentes por no mencionar que el Ejemplo 6.3.1 aún tiene un gran valor educativo. Mucho se puede aprender sobre logaritmos y exponenciales verificando analíticamente las soluciones obtenidas en el Ejemplo 6.3.1. Por ejemplo, para verificar nuestra solución$2000 = 1000 \cdot 3^{-0.1 t}$, sustituimos$t = -\frac{10\ln(2)}{\ln(3)}$ y obtenemos

\[\begin{array}{rclr} 2000 & \stackrel{?}{=} & 1000 \cdot 3^{-0.1 \left(-\frac{10\ln(2)}{\ln(3)}\right)} & \\ 2000 & \stackrel{?}{=} & 1000 \cdot 3^{\frac{\ln(2)}{\ln(3)}} & \\ 2000 & \stackrel{?}{=} & 1000 \cdot 3^{\log_{3}(2)} & \mbox{Change of Base}\\ 2000 & \stackrel{?}{=} & 1000 \cdot 2 & \mbox{Inverse Property}\\ 2000 & \stackrel{\checkmark}{=} & 2000 & \\ \end{array}\nonumber\]

Las otras soluciones se pueden verificar usando una combinación de propiedades logarítmicas e inversas. Algunos se caen bastante rápido, mientras que otros están más involucrados. Se los dejamos al lector.

Dado que las funciones exponenciales son continuas en sus dominios, se aplica el Teorema del Valor Intermedio 3.1. Al igual que con las funciones algebraicas de la Sección 5.3, esto nos permite resolver desigualdades utilizando diagramas de signos como se demuestra a continuación.

Ejemplo 6.3.2

Resolver las siguientes desigualdades. Verifica tu respuesta gráficamente usando una calculadora.

$2^{x^2-3x} - 16 \geq 0$
$\dfrac{e^{x}}{e^{x}-4} \leq 3$
$x e^{2x} < 4x$

Solución.

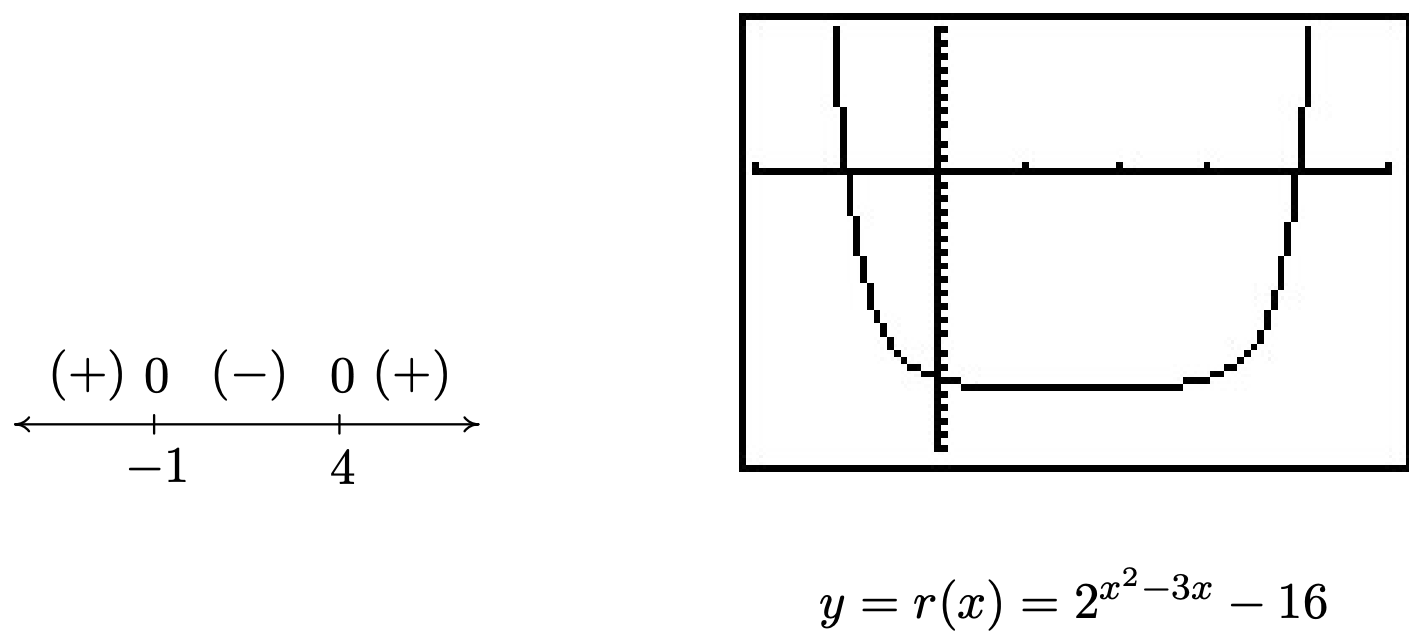
Como ya tenemos de un$0$ lado de la desigualdad, nos fijamos$r(x) = 2^{x^2-3x} - 16$. El dominio de$r$ es todo números reales, por lo que para construir nuestro diagrama de signos, necesitamos encontrar los ceros de$r$. Ajuste$r(x) = 0$ da$2^{x^2-3x} - 16 = 0$ o$2^{x^2-3x} = 16$. Ya que$16 = 2^{4}$ tenemos$2^{x^2-3x} = 2^{4}$, así por la propiedad uno-a-uno de las funciones exponenciales,$x^2 -3x = 4$. Resolviendo$x^2 -3x - 4 = 0$ da$x=4$ y$x=-1$. Del diagrama de signos, vemos$r(x) \geq 0$ en$(-\infty, -1] \cup [4, \infty)$, que corresponde a donde la gráfica de$y=r(x) = 2^{x^2-3x} - 16$, está sobre o por encima del$x$ eje -eje.
$Screen Shot 2022-04-18 en 1.06.53 AM.png$
El primer paso que debemos dar para resolver$\frac{e^{x}}{e^{x}-4} \leq 3$ es ponernos de un$0$ lado de la desigualdad. Para ello, restamos$3$ de ambos lados y obtenemos un denominador común
\[\begin{array}{rclr} \dfrac{e^{x}}{e^{x}-4} & \leq & 3 & \\ \dfrac{e^{x}}{e^{x}-4} - 3 & \leq & 0 & \\ \dfrac{e^{x}}{e^{x}-4} - \dfrac{3 \left(e^{x}-4\right)}{e^{x}-4} & \leq & 0 & \mbox{Common denomintors.} \\ \dfrac{12 - 2e^{x}}{e^{x}-4} & \leq & 0 & \\ \end{array}\nonumber\]

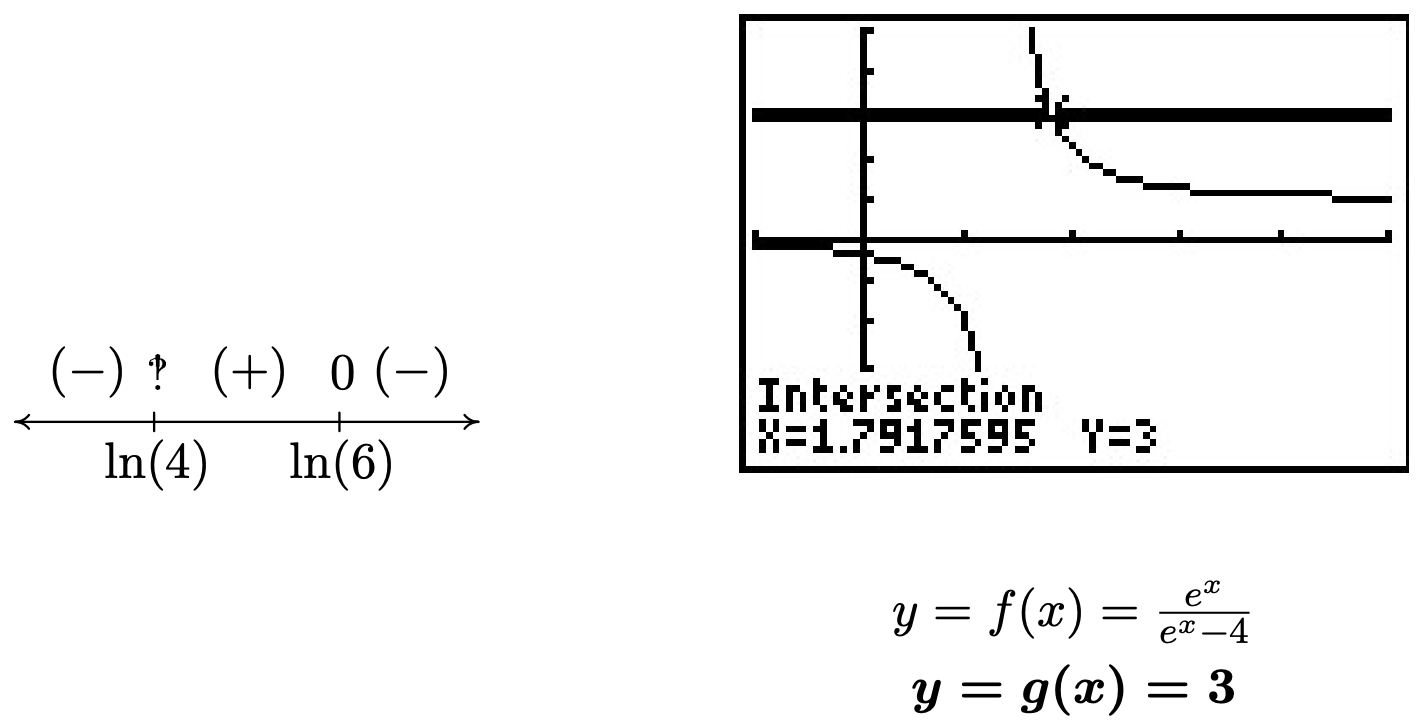
Nos fijamos$r(x) = \frac{12 - 2e^{x}}{e^{x}-4}$ y notamos que$r$ está indefinido cuando su denominador$e^{x}-4=0$, o cuándo$e^{x} = 4$. Resolver esto da$x = \ln(4)$, por lo que el dominio de$r$ es$(-\infty, \ln(4)) \cup (\ln(4), \infty)$. Para encontrar los ceros de$r$, resolvemos$r(x) = 0$ y obtenemos$12 - 2e^{x} = 0$. Resolviendo para$e^{x}$, encontramos$e^{x} = 6$, o$x = \ln(6)$. Cuando construimos nuestro diagrama de signos, encontrar valores de prueba puede ser un poco complicado ya que necesitamos verificar valores alrededor$\ln(4)$ y$\ln(6)$. Recordemos que la función$\ln(x)$ está aumentando ⁴ lo que significa$\ln(3) < \ln(4) < \ln(5) < \ln(6) < \ln(7)$. Si bien la perspectiva de determinar el signo de$r\left(\ln(3)\right)$ puede ser muy inquietante, recuérdalo$e^{\ln(3)} = 3$, por lo que\[r\left(\ln(3)\right) = \frac{12 - 2e^{\ln(3)}}{e^{\ln(3)}-4} = \frac{12-2(3)}{3-4} = -6\nonumber\] determinamos los signos de$r\left(\ln(5)\right)$ y de$r\left(\ln(7)\right)$ manera similar. ⁵ Del diagrama de señales, encontramos que nuestra respuesta es$(-\infty,\ln(4)) \cup [\ln(6), \infty)$. Usando la calculadora, vemos que la gráfica de$f(x) = \frac{e^{x}}{e^{x}-4}$ está debajo de la gráfica de$g(x) = 3$ on$(-\infty,\ln(4)) \cup (\ln(6), \infty)$, y se cruzan en$x = \ln(6) \approx 1.792$.

$Screen Shot 2022-04-18 en 1.21.48 AM.png$
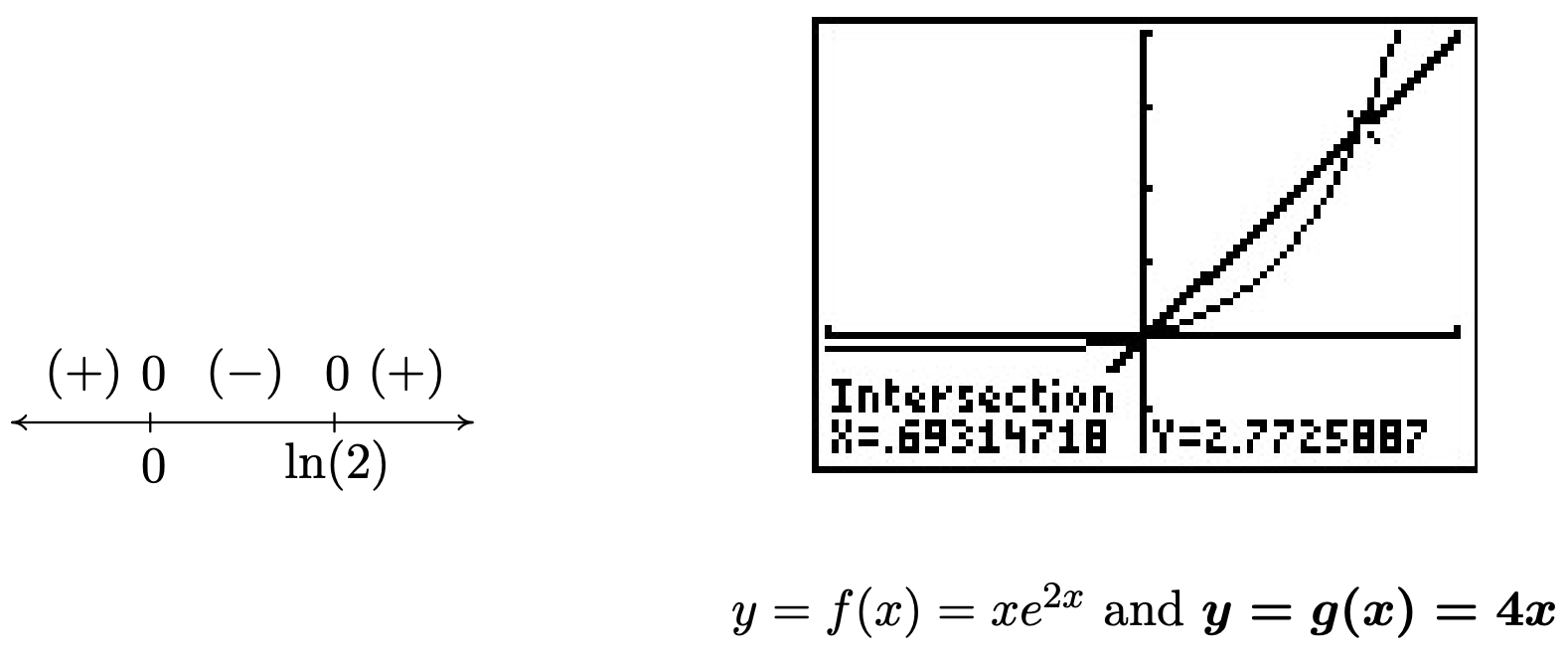
Como antes, empezamos a resolver$x e^{2x} < 4x$ poniéndonos de un$0$ lado de la desigualdad,$x e^{2x} - 4x < 0$. Establecemos$r(x) = xe^{2x} - 4x$ y como no hay denominadores, radicales pares indexados, ni registros, el dominio de$r$ es todo números reales. El fraguado$r(x) = 0$ produce$x e^{2x} - 4x = 0$. Nosotros factorizamos para obtener$x \left(e^{2x} - 4\right) = 0$ cuál da$x=0$ o$e^{2x} - 4 = 0$. Para resolver esto último, aislamos lo exponencial y tomamos bitácoras para obtener$2x = \ln(4)$, o$x = \frac{\ln(4)}{2} = \ln(2)$. (¿Se puede explicar la última igualdad usando propiedades de registros?) Al igual que en el ejemplo anterior, debemos tener cuidado al elegir los valores de prueba. Ya que$\ln(1) = 0$, elegimos$\ln\left(\frac{1}{2}\right)$,$\ln\left(\frac{3}{2}\right)$ y$\ln(3)$. Evaluando, ⁶ obtenemos
\[\begin{array}{rclr} r\left(\ln\left(\frac{1}{2}\right)\right) & = & \ln\left(\frac{1}{2}\right) e^{2\ln\left(\frac{1}{2}\right)} - 4\ln\left(\frac{1}{2}\right) & \\ &= & \ln\left(\frac{1}{2}\right)e^{\ln\left(\frac{1}{2}\right)^2}- 4\ln\left(\frac{1}{2}\right) & \text{Power Rule} \\ & = & \ln\left(\frac{1}{2}\right)e^{\ln\left(\frac{1}{4}\right)}- 4\ln\left(\frac{1}{2}\right) & \\ & = & \frac{1}{4} \ln\left(\frac{1}{2}\right) - 4 \ln\left(\frac{1}{2}\right) = -\frac{15}{4} \ln\left(\frac{1}{2}\right) & \end{array}\nonumber\]

Ya que$\frac{1}{2} < 1$,$\ln\left(\frac{1}{2}\right) < 0$ y obtenemos$r(\ln\left(\frac{1}{2}\right))$ es$(+)$, así$r(x) < 0$ sucesivamente$(0 ,\ln(2))$. La calculadora confirma que la gráfica de$f(x) = x e^{2x}$ está por debajo de la gráfica de$g(x) = 4x$ en estos intervalos. ⁷

$Screen Shot 2022-04-18 en 1.23.37 AM.png$

Ejemplo 6.3.3

Recordemos del Ejemplo 6.1.2 que la temperatura del café$T$ (en grados Fahrenheit)$t$ minutos después de servirlo puede ser modelada por$T(t) = 70 + 90 e^{-0.1 t}$. ¿Cuándo estará el café más caliente que$100^{\circ}\mbox{F}$?

Solución

Tenemos que encontrar cuándo$T(t) > 100$, o en otras palabras, necesitamos resolver la desigualdad$70 + 90 e^{-0.1 t} > 100$. Ponerse de un$0$ lado de la desigualdad, tenemos$90 e^{-0.1 t} - 30 > 0$, y nos fijamos$r(t) = 90 e^{-0.1 t} - 30$. El dominio de$r$ está restringido artificialmente debido al contexto del problema a$[0, \infty)$, por lo que se procede a encontrar los ceros de$r$. Resolver$90 e^{-0.1 t} - 30=0$ resulta en$e^{-0.1t} = \frac{1}{3}$ lo$t = -10\ln\left(\frac{1}{3}\right)$ que, tras una rápida aplicación de la Regla del Poder nos deja con$t = 10 \ln(3)$. Si queremos evitar usar la calculadora para elegir valores de prueba, notamos que desde$1 < 3$,$0 = \ln(1) < \ln(3)$ así que$10\ln(3) > 0$. Entonces elegimos$t = 0$ como valor de prueba en$[0, 10 \ln(3))$. Ya que$3 < 4$$10 \ln(3) < 10 \ln(4)$,, entonces esta última es nuestra elección de un valor de prueba para el intervalo$(10 \ln(3), \infty)$. Nuestro diagrama de signos está abajo, y junto a él está nuestra gráfica$y=T(t)$ del Ejemplo 6.1.2 con la línea horizontal$y = 100$.

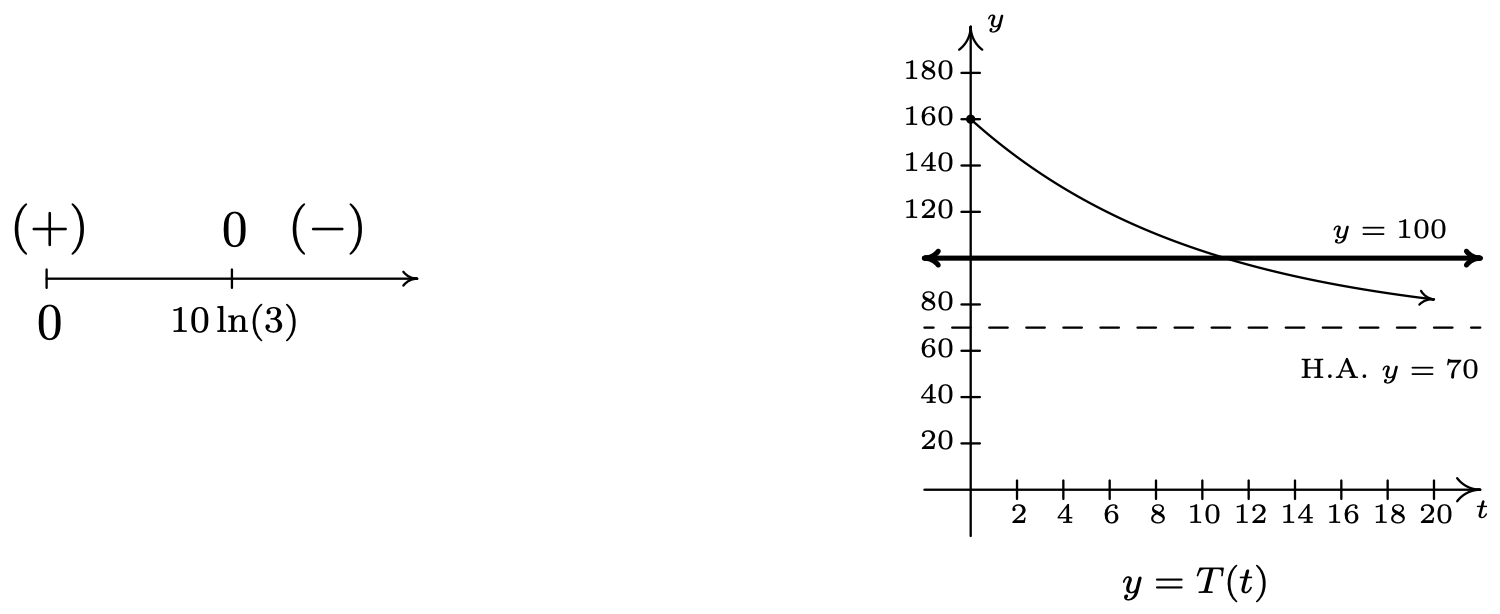
$Screen Shot 2022-04-18 en 1.30.29 AM.png$

Para interpretar lo que esto significa en el contexto del mundo real, necesitamos una aproximación razonable del número$10 \ln(3) \approx 10.986$. Esto significa que el café tarda aproximadamente$11$ minutos en enfriarse$100^{\circ}\mbox{F}$. Hasta entonces, el café está más caliente que eso. ⁸

Cerramos esta sección encontrando la inversa de una función que es una composición de una función racional con una función exponencial.

Ejemplo 6.3.4

La función$f(x) = \dfrac{5e^{x}}{e^{x}+1}$ es uno a uno. Encuentre una fórmula para$f^{-1}(x)$ y verifique su respuesta gráficamente usando su calculadora.

Solución

Comenzamos por escribir$y=f(x)$, e intercambiamos los roles de$x$ y$y$. Para resolver$y$, primero limpiamos los denominadores y luego aislamos la función exponencial.

\[\begin{array}{rclr} y & = & \dfrac{5e^{x}}{e^{x}+1} & \\ [12pt] x & = & \dfrac{5e^{y}}{e^{y}+1} & \mbox{Switch $x$ and $y$} \\ [12pt] x \left(e^{y}+1\right) & = & 5e^{y} & \\[4pt] x e^{y}+x & = & 5e^{y} & \\[4pt] x & = & 5e^{y} - x e^{y} & \\[4pt] x & = & e^{y}(5 - x) & \\[4pt] e^{y}& = & \dfrac{x}{5-x} & \\[12pt] \ln\left(e^{y}\right) & = & \ln\left(\dfrac{x}{5-x}\right) & \\[12pt] y & = & \ln\left(\dfrac{x}{5-x}\right) & \\ \end{array}\nonumber\]

Nosotros reclamamos$f^{-1}(x) = \ln\left(\frac{x}{5-x}\right)$. Para verificar esto analíticamente, necesitaríamos verificar las composiciones$\left(f^{-1} \circ f\right)(x) = x$ para todos$x$ en el dominio de$f$ y eso$\left(f \circ f^{-1}\right)(x) = x$ para todos$x$ en el dominio de$f^{-1}$. Esto se lo dejamos al lector. Para verificar nuestra solución gráficamente, graficamos$y = f(x) = \frac{5e^{x}}{e^{x}+1}$ y$y = g(x) = \ln\left(\frac{x}{5-x}\right)$ en el mismo conjunto de ejes y observamos la simetría alrededor de la línea$y=x$. Tenga en cuenta que el dominio de$f$ es el rango de$g$ y viceversa.

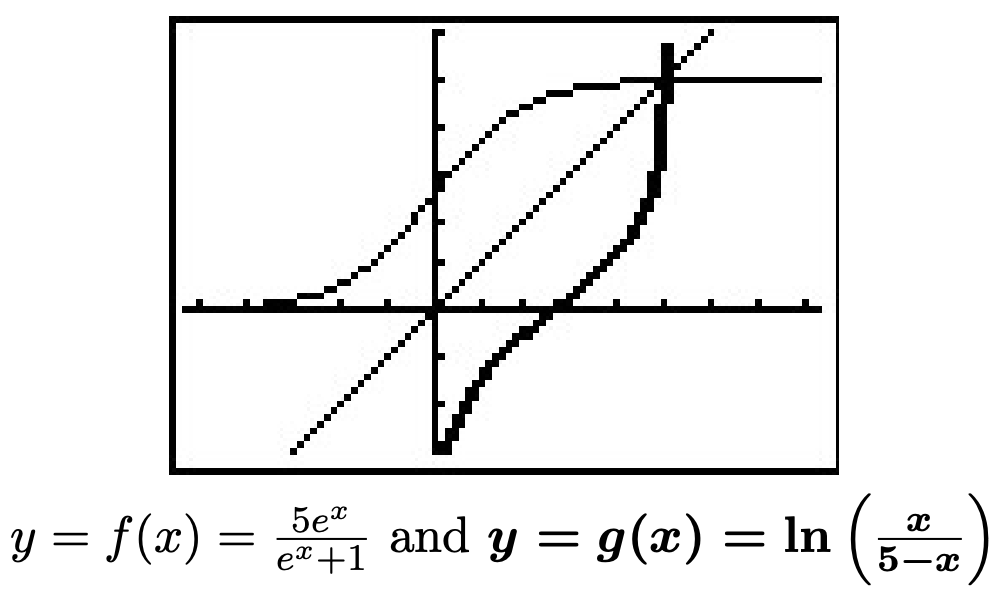
Screen Shot 2022-04-18 en 1.44.42 AM.png

6.3.1. Ejercicios

En los Ejercicios 1 - 33, resuelve la ecuación analíticamente.

$2^{4x} = 8$[expeqnfirst]
$3^{(x - 1)} = 27$
$5^{2x-1} = 125$
$4^{2x} = \frac{1}{2}$
$8^{x} = \frac{1}{128}$
$2^{(x^{3} - x)} = 1$
$3^{7x} = 81^{4-2x}$
$9 \cdot 3^{7x} = \left(\frac{1}{9}\right)^{2x}$
$3^{2x} = 5$
$5^{-x} = 2$
$5^{x} = -2$
$3^{(x - 1)} = 29$
$(1.005)^{12x} = 3$
$e^{-5730k} = \frac{1}{2}$
$2000e^{0.1t} = 4000$
$500\left(1-e^{2x}\right) = 250$
$70 + 90e^{-0.1t} = 75$
$30-6e^{-0.1x}=20$
$\dfrac{100e^{x}}{e^{x}+2}=50$
$\dfrac{5000}{1+2e^{-3t}}=2500$
$\dfrac{150}{1 + 29e^{-0.8t}} = 75$
$25\left(\frac{4}{5}\right)^{x} = 10$
$e^{2x} = 2e^{x}$
$7e^{2x} = 28e^{-6x}$
$3^{(x - 1)} = 2^{x}$
$3^{(x - 1)} = \left(\frac{1}{2}\right)^{(x + 5)}$
$7^{3+7x} = 3^{4-2x}$
$e^{2x} - 3e^{x}-10=0$
$e^{2x} = e^{x}+6$
$4^{x} + 2^{x} = 12$
$e^{x}-3e^{-x}=2$
$e^{x}+15e^{-x}=8$
$3^{x}+25\cdot3^{-x}=10$[expeqnlast]

En los Ejercicios 34 - 39, resolver la desigualdad analíticamente.

$e^{x} > 53$[expineqfirst]
$1000\left(1.005\right)^{12t} \geq 3000$
$2^{(x^{3} - x)} < 1$
$25\left(\frac{4}{5}\right)^{x} \geq 10$
$\dfrac{150}{1 + 29e^{-0.8t}} \leq 130$
$\vphantom{\dfrac{150}{1 + 29e^{-0.8t}}} 70 + 90e^{-0.1t} \leq 75$[expineqlast]

En Ejercicios 40 - 45, usa tu calculadora para ayudarte a resolver la ecuación o desigualdad.

$2^{x} = x^2$[calcexpineqfirst]
$e^{x} = \ln(x) + 5$
$e^{\sqrt{x}} = x + 1$
$e^{-x} - xe^{-x} \geq 0$
$3^{(x - 1)} < 2^{x}$
$e^{x} < x^{3} - x$[calcexpineqlast]
[onetoonelogexercise] Ya que$f(x) = \ln(x)$ es una función estrictamente creciente, si$0 < a < b$ entonces$\ln(a) < \ln(b)$. Usa este hecho para resolver la desigualdad$e^{(3x - 1)} > 6$ sin un diagrama de signos. Utiliza esta técnica para resolver las desigualdades en los Ejercicios 34 - 39. (NOTA: ¡Aísle primero la función exponencial!)
[hiperbolicsina] Calcular la inversa de$f(x) = \dfrac{e^{x} - e^{-x}}{2}$. Indicar el dominio y el rango de ambos$f$ y$f^{-1}$.
En el Ejemplo 6.3.4, encontramos que la inversa de$f(x) = \dfrac{5e^{x}}{e^{x}+1}$ era$f^{-1}(x) = \ln\left(\dfrac{x}{5-x}\right)$ pero dejamos algunos cabos sueltos para que los amarraras.
1. Demostrar eso$\left(f^{-1} \circ f\right)(x) = x$ para todos$x$ en el dominio de$f$ y eso$\left(f \circ f^{-1}\right)(x) = x$ para todos$x$ en el dominio de$f^{-1}$.
2. Encuentra el rango de$f$ encontrando el dominio de$f^{-1}$.
3. Dejar$g(x) = \dfrac{5x}{x+1}$ y$h(x) = e^{x}$. Demuestre eso$f = g \circ h$ y aquello$(g \circ h)^{-1} = h^{-1} \circ g^{-1}$. (Sabemos que esto es cierto en general por el Ejercicio 31 en la Sección 5.2, pero es agradable ver un ejemplo específico de la propiedad.)
Con la ayuda de tus compañeros, resuelve la desigualdad$e^{x} > x^{n}$ para una variedad de números naturales$n$. ¿Qué conjeturas sobre la “velocidad” a la que$f(x) = e^{x}$ crece frente a cualquier polinomio?

6.3.2. RESPUESTAS

$x = \frac{3}{4}$
$x = 4$
$x=2$
$x = -\frac{1}{4}$
$x = -\frac{7}{3}$
$x = -1, \, 0, \, 1$
$x = \frac{16}{15}$
$x=-\frac{2}{11}$
$x = \frac{\ln(5)}{2\ln(3)}$
$x = -\frac{\ln(2)}{\ln(5)}$
Sin solución.
$x = \frac{\ln(29) + \ln(3)}{\ln(3)}$
$x = \frac{\ln(3)}{12\ln(1.005)}$
$k = \frac{\ln\left(\frac{1}{2}\right)}{-5730} = \frac{\ln(2)}{5730}$
$t=\frac{\ln(2)}{0.1} = 10\ln(2)$
$x=\frac{1}{2}\ln\left(\frac{1}{2}\right) = -\frac{1}{2}\ln(2)$
$t = \frac{\ln\left(\frac{1}{18}\right)}{-0.1} =10 \ln(18)$
$x=-10\ln\left(\frac{5}{3}\right) = 10\ln\left(\frac{3}{5}\right)$
$x=\ln(2)$
$t=\frac{1}{3}\ln(2)$
$t = \frac{\ln\left(\frac{1}{29}\right)}{-0.8} = \frac{5}{4}\ln(29)$
$x = \frac{\ln\left(\frac{2}{5}\right)}{\ln\left(\frac{4}{5}\right)} = \frac{\ln(2)-\ln(5)}{\ln(4) - \ln(5)}$
$x = \ln(2)$
$x = -\frac{1}{8} \ln\left(\frac{1}{4} \right) = \frac{1}{4}\ln(2)$
$x = \frac{\ln(3)}{\ln(3) - \ln(2)}$
$x = \frac{\ln(3) + 5\ln\left(\frac{1}{2}\right)}{\ln(3) - \ln\left(\frac{1}{2}\right)} = \frac{\ln(3)-5\ln(2)}{\ln(3)+\ln(2)}$
$x = \frac{4 \ln(3) - 3 \ln(7)}{7 \ln(7) + 2 \ln(3)}$
$x=\ln(5)$
$x=\ln(3)$
$x=\frac{\ln(3)}{\ln(2)}$
$x=\ln(3)$
$x=\ln(3)$,$\ln(5)$
$x=\frac{\ln(5)}{\ln(3)}$
$(\ln(53), \infty)$
$\left[\frac{\ln(3)}{12\ln(1.005)}, \infty\right)$
$(-\infty, -1) \cup (0, 1)$
$\left(-\infty, \frac{\ln\left(\frac{2}{5}\right)}{\ln\left(\frac{4}{5}\right)} \right] = \left(-\infty, \frac{\ln(2)-\ln(5)}{\ln(4)-\ln(5)} \right]$
$\left(-\infty, \frac{\ln\left(\frac{2}{377}\right)}{-0.8} \right] = \left(-\infty, \frac{5}{4}\ln\left(\frac{377}{2}\right) \right]$
$\left[\frac{\ln\left(\frac{1}{18}\right)}{-0.1}, \infty\right) = [10\ln(18), \infty)$
$x \approx -0.76666, \, x = 2, \, x = 4$
$x \approx 0.01866, \, x \approx 1.7115$
$x = 0$
$(-\infty, 1]$
$\approx (-\infty, 2.7095)$
$\approx (2.3217, 4.3717)$
$x > \frac{1}{3}(\ln(6) + 1)$
$f^{-1} = \ln\left(x + \sqrt{x^{2} + 1}\right)$. Ambos$f$ y$f^{-1}$ tienen dominio$(-\infty, \infty)$ y rango$(-\infty, \infty)$.

Referencia

¹ Se pueden utilizar troncos naturales o troncos comunes. Elegimos troncos naturales. (En Cálculo, aprenderás que estos son los más 'matemáticos' de los logaritmos).

² Esta es también la parte 'si' de la declaración$\log _{b}(u)=\log _{b}(w)$ si y sólo si$u = w$ en el Teorema 6.4.

³ Por favor resista la tentación de dividir ambos lados por 'ln' en lugar de ln (2). Al igual que no tendría sentido dividir ambos lados por el símbolo de raíz cuadrada$‘\sqrt ’$ al resolver$x \sqrt{2}=5$, no tiene sentido dividir por 'ln'.

⁴ Esto se debe a que la base de$\ln (x)$ es$e>1$. Si la base$b$ estuviera en el intervalo$0<b<1$, entonces$\log _{b}(x)$ disminuiría.

⁵ Podríamos, por supuesto, usar la calculadora, pero ¿qué divertido sería eso?

⁶ En este punto se puede utilizar una calculadora. Como es habitual, procedemos sin disculpas, con el método analítico.

⁷ Nota:$\ln (2) \approx 0.693$.

⁸ Los críticos pueden señalar que como necesitábamos usar la calculadora para interpretar nuestra respuesta de todos modos, ¿por qué no usarla antes para simplificar los cálculos? Es una pregunta justa a la que respondemos injustamente: es nuestro libro