6.5: Aplicaciones de funciones exponenciales y logarítmicas

Como mencionamos en la Sección 6.1, las funciones exponenciales y logarítmicas se utilizan para modelar una amplia variedad de comportamientos en el mundo real. En los ejemplos que siguen, tenga en cuenta que si bien las aplicaciones se extraen de muchas disciplinas diferentes, las matemáticas siguen siendo esencialmente las mismas. Debido a la naturaleza aplicada de los problemas que examinaremos en esta sección, la calculadora se utiliza a menudo para expresar nuestras respuestas como aproximaciones decimales.

6.5.1. Aplicaciones de Funciones Exponenciales

Quizás la aplicación más conocida de las funciones exponenciales proviene del mundo financiero. Supongamos\(\$ 100\) que tienes que invertir en tu banco local y ellos están ofreciendo una tasa de interés porcentual\(5 \, \%\) anual enorme. Esto significa que después de un año, el banco te pagará\(5 \%\) de eso\(\$100\), o\(\$ 100(0.05) =\$ 5\) en intereses, así que ahora tienes\(\$105\). ¹ Esto está de acuerdo con la fórmula para el interés simple con el que sin duda te has topado en algún momento antes.

Ecuación 6.1. Interés Sencillo

El monto de intereses\(I\) devengados a tasa anual\(r\) sobre ^una inversión a\(P\) después de\(t\) años es\[I = Prt\nonumber\] El monto\(A\) en la cuenta después de\(t\) años es dado por\[A = P + I = P + Prt = P(1+rt)\nonumber\]

---

^a Llamado el director

Supongamos, sin embargo, que seis meses en el año, se oye hablar de un mejor trato en un banco rival. ² Naturalmente, retiras tu dinero e intentas invertirlo a la tasa más alta ahí. Ya que seis meses es medio año, ese inicial\(\$100\) rinde\(\$100(0.05)\left(\frac{1}{2}\right) = \$ 2.50\) en intereses. Te\(\$102.50\) quitas con el competidor y descubres que esas restricciones que puedan aplicarse realmente te aplican, y regresas a tu banco que felizmente acepta tu\(\$102.50\) por los seis meses restantes del año. Para su sorpresa y deleite, al final del año se lee su declaración\(\$105.06\), no\(\$105\) como había esperado. ³ ¿De dónde salieron esos seis centavos extra? Durante los primeros seis meses del año, se ganaron intereses sobre el principal original de\(\$100\), pero durante el segundo seis meses, se ganaron intereses sobre\(\$102.50\), es decir, usted ganó intereses sobre sus intereses. Este es el concepto básico detrás del interés compuesto. En la discusión anterior, diríamos que el interés se agravó dos veces, o semestralmente. ⁴ Si se puede ganar más dinero ganando intereses sobre intereses ya devengados, una pregunta natural es qué sucede si el interés se agrava con más frecuencia, digamos\(4\) veces al año, que es cada tres meses, o 'trimestralmente'. En este caso, el dinero está en la cuenta por tres meses, o\(\frac{1}{4}\) de un año, a la vez. Después del primer trimestre, tenemos\(A = P(1+rt) = \$100 \left(1 + 0.05 \cdot \frac{1}{4} \right) = \$101.25\). Ahora invertimos el\(\$101.25\) para los próximos tres meses y encontramos que al final del segundo trimestre, tenemos\(A = \$101.25 \left(1 + 0.05 \cdot \frac{1}{4} \right)\approx \$102.51\). Continuando de esta manera, el saldo al final del tercer trimestre es\(\$103.79\), y, por fin, obtenemos\(\$105.08\). Los dos centavos extra apenas parecen valer la pena, pero vemos que de hecho obtenemos más dinero cuanto más a menudo nos compongamos. Para desarrollar una fórmula para este fenómeno, necesitamos hacer algunos cálculos abstractos. Supongamos que deseamos invertir nuestro capital\(P\) a una tasa anual\(r\) y componer los\(n\) tiempos de interés por año. Esto significa que el dinero se asienta en la cuenta\(\frac{1}{n}^{\mbox{\tiny th}}\) de un año entre compuestos. Dejar\(A_{k}\) denotar la cantidad en la cuenta después de la\(k^{\mbox{\tiny th}}\) capitalización. Entonces\(A_{1} = P\left(1 + r\left(\frac{1}{n}\right)\right)\) lo que simplifica a\(A_{1} = P \left(1 + \frac{r}{n}\right)\). Después de la segunda composición, usamos\(A_{1}\) como nuestro nuevo director y obtenemos\(A_{2} = A_{1} \left(1 + \frac{r}{n}\right) = \left[P \left(1 + \frac{r}{n}\right)\right]\left(1 + \frac{r}{n}\right) = P \left(1 + \frac{r}{n}\right)^2\). Continuando con esta moda, obtenemos\(A_{3} =P \left(1 + \frac{r}{n}\right)^3\),\(A_{4} =P \left(1 + \frac{r}{n}\right)^4\), y así sucesivamente, así que\(A_{k} = P \left(1 + \frac{r}{n}\right)^k\). Ya que componemos los\(n\) tiempos de interés por año, después de\(t\) años, tenemos\(nt\) compuestos. Acabamos de derivar la fórmula general para el interés compuesto a continuación.

Ecuación 6.2. Interés Compuesto

Si un principal inicial\(P\) se invierte a una tasa anual\(r\) y el interés se compone\(n\) veces al año, el monto\(A\) en la cuenta después de\(t\) años es\[A(t) = P \left(1 + \frac{r}{n}\right)^{nt}\nonumber\]

Si tomamos\(P = 100\),, y\(r = 0.05\)\(n = 4\), la Ecuación 6.2 se convierte en la\(A(t) = 100\left(1+ \frac{0.05}{4}\right)^{4t}\) que se reduce a\(A(t) = 100(1.0125)^{4t}\). Para verificar esta nueva fórmula con nuestros cálculos anteriores, encontramos\(A\left(\frac{1}{4}\right) = 100(1.0125)^{4 \left(\frac{1}{4}\right)} = 101.25\),\(A\left(\frac{1}{2}\right) \approx \$102.51\),\(A\left(\frac{3}{4}\right) \approx \$103.79\), y\(A(1) \approx \$105.08\).

Ejemplo 6.5.1

Supongamos que\(\$2000\) se invierte en una cuenta que ofrece\(7.125 \%\) compuestos mensuales.

1. Expresar el monto\(A\) en la cuenta en función del plazo de la inversión\(t\) en años.
2. ¿Cuánto hay en la cuenta después de\(5\) años?
3. ¿Cuánto tiempo tardará en duplicarse la inversión inicial?
4. Encontrar e interpretar la tasa promedio de cambio ⁵ del monto en la cuenta desde el final del cuarto año hasta el final del quinto año, y desde el final del trigésimo cuarto año hasta el final del trigésimo quinto año.

Solución.

1. Sustituir\(P = 2000\),\(r = 0.07125\), y\(n = 12\) (ya que el interés se compone mensualmente) en la Ecuación 6.2 rendimientos\(A(t) = 2000\left(1 + \frac{0.07125}{12}\right)^{12t}=2000 (1.0059375)^{12t}\).
2. Ya que\(t\) representa la duración de la inversión en años, sustituimos\(t=5\) en\(A(t)\) para encontrar\(A(5) = 2000 (1.0059375)^{12(5)} \approx 2852.92\). Después de\(5\) años, tenemos aproximadamente\(\$2852.92\).
3. Nuestra inversión inicial es\(\$2000\), así que para encontrar el tiempo que tarda esto en duplicarse, necesitamos encontrar\(t\) cuándo\(A(t) = 4000\). Obtenemos\(2000 (1.0059375)^{12t}=4000\), o\((1.0059375)^{12t}=2\). Tomando troncos naturales como en la Sección 6.3, obtenemos\(t = \frac{\ln(2)}{12 \ln(1.0059375)} \approx 9.75\). De ahí que tarde aproximadamente\(9\) años\(9\) meses para que la inversión se duplique.
4. Para encontrar la tasa promedio de cambio de\(A\) desde el final del cuarto año hasta el final del quinto año, calculamos\(\frac{A(5)-A(4)}{5-4} \approx 195.63\). De igual manera, la tasa promedio de cambio de\(A\) desde el cierre del trigésimo cuarto año hasta el final del trigésimo quinto año es\(\frac{A(35)-A(34)}{35-34} \approx 1648.21\). Esto significa que el valor de la inversión está aumentando a un ritmo aproximado\(\$195.63\) anual entre el final del cuarto y quinto año, mientras que esa tasa salta a\(\$1648.21\) por año entre el final del trigésimo cuarto y trigésimo quinto años. Entonces, no sólo es cierto que cuanto más esperes, cuanto más dinero tengas, sino también cuanto más esperes, más rápido aumenta el dinero. ⁶

Hemos observado que cuantas más veces compongas los intereses por año, más dinero ganarás en un año. Vamos a llevar esta noción al límite. ⁷ Considerar una inversión de\(\$ 1\) invertido a\(100 \%\) intereses por\(1\) año compuesto\(n\) veces al año. La ecuación 6.2 nos dice que la cantidad de dinero en la cuenta tras\(1\) año es\(A = \left(1+\frac{1}{n}\right)^{n}\). A continuación se muestra una tabla de valores relativos\(n\) y\(A\).

\[\begin{array}{|r||r|} \hline n & A \\ \hline 1 & 2 \\ \hline 2 & 2.25 \\ \hline 4 & \approx 2.4414 \\ \hline 12 & \approx 2.6130 \\ \hline 360 & \approx 2.7145 \\ \hline 1000 & \approx 2.7169 \\ \hline 10000 & \approx 2.7181 \\ \hline 100000 & \approx 2.7182 \\ \hline \end{array}\nonumber\]

Según lo prometido, cuantos más compuestos al año, más dinero haya en la cuenta, pero también observamos que el incremento de dinero está disminuyendo mucho. Estamos presenciando un 'tira y rayo' matemático. Si bien estamos componiendo más veces al año y, por lo tanto, nos interesamos más a menudo en nuestro interés, la cantidad de tiempo entre compuestos es cada vez más pequeña, por lo que hay menos tiempo para acumular interés adicional. Con Cálculo, podemos mostrar ⁸ que como\(n \rightarrow \infty\),\(A = \left(1+\frac{1}{n}\right)^{n} \rightarrow e\), donde\(e\) está la base natural presentada por primera vez en la Sección 6.1. Llevar el número de compuestos por año al infinito da como resultado lo que se llama interés continuamente compuesto.

Teorema 6.8.

Si inviertes\(\$1\) a\(100 \%\) intereses compuestos continuamente, entonces tendrás\(\$ e\) al final de un año.

Usando esta definición de\(e\) y un poco de Cálculo, podemos tomar la Ecuación 6.2 y producir una fórmula para el interés continuamente compuesto.

Ecuación 6.3. Interés continuamente compuesto

Si un principal inicial\(P\) se invierte a una tasa anual\(r\) y el interés se compone continuamente, el monto\(A\) en la cuenta después de\(t\) años es\[A(t) = P e^{rt}\nonumber\]

Si tomamos el escenario del Ejemplo 6.5.1 y comparamos la composición mensual con la composición continua a lo largo de los\(35\) años, encontramos que la capitalización mensual rinde\(A(35) = 2000 (1.0059375)^{12(35)}\) que es aproximadamente\(\$ 24,\!035.28\), mientras que la composición continua da\(A(35) = 2000e^{0.07125 (35)}\) cuál es aproximadamente\(\$ 24,\!213.18\) - una diferencia de menos de\(1 \%\).

Las ecuaciones 6.2 y 6.3 utilizan funciones exponenciales para describir el crecimiento de una inversión. Curiosamente, los mismos principios que rigen el interés compuesto también se utilizan para modelar el crecimiento a corto plazo de las poblaciones. En Biología, La Ley del Crecimiento Desinhibido establece como premisa que la velocidad instantánea a la que una población aumenta en cualquier momento es directamente proporcional a la población en ese momento. ⁹ En otras palabras, cuantos más organismos haya en un momento dado, más rápido se reproducen. La formulación de la ley como se establece da como resultado una ecuación diferencial, que requiere de Cálculo para resolver. Su solución se expone a continuación.

Ecuación 6.4. Crecimiento desinhibido

Si una población aumenta según La Ley del Crecimiento Desinhibido, el número de organismos\(N\) en el momento\(t\) viene dado por la fórmula\[N(t) = N_0e^{kt},\nonumber\] donde\(N(0) = N_0\) (léase '\(N\)nought') es el número inicial de organismos y\(k>0\) es la constante de proporcionalidad que satisface la ecuación

\[\left(\mbox{instantaneous rate of change of $N(t)$ at time $t$}\right) = k \, N(t)\nonumber\]

Vale la pena tomarse un tiempo para comparar las Ecuaciones 6.3 y 6.4. En la Ecuación 6.3, usamos\(P\) para denotar la inversión inicial; en la Ecuación 6.4, usamos\(N_0\) para denotar la población inicial. En la Ecuación 6.3,\(r\) denota la tasa de interés anual, por lo que no debería ser demasiado sorprendente que la\(k\) de la Ecuación 6.4 corresponda también a una tasa de crecimiento. Si bien las Ecuaciones 6.3 y 6.4 se ven completamente diferentes, ambas representan el mismo concepto matemático.

Ejemplo 6.5.2

Para realizar investigaciones de artrosclerosis, las células epiteliales se cosechan del tejido umbilical desechado y se cultivan en el laboratorio. Un técnico observa que un cultivo de doce mil células crece a cinco millones de células en una semana. Suponiendo que las células sigan La Ley del Crecimiento Desinhibido, encuentre una fórmula para el número de células,\(N\), en miles, después de\(t\) días.

Solución

Empezamos con\(N(t) = N_0e^{kt}\). Ya que\(N\) es dar el número de celdas en miles, tenemos\(N_0 = 12\), así\(N(t) = 12e^{kt}\). Para completar la fórmula, necesitamos determinar la tasa de crecimiento\(k\). Sabemos que después de una semana, el número de células ha crecido hasta los cinco millones. Ya que\(t\) mide días y las unidades de\(N\) son en miles, esto se traduce matemáticamente a\(N(7) = 5000\). Obtenemos la ecuación\(12e^{7k} = 5000\) que da\(k = \frac{1}{7} \ln\left(\frac{1250}{3}\right)\). De ahí,\(N(t) = 12e^{ \frac{t}{7} \ln\left(\frac{1250}{3}\right)}\). Por supuesto, en la práctica, nos aproximaríamos\(k\) a alguna precisión deseada, digamos\(k \approx 0.8618\), que podemos interpretar como una tasa de crecimiento\(86.18 \%\) diario para las células.

Mientras que las Ecuaciones 6.3 y 6.4 modelan el crecimiento de las cantidades, podemos usar ecuaciones como ellas para describir la disminución de cantidades. Un ejemplo que ya hemos visto es Ejemplo 6.1.1 en la Sección 6.1. Ahí, el valor de un automóvil disminuyó de su precio de compra de\(\$25,\!000\) a nada en absoluto. Otro fenómeno del mundo real que sigue su ejemplo es la desintegración radiactiva. Hay elementos que son inestables y emiten energía de manera espontánea. Al hacerlo, la cantidad del elemento en sí disminuye. La suposición detrás de este modelo es que la tasa de decaimiento de un elemento en un momento determinado es directamente proporcional a la cantidad del elemento presente en ese momento. En otras palabras, cuanto más elemento haya, más rápido decae el elemento. Este es precisamente el mismo tipo de hipótesis que impulsa La Ley del Crecimiento Desinhibido, y como tal, la ecuación que rige la desintegración radiactiva es inquietantemente similar a la Ecuación 6.4 con la excepción de que la constante de velocidad\(k\) es negativa.

Ecuación 6.5. Desintegración radiactiva

La cantidad de un elemento radiactivo\(A\) en el tiempo\(t\) viene dada por la fórmula\[A(t) = A_0e^{kt},\nonumber\] donde\(A(0) = A_0\) es la cantidad inicial del elemento y\(k<0\) es la constante de proporcionalidad que satisface la ecuación

\[\left(\mbox{instantaneous rate of change of $A(t)$ at time $t$}\right) = k \, A(t)\nonumber\]

Ejemplo 6.5.3

El yodo-131 es un isótopo radiactivo comúnmente utilizado para ayudar a detectar qué tan bien está funcionando la tiroides. Supongamos que la decadencia del Yodo-131 sigue el modelo dado en la Ecuación 6.5, y que la semivida ¹⁰ del yodo-131 es aproximadamente de\(8\) días. Si inicialmente está presente\(5\) gramos de yodo-131, encuentre una función que dé la cantidad de yodo-131,\(A\), en gramos,\(t\) días después.

Solución

Desde que empezamos con\(5\) gramos inicialmente, la Ecuación 6.5 da\(A(t) = 5e^{kt}\). Dado que la vida media es de\(8\)\(8\) días, la mitad del yodo-131 tarda días en decairse, dejando atrás la mitad del mismo. De ahí,\(A(8) = 2.5\) lo que significa\(5e^{8k} = 2.5\). Resolviendo\(k = \frac{1}{8} \ln\left(\frac{1}{2}\right) = -\frac{\ln(2)}{8} \approx -0.08664\), obtenemos, lo que podemos interpretar como una pérdida de material a un ritmo\(8.664 \%\) diario. De ahí,\(A(t) = 5 e^{-\frac{t\ln(2)}{8}} \approx 5 e^{-0.08664t}\).

Ahora dirigimos nuestra atención a algunos modelos matemáticamente más sofisticados. Uno de esos modelos es la Ley de Enfriamiento de Newton, que encontramos por primera vez en el Ejemplo 6.1.2 de la Sección 6.1. En ese ejemplo tuvimos una taza de café enfriando de\(160^{\circ}\mbox{F}\) a temperatura ambiente\(70^{\circ}\mbox{F}\) según la fórmula\(T(t) = 70 + 90 e^{-0.1 t}\), donde\(t\) se midió en minutos. En esta situación, sabemos que el límite físico de la temperatura del café es la temperatura ambiente, ¹¹ y la ecuación diferencial que da origen a nuestra fórmula para lo\(T(t)\) toma en cuenta. Mientras que el modelo de desintegración radiactiva tuvo una tasa de desintegración en el momento\(t\) directamente proporcional a la cantidad del elemento que permaneció en el momento\(t\), la Ley de Enfriamiento de Newton establece que la velocidad de enfriamiento del café en un momento dado\(t\) es directamente proporcional a la cantidad de existe entre el café en el momento\(t\) y la temperatura ambiente, no la temperatura del café en sí. Es decir, el café se enfría más rápido cuando se sirve por primera vez, y a medida que su temperatura se acerca a la temperatura ambiente, el café se enfría cada vez más lentamente. Por supuesto, si sacamos un artículo del refrigerador y lo dejamos reposar en la cocina, la temperatura del objeto subirá a temperatura ambiente, y dado que la física detrás del calentamiento y enfriamiento es la misma, combinamos ambos casos en la siguiente ecuación.

Ecuación 6.6. Ley de Newton de Enfriamiento (Calentamiento)

La temperatura\(T\) de un objeto en el tiempo\(t\) viene dada por la fórmula\[T(t) = T_{a} + \left(T_0 - T_{a}\right) e^{-kt},\nonumber\] donde\(T(0) = T_0\) es la temperatura inicial del objeto,\(T_{a}\) es la temperatura ambiente ^a y\(k>0\) es la constante de proporcionalidad que satisface la ecuación

\[\left(\mbox{instantaneous rate of change of $T(t)$ at time $t$}\right) = k \, \left(T(t) - T_{a}\right)\nonumber\]

---

^a Es decir, la temperatura de los alrededores.

Si volvemos a examinar la situación en el Ejemplo 6.1.2 con\(T_0 = 160\),\(T_{a} = 70\), y\(k = 0.1\), obtenemos, de acuerdo con la Ecuación 6.6,\(T(t) = 70 + (160 - 70)e^{-0.1t}\) que reduce a la fórmula original dada. La constante de velocidad\(k = 0.1\) indica que el café se está enfriando a una velocidad igual a\(10 \%\) la diferencia entre la temperatura del café y su entorno. Nótese en la Ecuación 6.6 que la constante\(k\) es positiva tanto para los escenarios de enfriamiento como de calentamiento. Lo que determina si la función\(T(t)\) está aumentando o disminuyendo es si\(T_0\) (la temperatura inicial del objeto) es mayor que\(T_{a}\) (la temperatura ambiente) o viceversa, como vemos en nuestro siguiente ejemplo.

Ejemplo 6.5.4.

Un\(40^{\circ}\mbox{F}\) asado se cocina en un\(350^{\circ}\mbox{F}\) horno. Después de\(2\) horas, la temperatura del asado es\(125^{\circ}\mbox{F}\).

1. Suponiendo que la temperatura del asado siga la Ley de Calentamiento de Newton, encuentre una fórmula para la temperatura del asado\(T\) en función de su tiempo en el horno,\(t\), en horas.
2. El asado se realiza cuando alcanza la temperatura interna\(165^{\circ}\mbox{F}\). ¿Cuándo se hará el asado?

Solución.

1. La temperatura inicial del asado es\(40^{\circ}\mbox{F}\), así\(T_0 = 40\). El ambiente en el que estamos colocando el asado es el\(350^{\circ}\mbox{F}\) horno, entonces\(T_{a} = 350\). La Ley del Calentamiento de Newton nos dice\(T(t) = 350 + (40-350)e^{-kt}\), o\(T(t) = 350 - 310e^{-kt}\). Para determinar\(k\), utilizamos el hecho de que después de\(2\) horas, el asado es\(125^{\circ}\mbox{F}\), lo que significa\(T(2) = 125\). Esto da lugar a la ecuación\(350 - 310e^{-2k} = 125\) que rinde\(k = -\frac{1}{2} \ln \left( \frac{45}{62} \right) \approx 0.1602\). La función de temperatura es\[T(t) = 350 - 310 e^{\frac{t}{2} \ln \left( \frac{45}{62} \right)} \approx 350- 310 e^{-0.1602 t}.\nonumber\]
2. Para determinar cuándo está hecho el asado, establecemos\(T(t) = 165\). Esto da de\(350- 310 e^{-0.1602 t} = 165\) quién es la solución\(t = -\frac{1}{0.1602} \ln \left( \frac{37}{62} \right) \approx 3.22\). Se tarda aproximadamente\(3\) horas y\(15\) minutos en cocer completamente el asado.

Si nos hubiéramos tomado el tiempo de graficar\(y=T(t)\) en el Ejemplo 6.5.4, habríamos encontrado que la asíntota horizontal estaba\(y = 350\), que corresponde a la temperatura del horno. También podemos llegar a esta conclusión aplicando un poco de 'sentido numérico'. Como t\(\rightarrow \infty,-0.1602 t \approx \text { very big }(-)\) para que\(e^{-0.1602 t} \approx \text { very small }(+)\). Cuanto mayor sea el valor de\(t\), menor\(e^{-0.1602 t}\) se vuelve así que\(T(t) \approx 350-\text { very small }(+)\), lo que indica que la gráfica de\(y=T(t)\) se acerca a su asíntota horizontal\(y=350\) desde abajo. Físicamente, esto significa que el asado eventualmente se calentará hasta\(350^{\circ}\mbox{F}\). ¹² A la función\(T\) se le denomina a veces un modelo de crecimiento limitado, ya que la función\(T\) permanece acotada como\(t \rightarrow \infty\). Si aplicamos los principios detrás de la Ley de Enfriamiento de Newton a un ejemplo biológico, dice que la tasa de crecimiento de una población es directamente proporcional a cuánto espacio tiene para crecer la población. En otras palabras, cuanto más espacio para la expansión, más rápida será la tasa de crecimiento. El modelo de crecimiento logístico combina La Ley del Crecimiento Desinhibido con un crecimiento limitado y establece que la tasa de crecimiento de una población varía conjuntamente con la propia población así como con el espacio que tiene para crecer la población.

Ecuación 6.7. Crecimiento Logístico

Si una población se comporta de acuerdo con los supuestos de crecimiento logístico, el número de organismos\(N\) en el momento\(t\) viene dado por la ecuación\[N(t) =\dfrac{L}{1 + Ce^{-kLt}},\nonumber\] dónde\(N(0) = N_0\) está la población inicial,\(L\) es la población limitante, a\(C\) es ^una medida de cómo mucho espacio hay para crecer dada por\[C = \dfrac{L}{N_0} - 1.\nonumber\] y\(k > 0\) es la constante de proporcionalidad que satisface la ecuación

\[\left(\mbox{instantaneous rate of change of $N(t)$ at time $t$}\right) = k \, N(t) \left(L - N(t)\right)\nonumber\]

---

^a Es decir, un\(t \rightarrow \infty, N(t) \rightarrow L\)

La función logística se utiliza no sólo para modelar el crecimiento de organismos, sino que también se utiliza a menudo para modelar la propagación de enfermedades y rumores. ¹³

Ejemplo 6.5.5

El número de personas\(N\), en cientos, en un colegio comunitario local que han escuchado el rumor de 'Carl le teme a Virginia Woolf' se puede modelar usando la ecuación logística

\[N(t) = \dfrac{84}{1+2799e^{-t}},\nonumber\]

donde\(t\geq 0\) es el número de días posteriores al 1 de abril de 2009.

1. Encontrar e interpretar\(N(0)\).
2. Encontrar e interpretar el comportamiento final de\(N(t)\).
3. ¿Cuánto falta para que la\(4200\) gente haya escuchado el rumor?
4. Consulta tus respuestas a 2 y 3 usando tu calculadora.

Solución.

1. Nos encontramos\(N(0) = \frac{84}{1+2799e^{0}} = \frac{84}{2800} = \frac{3}{100}\). Ya que\(N(t)\) mide el número de personas que han escuchado el rumor en cientos,\(N(0)\) corresponde a\(3\) personas. Ya que\(t=0\) corresponde al 1 de abril de 2009, podemos concluir que ese día, la\(3\) gente ha escuchado el rumor. ¹⁴
2. Simplemente podríamos señalar que\(N(t)\) está escrito en la forma de la Ecuación 6.7, e identificar\(L = 84\). No obstante, para ver por qué es la respuesta\(84\), procedemos analíticamente. Dado que el dominio de\(N\) está restringido a\(t \geq 0\), el único comportamiento final de significación es\(t \rightarrow \infty\). Como hemos visto antes, ¹⁵ como\(t \rightarrow \infty\), tenemos\(1997 e^{-t} \rightarrow 0^{+}\) y así\(N(t) \approx \frac{84}{1+\text { very small }(+)} \approx 84\). De ahí, como\(t \rightarrow \infty\),\(N(t) \rightarrow 84\). Esto quiere decir que a medida que pasa el tiempo, se acerca el número de personas que habrán escuchado el rumor\(8400\).
3. Para saber cuánto tiempo lleva hasta que la\(4200\) gente haya escuchado el rumor, nos fijamos\(N(t) = 42\). Resolver\(\frac{84}{1+2799e^{-t}} = 42\) da\(t = \ln(2799) \approx 7.937\). Tarda alrededor de\(8\) días hasta que la\(4200\) gente haya escuchado el rumor.
4. Gráficamos\(y=N(x)\) usando la calculadora y vemos que la línea\(y=84\) es la asíntota horizontal de la gráfica, confirmando nuestra respuesta a la parte 2, y la gráfica cruza la línea\(y=42\) en\(x = \ln(2799) \approx 7.937\), lo que confirma nuestra respuesta a la parte 3.

   

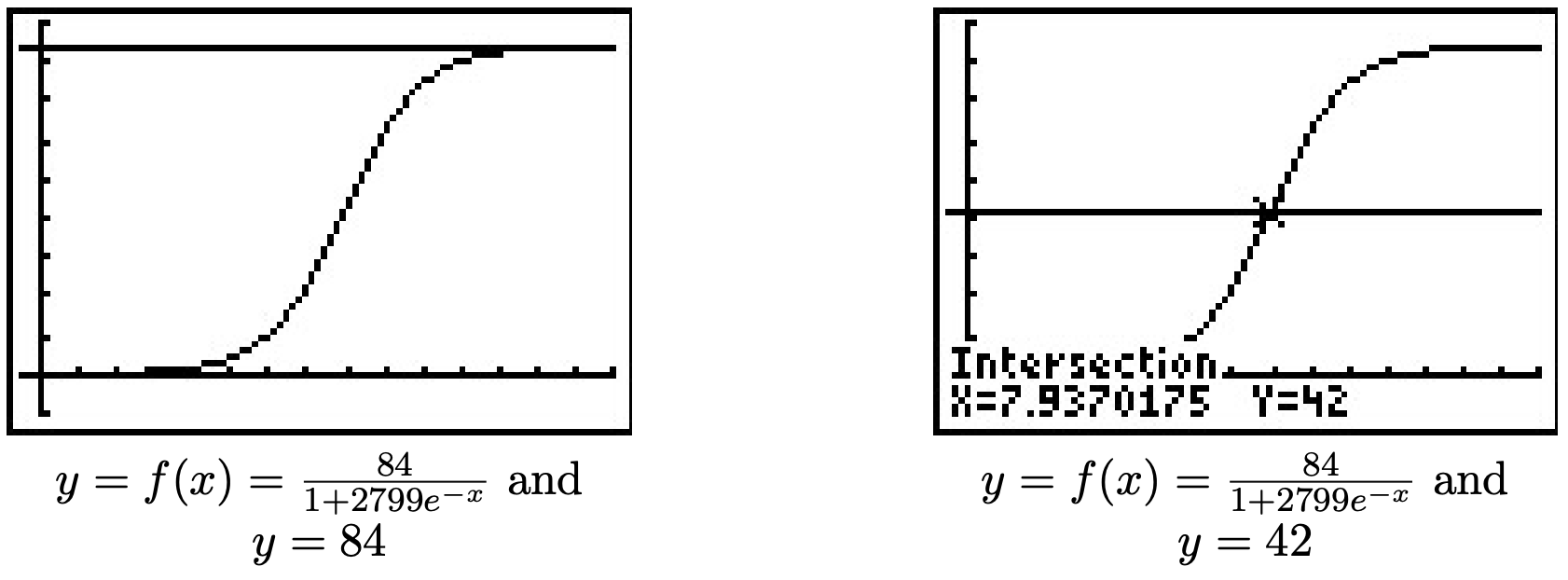
Si nos tomamos el tiempo para analizar la gráfica\(y=N(x)\) anterior, podemos ver gráficamente cómo el crecimiento logístico combina características de crecimiento desinhibido y limitado. La curva parece elevarse pronunciadamente, luego en algún momento, comienza a nivelarse. Al punto en el que esto sucede se le llama punto de inflexión o a veces se le llama el 'punto de retornos disminuidos'. En este punto, a pesar de que la función sigue aumentando, la velocidad a la que lo hace comienza a disminuir. Resulta que el punto de rendimientos decrecientes siempre ocurre a la mitad de la población limitante. (En nuestro caso, cuando\(y=42\).) Si bien estos conceptos se cuantifican con mayor precisión usando Cálculo, a continuación se muestran dos vistas de la gráfica de\(y=N(x)\), una en el intervalo\([0,8]\) y la otra en\([8,15]\). El primero se ve sorprendentemente como crecimiento desinhibido; el segundo como crecimiento limitado.

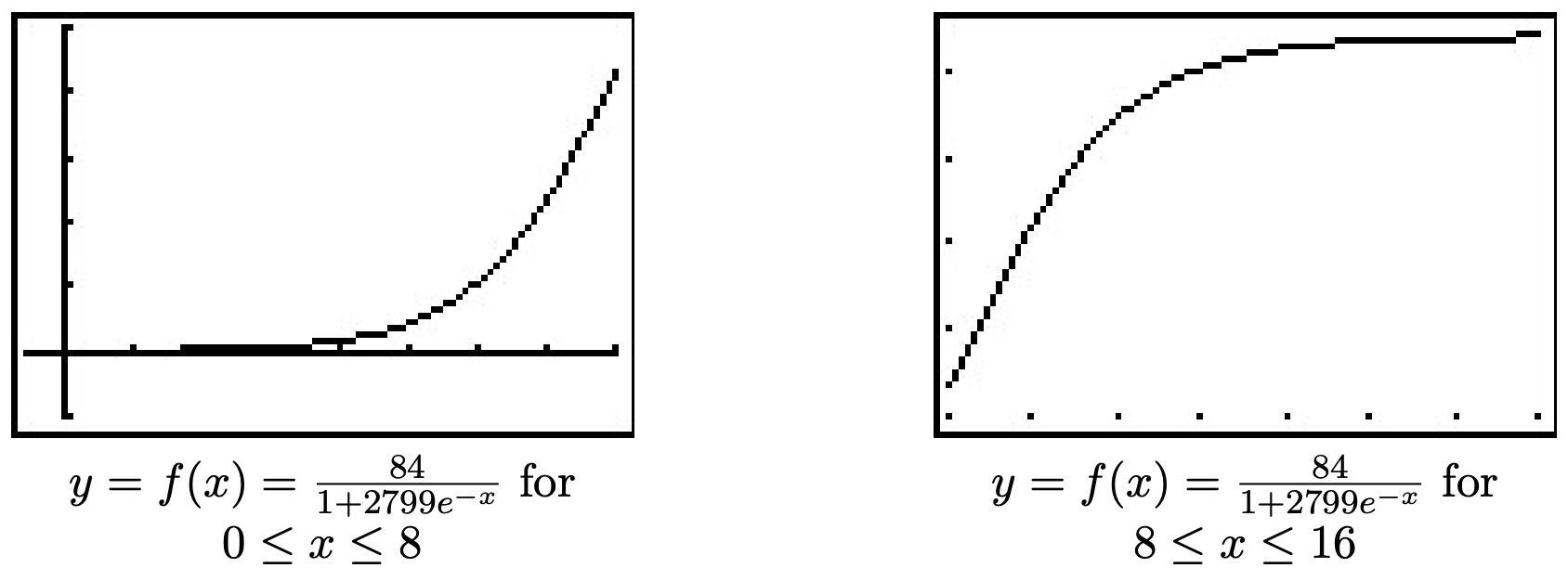
6.5.2 Aplicaciones de logaritmos

Así como muchos fenómenos físicos pueden ser modelados por funciones exponenciales, lo mismo ocurre con las funciones logarítmicas. En los Ejercicios 75, 76 y 77 de la Sección 6.1, mostramos que los logaritmos son útiles para medir las intensidades de los sismos (la escala de Richter), el sonido (decibelios) y los ácidos y bases (pH). Ahora presentamos todavía un uso diferente de la función de logaritmo básico, la fortaleza de la contraseña.

Ejemplo 6.5.6

La entropía de información\(H\), en bits, de una contraseña generada aleatoriamente que consta de\(L\) caracteres viene dada por\(H = L \log_{2}(N)\), donde\(N\) está el número de símbolos posibles para cada carácter en la contraseña. En general, cuanto mayor sea la entropía, más fuerte será la contraseña.

1. Si una contraseña de ^16\(7\) caracteres que distingue entre mayúsculas y minúsculas se compone únicamente de letras y números, busque la entropía de información asociada.
2. ¿Cuántas opciones posibles de símbolo por carácter se requieren para producir una contraseña de\(7\) carácter con una entropía de información de\(50\) bits?

Solución.

1. Hay\(26\) letras en el alfabeto,\(52\) si las letras mayúsculas y minúsculas se cuentan como diferentes. Hay\(10\) dígitos (\(0\)a través\(9\)) para un total de\(N=62\) símbolos. Dado que la contraseña debe tener\(7\) caracteres largos,\(L = 7\). Por lo tanto,\(H = 7 \log_{2}(62) = \frac{7 \ln(62)}{\ln(2)} \approx 41.68\).
2. Tenemos\(L = 7\) y\(H=50\) y tenemos que encontrar\(N\). Resolver la ecuación\(50 = 7 \log_{2}(N)\) da\(N = 2^{50/7} \approx 141.323\), así que necesitaríamos\(142\) diferentes símbolos para elegir. ¹⁷

Los sistemas químicos conocidos como soluciones tampón tienen la capacidad de ajustarse a pequeños cambios en la acidez para mantener un rango de valores de pH. Las soluciones tampón tienen una amplia variedad de aplicaciones, desde mantener una pecera saludable hasta regular los niveles de pH en sangre. Nuestro siguiente ejemplo muestra cómo el pH en una solución tampón es un poco más complicado que el pH que encontramos por primera vez en el Ejercicio 77 en la Sección 6.1.

Ejemplo 6.5.7

La sangre es una solución tampón. Cuando el dióxido de carbono es absorbido en el torrente sanguíneo produce ácido carbónico y disminuye el pH. El cuerpo compensa produciendo bicarbonato, una base débil para neutralizar parcialmente el ácido. La ecuación ¹⁸ que modela el pH de la sangre en esta situación\(x\) es\(\mbox{pH} = 6.1 + \log\left(\frac{800}{x} \right)\), donde está la presión parcial de dióxido de carbono en sangre arterial, medida en torr. Encontrar la presión parcial del dióxido de carbono en la sangre arterial si el pH es\(7.4\).

Solución

Nos fijamos\(\mbox{pH} = 7.4\) y conseguimos\(7.4 = 6.1 + \log\left(\frac{800}{x} \right)\), o\(\log\left(\frac{800}{x} \right) = 1.3\). Resolviendo, encontramos\(x = \frac{800}{10^{1.3}} \approx 40.09\). De ahí que la presión parcial del dióxido de carbono en la sangre sea de aproximadamente\(40\) torr.

Otro lugar donde se utilizan logaritmos es en el análisis de datos. Supongamos, por ejemplo, que deseamos modelar la propagación de la influenza A (H1N1), la llamada 'Gripe Porcina'. A continuación se muestran datos tomados de la Organización Mundial de la Salud (OMS) donde\(t\) representa el número de días transcurridos desde el 28 de abril de 2009, y\(N\) representa el número de casos confirmados de virus H1N1 a nivel mundial.

\[\begin{array}{|c||c|c|c|c|c|c|c|c|c|c|c|c|c|} \hline t & 1 & 2 & 3 & 4 & 5 & 6 & 7 & 8 & 9 & 10 & 11 & 12 & 13 \\ \hline N & 148 & 257 & 367 & 658 & 898 & 1085 & 1490 & 1893 & 2371 & 2500 & 3440 & 4379 & 4694 \\ \hline \end{array}\nonumber\]

\[\begin{array}{|c||c||c|c|c|c|c|c|} \hline t & 14 & 15 & 16 & 17 & 18 & 19& 20 \\ \hline N & 5251 & 5728 & 6497 & 7520 & 8451 & 8480 & 8829 \\ \hline \end{array}\nonumber\]

Hacer un diagrama de dispersión de los datos tratando\(t\) como la variable independiente y\(N\) como la variable dependiente da

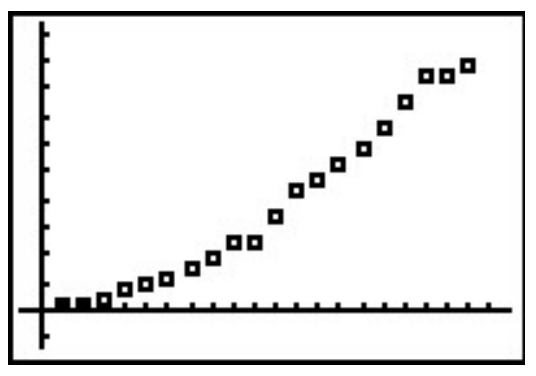
¿Qué modelos son sugeridos por la forma de los datos? Pensando en la Sección 2.5, intentamos una Regresión Cuadrática, con resultados bastante buenos.

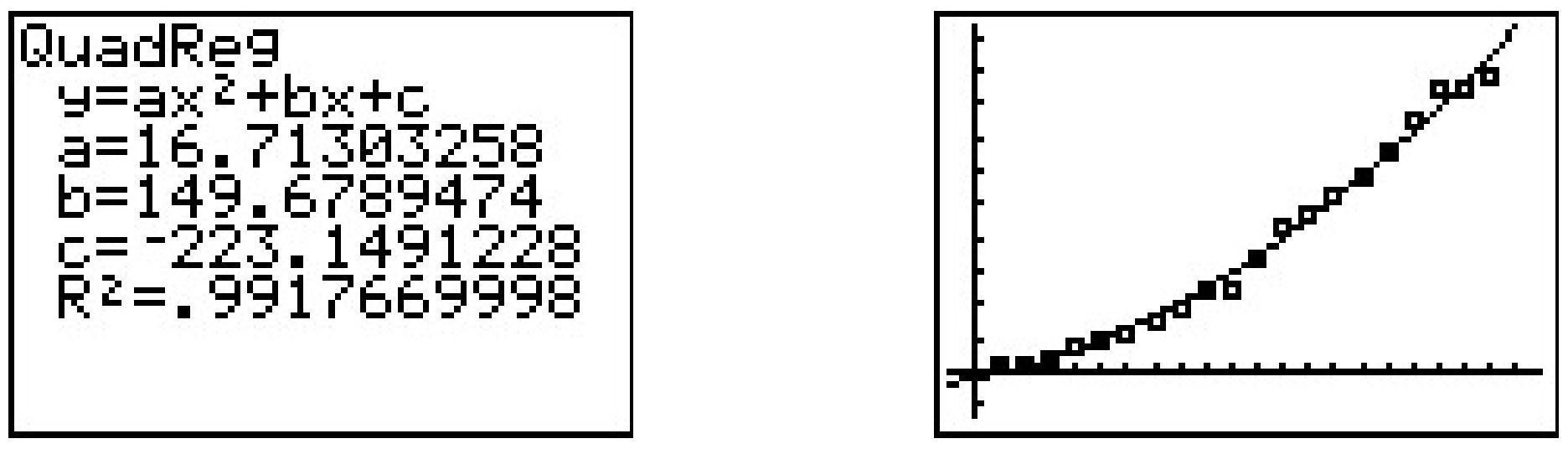
No obstante, ¿hay alguna razón científica para que los datos sean cuadráticos? ¿Hay otros modelos que se ajusten igualmente bien a los datos, o mejor? Los científicos suelen utilizar logaritmos en un intento de 'linealizar' los conjuntos de datos, es decir, transformar los conjuntos de datos para producir unos que resulten en líneas rectas. Para ver cómo esto podría funcionar, supongamos que adivinamos la relación entre\(N\) y\(t\) era algún tipo de función de poder, no necesariamente cuadrática, digamos\(N = B t^{A}\). Para tratar de determinar el\(A\) y\(B\), podemos tomar el tronco natural de ambos lados y obtener\(\ln(N) = \ln\left(B t^{A}\right)\). Usando propiedades de troncos para expandir el lado derecho de esta ecuación, obtenemos\(\ln(N) = A \ln(t) + \ln(B)\). Si establecemos\(X = \ln(t)\) y\(Y = \ln(N)\), esta ecuación se vuelve\(Y = AX + \ln(B)\). En otras palabras, tenemos una línea con pendiente\(A\) e\(Y\) -intercepción\(\ln(B)\). Entonces, en lugar de trazar\(N\) versus\(t\), trazamos\(\ln(N)\) versus\(\ln(t)\).

\[\begin{array}{|c||c|c|c|c|c|c|c|c|c|c|c|c|c|} \hline \ln(t) & 0 & 0.693 & 1.099 & 1.386& 1.609 & 1.792 & 1.946 & 2.079 & 2.197 & 2.302 & 2.398 & 2.485 & 2.565 \\ \hline \ln(N) & 4.997 & 5.549 & 5.905 & 6.489 & 6.800 & 6.989 & 7.306 & 7.546 & 7.771 & 7.824 & 8.143 & 8.385 & 8.454 \\ \hline \end{array}\nonumber\]

\[\begin{array}{|c||c||c|c|c|c|c|c|} \hline \ln(t) & 2.639 & 2.708 & 2.773 & 2.833 & 2.890 & 2.944 & 2.996 \\ \hline \ln(N) & 8.566 & 8.653 & 8.779 & 8.925 & 9.042 & 9.045 & 9.086 \\ \hline \end{array}\nonumber\]

Ejecutar una regresión lineal en los datos da

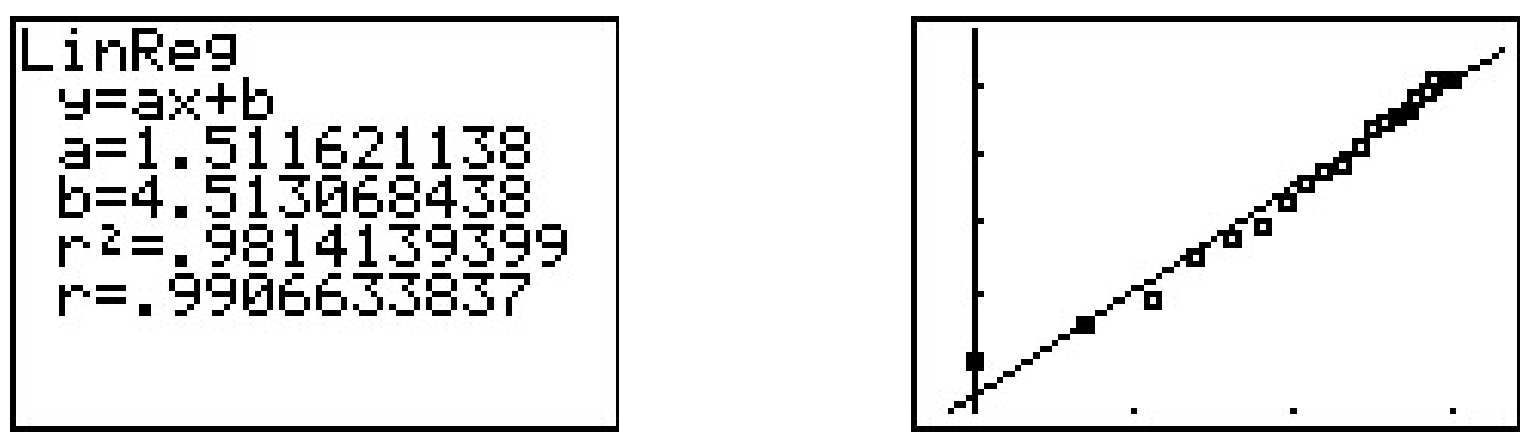
La pendiente de la línea de regresión es\(a \approx 1.512\) la que corresponde a nuestro exponente\(A\). El\(y\) -intercepto\(b \approx 4.513\) corresponde a\(\ln(B)\), así que\(B \approx 91.201\). De ahí que obtengamos el modelo\(N = 91.201 t^{1.512}\), algo de la Sección 5.3. Por supuesto, la calculadora tiene una función incorporada de 'Regresión de potencia'. Si aplicamos esto a nuestro conjunto de datos original, obtenemos el mismo modelo al que llegamos antes. ¹⁹

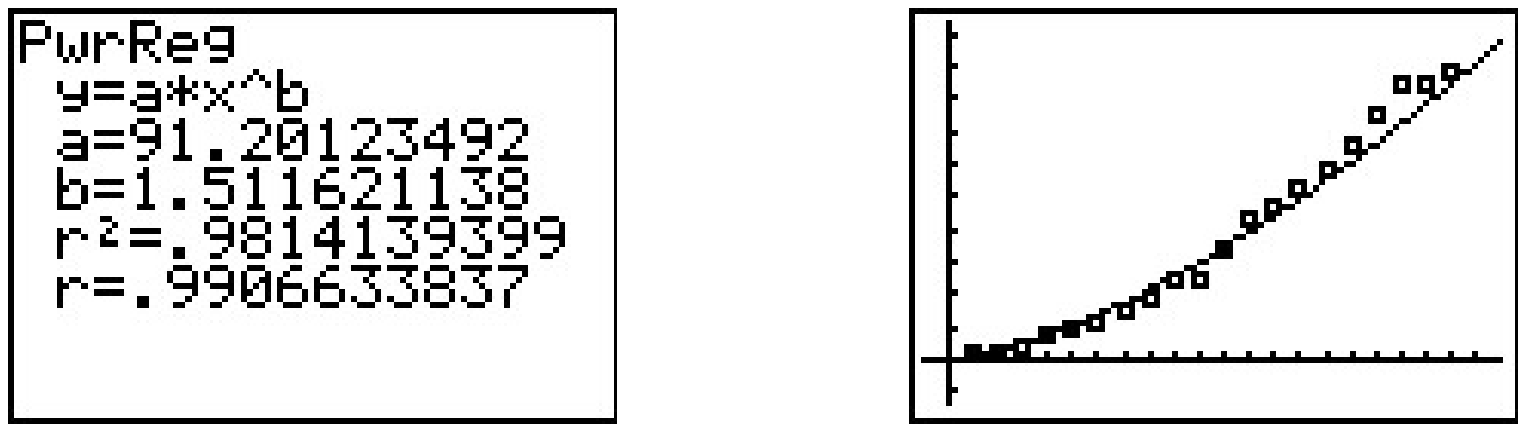
Todo esto está bien, pero el modelo cuadrático parece encajar mejor con los datos, y aún no hemos mencionado ningún principio científico que nos lleve a creer que la propagación real de la gripe sigue cualquier tipo de función de poder en absoluto. Si vamos a atacar estos datos desde una perspectiva científica, parece tener sentido que, al menos en las primeras etapas del brote, cuanta más gente tenga la gripe, más rápido se propagará, lo que nos lleva a proponer un modelo de crecimiento desinhibido. Si asumimos\(N = B e^{At}\) entonces, tomando bitácoras como antes, obtenemos\(\ln(N) = At + \ln(B)\). Si nos fijamos\(X = t\) y\(Y = \ln(N)\), entonces, una vez más, obtenemos\(Y = AX + \ln(B)\), una línea con pendiente\(A\) e\(Y\) -interceptar\(\ln(B)\). Trazar\(\ln(N)\) versus\(t\) da la siguiente regresión lineal.

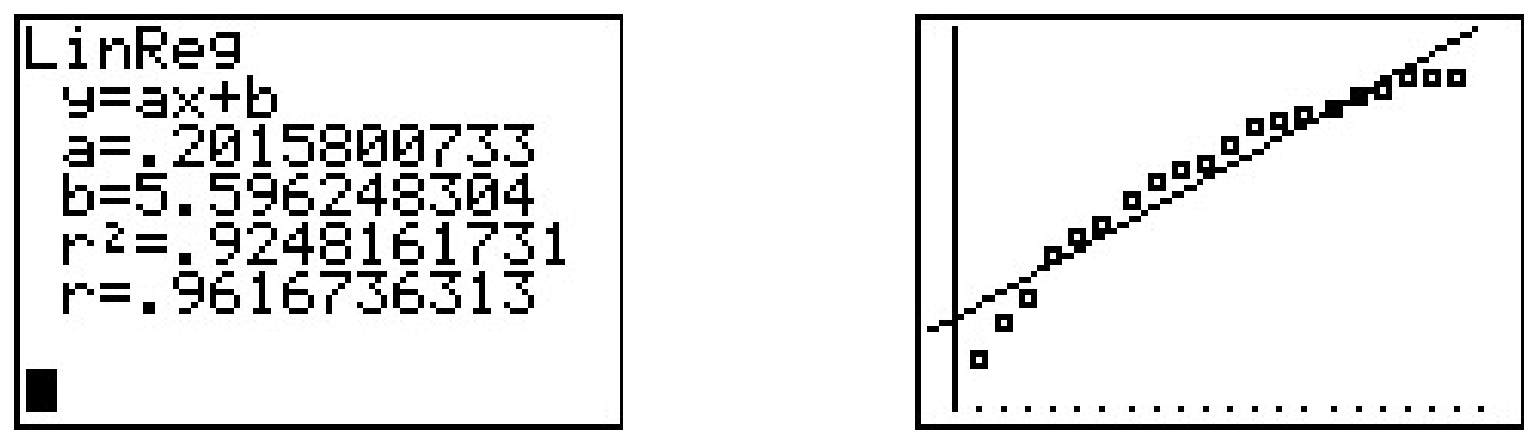
Vemos que la pendiente es\(a \approx 0.202\) y a la que corresponde\(A\) en nuestro modelo, y la\(y\) -intercepción es la\(b \approx 5.596\) que corresponde a\(\ln(B)\). Obtenemos\(B \approx 269.414\), para que nuestro modelo sea\(N = 269.414e^{0.202t}\). Por supuesto, la calculadora tiene una función incorporada de 'Regresión Exponencial' que produce lo que parece ser un modelo diferente\(N = 269.414 (1.22333419)^{t}\). Usando propiedades de exponentes, escribimos\(e^{0.202t} = \left(e^{0.202}\right)^t \approx (1.223848)^{t}\), que, si hubiéramos llevado más decimales, habría coincidido exactamente con la base del modelo de calculadora.

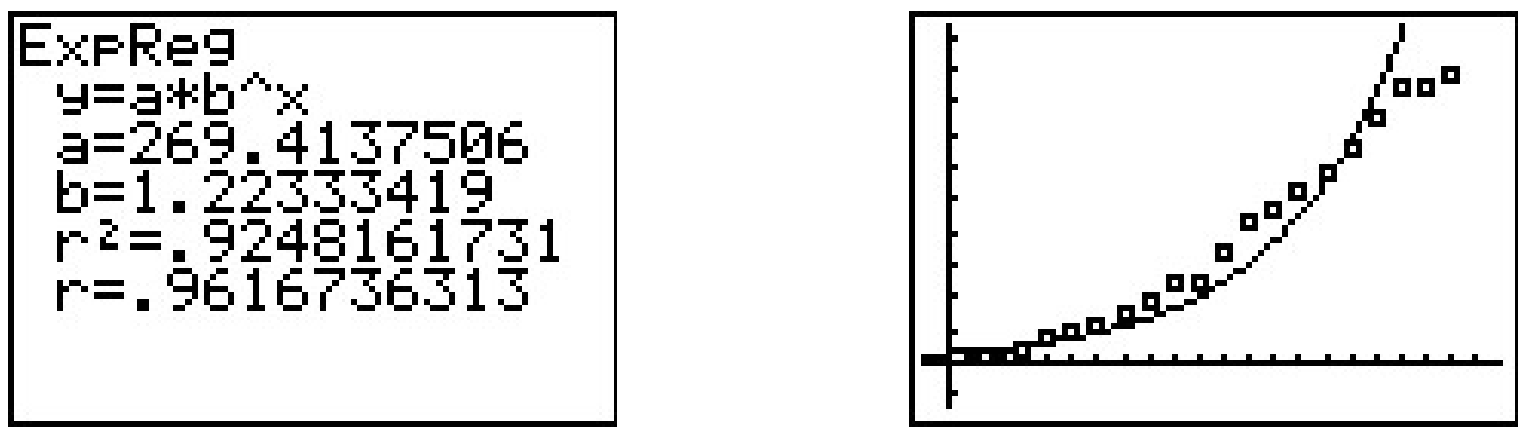
El modelo exponencial no se ajustaba tanto a los datos como al modelo cuadrático o de función de potencia, pero es lógico pensar que, tal vez, la propagación de la gripe no es diferente a la de la propagación de un rumor y que se puede utilizar un modelo logístico para modelar los datos. La calculadora tiene una función de 'Regresión Logística', y su uso produce el modelo\(N = \frac{10739.147}{1 + 42.416 e^{0.268 t}}\).

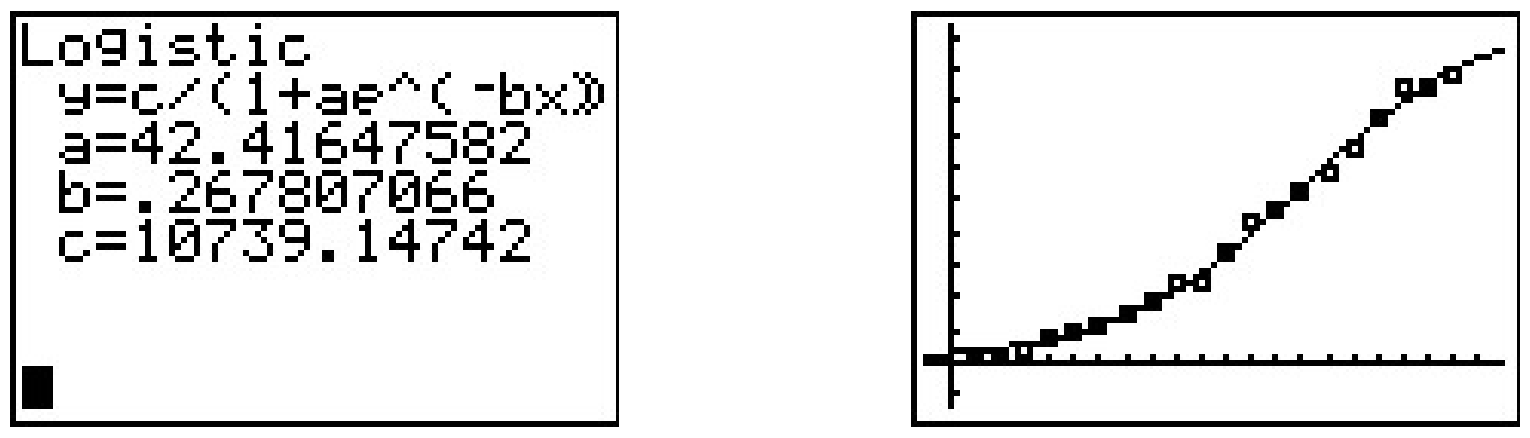
Esto parece ser un ajuste excelente, pero no existe un coeficiente amistoso de determinación,\(R^2\), por el cual juzgar esto numéricamente. Hay buenas razones para ello, pero están mucho más allá del alcance del texto. ¿Cuál de los modelos, cuadrático, de potencia, exponencial o logístico es el 'mejor modelo'? Si por 'mejor' queremos decir 'se ajusta más cerca de los datos', entonces los modelos cuadráticos y logísticos son posiblemente los ganadores con el modelo de función de potencia en un segundo cercano. No obstante, si pensamos en la ciencia detrás de la propagación de la gripe, el modelo logístico obtiene ventaja. Por un lado, toma en cuenta que solo un número finito de personas alguna vez contraerá la gripe (según nuestro modelo,\(10,\!739\)), mientras que el modelo cuadrático predice que no hay límite para el número de casos. Como hemos dicho varias veces antes en el texto, los modelos matemáticos, independientemente de su sofisticación, son precisamente eso: modelos, y todos tienen sus limitaciones. ²⁰

6.5.3. Ejercicios

Para cada uno de los escenarios dados en los Ejercicios 1 - 6

• Encontrar el monto\(A\) en la cuenta en función del plazo de la inversión\(t\) en años.
• Determinar cuánto hay en la cuenta después de\(5\) años,\(10\) años,\(30\) años y\(35\) años. Redondee sus respuestas al centavo más cercano.
• Determinar cuánto tiempo tardará en duplicarse la inversión inicial. Redondea tu respuesta al año más cercano.
• Encontrar e interpretar la tasa promedio de cambio del monto en la cuenta desde el final del cuarto año hasta el final del quinto año, y desde el final del trigésimo cuarto año hasta el final del trigésimo quinto año. Redondee su respuesta a dos decimales.

1. \(\$500\)se invierte en una cuenta que ofrece\(0.75 \%\), compuesta mensualmente.
2. \(\$500\)se invierte en una cuenta que ofrece\(0.75 \%\), compuesta continuamente.
3. \(\$1000\)se invierte en una cuenta que ofrece\(1.25 \%\), compuesta mensualmente.
4. \(\$1000\)se invierte en una cuenta que ofrece\(1.25 \%\), compuesta continuamente.
5. \(\$5000\)se invierte en una cuenta que ofrece\(2.125 \%\), compuesta mensualmente.
6. \(\$5000\)se invierte en una cuenta que ofrece\(2.125 \%\), compuesta continuamente.
7. Mira hacia atrás en tus respuestas a los Ejercicios 1 - 6. ¿Qué se puede decir de la diferencia entre la composición mensual y la agravación continua del interés en esas situaciones? Con la ayuda de tus compañeros de clase, discute escenarios donde la diferencia entre el interés mensual y el continuamente compuesto sería más dramática. Intente variar la tasa de interés, el plazo de la inversión y el principal. Usa cálculos para respaldar tu respuesta.
8. ¿Cuánto dinero se necesita invertir ahora para obtener\(\$2000\) en 3 años si la tasa de interés en una cuenta de ahorro es\(0.25 \%\), compuesta continuamente? Redondea tu respuesta al centavo más cercano.
9. ¿Cuánto dinero hay que invertir ahora para obtener\(\$5000\) en 10 años si la tasa de interés en un CD es\(2.25 \%\), compuesta mensualmente? Redondee su respuesta al centavo más cercano.
10. El 31 de mayo de 2009, la Tasa de Porcentaje Anual listada en el banco de Jeff para las cuentas de ahorro regulares se\(0.25\%\) compuso mensualmente. Utilice la Ecuación 6.2 para responder a lo siguiente.
    1. \(P = 2000\)¿Si qué es\(A(8)\)?
    2. Resuelve la ecuación\(A(t) = 4000\) para\(t\).
    3. ¿Qué principal se\(P\) debe invertir para que el saldo de la cuenta sea de 2000 dólares es de tres años?
11. El banco de Jeff también ofrece un Certificado de Depósito (CD) de 36 meses con una APR de\(2.25\%\).
    1. \(P = 2000\)¿Si qué es\(A(8)\)?
    2. Resuelve la ecuación\(A(t) = 4000\) para\(t\).
    3. ¿Qué capital se\(P\) debe invertir para que el saldo de la cuenta sea de 2000 dólares en tres años?
    4. El Rendimiento Porcentaje Anual es la tasa de interés que devuelve la misma cantidad de interés después de un año que lo hace el interés compuesto. Con la ayuda de tus compañeros, computa el APY para esta inversión.
12. Una empresa financiera ofrece una promoción en\(\$5000\) préstamos. El prestatario no tiene que realizar ningún pago durante los primeros tres años, sin embargo, se seguirán cobrando intereses al préstamo en\(29.9 \%\) compuesto continuamente. ¿Qué monto se adeudará al término del periodo de tres años, suponiendo que no se realicen pagos? Si la promoción se extiende tres años adicionales, y no se realizan pagos, ¿qué monto se adeudaría?
13. Utilice la Ecuación 6.2 para mostrar que el tiempo que tarda una inversión en duplicar su valor sí depende del principal\(P\), sino más bien, depende únicamente de la TAE y del número de compuestos por año. Deja\(n = 12\) y con la ayuda de tus compañeros de clase computar el tiempo de duplicación para una variedad de tarifas\(r\). Entonces busca la Regla del 72 y compara tus respuestas con lo que dice esa regla. Si realmente te interesa ²¹ en Matemáticas Financieras, también podrías comparar y contrastar la Regla del 72 con la Regla del 70 y la Regla del 69.

En los Ejercicios 14 - 18, enumeramos algunos isótopos radiactivos y sus semividas asociadas. Supongamos que cada uno decae según la fórmula\(A(t)=A_{0} e^{k t}\) donde\(A_{0}\) está la cantidad inicial del material y\(k\) es la constante de decaimiento. Para cada isótopo:

• Encuentra la constante de decaimiento\(k\). Redondee su respuesta a cuatro decimales.
• Encontrar una función que da la cantidad de isótopo\(A\) que queda después del tiempo\(t\). (Conservar las unidades de\(A\) y\(t\) las mismas que los datos dados.)
• Determinar cuánto tiempo tarda\(90 \%\) del material en descomponerse. Redondee su respuesta a dos decimales. (SUMINISTRO: Si\(90 \%\) del material se decae, ¿cuánto queda?)

14. Cobalto 60, utilizado en irradiación de alimentos, cantidad inicial 50 gramos, vida media de\(5.27\) años.
15. Fósforo 32, utilizado en agricultura, cantidad inicial 2 miligramos,\(14\) días de vida media.
16. Cromo 51, utilizado para rastrear glóbulos rojos, cantidad inicial 75 miligramos,\(27.7\) días de vida media.
17. Americio 241, utilizado en detectores de humo, cantidad inicial 0.29 microgramos,\(432.7\) años de vida media.
18. Uranio 235, utilizado para la energía nuclear, cantidad inicial\(1\) kg gramos, vida media\(704\) millones de años.
19. Con la ayuda de tus compañeros de clase, demuestra que el tiempo que tarda\(90 \%\) de cada isótopo enumerado en los Ejercicios 14 - 18 en descomponerse no depende de la cantidad inicial de la sustancia, sino más bien, solo de la constante de decaimiento\(k\). Encuentra una fórmula, en términos de\(k\) solo, para determinar cuánto tiempo tarda un isótopo radiactivo en descomponerse.\(90 \%\)
20. En el Ejemplo 6.1.1 de la Sección 6.1,\(V(x) = 25 \left(\frac{4}{5}\right)^{x}\) se utilizó la función exponencial para modelar el valor de un automóvil a lo largo del tiempo. Utilice las propiedades de registros y/o exponentes para reescribir el modelo en el formulario\(V(t) = 25e^{kt}\).
21. El Producto Interno Bruto (PIB) de EU (en miles de millones de dólares)\(t\) años después del año 2000 puede modelarse por:\[G(t) = 9743.77 e^{0.0514t}\nonumber\]
    1. Encontrar e interpretar\(G(0)\).
    2. Según el modelo, ¿cuál debería haber sido el PIB en 2007? ¿En 2010? (Según el Departamento de Comercio de Estados Unidos, el PIB de 2007 fue de\(\$14,369.1\) mil millones y el PIB de 2010 fue de\(\$14,657.8\) mil millones).
22. El diámetro\(D\) de un tumor, en milímetros,\(t\) días después de ser detectado viene dado por:\[D(t) = 15e^{0.0277t}\nonumber\]
    1. ¿Cuál era el diámetro del tumor cuando se detectó originalmente?
    2. ¿Cuánto tiempo hasta que se duplique el diámetro del tumor?
23. En condiciones óptimas, el crecimiento de una determinada cepa de E. Coli se modela por la Ley de Crecimiento Desinhibido\(N(t)=N_{0} e^{k t}\) donde\(N_{0}\) está el número inicial de bacterias y\(t\) es el tiempo transcurrido, medido en minutos. A partir de numerosos experimentos, se ha determinado que el tiempo de duplicación de este organismo es de 20 minutos. Supongamos que inicialmente están presentes 1000 bacterias.
    1. Encuentra la constante de crecimiento\(k\). Redondee su respuesta a cuatro decimales.
    2. Encuentra una función que dé el número de bacterias\(N(t)\) después de\(t\) minutos.
    3. ¿Cuánto tiempo hasta que haya 9000 bacterias? Redondee su respuesta al minuto más cercano.
24. La levadura se usa a menudo en experimentos biológicos. Un técnico de investigación estima que una muestra de suspensión de levadura contiene 2.5 millones de organismos por centímetro cúbico (cc). Dos horas después, estima que la densidad poblacional es de 6 millones de organismos por cc. \(t\)Sea el tiempo transcurrido desde la primera observación, medido en horas. Supongamos que el crecimiento de levaduras sigue la Ley de Crecimiento Desinhibido\(N(t)=N_{0} e^{k t}\).
    1. Encuentra la constante de crecimiento\(k\). Redondee su respuesta a cuatro decimales.
    2. Encuentra una función que dé el número de levaduras (en millones) por cc\(N(t)\) después de\(t\) horas.
    3. ¿Cuál es el tiempo de duplicación para esta cepa de levadura?
25. La Ley de Crecimiento Desinhibido también se aplica a situaciones en las que un animal es reintroducido en un ambiente adecuado. Tal caso es la reintroducción de lobos al Parque Nacional Yellowstone. Según el Servicio de Parques Nacionales, la población de lobos en el Parque Nacional Yellowstone era de 52 en 1996 y 118 en 1999. Utilizando estos datos, encontrar una función de la forma\(N(t)=N_{0} e^{k t}\) que modela el número de lobos\(t\) años después de 1996. (Utilizar\(t = 0\) para representar el año 1996. Además, redondee su valor de\(k\) a cuatro decimales.) Según el modelo, ¿cuántos lobos había en Yellowstone en 2002? (El número registrado es 272.)
26. Durante los primeros años de una comunidad, no es raro que la población crezca de acuerdo con la Ley de Crecimiento Desinhibido. Según la entrada de Wikipedia de Painesville, en 1860, el pueblo de Painesville tenía una población de 2649 habitantes. En 1920, la población era de 7272. Utilizar estos dos puntos de datos para ajustarse a un modelo del formulario\(N(t)=N_{0} e^{k t}\) fueron\(N(t)\) es el número de Residentes de Painesville\(t\) años después de 1860. (Utilizar\(t = 0\) para representar el año 1860. Además, redondear el valor de\(k\) a cuatro decimales.) Según este modelo, ¿cuál era la población de Painesville en 2010? (El censo de 2010 dio a la población en 19.563) ¿Cuáles podrían ser algunas de las causas de una discrepancia tan vasta? Para más información sobre esto, consulte el Ejercicio 37.
27. La población de Sasquatch en el condado de Bigfoot está modelada por\[P(t) = \dfrac{120}{1 + 3.167e^{-0.05t}}\nonumber\] dónde\(P(t)\) está la población de Sasquatch\(t\) años después\(2010\).
    1. Encontrar e interpretar\(P(0)\).
    2. Encuentra la población de Sasquatch en el condado de Bigfoot en 2013. Redondee su respuesta al Sasquatch más cercano.
    3. ¿Cuándo llegará a 60 la población de Sasquatch en el condado de Bigfoot? Redondee su respuesta al año más cercano.
    4. Encontrar e interpretar el comportamiento final de la gráfica de\(y = P(t)\). Comprueba tu respuesta usando una utilidad gráfica.
28. La vida media del isótopo radiactivo Carbono-14 es de aproximadamente 5730 años.
    1. Utilice la Ecuación 6.5 para expresar la cantidad de Carbono-14 que queda de un\(N\) miligramos inicial en función del tiempo\(t\) en años.
    2. ¿Qué porcentaje de la cantidad original de Carbono-14 queda después de 20,000 años?
    3. Si en una cueva se encuentra una vieja herramienta de madera y se estima que la cantidad de Carbono-14 presente en ella es solo 42% de la cantidad original, aproximadamente ¿qué edad tiene la herramienta?
    4. La datación por radiocarbono no es tan fácil como estos ejercicios podrían llevarte a creer. Con la ayuda de tus compañeros, investiga la datación por radiocarbono y discute por qué nuestro modelo está algo sobresimplificado.
29. El carbono-14 no se puede utilizar para fechar material inorgánico como rocas, pero existen muchos otros métodos de datación radiométrica que estiman la edad de las rocas. Uno de ellos, la datación Rubidio-Estroncio, utiliza Rubidio-87 que decae a Estroncio-87 con una vida media de 50 mil millones de años. Utilice la Ecuación 6.5 para expresar la cantidad de Rubidio-87 que queda de 2.3 microgramos iniciales en función del tiempo\(t\) en miles de millones de años. Investiga esta y otras técnicas radiométricas y discute los márgenes de error para diversos métodos con tus compañeros de clase.
30. Utilice la Ecuación 6.5 para mostrar\(k = -\dfrac{\ln(2)}{h}\) dónde\(h\) está la vida media del isótopo radiactivo.
31. Un asado de cerdo ²² se sacó de un ahumador de madera dura cuando su temperatura interna había alcanzado\(180^{\circ}\) F y se dejó reposar en una casa\(75^{\circ}\) F durante 20 minutos después de lo cual su temperatura interna había bajado a\(170^{\circ}\) F. Suponiendo que la temperatura del asado sigue la Ley de Enfriamiento de Newton (Ecuación 6.6),
    1. Exprese la temperatura\(T\) (en\(^{\circ}\) F) en función del tiempo\(t\) (en minutos).
    2. Encuentra la hora en la que el asado habría caído a\(140^{\circ}\) F si no hubiera sido tallado y comido.
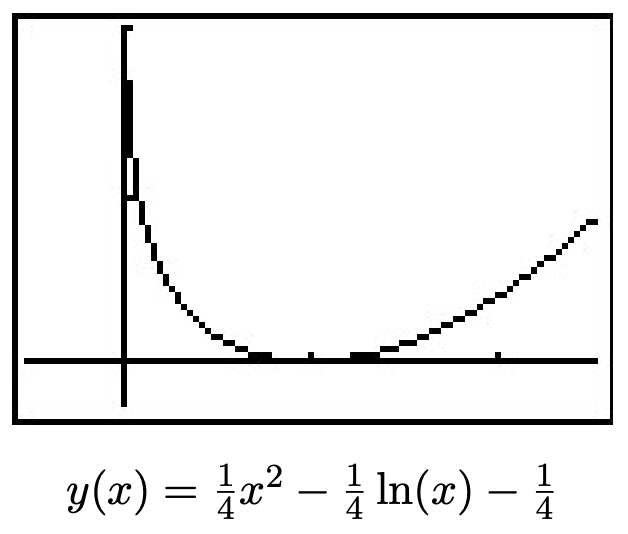
32. En referencia al Ejercicio 44 en la Sección 5.3, si la velocidad de Fritzy the Fox es la misma que la velocidad de Chewbacca the Bunny, la curva de persecución de Fritzy viene dada por

    \[y(x) = \frac{1}{4} x^2-\frac{1}{4} \ln(x)-\frac{1}{4}\nonumber\]

    Utilice su calculadora para graficar esta ruta para\(x > 0\). Describir el comportamiento de\(y\) as\(x \rightarrow 0^{+}\) e interpretarlo físicamente.

33. La corriente\(i\) medida en amperios en cierto circuito electrónico con un voltaje constante de 120 voltios está dada por\(i(t) = 2 - 2e^{-10t}\) donde\(t \geq 0\) está el número de segundos después de que se encienda el circuito. Determinar el valor de\(i\) as\(t \rightarrow \infty\). (A esto se le llama la corriente de estado estacionario.)
34. Si el voltaje en el circuito en el Ejercicio 33 anterior se desconecta después de 30 segundos, la corriente viene dada por la función definida por partes

    \[i(t) = \left\{ \begin{array}{rcl} 2 - 2e^{-10t} & \mbox{if} & 0 \leq t < 30 \\ [6pt] \left(2 - 2e^{-300}\right) e^{-10t+300} & \mbox{if} & t \geq 30 \end{array} \right.\nonumber\]

    Con la ayuda de tu calculadora, grafica\(y = i(t)\) y discute con tus compañeros de clase el significado físico de las dos partes de la gráfica\(0 \leq t < 30\) y\(t \geq 30\).

35. En el Ejercicio 6a de la Sección 2.5, declaramos que el cable de un puente colgante formaba una parábola pero que un cable colgante libre no lo hacía. Un cable colgante libre forma a y su forma básica viene dada por\(y = \frac{1}{2}\left(e^{x} + e^{-x}\right)\). Usa tu calculadora para graficar esta función. ¿Cuáles son su dominio y alcance? ¿Cuál es su comportamiento final? ¿Es invertible? ¿Cómo cree que se relaciona con la función dada en el Ejercicio 47 en la Sección 6.3 y la que se da en la respuesta al Ejercicio 38 en la Sección 6.4? Al voltear boca abajo, la catenaria hace un arco. El Arco Gateway en St. Louis, Missouri tiene la forma\[y = 757.7 - \frac{127.7}{2}\left(e^{\frac{x}{127.7}} + e^{-\frac{x}{127.7}}\right)\nonumber\] donde\(x\) y\(y\) se miden en pies y\(-315 \leq x \leq 315\). Encuentra el punto más alto en el arco.
36. En el Ejercicio 6a de la Sección 2.5, examinamos el conjunto de datos que se da a continuación, que mostraron cómo dos gatos y sus crías supervivientes pueden producir más de 80 millones de gatos en solo diez años. Es prácticamente imposible ver estos datos trazados en su calculadora, así que trazar\(x\) versus\(\ln(x)\) como se hizo en la página 480. Encuentre un modelo lineal para estos nuevos datos y comente su bondad de ajuste. Encuentre un modelo exponencial para los datos originales y comente su bondad de ajuste.

    \ (\ begin {array} {|l|r|r|r|r|r|r|r|r|r|r|r|r|}
    \ hline\ text {Año} x & 1 & 2 & 3 & 4 & 5 & 6 & 7 & 8 & 9\\ hline
    \ texto {Número de} & & & & & & & & & & & & &\
    \ texto {Gatos} N (x) & & Amp; 12 & 66 & 382 & 2201 & 12680 & 73041 & 420715 & 2423316 & 13968290 & 80399780\
    \ hline
    \ end {array}\)

37. Este ejercicio es un seguimiento del Ejercicio 26 que explora más a fondo el crecimiento poblacional de Painesville, Ohio. Según Wikipedia, la población de Painesville, Ohio viene dada por\ [\ begin {aligned}
    &\ begin {array} {|l|r|r|r|r|r|r|r|r|r|r|r|r|r|}
    \ hline\ text {Año} t & 1860 & 1870 & 1880 & 1890 & 1900 & 1910 & 1920 & 1930 & 1940 & 1950\
    \ hline\ text {Población} & 2649 & 3728 & 3841 & 4755 & 5024 & 5501 & 7272 & 10944 & 12235 & 14432\\ hline\
    \ hline
    \ end {array}\\
    &\ begin {array} {|l|r|r|r|r|r|r|}
    \ hline\ texto {Año} t & 1960 & 1970 & 1980 & 1990 & 2000\\
    \ hline\ text {Población} & 16116 & 16536 & 16351 & 15699 & 17503\\ hline
    \\ hline
    \ end {array}
    \ end {alineado}\ nonumber\]
    1. Utilice una utilidad gráfica para realizar una regresión exponencial en los datos desde 1860 hasta 1920 solamente, dejando\(t = 0\) representar el año 1860 como antes. ¿Cómo se compara este modelo de calculadora con el modelo que encontraste en el Ejercicio 26? Utilizar el modelo exponencial de la calculadora para predecir la población en 2010. (El censo de 2010 dio la población en 19.563 habitantes)
    2. El modelo logístico ajustado a todos los puntos de datos dados para la población de Painesville\(t\) años después de 1860 (nuevamente, usando\(t = 0\) como 1860) es\[P(t) = \dfrac{18691}{1+9.8505e^{-0.03617t}}\nonumber\] Según este modelo, ¿cuál debería haber sido la población de Painesville en 2010? (El censo de 2010 dio a la población en 19.563.) ¿Cuál es el límite de población de Painesville?
38. Según OhioBiz, los datos del censo para el condado de Lake, Ohio son los siguientes:\ [\ begin {aligned}
    &\ begin {array} {|l|r|r|r|r|r|r|r|r|r|r|r|r|}
    \ hline\ text {Año} t & 1860 & 1870 & 1880 & 1890 & 1900 & 1910 & 1920 & 1930 & 1940 & amp; 1950\\
    \ hline\ text {Población} & 15576 & 15935 & 16326 & 18235 & 21680 & 22927 & 28667 & 41674 & 50020 & 75979\\\ hline
    \ end {array}
    \\
    &\ begin {array} {|l|r|r|r|r|r|r| r|}
    \ hline\ text {Año} t & 1960 & 1970 & 1980 & 1990 & 2000\\
    \ hline\ texto {Población} & 148700 & 197200 & 212801 & 215499 & 227511\
    \ hline
    \ end {array}
    \ end {alineado}\ nonumber\]
    1. Utilice su calculadora para ajustar un modelo logístico a estos datos, utilizando\(x = 0\) para representar el año 1860.
    2. Grafique estos datos y su función logística en su calculadora para juzgar la razonabilidad del ajuste.
    3. Utilice este modelo para estimar la población del condado de Lake en 2010. (El censo de 2010 dio la población a 230.041.)
    4. Según su modelo, ¿cuál es el límite de población del condado de Lake, Ohio?
39. Según facebook, el número de usuarios activos de facebook ha crecido significativamente desde su lanzamiento inicial desde un dormitorio de Harvard en febrero de 2004. El siguiente cuadro tiene el número aproximado\(U(x)\) de usuarios activos, en,\(x\) meses después de febrero de 2004. Por ejemplo, la primera entrada\((10, 1)\) significa que hubo\(1\) millones de usuarios activos en diciembre de 2004 y la última entrada\((77, 500)\) significa que hubo\(500\) millones de usuarios activos en julio de 2010.

    Con la ayuda de tus compañeros, encuentra un modelo para estos datos.

40. Cada lunes durante el periodo de registro previo al Semestre de Otoño en LCCC, el Consejo de Planeación de Inscripción obtiene un informe elaborado por los analistas de datos en Efectividad Institucional y Plane ²³ Si bien los datos de inscripción en curso se analizan de muchas maneras diferentes, nos centraremos únicamente en el recuento general de personal. A continuación se muestra una tabla de los datos de inscripción para el Semestre de Otoño 2008. Comienza 21 semanas antes del “Día de Apertura” y termina en el “Día 15” del semestre, pero hemos vuelto a etiquetar la fila superior para que sea a\(x = 1\) través para\(x = 24\) que las matemáticas sean más fáciles. (Así,\(x = 22\) es el Día de Inauguración.) \ [\ begin {aligned}
    &\ begin {array} {|l|r|r|r|r|r|r|r|r|r|r|}
    \ hline\ text {Semana} x & 1 & 2 & 3 & 4 & 5 & 6 & 7 & 8
    \\ hline\ texto {Total} & & & & & & & &\
    \ texto { Headcount} & 1194 & 1564 & 2001 & 2475 & 2802 & 3141 & 3527 & 3790\\ hline
    
    \ end {array}\\
    &\ begin {array} {|l|r|r|r|r|r|r|r|r|r|r|}
    \ hline\ text {Semana} x & 9 y 10 y 11 y 12 y 13 & amp; 14 & 15 & 16\\
    \ hline\ text {Total} & & & & & & & & &\
    \ text {Headcount} & 4065 & 4371 & 4611 & 4945 & 5300 & 5657 & 6056 & 6478\
    \ hline
    \ end {array}
    \ end {alineado}\ nonumber\]\ [\ begin {array} {|l|r|r|r|r|r|r|r|r|r|r|}
    \ hline\ text {Semana} x & 17 & 18 & 19 & 20 & 21 & 22 & 23 & 24\
    \ hline\ texto {Total} & & & & & & & & & & &\
    \ text {Headcount} & 7161 & 7772 & 8505 & 9256 & 10201 & 10743 & 11102 & 11181\
    \ hline
    \ end {array}\ nonumber\]

    Con la ayuda de tus compañeros, encuentra un modelo para estos datos. A diferencia de la mayoría de los fenómenos que hemos estudiado en esta sección, no existe una ecuación diferencial única que gobierne el crecimiento de la matrícula. Por lo tanto, no hay razón científica para confiar en una función logística aunque la gráfica de datos pueda llevarnos a ese modelo. ¿Cuáles son algunos de los factores que influyen en la inscripción en un colegio comunitario y cómo puedes tomarlos en cuenta matemáticamente?

41. Cuando escribimos este ejercicio, el Informe de Planeación de Inscripción para el Semestre de Otoño 2009 contaba con solo 10 puntos de datos para las primeras 10 semanas del periodo de registro. Esos números se dan a continuación. \ [\ begin {array} {|l|r|r|r|r|r|r|r|r|r|}
    \ hline\ text {Semana} x & 17 & 18 & 19 & 20 & 21 & 22 & 23 & 24\
    \ hline\ texto {Total} & & & & & & & & & & &
    \\ texto {recuento} & 7161 & 7772 & 8505 & 9256 & 10201 & 10743 & 11102 & 11181\
    \ hline
    \ end {array}\ nonumber\]

    Con la ayuda de tus compañeros, encuentra un modelo para estos datos y haz una predicción para la inscripción del Día de Apertura así como la inscripción del Día 15. (ADVERTENCIA: El periodo de registro para 2009 fue una semana más corto que en 2008 por lo que sería el Día de Apertura\(x = 21\) y el Día 15 es\(x = 23\).)

6.5.4. RESPUESTAS

1. • \(A(t) = 500\left(1 + \frac{0.0075}{12}\right)^{12t}\)
   • \(A(5) \approx \$ 519.10\),\(A(10) \approx \$ 538.93\),\(A(30) \approx \$ 626.12\),\(A(35) \approx \$ 650.03\)
   • Tomará aproximadamente\(92\) años para que la inversión se duplique.
   • La tasa promedio de cambio desde el final del cuarto año hasta el final del quinto año es aproximadamente\(3.88\). Esto quiere decir que la inversión está creciendo a una tasa promedio anual en este punto.\(\$3.88\) La tasa promedio de cambio desde el final del trigésimo cuarto año hasta el final del trigésimo quinto año es aproximadamente\(4.85\). Esto quiere decir que la inversión está creciendo a una tasa promedio anual en este punto.\(\$4.85\)
2. • \(A(t) = 500e^{0.0075t}\)
   • \(A(5) \approx \$ 519.11\),\(A(10) \approx \$ 538.94\),\(A(30) \approx \$ 626.16\),\(A(35) \approx \$ 650.09\)
   • Tomará aproximadamente\(92\) años para que la inversión se duplique.
   • La tasa promedio de cambio desde el final del cuarto año hasta el final del quinto año es aproximadamente\(3.88\). Esto quiere decir que la inversión está creciendo a una tasa promedio anual en este punto.\(\$3.88\) La tasa promedio de cambio desde el final del trigésimo cuarto año hasta el final del trigésimo quinto año es aproximadamente\(4.86\). Esto quiere decir que la inversión está creciendo a una tasa promedio anual en este punto.\(\$4.86\)
3. • \(A(t) = 1000\left(1 + \frac{0.0125}{12}\right)^{12t}\)
   • \(A(5) \approx \$ 1064.46\),\(A(10) \approx \$ 1133.07\),\(A(30) \approx \$ 1454.71\),\(A(35) \approx \$ 1548.48\)
   • Tomará aproximadamente\(55\) años para que la inversión se duplique.
   • La tasa promedio de cambio desde el final del cuarto año hasta el final del quinto año es aproximadamente\(13.22\). Esto quiere decir que la inversión está creciendo a una tasa promedio anual en este punto.\(\$13.22\) La tasa promedio de cambio desde el final del trigésimo cuarto año hasta el final del trigésimo quinto año es aproximadamente\(19.23\). Esto quiere decir que la inversión está creciendo a una tasa promedio anual en este punto.\(\$19.23\)
4. • \(A(t) = 1000e^{0.0125t}\)
   • \(A(5) \approx \$ 1064.49\),\(A(10) \approx \$ 1133.15\),\(A(30) \approx \$ 1454.99\),\(A(35) \approx \$ 1548.83\)
   • Tomará aproximadamente\(55\) años para que la inversión se duplique.
   • La tasa promedio de cambio desde el final del cuarto año hasta el final del quinto año es aproximadamente\(13.22\). Esto quiere decir que la inversión está creciendo a una tasa promedio anual en este punto.\(\$13.22\) La tasa promedio de cambio desde el final del trigésimo cuarto año hasta el final del trigésimo quinto año es aproximadamente\(19.24\). Esto quiere decir que la inversión está creciendo a una tasa promedio anual en este punto.\(\$19.24\)
5. • \(A(t) = 5000\left(1 + \frac{0.02125}{12}\right)^{12t}\)
   • \(A(5) \approx \$ 5559.98\),\(A(10) \approx \$ 6182.67\),\(A(30) \approx \$ 9453.40\),\(A(35) \approx \$ 10512.13\)
   • Tomará aproximadamente\(33\) años para que la inversión se duplique.
   • La tasa promedio de cambio desde el final del cuarto año hasta el final del quinto año es aproximadamente\(116.80\). Esto quiere decir que la inversión está creciendo a una tasa promedio anual en este punto.\(\$116.80\) La tasa promedio de cambio desde el final del trigésimo cuarto año hasta el final del trigésimo quinto año es aproximadamente\(220.83\). Esto quiere decir que la inversión está creciendo a una tasa promedio anual en este punto.\(\$220.83\)
6. • \(A(t) = 5000e^{0.02125t}\)
   • \(A(5) \approx \$ 5560.50\),\(A(10) \approx \$ 6183.83\),\(A(30) \approx \$ 9458.73\),\(A(35) \approx \$ 10519.05\)
   • Tomará aproximadamente\(33\) años para que la inversión se duplique.
   • La tasa promedio de cambio desde el final del cuarto año hasta el final del quinto año es aproximadamente\(116.91\). Esto quiere decir que la inversión está creciendo a una tasa promedio anual en este punto.\(\$116.91\) La tasa promedio de cambio desde el final del trigésimo cuarto año hasta el final del trigésimo quinto año es aproximadamente\(221.17\). Esto quiere decir que la inversión está creciendo a una tasa promedio anual en este punto.\(\$221.17\)

8. \(P = \frac{2000}{e^{0.0025 \cdot 3}} \approx \$ 1985.06\)
9. \(P = \frac{5000}{\left(1 + \frac{0.0225}{12}\right)^{12 \cdot 10}} \approx \$ 3993.42\)
10. 1. \(A(8) = 2000\left(1 + \frac{0.0025}{12}\right)^{12 \cdot 8} \approx \$2040.40\)
    2. \(t = \dfrac{\ln(2)}{12 \ln\left(1 + \frac{0.0025}{12}\right)} \approx 277.29\)años
    3. \(P = \dfrac{2000}{\left(1 + \frac{0.0025}{12}\right)^{36}} \approx \$1985.06\)
11. 1. \(A(8) = 2000\left(1 + \frac{0.0225}{12}\right)^{12 \cdot 8} \approx \$2394.03\)
    2. \(t = \dfrac{\ln(2)}{12 \ln\left(1 + \frac{0.0225}{12}\right)} \approx 30.83\)años
    3. \(P = \dfrac{2000}{\left(1 + \frac{0.0225}{12}\right)^{36}} \approx \$1869.57\)
    4. \(\left(1 + \frac{0.0225}{12}\right)^{12} \approx 1.0227\)por lo que el APY es 2.27%
12. \(A(3) = 5000e^{0.299 \cdot 3} \approx \$12,226.18\),\(A(6) = 5000e^{0.299 \cdot 6} \approx \$30,067.29\)

14. • \(k = \frac{\ln(1/2)}{5.27} \approx -0.1315\)
    • \(A(t) = 50e^{-0.1315t}\)
    • \(t = \frac{\ln(0.1)}{-0.1315} \approx 17.51\)años.
15. • \(k = \frac{\ln(1/2)}{14} \approx -0.0495\)
    • \(A(t) = 2e^{-0.0495t}\)
    • \(t = \frac{\ln(0.1)}{-0.0495} \approx 46.52\)días.
16. • \(k = \frac{\ln(1/2)}{27.7} \approx -0.0250\)
    • \(A(t) = 75e^{-0.0250t}\)
    • \(t = \frac{\ln(0.1)}{-0.025} \approx 92.10\)días.
17. • \(k = \frac{\ln(1/2)}{432.7} \approx -0.0016\)
    • \(A(t) = 0.29e^{-0.0016t}\)
    • \(t = \frac{\ln(0.1)}{-0.0016} \approx 1439.11\)años.
18. • \(k = \frac{\ln(1/2)}{704} \approx -0.0010\)
    • \(A(t) = e^{-0.0010t}\)
    • \(t = \frac{\ln(0.1)}{-0.0010} \approx 2302.58\)millones de años, o\(2.30\) mil millones de años.
19. \(t = \frac{\ln(0.1)}{k} = -\frac{\ln(10)}{k}\)
20. \(V(t) = 25e^{\ln\left(\frac{4}{5}\right)t} \approx 25e^{-0.22314355t}\)
21. 1. \(G(0) = 9743.77\)Esto quiere decir que el PIB de EU en 2000 fue de\(\$9743.77\) mil millones de dólares.
    2. \(G(7) = 13963.24\)y\(G(10) = 16291.25\), así el modelo predijo un PIB de\(\$ 13,963.24\) mil millones en 2007 y\(\$ 16,291.25\) mil millones en 2010.
22. 1. \(D(0) = 15\), por lo que el tumor tenía 15 milímetros de diámetro cuando se detectó por primera vez.
    2. \(t = \frac{\ln(2)}{0.0277} \approx 25\)días.
23. 1. \(k = \frac{\ln(2)}{20} \approx 0.0346\)
    2. \(N(t) = 1000e^{0.0346 t}\)
    3. \(t = \frac{\ln(9)}{0.0346} \approx 63\)minutos
24. 1. \(k = \frac{1}{2}\frac{\ln(6)}{2.5} \approx 0.4377\)
    2. \(N(t) = 2.5e^{0.4377 t}\)
    3. \(t = \frac{\ln(2)}{0.4377} \approx 1.58\)horas
25. \(N_{0}=52, k=\frac{1}{3} \ln \left(\frac{118}{52}\right) \approx 0.2731, N(t)=52 e^{0.2731 t} \cdot N(6) \approx 268\).
26. \(N_{0}=2649, k=\frac{1}{60} \ln \left(\frac{7272}{2649}\right) \approx 0.0168, N(t)=2649 e^{0.0168 t} \cdot N(150) \approx 32923\), por lo que la población de Painesville en 2010 basada en este modelo habría sido de 32 mil 923.
27. 1. \(P(0) = \frac{120}{4.167} \approx 29\). Hay 29 Sasquatch en el condado de Bigfoot en 2010.
    2. \(P(3) = \frac{120}{1+3.167e^{-0.05(3)}} \approx 32\)Sasquatch.
    3. \(t = 20 \ln(3.167) \approx 23\)años.
    4. Como\(t \rightarrow \infty\),\(P(t) \rightarrow 120\). Con el paso del tiempo, la Población Sasquatch en el condado de Bigfoot se acercará a 120. Gráficamente,\(y = P(x)\) tiene una asíntota horizontal\(y=120\).
28. 1. \(A(t) = Ne^{-\left(\frac{\ln(2)}{5730}\right)t} \approx Ne^{-0.00012097t}\)
    2. \(A(20000) \approx 0.088978 \cdot N\)por lo que alrededor de 8.9% permanece
    3. \(t \approx \dfrac{\ln(.42)}{-0.00012097} \approx 7171\)años
29. \(A(t) = 2.3e^{-0.0138629t}\)

31. 1. \(T(t) = 75 + 105e^{-0.005005t}\)
    2. El asado se habría enfriado a\(140^{\circ}\) F en unos 95 minutos.
32. De la gráfica, aparece que como\(x \rightarrow 0^{+}\),\(y \rightarrow \infty\). Esto se debe a la presencia del\(\ln(x)\) término en la función. Esto quiere decir que Fritzy nunca atrapará a Chewbacca, lo cual tiene sentido ya que Chewbacca tiene ventaja y Fritzy sólo corre tan rápido como él.

    

33. La corriente de estado estacionario es de 2 amperios.

36. La regresión lineal en los datos a continuación es\(y = 1.74899x + 0.70739\) con\(r^{2} \approx 0.999995\). Este es un ajuste excelente. \ [\ begin {array} {|l|r|r|r|r|r|r|r|r|r|r|r|r|}
    \ hline x & 1 & 2 & 3 & 4 & 5 & 6 & 7 & 8 & 9 & 10
    \\ hline\ ln (N (x)) & 2.4849 & 4.1897 & 5.9454 & 7.6967 & 9.4478 & 11.1988 & 12.1988 9497 y 14.7006 y 16.4523 y amp; 18.2025\\
    \ hline
    \ end {array}\ nonumber\]

    \(N(x) = 2.02869(5.74879)^{x} = 2.02869e^{1.74899x}\)con\(r^{2} \approx 0.999995\). Este también es un excelente ajuste y corresponde a nuestro modelo linealizado porque\(\ln(2.02869) \approx 0.70739\).

37. 1. La calculadora da:\(y = 2895.06 (1.0147)^{x}\). Graficando esto junto con nuestra respuesta del Ejercicio 26 a lo largo del intervalo\([0,60]\) muestra que están bastante cerca. A partir de este modelo,\(y(150) \approx 25840\) que una vez más rebasa el valor real de los datos.
    2. \(P(150) \approx 18717\), por lo que este modelo predice 17,914 personas en Painesville en 2010, un número más conservador de lo que se registró en el censo de 2010. Como\(t \rightarrow \infty\),\(P(t) \rightarrow 18691\). Por lo que la población limitante de Painesville basada en este modelo es de 18 mil 691 personas.
38. 1. \(y = \dfrac{242526}{1+874.62e^{-0.07113x}}\), donde\(x\) es el número de años transcurridos desde 1860.
    2. La gráfica de los datos y la curva está por debajo.

       

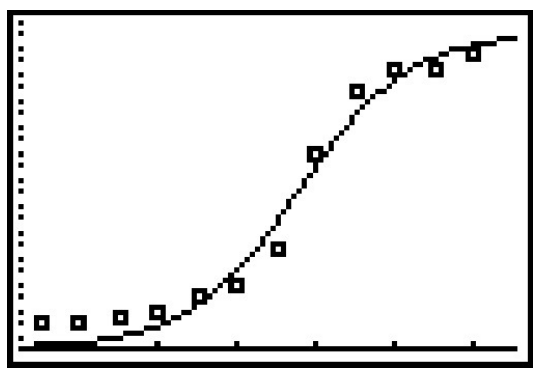
    3. \(y(140) \approx 232889\), por lo que este modelo predice 232,889 personas en el condado de Lake en 2010.
    4. Como\(x \rightarrow \infty\),\(y \rightarrow 242526\), por lo que la población limitante del Condado de Lake basada en este modelo es de 242,526 personas.

---

Referencia

¹ Cuán generoso de los

² Pueden aplicarse algunas restricciones.

³ En realidad, el saldo final debería ser de $105.0625.

⁴ Utilizando esta convención, el interés simple después de un año es lo mismo que agrava el interés solo una vez.

⁵ Ver Definición 2.3 en la sección 2.1.

⁶ De hecho, la tasa de incremento del monto en la cuenta también es exponencial. Esta es la cualidad que realmente define las funciones exponenciales y remitimos al lector a un curso en Cálculo.

⁷ Una vez que hayas tenido un semestre de Cálculo, podrás apreciar completamente este juego de palabras muy cojo.

⁸ O defina, dependiendo de tu punto de vista.

⁹ La tasa promedio de cambio de una función a lo largo de un intervalo se introdujo por primera vez en la Sección 2.1. Las tasas de cambio instantáneas son el negocio de Cálculo, como se menciona en la Página 161.

¹⁰ El tiempo que tarda la mitad de la sustancia en descomponerse.

¹¹ La Segunda Ley de la Termodinámica establece que el calor puede fluir espontáneamente de un objeto más caliente a uno más frío, pero no al revés. De esta manera, el café no pudo continuar liberando calor al aire para que se enfriara por debajo de la temperatura ambiente.

¹² momento en el que sería más tostado que asado.

¹³ Que puede ser tan dañina como las enfermedades.

¹⁴ O, más probablemente, tres personas iniciaron el rumor. Apuesto a que Jeff, Jamie y Jason lo empezaron. ¡Tanto por decirle algo a tus mejores amigos en confianza!

¹⁵ Véase, por ejemplo, Ejemplo 6.1.2.

¹⁶ Es decir, las letras mayúsculas y minúsculas se tratan como caracteres diferentes.

¹⁷ Dado que solo hay 94 caracteres de teclado ASCII distintos, para lograr esta fuerza, se debe aumentar el número de caracteres en la contraseña.

¹⁸ Derivado de la Ecuación de Henderson-Hasselbalch. Ver Ejercicio 43 en la Sección 6.2. El propio Hasselbalch estaba estudiando el dióxido de carbono que se disuelve en la sangre, un proceso llamado acidosis metabólica.

¹⁹ Los críticos pueden preguntarse por qué los autores del libro han optado por discutir incluso la linealización de datos cuando la calculadora tiene una Regresión de Poder incorporada y lista para funcionar. Nuestra respuesta: habla con tu facultad de ciencias

²⁰ Hablando de limitaciones, al 3 de junio de 2009, había 19.273 casos confirmados de influenza A (H1N1). Esto está muy por encima de nuestra predicción de 10,739. Cada vez que se emite un nuevo reporte, el conjunto de datos aumenta y el modelo debe ser recalculado. Dejamos este recálculo al lector.

²¹ ¡Impresionante juego de palabras!

²² Este asado lo disfrutaron Jeff y su familia el 10 de junio de 2009. ¡Esto es un dato real, amigos!

²³ Los autores agradecen a la Dra. Wendy Marley y a su personal estos datos y a la Dra. Marcia Ballinger el permiso para utilizarlos en este problema.