8.1: Sistemas de Ecuaciones Lineales- Eliminación Gaussiana

Hasta ahora, cuando nos ocupábamos de resolver diferentes tipos de ecuaciones solo había una ecuación por resolver a la vez. Dada una ecuación\(f(x) = g(x)\), podríamos verificar nuestras soluciones geométricamente encontrando dónde se cruzan las gráficas\(y=f(x)\) y dónde se\(y=g(x)\) cruzan. Las\(x\) coordenadas de estos puntos de intersección corresponden a las soluciones a la ecuación\(f(x) = g(x)\), y las\(y\) coordenadas se ignoraron en gran medida. Si modificamos el problema y pedimos los puntos de intersección de las gráficas de\(y=f(x)\) y\(y=g(x)\), donde tanto la solución como\(y\) son de interés, tenemos lo que se conoce como un sistema de ecuaciones, generalmente escrito como\[\left\{ \begin{array}{rcl} y & = & f(x) \\ y & = & g(x) \\ \end{array} \right.\nonumber\] La notación 'corchete rizado' significa que\(x\) son encontrar todos los pares de puntos\((x,y)\) que satisfagan ambas ecuaciones. Comenzamos nuestro estudio de sistemas de ecuaciones revisando algunas nociones básicas de Álgebra Intermedia.

Definición 8.1.

Una ecuación lineal en dos variables es una ecuación de la forma\(a_{1} x + a_{2} y = c\) donde\(a_{1}\),\(a_{2}\) y\(c\) son números reales y al menos uno de\(a_{1}\) y\(a_{2}\) es distinto de cero.

Por razones que quedarán claras más adelante en la sección, estamos usando subíndices en la Definición 8.1 para indicar números reales diferentes, pero fijos, y esos subíndices no tienen un significado matemático más allá de eso. Por ejemplo,\(3x - \frac{y}{2} = 0.1\) es una ecuación lineal en dos variables con\(a_{1} = 3\),\(a_{2} = -\frac{1}{2}\) y\(c = 0.1\). También podemos considerar\(x = 5\) que es una ecuación lineal en dos variables ¹ identificando\(a_{1} = 1\),\(a_{2} = 0\), y\(c = 5\). Si\(a_{1}\) y\(a_{2}\) son ambos\(0\), entonces dependiendo de\(c\), obtenemos o una ecuación que siempre es verdadera, llamada identidad, o una ecuación que nunca es cierta, llamada contradicción. (Si\(c = 0\), entonces obtenemos\(0 = 0\), que siempre es cierto. Si\(c \neq 0\), entonces tendríamos\(0 \neq 0\), lo cual nunca es cierto.) A pesar de que las identidades y contradicciones tienen un papel importante que desempeñar en las próximas secciones, no las consideramos ecuaciones lineales. La clave para identificar ecuaciones lineales es señalar que las variables involucradas son a la primera potencia y que los coeficientes de las variables son números. Algunos ejemplos de ecuaciones que son no lineales son\(x^2 + y = 1\),\(xy = 5\) y\(e^{2x} + \ln(y) = 1\). Dejamos que el lector explique por qué estos no satisfacen la Definición 8.1. Por lo que sabemos de las Secciones 1.2 y 2.1, las gráficas de ecuaciones lineales son líneas. Si acoplamos dos o más ecuaciones lineales juntas, en efecto para encontrar los puntos de intersección de dos o más líneas, obtenemos un sistema de ecuaciones lineales en dos variables. Nuestro primer ejemplo revisa algunas de las técnicas básicas aprendidas por primera vez en Álgebra Intermedia.

Ejemplo 8.1.1

Resuelve los siguientes sistemas de ecuaciones. Comprueba tu respuesta algebraica y gráficamente.

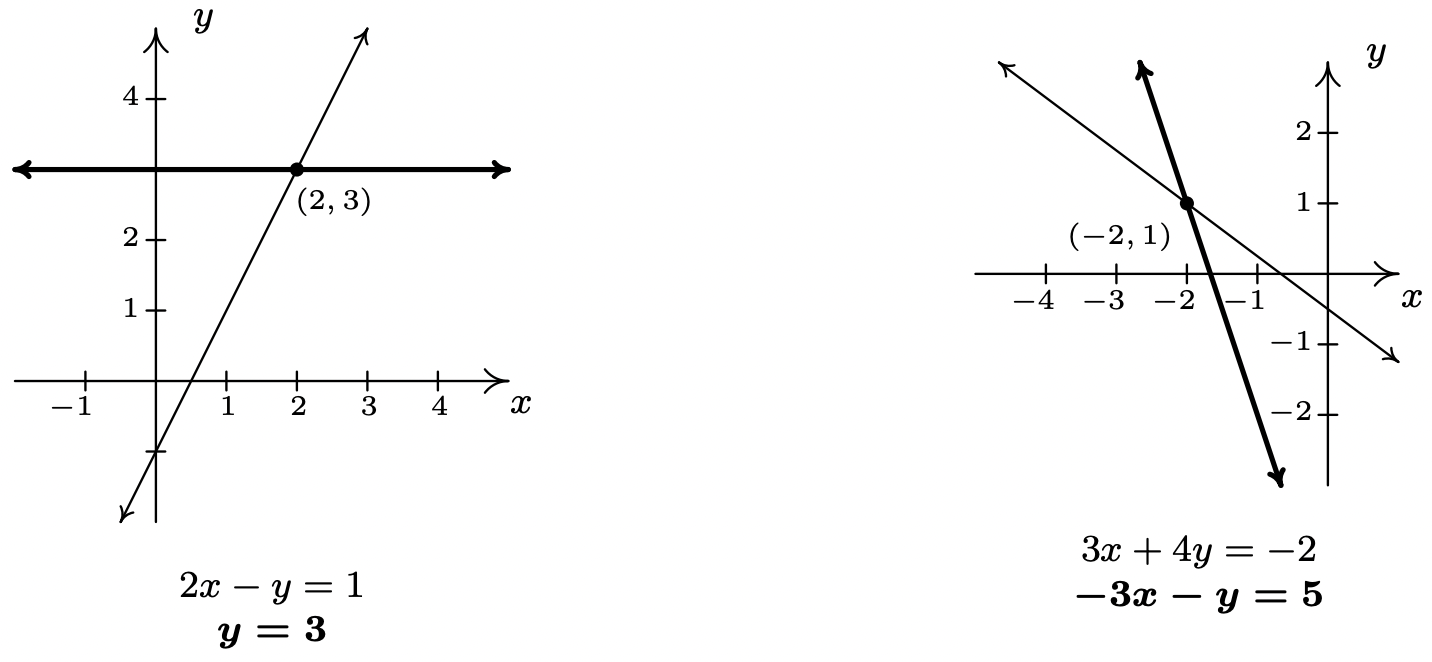
1. \(\left\{ \begin{array}{rcr} 2x - y & = & 1 \\ y & = & 3 \\ \end{array} \right.\)
2. \(\left\{ \begin{array}{rcr} 3x+4y & = & -2 \\ -3x-y & = & 5 \\ \end{array} \right.\)
3. \(\left\{ \begin{array}{rcr} \frac{x}{3} -\frac{4y}{5} & = & \frac{7}{5} \\[4pt] \frac{2x}{9} + \frac{y}{3} & = & \frac{1}{2} \\ \end{array} \right.\)
4. \(\left\{ \begin{array}{rcr} 2x - 4y & = & 6 \\ 3x -6y & = & 9\\ \end{array} \right.\)
5. \(\left\{ \begin{array}{rcr} 6x + 3y & = & 9 \\ 4x + 2y & = & 12 \\ \end{array} \right.\)
6. \(\left\{ \begin{array}{rcr} x - y & = & 0 \\ x + y & = & 2 \\ -2x + y & = & -2 \end{array} \right.\)

Solución

1. Nuestro primer sistema está casi resuelto para nosotros. Eso nos dice la segunda ecuación\(y=3\). Para encontrar el valor correspondiente de\(x\), sustituimos este valor por\(y\) en la primera ecuación a obtener\(2x - 3 = 1\), de manera que\(x = 2\). Nuestra solución al sistema es\((2,3)\). Para comprobar esto algebraicamente, sustituimos\(x=2\) y\(y=3\) en cada ecuación y vemos que están satisfechos. Vemos\(2(2) - 3 = 1\), y\(3=3\), según se requiera. Para verificar nuestra respuesta gráficamente, graficamos las líneas\(2x-y = 1\)\(y=3\) y verificamos que se cruzan en\((2,3)\).
2. Para resolver el segundo sistema, utilizamos el método de adición para eliminar la variable\(x\). Tomamos las dos ecuaciones como dadas y 'sumamos iguales a iguales' para obtener

   \[\begin{array}{lrcr} & 3x+4y & = & -2 \\ + & (-3x-y & = & 5 ) \\ \hline & 3y & = & 3\end{array}\nonumber\]

   Esto nos da\(y = 1\). Ahora sustituimos\(y=1\) en cualquiera de las dos ecuaciones, digamos\(-3x-y = 5\), para conseguir\(-3x-1 = 5\) así eso\(x = -2\). Nuestra solución es\((-2,1)\). Sustituyendo\(x=-2\) y\(y=1\) en la primera ecuación da\(3(-2) + 4(1) = -2\), lo cual es cierto, y, de igual manera, cuando\((-2, 1)\) registramos la segunda ecuación, obtenemos\(-3(-2) - 1 = 5\), que también es cierto. Geométricamente, las líneas\(3x+4y = -2\) y se\(-3x-y=5\) cruzan en\((-2,1)\).

   

3. Las ecuaciones en el tercer sistema son más accesibles si aclaramos los denominadores. Multiplicamos ambos lados de la primera ecuación por\(15\) y ambos lados de la segunda ecuación por\(18\) para obtener el sistema más amable, más gentil\[\left\{ \begin{array}{rcr} 5x - 12y & = & 21 \\ 4x + 6y & = & 9 \\ \end{array} \right.\nonumber\] Sumando estas dos ecuaciones directamente no logra eliminar ninguna de las variables, pero observamos que si multiplicamos la primera ecuación por\(4\) y el segundo por\(-5\), estaremos en condiciones de eliminar el\(x\) término

   \[\begin{array}{lrcr} & 20x-48y & = & 84 \\ + & (-20x-30y & = & -45 ) \\ \hline & -78y & = & 39\end{array}\nonumber\]

   De esto obtenemos\(y = -\frac{1}{2}\). Podemos evitar temporalmente demasiadas molestias eligiendo sustituir\(y = -\frac{1}{2}\) en una de las ecuaciones equivalentes que encontramos al borrar denominadores, digamos en\(5x - 12y = 21\). Obtenemos\(5x + 6 = 21\) lo que da\(x=3\). Nuestra respuesta es\(\left(3, -\frac{1}{2}\right)\). En este punto, no tenemos otra opción\(-\) para comprobar algebraicamente una respuesta, debemos ver si la respuesta satisface ambas ecuaciones originales, así que sustituimos\(x = 3\) y\(y = -\frac{1}{2}\) en ambas\(\frac{x}{3} -\frac{4y}{5} = \frac{7}{5}\) y\(\frac{2x}{9} + \frac{y}{3} = \frac{1}{2}\). Dejamos al lector verificar que la solución es correcta. Graficar ambas líneas involucradas con un cuidado considerable produce un punto de intersección de\(\left(3, -\frac{1}{2}\right)\).

4. Una calma escalofriante se asienta sobre nosotros a medida que nos acercamos con cautela a nuestro cuarto sistema. ¿Sus coeficientes enteros amigables desmienten algo más siniestro? Observamos que si multiplicamos ambos lados de la primera ecuación por\(3\) y ambos lados de la segunda ecuación por\(-2\), estamos listos para eliminar el\(x\)

   \[\begin{array}{lrcr} & 6x-12y & = & 18 \\ + & (-6x+12y & = & -18 ) \\ \hline & 0 & = & 0\end{array}\nonumber\]

   Eliminamos no sólo el\(x\), sino el\(y\) también y nos quedamos con la identidad\(0=0\). Esto significa que estas dos ecuaciones lineales diferentes son, de hecho, equivalentes. En otras palabras, si un par ordenado\((x,y)\) satisface la ecuación\(2x-4y = 6\), automáticamente satisface la ecuación\(3x-6y = 9\). Una forma de describir el conjunto de soluciones para este sistema es usar el método de roster ² y escribir\(\{(x,y) \, | \, 2x-4y = 6\}\). Si bien esto es correcto (y corresponde exactamente a lo que sucede gráficamente, como veremos en breve), aprovechamos esta oportunidad para introducir la noción de solución paramétrica a un sistema. Nuestro primer paso es resolver\(2x-4y = 6\) para una de las variables, digamos\(y = \frac{1}{2} x - \frac{3}{2}\). Para cada valor de\(x\), la fórmula\(y = \frac{1}{2} x - \frac{3}{2}\) determina el\(y\) -valor correspondiente de una solución. Como no tenemos ninguna restricción sobre\(x\), se llama variable libre. Dejamos\(x=t\), un llamado 'parámetro', y obtenemos\(y = \frac{1}{2} t - \frac{3}{2}\). Nuestro conjunto de soluciones puede describirse como\(\left\{ \left(t, \frac{1}{2} t - \frac{3}{2}\right) \, | \, -\infty < t < \infty \right\}\). ³ Para valores específicos de\(t\), podemos generar soluciones. Por ejemplo, nos\(t=0\) da la solución\(\left(0,-\frac{3}{2}\right)\); nos\(t = 117\) da\((117,57)\), y si bien podemos verificar fácilmente que cada una de estas soluciones particulares satisfaga ambas ecuaciones, la pregunta es ¿cómo verificamos nuestra respuesta general algebraicamente? Igual que siempre. Afirmamos que para cualquier número real\(t\), el par\(\left(t, \frac{1}{2} t - \frac{3}{2}\right)\) satisface ambas ecuaciones. Sustituyendo\(x = t\) y\(y = \frac{1}{2} t - \frac{3}{2}\) en\(2x - 4y = 6\) da\(2t - 4\left(\frac{1}{2} t - \frac{3}{2}\right) = 6\). Simplificando, obtenemos\(2t - 2t + 6 = 6\), lo que siempre es cierto. Del mismo modo, cuando hacemos estas sustituciones en la ecuación\(3x-6y = 9\), obtenemos\(3t - 6\left(\frac{1}{2} t - \frac{3}{2}\right) = 9\) cuál se reduce a\(3t - 3t + 9 = 9\), así que se comprueba, también. Geométricamente,\(2x-4y = 6\) y\(3x-6y=9\) son la misma línea, lo que significa que se cruzan en cada punto de sus gráficas. Se anima al lector a pensar en cómo nuestra solución paramétrica dice exactamente eso.

   

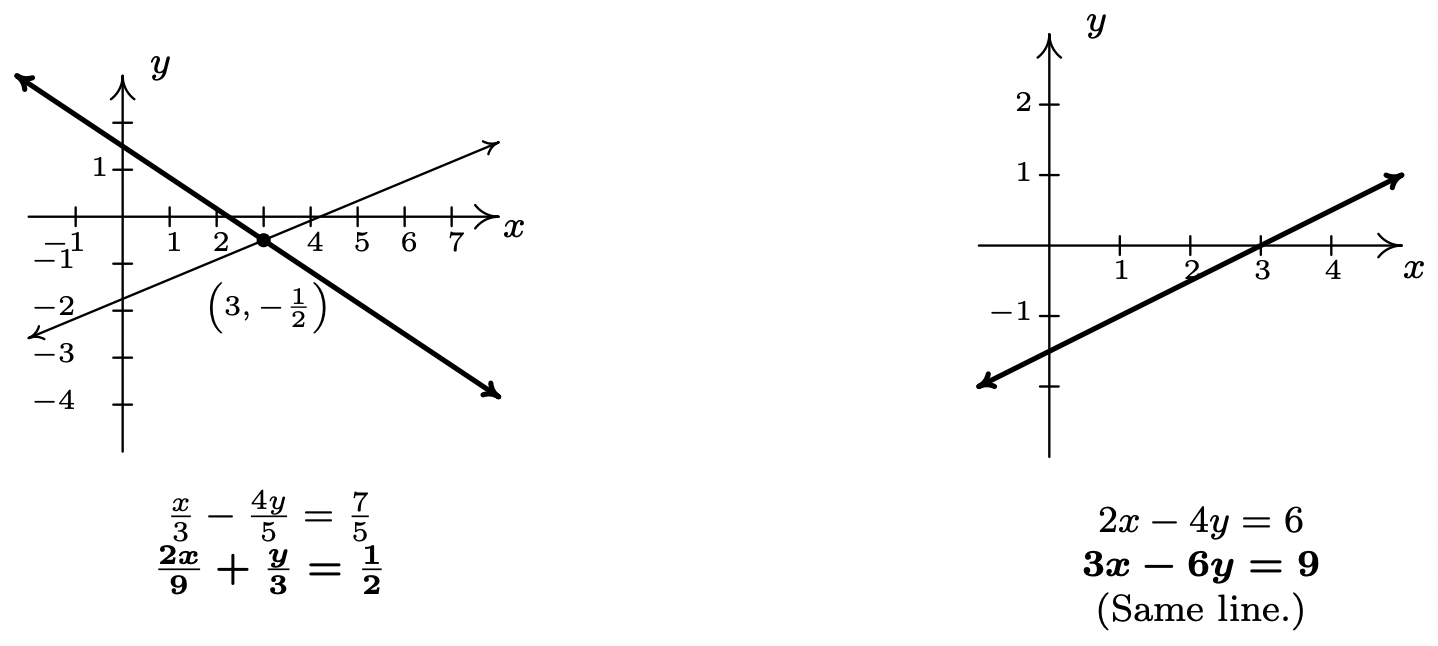
5. Multiplicando ambos lados de la primera ecuación por\(2\) y ambos lados de la segunda ecuación por\(-3\), establecemos el escenario para eliminar\(x\)

   \[\begin{array}{lrcr} & 12x + 6y & = & 18 \\ + & (-12x-6y & = & -36 ) \\ \hline & 0 & = & -18 \end{array}\nonumber\]

   Al igual que en el ejemplo anterior, ambos\(x\) y\(y\) abandonaron la ecuación, pero nos quedamos con una contradicción irrevocable,\(0 = -18\). Esto nos dice que es imposible encontrar un par\((x,y)\) que satisfaga ambas ecuaciones; es decir, el sistema no tiene solución. Gráficamente, las líneas\(6x + 3y =9\) y\(4x + 2y = 12\) son distintas y paralelas, por lo que no se cruzan.

6. Podemos comenzar a resolver nuestro último sistema sumando las dos primeras ecuaciones

   \[\begin{array}{lrcr} & x - y & = & 0 \\ + & (x + y & = & 2 ) \\ \hline & 2x & = & 2 \end{array}\nonumber\]

   que da\(x = 1\). Sustituir esto en la primera ecuación da\(1 - y = 0\) así que\(y = 1\). Parece que hemos determinado una solución a nuestro sistema,\((1,1)\). Si bien esto comprueba en las dos primeras ecuaciones, cuando sustituimos\(x=1\) y\(y=1\) en la tercera ecuación, obtenemos\(-2(1) + (1) = -2\) lo que simplifica a la contradicción\(-1 = -2\). Graficando las líneas\(x-y=0\),\(x+y = 2\), y\(-2x+y=-2\), vemos que las dos primeras líneas, de hecho, se cruzan en\((1,1)\), sin embargo, las tres líneas nunca se cruzan en el mismo punto simultáneamente, que es lo que se requiere si se va a encontrar una solución al sistema.

   

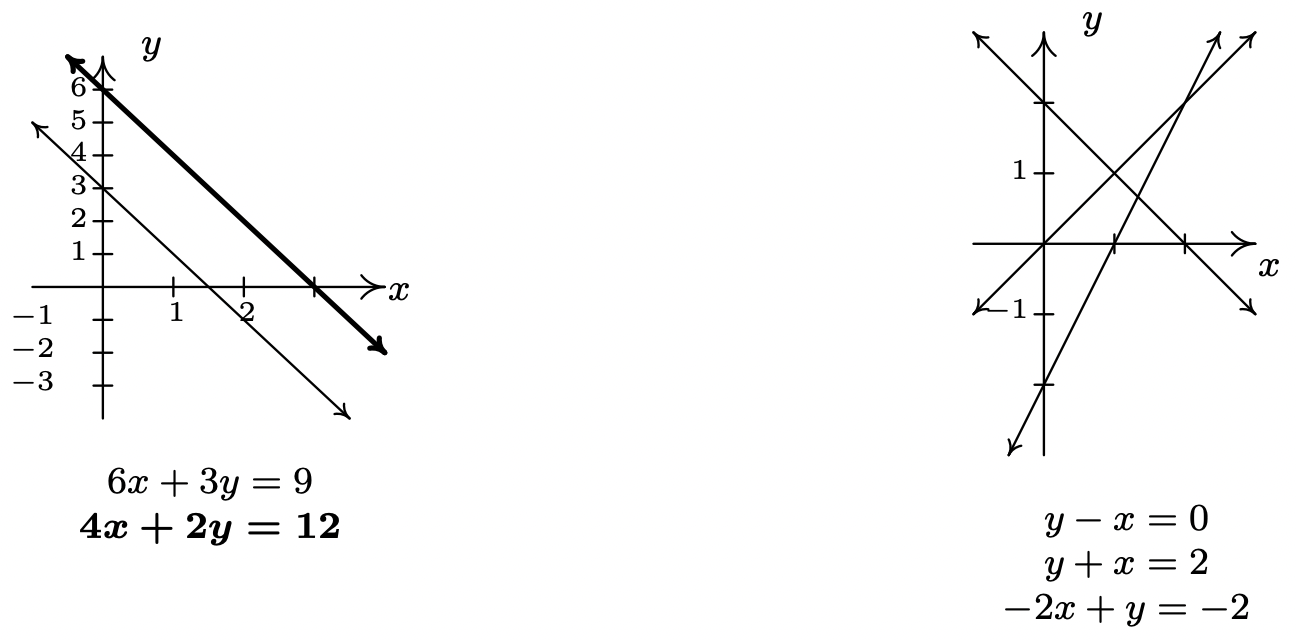
Algunos comentarios sobre el Ejemplo 8.1.1 están en orden. Es claro que algunos sistemas de ecuaciones tienen soluciones, y otros no. A los que tienen soluciones se les llama consistentes, a los que no tienen solución se les llama inconsistentes. También distinguimos los dos tipos diferentes de comportamiento entre sistemas consistentes. Los que admiten variables libres se denominan dependientes; los que no tienen variables libres se denominan independientes. ⁴ Usando este nuevo vocabulario, clasificamos los números 1, 2 y 3 en el Ejemplo 8.1.1 como sistemas independientes consistentes, el número 4 es consistente dependiente y los números 5 y 6 son inconsistentes. ⁵ El sistema en 6 anterior se llama sobredeterminado, ya que tenemos más ecuaciones que variables. ⁶ No es sorprendente que un sistema con más variables que ecuaciones se llame subdeterminado. Si bien el sistema en el número 6 anterior está sobredeterminado e inconsistente, existen sistemas consistentes sobredeterminados (tanto dependientes como independientes) y dejamos que el lector piense en lo que sucede algebraica y geométricamente en estos casos. Del mismo modo, existen sistemas subdeterminados consistentes e inconsistentes, ⁷ pero un sistema consistente subdeterminado de ecuaciones lineales es necesariamente dependiente. ⁸

Para mover esta sección más allá de una revisión del Álgebra Intermedia, ahora definimos lo que se entiende por una ecuación lineal en\(n\) variables.

Definición 8.2.

Una ecuación lineal en n variables,\(x_{1}\),\(x_{2}\),...\(x_{n}\), es una ecuación de la forma\(a_{1} x_{1} + a_{2} x_{2} + \ldots + a_{n} x_{n} = c\) donde\(a_{1}\),\(a_{2}\),...\(a_{n}\) y\(c\) son números reales y al menos uno de\(a_{1}\),\(a_{2}\),...,\(a_{n}\) es distinto de cero.

En lugar de usar variables más familiares como\(x\)\(y\), e incluso\(z\) y/o\(w\) en la Definición 8.2, usamos subíndices para distinguir las diferentes variables. No tenemos idea de cuántas variables pueden estar involucradas, así que usamos números para distinguirlas en lugar de letras. (Hay un suministro interminable de números distintos.) Como ejemplo, la ecuación lineal\(3x_{1} - x_{2} = 4\) representa la misma relación entre las variables\(x_{1}\) y\(x_{2}\) como lo\(3x-y=4\) hace la ecuación entre las variables\(x\) y\(y\). Además, así como no podemos combinar los términos en la expresión\(3x-y\), no podemos combinar los términos en la expresión\(3x_{1} - x_{2}\). El acoplamiento de más de una ecuación lineal en\(n\) variables da como resultado un sistema de ecuaciones lineales en n variables. A la hora de resolver estos sistemas, cada vez es más importante hacer un seguimiento de qué operaciones se realizan a qué ecuaciones y desarrollar una estrategia basada en el tipo de manipulaciones que ya hemos empleado. Para ello, primero recordamos las maniobras que pueden aplicarse a un sistema de ecuaciones lineales que dan como resultado un sistema equivalente. ⁹

Teorema 8.1.

Dado un sistema de ecuaciones, los siguientes movimientos darán como resultado un sistema equivalente de ecuaciones.

• Intercambien la posición de dos ecuaciones cualesquiera.
• Reemplazar una ecuación con un múltiplo distinto de cero de sí mismo. ^a
• Reemplazar una ecuación por sí misma más un múltiplo distinto de cero de otra ecuación.

---

^a Es decir, una ecuación que resulta de multiplicar ambos lados de la ecuación por el mismo número distinto de cero.

Hemos visto bastantes instancias del segundo y tercer movimiento en el Teorema 8.1 cuando resolvimos los sistemas en el Ejemplo 8.1.1. El primer movimiento, si bien obviamente admite un sistema equivalente, parece tonto. Nuestra percepción cambiará a medida que consideremos más ecuaciones y más variables en esta, y secciones posteriores.

Considerar el sistema de ecuaciones

\[\left\{ \begin{array}{rcr} x-\frac{1}{3}y+\frac{1}{2}z & = & 1 \\[4pt] y - \frac{1}{2} z & = & 4 \\[4pt] z & = & -1 \\ \end{array} \right.\nonumber\]

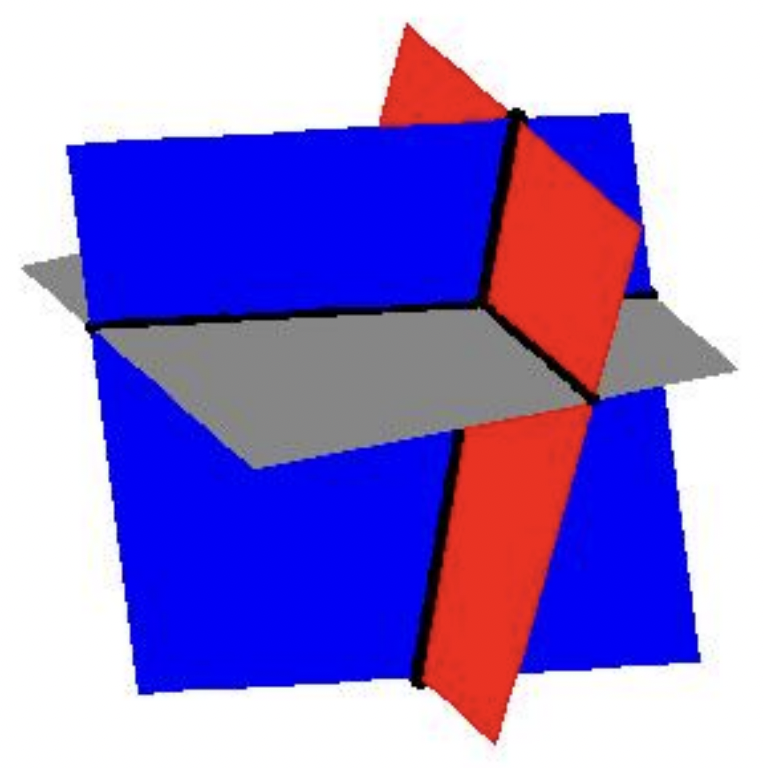
Claramente\(z = -1\), y sustituimos esto en la segunda ecuación\(y - \frac{1}{2} (-1) = 4\) para obtener\(y = \frac{7}{2}\). Por último, sustituimos\(y = \frac{7}{2}\) y\(z=-1\) en la primera ecuación para obtener\(x - \frac{1}{3}\left(\frac{7}{2}\right) + \frac{1}{2}(-1) = 1\), así que eso\(x = \frac{8}{3}\). El lector puede verificar que estos valores de\(x\),\(y\) y\(z\) satisfacer las tres ecuaciones originales. Es tentador para nosotros escribir la solución a este sistema extendiendo la\((x,y)\) notación habitual\((x,y,z)\) y enumerando nuestra solución como\(\left(\frac{8}{3},\frac{7}{2},-1\right)\). La pregunta rápidamente se convierte en ¿qué representa un 'triple ordenado' como\(\left(\frac{8}{3},\frac{7}{2},-1\right)\) representa? Así como los pares ordenados se utilizan para ubicar puntos en el plano bidimensional, se pueden usar triples ordenados para ubicar puntos en el espacio. ¹⁰ Además, al igual que las ecuaciones que involucran las variables\(x\) y\(y\) describen gráficas de líneas unidimensionales y curvas en el plano bidimensional, ecuaciones que involucran variables\(x\)\(y\), y\(z\) describen objetos llamados superficies en el espacio tridimensional. Cada una de las ecuaciones del sistema anterior se puede visualizar como un plano situado en tres espacios. Geométricamente, el sistema está tratando de encontrar la intersección, o punto común, de los tres planos. Si imaginas tres hojas de papel de cuaderno cada una representando una porción de estos planos, comenzará a ver las complejidades que implica cómo tres de esos planos pueden cruzarse. A continuación se muestra un boceto de los tres planos. Resulta que dos cualesquiera de estos planos se cruzan en una línea, ¹¹ por lo que nuestro punto de intersección es donde se encuentran las tres líneas.

Dado que la geometría para ecuaciones que involucran más de dos variables es complicada, enfocaremos nuestros esfuerzos en el álgebra. Regresando al sistema

\[\left\{ \begin{array}{rcr} x-\frac{1}{3}y+\frac{1}{2}z & = & 1 \\[4pt] y - \frac{1}{2} z & = & 4 \\[4pt] z & = & -1 \\ \end{array} \right.\nonumber\]

notamos que la razón por la que fue tan fácil de resolver es que la tercera ecuación está resuelta para\(z\), la segunda ecuación implica solo\(y\) y\(z\), y como el coeficiente de\(y\) es\(1\), facilita la resolución por\(y\) usar nuestro valor conocido para\(z\). Por último, el coeficiente de\(x\) en la primera ecuación está\(1\) facilitando la sustitución de los valores conocidos de\(y\)\(z\) y luego resolverlos\(x\). Formalizamos este patrón a continuación para los sistemas más generales de ecuaciones lineales. Nuevamente, utilizamos variables subcriptadas para describir el caso general. La variable con el subíndice más pequeño en una ecuación dada se llama típicamente la variable principal de esa ecuación.

Definición 8.3: Forma triangular

Un sistema de ecuaciones lineales con variables\(x_{1}\),\(x_{2}\),...\(x_{n}\) se dice que está en forma triangular siempre que se mantengan todas las siguientes condiciones:

1. Los subíndices de las variables en cada ecuación siempre están aumentando de izquierda a derecha.
2. La variable principal en cada ecuación tiene coeficiente\(1\).
3. El subíndice en la variable principal en una ecuación dada es mayor que el subíndice en la variable principal en la ecuación anterior.
4. Cualquier ecuación sin variables ^a no puede colocarse por encima de una ecuación con variables.

---

necesariamente ^una identidad o contradicción

En nuestro sistema anterior, si hacemos las elecciones obvias\(x = x_{1}\)\(y = x_{2}\),, y\(z = x_{3}\), vemos que el sistema está en forma triangular. ¹² Un ejemplo de un sistema más complicado en forma triangular es

\[\left\{ \begin{array}{rcr} x_1 - 4x_3 + x_4 - x_6 & = & 6 \\ x_2 + 2x_3 & = & 1 \\ x_4 + 3x_5 - x_6 & = & 8 \\ x_5 + 9x_6 & = & 10 \end{array} \right.\nonumber\]

Nuestro objetivo en adelante será transformar un sistema dado de ecuaciones lineales en forma triangular utilizando los movimientos del Teorema 8.1.

Ejemplo 8.1.2

Utilice el Teorema 8.1 para poner los siguientes sistemas en forma triangular y luego resolver el sistema si es posible. Clasifique cada sistema como consistente independiente, consistente dependiente o inconsistente.

1. \(\left\{ \begin{array}{rcr} 3x-y+z & = & 3 \\ 2x-4y+3z & = & 16 \\ x-y+z & = & 5 \\ \end{array} \right.\)
2. \(\left\{ \begin{array}{rcr} 2x+3y-z & = & 1 \\ 10x-z & = & 2 \\ 4x-9y+2z & = & 5 \\ \end{array} \right.\)
3. \(\left\{ \begin{array}{rcr} 3x_{1} +x_{2} + x_{4} & = & 6 \\ 2x_{1} + x_{2} -x_{3} & = & 4 \\ x_{2} -3x_{3} -2x_{4} & = & 0 \end{array} \right.\)

Solución

1. Para la definición, etiquetamos la ecuación superior en el sistema\(E1\), la ecuación debajo de eso\(E2\), y así sucesivamente. Ahora intentamos poner el sistema en forma triangular utilizando un algoritmo conocido como Eliminación Gaussiana. Lo que esto significa es que, a partir de\(x\), transformamos el sistema para que se cumplan las condiciones 2 y 3 de la Definición 8.3. Después pasamos a la siguiente variable, en este caso\(y\), y repetimos. Dado que las variables en todas las ecuaciones tienen un orden consistente de izquierda a derecha, nuestro primer movimiento es obtener un lugar\(x\) in\(E1\) con un coeficiente de\(1\). Si bien hay muchas formas de hacer esto, la más fácil es aplicar el primer movimiento enumerado en el Teorema 8.1 e intercambiar\(E1\) y\(E3\).

   \[\begin{array}{ccc} \left\{ \begin{array}{lrcr} (E1) & 3x-y+z & = & 3 \\ (E2) & 2x-4y+3z & = & 16 \\ (E3) & x-y+z & = & 5 \\ \end{array} \right. & \xrightarrow{\text{Switch $E1$ and $E3$}} & \left\{ \begin{array}{lrcr} (E1) & x-y+z & = & 5 \\ (E2) & 2x-4y+3z & = & 16 \\ (E3) & 3x-y+z & = & 3 \\ \end{array} \right. \end{array}\nonumber\]

   Para satisfacer la Definición 8.3, necesitamos eliminar los\(x\)'s de\(E2\) y\(E3\). Logramos esto reemplazando cada uno de ellos con una suma de sí mismos y un múltiplo de\(E1\). Para eliminar el\(x\) de\(E2\), necesitamos multiplicar\(E1\) por\(-2\) luego sumar; para eliminar el\(x\) de\(E3\), necesitamos multiplicar\(E1\) por\(-3\) luego sumar. Aplicando el tercer movimiento listado en el Teorema 8.1 dos veces, obtenemos

   \[\begin{array}{ccc} \left\{ \begin{array}{lrcr} (E1) & x-y+z & = & 5 \\ (E2) & 2x-4y+3z & = & 16 \\ (E3) & 3x-y+z & = & 3 \\ \end{array} \right. & \xrightarrow[\text{Replace $E3$ with $-3E1 + E3$}]{\text{Replace $E2$ with $-2E1 + E2$}} & \left\{ \begin{array}{lrcr} (E1) & x-y+z & = & 5 \\ (E2) & -2y+z & = & 6 \\ (E3) & 2y-2z & = & -12 \\ \end{array} \right. \end{array}\nonumber\]

   Ahora hacemos cumplir las condiciones establecidas en la Definición 8.3 para la variable\(y\). Para ello necesitamos obtener el coeficiente de\(y\) en\(E2\) igual a\(1\). Aplicamos el segundo movimiento enumerado en el Teorema del Teorema 8.1 y\(E2\) reemplazamos por sí mismo tiempos\(-\frac{1}{2}\).

   \[\begin{array}{ccc} \left\{ \begin{array}{lrcr} (E1) & x-y+z & = & 5 \\ (E2) & -2y+z & = & 6 \\ (E3) & 2y-2z & = & -12 \\ \end{array} \right. & \xrightarrow{\text{Replace $E2$ with $-\frac{1}{2}E2$}} & \left\{ \begin{array}{lrcr} (E1) & x-y+z & = & 5 \\ (E2) & y - \frac{1}{2}z & = & -3\\ (E3) & 2y-2z & = & -12 \\ \end{array} \right. \end{array}\nonumber\]

   Para eliminar el\(y\) in\(E3\),\(-2E2\) le sumamos.

   \[\begin{array}{ccc} \left\{ \begin{array}{lrcr} (E1) & x-y+z & = & 5 \\ (E2) & y - \frac{1}{2}z & = & -3\\ (E3) & 2y-2z & = & -12 \\ \end{array} \right. & \xrightarrow{\text{Replace $E3$ with $-2E2 + E3$}} & \left\{ \begin{array}{lrcr} (E1) & x-y+z & = & 5 \\ (E2) & y - \frac{1}{2}z & = & -3\\ (E3) & -z & = & -6 \\ \end{array} \right. \end{array}\nonumber\]

   Finalmente, aplicamos el segundo movimiento del Teorema 8.1 por última vez y multiplicamos\(E3\) por\(-1\) para satisfacer las condiciones de la Definición 8.3 para la variable\(z\).

   \[\begin{array}{ccc} \left\{ \begin{array}{lrcr} (E1) & x-y+z & = & 5 \\ (E2) & y - \frac{1}{2}z & = & -3\\ (E3) & -z & = & -6 \\ \end{array} \right. & \xrightarrow{\text{Replace $E3$ with $-1E3$}} & \left\{ \begin{array}{lrcr} (E1) & x-y+z & = & 5 \\ (E2) & y - \frac{1}{2}z & = & -3\\ (E3) & z & = & 6 \\ \end{array} \right. \end{array}\nonumber\]

   Ahora procedemos a sustituir. Conectarse\(z=6\) a\(E2\) da\(y - 3 = -3\) para que\(y = 0\). Con\(y=0\) y\(z=6\),\(E1\) se convierte\(x - 0 + 6 = 5\), o\(x = -1\). Nuestra solución es\((-1,0,6)\). Dejamos al lector verificar que sustituir los valores respectivos por\(x\),\(y\), y\(z\) en el sistema original da como resultado tres identidades. Ya que hemos encontrado una solución, el sistema es consistente; como no hay variables libres, es independiente.

2. Procediendo como hicimos en 1, nuestro primer paso es obtener una ecuación con\(x\) en la\(E1\) posición con\(1\) como su coeficiente. Como no hay una solución fácil, multiplicamos\(E1\) por\(\frac{1}{2}\).

   \[\begin{array}{ccc} \left\{ \begin{array}{lrcr} (E1) & 2x+3y-z & = & 1 \\ (E2) & 10x-z & = & 2 \\ (E3) & 4x-9y+2z & = & 5 \\ \end{array} \right. & \xrightarrow{\text{Replace $E1$ with $\frac{1}{2}E1$}} & \left\{ \begin{array}{lrcr} (E1) & x+\frac{3}{2}y-\frac{1}{2}z & = & \frac{1}{2} \\ (E2) & 10x-z & = & 2 \\ (E3) & 4x-9y+2z & = & 5 \\ \end{array} \right. \end{array}\nonumber\]

   Ahora es el momento de encargarse de los\(x\)'s en\(E2\) y\(E3\).

   \[\begin{array}{ccc} \left\{ \begin{array}{lrcr} (E1) & x+\frac{3}{2}y-\frac{1}{2}z & = & \frac{1}{2} \\ (E2) & 10x-z & = & 2 \\ (E3) & 4x-9y+2z & = & 5 \\ \end{array} \right. & \xrightarrow[\text{Replace $E3$ with $-4E1 + E3$}]{\text{Replace $E2$ with $-10E1 + E2$}} & \left\{ \begin{array}{lrcr} (E1) & x+\frac{3}{2}y-\frac{1}{2}z & = & \frac{1}{2} \\ (E2) & -15y+4z & = & -3 \\ (E3) & -15y+4z & = & 3 \\ \end{array} \right. \end{array}\nonumber\]

   Nuestro siguiente paso es obtener el coeficiente de\(y\) en\(E2\) igual a\(1\). Para ello, tenemos

   \[\begin{array}{ccc} \left\{ \begin{array}{lrcr} (E1) & x+\frac{3}{2}y-\frac{1}{2}z & = & \frac{1}{2} \\[4pt] (E2) & -15y+4z & = & -3 \\[4pt] (E3) & -15y+4z & = & 3 \\ \end{array} \right. & \xrightarrow{\text{Replace $E2$ with $-\frac{1}{15}E2$}} & \left\{ \begin{array}{lrcr} (E1) & x+\frac{3}{2}y-\frac{1}{2}z & = & \frac{1}{2} \\[4pt] (E2) & y - \frac{4}{15}z & = & \frac{1}{5} \\[4pt] (E3) & -15y+4z & = & 3 \\ \end{array} \right. \end{array}\nonumber\]

   Por último, nos deshacemos\(E3\) de\(y\).

   \[\begin{array}{ccc} \left\{ \begin{array}{lrcr} (E1) & x+\frac{3}{2}y-\frac{1}{2}z & = & \frac{1}{2} \\[4pt] (E2) & y - \frac{4}{15}z & = & \frac{1}{5} \\[4pt] (E3) & -15y+4z & = & 3 \\ \end{array} \right. & \xrightarrow{\text{Replace $E3$ with $15E2 + E3$}} & \left\{ \begin{array}{lrcr} (E1) & x-y+z & = & 5 \\[4pt] (E2) & y - \frac{1}{2}z & = & -3\\[4pt] (E3) & 0 & = & 6 \\ \end{array} \right. \end{array}\nonumber\]

   La última ecuación,\(0=6\), es una contradicción por lo que el sistema no tiene solución. Según el Teorema 8.1, ya que este sistema no tiene soluciones, tampoco el original, así tenemos un sistema inconsistente.

3. Para nuestro último sistema, comenzamos multiplicando\(E1\) por\(\frac{1}{3}\) para obtener un coeficiente de\(1\) on\(x_{1}\).

   \[\begin{array}{ccc} \left\{ \begin{array}{lrcr} (E1) & 3x_1 +x_2 + x_4 & = & 6 \\ (E2) & 2x_1 + x_2 -x_3 & = & 4 \\ (E3) & x_2 -3x_3 -2x_4 & = & 0 \\ \end{array} \right. & \xrightarrow{\text{Replace $E1$ with $\frac{1}{3}E1$}} & \left\{ \begin{array}{lrcr} (E1) & x_1 + \frac{1}{3}x_2 + \frac{1}{3}x_4 & = & 2 \\ (E2) & 2x_1 + x_2 -x_3 & = & 4 \\ (E3) & x_2 -3x_3 -2x_4 & = & 0 \\ \end{array} \right. \end{array}\nonumber\]

   A continuación eliminamos\(x_{1}\) de\(E2\)

   \[\begin{array}{ccc} \left\{ \begin{array}{lrcr} (E1) & x_1 + \frac{1}{3}x_2 + \frac{1}{3}x_4 & = & 2 \\ [3pt] (E2) & 2x_1 + x_2 -x_3 & = & 4 \\[4pt] (E3) & x_2 -3x_3 -2x_4 & = & 0 \\ \end{array} \right. & \xrightarrow[\text{with $-2E1 + E2$}]{\text{Replace $E2$}} & \left\{ \begin{array}{lrcr} (E1) & x_1 + \frac{1}{3}x_2 + \frac{1}{3}x_4 & = & 2 \\[4pt] (E2) & \frac{1}{3} x_2 -x_3 -\frac{2}{3}x_4 & = & 0 \\[4pt] (E3) & x_2 -3x_3 -2x_4 & = & 0 \\ \end{array} \right. \end{array}\nonumber\]

   Cambiamos\(E2\) y\(E3\) para obtener un coeficiente de\(1\) for\(x_{2}\).

   \[\begin{array}{ccc} \left\{ \begin{array}{lrcr} (E1) & x_1 + \frac{1}{3}x_2 + \frac{1}{3}x_4 & = & 2 \\ [3pt] (E2) & \frac{1}{3} x_2 -x_3 -\frac{2}{3}x_4 & = & 0 \\[4pt] (E3) & x_2 -3x_3 -2x_4 & = & 0 \\ \end{array} \right. & \xrightarrow{\text{Switch $E2$ and $E3$}} & \left\{ \begin{array}{lrcr} (E1) & x_1 + \frac{1}{3}x_2 + \frac{1}{3}x_4 & = & 2 \\ [3pt] (E2) & x_2 -3x_3 -2x_4 & = & 0 \\[4pt] (E3) & \frac{1}{3} x_2 -x_3 -\frac{2}{3}x_4 & = & 0 \\ \end{array} \right.\end{array}\nonumber\]

   Por último, eliminamos\(x_{2}\) en\(E3\).

   \[\begin{array}{ccc} \left\{ \begin{array}{lrcr} (E1) & x_1 + \frac{1}{3}x_2 + \frac{1}{3}x_4 & = & 2 \\ [3pt] (E2) & x_2 -3x_3 -2x_4 & = & 0 \\[4pt] (E3) & \frac{1}{3} x_2 -x_3 -\frac{2}{3}x_4 & = & 0 \\ \end{array} \right. & \xrightarrow[\text{with $-\frac{1}{3}E2 + E3$}]{\text{Replace $E3$} } & \left\{ \begin{array}{lrcr} (E1) & x_1 + \frac{1}{3}x_2 + \frac{1}{3}x_4 & = & 2 \\ [3pt] (E2) & x_2 -3x_3 -2x_4 & = & 0 \\ [3pt] (E3) & 0 & = & 0 \\ \end{array} \right.\end{array}\nonumber\]

   Ecuación\(E3\) reduce a\(0=0\), lo que siempre es cierto. Como no tenemos ecuaciones con\(x_{3}\) o\(x_{4}\) como variables principales, ambas son libres, lo que significa que tenemos un sistema dependiente consistente. Parametrizamos el conjunto de soluciones dejando\(x_{3} = s\) y\(x_{4} = t\) y obtenemos de\(E2\) eso\(x_{2} = 3s + 2t\). Sustituyendo esto y\(x_{4} = t\) en\(E1\), tenemos\(x_{1} + \frac{1}{3}\left( 3s+2t \right) + \frac{1}{3}t = 2\) lo que da\(x_{1} = 2 - s - t\). Nuestra solución es el conjunto\(\{ (2-s-t,2s+3t,s,t) \, | \, -\infty < s, t < \infty\}\). ¹³ Dejamos al lector verificar que las sustituciones\(x_{1} = 2-s-t\),\(x_{2} = 3s+2t\),\(x_{3} = s\) y\(x_{4} = t\) satisfacer las ecuaciones en el sistema original.

Como todos los algoritmos, la Eliminación Gaussiana tiene la ventaja de producir siempre lo que necesitamos, pero también puede ser ineficiente a veces. Por ejemplo, al resolver 2 anterior, queda claro después de que eliminamos los\(x\)'s en el segundo paso para obtener el sistema

\[\left\{ \begin{array}{lrcr} (E1) & x+\frac{3}{2}y-\frac{1}{2}z & = & \frac{1}{2} \\[4pt] (E2) & -15y+4z & = & -3 \\[4pt] (E3) & -15y+4z & = & 3 \\ \end{array} \right.\nonumber\]

que las ecuaciones\(E2\) y\(E3\) cuando se toman juntas forman una contradicción ya que tenemos lados idénticos de la mano izquierda y diferentes lados de la derecha. El algoritmo da dos pasos más para llegar a esta contradicción. También observamos que la sustitución en la Eliminación Gaussiana se retrasa hasta que se haga toda la eliminación, por lo que se denomina sustitución por retroceso. Esto también puede ser ineficiente en muchos casos. Ten la seguridad, la técnica de sustitución como la habrás aprendido en Álgebra Intermedia volverá a tomar protagonismo en la Sección 8.7. Por último, observamos que el sistema en 3 anterior está subdeterminado, y como es consistente, tenemos variables libres en nuestra respuesta. Cerramos esta sección con una aplicación estándar tipo 'mezcla' de sistemas de ecuaciones lineales.

Ejemplo 8.1.3

Lucas necesita crear\(500\) mililitros (mL) de una solución\(40 \%\) ácida. Tiene soluciones de stock\(30 \%\) y\(90 \%\) ácido así como toda el agua destilada que quiere. Establecer y resolver un sistema de ecuaciones lineales que determine todas las combinaciones posibles de las soluciones madre y agua que producirían la solución requerida.

Solución

Estamos tras tres incógnitas, la cantidad (en mL) de la solución\(30 \%\) madre (a la que llamaremos\(x\)), la cantidad (en mL) de la solución\(90 \%\) madre (a la que llamaremos\(y\)) y la cantidad (en mL) de agua (a la que llamaremos\(w\)). Ahora necesitamos determinar algunas relaciones entre estas variables. Nuestro objetivo es producir\(500\) mililitros de una solución\(40 \%\) ácida. Este producto tiene dos características definitorias. Primero, debe ser\(500\) mL; segundo, debe ser\(40 \%\) ácido. Tomamos cada una de estas cualidades a su vez. Primero, el volumen total de\(500\) mL debe ser la suma de los volúmenes aportados de las dos soluciones madre y el agua. Eso es\[\mbox{amount of $30 \%$ stock solution} + \mbox{amount of $90 \%$ stock solution} + \mbox{amount of water} = 500 \, \mbox{mL}\nonumber\] Usando nuestras variables definidas, esto se reduce a\(x+y+w = 500\). A continuación, tenemos que asegurarnos de que la solución final sea\(40 \%\) ácida. Dado que el agua no contiene ácido, el ácido vendrá únicamente de las soluciones madre. Encontramos\(40 \%\) que\(500\) mL es\(200\) mL lo que significa que la solución final debe contener\(200\) mL de ácido. Tenemos\[\mbox{amount of acid in $30 \%$ stock solution} + \mbox{amount of acid $90 \%$ stock solution} = 200 \, \mbox{mL}\nonumber\] La cantidad de ácido en\(x\) mL de\(30 \%\) stock es\(0.30x\) y la cantidad de ácido en\(y\) mL de\(90 \%\) solución es\(0.90y\). Nosotros tenemos\(0.30x + 0.90y = 200\). Convirtiendo a fracciones, ¹⁴ nuestro sistema de ecuaciones se convierte

\[\left\{ \begin{array}{rcl} x+y+w & = & 500 \\ \frac{3}{10}x + \frac{9}{10}y & = & 200 \\ \end{array} \right.\nonumber\]

Primero eliminamos el\(x\) de la segunda ecuación

\[\begin{array}{ccc} \left\{ \begin{array}{lrcr} (E1) & x+y+w & = & 500 \\ (E2) & \frac{3}{10}x + \frac{9}{10}y & = & 200 \\ \end{array} \right. & \xrightarrow{\text{Replace $E2$ with $-\frac{3}{10}E1 + E2$}} & \left\{ \begin{array}{lrcr} (E1) & x+y+w & = & 500 \\ (E2) & \frac{3}{5}y - \frac{3}{10}w & = & 50 \\ \end{array} \right. \end{array}\nonumber\]

A continuación, obtenemos un coeficiente de\(1\) sobre la variable principal en\(E2\)

\[\begin{array}{ccc} \left\{ \begin{array}{lrcr} (E1) & x+y+w & = & 500 \\ (E2) & \frac{3}{5}y - \frac{3}{10}w & = & 50 \\ \end{array} \right. & \xrightarrow{\text{Replace $E2$ with $\frac{5}{3}E2$}} & \left\{ \begin{array}{lrcr} (E1) & x+y+w & = & 500 \\ (E2) & y - \frac{1}{2}w & = & \frac{250}{3} \\ \end{array} \right. \end{array}\nonumber\]

Observe que no tenemos ninguna ecuación que determinar\(w\), y como tal,\(w\) es libre. Nos fijamos\(w = t\) y de\(E2\) get\(y = \frac{1}{2} t + \frac{250}{3}\). Sustituyendo en\(E1\) da\(x + \left(\frac{1}{2} t + \frac{250}{3}\right) + t = 500\) para que\(x = -\frac{3}{2} t + \frac{1250}{3}\). Este sistema es consistente, dependiente y su conjunto de soluciones lo es\(\{ \left(-\frac{3}{2} t + \frac{1250}{3}, \frac{1}{2} t + \frac{250}{3}, t\right) \, | \, - \infty < t < \infty\}\). Si bien esta respuesta comprueba algebraicamente, hemos descuidado tomar en cuenta eso\(x\),\(y\) y\(w\), al ser cantidades de ácido y agua, tienen que ser no negativas. Es decir,\(x \geq 0\),\(y \geq 0\) y\(w \geq 0\). La restricción nos\(x \geq 0\) da\(-\frac{3}{2} t + \frac{1250}{3} \geq 0\), o\(t \leq \frac{2500}{9}\). De\(y \geq 0\), obtenemos\(\frac{1}{2} t + \frac{250}{3} \geq 0\) o\(t \geq -\frac{500}{3}\). La condición\(z \geq 0\) rinde\(t \geq 0\), y vemos que cuando tomamos la intersección teórica establecida de estos intervalos, obtenemos\(0 \leq t \leq \frac{2500}{9}\). Nuestra respuesta final es\(\{ \left(-\frac{3}{2} t + \frac{1250}{3}, \frac{1}{2} t + \frac{250}{3}, t\right) \, | \,0 \leq t \leq \frac{2500}{9} \}\). ¿De qué utilidad práctica es nuestra respuesta? Supongamos que solo quedan\(100\) mL de la\(90 \%\) solución y está por caducar. ¿Podemos usarlo todo para hacer nuestra solución requerida? Tendríamos\(y = 100\) así que\(\frac{1}{2} t + \frac{250}{3} = 100\), y conseguimos\(t = \frac{100}{3}\). Esto significa que la cantidad de\(30 \%\) solución requerida es\(x = -\frac{3}{2} t + \frac{1250}{3} = -\frac{3}{2} \left(\frac{100}{3}\right) + \frac{1250}{3} = \frac{1100}{3}\) mL, y para el agua,\(w = t = \frac{100}{3}\) mL. Se invita al lector a verificar que la mezcla de estas tres cantidades de nuestras soluciones constituyentes produce la mezcla\(40 \%\) ácida requerida.

8.1.1. Ejercicios

(Revisar ejercicios) En los Ejercicios 1 - 8, haz un viaje por el carril de la memoria y resuelve el sistema dado usando sustitución y/o eliminación. Clasifique cada sistema como consistente independiente, consistente dependiente o inconsistente. Consulta tus respuestas tanto algebraica como gráficamente.

1. \(\left\{ \begin{array}{rcr} x+2y & = & 5 \\ x & = & 6 \end{array} \right.\)
2. \(\left\{ \begin{array}{rcr} 2y-3x & = & 1 \\ y & = & -3 \end{array} \right.\)
3. \(\left\{ \begin{array}{rcr} \frac{x+2y}{4} & = & -5 \\[5pt] \frac{3x-y}{2} & = & 1 \end{array} \right.\)
4. \(\left\{ \begin{array}{rcr} \frac{2}{3} x-\frac{1}{5}y & = & 3 \\[5pt] \frac{1}{2}x+\frac{3}{4}y& = & 1 \end{array} \right.\)
5. \(\left\{ \begin{array}{rcr} \frac{1}{2}x-\frac{1}{3}y & = & -1 \\[4pt] 2y-3x & = & 6 \end{array} \right.\)
6. \(\left\{ \begin{array}{rcr} x+4y & = & 6 \\[4pt] \frac{1}{12}x+\frac{1}{3}y& = & \frac{1}{2} \end{array} \right.\)
7. \(\left\{ \begin{array}{rcr} 3y-\frac{3}{2}x & = & -\frac{15}{2} \\[4pt] \frac{1}{2}x-y & = & \frac{3}{2} \end{array} \right.\)
8. \(\left\{ \begin{array}{rcr} \frac{5}{6}x+\frac{5}{3}y & = & -\frac{7}{3} \\[4pt] -\frac{10}{3}x-\frac{20}{3}y & = & 10 \end{array} \right.\)

En los Ejercicios 9 - 26, ponga cada sistema de ecuaciones lineales en forma triangular y resuelva el sistema si es posible. Clasifique cada sistema como consistente independiente, consistente dependiente o inconsistente.

9. \(\left\{ \begin{array}{rcr} -5x + y & = & 17 \\ x + y & = & 5 \end{array} \right.\)
10. \(\left\{ \begin{array}{rcr} x + y + z & = & 3 \\ 2x - y + z & = & 0 \\ -3x + 5y + 7z & = & 7 \end{array} \right.\)
11. \(\left\{ \begin{array}{rcr} 4x - y + z & = & 5 \\ 2y + 6z & = & 30 \\ x + z & = & 5 \end{array} \right.\)
12. \(\left\{ \begin{array}{rcr} 4x - y + z & = & 5 \\ 2y + 6z & = & 30 \\ x + z & = & 6 \end{array} \right.\)
13. \(\left\{ \begin{array}{rcr} x + y + z & = & -17 \\ y - 3z & = & 0 \end{array} \right.\)
14. \(\left\{ \begin{array}{rcr} x-2y+3z & = & 7 \\ -3x+y+2z & = & -5 \\ 2x+2y+z & = & 3 \end{array} \right.\)
15. \(\left\{ \begin{array}{rcr} 3x-2y+z & = & -5 \\ x+3y-z & = & 12 \\ x+y+2z & = & 0 \end{array} \right.\)
16. \(\left\{ \begin{array}{rcr} 2x-y+z& = & -1 \\ 4x+3y+5z & = & 1 \\ 5y+3z & = & 4 \end{array} \right.\)
17. \(\left\{ \begin{array}{rcr} x-y+z & = & -4 \\ -3x+2y+4z & = & -5 \\ x-5y+2z & = & -18 \end{array} \right.\)
18. \(\left\{ \begin{array}{rcr} 2x-4y+z & = & -7 \\ x-2y+2z & = & -2 \\ -x+4y-2z & = & 3 \end{array} \right.\)
19. \(\left\{ \begin{array}{rcr} 2x-y+z & = & 1 \\ 2x+2y-z & = & 1 \\ 3x+6y+4z & = & 9 \end{array} \right.\)
20. \(\left\{ \begin{array}{rcr} x-3y-4z & = & 3 \\ 3x+4y-z & = & 13 \\ 2x-19y-19z & = & 2 \end{array} \right.\)
21. \(\left\{ \begin{array}{rcr} x+y+z & = & 4 \\ 2x-4y-z& = & -1 \\ x-y & = & 2 \end{array} \right.\)
22. \(\left\{ \begin{array}{rcr} x-y+z & = & 8 \\ 3x+3y-9z & = & -6 \\ 7x-2y+5z & = & 39 \end{array} \right.\)
23. \(\left\{ \begin{array}{rcr} 2x-3y+z & = & -1 \\ 4x-4y+4z & = & -13 \\ 6x-5y+7z & = & -25 \end{array} \right.\)
24. \(\left\{ \begin{array}{rcr} 2x_{1} + x_{2} - 12x_{3} - x_{4} & = & 16 \\ -x_{1} + x_{2} + 12x_{3} - 4x_{4} & = & -5 \\ 3x_{1} + 2x_{2} - 16x_{3} - 3x_{4} & = & 25 \\ x_{1} + 2x_{2} - 5x_{4} & = & 11 \end{array} \right.\)
25. \(\left\{ \begin{array}{rcr} x_{1} - x_{3} & = & -2 \\ 2x_{2} - x_{4} & = & 0 \\ x_{1} - 2x_{2} + x_{3} & = & 0 \\ -x_{3} + x_{4} & = & 1 \end{array} \right.\)
26. \(\left\{ \begin{array}{rcr} x_{1} - x_{2} - 5x_{3} + 3x_{4} & = & -1 \\ x_{1} + x_{2} + 5x_{3} - 3x_{4} & = & 0 \\ x_{2} + 5x_{3} - 3x_{4} & = & 1 \\ x_{1} - 2x_{2} - 10x_{3} + 6x_{4} & = & -1 \end{array} \right.\)
27. Encuentra otras dos formas de la solución paramétrica al Ejercicio 11 anterior reorganizando las ecuaciones para que\(x\) o\(y\) pueda ser la variable libre.
28. Un buffet local cobra\(\$7.50\) por persona por el buffet básico y\(\$9.25\) por el buffet de lujo (que incluye patas de cangrejo). Si 27 comensales salieron a comer y la factura total era\(\$227.00\) antes de impuestos, ¿cuántos eligieron el buffet básico y cuántos eligieron el buffet de lujo?
29. En The Old Home Fill'er Up and Keep on A-truckin' Cafe, Mavis mezcla dos tipos diferentes de granos de café para producir una mezcla casera. El primer tipo cuesta $3 por libra y el segundo cuesta $8 por libra. ¿Cuánto de cada tipo usa Mavis para hacer 50 libras de una mezcla que cuesta $6 por libra?
30. Skippy tiene un total de\(\$\) 10,000 para dividir entre dos inversiones. Una cuenta ofrece interés\(3\%\) simple, y la otra cuenta ofrece interés\(8\%\) simple. Por razones fiscales, sólo puede ganar\(\$500\) en intereses todo el año. ¿Cuánto dinero debe invertir Skippy en cada cuenta para ganar\(\$500\) en intereses del año?
31. Una solución\(10 \%\) salina se debe mezclar con agua pura para producir 75 galones de una solución\(3\%\) salina. ¿Cuánto de cada uno se necesita?
32. [herbalteablend] En The Critter's Head Shop y Patchouli Emporium junto con sus malas hierbas secas, semillas de girasol y postales astrológicas venden una mezcla de té de hierbas. En peso, el té de hierbas Tipo I es 30% menta, 40% escaramujos y 30% manzanilla, Tipo II tiene porcentajes 40%, 20% y 40%, respectivamente, y Tipo III tiene porcentajes 35%, 30% y 35%, respectivamente. ¿Cuánto de cada tipo de té se necesita para hacer 2 libras de una nueva mezcla de té que sea partes iguales de menta, escaramujos y manzanilla?
33. Discuta con sus compañeros de clase cómo abordaría el Ejercicio 32 anterior si necesitaran usar hasta una libra de té Tipo I para hacer espacio en la repisa para un bote nuevo.
34. Si tratara de hacer 100 mL de una solución\(60\%\) ácida usando soluciones madre en\(20\%\) y\(40\%\), respectivamente, ¿cómo sería la forma triangular del sistema resultante? Explique.

RESPUESTAS

1. 
   Solución consistente e independiente\(\left(6, -\frac{1}{2}\right)\)

2. 
   Solución consistente e independiente\(\left(-\frac{7}{3}, -3\right)\)

3. 
   Solución consistente e independiente\(\left(-\frac{16}{7}, -\frac{62}{7}\right)\)

4. 
   Solución consistente e independiente\(\left(\frac{49}{12}, -\frac{25}{18}\right)\)

5. 
   Solución dependiente consistente\(\left(t, \frac{3}{2}t+3\right)\)
   para todos los números reales\(t\)

6. 
   Solución dependiente consistente\(\left(6-4t, t\right)\)
   para todos los números reales\(t\)

7. Inconsistente
   Sin solución

8. Inconsistente
   Sin solución

Debido a que la forma triangular no es única, solo damos una respuesta posible a esa parte de la pregunta. El tuyo puede ser diferente y seguir siendo correcto.

9. \(\left\{ \begin{array}{rcr} x + y & = & 5 \\ y & = & 7 \end{array} \right.\)

   Consistente e independiente

   Solución\((-2, 7)\)

10. \(\left\{ \begin{array}{rcr} x - \frac{5}{3}y - \frac{7}{3}z & = & -\frac{7}{3} \\[4pt] y + \frac{5}{4}z & = & 2 \\ z & = & 0 \end{array} \right.\)

    Consistente e independiente

    Solución\((1, 2, 0)\)

11. \(\left\{ \begin{array}{rcr} x - \frac{1}{4}y + \frac{1}{4}z & = & \frac{5}{4} \\[4pt] y + 3z & = & 15 \\ 0 & = & 0 \end{array} \right.\)

    Dependiente consistente

    Solución\((-t + 5, -3t + 15, t)\)

    para todos los números reales\(t\)

12. \(\left\{ \begin{array}{rcr} x - \frac{1}{4}y + \frac{1}{4}z & = & \frac{5}{4} \\[4pt] y + 3z & = & 15 \\ 0 & = & 1 \end{array} \right.\)

    Inconsistente

    Sin solución

13. \(\left\{ \begin{array}{rcr} x + y + z & = & -17 \\ y - 3z & = & 0 \end{array} \right.\)

    Dependiente consistente

    Solución\((-4t - 17, 3t, t)\)

    para todos los números reales\(t\)

14. \(\left\{ \begin{array}{rcr} x-2y+3z & = & 7 \\ y - \frac{11}{5}z & = & -\frac{16}{5} \\ z & = & 1 \\ \end{array} \right.\)

    Consistente e independiente

    Solución\((2,-1,1)\)

15. \(\left\{ \begin{array}{rcr} x+y+2z & = & 0 \\ y - \frac{3}{2}z & = & 6 \\ z & = & -2 \\ \end{array} \right.\)

    Consistente e independiente

    Solución\((1,3,-2)\)

16. \(\left\{ \begin{array}{rcr} x - \frac{1}{2} y + \frac{1}{2} z & = & -\frac{1}{2} \\[4pt] y + \frac{3}{5} z & = & \frac{3}{5} \\ 0 & = & 1 \\ \end{array} \right.\)

    Inconsistente

    no hay solución

17. \(\left\{ \begin{array}{rcr} x-y+z & = & -4 \\ y - 7z & = & 17 \\ z & = & -2 \\ \end{array} \right.\)

    Consistente e independiente

    Solución\((1,3,-2)\)

18. \(\left\{ \begin{array}{rcr} x-2y+2z & = & -2 \\ y & = & \frac{1}{2} \\ z & = & 1 \\ \end{array} \right.\)

    
    Solución consistente e independiente\(\left(-3,\frac{1}{2},1\right)\)

19. \(\left\{ \begin{array}{rcr} x-\frac{1}{2} y+\frac{1}{2} z & = & \frac{1}{2} \\[4pt] y - \frac{2}{3} z & = & 0 \\ z & = & 1 \\ \end{array} \right.\)

    Consistente e independiente

    Solución\(\left(\frac{1}{3},\frac{2}{3},1\right)\)

20. \(\left\{ \begin{array}{rcr} x-3y-4z & = & 3 \\ y + \frac{11}{13} z & = & \frac{4}{13} \\ 0 & = & 0 \\ \end{array} \right.\)

    Dependiente consistente

    Solución\(\left(\frac{19}{13} t + \frac{51}{13},-\frac{11}{13} t+\frac{4}{13},t\right)\)

    para todos los números reales\(t\)

21. \(\left\{ \begin{array}{rcr} x+y+z & = & 4 \\ y + \frac{1}{2} z & = & \frac{3}{2} \\ 0 & = & 1 \\ \end{array} \right.\)

    Inconsistente

    no hay solución

22. \(\left\{ \begin{array}{rcr} x- y + z & = & 8 \\ y -2z & = & -5 \\ z & = & 1 \\ \end{array} \right.\)

    Consistente e independiente

    Solución\(\left(4,-3,1\right)\)

23. \(\left\{ \begin{array}{rcr} x- \frac{3}{2} y + \frac{1}{2} z & = & -\frac{1}{2} \\[3pt] y + z & = & -\frac{11}{2} \\ 0 & = & 0 \\ \end{array} \right.\)

    Dependiente consistente

    Solución\(\left(-2t - \frac{35}{4},-t - \frac{11}{2},t\right)\)

    para todos los números reales\ (t\

24. \(\left\{ \begin{array}{rcr} x_{1} + \frac{2}{3}x_{2} - \frac{16}{3}x_{3} - x_{4} & = & \frac{25}{3} \\[4pt] x_{2} + 4x_{3} - 3x_{4} & = & 2 \\ 0 & = & 0 \\ 0 & = & 0 \end{array} \right.\)

    Dependiente consistente

    Solución\((8s - t + 7, -4s + 3t + 2, s, t)\)

    para todos los números reales\(s\) y\(t\)

25. \(\left\{ \begin{array}{rcr} x_{1} - x_{3} & = & -2 \\[4pt] x_{2} - \frac{1}{2}x_{4} & = & 0 \\[4pt] x_{3} - \frac{1}{2} x_{4} & = & 1 \\[4pt] x_{4} & = & 4 \end{array} \right.\)

    Consistente e independiente

    Solución\((1, 2, 3, 4)\)

26. \(\left\{ \begin{array}{rcr} x_{1} - x_{2} - 5x_{3} + 3x_{4} & = & -1 \\ x_{2} + 5x_{3} - 3x_{4} & = & \frac{1}{2} \\ 0 & = & 1 \\ 0 & = & 0 \end{array} \right.\)

    Inconsistente

    Sin solución

27. Si\(x\) es la variable libre entonces la solución es\((t, 3t, -t + 5)\) y si\(y\) es la variable libre entonces la solución es\(\left(\frac{1}{3}t, t, -\frac{1}{3}t + 5\right)\).
28. \(13\)eligió el buffet básico y\(14\) eligió el buffet de lujo.
29. Mavis necesita 20 libras de $3 por libra de café y 30 libras de $8 por libra de café.
30. Skippy necesita invertir\(\$\) 6000 en la\(3\%\) cuenta y\(\$\) 4000 en la\(8 \%\) cuenta.
31. \(22.5\)galones de la\(10 \%\) solución y\(52.5\) galones de agua pura.
32. \(\frac{4}{3}- \frac{1}{2}t\)libras de Tipo I,\(\frac{2}{3} - \frac{1}{2}t\) libras de Tipo II y\(t\) libras de Tipo III donde\(0 \leq t \leq \frac{4}{3}\).

---

Referencia

¹ Los críticos pueden argumentar que\(x = 5\) es claramente una ecuación en una variable. También se puede considerar una ecuación en 117 variables con los coeficientes de 116 variables establecidos en 0. Al igual que con muchas convenciones en Matemáticas, el contexto aclarará la situación.

² Véase la Sección 1.2 para una revisión de esta.

³ Tenga en cuenta que podríamos haber elegido con la misma facilidad\(2x − 4y = 6\) para resolver\(x\) para obtener\(x = 2y + 3\). Dejando\(y\) ser el parámetro\(t\), tenemos eso por cualquier valor de\(t\),\(x = 2t + 3\), cual\(\{(2 t+3, t) \mid-\infty<t<\infty\}\). No hay una forma correcta de parametrizar el conjunto de soluciones, por lo que siempre es mejor verificar tus respuestas.

⁴ En el caso de sistemas de ecuaciones lineales, independientemente del número de ecuaciones o variables, los sistemas independientes consistentes tienen exactamente una solución. Se anima al lector a pensar por qué este es el caso de las ecuaciones lineales en dos variables. Pista: pensar geométricamente.

⁵ Los adjetivos 'dependiente' e 'independiente' se aplican únicamente a sistemas consistentes —describen el tipo de soluciones. ¿Existe una variable libre (dependiente) o no (independiente)?

⁶ Si pensamos que si cada variable es una cantidad desconocida, entonces ostensiblemente, para recuperar dos cantidades desconocidas, necesitamos dos piezas de información -es decir, dos ecuaciones. Tener más de dos ecuaciones sugiere que tenemos más información de la necesaria para determinar los valores de las incógnitas. Si bien este no es necesariamente el caso, sí explica la elección de la terminología 'sobredeterminada'.

⁷ Necesitamos más de dos variables para dar un ejemplo de estas últimas.

⁸ Nuevamente, la experiencia con sistemas con más variables ayuda a ver esto aquí, al igual que un curso sólido en Álgebra Lineal.

⁹ Es decir, un sistema con el mismo conjunto de soluciones.

¹⁰ Se le pidió que pensara sobre esto en el Ejercicio 40 de la Sección 1.1.

¹¹ De hecho, estas líneas son descritas por las soluciones paramétricas a los sistemas formados tomando dos de estas ecuaciones por sí mismas.

¹² Si se usan letras en lugar de variables subinscritas, la Definición 8.3 puede modificarse adecuadamente usando el orden alfabético de las variables en lugar del orden numérico en los subíndices de las variables.

¹³ Aquí, cualquier elección de\(s\) y\(t\) determinará una solución que es un punto en el espacio de 4 dimensiones. Sí, también tenemos problemas para visualizar eso.

¹⁴ ¡Hacemos esto solo porque creemos que los estudiantes pueden usar toda la práctica con fracciones que puedan obtener!