8.7: Sistemas de Ecuaciones No Lineales y Desigualdades
- Page ID
- 119475
En esta sección, estudiamos sistemas de ecuaciones no lineales y desigualdades. A diferencia de los sistemas de ecuaciones lineales para los que hemos desarrollado varias técnicas de solución algorítmica, no existe un algoritmo general para resolver sistemas de ecuaciones no lineales. Además, todos los peligros habituales de las ecuaciones no lineales como soluciones extrañas y dominios de función inusuales están nuevamente presentes. Junto con las probadas y verdaderas técnicas de sustitución y eliminación, a menudo necesitaremos a partes iguales de tenacidad e ingenio para ver un problema hasta el final. Puede ser necesario revisar temas a lo largo del texto que pertenecen a la resolución de ecuaciones que involucran las diversas funciones que hemos estudiado hasta el momento. Para que la sección ruede comenzamos con un ejemplo bastante rutinario.
Resuelve los siguientes sistemas de ecuaciones. Verifica tus respuestas algebraica y gráficamente.
- \ (\ izquierda\ {\ begin {array} {r}
x^ {2} +y^ {2} =&4\\
4 x^ {2} +9 y^ {2} =& 36
\ end {array}\ derecha.\) - \ (\ left\ {\ begin {array} r
x^ {2} +y^ {2} =&4\\
4 x^ {2} -9 y^ {2} =&36
\ end {array}\ derecha.\) - \ (\ text {3.}\ left\ {\ begin {array} {r}
x^ {2} +y^ {2} =4\\
y-2 x=0
\ end {array}\ right.\) - \ (\ izquierda\ {\ begin {array} {r}
x^ {2} +y^ {2} =4\
y-x^ {2} =0
\ end {array}\ derecha.\)
Solución
- Dado que ambas ecuaciones contienen\(x^{2}\) y\(y^{2}\) solo, podemos eliminar una de las variables como hicimos en la Sección 8.1. \ [\ left\ {\ begin {array} {lrrl}
(E 1)\ quad x^2+y^2&=&4 &\ quad\ xrightarrow {\ text {Reemplazar} E2\ text {con}}\\
(E 2)\ quad 4x^2+9y^2&=&36 &\ quad -4E1 + E2\ end {array}\ derecha. \ quad\ left\ {\ begin {array} {lr} (E1)\ quad x^2+y^2 &=&4\\ (E2)\ quad\\\\\\ 5y^2 &=&20\ end {array}\ derecha. \ nonumber\] De\(5 y^{2}=20\), obtenemos\(y^{2}=4\) o\(y=\pm 2\). Para encontrar los\(x\) valores asociados, sustituimos cada valor de\(y\) en una de las ecuaciones para encontrar el valor resultante de\(x\). Escogiendo\(x^{2}+y^{2}=4\), nos encontramos con eso para ambos\(y = −2\) y\(y = 2\), obtenemos\(x = 0\). Nuestra solución es así {(0, 2), (0, −2)}. Para verificar esto algebraicamente, necesitamos demostrar que ambos puntos satisfacen ambas ecuaciones originales. Dejamos que el lector verifique esto. Para verificar nuestra respuesta gráficamente, esbozamos ambas ecuaciones y buscamos sus puntos de intersección. La gráfica de\(x^{2}+y^{2}=4\) es un círculo centrado en (0, 0) con un radio de 2, mientras que la gráfica de\(4 x^{2}+9 y^{2}=36\), cuando se escribe en la forma estándar\(\frac{x^{2}}{9}+\frac{y^{2}}{4}=1\) se reconoce fácilmente como una elipse centrada en (0, 0) con un eje mayor a lo largo del eje x de longitud 6 y un eje menor a lo largo del eje y de longitud 4. Vemos en la gráfica que las dos curvas se cruzan en sus intercepciones y solamente, (0, ±2). - Procedemos como antes para eliminar una de las variables\ [\ left\ {\ begin {array} {lrrl}
(E 1)\ quad\ x^2+\\ y^2&=&4 &\ quad\ xrightarrow {\ text {Reemplazar} E2\ text {con}}\\
(E 2)\ quad 4x^2-9y^2&=&36 &\ quad -4E1 + E2\ end {array}\ derecho. \ quad\ left\ {\ begin {array} {lr} (E1)\ quad x^2+y^2 &=&4\\ (E2)\ quad -13y^2 &=&20\ end {array}\ right. \ nonumber\] Dado que la ecuación no\(-13 y^{2}=20\) admite ninguna solución real, el sistema es inconsistente. Para verificar esto gráficamente, observamos que\(x^{2}+y^{2}=4\) es el mismo círculo que antes, pero al escribir la segunda ecuación en forma estándar,\(\frac{x^{2}}{9}-\frac{y^{2}}{4}=1\), encontramos una hipérbola centrada en (0, 0) abriéndose a la izquierda y derecha con un eje transversal de longitud 6 y un eje conjugado de longitud 4. Vemos que el círculo y la hipérbola no tienen puntos en común.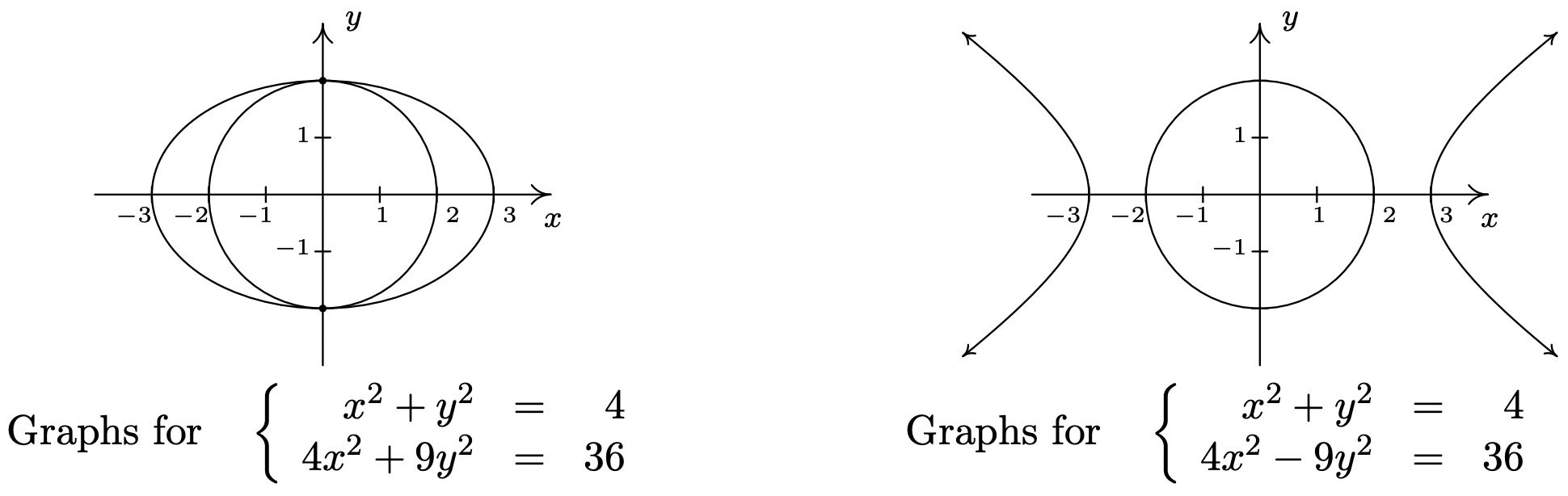
- Como no hay términos similares entre las dos ecuaciones, la eliminación no nos servirá de nada. Pasamos a la sustitución y a partir de la ecuación\(y − 2x = 0\), obtenemos\(y = 2x\). Sustituyendo esto en\(x^{2}+y^{2}=4\) da\(x^{2}+(2 x)^{2}=4\). Resolviendo, encontramos\(5 x^{2}=4\) o\(x=\pm \frac{2 \sqrt{5}}{5}\). Volviendo a la ecuación que usamos para la sustitución\(y = 2x\),, encontramos\(y=\frac{4 \sqrt{5}}{5}\) cuándo\(x=\frac{2 \sqrt{5}}{5}\), entonces una solución es\(\left(\frac{2 \sqrt{5}}{5}, \frac{4 \sqrt{5}}{5}\right)\). De igual manera, encontramos que la otra solución es\(\left(-\frac{2 \sqrt{5}}{5},-\frac{4 \sqrt{5}}{5}\right)\). Dejamos al lector que ambos puntos satisfacen ambas ecuaciones, para que nuestra respuesta final sea\(\left\{\left(\frac{2 \sqrt{5}}{5}, \frac{4 \sqrt{5}}{5}\right),\left(-\frac{2 \sqrt{5}}{5},-\frac{4 \sqrt{5}}{5}\right)\right\}\). La gráfica de\(x^{2}+y^{2}=4\) es nuestro círculo de antes y la gráfica de\(y − 2x = 0\) es una línea a través del origen con pendiente 2. Aunque no podemos verificar los valores numéricos de los puntos de intersección a partir de nuestro boceto, sí vemos que tenemos dos soluciones: una en el Cuadrante I y otra en el Cuadrante III según sea necesario.
- Si bien puede ser tentador resolver\(y-x^{2}=0\) como\(y=x^{2}\) y sustituir, observamos que este sistema está configurado para su eliminación. 1\ [\ left\ {\ begin {array} {ll}
(E 1)\ quad x^2+\\ y^2&=&4 &\ quad\ xrightarrow {\ text {Reemplazar} E2\ text {con}}\\
(E 2)\ quad y\ -\ x^2&=&0 &\ quad\\\\ E1 + E2\ end {array} derecha\. \ quad\ left\ {\ begin {array} {lr} (E1)\ quad x^2+y^2 &=&4\\ (E2)\ quad y^2+y &=&4\ end {array}\ right. \ nonumber\] De\(y^{2}+y=4\) obtenemos\(y^{2}+y-4=0\) lo que da\(y=\frac{-1 \pm \sqrt{17}}{2}\). Debido a la naturaleza complicada de estas respuestas, merece la pena hacer un boceto rápido de ambas ecuaciones para evitar cualquier solución extraña que podamos encontrar. Vemos que el círculo\(x^{2}+y^{2}=4\) cruza\(y=x^{2}\) exactamente dos veces la parábola, y ambos puntos tienen un\(y\) valor positivo. De las dos soluciones para\(y\), solo\(y=\frac{-1+\sqrt{17}}{2}\) es positiva, así que para obtener nuestra solución, sustituimos esto en\(y-x^{2}=0\) y resolvemos para\(x\). Obtenemos\(x=\pm \sqrt{\frac{-1+\sqrt{17}}{2}}=\pm \frac{\sqrt{-2+2 \sqrt{17}}}{2}\). Nuestra solución es\(\left\{\left(\frac{\sqrt{-2+2 \sqrt{17}}}{2}, \frac{-1+\sqrt{17}}{2}\right),\left(-\frac{\sqrt{-2+2 \sqrt{17}}}{2}, \frac{-1+\sqrt{17}}{2}\right)\right\}\), la cual dejamos al lector para verificar.
Un par de comentarios sobre el Ejemplo 8.7.1 están en orden. Primero señalar que, a diferencia de los sistemas de ecuaciones lineales, es posible que un sistema de ecuaciones no lineales tenga más de una solución sin tener infinitamente muchas soluciones. De hecho, si bien caracterizamos los sistemas de ecuaciones no lineales como “consistentes” o “inconsistentes”, generalmente no usamos las etiquetas “dependientes” o “independientes”. En segundo lugar, como vimos con el número 4, a veces hacer un boceto rápido de la situación problemática puede ahorrar mucho tiempo y esfuerzo. Si bien en general las curvas en un sistema de ecuaciones no lineales pueden no ser fácilmente visualizadas, a veces vale la pena aprovechar cuando están. Nuestro siguiente ejemplo proporciona una revisión considerable de muchos de los temas introducidos en este texto.
Resuelve los siguientes sistemas de ecuaciones. Verifica tus respuestas algebraica y gráficamente, según corresponda.
- \ (\ left\ {\ begin {array} {l}
x^ {2} +2 x y-16=0\\
y^ {2} +2 x y-16=0
\ end {array}\ right.\) - \ (\ izquierda\ {\ begin {array} {l}
y+4 e^ {2 x} =1\\
y^ {2} +2 e^ {x} =1
\ end {array}\ derecha.\) - \ (\ izquierda\ {\ comenzar {alineado}
z (x-2) &=x\\
y z &=y\\
(x-2) ^ {2} +y^ {2} &=1
\ end {alineado}\ derecho.\)
Solución
- A primera vista, no parece que la eliminación nos vaya a servir de nada ya que está claro que no podemos eliminar por completo una de las variables. La alternativa, resolver una de las ecuaciones para una variable y sustituirla por la otra, está llena de desagradabilidad. Volviendo a la eliminación, observamos que es posible eliminar el\(xy\) término problemático, y también el término constante, al eliminar y hacerlo obtenemos una relación más manejable entre\(x\) y\(y\)\ [\ left\ {\ begin {array} {ll} (E 1)\ quad x^2+\\ 2xy-16&=&0 &\ quad\ xrightarrow {\ text {Reemplazar} E2\ text {con}}\\
(E 2)\ quad y^2+\\ 2xy-16&=&0 &\ quad\\\\\ -E1 + E2\ end {array}\ right. \ quad\ left\ {\ begin {array} {lr} (E1)\ quad x^2+2xy-16 &=&0\\ (E2)\ quad\\\\\\\\\\ y^2-x^2 &=&0\ end {array}\\ derecha. \ nonumber\] Obtenemos\(y^{2}-x^{2}=0\) o\(y=\pm x\). Sustituyendo\(y = x\) en\(E\) 1 obtenemos\(x^{2}+2 x^{2}-16=0\) así que eso\(x^{2}=\frac{16}{3}\) o\(x=\pm \frac{4 \sqrt{3}}{3}\). Por otro lado, cuando sustituimos por\(y = −x\)\(E\) 1, obtenemos\(x^{2}-2 x^{2}-16=0\) o\(x^{2}=-16\) lo que no da soluciones reales. Sustituir cada uno de\(x=\pm \frac{4 \sqrt{3}}{3}\) en la ecuación de sustitución\(y = x\) produce la solución\(\left\{\left(\frac{4 \sqrt{3}}{3}, \frac{4 \sqrt{3}}{3}\right),\left(-\frac{4 \sqrt{3}}{3},-\frac{4 \sqrt{3}}{3}\right)\right\}\). Dejamos al lector demostrar que ambos puntos satisfacen ambas ecuaciones y ahora volvemos a verificar nuestra solución gráficamente. Comenzamos resolviendo\(x^{2}+2 x y-16=0\)\(y\) para obtener\(y=\frac{16-x^{2}}{2 x}\). Esta función se grafica fácilmente utilizando las técnicas de la Sección 4.2. Resolver la segunda ecuación\(y^{2}+2 x y-16=0\), porque\(y\), sin embargo, es más complicado. Utilizamos la fórmula cuadrática para obtener\(y=-x \pm \sqrt{x^{2}+16}\) lo que requeriría el uso de Cálculo o una calculadora para graficar. Lo creas o no, tampoco necesitamos porque la ecuación se\(y^{2}+2 x y-16=0\) puede obtener de la ecuación\(x^{2}+2 x y-16=0\) intercambiando\(y\) y\(x\). Pensando en la Sección 5.2, esto significa que podemos obtener la gráfica de\(y^{2}+2 x y-16=0\) reflejando la gráfica de\(x^{2}+2 x y-16=0\) a través de la línea\(y = x\). Hacerlo confirma que las dos gráficas se cruzan dos veces: una en el Cuadrante I, y otra en el Cuadrante III según se requiera.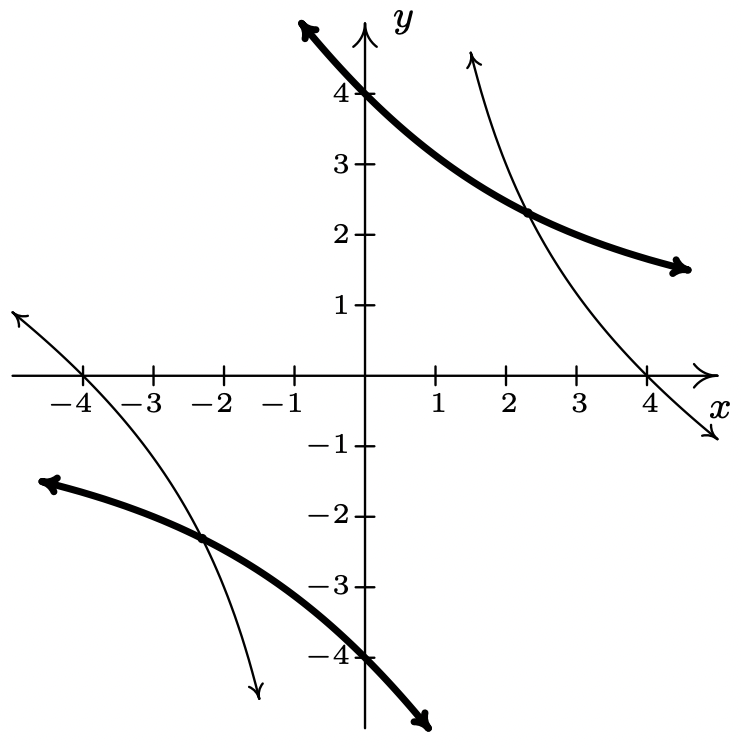
Las gráficas de\(x^{2}+2 x y-16=0\) y\(y^{2}+2 x y-16=0\) - A diferencia del problema anterior, parece que no hay sustitución evitable y un poco de descontento algebraico. Resolviendo\(y+4 e^{2 x}=1\) para\(y\), obtenemos\(y=1-4 e^{2 x}\) cuál, cuando se sustituye en la segunda ecuación, rinde\(\left(1-4 e^{2 x}\right)^{2}+2 e^{x}=1\). Después de expandirnos y reunir términos similares, obtenemos\(16 e^{4 x}-8 e^{2 x}+2 e^{x}=0\). El factoring nos da\(2 e^{x}\left(8 e^{3 x}-4 e^{x}+1\right)=0\), y como\(2 e^{x} \neq 0\) para cualquier real\(x\), nos queda resolver\(8 e^{3 x}-4 e^{x}+1=0\). Tenemos tres términos, y a pesar de que esto no es un 'cuadrático encubierto', podemos beneficiarnos de la sustitución\(u=e^{x}\). La ecuación se convierte\(8 u^{3}-4 u+1=0\). Utilizando las técnicas establecidas en la Sección 3.3, encontramos que\(u=\frac{1}{2}\) es un cero y utilizamos división sintética para factorizar el lado izquierdo\(\left(u-\frac{1}{2}\right)\left(8 u^{2}+4 u-2\right)\). Utilizamos la fórmula cuadrática para resolver\(8 u^{2}+4 u-2=0\) y encontrar\(u=\frac{-1 \pm \sqrt{5}}{4}\). Ya que\(u=e^{x}\), ahora debemos resolver\(e^{x}=\frac{1}{2}\) y\(e^{x}=\frac{-1 \pm \sqrt{5}}{4}\). De\(e^{x}=\frac{1}{2}\), obtenemos\(x=\ln \left(\frac{1}{2}\right)=-\ln (2)\). En cuanto a\(e^{x}=\frac{-1 \pm \sqrt{5}}{4}\), primero señalamos que\(\frac{-1-\sqrt{5}}{4}<0\), por lo tanto, no\(e^{x}=\frac{-1-\sqrt{5}}{4}\) tiene soluciones reales. Nos quedamos con\(e^{x}=\frac{-1+\sqrt{5}}{4}\), así que eso\(x=\ln \left(\frac{-1+\sqrt{5}}{4}\right)\). Ahora volvemos\(y=1-4 e^{2 x}\) a encontrar los\(y\) valores que acompañan a cada una de nuestras soluciones para\(x\). Para\(x=-\ln (2)\), obtenemos\[ \begin{aligned} y &=1-4 e^{2 x} \\ &=1-4 e^{-2 \ln (2)} \\ &=1-4 e^{\ln \left(\frac{1}{4}\right)} \\ &=1-4\left(\frac{1}{4}\right) \\ &=0 \end{aligned}\nonumber\] For\(x=\ln \left(\frac{-1+\sqrt{5}}{4}\right)\), tenemos\[ \begin{aligned} y &=1-4 e^{2 x} \\ &=1-4 e^{2 \ln \left(\frac{-1+\sqrt{5}}{4}\right)} \\ &=1-4 e^{\ln \left(\frac{-1+\sqrt{5}}{4}\right)^{2}} \\ &=1-4\left(\frac{-1+\sqrt{5}}{4}\right)^{2} \\ &=1-4\left(\frac{3-\sqrt{5}}{8}\right) \\ &=\frac{-1+\sqrt{5}}{2} \end{aligned}\] Obtenemos dos soluciones,\(\left\{(0,-\ln (2)),\left(\ln \left(\frac{-1+\sqrt{5}}{4}\right), \frac{-1+\sqrt{5}}{2}\right)\right\}\). Es una buena revisión de las propiedades de logaritmos para verificar ambas soluciones, por lo que dejamos eso al lector. Somos capaces de bosquejar\(y=1-4 e^{2 x}\) usando transformaciones, pero la segunda ecuación es más difícil y recurrimos a la calculadora. Observamos que para graficar\(y^{2}+2 e^{x}=1\), necesitamos graficar tanto las raíces positivas como las negativas,\(y=\pm \sqrt{1-2 e^{x}}\). Después de un cuidadoso zoom, 2 obtenemos
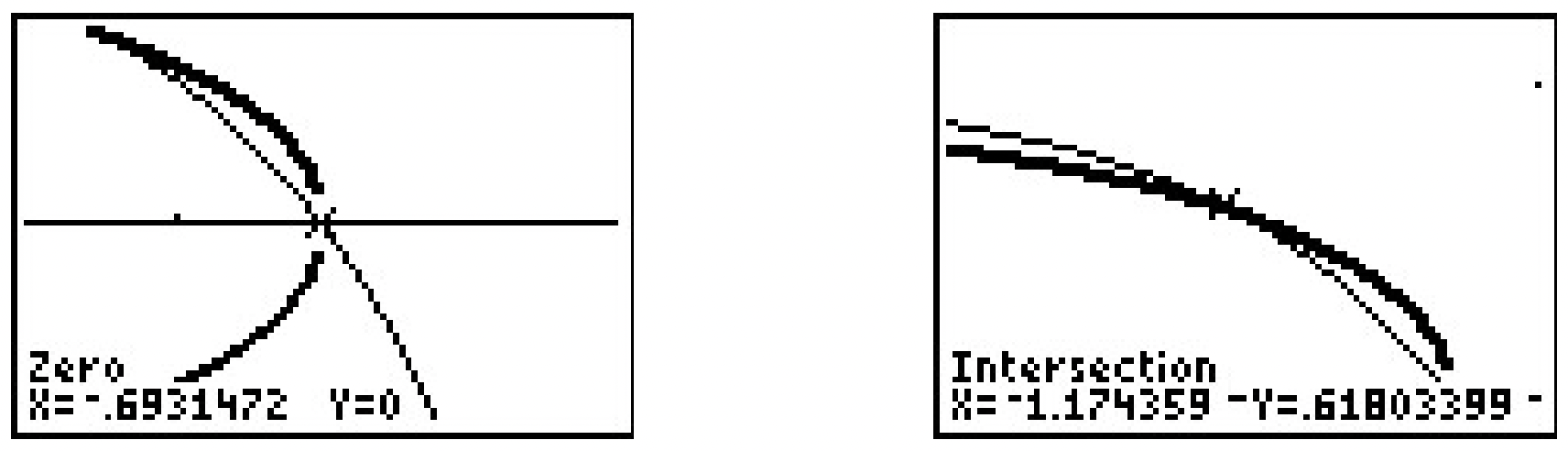
Las gráficas de\(y=1-4 e^{2 x}\) y\(y=\pm \sqrt{1-2 e^{x}}\). - Nuestro último sistema involucra tres variables y da algunas ideas sobre cómo mantener dichos sistemas organizados. Etiquetando las ecuaciones como antes, tenemos\[ \left \{\begin{array}{lr} E 1& \quad z(x-2)&=&x\\ E 2& y z&=&y\\ E 3&(x-2)^{2}+y^{2}&=&1 \end{array}\right.\nonumber\] La ecuación más fácil para comenzar parece ser\(E\) 2. Si bien puede ser tentador dividir ambos lados de\(E\) 2 por\(y\), advertimos contra esta práctica porque presupone\(y \neq 0\). En cambio, tomamos\(E\) 2 y lo reescribimos\(y z-y=0\) así\(y(z-1)=0\). De esto, obtenemos dos casos:\(y = 0\) o\(z = 1\). Tomamos cada caso a su vez.
Caso 1:\(y = 0\). Sustituyendo\(y = 0\) en\(E\) 1 y\(E\) 3, obtenemos
\ [\ left\ {\ begin {array} {lr}
E 1&\ quad z (x-2) &=&x\
E 3& (x-2) ^ {2} &=&1
\ end {array}\ right. \ nonumber\]Resolviendo\(E\) 3 para\(x\) da\(x = 1\) o\(x = 3\). Sustituir estos valores en\(E\) 1 da\(z = −1\) cuándo\(x = 1\) y\(z = 3\) cuándo\(x = 3\). Obtenemos dos soluciones, (1, 0, −1) y (3, 0, 3).
Caso 2:\(z = 1\). Sustituir\(z = 1\) en\(E\) 1 y\(E\) 3 nos da
\ [\ left\ {\ begin {array} {lr}
E 1&\ quad (1) (x-2) &=&x\
E 3& (1-2) ^ {2} +y^ {2} &=&1
\ end {array}\ right. \ nonumber\]La ecuación\(E\) 1 nos da\(x − 2 = x\) o −2 = 0, lo cual es una contradicción. Esto significa que no tenemos solución al sistema en este caso, a pesar de que\(E\) 3 es solucionable y da y = 0. De ahí que nuestra respuesta final sea {(1, 0, −1), (3, 0, 3)}. Estos puntos son bastante fáciles de comprobar algebraicamente en nuestras tres ecuaciones originales, de manera que eso se deja al lector. En cuanto a verificar gráficamente estas soluciones, requieren trazar superficies en tres dimensiones y buscar puntos de intersección. Si bien esto está más allá del alcance de este libro, proporcionamos una instantánea de las gráficas de nuestras tres ecuaciones cerca de uno de los puntos de solución, (1, 0, −1).
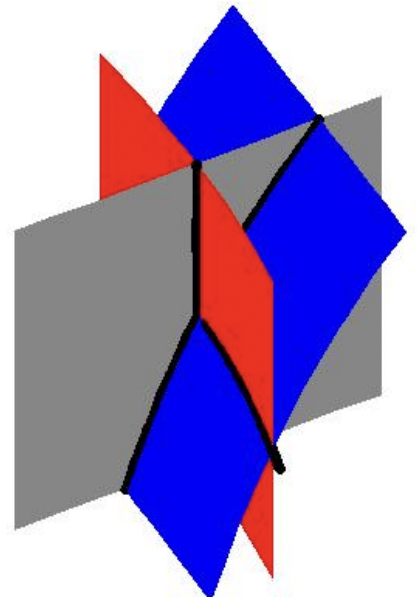
El Ejemplo 8.7.2 muestra parte del ingenio y tenacidad mencionados al inicio de la sección. A veces solo hay que mirar un sistema de la manera correcta para encontrar el método más eficiente para resolverlo. A veces solo hay que probar algo.
Cerramos esta sección discutiendo cómo las desigualdades no lineales pueden ser utilizadas para describir regiones en el plano que introdujimos por primera vez en la Sección 2.4. Antes de embarcarnos en algunos ejemplos, un poco de motivación está en orden. Supongamos que deseamos resolver\(x^2 < 4 - y^2\). Si imitamos los algoritmos para resolver desigualdades no lineales en una variable, reuniríamos todos los términos por un lado y dejaríamos un\(0\) en el otro para obtener\(x^2 + y^2 -4 < 0\). Entonces encontraríamos los ceros del lado izquierdo, es decir, dónde está\(x^2 + y^2 - 4 = 0\), o\(x^2 + y^2 = 4\). En lugar de obtener algunos números que dividen la recta numérica real en intervalos, obtenemos una ecuación de una curva, en este caso, un círculo, que divide el plano en dos regiones -la 'interior' y 'exterior' del círculo- con el círculo mismo como límite entre los dos. Así como usamos valores de prueba para determinar si un intervalo pertenece o no a la solución de la desigualdad, utilizamos puntos de prueba en cada una de las regiones para ver cuál de estos pertenece a nuestro conjunto de soluciones. 3 Elegimos\((0,0)\) representar la región dentro del círculo y\((0,3)\) representar los puntos fuera del círculo. Cuando sustituimos\((0,0)\) en\(x^2 + y^2 -4 < 0\), obtenemos\(-4 < 4\) lo que es cierto. Esto significa\((0,0)\) y todos los demás puntos dentro del círculo son parte de la solución. Por otro lado, cuando sustituimos\((0,3)\) en la misma desigualdad, obtenemos\(5 < 0\) lo que es falso. Esto significa que\((0,3)\) junto con todos los demás puntos fuera del círculo no son parte de la solución. ¿Qué pasa con los puntos en el círculo mismo? Escogiendo un punto en el círculo, digamos\((0,2)\), obtenemos\(0 < 0\), lo que significa que el círculo en sí no satisface la desigualdad. 4 Como resultado, dejamos el círculo discontinuas en el diagrama final.
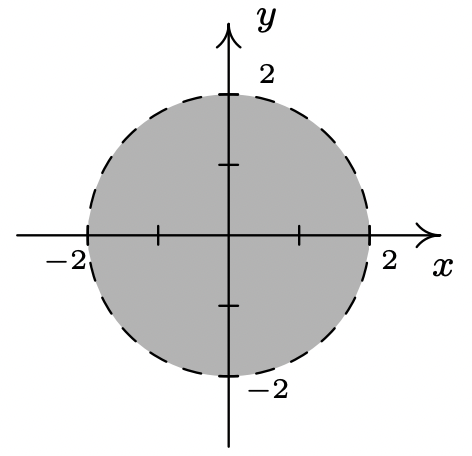
La solución para\(x^{2}<4-y^{2}\)
Ponemos a buen uso esta técnica en el siguiente ejemplo.
Esboce la solución a las siguientes desigualdades no lineales en el plano.
- \(y^{2}-4 \leq x<y+2\)
- \ (\ izquierda\ {\ comenzar {alineado}
x^ {2} +y^ {2} &\ geq 4\\
x^ {2} -2 x+y^ {2} -2 y &\ leq 0
\ end {alineado}\ derecho.\)
Solución
- La desigualdad\(y^{2}-4 \leq x<y+2\) es una desigualdad compuesta. Se traduce como\(y^{2}-4 \leq x\) y\(x<y+2\). Como es habitual, resolvemos cada desigualdad y tomamos la intersección teórica del conjunto para determinar la región que satisface ambas desigualdades. Para resolver\(y^{2}-4 \leq x\), escribimos\(y^{2}-x-4 \leq 0\). La curva\(y^{2}-x-4=0\) describe una parábola ya que exactamente una de las variables es cuadrada. Reescribiendo esto en forma estándar, obtenemos\(y^{2}=x+4\) y vemos que el vértice es (−4, 0) y la parábola se abre a la derecha. Usando los puntos de prueba (−5, 0) y (0, 0), encontramos que la solución a la desigualdad incluye la región a la derecha de, o 'dentro', de la parábola. Los puntos en la propia parábola también forman parte de la solución, ya que el vértice (−4, 0) satisface la desigualdad. Ahora dirigimos nuestra atención a\(x<y+2\). Procediendo como antes, escribimos\(x-y-2<0\) y enfocamos nuestra atención en\(x − y − 2 = 0\), que es la línea\(y = x − 2\). Usando los puntos de prueba (0, 0) y (0, −4), encontramos puntos en la región por encima de la línea que\(y = x − 2\) satisfacen la desigualdad. Los puntos en la línea\(y = x − 2\) no satisfacen la desigualdad, ya que la intersección y (0, −2) no lo hace. Vemos que estas dos regiones sí se superponen, y para hacer la gráfica más precisa, buscamos la intersección de estas dos curvas. Es decir, necesitamos resolver el sistema de ecuaciones no lineales\[ \left\{\begin{array}{l} (E 1) \quad y^{2}&=&x+4 \\ (E 2) \quad y&=&x-2 \end{array}\right.\nonumber\] Resolviendo\(E\) 1 para\(x\), obtenemos\(x=y^{2}-4\). Sustituyendo esto en\(E\) 2 da\(y=y^{2}-4-2\), o\(y^{2}-y-6=0\). Encontramos\(y = −2\) y\(y = 3\) y desde entonces\(x=y^{2}-4\), obtenemos que las gráficas se cruzan en (0, −2) y (5, 3). Armando todo esto, obtenemos nuestra respuesta final a continuación.
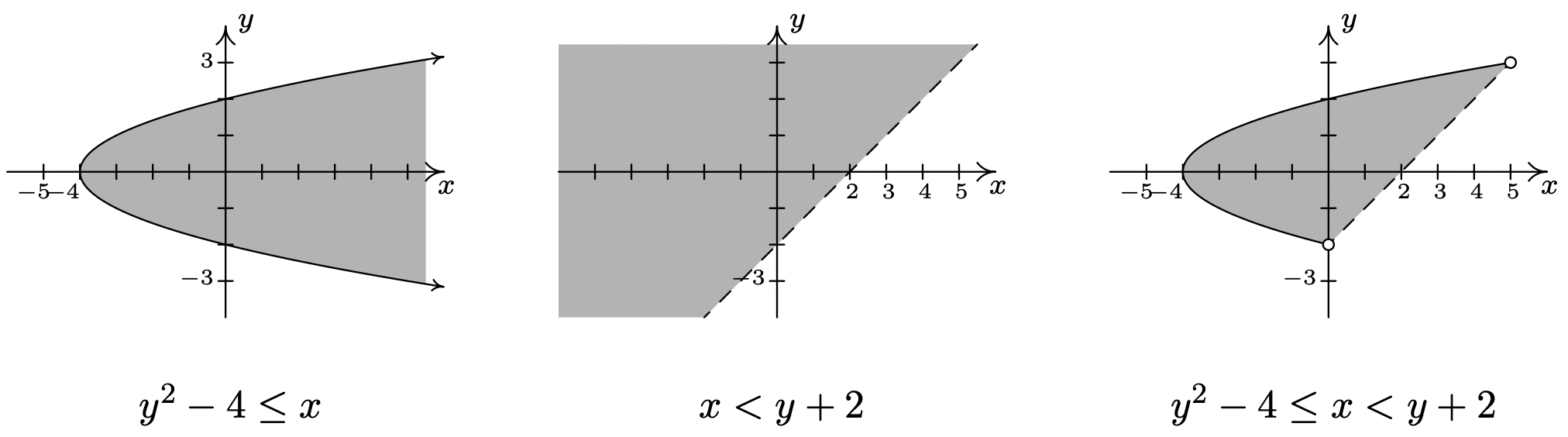
- Para resolver este sistema de desigualdades, necesitamos encontrar todos los puntos\((x, y)\) que satisfagan ambas desigualdades. Para ello, resolvemos cada desigualdad por separado y tomamos la intersección teórica del conjunto de los conjuntos de soluciones. Comenzamos con la desigualdad como la\(x^{2}+y^{2} \geq 4\) que reescribimos\(x^{2}+y^{2}-4 \geq 0\). Los puntos que satisfacen\(x^{2}+y^{2}-4=0\) forman nuestro círculo amistoso\(x^{2}+y^{2}=4\). Usando los puntos de prueba (0, 0) y (0, 3) encontramos que nuestra solución comprende la región fuera del círculo. En cuanto al círculo mismo, el punto (0, 2) satisface la desigualdad, por lo que el círculo mismo es parte del conjunto de soluciones. Pasando a la desigualdad\(x^{2}-2 x+y^{2}-2 y \leq 0\), empezamos con\(x^{2}-2 x+y^{2}-2 y=0\). Completando los cuadrados, obtenemos\((x-1)^{2}+(y-1)^{2}=2\), que es un círculo centrado en (1, 1) con un radio de\(\sqrt{2}\). Al elegir (1, 1) representar el interior del círculo, (1, 3) como un punto fuera del círculo y (0, 0) como un punto en el círculo, encontramos que la solución a la desigualdad es el interior del círculo, incluyendo el círculo mismo. Nuestra respuesta final, entonces, consiste en los puntos dentro o fuera del círculo\(x^{2}+y^{2}=4\) que se encuentran sobre o dentro del círculo\((x-1)^{2}+(y-1)^{2}=2\). Para producir la gráfica más precisa, necesitamos encontrar dónde se cruzan estos círculos. Para ello, resolvemos el sistema\[\left\{\begin{array}{r} (E 1)& \quad x^{2}+y^{2}&=&4 \\ (E 2)& \quad x^{2}-2 x+y^{2}-2 y&=&0 \end{array}\right.\n\nonumber\] Podemos eliminar tanto el\(x^{2}\) como\(E2\) reemplazándolo\(y^{2}\) por\(-E 1+E 2\). Hacerlo produce\(−2x − 2y = −4\). Resolviendo esto para\(y\), obtenemos\(y = 2 − x\). Sustituyendo esto en\(E1\) da\(x^{2}+(2-x)^{2}=4\) lo que simplifica a\(x^{2}+4-4 x+x^{2}=4\) o\(2 x^{2}-4 x=0\). Factorización de rendimientos\(2x(x − 2)\) que da\(x = 0\) o\(x = 2\). Sustituyendo estos valores en\(y = 2 − x\) da los puntos (0, 2) y (2, 0). Las gráficas intermedias y la solución final están a continuación.
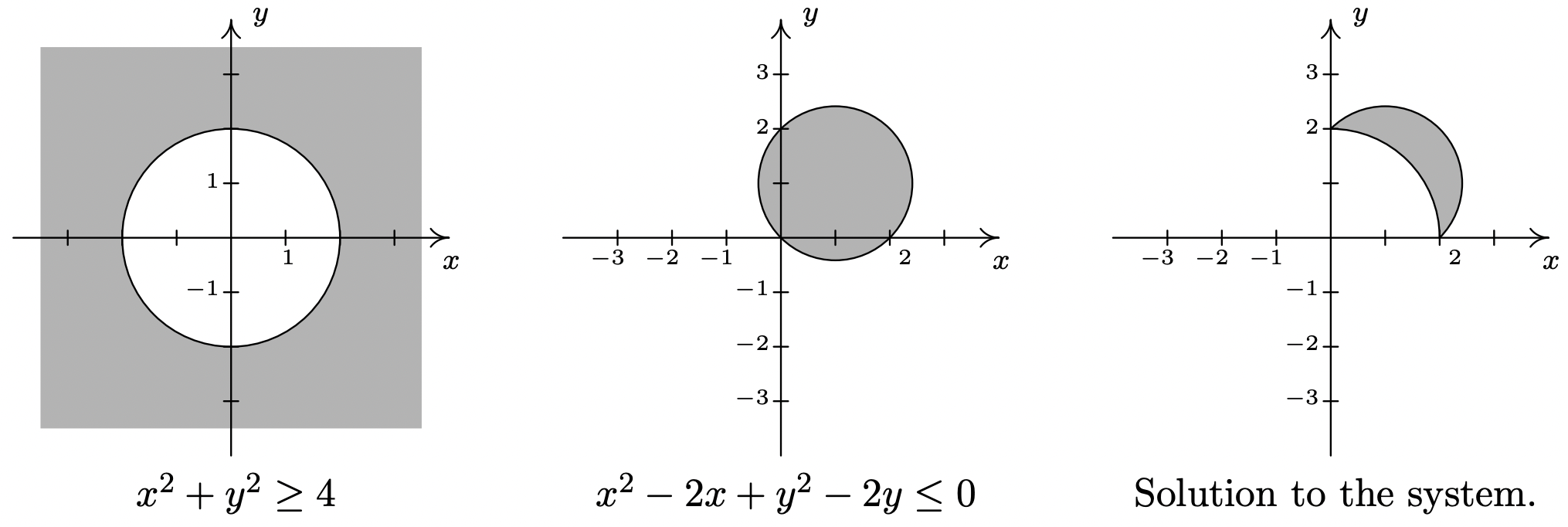
8.7.1 Ejercicios
En los Ejercicios 1 - 6, resolver el sistema dado de ecuaciones no lineales. Esboce la gráfica de ambas ecuaciones en el mismo conjunto de ejes para verificar el conjunto de soluciones.
- \ (\ izquierda\ {\ comenzar {alineado}
x^ {2} -y &=4\\
x^ {2} +y^ {2} &=4
\ end {alineado}\ derecho.\) - \ (\ izquierda\ {\ begin {array} {r}
x^ {2} +y^ {2} =4\\
x^ {2} -y=5
\ end {array}\ derecha.\) - \ (\ izquierda\ {\ comenzar {alineado}
x^ {2} +y^ {2} &=16\\
16 x^ {2} +4 y^ {2} &=64
\ end {alineado}\ derecho.\) - \ (\ izquierda\ {\ begin {array} {rrr}
x^ {2} +y^ {2} & =&16\\
9 x^ {2} -16 y^ {2} & =&144
\ end {array}\ derecha.\) - \ (\ izquierda\ {\ begin {array} {rlr}
x^ {2} +y^ {2} & =&16\\
\ frac {1} {9} y^ {2} -\ frac {1} {16} x^ {2} & =&1
\ end {array}\ derecha.\) - \ (\ izquierda\ {\ begin {array} {rlr}
x^ {2} +y^ {2} & = & 16\\
x-y & = & 2
\ end {matriz}\ derecha.\)
En los Ejercicios 7 - 15, resolver el sistema dado de ecuaciones no lineales. Usa una gráfica para ayudarte a evitar posibles soluciones extrañas.
- \ (\ izquierda\ {\ comenzar {alineado}
x^ {2} -y^ {2} &=1\\
x^ {2} +4 y^ {2} &=4
\ end {alineado}\ derecho.\) - \ (\ izquierda\ {\ comenzar {alineado}
\ sqrt {x+1} -y &=0\\
x^ {2} +4 y^ {2} &=4
\ end {alineado}\ derecho.\) - \ (\ izquierda\ {\ comenzar {alineado}
x+2 y^ {2} &=2\\
x^ {2} +4 y^ {2} &=4
\ end {alineado}\ derecho.\) - \ (\ izquierda\ {\ comenzar {alineado}
(x-2) ^ {2} +y^ {2} &=1\\
x^ {2} +4 y^ {2} &=4
\ end {alineado}\ derecho.\) - \ (\ left\ {\ begin {array} {rlr}
x^ {2} +y^ {2} & =&25\\
y-x & =&1
\ end {array}\ right.\) - \ (\ izquierda\ {\ comenzar {alineado}
x^ {2} +y^ {2} &=25\\
x^ {2} + (y-3) ^ {2} &=10
\ end {alineado}\ derecho.\) - \ (\ izquierda\ {\ begin {array} {l}
y=x^ {3} +8\\
y=10 x-x^ {2}
\ end {array}\ derecha.\) - \ (\ izquierda\ {\ begin {array} {l}
x^ {2} -x y=8\\
y^ {2} -x y=8
\ end {array}\ derecha.\) - \ (\ izquierda\ {\ begin {array} {rlr}
x^ {2} +y^ {2} & = & 25\\
4 x^ {2} -9 y & = & 0\\
3 y^ {2} -16 x & = & 0
\ end {array}\ derecha.\) - Un cierto cultivo de bacterias sigue la Ley de Crecimiento No Enbitado, Ecuación 6.4. Después de 10 minutos, hay 10 mil bacterias. Cinco minutos después, hay 14 mil bacterias. ¿Cuántas bacterias estuvieron presentes inicialmente? ¿Cuánto tiempo antes de que haya 50,000 bacterias?
Considere el sistema de ecuaciones no lineales a continuación
\ (\ izquierda\ {\ begin {array} {l}
\ frac {4} {x} +\ frac {3} {y} =1\\
\ frac {3} {x} +\ frac {2} {y} =-1
\ end {array}\ derecha.\)
Si lo dejamos\(u=\frac{1}{x}\) y\(v=\frac{1}{y}\) entonces el sistema se convierte
\ (\ left\ {\ begin {array} {lr}
4 u+3 v&=&1\\
3 u+2 v&=&-1
\ end {array}\ right.\)
Este sistema asociado de ecuaciones lineales puede entonces resolverse utilizando cualquiera de las técnicas presentadas anteriormente en el capítulo para encontrar eso\(u = −5\) y\(v = 7\). Así\(x=\frac{1}{u}=-\frac{1}{5}\) y\(y=\frac{1}{v}=\frac{1}{7}\).
Decimos que el sistema original es lineal en forma porque sus ecuaciones no son lineales sino que algunas sustituciones revelan una estructura que podemos tratar como un sistema de ecuaciones lineales. Cada sistema en los Ejercicios 17 - 19 es lineal en forma. Hacer las sustituciones apropiadas y resolver para\(x\) y\(y\).
- \ (\ izquierda\ {\ begin {array} {rrr}
4 x^ {3} +3\ sqrt {y} = & 1\\
3 x^ {3} +2\ sqrt {y} = & -1
\ end {array}\ derecha.\) - \ (\ izquierda\ {\ comenzar {alineado}
4 e^ {x} +3 e^ {-y} &=1\\
3 e^ {x} +2 e^ {-y} &=-1
\ end {alineado}\ derecho.\) - \ (\ left\ {\ begin {array} {lr}
4\ ln (x) +3 y^ {2} &=&1\\
3\ ln (x) +2 y^ {2} &=&-1
\ end {array}\ right.\) - Resuelve el siguiente sistema\ [\ left\ {\ begin {alineado}
x^ {2} +\ sqrt {y} +\ log _ {2} (z) &=6\\
3 x^ {2} -2\ sqrt {y} +2\ log _ {2} (z) &=5\\
-5 x^ {2} +3\ sqrt {y} +4\ log _ {2} (z) =13
\ end {alineado}\ derecho. \ nonumber\]
En los Ejercicios 21 - 26, esbozar la solución a cada sistema de desigualdades no lineales en el plano.
- \ (\ izquierda\ {\ comenzar {alineado}
x^ {2} -y^ {2} &\ leq 1\\
x^ {2} +4 y^ {2} &\ geq 4
\ end {alineado}\ derecho.\) - \ (\ izquierda\ {\ comenzar {alineado}
x^ {2} +y^ {2} &<25\\
x^ {2} + (y-3) ^ {2} &\ geq 10
\ end {alineado}\ derecho.\) - \ (\ izquierda\ {\ comenzar {alineado}
(x-2) ^ {2} +y^ {2} &<1\\
x^ {2} +4 y^ {2} &<4
\ end {alineado}\ derecho.\) - \ (\ left\ {\ begin {array} {rrr}
y & > & 10 x-x^ {2}\\
y & < & x^ {3} +8
\ end {array}\ right.\) - \ (\ izquierda\ {\ comenzar {alineado}
x+2 y^ {2} &>2\\
x^ {2} +4 y^ {2} &\ leq 4
\ final {alineado}\ derecho.\) - \ (\ izquierda\ {\ comenzar {alineado}
x^ {2} +y^ {2} &\ geq 25\\
y-x &\ leq 1
\ end {alineado}\ derecho.\) - Sistemas de ecuaciones no lineales aparecen en Cálculo de tercer semestre en medio de algunos problemas realmente geniales. El sistema de abajo vino de un problema en el que nos pidieron encontrar las dimensiones de una caja rectangular con un volumen de 1000 pulgadas cúbicas que tiene una superficie mínima. Las variables\(x\),\(y\) y\(z\) son las dimensiones de la caja y λ se llama multiplicador Lagrange. Con la ayuda de tus compañeros, resuelve el sistema. 5\ [\ izquierda\ {\ comenzar {alineado}
2 y+2 z &=\ lambda y z\\
2 x+2 z &=\ lambda x z\\
2 y+2 x &=\ lambda x y\\
x y z &=1000
\ end {alineado}\ derecho. \ nonumber\] - Según el Teorema 3.16 de la Sección 3.4, el polinomio\(p(x)=x^{4}+4\) puede ser factorizado en los factores lineales del producto e irreducibles cuadráticos. En este ejercicio se presenta un método para obtener esa factorización.
- Demostrar que no\(p\) tiene ceros reales.
- Debido a que no\(p\) tiene ceros reales, su factorización debe ser de la forma\(\left(x^{2}+a x+b\right)\left(x^{2}+c x+d\right)\) donde cada factor sea una cuadrática irreducible. Amplíe esta cantidad y reúna términos similares.
- Crear y resolver el sistema de ecuaciones no lineales que resulta de equiparar los coeficientes de expansión encontrados anteriormente con los de\(x^{4}+4\). Deberías obtener cuatro ecuaciones en las cuatro incógnitas\(a\),\(b\),\(c\) y\(d\). Escribe p (x) en forma factorizada.
- Factor\(q(x)=x^{4}+6 x^{2}-5 x+6\).
8.7.2 Respuestas
- \((\pm 2,0),(\pm \sqrt{3},-1)\)
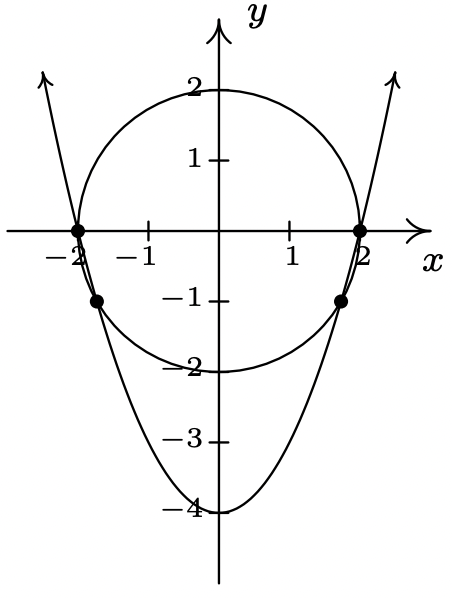
- Sin solución
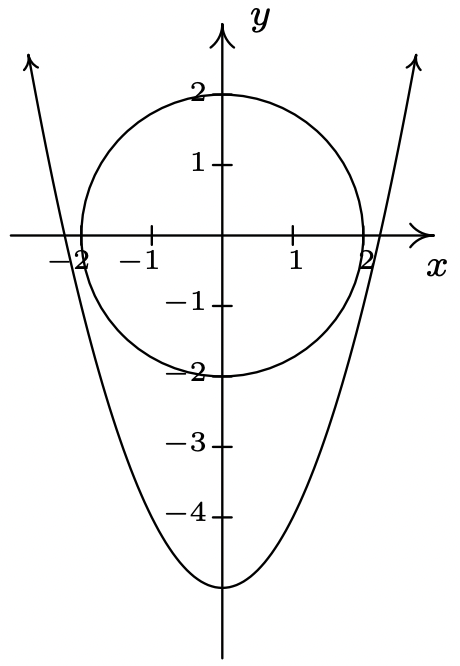
- \((0, \pm 4)\)
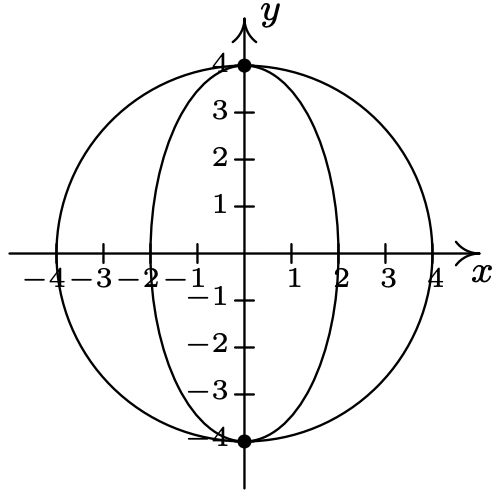
- \((\pm 4,0)\)
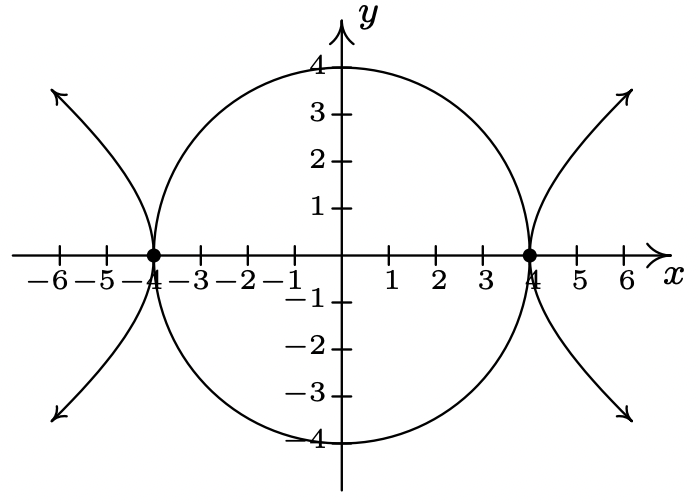
- \(\left(\pm \frac{4 \sqrt{7}}{5}, \pm \frac{12 \sqrt{2}}{5}\right)\)
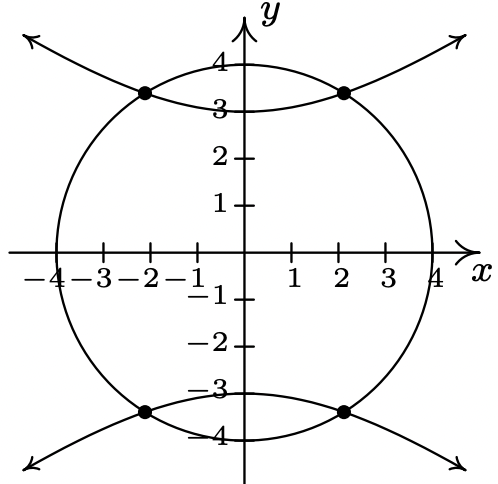
- \((1+\sqrt{7},-1+\sqrt{7}),(1-\sqrt{7},-1-\sqrt{7})\)
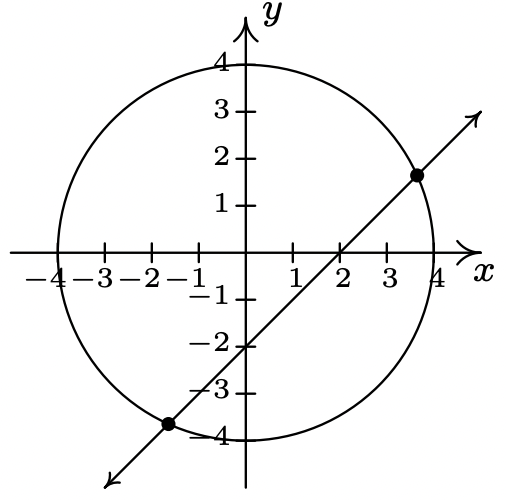
- \(\left(\pm \frac{2 \sqrt{10}}{5}, \pm \frac{\sqrt{15}}{5}\right)\)
- \((0,1)\)
- \((0, \pm 1),(2,0)\)
- \(\left(\frac{4}{3}, \pm \frac{\sqrt{5}}{3}\right)\)
- \((3,4),(-4,-3)\)
- \((\pm 3,4)\)
- \((-4,-56),(1,9),(2,16)\)
- \((-2,2),(2,-2)\)
- \((3,4)\)
- Inicialmente, hay\(\frac{250000}{49} \approx 5102\) bacterias. La colonia tardará\(\frac{5 \ln (49 / 5)}{\ln (7 / 5)} \approx 33.92\) minutos en crecer hasta 50 mil bacterias.
- \((-\sqrt[3]{5}, 49)\)
- Sin solución
- \(\left(e^{-5}, \pm \sqrt{7}\right)\)
- (1, 4, 8), (−1, 4, 8)
-
\ (\ izquierda\ {\ comenzar {alineado}
x^ {2} -y^ {2} &\ leq 1\\
x^ {2} +4 y^ {2} &\ geq 4
\ end {alineado}\ derecho.\)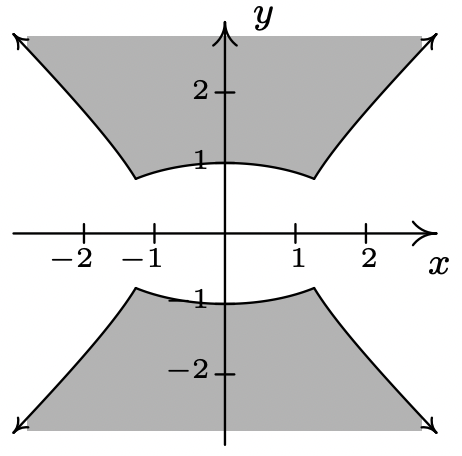
-
\ (\ izquierda\ {\ comenzar {alineado}
x^ {2} +y^ {2} &<25\\
x^ {2} + (y-3) ^ {2} &\ geq 10
\ end {alineado}\ derecho.\)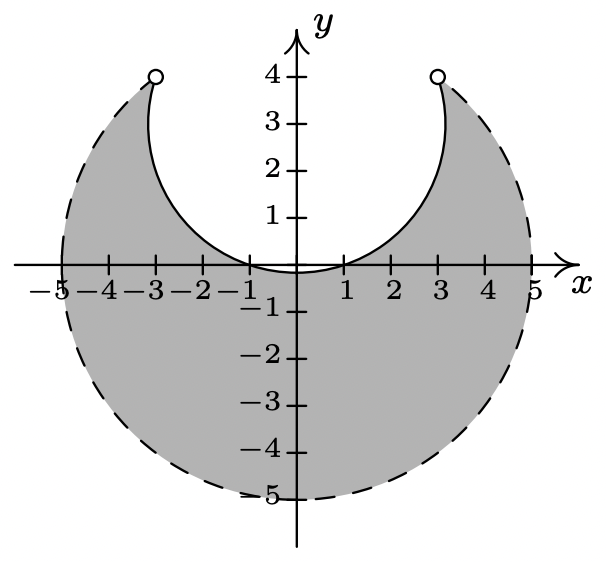
-
\ (\ izquierda\ {\ comenzar {alineado}
(x-2) ^ {2} +y^ {2} &<1\\
x^ {2} +4 y^ {2} &<4
\ end {alineado}\ derecho.\)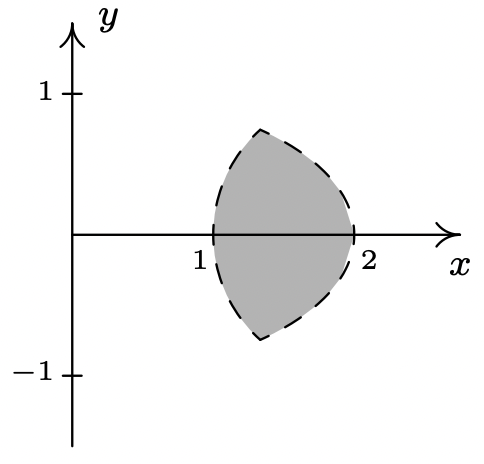
-
\ (\ izquierda\ {\ begin {array} {lr}
y> & 10 x-x^ {2}\\
y< & x^ {3} +8
\ end {array}\ derecha.\)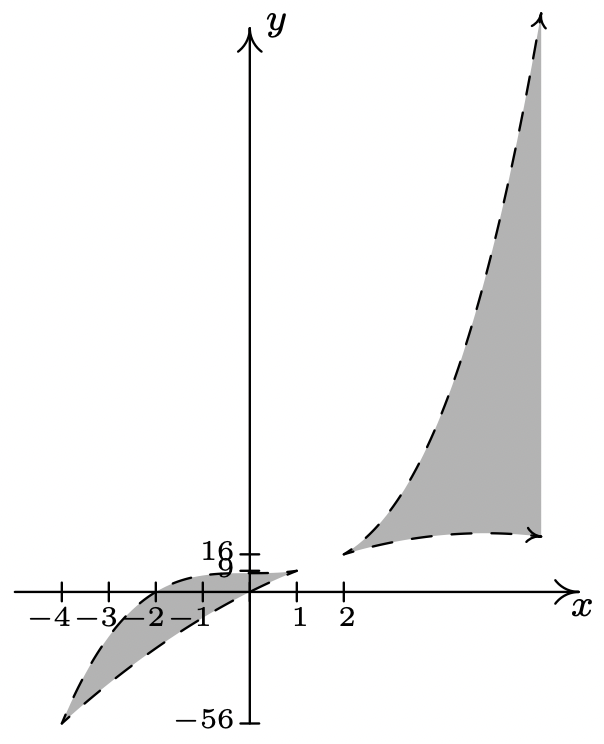
-
\ (\ izquierda\ {\ comenzar {alineado}
x+2 y^ {2} &>2\\
x^ {2} +4 y^ {2} &\ leq 4
\ final {alineado}\ derecho.\)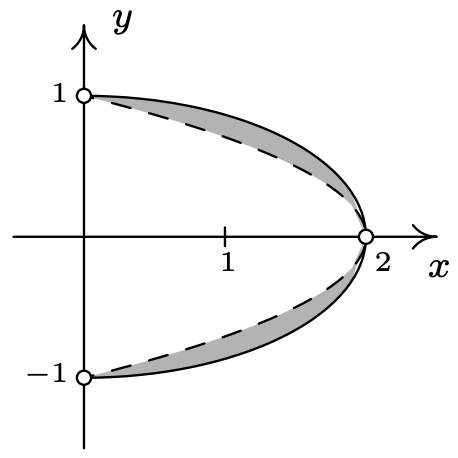
-
\ (\ izquierda\ {\ comenzar {alineado}
x^ {2} +y^ {2} &\ geq 25\\
y-x &\ leq 1
\ end {alineado}\ derecho.\)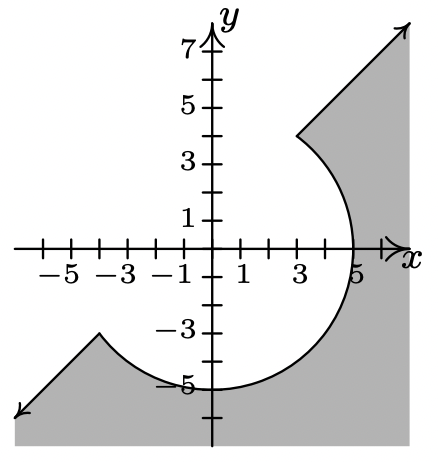
- \(x=10, y=10, z=10, \lambda=\frac{2}{5}\)
- \(\text { (c) } x^{4}+4=\left(x^{2}-2 x+2\right)\left(x^{2}+2 x+2\right)\)
- \(x^{4}+6 x^{2}-5 x+6=\left(x^{2}-x+1\right)\left(x^{2}+x+6\right)\)
Referencia
1 Animamos al lector a resolver el sistema usando la sustitución para ver que se obtiene la misma solución.
2 La calculadora tiene problemas para confirmar la solución (− ln (2), 0) debido a sus problemas en la representación gráfica de las funciones de raíz cuadrada. Si conectamos mentalmente las dos ramas de la curva más gruesa, vemos la intersección.
3 La teoría detrás de por qué todo esto funciona es, sorprendentemente, la misma teoría que garantiza que los diagramas de signos funcionen de la manera que hacen -la continuidad y el Teorema del Valor Intermedio- pero en este caso, aplicada a funciones de más de una variable.
4 Otra forma de ver esto es que los puntos en el círculo satisfacen\(x^{2}+y^{2}-4=0\), por lo que no satisfacen\(x^{2}+y^{2}-4<0\).
5 Si el uso de λ te molesta, cámbialo a\(w\) cuando resuelvas el sistema.


