9.1: Secuencias

Cuando introdujimos por primera vez una función como un tipo especial de relación en la Sección 1.3, no pusimos ninguna restricción en el dominio de la función. Todo lo que dijimos fue que el conjunto de\(x\) -coordenadas de los puntos en la función\(F\) se llama dominio, y resulta que cualquier subconjunto de los números reales, independientemente de lo extraño que pueda ser ese subconjunto, puede ser el dominio de una función. A medida que nuestra exploración de funciones continuó más allá de la Sección 1.3, vimos cada vez menos funciones con dominios 'extraños'. Vale la pena su tiempo para remontarse por el texto para ver que los dominios de las funciones polinomiales, racionales, exponenciales, logarítmicas y algebraicas discutidas hasta ahora tienen dominios bastante predecibles que casi siempre consisten en solo una colección de intervalos en la línea real. Esto puede llevar a algunos lectores a creer que las únicas funciones importantes en un texto de Álgebra Universitaria tienen dominios que consisten en intervalos y todo lo demás era una tontería introductoria. En esta sección, introducimos secuencias que son una clase importante de funciones cuyos dominios son el conjunto de números naturales. ¹ Antes de llegar muy por delante de nosotros mismos, veamos lo que significa matemáticamente el término 'secuencia'. Informalmente, podemos pensar en una secuencia como una lista infinita de números. Por ejemplo, considere la secuencia

\[\label{seq1} \frac{1}{2}, -\frac{3}{4}, \frac{9}{8}, -\frac{27}{16}, \ldots \tag{1}\]

Como es habitual, los periodos de elipsis,\(\ldots\), indican que el patrón propuesto continúa para siempre. A cada uno de los números de la lista se le llama término, y nosotros llamamos\(\frac{1}{2}\) al 'primer término',\(-\frac{3}{4}\) al 'segundo término',\(\frac{9}{8}\) al 'tercer término' y así sucesivamente. Al numerarlos de esta manera, estamos configurando una función, a la que llamaremos\(a\) por tradición, entre los números naturales y los términos en la secuencia.

\[\begin{array}{|r||r|} \hline n & a(n) \\[2pt] \hline 1 & \frac{1}{2} \\[3pt] \hline 2 & -\frac{3}{4} \\[3pt] \hline 3 & \frac{9}{8} \\[3pt] \hline 4 & -\frac{27}{16} \\[3pt] \hline \vdots & \vdots \\[2pt] \hline \end{array}\nonumber\]

En otras palabras,\(a(n)\) es el\(n^{\text{th}}\) término en la secuencia. Formalizamos estas ideas en nuestra definición de una secuencia e introducimos alguna notación acompañante.

Definición 9.1.

Una secuencia es una función\(a\) cuyo dominio son los números naturales. El valor a menudo\(a(n)\) se escribe como\(a_{n}\) y se llama el \(n^{\textbf{th}}\)término de la secuencia. La secuencia en sí se suele denotar usando la notación:\(a_{n}\),\(n \geq 1\) o la notación:\(\left\{ a_{n} \right\}_{n = 1}^{\infty}\).

Aplicando la notación proporcionada en la Definición 9.1 a la secuencia dada (1)\(a_1 = \frac{1}{2}\), tenemos\(a_{2} = -\frac{3}{4}\),\(a_{3} = \frac{9}{8}\) y así sucesivamente. Ahora supongamos que queríamos saber\(a_{117}\), es decir, el\(117^{\text{th}}\) término en la secuencia. Si bien el patrón de la secuencia es evidente, nos beneficiaría enormemente tener una fórmula explícita para\(a_{n}\). Desafortunadamente, no existe un algoritmo general que produzca una fórmula para cada secuencia, por lo que cualquier fórmula que sí desarrollemos vendrá de ese mayor de los maestros, la experiencia. En otras palabras, es hora de un ejemplo.

Ejemplo 9.1.1.

Escribe los primeros cuatro términos de las siguientes secuencias.

1. \(a_{n} = \dfrac{5^{n-1}}{3^{n}}\),\(n \geq 1\)
2. \(b_{k} = \dfrac{(-1)^{k}}{2k+1}\),\(k \geq 0\)
3. \(\left\{ 2n - 1 \right\}_{n=1}^{\infty} \vphantom{\left\{\dfrac{1 + (-1)^{i}}{i} \right\}_{i=2}^{\infty}}\)
4. \(\left\{\dfrac{1 + (-1)^{i}}{i} \right\}_{i=2}^{\infty}\)
5. \(a_1 = 7\),\(a_{n + 1} = 2 - a_{n}\),\(n \geq 1\)
6. [factorialintroex]\(f_0 = 1\),\(f_{n} =n \cdot f_{n-1}\),\(n \geq 1\)

Solución

1. Ya que se nos da\(n \geq 1\), los primeros cuatro términos de la secuencia son\(a_1\),\(a_{2}\),\(a_{3}\) y\(a_{4}\). Dado que la notación\(a_1\) significa lo mismo que\(a(1)\), obtenemos nuestro primer término reemplazando cada ocurrencia de\(n\) en la fórmula para\(a_{n}\) con\(n=1\) para obtener\(a_1 = \frac{5^{1-1}}{3^{1}} = \frac{1}{3}\). Procediendo de manera similar, obtenemos\(a_{2} = \frac{5^{2-1}}{3^{2}} =\frac{5}{9}\),\(a_{3} = \frac{5^{3-1}}{3^{3}} =\frac{25}{27}\) y\(a_{4} = \frac{5^{4-1}}{3^{4}} =\frac{125}{81}\).
2. Para esta secuencia tenemos\(k \geq 0\), por lo que los primeros cuatro términos son\(b_0\),\(b_1\),\(b_{2}\) y\(b_{3}\). Procediendo como antes, sustituyendo en este caso la variable\(k\) por el número entero apropiado, comenzando con\(0\), obtenemos\(b_0 = \frac{(-1)^{0}}{2(0)+1} = 1\),\(b_1 = \frac{(-1)^{1}}{2(1)+1} = - \frac{1}{3}\),\(b_{2} = \frac{(-1)^{2}}{2(2)+1} = \frac{1}{5}\) y\(b_{3} = \frac{(-1)^{3}}{2(3)+1} = -\frac{1}{7}\). (Esta secuencia se denomina secuencia alterna ya que los signos se alternan entre\(+\) y\(-\). Se anima al lector a pensar qué componente de la fórmula está produciendo este efecto.)
3. De\(\left\{ 2n - 1 \right\}_{n=1}^{\infty}\), tenemos eso\(a_{n} = 2n -1\),\(n \geq 1\). Obtenemos\(a_1 = 1\),\(a_{2} = 3\),\(a_{3} = 5\) y\(a_{4} = 7\). (Los primeros cuatro términos son los primeros cuatro números naturales impares. Se anima al lector a examinar si este patrón continúa indefinidamente o no.)
4. Aquí, estamos usando la letra\(i\) como contador, no como la unidad imaginaria que vimos en la Sección 3.4. Procediendo como antes, nos fijamos\(a_{i} = \frac{1 + (-1)^{i}}{i}\),\(i \geq 2\). Encontramos\(a_{2} = 1\),\(a_{3} = 0\),\(a_{4} = \frac{1}{2}\) y\(a_{5} = 0\).
5. Para obtener los términos de esta secuencia, comenzamos con\(a_1 = 7\) y usamos la ecuación\(a_{n + 1} = 2 - a_{n}\)\(n \geq 1\) para generar términos sucesivos. Cuando\(n = 1\), esta ecuación se convierte en\(a_{1 + 1} = 2 - a_1\) lo que simplifica a\(a_{2} = 2 - a_1 = 2 - 7 = -5\). Cuando\(n = 2\), la ecuación se vuelve\(a_{2 + 1} = 2 - a_{2}\) así que obtenemos\(a_{3} = 2 - a_{2} = 2 - (-5) = 7\). Por último, cuando\(n = 3\),\(a_{3 + 1} = 2 - a_{3}\) así lo conseguimos\(a_{4} = 2 - a_{3} = 2-7 = -5\).
6. Al igual que con el problema anterior, se nos da un lugar para comenzar\(f_0 = 1\) y se nos da una fórmula para construir otros términos de la secuencia. Sustituyendo\(n = 1\) en la ecuación\(f_{n} = n \cdot f_{n-1}\), obtenemos\(f_1 = 1 \cdot f_0 = 1 \cdot 1 = 1\). Avanzando a\(n = 2\), obtenemos\(f_{2} = 2 \cdot f_1 = 2 \cdot 1 = 2\). Por último,\(f_{3} = 3 \cdot f_{2} = 3 \cdot 2 = 6\).

Algunos comentarios sobre el Ejemplo 9.1.1 están en orden. Primero notamos que como las secuencias son funciones, podemos graficarlas de la misma manera que graficamos las funciones. Por ejemplo, si queremos graficar la secuencia\(\left\{ b_{k} \right\}_{k=0}^{\infty}\) del Ejemplo 9.1.1, graficamos la ecuación\(y=b(k)\) para los valores\(k \geq 0\). Es decir, trazamos los puntos\((k, b(k))\) para los valores de\(k\) en el dominio,\(k = 0, 1, 2, \ldots\). La colección resultante de puntos es la gráfica de la secuencia. Tenga en cuenta que no conectamos los puntos de una manera agradable como estamos acostumbrados a hacer, porque el dominio es solo los números enteros en este caso, no una colección de intervalos de números reales. Si sientes una sensación de nostalgia, deberías ver la Sección 1.2.

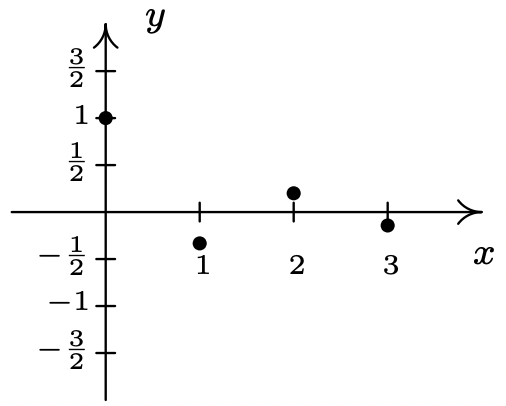
Graficando\(y = b_{k} = \dfrac{(-1)^{k}}{2k+1}\),\(k \geq 0\)

Hablando de ello\(\left\{ b_{k} \right\}_{k=0}^{\infty}\), el lector astuto y de mentalidad matemática notará correctamente que esto técnicamente no es una secuencia, ya que según la Definición 9.1, las secuencias son funciones cuyos dominios son los números naturales, no los números enteros, como es el caso de \(\left\{ b_{k} \right\}_{k=0}^{\infty}\). En otras palabras, para satisfacer la Definición 9.1, necesitamos desplazar la variable\(k\) para que comience en\(k=1\) lugar de\(k=0\). Para ver cómo podemos hacer esto, ayuda pensar gráficamente en el problema. Lo que queremos es desplazar la gráfica de\(y=b(k)\) a la derecha una unidad, y pensando de nuevo a la Sección 1.7, podemos lograr esto reemplazando\(k\) con\(k-1\) en la definición de\(\left\{ b_{k} \right\}_{k=0}^{\infty}\). En concreto, vamos a\(c_{k}=b_{k-1}\) dónde\(k-1 \geq 0\). Obtenemos\(c_{k} = \frac{(-1)^{k-1}}{2(k-1)+1} = \frac{(-1)^{k-1}}{2k-1}\), donde ahora\(k \geq 1\). Dejamos al lector verificar que\(\left\{ c_{k} \right\}_{k=1}^{\infty}\) genera la misma lista de números que hace\(\left\{ b_{k} \right\}_{k=0}^{\infty}\), pero el primero satisface la Definición 9.1, mientras que el segundo no. Como tantas cosas en este texto, reconocemos que este punto es pedante y nos unimos a la gran mayoría de autores que adoptan una visión más relajada de la Definición 9.1 para incluir cualquier función que genere una lista de números que luego se pueda emparejar con los números naturales. ² Finalmente, deseamos anotar las secuencias en partes\(5\) y\(6\) son ejemplos de secuencias descritas recursivamente. En cada instancia, se da un valor inicial de la secuencia que luego es seguido por una ecuación de recursión\(-\) una fórmula que nos permite usar términos conocidos de la secuencia para determinar otros términos. A los términos de la secuencia en parte\(6\) se les da un nombre especial:\(f_{n}=n!\) se llama \(n\)-factorial. Usando el '!' notación, podemos describir la secuencia factorial como:\(0! = 1\) y\(n! = n(n-1)!\) para\(n \geq 1\). Después\(0! = 1\) de los siguientes cuatro términos, escritos en detalle, son\(1! = 1 \cdot 0! = 1 \cdot 1 = 1\),\(2! = 2 \cdot 1! = 2 \cdot 1 = 2\),\(3! = 3 \cdot 2! = 3 \cdot 2 \cdot 1 = 6\) y\(4! = 4 \cdot 3! = 4 \cdot 3 \cdot 2 \cdot 1 = 24\). A partir de esto, vemos una forma más informal de computación\(n!\), que es\(n! = n\cdot(n -1)\cdot(n -2) \cdots 2 \cdot 1\) con\(0! = 1\) como caso especial. (Estudiaremos factoriales con mayor detalle en la Sección 9.4.) Los mundialmente famosos Números de Fibonacci se definen recursivamente y se exploran en los ejercicios. Si bien ninguna de las secuencias resultó ser la secuencia en (1), sí nos dan una idea de qué tipo de patrones buscar. En la siguiente definición se dan dos patrones en particular.

Definición 9.2. Secuencias aritméticas y geométricas

Supongamos que\(\left\{ a_{n} \right\}_{n=k}^{\infty}\) es ^una secuencia

• Si hay un número\(d\) así que\(a_{n + 1} = a_{n} + d\) para todos\(n \geq k\), entonces\(\left\{ a_{n} \right\}_{n=k}^{\infty}\) se llama una secuencia aritmética. El número\(d\) se llama la diferencia común.
• Si hay un número\(r\) así que\(a_{n + 1} = r a_{n}\) para todos\(n \geq k\), entonces\(\left\{ a_{n} \right\}_{n=k}^{\infty}\) se llama una secuencia geométrica. Al número\(r\) se le llama la relación común.

---

^a Tenga en cuenta que hemos ajustado por el hecho de que no todas las 'secuencias' comienzan en\(n = 1\).

Tanto las secuencias aritméticas como las geométricas se definen en términos de ecuaciones de recursión. En inglés, una secuencia aritmética es aquella en la que procedemos de un término a otro sumando siempre el número fijo\(d\). El nombre 'diferencia común' proviene de una ligera reescritura de la ecuación de recursión de\(a_{n + 1} = a_{n} + d\) a\(a_{n + 1} - a_{n} = d\). Análogamente, una secuencia geométrica es aquella en la que procedemos de un término a otro multiplicando siempre por el mismo número fijo\(r\). Si\(r \neq 0\), podemos reorganizar la ecuación de recursión para obtener\(\frac{a_{n+1}}{a_{n}} = r\), de ahí el nombre 'relación común'. Algunas secuencias son aritméticas, algunas son geométricas y otras no son como ilustra el siguiente ejemplo. ³

Ejemplo 9.1.2.

Determinar si las siguientes secuencias son aritméticas, geométricas o ninguna. Si es aritmética, encuentra la diferencia común\(d\); si es geométrica, encuentra la relación común\(r\).

1. \(a_{n} = \dfrac{5^{n-1}}{3^{n}}\),\(n \geq 1\)
2. \(b_{k} = \dfrac{(-1)^{k}}{2k+1}\),\(k \geq 0\)
3. \(\left\{ 2n - 1 \right\}_{n=1}^{\infty} \vphantom{\dfrac{1}{2}, -\dfrac{3}{4}, \dfrac{9}{8}, -\dfrac{27}{16}, \ldots}\)
4. \(\dfrac{1}{2}, -\dfrac{3}{4}, \dfrac{9}{8}, -\dfrac{27}{16}, \ldots\)

Solución

Una buena regla general a tener en cuenta al trabajar con secuencias es “¡En caso de duda, escríbalo!” Escribir los primeros términos puede ayudarte a identificar el patrón de la secuencia en caso de que exista uno.

1. Del Ejemplo 9.1.1, sabemos que los primeros cuatro términos de esta secuencia son\(\frac{1}{3}, \, \frac{5}{9}, \, \frac{25}{27}\) y\(\frac{125}{81}\). Para ver si se trata de una secuencia aritmética, observamos las sucesivas diferencias de términos. Nos encontramos con eso\(a_{2} - a_1 = \frac{5}{9} - \frac{1}{3} = \frac{2}{9}\) y\(a_{3} - a_{2} = \frac{25}{27} - \frac{5}{9} = \frac{10}{27}\). Como obtenemos números diferentes, no hay 'diferencia común' y hemos establecido que la secuencia no es aritmética. Para investigar si es geométrico o no, calculamos las proporciones de términos sucesivos. Las tres primeras proporciones\[\frac{a_2}{a_1} = \frac{\frac{5}{9}}{\frac{1}{3}} = \frac{5}{3}, \;\;\; \frac{a_3}{a_2} = \frac{\frac{25}{27}}{\frac{5}{9}} = \frac{5}{3} \;\; \mbox{ and } \;\; \frac{a_4}{a_3} = \frac{\frac{125}{81}}{\frac{25}{27}} = \frac{5}{3}\nonumber\] sugieren que la secuencia es geométrica. Para probarlo, debemos demostrarlo\(\frac{a_{n+1}}{a_{n}} = r\) para todos\(n\).

   \[\frac{a_{n+1}}{a_{n}}=\frac{\frac{5^{(n+1)-1}}{3^{n+1}}}{\frac{5^{n-1}}{3^{n}}}=\frac{5^{n}}{3^{n+1}} \cdot \frac{3^{n}}{5^{n-1}}=\frac{5}{3}\nonumber\]

   Esta secuencia es geométrica con cociente común\(r = \frac{5}{3}\).

2. Nuevamente, tenemos Ejemplo 9.1.1 para agradecer por proporcionar los primeros cuatro términos de esta secuencia:\(1, \, -\frac{1}{3}, \, \frac{1}{5}\) y\(-\frac{1}{7}\). Nos encontramos\(b_1 - b_0 = -\frac{4}{3}\) y\(b_{2} - b_1 = \frac{8}{15}\). De ahí que la secuencia no sea aritmética. Para ver si es geométrico, calculamos\(\frac{b_1}{b_0} = -\frac{1}{3}\) y\(\frac{b_{2}}{b_1} = -\frac{3}{5}\). Como no existe una 'relación común', concluimos que la secuencia tampoco es geométrica.
3. Como vimos en el Ejemplo 9.1.1, la secuencia\(\left\{ 2n - 1 \right\}_{n=1}^{\infty}\) genera los números impares:\(1, 3, 5, 7, \ldots\). Computando las primeras diferencias, encontramos\(a_{2} - a_1 = 2\),\(a_{3} - a_{2} = 2\), y\(a_{4} - a_{3} = 2\). Esto sugiere que la secuencia es aritmética. Para verificar esto, encontramos\[a_{n+1}-a_{n}=(2(n+1)-1)-(2 n-1)=2 n+2-1-2 n+1=2\nonumber\] Esto establece que la secuencia es aritmética con diferencia común\(d = 2\). Para ver si es geométrico, calculamos\(\frac{a_{2}}{a_1} = 3\) y\(\frac{a_{3}}{a_{2}} = \frac{5}{3}\). Dado que estas proporciones son diferentes, concluimos que la secuencia no es geométrica.
4. Conocimos nuestra última secuencia al inicio de la sección. Dado eso\(a_{2} - a_1 = -\frac{5}{4}\) y\(a_{3} - a_{2} = \frac{15}{8}\), la secuencia no es aritmética. Computar las primeras proporciones, sin embargo, nos da\(\frac{a_{2}}{a_1} = -\frac{3}{2}\),\(\frac{a_{3}}{a_{2}} = -\frac{3}{2}\) y\(\frac{a_{4}}{a_{3}} = -\frac{3}{2}\). Dado que estos son los únicos términos que se nos dan, asumimos que el patrón de proporciones continúa de esta manera y concluimos que la secuencia es geométrica.

Ahora estamos a un paso de determinar una fórmula explícita para la secuencia dada en (1). Sabemos que es una secuencia geométrica y nuestro siguiente resultado nos da la fórmula explícita que requerimos.

Ecuación 9.1. Fórmulas para secuencias aritméticas y geométricas

• Una secuencia aritmética con primer término\(a\) y diferencia común\(d\) viene dada por\[a_{n} = a + (n-1) d, \quad n \geq 1\nonumber\]
• Una secuencia geométrica con primer término\(a\) y relación común\(r \neq 0\) viene dada por\[a_{n} = ar^{n-1}, \quad n \geq 1\nonumber\]

Si bien las pruebas formales de las fórmulas de la Ecuación 9.1 requieren las técnicas establecidas en la Sección 9.3, intentamos motivarlas aquí. De acuerdo con la Definición 9.2, dada una secuencia aritmética con primer término\(a\) y diferencia común\(d\), la forma en que obtenemos de un término al siguiente es sumando\(d\). De ahí que los términos de la secuencia sean:\(a\),\(a+d\),\(a+2d\),\(a+3d\),... Vemos que para llegar al término\(n\) th, sumamos\(a\) exactamente\(d\) a los\((n-1)\) tiempos, que es lo que dice la fórmula. La derivación de la fórmula para series geométricas sigue de manera similar. Aquí, comenzamos con\(a\) y pasamos de un término a otro multiplicando por\(r\). Obtenemos\(a, ar, ar^2, ar^3\) y así sucesivamente. El\(n\) término es el resultado de multiplicar\(a\) por\((n-1)\) tiempos\(r\) exactos. Observamos aquí que la razón que\(r=0\) se excluye de la Ecuación 9.1 es evitar una instancia de la\(0^{0}\) cual es una forma indeterminante. ⁴ Con la Ecuación 9.1 en su lugar, finalmente tenemos las herramientas necesarias para encontrar una fórmula explícita para el término\(n\) th de la secuencia dada en (1). Sabemos por el Ejemplo 9.1.2 que es geométrico con relación común\(r = -\frac{3}{2}\). El primer término es\(a = \frac{1}{2}\) así por la Ecuación 9.1 obtenemos\(a_{n} = ar^{n-1} = \frac{1}{2} \left( - \frac{3}{2}\right)^{n-1}\) para\(n \geq 1\). Después de un toque de simplificación, obtenemos\(a_{n} = \frac{(-3)^{n-1}}{2^{n}}\) para\(n \geq 1\). Tenga en cuenta que podemos verificar fácilmente nuestra respuesta sustituyendo en valores de\(n\) y viendo que la fórmula genera la secuencia dada en (1). Esto se lo dejamos al lector. Nuestro siguiente ejemplo nos da más práctica para encontrar patrones.

Ejemplo 9.1.3.

Encuentra una fórmula explícita para el\(n^{\mathrm{th}}\) término de las siguientes secuencias.

1. \(0.9, 0.09, 0.009, 0.0009, \ldots\)
2. \(\dfrac{2}{5}, 2, -\dfrac{2}{3}, -\dfrac{2}{7}, \ldots\)
3. \(1, -\dfrac{2}{7}, \dfrac{4}{13}, -\dfrac{8}{19}, \ldots\)

Solución

1. Aunque esta secuencia pueda parecer extraña, el lector puede verificar que en realidad es una secuencia geométrica con relación común\(r = 0.1 = \frac{1}{10}\). Con\(a = 0.9 = \frac{9}{10}\), conseguimos\(a_{n} = \frac{9}{10} \left(\frac{1}{10}\right)^{n-1}\) para\(n \geq 0\). Simplificando, obtenemos\(a_{n} = \frac{9}{10^{n}}\),\(n \geq 1\). Hay más en esta secuencia de lo que parece y volveremos a este ejemplo en la siguiente sección.
2. Como puede verificar el lector, esta secuencia no es ni aritmética ni geométrica. En un intento de encontrar un patrón, reescribimos el segundo término con un denominador para que todos los términos aparezcan como fracciones. Nosotros tenemos\(\frac{2}{5}, \frac{2}{1}, -\frac{2}{3}, -\frac{2}{7}, \ldots\). Si asociamos el '\(-\)' negativo de los dos últimos términos con los denominadores obtenemos\(\frac{2}{5}, \frac{2}{1}, \frac{2}{-3}, \frac{2}{-7}, \ldots\). Esto nos dice que podemos esbozar tentativamente la fórmula para la secuencia como\(a_{n} = \frac{2}{d_{n}}\) dónde\(d_{n}\) está la secuencia de denominadores. Al mirar a los denominadores\(5,1,-3,-7, \ldots\), encontramos que van de un término a otro restando\(4\) que es lo mismo que sumar\(-4\). Esto significa que tenemos una secuencia aritmética en nuestras manos. Usando la Ecuación 9.1 con\(a = 5\) y\(d = -4\), obtenemos el denominador\(n\) th por la fórmula\(d_{n} = 5 + (n-1)(-4) = 9-4n\) para\(n \geq 1\). Nuestra respuesta final es\(a_{n} = \frac{2}{9-4n}\),\(n \geq 1\).
3. La secuencia como se da no es ni aritmética ni geométrica, por lo que procedemos como en el último problema para tratar de obtener patrones individualmente para el numerador y denominador. Dejando\(c_{n}\) y\(d_{n}\) denotar la secuencia de numeradores y denominadores, respectivamente, tenemos\(a_{n} = \frac{c_{n}}{d_{n}}\). Después de cierta experimentación, ⁵ elegimos escribir el primer término como fracción y asociar los negativos '\(-\)' con los numeradores. Esto rinde\(\frac{1}{1}, \frac{-2}{7}, \frac{4}{13}, \frac{-8}{19}, \ldots\). Los numeradores forman la secuencia\(1, -2, 4, -8, \ldots\) que es geométrica con\(a=1\) y\(r = -2\), así obtenemos\(c_{n} = (-2)^{n-1}\), para\(n \geq 1\). Los denominadores\(1, 7, 13, 19, \ldots\) forman una secuencia aritmética con\(a = 1\) y\(d = 6\). De ahí, obtenemos\(d_{n} = 1 + 6(n-1) = 6n-5\), para\(n \geq 1\). Obtenemos nuestra fórmula para\(a_{n} = \frac{c_{n}}{d_{n}} = \frac{(-2)^{n-1}}{6n-5}\), para\(n \geq 1\). Dejamos que el lector demuestre que esto echa un cheque.

Si bien el último problema en el Ejemplo 9.1.3 no fue ni geométrico ni aritmético, sí resolvió en una combinación de estos dos tipos de secuencias. Si se entregara la secuencia\(2, 5, 10, 17, \ldots\), sería difícil encontrar una fórmula para\(a_{n}\) si restringimos nuestra atención a estos dos arquetipos. Dijimos antes que no existe un algoritmo general para encontrar la fórmula explícita para el término\(n\) th de una secuencia dada, y es sólo a través de la experiencia obtenida de la evaluación de secuencias a partir de fórmulas explícitas que aprendemos a comenzar a reconocer patrones numéricos. El patrón\(1, 4, 9, 16, \ldots\) es bastante reconocible como los cuadrados, por lo que la fórmula\(a_{n} = n^2\),\(n \geq 1\) puede no ser demasiado difícil de determinar. Con esto en mente, es posible ver\(2, 5, 10, 17, \ldots\) como la secuencia\(1 + 1, 4 + 1, 9 + 1, 16 + 1 , \ldots\), así que\(a_{n} = n^2 + 1\),\(n \geq 1\). Por supuesto, dado que solo se nos da una pequeña muestra de la secuencia, no deberíamos decepcionarnos demasiado para descubrir que esta no es la única fórmula que genera esta secuencia. Por ejemplo, considere la secuencia definida por\(b_{n} = -\frac{1}{4} n^4 + \frac{5}{2} n^3 - \frac{31}{4} n^2 + \frac{25}{2} n - 5\),\(n \geq 1\). Se anima al lector a verificar que también produce los términos\(2, 5, 10, 17\). De hecho, se puede demostrar que dada cualquier muestra finita de una secuencia, hay infinitamente muchas fórmulas explícitas todas las cuales generan esos mismos puntos finitos. Esto significa que habrá infinitamente muchas respuestas correctas a algunos de los ejercicios de esta sección. ⁶ El hecho de que tu respuesta no coincida con la nuestra no significa que esté mal. Como siempre, en caso de duda, escribe tu respuesta. Siempre y cuando produzca los mismos términos en el mismo orden que lo que quiere el problema, tu respuesta es correcta.

Las secuencias juegan un papel importante en las Matemáticas de las Finanzas, como ya hemos visto con la Ecuación 6.2 en la Sección 6.5. Recordemos que si invertimos\(P\) dólares a una tasa porcentual anual\(r\) y componemos los\(n\) tiempos de interés por año, la fórmula para\(A_{k}\), el monto en la cuenta después de períodos\(k\) compuestos, es\(A_{k} = P\left(1 + \frac{r}{n}\right)^{k} = \left[P\left(1 + \frac{r}{n}\right)\right]\left(1 + \frac{r}{n}\right)^{k-1}\),\(k \geq 1\). Ahora vemos esto como una secuencia geométrica con primer término\(P\left(1 + \frac{r}{n}\right)\) y relación común\(\left(1 + \frac{r}{n}\right)\). En la planeación del retiro, rara vez ocurre que un inversionista deposite una cantidad fija de dinero en una cuenta y espera a que crezca. Por lo general, los pagos adicionales de principal se realizan a intervalos regulares y el valor de la inversión crece en consecuencia. Este tipo de inversión se llama anualidad y se discutirá en la siguiente sección una vez que hayamos desarrollado más maquinaria matemática.

9.1.1 Ejercicios

En los Ejercicios 1 - 3, escriba los primeros cuatro términos de la secuencia dada.

1. \(a_{n} = 2^{n} - 1 \vphantom{d_{j} = (-1)^{\dfrac{j(j+1)}{2}}}\),\(n \geq 0\)
2. \(d_{j} = (-1)^{\frac{j(j+1)}{2}}\),\(j \geq 1\)
3. \(\left\{ 5k - 2 \right\}_{k=1}^{\infty} \vphantom{\left\{ \dfrac{n^2+1}{n+1} \right\}_{n=0}^{\infty}}\)
4. \(\left\{ \dfrac{n^2+1}{n+1} \right\}_{n=0}^{\infty}\)
5. \(\left\{ \dfrac{x^{n}}{n^{2}} \right\}_{n=1}^{\infty}\)
6. \(\left\{ \dfrac{\ln(n)}{n} \right\}_{n=1}^{\infty} \vphantom{\left\{ \dfrac{x^{n}}{n^{2}} \right\}_{n=1}^{\infty}}\)
7. \(a_1 = 3\),\(a_{n+ 1} = a_{n} - 1\),\(n \geq 1 \vphantom{d_{m} = \dfrac{d_{m-1}}{100}}\)
8. \(d_0 = 12\),\(d_{m} = \dfrac{d_{m-1}}{100}\),\(m \geq 1\)
9. \(b_{1}=2, b_{k+1}=3 b_{k}+1, k \geq 1\)
10. \(c_{0}=-2, c_{j}=\frac{c_{j-1}}{(j+1)(j+2)}, j \geq 1\)
11. \(a_1 = 117\),\(a_{n + 1} = \dfrac{1}{a_{n}}\),\(n \geq 1\)
12. \(s_0 = 1\),\(s_{n + 1} = x^{n + 1} + s_{n}\),\(n \geq 0\)
13. \(F_0 = 1\),\(F_1 = 1\),\(F_{n} = F_{n - 1} + F_{n - 2}\),\(n \geq 2\) (Esta es la famosa Secuencia de Fibonacci)

En los Ejercicios 14 - 21 determinar si la secuencia dada es aritmética, geométrica o ninguna. Si es aritmética, encuentra la diferencia común\(d\); si es geométrica, encuentra la relación común\(r\).

14. \(\left\{ 3n-5 \right\}_{n=1}^{\infty}\)
15. \(a_{n} = n^2+3n+2\),\(n \geq 1\)
16. \(\dfrac{1}{3}\),\(\dfrac{1}{6}\),\(\dfrac{1}{12}\),\(\dfrac{1}{24} \vphantom{\left\{ 3 \left(\dfrac{1}{5}\right)^{n-1} \right\}_{n=1}^{\infty}}\),...
17. \(\left\{ 3 \left(\dfrac{1}{5}\right)^{n-1} \right\}_{n=1}^{\infty}\)
18. \(17\),\(5\),\(-7\),\(-19\),...
19. \(2\),\(22\),\(222\),\(2222\),...
20. \(0.9\),\(9\),\(90\),\(900 \vphantom{a_{n} = \dfrac{n!}{2}}\),...
21. \(a_{n} = \dfrac{n!}{2}\),\(n \geq 0\).

En los Ejercicios 22 - 30, encuentra una fórmula explícita para el\(n^{\mathrm{th}}\) término de la secuencia dada. Utilice las fórmulas de la Ecuación 9.1 según sea necesario.

22. \(3\),\(5\),\(7\),\(9 \vphantom{-\dfrac{1}{8}}\),...
23. \(1\),\(-\dfrac{1}{2}\),\(\dfrac{1}{4}\),\(-\dfrac{1}{8}\),...
24. \(1\),\(\dfrac{2}{3}\),\(\dfrac{4}{5}\),\(\dfrac{8}{7}\),...
25. \(1\),\(\dfrac{2}{3}\),\(\dfrac{1}{3}\),\(\dfrac{4}{27} \vphantom{\dfrac{x^7}{7}}\),...
26. \(1\),\(\dfrac{1}{4}\),\(\dfrac{1}{9}\),\(\dfrac{1}{16} \vphantom{-\dfrac{x^7}{7}}\),...
27. \(x\),\(-\dfrac{x^3}{3}\),\(\dfrac{x^5}{5}\),\(-\dfrac{x^7}{7}\),...
28. \(0.9, 0.99, 0.999, 0.9999, \ldots\)
29. \(27, 64, 125, 216, \ldots\)
30. \(1, 0, 1, 0, \ldots\)
31. Encuentra una secuencia que sea tanto aritmética como geométrica. (Pista: Comience con\(a_{n} = c\) para todos\(n\).)
32. Mostrar que una secuencia geométrica puede transformarse en una secuencia aritmética tomando el logaritmo natural de los términos.
33. A Thomas Robert Malthus se le atribuye decir: “El poder de la población es indefinidamente mayor que el poder en la tierra para producir subsistencia para el hombre. La población, cuando no se controla, aumenta en una proporción geométrica. La subsistencia solo aumenta en una relación aritmética. Un ligero conocimiento de los números mostrará la inmensidad del primer poder en comparación con el segundo”. (Consulte esta página web para más información.) Discuta esta cita con tus compañeros de clase desde el punto de vista de las secuencias.
34. Este problema clásico que involucra secuencias muestra el poder de las secuencias geométricas. Supongamos que una benefactora adinerada acepta darte hoy un centavo y luego duplicar la cantidad que te da cada día durante 30 días. Entonces, por ejemplo, obtienes dos centavos el segundo día y cuatro centavos al tercer día. ¿Cuántos centavos obtienes en el\(30^{\mbox{\scriptsize th}}\) día? ¿Cuál es el valor en dólares del regalo que has recibido?
35. Investiga los términos 'media aritmética' y 'media geométrica'. Con la ayuda de tus compañeros de clase, demuestra que un término dado de una secuencia aritmética\(a_{k}\),\(k \geq 2\) es la media aritmética del término inmediatamente anterior,\(a_{k-1}\) éste e inmediatamente después de él,\(a_{k+1}\). Estado y probar un resultado análogo para secuencias geométricas.
36. Discuta con sus compañeros de clase cómo podrían cambiar los resultados de esta sección si examináramos secuencias de otras cosas matemáticas como números complejos o matrices. Encuentra una fórmula explícita para el\(n^{\mbox{\scriptsize th}}\) término de la secuencia\(i, -1, -i, 1, i, \ldots\). Enumere los cuatro primeros términos de las secuencias matriciales que discutimos en el Ejercicio 8.3.1 en la Sección 8.3.

9.1.2 Respuestas

1. \(0, 1, 3, 7\)
2. \(-1, -1, 1, 1\)
3. \(3, 8, 13, 18\)
4. \(1, 1, \frac{5}{3}, \frac{5}{2}\)
5. \(x, \frac{x^{2}}{4}, \frac{x^{3}}{9}, \frac{x^{4}}{16}\)
6. \(0, \frac{\ln(2)}{2}, \frac{\ln(3)}{3}, \frac{\ln(4)}{4}\)
7. \(3, 2, 1, 0\)
8. \(12, 0.12, 0.0012, 0.000012\)
9. \(2, 7, 22, 67\)
10. \(-2, -\frac{1}{3}, -\frac{1}{36}, -\frac{1}{720}\)
11. \(117, \frac{1}{117}, 117, \frac{1}{117}\)
12. \(1, x + 1, x^{2} + x + 1, x^{3} + x^{2} + x + 1\)
13. \(1, 1, 2, 3\)
14. aritmética,\(d = 3\)
15. ni
16. geométrica,\(r = \frac{1}{2}\)
17. geométrica,\(r = \frac{1}{5}\)
18. aritmética,\(d = -12\)
19. ni
20. geométrica,\(r = 10\)
21. ni
22. \(a_{n} = 1 + 2n, \; n \geq 1\)
23. \(a_{n} = \left(-\frac{1}{2}\right)^{n - 1}, \; n \geq 1\)
24. \(a_{n} = \frac{2^{n - 1}}{2n - 1}, \; n \geq 1\)
25. \(a_{n} = \frac{n}{3^{n - 1}}, \; n \geq 1\)
26. \(a_{n} = \frac{1}{n^{2}}, \; n \geq 1\)
27. \(\frac{(-1)^{n - 1}x^{2n - 1}}{2n -1}, \; n \geq 1\)
28. \(a_{n} = \frac{10^{n} - 1}{10^{n}}, \; n \geq 1\)
29. \(a_{n} = (n + 2)^{3}, \; n \geq 1\)
30. \(a_{n} = \frac{1 + (-1)^{n-1}}{2}, \; n \geq 1\)

---

Referencia

¹ Recordemos que este es el conjunto {1, 2, 3,.}.

² Básicamente estamos hablando de los subconjuntos 'contablementeinfinitos' de la recta numérica real cuando hacemos esto.

³ Las secuencias que son tanto aritméticas como geométricas se discuten en los Ejercicios.

⁴ Consulte las notas al pie de página 237 en la Sección 3.1 y en la página 418 de la Sección 6.1.

⁵ Aquí tomamos 'experimentación' para significar una sesión frustrante de conjeturar y verificar.

⁶ Para obtener más información sobre esto, consulte Cuando cada respuesta es correcta: por qué las secuencias y los patrones numéricos fallan en la prueba.