10.1: Los ángulos y su medida
- Page ID
- 119460
Esta sección inicia nuestro estudio de la Trigonometría y para comenzar, recordamos algunas definiciones básicas de Geometría. Un rayo generalmente se describe como una 'media línea' y puede pensarse como un segmento de línea en el que uno de los dos puntos finales es empujado infinitamente distante del otro, como se muestra a continuación. El punto a partir del cual se origina el rayo se denomina punto inicial del rayo.
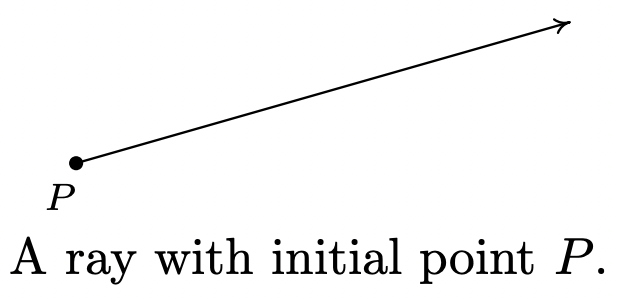
Cuando dos rayos comparten un punto inicial común forman un ángulo y el punto inicial común se llama el vértice del ángulo. Dos ejemplos de lo que comúnmente se consideran ángulos son
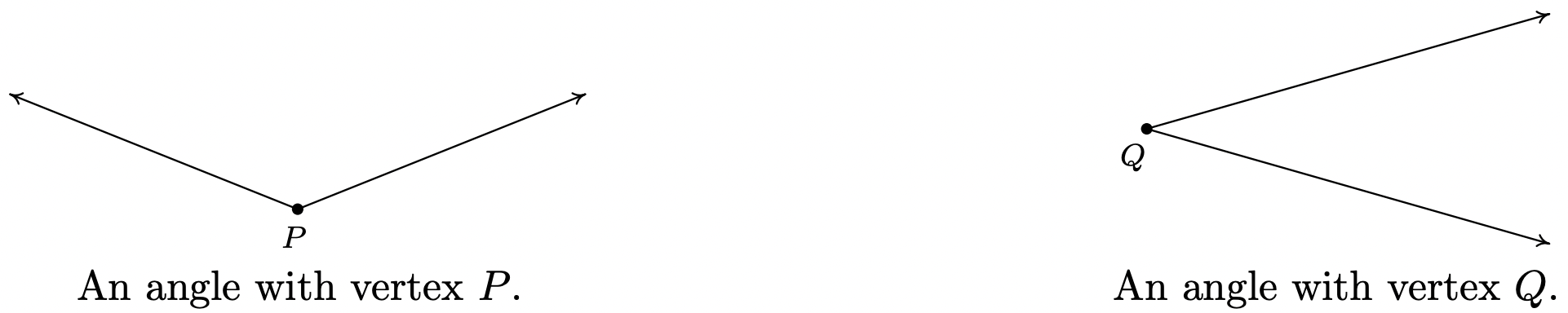
Sin embargo, las dos figuras a continuación también representan ángulos, aunque estos son, en cierto sentido, casos extremos. En el primer caso, los dos rayos son directamente opuestos entre sí formando lo que se conoce como ángulo recto; en el segundo, los rayos son idénticos por lo que el 'ángulo' es indistinguible del propio rayo.
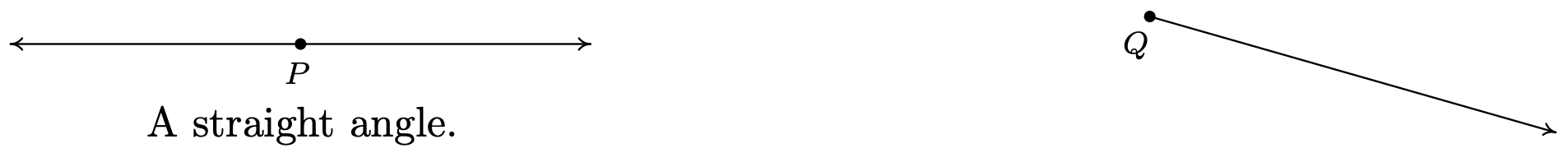
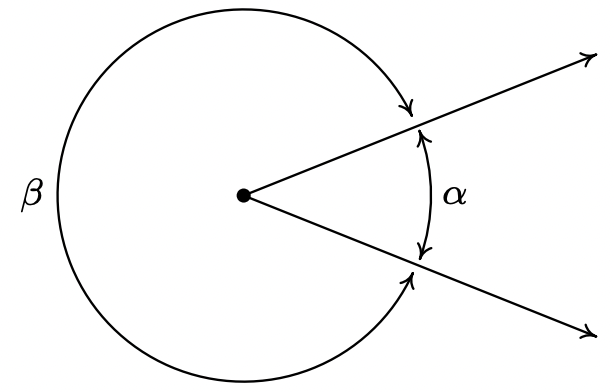
La medida de un ángulo es un número que indica la cantidad de rotación que separa los rayos del ángulo. Hay un problema inmediato con esto, como se muestra a continuación.

¿Qué cantidad de rotación intentamos cuantificar? Lo que acabamos de descubrir es que tenemos al menos dos ángulos descritos por este diagrama. 1 Claramente estos dos ángulos tienen medidas diferentes porque uno parece representar una rotación mayor que el otro, por lo que debemos etiquetarlos de manera diferente. En este libro, utilizamos letras griegas minúsculas como\(\alpha\) (alfa),\(\beta\) (beta),\(\gamma\) (gamma) y\(\theta\) (theta) para etiquetar ángulos. Entonces, por ejemplo, tenemos
Un sistema comúnmente utilizado para medir ángulos es la medida de grados. Las cantidades medidas en grados se denotan con el símbolo '\(^{\circ}\)' familiar. Una revolución completa como se muestra a continuación es\(360^{\circ}\), y partes de una revolución se miden proporcionalmente. 2 Así la mitad de una revolución (un ángulo recto) mide\(\frac{1}{2} \left(360^{\circ}\right) = 180^{\circ}\), un cuarto de revolución (un ángulo recto) mide\(\frac{1}{4} \left(360^{\circ}\right) = 90^{\circ}\) y así sucesivamente.
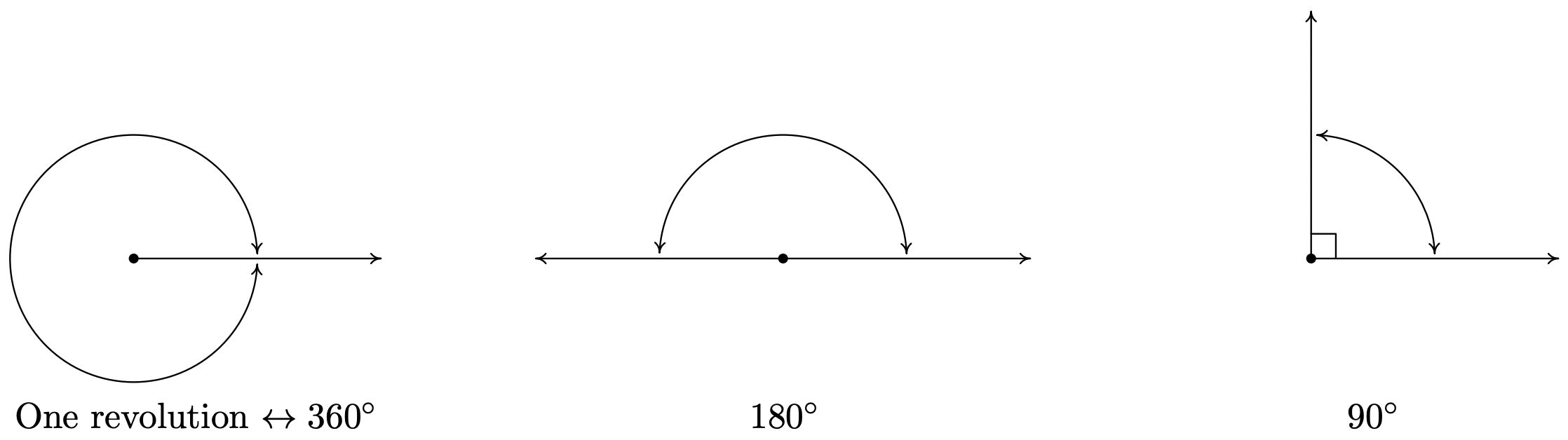
Tenga en cuenta que en la figura anterior, hemos utilizado el pequeño cuadrado '\(\square\)' para denotar un ángulo recto, como es común en Geometría. Recordemos que si un ángulo mide estrictamente entre\(0^{\circ}\) y\(90^{\circ}\) se llama ángulo agudo y si mide estrictamente entre\(90^{\circ}\) y\(180^{\circ}\) se llama ángulo obtuso. Es importante señalar que, teóricamente, podemos conocer la medida de cualquier ángulo siempre y cuando sepamos la proporción que representa de toda la revolución. 3 Por ejemplo, la medida de un ángulo que representa una rotación\(\frac{2}{3}\) de una revolución mediría\(\frac{2}{3} \left(360^{\circ}\right) = 240^{\circ}\), la medida de un ángulo que constituye solo\(\frac{1}{12}\) de una revolución mide\(\frac{1}{12} \left(360^{\circ}\right) = 30^{\circ}\) y un ángulo que indica que no hay rotación en absoluto se mide como\(0^{\circ}\).
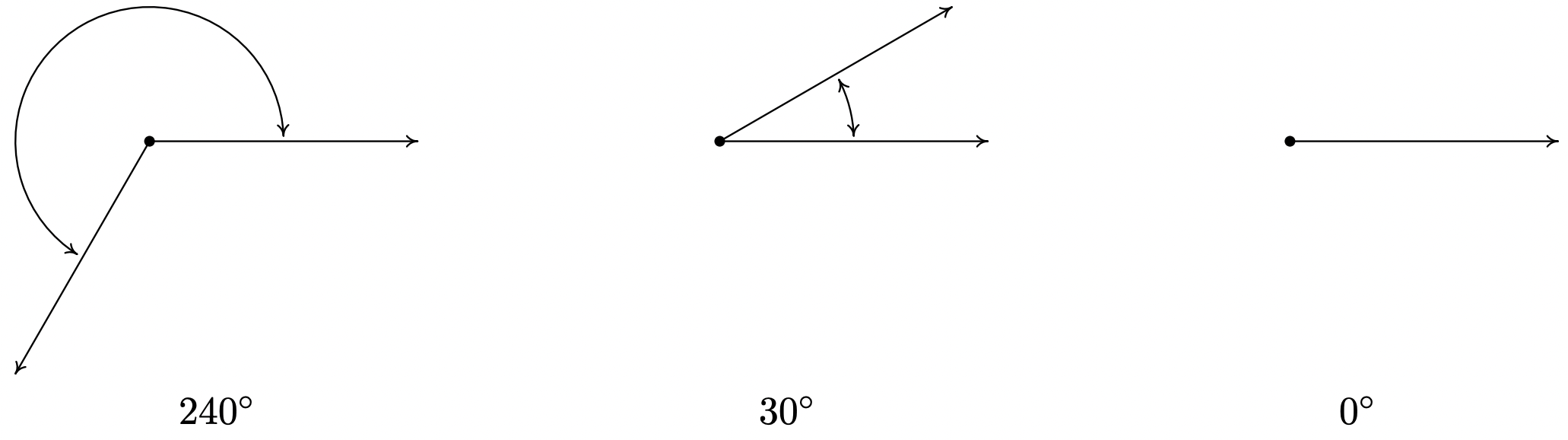
Usando nuestra definición de medida de grado, tenemos que\(1^{\circ}\) representa la medida de un ángulo que constituye\(\frac{1}{360}\) una revolución. A pesar de que puede ser difícil de dibujar, no es difícil imaginar un ángulo con una medida menor que\(1^{\circ}\). Hay dos formas de subdividir grados. El primero, y el más familiar, son los grados decimales. Por ejemplo, un ángulo con una medida de\(30.5^{\circ}\) representaría una rotación a medio camino entre\(30^{\circ}\) y\(31^{\circ}\), o equivalentemente,\(\frac{30.5}{360} = \frac{61}{720}\) de una rotación completa. Esto se puede llevar al límite usando Cálculo para que las medidas como\(\sqrt{2}^{\, \circ}\) tengan sentido. 4 La segunda forma de dividir grados es el sistema Grado - Minuto - Segundo (DMS). En este sistema, un grado se divide equitativamente en sesenta minutos, y a su vez, cada minuto se divide equitativamente en sesenta segundos. 5 En símbolos, escribimos\(1^{\circ} = 60'\) y\(1' = 60''\), de lo que se deduce que\(1^{\circ} = 3600''\). Para convertir una medida de\(42.125^{\circ}\) al sistema DMS, comenzamos por señalar eso\(42.125^{\circ} = 42^{\circ} + 0.125^{\circ}\). Convirtiendo la cantidad parcial de grados a minutos, encontramos\(0.125^{\circ} \left( \frac{60'}{1^{\circ}} \right) = 7.5' = 7' + 0.5'\). Convertir la cantidad parcial de minutos a segundos da\(0.5' \left(\frac{60''}{1'} \right) = 30''\). Poniéndolo todo junto rinde
\[\begin{array}{rcl} 42.125^{\circ} & = & 42^{\circ} + 0.125^{\circ} \\ & = & 42^{\circ} + 7.5' \\ & = & 42^{\circ} + 7' + 0.5' \\ & = & 42^{\circ} + 7' + 30'' \\ & = & 42^{\circ} 7' 30'' \\ \end{array}\nonumber\]
Por otro lado, para convertir\(117^{\circ}15'45''\) a grados decimales, primero calculamos\(15' \left(\frac{1^{\circ}}{60'}\right) = \frac{1}{4}^{\circ}\) y\(45'' \left(\frac{1^{\circ}}{3600''}\right) = \frac{1}{80}^{\circ}\). Entonces encontramos
\[\begin{array}{rcl} 117^{\circ}15'45'' & = & 117^{\circ} + 15' + 45'' \\[4pt] & = & 117^{\circ} + \frac{1}{4}^{\circ} + \frac{1}{80}^{\circ} \\[4pt] & = & \frac{9381}{80}^{\circ} \\[4pt] & = & 117.2625^{\circ} \\ \end{array}\nonumber\]
Recordemos que dos ángulos agudos se denominan ángulos complementarios si sus medidas se suman a\(90^{\circ}\). Dos ángulos, ya sea un par de ángulos rectos o un ángulo agudo y un ángulo obtuso, se denominan ángulos suplementarios si sus medidas se suman a\(180^{\circ}\). En el diagrama de abajo, los ángulos\(\alpha\) y\(\beta\) son ángulos suplementarios mientras que el par\(\gamma\) y\(\theta\) son ángulos complementarios.
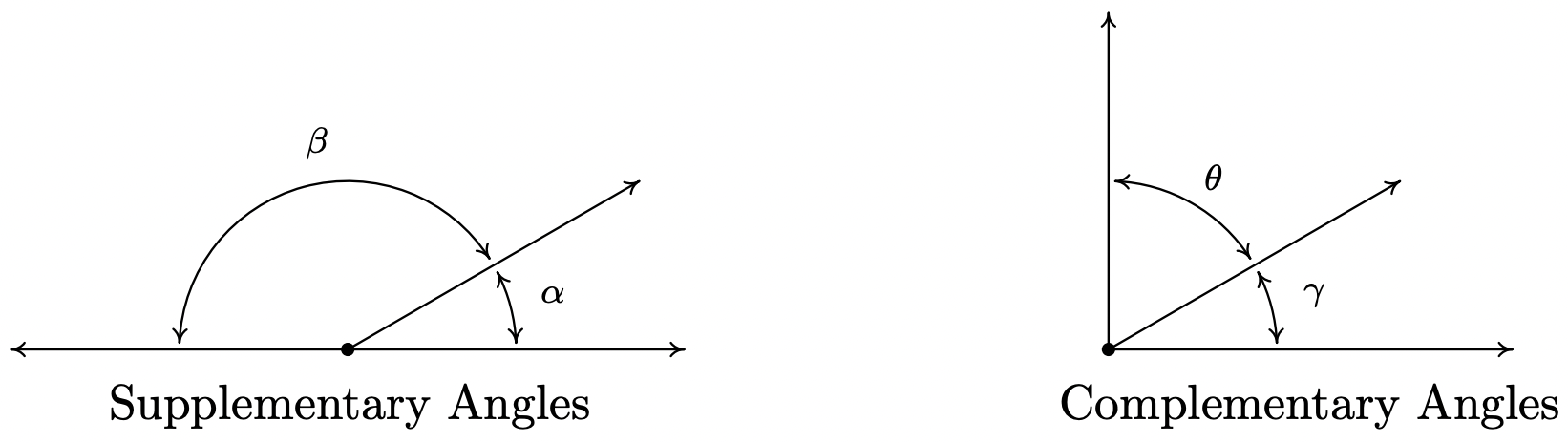
En la práctica, la distinción entre el ángulo en sí y su medida es borrosa de manera que la oración '\(\alpha\)es un ángulo que mide\(42^{\circ}\)' a menudo se abrevia como '\(\alpha = 42^{\circ}\).' Ahora es el momento de dar un ejemplo.
Dejar\(\alpha = 111.371^{\circ}\) y\(\beta = 37^{\circ}28'17''\).
- Convertir\(\alpha\) al sistema DMS. Redondee su respuesta al segundo más cercano.
- Convertir\(\beta\) a grados decimales. Redondea tu respuesta a la milésima de grado más cercana.
- Sketch\(\alpha\) y\(\beta\).
- Encuentra un ángulo suplementario para\(\alpha\).
- Encuentra un ángulo complementario para\(\beta\).
Solución
- Para convertir\(\alpha\) al sistema DMS, comenzamos con\(111.371^{\circ} = 111^{\circ}+ 0.371^{\circ}\). A continuación convertimos\(0.371^{\circ} \left(\frac{60'}{1^{\circ}}\right) = 22.26'\). Escribiendo\(22.26' = 22'+ 0.26'\), convertimos\(0.26' \left( \frac{60''}{1'} \right) = 15.6''\). Por lo tanto,
\[\begin{array}{rcl} 111.371^{\circ} & = & 111^{\circ} + 0.371^{\circ} \\ & = & 111^{\circ} + 22.26' \\ & = & 111^{\circ} + 22' + 0.26' \\ & = & 111^{\circ} + 22' + 15.6'' \\ & = & 111^{\circ}22'15.6'' \\ \end{array}\nonumber\]
Redondeando a segundos, obtenemos\(\alpha \approx 111^{\circ}22'16''\).
- Para convertir\(\beta\) a grados decimales, convertimos\(28' \left(\frac{1^{\circ}}{60'}\right) = \frac{7}{15}^{\, \circ}\) y\(17''\left(\frac{1^{\circ}}{3600'}\right) = \frac{17}{3600}^{\, \circ}\). Poniéndolo todo junto, tenemos
\[\begin{array}{rcl} 37^{\circ}28'17'' & = & 37^{\circ} + 28' + 17'' \\[4pt] & = & 37^{\circ} + \frac{7}{15}^{\, \circ} + \frac{17}{3600}^{\, \circ} \\[4pt] & = & \frac{134897}{3600}^{\circ} \\[4pt] & \approx & 37.471^{\circ} \\ \end{array}\nonumber\]
- Para bosquejar\(\alpha\), primero notamos eso\(90^{\circ} < \alpha < 180^{\circ}\). Si dividimos este rango a la mitad, obtenemos\(90^{\circ} < \alpha < 135^{\circ}\), y una vez más, tenemos\(90^{\circ} < \alpha < 112.5^{\circ}\). Esto nos da una estimación bastante buena para\(\alpha\), como se muestra a continuación. 6 Procediendo de manera similar para\(\beta\), nos encontramos\(0^{\circ} < \beta < 90^{\circ}\), entonces\(0^{\circ} < \beta < 45^{\circ}\),\(22.5^{\circ} < \beta < 45^{\circ}\), y por último,\(33.75^{\circ} < \beta < 45^{\circ}\).
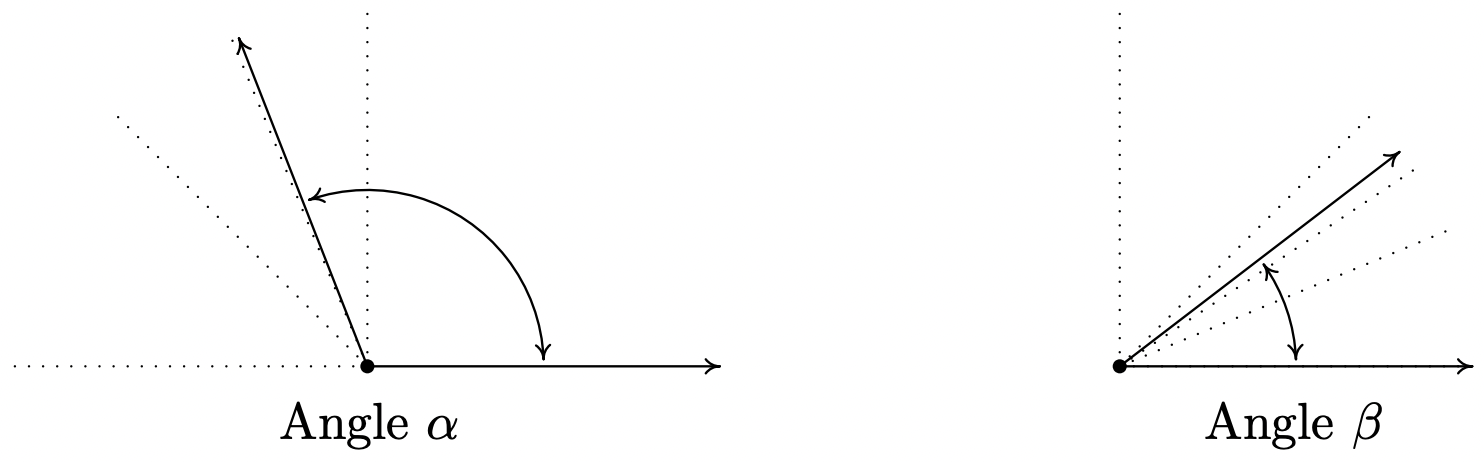
- Para encontrar un ángulo suplementario para\(\alpha\), buscamos un ángulo\(\theta\) para que\(\alpha + \theta = 180^{\circ}\). Obtenemos\(\theta = 180^{\circ} - \alpha = 180^{\circ} - 111.371^{\circ} = 68.629^{\circ}\).
- Para encontrar un ángulo complementario para\(\beta\), buscamos un ángulo\(\gamma\) para que\(\beta + \gamma = 90^{\circ}\). Obtenemos\(\gamma = 90^{\circ} - \beta = 90^{\circ} - 37^{\circ}28'17''\). Si bien podríamos llegar a la calculadora para obtener una respuesta aproximada, elegimos en su lugar hacer un poco de aritmética sexagesimal 7. Primero reescribimos\(90^{\circ} = 90^{\circ} 0' 0'' = 89^{\circ}60' 0'' = 89^{\circ}59'60''\). En esencia, estamos 'pidiendo prestado'\(1^{\circ} = 60'\) del lugar de grado, y luego tomando prestado\(1' = 60''\) del lugar de minutos. 8 Esto rinde,\(\gamma = 90^{\circ} - 37^{\circ}28'17'' = 89^{\circ}59'60'' - 37^{\circ}28'17'' = 52^{\circ}31'43''\).
Hasta este punto, solo hemos discutido ángulos que miden entre\(0^{\circ}\) y\(360^{\circ}\), inclusivo. En última instancia, queremos utilizar el arsenal de Álgebra que hemos acumulado en los Capítulos 1 al 9 no sólo para resolver problemas geométricos que involucran ángulos, sino también para extender su aplicabilidad a otros fenómenos del mundo real. Un primer paso en esta dirección es extender nuestra noción de “ángulo” de simplemente medir una extensión de rotación a cantidades que pueden asociarse con números reales. Para ello, se introduce el concepto de ángulo orientado. Como su nombre indica, en un ángulo orientado, la dirección de la rotación es importante. Imaginamos que el ángulo se barre comenzando desde un lado inicial y terminando en un lado terminal, como se muestra a continuación. Cuando la rotación es en sentido antihorario 9 desde el lado inicial hasta el lado terminal, decimos que el ángulo es positivo; cuando la rotación es en sentido horario, decimos que el ángulo es negativo.
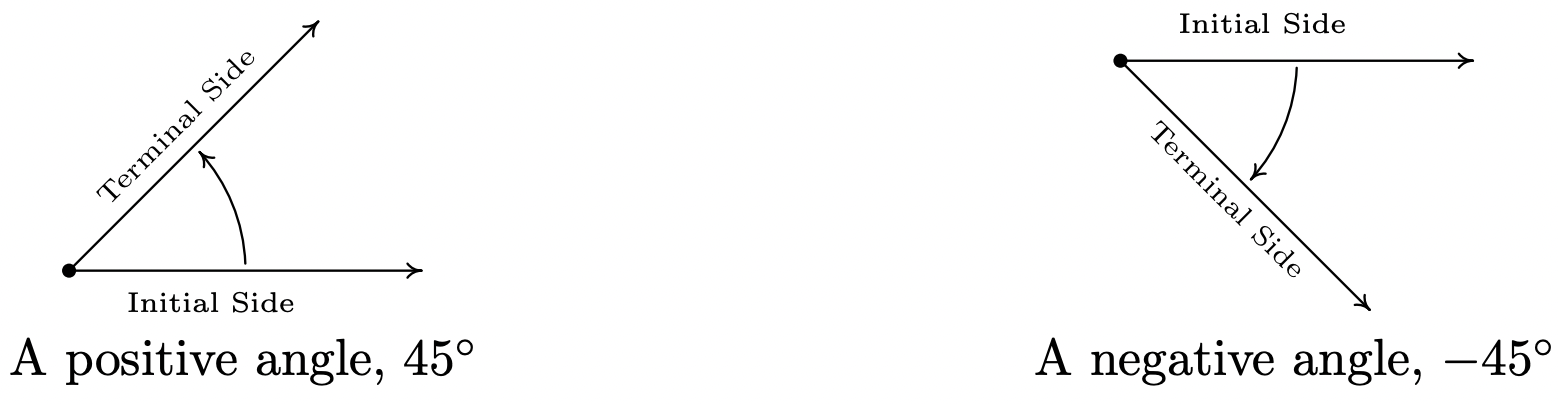
En este punto, también extendemos nuestras rotaciones permisibles para incluir ángulos que abarcan más de una revolución. Por ejemplo, para bosquejar un ángulo con medida\(450^{\circ}\) comenzamos con un lado inicial, giramos en sentido antihorario una revolución completa (para encargarnos de la 'primera'\(360^{\circ}\)) luego continuamos con una rotación adicional en sentido contrario a\(90^{\circ}\) las agujas del reloj, como se ve a continuación.
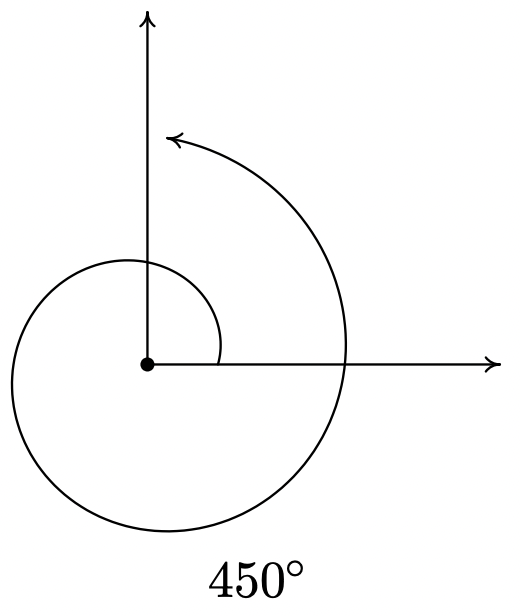
Para conectar aún más los ángulos con el Álgebra que ha venido antes, a menudo superpondremos un diagrama de ángulos en el plano de coordenadas. Se dice que un ángulo está en posición estándar si su vértice es el origen y su lado inicial coincide con el\(x\) eje positivo. Los ángulos en posición estándar se clasifican de acuerdo a dónde se encuentra su lado terminal. Por ejemplo, un ángulo en posición estándar cuyo lado terminal se encuentra en el Cuadrante I se denomina 'ángulo del cuadrante I'. Si el lado terminal de un ángulo se encuentra en uno de los ejes de coordenadas, se denomina ángulo cuadrangular. Dos ángulos en posición estándar se denominan coterminales si comparten el mismo lado de terminal. 10 En la siguiente figura,\(\alpha = 120^{\circ}\) y\(\beta = -240^{\circ}\) se encuentran dos ángulos coterminales del Cuadrante II dibujados en posición estándar. Tenga en cuenta que\(\alpha = \beta + 360^{\circ}\), o equivalentemente,\(\beta = \alpha - 360^{\circ}\). Dejamos como ejercicio al lector verificar que los ángulos coterminales siempre difieran en un múltiplo de\(360^{\circ}\). 11 Más precisamente, si\(\alpha\) y\(\beta\) son ángulos coterminales, entonces\(\beta = \alpha + 360^{\circ} \cdot k\) donde\(k\) es un entero. 12
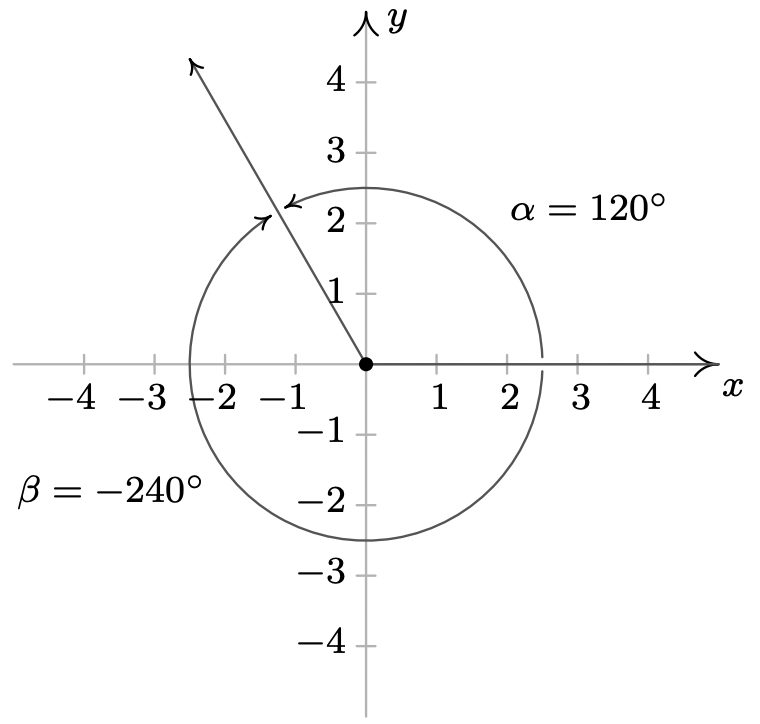
Dos ángulos coterminales,\(\alpha = 120^{\circ}\) y\(\beta = -240^{\circ}\), en posición estándar.
Grafique cada uno de los ángulos (orientados) a continuación en posición estándar y clasifíquelos según dónde se encuentre su lado terminal. Encuentra tres ángulos coterminales, al menos uno de los cuales es positivo y uno de los cuales es negativo.
- \(\alpha = 60^{\circ}\)
- \(\beta = -225^{\circ}\)
- \(\gamma = 540^{\circ}\)
- \(\phi = -750^{\circ}\)
Solución.
- Para graficar\(\alpha = 60^{\circ}\), dibujamos un ángulo con su lado inicial en el\(x\) eje positivo y giramos en sentido antihorario\(\frac{60^{\circ}}{360^{\circ}} = \frac{1}{6}\) de una revolución. Vemos que\(\alpha\) es un ángulo del Cuadrante I. Para encontrar ángulos que son coterminales, buscamos ángulos\(\theta\) de la forma\(\theta = \alpha + 360^{\circ} \cdot k\), para algún entero\(k\). Cuando\(k = 1\), obtenemos\(\theta = 60^{\circ} + 360^{\circ} = 420^{\circ}\). Sustituyendo\(k = -1\) da\(\theta = 60^{\circ} - 360^{\circ} = -300^{\circ}\). Por último, si lo dejamos\(k = 2\), lo conseguimos\(\theta = 60^{\circ} + 720^{\circ} = 780^{\circ}\).
- Dado que\(\beta = - 225^{\circ}\) es negativo, partimos en el\(x\) eje positivo y giramos en sentido horario\(\frac{225^{\circ}}{360^{\circ}} = \frac{5}{8}\) de una revolución. Vemos que\(\beta\) es un ángulo del Cuadrante II. Para encontrar ángulos coterminales, procedemos como antes y calculamos\(\theta = -225^{\circ} + 360^{\circ} \cdot k\) para valores enteros de\(k\). Encontramos\(135^{\circ}\),\(-585^{\circ}\) y todos\(495^{\circ}\) somos coterminales con\(-225^{\circ}\).
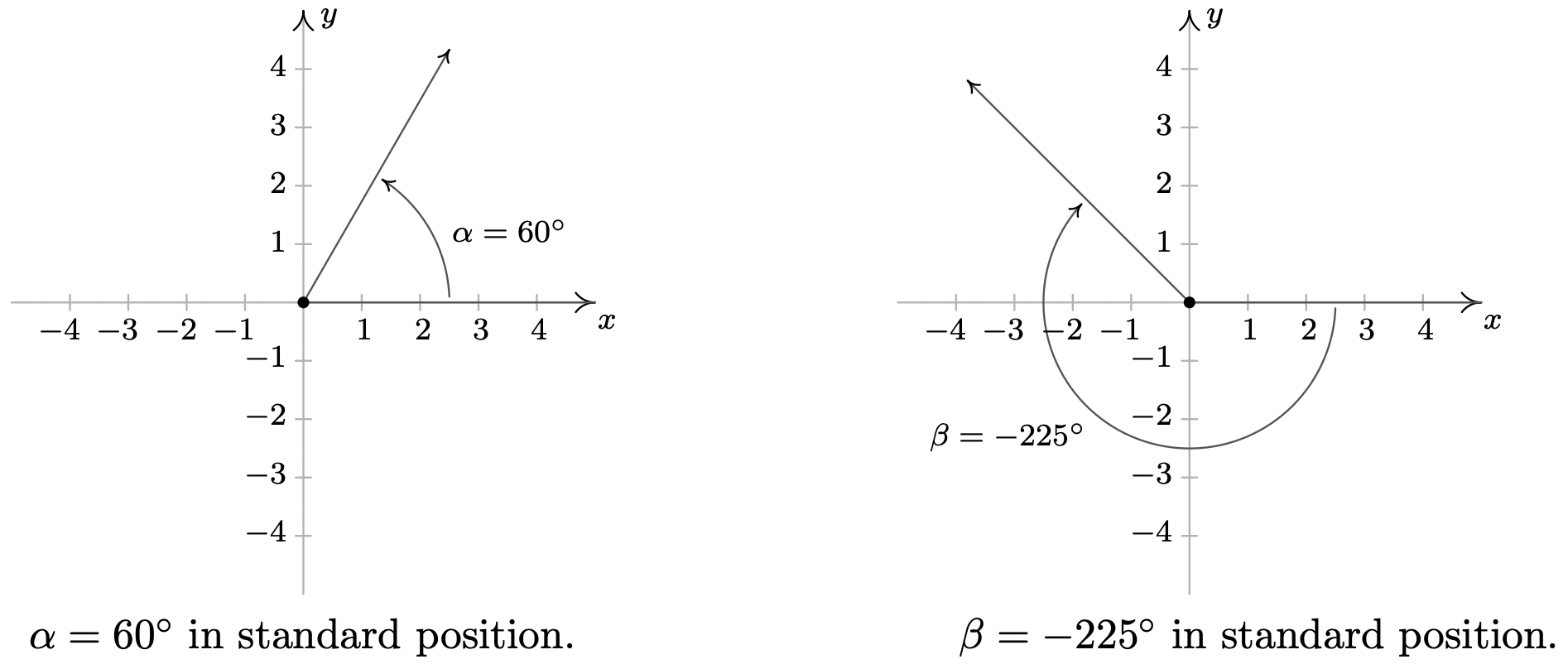
- Dado que\(\gamma = 540^{\circ}\) es positivo, giramos en sentido antihorario desde el\(x\) eje positivo. Una revolución completa explica\(360^{\circ}\), con\(180^{\circ}\), o\(\frac{1}{2}\) de una revolución restante. Dado que el lado terminal de\(\gamma\) se encuentra en el\(x\) eje negativo,\(\gamma\) es un ángulo cuadrangular. Todos los ángulos coterminales con\(\gamma\) son de la forma\(\theta = 540^{\circ} + 360^{\circ} \cdot k\), donde\(k\) es un entero. Trabajando a través de la aritmética, encontramos tres ángulos de este tipo:\(180^{\circ}\),\(-180^{\circ}\) y\(900^{\circ}\).
- La letra griega\(\phi\) se pronuncia 'fee' o 'fie' y como\(\phi\) es negativa, comenzamos nuestra rotación en sentido horario desde el\(x\) eje positivo. Dos revoluciones completas dan cuenta\(720^{\circ}\), con solo\(30^{\circ}\) o\(\frac{1}{12}\) de una revolución por recorrer. Encontramos que\(\phi\) es un ángulo del Cuadrante IV. Para encontrar ángulos coterminales, calculamos\(\theta = -750^{\circ} + 360^{\circ} \cdot k\) para unos cuantos enteros\(k\) y obtenemos\(-390^{\circ}\),\(-30^{\circ}\) y\(330^{\circ}\).
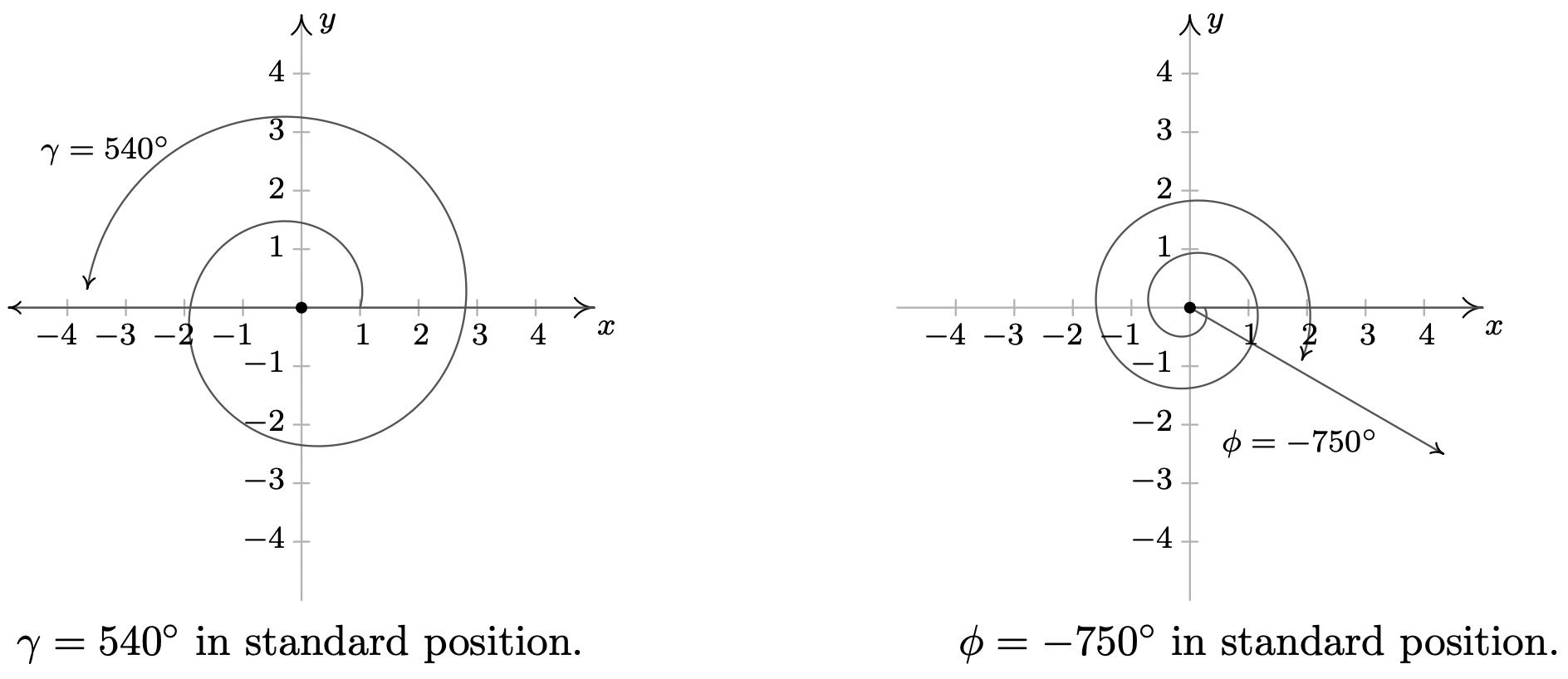
Tenga en cuenta que como hay infinitamente muchos enteros, cualquier ángulo dado tiene infinitamente muchos ángulos coterminales, y se anima al lector a trazar los pocos conjuntos de ángulos coterminales que se encuentran en el Ejemplo 10.1.2 para ver esto. Ahora estamos a un paso de casar completamente ángulos con los números reales y el resto del Álgebra. Para ello, recordamos esta definición de Geometría.
El número real\(\pi\) se define como la relación entre la circunferencia de un círculo y su diámetro. En símbolos, dado un círculo de circunferencia\(C\) y diámetro\(d\),
\[\pi = \dfrac{C}{d}\nonumber\]
Si bien la Definición 10.1 es muy posiblemente la definición 'estándar' de\(\pi\), los autores serían negligentes si no mencionáramos que enterrado en esta definición es en realidad un teorema. Como probablemente sepa el lector, el número\(\pi\) es una constante matemática, es decir, no importa qué círculo se seleccione, la relación de su circunferencia a su diámetro tendrá el mismo valor que cualquier otro círculo. Si bien esto es cierto, está lejos de ser obvio y conduce a un escenario contradictorio que se explora en los Ejercicios. Dado que el diámetro de un círculo es el doble de su radio, podemos reorganizar rápidamente la ecuación en la Definición 10.1 para obtener una fórmula más útil para nuestros propósitos, a saber:\(2 \pi = \dfrac{C}{r}\)
Esto nos dice que para cualquier círculo, la relación de su circunferencia a su radio también es siempre constante; en este caso la constante es\(2\pi\). Supongamos que ahora tomamos una porción del círculo, así que en lugar de comparar toda la circunferencia\(C\) con el radio, comparamos algunas\(s\) unidades de medición de arco en longitud con el radio, como se muestra a continuación. \(\theta\)Sea el ángulo central subtendido por este arco, es decir, un ángulo cuyo vértice es el centro del círculo y cuyos rayos determinantes pasan por los puntos finales del arco. Usando argumentos de proporcionalidad, es lógico razonar que la relación también\(\dfrac{s}{r}\) debe ser una constante entre todos los círculos, y es esta relación la que define la medida radianes de un ángulo.
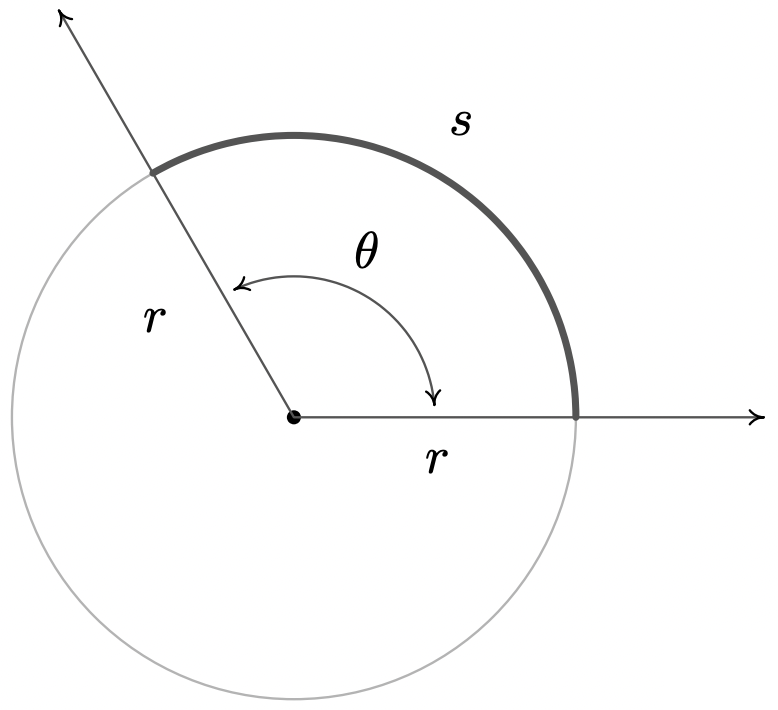
La medida radianes de\(\theta\) es\(\dfrac{s}{r}\).
Para tener una mejor idea de la medida de radianes, observamos que un ángulo con medida de radianes\(1\) significa que la longitud del arco correspondiente\(s\) es igual al radio del círculo\(r\), de ahí\(s = r\). Cuando la medida del radián es\(2\), tenemos\(s = 2r\); cuando la medida del radián es\(3\)\(s = 3r\), y así sucesivamente. Así, la medida radianes de un ángulo nos\(\theta\) dice cuántas 'longitudes de radio' necesitamos barrer a lo largo del círculo para subtender el ángulo\(\theta\).
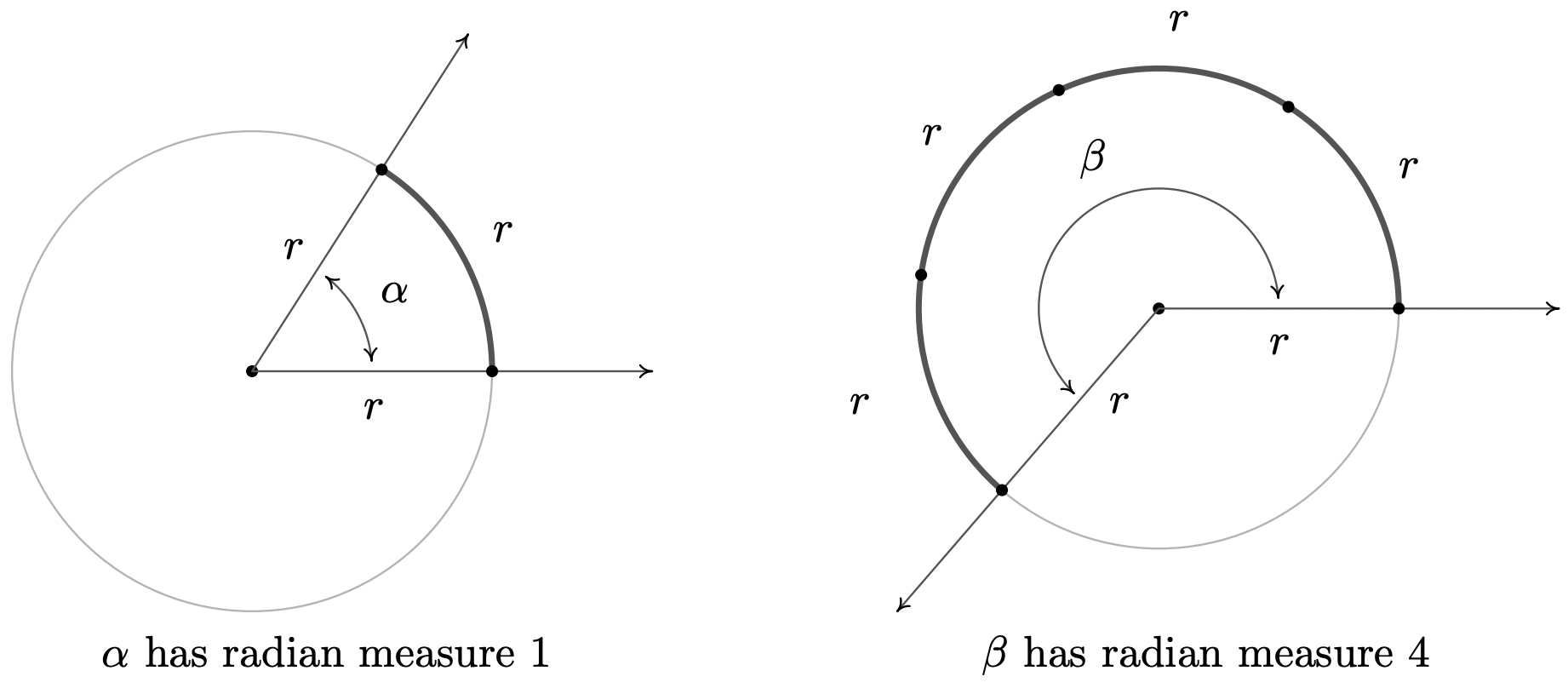
Dado que una revolución barre toda la circunferencia\(2\pi r\), una revolución tiene medida de radianes\(\dfrac{2 \pi r}{r} = 2 \pi\). De esto podemos encontrar la medida radianes de otros ángulos centrales usando proporciones, al igual que hicimos con grados. Por ejemplo, la mitad de una revolución tiene medida radianes\(\frac{1}{2} (2 \pi) = \pi\), un cuarto de revolución tiene medida radianes\(\frac{1}{4} (2 \pi) = \frac{\pi}{2}\), y así sucesivamente. Obsérvese que, por definición, la medida radianes de un ángulo es una longitud dividida por otra longitud de manera que estas mediciones son en realidad adimensionales y se consideran números 'puros'. Por esta razón, no utilizamos ningún símbolo para denotar la medida de radianes, sino que usamos la palabra 'radianes' para denotar estas unidades adimensionales según sea necesario. Por ejemplo, decimos que una revolución mide '\(2\pi\)radianes', la mitad de una revolución mide '\(\pi\)radianes', y así sucesivamente.
Al igual que con la medida de grado, la distinción entre el ángulo en sí y su medida suele ser borrosa en la práctica, así que cuando escribimos\(\theta = \frac{\pi}{2}\) '', queremos decir que\(\theta\) es un ángulo que mide\(\frac{\pi}{2}\) radianes. 13 Extendemos la medida de radianes a ángulos orientados, tal como hicimos con grados de antemano, de manera que una medida positiva indica rotación en sentido antihorario y una medida negativa indica rotación en sentido horario. 14 Al igual que antes, dos ángulos positivos\(\alpha\) y\(\beta\) son complementarios si\(\alpha + \beta = \pi\) y complementarios si\(\alpha + \beta = \frac{\pi}{2}\). Por último, dejamos al lector demostrar que al usar la medida de radianes, dos ángulos\(\alpha\) y\(\beta\) son coterminales si y sólo si\(\beta = \alpha + 2\pi k\) para algún entero\(k\).
Grafique cada uno de los ángulos (orientados) a continuación en posición estándar y clasifíquelos según dónde se encuentre su lado terminal. Encuentra tres ángulos coterminales, al menos uno de los cuales es positivo y uno de los cuales es negativo.
- \(\alpha = \dfrac{\pi}{6}\)
- \(\beta = -\dfrac{4\pi}{3}\)
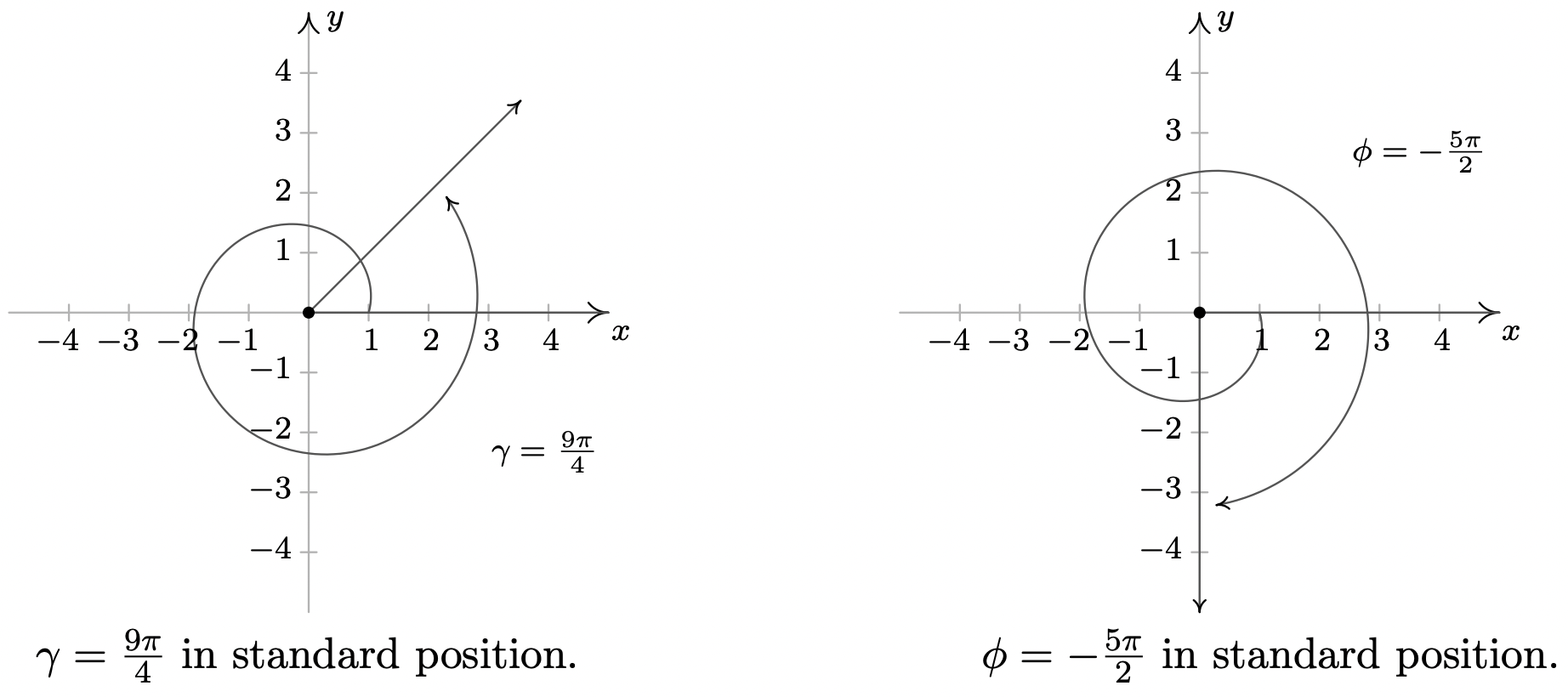
- \(\gamma = \dfrac{9 \pi}{4}\)
- \(\phi = - \dfrac{5 \pi}{2}\)
Solución.
- El ángulo\(\alpha = \frac{\pi}{6}\) es positivo, por lo que dibujamos un ángulo con su lado inicial en el\(x\) eje positivo y giramos en sentido antihorario\(\frac{\left( \pi / 6\right)}{2 \pi} = \frac{1}{12}\) de una revolución. Así\(\alpha\) es un ángulo del Cuadrante I. \(\theta\)Los ángulos coterminales son de la forma\(\theta = \alpha + 2\pi \cdot k\), para algún entero\(k\). Para facilitar un poco la aritmética, observamos que\(2\pi = \frac{12 \pi}{6}\), así cuando\(k = 1\), obtenemos\(\theta = \frac{\pi}{6} + \frac{12 \pi}{6} = \frac{13 \pi}{6}\). Sustituyendo\(k = -1\) da\(\theta = \frac{\pi}{6} - \frac{12 \pi}{6} = -\frac{11 \pi}{6}\) y cuando dejamos\(k = 2\), obtenemos\(\theta = \frac{\pi}{6} + \frac{24 \pi}{6} = \frac{25 \pi}{6}\).
- Dado que\(\beta = - \frac{4\pi}{3}\) es negativo, partimos en el\(x\) eje positivo y giramos en sentido horario\(\frac{\left(4 \pi / 3\right)}{2\pi} = \frac{2}{3}\) de una revolución. Encontramos\(\beta\) que es un ángulo del Cuadrante II. Para encontrar ángulos coterminales, procedemos como antes de usar\(2\pi = \frac{6 \pi}{3}\), y calculamos\(\theta = -\frac{4 \pi}{3} + \frac{6 \pi}{3} \cdot k\) para valores enteros de\(k\). Obtenemos\(\frac{2\pi}{3}\),\(-\frac{10 \pi}{3}\) y\(\frac{8 \pi}{3}\) como ángulos coterminales.
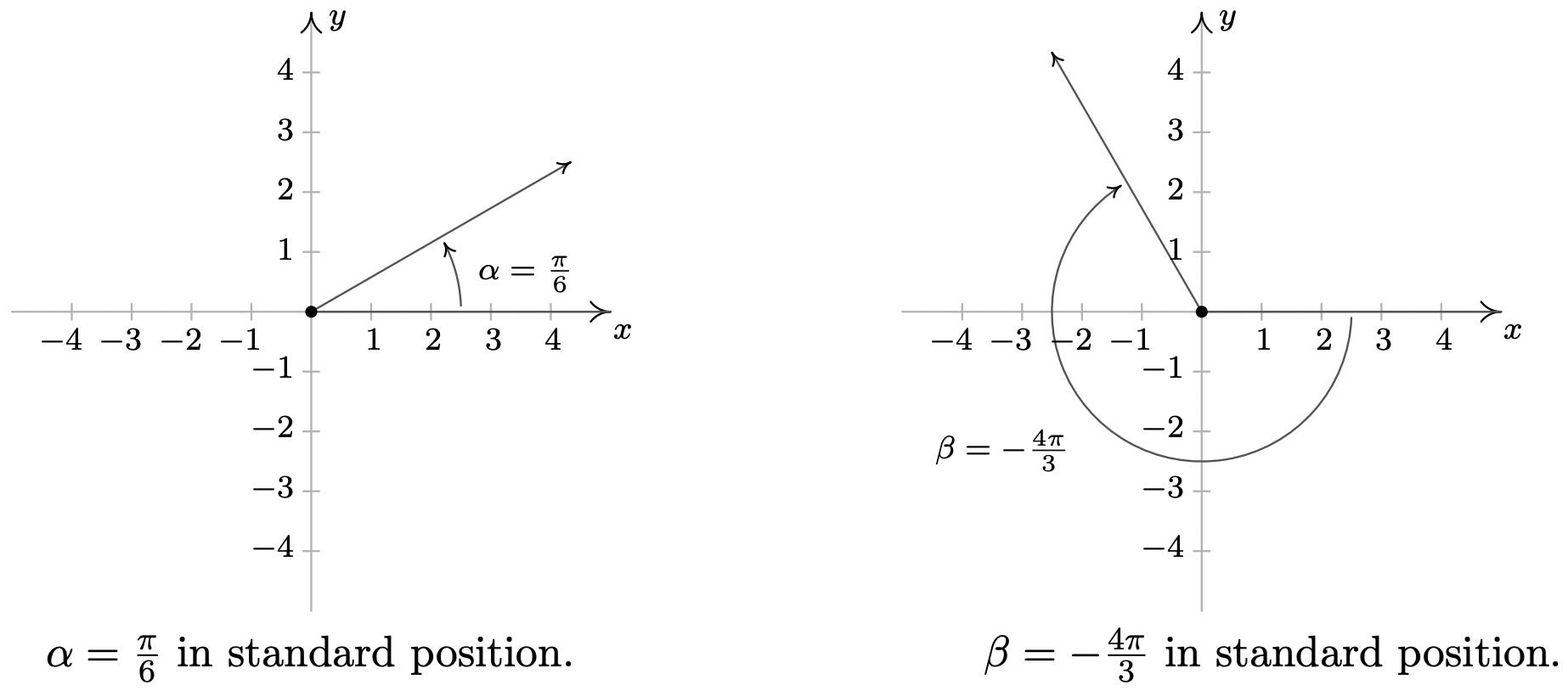
- Dado que\(\gamma = \frac{9 \pi}{4}\) es positivo, giramos en sentido antihorario desde el\(x\) eje positivo. Una revolución completa da cuenta\(2 \pi = \frac{8 \pi}{4}\) de la medida radianes con\(\frac{\pi}{4}\) o\(\frac{1}{8}\) de una revolución restante. Tenemos\(\gamma\) como cuadrante I ángulo. Todos los ángulos coterminales con\(\gamma\) son de la forma\(\theta = \frac{9 \pi}{4} + \frac{8\pi}{4} \cdot k\), donde\(k\) es un entero. Trabajando a través de la aritmética, encontramos:\(\frac{\pi}{4}\),\(-\frac{7 \pi}{4}\) y\(\frac{17 \pi}{4}\).
- Para graficar\(\phi = -\frac{5 \pi}{2}\), comenzamos nuestra rotación en el sentido de las agujas del reloj desde el\(x\) eje positivo. Como\(2 \pi = \frac{4 \pi}{2}\), después de una revolución completa en el sentido de las agujas del reloj, tenemos\(\frac{\pi}{2}\) o\(\frac{1}{4}\) de una revolución restante. Dado que el lado terminal de\(\phi\) se encuentra en el\(y\) eje negativo,\(\phi\) es un ángulo cuadrangular. Para encontrar ángulos coterminales, calculamos\(\theta = -\frac{5 \pi}{2} + \frac{4 \pi}{2} \cdot k\) para unos cuantos enteros\(k\) y obtenemos\(-\frac{\pi}{2}\),\(\frac{3 \pi}{2}\) y\(\frac{7 \pi}{2}\).
Cabe mencionar que podríamos haber trazado los ángulos en el Ejemplo 10.1.3 convirtiéndolos primero a medida de grado y siguiendo el procedimiento establecido en el Ejemplo 10.1.2. Si bien convertir ida y vuelta de grados y radianes es sin duda una buena habilidad para tener, lo mejor es que aprendas a 'pensar en radianes' así como puedas 'pensar en grados'. Sin embargo, los autores quedarían abandonados en nuestros deberes si ignoráramos por completo la conversión básica entre estos sistemas. Dado que una revolución mide en sentido antihorario\(360^{\circ}\) y el mismo ángulo mide\(2 \pi\) radianes, podemos usar la proporción\(\frac{2 \pi \, \text{radians}}{360^{\circ}}\), o su equivalente reducido\(\frac{\pi \, \text{radians}}{180^{\circ}}\), como factor de conversión entre los dos sistemas. Por ejemplo, para convertir\(60^{\circ}\) a radianes nos encontramos\(60^{\circ} \left( \frac{\pi \, \text{radians}}{180^{\circ}}\right) = \frac{\pi}{3} \, \text{radians}\), o simplemente\(\frac{\pi}{3}\). Para convertir de la medida de radianes de nuevo a grados, multiplicamos por la proporción\(\frac{180^{\circ}}{\pi \, \text{radian}}\). Por ejemplo,\(-\frac{5 \pi}{6} \, \text{radians}\) es igual a\(\left(-\frac{5 \pi}{6} \, \text{radians} \right) \left( \frac{180^{\circ}}{\pi \, \text{radians}}\right) = -150^{\circ}\). 15 De particular interés es el hecho de que un ángulo que mide\(1\) en medida radianes es igual a\(\frac{180^{\circ}}{\pi} \approx 57.2958^{\circ}\).
Resumimos estas conversiones a continuación.
- Para convertir medida de grado en medida de radianes, multiplique por\(\dfrac{\pi \, \text{radians}}{180^{\circ}}\)
- Para convertir la medida de radianes en medida de grado, multiplique por\(\dfrac{180^{\circ}}{\pi \, \text{radians}}\)
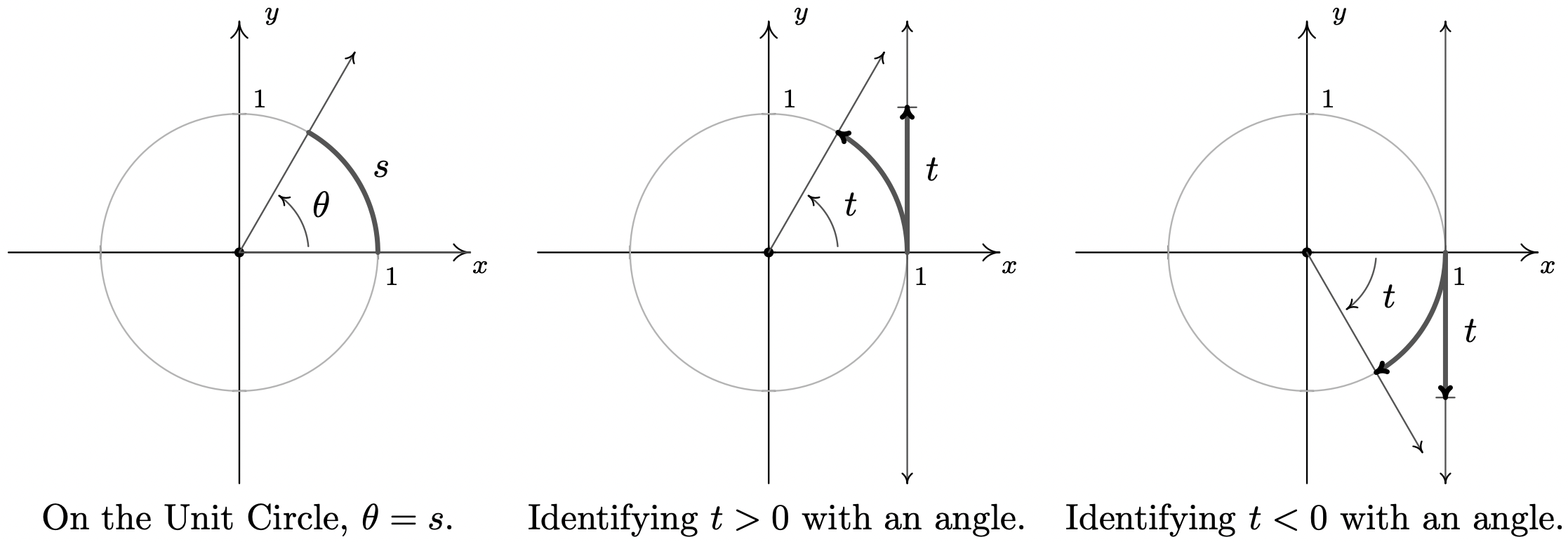
A la luz del Ejemplo 10.1.3 y la Ecuación 10.1, el lector bien puede preguntarse cuál es el atractivo de la medida de radianes. Los números involucrados son, ciertamente, mucho más complicados que la medida de grado. La respuesta radica en la facilidad con la que los ángulos en la medida de radianes pueden identificarse con números reales. Considere el Círculo de Unidad\(x^2 + y^2 = 1\), como se dibuja a continuación, el ángulo\(\theta\) en posición estándar y las\(s\) unidades de medición de arco correspondientes en longitud. Por definición, y el hecho de que el Círculo Unitario tenga radio 1, la medida radianes de\(\theta\) es\(\dfrac{s}{r}=\dfrac{s}{1} = s\) tal que, una vez más desdibujando la distinción entre un ángulo y su medida, tenemos\(\theta = s\). Para identificar números reales con ángulos orientados, aprovechamos este hecho esencialmente “envolviendo” la recta numérica real alrededor del Círculo de Unidad y asociando a cada número real\(t\) un arco orientado en el Círculo de Unidad con punto inicial\((1,0)\).
Al ver la línea vertical\(x=1\) como otra línea numérica real demarcada como el\(y\) eje -eje, dado un número real\(t>0\), 'envolvemos' el intervalo (vertical)\([0,t]\) alrededor del Círculo de Unidad en sentido antihorario. El arco resultante tiene una longitud de\(t\) unidades y por lo tanto el ángulo correspondiente tiene una medida de radianes igual a\(t\). Si\(t<0\), envolvemos el intervalo en\([t,0]\) sentido horario alrededor del Círculo de Unidad. Como hemos definido la rotación en el sentido de las agujas del reloj como tener medida de radianes negativos, el ángulo determinado por este arco tiene una medida de radianes igual a\(t\). Si\(t=0\), estamos en el punto\((1,0)\) del\(x\) eje -que corresponde a un ángulo con medida de radianes\(0\). De esta manera, identificamos cada número real\(t\) con el ángulo correspondiente con la medida de radianes\(t\).
Esboza el arco orientado en el Círculo de Unidad correspondiente a cada uno de los siguientes números reales.
- \(t=\dfrac{3 \pi}{4}\)
- \(t = - 2 \pi\)
- \(t = -2\)
- \(t = 117\)
Solución.
- El arco asociado con\(t = \frac{3 \pi}{4}\) es el arco en el Círculo de Unidad que subtiende el ángulo\(\frac{3 \pi}{4}\) en la medida de radianes. Ya que\(\frac{3 \pi}{4}\) es\(\frac{3}{8}\) de una revolución, tenemos un arco que comienza en el punto que\((1,0)\) avanza en sentido antihorario hasta la mitad del cuadrante II.
- Como una revolución es\(2\pi\) radianes, y\(t=-2\pi\) es negativa, graficamos el arco que comienza en\((1,0)\) y procede en el sentido de las agujas del reloj para una revolución completa.
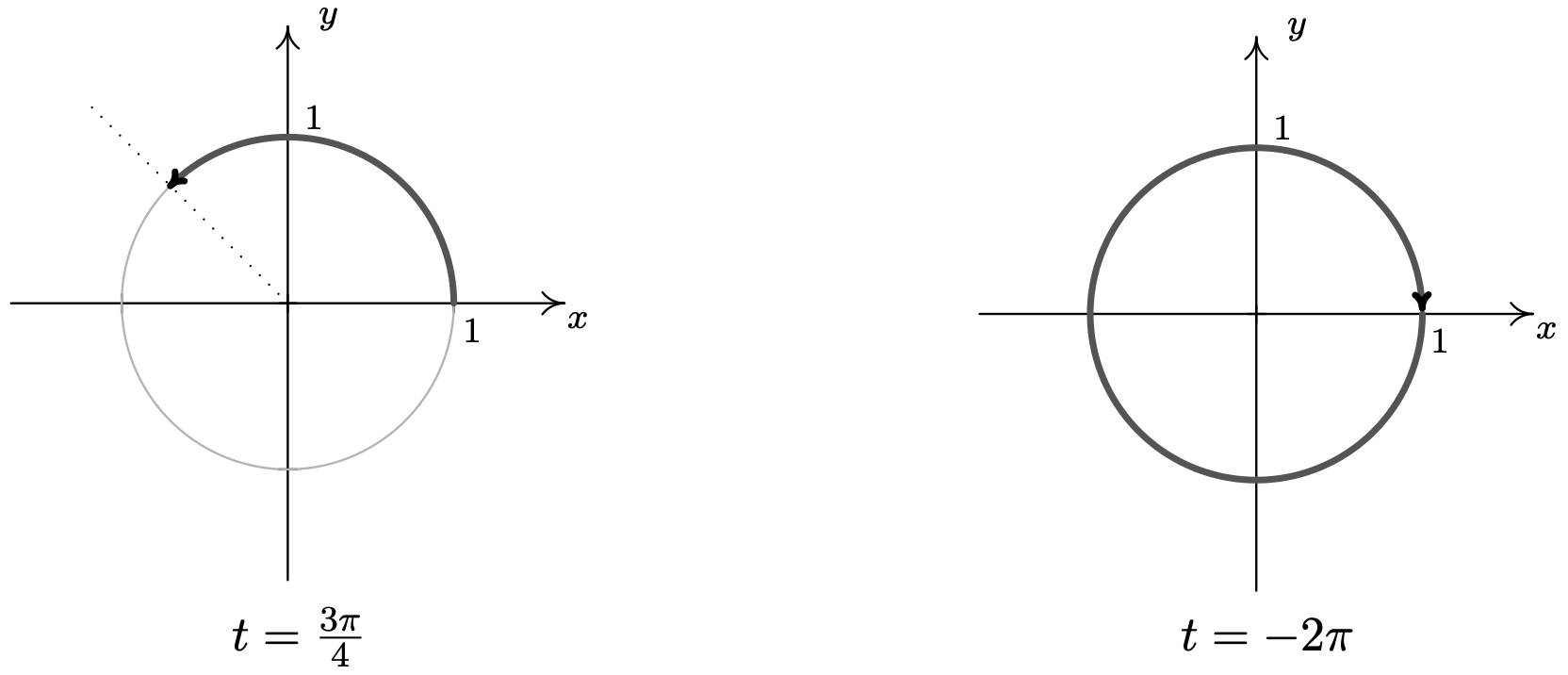
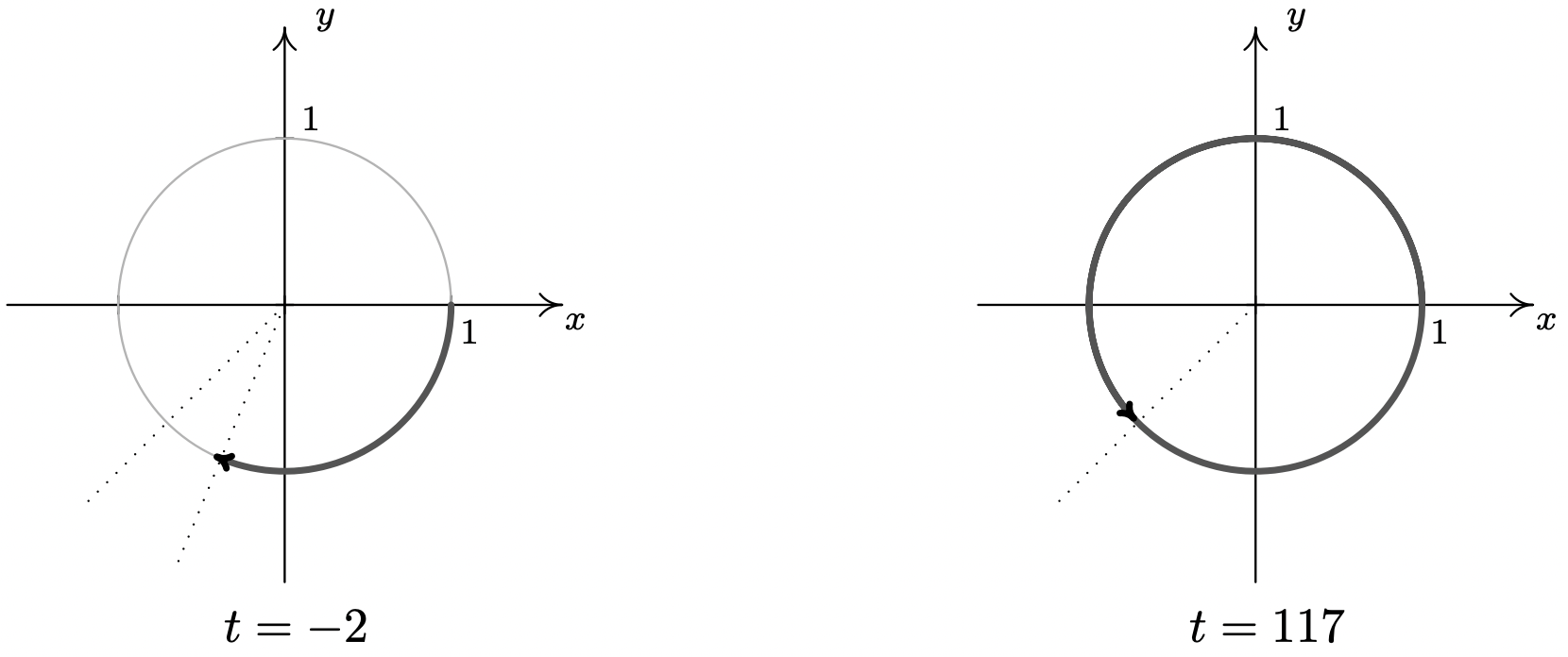
- Al igual que\(t=-2\pi\),\(t=-2\) es negativo, así que comenzamos nuestro arco en\((1,0)\) y procedemos en sentido horario alrededor del círculo unitario. Desde\(\pi \approx 3.14\) y\(\frac{\pi}{2} \approx 1.57\), nos encontramos con que\(2\) los radianes giratorios en sentido horario desde el punto nos\((1,0)\) aterrizan en el Cuadrante III. Para colocar con mayor precisión el punto final, procedemos como hicimos en el Ejemplo 10.1.1, reduciendo sucesivamente a la mitad la medida del ángulo hasta encontrar\(\frac{5 \pi}{8} \approx 1.96\) lo que nos dice que nuestro arco se extiende un poco más allá de la marca de cuarto en el Cuadrante III.
- Dado que\(117\) es positivo, el arco correspondiente a\(t=117\) comienza en\((1,0)\) y avanza en sentido antihorario. Como\(117\) es mucho mayor que\(2\pi\), envolvemos el Círculo de Unidades varias veces antes de finalmente llegar a nuestro punto final. Nos aproximamos\(\frac{117}{2\pi}\) como\(18.62\) lo que nos dice completamos\(18\) revoluciones en sentido contrario a las agujas del reloj con\(0.62\), o simplemente tímida\(\frac{5}{8}\) de una revolución de sobra. En otras palabras, el lado terminal del ángulo que mide\(117\) radianes en posición estándar está poco antes de estar a mitad de camino a través del Cuadrante III.
10.1.1 Aplicaciones de la Medida Radiana: Movimiento Circular
Ahora que hemos emparejado ángulos con números reales a través de la medida de radianes, nos espera todo un mundo de aplicaciones. Nuestra primera excursión a este reino viene por medio de movimiento circular. Supongamos que un objeto se mueve como se muestra a continuación a lo largo de una trayectoria circular\(r\) de radio desde el punto\(P\) hasta el punto\(Q\) en una cantidad de tiempo\(t\).
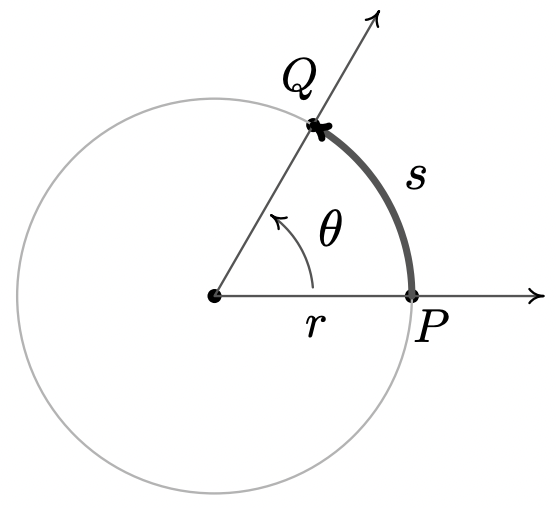
Aquí\(s\) representa un desplazamiento por lo que\(s > 0\) significa que el objeto está viajando en sentido contrario a las agujas del reloj e\(s<0\) indica movimiento en sentido horario. Tenga en cuenta que con esta convención la fórmula que usamos para definir la medida de radianes, es decir\(\theta = \dfrac{s}{r}\), aún se mantiene ya que un valor negativo de\(s\) incurrido a partir de un desplazamiento en sentido horario coincide con el negativo que asignamos\(\theta\) para una rotación en sentido horario. En Física, la velocidad promedio del objeto, denotada\(\overline{v}\) y leída como '\(v\)-bar', se define como la tasa promedio de cambio de la posición del objeto con respecto al tiempo. 16 Como resultado, tenemos\(\overline{v} = \frac{\text{displacement}}{\text{time}} = \dfrac{s}{t}\). La cantidad\(\overline{v}\) tiene unidades de\(\frac{\text{length}}{\text{time}}\) y transmite dos ideas: la dirección en la que se mueve el objeto y la rapidez con la que cambia la posición del objeto. El aporte de dirección en la cantidad\(\overline{v}\) es ya sea para hacerla positiva (en el caso de movimiento en sentido contrario a las agujas del reloj) o negativa (en el caso del movimiento en sentido horario), de manera que la cantidad\(\left| \overline{v} \right|\) cuantifique la rapidez con la que se mueve el objeto, es la velocidad del objeto. Midiendo\(\theta\) en radianes tenemos\(\theta = \dfrac{s}{r}\) así\(s = r \theta\) y\[\overline{v} = \frac{s}{t} = \frac{r \theta}{t} = r \cdot \frac{\theta}{t}\nonumber\] La cantidad\(\dfrac{\theta}{t}\) se llama la velocidad angular promedio del objeto. Se denota por\(\overline{\omega}\) y se lee 'omega-bar'. La cantidad\(\overline{\omega}\) es la tasa promedio de cambio del ángulo\(\theta\) con respecto al tiempo y por lo tanto tiene unidades\(\frac{\text{radians}}{\text{time}}\). Si\(\overline{\omega}\) es constante a lo largo de la duración del movimiento, entonces se puede mostrar 17 que las velocidades medias involucradas, es decir\(\overline{v}\) y\(\overline{\omega}\), son las mismas que sus contrapartes instantáneas,\(v\) y\(\omega\), respectivamente. En este caso,\(v\) se llama simplemente la 'velocidad' del objeto y es la velocidad instantánea de cambio de la posición del objeto con respecto al tiempo. 18 De igual manera,\(\omega\) se llama la 'velocidad angular' y es la velocidad instantánea de cambio del ángulo con respecto al tiempo.
Si la trayectoria del objeto se 'desencrespó' de un círculo para formar un segmento de línea, entonces la velocidad del objeto en ese segmento de línea sería la misma que la velocidad en el círculo. Por esta razón, a la cantidad\(v\) se le suele llamar la velocidad lineal del objeto con el fin de distinguirla de la velocidad angular,\(\omega\). Armando las ideas del párrafo anterior, obtenemos lo siguiente.
Para un objeto que se mueve en una trayectoria circular de radio\(r\) con velocidad angular constante\(\omega\), la velocidad (lineal) del objeto viene dada por\(v = r \omega\).
Tenemos que hablar de unidades aquí. Las unidades de\(v\) son\(\frac{\text{length}}{\text{time}}\), las unidades de\(r\) son de longitud solamente, y las unidades de\(\omega\) son\(\frac{\text{radians}}{\text{time}}\). Así, el lado izquierdo de la ecuación\(v = r \omega\) tiene unidades\(\frac{\text{length}}{\text{time}}\), mientras que el lado derecho tiene unidades\(\text{length} \cdot \frac{\text{radians}}{\text{time}} = \frac{\text{length} \cdot \text{radians}}{\text{time}}\). La supuesta contradicción en unidades se resuelve recordando que los radianes son una cantidad adimensional y los ángulos en medida de radianes se identifican con números reales para que las unidades se\(\frac{\text{length} \cdot \text{radians}}{\text{time}}\) reduzcan a las unidades\(\frac{\text{length}}{\text{time}}\). Estamos muy atrasados por un ejemplo.
Suponiendo que la superficie de la Tierra es una esfera, cualquier punto de la Tierra puede considerarse como un objeto que viaja en un círculo que completa una revolución en (aproximadamente) 24 horas. El camino trazado por el punto durante este periodo de 24 horas es la Latitud de ese punto. Lakeland Community College se encuentra en latitud\(41.628^{\circ}\) norte, y se puede mostrar 19 que el radio de la tierra en esta Latitud es de aproximadamente\(2960\) millas. Encuentra la velocidad lineal, en millas por hora, de Lakeland Community College a medida que el mundo gira.
Solución
Para usar la fórmula\(v = r \omega\), primero necesitamos calcular la velocidad angular\(\omega\). La tierra hace una revolución en 24 horas, y una revolución son\(2 \pi\) radianes, entonces, donde\(\omega = \frac{2 \pi \, \text{radians}}{24 \, \text{hours}} = \frac{\pi}{12 \, \text{hours}}\), una vez más, estamos usando el hecho de que los radianes son números reales y son adimensionales. (Por el bien de la simplicidad, también estamos asumiendo que estamos viendo la rotación de la tierra como en sentido contrario a las agujas del reloj)\(\omega > 0\). Por lo tanto, la velocidad lineal es\[v = 2960 \, \text{miles} \cdot \frac{\pi}{12 \, \text{hours}} \approx 775 \, \frac{\text{miles}}{\text{hour}}\nonumber\]
Vale la pena señalar que la cantidad\(\frac{1 \, \text{revolution}}{24 \, \text{hours}}\) en el Ejemplo 10.1.5 se llama la frecuencia ordinaria del movimiento y generalmente se denota por la variable\(f\). La frecuencia ordinaria es una medida de la frecuencia con la que un objeto realiza un ciclo completo del movimiento. El hecho que\(\omega = 2\pi f\) sugiere que también\(\omega\) es una frecuencia. En efecto, se le llama la frecuencia angular del movimiento. En una nota relacionada, la cantidad\(T = \dfrac{1}{f}\) se llama el período del movimiento y es la cantidad de tiempo que tarda el objeto en completar un ciclo del movimiento. En el escenario del Ejemplo 10.1.5, el periodo de la moción es de 24 horas, o un día.
Los conceptos de frecuencia y período ayudan a enmarcar la ecuación\(v = r \omega\) bajo una nueva luz. Es decir, si\(\omega\) es fijo, los puntos que están más lejos del centro de rotación necesitan viajar más rápido para mantener la misma frecuencia angular ya que tienen que viajar más lejos para hacer una revolución en el tiempo de un período. La distancia del objeto al centro de rotación es el radio del círculo,\(r\), y es el 'factor de ampliación' que relaciona\(\omega\) y\(v\). Tendremos más que decir sobre frecuencias y periodos en la Sección 11.5. Si bien hemos discutido exhaustivamente las velocidades asociadas al movimiento circular, todavía tenemos que discutir una pregunta más natural: si un objeto se mueve en una trayectoria circular de radio\(r\) con una velocidad angular fija (frecuencia)\(\omega\), ¿cuál es la posición del objeto en el momento\(t\)? La respuesta a esta pregunta es el corazón mismo de la Trigonometría y se responde en la siguiente sección.
10.1.2. Ejercicios
En Ejercicios 1 - 4, convierte los ángulos en el sistema DMS. Redondea cada una de tus respuestas al segundo más cercano.
- \(63.75^{\circ}\)
- \(200.325^{\circ}\)
- \(-317.06^{\circ}\)
- \(179.999^{\circ}\)
En Ejercicios 5 - 8, convierte los ángulos en grados decimales. Redondea cada una de tus respuestas a tres decimales.
- \(125^{\circ} 50'\)
- \(-32^{\circ} 10' 12''\)
- \(502^{\circ} 35'\)
- \(237^{\circ} 58' 43''\)
En los Ejercicios 9 - 28, grafica el ángulo orientado en posición estándar. Clasifica cada ángulo según donde se encuentre su lado terminal y luego dé dos ángulos coterminales, uno de los cuales es positivo y el otro negativo.
- \(330^{\circ}\)
- \(-135^{\circ}\)
- \(120^{\circ}\)
- \(405^{\circ}\)
- \(-270^{\circ}\)
- \(\dfrac{5\pi}{6}\)
- \(-\dfrac{11\pi}{3}\)
- \(\dfrac{5\pi}{4}\)
- \(\dfrac{3\pi}{4}\)
- \(-\dfrac{\pi}{3}\)
- \(\dfrac{7\pi}{2}\)
- \(\dfrac{\pi}{4}\)
- \(-\dfrac{\pi}{2}\)
- \(\dfrac{7\pi}{6}\)
- \(-\dfrac{5\pi}{3}\)
- \(3\pi\)
- \(-2\pi\)
- \(-\dfrac{\pi}{4}\)
- \(\dfrac{15\pi}{4}\)
- \(-\dfrac{13\pi}{6}\)
En los Ejercicios 29 - 36, convertir el ángulo de medida de grado en medida de radianes, dando el valor exacto en términos de\(\pi\).
- \(0^{\circ}\)
- \(240^{\circ}\)
- \(135^{\circ}\)
- \(-270^{\circ}\)
- \(-315^{\circ}\)
- \(150^{\circ}\)
- \(45^{\circ}\)
- \(-225^{\circ}\)
En los Ejercicios 37 - 44, convierte el ángulo de medida de radianes en medida de grado.
- \(\pi\)
- \(-\dfrac{2\pi}{3}\)
- \(\dfrac{7\pi}{6}\)
- \(\dfrac{11\pi}{6}\)
- \(\dfrac{\pi}{3}\)
- \(\dfrac{5\pi}{3}\)
- \(-\dfrac{\pi}{6}\)
- \(\dfrac{\pi}{2}\)
En los Ejercicios 45 - 49, dibuje el arco orientado en el Círculo de Unidad que corresponde al número real dado.
- \(t=\frac{5 \pi}{6}\)
- \(t=-\pi\)
- \(t = 6\)
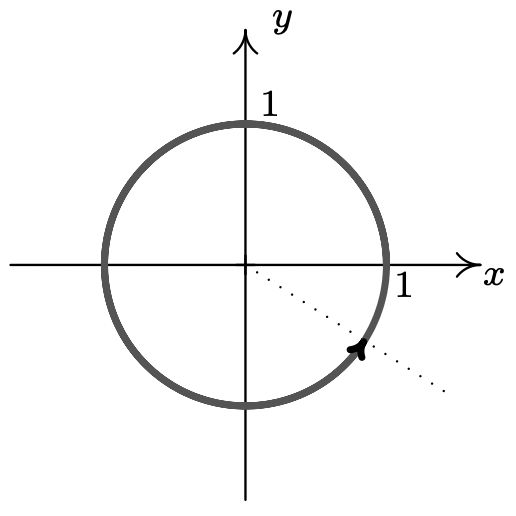
- \(t = -2\)
- \(t = 12\)
- Un yoyo que tiene 2.25 pulgadas de diámetro gira a una velocidad de 4500 revoluciones por minuto. ¿Qué tan rápido gira el borde del yoyo en millas por hora? Redondee su respuesta a dos decimales.
- ¿Cuántas revoluciones por minuto tendría que completar el yoyo en el ejercicio 50 si el borde del yoyo va a estar girando a una velocidad de 42 millas por hora? Redondee su respuesta a dos decimales.
- En el truco del yo-yo 'La vuelta al mundo', el intérprete lanza el yoyo para que barre un círculo vertical cuyo radio es la cuerda del yo-yo. Si la cuerda de yoyo mide 28 pulgadas de largo y el yoyo tarda 3 segundos en completar una revolución del círculo, calcula la velocidad del yoyo en millas por hora. Redondee su respuesta a dos decimales.
- Un disco duro de computadora contiene un disco circular con diámetro de 2.5 pulgadas y gira a una velocidad de 7200 RPM (revoluciones por minuto). Encuentre la velocidad lineal de un punto en el borde del disco en millas por hora.
- Una roca se quedó atascada en la banda de rodadura de mi llanta y cuando conducía 70 millas por hora, la roca se soltó y chocó contra el interior del pozo de la rueda del auto. ¿Qué tan rápido, en millas por hora, viajaba la roca cuando salió de la banda de rodadura? (La llanta tiene un diámetro de 23 pulgadas).
- La Rueda Gigante en Cedar Point es un círculo con 128 pies de diámetro que se asienta sobre una plataforma de 8 pies de altura haciendo que su altura total sea de 136 pies. (¿Recuerdas esto del Ejercicio 17 en la Sección 7.2?) Se completa dos revoluciones en 2 minutos y 7 segundos. 20 Suponiendo que los jinetes están al borde del círculo, ¿qué tan rápido viajan en millas por hora?
- Considere el círculo de radio que se\(r\) muestra a continuación con ángulo central\(\theta\), medido en radianes, y arco subtendido de longitud\(s\). Demostrar que el área del sector sombreado es\(A = \frac{1}{2} r^{2} \theta\).
(Pista: Usa la proporción\(\frac{A}{\text{area of the circle}} = \frac{s}{\text{circumference of the circle}}\).)
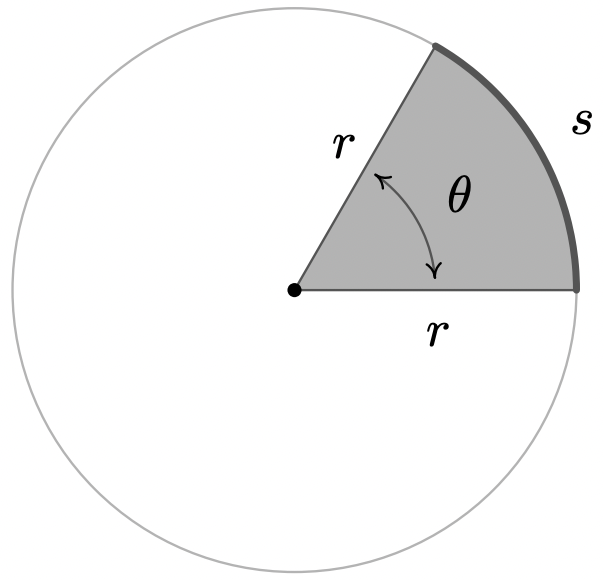
En los Ejercicios 57 - 62, utilice el resultado del Ejercicio 56 para computar las áreas de los sectores circulares con los ángulos centrales y radios dados.
- \(\theta = \dfrac{\pi}{6}, \; r = 12\)
- \(\theta = \dfrac{5\pi}{4}, \; r = 100\)
- \(\theta = 330^{\circ}, \; r = 9.3\)
- \(\theta =\pi, \; r = 1\)
- \(\theta = 240^{\circ}, \; r = 5\)
- \(\theta = 1^{\circ}, \; r = 117\)
- Imagina una cuerda atada alrededor de la Tierra en el ecuador. Demuestre que es necesario agregar solo\(2\pi\) pies de longitud a la cuerda para levantarla un pie sobre el suelo alrededor de todo el ecuador. (NO es necesario conocer el radio de la Tierra para mostrar esto.)
- Con la ayuda de tus compañeros, busca una prueba que efectivamente\(\pi\) sea una constante.
10.1.3 Respuestas
- \(63^{\circ} 45'\)
- \(200^{\circ} 19' 30''\)
- \(-317^{\circ} 3' 36''\)
- \(179^{\circ} 59' 56''\)
- \(125.833^{\circ}\)
- \(-32.17^{\circ}\)
- \(502.583^{\circ}\)
- \(237.979^{\circ}\)
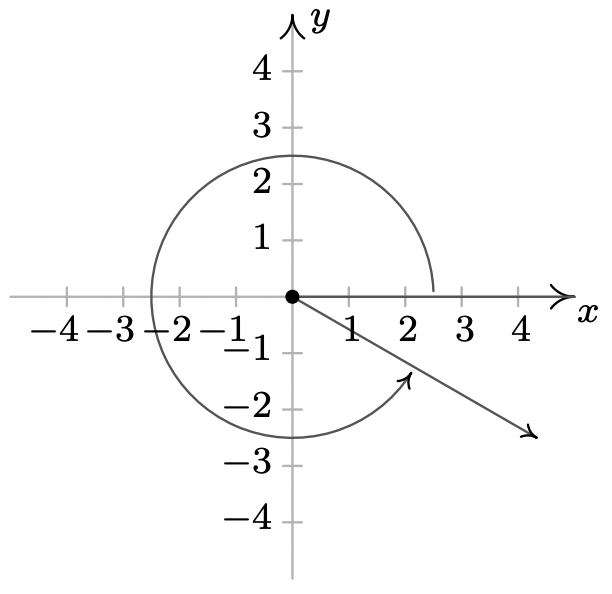
- \(330^{\circ}\)es un coterminal de ángulo cuadrante IV con\(690^{\circ}\) y\(-30^{\circ}\)
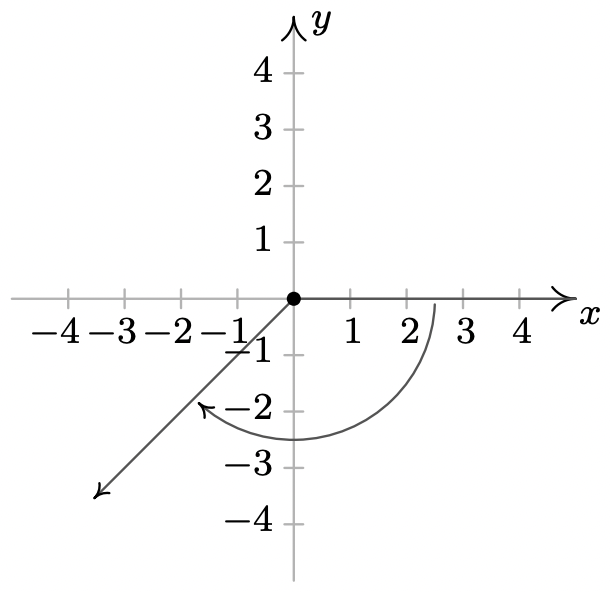
- \(-135^{\circ}\)es un coterminal de ángulo Cuadrante III con\(225^{\circ}\) y\(-495^{\circ}\)
- \(120^{\circ}\)es un coterminal de ángulo Cuadrante II con\(480^{\circ}\) y\(-240^{\circ}\)
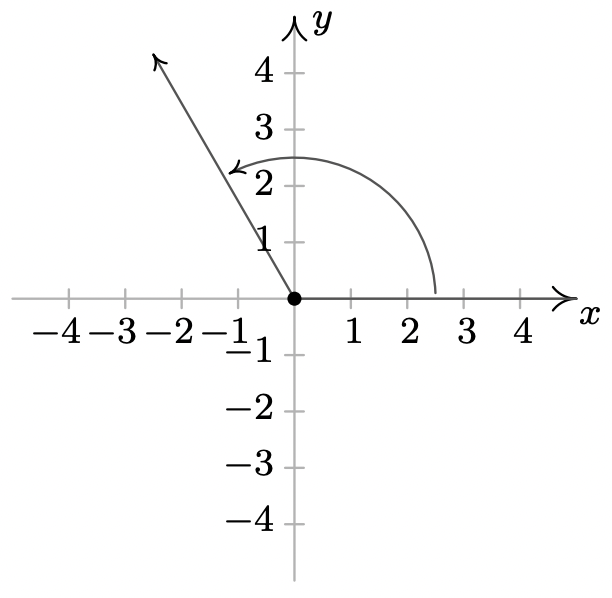
- \(405^{\circ}\)es un coterminal de ángulo cuadrante I con\(45^{\circ}\) y\(-315^{\circ}\)
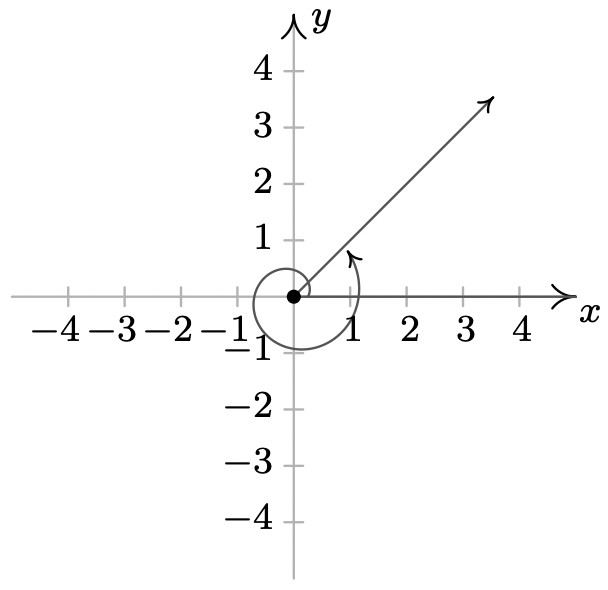
- \(-270^{\circ}\)se encuentra en el coterminal\(y\) del eje positivo con\(90^{\circ}\) y\(-630^{\circ}\)
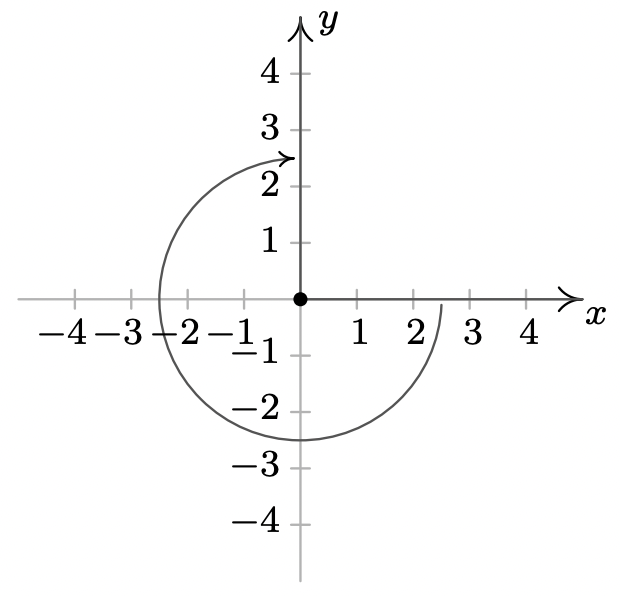
- \(\dfrac{5\pi}{6}\)es un coterminal de ángulo Cuadrante II con\(\dfrac{17\pi}{6}\) y\(-\dfrac{7\pi}{6}\)
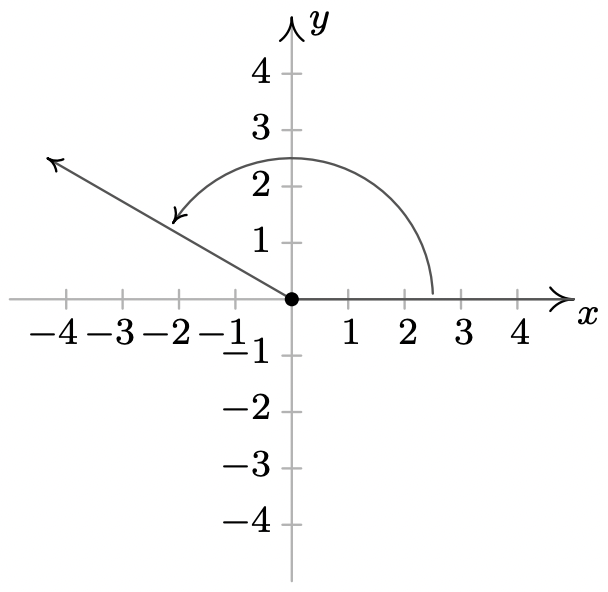
- \(-\dfrac{11\pi}{3}\)es un coterminal de ángulo cuadrante I con\(\dfrac{\pi}{3}\) y\(-\dfrac{5\pi}{3}\)
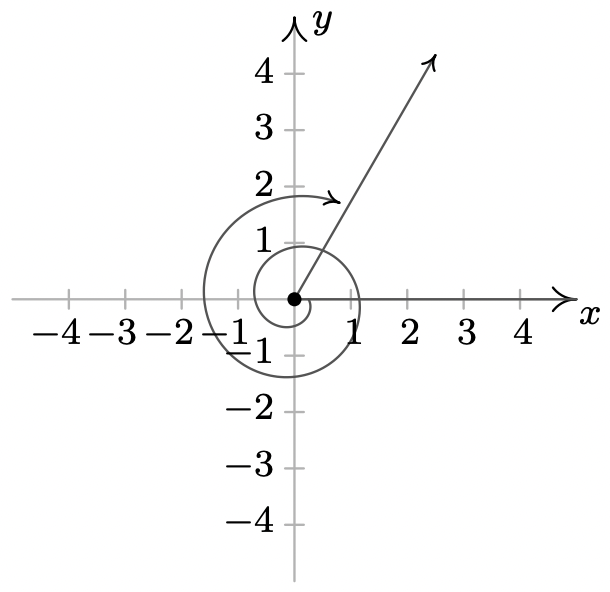
- \(\dfrac{5\pi}{4}\)es un coterminal de ángulo Cuadrante III con\(\dfrac{13\pi}{4}\) y\(-\dfrac{3\pi}{4}\)
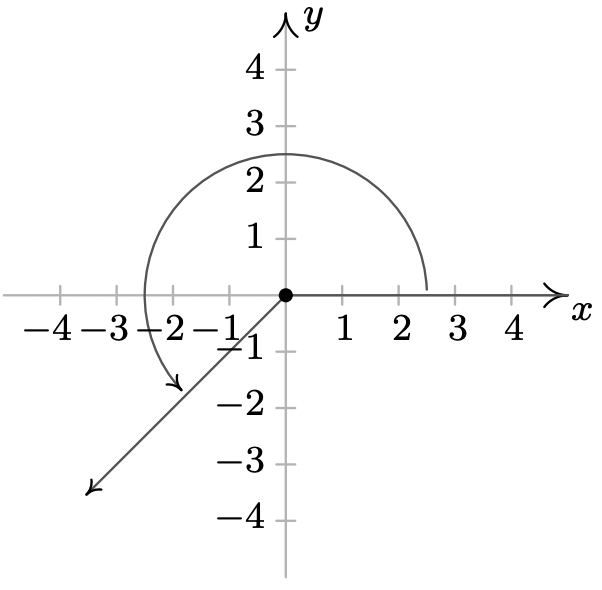
- \(\dfrac{3\pi}{4}\)es un coterminal de ángulo Cuadrante II con\(\dfrac{11\pi}{4}\) y\(-\dfrac{5\pi}{4}\)
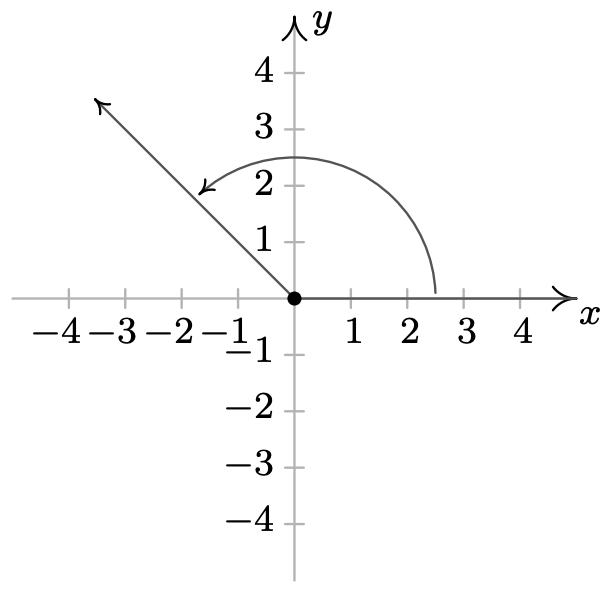
- \(-\dfrac{\pi}{3}\)es un coterminal de ángulo cuadrante IV con\(\dfrac{5\pi}{3}\) y\(-\dfrac{7\pi}{3}\)
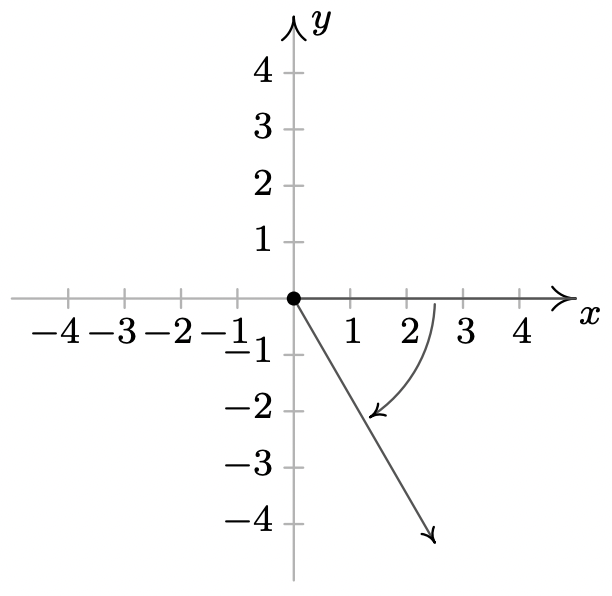
- \(\dfrac{7\pi}{2}\)se encuentra en el coterminal\(y\) del eje negativo con\(\dfrac{3\pi}{2}\) y\(-\dfrac{\pi}{2}\)
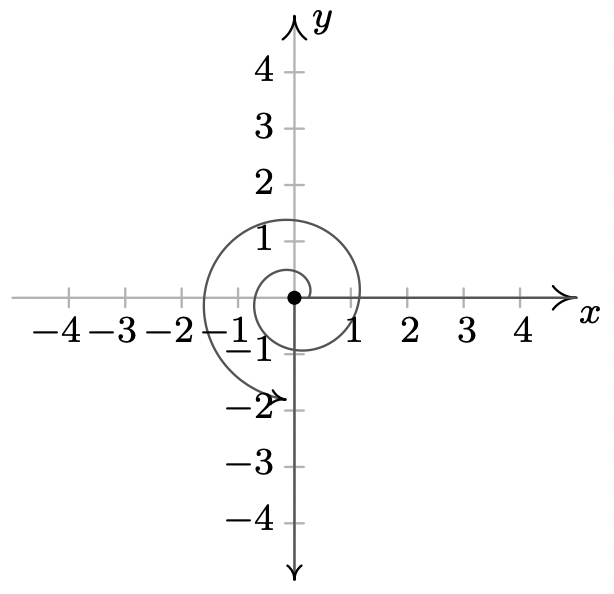
- \(\dfrac{\pi}{4}\)es un coterminal de ángulo cuadrante I con\(\dfrac{9 \pi}{4}\) y\(-\dfrac{7\pi}{4}\)
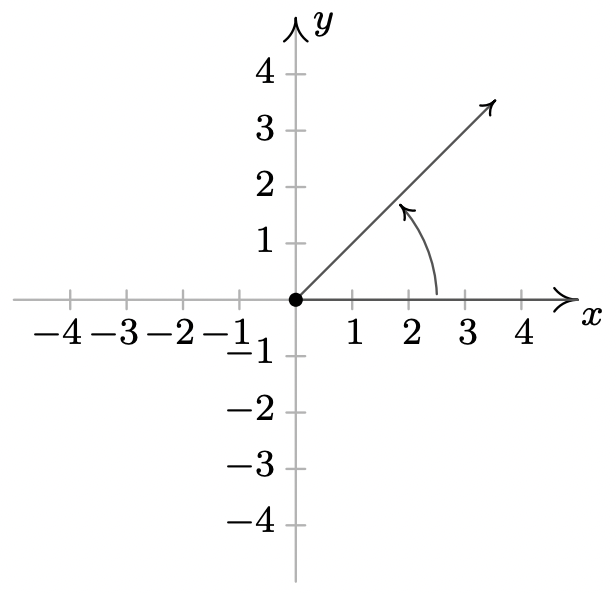
- \(-\dfrac{\pi}{2}\)se encuentra en el coterminal\(y\) del eje negativo con\(\dfrac{3\pi}{2}\) y\(-\dfrac{5\pi}{2}\)
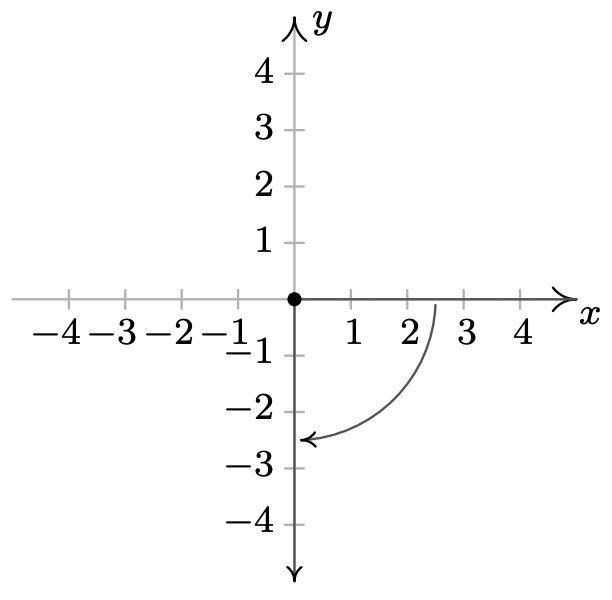
- \(\dfrac{7\pi}{6}\)es un coterminal de ángulo Cuadrante III con\(\dfrac{19 \pi}{6}\) y\(-\dfrac{5\pi}{6}\)
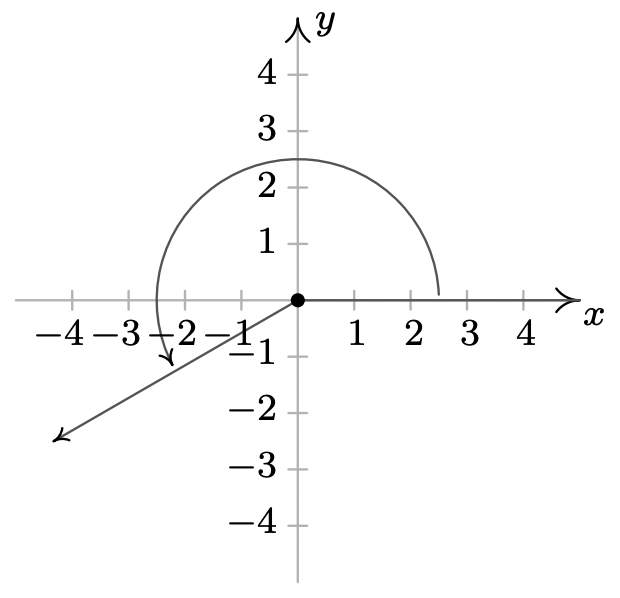
- \(-\dfrac{5\pi}{3}\)es un coterminal de ángulo cuadrante I con\(\dfrac{\pi}{3}\) y\(-\dfrac{11\pi}{3}\)
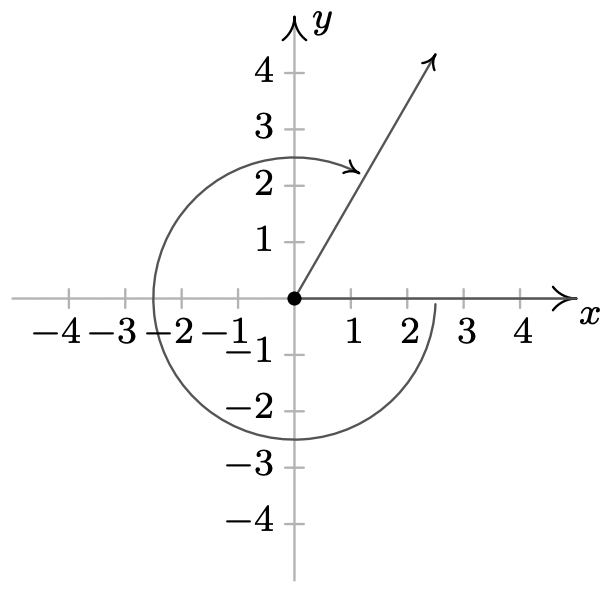
- \(3\pi\)se encuentra en el coterminal\(x\) del eje negativo con\(\pi\) y\(-\pi\)
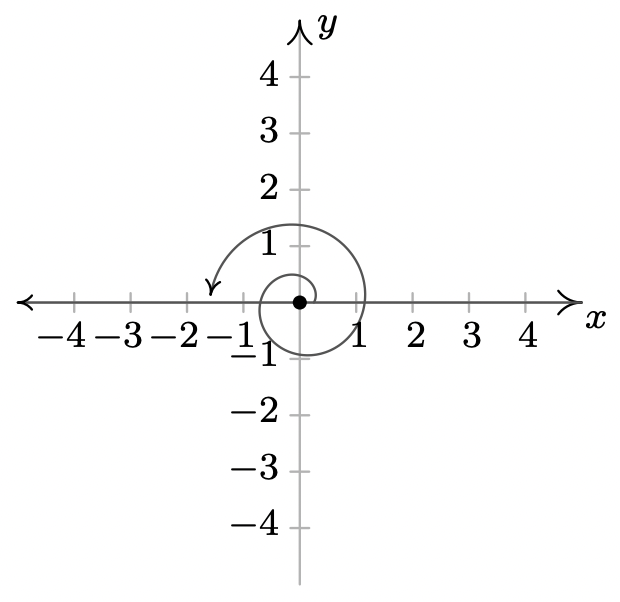
- \(-2\pi\)se encuentra en el coterminal\(x\) del eje positivo con\(2\pi\) y\(-4\pi\)
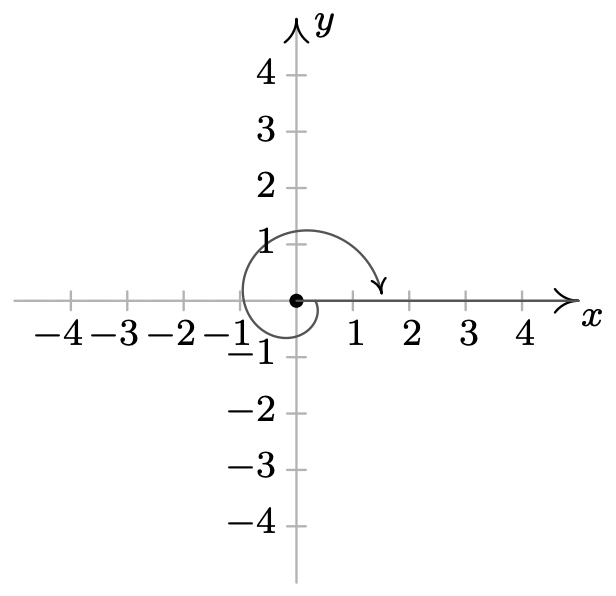
- \(-\dfrac{\pi}{4}\)es un coterminal de ángulo cuadrante IV con\(\dfrac{7 \pi}{4}\) y\(-\dfrac{9\pi}{4}\)
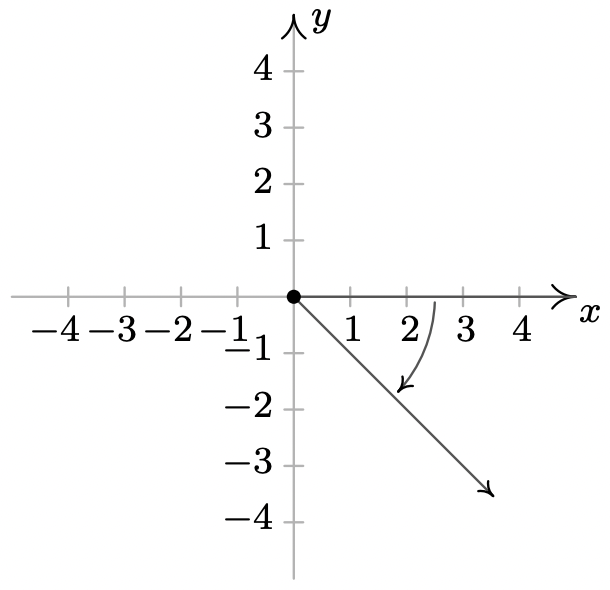
- \(\dfrac{15\pi}{4}\)es un coterminal de ángulo cuadrante IV con\(\dfrac{7\pi}{4}\) y\(-\dfrac{\pi}{4}\)
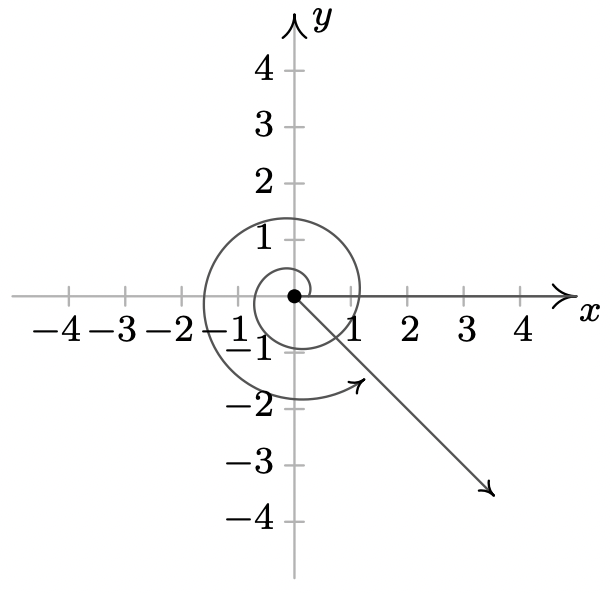
- \(-\dfrac{13\pi}{6}\)es un coterminal de ángulo cuadrante IV con\(\dfrac{11\pi}{6}\) y\(-\dfrac{\pi}{6}\)
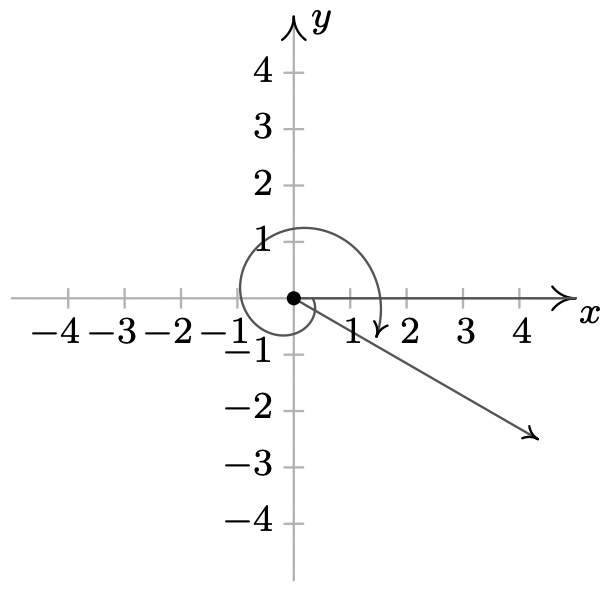
- \(0\)
- \(\dfrac{4\pi}{3}\)
- \(\dfrac{3\pi}{4}\)
- \(-\dfrac{3\pi}{2}\)
- \(-\dfrac{7\pi}{4}\)
- \(\dfrac{5\pi}{6}\)
- \(\dfrac{\pi}{4}\)
- \(-\dfrac{5\pi}{4}\)
- \(180^{\circ}\)
- \(-120^{\circ}\)
- \(210^{\circ}\)
- \(330^{\circ}\)
- \(60^{\circ}\)
- \(300^{\circ}\)
- \(-30^{\circ}\)
- \(90^{\circ}\)
- \(t = \dfrac{5\pi}{6}\)
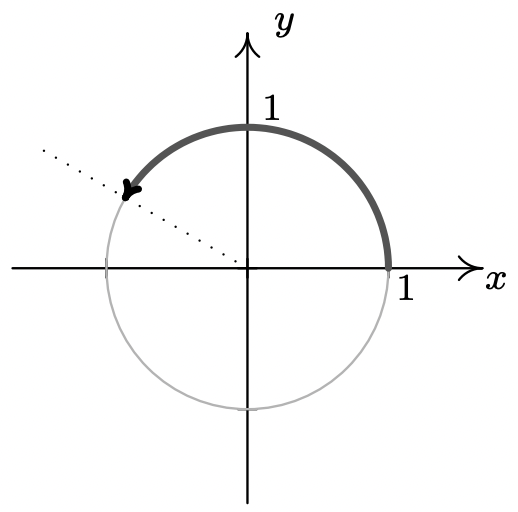
- \(t = -\pi\)
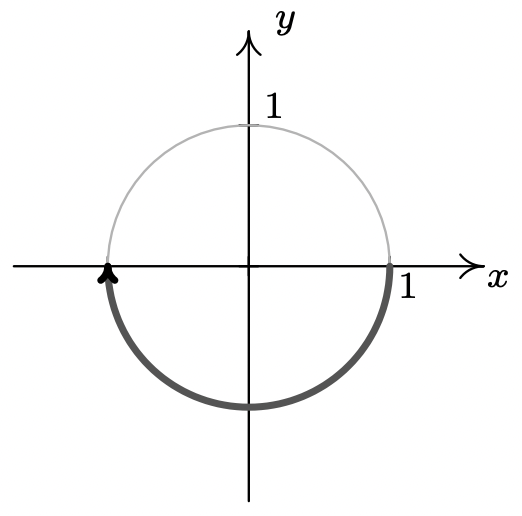
- \(t = 6\)
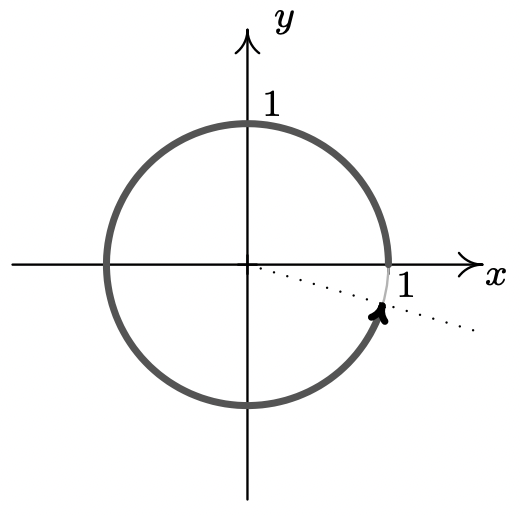
- \(t = -2\)
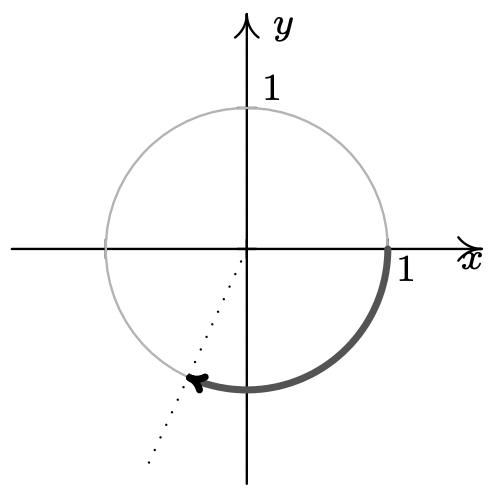
- \(t = 12\)(entre 1 y 2 revoluciones)
- Cerca de 30.12 millas por hora
- Cerca de 6274.52 revoluciones por minuto
- Cerca de 3.33 millas por hora
- Cerca de 53.55 millas por hora
- 70 millas por hora
- Cerca de 4.32 millas por hora
- \(12\pi\)unidades cuadradas
- \(6250\pi\)unidades cuadradas
- \(79.2825\pi \approx 249.07\)unidades cuadradas
- \(\dfrac{\pi}{2}\)unidades cuadradas
- \(\dfrac{50\pi}{3}\)unidades cuadradas
- \(38.025 \pi \approx 119.46\)unidades cuadradas
Referencia
1 La frase 'al meno' se justificará en poco tiempo.
2 La elección de '360' se atribuye con mayor frecuencia a los babilonios.
3 Así es como se califica un prolongador.
4 Impresionante juego de palabras matemáticas a un lado, esta es la misma idea detrás de definir exponentes irracionales en la Sección 6.1.
5 ¿Este tipo de sistema le parece familiar?
6 Si este proceso parece embrujosamente familiar, debería. Compare este método con el Método de Bisección introducido en la Sección 3.3.
7 Al igual que 'recto latus', este es también un término matemático real.
8 Este es exactamente el mismo tipo de 'préstamo' que solías hacer en la Escuela Primaria cuando tratabas de encontrar 300 − 125. En aquel entonces, estabas trabajando en un sistema base diez; aquí, es la base sesenta.
9 'Widdershins'
10 Tenga en cuenta que al estar en posición estándar comparten automáticamente el mismo lado inicial que es el eje x positivo.
11 Cabe señalar que todas las patologías de la Trigonometría Analítica resultan de este hecho inocuo.
12 Recordemos que esto significa\(k=0, \pm 1, \pm 2, \ldots\).
13 Los autores son muy conscientes de que ahora estamos identificando radianes con números reales. Esto lo justificaremos en breve.
14 Esto, a su vez, dota también de orientación a los arcos subtendidos. Abordamos esto en poco tiempo.
15 Tenga en cuenta que el signo negativo indica rotación en el sentido de las agujas del reloj en ambos sistemas, y así se transporta en consecuencia.
16 Véase Definición 2.3 en la Sección 2.1 para una revisión de este concepto.
20 Fuente: Página web de Cedar Point.


