10.2: El círculo unitario - coseno y seno
- Page ID
- 119452
En la Sección 10.1.1, introdujimos el movimiento circular y derivamos una fórmula que describe la velocidad lineal de un objeto que se mueve en una trayectoria circular a una velocidad angular constante. Uno de los objetivos de esta sección es describir la posición de tal objeto. Para ello, considere un ángulo\(\theta\) en posición estándar y deje\(P\) denotar el punto donde el lado terminal de\(\theta\) intersecta el Círculo de Unidad. Al asociar el punto\(P\) con el ángulo\(\theta\), estamos asignando una posición en el Círculo de Unidad al ángulo\(\theta\). La\(x\) coordenada de\(P\) se llama coseno de\(\theta\), escrito\(\cos(\theta)\), mientras que la\(y\) coordenada de\(P\) se llama seno de\(\theta\), escrito\(\sin(\theta)\). 1 Se alienta al lector a verificar que estas reglas utilizadas para hacer coincidir un ángulo con su coseno y seno, de hecho, satisfacen la definición de una función. Es decir, para cada ángulo\(\theta\), solo hay un valor asociado de\(\cos(\theta)\) y solo un valor asociado de\(\sin(\theta)\).
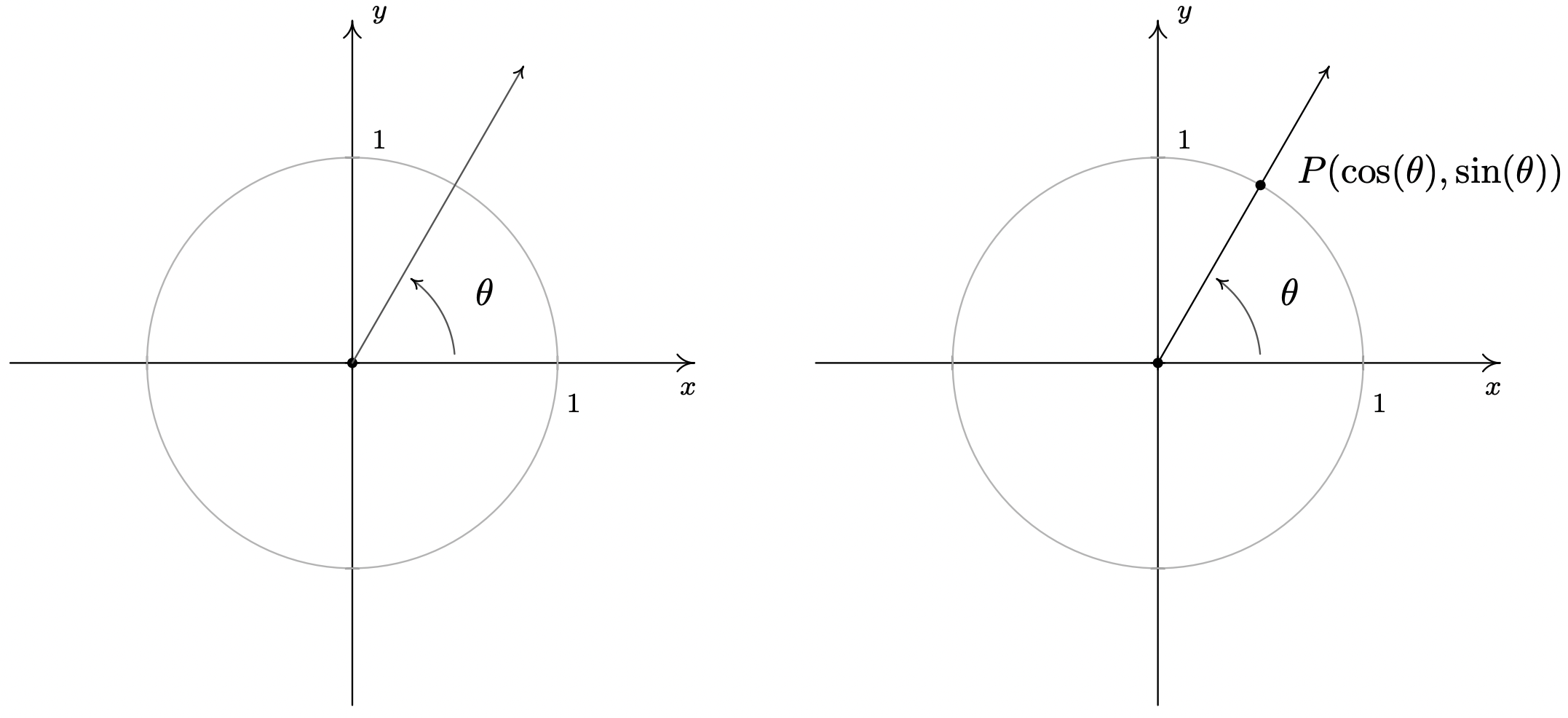
Encuentra el coseno y el seno de los siguientes ángulos.
- \(\theta = 270^{\circ}\)
- \(\theta = - \pi\)
- \(\theta = 45^{\circ}\)
- \(\theta = \frac{\pi}{6}\)
- \(\theta = 60^{\circ}\)
Solución.
- Para encontrar\(\cos\left(270^{\circ}\right)\) y\(\sin\left(270^{\circ}\right)\), trazamos el ángulo\(\theta =270^{\circ}\) en posición estándar y encontramos el punto en el lado terminal del\(\theta\) cual se encuentra en el Círculo de Unidad. Dado que\(270^{\circ}\) representa\(\frac{3}{4}\) una revolución en sentido antihorario, el lado terminal de\(\theta\) se encuentra a lo largo del\(y\) eje negativo. De ahí que el punto que buscamos es\((0,-1)\) así que\(\cos\left(270^{\circ}\right) = 0\) y\(\sin\left(270^{\circ}\right) = -1\).
- El ángulo\(\theta=-\pi\) representa la mitad de una revolución en sentido horario, por lo que su lado terminal se encuentra en el\(x\) eje negativo. El punto en el Círculo de Unidad que se encuentra en el\(x\) eje negativo es el\((-1,0)\) que significa\(\cos(-\pi) = -1\) y\(\sin(-\pi) = 0\).
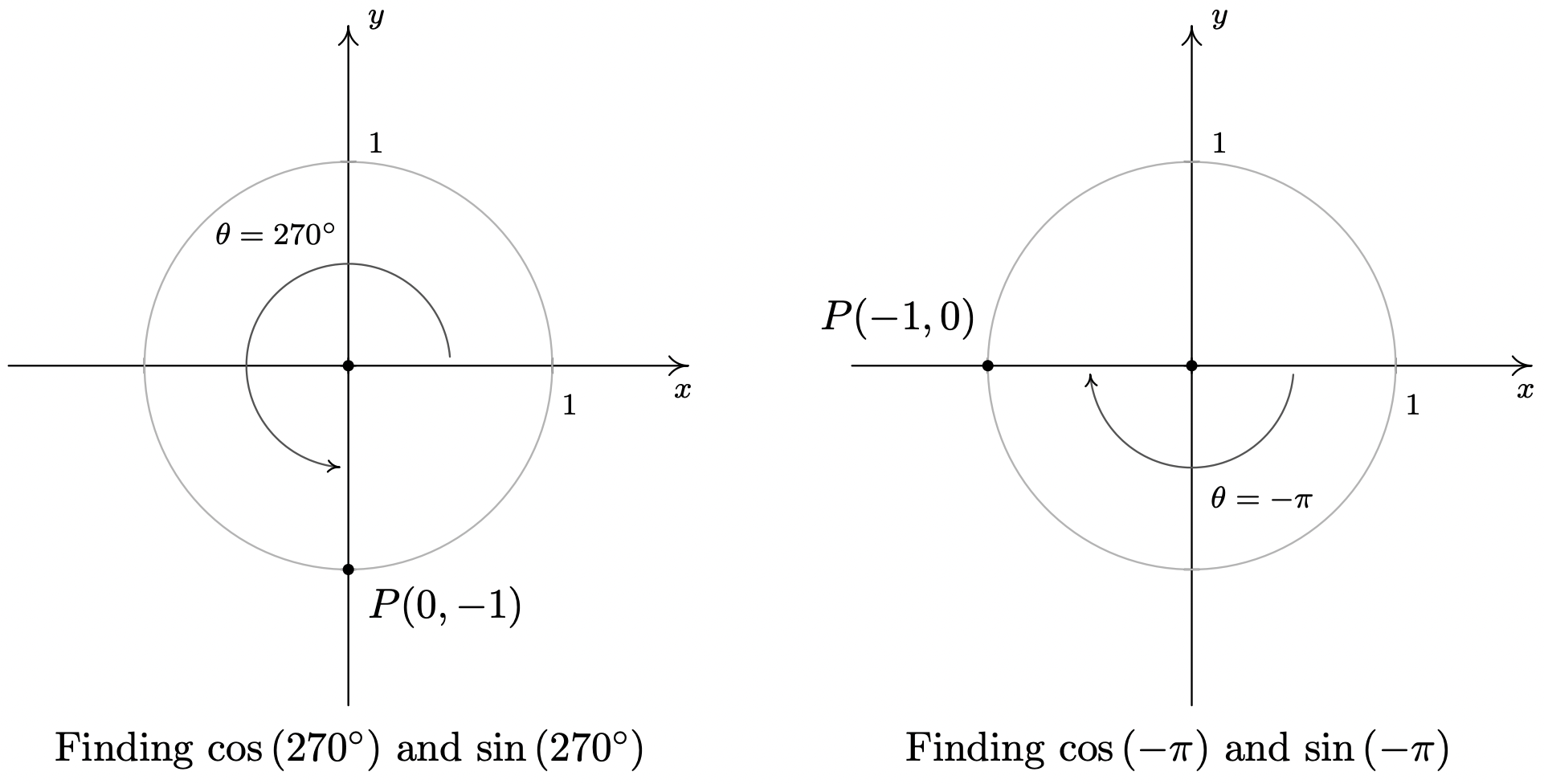
- Cuando bosquejamos\(\theta = 45^{\circ}\) en posición estándar, vemos que su terminal no se encuentra a lo largo de ninguno de los ejes de coordenadas, lo que dificulta un poco nuestro trabajo de encontrar los valores coseno y seno. Dejar\(P(x,y)\) denotar el punto en el lado terminal del\(\theta\) cual se encuentra en el Círculo de Unidad. Por definición,\(x = \cos\left(45^{\circ}\right)\) y\(y = \sin\left(45^{\circ}\right)\). Si dejamos caer un segmento de línea\(P\) perpendicular desde el\(x\) eje -eje, obtenemos un\(45^{\circ} - 45^{\circ} - 90^{\circ}\) triángulo rectángulo cuyas patas tienen longitudes\(x\) y\(y\) unidades. De Geometría, 2 obtenemos\(y=x\). Ya que\(P(x,y)\) se encuentra en el Círculo de Unidades, tenemos\(x^2+y^2 = 1\). Sustituir\(y=x\) en esta ecuación rinde\(2x^2 = 1\), o\(x =\pm \sqrt{\frac{1}{2}} = \pm \frac{\sqrt{2}}{2}\). Ya que\(P(x,y)\) se encuentra en el primer cuadrante\(x>0\),, así\(x = \cos\left(45^{\circ}\right) = \frac{\sqrt{2}}{2}\) y con\(y=x\) nosotros tenemos\(y = \sin\left(45^{\circ}\right) = \frac{\sqrt{2}}{2}\).
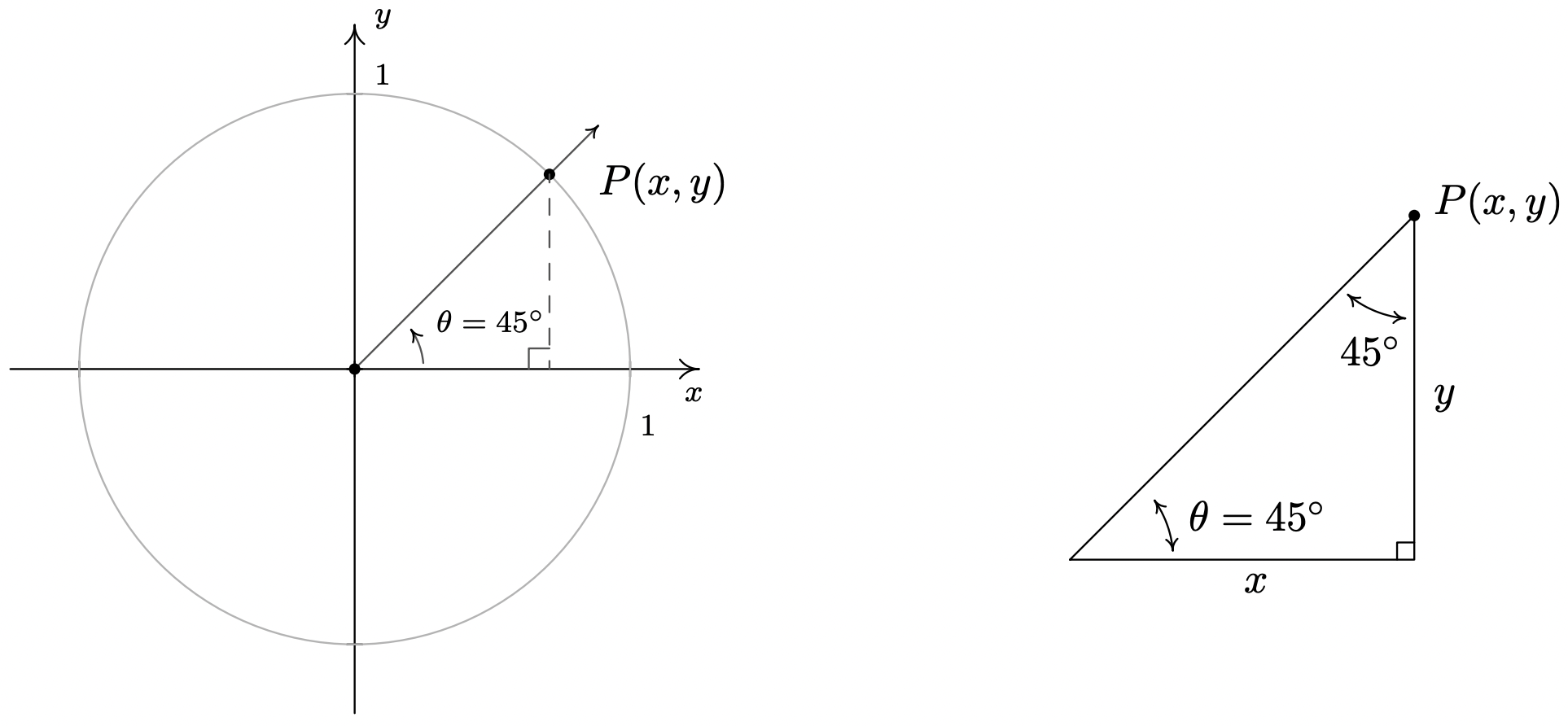
- Como antes, el lado terminal de\(\theta = \frac{\pi}{6}\) no se encuentra en ninguno de los ejes de coordenadas, por lo que procedemos utilizando un enfoque triangular. Dejando\(P(x,y)\) denotar el punto en el lado terminal del\(\theta\) cual se encuentra en el Círculo de Unidad, soltamos un segmento de línea\(P\) perpendicular desde el\(x\) eje -eje para formar un\(30^{\circ} - 60^{\circ} - 90^{\circ}\) triángulo rectángulo. Después de un poco de Geometría 3 nos parece\(y = \frac{1}{2}\) así\(\sin\left(\frac{\pi}{6}\right) = \frac{1}{2}\). Ya que\(P(x,y)\) se encuentra en el Círculo de Unidades, sustituimos\(y = \frac{1}{2}\) en\(x^2 + y^2 = 1\) para obtener\(x^{2} = \frac{3}{4}\), o\(x = \pm \frac{\sqrt{3}}{2}\). Aquí,\(x > 0\) entonces\(x = \cos\left(\frac{\pi}{6}\right) = \frac{\sqrt{3}}{2}\).
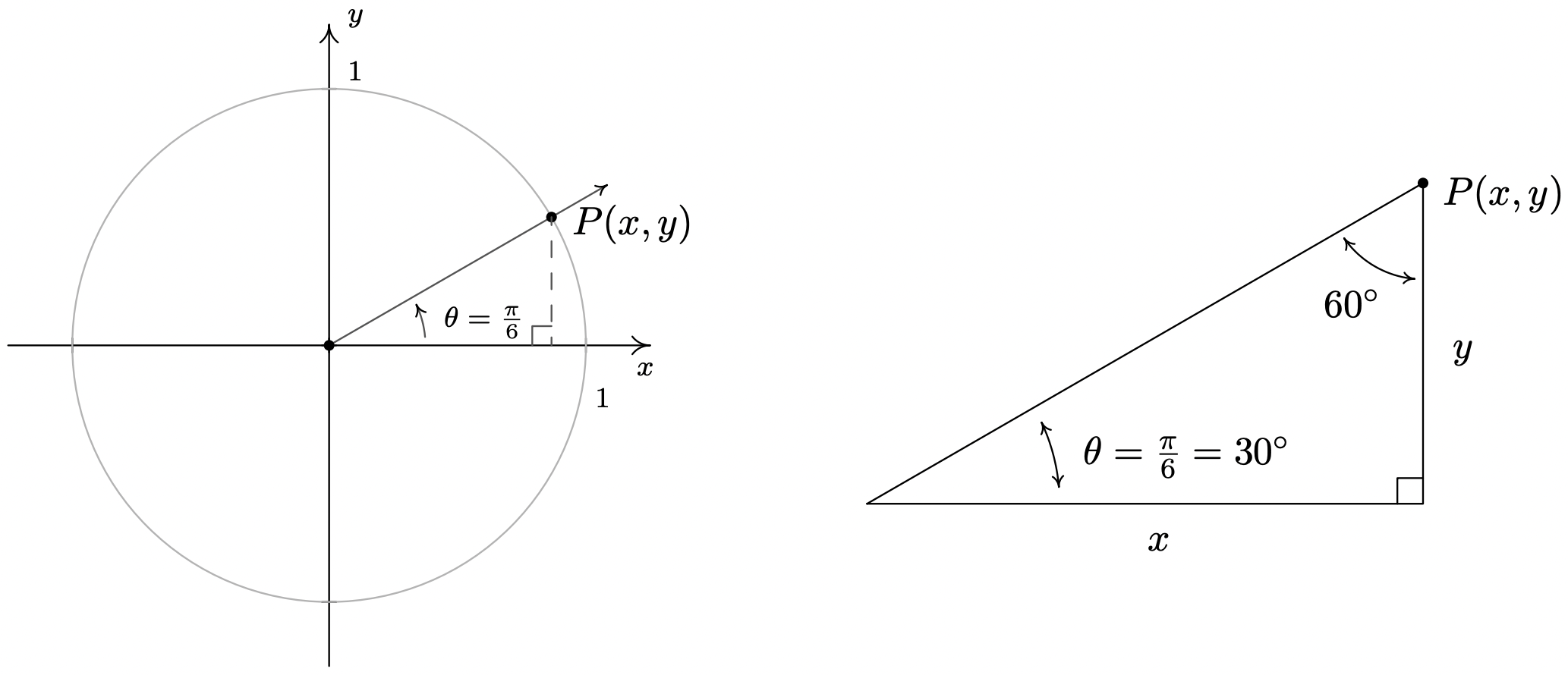
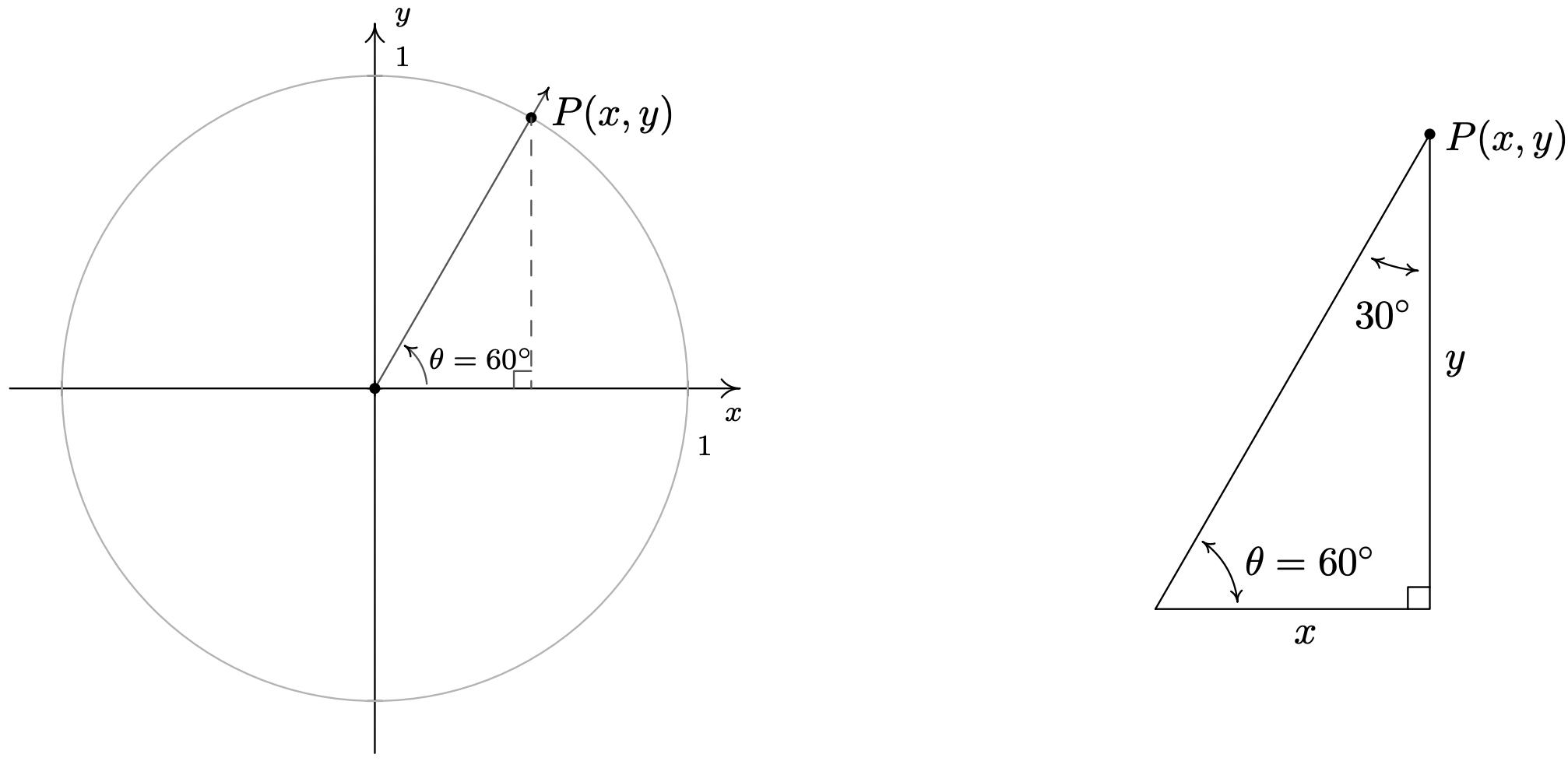
- Trazando\(\theta = 60^{\circ}\) en posición estándar, encontramos que no es un ángulo cuadrangular y se establece usando un enfoque de triángulo. Una vez más, obtenemos un\(30^{\circ} - 60^{\circ} - 90^{\circ}\) triángulo rectángulo y, después de los cálculos habituales, encontramos\(x = \cos\left(60^{\circ}\right) = \frac{1}{2}\) y\(y = \sin\left(60^{\circ}\right) = \frac{\sqrt{3}}{2}\).
En el Ejemplo 10.2.1, fue bastante fácil encontrar el coseno y el seno de los ángulos cuadrangulares, pero para los ángulos no cuadránticos, la tarea estuvo mucho más involucrada. En estos últimos casos, aprovechamos bien el hecho de que el punto\(P(x,y) = (\cos(\theta), \sin(\theta))\) se encuentra en el Círculo Unitario,\(x^2+y^2 = 1\). Si sustituimos\(x=\cos(\theta)\) y\(y = \sin(\theta)\) en\(x^2+y^2=1\), obtenemos\(\left(\cos(\theta)\right)^2 + \left(\sin(\theta)\right)^2 = 1\). Una desafortunada convención 4, que los autores se ven obligados a perpetuar, es escribir\(\left(\cos(\theta)\right)^2\) como\(\cos^{2}(\theta)\) y\(\left(\sin(\theta)\right)^2\) como\(\sin^{2}(\theta)\). Reescribir la identidad usando esta convención da como resultado el siguiente teorema, que es sin duda uno de los resultados más importantes en Trigonometría.
Para cualquier ángulo\(\theta\),\(\cos^{2}(\theta) + \sin^{2}(\theta) = 1\).
El sobrenombre 'Pitágoras' trae a la mente el Teorema de Pitágoras, del cual se derivan en última instancia tanto la Fórmula de Distancia como la ecuación para un círculo. 5 La palabra 'Identidad' nos recuerda que, independientemente del ángulo\(\theta\), la ecuación en el Teorema 10.1 es siempre cierta. Si uno de\(\cos(\theta)\) o\(\sin(\theta)\) es conocido, el Teorema 10.1 puede ser utilizado para determinar el otro, hasta un signo (\(\pm\)). Si, además, sabemos dónde se\(\theta\) encuentra el lado terminal de cuando está en posición estándar, entonces podemos eliminar la ambigüedad de la (\(\pm\)) y determinar completamente el valor faltante como ilustra el siguiente ejemplo.
Utilizando la información dada sobre\(\theta\), encuentra el valor indicado.
- Si\(\theta\) es un ángulo del Cuadrante II con\(\sin(\theta) = \frac{3}{5}\), encontrar\(\cos(\theta)\).
- Si\(\pi < \theta < \frac{3\pi}{2}\) con\(\cos(\theta) = -\frac{\sqrt{5}}{5}\), encuentra\(\sin(\theta)\).
- Si\(\sin(\theta) = 1\), encuentra\(\cos(\theta)\).
Solución.
- Cuando sustituimos\(\sin(\theta) = \frac{3}{5}\) en La identidad pitagórica\(\cos^{2}(\theta) + \sin^{2}(\theta) = 1\),, obtenemos\(\cos^{2}(\theta) + \frac{9}{25} = 1\). Resolviendo, encontramos\(\cos(\theta) = \pm \frac{4}{5}\). Dado que\(\theta\) es un ángulo del Cuadrante II, su lado terminal, cuando se traza en posición estándar, se encuentra en el Cuadrante II. Dado que las\(x\) coordenadas -son negativas en el Cuadrante II, también lo\(\cos(\theta)\) es. De ahí,\(\cos(\theta) = - \frac{4}{5}\).
- Sustituyendo\(\cos(\theta) = -\frac{\sqrt{5}}{5}\) en\(\cos^{2}(\theta) + \sin^{2}(\theta) = 1\) da\(\sin(\theta) = \pm \frac{2}{\sqrt{5}} = \pm \frac{2 \sqrt{5}}{5}\). Ya que se nos da eso\(\pi < \theta < \frac{3\pi}{2}\), sabemos que\(\theta\) es un ángulo del Cuadrante III. De ahí que tanto su seno como su coseno sean negativos y concluimos\(\sin(\theta) = -\frac{2 \sqrt{5}}{5}\).
- Cuando sustituimos\(\sin(\theta) = 1\) en\(\cos^{2}(\theta) + \sin^{2}(\theta) = 1\), nos encontramos\(\cos(\theta) = 0\).
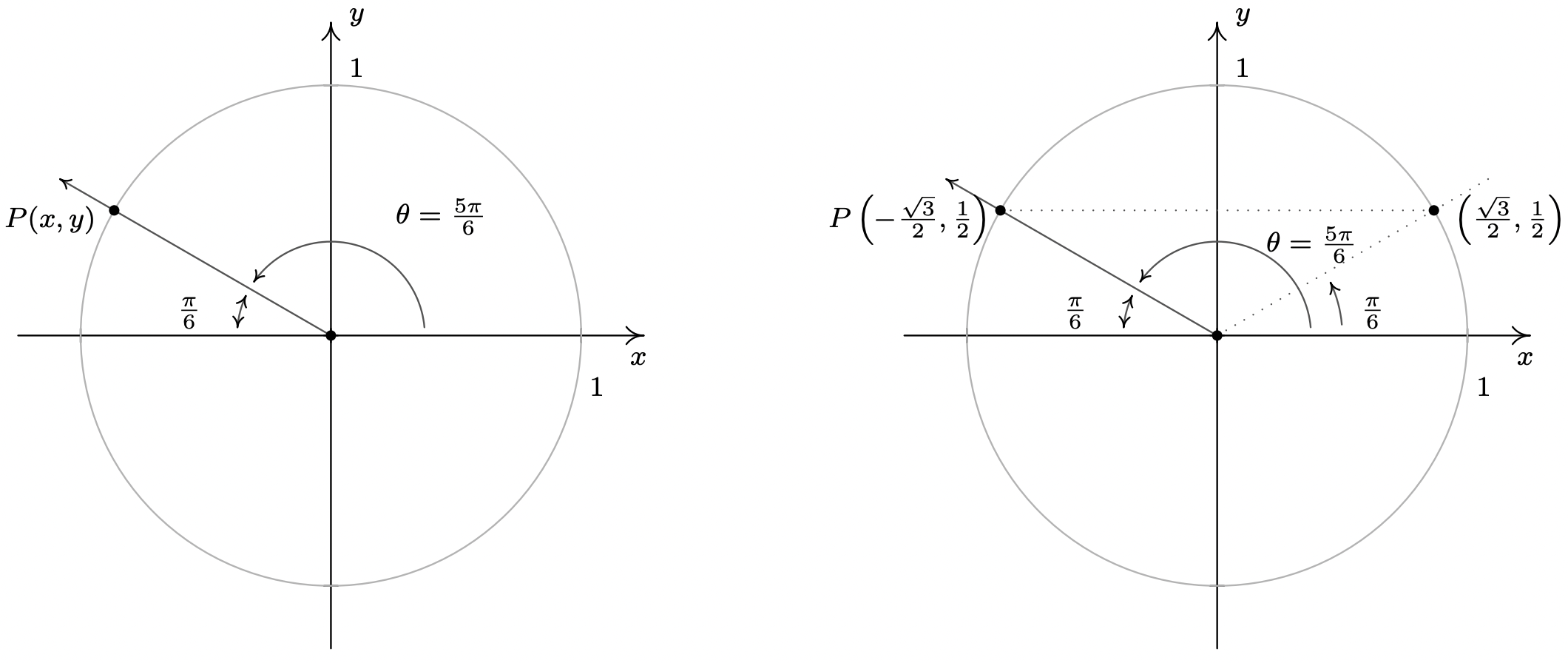
Otra herramienta que ayuda inmensamente en la determinación de cosenos y senos de ángulos es la simetría inherente al Círculo de Unidad. Supongamos, por ejemplo, que deseamos conocer el coseno y el seno de\(\theta = \frac{5 \pi}{6}\). Trazamos\(\theta\) en posición estándar abajo y, como de costumbre, vamos a\(P(x,y)\) denotar el punto en el lado terminal del\(\theta\) cual se encuentra en el Círculo Unitario. Tenga en cuenta que el lado terminal de las\(\theta\) mentiras\(\frac{\pi}{6}\) radianes corto de una media revolución. En el Ejemplo 10.2.1, determinamos que\(\cos\left(\frac{\pi}{6}\right) = \frac{\sqrt{3}}{2}\) y\(\sin\left( \frac{\pi}{6} \right) = \frac{1}{2}\). Esto significa que el punto en el lado terminal del ángulo\(\frac{\pi}{6}\), cuando se traza en posición estándar, es\(\left(\frac{\sqrt{3}}{2}, \frac{1}{2}\right)\). De la siguiente figura, queda claro que el punto que\(P(x,y)\) buscamos se puede obtener reflejando ese punto alrededor del\(y\) eje -eje. De ahí,\(\cos\left(\frac{5\pi}{6}\right) = -\frac{\sqrt{3}}{2}\) y\(\sin\left( \frac{5\pi}{6} \right) = \frac{1}{2}\).
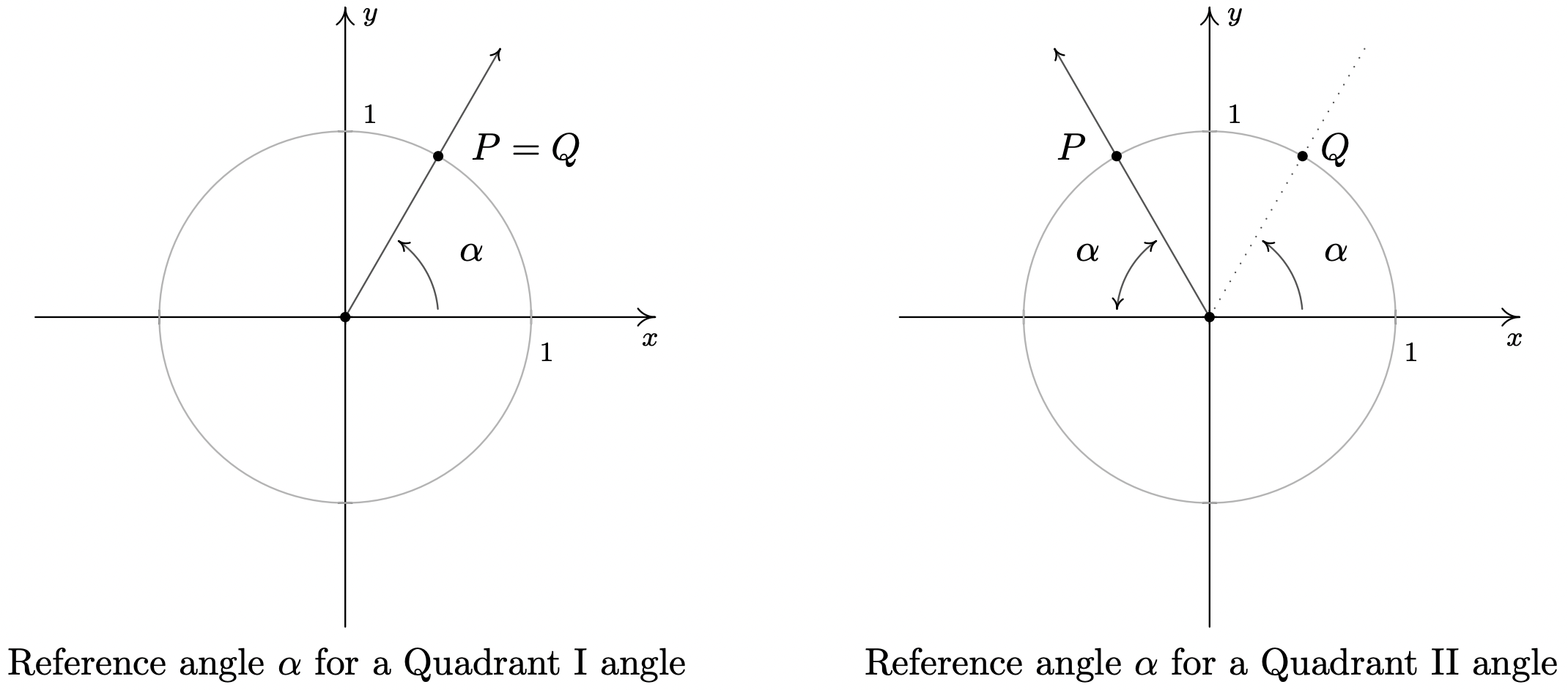
En el escenario anterior, el ángulo\(\frac{\pi}{6}\) se denomina ángulo de referencia para el ángulo\(\frac{5 \pi}{6}\). En general, para un ángulo no cuadrántico\(\theta\), el ángulo de referencia para\(\theta\) (generalmente denotado\(\alpha\)) es el ángulo agudo realizado entre el lado terminal\(\theta\) y el\(x\) eje. Si\(\theta\) es un ángulo Cuadrante I o IV,\(\alpha\) es el ángulo entre el lado terminal\(\theta\) y el\(x\) eje positivo; si\(\theta\) es un ángulo Cuadrante II o III,\(\alpha\) es el ángulo entre el lado terminal de\(\theta\) y el negativo \(x\)-eje. Si dejamos\(P\) denotar el punto\((\cos(\theta), \sin(\theta))\), entonces\(P\) yace en el Círculo de Unidades. Dado que el Círculo de Unidad posee simetría con respecto al\(x\) -eje,\(y\) -eje y origen, independientemente de dónde\(\theta\) se encuentre el lado terminal, existe un punto\(Q\) simétrico con el\(P\) que determina el ángulo\(\theta\) de referencia,\(\alpha\) como se ve a continuación.
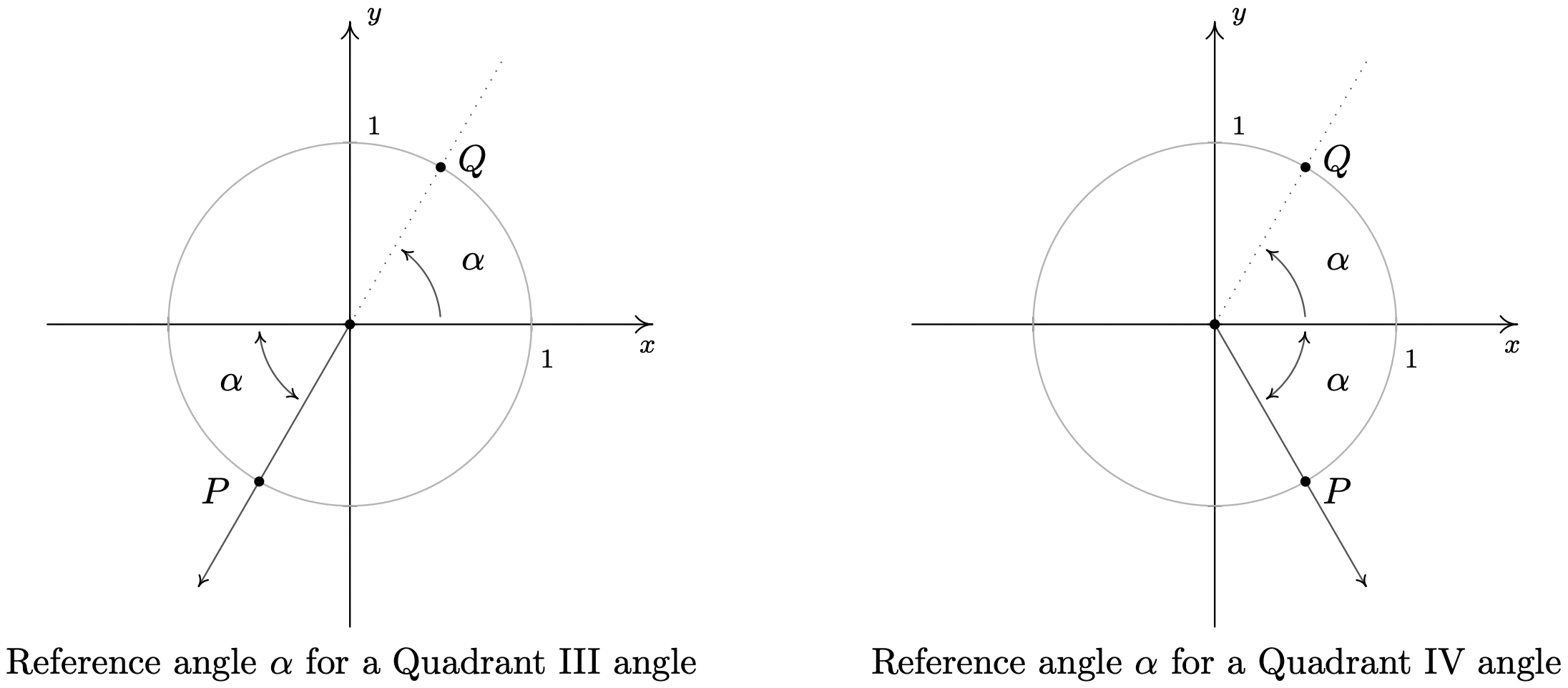
Acabamos de esbozar la prueba del siguiente teorema.
Supongamos que\(\alpha\) es el ángulo de referencia para\(\theta\). Entonces\(\cos(\theta) = \pm \cos(\alpha)\) y\(\sin(\theta) = \pm \sin(\alpha)\), donde la elección de la (\(\pm\)) depende del cuadrante en el que se\(\theta\) encuentra el lado terminal de.
A la luz del Teorema 10.2, conviene conocer los valores coseno y seno para ciertos ángulos comunes. En la siguiente tabla, resumimos los valores que consideramos esenciales y que deben ser memorizados.
\[\begin{array}{|c|c||c|c|} \hline \theta (\mbox{degrees}) & \theta (\mbox{radians}) & \cos(\theta) & \sin(\theta) \\ \hline 0^{\circ} & 0 & 1 & 0 \\ \hline 30^{\circ} & \frac{\pi}{6} & \frac{\sqrt{3}}{2} & \frac{1}{2} \\[4pt] \hline 45^{\circ} & \frac{\pi}{4} & \frac{\sqrt{2}}{2} & \frac{\sqrt{2}}{2} \\[4pt] \hline 60^{\circ} & \frac{\pi}{3} & \frac{1}{2} & \frac{\sqrt{3}}{2} \\[4pt] \hline 90^{\circ} & \frac{\pi}{2} & 0 & 1 \\[4pt] \hline \end{array}\nonumber\]
Encuentra el coseno y el seno de los siguientes ángulos.
- \(\theta = 225^{\circ}\)
- \(\theta = \frac{11 \pi}{6}\)
- \(\theta = -\frac{5 \pi}{4}\)
- \(\theta = \frac{7 \pi}{3}\)
Solución.
- Comenzamos trazando\(\theta = 225^{\circ}\) en posición estándar y encontramos que su lado terminal rebasa el\(x\) eje negativo para aterrizar en el Cuadrante III. De ahí, obtenemos\(\theta\) el ángulo de referencia\(\alpha\) restando:\(\alpha = \theta - 180^{\circ} = 225^{\circ} - 180^{\circ} = 45^{\circ}\). Ya que\(\theta\) es un ángulo Cuadrante III, ambos\(\cos(\theta) < 0\) y\(\sin(\theta) < 0\). El Teorema del Ángulo de Referencia rinde:\(\cos\left(225^{\circ}\right) = -\cos\left(45^{\circ}\right) = -\frac{\sqrt{2}}{2}\) y\(\sin\left(225^{\circ}\right) = - \sin\left(45^{\circ}\right) = -\frac{\sqrt{2}}{2}\).
- El lado terminal de\(\theta = \frac{11\pi}{6}\), cuando se traza en posición estándar, se encuentra en el Cuadrante IV, apenas tímido del\(x\) eje positivo. Para encontrar\(\theta\) el ángulo de referencia\(\alpha\), restamos:\(\alpha = 2\pi - \theta = 2\pi - \frac{11 \pi}{6} = \frac{\pi}{6}\). Ya que\(\theta\) es un ángulo Cuadrante IV,\(\cos(\theta) > 0\) y\(\sin(\theta) < 0\), así el Teorema del Ángulo de Referencia da:\(\cos\left(\frac{11 \pi}{6} \right) = \cos\left(\frac{\pi}{6} \right) = \frac{\sqrt{3}}{2}\) y\(\sin\left(\frac{11\pi}{6}\right) = -\sin\left(\frac{\pi}{6}\right) = -\frac{1}{2}\).
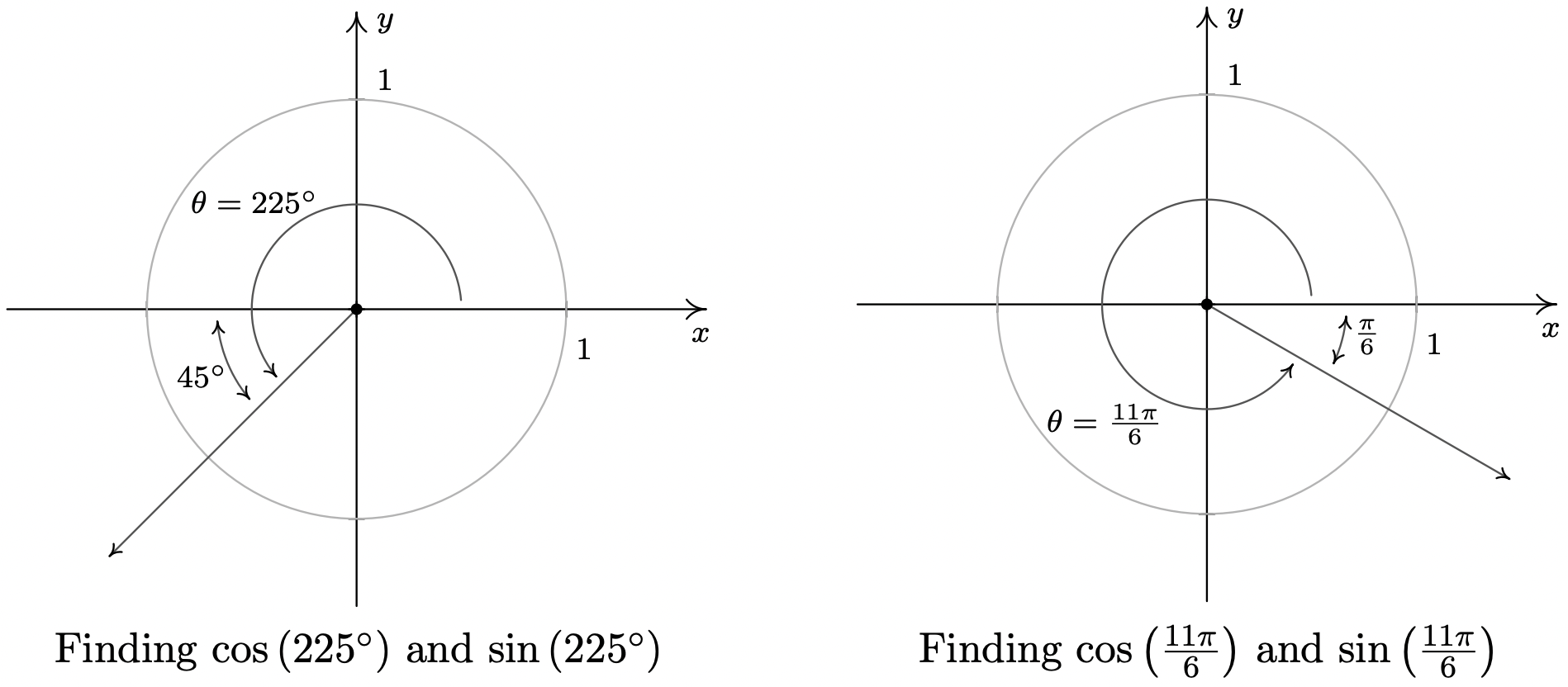
- Para trazar\(\theta = -\frac{5\pi}{4}\), giramos en el sentido de las agujas del reloj un ángulo\(\frac{5 \pi}{4}\) desde el\(x\) eje positivo. El lado terminal de\(\theta\), por lo tanto, se encuentra en el Cuadrante II formando un ángulo de\(\alpha = \frac{5 \pi}{4} - \pi = \frac{\pi}{4}\) radianes con respecto al\(x\) eje negativo. Dado que\(\theta\) es un ángulo del Cuadrante II, el Teorema del Ángulo de Referencia da:\(\cos\left(-\frac{5 \pi}{4}\right) = -\cos\left(\frac{\pi}{4}\right) = -\frac{\sqrt{2}}{2}\) y\(\sin\left(-\frac{5 \pi}{4}\right) = \sin\left(\frac{\pi}{4}\right) = \frac{\sqrt{2}}{2}\).
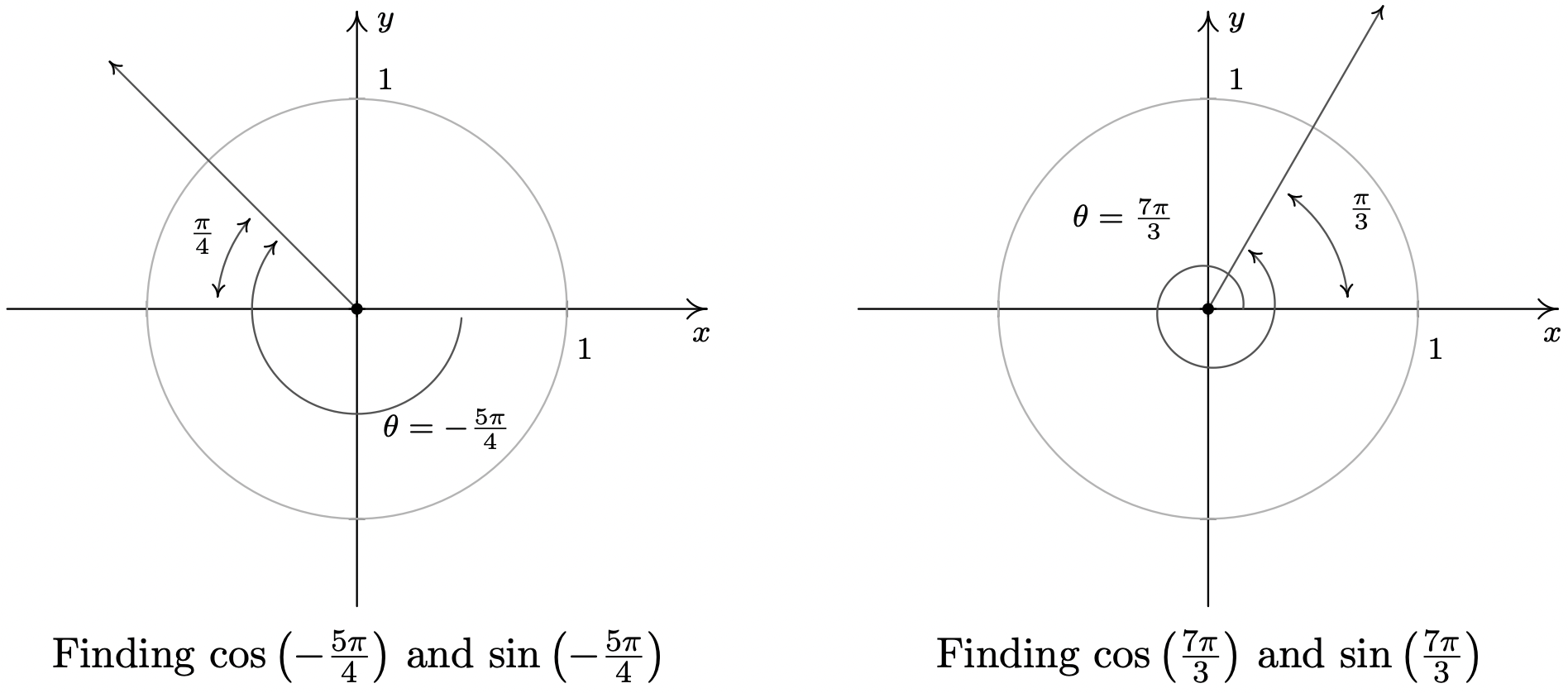
- Dado que el ángulo\(\theta = \frac{7 \pi}{3}\) mide más de\(2 \pi = \frac{6 \pi}{3}\), encontramos el lado terminal de\(\theta\) girando una revolución completa seguida de un\(\alpha = \frac{7 \pi}{3} - 2\pi = \frac{\pi}{3}\) radianes adicionales. Desde\(\theta\) y\(\alpha\) son coterminales,\(\cos\left(\frac{7\pi}{3}\right) = \cos\left(\frac{\pi}{3}\right) = \frac{1}{2}\) y\(\sin\left(\frac{7\pi}{3}\right) = \sin\left(\frac{\pi}{3}\right) = \frac{\sqrt{3}}{2}\).
El lector puede haber notado que cuando se expresa en medida de radianes, el ángulo de referencia para un ángulo no cuadrántico es fácil de detectar. Fracción reducida múltiplos de\(\pi\) con denominador de\(6\) tener\(\frac{\pi}{6}\) como ángulo de referencia, aquellos con denominador de\(4\) tener\(\frac{\pi}{4}\) como ángulo de referencia, y aquellos con denominador de\(3\) tener\(\frac{\pi}{3}\) como ángulo de referencia. 6 El Teorema del Ángulo de Referencia en conjunto con la tabla de valores de coseno y seno de la Página 722 se puede utilizar para generar la siguiente figura, que los autores consideran que debe estar comprometida con la memoria.
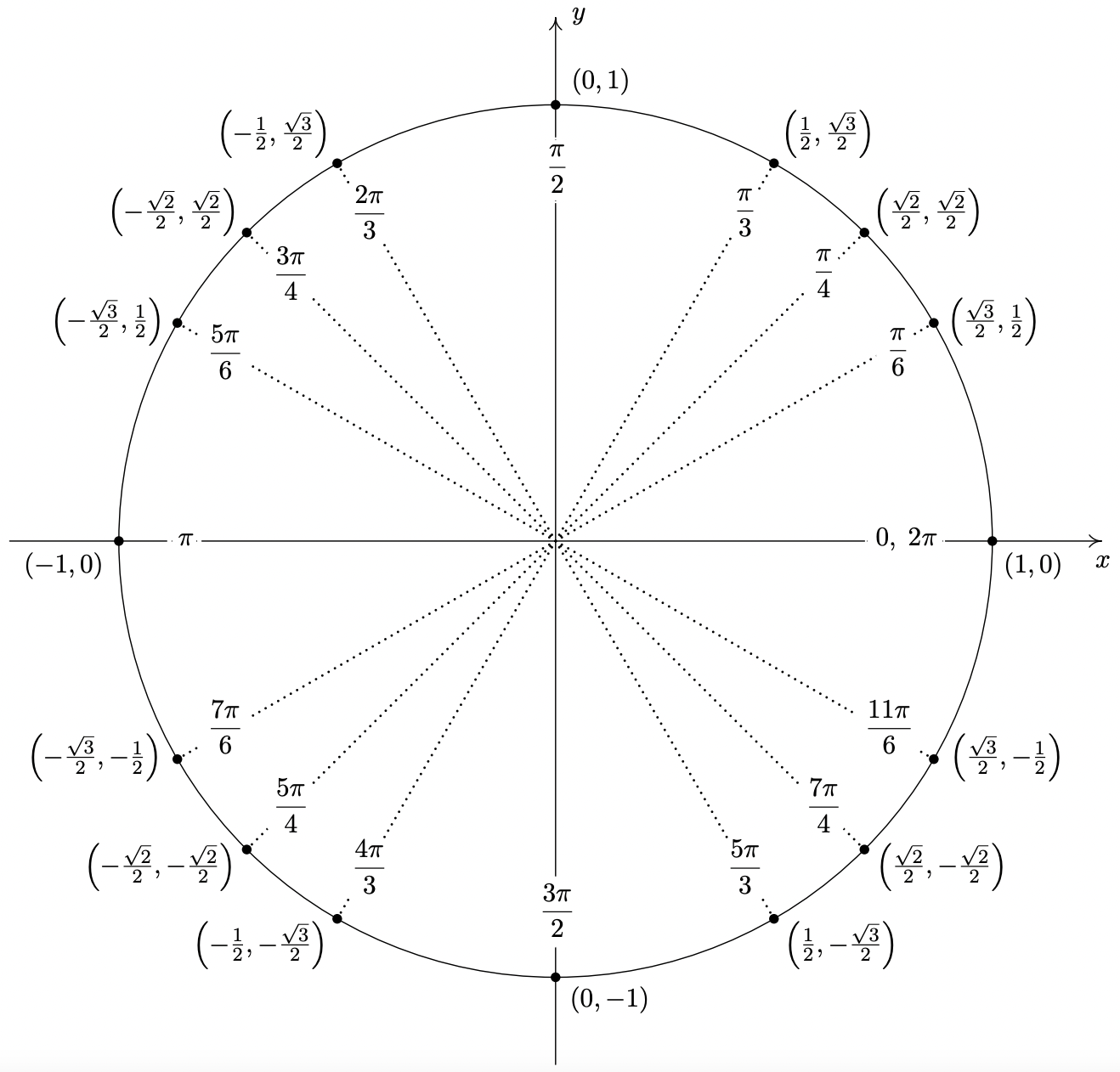 Puntos Importantes en el Círculo de Unidades
Puntos Importantes en el Círculo de UnidadesEl siguiente ejemplo resume todas las ideas importantes discutidas hasta ahora en la sección.
Supongamos que\(\alpha\) es un ángulo agudo con\(\cos(\alpha) = \frac{5}{13}\).
- Encuentra\(\sin(\alpha)\) y usa esto para trazar\(\alpha\) en posición estándar.
- Encuentra el seno y el coseno de los siguientes ángulos:
- \(\theta = \pi + \alpha\)
- \(\theta = 2\pi - \alpha\)
- \(\theta = 3\pi - \alpha\)
- \(\theta = \frac{\pi}{2} + \alpha\)
Solución.
- Procediendo como en el Ejemplo 10.2.2, sustituimos\(\cos(\alpha) = \frac{5}{13}\) en\(\cos^{2}(\alpha) + \sin^{2}(\alpha) = 1\) y encontramos\(\sin(\alpha) = \pm \frac{12}{13}\). Ya que\(\alpha\) es un ángulo agudo (y por lo tanto Cuadrante I),\(\sin(\alpha)\) es positivo. De ahí,\(\sin(\alpha) = \frac{12}{13}\). Para trazar\(\alpha\) en posición estándar, comenzamos nuestra rotación sobre el\(x\) eje positivo al rayo que contiene el punto\((\cos(\alpha), \sin(\alpha)) = \left(\frac{5}{13}, \frac{12}{13}\right)\).
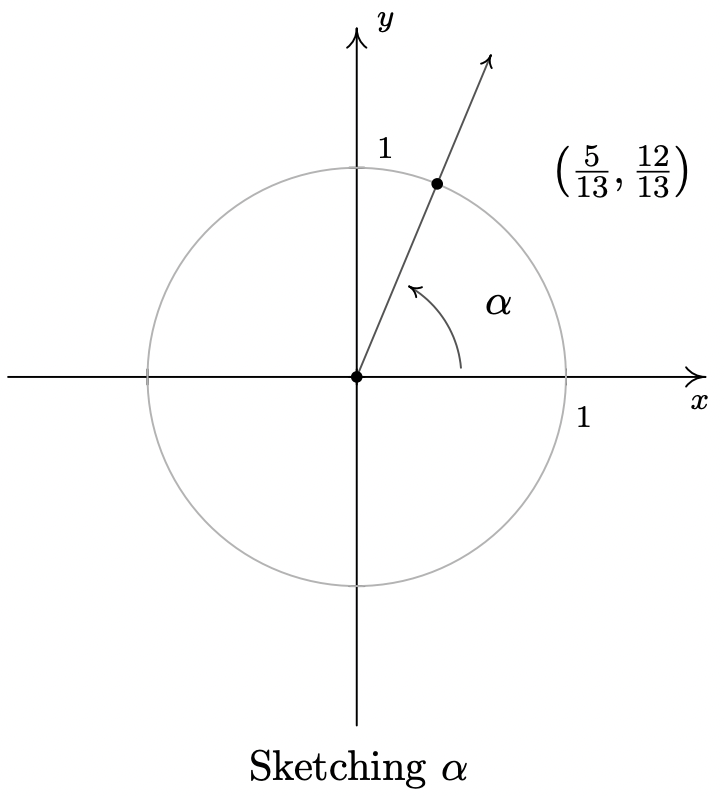
-
- Para encontrar el coseno y el seno de\(\theta = \pi + \alpha\), primero trazamos\(\theta\) en posición estándar. Podemos imaginar la suma de los ángulos\(\pi + \alpha\) como una secuencia de dos rotaciones: una rotación de\(\pi\) radianes seguida de una rotación de\(\alpha\) radianes. 7 Vemos que\(\alpha\) es el ángulo de referencia para\(\theta\), así por El Teorema del Ángulo de Referencia,\(\cos(\theta) = \pm \cos(\alpha) = \pm \frac{5}{13}\) y\(\sin(\theta) = \pm \sin(\alpha) = \pm \frac{12}{13}\). Dado que el lado terminal de las\(\theta\) caídas en el Cuadrante III, ambos\(\cos(\theta)\) y\(\sin(\theta)\) son negativos, por lo tanto,\(\cos(\theta) = - \frac{5}{13}\) y\(\sin(\theta) = - \frac{12}{13}\).
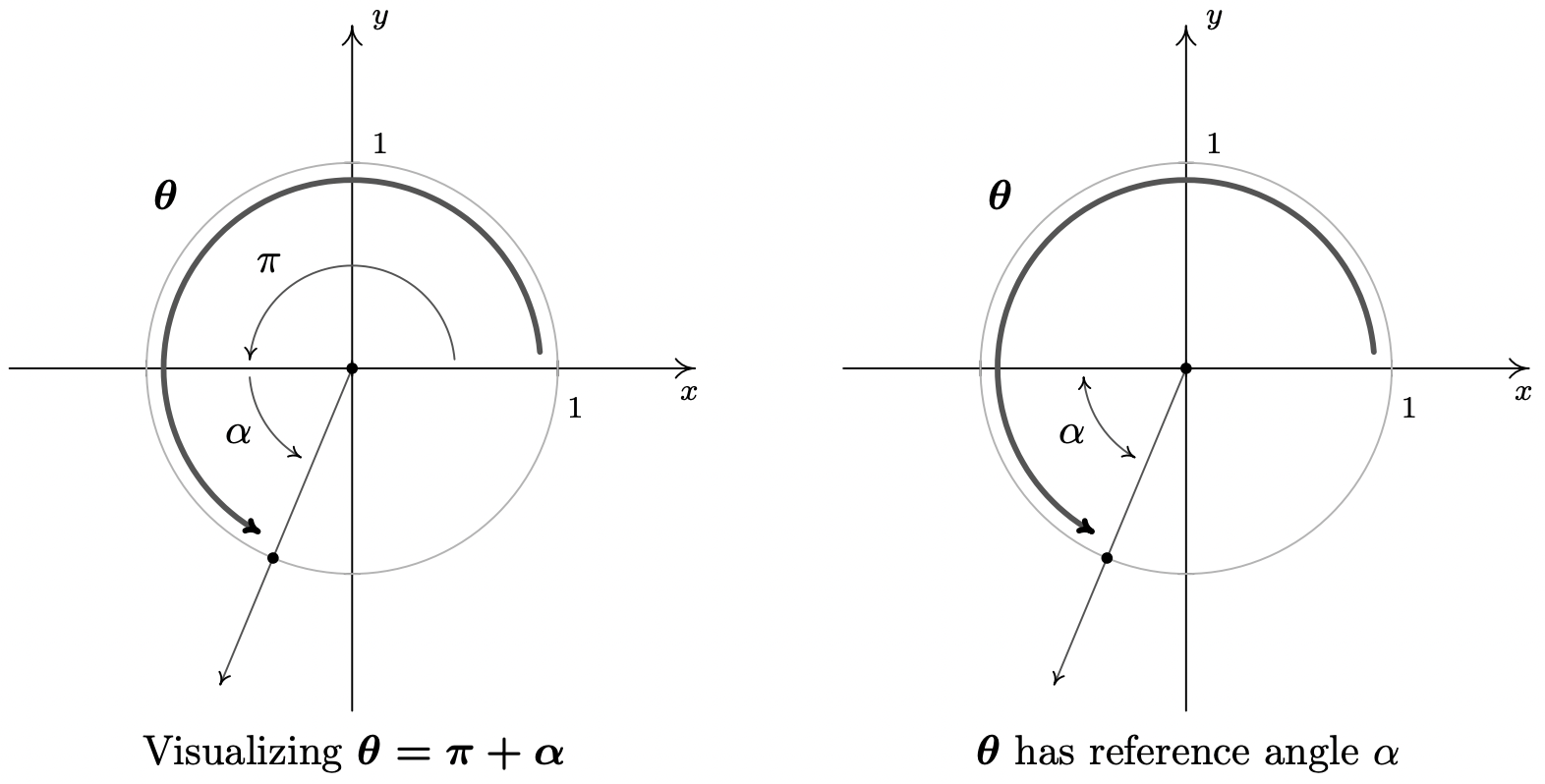
- Reescribiendo\(\theta = 2\pi - \alpha\) como\(\theta = 2\pi + (-\alpha)\), podemos trazar\(\theta\) visualizando una revolución completa en sentido antihorario seguida de una revolución en el sentido de las agujas del reloj, o “retrocediendo”, de\(\alpha\) radianes. Vemos que\(\alpha\) es\(\theta\) el ángulo de referencia, y dado que\(\theta\) es un ángulo Cuadrante IV, el Teorema del Ángulo de Referencia da:\(\cos(\theta) = \frac{5}{13}\) y\(\sin(\theta) = -\frac{12}{13}\).
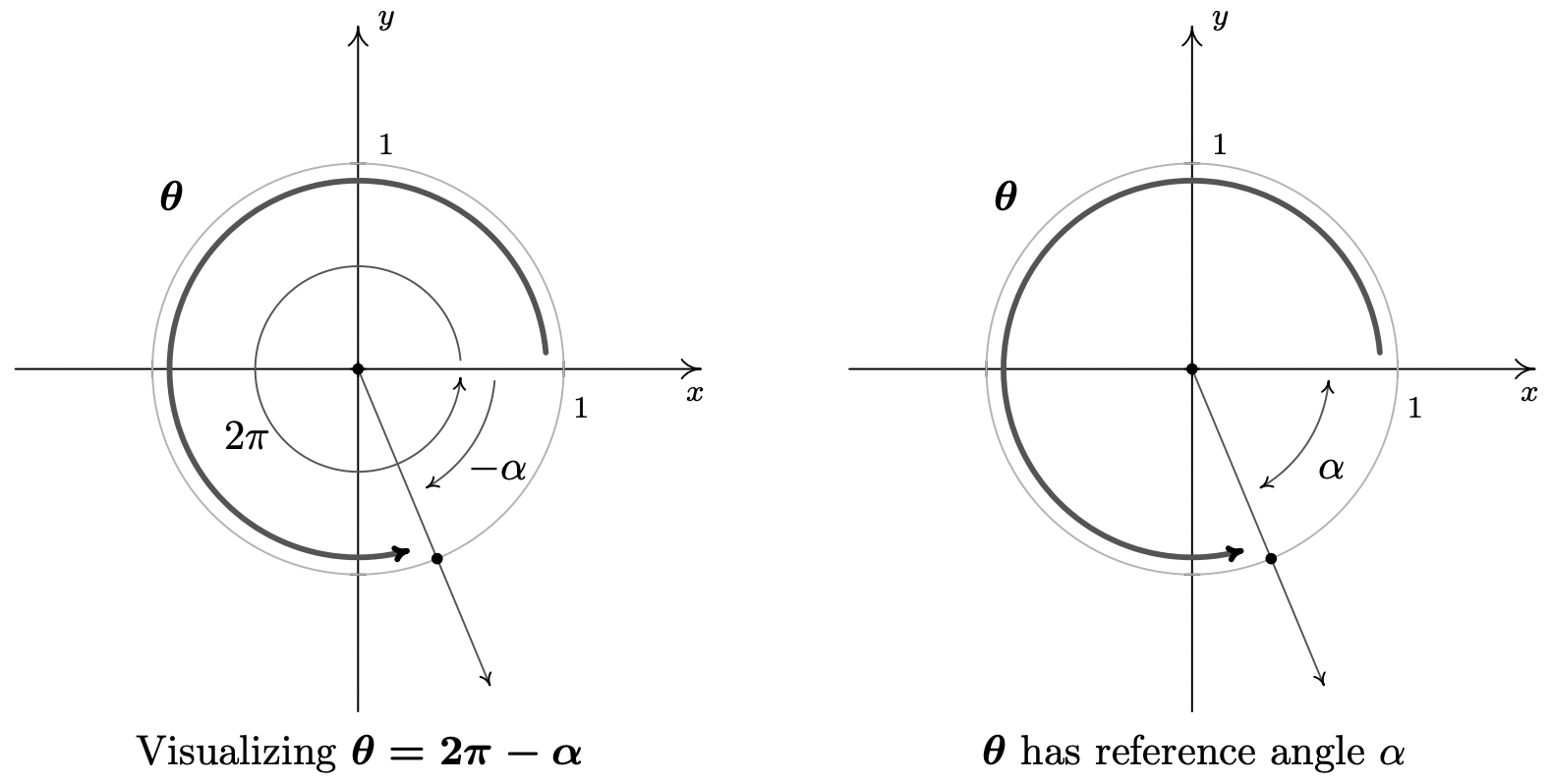
- Siguiendo el ejemplo del problema anterior, reescribimos\(\theta = 3\pi - \alpha\) como\(\theta = 3\pi + (-\alpha)\). El ángulo\(3\pi\) representa una revolución y media en sentido contrario a las agujas del reloj, de manera que cuando “retrocedemos”\(\alpha\) radianes, terminamos en el Cuadrante II. Usando el Teorema del Ángulo de Referencia, obtenemos\(\cos(\theta) = -\frac{5}{13}\) y\(\sin(\theta) = \frac{12}{13}\).
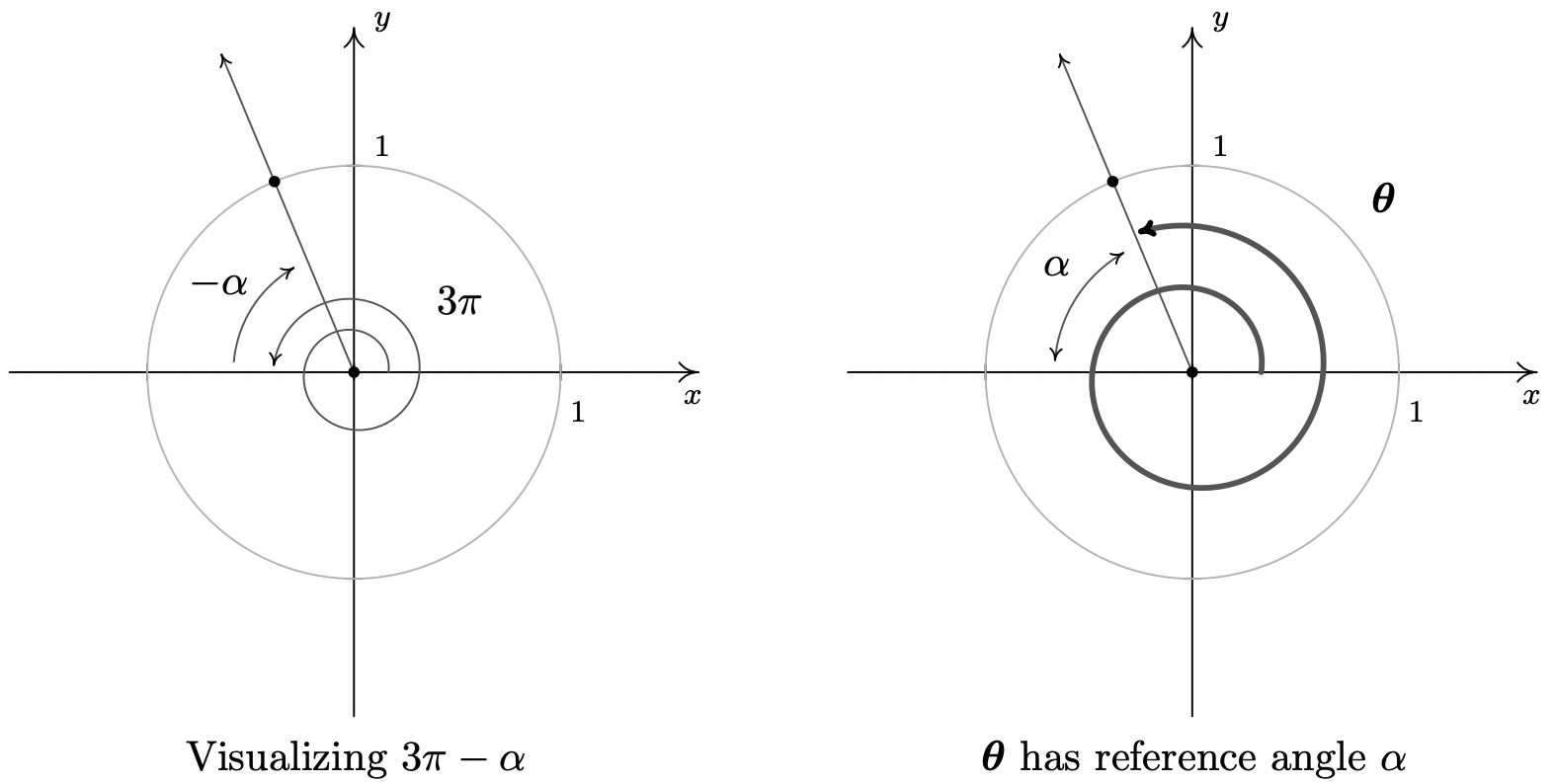
- Para trazar\(\theta = \frac{\pi}{2} + \alpha\), primero giramos\(\frac{\pi}{2}\) radianes y hacemos un seguimiento con\(\alpha\) radianes. El ángulo de referencia aquí no lo es\(\alpha\), por lo que El Teorema del Ángulo de Referencia no es de aplicación inmediata. (Es importante que veas por qué es así. Tómese un momento para pensar en esto antes de seguir leyendo.) Que\(Q(x,y)\) sea el punto en el lado terminal del\(\theta\) cual se encuentra en el Círculo de Unidad para que\(x = \cos(\theta)\) y\(y = \sin(\theta)\). Una vez que\(\alpha\) graficamos en posición estándar, usamos el hecho de que ángulos iguales subtienden acordes iguales para mostrar que las líneas punteadas en la figura de abajo son iguales. De ahí,\(x = \cos(\theta) = -\frac{12}{13}\). De igual manera, encontramos\(y = \sin(\theta) = \frac{5}{13}\).
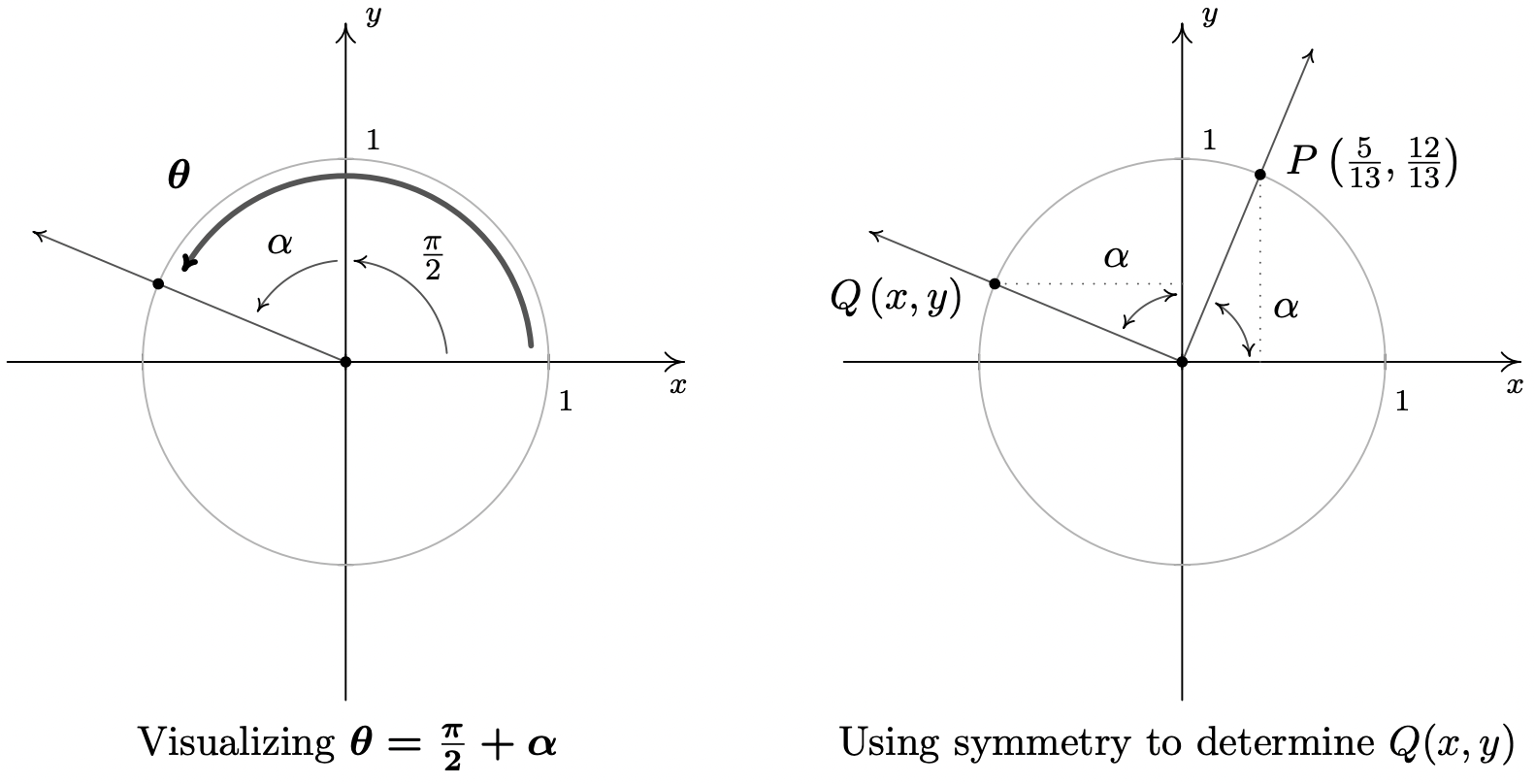
- Para encontrar el coseno y el seno de\(\theta = \pi + \alpha\), primero trazamos\(\theta\) en posición estándar. Podemos imaginar la suma de los ángulos\(\pi + \alpha\) como una secuencia de dos rotaciones: una rotación de\(\pi\) radianes seguida de una rotación de\(\alpha\) radianes. 7 Vemos que\(\alpha\) es el ángulo de referencia para\(\theta\), así por El Teorema del Ángulo de Referencia,\(\cos(\theta) = \pm \cos(\alpha) = \pm \frac{5}{13}\) y\(\sin(\theta) = \pm \sin(\alpha) = \pm \frac{12}{13}\). Dado que el lado terminal de las\(\theta\) caídas en el Cuadrante III, ambos\(\cos(\theta)\) y\(\sin(\theta)\) son negativos, por lo tanto,\(\cos(\theta) = - \frac{5}{13}\) y\(\sin(\theta) = - \frac{12}{13}\).
Nuestro siguiente ejemplo nos pide resolver algunas ecuaciones trigonométricas muy básicas. 8
Encuentra todos los ángulos que satisfacen la ecuación dada.
- \(\cos(\theta) = \dfrac{1}{2}\)
- \(\sin(\theta) = -\dfrac{1}{2}\)
- \(\cos(\theta) = 0\).
Solución
Dado que no hay contexto en el problema para indicar si usar grados o radianes, por defecto usaremos la medida de radianes en nuestras respuestas a cada uno de estos problemas. Esta elección se justificará más adelante en el texto cuando estudiemos lo que se conoce como Trigonometría Analítica. En esas secciones por venir, la medida de radianes será la única medida de ángulo apropiada por lo que ahora vale la pena pasar a ser “fluido en radianes”.
- Si\(\cos(\theta) = \frac{1}{2}\), entonces el lado terminal de\(\theta\), cuando se traza en posición estándar, cruza el Círculo de Unidad en\(x = \frac{1}{2}\). Esto significa que\(\theta\) es un ángulo Cuadrante I o IV con ángulo de referencia\(\frac{\pi}{3}\).
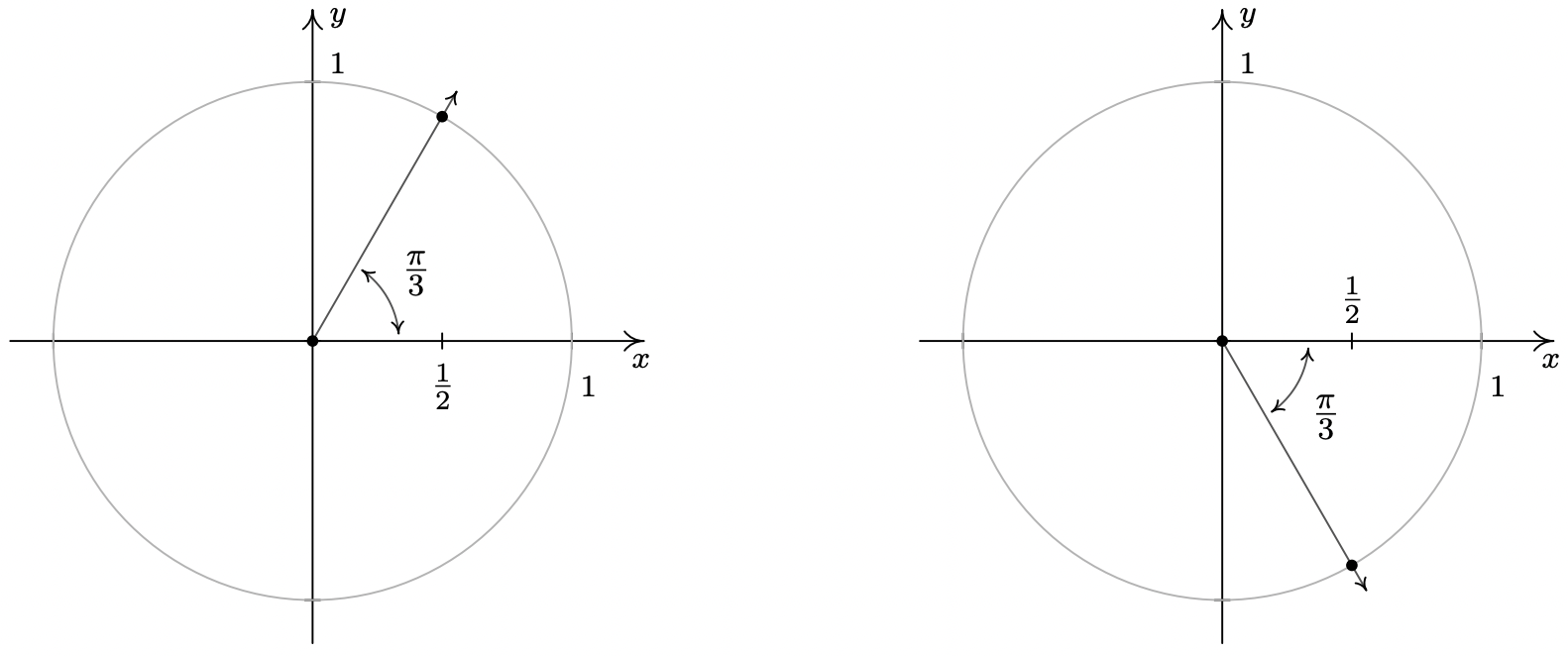
Una solución en el Cuadrante I es\(\theta = \frac{\pi}{3}\), y como todas las demás soluciones del Cuadrante I deben ser coterminales con\(\frac{\pi}{3}\), encontramos\(\theta = \frac{\pi}{3} + 2\pi k\) para enteros\(k\). 9 Procediendo de manera similar para el caso del Cuadrante IV, encontramos la solución para\(\cos(\theta) = \frac{1}{2}\) aquí es\(\frac{5 \pi}{3}\), por lo que nuestra respuesta en este Cuadrante es\(\theta = \frac{5\pi}{3} + 2\pi k\) para enteros\(k\).
- Si\(\sin(\theta) = -\frac{1}{2}\), entonces cuando\(\theta\) se traza en posición estándar, su lado terminal intersecta el Círculo de Unidad en\(y=-\frac{1}{2}\). A partir de esto, determinamos que\(\theta\) es un ángulo Cuadrante III o Cuadrante IV con ángulo de referencia\(\frac{\pi}{6}\).
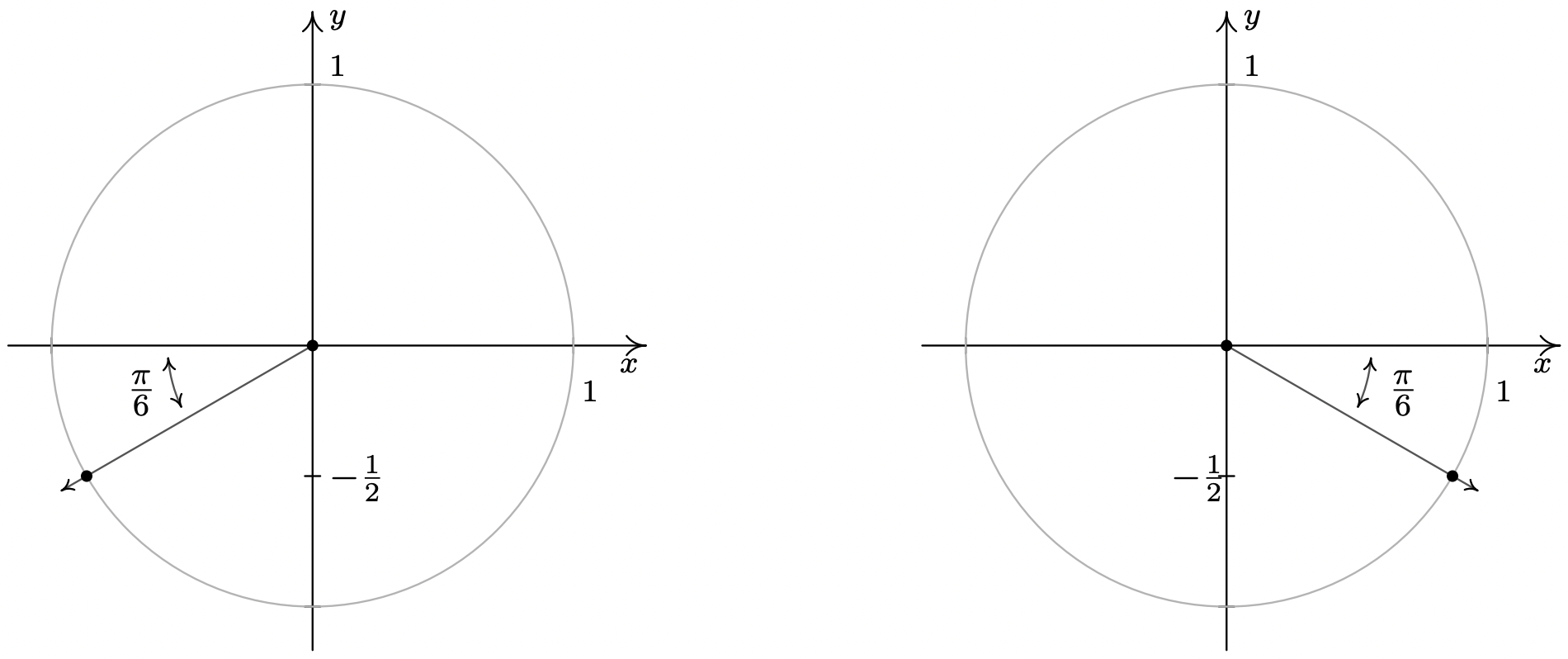
En el Cuadrante III, una solución es\(\frac{7\pi}{6}\), por lo que capturamos todas las soluciones del Cuadrante III agregando múltiplos enteros de\(2\pi\):\(\theta = \frac{7\pi}{6} + 2\pi k\). En el Cuadrante IV, una solución es\(\frac{11\pi}{6}\) así que todas las soluciones aquí son de la forma\(\theta = \frac{11\pi}{6} + 2\pi k\) para enteros\(k\).
- Los ángulos con\(\cos(\theta) = 0\) son ángulos cuadránticos cuyos lados terminales, cuando se trazan en posición estándar, se encuentran a lo largo del\(y\) eje.
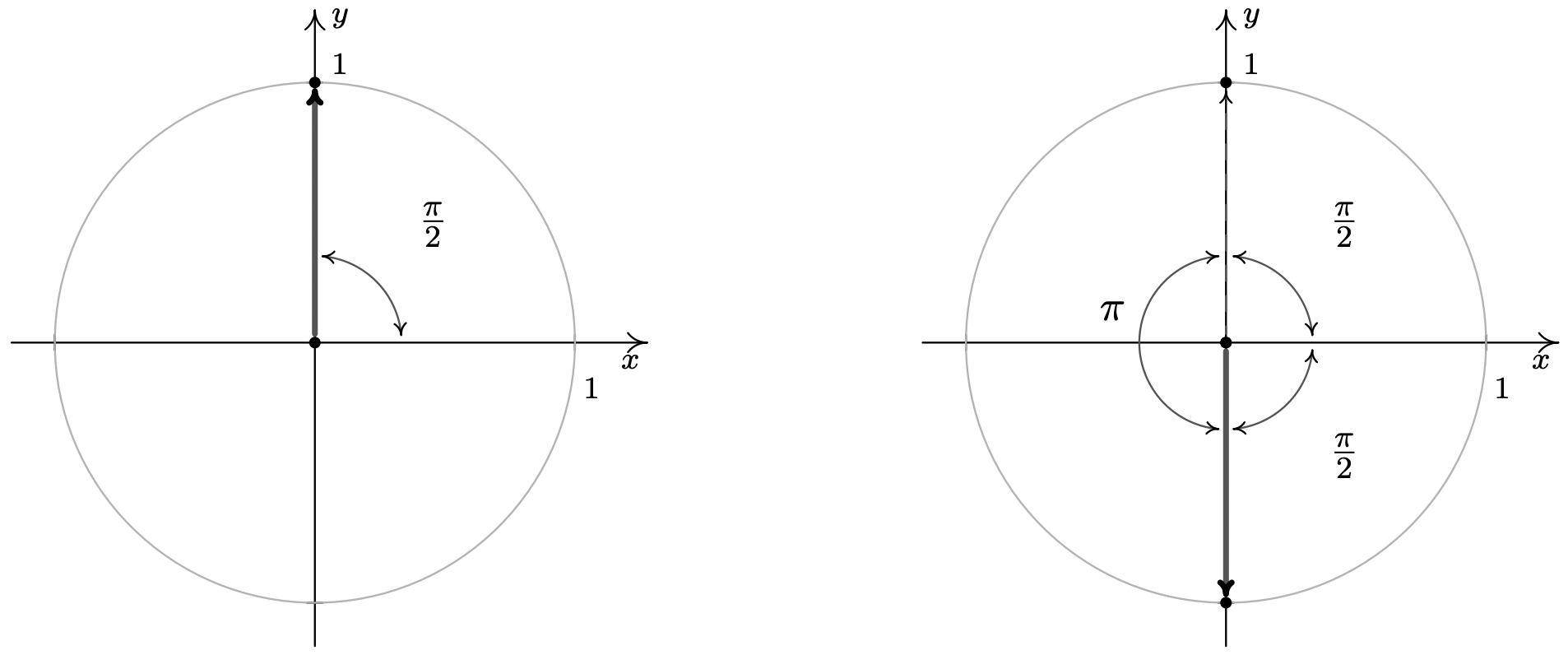
Si bien, técnicamente hablando,\(\frac{\pi}{2}\) no es un ángulo de referencia, podemos usarlo para encontrar nuestras respuestas. Si seguimos el procedimiento establecido en los ejemplos anteriores, encontramos\(\theta = \frac{\pi}{2} + 2\pi k\) y\(\theta = \frac{3\pi}{2} + 2\pi k\) para enteros,\(k\). Si bien esta solución es correcta, se puede acortar a\(\theta = \frac{\pi}{2} + \pi k\) para enteros\(k\). (¿Puedes ver por qué funciona esto a partir del diagrama?)
Uno de los elementos clave a tomar del Ejemplo 10.2.5 es que, en general, las soluciones a las ecuaciones trigonométricas consisten en infinitamente muchas respuestas. Para tener una idea de estas respuestas, se anima al lector a seguir nuestro mantra del Capítulo 9, es decir, '¡En caso de duda, escríbalo!' Esto es especialmente importante a la hora de verificar las respuestas a los ejercicios. Por ejemplo, otra solución de Cuadrante IV a\(\sin(\theta) = -\frac{1}{2}\) es\(\theta = -\frac{\pi}{6}\). De ahí que la familia de respuestas del Cuadrante IV al número 2 anterior podría haberse escrito fácilmente\(\theta = -\frac{\pi}{6} + 2\pi k\) para enteros\(k\). Si bien en la superficie, esta familia puede verse diferente a la solución declarada de\(\theta = \frac{11\pi}{6} + 2\pi k\) para enteros\(k\), dejamos que el lector muestre que representan la misma lista de ángulos.
10.2.1 Más allá del círculo de unidades
Comenzamos la sección con una búsqueda para describir la posición de una partícula que experimenta movimiento circular. Al definir las funciones coseno y seno, asignamos a cada ángulo una posición en el Círculo de Unidad. En esta subsección, ampliamos nuestro alcance para incluir círculos de radio\(r\) centrados en el origen. Considera por el momento el ángulo agudo\(\theta\) dibujado a continuación en posición estándar. \(Q(x,y)\)Sea el punto en el lado terminal del\(\theta\) cual se encuentra en el círculo\(x^2+y^2 = r^2\), y dejar que\(P(x',y')\) sea el punto en el lado terminal del\(\theta\) cual se encuentra en el Círculo de Unidad. Ahora considere soltar perpendiculares desde\(P\) y\(Q\) para crear dos triángulos rectos,\(\Delta OPA\) y\(\Delta OQB\). Estos triángulos son similares, 10 así se deduce que\(\frac{x}{x'} = \frac{r}{1} = r\), así\(x = r x'\) y, de manera similar, nos encontramos\(y = r y'\). Ya que, por definición\(y' = \sin(\theta)\),\(x' = \cos(\theta)\) y, obtenemos las coordenadas de\(Q\) ser\(x = r \cos(\theta)\) y\(y = r \sin(\theta)\). Al reflejar estos puntos a través del\(x\) eje\(y\) -eje, -eje y origen, obtenemos el resultado para todos los ángulos no cuadránticos\(\theta\), y dejamos al lector verificar que estas fórmulas se mantienen para los ángulos cuadrantales.
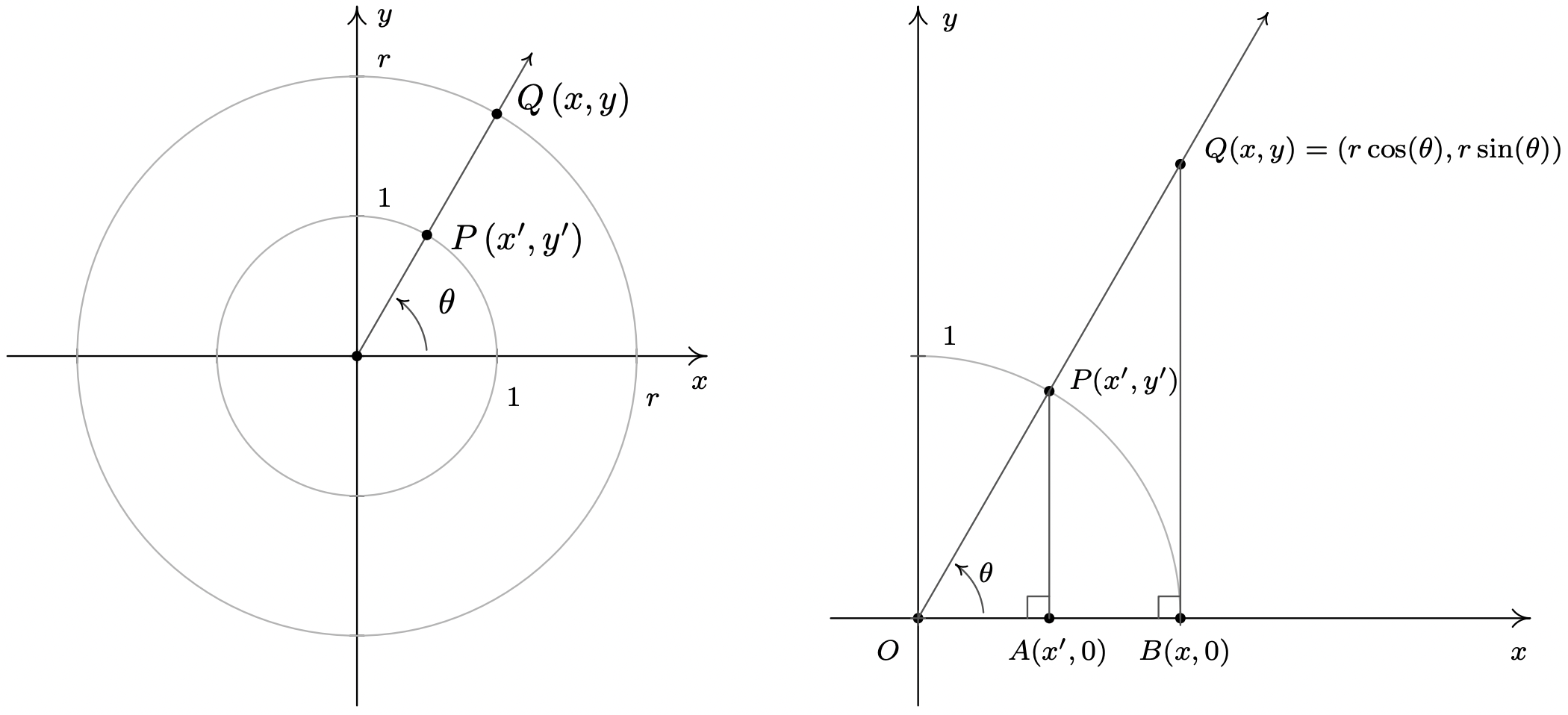
No sólo podemos describir las coordenadas de\(Q\) en términos de\(\cos(\theta)\) y\(\sin(\theta)\) sino como el radio del círculo es\(r = \sqrt{x^2 + y^2}\), también podemos expresar\(\cos(\theta)\) y\(\sin(\theta)\) en términos de las coordenadas de\(Q\). Estos resultados se resumen en el siguiente teorema.
Si\(Q(x,y)\) es el punto en el lado terminal de un ángulo\(\theta\), trazado en posición estándar, que se encuentra en el círculo\(x^2+y^2 = r^2\) entonces\(x = r \cos(\theta)\) y\(y = r \sin(\theta)\). Por otra parte,
\[\begin{array}{ccc} \cos(\theta)= \dfrac{x}{r} = \dfrac{x}{\sqrt{x^2+y^2}} & \text{and} & \sin(\theta) = \dfrac{y}{r} = \dfrac{y}{\sqrt{x^2+y^2}} \\ \end{array}\nonumber\]
Tenga en cuenta que en el caso del Círculo de Unidad tenemos\(r = \sqrt{x^2+y^2} = 1\), por lo que el Teorema 10.3 se reduce a nuestras definiciones de\(\cos(\theta)\) y\(\sin(\theta)\).
- Supongamos que el lado terminal de un ángulo\(\theta\), cuando se traza en posición estándar, contiene el punto\(Q(4,-2)\). Encontrar\(\sin(\theta)\) y\(\cos(\theta)\).
- En el Ejemplo 10.1.5 de la Sección 10.1, aproximamos el radio de la tierra en latitud\(41.628^{\circ}\) norte para ser\(2960\) millas. Justifica esta aproximación si el radio de la Tierra en el Ecuador es de aproximadamente\(3960\) millas.
Solución.
- Usando el Teorema 10.3 con\(x = 4\) y\(y = -2\), nos encontramos con\(r = \sqrt{(4)^2 + (-2)^2} = \sqrt{20} = 2 \sqrt{5}\) lo que\(\cos(\theta) = \frac{x}{r} = \frac{4}{2 \sqrt{5}} = \frac{2 \sqrt{5}}{5}\) y\(\sin(\theta) = \frac{y}{r} = \frac{-2}{2 \sqrt{5}} = -\frac{\sqrt{5}}{5}\).
- Suponiendo que la Tierra es una esfera, una sección transversal a través de los polos produce un círculo de radio\(3960\) millas. Viendo el Ecuador como el\(x\) eje -eje, el valor que buscamos es la\(x\) coordenada -del punto\(Q(x,y)\) indicado en la siguiente figura.
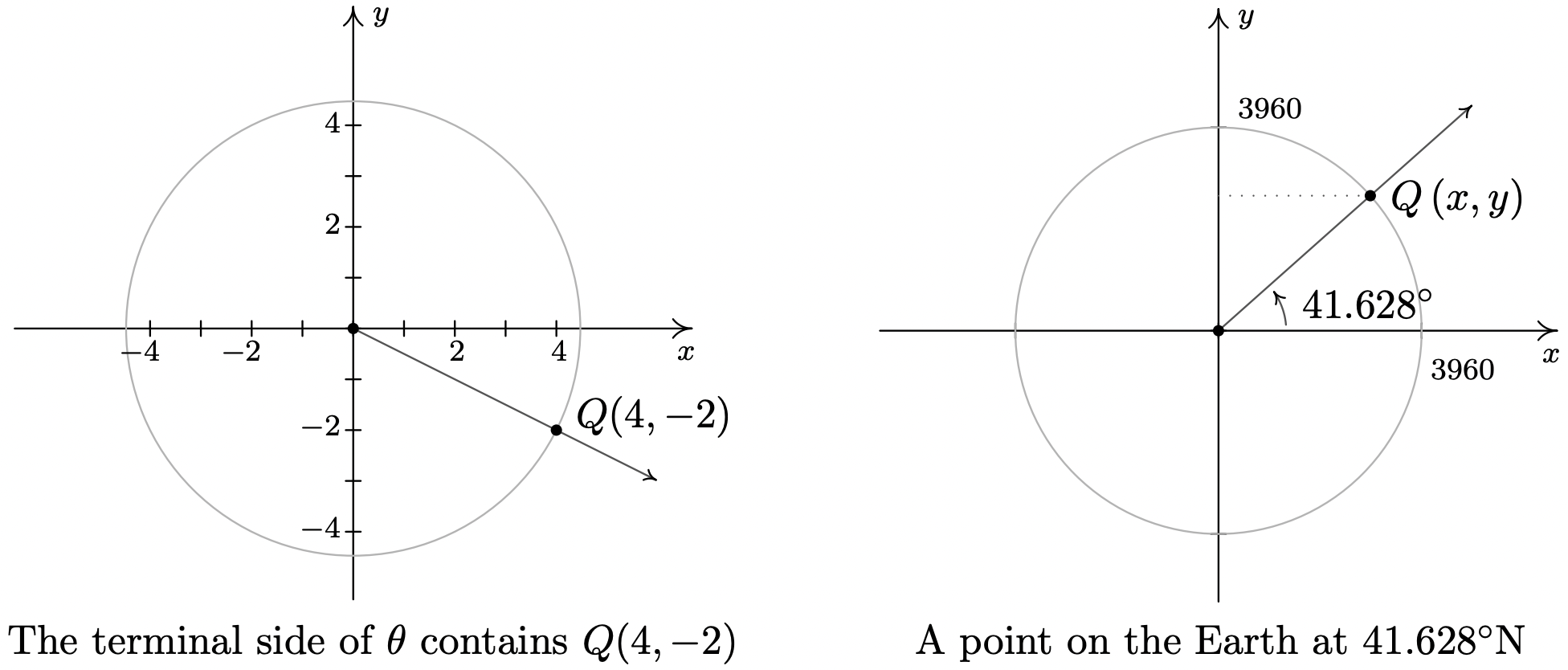
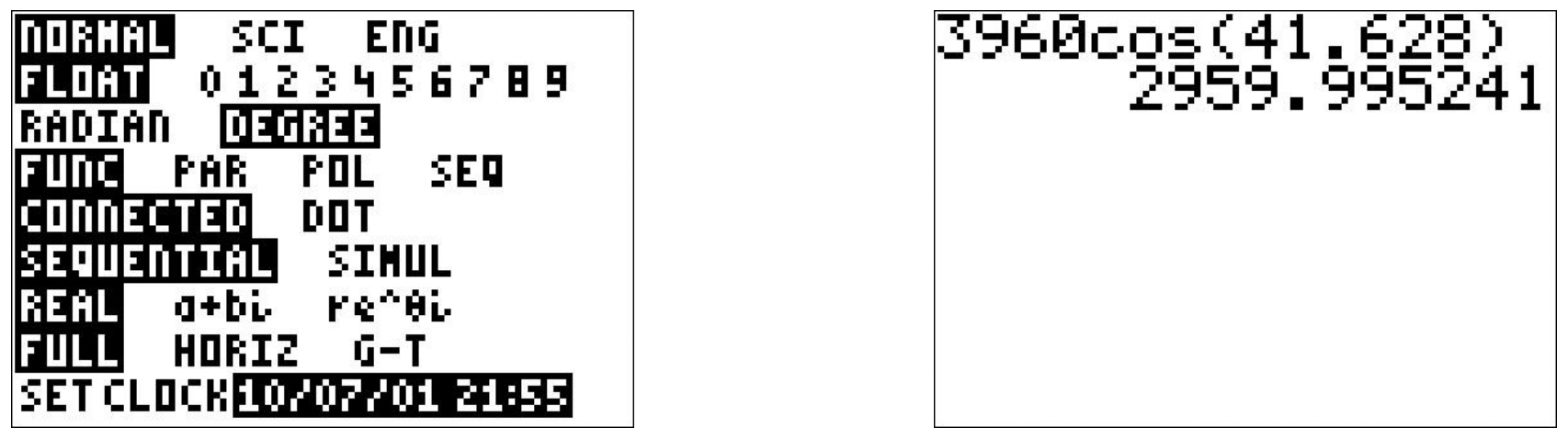
Usando el Teorema 10.3, obtenemos\(x = 3960 \cos\left(41.628^{\circ}\right)\). Usando una calculadora en modo 'grado', encontramos\(3960 \cos\left(41.628^{\circ}\right) \approx 2960\). De ahí que el radio de la Tierra en Latitud Norte\(41.628^{\circ}\) sea de aproximadamente\(2960\) millas.
El teorema 10.3 nos da lo que necesitamos para describir la posición de un objeto viajando en una trayectoria circular de radio\(r\) con velocidad angular constante\(\omega\). Supongamos que en el momento\(t\), el objeto ha barrido un ángulo que mide\(\theta\) radianes. Si asumimos que el objeto está en el punto\((r,0)\) cuando\(t=0\), el ángulo\(\theta\) está en posición estándar. Por definición,\(\omega = \frac{\theta}{t}\) que reescribimos como\(\theta = \omega t\). Según el Teorema 10.3, la ubicación del objeto\(Q(x,y)\) en el círculo se encuentra utilizando las ecuaciones\(x = r \cos(\theta) = r \cos(\omega t)\) y\(y = r \sin(\theta) = r \sin(\omega t)\). De ahí que, en el momento\(t\), el objeto esté en el punto\((r \cos(\omega t), r \sin(\omega t))\). Acabamos de argumentar lo siguiente.
Supongamos que un objeto está viajando en una trayectoria circular de radio\(r\) centrada en el origen con velocidad angular constante\(\omega\). Si\(t=0\) corresponde al punto\((r,0)\), entonces las\(y\) coordenadas\(x\) y del objeto son funciones de\(t\) y están dadas por\(x = r \cos(\omega t)\) y\(y = r \sin(\omega t)\). Aquí,\(\omega > 0\) indica una dirección en sentido contrario a las agujas del reloj e\(\omega < 0\) indica un sentido horario.
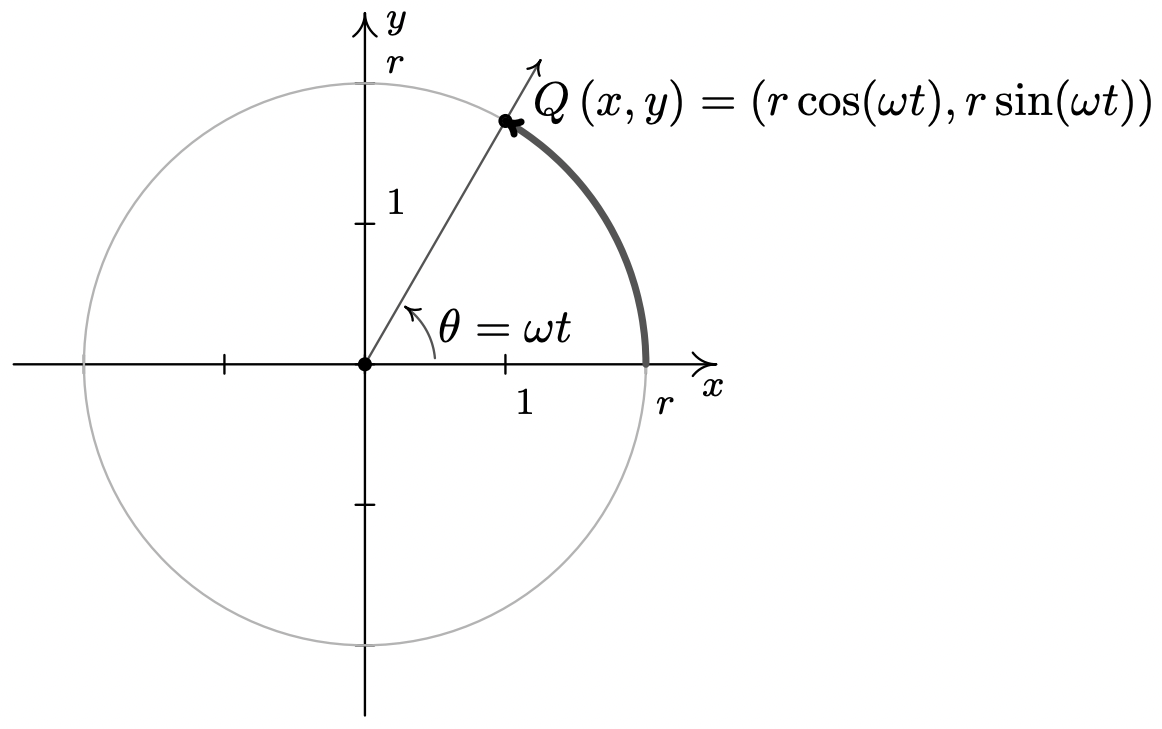
Ecuaciones para Movimiento Circular
Supongamos que estamos en la situación del Ejemplo 10.1.5. Encuentra las ecuaciones de movimiento de Lakeland Community College a medida que la tierra gira.
Solución
Del Ejemplo 10.1.5, tomamos\(r = 2960\) millas y y\(\omega = \frac{\pi}{12 \, \text{hours}}\). De ahí que las ecuaciones de movimiento son\(x = r \cos(\omega t) = 2960 \cos\left(\frac{\pi}{12} t\right)\) y\(y = r \sin(\omega t) = 2960 \sin\left(\frac{\pi}{12} t\right)\), dónde\(x\) y\(y\) se miden en millas y\(t\) se miden en horas.
Además del movimiento circular, el Teorema 10.3 también es la clave para desarrollar lo que suele llamarse trigonometría de 'triángulo recto'. 11 Como veremos en las secciones venideras, muchas aplicaciones en trigonometría implican encontrar las medidas de los ángulos en, y longitudes de los lados de, triángulos rectos. En efecto, hicimos buen uso de algunas propiedades de los triángulos rectos para encontrar los valores exactos del coseno y seno de muchos de los ángulos en el Ejemplo 10.2.1, por lo que el siguiente desarrollo no debería ser una gran sorpresa. Considera el triángulo rectángulo genérico de abajo con el ángulo agudo correspondiente\(\theta\). El lado con longitud\(a\) se llama el lado del triángulo adyacente a\(\theta\); el lado con longitud\(b\) se llama el lado del triángulo opuesto\(\theta\); y el lado restante de longitud\(c\) (el lado opuesto al ángulo recto) se llama hipotenusa. Ahora imaginamos dibujar este triángulo en el Cuadrante I para que el ángulo\(\theta\) esté en posición estándar con el lado adyacente para que\(\theta\) quede a lo largo del\(x\) eje positivo.
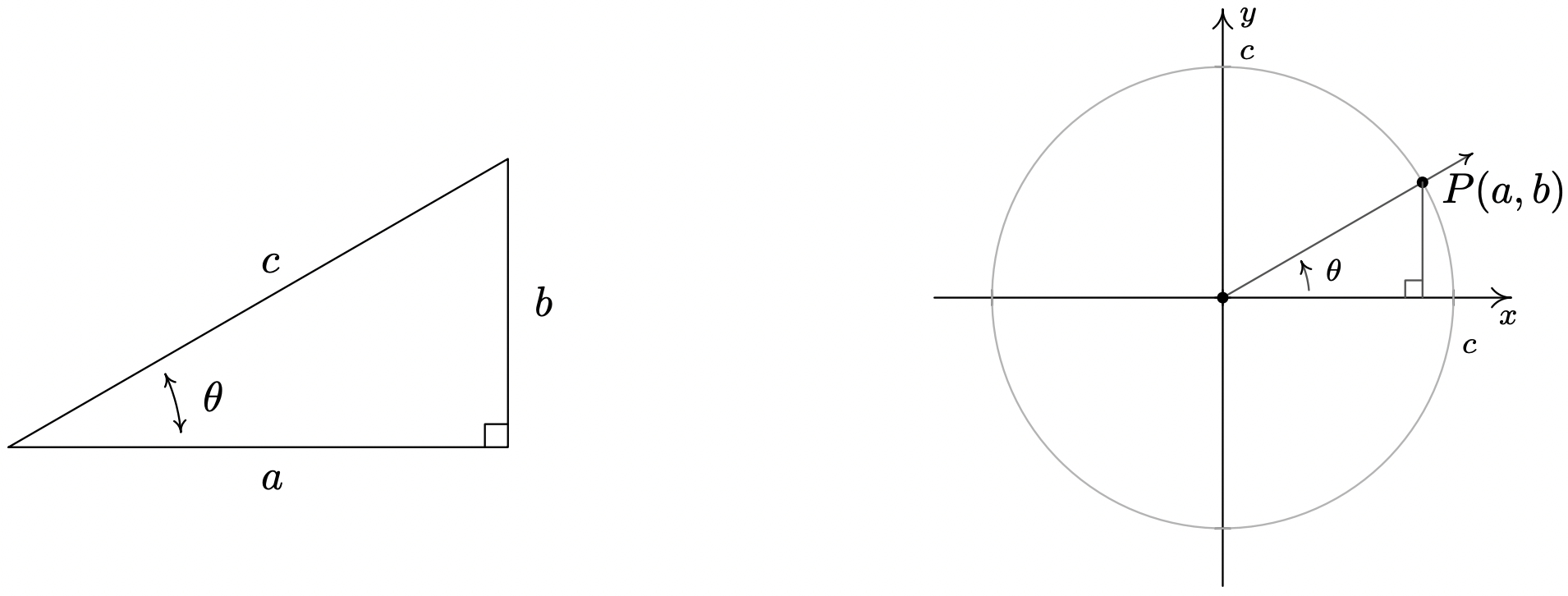
Según el Teorema de Pitágoras,\(a^2+b^2=c^2\), de manera que el punto\(P(a,b)\) se encuentra en un círculo de radio\(c\). El teorema 10.3 nos dice que\(\cos(\theta) = \frac{a}{c}\) y\(\sin(\theta) = \frac{b}{c}\), así hemos determinado el coseno y el seno de\(\theta\) en términos de las longitudes de los lados del triángulo rectángulo. Así tenemos el siguiente teorema.
Supongamos que\(\theta\) es un ángulo agudo que reside en un triángulo rectángulo. Si la longitud del lado adyacente a\(\theta\) es\(a\), la longitud del lado opuesto\(\theta\) es\(b\), y la longitud de la hipotenusa es\(c\), entonces\(\cos(\theta) = \dfrac{a}{c}\) y\(\sin(\theta) = \dfrac{b}{c}\).
Encuentra la medida del ángulo faltante y las longitudes de los lados faltantes de:
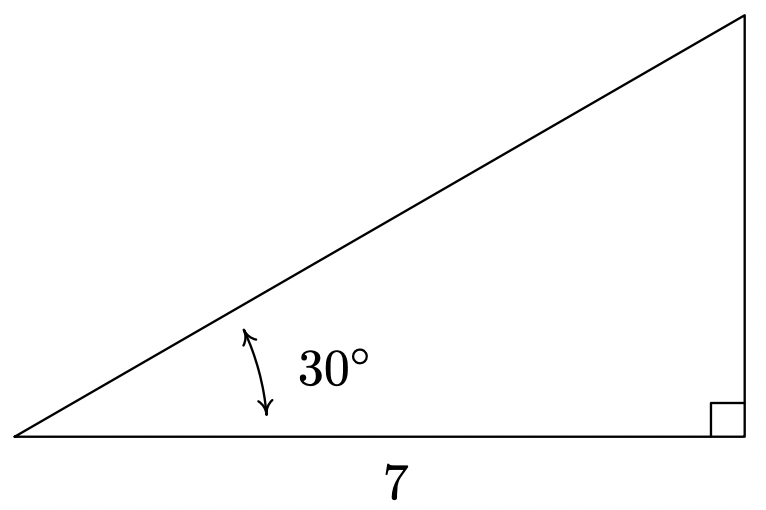
Solución
La primera y más sencilla tarea es encontrar la medida del ángulo faltante. Ya que la suma de ángulos de un triángulo es\(180^{\circ}\), sabemos que el ángulo faltante tiene medida\(180^{\circ} - 30^{\circ} - 90^{\circ} = 60^{\circ}\). Ahora procedemos a encontrar las longitudes de los dos lados restantes del triángulo. Dejar\(c\) denotar la longitud de la hipotenusa del triángulo. Por Teorema 10.4, tenemos\(\cos\left(30^{\circ}\right) = \frac{7}{c}\), o\(c = \frac{7}{\cos\left(30^{\circ}\right)}\). Ya que\(\cos\left(30^{\circ}\right) = \frac{\sqrt{3}}{2}\), tenemos, después de la habitual fracción de gimnasia,\(c = \frac{14 \sqrt{3}}{3}\). En este punto, tenemos dos formas de proceder para encontrar la longitud del lado opuesto al\(30^{\circ}\) ángulo, que vamos a denotar\(b\). Sabemos que la longitud del lado adyacente es\(7\) y la longitud de la hipotenusa es\(\frac{14 \sqrt{3}}{3}\), por lo que podríamos usar el Teorema de Pitágoras para encontrar el lado faltante y resolver\((7)^2 + b^2 = \left( \frac{14 \sqrt{3}}{3} \right)^{2}\) para\(b\). Alternativamente, podríamos usar el Teorema 10.4, es decir, eso\(\sin\left(30^{\circ}\right) = \frac{b}{c}\). Escogiendo este último, nos encontramos\(b = c \sin\left(30^{\circ}\right) = \frac{14 \sqrt{3}}{3} \cdot \frac{1}{2} = \frac{7 \sqrt{3}}{3}\). El triángulo con todos sus datos se registra a continuación.
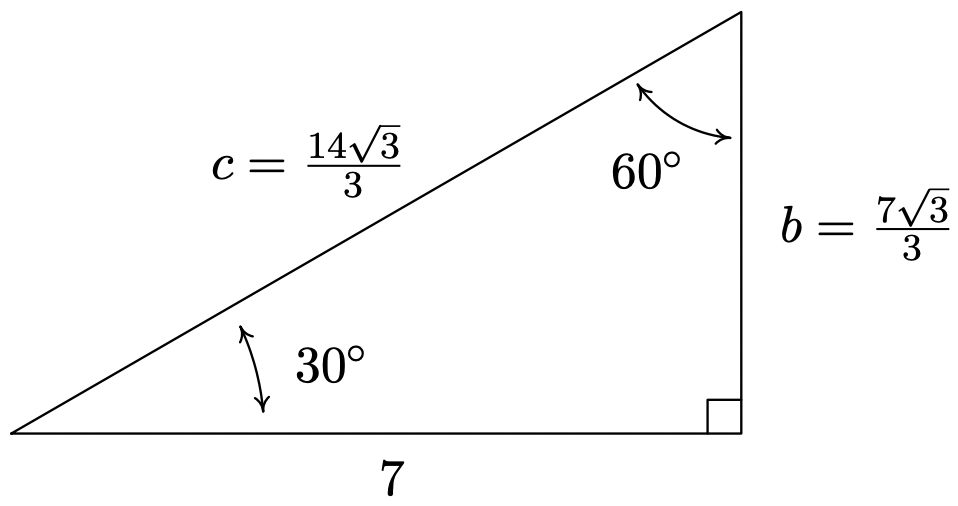
Cerramos esta sección señalando que podemos extender fácilmente las funciones coseno y seno a números reales identificando un número real\(t\) con los\(\theta = t\) radianes angulares. Usando esta identificación, definimos\(\cos(t) = \cos(\theta)\) y\(\sin(t) = \sin(\theta)\). En la práctica, esto significa expresiones como\(\cos(\pi)\) y se\(\sin(2)\) pueden encontrar considerando las entradas como ángulos en la medida de radianes o números reales; la elección es la del lector Si trazamos la identificación de números reales\(t\) con ángulos\(\theta\) en medida de radianes hasta sus raíces en la página 704, podemos deletrear esta correspondencia con mayor precisión. Para cada número real\(t\), asociamos\(t\) unidades de arco orientado en longitud con punto inicial\((1,0)\) y punto final\(P(\cos(t), \sin(t))\).
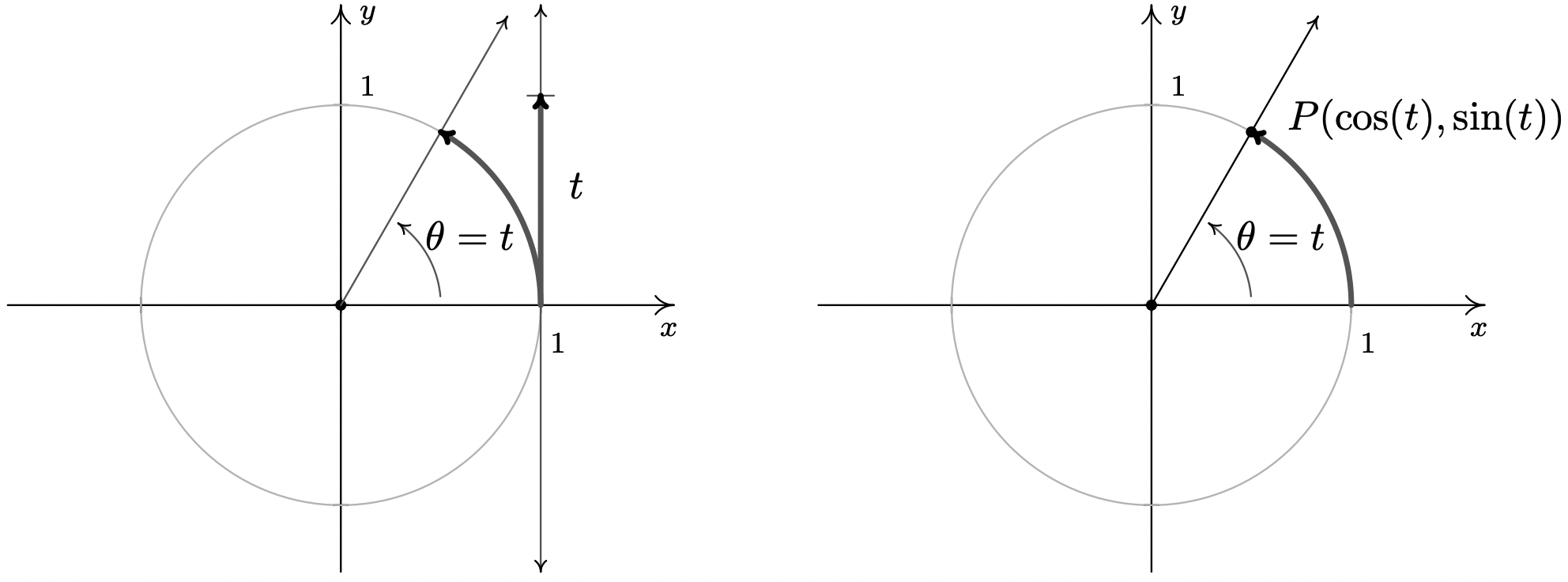
De la misma manera estudiamos las funciones polinomiales, racionales, exponenciales y logarítmicas, estudiaremos las funciones trigonométricas\(f(t) = \cos(t)\) y\(g(t) = \sin(t)\). El primer orden del día es encontrar los dominios y rangos de estas funciones. Ya sea que pensemos en identificar el número real\(t\) con los\(\theta = t\) radianes angulares, o pensemos en envolver un arco orientado alrededor del Círculo de Unidad para encontrar coordenadas en el Círculo de Unidad, debe quedar claro que tanto las funciones coseno como sinusoidal están definidas para todos los números reales\(t\). En otras palabras, el dominio de\(f(t) = \cos(t)\) y de\(g(t) = \sin(t)\) es\((-\infty, \infty)\). Dado que\(\cos(t)\) y\(\sin(t)\) representan\(x\) -y\(y\) -coordenadas, respectivamente, de puntos en el Círculo de Unidad, ambas asumen todos los valores entre\(-1\) an\(1\), inclusive. En otras palabras, el rango de\(f(t) = \cos(t)\) y de\(g(t) = \sin(t)\) es el intervalo\([-1,1]\). Para resumir:
|
|
Supongamos, como en los Ejercicios, se nos pide que resolvamos una ecuación como\(\sin(t) = -\frac{1}{2}\). Como ya hemos mencionado, la distinción entre\(t\) como número real y como ángulo\(\theta = t\) radianes suele ser borrosa. En efecto,\(\sin(t) = -\frac{1}{2}\) resolvemos exactamente de la misma manera 12 que hicimos en el Ejemplo 10.2.5 número 2. Nuestra solución es sólo cosméticamente diferente en que la variable utilizada es más\(t\) bien que\(\theta\):\(t = \frac{7\pi}{6} + 2\pi k\) o\(t = \frac{11\pi}{6} + 2\pi k\) para enteros,\(k\). Estudiaremos las funciones coseno y seno con mayor detalle en la Sección 10.5. Hasta entonces, hay que tener en cuenta que todas las propiedades del coseno y seno desarrolladas en las siguientes secciones que las consideran como funciones de ángulos en la medida de radianes se aplican igualmente bien si las entradas son consideradas como números reales.
10.2.2 Ejercicios
En los Ejercicios 1 - 20, encuentra el valor exacto del coseno y seno del ángulo dado.
- \(\theta = 0\)
- \(\theta = \dfrac{\pi}{4}\)
- \(\theta = \dfrac{\pi}{3}\)
- \(\theta = \dfrac{\pi}{2}\)
- \(\theta = \dfrac{2\pi}{3}\)
- \(\theta = \dfrac{3\pi}{4}\)
- \(\theta = \pi\)
- \(\theta = \dfrac{7\pi}{6}\)
- \(\theta = \dfrac{5\pi}{4}\)
- \(\theta = \dfrac{4\pi}{3}\)
- \(\theta = \dfrac{3\pi}{2}\)
- \(\theta = \dfrac{5\pi}{3}\)
- \(\theta = \dfrac{7\pi}{4}\)
- \(\theta = \dfrac{23\pi}{6}\)
- \(\theta = -\dfrac{13\pi}{2}\)
- \(\theta = -\dfrac{43\pi}{6}\)
- \(\theta = -\dfrac{3\pi}{4}\)
- \(\theta = -\dfrac{\pi}{6}\)
- \(\theta = \dfrac{10\pi}{3}\)
- \(\theta = 117\pi\)
En Ejercicios 21 - 30, utilice los resultados desarrollados a lo largo de la sección para encontrar el valor solicitado.
- Si\(\sin(\theta) = -\dfrac{7}{25}\) con\(\theta\) en el Cuadrante IV, ¿qué es\(\cos(\theta)\)?
- Si\(\cos(\theta) = \dfrac{4}{9}\) con\(\theta\) en el Cuadrante I, ¿qué es\(\sin(\theta)\)?
- Si\(\sin(\theta) = \dfrac{5}{13}\) con\(\theta\) en el Cuadrante II, ¿qué es\(\cos(\theta)\)?
- Si\(\cos(\theta) = -\dfrac{2}{11}\) con\(\theta\) en el Cuadrante III, ¿qué es\(\sin(\theta)\)?
- Si\(\sin(\theta) = -\dfrac{2}{3}\) con\(\theta\) en el Cuadrante III, ¿qué es\(\cos(\theta)\)?
- Si\(\cos(\theta) = \dfrac{28}{53}\) con\(\theta\) en el Cuadrante IV, ¿qué es\(\sin(\theta)\)?
- Si\(\sin(\theta) = \dfrac{2\sqrt{5}}{5}\) y\(\dfrac{\pi}{2} < \theta < \pi\), ¿qué es\(\cos(\theta)\)?
- Si\(\cos(\theta) = \dfrac{\sqrt{10}}{10}\) y\(2\pi < \theta < \dfrac{5\pi}{2}\), ¿qué es\(\sin(\theta)\)?
- Si\(\sin(\theta) = -0.42\) y\(\pi < \theta < \dfrac{3\pi}{2}\), ¿qué es\(\cos(\theta)\)?
- Si\(\cos(\theta) = -0.98\) y\(\dfrac{\pi}{2} < \theta < \pi\), ¿qué es\(\sin(\theta)\)?
En los Ejercicios 31 - 39, encuentra todos los ángulos que satisfacen la ecuación dada.
- \(\sin(\theta) = \dfrac{1}{2}\)
- \(\cos(\theta) = -\dfrac{\sqrt{3}}{2}\)
- \(\sin(\theta) = 0\)
- \(\cos(\theta) = \dfrac{\sqrt{2}}{2}\)
- \(\sin(\theta) = \dfrac{\sqrt{3}}{2}\)
- \(\cos(\theta) = -1\)
- \(\sin(\theta) = -1\)
- \(\cos(\theta) = \dfrac{\sqrt{3}}{2}\)
- \(\cos(\theta) = -1.001\)
En Ejercicios 40 - 48, resuelve la ecuación para\(t\). (Ver los comentarios siguientes Teorema 10.5.)
- \(\cos(t) = 0\)
- \(\sin(t) = -\dfrac{\sqrt{2}}{2}\)
- \(\cos(t) = 3\)
- \(\sin(t) = -\dfrac{1}{2}\)
- \(\cos(t) = \dfrac{1}{2}\)
- \(\sin(t) = -2\)
- \(\cos(t) = 1\)
- \(\sin(t) = 1\)
- \(\cos(t) = -\dfrac{\sqrt{2}}{2}\)
En los Ejercicios 49 - 54, usa tu calculadora para aproximar el valor dado a tres decimales. ¡Asegúrate de que tu calculadora esté en el modo de medición de ángulo adecuado!
- \(\sin(78.95^{\circ})\)
- \(\cos(-2.01)\)
- \(\sin(392.994)\)
- \(\cos(207^{\circ})\)
- \(\sin\left( \pi^{\circ} \right)\)
- \(\cos(e)\)
En Ejercicios 55 - 58, encuentra la medida del ángulo faltante y las longitudes de los lados faltantes. (Ver Ejemplo 10.2.8)
- Encontrar\(\theta\),\(b\), y\(c\).
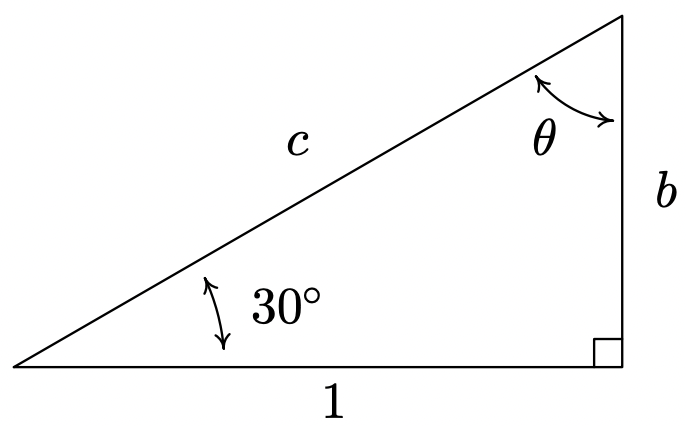
- Encontrar\(\theta\),\(a\), y\(c\).
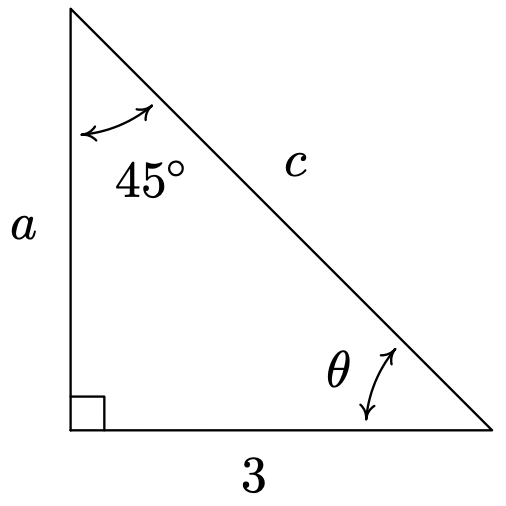
- Encontrar\(\alpha\),\(a\), y\(b\).
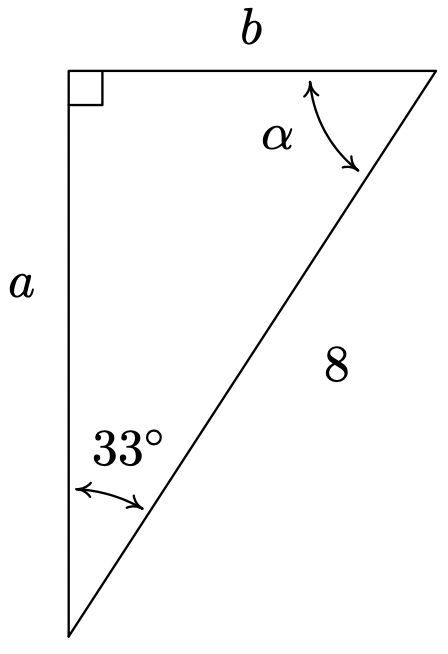
- Encontrar\(\beta\),\(a\), y\(c\).
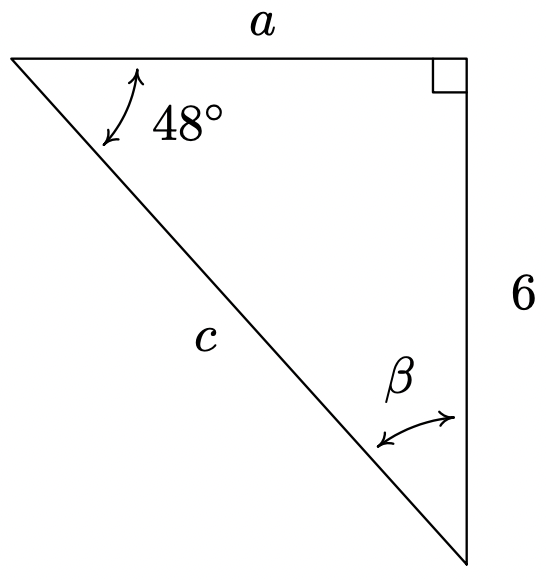
En los Ejercicios 59 - 64, asumir que\(\theta\) es un ángulo agudo en un triángulo rectángulo y utilizar el Teorema 10.4 para encontrar el lado solicitado.
- Si\(\theta = 12^{\circ}\) y el lado adyacente a\(\theta\) tiene longitud 4, ¿cuánto dura la hipotenusa?
- Si\(\theta = 78.123^{\circ}\) y la hipotenusa tiene longitud 5280, ¿a cuánto tiempo está adyacente el lado\(\theta\)?
- Si\(\theta = 59^{\circ}\) y el lado opuesto\(\theta\) tiene longitud 117.42, ¿cuánto dura la hipotenusa?
- Si\(\theta = 5^{\circ}\) y la hipotenusa tiene longitud 10, ¿cuánto tiempo es el lado opuesto\(\theta\)?
- Si\(\theta = 5^{\circ}\) y la hipotenusa tiene longitud 10, ¿cuánto tiempo es adyacente el lado\(\theta\)?
- Si\(\theta = 37.5^{\circ}\) y el lado opuesto\(\theta\) tiene longitud 306, ¿cuánto tiempo es adyacente el lado\(\theta\)?
En los Ejercicios 65 - 68, deja\(\theta\) ser el ángulo en posición estándar cuyo lado terminal contiene el punto dado luego computar\(\cos(\theta)\) y\(\sin(\theta)\).
- \(P(-7, 24)\)
- \(Q(3, 4)\)
- \(R(5, -9)\)
- \(T(-2, -11)\)
En los Ejercicios 69 - 72, encuentra las ecuaciones de movimiento para el escenario dado. Supongamos que el centro del movimiento es el origen, el movimiento es antihorario y eso\(t = 0\) corresponde a una posición a lo largo del\(x\) eje positivo. (Ver Ecuación 10.3 y Ejemplo 10.1.5.)
- Un punto en el borde del yoyo giratorio en el Ejercicio 50 de la Sección 10.1.
Recordar: El diámetro del yoyo es de 2.25 pulgadas y gira a 4500 revoluciones por minuto.
- El yoyo en el Ejercicio 52 de la Sección 10.1.
Recordar: El radio del círculo es de 28 pulgadas y completa una revolución en 3 segundos.
- Un punto en el borde del disco duro en el Ejercicio 53 de la Sección 10.1.
Recordar: El diámetro del disco duro es de 2.5 pulgadas y gira a 7200 revoluciones por minuto.
- Un pasajero en la Rueda Grande en el Ejercicio 55 de la Sección 10.1.
Recordar: El diámetro es de 128 pies y completa 2 revoluciones en 2 minutos, 7 segundos.
- Considera los números:\(0\),\(1\),\(2\),\(3\),\(4\). Toma la raíz cuadrada de cada uno de estos números, luego divide cada uno por\(2\). Los números resultantes deberían parecer asombrosamente familiares. (Ver los valores en la tabla en 722.)
- Dejar\(\alpha\) y\(\beta\) ser los dos ángulos agudos de un triángulo rectángulo. (Así\(\alpha\) y\(\beta\) son ángulos complementarios.) Demuestre eso\(\sin(\alpha) = \cos(\beta)\) y\(\sin(\beta) = \cos(\alpha)\). El hecho de que las cofunciones de los ángulos complementarios sean iguales en este caso no es un accidente y se dará un resultado más general en la Sección 10.4.
- En el escenario de la Ecuación 10.3, asumimos que at\(t=0\), el objeto estaba en el punto\((r,0)\). Si este no es el caso, podemos ajustar las ecuaciones de movimiento introduciendo un 'retardo de tiempo'. Si\(t_{0} > 0\) es la primera vez que el objeto pasa por el punto\((r,0)\), muestra, con la ayuda de tus compañeros de clase, las ecuaciones de movimiento son\(x = r \cos(\omega (t - t_{0}))\) y\(y = r \sin(\omega (t-t_{0}))\).
10.2.3 Respuestas
- \(\cos(0) = 1\),\(\; \sin(0) = 0\)
- \(\cos \left(\dfrac{\pi}{4} \right) = \dfrac{\sqrt{2}}{2}\),\(\; \sin \left(\dfrac{\pi}{4} \right) = \dfrac{\sqrt{2}}{2}\)
- \(\cos \left(\dfrac{\pi}{3}\right) = \dfrac{1}{2}\),\(\; \sin \left(\dfrac{\pi}{3}\right) = \dfrac{\sqrt{3}}{2}\)
- \(\cos \left(\dfrac{\pi}{2}\right) = 0\),\(\; \sin \left(\dfrac{\pi}{2}\right) = 1\)
- \(\cos\left(\dfrac{2\pi}{3}\right) = -\dfrac{1}{2}\),\(\; \sin \left(\dfrac{2\pi}{3}\right) = \dfrac{\sqrt{3}}{2}\)
- \(\cos \left(\dfrac{3\pi}{4} \right) = -\dfrac{\sqrt{2}}{2}\),\(\; \sin \left(\dfrac{3\pi}{4} \right) = \dfrac{\sqrt{2}}{2}\)
- \(\cos(\pi) = -1\),\(\; \sin(\pi) = 0\)
- \(\cos\left(\dfrac{7\pi}{6}\right) = -\dfrac{\sqrt{3}}{2}\),\(\; \sin\left(\dfrac{7\pi}{6}\right) = -\dfrac{1}{2}\)
- \(\cos \left(\dfrac{5\pi}{4} \right) = -\dfrac{\sqrt{2}}{2}\),\(\; \sin \left(\dfrac{5\pi}{4} \right) = -\dfrac{\sqrt{2}}{2}\)
- \(\cos\left(\dfrac{4\pi}{3}\right) = -\dfrac{1}{2}\),\(\; \sin \left(\dfrac{4\pi}{3}\right) = -\dfrac{\sqrt{3}}{2}\)
- \(\cos \left(\dfrac{3\pi}{2}\right) = 0\),\(\; \sin \left(\dfrac{3\pi}{2}\right) = -1\)
- \(\cos\left(\dfrac{5\pi}{3}\right) = \dfrac{1}{2}\),\(\; \sin \left(\dfrac{5\pi}{3}\right) = -\dfrac{\sqrt{3}}{2}\)
- \(\cos \left(\dfrac{7\pi}{4} \right) = \dfrac{\sqrt{2}}{2}\),\(\; \sin \left(\dfrac{7\pi}{4} \right) = -\dfrac{\sqrt{2}}{2}\)
- \(\cos\left(\dfrac{23\pi}{6}\right) = \dfrac{\sqrt{3}}{2}\),\(\; \sin\left(\dfrac{23\pi}{6}\right) = -\dfrac{1}{2}\)
- \(\cos \left(-\dfrac{13\pi}{2}\right) = 0\),\(\; \sin \left(-\dfrac{13\pi}{2}\right) = -1\)
- \(\cos\left(-\dfrac{43\pi}{6}\right) = -\dfrac{\sqrt{3}}{2}\),\(\; \sin\left(-\dfrac{43\pi}{6}\right) = \dfrac{1}{2}\)
- \(\cos \left(-\dfrac{3\pi}{4} \right) = -\dfrac{\sqrt{2}}{2}\),\(\; \sin \left(-\dfrac{3\pi}{4} \right) = -\dfrac{\sqrt{2}}{2}\)
- \(\cos\left(-\dfrac{\pi}{6}\right) = \dfrac{\sqrt{3}}{2}\),\(\; \sin\left(-\dfrac{\pi}{6}\right) = -\dfrac{1}{2}\)
- \(\cos\left(\dfrac{10\pi}{3}\right) = -\dfrac{1}{2}\),\(\; \sin \left(\dfrac{10\pi}{3}\right) = -\dfrac{\sqrt{3}}{2}\)
- \(\cos(117\pi) = -1\),\(\; \sin(117\pi) = 0\)
- Si\(\sin(\theta) = -\dfrac{7}{25}\) con\(\theta\) en el Cuadrante IV, entonces\(\cos(\theta) = \dfrac{24}{25}\).
- Si\(\cos(\theta) = \dfrac{4}{9}\) con\(\theta\) en el Cuadrante I, entonces\(\sin(\theta) = \dfrac{\sqrt{65}}{9}\).
- Si\(\sin(\theta) = \dfrac{5}{13}\) con\(\theta\) en el Cuadrante II, entonces\(\cos(\theta) = -\dfrac{12}{13}\).
- Si\(\cos(\theta) = -\dfrac{2}{11}\) con\(\theta\) en el Cuadrante III, entonces\(\sin(\theta) = -\dfrac{\sqrt{117}}{11}\).
- Si\(\sin(\theta) = -\dfrac{2}{3}\) con\(\theta\) en el Cuadrante III, entonces\(\cos(\theta) = -\dfrac{\sqrt{5}}{3}\).
- Si\(\cos(\theta) = \dfrac{28}{53}\) con\(\theta\) en el Cuadrante IV, entonces\(\sin(\theta) = -\dfrac{45}{53}\).
- Si\(\sin(\theta) = \dfrac{2\sqrt{5}}{5}\) y\(\dfrac{\pi}{2} < \theta < \pi\), entonces\(\cos(\theta) = -\dfrac{\sqrt{5}}{5}\).
- Si\(\cos(\theta) = \dfrac{\sqrt{10}}{10}\) y\(2\pi < \theta < \dfrac{5\pi}{2}\), entonces\(\sin(\theta) = \dfrac{3 \sqrt{10}}{10}\).
- Si\(\sin(\theta) = -0.42\) y\(\pi < \theta < \dfrac{3\pi}{2}\), entonces\(\cos(\theta) = -\sqrt{0.8236} \approx -0.9075\).
- Si\(\cos(\theta) = -0.98\) y\(\dfrac{\pi}{2} < \theta < \pi\), entonces\(\sin(\theta) = \sqrt{0.0396} \approx 0.1990\).
- \(\sin(\theta) = \dfrac{1}{2}\)cuando\(\theta = \dfrac{\pi}{6} + 2\pi k\) o\(\theta = \dfrac{5\pi}{6} + 2\pi k\) para cualquier entero\(k\).
- \(\cos(\theta) = -\dfrac{\sqrt{3}}{2}\)cuando\(\theta = \dfrac{5\pi}{6} + 2\pi k\) o\(\theta = \dfrac{7\pi}{6} + 2\pi k\) para cualquier entero\(k\).
- \(\sin(\theta) = 0\)cuando\(\theta = \pi k\) para cualquier entero\(k\).
- \(\cos(\theta) = \dfrac{\sqrt{2}}{2}\)cuando\(\theta = \dfrac{\pi}{4} + 2\pi k\) o\(\theta = \dfrac{7\pi}{4} + 2\pi k\) para cualquier entero\(k\).
- \(\sin(\theta) = \dfrac{\sqrt{3}}{2}\)cuando\(\theta = \dfrac{\pi}{3} + 2\pi k\) o\(\theta = \dfrac{2\pi}{3} + 2\pi k\) para cualquier entero\(k\).
- \(\cos(\theta) = -1\)cuando\(\theta = (2k + 1)\pi\) para cualquier entero\(k\).
- \(\sin(\theta) = -1\)cuando\(\theta = \dfrac{3\pi}{2} + 2\pi k\) para cualquier entero\(k\).
- \(\cos(\theta) = \dfrac{\sqrt{3}}{2}\)cuando\(\theta = \dfrac{\pi}{6} + 2\pi k\) o\(\theta = \dfrac{11\pi}{6} + 2\pi k\) para cualquier entero\(k\).
- \(\cos(\theta) = -1.001\)nunca pasa
- \(\cos(t) = 0\)cuando\(t = \dfrac{\pi}{2} + \pi k\) para cualquier entero\(k\).
- \(\sin(t) = -\dfrac{\sqrt{2}}{2}\)cuando\(t = \dfrac{5\pi}{4} + 2\pi k\) o\(t = \dfrac{7\pi}{4} + 2\pi k\) para cualquier entero\(k\).
- \(\cos(t) = 3\)nunca pasa.
- \(\sin(t) = -\dfrac{1}{2}\)cuando\(t = \dfrac{7\pi}{6} + 2\pi k\) o\(t = \dfrac{11\pi}{6} + 2\pi k\) para cualquier entero\(k\).
- \(\cos(t) = \dfrac{1}{2}\)cuando\(t = \dfrac{\pi}{3} + 2\pi k\) o\(t = \dfrac{5\pi}{3} + 2\pi k\) para cualquier entero\(k\).
- \(\sin(t) = -2\)nunca pasa
- \(\cos(t) = 1\)cuando\(t = 2\pi k\) para cualquier entero\(k\).
- \(\sin(t) = 1\)cuando\(t = \dfrac{\pi}{2} + 2\pi k\) para cualquier entero\(k\).
- \(\cos(t) = -\dfrac{\sqrt{2}}{2}\)cuando\(t = \dfrac{3\pi}{4} + 2\pi k\) o\(t = \dfrac{5\pi}{4} + 2\pi k\) para cualquier entero\(k\).
- \(\sin(78.95^{\circ}) \approx 0.981\)
- \(\cos(-2.01) \approx -0.425\)
- \(\sin(392.994) \approx -0.291\)
- \(\cos(207^{\circ}) \approx -0.891\)
- \(\sin\left( \pi^{\circ} \right) \approx 0.055\)
- \(\cos(e) \approx -0.912\)
- \(\theta = 60^{\circ}\),\(b = \dfrac{ \sqrt{3}}{3}\),\(c=\dfrac{2 \sqrt{3}}{3}\)
- \(\theta = 45^{\circ}\),\(a = 3\),\(c = 3\sqrt{2}\)
- \(\alpha = 57^{\circ}\),\(a = 8 \cos(33^{\circ}) \approx 6.709\),\(b = 8 \sin(33^{\circ}) \approx 4.357\)
- \(\beta = 42^{\circ}\),\(c = \dfrac{6}{\sin(48^{\circ})} \approx 8.074\),\(a = \sqrt{c^2 - 6^2} \approx 5.402\)
- La hipotenusa tiene longitud\(\dfrac{4}{\cos(12^{\circ})}\approx 4.089\).
- El lado adyacente a\(\theta\) tiene longitud\(5280\cos(78.123^{\circ}) \approx 1086.68\).
- La hipotenusa tiene longitud\(\dfrac{117.42}{\sin(59^{\circ})}\approx 136.99\).
- El lado opuesto\(\theta\) tiene longitud\(10\sin(5^{\circ}) \approx 0.872\).
- El lado adyacente a\(\theta\) tiene longitud\(10\cos(5^{\circ}) \approx 9.962\).
- La hipotenusa tiene longitud\(c = \dfrac{306}{\sin(37.5^{\circ})}\approx 502.660\), por lo que el lado adyacente a\(\theta\) tiene longitud\(\sqrt{c^2 - 306^{2}} \approx 398.797\).
- \(\cos(\theta) = -\dfrac{7}{25}, \; \sin(\theta) = \dfrac{24}{25}\)
- \(\cos(\theta) = \dfrac{3}{5}, \; \sin(\theta) = \dfrac{4}{5}\)
- \(\cos(\theta) = \dfrac{5\sqrt{106}}{106}, \; \sin(\theta) = -\dfrac{9\sqrt{106}}{106}\)
- \(\cos(\theta) = -\dfrac{2\sqrt{5}}{25}, \; \sin(\theta) = -\dfrac{11\sqrt{5}}{25}\)
- \(r = 1.125\)pulgadas,\(\omega = 9000 \pi \, \frac{\text{radians}}{\text{minute}}\),\(x = 1.125 \cos(9000 \pi \, t)\),\(y = 1.125 \sin(9000 \pi \, t)\). Aquí\(x\) y\(y\) se miden en pulgadas y\(t\) se mide en minutos.
- \(r = 28\)pulgadas,\(\omega = \frac{2\pi}{3} \, \frac{\text{radians}}{\text{second}}\),\(x = 28 \cos\left(\frac{2\pi}{3} \, t \right)\),\(y = 28 \sin\left(\frac{2\pi}{3} \, t \right)\). Aquí\(x\) y\(y\) se miden en pulgadas y\(t\) se miden en segundos.
- \(r = 1.25\)pulgadas,\(\omega = 14400 \pi \, \frac{\text{radians}}{\text{minute}}\),\(x = 1.25 \cos(14400 \pi \, t)\),\(y = 1.25 \sin(14400 \pi \, t)\). Aquí\(x\) y\(y\) se miden en pulgadas y\(t\) se mide en minutos.
- \(r = 64\)pies,\(\omega = \frac{4\pi}{127} \, \frac{\text{radians}}{\text{second}}\),\(x = 64 \cos\left(\frac{4\pi}{127} \, t \right)\),\(y = 64 \sin\left(\frac{4\pi}{127} \, t \right)\). Aquí\(x\) y\(y\) se miden en pies y\(t\) se miden en segundos
Referencia
1 La etimología del nombre 'seno' es bastante colorida, y se invita al lector interesado a investigarlo; la 'co' en 'coseno' se explica en la Sección 10.4.
2 ¿Se puede mostrar esto?
3 Otra vez, ¿puedes mostrar esto?
4 Esto es lamentable desde una perspectiva de 'notación de función'. Ver Sección 10.6.
5 Consulte las Secciones 1.1 y 7.2 para más detalles.
6 ¡Por una vez, tenemos algo conveniente en usar la medida de radianes en contraste con las tonterías teóricas abstractas sobre usarlas como una forma 'natural' de hacer coincidir ángulos orientados con números reales!
7 Ya que\(\pi+\alpha=\alpha+\pi\), se\(\theta\) puede trazar invirtiendo el orden de rotaciones dado aquí. Deberías hacer esto.
8 Estudiaremos las ecuaciones trigonométricas de manera más formal en la Sección 10.7. ¡Disfruta de estos ejercicios relativamente sencillos mientras duren!
9 Recordemos en la Sección 10.1, dos ángulos en la medida de radianes son coterminales si y solo si difieren en un múltiplo entero de\(2 \pi\). Por lo tanto, para describir todos los ángulos coterminales con un ángulo dado, agregamos\(2 \pi k\) para enteros\(k=0, \pm 1, \pm 2, \ldots\)
10 ¿Recuerdas por qué?
11 Es posible que hayas estado expuesto a esto en la Preparatoria.
12 Bueno, para ser pedantes, técnicamente estaríamos usando 'números de referencia' o 'arcos de referencia' en lugar de 'ángulos de referencia' —pero la idea es la misma.


