10.7: Ecuaciones trigonométricas y desigualdades

En las Secciones 10.2, 10.3 y más recientemente 10.6, resolvimos algunas ecuaciones básicas que involucran las funciones trigonométricas. A continuación resumimos las técnicas que hemos empleado hasta ahora. Tenga en cuenta que usamos la letra neutra\(u\) '' como argumento ¹ de cada función circular para la generalidad.

Estrategias para resolver ecuaciones básicas que involucran funciones trigonométricas

• Para resolver\(\cos(u) = c\) o\(\sin(u) = c\) para\(-1 \leq c \leq 1\), primero resolver para\(u\) en el intervalo\([0,2\pi)\) y agregar múltiplos enteros del periodo\(2\pi\). Si\(c < -1\) o de\(c > 1\), no hay soluciones reales.
• Para resolver\(\sec(u) = c\) o\(\csc(u) = c\) para\(c \leq -1\) o\(c \geq 1\), convertir a coseno o seno, respectivamente, y resolver como arriba. Si\(-1 < c < 1\), no hay soluciones reales.
• Para resolver\(\tan(u) = c\) para cualquier número real\(c\), primero resuelva para\(u\) en el intervalo\(\left(-\frac{\pi}{2}, \frac{\pi}{2}\right)\) y agregue múltiplos enteros del período\(\pi\).
• Para resolver\(\cot(u) = c\) para\(c \neq 0\), convertir a tangente y resolver como arriba. Si\(c = 0\), la solución a\(\cot(u) = 0\) es\(u = \frac{\pi}{2} + \pi k\) para enteros\(k\).

Usando las pautas anteriores, podemos resolver cómodamente\(\sin(x) = \frac{1}{2}\) y encontrar la solución\(x = \frac{\pi}{6} + 2\pi k\) o\(x = \frac{5\pi}{6} + 2\pi k\) para enteros\(k\). ¿Cómo resolvemos algo así como\(\sin(3x) = \frac{1}{2}\)? Dado que esta ecuación tiene la forma\(\sin(u) = \frac{1}{2}\), sabemos que las soluciones toman la forma\(u= \frac{\pi}{6} + 2\pi k\) o\(u = \frac{5\pi}{6} + 2\pi k\) para enteros\(k\). Ya que el argumento de seno aquí es\(3x\), tenemos\(3x= \frac{\pi}{6} + 2\pi k\) o\(3x = \frac{5\pi}{6} + 2\pi k\) para enteros\(k\). Para resolver para\(x\), dividimos ambos lados ² de estas ecuaciones por\(3\), y obtenemos\(x = \frac{\pi}{18} + \frac{2\pi}{3} k\) o\(x = \frac{5\pi}{18} + \frac{2\pi}{3}k\) para enteros\(k\). Esta es la técnica empleada en el siguiente ejemplo.

Ejemplo 10.7.1

Resuelve las siguientes ecuaciones y revisa tus respuestas analíticamente. Enumere las soluciones que se encuentran en el intervalo\([0,2\pi)\) y verifíquelas usando una utilidad gráfica.

1. \(\cos(2x) = -\frac{\sqrt{3}}{2}\)
2. \(\csc\left(\frac{1}{3}x-\pi \right) = \sqrt{2}\)
3. \(\cot\left(3x \right) = 0\)
4. \(\sec^{2}(x) = 4\)
5. \(\tan\left(\frac{x}{2}\right) = -3\)
6. \(\sin(2x) = 0.87\)

Solución

1. Las soluciones a\(\cos(u) =-\frac{\sqrt{3}}{2}\) son\(u = \frac{5\pi}{6} + 2\pi k\) o\(u = \frac{7\pi}{6} + 2\pi k\) para enteros\(k\). Ya que el argumento del coseno aquí es\(2x\), esto significa\(2x = \frac{5\pi}{6} + 2\pi k\) o\(2x = \frac{7\pi}{6} + 2\pi k\) para enteros\(k\). Resolviendo para\(x\) da\(x = \frac{5\pi}{12} + \pi k\) o\(x = \frac{7\pi}{12} + \pi k\) para enteros\(k\). Para verificar estas respuestas analíticamente, las sustituimos en la ecuación original. Para cualquier entero\(k\) tenemos

   \[\begin{array}{rclr} \cos\left( 2\left[\frac{5\pi}{12} + \pi k\right]\right) & = & \cos\left(\frac{5\pi}{6} + 2\pi k\right) & \\[4pt] & = & \cos\left(\frac{5\pi}{6}\right) & \text{(the period of cosine is $2\pi$)} \\[4pt] & = & -\frac{\sqrt{3}}{2} & \\ \end{array}\nonumber\]

   De igual manera, encontramos\(\cos\left( 2\left[\frac{7\pi}{12} + \pi k\right]\right) = \cos\left(\frac{7\pi}{6} + 2\pi k\right) = \cos\left(\frac{7\pi}{6}\right) = -\frac{\sqrt{3}}{2}\). Para determinar en cuál de nuestras soluciones se encuentran\([0,2\pi)\), sustituimos los valores enteros por\(k\). Las soluciones que mantenemos provienen de los valores de\(k = 0\) y\(k =1\) y son\(x = \frac{5\pi}{12}\),\(\frac{7\pi}{12}\),\(\frac{17\pi}{12}\) y\(\frac{19\pi}{12}\). Usando una calculadora, hacemos una gráfica\(y = \cos(2x)\) y\(y = -\frac{\sqrt{3}}{2}\) otra vez\([0,2\pi)\) y examinamos dónde se cruzan estas dos gráficas. Vemos que las\(x\) coordenadas de los puntos de intersección corresponden a las representaciones decimales de nuestras respuestas exactas.

2. Como esta ecuación tiene la forma\(\csc(u) = \sqrt{2}\), reescribimos esto como\(\sin(u) = \frac{\sqrt{2}}{2}\) y find\(u = \frac{\pi}{4} + 2\pi k\) o\(u = \frac{3\pi}{4} + 2\pi k\) para enteros\(k\). Como el argumento de cosecante aquí es\(\left(\frac{1}{3}x-\pi \right)\),

   \[\frac{1}{3}x-\pi = \frac{\pi}{4} + 2\pi k \quad \text{or} \quad \frac{1}{3}x-\pi = \frac{3\pi}{4} + 2\pi k\nonumber\]

   Para resolver\(\frac{1}{3}x-\pi = \frac{\pi}{4} + 2\pi k\), primero agregamos\(\pi\) a ambos lados

   \[\frac{1}{3} x = \frac{\pi}{4} + 2\pi k + \pi\nonumber\]

   Un error común es tratar los términos\(2\pi k\) '' y\(\pi\) '' como términos “similares” e intentar combinarlos cuando no lo son. ³ Podemos, sin embargo, combinar los términos\(\pi\) '' y\(\frac{\pi}{4}\) '' para obtener

   \[\frac{1}{3} x = \frac{5\pi}{4} + 2\pi k\nonumber\]

   Ahora terminamos multiplicando ambos lados por\(3\) para conseguir

   \[x = 3 \left( \frac{5\pi}{4} + 2\pi k \right) = \frac{15 \pi}{4} + 6\pi k\nonumber\]

   Resolviendo la otra ecuación,\(\frac{1}{3}x-\pi = \frac{3\pi}{4} + 2\pi k\) produce\(x = \frac{21\pi}{4} + 6 \pi k\) para enteros\(k\). Para verificar la primera familia de respuestas, sustituimos, combinamos términos de línea y simplificamos.

   \[\begin{array}{rclr} \csc\left(\frac{1}{3} \left[ \frac{15\pi}{4} + 6 \pi k \right] - \pi \right) & = & \csc\left(\frac{5\pi}{4} + 2\pi k - \pi \right) & \\[4pt] & = & \csc\left(\frac{\pi}{4} + 2\pi k\right) & \\[4pt] & = & \csc\left(\frac{\pi}{4}\right) & \text{(the period of cosecant is $2\pi$)} \\ & = & \sqrt{2} & \\ \end{array}\nonumber\]

   La familia\(x= \frac{21\pi}{4} + 6 \pi k\) revisa de manera similar. A pesar de tener infinitamente muchas soluciones, encontramos que ninguna de ellas se encuentra en\([0,2\pi)\). Para verificar esto gráficamente, utilizamos una identidad recíproca para reescribir el cosecante como seno y lo encontramos\(y = \frac{1}{\sin\left(\frac{1}{3}x-\pi\right)}\) y\(y =\sqrt{2}\) no se cruzan en absoluto a lo largo del intervalo\([0,2\pi)\).

   
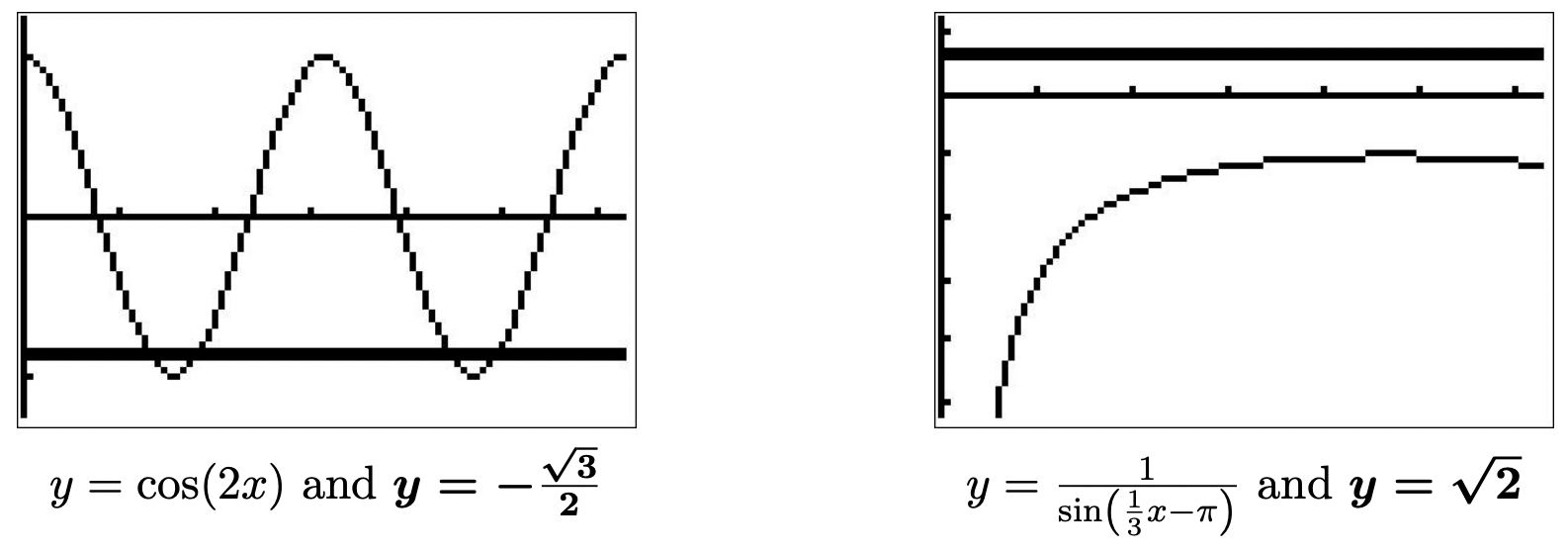
3. Ya que\(\cot(3x) = 0\) tiene la forma\(\cot(u) = 0\), sabemos\(u = \frac{\pi}{2} + \pi k\), entonces, en este caso,\(3x = \frac{\pi}{2} + \pi k\) para enteros\(k\). Resolviendo para\(x\) rendimientos\(x = \frac{\pi}{6} + \frac{\pi}{3} k\). Verificando nuestras respuestas, obtenemos

   \[\begin{array}{rclr} \cot\left(3\left[ \frac{\pi}{6} + \frac{\pi}{3} k\right]\right) & = & \cot\left(\frac{\pi}{2} + \pi k\right) & \\[4pt] & = & \cot\left(\frac{\pi}{2}\right) & \text{(the period of cotangent is $\pi$)} \\[4pt] & = & 0 & \\ \end{array}\nonumber\]

   Como\(k\) corre a través de los enteros, obtenemos seis respuestas, correspondientes a\(k=0\) through\(k=5\), que se encuentran en\([0, 2\pi)\):\(x = \frac{\pi}{6}\),\(\frac{\pi}{2}\),\(\frac{5\pi}{6}\),\(\frac{7\pi}{6}\),\(\frac{3\pi}{2}\) y\(\frac{11\pi}{6}\). Para confirmarlos gráficamente, hay que tener cuidado. En muchas calculadoras, no hay botón de función para cotangente. Elegimos ⁴ para usar la identidad del cociente\(\cot(3x) = \frac{\cos(3x)}{\sin(3x)}\). Graficando\(y = \frac{\cos(3x)}{\sin(3x)}\) y\(y = 0\) (el\(x\) eje), vemos que las\(x\) coordenadas de los puntos de intersección coinciden aproximadamente con nuestras soluciones.

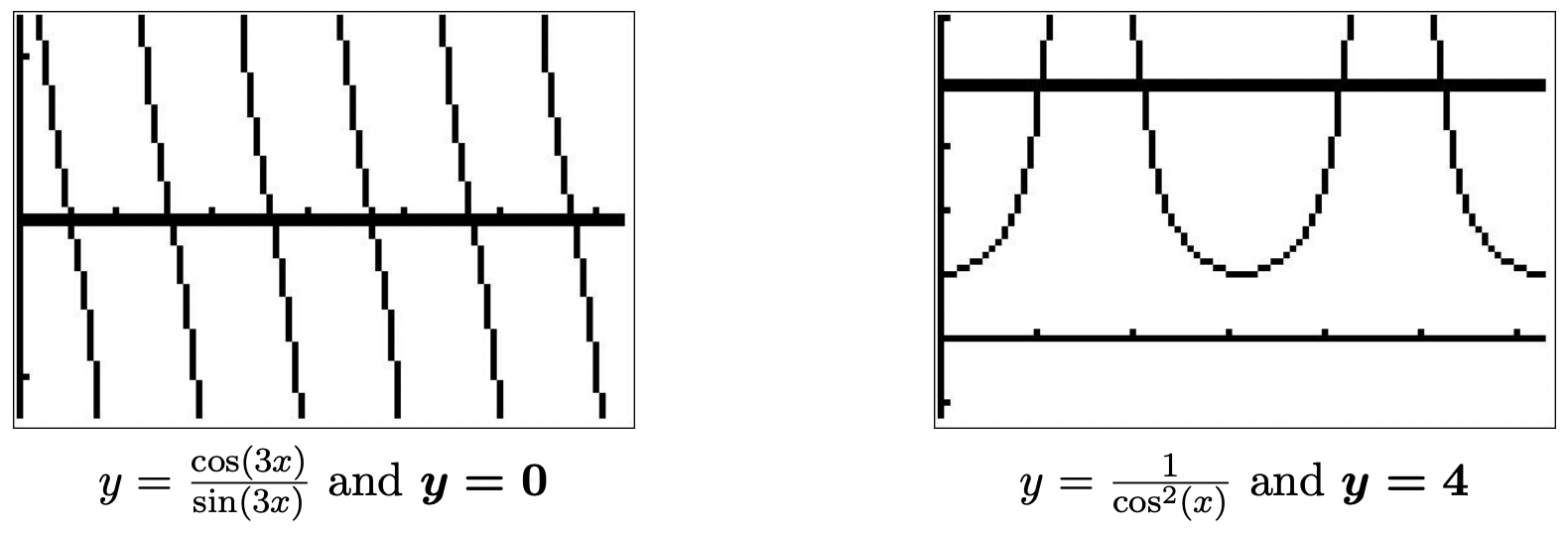
4. La complicación en resolver una ecuación como no\(\sec^{2}(x) = 4\) viene del argumento de secante, que es justo\(x\), sino más bien, el hecho de que la secante esté siendo cuadrada. Para que esta ecuación se vea como una de las formas listadas en la página 857, extraemos raíces cuadradas para obtener\(\sec(x) = \pm 2\). Convertiéndonos a cosenos, tenemos\(\cos(x) = \pm \frac{1}{2}\). Para\(\cos(x) = \frac{1}{2}\), obtenemos\(x = \frac{\pi}{3} + 2\pi k\) o\(x = \frac{5\pi}{3} + 2\pi k\) para enteros\(k\). Para\(\cos(x) = -\frac{1}{2}\), obtenemos\(x = \frac{2\pi}{3} + 2\pi k\) o\(x = \frac{4\pi}{3} + 2\pi k\) para enteros\(k\). Si damos un paso atrás y pensamos en estas familias de soluciones geométricamente, vemos que estamos encontrando las medidas de todos los ángulos con un ángulo de referencia de\(\frac{\pi}{3}\). Como resultado, estas soluciones se pueden combinar y podemos escribir nuestras soluciones como\(x = \frac{\pi}{3} + \pi k\) y\(x = \frac{2\pi}{3} + \pi k\) para enteros\(k\). Para verificar la primera familia de soluciones, observamos que, dependiendo del entero\(k\),\(\sec\left(\frac{\pi}{3} + \pi k\right)\) no siempre es igual\(\sec\left(\frac{\pi}{3}\right)\). No obstante, es cierto que para todos los enteros\(k\),\(\sec\left(\frac{\pi}{3} + \pi k\right) = \pm \sec\left(\frac{\pi}{3}\right) = \pm 2\). (¿Se puede mostrar esto?) Como consecuencia de ello,

   \[\begin{array}{rclr} \sec^{2}\left(\frac{\pi}{3} + \pi k\right) & = & \left( \pm \sec\left(\frac{\pi}{3}\right)\right)^2 & \\[4pt] & = & (\pm 2)^2 & \\[4pt] & = & 4 & \\ \end{array}\nonumber\]

   Lo mismo vale para la familia\(x =\frac{2\pi}{3} + \pi k\). Las soluciones en las que se encuentran\([0,2\pi)\) provienen de los valores\(k = 0\) y\(k=1\), es decir\(x = \frac{\pi}{3}\),\(\frac{2\pi}{3}\),\(\frac{4\pi}{3}\) y\(\frac{5\pi}{3}\). Para confirmar gráficamente, utilizamos una identidad recíproca para reescribir la secante como coseno. Las\(x\) coordenadas de los puntos de intersección de\(y = \frac{1}{(\cos(x))^2}\) y\(y = 4\) verificar nuestras respuestas.

   
5. La ecuación\(\tan\left(\frac{x}{2}\right) = -3\) tiene la forma\(\tan(u) = -3\), cuya solución es\(u = \arctan(-3) + \pi k\). De ahí\(\frac{x}{2} = \arctan(-3) + \pi k\),, así\(x = 2\arctan(-3) + 2\pi k\) para los enteros\(k\). Para verificar, notamos

   \[\begin{array}{rclr} \tan\left(\frac{2\arctan(-3) + 2\pi k}{2}\right) & = & \tan\left( \arctan(-3) + \pi k \right) & \\[4pt] & = & \tan\left(\arctan(-3) \right) & \text{(the period of tangent is $\pi$)} \\[4pt] & = & -3 & (\text{See Theorem 10.27}) \\ \end{array}\nonumber\]

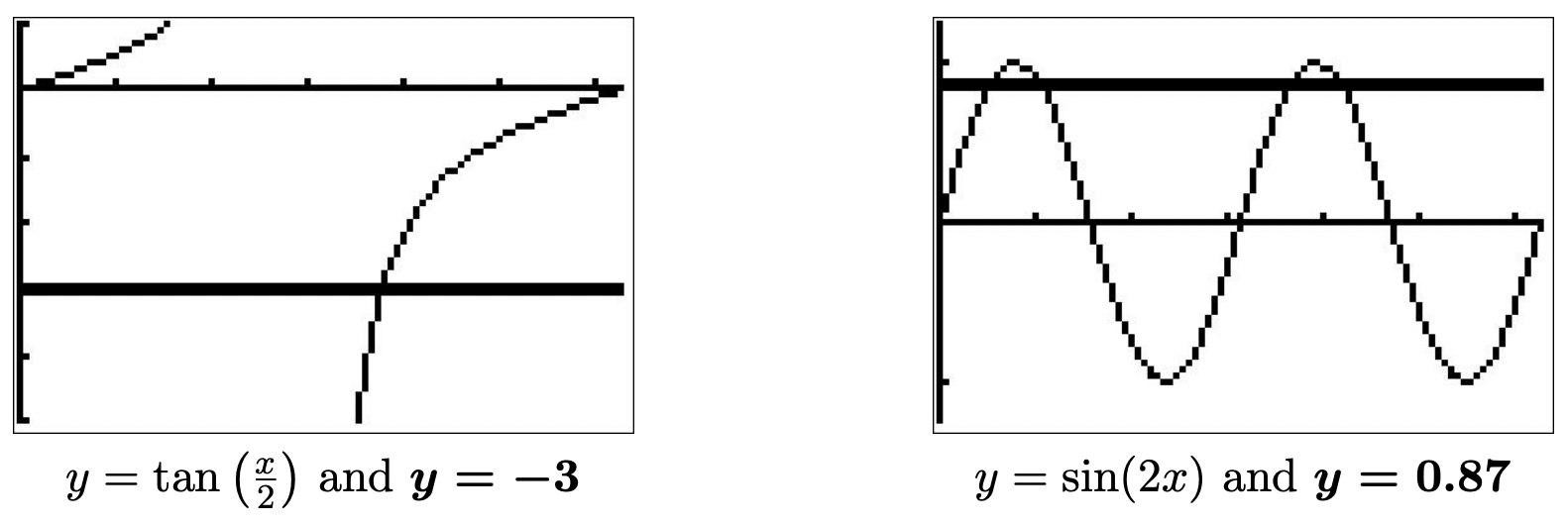
   Para determinar cuál de nuestras respuestas se encuentra en el intervalo\([0,2\pi)\), primero necesitamos hacernos una idea del valor de\(2\arctan(-3)\). Si bien podríamos encontrar fácilmente una aproximación usando una calculadora, ⁵ procedemos analíticamente. Ya que\(-3 < 0\), se deduce que\(-\frac{\pi}{2} < \arctan(-3) < 0\). Multiplicando por\(2\) da\(-\pi < 2\arctan(-3) < 0\). Ahora estamos en condiciones de argumentar cuál de las soluciones\(x = 2\arctan(-3) + 2\pi k\) se encuentra\([0,2\pi)\). Porque\(k = 0\), obtenemos\(x = 2\arctan(-3) < 0\), así descartamos esta respuesta y todas las respuestas\(x = 2\arctan(-3) + 2\pi k\) donde\(k < 0\). A continuación, volvemos nuestra atención\(k = 1\) y conseguimos\(x = 2\arctan(-3) + 2\pi\). Empezando por la desigualdad\(-\pi < 2\arctan(-3) < 0\), sumamos\(2\pi\) y obtenemos\(\pi < 2\arctan(-3) +2\pi < 2\pi\). Esto significa que\(x = 2\arctan(-3) + 2\pi\) se encuentra en\([0,2\pi)\). Avanzando\(k\) a\(2\) produce\(x = 2\arctan(-3) + 4\pi\). Una vez más, nos sale de\(-\pi < 2\arctan(-3) < 0\) eso\(3\pi < 2\arctan(-3) + 4\pi < 4\pi\). Ya que esto está fuera del intervalo\([0,2\pi)\), descartamos\(x = 2\arctan(-3) + 4\pi\) y todas las soluciones de la forma\(x = 2\arctan(-3) + 2\pi k\) para\(k > 2\). Gráficamente, vemos\(y = \tan\left(\frac{x}{2}\right)\) e\(y = -3\) intersectamos solo una vez\([0,2\pi)\) a las\(x = 2\arctan(-3) + 2\pi\approx 3.7851\).

6. Para resolver\(\sin(2x) = 0.87\), primero señalamos que tiene la forma\(\sin(u) = 0.87\), que tiene la familia de soluciones\(u = \arcsin(0.87) + 2\pi k\) o\(u =\pi - \arcsin(0.87) + 2\pi k\) para enteros\(k\). Ya que el argumento de seno aquí es\(2x\), obtenemos\(2x = \arcsin(0.87) + 2\pi k\) o\(2x =\pi - \arcsin(0.87) + 2\pi k\) que da\(x = \frac{1}{2} \arcsin(0.87) + \pi k\) o\(x =\frac{\pi}{2} - \frac{1}{2}\arcsin(0.87) + \pi k\) para enteros\(k\). Para verificar,

   \[\begin{array}{rclr} \sin\left(2\left[\frac{1}{2} \arcsin(0.87) + \pi k\right]\right) & = & \sin\left(\arcsin(0.87) + 2\pi k\right) & \\[4pt] & = & \sin\left(\arcsin(0.87)\right) & \text{(the period of sine is $2\pi$)} \\[4pt] & = & 0.87& (\text{See Theorem 10.26})\\ \end{array}\nonumber\]

   Para la familia\(x =\frac{\pi}{2} - \frac{1}{2}\arcsin(0.87) + \pi k\), obtenemos

   \[\begin{array}{rclr} \sin\left(2\left[\frac{\pi}{2} - \frac{1}{2} \arcsin(0.87) + \pi k\right]\right) & = & \sin\left(\pi - \arcsin(0.87) + 2\pi k\right) & \\[4pt] & = & \sin\left(\pi - \arcsin(0.87)\right) & \text{(the period of sine is $2\pi$)} \\[4pt] & = & \sin\left(\arcsin(0.87)\right) & \text{($\sin(\pi - t) = \sin(t)$)} \\[4pt] & = & 0.87& (\text{See Theorem 10.26}) \\ \end{array}\nonumber\]

   Para determinar en cuál de estas soluciones se encuentran\([0,2\pi)\), primero necesitamos hacernos una idea del valor de\(x=\frac{1}{2} \arcsin(0.87)\). Una vez más, podríamos usar la calculadora, pero aquí adoptamos una ruta analítica. Por definición,\(0 < \arcsin(0.87) < \frac{\pi}{2}\) para que multiplicar a través de por nos\(\frac{1}{2}\) da\(0 < \frac{1}{2} \arcsin(0.87) < \frac{\pi}{4}\). Comenzando con la familia de soluciones\(x = \frac{1}{2} \arcsin(0.87) + \pi k\), utilizamos el mismo tipo de argumentos que en nuestra solución al número 5 anterior y solo encontramos las soluciones correspondientes\(k =0\) y se\(k=1\) encuentran en\([0,2\pi)\):\(x = \frac{1}{2} \arcsin(0.87)\) y\(x = \frac{1}{2} \arcsin(0.87) + \pi\). A continuación, pasamos a la familia\(x =\frac{\pi}{2} - \frac{1}{2}\arcsin(0.87) + \pi k\) para los enteros\(k\). Aquí, necesitamos obtener una mejor estimación de\(\frac{\pi}{2} - \frac{1}{2} \arcsin(0.87)\). A partir de la desigualdad\(0 < \frac{1}{2}\arcsin(0.87) < \frac{\pi}{4}\), primero multiplicamos por\(-1\) y luego agregamos\(\frac{\pi}{2}\) para obtener\(\frac{\pi}{2} > \frac{\pi}{2} -\frac{1}{2} \arcsin(0.87) > \frac{\pi}{4}\), o\(\frac{\pi}{4} < \frac{\pi}{2} -\frac{1}{2} \arcsin(0.87) < \frac{\pi}{2}\). Procediendo con los argumentos habituales, encontramos las únicas soluciones que se encuentran en\([0,2\pi)\) corresponden a\(k = 0\) y\(k=1\), es decir,\(x =\frac{\pi}{2} - \frac{1}{2}\arcsin(0.87)\) y\(x = \frac{3\pi}{2} - \frac{1}{2}\arcsin(0.87)\). Todo dicho, hemos encontrado cuatro soluciones para\(\sin(2x) = 0.87\) en\([0,2\pi)\):\(x =\frac{1}{2} \arcsin(0.87)\),\(x=\frac{1}{2} \arcsin(0.87) + \pi\),\(x =\frac{\pi}{2} - \frac{1}{2}\arcsin(0.87)\) y\(x = \frac{3\pi}{2} - \frac{1}{2}\arcsin(0.87)\). Al graficar\(y = \sin(2x)\) y\(y = 0.87\), confirmamos nuestros resultados.

   

Cada uno de los problemas del Ejemplo 10.7.1 presentaba una función trigonométrica. Si una ecuación involucra dos funciones trigonométricas diferentes o si la ecuación contiene la misma función trigonométrica pero con argumentos diferentes, necesitaremos usar identidades y Álgebra para reducir la ecuación a la misma forma que las dadas en la página 857.

Ejemplo 10.7.2

Resuelva las siguientes ecuaciones y enumere las soluciones que se encuentran en el intervalo\([0,2\pi)\). Verifica tus soluciones\([0,2\pi)\) gráficamente.

1. \(3\sin^{3}(x) = \sin^{2}(x)\)
2. \(\sec^{2}(x) = \tan(x) + 3\)
3. \(\cos(2x) = 3\cos(x) - 2\)
4. \(\cos(3x) = 2- \cos(x)\)
5. \(\cos(3x) = \cos(5x)\)
6. \(\sin(2x) =\sqrt{3} \cos(x)\)
7. \(\sin(x)\cos\left(\frac{x}{2}\right) + \cos(x)\sin\left(\frac{x}{2}\right) = 1\)
8. \(\cos(x) - \sqrt{3} \sin(x) = 2\)

Solución.

1. Resistimos la tentación de dividir ambos lados de\(3\sin^{3}(x) = \sin^{2}(x)\) por\(\sin^{2}(x)\) (¿Qué sale mal si lo haces?) y en su lugar reunir todos los términos a un lado de la ecuación y factor.

   \[\begin{array}{rclr} 3\sin^{3}(x) & = & \sin^{2}(x) & \\ 3\sin^{3}(x) - \sin^{2}(x) & = & 0 & \\ \sin^{2}(x) (3 \sin(x) - 1) & = & 0 & \text{Factor out $\sin^{2}(x)$ from both terms.} \\ \end{array}\nonumber\]

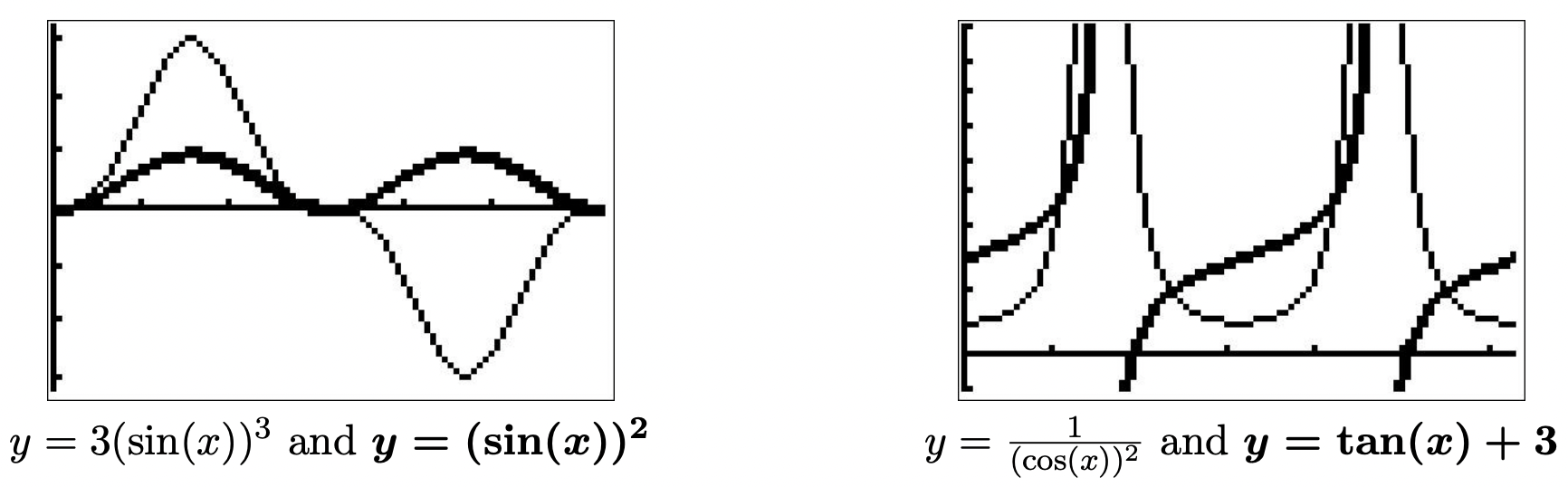
   Obtenemos\(\sin^{2}(x) = 0\) o\(3\sin(x) - 1 = 0\). Resolviendo para\(\sin(x)\), encontramos\(\sin(x) = 0\) o\(\sin(x) = \frac{1}{3}\). La solución a la primera ecuación es\(x = \pi k\), con\(x = 0\) y\(x = \pi\) siendo las dos soluciones en las que se encuentran\([0,2\pi)\). Para resolver\(\sin(x) = \frac{1}{3}\), usamos la función arcsine para obtener\(x = \arcsin\left(\frac{1}{3}\right) + 2\pi k\) o\(x = \pi - \arcsin\left(\frac{1}{3}\right) + 2\pi k\) para enteros\(k\). Aquí encontramos las dos soluciones que se encuentran en\([0,2\pi)\) ser\(x = \arcsin\left(\frac{1}{3}\right)\) y\(x = \pi - \arcsin\left(\frac{1}{3}\right)\). Para verificar gráficamente, trazamos\(y = 3(\sin(x))^3\)\(y = (\sin(x))^2\) y encontramos las\(x\) coordenadas -de los puntos de intersección de estas dos curvas. Se requiere algo de zoom adicional cerca\(x=0\) y\(x=\pi\) para verificar que estas dos curvas de hecho se cruzan cuatro veces. ⁶

2. El análisis de\(\sec^{2}(x) = \tan(x) + 3\) revela dos funciones trigonométricas diferentes, por lo que una identidad está en orden. Ya que\(\sec^{2}(x) = 1 + \tan^{2}(x)\), obtenemos

   \[\begin{array}{rclr} \sec^{2}(x) & = & \tan(x) + 3 & \\ 1 + \tan^{2}(x) & = & \tan(x) + 3& \text{(Since $\sec^{2}(x) = 1 + \tan^{2}(x)$.)} \\ \tan^{2}(x) - \tan(x) -2 & = & 0 & \\ u^2 - u - 2 & = & 0 & \text{Let $u = \tan(x)$.} \\ (u + 1)(u - 2) & = & 0 & \\ \end{array}\nonumber\]

   Esto da\(u = -1\) o\(u = 2\). Ya que\(u = \tan(x)\), tenemos\(\tan(x) = -1\) o\(\tan(x) = 2\). De\(\tan(x) = -1\), obtenemos\(x = -\frac{\pi}{4} + \pi k\) para enteros\(k\). Para resolver\(\tan(x) = 2\), empleamos la función arcotangente y obtenemos\(x = \arctan(2) + \pi k\) para enteros\(k\). Desde el primer conjunto de soluciones, obtenemos\(x = \frac{3\pi}{4}\) y\(x = \frac{5\pi}{4}\) como nuestras respuestas que se encuentran en\([0,2\pi)\). Usando el mismo tipo de argumento que vimos en el Ejemplo 10.7.1, obtenemos\(x=\arctan(2)\) y\(x = \pi + \arctan(2)\) como respuestas de nuestro segundo conjunto de soluciones en las que se encuentran\([0,2\pi)\). Usando una identidad recíproca, reescribimos la secante como coseno y gráfica\(y = \frac{1}{(\cos(x))^2}\) y\(y = \tan(x) + 3\) para encontrar los\(x\) -valores de los puntos donde se cruzan.

   
3. En la ecuación\(\cos(2x) = 3\cos(x) - 2\), tenemos la misma función circular, es decir, coseno, en ambos lados pero los argumentos difieren. Usando la identidad\(\cos(2x) = 2\cos^{2}(x) - 1\), obtenemos un 'cuadrático disfrazado' y procedemos como lo hemos hecho en el pasado.

   \[\begin{array}{rclr} \cos(2x) & = & 3\cos(x) - 2 & \\ 2\cos^{2}(x) -1 & = & 3\cos(x) -2 & \text{(Since $\cos(2x) = 2\cos^{2}(x) -1$.)} \\ 2\cos^{2}(x) - 3\cos(x) +1 & = & 0 & \\ 2 u^2 - 3 u + 1 & = & 0 & \text{Let $u = \cos(x)$.}\\ (2u - 1)(u - 1) & = & 0 & \\ \end{array}\nonumber\]

   Esto da\(u = \frac{1}{2}\) o\(u = 1\). Ya que\(u = \cos(x)\), obtenemos\(\cos(x) = \frac{1}{2}\) o\(\cos(x) = 1\). Resolviendo\(\cos(x) = \frac{1}{2}\), obtenemos\(x = \frac{\pi}{3} + 2\pi k\) o\(x = \frac{5\pi}{3} + 2\pi k\) para enteros\(k\). De\(\cos(x) = 1\), obtenemos\(x = 2\pi k\) para enteros\(k\). Las respuestas en las que\([0,2\pi)\) se encuentran son\(x =0\),\(\frac{\pi}{3}\), y\(\frac{5\pi}{3}\). Graficando\(y = \cos(2x)\) y\(y = 3\cos(x) - 2\), después de un pequeño esfuerzo extra, encontramos que las curvas se cruzan en tres lugares\([0,2\pi)\), y las\(x\) coordenadas de estos puntos confirman nuestros resultados.

4. Para resolverlo\(\cos(3x) = 2- \cos(x)\), utilizamos la misma técnica que en el problema anterior. Del Ejemplo 10.4.3, número 4, lo sabemos\(\cos(3x) = 4\cos^{3}(x) - 3\cos(x)\). Esto transforma la ecuación en un polinomio en términos de\(\cos(x)\).

   \[\begin{array}{rclr} \cos(3x) & = &2- \cos(x) & \\ 4\cos^{3}(x) - 3\cos(x) & = & 2- \cos(x) & \\ 2\cos^{3}(x) - 2\cos(x) -2 & = & 0 & \\ 4 u^3 - 2 u -2 & = & 0 & \text{Let $u = \cos(x)$.} \\ \end{array}\nonumber\]

   Para resolverlo\(4u^3-2u-2=0\), necesitamos las técnicas del Capítulo 3 para factorizar\(4u^3-2u-2\) en\((u-1)\left(4u^2+4u+2\right)\). Obtenemos cualquiera\(u-1 = 0\) o\(4u^2+2u+2=0\), y como el discriminante de este último es negativo, la única solución real a\(4u^3-2u-2=0\) es\(u = 1\). Ya que\(u = \cos(x)\), obtenemos\(\cos(x) = 1\), así\(x = 2\pi k\) para enteros\(k\). La única solución en la que se encuentra\([0,2\pi)\) es\(x = 0\). Graficar\(y = \cos(3x)\) y\(y = 2- \cos(x)\) sobre el mismo conjunto de ejes\([0,2\pi)\) muestra que las gráficas se cruzan en lo que parece ser\((0,1)\), según se requiera.

   
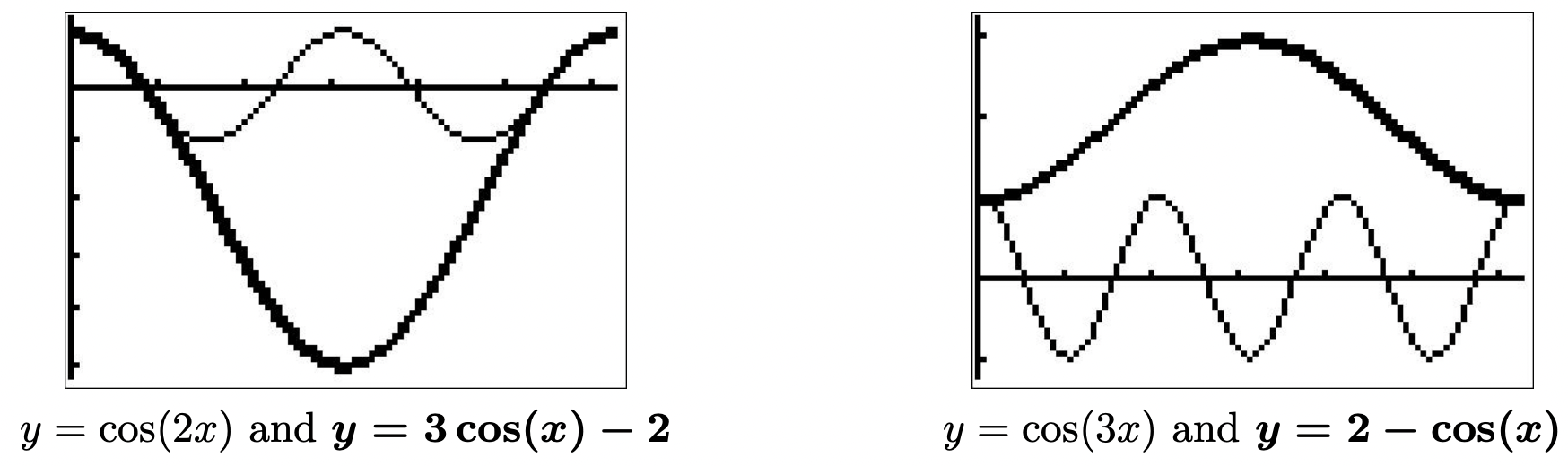
5. Si bien podríamos abordar\(\cos(3x) = \cos(5x)\) de la misma manera que hicimos los dos problemas anteriores, elegimos mostrar la utilidad de Suma a Identidades de Producto. De\(\cos(3x) = \cos(5x)\), obtenemos\(\cos(5x) - \cos(3x) = 0\), y es la presencia de\(0\) en el lado derecho lo que indica un cambio a un producto sería un buen movimiento. ⁷ Usando el Teorema 10.21, tenemos eso\(\cos(5x) - \cos(3x) = - 2 \sin\left( \frac{5x + 3x}{2}\right)\sin\left( \frac{5x - 3x}{2}\right) = -2 \sin(4x)\sin(x)\). De ahí que la ecuación\(\cos(5x) = \cos(3x)\) sea equivalente a\(-2 \sin(4x) \sin(x) = 0\). A partir de esto, obtenemos\(\sin(4x) = 0\) o\(\sin(x)\) = 0. Resolver\(\sin(4x) = 0\) da\(x = \frac{\pi}{4} k\) para enteros\(k\), y la solución a\(\sin(x) = 0\) es\(x = \pi k\) para enteros\(k\). El segundo conjunto de soluciones está contenido en el primer conjunto de soluciones, ⁸ por lo que nuestra solución final\(\cos(5x) = \cos(3x)\) es\(x = \frac{\pi}{4} k\) para enteros\(k\). Hay ocho de estas respuestas que se encuentran en\([0,2\pi)\):\(x = 0\),\(\frac{\pi}{4}\),\(\frac{\pi}{2}\),\(\frac{3\pi}{4}\),\(\pi\),\(\frac{5\pi}{4}\),\(\frac{3\pi}{2}\) y\(\frac{7\pi}{4}\). Nuestra gráfica de las gráficas de\(y = \cos(3x)\) y\(y = \cos(5x)\) abajo (después de un zoom cuidadoso) confirma esto.
6. Al examinar la ecuación\(\sin(2x) =\sqrt{3} \cos(x)\), no sólo tenemos involucradas diferentes funciones circulares, a saber, seno y coseno, también tenemos diferentes argumentos con los que lidiar, es decir,\(2x\) y\(x\). El uso de la identidad\(\sin(2x) = 2 \sin(x) \cos(x)\) hace que todos los argumentos sean iguales y procedemos como resolveríamos cualquier ecuación no lineal: reunimos todos los términos distintos de cero en un lado de la ecuación y el factor.

   \[\begin{array}{rclr} \sin(2x) & = & \sqrt{3} \cos(x) & \\ 2 \sin(x) \cos(x) & = & \sqrt{3} \cos(x) & \text{(Since $\sin(2x) = 2\sin(x) \cos(x)$.)} \\ 2\sin(x) \cos(x) - \sqrt{3} \cos(x) & = & 0 & \\ \cos(x) (2 \sin(x) - \sqrt{3}) & = & 0 & \\ \end{array}\nonumber\]

   de la que obtenemos\(\cos(x) = 0\) o\(\sin(x) = \frac{\sqrt{3}}{2}\). De\(\cos(x) = 0\), obtenemos\(x = \frac{\pi}{2} + \pi k\) para enteros\(k\). De\(\sin(x) = \frac{\sqrt{3}}{2}\), obtenemos\(x = \frac{\pi}{3} + 2\pi k\) o\(x = \frac{2\pi}{3} + 2\pi k\) para enteros\(k\). Las respuestas en las que\([0,2\pi)\) se encuentran son\(x = \frac{\pi}{2}\),\(\frac{3\pi}{2}\),\(\frac{\pi}{3}\) y\(\frac{2\pi}{3}\). Gráficamos\(y = \sin(2x)\)\(y = \sqrt{3} \cos(x)\) y, después de un cuidadoso zoom, verificamos nuestras respuestas.

   
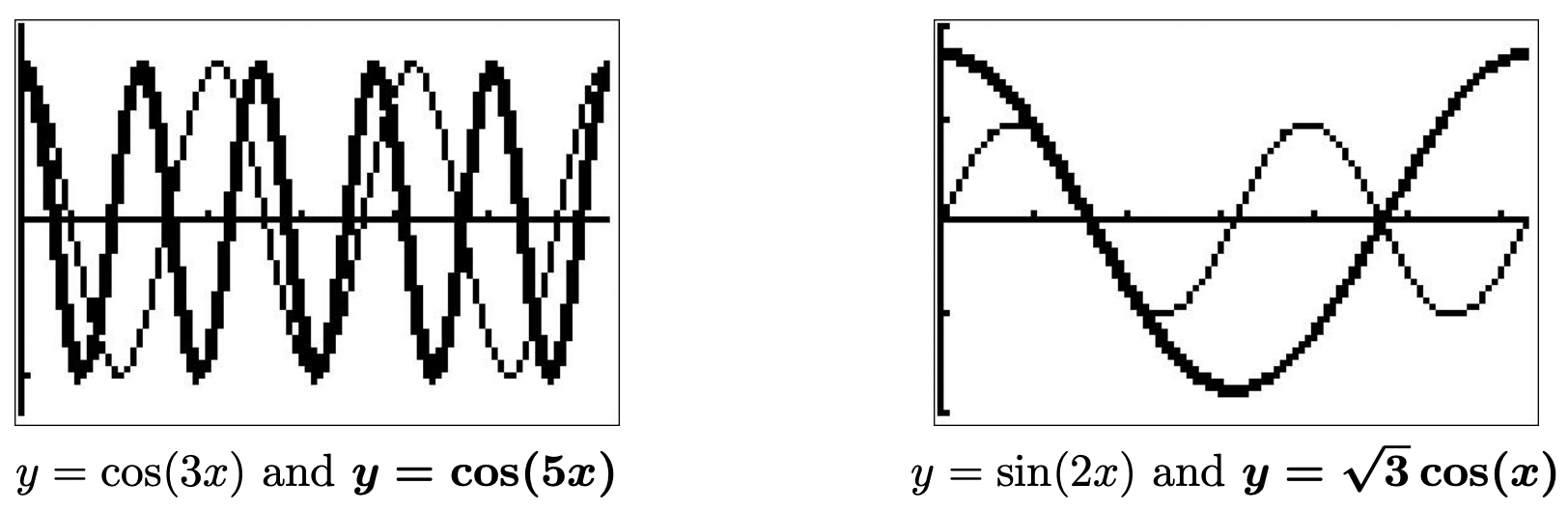
7. A diferencia del problema anterior, parece que no hay una manera rápida de conseguir que las funciones circulares o sus argumentos coincidan en la ecuación\(\sin(x)\cos\left(\frac{x}{2}\right) + \cos(x)\sin\left(\frac{x}{2}\right) = 1\). Sin embargo, si lo miramos el tiempo suficiente, nos damos cuenta de que el lado izquierdo es la forma expandida de la fórmula de suma para\(\sin\left(x + \frac{x}{2}\right)\). De ahí que nuestra ecuación original sea equivalente a\(\sin\left(\frac{3}{2} x\right) = 1\). Resolviendo, encontramos\(x = \frac{\pi}{3} + \frac{4\pi}{3} k\) para enteros\(k\). Dos de estas soluciones se encuentran en\([0,2\pi)\):\(x = \frac{\pi}{3}\) y\(x = \frac{5\pi}{3}\). Graficando\(y = \sin(x)\cos\left(\frac{x}{2}\right) + \cos(x)\sin\left(\frac{x}{2}\right)\) y\(y = 1\) validando nuestras soluciones.
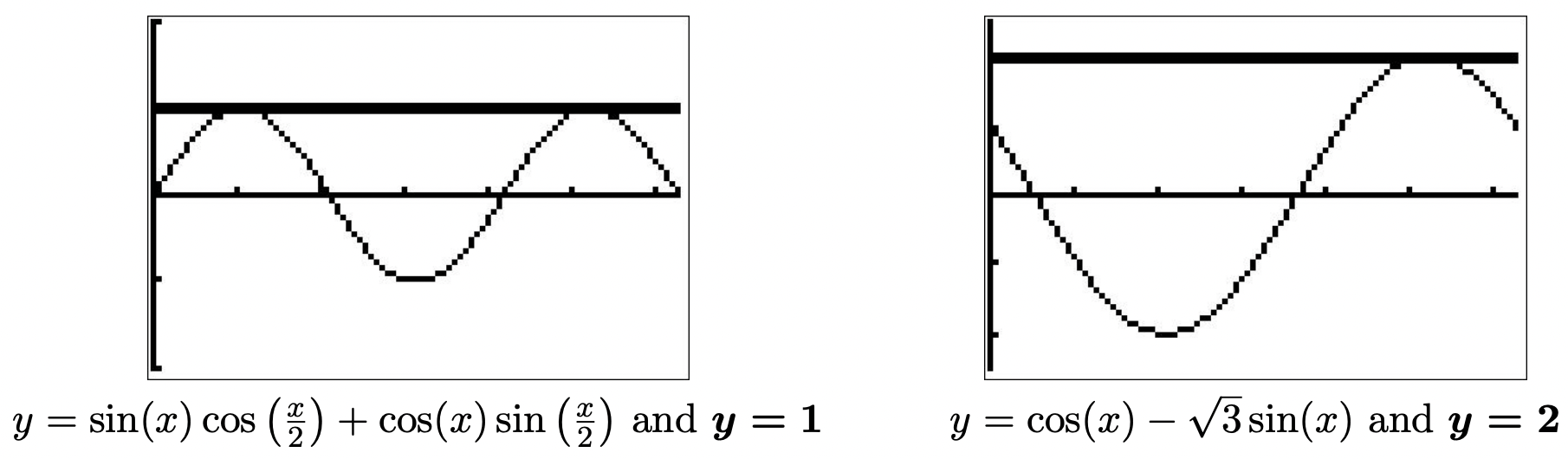
8. Con la ausencia de ángulos dobles o cuadrados, no parece haber mucho que podamos hacer. Sin embargo, como los argumentos del coseno y del seno son los mismos, podemos reescribir el lado izquierdo de esta ecuación como sinusoide. ⁹ Para ajustarnos\(f(x) = \cos(x) - \sqrt{3} \sin(x)\) a la forma\(A\sin(\omega t + \phi) + B\), utilizamos lo que aprendimos en el Ejemplo 10.5.3 y encontramos\(A = 2\),\(B = 0\),\(\omega = 1\) y\(\phi = \frac{5\pi}{6}\). De ahí que podamos reescribir la ecuación\(\cos(x) - \sqrt{3} \sin(x) = 2\) como\(2 \sin\left(x + \frac{5\pi}{6}\right) = 2\), o\(\sin\left(x + \frac{5\pi}{6}\right) = 1\). Resolviendo esto último, obtenemos\(x = - \frac{\pi}{3} + 2\pi k\) para enteros\(k\). Sólo una de estas soluciones,\(x = \frac{5\pi}{3}\), que corresponde a\(k=1\), yace en\([0,2\pi)\). Geométricamente, lo vemos\(y = \cos(x) - \sqrt{3} \sin(x)\) e\(y = 2\) intersectamos solo una vez, apoyando nuestra respuesta.

   

Repetimos aquí los consejos dados a la hora de resolver sistemas de ecuaciones no lineales en la sección 8.7 —cuando se trata de resolver ecuaciones que involucran las funciones trigonométricas, ayuda simplemente intentar algo.

A continuación, nos enfocamos en resolver desigualdades que involucran las funciones trigonométricas. Dado que estas funciones son continuas en sus dominios, podemos usar la técnica de diagrama de signos que hemos utilizado en el pasado para resolver las desigualdades. ¹⁰

Ejemplo 10.7.3

Resolver las siguientes desigualdades en\([0,2\pi)\). Exprese sus respuestas usando notación de intervalos y verifique sus respuestas gráficamente.

1. \(2\sin(x) \leq 1\)
2. \(\sin(2x) > \cos(x)\)
3. \(\tan(x) \geq 3\)

Solución

1. Comenzamos a resolver\(2\sin(x) \leq 1\) recogiendo todos los términos en un lado de la ecuación y cero en el otro para obtener\(2\sin(x) - 1 \leq 0\). A continuación, dejamos\(f(x) = 2\sin(x) - 1\) y señalamos que nuestra desigualdad original equivale a resolver\(f(x) \leq 0\). Ahora miramos para ver dónde, si alguna vez,\(f\) está indefinido y dónde\(f(x) = 0\). Dado que el dominio de\(f\) es todo números reales, podemos comenzar inmediatamente a encontrar los ceros de\(f\). Resolviendo\(f(x) = 0\), tenemos\(2\sin(x) - 1=0\) o\(\sin(x) = \frac{1}{2}\). Las soluciones aquí son\(x = \frac{\pi}{6} + 2\pi k\) y\(x = \frac{5\pi}{6} + 2\pi k\) para enteros\(k\). Ya que estamos restringiendo nuestra atención a\([0,2\pi)\), solo\(x = \frac{\pi}{6}\) y\(x = \frac{5\pi}{6}\) nos preocupan. A continuación, elegimos valores de prueba en\([0,2\pi)\) distintos de los ceros y determinamos si ahí\(f\) es positivo o negativo. Porque\(x = 0\) tenemos\(f(0) = -1\), porque\(x = \frac{\pi}{2}\) obtenemos\(f\left(\frac{\pi}{2}\right) = 1\) y para\(x = \pi\) nosotros obtenemos\(f(\pi) = -1\). Ya que nuestra desigualdad original es equivalente a\(f(x) \leq 0\), estamos buscando donde la función es negativa\((-)\) o\(0\), y obtenemos los intervalos\(\left[0, \frac{\pi}{6}\right] \cup \left[\frac{5\pi}{6}, 2\pi \right)\). Podemos confirmar nuestra respuesta gráficamente viendo dónde está la gráfica de\(y = 2\sin(x)\) cruces o está debajo de la gráfica de\(y = 1\).

   

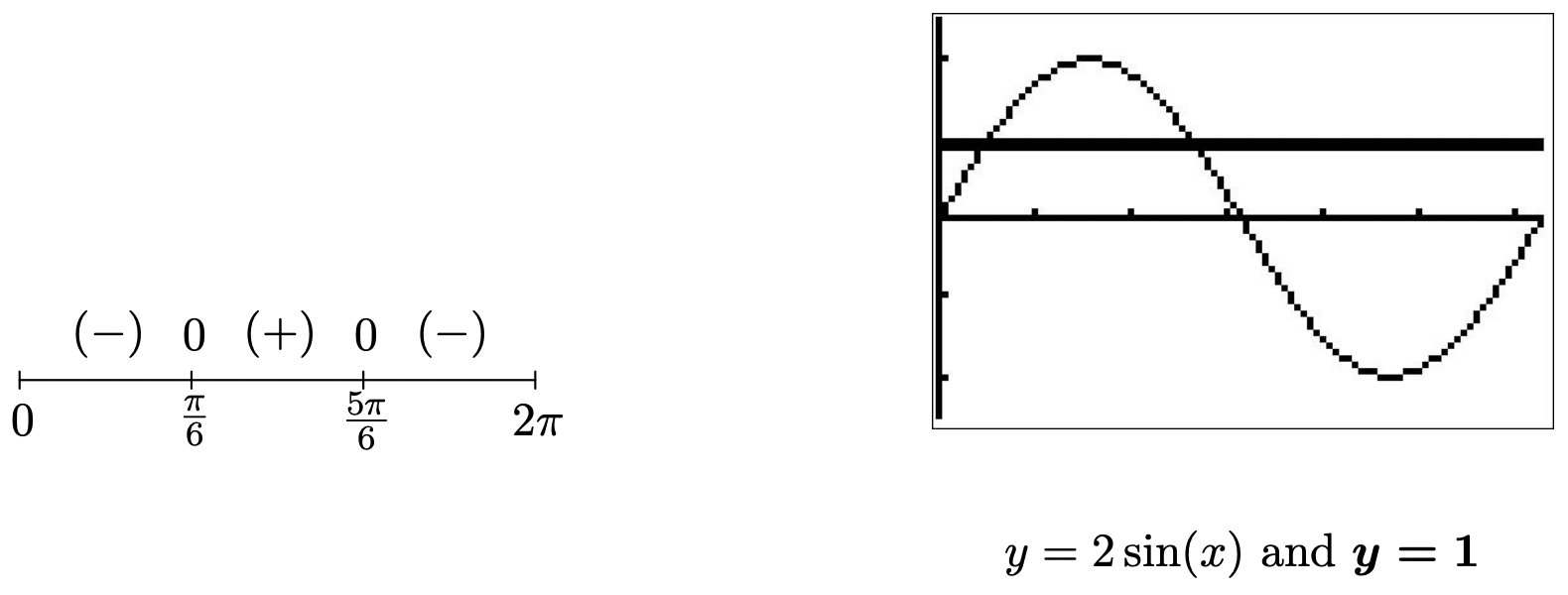
2. Primero reescribimos\(\sin(2x) > \cos(x)\) como\(\sin(2x) - \cos(x) > 0\) y dejamos\(f(x) = \sin(2x) - \cos(x)\). Nuestra desigualdad original es así equivalente a\(f(x) > 0\). El dominio de\(f\) es todo números reales, por lo que podemos avanzar a encontrar los ceros de\(f\). Ajuste de\(f(x) = 0\) rendimientos\(\sin(2x) - \cos(x) = 0\), que, por medio de la identidad de doble ángulo para seno, se convierte en\(2\sin(x)\cos(x) - \cos(x) = 0\) o\(\cos(x) (2\sin(x) - 1) = 0\). De\(\cos(x) = 0\), obtenemos\(x = \frac{\pi}{2} + \pi k\) para enteros\(k\) de los cuales solo\(x = \frac{\pi}{2}\) y se\(x = \frac{3\pi}{2}\) encuentran en\([0,2\pi)\). Para\(2\sin(x) - 1 = 0\), obtenemos\(\sin(x) = \frac{1}{2}\) cuál da\(x = \frac{\pi}{6} + 2\pi k\) o\(x = \frac{5\pi}{6} + 2\pi k\) para enteros\(k\). De esos, solo\(x = \frac{\pi}{6}\) y\(x = \frac{5\pi}{6}\) yacen en\([0,2\pi)\). A continuación, elegimos nuestros valores de prueba. Porque\(x =0\) encontramos\(f(0) = -1\); cuando\(x = \frac{\pi}{4}\) obtenemos\(f\left(\frac{\pi}{4}\right) =1 - \frac{\sqrt{2}}{2} = \frac{2 - \sqrt{2}}{2}\); porque\(x = \frac{3\pi}{4}\) obtenemos\(f\left(\frac{3\pi}{4}\right) =-1 + \frac{\sqrt{2}}{2} = \frac{\sqrt{2} - 2}{2}\); cuando\(x=\pi\) tenemos\(f(\pi) = 1\), y por último,\(x = \frac{7\pi}{4}\) porque obtenemos\(f\left(\frac{7\pi}{4}\right) = -1 - \frac{\sqrt{2}}{2} = \frac{-2 - \sqrt{2}}{2}\). Ya vemos\(f(x) > 0\)\(\left(\frac{\pi}{6}, \frac{\pi}{2}\right) \cup \left(\frac{5\pi}{6}, \frac{3\pi}{2}\right)\), así que esta es nuestra respuesta. Podemos usar la calculadora para comprobar que la gráfica de\(y = \sin(2x)\) está efectivamente por encima de la gráfica de\(y = \cos(x)\) en esos intervalos.

   

3. Procediendo como en los dos últimos problemas, reescribimos\(\tan(x) \geq 3\) como\(\tan(x) - 3 \geq 0\) y dejamos\(f(x) = \tan(x) - 3\). Observamos que on\([0,2\pi)\), no\(f\) está definido en\(x =\frac{\pi}{2}\) y\(\frac{3\pi}{2}\), por lo que esos valores necesitarán el descargo de responsabilidad habitual en el diagrama de signos. ¹¹ Al pasar a ceros, la resolución\(f(x) = \tan(x) - 3 = 0\) requiere la función arcotangente. Encontramos\(x = \arctan(3) + \pi k\) para enteros\(k\) y de estos, solo\(x = \arctan(3)\) y\(x = \arctan(3) + \pi\) yacemos en\([0,2\pi)\). Ya que\(3 > 0\), sabemos\(0 < \arctan(3) < \frac{\pi}{2}\) cuál nos permite posicionar estos ceros correctamente en el diagrama de signos. Para elegir valores de prueba, comenzamos con\(x=0\) y encontramos\(f(0) = -3\). Encontrar un valor de prueba conveniente en el intervalo\(\left(\arctan(3), \frac{\pi}{2}\right)\) es un poco más desafiante. Hay que tener en cuenta que la función arcotangente va en aumento y está delimitada arriba por\(\frac{\pi}{2}\). Esto significa que el número\(x = \arctan(117)\) está garantizado ¹² para estar entre\(\arctan(3)\) y\(\frac{\pi}{2}\). Eso lo vemos\(f(\arctan(117)) = \tan(\arctan(117)) - 3 = 114\). Para nuestro próximo valor de prueba, tomamos\(x = \pi\) y encontramos\(f(\pi) = -3\). Para encontrar nuestro próximo valor de prueba, observamos que desde\(\arctan(3) < \arctan(117) < \frac{\pi}{2}\), se deduce ¹³ que\(\arctan(3) + \pi < \arctan(117) + \pi < \frac{3\pi}{2}\). Evaluar\(f\) a\(x = \arctan(117) + \pi\) rendimientos\(f(\arctan(117)+\pi) = \tan(\arctan(117) + \pi) -3 = \tan(\arctan(117)) - 3 = 114\). Elegimos nuestro último valor de prueba para ser\(x = \frac{7\pi}{4}\) y encontrar\(f\left(\frac{7\pi}{4}\right) = -4\). Ya que queremos\(f(x) \geq 0\), vemos que nuestra respuesta es\(\left[ \arctan(3), \frac{\pi}{2}\right) \cup \left[\arctan(3)+\pi, \frac{3\pi}{2}\right)\). Usando las gráficas de\(y = \tan(x)\) y\(y = 3\), vemos cuando la gráfica de la primera está por encima (o cumple) la gráfica de la segunda.

   

Cerramos esta sección con un ejemplo que pone en buen uso la resolución de ecuaciones y desigualdades — encontrando dominios de funciones.

Ejemplo 10.7.4

Expresar el dominio de las siguientes funciones usando notación de intervalo extendido. ¹⁴

1. \(f(x) = \csc\left(2x + \frac{\pi}{3}\right)\)
2. \(f(x) = \dfrac{\sin(x)}{2\cos(x) - 1}\)
3. \(f(x) = \sqrt{1 - \cot(x)}\)

Solución

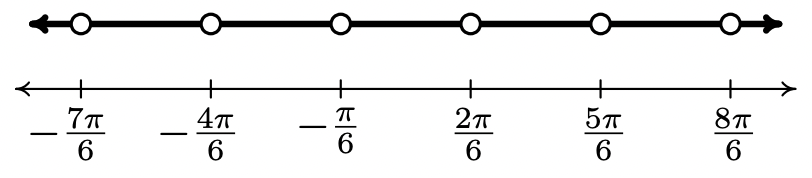
1. Para encontrar el dominio de\(f(x) = \csc\left(2x + \frac{\pi}{3}\right)\), reescribimos\(f\) en términos de seno como\(f(x) = \frac{1}{\sin\left(2x + \frac{\pi}{3}\right)}\). Dado que la función sinusoidal se define en todas partes, nuestra única preocupación proviene de los ceros en el denominador. Resolviendo\(\sin\left(2x + \frac{\pi}{3}\right) = 0\), obtenemos\(x = -\frac{\pi}{6} + \frac{\pi}{2} k\) para enteros\(k\). En notación set-builder, nuestro dominio es\(\left\{x: x \neq-\frac{\pi}{6}+\frac{\pi}{2} k \text { for integers } k\right\}\). Para ayudar a visualizar el dominio, seguimos el viejo mantra 'En caso de duda, ¡escríbalo! ' Obtenemos\(\left\{x: x \neq-\frac{\pi}{6}, \frac{2 \pi}{6},-\frac{4 \pi}{6}, \frac{5 \pi}{6},-\frac{7 \pi}{6}, \frac{8 \pi}{6}, \ldots\right\}\), donde hemos mantenido a los denominadores\(6\) en todo momento para ayudar a ver el patrón. Graficando la situación en una línea numérica, tenemos

   

   Procediendo como lo hicimos en la página 756 en la Sección 10.3.1, dejamos\(x_{k}\) denotar el número\(k\) th excluido del dominio y tenemos\(x_{k} = -\frac{\pi}{6} + \frac{\pi}{2} k = \frac{(3k-1)\pi}{6}\) para enteros\(k\). Los intervalos que comprenden el dominio son de la forma\(\left(x_{k}, x_{k+1} \right) = \left(\frac{(3k-1)\pi}{6}, \frac{(3k+2)\pi}{6} \right)\) como\(k\) recorridos a través de los números enteros. Usando notación de intervalo extendido, tenemos que el dominio es

   \[\bigcup_{k = -\infty}^{\infty} \left(\dfrac{(3k-1)\pi}{6}, \dfrac{(3k+2)\pi}{6} \right)\nonumber\]

   Podemos verificar nuestra respuesta sustituyendo en valores de\(k\) para ver que coincide con nuestro diagrama.

2. Dado que los dominios de\(\sin(x)\) y\(\cos(x)\) son todos números reales, la única preocupación a la hora de encontrar el dominio de\(f(x) = \frac{\sin(x)}{2\cos(x) - 1}\) es la división por cero por lo que establecemos el denominador igual a cero y resolvemos. De\(2\cos(x) - 1 = 0\) obtenemos\(\cos(x) = \frac{1}{2}\) así que\(x = \frac{\pi}{3} + 2\pi k\) o\(x = \frac{5\pi}{3} + 2\pi k\) para enteros\(k\). Usando la notación set-builder, el dominio es\(\left\{x: x \neq \frac{\pi}{3}+2 \pi k \text { and } x \neq \frac{5 \pi}{3}+2 \pi k \text { for integers } k\right\}\)\(\left\{ x : x \neq \pm \frac{\pi}{3}, \pm \frac{5\pi}{3}, \pm \frac{7\pi}{3}, \pm \frac{11\pi}{3}, \ldots \right\}\), o, entonces tenemos

   

   A diferencia del ejemplo anterior, tenemos dos familias diferentes de puntos a considerar, y presentamos dos formas de lidiar con este tipo de situaciones. Una forma es generalizar lo que hicimos en el ejemplo anterior y usar las fórmulas que encontramos en nuestro trabajo de dominio para describir los intervalos. Para ello, dejamos\(a_{k} = \frac{\pi}{3} + 2\pi k = \frac{(6k+1)\pi}{3}\) y\(b_{k} = \frac{5\pi}{3} + 2\pi k = \frac{(6k+5) \pi}{3}\) para enteros\(k\). El objetivo ahora es escribir el dominio en términos de los\(a\)'s\(b\) an's. encontramos\(a_0 = \frac{\pi}{3}\),,,\(a_{1} = \frac{7\pi}{3}\),\(a_{-1} = -\frac{5\pi}{3}\),\(a_{2} = \frac{13\pi}{3}\),\(a_{-2} = -\frac{11\pi}{3}\),\(b_0 = \frac{5\pi}{3}\),\(b_{1} = \frac{11\pi}{3}\),\(b_{-1} = -\frac{\pi}{3}\),\(b_{2} = \frac{17\pi}{3}\) y\(b_{-2} = -\frac{7\pi}{3}\). Por lo tanto, en términos de los\(a\)'s y\(b\)'s, nuestro dominio es

   \[\ldots\left(a_{-2}, b_{-2}\right) \cup\left(b_{-2}, a_{-1}\right) \cup\left(a_{-1}, b_{-1}\right) \cup\left(b_{-1}, a_{0}\right) \cup\left(a_{0}, b_{0}\right) \cup\left(b_{0}, a_{1}\right) \cup\left(a_{1}, b_{1}\right) \cup \ldots\nonumber\]

   Si agrupamos estos intervalos en pares,\(\left(a_{-2}, b_{-2} \right) \cup \left(b_{-2}, a_{-1} \right)\),\(\left(a_{-1}, b_{-1} \right)\cup \left(b_{-1}, a_0 \right)\),\(\left(a_0, b_0 \right)\cup \left(b_0, a_{1} \right)\) y así sucesivamente, vemos un patrón emerger de la forma\(\left(a_{k}, b_{k} \right)\cup \left(b_{k}, a_{k+1} \right)\) para enteros\(k\) para que nuestro dominio pueda escribirse como

   \[\bigcup_{k=-\infty}^{\infty}\left(a_{k}, b_{k}\right) \cup\left(b_{k}, a_{k+1}\right)=\bigcup_{k=-\infty}^{\infty}\left(\frac{(6 k+1) \pi}{3}, \frac{(6 k+5) \pi}{3}\right) \cup\left(\frac{(6 k+5) \pi}{3}, \frac{(6 k+7) \pi}{3}\right)\nonumber\]

   Una segunda aproximación al problema explota la naturaleza periódica de\(f\). Desde\(\cos(x)\) y\(\sin(x)\) tienen periodo\(2\pi\), no es demasiado difícil mostrar que la función\(f\) se repite cada\(2\pi\) unidad. ¹⁵ Esto significa que si podemos encontrar una fórmula para el dominio en un intervalo de longitud\(2\pi\), podemos expresar todo el dominio traduciendo nuestra respuesta izquierda y derecha en el\(x\) eje -mediante la adición de múltiplos enteros de\(2\pi\). Uno de esos intervalos que surge de nuestro trabajo de dominio es\(\left[\frac{\pi}{3}, \frac{7\pi}{3}\right]\). La porción del dominio aquí es\(\left(\frac{\pi}{3}, \frac{5\pi}{3}\right) \cup \left(\frac{5\pi}{3}, \frac{7\pi}{3}\right)\). Añadiendo múltiplos enteros de\(2\pi\), obtenemos la familia de intervalos\(\left(\frac{\pi}{3} + 2\pi k, \frac{5\pi}{3} + 2\pi k \right) \cup \left(\frac{5\pi}{3} + 2\pi k, \frac{7\pi}{3} + 2\pi k\right)\) para enteros\(k\). Dejamos al lector demostrar que conseguir denominadores comunes lleva a nuestra respuesta anterior.

3. Para encontrar el dominio de\(f(x) = \sqrt{1-\cot(x)}\), primero observamos que, debido a la presencia del\(\cot(x)\) término,\(x \neq \pi k\) para enteros\(k\). A continuación, recordamos que para que se defina la raíz cuadrada, necesitamos\(1 - \cot(x) \geq 0\). A diferencia de las desigualdades que resolvimos en el Ejemplo 10.7.3, no estamos restringidos aquí a un intervalo dado. Nuestra estrategia es resolver esta desigualdad sobre\((0,\pi)\) (el mismo intervalo que genera un ciclo fundamental de cotangente) y luego agregar múltiplos enteros del periodo, en este caso,\(\pi\). Dejamos\(g(x) = 1 - \cot(x)\) y nos pusimos a hacer un diagrama de signos para\(g\) sobre el intervalo\((0,\pi)\) para encontrar dónde\(g(x) \geq 0\). Observamos que\(g\) está indefinido\(x = \pi k\) para para enteros\(k\), en particular, en los puntos finales de nuestro intervalo\(x = 0\) y\(x = \pi\). A continuación, buscamos los ceros de\(g\). Resolviendo\(g(x) = 0\), obtenemos\(\cot(x) = 1\) o\(x = \frac{\pi}{4} + \pi k\) para enteros\(k\) y sólo uno de estos,\(x = \frac{\pi}{4}\), yace en\((0,\pi)\). Escogiendo los valores de prueba\(x = \frac{\pi}{6}\) y\(x = \frac{\pi}{2}\), obtenemos\(g\left(\frac{\pi}{6}\right) = 1 - \sqrt{3}\), y\(g\left(\frac{\pi}{2}\right) = 1\).

   

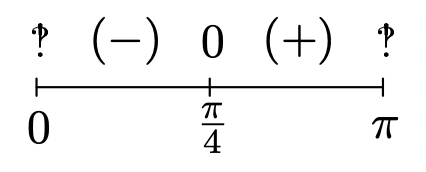
   Nos encontramos\(g(x) \geq 0\) en\(\left[\frac{\pi}{4}, \pi \right)\). Sumando múltiplos del periodo obtenemos nuestra solución para que consista en los intervalos\(\left[\frac{\pi}{4} + \pi k, \pi + \pi k \right) = \left[\frac{(4k+1)\pi}{4}, (k+1)\pi \right)\). Usando notación de intervalo extendido, expresamos nuestra respuesta final como

   \[\bigcup_{k = -\infty}^{\infty} \left[\dfrac{(4k+1)\pi}{4}, (k+1)\pi \right)\nonumber\]

Cerramos esta sección con un ejemplo que demuestra cómo resolver ecuaciones y desigualdades que involucran las funciones trigonométricas inversas.

Ejemplo 10.7.5

Resolver analíticamente las siguientes ecuaciones y desigualdades. Comprueba tus respuestas usando una utilidad gráfica.

1. \(\arcsin (2 x)=\frac{\pi}{3}\)
2. \(4 \arccos (x)-3 \pi=0\)
3. \(3 \operatorname{arcsec}(2 x-1)+\pi=2 \pi\)
4. \(4 \arctan ^{2}(x)-3 \pi \arctan (x)-\pi^{2}=0\)
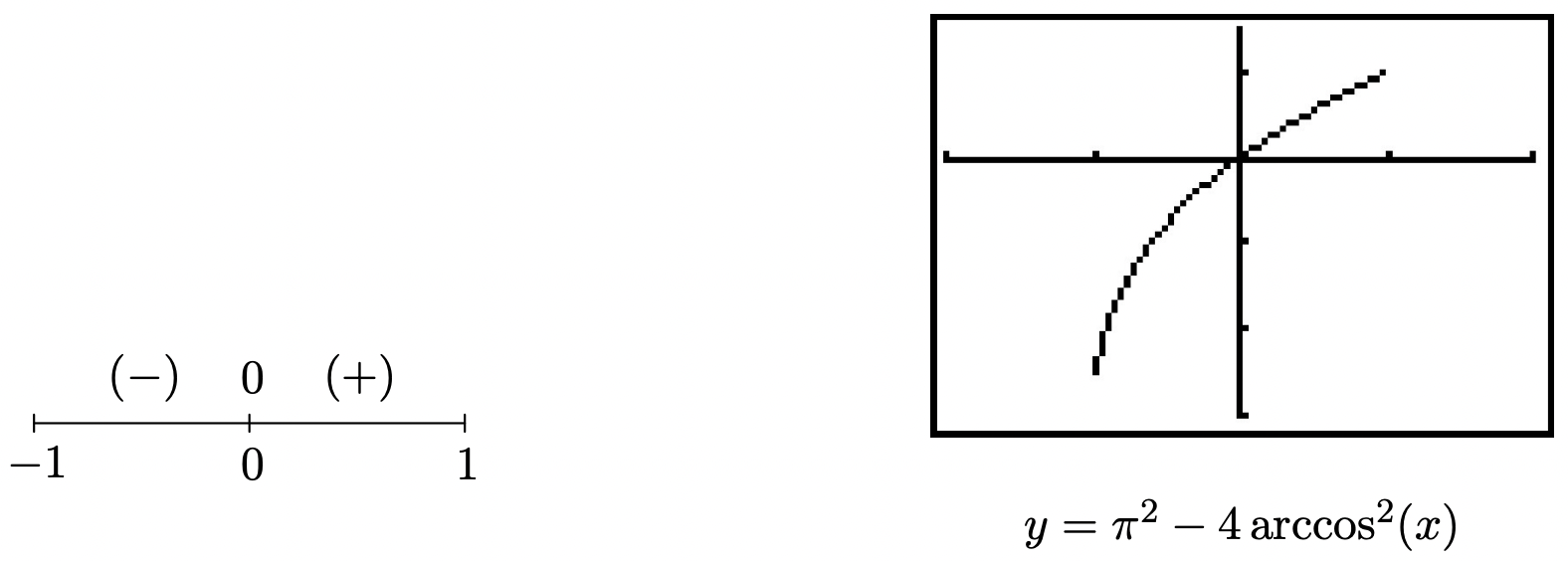
5. \(\pi^{2}-4 \arccos ^{2}(x)<0\)
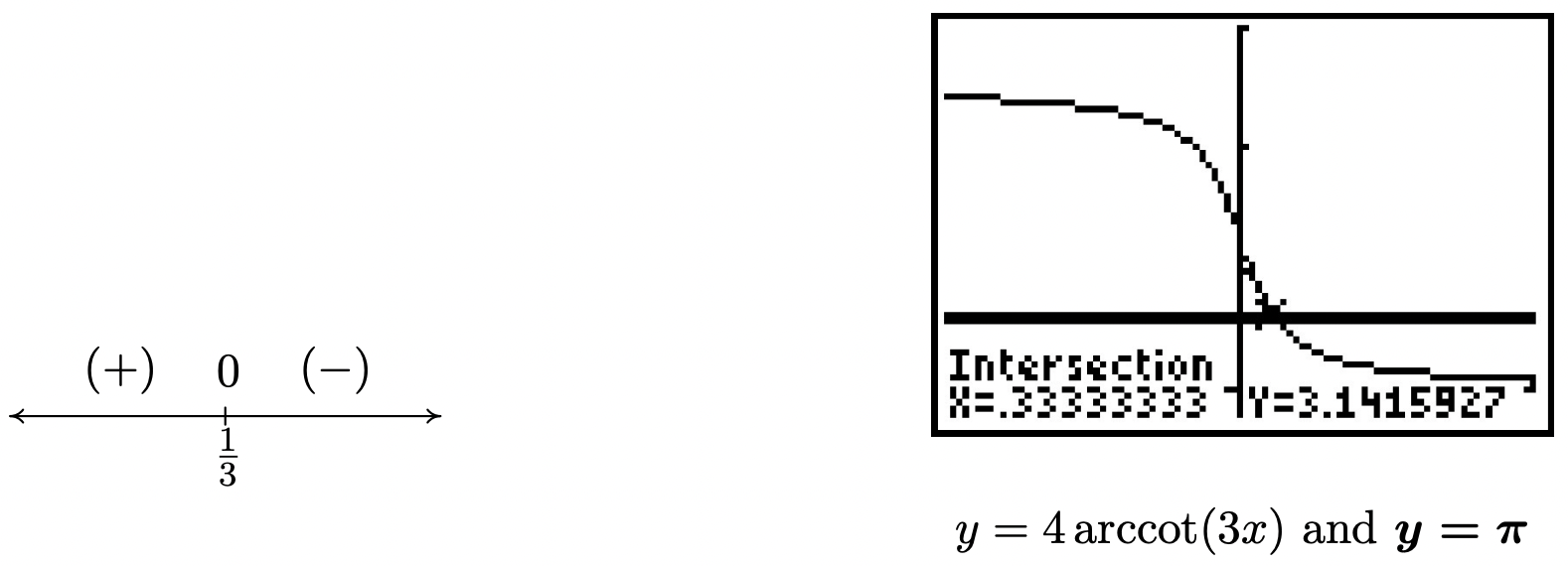
6. \(4 \operatorname{arccot}(3 x)>\pi\)

Solución

1. Para resolver\(\arcsin (2 x)=\frac{\pi}{3}\), primero notamos que\(\frac{\pi}{3}\) está en el rango de la función arcoseno (¡así existe una solución!) A continuación, explotamos la propiedad inversa de seno y arcoseno a partir del Teorema 10.26\[\begin{aligned} \arcsin (2 x) &=\frac{\pi}{3} \\ \sin (\arcsin (2 x)) &=\sin \left(\frac{\pi}{3}\right) \\ 2 x &=\frac{\sqrt{3}}{2} \quad \text { Since } \sin (\arcsin (u))=u \\ x &=\frac{\sqrt{3}}{4} \end{aligned}\nonumber\] Graficando\(y=\arcsin (2 x)\) y la línea horizontal\(y=\frac{\pi}{3}\), vemos que se cruzan en\(\frac{\sqrt{3}}{4} \approx 0.4430\).
2. Nuestro primer paso para resolver\(4 \arccos (x)-3 \pi=0\) es aislar el arcoseno. Al hacerlo, conseguimos\(\arccos (x)=\frac{3 \pi}{4}\). Ya que\(\frac{3 \pi}{4}\) está en el rango del arccosino, podemos aplicar Teorema 10.26\[\begin{aligned} \arccos (x) &=\frac{3 \pi}{4} \\ \cos (\arccos (x)) &=\cos \left(\frac{3 \pi}{4}\right) \\ x &=-\frac{\sqrt{2}}{2} \quad \text { Since } \cos (\arccos (u))=u \end{aligned}\nonumber\] La calculadora confirma\(y=4 \arccos (x)-3 \pi\) cruces\(y=0\) (el eje x) en\(-\frac{\sqrt{2}}{2} \approx-0.7071\).

   

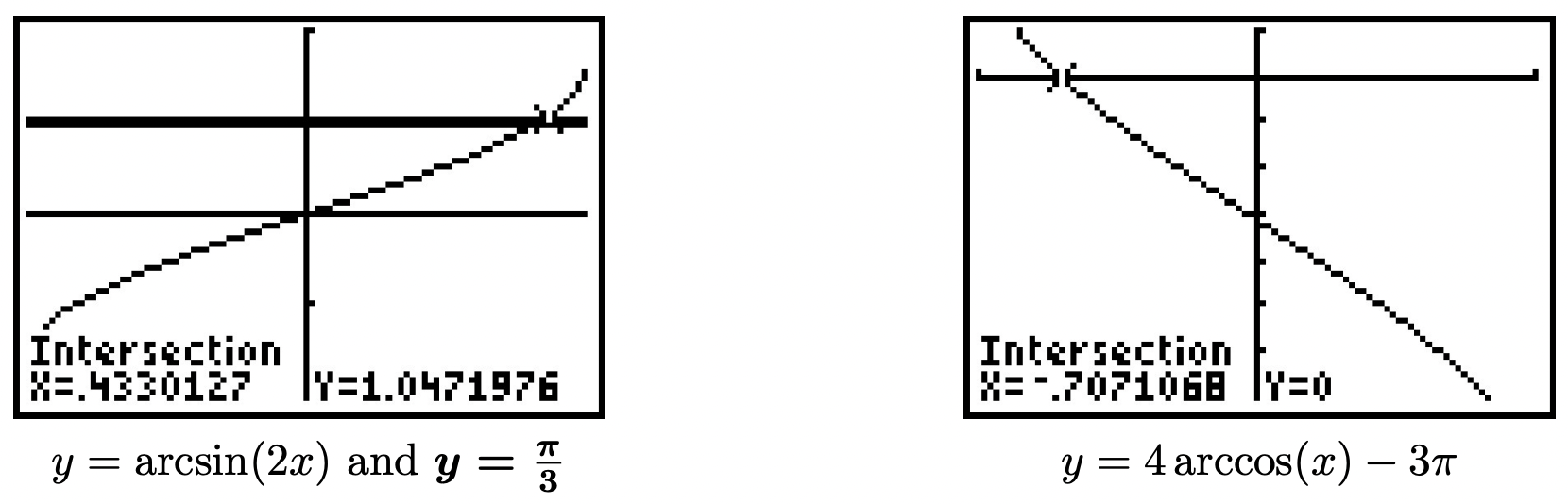
3. De\(3 \operatorname{arcsec}(2 x-1)+\pi=2 \pi\), obtenemos\(\operatorname{arcsec}(2 x-1)=\frac{\pi}{3}\). Como vimos en la Sección 10.6, existen dos rangos posibles para la función secante al arco. Afortunadamente, ambos rangos contienen\(\frac{\pi}{3}\). Aplicando el Teorema 10.28/10.29, obtenemos\[\begin{aligned} \operatorname{arcsec}(2 x-1) &=\frac{\pi}{3} \\ \sec (\operatorname{arcsec}(2 x-1)) &=\sec \left(\frac{\pi}{3}\right) \\ 2 x-1 &=2 \quad \text { Since } \sec (\operatorname{arcsec}(u))=u \\ x &=\frac{3}{2} \end{aligned}\nonumber\] Para verificar usando nuestra calculadora, necesitamos graficar\(y=3 \operatorname{arcsec}(2 x-1)+\pi\). Para ello, hacemos uso de la identidad\(\operatorname{arcsec}(u)=\arccos \left(\frac{1}{u}\right)\) de los Teoremas 10.28 y 10.29. ¹⁶ Vemos la gráfica de\(y=3 \arccos \left(\frac{1}{2 x-1}\right)+\pi\) y la línea horizontal se\(y=2 \pi\) cruzan en\(\frac{3}{2}=1.5\).

4. Con la presencia de ambos\(\arctan ^{2}(x)\left(=(\arctan (x))^{2}\right)\) y\(\arctan (x)\), sustituimos\(u=\arctan (x)\). La ecuación\(4 \arctan ^{2}(x)-3 \pi \arctan (x)-\pi^{2}=0\) se convierte\(4 u^{2}-3 \pi u-\pi^{2}=0\). Factoring, ¹⁷ obtenemos\((4 u+\pi)(u-\pi)=0\), así\(u=\arctan (x)=-\frac{\pi}{4}\) o\(u=\arctan (x)=\pi\). Ya que\(-\frac{\pi}{4}\) está en el rango de arcotangente, pero no lo\(\pi\) es, solo obtenemos soluciones de la primera ecuación. Usando el Teorema 10.27, obtenemos\ [\ begin {aligned}\ arctan (x) &=-\ frac {\ pi} {4}\\\ tan (\ arctan (\ arctan (x)) &=\ tan\ left (-\ frac {\ pi} {4}\\ right)\\
   x &=-1\ quad\ text {Since}\ tan (\ arctan (u)) =u end\ {alineado}\ nonumber\] La calculadora verifica nuestro resultado.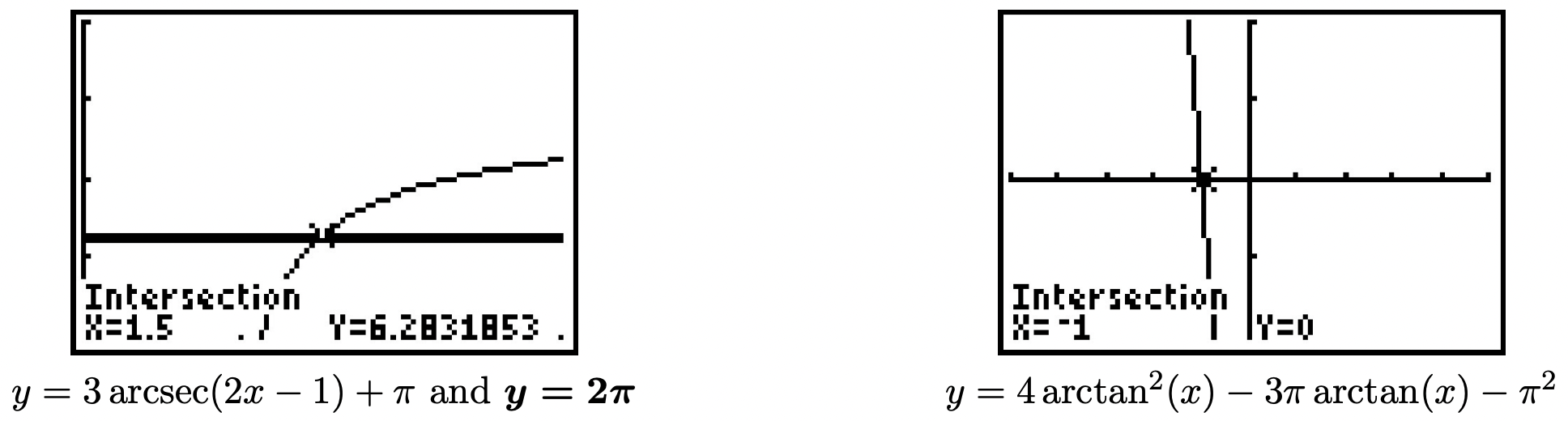

   

5. Dado que las funciones trigonométricas inversas son continuas en sus dominios, podemos resolver desigualdades con estas funciones mediante diagramas de signos. Dado que todos los términos distintos de cero de\(\pi^{2}-4 \arccos ^{2}(x)<0\) están en un lado de la desigualdad, dejamos\(f(x)=\pi^{2}-4 \arccos ^{2}(x)\) y notamos que el dominio de\(f\) está limitado por el\(\arccos (x)\) a [−1, 1]. A continuación, encontramos los ceros de\(f\) fijando\(f(x)=\pi^{2}-4 \arccos ^{2}(x)=0\). Obtenemos\(\arccos (x)=\pm \frac{\pi}{2}\), y como el alcance del arcoseno es\([0, \pi]\), enfocamos nuestra atención en\(\arccos (x)=\frac{\pi}{2}\). Usando el Teorema 10.26, obtenemos\(x=\cos \left(\frac{\pi}{2}\right)=0\) como nuestro único cero. De ahí que tengamos dos intervalos de prueba, [−1, 0) y (0, 1]. Eligiendo valores de prueba\(x=\pm 1\), obtenemos\(f(-1)=-3 \pi^{2}<0\) y\(f(1)=\pi^{2}>0\). Ya que estamos buscando donde\(f(x)=\pi^{2}-4 \arccos ^{2}(x)<0\), nuestra respuesta es [−1, 0). La calculadora confirma que para estos valores de\(x\), la gráfica de\(y=\pi^{2}-4 \arccos ^{2}(x)\) está por debajo\(y=0\) (el eje x).

   

6. Para comenzar, reescribimos\(4 \operatorname{arccot}(3 x)>\pi \text { as } 4 \operatorname{arccot}(3 x)-\pi>0\). Dejamos\(f(x)=4 \operatorname{arccot}(3 x)-\pi\), y notamos que el dominio de\(f\) es todos los números reales,\((-\infty, \infty)\). Para encontrar los ceros de\(f\), establecemos\(f(x)=4 \operatorname{arccot}(3 x)-\pi=0\) y resolvemos. Obtenemos\(\operatorname{arccot}(3 x)=\frac{\pi}{4}\), y dado que\(\frac{\pi}{4}\) está en el rango de arccotangente, podemos aplicar el Teorema 10.27 y resolver\[\begin{aligned} \operatorname{arccot}(3 x) &=\frac{\pi}{4} \\ \cot (\operatorname{arccot}(3 x)) &=\cot \left(\frac{\pi}{4}\right) \\ 3 x &=1 \quad \text { Since } \cot (\operatorname{arccot}(u))=u . \\ x &=\frac{1}{3} \end{aligned}\nonumber\] A continuación, hacemos un diagrama de signos para\(f\). Ya que el dominio de\(f\) es todo números reales, y sólo hay un cero de\(f\),\(x=\frac{1}{3}\), tenemos dos intervalos de prueba,\(\left(-\infty, \frac{1}{3}\right)\) y\(\left(\frac{1}{3}, \infty\right)\). Idealmente, deseamos encontrar valores de prueba\(x\) en estos intervalos para que\(\operatorname{arccot}(4 x)\) correspondan a uno de nuestros ángulos 'comunes' de uso frecuente. Después de un poco de cómputos, ¹⁸ elegimos\(x = 0\) por\(x<\frac{1}{3}\) y para\(x>\frac{1}{3}\), elegimos\(x=\frac{\sqrt{3}}{3}\). Nos encontramos\(f(0)=\pi>0\) y\(f\left(\frac{\sqrt{3}}{3}\right)=-\frac{\pi}{3}<0\). Ya que estamos buscando donde\(f(x)=4 \operatorname{arccot}(3 x)-\pi>0\), obtenemos nuestra respuesta\(\left(-\infty, \frac{1}{3}\right)\). Para verificar gráficamente, utilizamos la técnica en el número 2c del Ejemplo 10.6.5 en la Sección 10.6 para graficar\(y=4 \operatorname{arccot}(3 x)\) y vemos que está por encima de la línea horizontal\(y=\pi \text { on }\left(-\infty, \frac{1}{3}\right)=(-\infty, 0 . \overline{3})\).

   

10.7.1 Ejercicios

En los Ejercicios 1 - 18, encuentre las soluciones exactas de la ecuación y luego enumere aquellas soluciones que están en el intervalo\([0, 2\pi)\).

1. \(\sin \left( 5x \right) = 0\)
2. \(\cos \left( 3x \right) = \dfrac{1}{2}\)
3. \(\sin \left( -2x \right) = \dfrac{\sqrt{3}}{2}\)
4. \(\tan \left( 6x \right) = 1\)
5. \(\csc \left( 4x \right) = -1\)
6. \(\sec \left( 3x \right) = \sqrt{2}\)
7. \(\cot \left( 2x \right) = -\dfrac{\sqrt{3}}{3}\)
8. \(\cos \left( 9x \right) = 9\)
9. \(\sin \left( \dfrac{x}{3} \right) = \dfrac{\sqrt{2}}{2}\)
10. \(\cos \left( x + \dfrac{5\pi}{6} \right) = 0\)
11. \(\sin \left( 2x - \dfrac{\pi}{3} \right) = -\dfrac{1}{2}\)
12. \(2\cos \left( x + \dfrac{7\pi}{4} \right) = \sqrt{3}\)
13. \(\csc(x) = 0\)
14. \(\tan \left( 2x - \pi \right) = 1\)
15. \(\tan^{2} \left( x \right) = 3\)
16. \(\sec^{2} \left( x \right) = \dfrac{4}{3}\)
17. \(\cos^{2} \left( x \right) = \dfrac{1}{2}\)
18. \(\sin^{2} \left( x \right) = \dfrac{3}{4}\)

En los Ejercicios 19 - 42, resuelve la ecuación, dando las soluciones exactas que se encuentran en\([0, 2\pi)\)

19. \(\sin \left( x \right) = \cos \left( x \right)\)
20. \(\sin \left( 2x \right) = \sin \left( x \right)\)
21. \(\sin \left( 2x \right) = \cos \left( x \right)\)
22. \(\cos \left( 2x \right) = \sin \left( x \right)\)
23. \(\cos \left( 2x \right) = \cos \left( x \right)\)
24. \(\cos(2x) = 2 - 5\cos(x)\)
25. \(3\cos(2x) + \cos(x) + 2 = 0\)
26. \(\cos(2x) = 5\sin(x) - 2\)
27. \(3\cos(2x) = \sin(x) + 2\)
28. \(2\sec^{2}(x) = 3 - \tan(x)\)
29. \(\tan^{2}(x) = 1-\sec(x)\)
30. \(\cot^{2}(x) = 3\csc(x) - 3\)
31. \(\sec(x) = 2\csc(x)\)
32. \(\cos(x)\csc(x)\cot(x) = 6-\cot^{2}(x)\)
33. \(\sin(2x) = \tan(x)\)
34. \(\cot^{4}(x) = 4\csc^{2}(x) - 7\)
35. \(\cos(2x) + \csc^{2}(x) = 0\)
36. \(\tan^{3} \left( x \right) = 3\tan \left( x \right)\)
37. \(\tan^{2} \left( x \right) = \dfrac{3}{2} \sec \left( x \right)\)
38. \(\cos^{3} \left( x \right) = -\cos \left( x \right)\)
39. \(\tan (2x) - 2\cos(x) = 0\)
40. \(\csc^{3}(x) + \csc^{2}(x) = 4\csc(x) + 4\)
41. \(2\tan(x) = 1 - \tan^{2}(x)\)
42. \(\tan \left( x \right) = \sec \left( x \right)\)

En los Ejercicios 43 - 58, resuelve la ecuación, dando las soluciones exactas que se encuentran en\([0, 2\pi)\)

43. \(\sin(6x) \cos(x) = -\cos(6x) \sin(x)\)
44. \(\sin(3x)\cos(x) = \cos(3x) \sin(x)\)
45. \(\cos(2x)\cos(x) + \sin(2x)\sin(x) = 1\)
46. \(\cos(5x)\cos(3x) - \sin(5x)\sin(3x) = \dfrac{\sqrt{3}}{2}\)
47. \(\sin(x) + \cos(x) = 1\)
48. \(\sin(x) + \sqrt{3} \cos(x) = 1\)
49. \(\sqrt{2} \cos(x) - \sqrt{2} \sin(x) = 1\)
50. \(\sqrt{3} \sin(2x) + \cos(2x) = 1\)
51. \(\cos(2x) - \sqrt{3} \sin(2x) = \sqrt{2}\)
52. \(3\sqrt{3}\sin(3x) - 3\cos(3x) = 3\sqrt{3}\)
53. \(\cos(3x) = \cos(5x)\)
54. \(\cos(4x) = \cos(2x)\)
55. \(\sin(5x) = \sin(3x)\)
56. \(\cos(5x) = -\cos(2x)\)
57. \(\sin(6x) + \sin(x) = 0\)
58. \(\tan(x) = \cos(x)\)

En los Ejercicios 59 - 68, resuelve la ecuación.

59. \(\arccos (2 x)=\pi\)
60. \(\pi-2 \arcsin (x)=2 \pi\)
61. \(4 \arctan (3 x-1)-\pi=0\)
62. \(6 \operatorname{arccot}(2 x)-5 \pi=0\)
63. \(4 \operatorname{arcsec}\left(\frac{x}{2}\right)=\pi\)
64. \(12 \operatorname{arccsc}\left(\frac{x}{3}\right)=2 \pi\)
65. \(9 \arcsin ^{2}(x)-\pi^{2}=0\)
66. \(9 \arccos ^{2}(x)-\pi^{2}=0\)
67. \(8 \operatorname{arccot}^{2}(x)+3 \pi^{2}=10 \pi \operatorname{arccot}(x)\)
68. \(6 \arctan (x)^{2}=\pi \arctan (x)+\pi^{2}\)

En Ejercicios 69 - 80, resolver la desigualdad. Exprese la respuesta exacta en notación de intervalos, restringiendo su atención\(0 \leq x \leq 2 \pi\).

69. \(\sin \left( x \right) \leq 0\)
70. \(\tan \left( x \right) \geq \sqrt{3}\)
71. \(\sec^{2} \left( x \right) \leq 4\)
72. \(\cos^{2} \left( x \right) > \dfrac{1}{2}\)
73. \(\cos \left( 2x \right) \leq 0\)
74. \(\sin \left( x + \dfrac{\pi}{3} \right) > \dfrac{1}{2}\)
75. \(\cot^{2} \left( x \right) \geq \dfrac{1}{3}\)
76. \(2\cos(x) \geq 1\)
77. \(\sin(5x) \geq 5\)
78. \(\cos(3x) \leq 1\)
79. \(\sec(x) \leq \sqrt{2}\)
80. \(\cot(x) \leq 4\)

En los Ejercicios 81 - 86, resolver la desigualdad. Exprese la respuesta exacta en notación de intervalos, restringiendo su atención a\(-\pi \leq x \leq \pi\).

81. \(\cos \left( x \right) > \dfrac{\sqrt{3}}{2}\)
82. \(\sin(x) > \dfrac{1}{3}\)
83. \(\sec \left( x \right) \leq 2\)
84. \(\sin^{2} \left( x \right) < \dfrac{3}{4}\)
85. \(\cot \left( x \right) \geq -1\)
86. \(\cos(x) \geq \sin(x)\)

En los Ejercicios 87 - 92, resolver la desigualdad. Exprese la respuesta exacta en notación de intervalos, restringiendo su atención a\(-2 \pi \leq x \leq 2 \pi\).

87. \(\csc \left( x \right) > 1\)
88. \(\cos(x) \leq \dfrac{5}{3}\)
89. \(\cot(x) \geq 5\)
90. \(\tan^{2} \left( x \right) \geq 1\)
91. \(\sin(2x) \geq \sin(x)\)
92. \(\cos(2x) \leq \sin(x)\)

En los Ejercicios 93 - 92, resolver la desigualdad dada.

93. \(\arcsin (2 x)>0\)
94. \(3 \arccos (x) \leq \pi\)
95. \(6 \operatorname{arccot}(7 x) \geq \pi\)
96. \(\pi>2 \arctan (x)\)
97. \(2 \arcsin (x)^{2}>\pi \arcsin (x)\)
98. \(12 \arccos (x)^{2}+2 \pi^{2}>11 \pi \arccos (x)\)

En los Ejercicios 99 - 107, expresar el dominio de la función utilizando la notación de intervalo extendido. (Consulte la página 756 en la Sección 10.3.1 para más detalles.)

99. \(f(x)=\frac{1}{\cos (x)-1}\)
100. \(f(x)=\frac{\cos (x)}{\sin (x)+1}\)
101. \(f(x)=\sqrt{\tan ^{2}(x)-1}\)
102. \(f(x)=\sqrt{2-\sec (x)}\)
103. \(f(x)=\csc (2 x)\)
104. \(f(x)=\frac{\sin (x)}{2+\cos (x)}\)
105. \(f(x)=3 \csc (x)+4 \sec (x)\)
106. \(f(x)=\ln (|\cos (x)|)\)
107. \(f(x)=\arcsin (\tan (x))\)
108. Con la ayuda de tus compañeros de clase, determina el número de soluciones a\(\sin(x) = \frac{1}{2}\) in\([0,2\pi)\). Luego encuentre el número de soluciones a\(\sin(2x) = \frac{1}{2}\),\(\sin(3x) = \frac{1}{2}\) y\(\sin(4x) = \frac{1}{2}\) en\([0,2\pi)\). Debería emerger un patrón. Explica cómo este patrón te ayudaría a resolver ecuaciones como\(\sin(11x) = \frac{1}{2}\). Ahora considere\(\sin\left(\frac{x}{2}\right) = \frac{1}{2}\),\(\sin\left(\frac{3x}{2}\right) = \frac{1}{2}\) y\(\sin\left(\frac{5x}{2}\right) = \frac{1}{2}\). ¿Qué encuentras? Reemplazar\(\dfrac{1}{2}\) con\(-1\) y repetir toda la exploración.

10.7.2. RESPUESTAS

1. \(x = \dfrac{\pi k}{5}; \; x = 0, \dfrac{\pi}{5}, \dfrac{2\pi}{5}, \dfrac{3\pi}{5}, \dfrac{4\pi}{5}, \pi, \dfrac{6\pi}{5}, \dfrac{7\pi}{5}, \dfrac{8\pi}{5}, \dfrac{9\pi}{5}\)
2. \(x = \dfrac{\pi}{9} + \dfrac{2\pi k}{3}\)o\(x = \dfrac{5\pi}{9} + \dfrac{2\pi k}{3}; \; x = \dfrac{\pi}{9}, \dfrac{5\pi}{9}, \dfrac{7\pi}{9}, \dfrac{11\pi}{9}, \dfrac{13\pi}{9}, \dfrac{17\pi}{9}\)
3. \(x = \dfrac{2\pi}{3} + \pi k\)o\(x = \dfrac{5\pi}{6} + \pi k; \; x = \dfrac{2\pi}{3}, \dfrac{5\pi}{6}, \dfrac{5\pi}{3}, \dfrac{11\pi}{6}\)
4. \(x = \dfrac{\pi}{24} + \dfrac{\pi k}{6}; \; x = \dfrac{\pi}{24}, \dfrac{5\pi}{24}, \dfrac{3\pi}{8}, \dfrac{13\pi}{24}, \dfrac{17\pi}{24}, \dfrac{7\pi}{8}, \dfrac{25\pi}{24}, \dfrac{29\pi}{24}, \dfrac{11\pi}{8}, \dfrac{37\pi}{24}, \dfrac{41\pi}{24}, \dfrac{15\pi}{8}\)
5. \(x = \dfrac{3\pi}{8} + \dfrac{\pi k}{2}; \; x = \dfrac{3\pi}{8}, \dfrac{7\pi}{8}, \dfrac{11\pi}{8}, \dfrac{15\pi}{8}\)
6. \(x = \dfrac{\pi}{12} + \dfrac{2\pi k}{3}\)o\(x = \dfrac{7\pi}{12} + \dfrac{2\pi k}{3}; \; x = \dfrac{\pi}{12}, \dfrac{7\pi}{12}, \dfrac{3\pi}{4}, \dfrac{5\pi}{4}, \dfrac{17\pi}{12}, \dfrac{23\pi}{12}\)
7. \(x = \dfrac{\pi}{3} + \dfrac{\pi k}{2}; \; x = \dfrac{\pi}{3}, \dfrac{5\pi}{6}, \dfrac{4\pi}{3}, \dfrac{11\pi}{6}\)
8. Sin solución
9. \(x = \dfrac{3\pi}{4} + 6\pi k\)o\(x = \dfrac{9\pi}{4} + 6\pi k; \; x = \dfrac{3\pi}{4}\)
10. \(x = -\dfrac{\pi}{3} + \pi k; \; x = \dfrac{2\pi}{3}, \dfrac{5\pi}{3}\)
11. \(x = \dfrac{3\pi}{4} + \pi k\)o\(x = \dfrac{13\pi}{12} + \pi k; \; x = \dfrac{\pi}{12}, \dfrac{3\pi}{4}, \dfrac{13\pi}{12}, \dfrac{7\pi}{4}\)
12. \(x = -\dfrac{19\pi}{12} + 2\pi k\)o\(x = \dfrac{\pi}{12} + 2\pi k; \; x = \dfrac{\pi}{12}, \dfrac{5\pi}{12}\)
13. Sin solución
14. \(x = \dfrac{5\pi}{8} + \dfrac{\pi k}{2}; \; x = \dfrac{\pi}{8}, \dfrac{5\pi}{8}, \dfrac{9\pi}{8}, \dfrac{13\pi}{8}\)
15. \(x = \dfrac{\pi}{3} + \pi k\)o\(x = \dfrac{2\pi}{3} + \pi k; \; x = \dfrac{\pi}{3}, \dfrac{2\pi}{3}, \dfrac{4\pi}{3}, \dfrac{5\pi}{3}\)
16. \(x = \dfrac{\pi}{6} + \pi k\)o\(x = \dfrac{5\pi}{6} + \pi k; \; x = \dfrac{\pi}{6}, \dfrac{5\pi}{6}, \dfrac{7\pi}{6}, \dfrac{11\pi}{6}\)
17. \(x = \dfrac{\pi}{4} + \dfrac{\pi k}{2}; \; x = \dfrac{\pi}{4}, \dfrac{3\pi}{4}, \dfrac{5\pi}{4}, \dfrac{7\pi}{4}\)
18. \(x = \dfrac{\pi}{3} + \pi k\)o\(x = \dfrac{2\pi}{3} + \pi k; \; x = \dfrac{\pi}{3}, \dfrac{2\pi}{3}, \dfrac{4\pi}{3}, \dfrac{5\pi}{3}\)
19. \(x = \dfrac{\pi}{4}, \dfrac{5\pi}{4}\)
20. \(x = 0, \dfrac{\pi}{3}, \pi, \dfrac{5\pi}{3}\)
21. \(x = \dfrac{\pi}{6}, \dfrac{\pi}{2}, \dfrac{5\pi}{6}, \dfrac{3\pi}{2}\)
22. \(x = \dfrac{\pi}{6}, \dfrac{5\pi}{6}, \dfrac{3\pi}{2}\)
23. \(x = 0, \dfrac{2\pi}{3}, \dfrac{4\pi}{3}\)
24. \(x=\dfrac{\pi}{3}, \dfrac{5\pi}{3}\)
25. \(x = \dfrac{2\pi}{3}, \dfrac{4\pi}{3}, \arccos\left(\dfrac{1}{3}\right), 2\pi -\arccos\left(\dfrac{1}{3}\right)\)
26. \(x=\dfrac{\pi}{6}, \dfrac{5\pi}{6}\)
27. \(x = \dfrac{7\pi}{6}, \dfrac{11\pi}{6}, \arcsin\left(\dfrac{1}{3}\right), \pi - \arcsin\left(\dfrac{1}{3}\right)\)
28. \(x=\dfrac{3\pi}{4}, \dfrac{7\pi}{4}, \arctan\left(\dfrac{1}{2}\right), \pi +\arctan\left(\dfrac{1}{2}\right)\)
29. \(x=0, \dfrac{2\pi}{3}, \dfrac{4\pi}{3}\)
30. \(x=\dfrac{\pi}{6}, \dfrac{5\pi}{6}, \dfrac{\pi}{2}\)
31. \(x=\arctan(2), \pi + \arctan(2)\)
32. \(x = \dfrac{\pi}{6}, \dfrac{7\pi}{6}, \dfrac{5\pi}{6}, \dfrac{11\pi}{6}\)
33. \(x = 0, \pi, \dfrac{\pi}{4}, \dfrac{3\pi}{4}, \dfrac{5\pi}{4}, \dfrac{7\pi}{4}\)
34. \(x = \dfrac{\pi}{6}, \dfrac{\pi}{4}, \dfrac{3\pi}{4}, \dfrac{5\pi}{6}, \dfrac{7\pi}{6}, \dfrac{5\pi}{4}, \dfrac{7\pi}{4}, \dfrac{11\pi}{6}\)
35. \(x = \dfrac{\pi}{2}, \dfrac{3\pi}{2}\)
36. \(x = 0, \dfrac{\pi}{3}, \dfrac{2\pi}{3}, \pi, \dfrac{4\pi}{3}, \dfrac{5\pi}{3}\)
37. \(x = \dfrac{\pi}{3}, \dfrac{5\pi}{3}\)
38. \(x = \dfrac{\pi}{2}, \dfrac{3\pi}{2}\)
39. \(x = \dfrac{\pi}{6}, \dfrac{\pi}{2}, \dfrac{5\pi}{6}, \dfrac{3\pi}{2}\)
40. \(x = \dfrac{\pi}{6}, \dfrac{5\pi}{6}, \dfrac{7\pi}{6}, \dfrac{3\pi}{2}, \dfrac{11\pi}{6}\)
41. \(x = \dfrac{\pi}{8}, \dfrac{5\pi}{8}, \dfrac{9\pi}{8}, \dfrac{13\pi}{8}\)
42. Sin solución
43. \(x = 0, \dfrac{\pi}{7}, \dfrac{2\pi}{7}, \dfrac{3\pi}{7}, \dfrac{4\pi}{7}, \dfrac{5\pi}{7}, \dfrac{6\pi}{7}, \pi, \dfrac{8\pi}{7}, \dfrac{9\pi}{7}, \dfrac{10\pi}{7}, \dfrac{11\pi}{7}, \dfrac{12\pi}{7}, \dfrac{13\pi}{7}\)
44. \(x=0, \dfrac{\pi}{2}, \pi, \dfrac{3\pi}{2}\)
45. \(x = 0\)
46. \(x = \dfrac{\pi}{48}, \dfrac{11\pi}{48}, \dfrac{13\pi}{48}, \dfrac{23\pi}{48}, \dfrac{25\pi}{48}, \dfrac{35\pi}{48}, \dfrac{37\pi}{48}, \dfrac{47\pi}{48}, \dfrac{49\pi}{48}, \dfrac{59\pi}{48}, \dfrac{61\pi}{48}, \dfrac{71\pi}{48}, \dfrac{73\pi}{48}, \dfrac{83\pi}{48}, \dfrac{85\pi}{48}, \dfrac{95\pi}{48}\)
47. \(x = 0, \dfrac{\pi}{2}\)
48. \(x = \dfrac{\pi}{2}, \dfrac{11\pi}{6}\)
49. \(x = \dfrac{\pi}{12}, \dfrac{17\pi}{12}\)
50. \(x= 0, \pi, \dfrac{\pi}{3}, \dfrac{4\pi}{3}\)
51. \(x = \dfrac{17 \pi}{24}, \dfrac{41 \pi}{24}, \dfrac{23\pi}{24}, \dfrac{47\pi}{24}\)
52. \(x = \dfrac{\pi}{6}, \dfrac{5\pi}{18}, \dfrac{5\pi}{6}, \dfrac{17\pi}{18}, \dfrac{3\pi}{2}, \dfrac{29\pi}{18}\)
53. \(x = 0, \dfrac{\pi}{4}, \dfrac{\pi}{2}, \dfrac{3\pi}{4}, \pi, \dfrac{5\pi}{4}, \dfrac{3\pi}{2}, \dfrac{7\pi}{4}\)
54. \(x = 0, \dfrac{\pi}{3}, \dfrac{2\pi}{3}, \pi, \dfrac{4\pi}{3}, \dfrac{5\pi}{3}\)
55. \(x = 0, \dfrac{\pi}{8}, \dfrac{3\pi}{8}, \dfrac{5\pi}{8}, \dfrac{7\pi}{8}, \pi, \dfrac{9\pi}{8}, \dfrac{11\pi}{8}, \dfrac{13\pi}{8}, \dfrac{15\pi}{8}\)
56. \(x = \dfrac{\pi}{7}, \dfrac{\pi}{3}, \dfrac{3\pi}{7}, \dfrac{5\pi}{7}, \pi, \dfrac{9\pi}{7}, \dfrac{11\pi}{7}, \dfrac{5\pi}{3}, \dfrac{13\pi}{7}\)
57. \(x = \dfrac{2\pi}{7}, \dfrac{4\pi}{7}, \dfrac{6\pi}{7}, \dfrac{8\pi}{7}, \dfrac{10\pi}{7}, \dfrac{12\pi}{7}, \dfrac{\pi}{5}, \dfrac{3\pi}{5}, \pi, \dfrac{7\pi}{5}, \dfrac{9\pi}{5}\)
58. \(x = \arcsin \left( \dfrac{-1 + \sqrt{5}}{2} \right) \approx 0.6662, \pi - \arcsin \left( \dfrac{-1 + \sqrt{5}}{2} \right) \approx 2.4754\)
59. \(x=-\frac{1}{2}\)
60. \(x = −1\)
61. \(x=\frac{2}{3}\)
62. \(x=-\frac{\sqrt{3}}{2}\)
63. \(x=2 \sqrt{2}\)
64. \(x = 6\)
65. \(x=\pm \frac{\sqrt{3}}{2}\)
66. \(x=\frac{1}{2}\)
67. \(x = −1, 0\)
68. \(x=-\sqrt{3}\)
69. \(\left[ \pi, 2\pi \right]\)
70. \(\left[ \dfrac{\pi}{3}, \dfrac{\pi}{2} \right) \cup \left[ \dfrac{4\pi}{3}, \dfrac{3\pi}{2} \right)\)
71. \(\left[ 0, \dfrac{\pi}{3} \right] \cup \left[ \dfrac{2\pi}{3}, \dfrac{4\pi}{3} \right] \cup \left[ \dfrac{5\pi}{3}, 2\pi \right]\)
72. \(\left[ 0, \dfrac{\pi}{4} \right) \cup \left( \dfrac{3\pi}{4}, \dfrac{5\pi}{4} \right) \cup \left( \dfrac{7\pi}{4}, 2\pi \right]\)
73. \(\left[ \dfrac{\pi}{4}, \dfrac{3\pi}{4} \right] \cup \left[ \dfrac{5\pi}{4}, \dfrac{7\pi}{4} \right]\)
74. \(\left[ 0, \dfrac{\pi}{2} \right) \cup \left( \dfrac{11\pi}{6}, 2\pi \right]\)
75. \(\left( 0, \dfrac{\pi}{3} \right] \cup \left[ \dfrac{2\pi}{3}, \pi \right) \cup \left( \pi, \dfrac{4\pi}{3} \right] \cup \left[ \dfrac{5\pi}{3}, 2\pi \right)\)
76. \(\left[0, \dfrac{\pi}{3}\right] \cup \left[\dfrac{5\pi}{3}, 2\pi\right]\)
77. Sin solución
78. \([0, 2\pi]\)
79. \(\left[0, \dfrac{\pi}{4} \right] \cup \left(\dfrac{\pi}{2}, \dfrac{3\pi}{2}\right) \cup \left[\dfrac{7\pi}{4}, 2\pi\right]\)
80. \(\left[\text{arccot}(4), \pi \right) \cup \left[ \pi + \text{arccot}(4), 2\pi\right)\)
81. \(\left( -\dfrac{\pi}{6}, \dfrac{\pi}{6} \right)\)
82. \(\left( \arcsin\left(\dfrac{1}{3}\right), \pi - \arcsin\left(\dfrac{1}{3}\right) \right)\)
83. \(\left[ -\pi, -\dfrac{\pi}{2} \right) \cup \left[ -\dfrac{\pi}{3}, \dfrac{\pi}{3} \right] \cup \left( \dfrac{\pi}{2}, \pi \right]\)
84. \(\left( -\dfrac{2\pi}{3}, -\dfrac{\pi}{3} \right) \cup \left( \dfrac{\pi}{3}, \dfrac{2\pi}{3} \right)\)
85. \(\left( -\pi, -\dfrac{\pi}{4} \right] \cup \left( 0, \dfrac{3\pi}{4} \right]\)
86. \(\left[ -\dfrac{3\pi}{4}, \dfrac{\pi}{4} \right]\)
87. \(\left( -2\pi, -\dfrac{3\pi}{2} \right) \cup \left( -\dfrac{3\pi}{2}, -\pi \right) \cup \left( 0, \dfrac{\pi}{2} \right) \cup \left( \dfrac{\pi}{2}, \pi \right)\)
88. \([-2\pi, 2\pi]\)
89. \(\left(-2\pi, \text{arccot}(5) - 2\pi\right] \cup \left(-\pi, \text{arccot}(5) - \pi\right] \cup \left(0, \text{arccot}(5)\right] \cup \left(\pi, \pi + \text{arccot}(5)\right]\)
90. \(\left[ -\dfrac{7\pi}{4}, -\dfrac{3\pi}{2} \right) \cup \left( -\dfrac{3\pi}{2}, -\dfrac{5\pi}{4} \right] \cup \left[ -\dfrac{3\pi}{4}, -\dfrac{\pi}{2} \right) \cup \left( -\dfrac{\pi}{2}, -\dfrac{\pi}{4} \right] \cup \left[ \dfrac{\pi}{4}, \dfrac{\pi}{2} \right) \cup \left( \dfrac{\pi}{2}, \dfrac{3\pi}{4} \right] \cup \left[ \dfrac{5\pi}{4}, \dfrac{3\pi}{2} \right) \cup \left( \dfrac{3\pi}{2}, \dfrac{7\pi}{4} \right]\)
91. \(\left[ -2\pi, -\dfrac{5\pi}{3} \right] \cup \left[ -\pi, -\dfrac{\pi}{3} \right] \cup \left[ 0, \dfrac{\pi}{3} \right] \cup \left[ \pi, \dfrac{5\pi}{3} \right]\)
92. \(\left[-\frac{11 \pi}{6},-\frac{7 \pi}{6}\right] \cup\left[\frac{\pi}{6}, \frac{5 \pi}{6}\right] \cup,\left\{-\frac{\pi}{2}, \frac{3 \pi}{2}\right\}\)
93. \(\left(0, \frac{1}{2}\right]\)
94. \(\left[\frac{1}{2}, 1\right]\)
95. \(\left(-\infty, \frac{\sqrt{3}}{7}\right]\)
96. \((-\infty, \infty)\)
97. \([-1,0)\)
98. \(\left[-1,-\frac{1}{2}\right) \cup\left(\frac{\sqrt{2}}{2}, 1\right]\)
99. \(\bigcup_{k=-\infty}^{\infty}(2 k \pi,(2 k+2) \pi)\)
100. \(\bigcup_{k=-\infty}^{\infty}\left(\frac{(4 k-1) \pi}{2}, \frac{(4 k+3) \pi}{2}\right)\)
101. \(\bigcup_{k=-\infty}^{\infty}\left\{\left[\frac{(4 k+1) \pi}{4}, \frac{(2 k+1) \pi}{2}\right) \cup\left(\frac{(2 k+1) \pi}{2}, \frac{(4 k+3) \pi}{4}\right]\right\}\)
102. \(\bigcup_{k=-\infty}^{\infty}\left\{\left[\frac{(6 k-1) \pi}{3}, \frac{(6 k+1) \pi}{3}\right] \cup\left(\frac{(4 k+1) \pi}{2}, \frac{(4 k+3) \pi}{2}\right)\right\}\)
103. \(\bigcup_{k=-\infty}^{\infty}\left(\frac{k \pi}{2}, \frac{(k+1) \pi}{2}\right)\)
104. \((-\infty, \infty)\)
105. \(\bigcup_{k=-\infty}^{\infty}\left(\frac{k \pi}{2}, \frac{(k+1) \pi}{2}\right)\)
106. \(\bigcup_{k=-\infty}^{\infty}\left(\frac{(2 k-1) \pi}{2}, \frac{(2 k+1) \pi}{2}\right)\)
107. \(\bigcup_{k=-\infty}^{\infty}\left[\frac{(4 k-1) \pi}{4}, \frac{(4 k+1) \pi}{4}\right]\)

---

Referencia

¹ Consulte los comentarios al inicio de la Sección 10.5 para una revisión de este concepto.

² ¡No olvides dividir\(2 \pi k\) por 3 también!

³ ¿Ves por qué?

⁴ Se anima al lector a ver qué pasa si en\(\cot (3 x)=\frac{1}{\tan (3 x)}\) su lugar hubiéramos elegido la identidad recíproca. El gráfico de la calculadora parece idéntico, pero ¿qué sucede cuando intentas encontrar los puntos de intersección?

⁵ Tu instructor te avisará si debes abandonar la ruta analítica en este punto y usar tu calculadora. Pero en serio, ¿qué divertido sería eso?

⁶ Tenga en cuenta que no estamos contando el\((2 \pi, 0)\) en nuestro conjunto de soluciones ya que no\(x=2 \pi\) está en el intervalo\([0,2 \pi)\). En las próximas soluciones, recuerde que si bien\(x=2 \pi\) puede ser una solución a la ecuación, no se cuenta entre las soluciones en\([0,2 \pi)\).

⁷ Como siempre, ¡la experiencia es el maestro más grande aquí!

⁸ Como siempre, en caso de duda, ¡escríbalo!

⁹ Estamos esencialmente 'deshaciendo' la fórmula de suma/diferencia para coseno o seno, dependiendo de la forma que usemos, ¡así que este problema en realidad está estrechamente relacionado con el anterior!

¹⁰ Consulte la página 214, Ejemplo 3.1.5, página 321, página 399, Ejemplo 6.3.2 y Ejemplo 6.4.2 para discusión de esta técnica.

¹¹ Consulte la página 321 para una discusión del carácter no estándar conocido como el interrobang.

¹² Podríamos haber elegido cualquier valor\(\arctan (t)\) donde\(t>3\).

^13.. sumando\(\pi\) a través de la desigualdad...

¹⁴ Consulte la página 756 para obtener detalles sobre esta notación.

¹⁵ Esto no significa necesariamente que el periodo de\(f\) es\(2 \pi\). La función tangente es comprender de\(\cos (x)\) y\(\sin (x)\), pero su periodo es la mitad del suyo. Se invita al lector a investigar el periodo de\(f\).

¹⁶ Ya que estamos comprobando soluciones donde arcsecant es positivo, lo sabemos\(u=2 x-1 \geq 1\), y así la identidad se aplica en ambos casos.

¹⁷ No es tan malo como parece... ¡no dejes que te\(\pi\) lancen!

¹⁸ Establecer\(3x\) igual a las cotangentes de los 'ángulos comunes' y elegir en consecuencia.