11.1: Aplicaciones de sinusoides

Última actualización
Guardar como PDF

Page ID: 119496

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

De la misma manera las funciones exponenciales pueden ser utilizadas para modelar una amplia variedad de fenómenos en la naturaleza, ¹ las funciones coseno y seno pueden ser utilizadas para modelar su parte justa de comportamientos naturales. En la sección 10.5, se introdujo el concepto de sinusoide como una función que puede escribirse ya sea en la forma$C(x)=A \cos (\omega x+\phi)+B \text { for } \omega>0$ o de manera equivalente, en la forma$S(x)=A \sin (\omega x+\phi)+B \text { for } \omega>0$. En su momento, permanecíamos indecisos en cuanto a qué forma preferimos, pero se acabó el tiempo para tal indecisión. Para mayor claridad de exposición nos enfocamos en la función sinusoidal ² en esta sección y cambiamos a la variable independiente$t$, ya que las aplicaciones en esta sección son dependientes del tiempo. Reintroducimos y resumimos todos los hechos y definiciones importantes sobre esta forma de la sinusoide a continuación.

Propiedades de la Sinusoide$S(t)=A \sin (\omega t+\phi)+B$

La amplitud es |A|
La frecuencia angular es ω y la frecuencia ordinaria es$f=\frac{\omega}{2 \pi}$
El periodo es$T=\frac{1}{f}=\frac{2 \pi}{\omega}$
La fase es φ y el desplazamiento de fase es$-\frac{\phi}{\omega}$
El desplazamiento vertical o línea base es B

Además de conocer estas fórmulas, es útil recordar lo que significan estas cantidades en contexto. La amplitud mide el desplazamiento máximo de la onda sinusoidal desde su línea base (determinado por el desplazamiento vertical), el periodo es el tiempo que tarda en completar un ciclo de la sinusoide, la frecuencia angular indica cuántos ciclos se completan en un intervalo de longitud$2 \pi$, y el ordinario frecuencia mide cuántos ciclos ocurren por unidad de tiempo. La fase indica a qué ángulo$\phi$ corresponde$t = 0$, y el desplazamiento de fase representa la cantidad de un 'inicio de cabeza' que tiene la sinusoide sobre la función sinusoidal no desplazada. La siguiente figura se repite de la Sección 10.5.

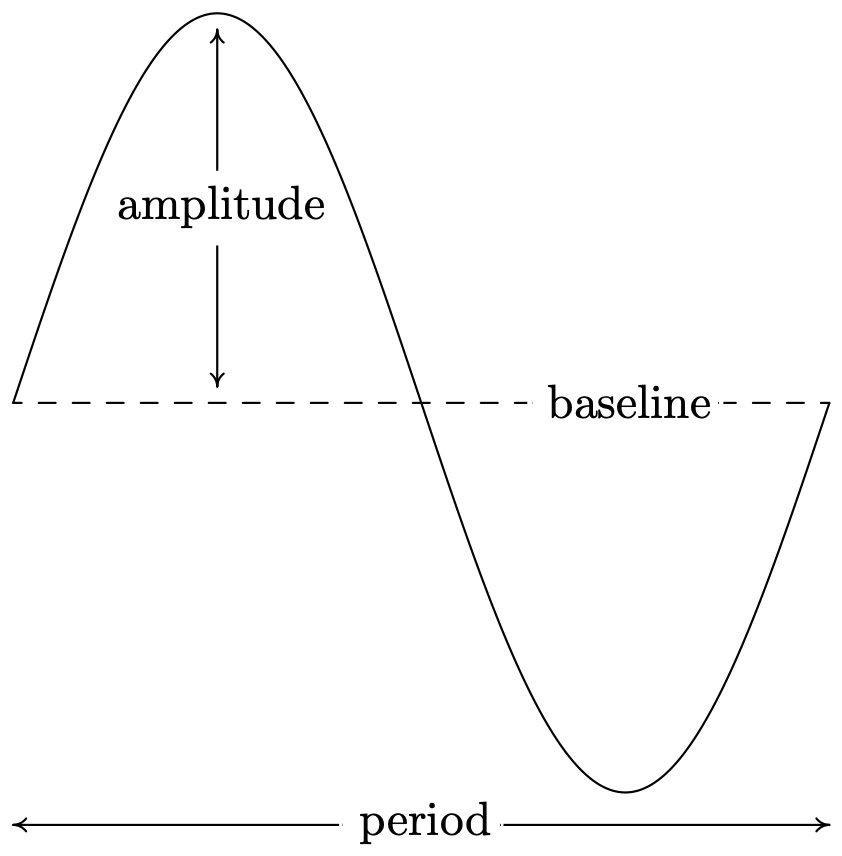
$Screen Shot 2022-05-17 a las 10.49.24 PM.png$

En la Sección 10.1.1, introdujimos el concepto de movimiento circular y en la Sección 10.2.1, desarrollamos fórmulas para el movimiento circular. Nuestra primera incursión en el movimiento sinusoidal le da un buen uso a estas nociones.

Ejemplo 11.1.1

Recordemos del Ejercicio 55 en la Sección 10.1 que La Rueda Gigante en Cedar Point es un círculo con un diámetro de 128 pies que se asienta sobre una plataforma de 8 pies de altura haciendo su altura total 136 pies. Se completa dos revoluciones en 2 minutos y 7 segundos. Suponiendo que los pasajeros están en el borde del círculo, encuentre una sinusoide que describa la altura de los pasajeros sobre el suelo$t$ segundos después de pasar el punto de la rueda más cercano al suelo.

Solución

A continuación, esbozamos la situación del problema y asumimos una rotación en sentido antihorario. ³

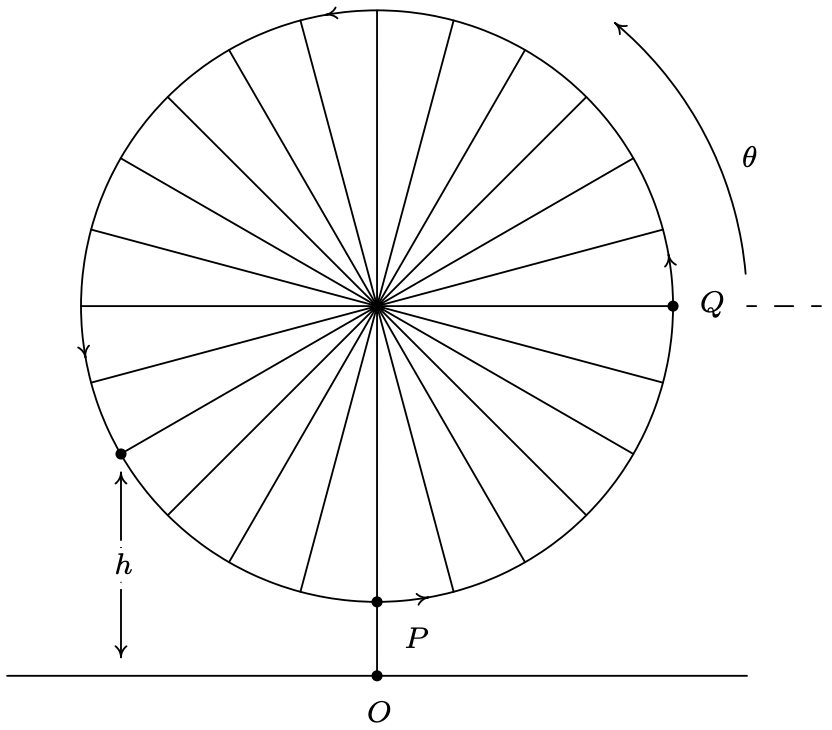
$Screen Shot 2022-05-20 en 2.57.04 PM.png$

Sabemos por las ecuaciones dadas en la página 732 de la Sección 10.2.1 que la coordenada y para el movimiento en sentido antihorario en un círculo de radio$r$ centrado en el origen con velocidad angular constante (frecuencia)$\omega$ viene dada por$y=r \sin (\omega t)$. Aquí,$t = 0$ corresponde al punto para$(r, 0)$ que$\theta$, el ángulo que mide la cantidad de rotación, esté en posición estándar. En nuestro caso, el diámetro de la rueda es de 128 pies, por lo que el radio es de$r$ = 64 pies. Dado que la rueda completa dos revoluciones en 2 minutos y 7 segundos (que es 127 segundos) el periodo$T=\frac{1}{2}(127)=\frac{127}{2}$ segundos. De ahí que la frecuencia angular sea$\omega=\frac{2 \pi}{T}=\frac{4 \pi}{127}$ radianes por segundo. Al juntar estas dos piezas de información, tenemos que$y=64 \sin \left(\frac{4 \pi}{127} t\right)$ describe la$y$ coordenada -en la Rueda Gigante después de$t$ segundos, asumiendo que está centrada en (0, 0) con$t = 0$ correspondiente al punto$Q$. Para encontrar una expresión para$h$, tomamos el punto$O$ en la figura como origen. Dado que la base del paseo de la Rueda Gigante está a 8 pies sobre el suelo y la Rueda Gigante en sí tiene un radio de 64 pies, su centro está a 72 pies sobre el suelo. Para dar cuenta de este desplazamiento vertical hacia arriba, ⁴ sumamos 72 a nuestra fórmula$y$ para obtener la nueva fórmula$h=y+72=64 \sin \left(\frac{4 \pi}{127} t\right)+72$. A continuación, necesitamos ajustar las cosas para que$t = 0$ corresponda al punto$P$ en lugar del punto$Q$. Aquí es donde entra en juego la fase. Geométricamente, necesitamos desplazar el ángulo$\theta$ θ en la figura hacia atrás$\frac{\pi}{2}$ radianes. De la Sección 10.2.1, sabemos$\theta=\omega t=\frac{4 \pi}{127} t$, por lo que (temporalmente) escribimos la altura en términos de$\theta$ como$h=64 \sin (\theta)+72$. Restar$\frac{\pi}{2}$ de$\theta$ da la respuesta final$h(t)=64 \sin \left(\theta-\frac{\pi}{2}\right)+72=64 \sin \left(\frac{4 \pi}{127} t-\frac{\pi}{2}\right)+72$. Podemos verificar la razonabilidad de nuestra respuesta graficando$y = h(t)$ sobre el inteval$\left[0, \frac{127}{2}\right]$.

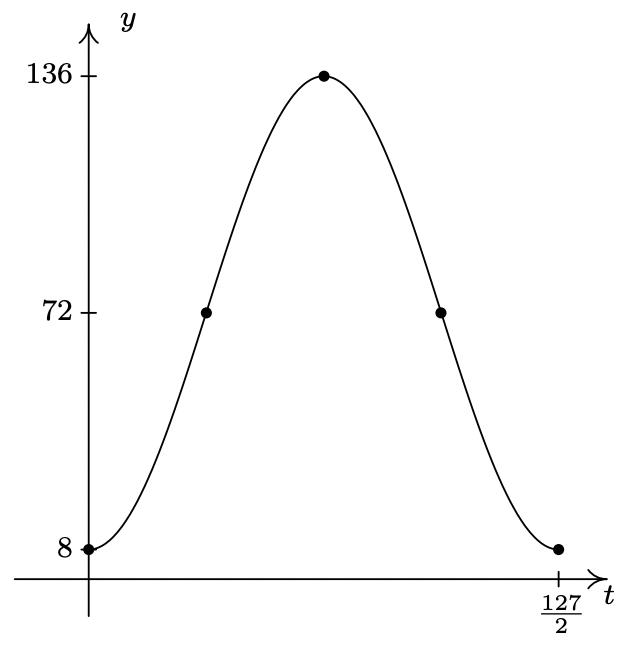
$Screen Shot 2022-05-20 en 3.11.56 PM.png$

Algunos comentarios sobre el Ejemplo 11.1.1 están en orden. Primero, tenga en cuenta que la amplitud de 64 en nuestra respuesta corresponde al radio de la Rueda Gigante. Esto significa que los pasajeros de la Rueda Gigante nunca se alejan más de 64 pies verticalmente del centro de la Rueda, lo cual tiene sentido. Segundo, el cambio de fase de nuestra respuesta resulta ser$\frac{\pi / 2}{4 \pi / 127}=\frac{127}{8}=15.875$. Esto representa el 'retraso de tiempo' (en segundos) que introducimos iniciando el movimiento en el punto en$P$ oposición al punto$Q$. Dicho de otra manera, los pasajeros que 'arrancan' en$P$ tardan 15.875 segundos en “ponerse al día” hasta el punto$Q$.

Nuestro siguiente ejemplo revisita los datos de luz diurna introducidos por primera vez en la Sección 2.5, Ejercicio 6b.

Ejemplo 11.1.2

Según el sitio web del Observatorio Naval de Estados Unidos, a continuación se da el número$H$ de horas de luz diurna que Fairbanks, Alaska$n$ recibió el día 21 del mes de 2009. Aquí$t = 1$ representa el 21 de enero de 2009,$t = 2$ representa el 21 de febrero de 2009, y así sucesivamente.

\[ \begin{array}{|l|r|r|r|r|r|r|r|r|r|r|r|r|} \hline \begin{array}{l} \text { Month } \\ \text { Number } \end{array} & 1 & 2 & 3 & 4 & 5 & 6 & 7 & 8 & 9 & 10 & 11 & 12 \\ \hline \begin{array}{l} \text { Hours of } \\ \text { Daylight } \end{array} & 5.8 & 9.3 & 12.4 & 15.9 & 19.4 & 21.8 & 19.4 & 15.6 & 12.4 & 9.1 & 5.6 & 3.3 \\ \hline \end{array}\nonumber\]

Encuentre una sinusoide que modele estos datos y use una utilidad gráfica para graficar su respuesta junto con los datos.
Compara tu respuesta con la primera parte con la obtenida usando la función de regresión de una calculadora.

Solución

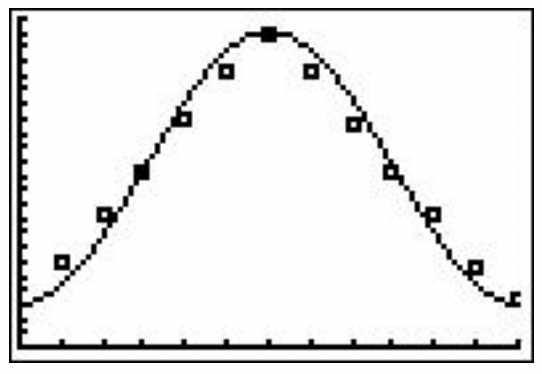
Para tener una idea de los datos, los trazamos a continuación.
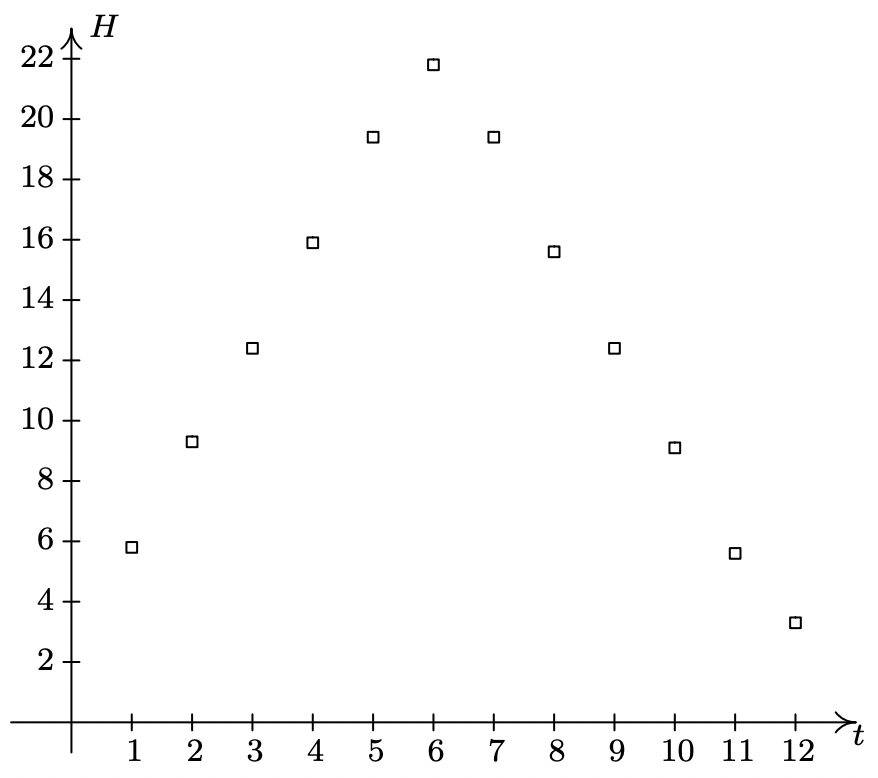
$Screen Shot 2022-05-20 a las 3.26.53 PM.png$

Los datos ciertamente parecen sinusoidales, ⁵ pero cuando se trata de ello, ajustar una sinusoide a los datos manualmente no es una ciencia exacta. Hacemos nuestro mejor esfuerzo para encontrar las constantes$A, \omega, \phi$ y$B$ para que la función coincida$H(t)=A \sin (\omega t+\phi)+B$ estrechamente con los datos. Primero vamos después del desplazamiento vertical$B$ cuyo valor determina la línea base. En una sinusoide típica, el valor de$B$ es el promedio de los valores máximo y mínimo. Entonces aquí llevamos$B=\frac{3.3+21.8}{2}=12.55$. A continuación se encuentra la amplitud$A$ que es el desplazamiento desde la línea base hasta los valores máximos (y mínimos). Nos encontramos$A=21.8-12.55=12.55-3.3=9.25$. En este punto, tenemos$H(t)=9.25 \sin (\omega t+\phi)+12.55$. A continuación, vamos tras la frecuencia angular$\omega$. Dado que los datos recopilados se encuentran en el lapso de un año (12 meses), tomamos el periodo$T=12$ meses. ⁶ Esto significa$\omega=\frac{2 \pi}{T}=\frac{2 \pi}{12}=\frac{\pi}{6}$. La última cantidad a encontrar es la fase$\phi$. A diferencia del ejemplo anterior, es más fácil en este caso encontrar el desplazamiento de fase$-\frac{\phi}{\omega}$. Desde que escogimos$A>0$, el desplazamiento de fase corresponde al primer valor de$t$ con$H(t) = 12.55$ (el valor de línea base). ⁷ Aquí, elegimos$t = 3$, ya que su$H$ valor correspondiente de 12.4 está más cerca de 12.55 que el siguiente valor, 15.9, que corresponde a$t = 4$. De ahí,$-\frac{\phi}{\omega}=3$, entonces$\phi=-3 \omega=-3\left(\frac{\pi}{6}\right)=-\frac{\pi}{2}$. Tenemos$H(t)=9.25 \sin \left(\frac{\pi}{6} t-\frac{\pi}{2}\right)+12.55$. A continuación se muestra una gráfica de nuestros datos con la curva$y = H(t)$.

$Screen Shot 2022-05-20 en 4.04.59 PM.png$
Usando el comando 'SinReg', graficamos la regresión de la calculadora a continuación.
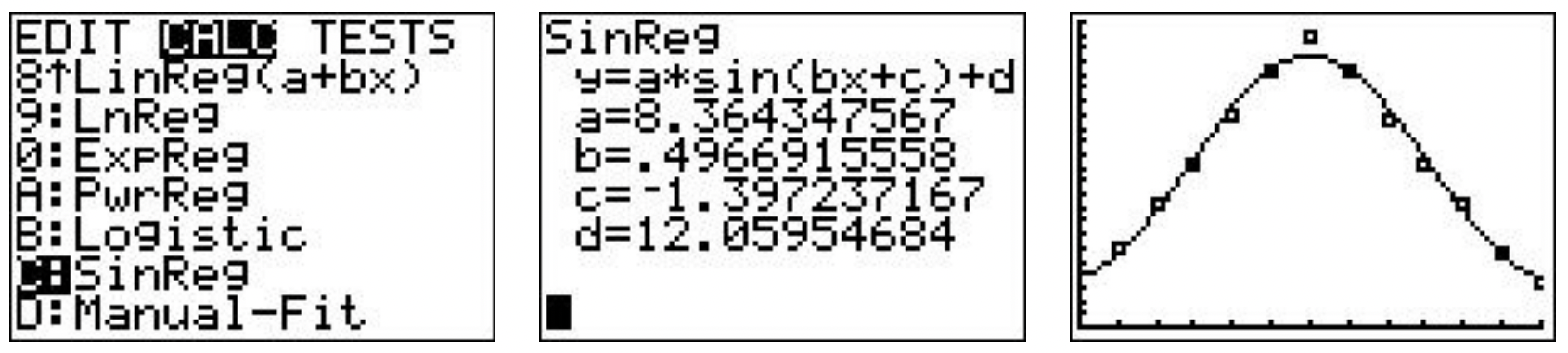
$Screen Shot 2022-05-20 a las 4.12.49 PM.png$

Si bien ambos modelos parecen ser ajustes razonables a los datos, el modelo de calculadora es posiblemente el mejor ajuste. La calculadora no nos da$r^{2}$ valor como lo hizo para las regresiones lineales en la Sección 2.5, ni nos da$R^{2}$ valor como lo hizo para las regresiones cuadráticas, cúbicas y cuárticas como en la Sección 3.1. El motivo de esto, al igual que el motivo de la ausencia de$R^{2}$ para el modelo logístico en la Sección 6.5, está más allá del alcance de este curso. Solo tendremos que usar nuestro propio buen juicio a la hora de elegir el mejor modelo sinusoidal.

11.1.1 Movimiento armónico

Una de las principales aplicaciones de los sinusoides en Ciencia e Ingeniería es el estudio del movimiento armónico. Las ecuaciones para el movimiento armónico pueden utilizarse para describir una amplia gama de fenómenos, desde el movimiento de un objeto sobre un resorte, hasta la respuesta de un circuito electrónico. En esta subsección, restringimos nuestra atención a modelar un sistema de resorte simple. Antes de saltar a las Matemáticas, hay algunos términos y conceptos de Física que necesitamos discutir. En Física, 'masa' se define como una medida de la resistencia de un objeto al movimiento en línea recta, mientras que 'peso' es la cantidad de fuerza (tracción) que la gravedad ejerce sobre un objeto. La masa de un objeto no puede cambiar, ⁸ mientras que su peso podría cambiar.

Un objeto que pesa 6 libras en la superficie de la Tierra pesaría 1 libra en la superficie de la Luna, pero su masa es la misma en ambos lugares. En el sistema inglés de unidades, 'libras' (lbs.) es una medida de fuerza (peso), y la unidad de masa correspondiente es la 'slug'. En el sistema SI, la unidad de fuerza es 'Newtons' (N) y la unidad de masa asociada es el 'kilogramo' (kg). Convertimos entre masa y peso usando la fórmula ⁹$w=m g$. Aquí,$w$ está el peso del objeto,$m$ es la masa y$g$ es la aceleración debido a la gravedad. En el sistema inglés,$g=32 \frac{\text { feet }}{\text { second}^{2}}$, y en el sistema SI,$g=9.8 \frac{\text { meters }}{\text { second}^{2}}$. De ahí que en la Tierra a$mass$ de 1 babosa$weighs$ 32 lbs. y a$mass$ de 1 kg$weighs$ 9.8 N. ¹⁰ Supongamos que sujetamos un objeto con masa$m$ a un resorte como se representa a continuación. El peso del objeto estirará el resorte. Se dice que el sistema está en 'equilibrio' cuando el peso del objeto está perfectamente equilibrado con la fuerza restauradora del resorte. La distancia que se estira la primavera para alcanzar el equilibrio depende de la 'constante de resorte' de la primavera. Generalmente denotada por la letra$k$, la constante de resorte relaciona la fuerza$F$ aplicada al resorte con la cantidad que estira$d$ el resorte de acuerdo con la Ley ¹¹ de Hooke$F=k d$. Si el objeto se libera por encima o por debajo de la posición de equilibrio, o si el objeto se libera con una velocidad ascendente o descendente, el objeto rebotará hacia arriba y hacia abajo en el extremo del resorte hasta que alguna fuerza externa lo detenga. Si dejamos$x(t)$ denotar el desplazamiento del objeto desde la posición de equilibrio en el tiempo$t$, entonces$x(t) = 0$ significa que el objeto está en la posición de equilibrio,$x(t)<0$ significa que el objeto está por encima de la posición de equilibrio, y$x(t)>0$ significa que el objeto está por debajo de la posición de equilibrio. La función$x(t)$ se llama la 'ecuación de movimiento' del objeto. ¹²

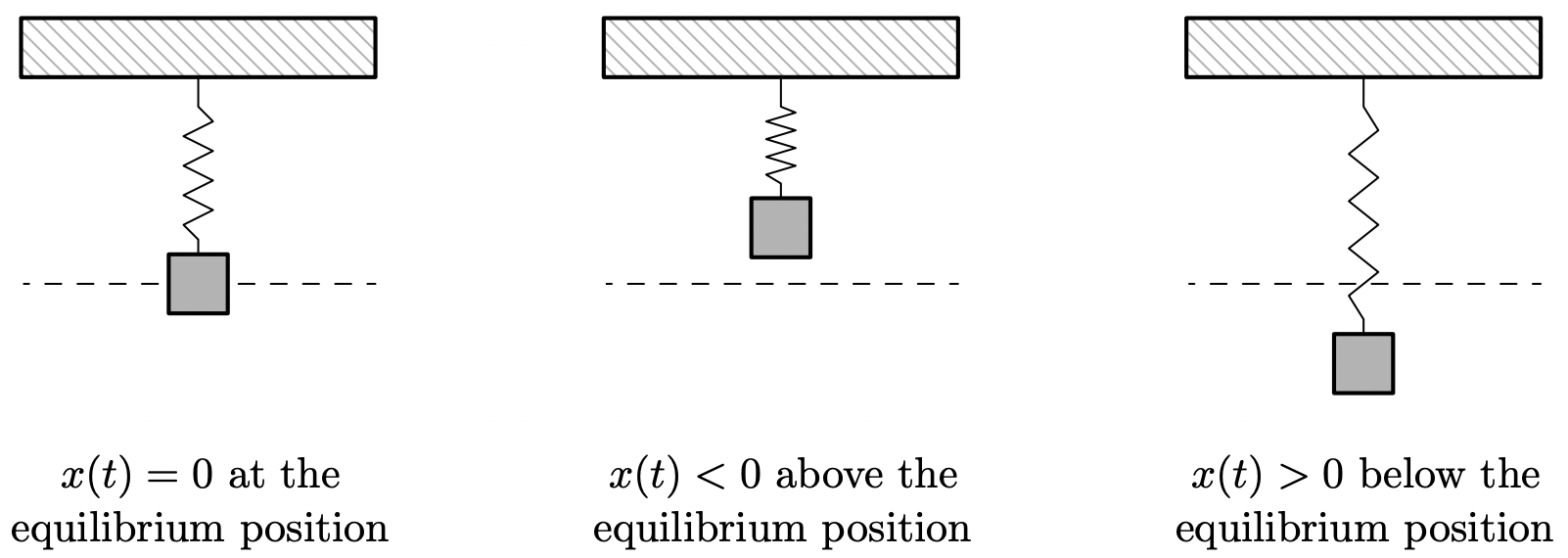
$Screen Shot 2022-05-20 a las 4.29.43 PM.png$

Si ignoramos todas las demás influencias en el sistema excepto la gravedad y la fuerza del resorte, entonces la Física nos dice que la gravedad y la fuerza del resorte lucharán entre sí para siempre y el objeto oscilará indefinidamente. En este caso, describimos el movimiento como 'libre' (es decir, no hay fuerza externa que cause el movimiento) y 'sin amortiguar' (es decir, ignoramos la fricción causada por el medio circundante, que en nuestro caso es el aire). El siguiente teorema, que proviene de Ecuaciones Diferenciales, da$x(t)$ como función$m$ de la masa del objeto, la constante de resorte$k$, el desplazamiento inicial$x_{0}$ del objeto y la velocidad inicial$v_{0}$ del objeto. Al igual que con$x(t)$,$x_{0}=0$ significa que el objeto se libera de la posición de equilibrio,$x_{0}<0$ significa que el objeto se libera por encima de la posición de equilibrio y$x_{0}>0$ significa que el objeto se libera por debajo de la posición de equilibrio. En lo que respecta a la velocidad$v_{0}$ inicial,$v_{0}=0$ significa que el objeto se libera 'del descanso',$v_{0}<0$ significa que el objeto se dirige hacia arriba y$v_{0}>0$ significa que el objeto se dirige hacia abajo. ¹³

Teorema 11.1. Ecuación para el movimiento armónico libre sin amortiguar

Supongamos que un objeto de masa$m$ está suspendido de un resorte con constante de resorte$k$. Si el desplazamiento inicial desde la posición de equilibrio es$x_{0}$ y la velocidad inicial del objeto es$v_{0}$, entonces el desplazamiento$x$ desde la posición de equilibrio en el tiempo$t$ viene dado por$x(t)=A \sin (\omega t+\phi)$ donde

$\omega=\sqrt{\frac{k}{m}} \text { and } A=\sqrt{x_{0}^{2}+\left(\frac{v_{0}}{\omega}\right)^{2}}$
$A \sin (\phi)=x_{0} \text { and } A \omega \cos (\phi)=v_{0}$.

Es un gran ejercicio de 'análisis dimensional' para verificar que las fórmulas dadas en el Teorema 11.1 funcionan para que$\omega$ tenga unidades$\frac{1}{s}$ y$A$ tenga unidades ft. o m, dependiendo del sistema que elijamos.

Ejemplo 11.1.3

Supongamos que un objeto que pesa 64 libras estira un resorte de 8 pies.

Si el objeto está unido al resorte y liberado 3 pies por debajo de la posición de equilibrio del reposo, encuentre la ecuación de movimiento del objeto,$x(t)$. ¿Cuándo pasa el objeto por primera vez por la posición de equilibrio? ¿El objeto se dirige hacia arriba o hacia abajo en este instante?
Si el objeto está unido al resorte y liberado 3 pies por debajo de la posición de equilibrio con una velocidad ascendente de 8 pies por segundo, encuentre la ecuación de movimiento del objeto,$x(t)$. ¿Cuál es la distancia más larga que recorre el objeto sobre la posición de equilibrio? ¿Cuándo ocurre esto por primera vez? Confirma tu resultado usando una utilidad gráfica.

Solución

Para poder utilizar las fórmulas en el Teorema 11.1, primero necesitamos determinar la constante elástica$k$ y la masa del objeto$m$. Para encontrar$k$, usamos la Ley de Hooke$F = kd$. Sabemos que el objeto pesa 64 lbs. y estira el resorte 8 ft.. Usando$F = 64$ y$d = 8$, obtenemos$64=k \cdot 8$, o$k=8 \frac{\mathrm{lbs.}}{\mathrm{ft.}}$. Para encontrar$m$, usamos$w = mg$ con$w = 64$ lbs. y$g=32 \frac{\mathrm{ft.}}{s^{2}}$. Conseguimos$m = 2$ babosas. Ahora podemos proceder a aplicar el Teorema 11.1.

Con$k = 8$ y$m = 2$, obtenemos$\omega=\sqrt{\frac{k}{m}}=\sqrt{\frac{8}{2}}=2$. Se nos dice que el objeto se libera 3 pies por debajo de la posición de equilibrio 'del descanso'. Esto significa$x_{0}=3$ y$v_{0}=0$. Por lo tanto,$A=\sqrt{x_{0}^{2}+\left(\frac{v_{0}}{\omega}\right)^{2}}=\sqrt{3^{2}+0^{2}}=3$. Para determinar la fase$\phi$, tenemos$A \sin (\phi)=x_{0}$, que en este caso$3 \sin (\phi)=3$ así lo da$\sin (\phi)=1$. Únicamente$\phi=\frac{\pi}{2}$ y ángulos coterminales a ella satisfacen esta condición, por lo que elegimos ¹⁴ la fase a ser$\phi=\frac{\pi}{2}$. De ahí que la ecuación del movimiento sea$x(t)=3 \sin \left(2 t+\frac{\pi}{2}\right)$. Para encontrar cuándo el objeto pasa por la posición de equilibrio resolvemos$x(t)=3 \sin \left(2 t+\frac{\pi}{2}\right)=0$. Pasando por el análisis habitual encontramos$t=-\frac{\pi}{4}+\frac{\pi}{2} k$ para enteros$k$. Como nos interesa la primera vez que el objeto pasa por la posición de equilibrio, buscamos el$t$ valor positivo más pequeño que en este caso es de$t=\frac{\pi}{4} \approx 0.78$ 8 segundos después del inicio del movimiento. El sentido común sugiere que si liberamos el objeto por debajo de la posición de equilibrio, el objeto debería estar viajando hacia arriba cuando pase por él por primera vez. Para verificar esta respuesta, graficamos un ciclo de$x(t)$. Dado que nuestro dominio aplicado en esta situación es$t \geq 0$, y el periodo de$x(t)$ es$T=\frac{2 \pi}{\omega}=\frac{2 \pi}{2}=\pi$, graficamos$x(t)$ sobre el intervalo$[0, \pi]$. Recordar eso$x(t)>0$ significa que el objeto está por debajo de la posición de equilibrio y$x(t)<0$ significa que el objeto está por encima de la posición de equilibrio, el hecho de que nuestra gráfica esté cruzando a través del$t$ eje -de x positiva a negativa$x$ en$t=\frac{\pi}{4}$ confirma nuestra respuesta.
La única diferencia entre este problema y el problema anterior es que ahora liberamos el objeto con una velocidad ascendente de$8 \frac{\mathrm{ft}}{s}$. Todavía tenemos$\omega=2$ y$x_{0}=3$, pero ahora tenemos$v_{0}=-8$, el negativo que indica que la velocidad se dirige hacia arriba. Aquí, obtenemos$A=\sqrt{x_{0}^{2}+\left(\frac{v_{0}}{\omega}\right)^{2}}=\sqrt{3^{2}+(-4)^{2}}=5$. 5. De$A \sin (\phi)=x_{0}$, obtenemos$5 \sin (\phi)=3$ lo que da$\sin (\phi)=\frac{3}{5}$. De$A \omega \cos (\phi)=v_{0}$, obtenemos$10 \cos (\phi)=-8$, o$\cos (\phi)=-\frac{4}{5}$. Esto quiere decir que$\phi$ es un ángulo del Cuadrante II que podemos describir en términos de arcoseno o arcoseno. Ya que$x(t)$ se expresa en términos de seno, elegimos expresarlo$\phi=\pi-\arcsin \left(\frac{3}{5}\right)$. De ahí,$x(t)=5 \sin \left(2 t+\left[\pi-\arcsin \left(\frac{3}{5}\right)\right]\right)$ .Dado que la amplitud de$x(t)$ es 5, el objeto viajará como máximo 5 pies por encima de la posición de equilibrio. Para encontrar cuando esto sucede, resolvemos la ecuación$x(t)=5 \sin \left(2 t+\left[\pi-\arcsin \left(\frac{3}{5}\right)\right]\right)=-5$, la negativa una vez más significa que el objeto está por encima de la posición de equilibrio. Pasando por las maquinaciones habituales, obtenemos$t=\frac{1}{2} \arcsin \left(\frac{3}{5}\right)+\frac{\pi}{4}+\pi k$ para enteros$k$. El menor de estos valores ocurre cuando$k = 0$, es decir,$t=\frac{1}{2} \arcsin \left(\frac{3}{5}\right)+\frac{\pi}{4} \approx 1.107$ segundos después del inicio del movimiento. Para verificar nuestra respuesta usando la calculadora, graficamos$y=5 \sin \left(2 x+\left[\pi-\arcsin \left(\frac{3}{5}\right)\right]\right)$ en una utilidad gráfica y confirmamos que las coordenadas del primer mínimo relativo sean aproximadamente (1.107, -5).
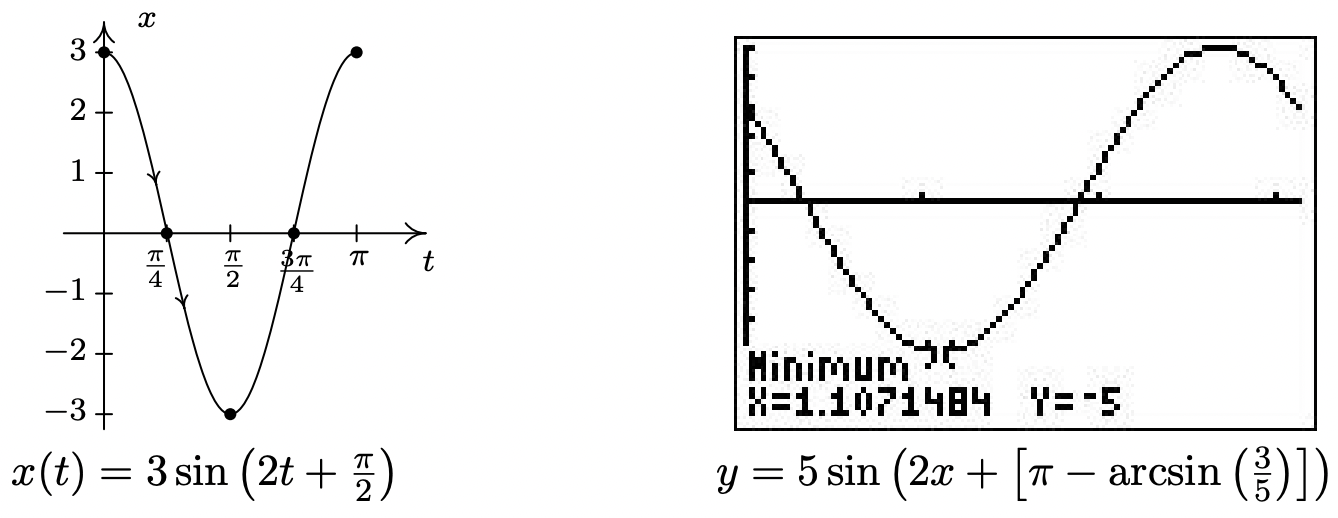
$Screen Shot 2022-05-23 en 3.21.46 PM.png$

Es posible, aunque fuera del alcance de este curso, modelar los efectos de la fricción y otras fuerzas externas que actúan sobre el sistema. ¹⁵ Si bien es posible que no tengamos los antecedentes de Física y Cálculo para derivar ecuaciones de movimiento para estos escenarios, ciertamente podemos analizarlos. Examinamos tres casos en el siguiente ejemplo.

Ejemplo 11.1.4

Escribe$x(t)=5 e^{-t / 5} \cos (t)+5 e^{-t / 5} \sqrt{3} \sin (t)$ en el formulario$x(t)=A(t) \sin (\omega t+\phi)$. Gráfica$x(t)$ usando una utilidad gráfica.
Escribe$x(t)=(t+3) \sqrt{2} \cos (2 t)+(t+3) \sqrt{2} \sin (2 t)$ en el formulario$x(t)=A(t) \sin (\omega t+\phi)$. Gráfica$x(t)$ usando una utilidad gráfica.
Encuentra el periodo de$x(t) = 5 sin(6t) − 5 sin (8t)$. Gráfica$x(t)$ usando una utilidad gráfica.

Solución

Empezamos a reescribir$x(t)=5 e^{-t / 5} \cos (t)+5 e^{-t / 5} \sqrt{3} \sin (t)$ factorizando$5 e^{-t / 5}$ desde ambos términos para obtener$x(t)=5 e^{-t / 5}(\cos (t)+\sqrt{3} \sin (t))$. Convertimos lo que queda entre paréntesis a la forma requerida usando las fórmulas introducidas en el Ejercicio 36 de la Sección 10.5. Encontramos$(\cos (t)+\sqrt{3} \sin (t))=2 \sin \left(t+\frac{\pi}{3}\right)$ así que$x(t)=10 e^{-t / 5} \sin \left(t+\frac{\pi}{3}\right)$. Graficando esto en la calculadora como$y=10 e^{-x / 5} \sin \left(x+\frac{\pi}{3}\right)$ revela algún comportamiento interesante. La naturaleza sinusoidal continúa indefinidamente, pero se está atenuando. En la sinusoide$A \sin (\omega x+\phi)$, el coeficiente$A$ de la función sinusoidal es la amplitud. En el caso de$y=10 e^{-x / 5} \sin \left(x+\frac{\pi}{3}\right)$, podemos pensar en la función$A(x)=10 e^{-x / 5}$ como la amplitud. Como$x \rightarrow \infty, 10 e^{-x / 5} \rightarrow 0$ lo que significa que la amplitud continúa reduciéndose hacia cero. En efecto, si graficamos$y=\pm 10 e^{-x / 5}$ junto con$y=10 e^{-x / 5} \sin \left(x+\frac{\pi}{3}\right)$, vemos que esta atenuación se lleva a cabo. Esta ecuación corresponde al movimiento de un objeto sobre un resorte donde hay una ligera fuerza que actúa para 'humedecer', o ralentizar la cámara. Un ejemplo de este tipo de fuerza sería la fricción del objeto contra el aire. En este modelo, el objeto oscila para siempre, pero con una amplitud cada vez menor.
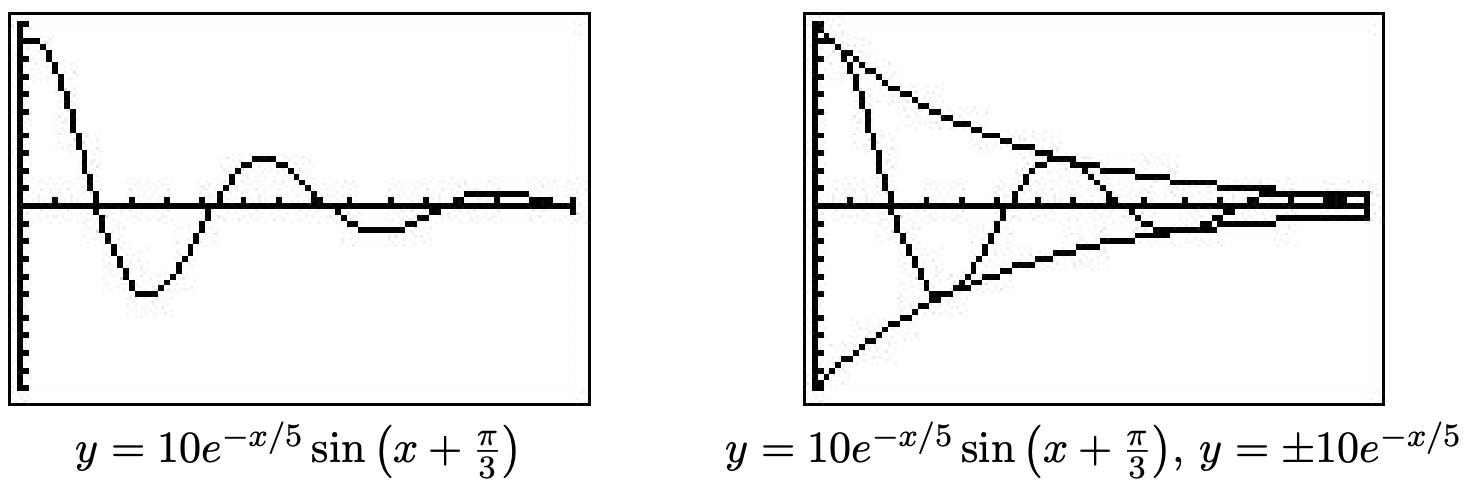
$Screen Shot 2022-05-23 a las 4.17.16 PM.png$
Procediendo como en el primer ejemplo, factorizamos$(t+3) \sqrt{2}$ de cada término en la función$x(t)=(t+3) \sqrt{2} \cos (2 t)+(t+3) \sqrt{2} \sin (2 t)$ a obtener$x(t)=(t+3) \sqrt{2}(\cos (2 t)+\sin (2 t))$. Nos encontramos$(\cos (2 t)+\sin (2 t))=\sqrt{2} \sin \left(2 t+\frac{\pi}{4}\right)$, así$x(t)=2(t+3) \sin \left(2 t+\frac{\pi}{4}\right)$. Graficando esto en la caculación como$y=2(x+3) \sin \left(2 x+\frac{\pi}{4}\right)$, encontramos que la amplitud de la sinusoide crece. Ya que nuestra función de amplitud aquí es$A(x)=2(x+3)=2 x+6$, que sigue creciendo sin ataduras ya que$x \rightarrow \infty$, esto no es de extrañar. El fenómeno aquí ilustrado es el movimiento 'forzado'. Es decir, imaginamos que todo el aparato en el que está unido el resorte también está oscilando. En este caso, estamos presenciando un efecto de 'resonancia': la frecuencia de la oscilación externa coincide con la frecuencia del movimiento del objeto en el resorte. ¹⁶
Por último, pero no menos importante, llegamos a$x(t) = 5 sin(6t)−5 sin(8t)$. Para encontrar el periodo de esta función, necesitamos determinar la longitud del intervalo más pequeño en el que ambos$f(t) = 5 sin(6t)$ y$g(t) = 5 sin(8t)$ completar un número entero de ciclos. Para ello, tomamos la relación de sus frecuencias y reducimos a términos más bajos:$\frac{6}{8}=\frac{3}{4}$. Esto nos dice que por cada 3 ciclos$f$ hace,$g$ hace 4. En otras palabras, el periodo de$x(t)$ es tres veces el periodo de$f(t)$ (que es cuatro veces el periodo de$g(t)$), o$\pi$. Gráficamos$y = 5 sin(6x) − 5 sin(8x)$$[0, \pi]$ sobre la calculadora para verificar esto. Esta ecuación de movimiento también resulta del movimiento 'forzado', pero aquí la frecuencia de la oscilación externa es diferente a la del objeto en el resorte. Dado que las sinusoides aquí tienen diferentes frecuencias, están 'desincrónicas' y no se amplifican entre sí como en el ejemplo anterior. Llevando las cosas un paso más allá, podemos usar una suma a la identidad del producto para reescribir$x(t) = 5 sin(6t) − 5 sin(8t) as x(t) = −10 sin(t) cos(7t)$. El menor factor de frecuencia en esta expresión,$−10 sin(t)$, juega un papel interesante en la gráfica de$x(t)$. A continuación graficamos$y = 5 sin(6x) − 5 sin(8x)$ y$y=\pm 10 \sin (x)$ más$[0,2 \pi]$. Este es un ejemplo del fenómeno 'beat', y se invita al lector curioso a explorar este concepto también. ¹⁷

11.1.2 Ejercicios

Los sonidos que escuchamos están conformados por ondas mecánicas. La nota 'A' por encima de la nota 'C media' es una onda sonora con frecuencia ordinaria$f=440 \text { Hertz }=440 \frac{\text { cycles }}{\text { second }}$. Encuentra una sinusoide que modele esta nota, asumiendo que la amplitud es 1 y el desplazamiento de fase es 0.
El voltaje$V$ en una fuente de corriente alterna tiene amplitud$220 \sqrt{2}$ y frecuencia ordinaria$f=60 \text { Hertz }$. Encuentra una sinusoide que modele este voltaje. Supongamos que la fase es 0.
The London Eye es una atracción turística popular en Londres, Inglaterra y es una de las Noria más grandes del mundo. Tiene un diámetro de 135 metros y hace una revolución (en sentido antihorario) cada 30 minutos. Está construido de manera que la parte más baja del Ojo alcance el nivel del suelo, lo que permite a los pasajeros simplemente caminar hacia, y fuera de, el viaje. Encuentra un sinsuoide que modele la altura$h$ del pasajero sobre el suelo en metros$t$ minutos después de que aborde el Ojo a nivel del suelo.
En la página 732 de la Sección 10.2.1, encontramos la$x$ coordenada -del movimiento en sentido antihorario sobre un círculo de radio$r$ con frecuencia angular$\omega$ a ser$x=r \cos (\omega t)$, donde$t = 0$ corresponde al punto$(r, 0)$. Supongamos que estamos en la situación del Ejercicio 3 anterior. Encuentra un sinsusoide que modele el desplazamiento horizontal$x$ del pasajero desde el centro del Ojo en metros$t$ minutos después de que aborde el Ojo. Aquí tomamos$x(t)>0$ para significar que el pasajero está a la derecha del centro, mientras que$x(t)<0$ significa que el pasajero está a la izquierda del centro.
En el Ejercicio 52 de la Sección 10.1, presentamos el truco del yoyo 'La vuelta al mundo' en el que se lanza un yoyo para que barre un círculo vertical. Al igual que en ese ejercicio, supongamos que la cuerda de yoyo mide 28 pulgadas y completa una revolución en 3 segundos. Si lo más cerca que el yoyo llega al suelo es de 2 pulgadas, encuentra un sinsuoide que modele la altura$h$ del yoyo sobre el suelo en pulgadas$t$ segundos después de que abandone su punto más bajo.
Supongamos que un objeto que pesa 10 libras está suspendido del techo por un resorte que se estira 2 pies hasta su posición de equilibrio cuando el objeto está unido.
1. Encuentra la constante$k$ de resorte$\frac{\mathrm{lbs} .}{\mathrm{ft} .}$ y la masa del objeto en babosas.
2. Encuentra la ecuación de movimiento del objeto si se libera desde 1 pie por debajo de la posición de equilibrio del reposo. ¿Cuándo es la primera vez que el objeto pasa por la posición de equilibrio? ¿En qué dirección se dirige?
3. Encuentra la ecuación de movimiento del objeto si se libera desde 6 pulgadas por encima de la posición de equilibrio con una velocidad descendente de 2 pies por segundo. Encuentra cuándo el objeto pasa por la posición de equilibrio dirigiéndose hacia abajo por tercera vez.
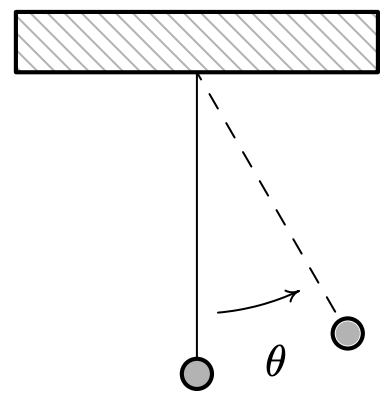
\[T=2 \pi \sqrt{\frac{l}{g}}\nonumber\]

donde$l$ es la longitud del péndulo y$g$ es la aceleración debida a la gravedad.
1. Encontrar una sinusoide que da el desplazamiento$\theta$ angular en función del tiempo,$t$. Arreglar las cosas así$\theta(0)=\theta_{0}$.
2. En el Ejercicio 40 sección 5.3, encontraste la longitud del péndulo necesaria en el antiguo reloj Seth-Thomas de Jeff para asegurar que el periodo del péndulo sea$\frac{1}{2}$ de un segundo. Suponiendo que el desplazamiento inicial del péndulo es$15^{\circ}$, encontrar una sinusoide que modele el desplazamiento del péndulo$\theta$ en función del tiempo,$t$, en segundos.
La siguiente tabla enumera la temperatura promedio del lago Erie medida en Cleveland, Ohio el primero del mes por cada mes durante los años 1971 — 2000. ¹⁹ Por ejemplo,$t = 3$ representa el promedio de las temperaturas registradas para el lago Erie cada 1 de marzo para los años 1971 a 2000.
\ [\ begin {array} {|l|r|r|r|r|r|r|r|r|r|r|r|r|r|}\ hline\ begin {array} {l}\ text {Mes}\\\ texto {Número,} t\ end {array} & 1 y 2 y 3 y 4 y 5 y 6 y 7 y 8 y 9 y 10 y 11 y 12\
\ hline\ begin {array} {l}\ text {Temperatura}\\\ izquierda ({} ^ {\ circ}\ mathrm {F}\ derecha), T\ end {array} & 36 & 33 & 34 & 38 & 47 & 57 & 67 & 74 & 73 & 67 & 56 & 46\\ hline
\ end {array}\ nonumber\]
1. Utilizando las técnicas discutidas en el Ejemplo 11.1.2, ajustar una sinusoide a estos datos.
2. Usando una utilidad gráfica, grafica tu modelo junto con el conjunto de datos para juzgar la razonabilidad del ajuste.
3. ^{Utilice el modelo que encontró en la parte 8a para predecir la temperatura promedio registrada para el lago Erie el 15 de ^abril y el 15 de septiembre durante los años 1971—2000.} ²⁰
4. Compara tus resultados con los obtenidos usando una utilidad gráfica.
La fracción de la luna iluminada a la medianoche Hora Estándar del Este del$t^{\text {th }}$ día de junio de 2009 se da en la siguiente tabla. ²¹
1. Utilizando las técnicas discutidas en el Ejemplo 11.1.2, ajustar una sinusoide a estos datos. ²²
2. Usando una utilidad gráfica, grafica tu modelo junto con el conjunto de datos para juzgar la razonabilidad del ajuste.
3. Usa el modelo que encontraste en la parte 9a para predecir la fracción de la luna iluminada el 1 de junio de 2009. ²³
4. Compara tus resultados con los obtenidos usando una utilidad gráfica.
Con la ayuda de tus compañeros, investiga los fenómenos mencionados en el Ejemplo 11.1.4, a saber, resonancia y latidos.
Con la ayuda de tus compañeros, investiga Modulación de Amplitud y Modulación de Frecuencia.
¿Qué otras cosas en el mundo podrían ser más o menos sinusoidales? Busca para ver qué modelos puedes encontrar para ellos y comparte tus resultados con tu clase.

11.1.3 Respuestas

$S(t)=\sin (880 \pi t)$
$V(t)=220 \sqrt{2} \sin (120 \pi t)$
$h(t)=28 \sin \left(\frac{2 \pi}{3} t-\frac{\pi}{2}\right)+30$
$x(t)=67.5 \cos \left(\frac{\pi}{15} t-\frac{\pi}{2}\right)=67.5 \sin \left(\frac{\pi}{15} t\right)$
$h(t)=28 \sin \left(\frac{2 \pi}{3} t-\frac{\pi}{2}\right)+30$
1. $k=5 \frac{\text { lbs. }}{\text { ft. }} \text { and } m=\frac{5}{16} \text { slugs }$
2. $x(t)=\sin \left(4 t+\frac{\pi}{2}\right)$. El objeto primero pasa por el punto de equilibrio cuando$t=\frac{\pi}{8} \approx 0.39$ 0.39 segundos después de que comienza el movimiento. En este momento, el objeto se dirige hacia arriba.
3. $x(t)=\frac{\sqrt{2}}{2} \sin \left(4 t+\frac{7 \pi}{4}\right)$. El objeto pasa por el punto de equilibrio dirigiéndose hacia abajo por tercera vez cuando$t=\frac{17 \pi}{16} \approx 3.34$ segundos.
1. $\theta(t)=\theta_{0} \sin \left(\sqrt{\frac{g}{l}} t+\frac{\pi}{2}\right)$
2. $\theta(t)=\frac{\pi}{12} \sin \left(4 \pi t+\frac{\pi}{2}\right)$
1. $T(t)=20.5 \sin \left(\frac{\pi}{6} t-\pi\right)+53.5$
2. Nuestra función y el conjunto de datos se representan a continuación. La sinusoide parece estar desplazada a la derecha de nuestros datos.
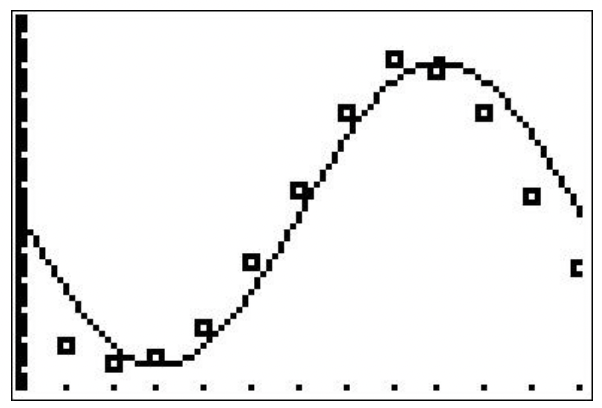
  $Screen Shot 2022-05-24 a las 12.25.45 AM.png$
3. La temperatura promedio de abril$15^{\text {th }}$ es aproximadamente$T(4.5) \approx 39.00^{\circ} \mathrm{F}$ y la temperatura promedio en septiembre$15^{\text {th }}$ es de aproximadamente$T(9.5) \approx 73.38^{\circ} \mathrm{F}$.
4. Usando una calculadora gráfica, obtenemos lo siguiente
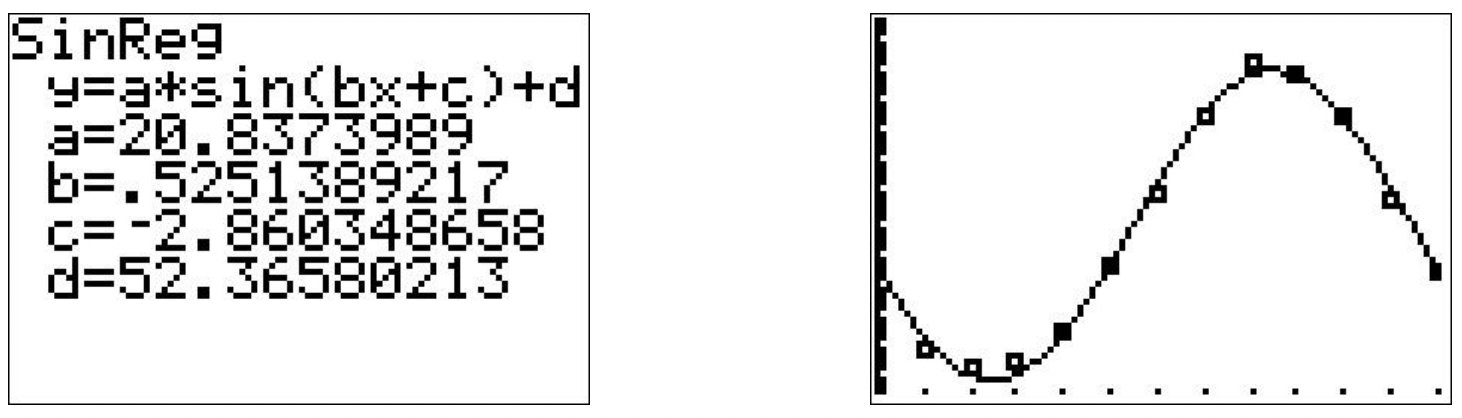
  $Screen Shot 2022-05-24 a las 12.31.40 AM.png$
  
  Este modelo predice que la temperatura promedio$15^{\mathrm{th}}$ para abril sea aproximadamente$42.43^{\circ} \mathrm{F}$ y la temperatura promedio en septiembre$15^{\text {th }}$ sea aproximadamente$70.05^{\circ} \mathrm{F}$. Este modelo parece ser más preciso.
1. Con base en la forma de los datos, o bien elegimos$A<0$ o encontramos el segundo valor del$t$ cual se aproxima estrechamente al valor de 'línea base',$F=0.505$. Elegimos este último para obtener$F(t)=0.475 \sin \left(\frac{\pi}{15} t-2 \pi\right)+0.505=0.475 \sin \left(\frac{\pi}{15} t\right)+0.505$.
2. Nuestra función y el conjunto de datos se representan a continuación. Es un ajuste bastante bueno.
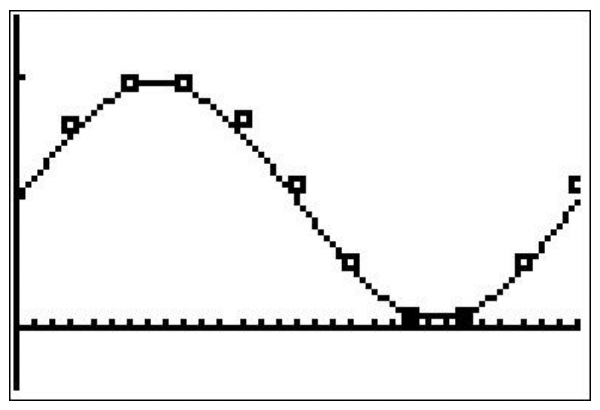
  $Screen Shot 2022-05-24 a las 12.45.05 AM.png$
3. La fracción de la luna iluminada el 1 de junio de 2009 es aproximadamente$F(1) \approx 0.60$
4. Usando una calculadora gráfica, obtenemos lo siguiente.
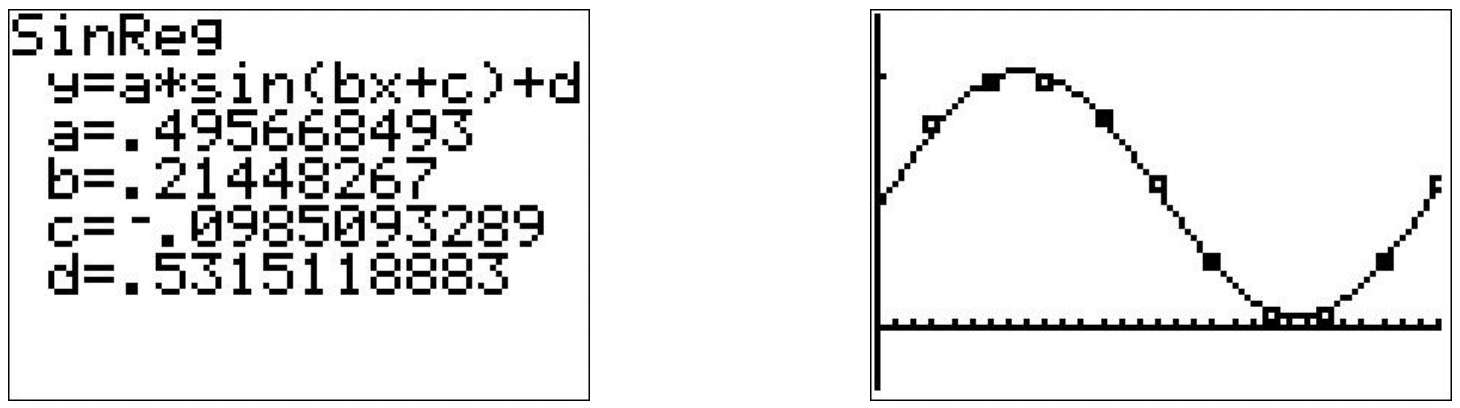
  $Screen Shot 2022-05-24 a las 12.46.50 AM.png$
  
  Este modelo predice que la fracción de la luna iluminada el 1 de junio de 2009 es aproximadamente de 0.59. Esto parece ser un mejor ajuste a los datos que nuestro primer modelo.

Referencia

¹ Ver Sección 6.5.

² Los haters sinusoidales pueden usar la identidad de co-función$\cos \left(\frac{\pi}{2}-\theta\right)=\sin (\theta)$ para convertir todos los senos en cosenos.

³ De lo contrario, podríamos simplemente observar el movimiento de la rueda desde el otro lado.

⁴ Estamos reajustando nuestra 'línea base' de$y = 0$ a$y =72$.

⁵ Bien, parece ser la forma '$\wedge$' que vimos en algunas de las gráficas de la Sección 2.2. Solo cómenos el humor.

⁶ A pesar de que los datos recopilados se encuentran en el intervalo [1, 12], que tiene una longitud de 11, necesitamos pensar en el punto de datos en t = 1 como una muestra representativa de la cantidad de luz diurna para cada día de enero. Es decir, representa$H(t)$ sobre el intervalo [0, 1]. De igual manera,$t = 2$ es una muestra de$H(t)$ más de [1, 2], y así sucesivamente.

⁷ Ver la figura en la página 882.

⁸ Bueno, asumiendo que el objeto no está sujeto a velocidades relativistas.

⁹ Esto es consecuencia de la Segunda Ley del Movimiento de Newton$F=m a$ donde$F$ está la fuerza,$m$ es la masa y$a$ es la aceleración. En nuestro entorno actual, la fuerza involucrada es el peso que es causado por la aceleración debida a la gravedad.

¹⁰ Tenga en cuenta que$1 \text { pound }=1 \frac{\text { slug foot }}{\text { second }^2}$ y$1 \text { Newton }=1 \frac{\mathrm{kg} \text { meter }}{\text { second }^2}$.

¹¹ ¿Te resulta familiar? Vimos la Ley de Hooke en la Sección 4.3.1.

¹² Para mantener las unidades compatibles, si estamos usando el sistema inglés, usamos pies (pies) para medir el desplazamiento. Si estamos en el sistema SI, medimos el desplazamiento en metros (m). El tiempo siempre se mide en segundos (s).

¹³ Las convenciones de signos aquí son trasladadas desde la Física. Si no fuera por la primavera, el objeto caería hacia el suelo, que es la dirección 'natural' o 'positiva'. Dado que la fuerza del resorte actúa en oposición directa a la gravedad, cualquier movimiento hacia arriba se considera 'negativo'.

¹⁴ Para confirmación, nosotros no eso$A \omega \cos (\phi)=v_{0}$, lo que en este caso se reduce a$6 \cos (\phi)=0$.

¹⁵ ¡Toma una buena clase de Ecuaciones Diferenciales para ver esto!

¹⁶ Se invita al lector a investigar las implicaciones destructivas de la resonancia.

¹⁷ Un buen lugar para comenzar es este artículo sobre beats.

¹⁸ Siempre$\theta$ se mantiene 'pequeño'. Carl recuerda que la 'Regla de Pulgar' es$20^{\circ}$ o menos. Consulta con tu amable físico de barrio para asegurarte.

¹⁹ Ver este sitio web: http://www.erh.noaa.gov/cle/climate/cle/normals/laketempcle.html.

²⁰ El promedio calculado es$41^{\circ} \mathrm{F}$ para abril$15^{\text {th }}$ y$71^{\circ} \mathrm{F}$ para septiembre$15^{\text {th }}$.

²¹ Ver este sitio web: http://www.usno.navy.mil/USNO/astronomical-applications/data-services/frac-moon-ill.

²² Es posible que desee trazar los datos antes de encontrar el cambio de fase.

²³ La fracción listada es 0.62.