11.3: La Ley de los Cosinos

En la Sección 11.2, desarrollamos la Ley de los Senos (Teorema 11.2) para permitirnos resolver triángulos en los casos 'Angle-Angle-Lado' (AAS), el 'Angle-Side-Angle' (ASA) y los ambiguos casos de 'Angle-Lado' (ASS). En esta sección, desarrollamos la Ley de Cosinos que maneja la resolución de triángulos en los casos de 'Lado de Ángulo Lateral' (SAS) y 'Lado Lateral Lateral' (SSS). ¹ Declaramos y probamos el teorema a continuación.

Teorema 11.5. Ley de Cosinos

Dado un triángulo con pares opuestos ángulo-lado\((\alpha, a),(\beta, b)\) y\((\gamma, c)\), se mantienen las siguientes ecuaciones

\(a^{2}=b^{2}+c^{2}-2 b c \cos (\alpha) \quad b^{2}=a^{2}+c^{2}-2 a c \cos (\beta) \quad c^{2}=a^{2}+b^{2}-2 a b \cos (\gamma)\)

o, resolviendo para el coseno en cada ecuación, tenemos

\(\cos (\alpha)=\frac{b^{2}+c^{2}-a^{2}}{2 b c} \quad \cos (\beta)=\frac{a^{2}+c^{2}-b^{2}}{2 a c} \quad \cos (\gamma)=\frac{a^{2}+b^{2}-c^{2}}{2 a b}\)

Para probar el teorema, consideramos un triángulo genérico con el vértice de ángulo\(\alpha\) en el origen con lado\(b\) posicionado a lo largo del\(x\) eje positivo.

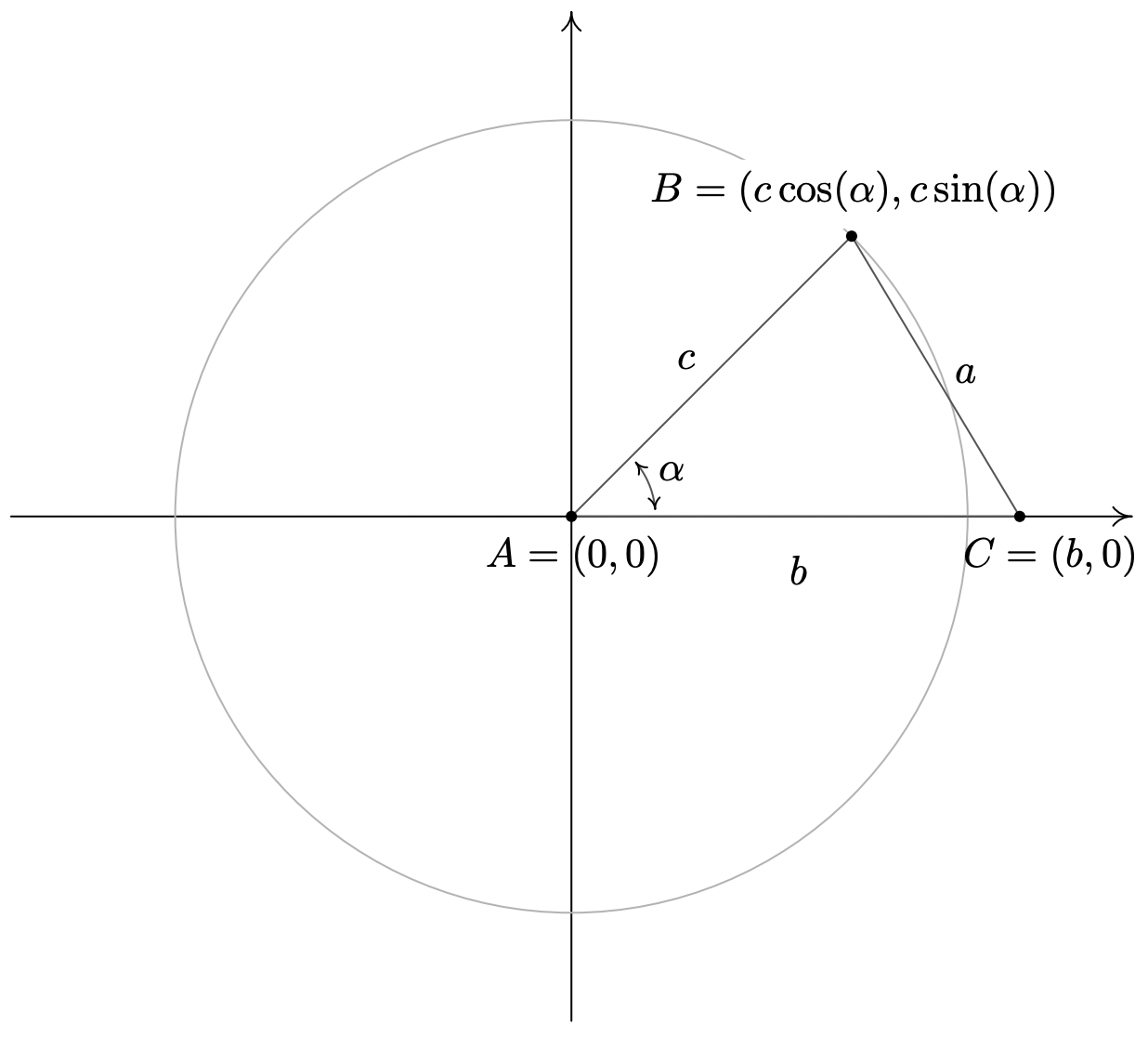
A partir de esta puesta a punto, inmediatamente encontramos que las coordenadas de\(A\) y\(C\) son\(A(0, 0)\) y\(C(b, 0)\). Del Teorema 10.3, sabemos que dado que el punto\(B(x, y)\) se encuentra en un círculo de radio\(c\), las coordenadas de\(B\) son\(B(x, y)=B(c \cos (\alpha), c \sin (\alpha))\). (Esto sería cierto aunque\(\alpha\) fuera un ángulo obtuso o recto así que aunque hemos dibujado el caso cuando α es agudo, los siguientes cálculos se mantienen para cualquier ángulo\(\alpha\) dibujado en posición estándar donde\(0<\alpha<180^{\circ}\).) Observamos que la distancia entre los puntos\(B\) y no\(C\) es otra que la longitud del lado\(a\). Usando la fórmula de distancia, Ecuación 1.1, obtenemos

\ [\ begin {alineado}
a &=\ sqrt {(c\ cos (\ alpha) -b) ^ {2} + (c\ sin (\ alpha) -0) ^ {2}}\\
a^ {2} &=\ left (\ sqrt {(c\ cos (\ alpha) -b) ^ {2} +c^ {2}\ sin ^ {2} (\ alpha)}\ derecha) ^ {2}\\
a^ {2} & =( c\ cos (\ alfa) -b) ^ {2} +c^ {2}\ sin ^ {2} (\ alfa)\\
a^ {2} &=c^ {2}\ cos ^ {2} (\ alfa) -2 b c\ cos (\ alfa) +b^ {2} +c^ {2}\ sin ^ {2} (\ alfa)\\
a^ {2} &=c^ {2}\ izquierda (\ cos ^ {2} (\ alfa) +\ sin ^ {2} (\ alfa)\ derecha) +b^ {2} -2 b c\ cos (\ alfa)\\
a^ {2} &=c^ {2} (1) +b^ {2} -2 b c\ cos (\ alfa)\ cuádruple\ cuádruple\ cuádruple\ cuádruple\ cuádruple\ cuádruple\ cuádruple\ texto {Desde}\ cos^2 (\ alfa) + \ sin^2 (\ alpha) =1\\
a^ {2} &=c^ {2} +b^ {2} -2 b c\ cos (\ alpha)
\ end {alineado}\ nonumber\]

Las fórmulas restantes dadas en el Teorema 11.5 se pueden mostrar simplemente reorientando el triángulo para colocar un vértice diferente en el origen. Dejamos estos detalles al lector. Lo importante de\(a\) y\(\alpha\) en la prueba anterior es que\((\alpha, a)\) es un par angle-lado opuesto y\(b\) y\(c\) son los lados adyacentes a\(\alpha\) — lo mismo puede decirse de cualquier otro par angle-lado opuesto en el triángulo. Observe que la prueba de la Ley de Cosinos se basa en la fórmula de distancia que tiene sus raíces en el Teorema de Pitágoras. Dicho esto, la Ley de Cosinos puede considerarse como una generalización del Teorema de Pitágoras. Si tenemos un triángulo en el que\(\gamma=90^{\circ}\), entonces\(\cos (\gamma)=\cos \left(90^{\circ}\right)=0\) así obtenemos la relación familiar\(c^{2}=a^{2}+b^{2}\). Lo que esto significa es que en el sentido matemático más amplio, la Ley de Cosines y el Teorema de Pitágoras equivalen a prácticamente lo mismo. ²

Ejemplo 11.3.1

Resuelve los siguientes triángulos. Dar respuestas exactas y aproximaciones decimales (redondeadas a centésimas) y esbozar el triángulo.

1. \(\beta=50^{\circ}, a=7 \text { units, } c=2 \text { units }\)
2. \(a=4 \text { units, } b=7 \text { units, } c=5 \text { units }\)

Solución

1. \(\cos (\alpha)=\frac{2-7 \cos \left(50^{\circ}\right)}{\sqrt{53-28 \cos \left(50^{\circ}\right)}}\)

   Dado que\(\alpha\) es un ángulo en un triángulo, sabemos que la medida radianes de\(\alpha\) debe estar entre 0 y\(\pi\) radianes. Esto coincide con el rango de la función arccosine, así que tenemos

   \(\alpha=\arccos \left(\frac{2-7 \cos \left(50^{\circ}\right)}{\sqrt{53-28 \cos \left(50^{\circ}\right)}}\right) \text { radians } \approx 114.99^{\circ}\)

   En este punto, podríamos encontrar el\(\gamma\) uso\(\gamma=180^{\circ}-\alpha-\beta \approx 180^{\circ}-114.99^{\circ}-50^{\circ}=15.01^{\circ}\), es decir, si confiamos en nuestra aproximación para\(\alpha\). Para minimizar la propagación del error, sin embargo, podríamos volver a utilizar la Ley de Cosinos, ⁴ en este caso utilizando\(\cos (\gamma)=\frac{a^{2}+b^{2}-c^{2}}{2 a b}\). Conectando\(a = 7\),\(b=\sqrt{53-28 \cos \left(50^{\circ}\right)}\) y\(c = 2\), obtenemos\(\gamma=\arccos \left(\frac{7-2 \cos \left(50^{\circ}\right)}{\sqrt{53-28 \cos \left(50^{\circ}\right)}}\right) \text { radians } \approx 15.01^{\circ}\). Esbozamos el triángulo a continuación.

   

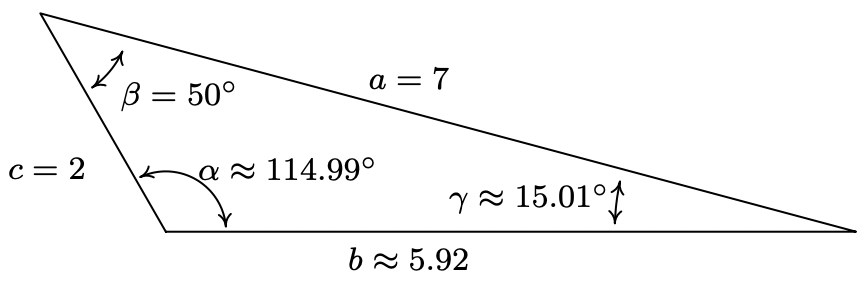
   Como mencionamos anteriormente, una vez que hemos determinado\(b\) es posible utilizar la Ley de los Sinos para encontrar los ángulos restantes. Aquí, sin embargo, debemos proceder con cautela como estamos en el caso ambiguo (ASS). Es recomendable encontrar primero el más pequeño de los ángulos desconocidos, ya que se nos garantiza que será agudo. ⁵ En este caso, encontraríamos\(\gamma\) ya que el lado opuesto\(\gamma\) es menor que el lado opuesto al otro ángulo desconocido,\(\alpha\). Usando el par ángulo-lado opuesto\((\beta, b)\), obtenemos\(\frac{\sin (\gamma)}{2}=\frac{\sin \left(50^{\circ}\right)}{\sqrt{53-28 \cos \left(50^{\circ}\right)}}\). Los cálculos habituales producen\(\gamma \approx 15.01^{\circ}\) y\(\alpha=180^{\circ}-\beta-\gamma \approx 180^{\circ}-50^{\circ}-15.01^{\circ}=114.99^{\circ}\).

2. Ya que se dan los tres lados y no hay ángulos, nos vemos obligados a utilizar la Ley de Cosinos. Siguiendo nuestra discusión en el problema anterior, encontramos\(\beta\) primero, ya que es opuesto al lado más largo,\(b\). Obtenemos\(\cos (\beta)=\frac{a^{2}+c^{2}-b^{2}}{2 a c}=-\frac{1}{5}\), así que conseguimos\(\beta=\arccos \left(-\frac{1}{5}\right) \text { radians } \approx 101.54^{\circ}\). Al igual que en el problema anterior, ahora que hemos obtenido un par ángulo-lado opuesto\((\beta, b)\), podríamos proceder utilizando la Ley de Sines. La Ley de Cosinos, sin embargo, nos ofrece una rara oportunidad de encontrar los ángulos restantes utilizando únicamente los datos que nos dieron en la declaración del problema. Usando esto, obtenemos\(\gamma=\arccos \left(\frac{5}{7}\right) \text { radians } \approx 44.42^{\circ}\) y\(\alpha=\arccos \left(\frac{29}{35}\right) \text { radians } \approx 34.05^{\circ}\).

   

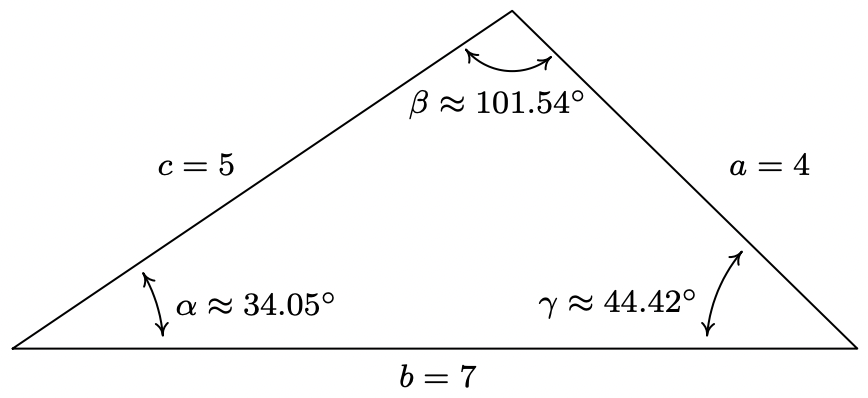
Observamos que, dependiendo de cuántos decimales se lleven a través de cálculos sucesivos, y dependiendo del enfoque que se utilice para resolver el problema, las respuestas aproximadas que obtenga pueden diferir ligeramente de las que obtengan los autores en los Ejemplos y los Ejercicios. Un gran ejemplo de ello es el número 2 en el Ejemplo 11.3.1, donde los valores aproximados que registramos para las medidas de los ángulos suman 180.01 ^◦, lo cual es geométricamente imposible. A continuación, tenemos una aplicación de la Ley de Cosinos

Ejemplo 11.3.2

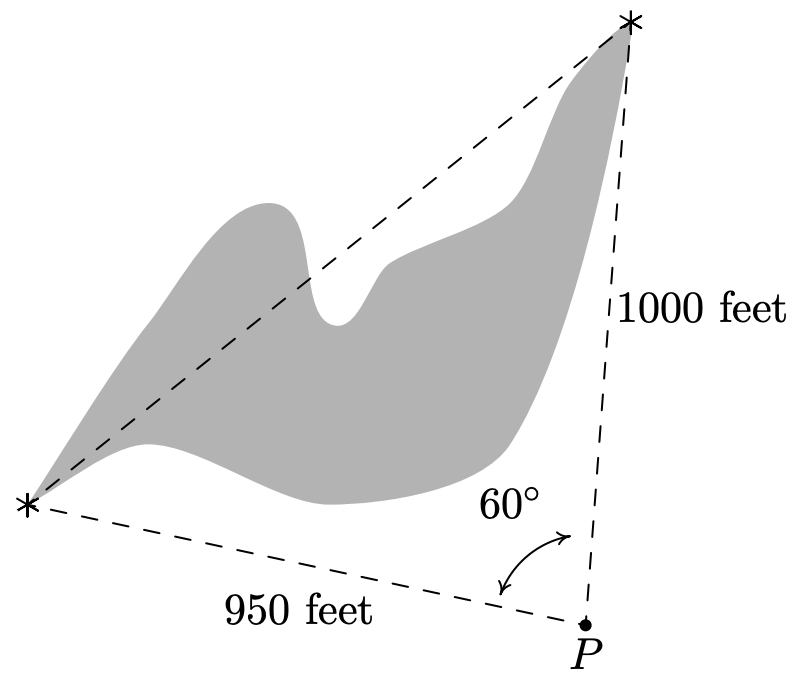
Un investigador desea determinar el ancho de un estanque vernal como se dibuja a continuación. Desde un punto\(P\), encuentra que la distancia al punto más oriental del estanque es de 950 pies, mientras que la distancia al punto más occidental del estanque\(P\) es de 1000 pies. Si el ángulo entre las dos líneas de visión es de 60 ^◦, encuentra el ancho del estanque.

Solución

Se nos dan las longitudes de dos lados y la medida de un ángulo incluido, por lo que podemos aplicar la Ley de Cosinos para encontrar la longitud del lado faltante opuesto al ángulo dado. Llamando a esta longitud\(w\left(\text { for width), we get } w^{2}=950^{2}+1000^{2}-2(950)(1000) \cos \left(60^{\circ}\right)=952500\right.\) de la que obtenemos\(w=\sqrt{952500} \approx 976 \text { feet }\).

En la Sección 11.2, se utilizó la prueba de la Ley de los Senos para desarrollar el Teorema 11.4 como fórmula alternativa para el área encerrada por un triángulo. En esta sección, utilizamos la Ley de Cosinos para derivar otra fórmula de este tipo: la Fórmula de Garza.

Teorema 11.6. Fórmula de Heron

Supongamos\(a\),\(b\) y\(c\) denota las longitudes de los tres lados de un triángulo. Dejar\(s\) ser el semiperímetro del triángulo, es decir, dejar\(s=\frac{1}{2}(a+b+c)\). Entonces el área\(A\) encerrada por el triángulo viene dada por

\(A=\sqrt{s(s-a)(s-b)(s-c)}\)

Demostramos el Teorema 11.6 usando el Teorema 11.4. Usando la convención de que el ángulo\(\gamma\) es opuesto al lado\(c\), tenemos\(A=\frac{1}{2} a b \sin (\gamma)\) desde el Teorema 11.4. Para simplificar los cálculos, comenzamos manipulando la expresión para\(A^{2}\).

\ (\ begin {alineado}
A^ {2} &=\ izquierda (\ frac {1} {2} a b\ sin (\ gamma)\ derecha) ^ {2}\\
&=\ frac {1} {4} a^ {2} b^ {2}\ sin ^ {2} (\ gamma)\\
&=\ frac {a^ {2} b^ {2}} 4}\ izquierda (1-\ cos ^ {2} (\ gamma)\ derecha)\ quad\ texto {desde}\ sin ^ {2} (\ gamma) =1-\ cos ^ {2} (\ gamma).
\ end {alineado}\)

La Ley de los Cosinos nos dice\(\cos (\gamma)=\frac{a^{2}+b^{2}-c^{2}}{2 a b}\), así que sustituyendo esto en nuestra ecuación por\(A^{2}\) da

\ (\ begin {alineado}
A^ {2} &=\ frac {a^ {2} b^ {2}} {4}\ izquierda (1-\ cos ^ {2} (\ gamma)\ derecha)\\
&=\ frac {a^ {2} b^ {2}} {4}\ izquierda [1-\ izquierda (\ frac {a^ {2} +b^ {2} +b^ {2}} -c^ {2}} {2 a b}\ derecha) ^ {2}\ derecha]\\
&=\ frac {a^ {2} b^ {2}} {4}\ izquierda [1-\ frac {\ izquierda (a^ {2} +b^ {2} -c^ {2}\ derecha) ^ {2}\ derecha) ^ {2}} {4 a^ {2} b^ { 2}}\ derecha]\\
&=\ frac {a^ {2} b^ {2}} {4}\ izquierda [\ frac {4 a^ {2} b^ {2} -\ izquierda (a^ {2} +b^ {2} -c^ {2}\ derecha) ^ {2}} {4 a^ {2} b^ {2}}\ derecha]\
&\ izquierda. =\ frac {4 a^ {2} b^ {2} -\ izquierda (a^ {2} +b^ {2} -c^ {2}\ derecha) ^ {2}} {16}\ derecha]\\
&=\ frac {(2 a b) ^ {2} -\ izquierda (a^ {2} +b^ {2} -c^ {2}\ derecha) ^ {2}} {16}\ quad\ quad\ quad\ quad\ text {diferencia de cuadrados.}\\
&=\ frac {\ izquierda (2 a b-\ izquierda [a^ {2} +b^ {2} -c^ {2}\ derecha]\ derecha)\ izquierda (2 a b+\ izquierda [a^ {2} +b^ {2} -c ^ {2}\ derecha]\ derecha)} {16}\\
&=\ frac {\ izquierda (c^ {2} -a^ {2} +2 a b-b^ {2}\ derecha)\ izquierda (a^ {2} +2 a b+b^ {2} -c^ {2}\ derecha)} {16}\ quad\ texto {os}
\ final {alineado}\)

\(\begin{aligned} A^{2} &=\frac{\left(c^{2}-\left[a^{2}-2 a b+b^{2}\right]\right)\left(\left[a^{2}+2 a b+b^{2}\right]-c^{2}\right)}{16} \\ &=\frac{\left(c^{2}-(a-b)^{2}\right)\left((a+b)^{2}-c^{2}\right)}{16}\quad \text { perfect square trinomials. } \\ &=\frac{(c-(a-b))(c+(a-b))((a+b)-c)((a+b)+c)}{16} \quad \text { difference of squares. } \\ &=\frac{(b+c-a)(a+c-b)(a+b-c)(a+b+c)}{16} \\ &=\frac{(b+c-a)}{2} \cdot \frac{(a+c-b)}{2} \cdot \frac{(a+b-c)}{2} \cdot \frac{(a+b+c)}{2} \end{aligned}\)

En esta etapa, reconocemos el último factor como el semiperimer,\(s=\frac{1}{2}(a+b+c)=\frac{a+b+c}{2}\). Para completar la prueba, observamos que

\((s-a)=\frac{a+b+c}{2}-a=\frac{a+b+c-2 a}{2}=\frac{b+c-a}{2}\)

De igual manera, encontramos\((s-b)=\frac{a+c-b}{2}\) y\((s-c)=\frac{a+b-c}{2}\). De ahí que obtengamos

\ (\ begin {alineado}
A^ {2} &=\ frac {(b+c-a)} {2}\ cdot\ frac {(a+c-b)} {2}\ cdot\ frac {(a+b-c)} {2}\ cdot\ frac {(a+b+c)} {2}\\
& =( s-a) (s-b) (s-c) s
\ end {alineado}\)

para que\(A=\sqrt{s(s-a)(s-b)(s-c)}\) c) según se requiera.

Cerramos con un ejemplo de la Fórmula de Garza.

Ejemplo 11.3.3

Encuentra el área encerrada del triángulo en el Ejemplo 11.3.1 número 2.

Solución

Se nos da\(a = 4\),\(b = 7\) y\(c = 5\). Usando estos valores, encontramos\(s=\frac{1}{2}(4+7+5)=8\),\((s-a)=8-4=4,(s-b)=8-7=1\) y\((s-c)=8-5=3\). Usando la Fórmula de Heron, obtenemos unidades\(A=\sqrt{s(s-a)(s-b)(s-c)}=\sqrt{(8)(4)(1)(3)}=\sqrt{96}=4 \sqrt{6} \approx 9.80\) cuadradas.

11.3.1 Ejercicios

En los Ejercicios 1 - 10, usa la Ley de Cosinos para encontrar el lado o los ángulos restantes si es posible.

1. \(a=7, b=12, \gamma=59.3^{\circ}\)
2. \(\alpha=104^{\circ}, b=25, c=37\)
3. \(\alpha=120^{\circ}, b=3, c=4\)
4. \(a=3, b=4, \gamma=90^{\circ}\)
5. \(\alpha=120^{\circ}, b=3, c=4\)
6. \(a=7, b=10, c=13\)
7. \(a=1, b=2, c=5\)
8. \(a=300, b=302, c=48\)
9. \(a=5, b=5, c=5\)
10. \(a=5, b=12, ; c=13\)

En los Ejercicios 11 - 16, resuelva para el lado (s) restante (s) y ángulo (s), si es posible, utilizando cualquier técnica apropiada.

11. \(a=18, \alpha=63^{\circ}, b=20\)
12. \(a=37, b=45, c=26\)
13. \(a=16, \alpha=63^{\circ}, b=20\)
14. \(a=22, \alpha=63^{\circ}, b=20\)
15. \(\alpha=42^{\circ}, b=117, c=88\)
16. \(\beta=7^{\circ}, \gamma=170^{\circ}, c=98.6\)
17. Encuentra el área de los triángulos dados en los Ejercicios 6, 8 y 10 anteriores.
18. La manecilla de la hora en mi antiguo reloj escolar de Seth Thomas en 4 pulgadas de largo y la manecilla de minutos mide 5.5 pulgadas de largo. Encuentra la distancia entre los extremos de las manecillas cuando el reloj lee las cuatro en punto. Redondee su respuesta a la centésima de pulgada más cercana.
19. Un geólogo quiere medir el diámetro de un cráter. Desde su campamento, está a 4 millas hasta el punto más septentrional del cráter y a 2 millas hasta el punto más al sur. Si el ángulo entre las dos líneas de visión es 117 ^◦, ¿cuál es el diámetro del cráter? Redondee su respuesta a la centésima de milla más cercana.
20. Desde el Aeropuerto Internacional Pedimaxus, un helicóptero turístico puede volar a Cliffs of Insanity Point siguiendo un rumbo de N8.2 ^◦ E por 192 millas y puede volar a Bigfoot Falls siguiendo un rumbo de S68.5 ^◦ E por 207 millas. ⁶ Encuentra la distancia entre Cliffs of Insanity Point y Bigfoot Falls. Redondee su respuesta a la milla más cercana.
21. Acantilados de Insanity Point y Bigfoot Falls de Exericse 20 por encima de ambos se encuentran en un tramo recto del Gran Cañón Sasquatch. ¿Qué rumbo tendría que seguir el helicóptero turístico para ir directamente de Bigfoot Falls a Cliffs of Insanity Point? Redondee su ángulo a la décima de grado más cercana.
22. Una naturalista emprende una caminata desde una cabaña en un rumbo de S80 ^◦ W. Después de 1.5 millas, cambia su rumbo a S17 ^◦ W y continúa caminando por 3 millas. Encuentra su distancia del lodge en este punto. Redondee su respuesta a la centésima de milla más cercana. ¿Qué rumbo debe seguir para regresar a la logia? Redondee su ángulo al grado más cercano.
23. El HMS Sasquatch sale de puerto en un rumbo de N23 ^◦ E y viaja 5 millas. Después cambia de rumbo y sigue un rumbo de S41 ^◦ E por 2 millas. ¿A qué distancia está el puerto? Redondee su respuesta a la centésima de milla más cercana. ¿Cuál es su rumbo a babor? Redondee su ángulo al grado más cercano.
24. El SS Bigfoot deja un puerto con destino a la isla de Nessie, que está a 300 millas de distancia con una dirección de N32 ^◦ E. Una tormenta entra y después de 100 millas, el capitán del Bigfoot descubre que se ha desviado del rumbo. Si su rumbo al puerto es ahora S70 ^◦ W, ¿a qué distancia está el SS Bigfoot de Nessie Island? Redondee su respuesta a la centésima de milla más cercana. ¿Qué rumbo debería fijar el capitán para dirigirse a la isla? Redondee su ángulo a la décima de grado más cercana.
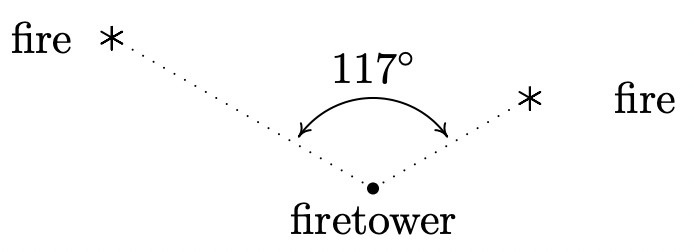
25. Desde un punto a 300 pies sobre el nivel del suelo en una torre de bomberos, un guardabosques detecta dos incendios en el Bosque Nacional Yeti. El ángulo de depresión ⁷ realizado por la línea de visión desde el guardabosques hasta el primer incendio es de 2.5 ^◦ y el ángulo de depresión realizado por la línea de visión desde el guardabosques hasta el segundo incendio es de 1.3 ^◦. El ángulo formado por las dos líneas de visión es de 117 ^◦. Encuentra la distancia entre los dos fuegos. Redondee su respuesta al pie más cercano. (Pista: Para utilizar el ángulo de 117 ^◦ entre las líneas de visión, primero deberá utilizar la trigonometría de ángulo recto para encontrar las longitudes de las líneas de visión. Esto le dará un caso Side-Angle-Side en el que aplicar la Ley de Cosinos.)

    

26. Si aplicas la Ley de Cosinos al caso ambiguo Angle-Side (ASS), el resultado es una ecuación cuadrática cuya variable es la del lado faltante. Si la ecuación no tiene ceros reales positivos entonces la información dada no arroja un triángulo. Si la ecuación tiene solo un cero real positivo entonces se forma exactamente un triángulo y si la ecuación tiene dos ceros reales positivos distintos entonces se forman dos triángulos distintos. Aplicar la Ley de Cosinos a los Ejercicios 11, 13 y 14 anteriores para demostrar este resultado.
27. Discuta con sus compañeros de clase por qué la Fórmula de Heron produce un área en unidades cuadradas a pesar de que se están multiplicando cuatro longitudes juntas.

11.3.2 Respuestas

1. \ (\ begin {array} {lll}
   \ alpha\ approx 35.54^ {\ circ} &\ beta\ approx 85.16^ {\ circ} &\ gamma=59.3^ {\ circ}\
   a=7 & b=12 & c\ approx 10.36
   \ end {array}\)
2. \ (\ begin {array} {lll}
   \ alpha=104^ {\ circ} &\ beta\ approx 29.40^ {\ circ} &\ gamma\ approx 46.60^ {\ circ}\\
   a\ approx 49.41 & b=25 & c=37
   \ end {array}\)
3. \ (\ begin {array} {lll}
   \ alpha\ approx 85.90^ {\ circ} &\ beta=8.2^ {\ circ} &\ gamma\ approx 85.90^ {\ circ}\
   a=153 & b\ approx 21.88 & c=153
   \ end {array}\)
4. \ (\ begin {array} {lll}
   \ alpha\ approx 36.87^ {\ circ} &\ beta\ approx 53.13^ {\ circ} &\ gamma=90^ {\ circ}\
   a=3 & b=4 & c=5
   \ end {array}\)
5. \ (\ begin {array} {lll}
   \ alpha=120^ {\ circ} &\ beta\ approx 25.28^ {\ circ} &\ gamma\ approx 34.72^ {\ circ}\\
   a=\ sqrt {37} & b=3 & c=4
   \ end {array}\)
6. \ (\ begin {array} {lll}
   \ alpha\ approx 32.31^ {\ circ} &\ beta\ approx 49.58^ {\ circ} &\ gamma\ approx 98.21^ {\ circ}\
   a=7 & b=10 & c=13
   \ end {array}\)
7. La información no produce un triángulo
8. \ (\ begin {array} {lll}
   \ alpha\ approx 83.05^ {\ circ} &\ beta\ approx 87.81^ {\ circ} &\ gamma\ approx 9.14^ {\ circ}\
   a=300 & b=302 & c=48
   \ end {array}\)
9. \ (\ begin {array} {lll}
   \ alpha=60^ {\ circ} &\ beta=60^ {\ circ} &\ gamma=60^ {\ circ}\
   a=5 & b=5 & c=5
   \ end {array}\)
10. \ (\ begin {array} {lll}
    \ alpha\ approx 22.62^ {\ circ} &\ beta\ approx 67.38^ {\ circ} &\ gamma=90^ {\ circ}\
    a=5 & b=12 & c=13
    \ end {array}\)
11. \ (\ begin {array} {lll}
    \ alpha=63^ {\ circ} &\ beta\ approx 98.11^ {\ circ} &\ gamma\ aproximadamente 18.89^ {\ circ}\
    a=18 & b=20 & c\ aprox 6.54\
    \ alpha=63^ {\ circ} &\ beta\ approx 81.89^ {\ circ} &\ gamma\ approx 35.11^ ^ {\ circ}\\
    a=18 & b=20 & c\ aprox. 11.62
    \ end {array}\)
12. \ (\ begin {array} {lll}
    \ alpha\ approx 55.30^ {\ circ} &\ beta\ approx 89.40^ {\ circ} &\ gamma\ approx 35.30^ {\ circ}\
    a=37 & b=45 & c=26
    \ end {array}\)
13. La información no produce un triángulo
14. \ (\ begin {array} {lll}
    \ alpha=63^ {\ circ} &\ beta\ approx 54.1^ {\ circ} &\ gamma\ approx 62.9^ {\ circ}\
    a=22 & b=20 & c\ approx 21.98
    \ end {array}\)
15. \ (\ begin {array} {lll}
    \ alpha=42^ {\ circ} &\ beta\ approx 89.23^ {\ circ} &\ gamma\ aproximadamente 48.77^ {\ circ}\\
    a\ aproximadamente 78.30 & b=117 & c=88
    \ end {array}\)
16. \ (\ begin {array} {lll}
    \ alpha\ approx 3^ {\ circ} &\ beta=7^ {\ circ} &\ gamma=170^ {\ circ}\\ a\
    aprox. 29.72 & b\ approx 69.2 & c=98,6
    \ end {array}\)
17. El área del triángulo dada en el Ejercicio 6 es de unidades\(\sqrt{1200}=20 \sqrt{3} \approx 34.64\) cuadradas.

    El área del triángulo dada en el Ejercicio 8 es de unidades\(\sqrt{51764375} \approx 7194.75\) cuadradas.

    El área del triángulo dada en el Ejercicio 10 es exactamente de 30 unidades cuadradas.

18. La distancia entre los extremos de las manecillas a las cuatro en punto es de aproximadamente 8.26 pulgadas.
19. El diámetro del cráter es de aproximadamente 5.22 millas.
20. Cerca de 313 millas
21. N31.8 ^◦ W
22. Ella está a unos 3.92 millas del albergue y su rumbo a la logia es N37 ^◦ E.
23. Se encuentra a unas 4.50 millas del puerto y su rumbo al puerto es S47 ^◦ W.
24. Se encuentra a unas 229.61 millas de la isla y el capitán debe establecer un rumbo de N16.4 ^◦ E para llegar a la isla.
25. Los incendios están a unos 17456 pies de distancia. (Trate de evitar errores de redondeo.)

---

Referencia

¹ Aquí, 'Lado de ángulo Lateral' significa que se nos dan dos lados y el ángulo 'incluido', es decir, el ángulo dado es adyacente a ambos lados dados.

² Esto no debería venir como un gran shock. Todos los teoremas en Trigonometría se pueden rastrear en última instancia a la definición de las funciones circulares junto con la fórmula de distancia y por lo tanto, el Teorema de Pitágoras.

³ después de simplificar..

⁴ Su instructor le permitirá saber qué procedimiento utilizar. Todo se reduce a cuánto confías en tu calculadora.

⁵ Solo puede haber un ángulo obtuso en el triángulo, y si hay uno, debe ser el más grande.

⁶ Consulte la Página 905 en la Sección 11.2 para una introducción a los rodamientos.

⁷ Véase el Ejercicio 78 en la Sección 10.3 para la definición de este ángulo.