11.4: Coordenadas polares

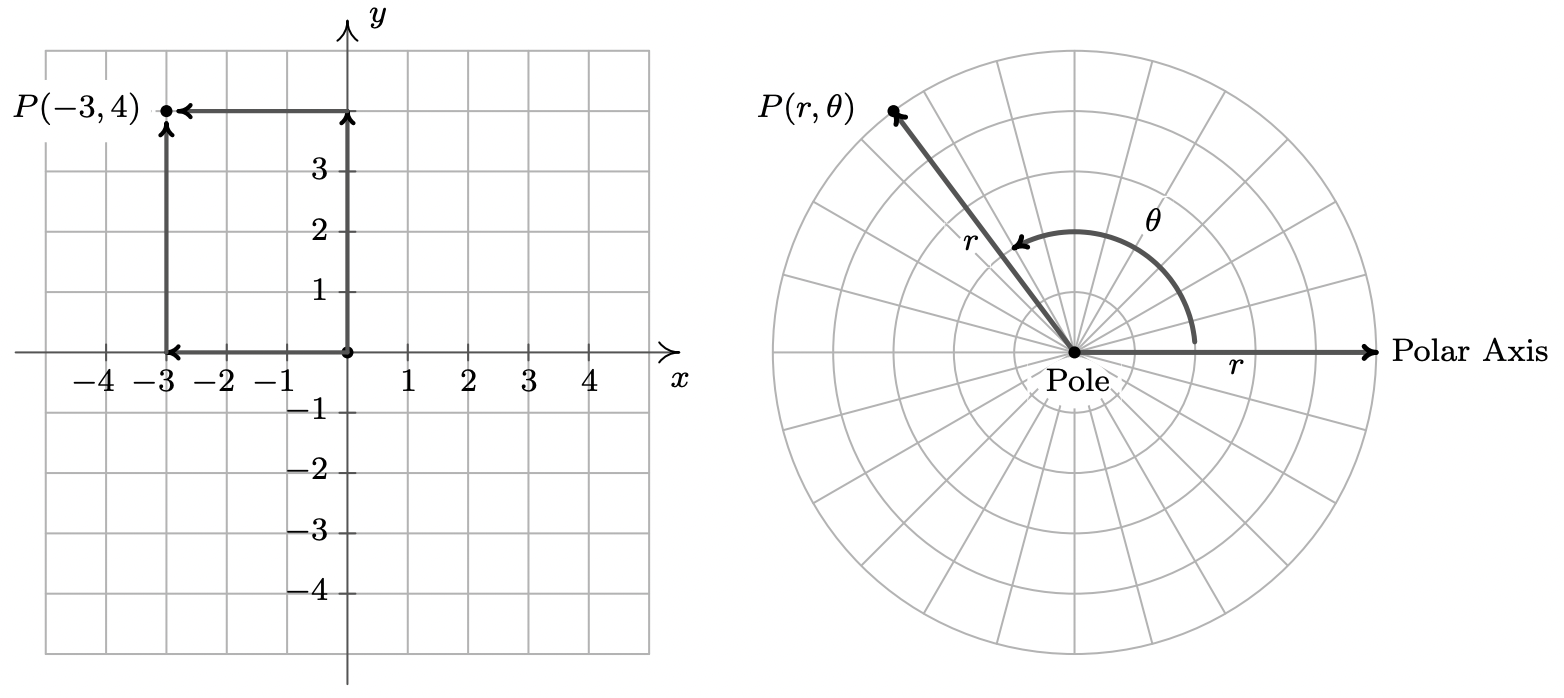
En la Sección 1.1, se introdujeron las coordenadas cartesianas de un punto en el plano como medio para asignar pares ordenados de números a puntos en el plano. Definimos el plano de coordenadas cartesianas usando dos líneas numéricas —una horizontal y otra vertical— que se cruzan en ángulo recto en un punto que llamamos el 'origen'. Para trazar un punto, digamos\(P(−3, 4)\), partimos en el origen, viajamos horizontalmente hacia la izquierda 3 unidades, luego subimos 4 unidades. Alternativamente, podríamos comenzar por el origen, viajar hasta 4 unidades, luego a la izquierda 3 unidades y llegar a la misma ubicación. En su mayor parte, los 'movimientos' del sistema cartesiano (arriba y arriba) describen un rectángulo, y la mayoría de los puntos pueden considerarse como la esquina diagonalmente a través del rectángulo desde el origen. ¹ Por esta razón, las coordenadas cartesianas de un punto suelen denominarse coordenadas 'rectangulares'. En esta sección, introducimos un nuevo sistema para asignar coordenadas a puntos en el plano — coordenadas polares. Comenzamos con un punto de origen, llamado polo, y un rayo llamado eje polar. Luego localizamos un punto\(P\) usando dos coordenadas,\((r, \theta)\), donde\(r\) representa una distancia dirigida desde el polo ² y\(\theta\) es una medida de rotación desde el eje polar. En términos generales, las coordenadas polares\((r, \theta)\) de un punto miden “qué tan lejos” está el punto del polo (eso es\(r\)), y 'qué tan lejos rotar' del eje polar, (eso es\(\theta\)).

Por ejemplo, si quisiéramos trazar el punto\(P\) con coordenadas polares, empezaríamos en el polo\(\left(4, \frac{5 \pi}{6}\right)\), nos moveríamos a lo largo del eje polar 4 unidades, luego giraríamos\(\frac{5 \pi}{6}\) radianes en sentido contrario a las agujas del reloj.

También podemos visualizar este proceso pensando primero en la rotación. ³ Para trazar de\(P\left(4, \frac{5 \pi}{6}\right)\) esta manera, giramos en\(\frac{5 \pi}{6}\) sentido antihorario desde el eje polar, luego nos movemos hacia afuera desde el polo 4 unidades.

Esencialmente estamos localizando un punto en el lado terminal del\(\frac{5 \pi}{6}\) cual se encuentra a 4 unidades del polo.

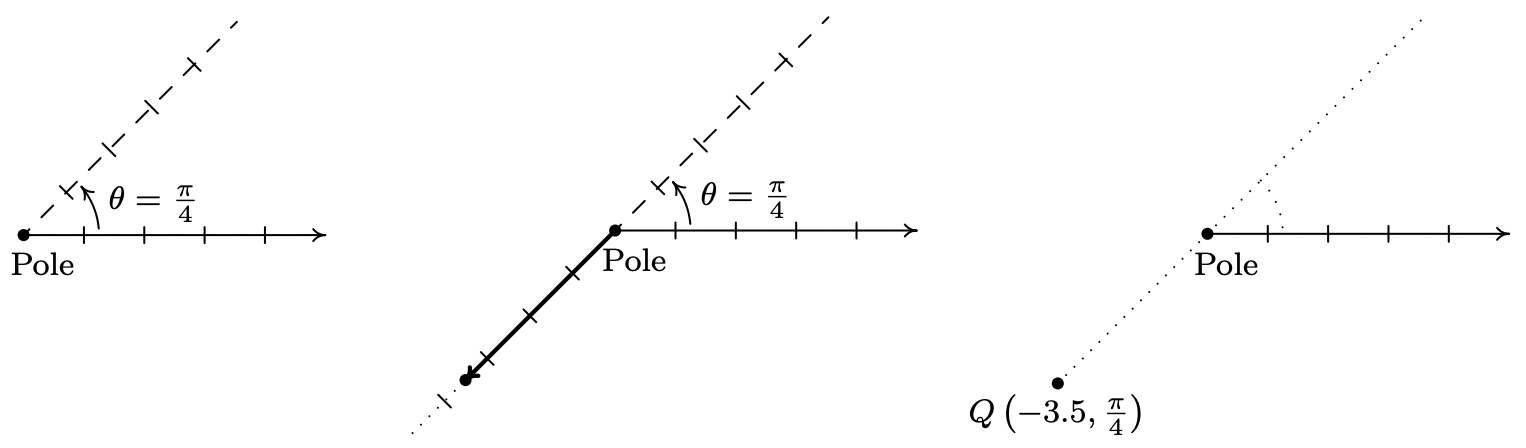
Si\(r<0\), comenzamos moviéndonos en dirección opuesta sobre el eje polar desde el polo. Por ejemplo, para trazar\(Q\left(-3.5, \frac{\pi}{4}\right)\) tenemos

Si primero interpretamos el ángulo, giramos\(\frac{\pi}{4}\) radianes, luego retrocedemos por el polo 3.5 unidades. Aquí estamos localizando un punto 3.5 unidades lejos del polo en el lado terminal de\(\frac{5 \pi}{4}\), no\(\frac{\pi}{4}\).

habrás adivinado,\(\theta<0\) significa que la rotación alejándose del eje polar es en el sentido de las agujas del reloj en lugar de antihorario. De ahí que para trazar\(R\left(3.5,-\frac{3 \pi}{4}\right)\) tenemos lo siguiente.

Desde un enfoque de 'ángulos primero', giramos\(-\frac{3 \pi}{4}\) y luego sacamos 3.5 unidades del poste. Vemos que\(R\) es el punto en el lado terminal del\(\theta=-\frac{3 \pi}{4}\) cual está a 3.5 unidades del polo.

Los puntos\(Q\) y\(R\) anteriores son, de hecho, el mismo punto a pesar de que sus representaciones de coordenadas polares son diferentes. A diferencia de las coordenadas cartesianas donde (\(a, b\)\(c, d\)) y () representan el mismo punto si y solo si\(a = c\) y\(b = d\), un punto puede ser representado por infinitamente muchos pares de coordenadas polares. Exploramos esta noción más en el siguiente ejemplo.

Ejemplo 11.4.1

Por cada punto en coordenadas polares dadas a continuación grafica el punto y luego da dos expresiones adicionales para el punto, una de las cuales tiene\(r > 0\) y la otra con\(r < 0\).

1. \(P\left(2,240^{\circ}\right)\)
2. \(P\left(-4, \frac{7 \pi}{6}\right)\)
3. \(P\left(117,-\frac{5 \pi}{2}\right)\)
4. \(P\left(-3,-\frac{\pi}{4}\right)\)

Solución

1. Ya sea que movemos 2 unidades a lo largo del eje polar y luego rotemos\(240^{\circ}\) o giremos\(240^{\circ}\) luego sacamos 2 unidades del polo, trazamos\(P\left(2,240^{\circ}\right)\) a continuación.

   

   Ahora nos pusimos a buscar descripciones alternas\((r, \theta)\) para el punto\(P\). Ya que\(P\) es 2 unidades del poste,\(r=\pm 2\). A continuación, elegimos ángulos\(\theta\) para cada uno de los\(r\) valores. La representación dada para\(P\) es\(\left(2,240^{\circ}\right)\) así que el ángulo\(\theta\) que elegimos para el\(r = 2\) caso debe ser coterminal con\(240^{\circ}\). (¿Ves por qué?) Uno de esos ángulos es\(\theta=-120^{\circ}\) así que una respuesta para este caso es\(\left(2,-120^{\circ}\right)\). Para el caso\(r = −2\), visualizamos nuestra rotación iniciando 2 unidades a la izquierda del poste. Desde esta posición, solo necesitamos rotar para llegar\(\theta=60^{\circ}\) a la ubicación coterminal con\(240^{\circ}\). De ahí que nuestra respuesta aquí sea\(\left(-2,60^{\circ}\right)\). Comprobamos nuestras respuestas trazándolas.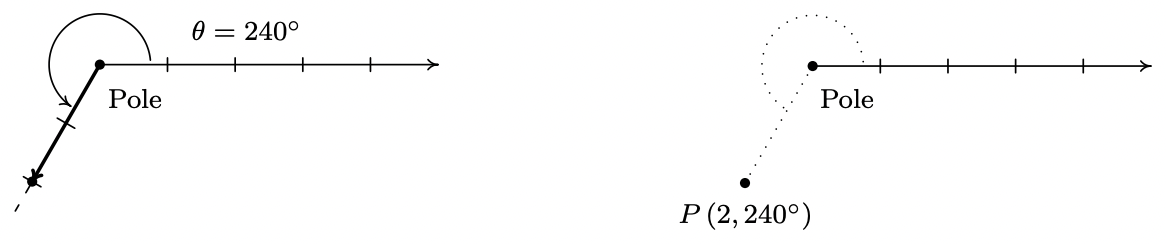

   

2. Trazamos\(\left(-4, \frac{7 \pi}{6}\right)\) moviendo primero 4 unidades a la izquierda del poste y luego rotando\(\frac{7 \pi}{6}\) radianes. Ya que\(r = −4 < 0\), encontramos nuestro punto se encuentra a 4 unidades del polo en el lado terminal de\(\frac{\pi}{6}\).

   

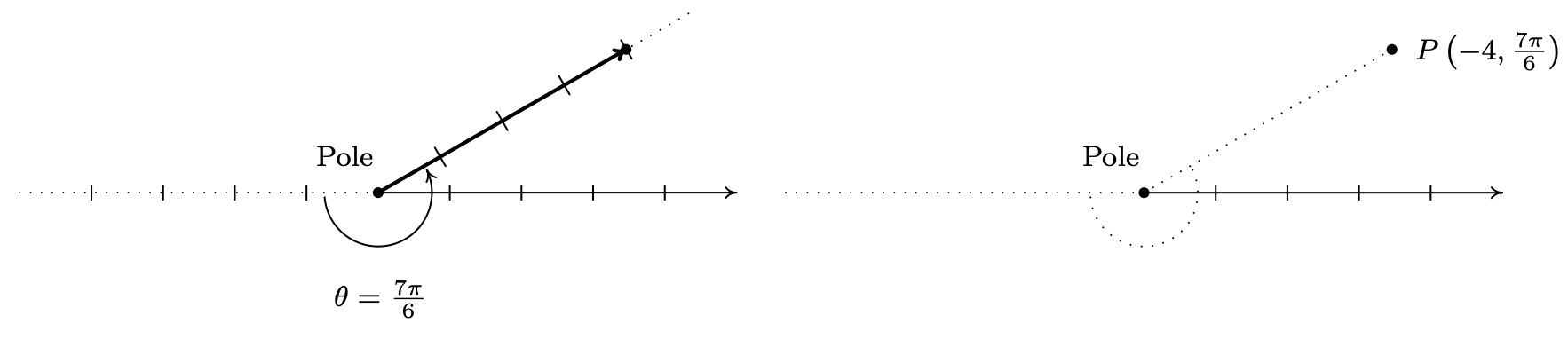
   Para encontrar descripciones alternativas para\(P\), observamos que la distancia desde\(P\) hasta el poste es de 4 unidades, por lo que cualquier representación\((r, \theta)\) para\(P\) debe tener\(r=\pm 4\). Como señalamos anteriormente,\(P\) se encuentra en el lado terminal de\(\frac{\pi}{6}\), por lo que esto, aunado a\(r=4\), nos da\(\left(4, \frac{\pi}{6}\right)\) como una de nuestras respuestas. Para encontrar una representación diferente para\(P\) con\(r = −4\), podemos elegir cualquier ángulo coterminal con el ángulo en la representación original de\(P\left(-4, \frac{7 \pi}{6}\right)\). Elegimos\(-\frac{5 \pi}{6}\) y obtenemos\(\left(-4,-\frac{5 \pi}{6}\right)\) como nuestra segunda respuesta.

   

3. Para trazar\(P\left(117,-\frac{5 \pi}{2}\right)\), nos movemos a lo largo del eje polar 117 unidades desde el polo y giramos\(\frac{5 \pi}{2}\) radianes en sentido horario como se ilustra a continuación.

   

   Ya que\(P\) está a 117 unidades del poste, cualquier representación\((r, \theta)\) para\(P\) satisface\(r=\pm 117\). Para el\(r = 117\) caso, podemos tomar\(\theta\) para ser cualquier ángulo coterminal con\(-\frac{5 \pi}{2}\). En este caso, elegimos\(\theta=\frac{3 \pi}{2}\), y obtenemos\(\left(117, \frac{3 \pi}{2}\right)\) como una sola respuesta. Para el\(r = −117\) caso, visualizamos moviendo a la izquierda 117 unidades desde el poste y luego rotando a través de un ángulo\(\theta\) para alcanzar\(P\). Encontramos que\(\theta=\frac{\pi}{2}\) satisface este requisito, por lo que nuestra segunda respuesta es\(\left(-117, \frac{\pi}{2}\right)\).

   

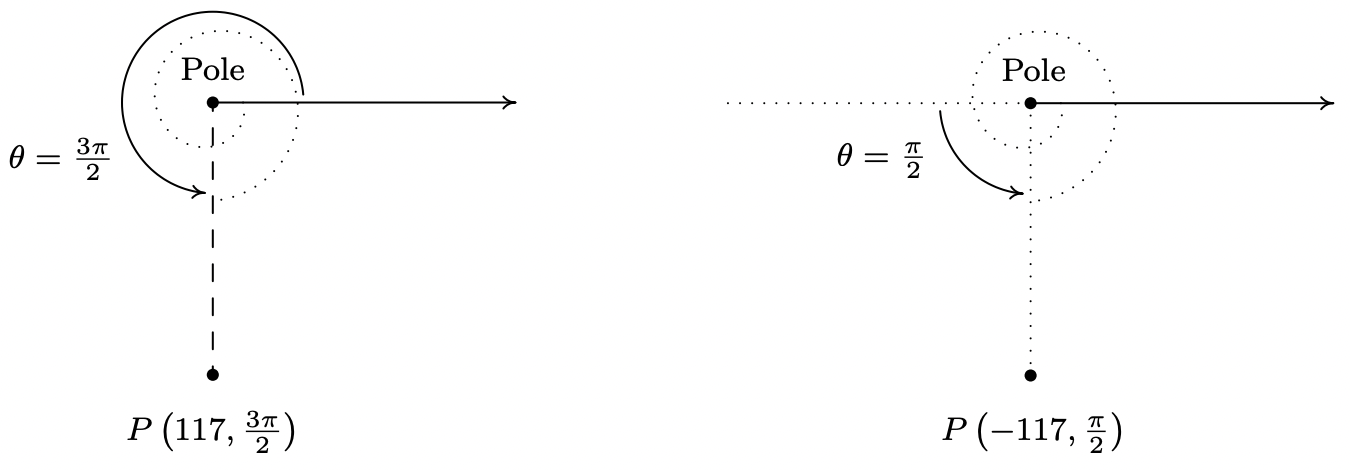
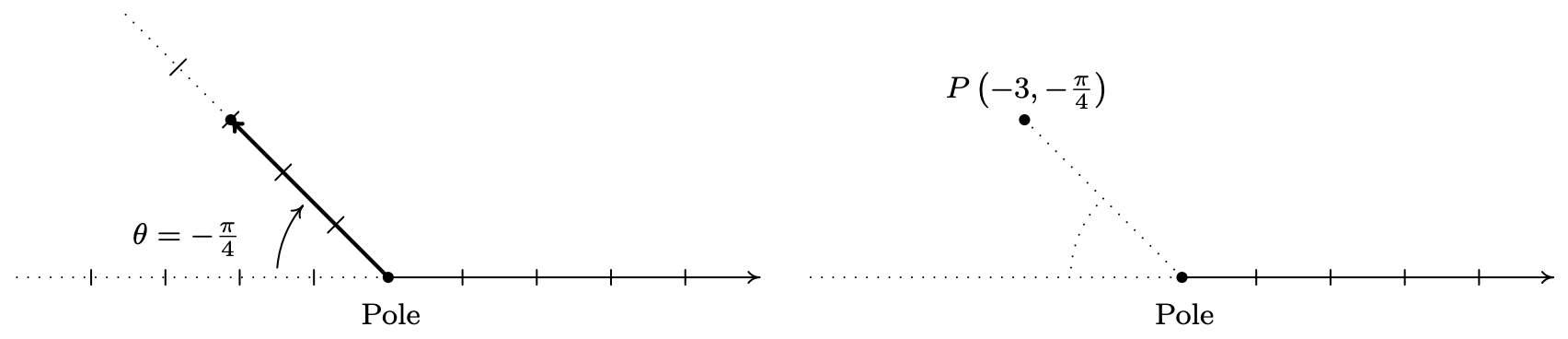
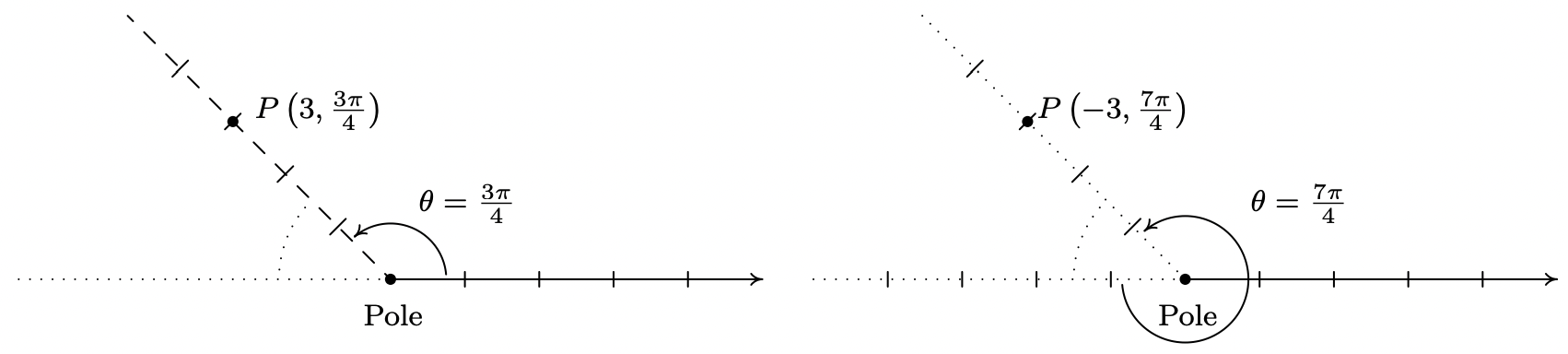
4. Nos movemos tres unidades a la izquierda del poste y damos seguimiento con una rotación de\(\frac{\pi}{4}\) radianes en sentido horario para trazar\(P\left(-3,-\frac{\pi}{4}\right)\). Vemos que\(P\) yace en el lado terminal de\(\frac{3 \pi}{4}\).

   

   Dado que\(P\) se encuentra en el lado terminal de\(\frac{3 \pi}{4}\), una representación alternativa para\(P\) es\(\left(3, \frac{3 \pi}{4}\right)\). Para encontrar una representación diferente para\(P\) con\(r = −3\), podemos elegir cualquier ángulo coterminal con\(-\frac{\pi}{4}\). Elegimos\(\theta=\frac{7 \pi}{4}\) para nuestra respuesta final\(\left(-3, \frac{7 \pi}{4}\right)\).

   

Ahora que hemos tenido alguna práctica con trazar puntos en coordenadas polares, no debería sorprendernos que cualquier punto dado expresado en coordenadas polares tenga infinitamente muchas otras representaciones en coordenadas polares. El siguiente resultado caracteriza cuando dos conjuntos de coordenadas polares determinan el mismo punto en el plano. Podría considerarse como una definición o un teorema, dependiendo de tu punto de vista. Lo declaramos como una propiedad del sistema de coordenadas polares.

Representaciones equivalentes de puntos en coordenadas polares

Supongamos\((r, \theta)\) y\(\left(r^{\prime}, \theta^{\prime}\right)\) son coordenadas polares donde\(r \neq 0, r^{\prime} \neq 0\) y los ángulos se miden en radianes. Entonces\((r, \theta)\) y\(\left(r^{\prime}, \theta^{\prime}\right)\) determinar el mismo punto\(P\) si y solo si uno de los siguientes es cierto:

• \(r^{\prime}=r\)y\(\theta^{\prime}=\theta+2 \pi k\) para algunos enteros\(k\)
• \(r^{\prime}=-r\)y\(\theta^{\prime}=\theta+(2 k+1) \pi\) para algunos enteros\(k\)

Todas las coordenadas polares de la forma\((0, \theta)\) representan el polo independientemente del valor de\(\theta\).

La clave para entender este resultado, y de hecho todo el sistema de coordenadas polares, es tener en cuenta que eso\((r, \theta)\) significa (distancia dirigida desde el polo, ángulo de rotación). Si\(r = 0\), entonces no importa cuánta rotación se realice, el punto nunca sale del poste. Así\((0, \theta)\) es el polo para todos los valores de\(\theta\). Ahora supongamos que ni\(r\) ni\(r^{\prime}\) es cero. Si\((r, \theta)\) y\(\left(r^{\prime}, \theta^{\prime}\right)\) determinar el mismo punto\(P\) entonces la distancia (distinta de cero) desde\(P\) el polo en cada caso debe ser la misma. Ya que esta distancia está controlada por la primera coordenada, tenemos eso ya sea\(r^{\prime}=r\) o\(r^{\prime}=-r\). Si\(r^{\prime}=r\), entonces al trazar\((r, \theta)\) y\(\left(r^{\prime}, \theta^{\prime}\right)\), los ángulos\(\theta\) y\(\theta^{\prime}\) tienen el mismo lado inicial. De ahí que si\((r, \theta)\) y\(\left(r^{\prime}, \theta^{\prime}\right)\) determinemos el mismo punto, debemos tener que que\(\theta^{\prime}\) sea coterminal con\(\theta\). Sabemos que esto significa\(\theta^{\prime}=\theta+2 \pi k\) para algún entero\(k\), según se requiera. Si, por otro lado,\(r^{\prime}=-r\), entonces al trazar\((r, \theta)\) y\(\left(r^{\prime}, \theta^{\prime}\right)\), el lado inicial de\(\theta^{\prime}\) se gira\(\pi\) radianes alejándose del lado inicial de\(\theta\). En este caso,\(\theta^{\prime}\) debe ser coterminal con\(\pi+\theta\). De ahí,\(\theta^{\prime}=\pi+\theta+2 \pi k\) que reescribimos como\(\theta^{\prime}=\theta+(2 k+1) \pi\) para algún entero\(k\). Por el contrario, si\(r^{\prime}=r\) y\(\theta^{\prime}=\theta+2 \pi k\) para algún entero\(k\), entonces los puntos\(P(r, \theta)\) y se\(P^{\prime}\left(r^{\prime}, \theta^{\prime}\right)\) encuentran a la misma distancia (dirigida) desde el polo en los lados terminales de los ángulos coterminales, y por lo tanto son el mismo punto. Ahora supongamos\(r^{\prime}=-r\) y\(\theta^{\prime}=\theta+(2 k+1) \pi\) para algún entero\(k\). Para trazar\(P\), primero nos movemos una distancia\(r\) dirigida del poste; para trazar\(P^{\prime}\), nuestro primer paso es movernos la misma distancia del polo que\(P\), pero en dirección opuesta. En esta etapa intermedia, tenemos dos puntos equidistantes del polo girados exactamente\(\pi\) radianes separados. Ya que\(\theta^{\prime}=\theta+(2 k+1) \pi=(\theta+\pi)+2 \pi k\) para algún entero\(k\), vemos que\(\theta^{\prime}\) es coterminal a\((\theta+\pi)\) y es este\(\pi\) radianes extra de rotación el que alinea los puntos\(P\) y\(P^{\prime}\).

A continuación, casamos el sistema de coordenadas polares con el sistema de coordenadas cartesianas (rectangulares). Para ello, identificamos el polo y el eje polar en el sistema polar al origen y al\(x\) eje positivo, respectivamente, en el sistema rectangular. Obtenemos el siguiente resultado.

Teorema 11.7. Conversión entre coordenadas rectangulares y polares

Supongamos que\(P\) se representa en coordenadas rectangulares como\((x, y)\) y en coordenadas polares como\((r, \theta)\). Entonces

• \(x=r \cos (\theta) \text { and } y=r \sin (\theta)\)
• \(x^{2}+y^{2}=r^{2}\)y\(\tan (\theta)=\frac{y}{x}\) (siempre\(x \neq 0\))

En el caso\(r > 0\), el Teorema 11.7 es una consecuencia inmediata del Teorema 10.3 junto con la identidad del cociente\(\tan (\theta)=\frac{\sin (\theta)}{\cos (\theta)}\). Si\(r < 0\), entonces sabemos que una representación alternativa para\((r, \theta)\) es\((-r, \theta+\pi)\). Desde\(\cos (\theta+\pi)=-\cos (\theta)\) y\(\sin (\theta+\pi)=-\sin (\theta)\), aplicando el teorema a\((-r, \theta+\pi)\) da\(x=(-r) \cos (\theta+\pi)=(-r)(-\cos (\theta))=r \cos (\theta)\) y\(y=(-r) \sin (\theta+\pi)=(-r)(-\sin(\theta))=r\sin(\theta)\). Además,\(x^{2}+y^{2}=(-r)^{2}=r^{2}\), y\(\frac{y}{x}=\tan (\theta+\pi)=\tan (\theta)\), así el teorema es cierto en este caso, también. El caso restante es\(r = 0\), en cuyo caso\((r, \theta)=(0, \theta)\) es el polo. Dado que el polo se identifica con el origen (0, 0) en coordenadas rectangulares, el teorema en este caso equivale a verificar '0 = 0'. El siguiente ejemplo le da buen uso al Teorema 11.7.

Ejemplo 11.4.2

Convierte cada punto en coordenadas rectangulares dadas a continuación en coordenadas polares con\(r \geq 0\) y\(0 \leq \theta<2 \pi\). Use valores exactos si es posible y redondee los valores aproximados a dos decimales. Comprueba tu respuesta convirtiéndolas de nuevo en coordenadas rectangulares.

1. \(P(2,-2 \sqrt{3})\)
2. \(Q(-3,-3)\)
3. \(R(0,-3)\)
4. \(S(-3,4)\)

Solución

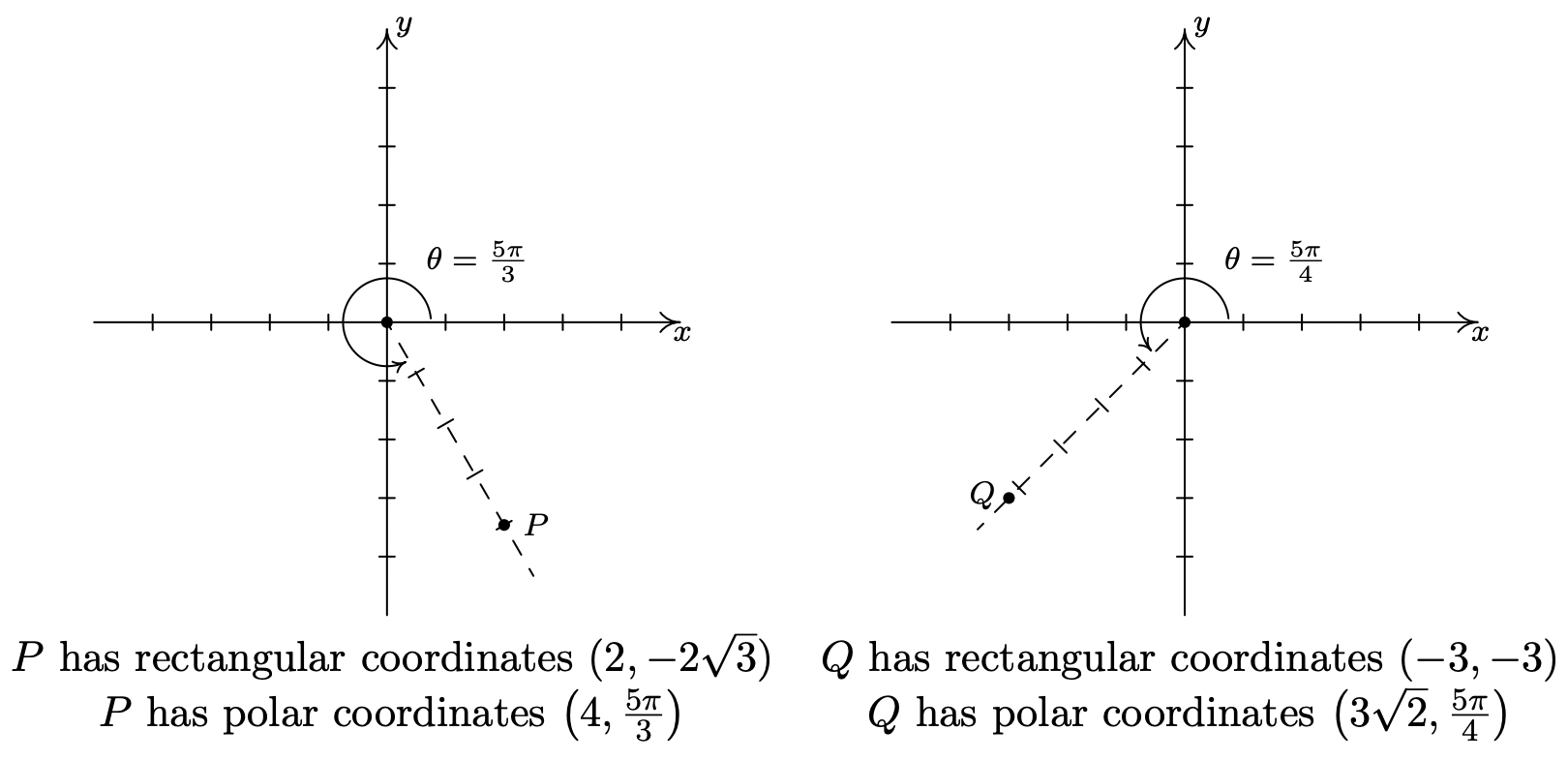
1. A pesar de que no se nos dice explícitamente que lo hagamos, podemos evitar muchos errores comunes tomándonos el tiempo para trazar los puntos antes de hacer cualquier cálculo. El trazado\(P(2,-2 \sqrt{3})\) muestra que se encuentra en el Cuadrante IV. Con\(x = 2\) y\(y=-2 \sqrt{3}\),\(r^{2}=x^{2}+y^{2}=(2)^{2}+(-2 \sqrt{3})^{2}=4+12=16\) así lo conseguimos\(r=\pm 4\). Ya que nos piden\(r \geq 0\), elegimos\(r = 4\). Para encontrar\(\theta\), tenemos eso\(\tan (\theta)=\frac{y}{c}=\frac{-2 \sqrt{3}}{2}=-\sqrt{3}\). Esto nos dice que\(\theta\) tiene un ángulo de referencia de\(\frac{\pi}{3}\), y como P se encuentra en el Cuadrante IV, sabemos que\(\theta\) es un ángulo del Cuadrante IV. Se nos pide tener\(0 \leq \theta<2 \pi\), así que elegimos\(\theta=\frac{5 \pi}{3}\). De ahí que nuestra respuesta sea\(\left(4, \frac{5 \pi}{3}\right)\). Para verificar,\((r, \theta)=\left(4, \frac{5 \pi}{3}\right)\) volvemos a convertir a coordenadas rectangulares y encontramos\(x=r \cos (\theta)=4 \cos \left(\frac{5 \pi}{3}\right)=4\left(\frac{1}{2}\right)=2\) y\(y=r \sin (\theta)=4 \sin \left(\frac{5 \pi}{3}\right)=4\left(-\frac{\sqrt{3}}{2}\right)=-2 \sqrt{3}\), según sea necesario.
2. El punto\(Q(-3,-3)\) está en el Cuadrante III. Usando\(x=y=-3\),\(r^{2}=(-3)^{2}+(-3)^{2}=18\) así lo conseguimos\(r=\pm \sqrt{18}=\pm 3 \sqrt{2}\). Ya que nos piden\(r \geq 0\), elegimos\(r=3 \sqrt{2}\). Encontramos\(\tan (\theta)=\frac{-3}{-3}=1\), lo que significa que\(\theta\) tiene un ángulo de referencia de\(\frac{\pi}{4}\). Ya que\(Q\) se encuentra en el Cuadrante III, elegimos\(\theta=\frac{5 \pi}{4}\), lo que satisface el requisito de que\(0 \leq \theta<2 \pi\). Nuestra respuesta final es\((r, \theta)=\left(3 \sqrt{2}, \frac{5 \pi}{4}\right)\). Para verificar, nos encontramos\(x=r \cos (\theta)=(3 \sqrt{2}) \cos \left(\frac{5 \pi}{4}\right)=(3 \sqrt{2})\left(-\frac{\sqrt{2}}{2}\right)=-3\) y\(y=r \sin (\theta)=(3 \sqrt{2}) \sin \left(\frac{5 \pi}{4}\right)=(3 \sqrt{2})\left(-\frac{\sqrt{2}}{2}\right)=-3\), así terminamos.

   

3. El punto\(R(0, −3)\) se encuentra a lo largo del\(y\) eje negativo. Si bien podríamos pasar por los cómputos habituales ⁴ para encontrar la forma polar de\(R\), en este caso podemos encontrar las coordenadas polares de\(R\) usar la definición. Dado que el polo se identifica con el origen, podemos decir fácilmente que el punto\(R\) es de 3 unidades del polo, lo que significa en la representación polar\((r, \theta)\) de que\(R\) conocemos\(r=\pm 3\). Ya que requerimos\(r \geq 0\), elegimos\(r = 3\). \(\theta\)Concerniente, el ángulo\(\theta=\frac{3 \pi}{2}\) satisface\(0 \leq \theta<2 \pi\) con su lado terminal a lo largo del\(y\) eje negativo, así que nuestra respuesta es\(\left(3, \frac{3 \pi}{2}\right)\). Para verificar, nosotros no\(x=r \cos (\theta)=3 \cos \left(\frac{3 \pi}{2}\right)=(3)(0)=0\) y\(y=r \sin (\theta)=3 \sin \left(\frac{3 \pi}{2}\right)=3(-1)=-3\).
4. El punto\(S(−3, 4)\) radica en el Cuadrante II. Con\(x = −3\) y\(y = 4\), nosotros\(r^{2}=(-3)^{2}+(4)^{2}=25\) así\(r=\pm 5\). Como es habitual, elegimos\(r=5 \geq 0\) y procedemos a determinar\(\theta\). Tenemos\(\tan(\theta)=\frac{y}{x}=\frac{4}{-3}=-\frac{4}{3}\), y como esta no es la tangente de uno de los ángulos comunes, recurrimos al uso de la función arcotangente. Ya que\(\theta\) se encuentra en el Cuadrante II y hay que satisfacer\(0 \leq \theta<2 \pi\), elegimos\(\theta=\pi-\arctan \left(\frac{4}{3}\right) \text { radians }\). De ahí que nuestra respuesta sea\((r, \theta)=\left(5, \pi-\arctan \left(\frac{4}{3}\right)\right) \approx(5,2.21)\). Para verificar nuestras respuestas se requiere un poco de tenacidad ya que necesitamos simplificar expresiones de la forma:\(\cos \left(\pi-\arctan \left(\frac{4}{3}\right)\right)\) y\(\sin \left(\pi-\arctan \left(\frac{4}{3}\right)\right)\). Estos son buenos ejercicios de revisión y, por lo tanto, se dejan al lector. Encontramos\(\cos \left(\pi-\arctan \left(\frac{4}{3}\right)\right)=-\frac{3}{5}\) y\(\sin \left(\pi-\arctan \left(\frac{4}{3}\right)\right)=\frac{4}{5}\), así que eso\(x=r \cos (\theta)=(5)\left(-\frac{3}{5}\right)=-3\) y\(y=r \sin (\theta)=(5)\left(\frac{4}{5}\right)=4\) lo que confirma nuestra respuesta.

   

Ahora que hemos tenido práctica la conversión de representaciones de puntos entre los sistemas de coordenadas rectangulares y polares, ahora nos pusimos a convertir ecuaciones de un sistema a otro. Así como hemos utilizado ecuaciones en\(x\) y\(y\) para representar relaciones en coordenadas rectangulares, ecuaciones en las variables\(r\) y\(\theta\) representar relaciones en coordenadas polares. Convertimos ecuaciones entre los dos sistemas usando el Teorema 11.7 como ilustra el siguiente ejemplo.

Ejemplo 11.4.3

1. Convierte cada ecuación en coordenadas rectangulares en una ecuación en coordenadas polares.
   1. \((x-3)^{2}+y^{2}=9\)
   2. \(y=-x\)
   3. \(y=x^{2}\)
2. Convierte cada ecuación en coordenadas polares en una ecuación en coordenadas rectangulares.
   1. \(r=-3\)
   2. \(\theta=\frac{4 \pi}{3}\)
   3. \(r=1-\cos (\theta)\)

Solución

1. Una estrategia para convertir una ecuación de coordenadas rectangulares a polares es reemplazar cada ocurrencia de\(x\) con\(r \cos (\theta)\) y cada ocurrencia de\(y\) con\(r \sin (\theta)\) y usar identidades para simplificar. Esta es la técnica que empleamos a continuación.
   1. Comenzamos sustituyendo\(x=r \cos (\theta)\) y\(y=\sin (\theta)\) entrando\((x-3)^{2}+y^{2}=9\) y simplificando. Sin dirección real en la que proceder, seguimos nuestros instintos matemáticos y vemos a dónde nos llevan. ⁵

      \ (\ begin {alineado}
      (r\ cos (\ theta) -3) ^ {2} + (r\ sin (\ theta)) ^ {2} &=9\\
      r^ {2}\ cos ^ {2} (\ theta) -6 r\ cos (\ theta) +9+r^ {2}\ sin ^ {2} (\ theta) &=9\
      r^ {2}\ izquierda (\ cos ^ {2} (\ theta) +\ sin ^ {2} (\ theta)\ derecha) -6 r\ cos (\ theta) &=0\ quad\ cuádruple \ text {Restar 9 de ambos lados.} \\
      r^ {2} -6 r\ cos (\ theta) &=0\ quad\ quad\ texto {Desde}\ cos^2 (\ theta) +\ sen ^2 (\ theta) =1\\
      r (r-6\ cos (\ theta)) &=0\ quad\ quad\ text {Factor.}
      \ end {alineado}\)

      Obtenemos\(r = 0\) o\(r=6 \cos (\theta)\). De la Sección 7.2 sabemos que la ecuación\((x-3)^{2}+y^{2}=9\) describe un círculo, y como\(r = 0\) describe solo un punto (es decir, el polo/origen), elegimos\(r=6 \cos (\theta)\) para nuestra respuesta final. ⁶

   2. Sustituyendo\(x=r \cos (\theta)\) y\(y=r \sin (\theta)\) en\(y = −x\) da\(r \sin (\theta)=-r \cos (\theta)\). Reordenando, obtenemos\(r \cos (\theta)+r \sin (\theta)=0\) o\(r(\cos (\theta)+\sin (\theta))=0\). Esto da\(r = 0\) o\(\cos (\theta)+\sin (\theta)=0\). Resolviendo esta última ecuación para\(\theta\), obtenemos\(\theta=-\frac{\pi}{4}+\pi k\) para enteros\(k\). Como hicimos en el ejemplo anterior, damos un paso atrás y pensamos geométricamente. Sabemos\(y = −x\) describe una línea a través del origen. Como antes,\(r = 0\) describe el origen, pero nada más. Considera la ecuación\(\theta=-\frac{\pi}{4}\). En esta ecuación, la variable\(r\) es libre, ⁷ lo que significa que puede asumir todos y cada uno de los valores incluidos\(r = 0\). Si imaginamos trazar puntos\(\left(r,-\frac{\pi}{4}\right)\) para todos los valores concebibles de\(r\) (positivo, negativo y cero), esencialmente estamos dibujando la línea que contiene el lado terminal de la\(\theta=-\frac{\pi}{4}\) cual no es otro que\(y = −x\). De ahí que podamos tomar como respuesta final\(\theta=-\frac{\pi}{4}\) aquí. ⁸
   3. Nosotros sustituimos\(x=r \cos (\theta)\) y\(y=r \sin (\theta)\) en\(y=x^{2}\) y obtenemos\(r \sin (\theta)=(r \cos (\theta))^{2}\), o\(r^{2} \cos ^{2}(\theta)-r \sin (\theta)=0\). Factoring, obtenemos\(r\left(r \cos ^{2}(\theta)-\sin (\theta)\right)=0\) así que\(r = 0\) o bien\(r \cos ^{2}(\theta)=\sin (\theta)\). Podemos resolver esta última ecuación para\(r\) dividiendo ambos lados de la ecuación por\(\cos ^{2}(\theta)\), pero como regla general, nunca dividimos por una cantidad que puede ser 0. En este caso particular, estamos a salvo ya que si\(\cos ^{2}(\theta)=0\), entonces\(\cos (\theta)=0\), y para\(r \cos ^{2}(\theta)=\sin (\theta)\) que la ecuación se mantenga, entonces también\(\sin (\theta)\) tendría que ser 0. Ya que no hay ángulos con ambos\(\cos (\theta)=0\) y\(\sin (\theta)=0\), no estamos perdiendo ninguna información dividiendo ambos lados de\(r \cos ^{2}(\theta)=\sin (\theta)\) por\(\cos ^{2}(\theta)\). Al hacerlo, obtenemos\(r=\frac{\sin (\theta)}{\cos ^{2}(\theta)}\), o\(r=\sec (\theta) \tan (\theta)\). Como antes, el\(r = 0\) caso se recupera en la solución\(r=\sec (\theta) \tan (\theta)\) (let\(\theta=0\)), por lo que declaramos este último como nuestra respuesta final.
2. Como regla general, convertir ecuaciones de coordenadas polares a rectangulares no es tan sencillo como el proceso inverso. Podríamos resolver\(r^{2}=x^{2}+y^{2}\) para\(r\) obtener\(r=\pm \sqrt{x^{2}+y^{2}}\) y resolver\(\tan (\theta)=\frac{y}{x}\) requiere la función arcotangente\(\theta=\arctan \left(\frac{y}{x}\right)+\pi k\) para obtener enteros\(k\). Ninguna de estas expresiones para\(r\) y\(\theta\) son especialmente fáciles de usar, por lo que optamos por una segunda estrategia —reorganizar la ecuación polar dada para que la expresión\(r^{2}=x^{2}+y^{2}\),\(r \cos (\theta)=x, r \sin (\theta)=y\) y/o se\(\tan (\theta)=\frac{y}{x}\) presenten.
   1. Empezando por\(r = −3\), podemos cuadrar ambos lados para conseguir\(r^{2}=(-3)^{2}\) o\(r^{2}=9\). Ahora podemos sustituir\(r^{2}=x^{2}+y^{2}\) para obtener la ecuación\(x^{2}+y^{2}=9\). Como hemos visto, ⁹ al cuadrado de una ecuación no produce, en general, una ecuación equivalente. La preocupación aquí es que la ecuación\(r^{2}=9\) podría ser satisfecha por más puntos que\(r=-3\). En la superficie, este parece ser el caso ya que\(r^{2}=9\) equivale a\(r=\pm 3\), no solo\(r = −3\). Sin embargo, cualquier punto con coordenadas polares se\((3, \theta)\) puede representar como\((-3, \theta+\pi)\), lo que significa que cualquier punto\((r, \theta)\) cuyas coordenadas polares satisfagan la relación\(r=\pm 3\) tiene una representación equivalente ¹⁰ que satisface\(r = −3\).
   2. Tomamos la tangente de ambos lados la ecuación\(\theta=\frac{4 \pi}{3}\) para obtener\(\tan (\theta)=\tan \left(\frac{4 \pi}{3}\right)=\sqrt{3}\). Ya que\(\tan (\theta)=\frac{y}{x}\), obtenemos\(\frac{y}{x}=\sqrt{3}\) o\(y=x \sqrt{3}\). Por supuesto, hacemos una pausa para preguntarnos si, geométricamente, las ecuaciones\(\theta=\frac{4 \pi}{3}\) y\(y=x \sqrt{3}\) generar el mismo conjunto de puntos. ¹¹ El mismo argumento presentado en el número 1b se aplica igualmente bien aquí así que ya hemos terminado.
   3. Una vez más, necesitamos manipular\(r=1-\cos (\theta)\) un poco antes de usar las fórmulas de conversión dadas en el Teorema 11.7. Podríamos cuadrar ambos lados de esta ecuación como hicimos en la parte 2a anterior para obtener una\(r^{2}\) en el lado izquierdo, pero eso no sirve de nada para el lado derecho. En cambio, multiplicamos ambos lados por\(r\) para obtener\(r^{2}=r-r \cos (\theta)\). Ahora tenemos una\(r^{2}\) y una\(r \cos (\theta)\) en la ecuación, que podemos manejar fácilmente, pero también tenemos otra con la que\(r\) lidiar. Reescribir la ecuación como\(r=r^{2}+r \cos (\theta)\) y cuadrar ambos lados rinde\(r^{2}=\left(r^{2}+r \cos (\theta)\right)^{2}\). Sustituyendo\(r^{2}=x^{2}+y^{2}\) y\(r \cos (\theta)=x\) da\(x^{2}+y^{2}=\left(x^{2}+y^{2}+x\right)^{2}\). Una vez más, hemos realizado algunas maniobras algebraicas que pueden haber alterado el conjunto de puntos descrito por la ecuación original. Primero, multiplicamos ambos lados por\(r\). Esto quiere decir que ahora\(r = 0\) es una solución viable a la ecuación. En la ecuación original,\(r=1-\cos (\theta)\), vemos que\(\theta=0\) da\(r = 0\), así que la multiplicación por\(r\) no introduce ningún punto nuevo. La cuadratura de ambos lados de esta ecuación es también una razón para hacer una pausa. ¿Hay puntos con coordenadas\((r, \theta)\) que satisfagan\(r^{2}=\left(r^{2}+r \cos (\theta)\right)^{2}\) pero no satisfagan\(r=r^{2}+r \cos (\theta)\)? Supongamos\(\left(r^{\prime}, \theta^{\prime}\right)\) que satisface\(r^{2}=\left(r^{2}+r \cos (\theta)\right)^{2}\). Entonces\(r^{\prime}=\pm\left(\left(r^{\prime}\right)^{2}+r^{\prime} \cos \left(\theta^{\prime}\right)\right)\). Si tenemos eso\(r^{\prime}=\left(r^{\prime}\right)^{2}+r^{\prime} \cos \left(\theta^{\prime}\right)\), ya terminamos. ¿Y si\(r^{\prime}=-\left(\left(r^{\prime}\right)^{2}+r^{\prime} \cos \left(\theta^{\prime}\right)\right)=-\left(r^{\prime}\right)^{2}-r^{\prime} \cos \left(\theta^{\prime}\right)\)? Afirmamos que las coordenadas\(\left(-r^{\prime}, \theta^{\prime}+\pi\right)\), que determinan el mismo punto que\(\left(r^{\prime}, \theta^{\prime}\right)\), satisfacen\(r=r^{2}+r \cos (\theta)\). Nosotros sustituimos\(r=-r^{\prime}\) y\(\theta=\theta^{\prime}+\pi\) en\(r=r^{2}+r \cos (\theta)\) para ver si obtenemos una declaración verdadera.

      \ (\ begin {alineado}
      -r^ {\ prime} &\ stackrel {?} {=}\ izquierda (-r^ {\ prime}\ derecha) ^ {2} +\ izquierda (-r^ {\ prime}\ cos\ izquierda (\ theta^ {\ prime} +\ pi\ derecha)\ derecha) &\\
      -\ izquierda (-\ izquierda (r^ {\ prime}\ derecha) ^ {2} -r^ {\ prime}\ cos izquierda (\ theta^ ^ {\ prime}\ derecha)\ derecha) &\ stackrel {?} {=}\ izquierda (r^ {\ prime}\ derecha) ^ {2} -r^ {\ prime}\ cos\ izquierda (\ theta^ {\ prime} +\ pi\ derecha) &\ text {Desde} r^ {\ prime} =-\ izquierda (r^ {\ prime}\ derecha) ^ {2} -r^ {\ prime}\ cos\ izquierda (\ theta^ {\ prime}\ derecha)\\
      \ izquierda (r^ {\ prime}\ derecha) ^ {2} +r^ {\ prime}\ cos\ izquierda (\ theta^ {\ prime}\ derecha) &\ stackrel {?} {=}\ izquierda (r^ {\ prime}\ derecha) ^ {2} -r^ {\ prime}\ izquierda (-\ cos\ izquierda (\ theta^ {\ prime}\ derecha)\ derecha) &\ text {Desde}\ cos\ izquierda (\ theta^ {\ prime} +\ pi\ derecha) =-\ cos\ izquierda (\ theta^ {\ prime} derecha)\\
      \ izquierda (r^ {\ prime}\ derecha) ^ {2} +r^ {\ prime}\ cos\ izquierda (\ theta^ {\ prime}\ derecha) &\ stackrel {\ marca de verificación} {=}\ izquierda (r^ {\ prime}\ derecha) ^ {2} +r^ {\ prime}\ cos\ izquierda (\ theta^ {\ prime}\ derecha) &
      \ end {alineado}\)

      Ya que ambas partes trabajaron para ser iguales,\(\left(-r^{\prime}, \theta^{\prime}+\pi\right)\) satisface\(r=r^{2}+r \cos (\theta)\) lo que significa que cualquier punto\((r, \theta)\) que satisfaga\(r^{2}=\left(r^{2}+r \cos (\theta)\right)^{2}\) tiene una representación que satisface\(r=r^{2}+r \cos (\theta)\), y estamos hechos.

En la práctica, gran parte de la verificación pedante de la equivalencia de ecuaciones en el Ejemplo 11.4.3 se deja sin decir. En efecto, en la mayoría de los libros de texto, las ecuaciones\(r = −3\) al cuadrado como llegar\(r^{2}=9\) sucede sin pensarlo dos veces. Su instructor decidirá en última instancia cuánta justificación, si la hay, está justificada. Si le quitas algo del Ejemplo 11.4.3, debería ser que las cosas relativamente bonitas en coordenadas rectangulares, como\(y=x^{2}\), puedan volverse feas en coordenadas polares, y viceversa. En la siguiente sección, dedicamos nuestra atención a graficar ecuaciones como las dadas en el Ejemplo 11.4.3 número 2 en el plano de coordenadas cartesianas sin convertir de nuevo a coordenadas rectangulares. Si nada más, el número 2c anterior muestra el precio que pagamos si insistimos en convertir siempre a volver al sistema de coordenadas rectangulares más familiar.

11.4.1 Ejercicios

En los Ejercicios 1 - 16, trazar el punto dado en coordenadas polares y luego dar tres expresiones diferentes para el punto de tal manera que

1. \(r<0 \text { and } 0 \leq \theta \leq 2 \pi,\)
2. \(r>0 \text { and } \theta \leq 0\)
3. \(r>0 \text { and } \theta \geq 2 \pi\)

1. \(\left(2, \frac{\pi}{3}\right)\)
2. \(\left(5, \frac{7 \pi}{4}\right)\)
3. \(\left(\frac{1}{3}, \frac{3 \pi}{2}\right)\)
4. \(\left(\frac{5}{2}, \frac{5 \pi}{6}\right)\)
5. \(\left(12,-\frac{7 \pi}{6}\right)\)
6. \(\left(3,-\frac{5 \pi}{4}\right)\)
7. \((2 \sqrt{2},-\pi)\)
8. \(\left(\frac{7}{2},-\frac{13 \pi}{6}\right)\)
9. \((-20,3 \pi)\)
10. \(\left(-4, \frac{5 \pi}{4}\right)\)
11. \(\left(-1, \frac{2 \pi}{3}\right)\)
12. \(\left(-3, \frac{\pi}{2}\right)\)
13. \(\left(-3,-\frac{11 \pi}{6}\right)\)
14. \(\left(-2.5,-\frac{\pi}{4}\right)\)
15. \(\left(-\sqrt{5},-\frac{4 \pi}{3}\right)\)
16. \((-\pi,-\pi)\)

En Ejercicios 17 - 36, convierte el punto de coordenadas polares en coordenadas rectangulares.

17. \(\left(5, \frac{7 \pi}{4}\right)\)
18. \(\left(2, \frac{\pi}{3}\right)\)
19. \(\left(11,-\frac{7 \pi}{6}\right)\)
20. \((-20,3 \pi)\)
21. \(\left(\frac{3}{5}, \frac{\pi}{2}\right)\)
22. \(\left(-4, \frac{5 \pi}{6}\right)\)
23. \(\left(9, \frac{7 \pi}{2}\right)\)
24. \(\left(-5,-\frac{9 \pi}{4}\right)\)
25. \(\left(42, \frac{13 \pi}{6}\right)\)
26. \((-117,117 \pi)\)
27. \((6, \arctan (2))\)
28. \((10, \arctan (3))\)
29. \(\left(-3, \arctan \left(\frac{4}{3}\right)\right)\)
30. \(\left(5, \arctan \left(-\frac{4}{3}\right)\right)\)
31. \(\left(2, \pi-\arctan \left(\frac{1}{2}\right)\right)\)
32. \(\left(-\frac{1}{2}, \pi-\arctan (5)\right)\)
33. \(\left(-1, \pi+\arctan \left(\frac{3}{4}\right)\right)\)
34. \(\left(\frac{2}{3}, \pi+\arctan (2 \sqrt{2})\right)\)
35. \((\pi, \arctan (\pi))\)
36. \(\left(13, \arctan \left(\frac{12}{5}\right)\right)\)

En Ejercicios 37 - 56, convertir el punto de coordenadas rectangulares en coordenadas polares con\(r \geq 0\) y\(0 \leq \theta<2 \pi\).

37. \((0,5)\)
38. \((3, \sqrt{3})\)
39. \((7,-7)\)
40. \((-3,-\sqrt{3})\)
41. \((-3,0)\)
42. \((-\sqrt{2}, \sqrt{2})\)
43. \((-4,-4 \sqrt{3})\)
44. \(\left(\frac{\sqrt{3}}{4},-\frac{1}{4}\right)\)
45. \(\left(-\frac{3}{10},-\frac{3 \sqrt{3}}{10}\right)\)
46. \((-\sqrt{5},-\sqrt{5})\)
47. \((6,8)\)
48. \((\sqrt{5}, 2 \sqrt{5})\)
49. \((-8,1)\)
50. \((-2 \sqrt{10}, 6 \sqrt{10})\)
51. \((-5,-12)\)
52. \(\left(-\frac{\sqrt{5}}{15},-\frac{2 \sqrt{5}}{15}\right)\)
53. \((24,-7)\)
54. \((12,-9)\)
55. \(\left(\frac{\sqrt{2}}{4}, \frac{\sqrt{6}}{4}\right)\)
56. \(\left(-\frac{\sqrt{65}}{5}, \frac{2 \sqrt{65}}{5}\right)\)

En los Ejercicios 57 - 76, convierte la ecuación de coordenadas rectangulares en coordenadas polares. Resuelve para\(r\) en todos menos #60 hasta #63. En Ejercicios 60 - 63, debes resolver para\(\theta\)

57. \(x = 6\)
58. \(x = −3\)
59. \(y = 7\)
60. \(y = 0\)
61. \(y = −x\)
62. \(y=x \sqrt{3}\)
63. \(y = 2x\)
64. \(x^{2}+y^{2}=25\)
65. \(x^{2}+y^{2}=117\)
66. \(y = 4x − 19\)
67. \(x = 3y + 1\)
68. \(y=-3 x^{2}\)
69. \(4 x=y^{2}\)
70. \(x^{2}+y^{2}-2 y=0\)
71. \(x^{2}-4 x+y^{2}=0\)
72. \(x^{2}+y^{2}=x\)
73. \(y^{2}=7 y-x^{2}\)
74. \((x+2)^{2}+y^{2}=4\)
75. \(x^{2}+(y-3)^{2}=9\)
76. \(4 x^{2}+4\left(y-\frac{1}{2}\right)^{2}=1\)

En Ejercicios 77 - 96, convierte la ecuación de coordenadas polares en coordenadas rectangulares.

77. \(r = 7\)
78. \(r = −3\)
79. \(r=\sqrt{2}\)
80. \(\theta=\frac{\pi}{4}\)
81. \(\theta=\frac{2 \pi}{3}\)
82. \(\theta=\pi\)
83. \(\theta=\frac{3 \pi}{2}\)
84. \(r=4 \cos (\theta)\)
85. \(5 r=\cos (\theta)\)
86. \(r=3 \sin (\theta)\)
87. \(r=-2 \sin (\theta)\)
88. \(r=7 \sec (\theta)\)
89. \(12 r=\csc (\theta)\)
90. \(r=-2 \sec (\theta)\)
91. \(r=-\sqrt{5} \csc (\theta)\)
92. \(r=2 \sec (\theta) \tan (\theta)\)
93. \(r=-\csc (\theta) \cot (\theta)\)
94. \(r^{2}=\sin (2 \theta)\)
95. \(r=1-2 \cos (\theta)\)
96. \(r=1+\sin (\theta)\)
97. Convierte el origen (0, 0) en coordenadas polares de cuatro maneras diferentes.
98. Con la ayuda de tus compañeros de clase, usa la Ley de Cosines para desarrollar una fórmula para la distancia entre dos puntos en coordenadas polares.

11.4.2 Respuestas

1. \ (\ begin {aligned}
   &\ left (2,\ frac {\ pi} {3}\ right),\ left (-2,\ frac {4\ pi} {3}\ right)\\
   &\ left (2, -\ frac {5\ pi} {3}\ right),\ left (2,\ frac {7\ pi} {3}\ right)
   \ end {alineado}\)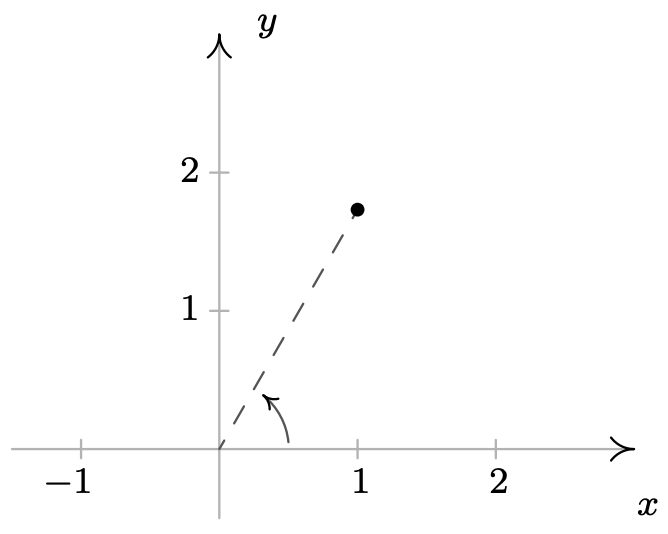

   

2. \ (\ begin {alineado}
   &\ left (5,\ frac {7\ pi} {4}\ derecho),\ left (-5,\ frac {3\ pi} {4}\ right)\\
   &\ left (5, -\ frac {\ pi} {4}\ right),\ left (5,\ frac {15\ pi} {4}\ right)
   \ end {alineado}\)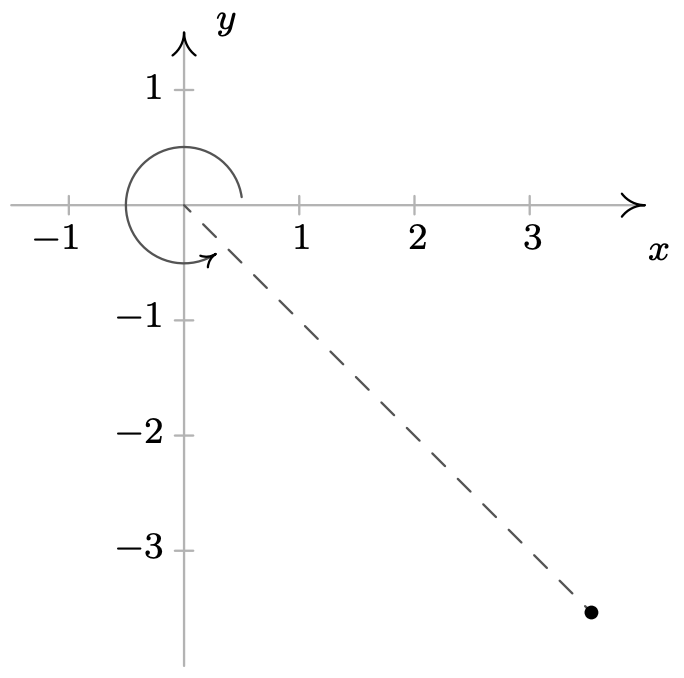

   

3. \ (\ begin {alineada}
   &\ izquierda (\ frac {1} {3},\ frac {3\ pi} {2}\ derecha),\ izquierda (-\ frac {1} {3},\ frac {\ pi} {2}\ derecha)\\
   &\ izquierda (\ frac {1} {3}, -\ frac {\ pi} {2}\ derecha),\ izquierda (\ frac {1} {3},\ frac {7\ pi} {2}\ derecha)
   \ final {alineado}\)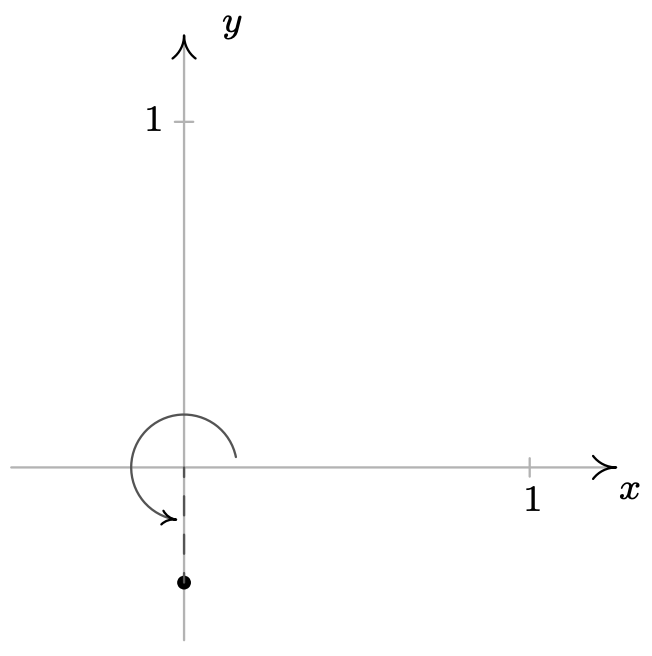

   

4. \ (\ begin {alineado}
   &\ izquierda (\ frac {5} {2},\ frac {5\ pi} {6}\ derecha),\ izquierda (-\ frac {5} {2},\ frac {11\ pi} {6}\ derecha)\\
   &\ izquierda (\ frac {5} {2}, -\ frac {7\ pi} {6} derecha),\ left (\ frac {5} {2},\ frac {17\ pi} {6}\ derecha)
   \ end {alineado}\)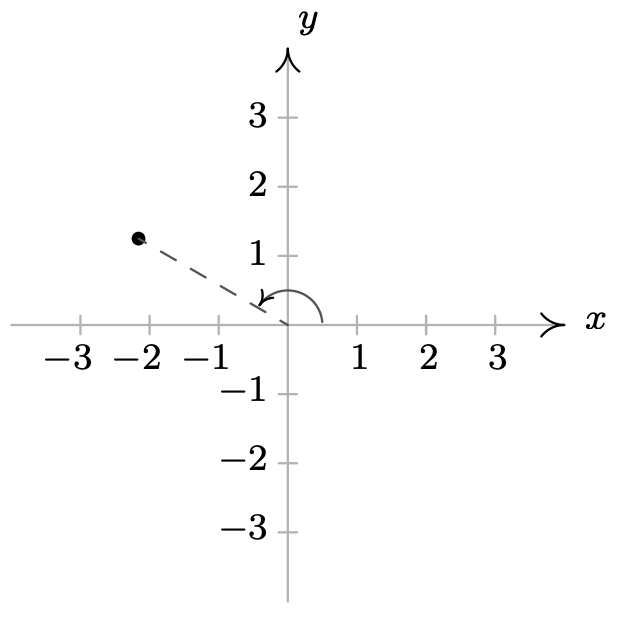

   

5. \ (\ begin {aligned}
   &\ left (12, -\ frac {7\ pi} {6}\ right),\ left (-12,\ frac {11\ pi} {6}\ right)\\
   &\ left (12, -\ frac {19\ pi} {6}\ right),\ left (12,\ frac {17\ pi} {6}\ right)
   \ end {alineado}\)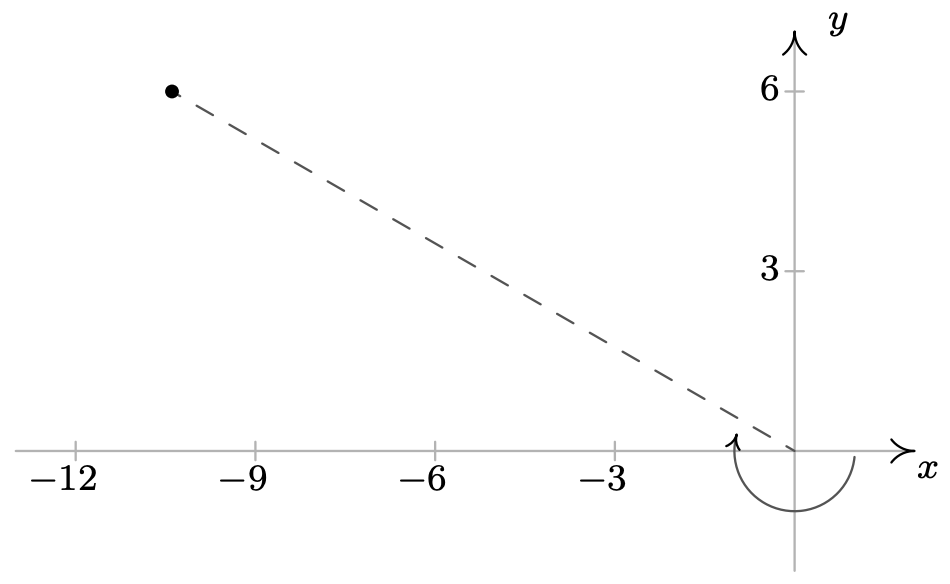

   

6. \ (\ begin {aligned}
   &\ left (3, -\ frac {5\ pi} {4}\ right),\ left (-3,\ frac {7\ pi} {4}\ right)\\
   &\ left (3, -\ frac {13\ pi} {4}\ right),\ left (3,\ frac {11\ pi} {4}\ right)
   \ end {alineado}\)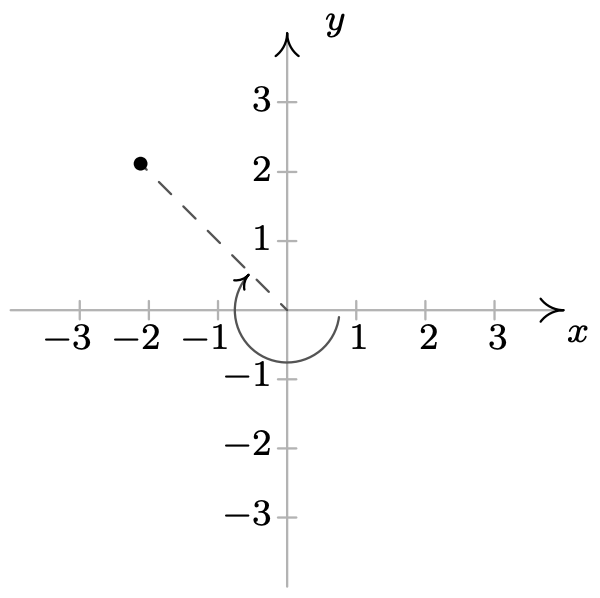

   

7. \ (\ begin {alineado}
   & (2\ sqrt {2}, -\ pi), (-2\ sqrt {2}, 0)\\
   & (2\ sqrt {2}, -3\ pi), (2\ sqrt {2}, 3\ pi)
   \ end {alineado}\)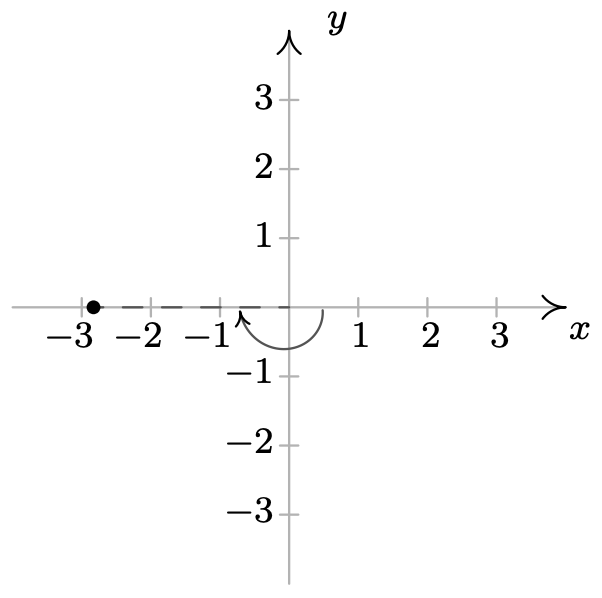

   

8. \ (\ begin {alineado}
   &\ izquierda (\ frac {7} {2}, -\ frac {13\ pi} {6}\ derecha),\ izquierda (-\ frac {7} {2},\ frac {5\ pi} {6}\ derecha)\\
   &\ izquierda (\ frac {7} {2}, -\ frac {\ pi} {6} derecha),\ left (\ frac {7} {2},\ frac {23\ pi} {6}\ derecha)
   \ end {alineado}\)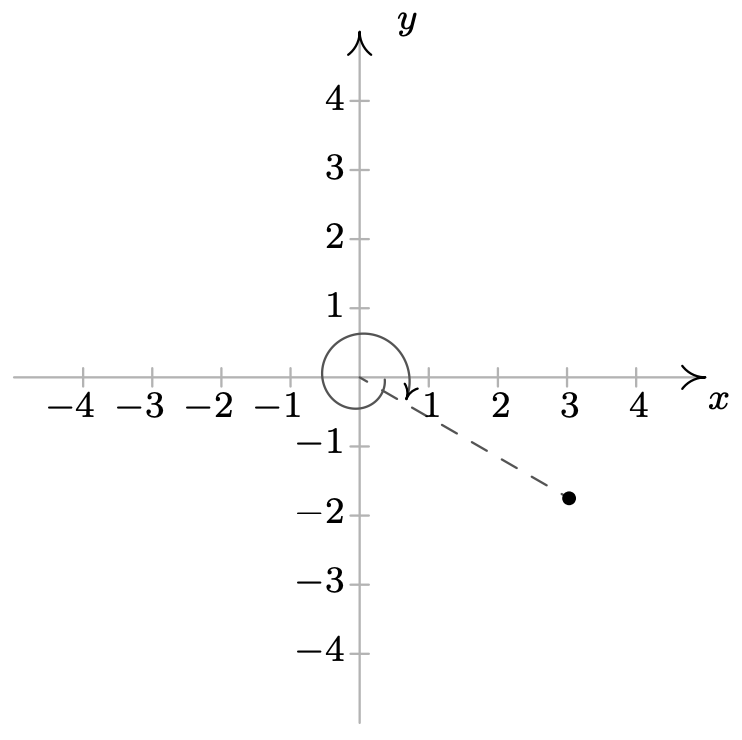

   

9. \ (\ begin {alineado}
   & (-20,3\ pi), (-20,\ pi)\\
   & (20, -2\ pi), (20,4\ pi)
   \ end {alineado}\)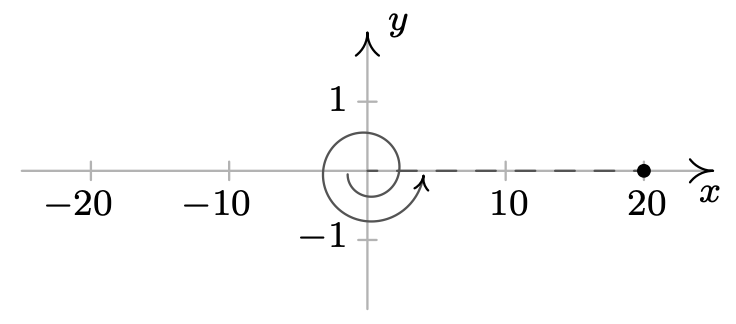

   

10. \ (\ begin {aligned}
    &\ left (-4,\ frac {5\ pi} {4}\ right),\ left (-4,\ frac {13\ pi} {4}\ right)\\
    &\ left (4, -\ frac {7\ pi} {4}\ right),\ left (4,\ frac {9\ pi} {4}\ right)
    \ end {alineado}\)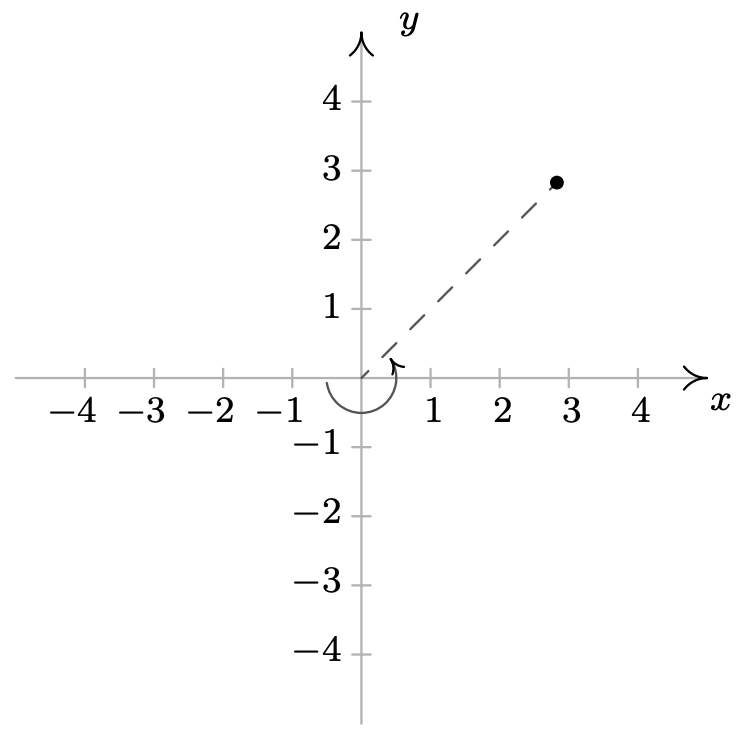

    

11. \ (\ begin {alineado}
    &\ left (-1,\ frac {2\ pi} {3}\ derecho),\ left (-1,\ frac {8\ pi} {3}\ right)\\
    &\ left (1, -\ frac {\ pi} {3}\ right),\ left (1,\ frac {11\ pi} {3}\ right)
    \ end {alineado}\)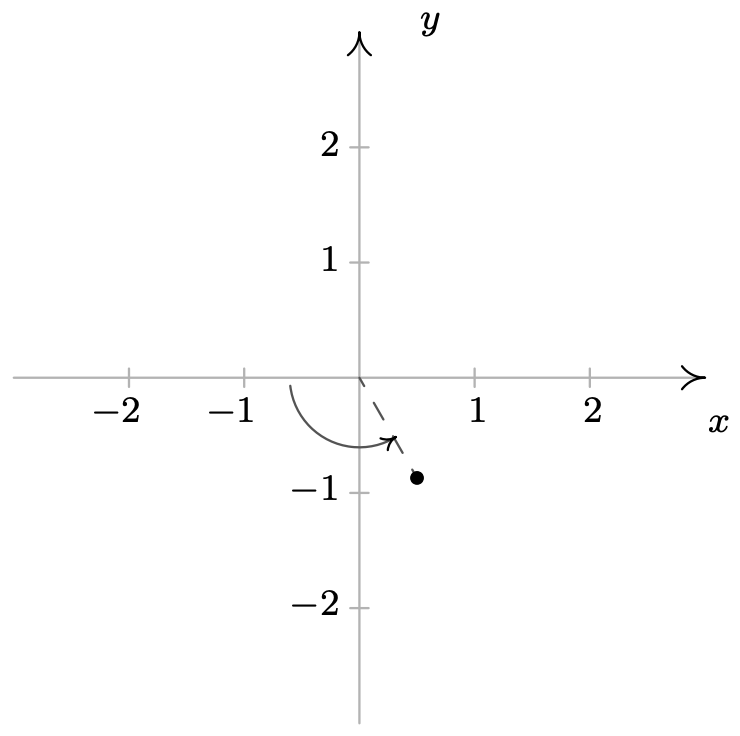

    

12. \ (\ begin {alineado}
    &\ left (-3,\ frac {\ pi} {2}\ derecha),\ left (-3,\ frac {5\ pi} {2}\ right)\\
    &\ left (3, -\ frac {\ pi} {2}\ right),\ left (3,\ frac {7\ pi} {2}\ right)
    \ end {alineado}\)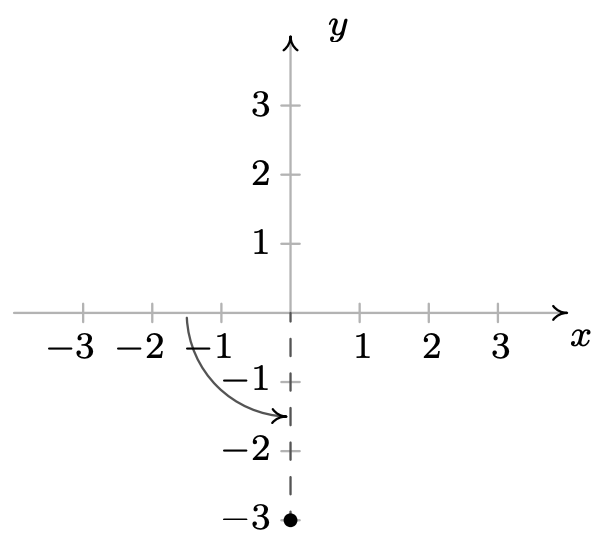

    

13. \ (\ begin {aligned}
    &\ left (-3, -\ frac {11\ pi} {6}\ right),\ left (-3,\ frac {\ pi} {6}\ right)\\
    &\ left (3, -\ frac {5\ pi} {6}\ right),\ left (3,\ frac {19\ pi} {6}\ right)
    \ end {alineado}\)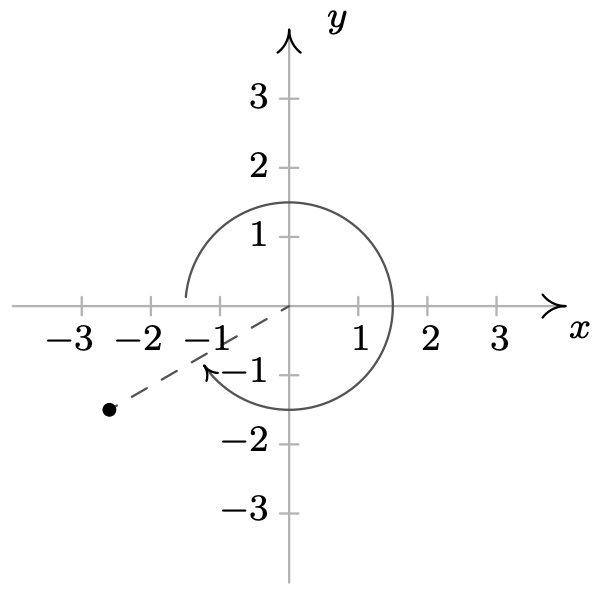

    

14. \ (\ begin {aligned}
    &\ left (-2.5, -\ frac {\ pi} {4}\ right),\ left (-2.5,\ frac {7\ pi} {4}\ right)\\
    &\ left (2.5, -\ frac {5\ pi} {4}\ right),\ left (2.5,\ frac {11\ pi} {4}\ right)
    \ end {alineado}\)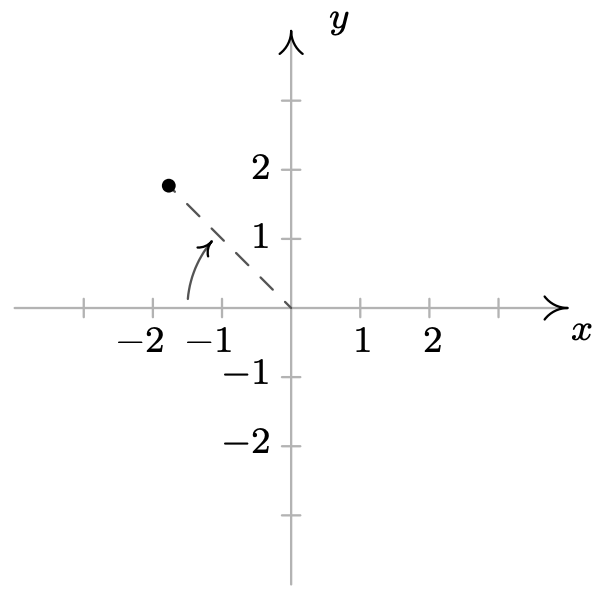

    

15. \ (\ begin {alineada}
    &\ izquierda (-\ sqrt {5}, -\ frac {4\ pi} {3}\ derecha),\ izquierda (-\ sqrt {5},\ frac {2\ pi} {3}\ derecha)\\
    &\ izquierda (\ sqrt {5}, -\ frac {\ pi} {3}\ derecha),\ izquierda (\ sqrt {5}, -\ frac {\ pi} {3}\ derecha),\ izquierda (\ sqrt {5}, - {5},\ frac {11\ pi} {3}
    \ derecha)\ end {alineado}\)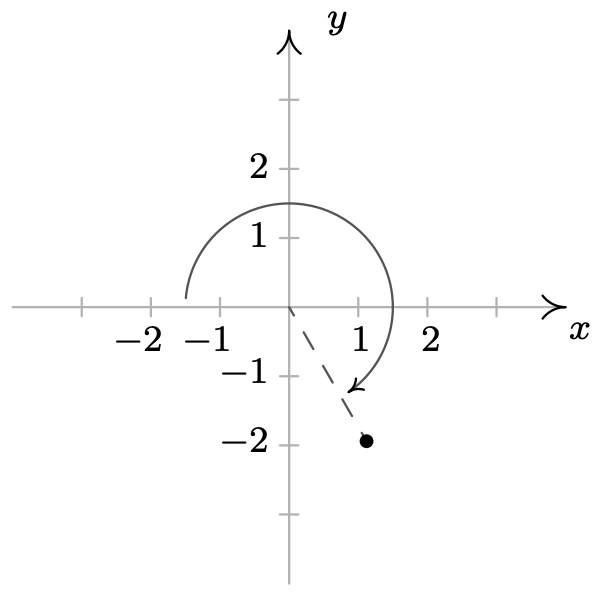

    

16. \ (\ begin {alineado}
    & (-\ pi, -\ pi), (-\ pi,\ pi)\\
    & (\ pi, -2\ pi), (\ pi, 2\ pi)
    \ end {alineado}\)

    

17. \(\left(\frac{5 \sqrt{2}}{2},-\frac{5 \sqrt{2}}{2}\right)\)
18. \((1, \sqrt{3})\)
19. \(\left(-\frac{11 \sqrt{3}}{2}, \frac{11}{2}\right)\)
20. \((20, 0)\)
21. \(\left(0, \frac{3}{5}\right)\)
22. \((2 \sqrt{3},-2)\)
23. \((0, −9)\)
24. \(\left(-\frac{5 \sqrt{2}}{2}, \frac{5 \sqrt{2}}{2}\right)\)
25. \((21 \sqrt{3}, 21)\)
26. \((117,0)\)
27. \(\left(\frac{6 \sqrt{5}}{5}, \frac{12 \sqrt{5}}{5}\right)\)
28. \((\sqrt{10}, 3 \sqrt{10})\)
29. \(\left(-\frac{9}{5},-\frac{12}{5}\right)\)
30. \((3,-4)\)
31. \(\left(-\frac{4 \sqrt{5}}{5}, \frac{2 \sqrt{5}}{5}\right)\)
32. \(\left(\frac{\sqrt{26}}{52},-\frac{5 \sqrt{26}}{52}\right)\)
33. \(\left(\frac{4}{5}, \frac{3}{5}\right)\)
34. \(\left(-\frac{2}{9},-\frac{4 \sqrt{2}}{9}\right)\)
35. \(\left(\frac{\pi}{\sqrt{1+\pi^{2}}}, \frac{\pi^{2}}{\sqrt{1+\pi^{2}}}\right)\)
36. \((5,12)\)
37. \(\left(5, \frac{\pi}{2}\right)\)
38. \(\left(2 \sqrt{3}, \frac{\pi}{6}\right)\)
39. \(\left(7 \sqrt{2}, \frac{7 \pi}{4}\right)\)
40. \(\left(2 \sqrt{3}, \frac{7 \pi}{6}\right)\)
41. \((3, \pi)\)
42. \(\left(2, \frac{3 \pi}{4}\right)\)
43. \(\left(8, \frac{4 \pi}{3}\right)\)
44. \(\left(\frac{1}{2}, \frac{11 \pi}{6}\right)\)
45. \(\left(\frac{3}{5}, \frac{4 \pi}{3}\right)\)
46. \(\left(\sqrt{10}, \frac{5 \pi}{4}\right)\)
47. \(\left(10, \arctan \left(\frac{4}{3}\right)\right)\)
48. \((5, \arctan (2))\)
49. \(\left(\sqrt{65}, \pi-\arctan \left(\frac{1}{8}\right)\right)\)
50. \((20, \pi-\arctan (3))\)
51. \(\left(13, \pi+\arctan \left(\frac{12}{5}\right)\right)\)
52. \(\left(\frac{1}{3}, \pi+\arctan (2)\right)\)
53. \(\left(25,2 \pi-\arctan \left(\frac{7}{24}\right)\right)\)
54. \(\left(15,2 \pi-\arctan \left(\frac{3}{4}\right)\right)\)
55. \(\left(\frac{\sqrt{2}}{2}, \frac{\pi}{3}\right)\)
56. \((\sqrt{13}, \pi-\arctan (2))\)
57. \(r=6 \sec (\theta)\)
58. \(r=-3 \sec (\theta)\)
59. \(r=7 \csc (\theta)\)
60. \(\theta=0\)
61. \(\theta=\frac{3 \pi}{4}\)
62. \(\theta=\frac{\pi}{3}\)
63. \(\theta=\arctan (2)\)
64. \(r=5\)
65. \(r=\sqrt{117}\)
66. \(r=\frac{19}{4 \cos (\theta)-\sin (\theta)}\)
67. \(x=\frac{1}{\cos (\theta)-3 \sin (\theta)}\)
68. \(r=\frac{-\sec (\theta) \tan (\theta)}{3}\)
69. \(r=4 \csc (\theta) \cot (\theta)\)
70. \(r=2 \sin (\theta)\)
71. \(r=4 \cos (\theta)\)
72. \(r=\cos (\theta)\)
73. \(r=7 \sin (\theta)\)
74. \(r=-4 \cos (\theta)\)
75. \(r=6 \sin (\theta)\)
76. \(r=\sin (\theta)\)
77. \(x^{2}+y^{2}=49\)
78. \(x^{2}+y^{2}=9\)
79. \(x^{2}+y^{2}=2\)
80. \(y = x\)
81. \(y=-\sqrt{3} x\)
82. \(y = 0\)
83. \(x = 0\)
84. \(x^{2}+y^{2}=4 x \text { or }(x-2)^{2}+y^{2}=4\)
85. \(5 x^{2}+5 y^{2}=x \text { or }\left(x-\frac{1}{10}\right)^{2}+y^{2}=\frac{1}{100}\)
86. \(x^{2}+y^{2}=3 y \text { or } x^{2}+\left(y-\frac{3}{2}\right)^{2}=\frac{9}{4}\)
87. \(x^{2}+y^{2}=-2 y \text { or } x^{2}+(y+1)^{2}=1\)
88. \(x = 7\)
89. \(y=\frac{1}{12}\)
90. \(x = −2\)
91. \(y=-\sqrt{5}\)
92. \(x^{2}=2 y\)
93. \(y^{2}=-x\)
94. \(\left(x^{2}+y^{2}\right)^{2}=2 x y\)
95. \(\left(x^{2}+2 x+y^{2}\right)^{2}=x^{2}+y^{2}\)
96. \(\left(x^{2}+y^{2}+y\right)^{2}=x^{2}+y^{2}\)
97. Cualquier punto del formulario\((0, \theta)\) funcionará, e.g\((0, \pi),(0,-117),\left(0, \frac{23 \pi}{4}\right) \text { and }(0,0)\).

---

Referencia

¹ Excluyendo, por supuesto, los puntos en los que una o ambas coordenadas son 0.

² Vamos a explicar más sobre esto momentáneamente.

³ Al igual que con cualquier cosa en Matemáticas, cuantas más formas tengas de mirar algo, mejor. Los autores animan al lector a tomarse el tiempo para pensar en ambos enfoques para trazar puntos dados en coordenadas polares.

⁴ Ya que\(x = 0\), tendríamos que determinar\(\theta\) geométricamente.

⁵ La experiencia es la madre de todo instinto, y la necesidad es la madre de la invención. Estudia este ejemplo y ve qué técnicas se emplean, luego haz tu mejor esfuerzo para obtener tus respuestas en la tarea para que coincidan con las de Jeff.

⁶ Tenga en cuenta que cuando sustituimos\(\theta=\frac{\pi}{2}\) en\(r=6 \cos (\theta)\), recuperamos el punto\(r = 0\), por lo que no estamos perdiendo nada despreciando\(r = 0\).

⁷ Véase Sección 8.1.

⁸ Podríamos tomarlo como cualquiera de\(\theta=-\frac{\pi}{4}+\pi k\) para enteros\(k\).

⁹ Ejercicio 5.3.1 en la Sección 5.3, por ejemplo...

¹⁰ Aquí, 'equivalente' significa que representan el mismo punto en el plano. Como pares ordenados,\((3, 0)\) y\((-3, \pi)\) son diferentes, pero cuando se interpretan como coordenadas polares, corresponden al mismo punto en el plano. Matemáticamente hablando, las relaciones son conjuntos de pares ordenados, por lo que las ecuaciones\(r^{2}=9\) y\(r = −3\) representan diferentes relaciones ya que corresponden a diferentes conjuntos de pares ordenados. Dado que las coordenadas polares se definieron geométricamente para describir la ubicación de los puntos en el plano, sin embargo, nos preocupamos solo por asegurar que los conjuntos de puntos en el plano generados por dos ecuaciones sean los mismos. Esto no era un tema, por cierto, cuando definimos por primera vez las relaciones como conjuntos de puntos en el plano en la Sección 1.2. En aquel entonces, se identificó un punto en el avión con un par ordenado único dado por sus coordenadas cartesianas.

¹¹ Además de tomar la tangente de ambos lados de una ecuación (¡Hay infinitamente muchas soluciones para\(\tan (\theta)=\sqrt{3}\), y\(\theta=\frac{4 \pi}{3}\) es solo una de ellas!) , también pasamos de\(\frac{y}{x}=\sqrt{3}\), en el que\(x\) no puede ser 0, a\(y=x \sqrt{3}\) en el que suponemos que\(x\) puede ser 0.