11.5: Gráficas de Ecuaciones Polares

En esta sección, discutimos cómo graficar ecuaciones en coordenadas polares en el plano de coordenadas rectangulares. Dado que cualquier punto dado en el plano tiene infinitamente muchas representaciones diferentes en coordenadas polares, nuestro 'Principio Fundamental de Gráficación' en esta sección no es tan limpio como lo fue para las gráficas de ecuaciones rectangulares en la página 23. Lo declaramos a continuación para que sea completo.

El principio fundamental de gráficos para ecuaciones polares

La gráfica de una ecuación en coordenadas polares es el conjunto de puntos que satisfacen la ecuación. Es decir, un punto\(P(r, \theta)\) está en la gráfica de una ecuación si y sólo si hay una representación de\(P\), digamos\(\left(r^{\prime}, \theta^{\prime}\right)\), tal que\(r^{\prime}\) y\(\theta^{\prime}\) satisfaga la ecuación.

Nuestro primer ejemplo se centra en algunas de las ecuaciones polares estructuralmente más simples.

Ejemplo 11.5.1

Grafica las siguientes ecuaciones polares.

1. \(r = 4\)
2. \(r=-3 \sqrt{2}\)
3. \(\theta=\frac{5 \pi}{4}\)
4. \(\theta=-\frac{3 \pi}{2}\)

Solución

En cada una de estas ecuaciones, sólo una de las variables\(r\) y\(\theta\) está presente haciendo libre a la otra variable. ¹ Esto hace que estas gráficas sean más fáciles de visualizar que otras.

1. En la ecuación\(r = 4\),\(\theta\) es libre. La gráfica de esta ecuación es, por lo tanto, todos los puntos que tienen una representación de coordenadas polares\((4, \theta)\), para cualquier elección de\(\theta\). Gráficamente esto se traduce en trazar todos los puntos a 4 unidades del origen. Esta es exactamente la definición de círculo, centrado en el origen, con un radio de 4.

   

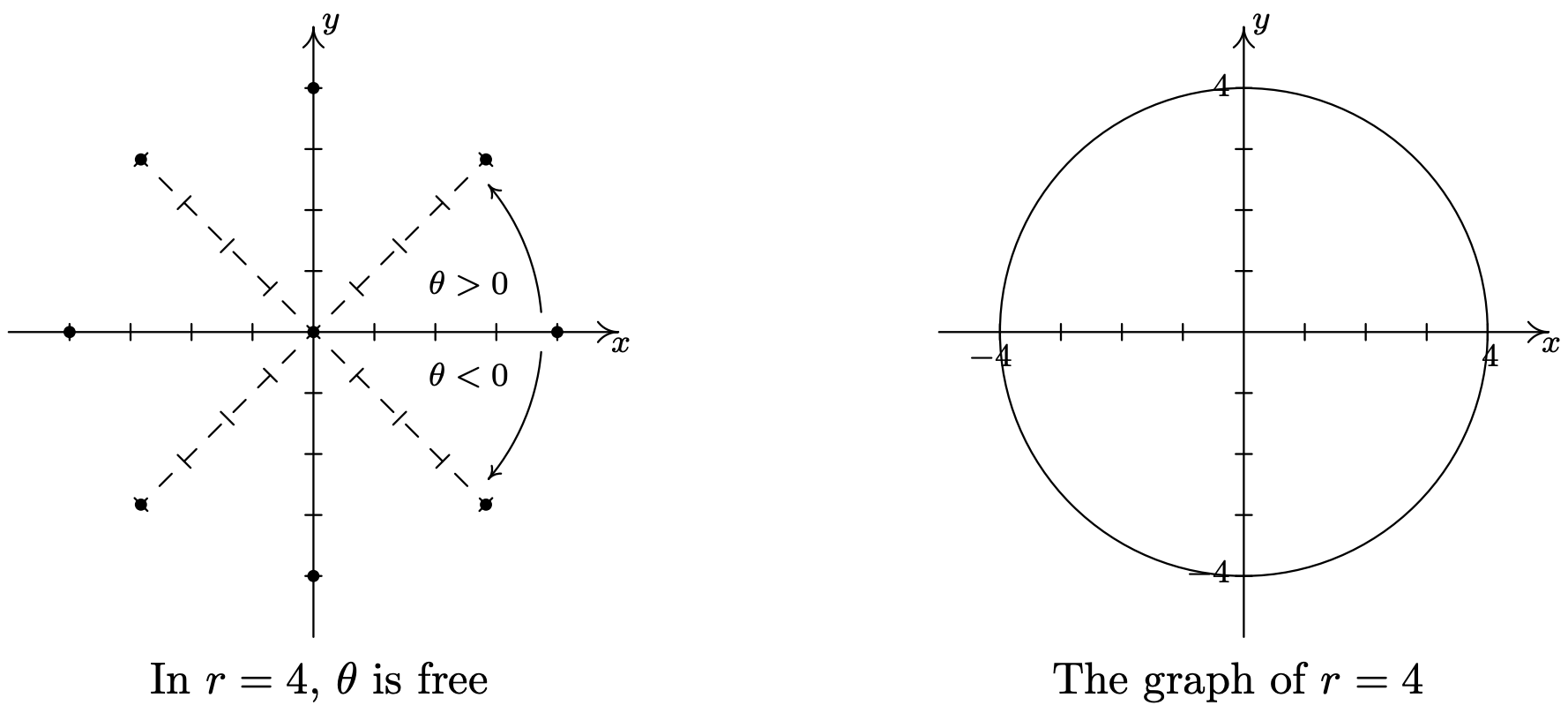
2. Una vez más tenemos\(\theta\) ser libres en la ecuación\(r=-3 \sqrt{2}\). Trazar todos los puntos de la forma nos\((-3 \sqrt{2}, \theta)\) da un círculo de radio\(3 \sqrt{2}\) centrado en el origen.

   

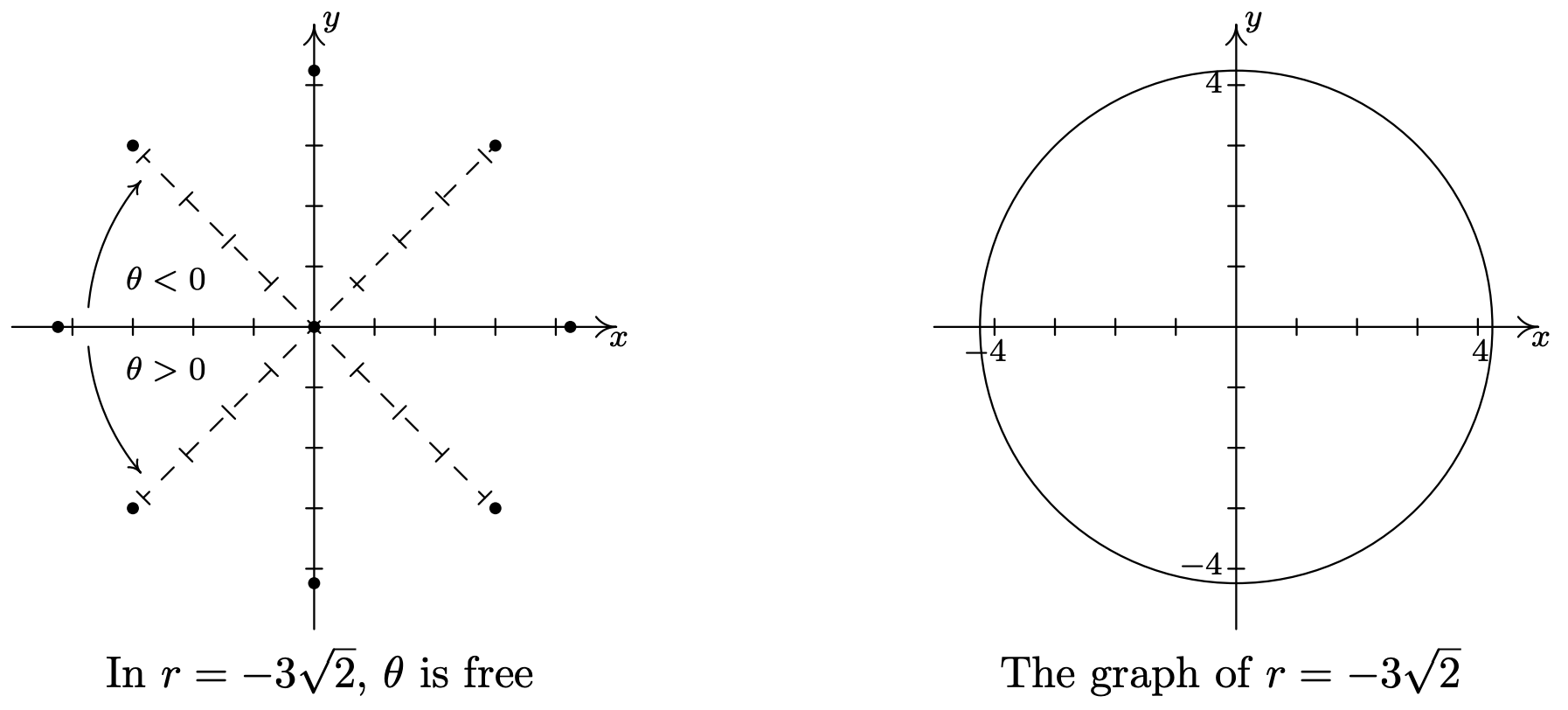
3. En la ecuación\(\theta=\frac{5 \pi}{4}\),\(r\) es libre, por lo que trazamos todos los puntos con representación polar\(\left(r, \frac{5 \pi}{4}\right)\). Lo que encontramos es que estamos trazando la línea que contiene el lado terminal de\(\theta=\frac{5 \pi}{4}\) cuando se traza en posición estándar.

   

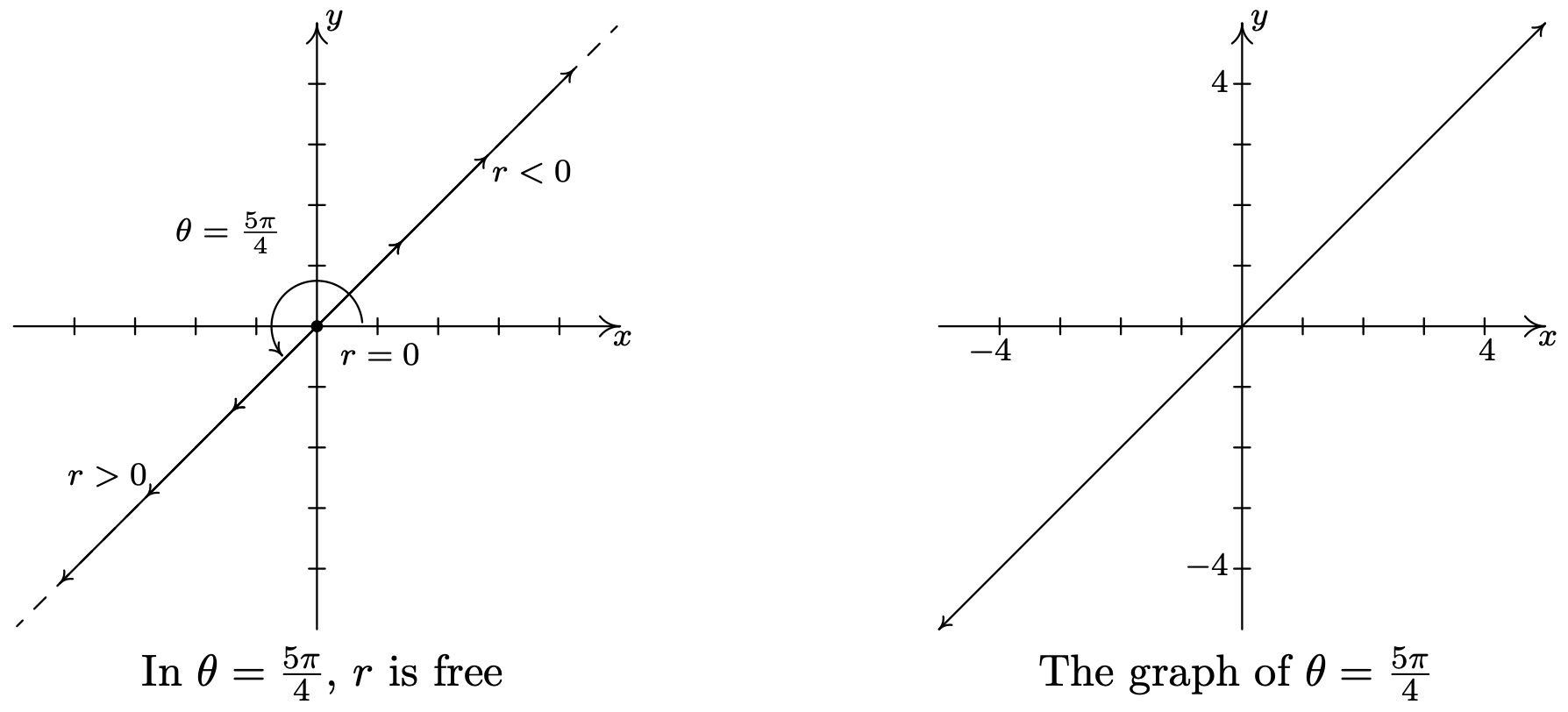
4. Al igual que en el ejemplo anterior, la variable\(r\) está libre en la ecuación\(\theta=-\frac{3 \pi}{2}\). Trazar\(\left(r,-\frac{3 \pi}{2}\right)\) para varios valores de nos\(r\) muestra que estamos trazando el\(y\) eje -eje.

   

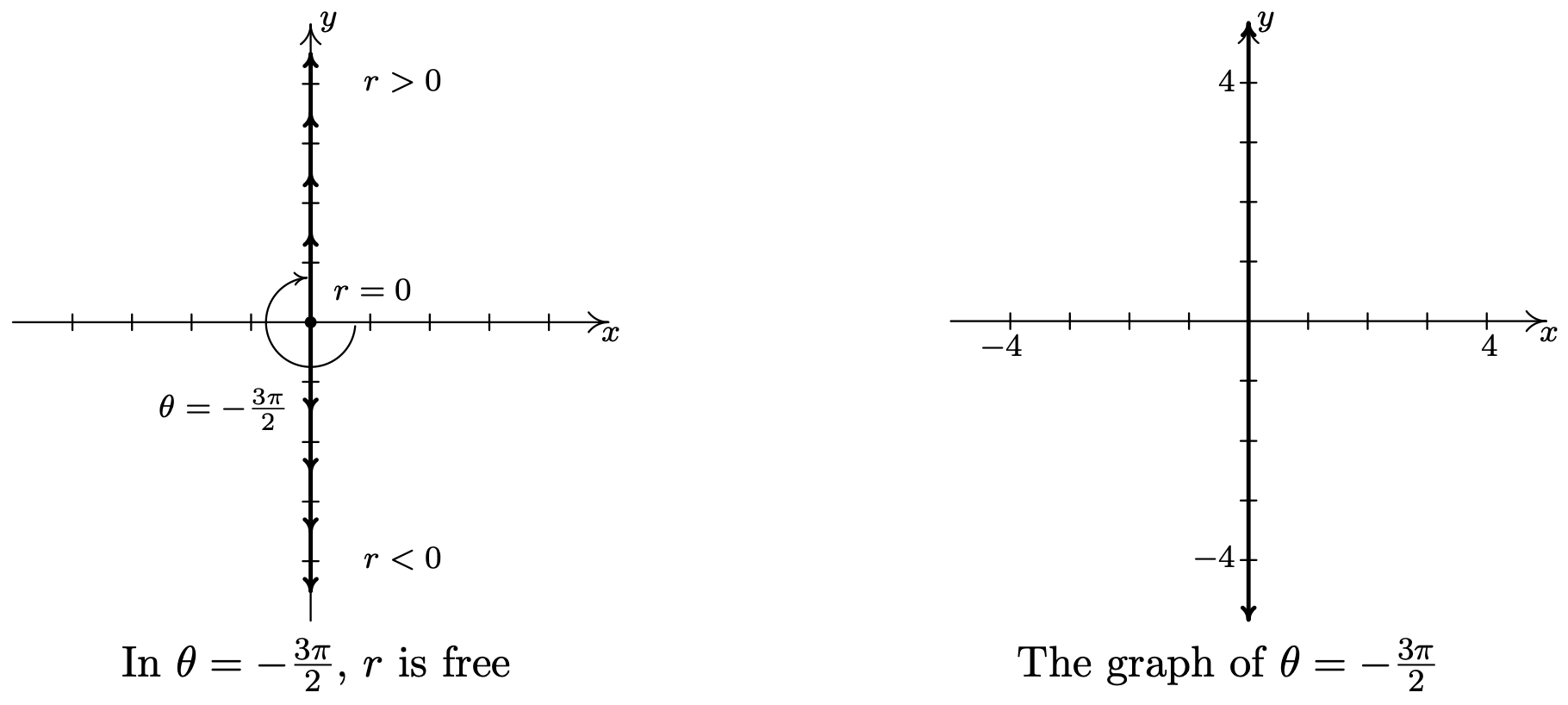
Ojalá, nuestra experiencia en el Ejemplo 11.5.1 deje claro el siguiente resultado.

Teorema 11.8. Gráficas de Constante\(r\) and \(\theta\)

Supongamos\(a\) y\(\alpha\) son constantes,\(a \neq 0\).

• La gráfica de la ecuación polar\(r = a\) en el plano cartesiano es un círculo centrado en el origen del radio\(|a|\).
• El gráfico de la ecuación polar\(\theta=\alpha\) en el plano cartesiano es la línea que contiene el lado terminal de\(\alpha\) cuando se traza en posición estándar.

Supongamos que deseamos graficar\(r=6 \cos (\theta)\). Una manera razonable de comenzar es tratar\(\theta\) como la variable independiente,\(r\) como la variable dependiente, evaluar\(r=f(\theta)\) en algunos valores 'amigables' de\(\theta\) y trazar los puntos resultantes. ² Generamos la siguiente tabla.

A pesar de tener nueve pares ordenados, solo obtenemos cuatro puntos distintos en la gráfica. Por esta razón, empleamos una estrategia ligeramente diferente. Gráficamos un ciclo de\(r=6 \cos (\theta)\) en el\(\theta r-\mathrm{plane}\) ³ y lo usamos para ayudar a graficar la ecuación en el\(xy\) plano. Vemos que como\(\theta\) rangos de 0 a\(\frac{\pi}{2}\),\(r\) va de 6 a 0. En el\(xy\) plano -esto significa que la curva inicia 6 unidades desde el origen en el\(x\) eje positivo\((\theta=0)\) y regresa gradualmente al origen en el momento en que la curva alcanza el\(y\) eje -eje\(\left(\theta=\frac{\pi}{2}\right)\). Las flechas dibujadas en la siguiente figura están destinadas a ayudarte a visualizar este proceso. En el\(\theta r \text {-plane }\), las flechas se dibujan de la\(\theta \text {-axis }\) a la curva\(r=6 \cos (\theta)\). En el\(xy\) plano -cada una de estas flechas inicia en el origen y se gira en el ángulo correspondiente\(\theta\), de acuerdo con la forma en que trazamos las coordenadas polares. Es una forma menos precisa de generar el gráfico que calcular los valores reales de las funciones, pero es marcadamente más rápida.

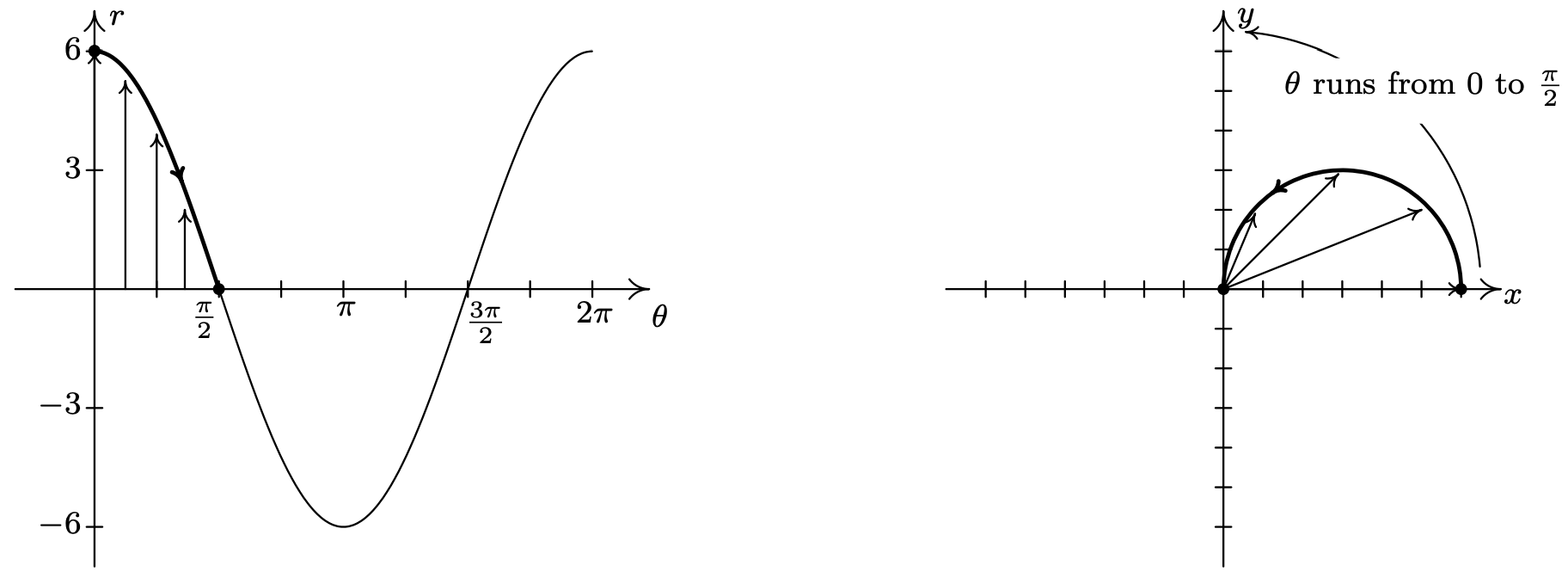
A continuación, repetimos el proceso como\(\theta\) rangos de\(\frac{\pi}{2}\) a\(\pi\). Aquí, los\(r\) valores son todos negativos. Esto significa que en el\(xy\) plano -en lugar de graficar en el Cuadrante II, graficamos en el Cuadrante IV, con todas las rotaciones angulares comenzando desde el\(x\) eje negativo.

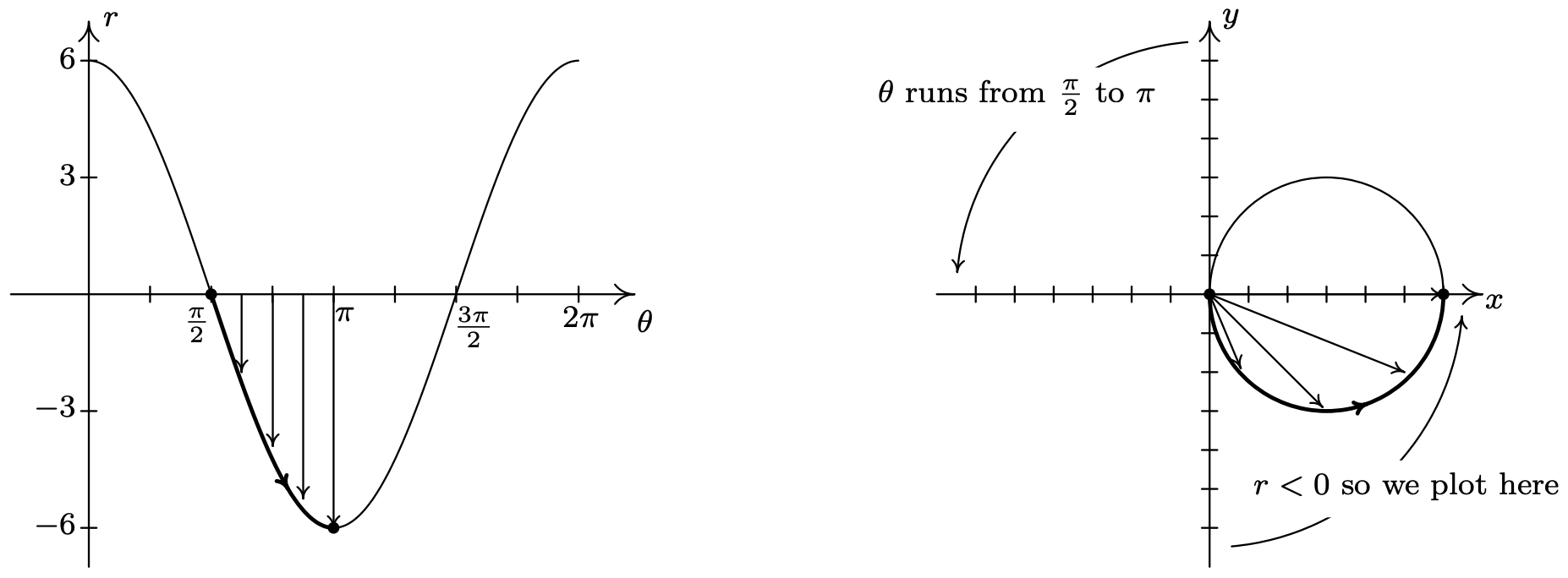
Como\(\theta\) rangos de\(\pi\) a\(\frac{3 \pi}{2}\), los\(r\) valores siguen siendo negativos, lo que significa que la gráfica se traza en el Cuadrante I en lugar del Cuadrante III. Dado que el\(|r|\) para estos valores de\(\theta\) coinciden los\(r\) valores para\(\theta\) in\(\left[0, \frac{\pi}{2}\right]\), tenemos que la curva comienza a retroceder en este punto. Avanzando más, encontramos que cuando\(\frac{3 \pi}{2} \leq \theta \leq 2 \pi\), retrocedemos la porción de la curva en el Cuadrante IV que primero trazamos como\(\frac{\pi}{2} \leq \theta \leq \pi\). Se invita al lector a verificar que trazar cualquier rango\(\theta\) fuera del intervalo\([0, \pi]\) da como resultado la retracción de alguna porción de la curva. ⁴ Presentamos la gráfica final a continuación.

Ejemplo 11.5.2

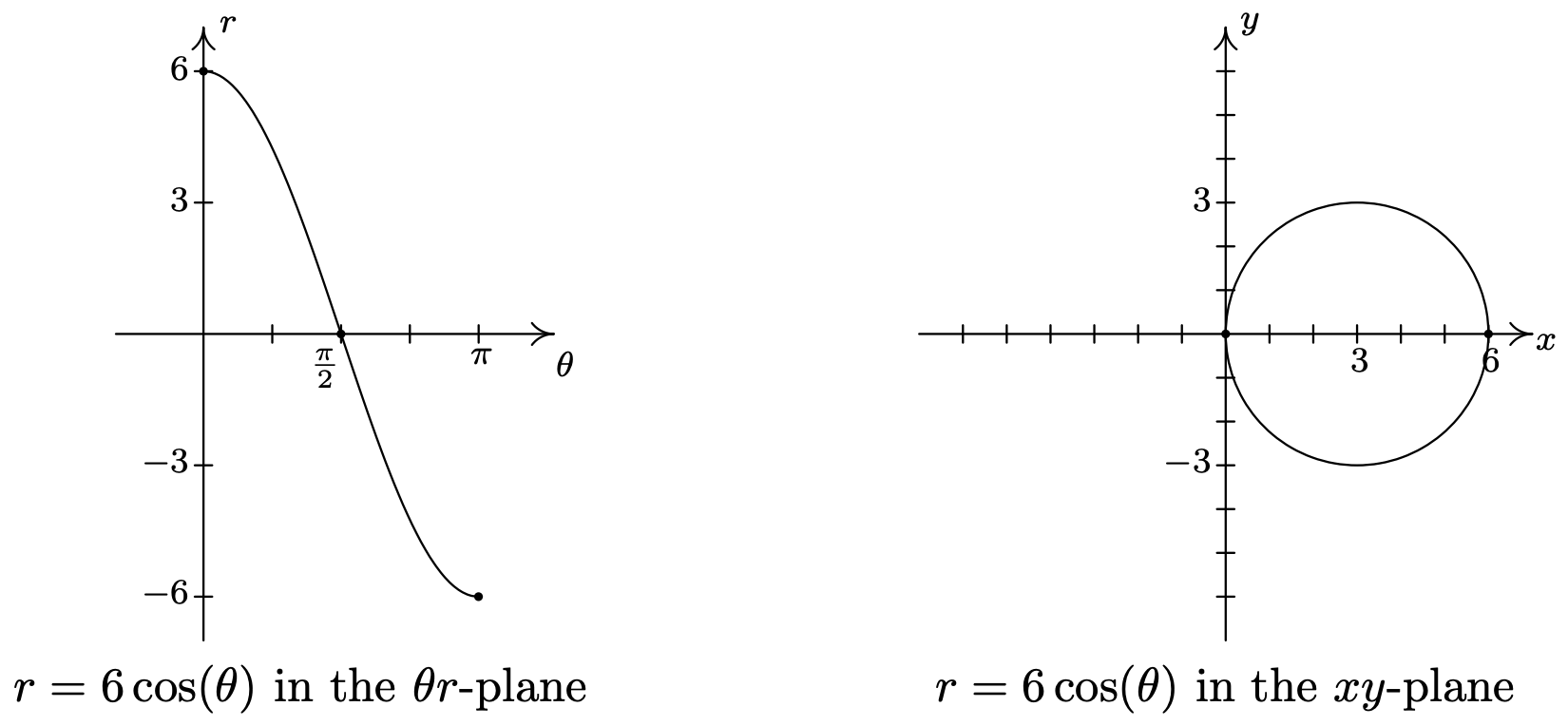
Grafica las siguientes ecuaciones polares.

1. \(r=4-2 \sin (\theta)\)
2. \(r=2+4 \cos (\theta)\)
3. \(r=5 \sin (2 \theta)\)
4. \(r^{2}=16 \cos (2 \theta)\)

Solución

1. Primero trazamos el ciclo fundamental de\(r=4-2 \sin (\theta)\) en el\(\theta r \text {-axes }\). Para ayudarnos a visualizar gráficamente lo que sucede,\([0,2 \pi]\) dividimos en los cuatro subintervalos habituales\(\left[0, \frac{\pi}{2}\right],\left[\frac{\pi}{2}, \pi\right]\),\(\left[\pi, \frac{3 \pi}{2}\right]\) y\(\left[\frac{3 \pi}{2}, 2 \pi\right]\), y procedemos como hicimos anteriormente. Como\(\theta\) rangos de 0 a\(\frac{\pi}{2}\),\(r\) disminuye de 4 a 2. Esto significa que la curva en el\(xy\) plano -inicia 4 unidades desde el origen en el\(x\) eje positivo y poco a poco tira hacia el origen a medida que se mueve hacia el\(y\) eje positivo.

   

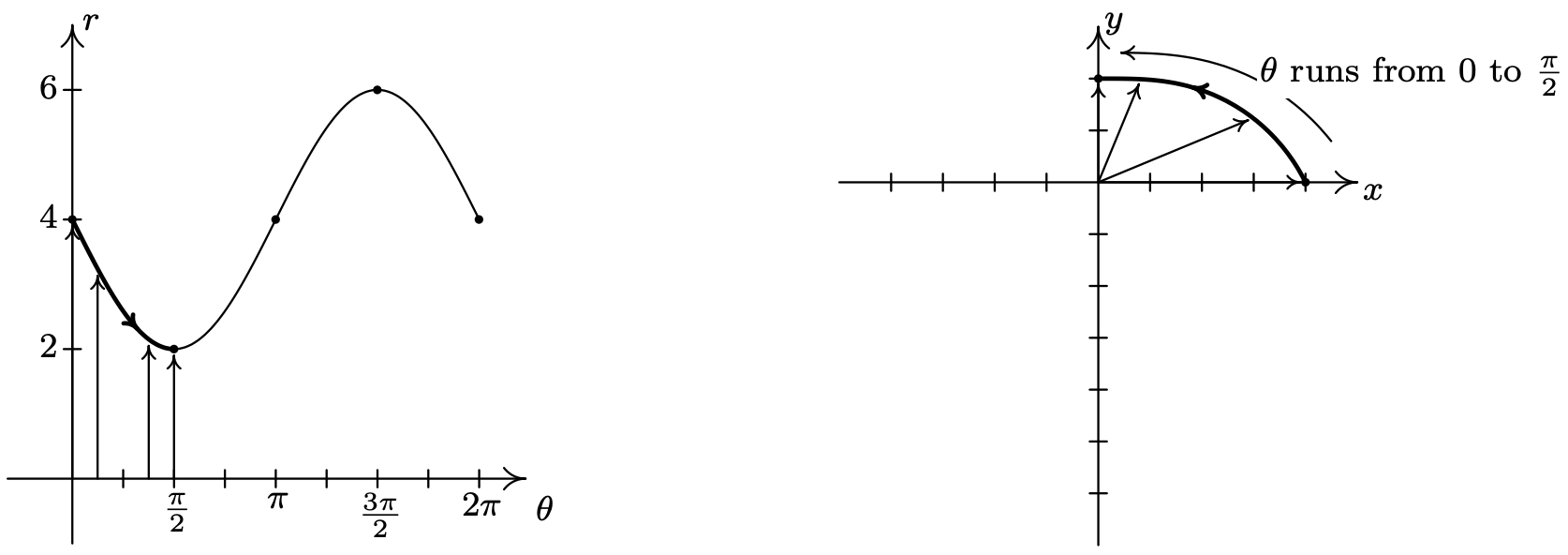
   A continuación, como\(\theta\) corre de\(\frac{\pi}{2}\) a\(\pi\), vemos que\(r\) aumenta de 2 a 4. Recogiendo donde lo dejamos, poco a poco retiramos la gráfica del origen hasta llegar al\(x\) eje negativo.

   

   A lo largo del intervalo\(\left[\pi, \frac{3 \pi}{2}\right]\), vemos que\(r\) aumenta de 4 a 6. En el\(xy\) plano -plano, la curva se aleja del origen a medida que viaja desde el\(x\) eje negativo al\(y\) eje negativo.

   

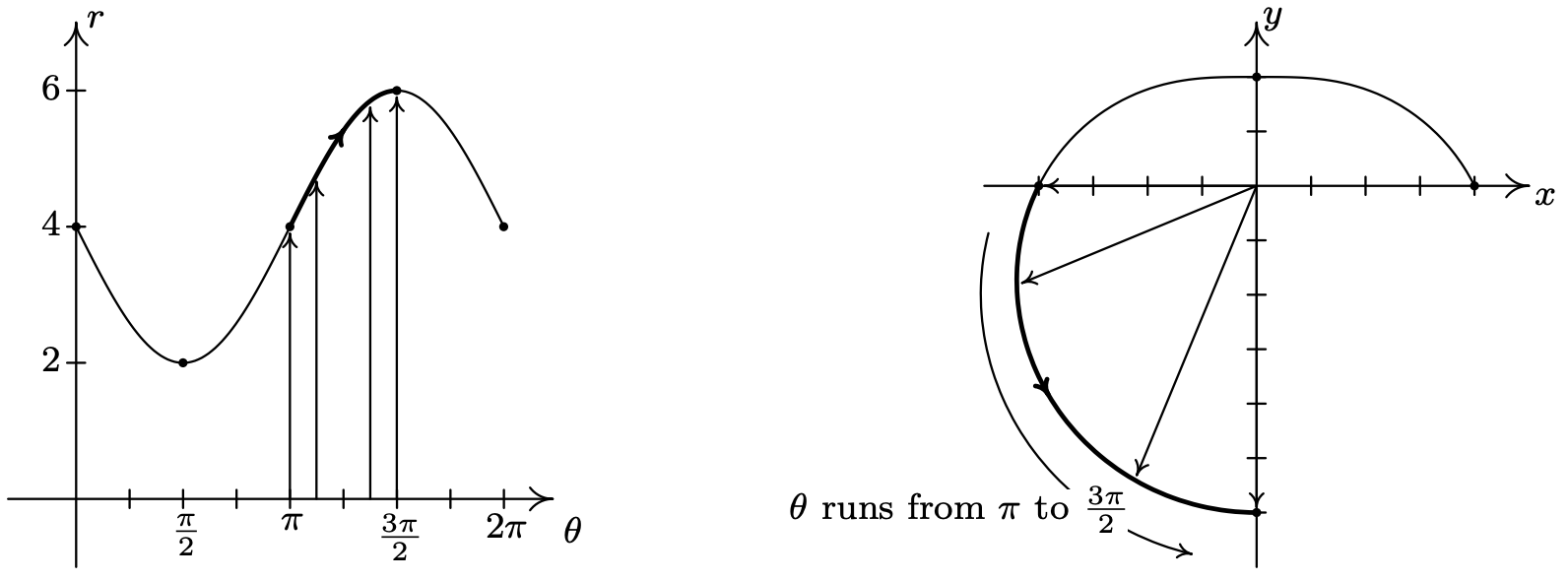
   Finalmente, a medida que\(\theta\) toma valores de\(\frac{3 \pi}{2}\) a\(2 \pi\),\(r\) disminuye de 6 volver a 4. La gráfica en el\(xy\) plano se extrae del\(y\) eje negativo para terminar donde empezamos.

   

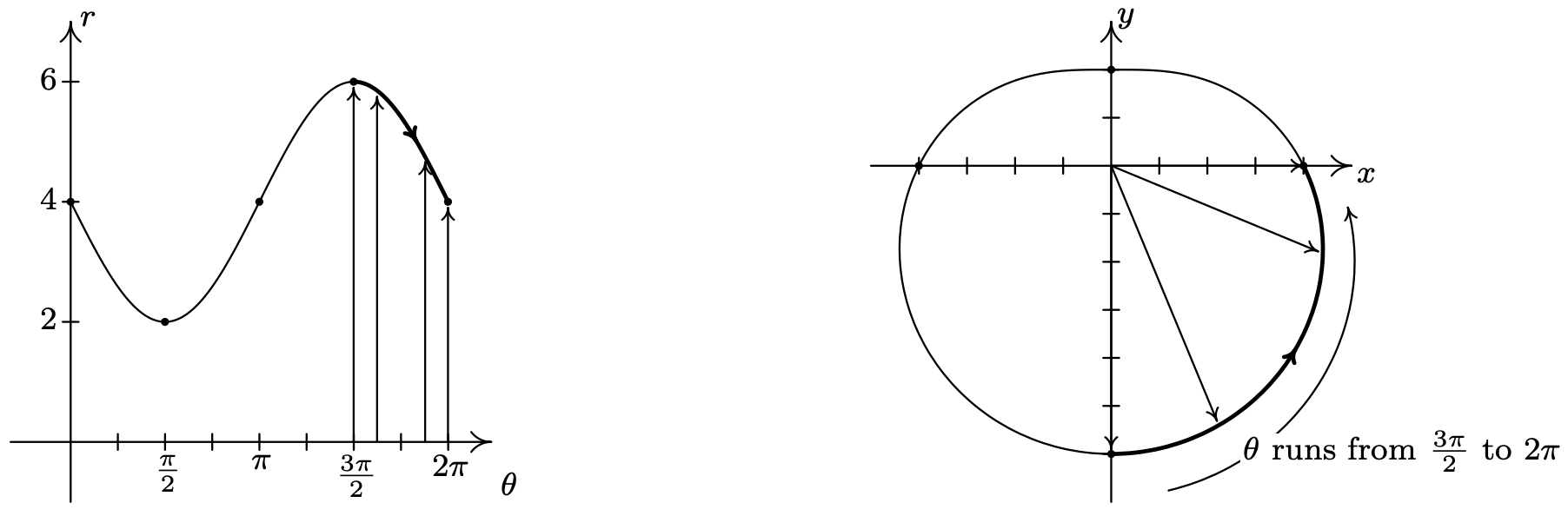
   Dejamos al lector verificar que trazar puntos correspondientes a valores de\(\theta\) fuera del intervalo\([0,2 \pi]\) da como resultado retraer porciones de la curva, por lo que estamos terminados.

   

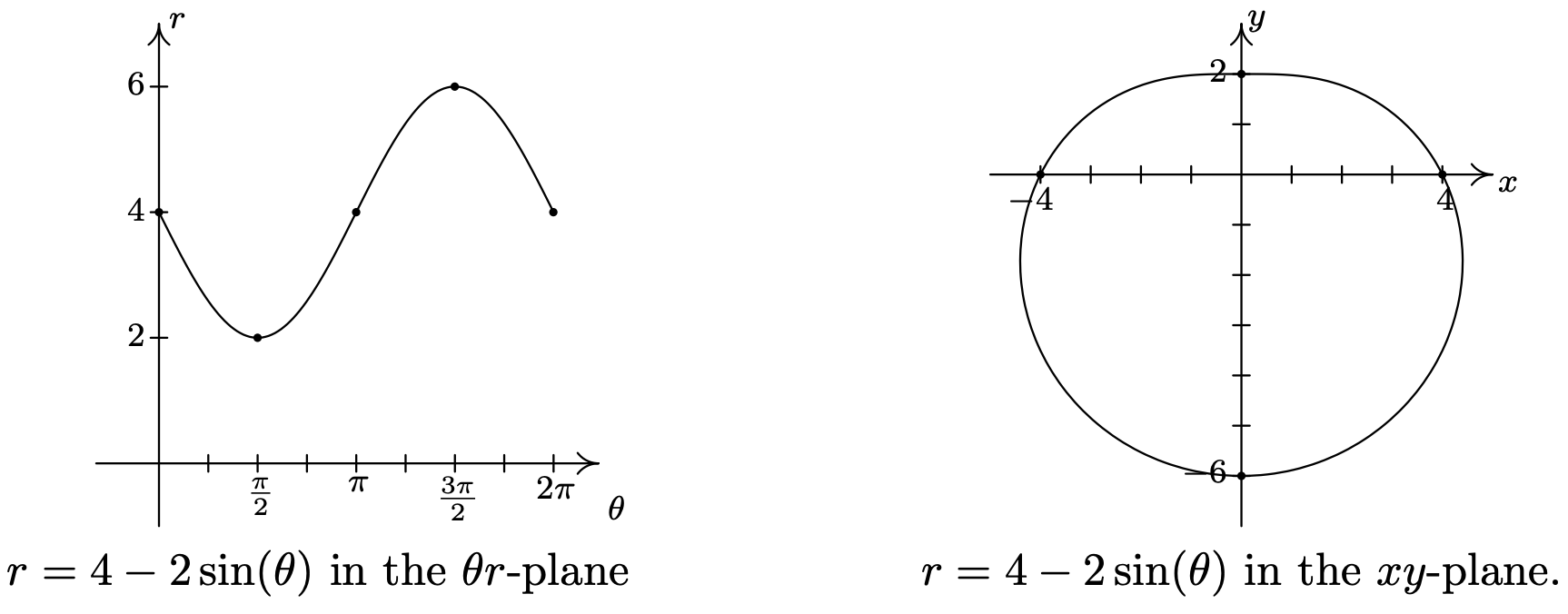
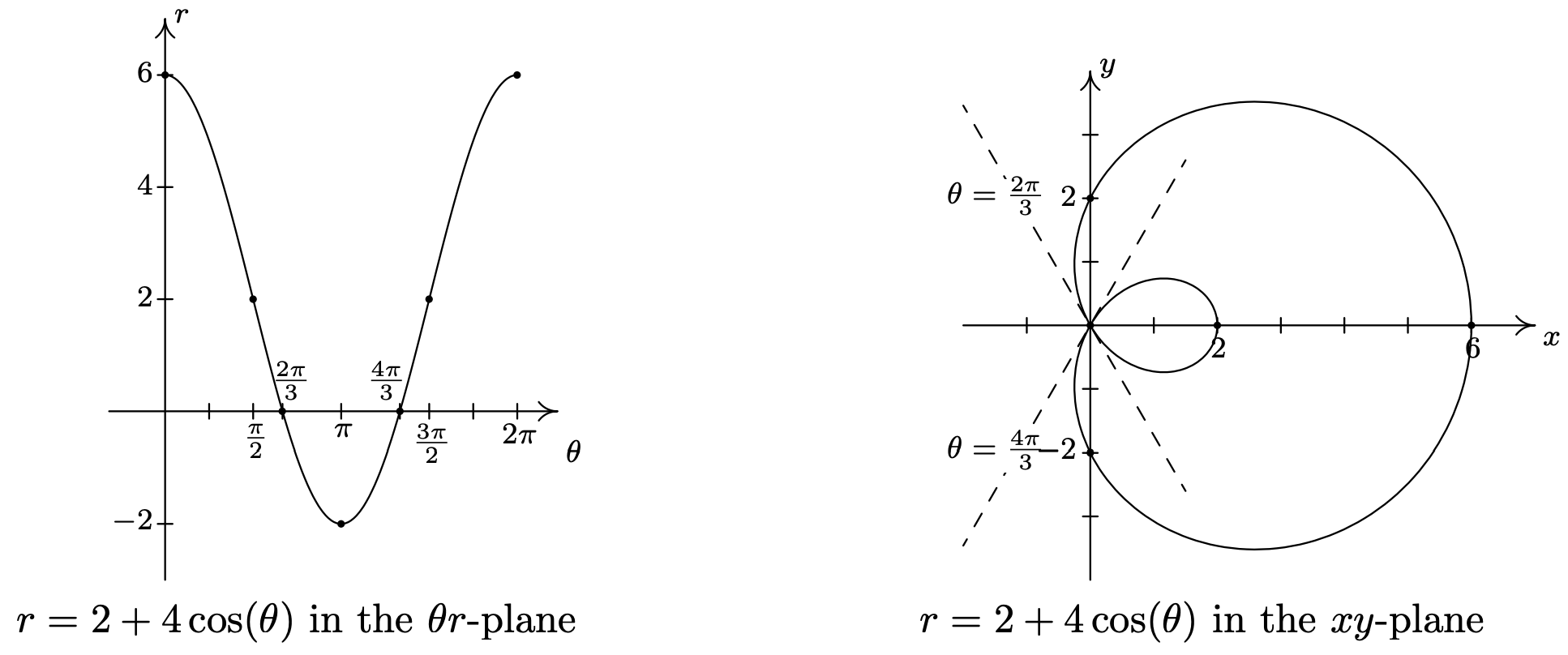
2. Lo primero a tener en cuenta al graficar\(r=2+4 \cos (\theta)\) en el\(\theta r \text {-plane }\) sobre el intervalo\([0,2 \pi]\) es que la gráfica cruza a través del\(\theta \text {-axis }\). Esto corresponde a la gráfica de la curva que pasa por el origen en el\(x y \text {-plane }\), y nuestra primera tarea es determinar cuándo sucede esto. Ajuste\(r = 0\) obtenemos\(2+4 \cos (\theta)=0\), o\(\cos (\theta)=-\frac{1}{2}\). Resolviendo para\(\theta\) en\([0,2 \pi]\) da\(\theta=\frac{2 \pi}{3}\) y\(\theta=\frac{4 \pi}{3}\). Dado que estos valores de\(\theta\) son importantes geométricamente, dividimos el intervalo\([0,2 \pi]\) en seis subintervalos:\(\left[0, \frac{\pi}{2}\right],\left[\frac{\pi}{2}, \frac{2 \pi}{3}\right],\left[\frac{2 \pi}{3}, \pi\right],\left[\pi, \frac{4 \pi}{3}\right],\left[\frac{4 \pi}{3}, \frac{3 \pi}{2}\right] \text { and }\left[\frac{3 \pi}{2}, 2 \pi\right]\). Como\(\theta\) rangos de 0 a\(\frac{\pi}{2}\),\(r\) disminuye de 6 a 2. Trazando esto en el\(xy\) plano, arrancamos 6 unidades desde el origen en el\(x\) eje positivo y lentamente tiramos hacia el\(y\) eje positivo.

   

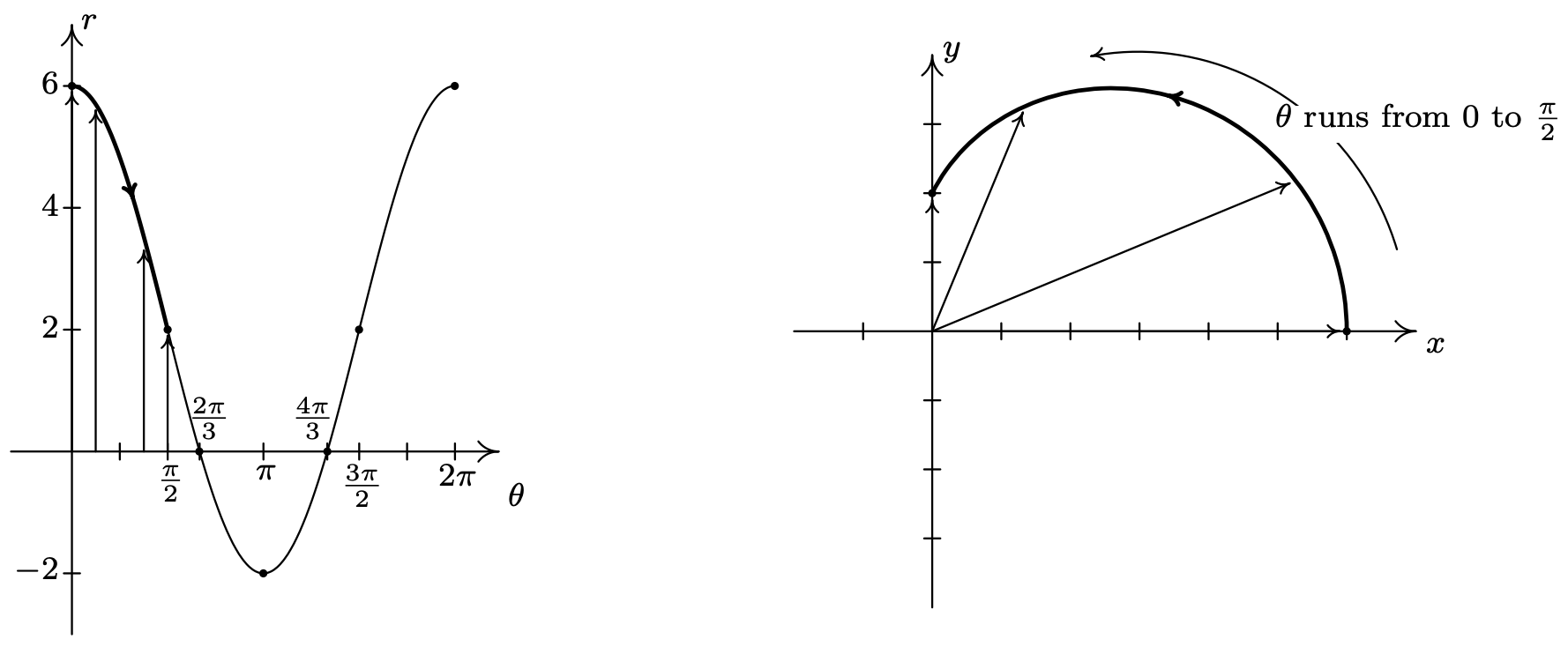
   En el intervalo\(\left[\frac{\pi}{2}, \frac{2 \pi}{3}\right]\),\(r\) disminuye de 2 a 0, lo que significa que la gráfica se dirige hacia (y eventualmente cruzará) el origen. No sólo alcanzamos el origen cuando\(\theta=\frac{2 \pi}{3}\), un teorema de Cálculo ⁵ afirma que la curva abraza la línea a\(\theta=\frac{2 \pi}{3}\) medida que se acerca al origen.

   

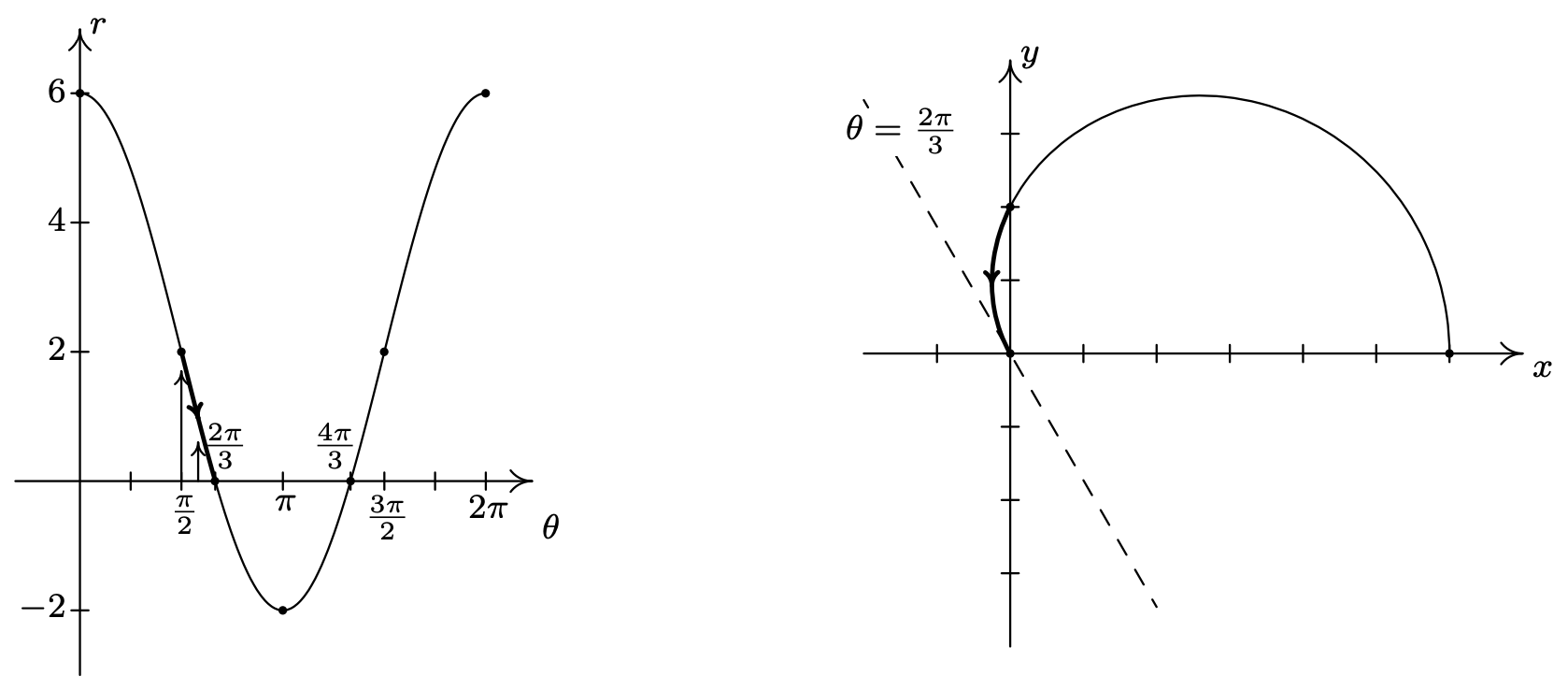
   En el intervalo\(\left[\frac{2 \pi}{3}, \pi\right]\),\(r\) varía de 0 a −2. Ya que\(r \leq 0\), la curva pasa por el origen en el\(xy\) plano -plano, siguiendo la línea\(\theta=\frac{2 \pi}{3}\) y continúa hacia arriba por el Cuadrante IV hacia el\(x\) eje positivo. ⁶ Dado que\(|r|\) va aumentando de 0 a 2, la curva se aleja del origen para terminar en un punto del\(x\) eje positivo.

   

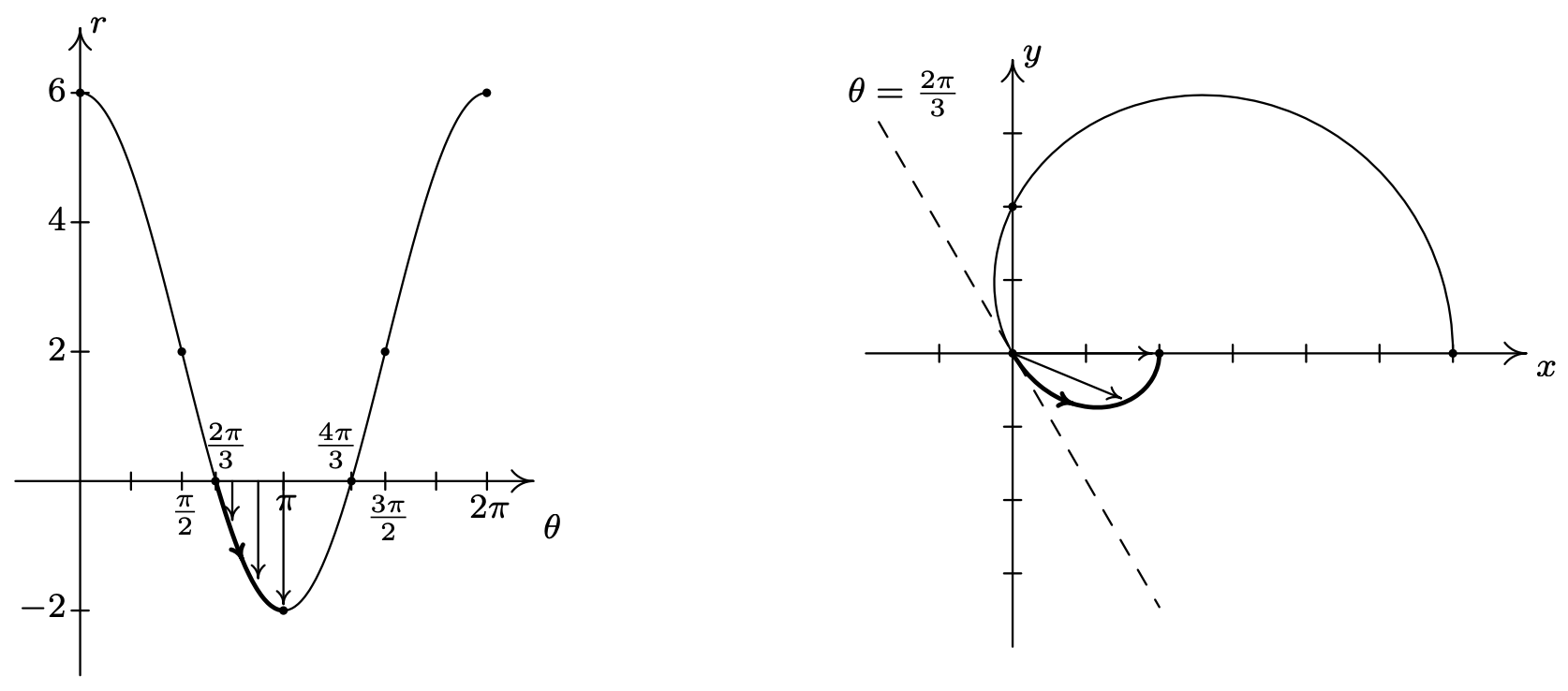
   A continuación, a\(\theta\) medida que avanza de\(\pi\) a\(\frac{4 \pi}{3}\),\(r\) varía de −2 a 0. Ya que\(r \leq 0\), continuamos nuestra gráfica en el primer cuadrante, rumbo al origen a lo largo de la línea\(\theta=\frac{4 \pi}{3}\).

   

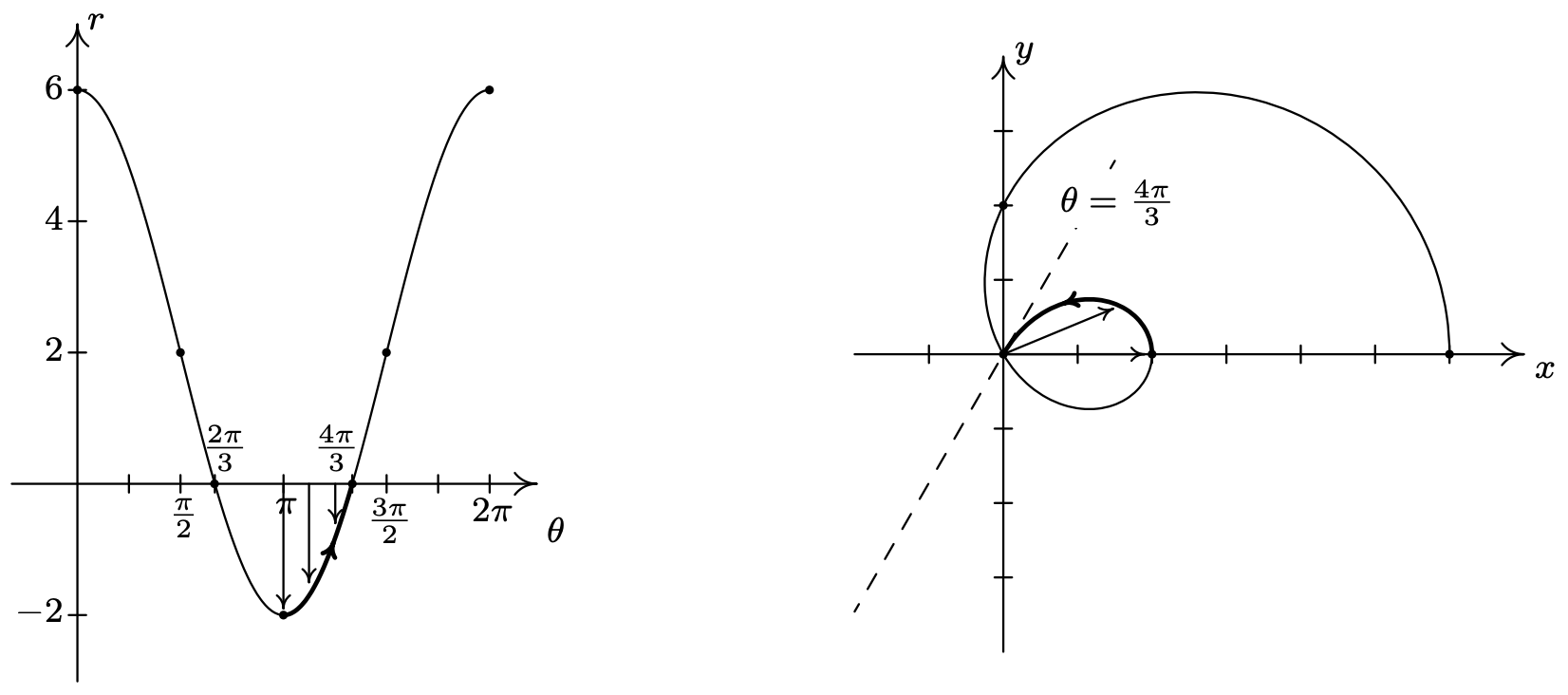
   En el intervalo\(\left[\frac{4 \pi}{3}, \frac{3 \pi}{2}\right]\),\(r\) vuelve a valores positivos y aumenta de 0 a 2. Nos abrazamos a la línea a\(\theta=\frac{4 \pi}{3}\) medida que avanzamos por el origen y nos dirigimos hacia el\(y\) eje negativo.

   

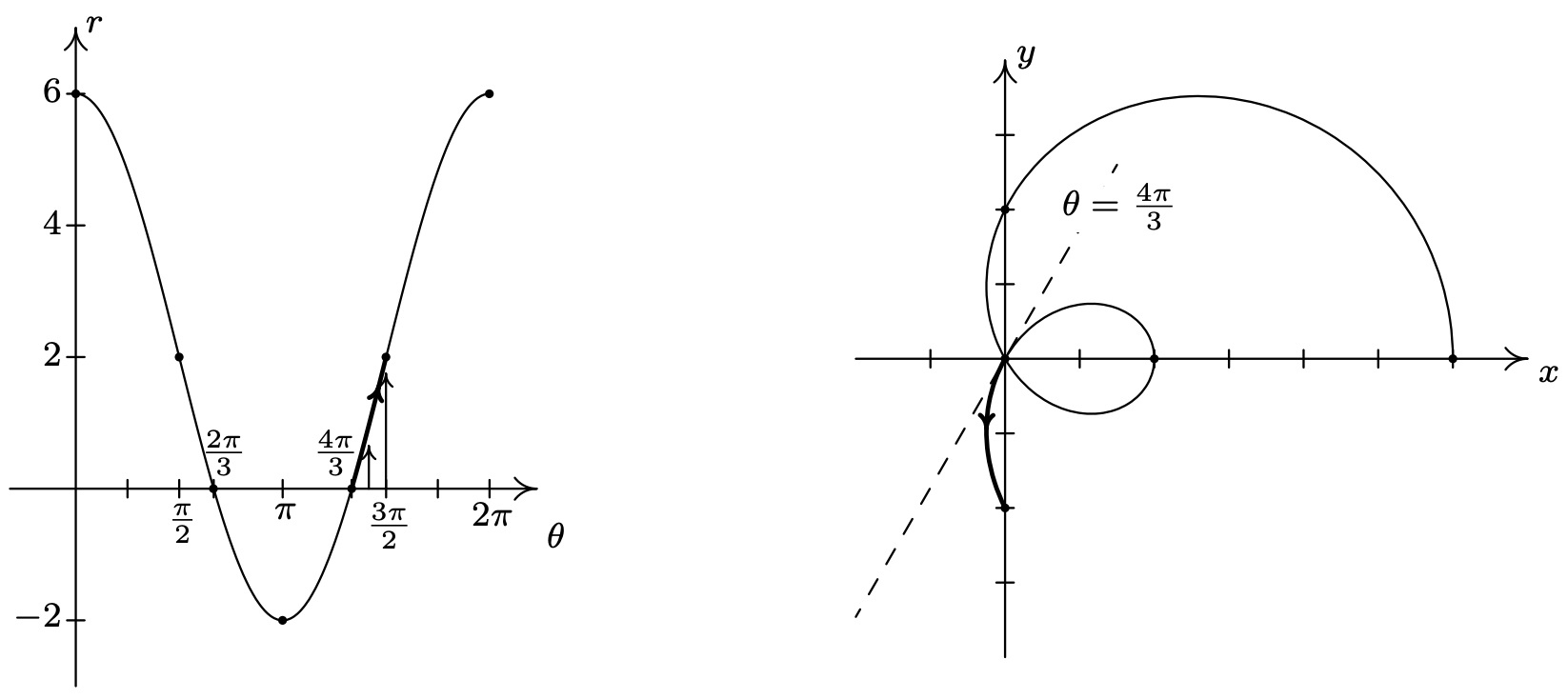
   A medida que redondeamos el intervalo, encontramos que como\(\theta\) corre\(\frac{3 \pi}{2}\) a través de a\(2 \pi\),\(r\) aumenta de 2 a 6, y terminamos de nuevo donde empezamos, 6 unidades desde el origen en el\(x\) eje positivo.

   

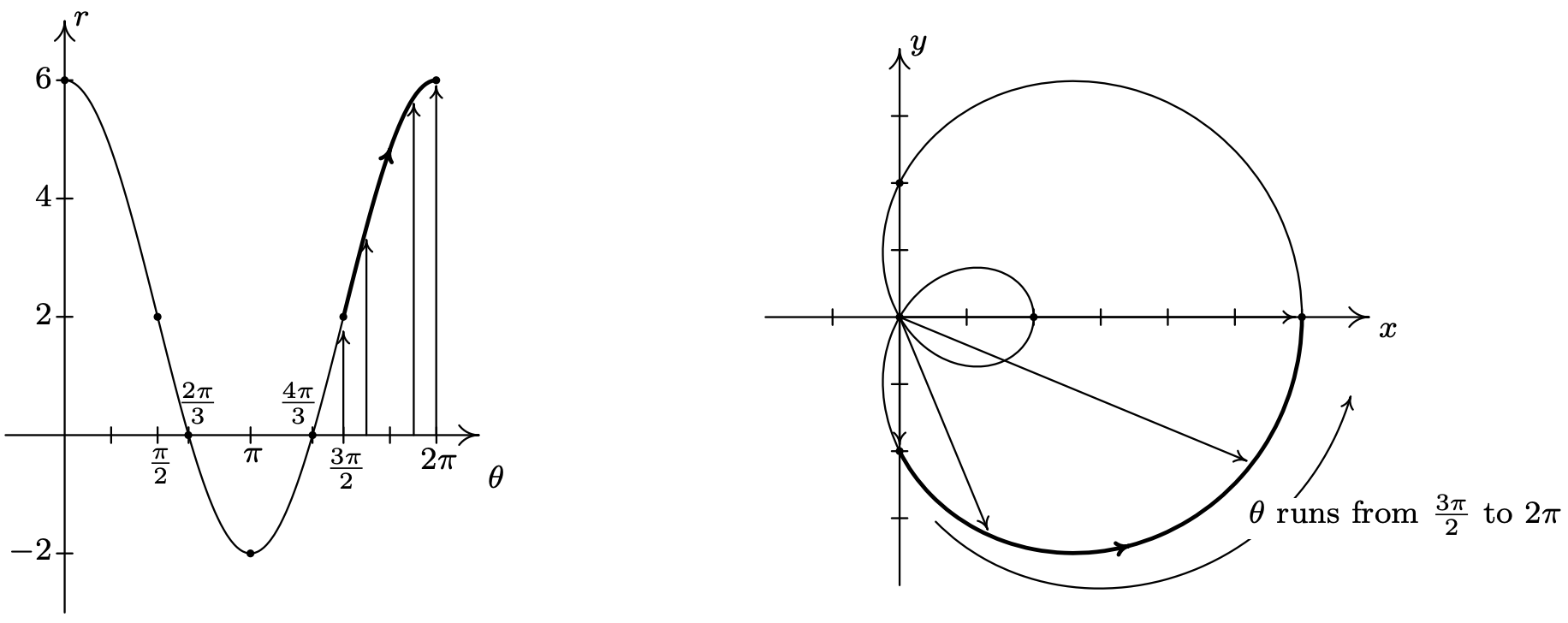
   Nuevamente, invitamos al lector a mostrar que trazar la curva para valores del\(\theta\) exterior\([0,2 \pi]\) da como resultado retraer una porción de la curva ya trazada. Nuestra gráfica final está a continuación.

   

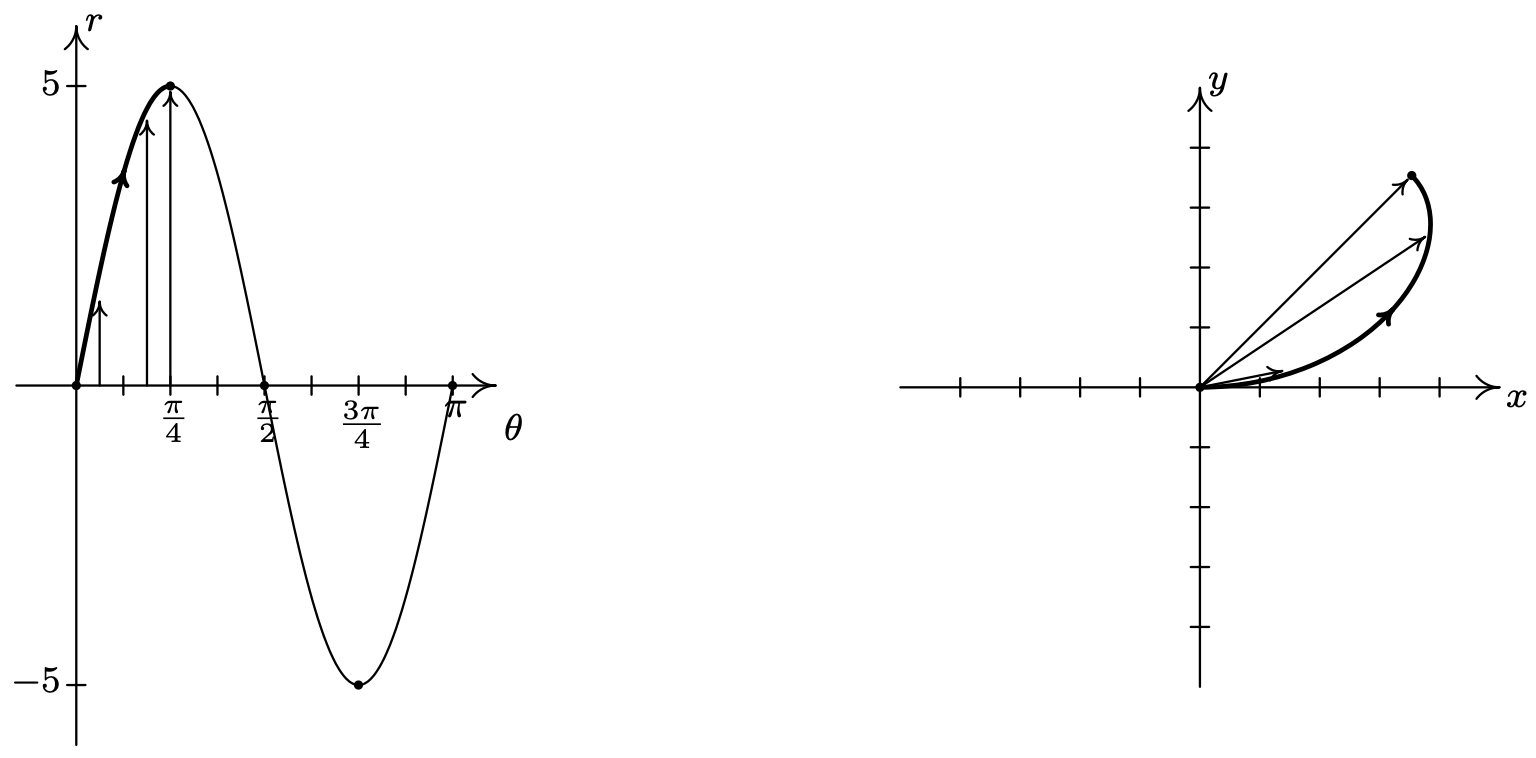
3. Como es habitual, comenzamos por graficar un ciclo fundamental de\(r=5 \sin (2 \theta)\) en el\(\theta r \text {-plane }\), que en este caso, ocurre como\(\theta\) rangos de 0 a\(\pi\). Particionamos nuestro intervalo en subintervalos para ayudarnos con la gráfica, es decir\(\left[0, \frac{\pi}{4}\right],\left[\frac{\pi}{4}, \frac{\pi}{2}\right],\left[\frac{\pi}{2}, \frac{3 \pi}{4}\right] \text { and }\left[\frac{3 \pi}{4}, \pi\right]\). Como\(\theta\) rangos de 0 a\(\frac{\pi}{4}\),\(r\) aumenta de 0 a 5. Esto significa que la gráfica de\(r=5 \sin (2 \theta)\) en el\(xy\) plano -comienza en el origen y gradualmente barre hacia fuera por lo que está a 5 unidades del origen en la línea\(\theta=\frac{\pi}{4}\).

   

   A continuación, vemos que\(r\) disminuye de 5 a 0 como\(\theta\) recorre\(\left[\frac{\pi}{4}, \frac{\pi}{2}\right]\), y además,\(r\) va rumbo negativo como\(\theta\) cruces\(\frac{\pi}{2}\). De ahí que dibujemos la curva abrazando la línea\(\theta=\frac{\pi}{2}\) (el\(y\) eje -) a medida que la curva se dirige hacia el origen.

   

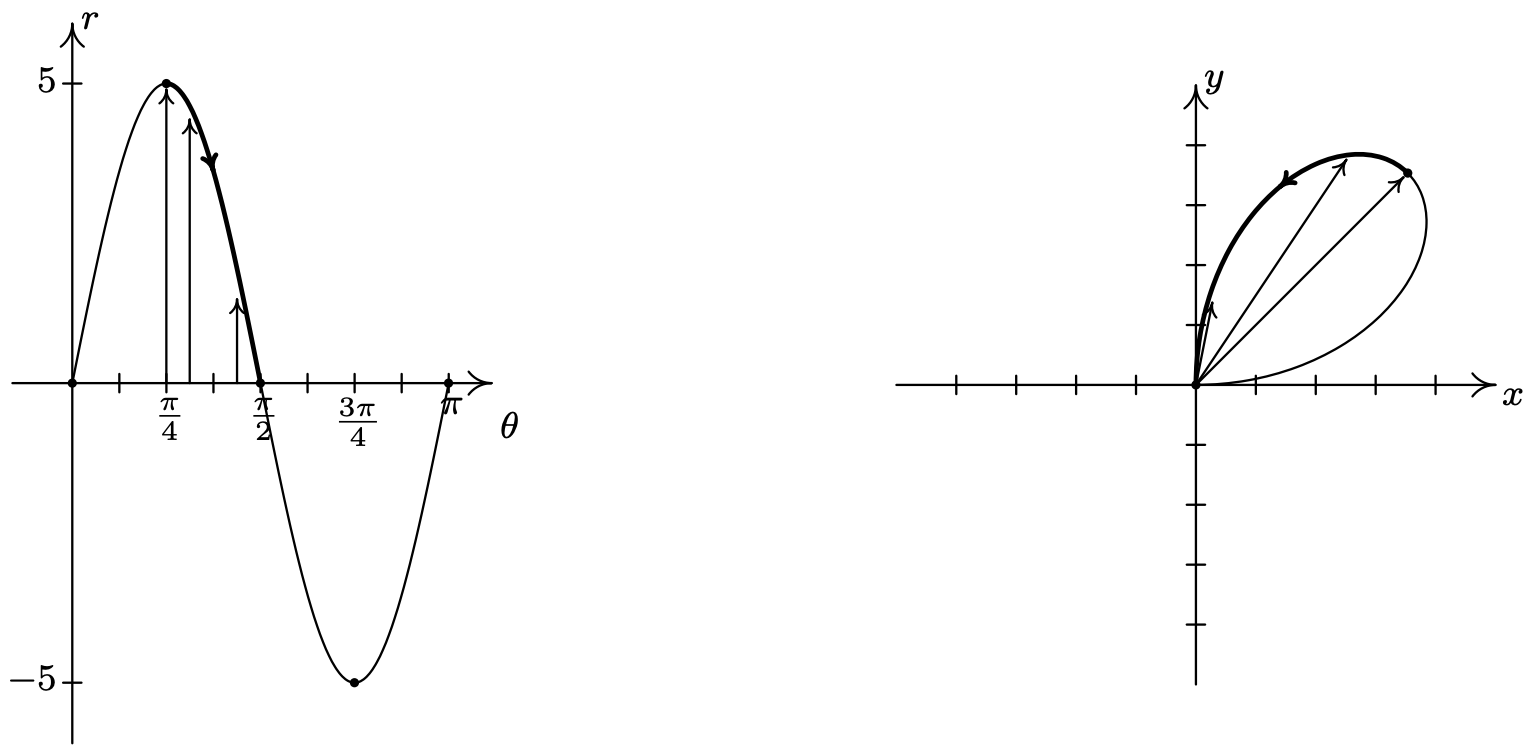
   A medida que se\(\theta\) ejecuta de\(\frac{\pi}{2}\) a\(\frac{3 \pi}{4}\)\(r\) se vuelve negativo y varía de 0 a −5. Ya que\(r \leq 0\), la curva se aleja del\(y\) eje negativo hacia el cuadrante IV.

   

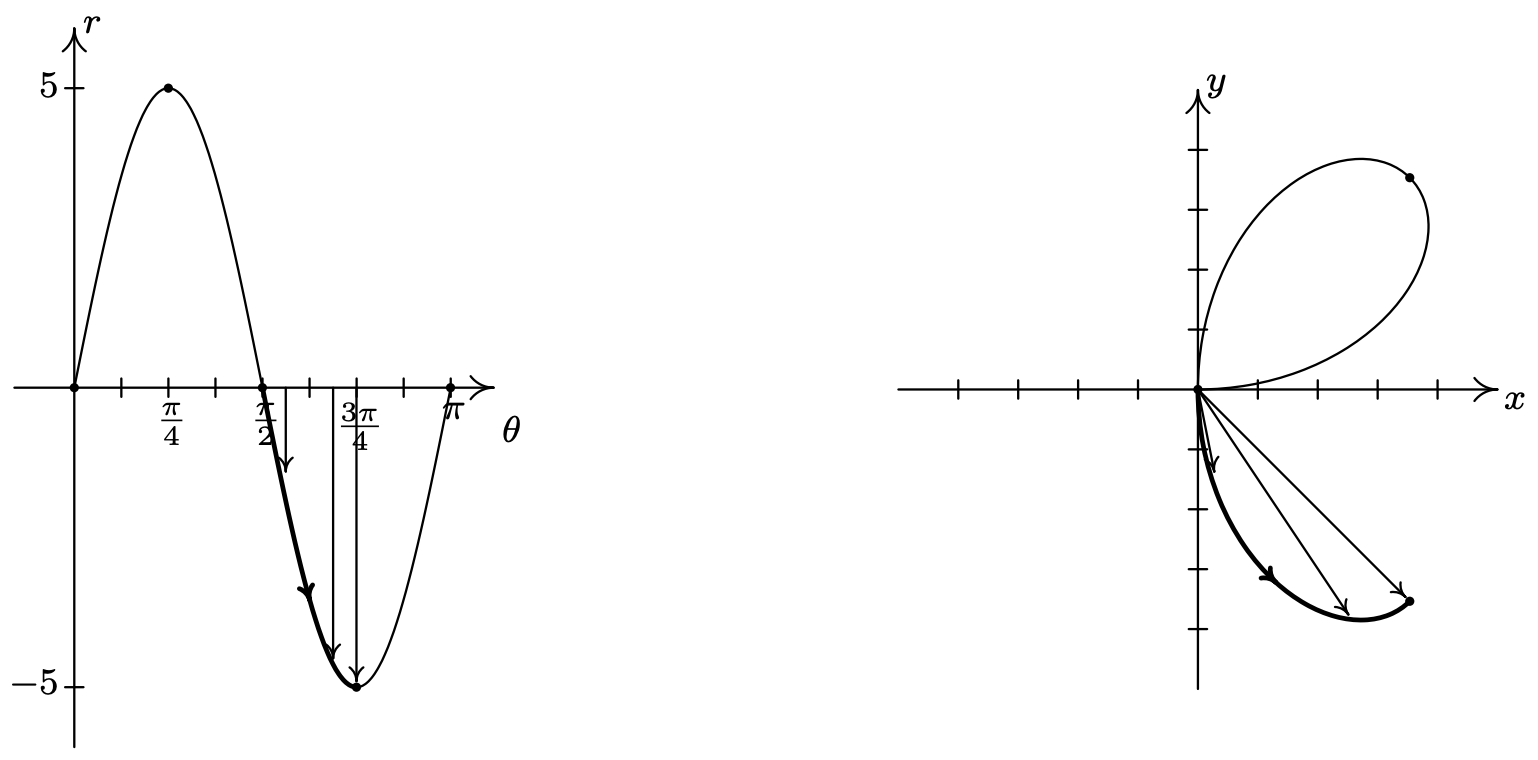
   Para\(\frac{3 \pi}{4} \leq \theta \leq \pi\),\(r\) aumenta de −5 a 0, por lo que la curva retrocede al origen.

   

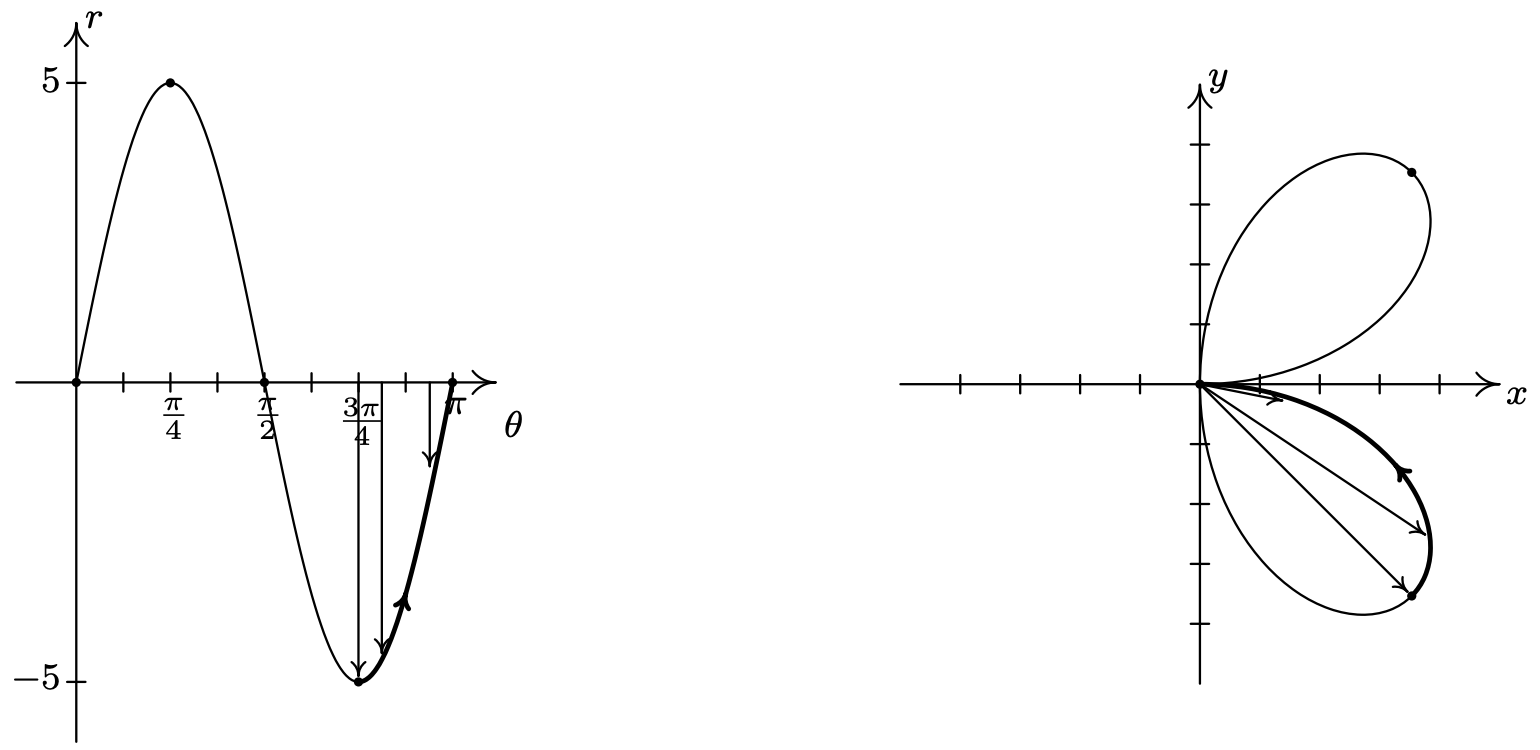
   A pesar de que hemos terminado con un ciclo completo de\(r=5 \sin (2 \theta)\), si seguimos trazando más allá\(\theta=\pi\), encontramos que la curva continúa en el tercer cuadrante! A continuación presentamos una gráfica de un segundo ciclo del\(r=5 \sin (2 \theta)\) cual continúa desde el primero. Las etiquetas en caja en el\(\theta \text {-axis }\) corresponden a las porciones con etiquetas coincidentes en la curva en el\(x y \text {-plane }\).

   

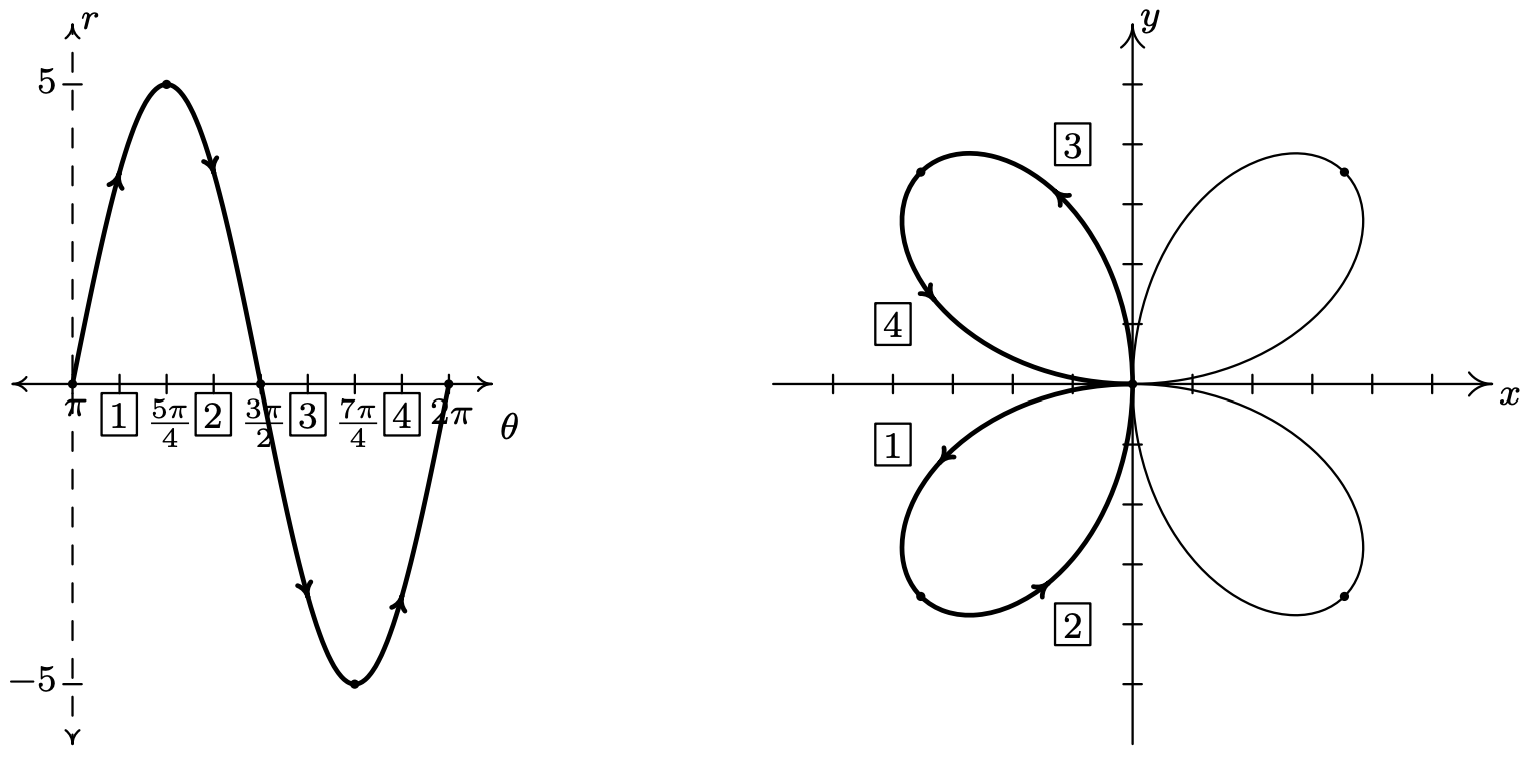
   Tenemos la gráfica final a continuación.

   

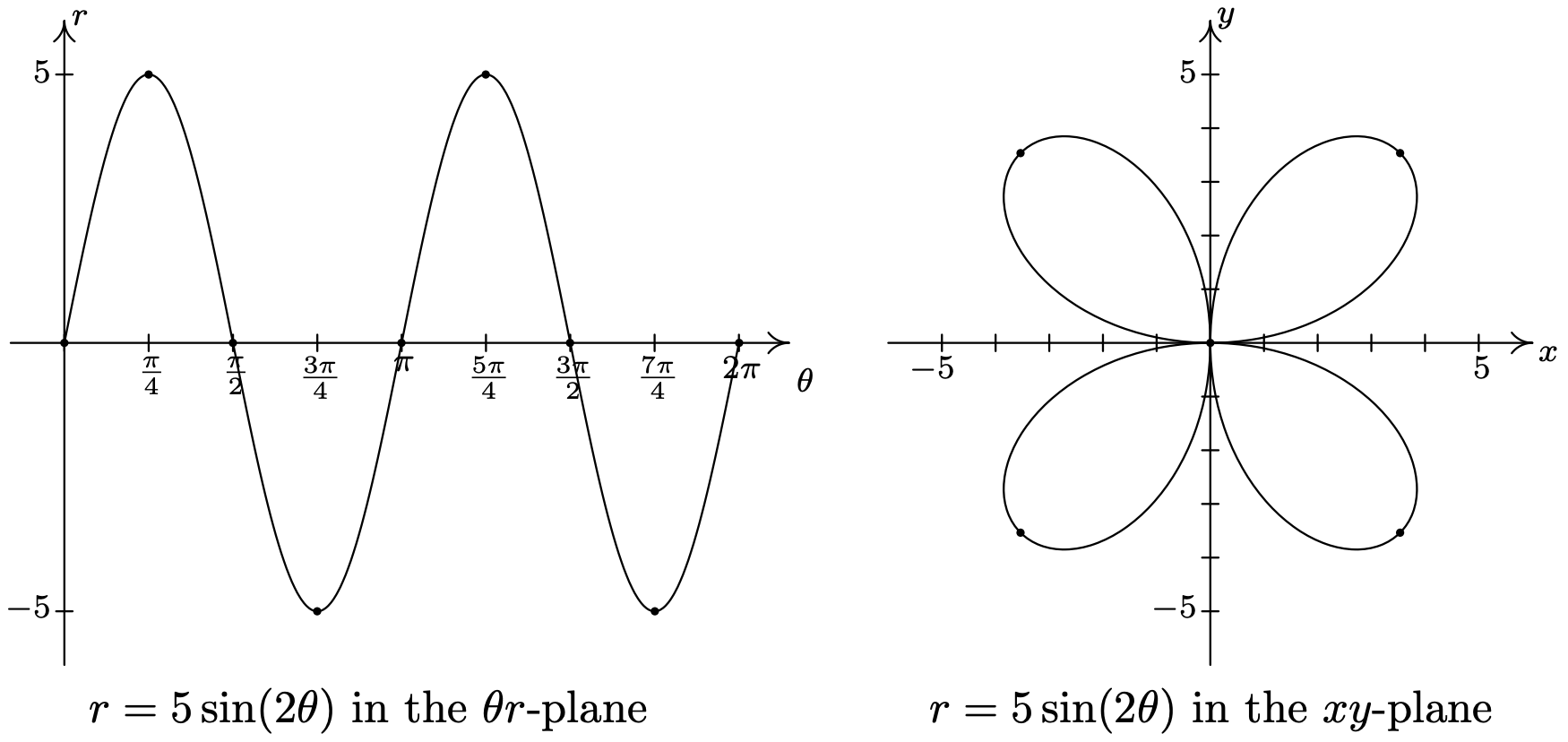
4. Graficar\(r^{2}=16 \cos (2 \theta)\) se complica por el\(r^{2}\), así que resolvemos conseguir\(r=\pm \sqrt{16 \cos (2 \theta)}=\pm4\sqrt{\cos(2\theta)}\). ¿Cómo hacemos un boceto de tal curva? En primer lugar, esbozamos un periodo fundamental del\(r=\cos (2 \theta)\) que hemos punteado en la siguiente figura. Cuando\(\cos (2 \theta)<0\),\(\sqrt{\cos (2 \theta)}\) es indefinido, así que no tenemos ningún valor en el intervalo\(\left(\frac{\pi}{4}, \frac{3 \pi}{4}\right)\). En los intervalos que quedan,\(\cos (2 \theta)\) va de 0 a 1, inclusive. De ahí que también\(\sqrt{\cos (2 \theta)}\) oscile entre 0 y 1. ⁷ A partir de esto, sabemos que\(r=\pm 4 \sqrt{\cos (2 \theta)}\) va continuamente de 0 a\(\pm 4\), respectivamente. A continuación graficamos ambos\(r=4 \sqrt{\cos (2 \theta)}\) y\(r=-4 \sqrt{\cos (2 \theta)}\) en el\(\theta r\) plano y los usamos para bosquejar las piezas correspondientes de la curva\(r^{2}=16 \cos (2 \theta)\) en el\(xy\) plano -plano. Como hemos visto en ejemplos anteriores, las líneas\(\theta=\frac{\pi}{4}\) y\(\theta=\frac{3 \pi}{4}\), que son los ceros de las funciones\(r=\pm 4 \sqrt{\cos (2 \theta)}\), nos sirven como guías para dibujar la curva tal como se pasa por el origen.

   

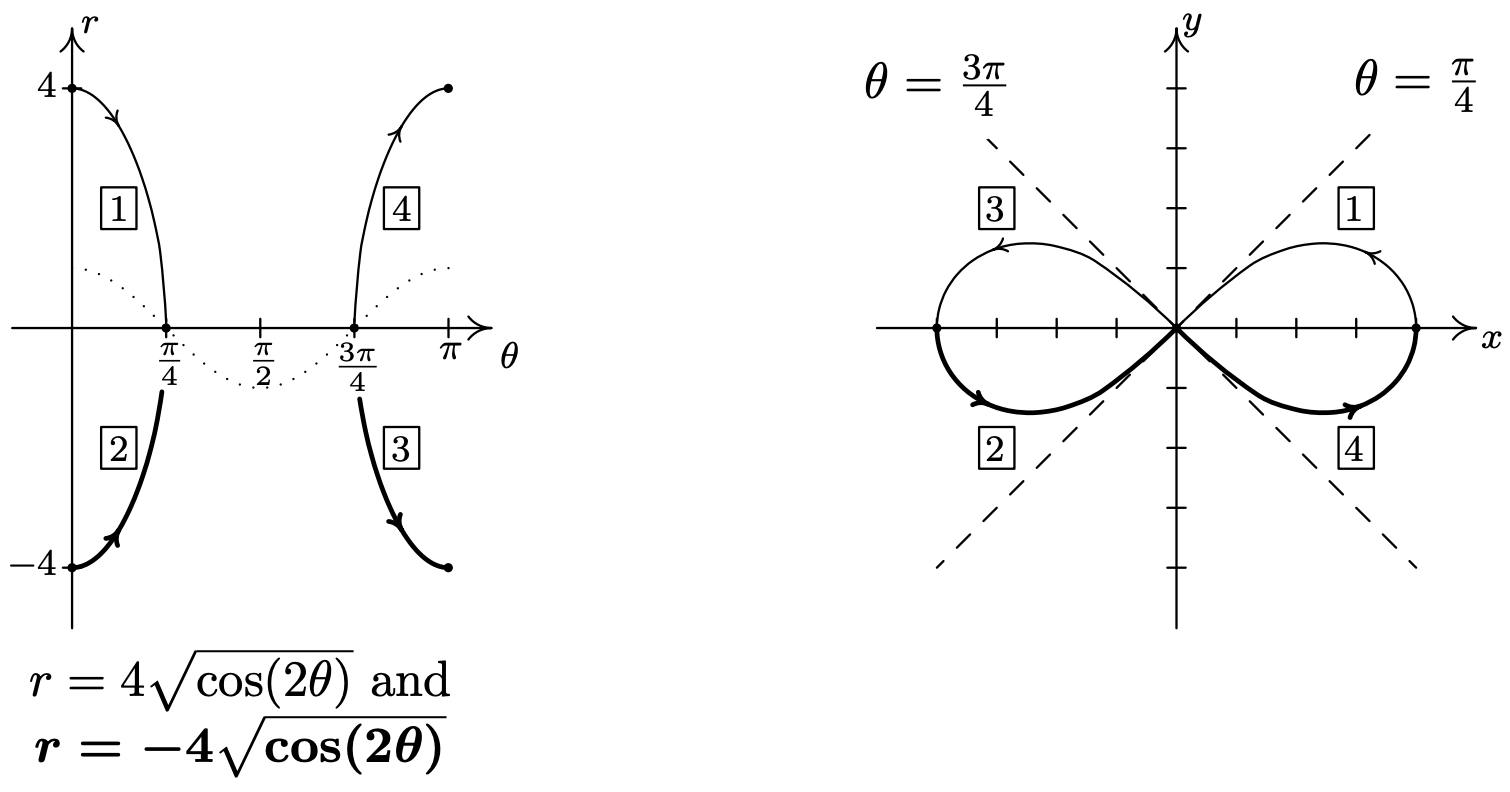
   A medida que trazamos puntos correspondientes a valores de\(\theta\) fuera del intervalo\([0, \pi]\), nos encontramos retrocediendo partes de la curva, ⁸ por lo que nuestra respuesta final está por debajo.

   

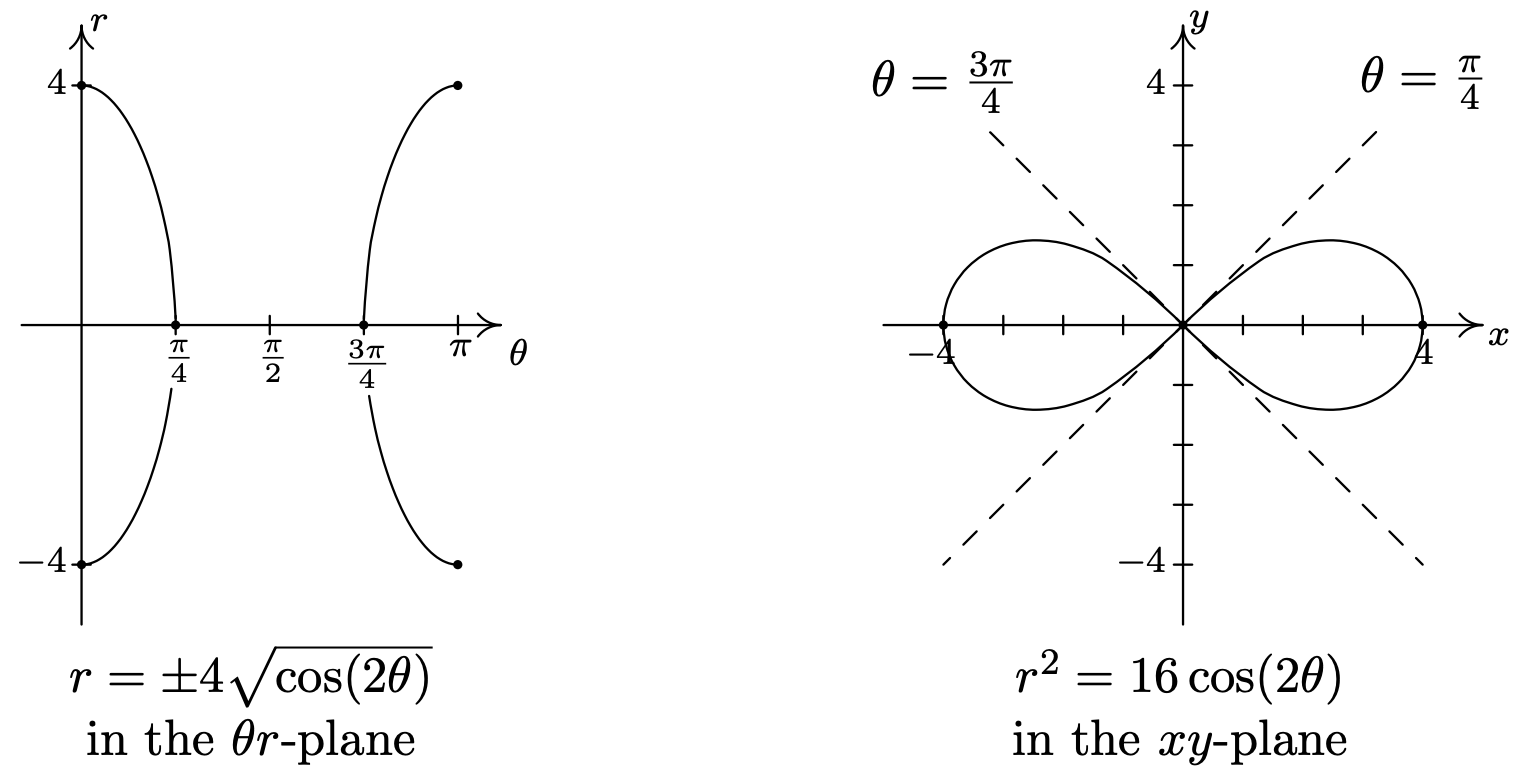
Algunas observaciones están en orden. En primer lugar, no existe relación, en general, entre el periodo de la función\(f(\theta)\) y la longitud del intervalo requerido para esbozar la gráfica completa de\(r=f(\theta)\) en el\(xy\) plano -plano. Como vimos en la página 941, a pesar de que el periodo de\(f(\theta)=6 \cos (\theta)\) es\(2 \pi\), esbozamos la gráfica completa de\(r=6 \cos (\theta)\) en el\(xy\) plano -solo usando los valores de\(\theta\) como\(\theta\) variaron de 0 a\(\pi\). En el Ejemplo 11.5.2, número 3, el periodo de\(f(\theta)=5 \sin (2 \theta)\) es\(\pi\), pero para obtener la gráfica completa de\(r=5 \sin (2 \theta)\), necesitábamos correr\(\theta\) de 0 a\(2 \pi\). Si bien muchas de las gráficas polares 'comunes' se pueden agrupar en familias, ⁹ los autores realmente sienten que tomarse el tiempo para trabajar cada gráfica de la manera que aquí se presenta es la mejor manera de no solo entender el sistema de coordenadas polares, sino también prepararte para lo que se necesita en Cálculo. En segundo lugar, la simetría observada en los ejemplos también es una ocurrencia común al graficar ecuaciones polares. Además de los tipos habituales de simetría discutidos hasta este punto en el texto (simetría sobre cada eje y el origen), es posible hablar de simetría rotacional. Dejamos la discusión de simetría a los Ejercicios. En nuestro siguiente ejemplo, se nos da la tarea de encontrar los puntos de intersección de las curvas polares. De acuerdo con el Principio de Gráfica Fundamental para Ecuaciones Polares en la página 938, para\(P\) que un punto esté en la gráfica de una ecuación polar, debe tener una representación\(P(r, \theta)\) que satisfaga la ecuación. Lo que complica las cosas en las coordenadas polares es que cualquier punto dado tiene infinitamente muchas representaciones. Como resultado, si un punto\(P\) está en la gráfica de dos ecuaciones polares diferentes, es totalmente posible que la representación\(P(r, \theta)\) que satisface una de las ecuaciones no satisfaga a la otra ecuación. Aquí, más que nunca, necesitamos confiar tanto en la Geometría como en el Álgebra para encontrar nuestras soluciones.

Ejemplo 11.5.3

Encuentra los puntos de intersección de las gráficas de las siguientes ecuaciones polares.

1. \(r=2 \sin (\theta) \text { and } r=2-2 \sin (\theta)\)
2. \(r=2 \text { and } r=3 \cos (\theta)\)
3. \(r=3 \text { and } r=6 \cos (2 \theta)\)
4. \(r=3 \sin \left(\frac{\theta}{2}\right) \text { and } r=3 \cos \left(\frac{\theta}{2}\right)\)

Solución

1. 
2. Como antes, hacemos un boceto rápido de\(r = 2\) y\(r=3 \cos (\theta)\) para tener idea del número y ubicación de los puntos de intersección. La gráfica de\(r = 2\) es un círculo, centrado en el origen, con un radio de 2. La gráfica de también\(r=3 \cos (\theta)\) es un círculo -pero ésta está centrada en el punto con coordenadas rectangulares\(\left(\frac{3}{2}, 0\right)\) y tiene un radio\(\frac{3}{2}\).

   

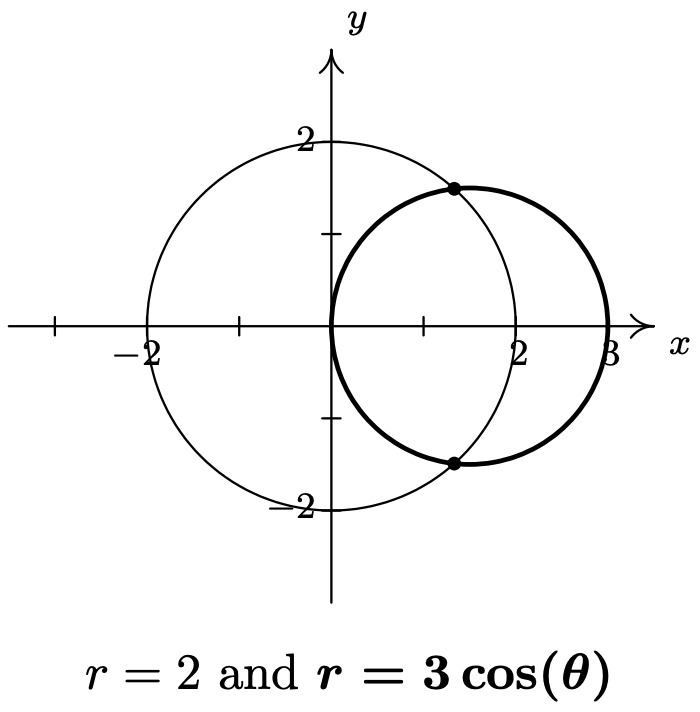
   Tenemos dos puntos de intersección para encontrar, uno en el Cuadrante I y otro en el Cuadrante IV. Procediendo como se indicó anteriormente, primero determinamos si alguno de los puntos de intersección\(P\) tiene una representación\((r, \theta)\) que satisfaga tanto\(r = 2\) y\(r=3 \cos (\theta)\). Equiparando estas dos expresiones para\(r\), obtenemos\(\cos (\theta)=\frac{2}{3}\). Para resolver esta ecuación, necesitamos la función arccosina. Obtenemos\(\theta=\arccos \left(\frac{2}{3}\right)+2 \pi k \text { or } \theta=2 \pi-\arccos \left(\frac{2}{3}\right)+2 \pi k \text { for integers } k\). A partir de estas soluciones, obtenemos\(\left(2, \arccos \left(\frac{2}{3}\right)\right)\) como una representación para nuestra respuesta en el Cuadrante I, y\(\left(2,2 \pi-\arccos \left(\frac{2}{3}\right)\right)\) como una representación para nuestra respuesta en el Cuadrante IV. Se anima al lector a verificar estos resultados algebraica y geométricamente.

3. Procediendo como arriba, primero\(r = 3\) graficamos y\(r=6 \cos (2 \theta)\) para hacernos una idea de cuántos puntos de intersección esperar y dónde se encuentran. La gráfica de\(r = 3\) es un círculo centrado en el origen con un radio de 3 y la gráfica de\(r=6 \cos (2 \theta)\) es otra rosa de cuatro hojas. ¹² Aparece como si hubiera ocho puntos de intersección, dos en cada cuadrante. Primero miramos para ver si hay algún punto\(P(r, \theta)\) con una representación que satisfaga tanto\(r = 3\) y\(r=6 \cos (2 \theta)\). Para estos puntos,\(6 \cos (2 \theta)=3 \text { or } \cos (2 \theta)=\frac{1}{2}\). Resolviendo, obtenemos\(\theta=\frac{\pi}{6}+\pi k \text { or } \theta=\frac{5 \pi}{6}+\pi k\) para enteros\(k\). De todas estas soluciones, obtenemos solo cuatro puntos distintos representados por\(\left(3, \frac{\pi}{6}\right),\left(3, \frac{5 \pi}{6}\right),\left(3, \frac{7 \pi}{6}\right) \text { and }\left(3, \frac{11 \pi}{6}\right)\). Para determinar las coordenadas de los cuatro puntos restantes, hay que considerar cómo pueden diferir las representaciones de los puntos de intersección. Sabemos por la Sección 11.4 que si\((r, \theta) \text { and }\left(r^{\prime}, \theta^{\prime}\right)\) representan el mismo punto y\(r \neq 0\), entonces, tampoco\(r=r^{\prime} \text { or } r=-r^{\prime}\). Si\(r=r^{\prime}\), entonces\(\theta^{\prime}=\theta+2 \pi k\), entonces una posibilidad es que un punto de intersección\(P\) tenga una representación\((r, \theta)\) que satisfaga\(r = 3\) y otra representación\((r, \theta+2 \pi k)\) para algún entero,\(k\) que satisfaga\(r=6 \cos (2 \theta)\). En este punto, ¹³ si reemplazamos cada ocurrencia de\(\theta\) en la ecuación\(r=6 \cos (2 \theta)\) con\((\theta+2 \pi k)\) y luego vemos si, al igualar las expresiones resultantes para\(r\), obtenemos más soluciones para\(\theta\). Ya que\(\cos (2(\theta+2 \pi k))=\cos (2 \theta+4 \pi k)=\cos (2 \theta)\) por cada entero\(k\), sin embargo, la ecuación se\(r=6 \cos (2(\theta+2 \pi k))\) reduce a la misma ecuación que teníamos antes\(r=6 \cos (2 \theta)\), lo que significa que no obtenemos soluciones adicionales. Pasando al caso donde\(r=-r^{\prime}\), tenemos eso\(\theta^{\prime}=\theta+(2 k+1) \pi\) para enteros\(k\). Miramos a ver si podemos encontrar puntos\(P\) que tengan una representación\((r, \theta)\) que satisfaga\(r = 3\) y otra,\((-r, \theta+(2 k+1) \pi)\), que satisfaga\(r=6 \cos (2 \theta)\). Para ello, sustituimos ¹⁴\((-r)\) por\(r\) y\((\theta+(2 k+1) \pi)\) para\(\theta\) en la ecuación\(r=6 \cos (2 \theta)\) y obtenemos\(-r=6 \cos (2(\theta+(2 k+1) \pi))\). Dado que\(\cos (2(\theta+(2 k+1) \pi))=\cos (2 \theta+(2 k+1)(2 \pi))=\cos (2 \theta)\) para todos los enteros\(k\), la ecuación se\(-r=6 \cos (2(\theta+(2 k+1) \pi))\) reduce a\(-r=6 \cos (2 \theta)\), o\(r=-6 \cos (2 \theta)\). Acoplar esta ecuación con\(r = 3\) da\(-6 \cos (2 \theta)=3\) o\(\cos (2 \theta)=-\frac{1}{2}\). Obtenemos\(\theta=\frac{\pi}{3}+\pi k \text { or } \theta=\frac{2 \pi}{3}+\pi k\). A partir de estas soluciones, obtenemos ¹⁵ los cuatro puntos de intersección restantes con representaciones\(\left(-3, \frac{\pi}{3}\right),\left(-3, \frac{2 \pi}{3}\right),\left(-3, \frac{4 \pi}{3}\right) \text { and }\left(-3, \frac{5 \pi}{3}\right)\), que podemos verificar fácilmente gráficamente.
4. Como es habitual, comenzamos por graficar\(r=3 \sin \left(\frac{\theta}{2}\right) \text { and } r=3 \cos \left(\frac{\theta}{2}\right)\). Utilizando las técnicas presentadas en el Ejemplo 11.5.2, encontramos que necesitamos trazar ambos\(\theta\) rangos de función de 0\(4 \pi\) a para obtener la gráfica completa. Para nuestra sorpresa y/o deleite, ¡parece como si estas dos ecuaciones describieran la misma curva!

   

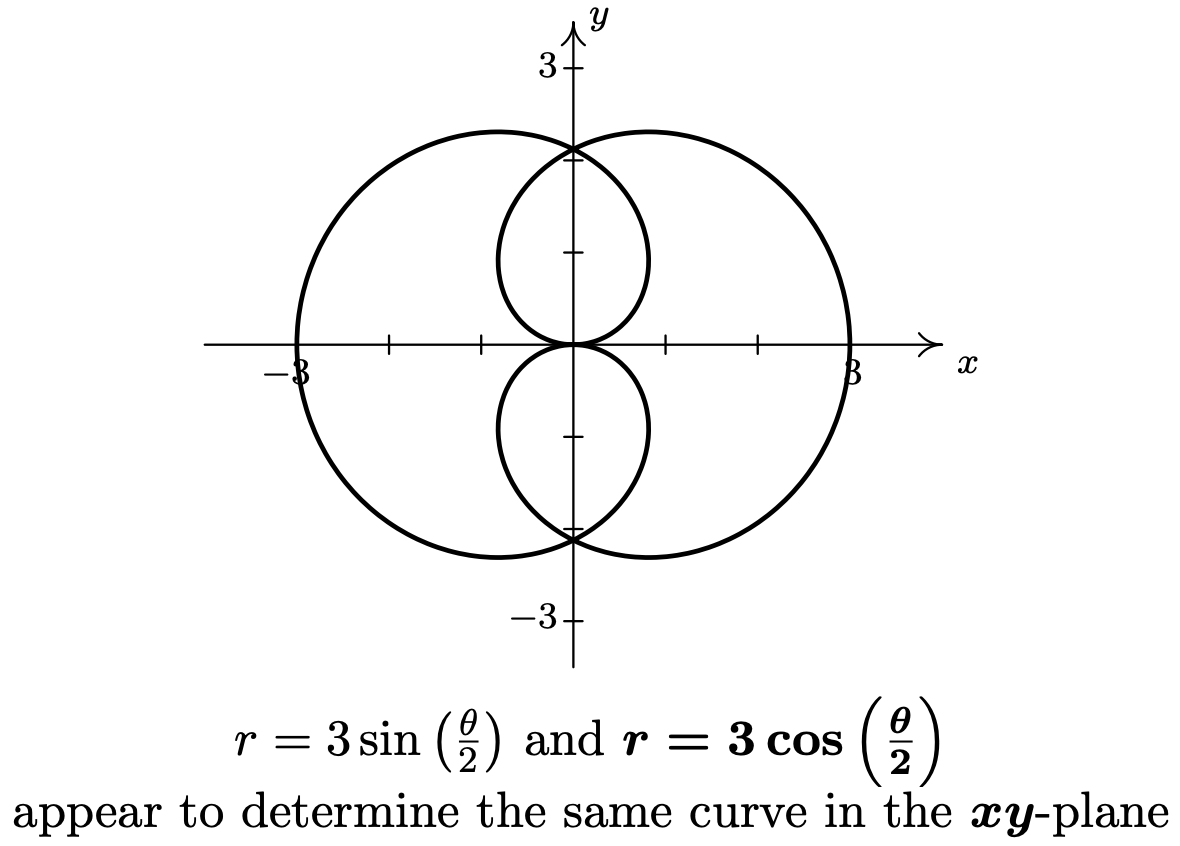
   plano Para verificar esta increíble afirmación, ¹⁶ necesitamos demostrar que, de hecho, las gráficas de estas dos ecuaciones se cruzan en todos los puntos del plano. Supongamos que\(P\) tiene una representación\((r, \theta)\) que satisface a ambos\(r=3 \sin \left(\frac{\theta}{2}\right) \text { and } r=3 \cos \left(\frac{\theta}{2}\right)\). Equiparar estas dos expresiones para\(r\) da la ecuación\(3 \sin \left(\frac{\theta}{2}\right)=3 \cos \left(\frac{\theta}{2}\right)\). Si bien normalmente desalentamos dividir por una expresión variable (en caso de que pudiera ser 0), observamos aquí que si\(3 \cos \left(\frac{\theta}{2}\right)=0\), entonces para que nuestra ecuación se mantenga,\(3 \sin \left(\frac{\theta}{2}\right)=0\) también. Dado que ningún ángulo tiene tanto coseno como seno iguales a cero, estamos seguros de dividir ambos lados de la ecuación\(3 \sin \left(\frac{\theta}{2}\right)=3 \cos \left(\frac{\theta}{2}\right)\) por\(3 \cos \left(\frac{\theta}{2}\right)\) para obtener\(\tan \left(\frac{\theta}{2}\right)=1\) cuál da\(\theta=\frac{\pi}{2}+2 \pi k\) para enteros\(k\). De estas soluciones, sin embargo, obtenemos solo un punto de intersección que puede ser representado por\(\left(\frac{3 \sqrt{2}}{2}, \frac{\pi}{2}\right)\). Ahora investigamos otras representaciones para los puntos de intersección. Supongamos que\(P\) es un punto de intersección con una representación\((r, \theta)\) que satisface\(r=3 \sin \left(\frac{\theta}{2}\right)\) y el mismo punto\(P\) tiene una representación diferente\((r, \theta+2 \pi k)\) para algún entero\(k\) que satisface\(r=3 \cos \left(\frac{\theta}{2}\right)\). Sustituyendo en este último, obtenemos\(r=3 \cos \left(\frac{1}{2}[\theta+2 \pi k]\right)=3 \cos \left(\frac{\theta}{2}+\pi k\right)\). Usando la fórmula sum para coseno, expandimos\(3 \cos \left(\frac{\theta}{2}+\pi k\right)=3 \cos \left(\frac{\theta}{2}\right) \cos (\pi k)-3 \sin \left(\frac{\theta}{2}\right) \sin (\pi k)=\pm 3 \cos \left(\frac{\theta}{2}\right)\), ya que\(\sin (\pi k)=0\) para todos los enteros\(k\), y\(\cos (\pi k)=\pm 1\) para todos los enteros k Si k es un entero par, obtenemos la\(r=3 \cos \left(\frac{\theta}{2}\right)\) misma ecuación que antes. Si\(k\) es extraño, obtenemos\(r=-3 \cos \left(\frac{\theta}{2}\right)\). Esta última expresión para\(r\) conduce a la ecuación\(3 \sin \left(\frac{\theta}{2}\right)=-3 \cos \left(\frac{\theta}{2}\right)\), o\(\tan \left(\frac{\theta}{2}\right)=-1\). Resolviendo obtenemos\(\theta=-\frac{\pi}{2}+2 \pi k\) para enteros\(k\), lo que da el punto de intersección\(\left(\frac{3 \sqrt{2}}{2},-\frac{\pi}{2}\right)\). A continuación, asumimos que\(P\) tiene una representación\((r, \theta)\) que satisface\(r=3 \sin \left(\frac{\theta}{2}\right)\) y una representación\((-r, \theta+(2 k+1) \pi)\) que satisface\(r=3 \cos \left(\frac{\theta}{2}\right)\) para algún entero\(k\). Sustituyendo\((-r)\)\(r\) y\((\theta+(2 k+1) \pi)\) en para\(\theta\) en\(r=3 \cos \left(\frac{\theta}{2}\right)\) da\(-r=3 \cos \left(\frac{1}{2}[\theta+(2 k+1) \pi]\right)\). Una vez más, usamos la fórmula de suma para coseno para obtener

   \ (\ begin {alineado}
   \ cos\ izquierda (\ frac {1} {2} [\ theta+ (2 k+1)\ pi]\ derecha) &=\ cos\ izquierda (\ frac {\ theta} {2} +\ frac {(2 k+1)\ pi} {2}\ derecha)\\
   &=\ cos\ izquierda (\ frac {\ theta} {2}\ derecha)\ cos\ izquierda (\ frac {(2 k+1)\ pi} {2}\ derecha) -\ sin\ izquierda (\ frac {\ theta} {2}\ derecha)\ sin\ izquierda (\ frac {(2 k+1)\ pi} {2}\ derecha)\\
   &=\ pm\ sin\ izquierda (\ frac {\ theta} {2}\ derecha)
   \ final {alineado}\)

   donde la última igualdad es verdadera desde\(\cos\left(\frac{(2 k+1) \pi}{2}\right)=0\) y\(\sin \left(\frac{(2 k+1) \pi}{2}\right)=\pm 1\) para enteros\(k\). De ahí, se\(-r=3 \cos \left(\frac{1}{2}[\theta+(2 k+1) \pi]\right)\) puede reescribir como\(r=\pm 3 \sin \left(\frac{\theta}{2}\right)\). Si elegimos\(k=0\), entonces\(\sin \left(\frac{(2 k+1) \pi}{2}\right)=\sin \left(\frac{\pi}{2}\right)=1\), y la ecuación\(-r=3 \cos \left(\frac{1}{2}[\theta+(2 k+1) \pi]\right)\) en este caso se reduce a\(-r=-3 \sin \left(\frac{\theta}{2}\right)\), ¡o\(r=3 \sin \left(\frac{\theta}{2}\right)\) cuál es la otra ecuación bajo consideración! Lo que esto significa es que si una representación polar\((r, \theta)\) para el punto\(P\) satisface\(r=3 \sin \left(\frac{\theta}{2}\right)\), entonces la representación\((-r, \theta+\pi)\) para\(P\) automáticamente satisface\(r=3 \cos \left(\frac{\theta}{2}\right)\). De ahí las ecuaciones\(r=3 \sin \left(\frac{\theta}{2}\right)\) y\(r=3 \cos \left(\frac{\theta}{2}\right)\) determinan el mismo conjunto de puntos en el plano.

Nuestro trabajo en el Ejemplo 11.5.3 justifica lo siguiente.

Lineamientos para Encontrar Puntos de Intersección de Gráficas de Ecuaciones Polares

Para encontrar los puntos de intersección de las gráficas de dos ecuaciones polares\(E_{1}\) y\(E_{2}\):

• Esbozar las gráficas de\(E_{1}\) y\(E_{2}\). Verifique si las curvas se cruzan en el origen (polo).
• Resolver para pares\((r, \theta)\) que satisfagan tanto\(E_{1}\) y\(E_{2}\).
• sustituir\((\theta+2 \pi k)\)\(\theta\) en cualquiera de\(E_{1}\) o\(E_{2}\) (pero no en ambos) y resolver por pares\((r, \theta)\) que satisfagan ambas ecuaciones. Ten en cuenta que\(k\) es un entero.
• Sustituir\(r\) y\((-r)\)\((\theta+(2 k+1) \pi)\) para\(\theta\) en cualquiera de\(E_{1}\) o\(E_{2}\) (pero no ambos) y resolver pares\((r, \theta)\) que satisfagan ambas ecuaciones. Ten en cuenta que\(k\) es un entero.

Nuestro último ejemplo une gráficos y puntos de intersección para describir regiones en el plano.

Ejemplo 11.5.4

Esboce la región en el\(xy\) plano -descrito por los siguientes conjuntos.

1. \(\left\{(r, \theta) \mid 0 \leq r \leq 5 \sin (2 \theta), 0 \leq \theta \leq \frac{\pi}{2}\right\}\)
2. \(\left\{(r, \theta) \mid 3 \leq r \leq 6 \cos (2 \theta), 0 \leq \theta \leq \frac{\pi}{6}\right\}\)
3. \(\left\{(r, \theta) \mid 2+4 \cos (\theta) \leq r \leq 0, \frac{2 \pi}{3} \leq \theta \leq \frac{4 \pi}{3}\right\}\)
4. \(\left\{(r, \theta) \mid 0 \leq r \leq 2 \sin (\theta), 0 \leq \theta \leq \frac{\pi}{6}\right\} \cup\left\{(r, \theta) \mid 0 \leq r \leq 2-2 \sin (\theta), \frac{\pi}{6} \leq \theta \leq \frac{\pi}{2}\right\}\)

Solución

Nuestro primer paso en estos problemas es esbozar las gráficas de las ecuaciones polares involucradas para tener una idea de la situación geométrica. Dado que todas las ecuaciones de este ejemplo se encuentran en el Ejemplo 11.5.2 o en el Ejemplo 11.5.3, la mayor parte del trabajo se realiza por nosotros.

1. Sabemos por el Ejemplo 11.5.2 número 3 que la gráfica de\(r=5 \sin (2 \theta)\) es una rosa. Además, sabemos por nuestro trabajo ahí que como\(0 \leq \theta \leq \frac{\pi}{2}\), estamos trazando la 'hoja' de la rosa que se encuentra en el primer cuadrante. La desigualdad\(0 \leq r \leq 5 \sin (2 \theta)\) significa que queremos capturar todos los puntos entre el origen\((r = 0)\) y la curva a\(r=5 \sin (2 \theta)\) medida que\(\theta\) recorre\(\left[0, \frac{\pi}{2}\right]\). De ahí que la región que buscamos sea la hoja misma.

   

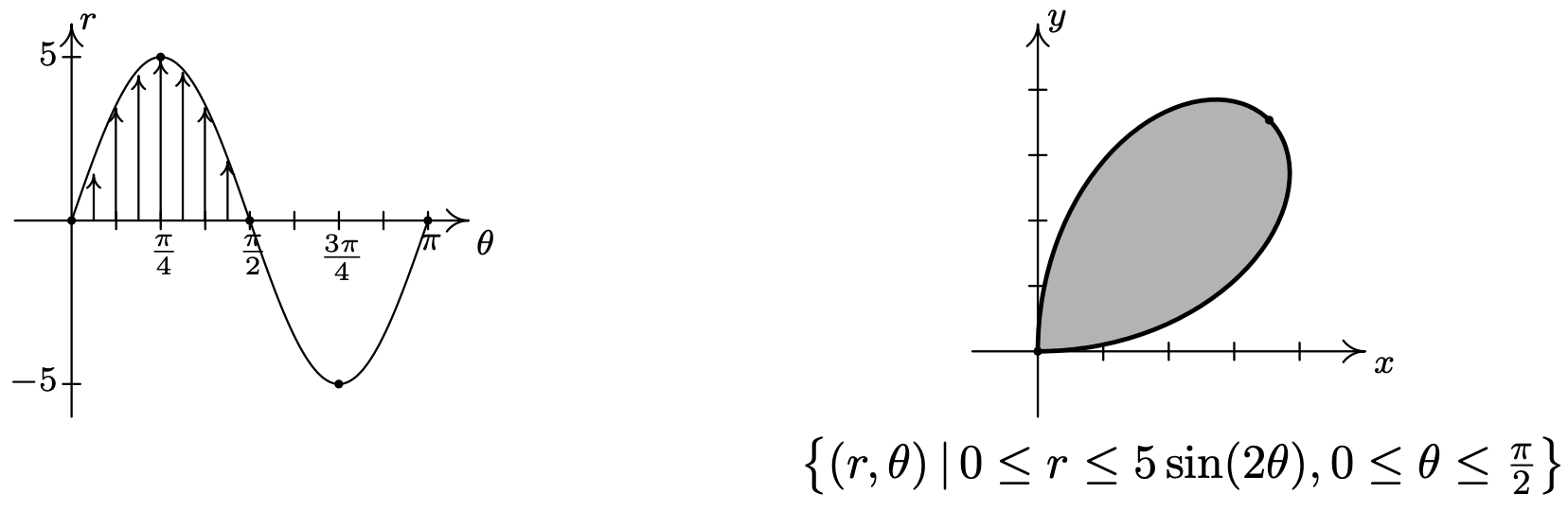
2. Sabemos por el Ejemplo 11.5.3 número 3 que\(r = 3\) y se\(r=6 \cos (2 \theta)\) cruzan en\(\theta=\frac{\pi}{6}\), por lo que la región que se está describiendo aquí es el conjunto de puntos cuya distancia dirigida\(r\) desde el origen es de al menos 3 pero no más que\(6 \cos (2 \theta)\) como\(\theta\) corre de 0 a\(\frac{\pi}{6}\). En otras palabras, estamos mirando los puntos fuera o en el círculo (desde\(r \geq 3\)) pero dentro o en la rosa (desde\(r \leq 6 \cos (2 \theta)\)). Damos sombra a la región de abajo.

   

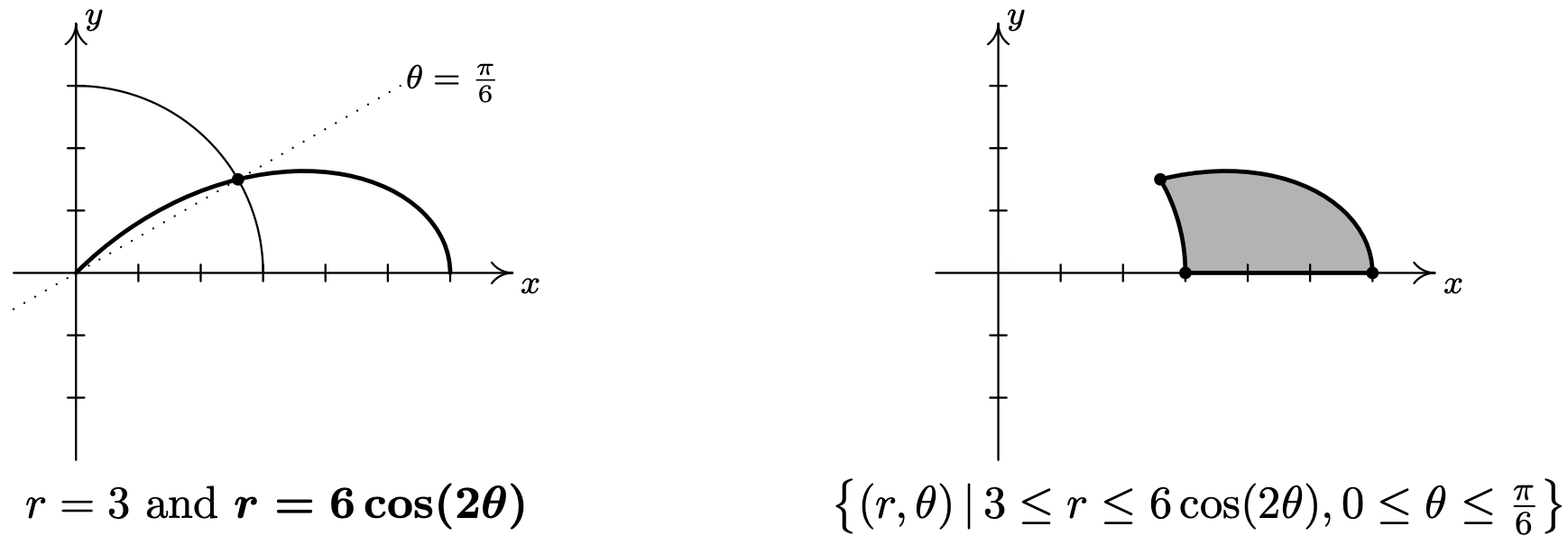
3. Del Ejemplo 11.5.2 número 2, sabemos que la gráfica de\(r=2+4 \cos (\theta)\) es una limaçon cuyo 'bucle interior' se traza como\(\theta\) corre a través de los valores dados\(\frac{2 \pi}{3}\) a\(\frac{4 \pi}{3}\). Dado que los valores\(r\) asumidos en este intervalo no son positivos, la desigualdad tiene\(2+4 \cos (\theta) \leq r \leq 0\) sentido, y estamos buscando todos los puntos entre el polo\(r = 0\) y el limaçon como\(\theta\) rangos sobre el intervalo\(\left[\frac{2 \pi}{3}, \frac{4 \pi}{3}\right]\). En otras palabras, sombreamos en el lazo interno del limaçon.

   

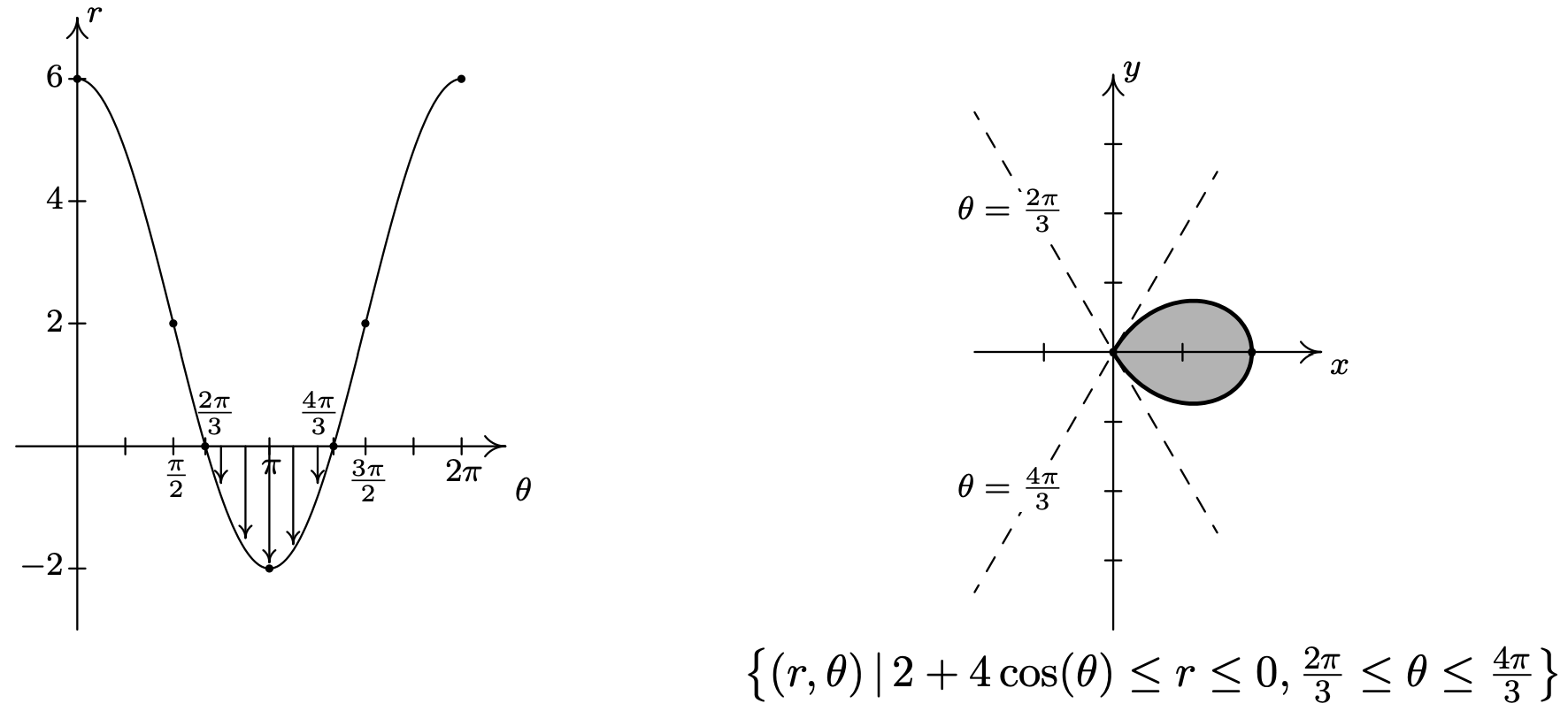
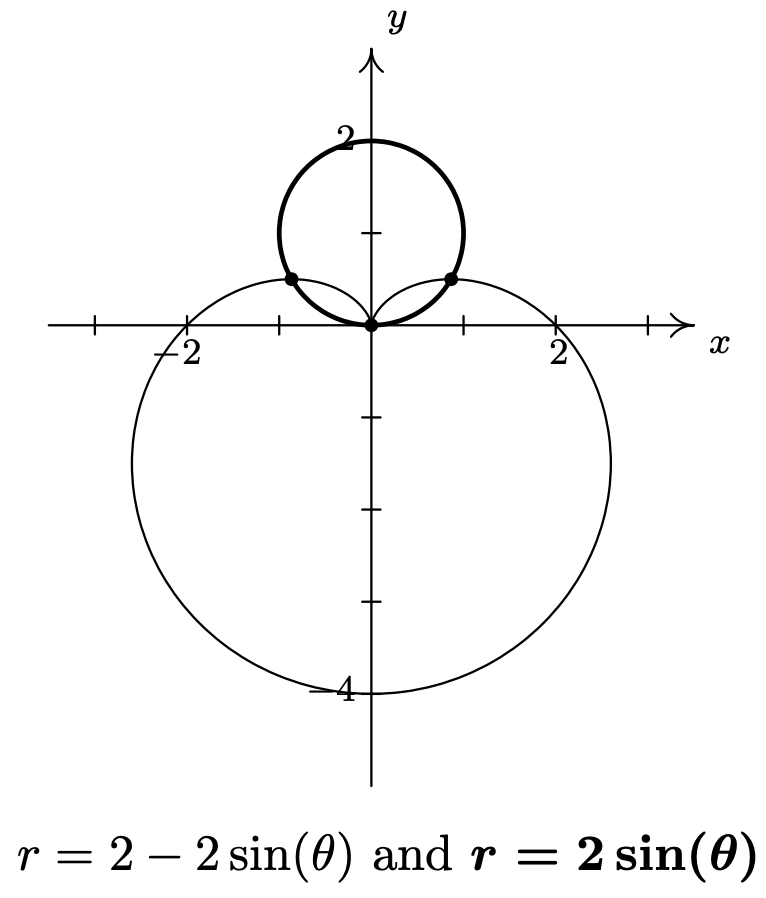
4. Tenemos dos regiones descritas aquí conectadas con el símbolo de unión\(\text { 'U.' }\) Sombreamos cada una por turno y encontramos nuestra respuesta final combinando las dos. En el Ejemplo 11.5.3, número 1, encontramos que las curvas\(r=2 \sin (\theta)\) y se\(r=2-2 \sin (\theta)\) cruzan cuando\(\theta=\frac{\pi}{6}\). De ahí que para la primera región\(\left\{(r, \theta) \mid 0 \leq r \leq 2 \sin (\theta), 0 \leq \theta \leq \frac{\pi}{6}\right\}\),, estamos sombreando la región entre el origen\((r = 0)\) hacia fuera al círculo\((r=2 \sin (\theta))\) como\(\theta\) rangos de 0 a\(\frac{\pi}{6}\), que es el ángulo de intersección de las dos curvas. Para la segunda región\(\left\{(r, \theta) \mid 0 \leq r \leq 2-2 \sin (\theta), \frac{\pi}{6} \leq \theta \leq \frac{\pi}{2}\right\}\),,\(\theta\) retoma donde lo dejó\(\frac{\pi}{6}\) y continúa hacia\(\frac{\pi}{2}\). En este caso, sin embargo, estamos sombreando desde el origen\((r = 0)\) hacia fuera hasta el cardioide\(r=2-2 \sin (\theta)\) que tira hacia el origen en\(\theta=\frac{\pi}{2}\). Juntar estas dos regiones nos da nuestra respuesta final.

   

11.5.1 Ejercicios

En los Ejercicios 1 - 20, trazar la gráfica de la ecuación polar a mano. Etiquete cuidadosamente sus gráficas.

1. \(\text { Circle: } r=6 \sin (\theta)\)
2. \(\text { Circle: } r=2 \cos (\theta)\)
3. \(\text { Rose: } r=2 \sin (2 \theta)\)
4. \(\text { Rose: } r=4 \cos (2 \theta)\)
5. \(\text { Rose: } r=5 \sin (3 \theta)\)
6. \(\text { Rose: } r=\cos (5 \theta)\)
7. \(\text { Rose: } r=\sin (4 \theta)\)
8. \(\text { Rose: } r=3 \cos (4 \theta)\)
9. \(\text { Cardioid: } r=3-3 \cos (\theta)\)
10. \(\text { Cardioid: } r=5+5 \sin (\theta)\)
11. \(\text { Cardioid: } r=2+2 \cos (\theta)\)
12. \(\text { Cardioid: } r=1-\sin (\theta)\)
13. \(\text { Limaçon: } r=1-2 \cos (\theta)\)
14. \(\text { Limaçon: } r=1-2 \sin (\theta)\)
15. \(\text { Limaçon: } r=2 \sqrt{3}+4 \cos (\theta)\)
16. \(\text { Limaçon: } r=3-5 \cos (\theta)\)
17. \(\text { Limaçon: } r=3-5 \sin (\theta)\)
18. \(\text { Limaçon: } r=2+7 \sin (\theta)\)
19. \(\text { Lemniscate: } r^{2}=\sin (2 \theta)\)
20. \(\text { Lemniscate: } r^{2}=4 \cos (2 \theta)\)

En los Ejercicios 21 - 30, encuentra las coordenadas polares exactas de los puntos de intersección de las gráficas de las ecuaciones polares. Recuerde verificar si hay intersección en el polo (origen).

21. \(r=3 \cos (\theta) \text { and } r=1+\cos (\theta)\)
22. \(r=1+\sin (\theta) \text { and } r=1-\cos (\theta)\)
23. \(r=1-2 \sin (\theta) \text { and } r=2\)
24. \(r=1-2 \cos (\theta) \text { and } r=1\)
25. \(r=2 \cos (\theta) \text { and } r=2 \sqrt{3} \sin (\theta)\)
26. \(r=3 \cos (\theta) \text { and } r=\sin (\theta)\)
27. \(r^{2}=4 \cos (2 \theta) \text { and } r=\sqrt{2}\)
28. \(r^{2}=2 \sin (2 \theta) \text { and } r=1\)
29. \(r=4 \cos (2 \theta) \text { and } r=2\)
30. \(r=2 \sin (2 \theta) \text { and } r=1\)

En Ejercicios 31 - 40, esboce la región en el\(xy\) plano descrito por el conjunto dado.

31. \(\{(r, \theta) \mid 0 \leq r \leq 3,0 \leq \theta \leq 2 \pi\}\)
32. \(\{(r, \theta) \mid 0 \leq r \leq 4 \sin (\theta), 0 \leq \theta \leq \pi\}\)
33. \(\left\{(r, \theta) \mid 0 \leq r \leq 3 \cos (\theta),-\frac{\pi}{2} \leq \theta \leq \frac{\pi}{2}\right\}\)
34. \(\left\{(r, \theta) \mid 0 \leq r \leq 2 \sin (2 \theta), 0 \leq \theta \leq \frac{\pi}{2}\right\}\)
35. \(\left\{(r, \theta) \mid 0 \leq r \leq 4 \cos (2 \theta),-\frac{\pi}{4} \leq \theta \leq \frac{\pi}{4}\right\}\)
36. \(\left\{(r, \theta) \mid 1 \leq r \leq 1-2 \cos (\theta), \frac{\pi}{2} \leq \theta \leq \frac{3 \pi}{2}\right\}\)
37. \(\left\{(r, \theta) \mid 1+\cos (\theta) \leq r \leq 3 \cos (\theta),-\frac{\pi}{3} \leq \theta \leq \frac{\pi}{3}\right\}\)
38. \(\left\{(r, \theta) \mid 1 \leq r \leq \sqrt{2 \sin (2 \theta)}, \frac{13 \pi}{12} \leq \theta \leq \frac{17 \pi}{12}\right\}\)
39. \(\left\{(r, \theta) \mid 0 \leq r \leq 2 \sqrt{3} \sin (\theta), 0 \leq \theta \leq \frac{\pi}{6}\right\} \cup\left\{(r, \theta) \mid 0 \leq r \leq 2 \cos (\theta), \frac{\pi}{6} \leq \theta \leq \frac{\pi}{2}\right\}\)
40. \(\left\{(r, \theta) \mid 0 \leq r \leq 2 \sin (2 \theta), 0 \leq \theta \leq \frac{\pi}{12}\right\} \cup\left\{(r, \theta) \mid 0 \leq r \leq 1, \frac{\pi}{12} \leq \theta \leq \frac{\pi}{4}\right\}\)

En los Ejercicios 41 - 50, utilice la notación set-builder para describir la región polar. Supongamos que la región contiene sus curvas delimitadoras.

41. La región dentro del círculo\(r = 5\).
42. La región dentro del círculo\(r = 5\) que se encuentra en el Cuadrante III.
43. La región dentro de la mitad izquierda del círculo\(r=6 \sin (\theta)\).
44. La región dentro del círculo\(r=4 \cos (\theta)\) que se encuentra en el Cuadrante IV.
45. La región dentro de la mitad superior del cardioide\(r=3-3 \cos (\theta)\)
46. La región dentro del cardioide\(r=2-2 \sin (\theta)\) que se encuentra en los Cuadrantes I y IV.
47. El interior del pétalo de la rosa\(r=3 \cos (4 \theta)\) que se encuentra en el\(x\) eje positivo
48. La región dentro del círculo\(r = 5\) pero fuera del círculo\(r = 3\).
49. La región que se encuentra dentro del círculo\(r=3 \cos (\theta)\) pero fuera del círculo\(r=\sin (\theta)\)
50. La región en el Cuadrante I que se encuentra dentro tanto del círculo\(r = 3\) como de la rosa\(r=6 \sin (2 \theta)\)

Si bien los autores realmente creen que graficar curvas polares a mano es fundamental para su comprensión del sistema de coordenadas polares, quedaríamos abandonados en nuestras funciones si ignoráramos totalmente la calculadora gráfica. De hecho, hay algunas curvas polares importantes que son simplemente demasiado difíciles de graficar a mano y que hacen de la calculadora una herramienta importante para tus estudios posteriores en Matemáticas, Ciencias e Ingeniería. Ahora damos una breve demostración de cómo utilizar la calculadora gráfica para trazar curvas polares. Lo primero que debes hacer es cambiar el MODO de tu calculadora a POL, que significa “polar”.

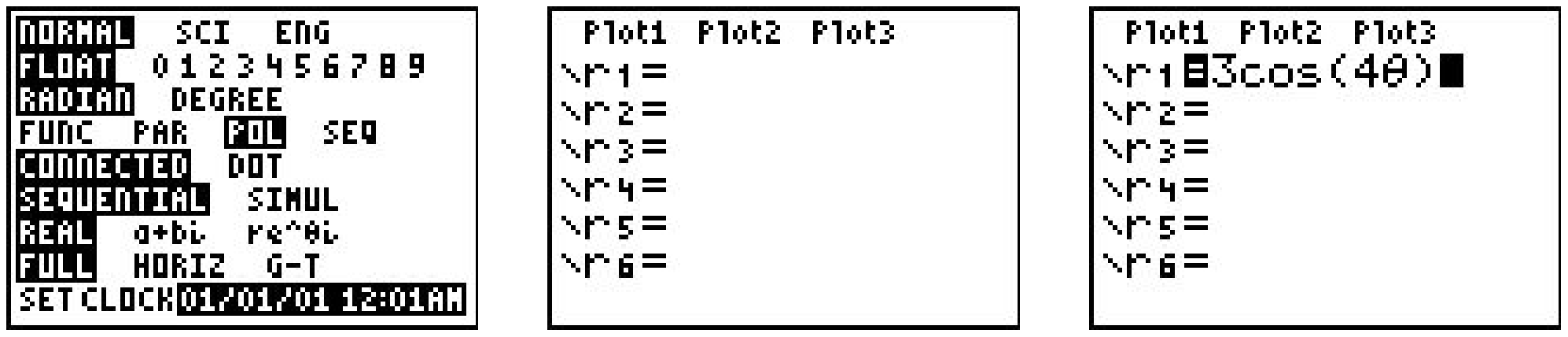
Esto cambia el\(\text { " } Y="\) menú como se ve arriba en el medio. Trazemos la rosa polar dada por\(r=3 \cos (4 \theta)\) del Ejercicio 8 anterior. Escribimos la función en el menú “r=” como se ve arriba a la derecha. Necesitamos configurar la ventana de visualización para que la curva se muestre correctamente, pero cuando miramos el menú VENTANA, encontramos tres líneas adicionales.

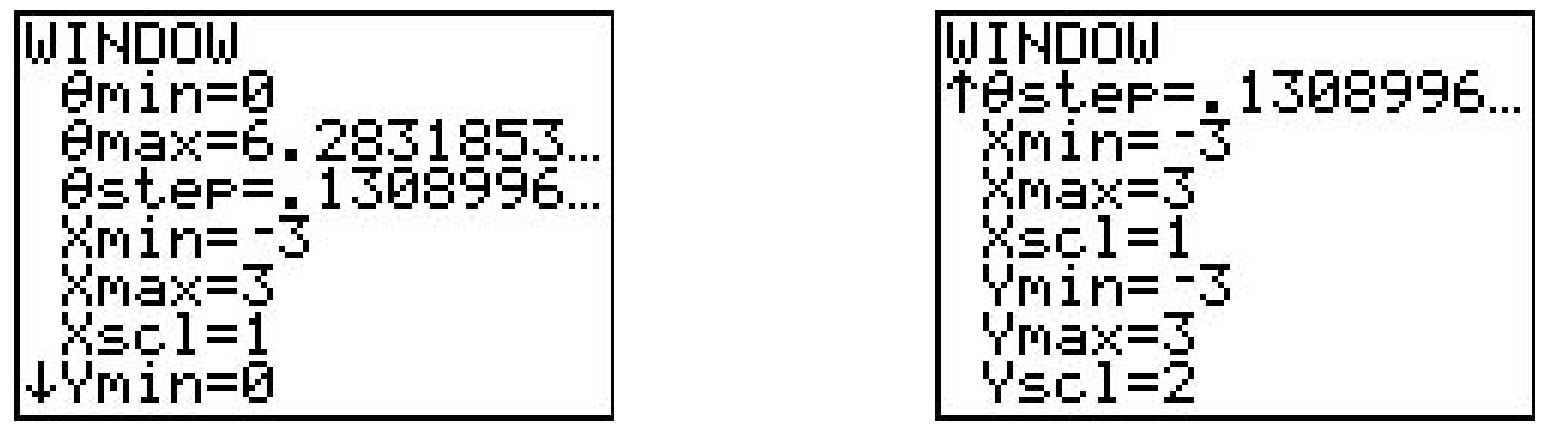
Para que la calculadora pueda trazar\(r=3 \cos (4 \theta)\) en el\(xy\) plano, necesitamos decirle no sólo las dimensiones cuáles\(x\) y\(y\) asumirán, sino también qué valores de\(\theta\) usar. De nuestro trabajo anterior, sabemos que necesitamos\(0 \leq \theta \leq 2 \pi\), por lo que ingresamos los datos que ves arriba. (Voy a decir más sobre el\(\theta \text {-step }\) en un momento.) Al golpear GRAPH se obtiene la curva de abajo a la izquierda que no se ve del todo bien. El problema aquí es que la pantalla de la calculadora tiene 96 píxeles de ancho pero solo 64 píxeles de alto. Para obtener una verdadera perspectiva geométrica, necesitamos golpear ZOOM CUADRADO (visto abajo en el medio) para producir una gráfica más precisa que presentamos a continuación a la derecha.

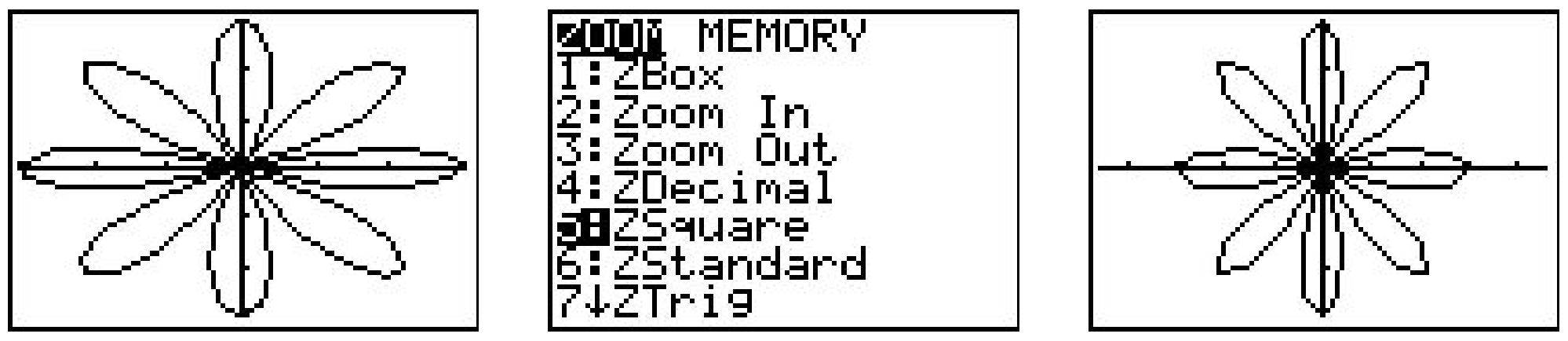
En modo de función, la calculadora dividió automáticamente el intervalo [Xmin, Xmax] en 96 subintervalos iguales. En modo polar, sin embargo, debemos especificar cómo dividir el intervalo\([\theta \min , \theta \max ]\) usando el\(\theta \text {step}\). Para la mayoría de las gráficas, a\(\theta \text {step}\) de 0.1 está bien. Si lo haces demasiado pequeño entonces la calculadora tarda mucho en graficar. Si lo haces demasiado grande, obtienes basura gruesuda como esta.

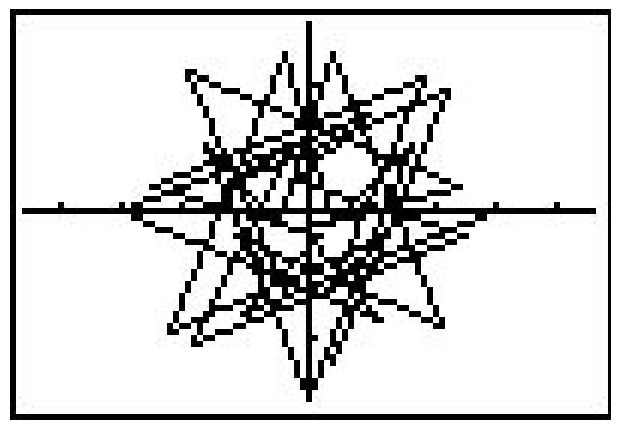
Tendrás que experimentar con los ajustes para obtener una gráfica agradable. Los ejercicios 51 - 60 te dan algunas curvas para graficar usando tu calculadora. Observe que algunos de ellos tienen límites explícitos\(\theta\) y otros no.

51. \(r=\theta, 0 \leq \theta \leq 12 \pi\)
52. \(r=\ln (\theta), 1 \leq \theta \leq 12 \pi\)
53. \(r=e^{.1 \theta}, 0 \leq \theta \leq 12 \pi\)
54. \(r=\theta^{3}-\theta,-1.2 \leq \theta \leq 1.2\)
55. \(r=\sin (5 \theta)-3 \cos (\theta)\)
56. \(r=\sin ^{3}\left(\frac{\theta}{2}\right)+\cos ^{2}\left(\frac{\theta}{3}\right)\)
57. \(r=\arctan (\theta),-\pi \leq \theta \leq \pi\)
58. \(r=\frac{1}{1-\cos (\theta)}\)
59. \(r=\frac{1}{2-\cos (\theta)}\)
60. \(r=\frac{1}{2-3 \cos (\theta)}\)
61. ¿Cuántos pétalos tiene la rosa polar\(r=\sin (2 \theta)\))? ¿Qué pasa\(r=\sin (3 \theta), r=\sin (4 \theta)\) y\(r=\sin (5 \theta)\)? ? Con la ayuda de tus compañeros, haz una conjetura sobre cuántos pétalos tiene la rosa\(r=\sin (n \theta)\) polar para cualquier número natural\(n\). Reemplazar seno por coseno y repetir la investigación. ¿Cuántos pétalos\(r=\cos (n \theta)\) tiene por cada número natural\(n\)?

Mirando hacia atrás a través de las gráficas de la sección, es claro que muchas curvas polares disfrutan de diversas formas de simetría. Sin embargo, clasificar la simetría para las curvas polares no es tan sencillo como lo fue para las ecuaciones de la página 26. En Ejercicios 62 - 64, te tenemos a ti y a tus compañeros de clase explorando algunas de las formas más básicas de simetría que se ven en las curvas polares comunes.

62. Mostrar que si\(f\) es par ¹⁷ entonces la gráfica de\(r=f(\theta)\) es simétrica alrededor del\(x\) eje -eje.
    1. Demostrar que\(f(\theta)=2+4 \cos (\theta)\) es parejo y verificar que la gráfica de\(r=2+4 \cos (\theta)\) es efectivamente simétrica alrededor del\(x\) eje -eje. (Ver Ejemplo 11.5.2 número 2.)
    2. Mostrar que no\(f(\theta)=3 \sin \left(\frac{\theta}{2}\right)\) es par, sin embargo la gráfica de\(r=3 \sin \left(\frac{\theta}{2}\right)\) es simétrica alrededor del\(x\) eje -eje. (Ver Ejemplo 11.5.3 número 4.)
63. Mostrar que si\(f\) es impar ¹⁸ entonces la gráfica de\(r=f(\theta)\) es simétrica sobre el origen.
    1. Mostrar que\(f(\theta)=5 \sin (2 \theta)\) es impar y verificar que la gráfica de\(r=5 \sin (2 \theta)\) es efectivamente simétrica sobre el origen. (Ver Ejemplo 11.5.2 número 3.)
    2. Mostrar que no\(f(\theta)=3 \cos \left(\frac{\theta}{2}\right)\) es extraño, sin embargo la gráfica de\(r=3 \cos \left(\frac{\theta}{2}\right)\) es simétrica sobre el origen. (Ver Ejemplo 11.5.3 número 4.)
64. Mostrar que si\(f(\pi-\theta)=f(\theta)\) para todos\(\theta\) en el dominio de\(f\) entonces la gráfica de\(r=f(\theta)\) es simétrica alrededor del\(y\) eje -.
    1. Para\(f(\theta)=4-2 \sin (\theta)\), mostrar eso\(f(\pi-\theta)=f(\theta)\) y la gráfica de\(r=4-2 \sin (\theta)\) es simétrica alrededor del\(y\) -eje, según sea necesario. (Ver Ejemplo 11.5.2 número 1.)
    2. Para\(f(\theta)=5 \sin (2 \theta)\), mostrar que\(f\left(\pi-\frac{\pi}{4}\right) \neq f\left(\frac{\pi}{4}\right)\), sin embargo la gráfica de\(r=5 \sin (2 \theta)\) es simétrica alrededor del\(y\) eje -. (Ver Ejemplo 11.5.2 número 3.)

En la Sección 1.7, se discutieron las transformaciones de las gráficas. En el Ejercicio 65 te tenemos a ti y a tus compañeros de clase explorando transformaciones de gráficas polares.

65. Para los Ejercicios 65a y 65b a continuación, vamos\(f(\theta)=\cos (\theta) \text { and } g(\theta)=2-\sin (\theta)\).
    1. Usando su calculadora gráfica, compare la gráfica de\(r=f(\theta)\) con cada una de las gráficas de\(r=f\left(\theta+\frac{\pi}{4}\right), r=f\left(\theta+\frac{3 \pi}{4}\right), r=f\left(\theta-\frac{\pi}{4}\right) \text { and } r=f\left(\theta-\frac{3 \pi}{4}\right)\). Repita este proceso para\(g(\theta)\). En general, ¿cómo crees que la gráfica de\(r=f(\theta+\alpha)\) compara con la gráfica de\(r=f(\theta)\)?
    2. Usando su calculadora gráfica, compare la gráfica de\(r=f(\theta)\) con cada una de las gráficas de\(r=2 f(\theta), r=\frac{1}{2} f(\theta), r=-f(\theta) \text { and } r=-3 f(\theta)\). Repita este proceso para\(g(\theta)\). En general, ¿cómo crees que la gráfica de\(r=k \cdot f(\theta)\) compara con la gráfica de\(r=f(\theta)\)? (¿Importa si\(k>0\) o\(k<0\)?)
66. A la luz de los Ejercicios 62 - 64, ¿cómo se\(r=f(-\theta)\) compararía la gráfica de con la gráfica de\(r=f(\theta)\) para una función genérica\(f\)? ¿Y las gráficas de\(r=-f(\theta) \text { and } r=f(\theta)\)? ¿Y qué pasa\(r=f(\theta) \text { and } r=f(\pi-\theta)\)? Pruebe sus conjeturas usando una variedad de funciones polares que se encuentran en esta sección con la ayuda de una utilidad gráfica.
67. Con la ayuda de tus compañeros, investiga micrófonos cardioides.
68. De vuelta en la Sección 1.2, en el párrafo anterior al Ejercicio 53, te dimos este enlace a una fascinante lista de curvas. Algunas de estas curvas tienen representaciones polares que te invitamos a investigar a ti y a tus compañeros de clase.

11.5.2 Respuestas

1. \(\text { Circle: } r=6 \sin (\theta)\)

   

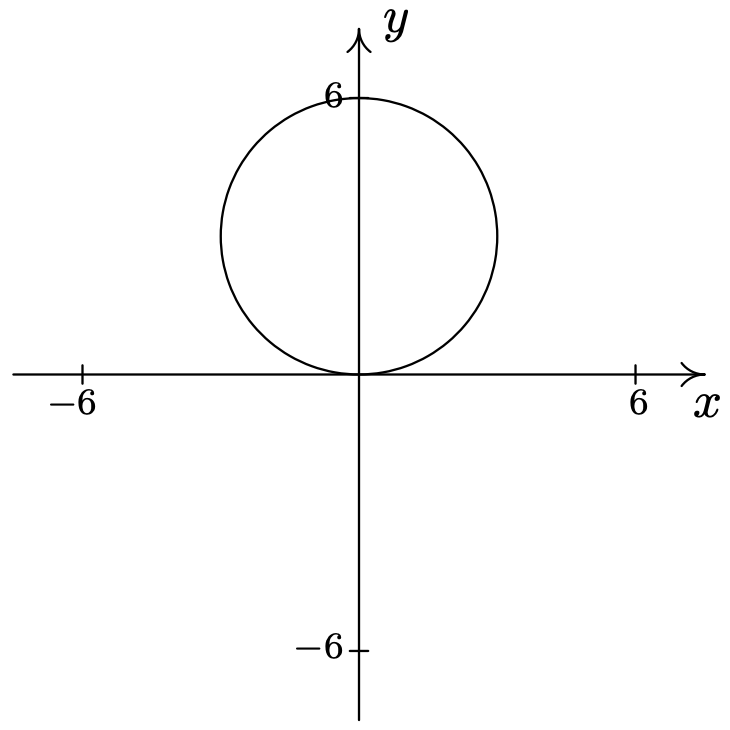
2. \(\text { Circle: } r=2 \cos (\theta)\)

   

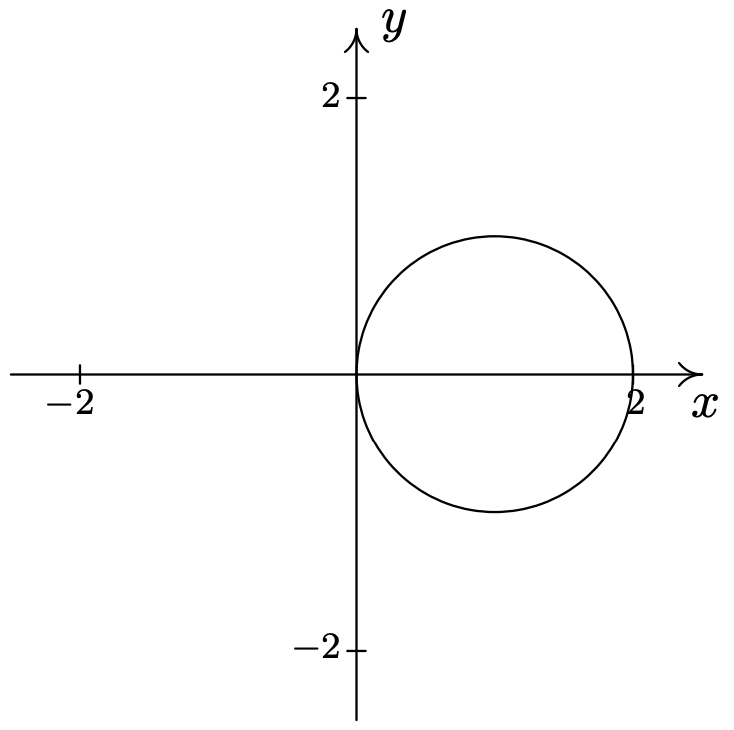
3. \(\text { Rose: } r=2 \sin (2 \theta)\)

   

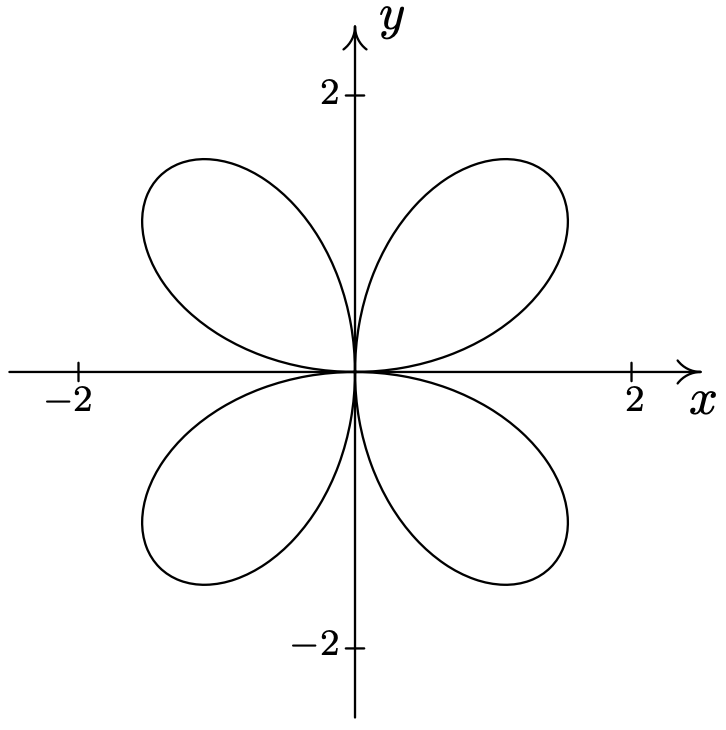
4. \(\text { Rose: } r=4 \cos (2 \theta)\)

   

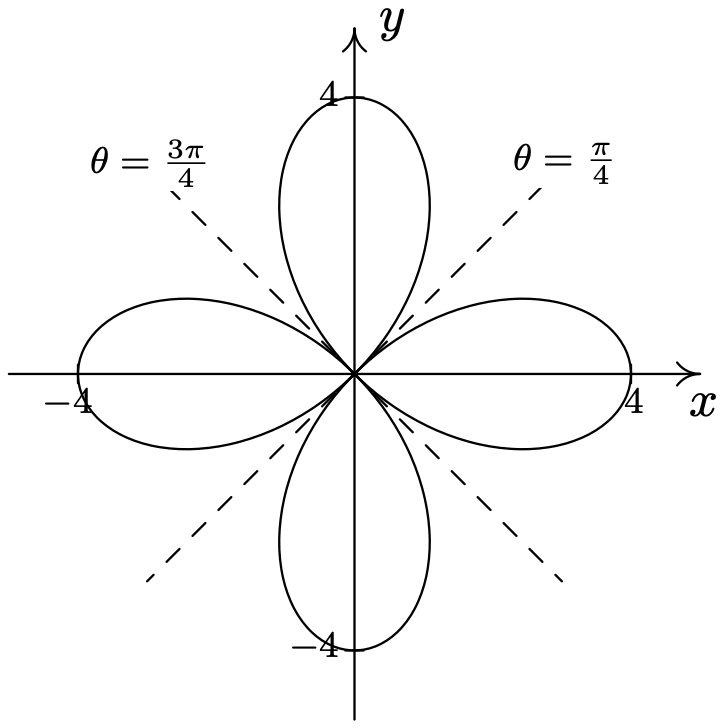
5. \(\text { Rose: } r=5 \sin (3 \theta)\)

   

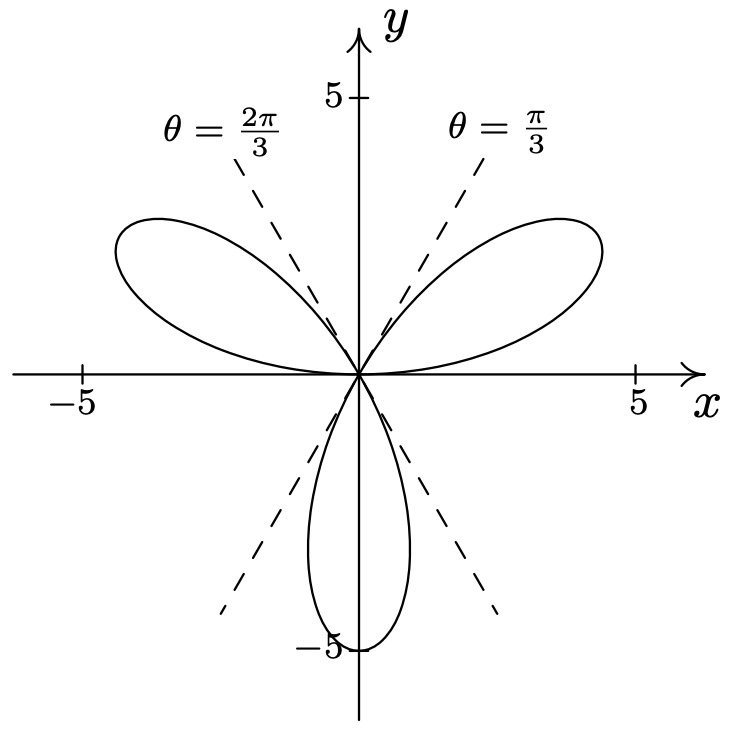
6. \(\text { Rose: } r=\cos (5 \theta)\)

   

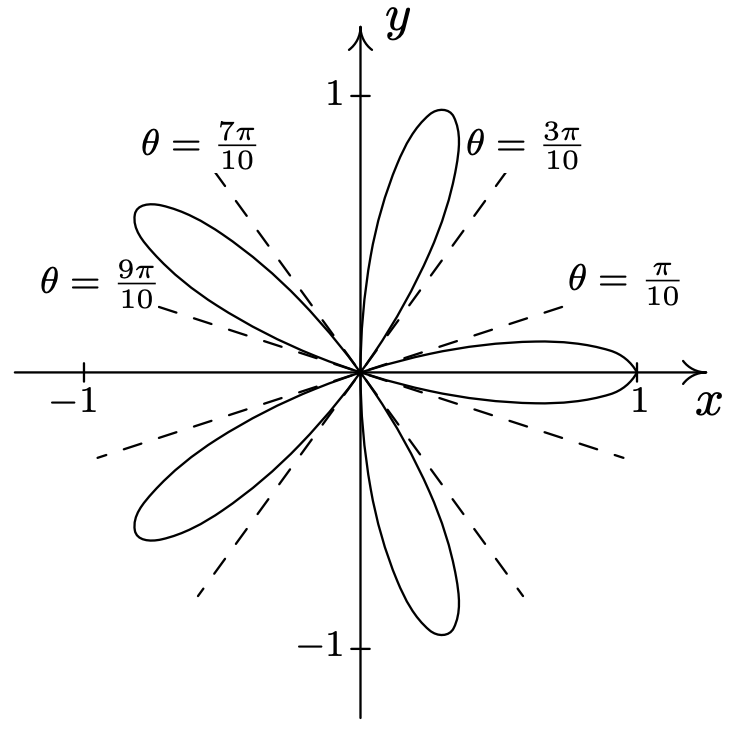
7. \(\text { Rose: } r=\sin (4 \theta)\)

   

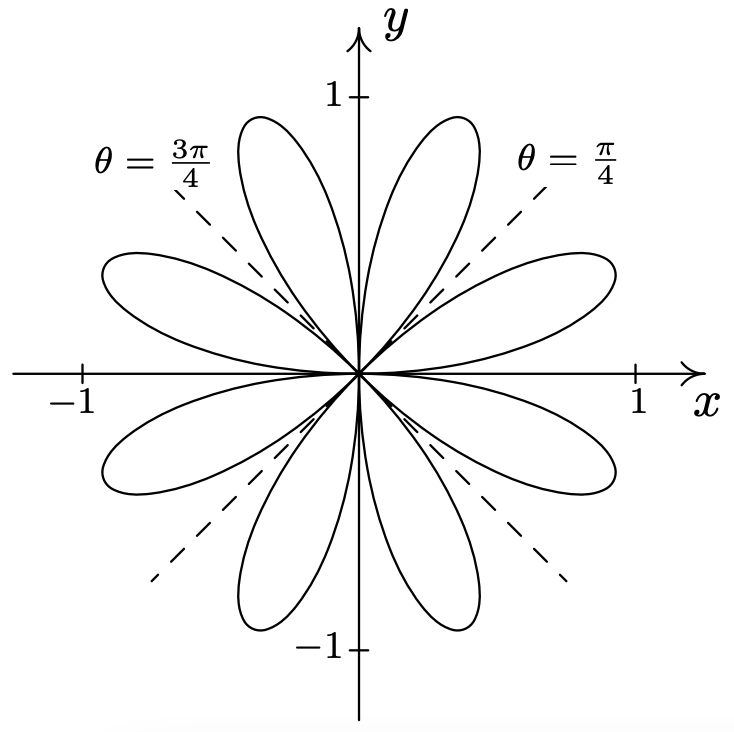
8. \(\text { Rose: } r=3 \cos (4 \theta)\)

   

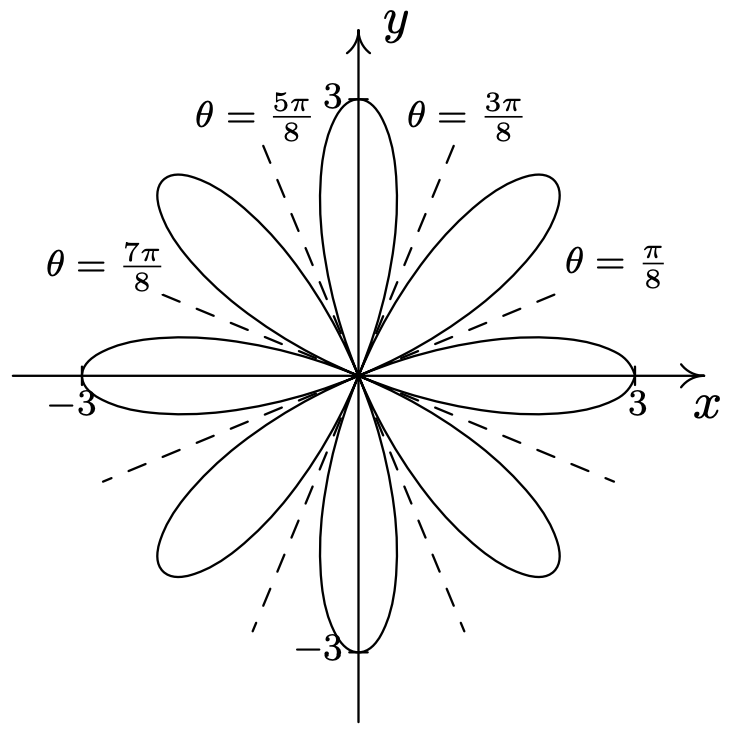
9. \(\text { Cardioid: } r=3-3 \cos (\theta)\)

   

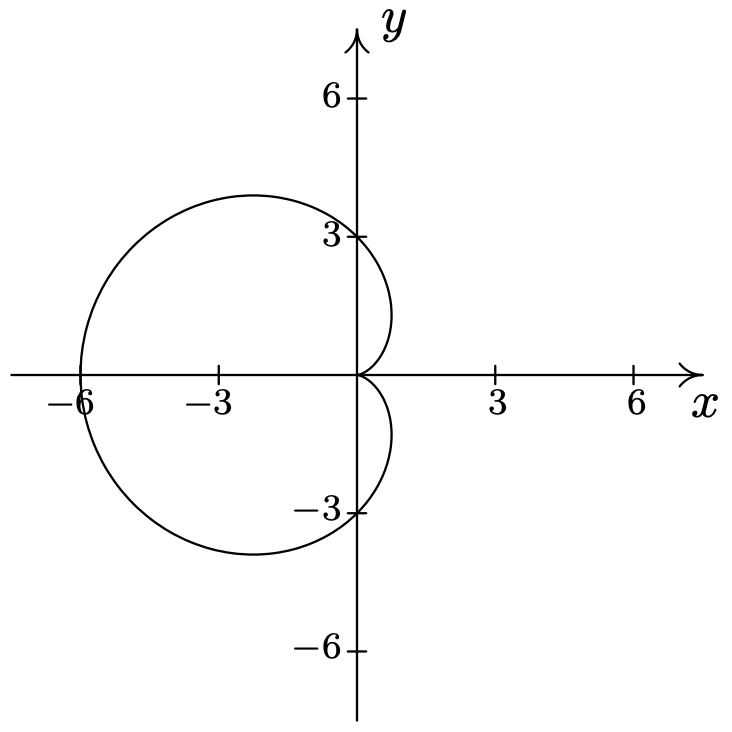
10. \(\text { Cardioid: } r=5+5 \sin (\theta)\)

    

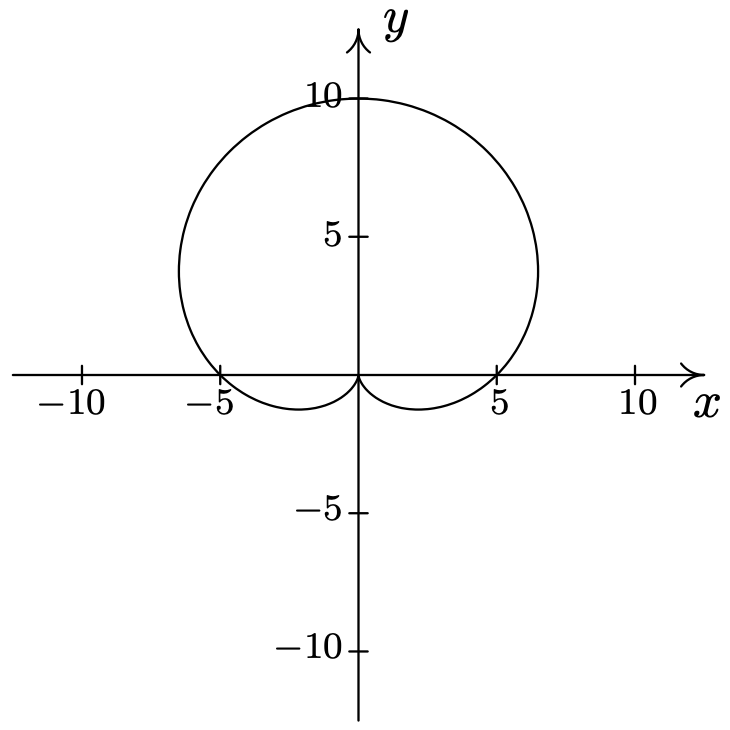
11. \(\text { Cardioid: } r=2+2 \cos (\theta)\)

    

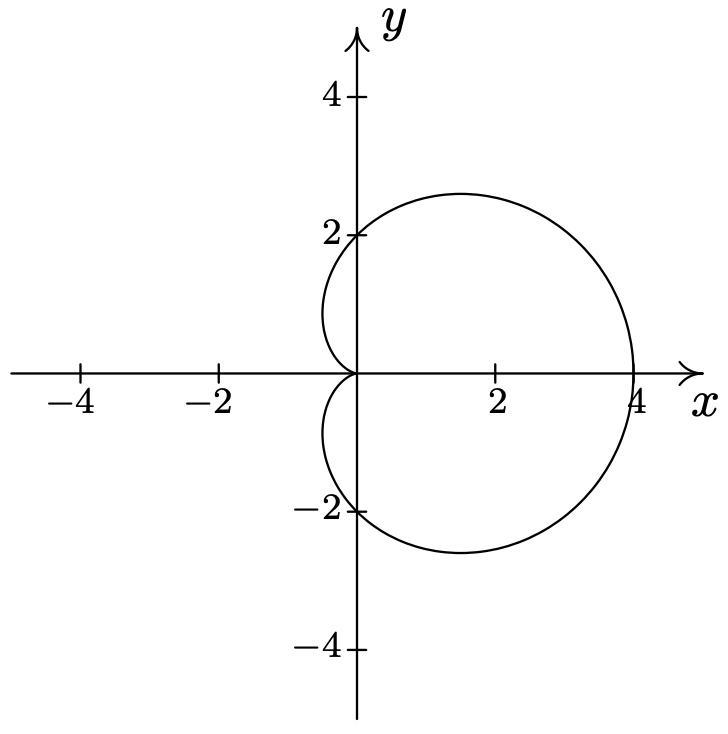
12. \(\text { Cardioid: } r=1-\sin (\theta)\)

    

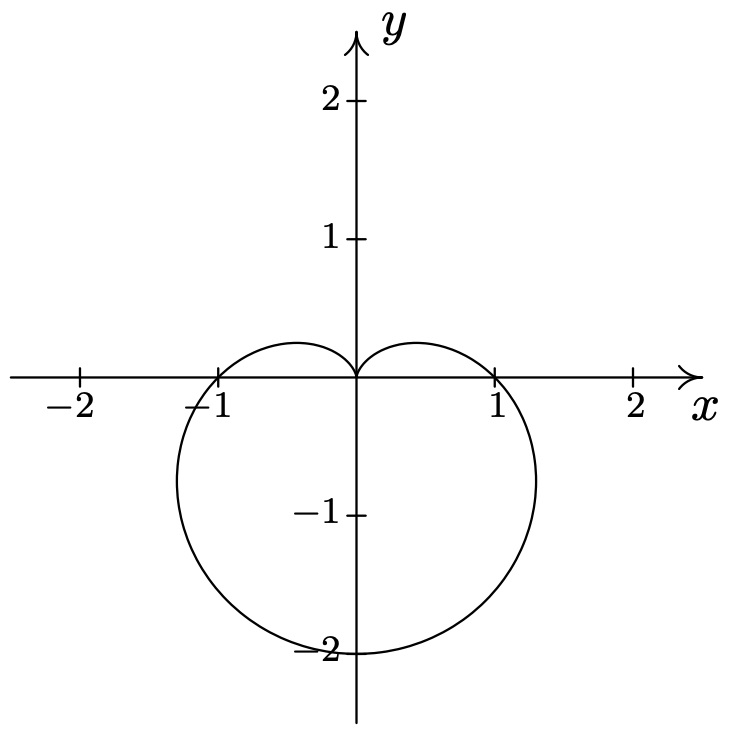
13. \(\text { Limaçon: } r=1-2 \cos (\theta)\)

    

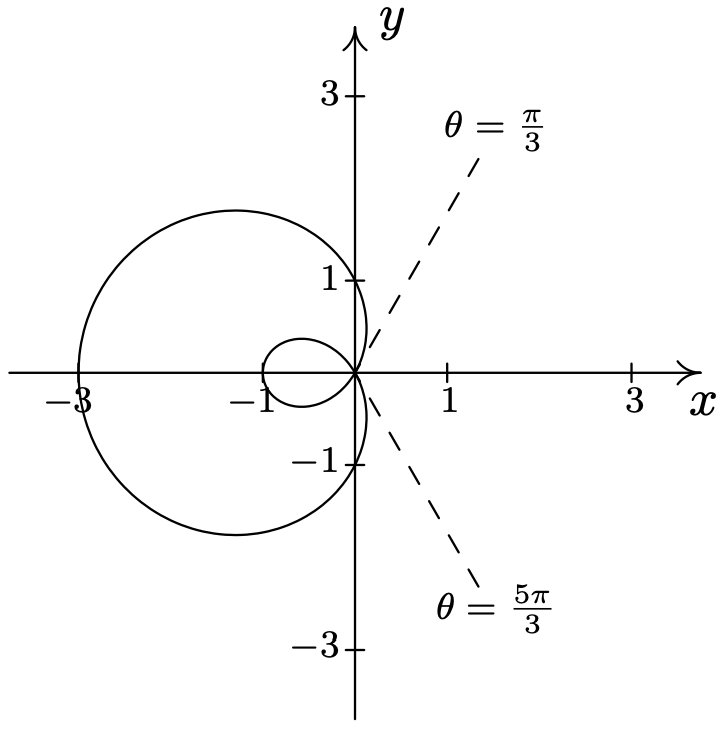
14. \(\text { Limaçon: } r=1-2 \sin (\theta)\)

    

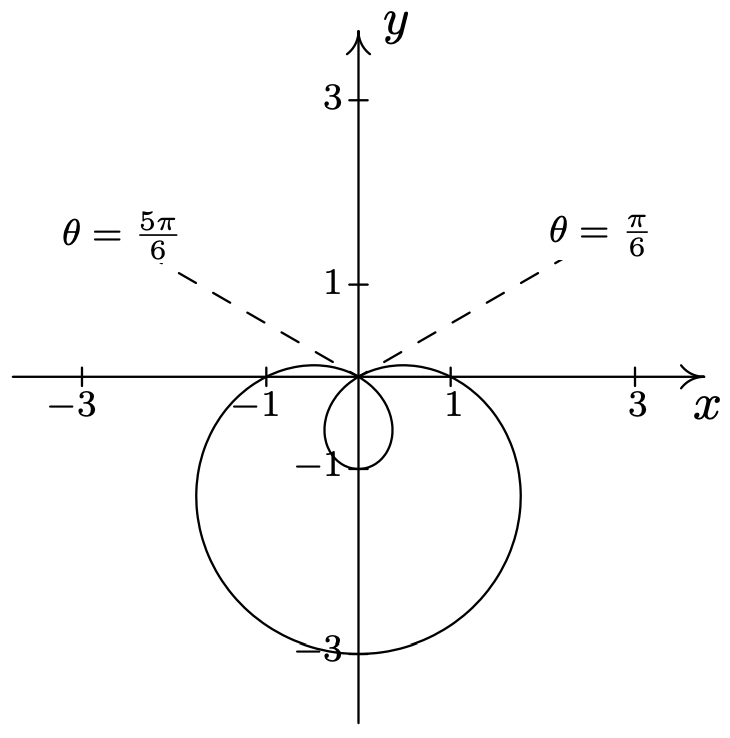
15. \(\text { Limaçon: } r=2 \sqrt{3}+4 \cos (\theta)\)

    

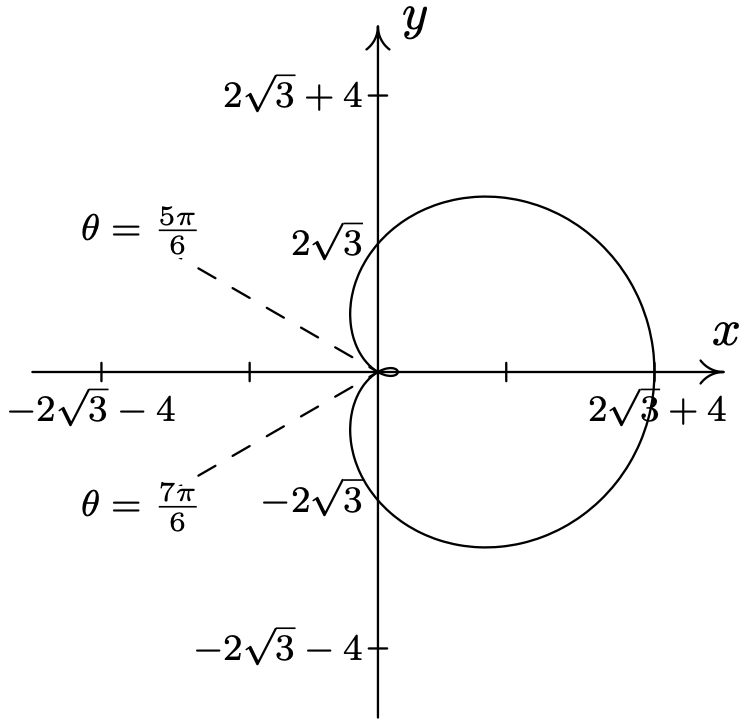
16. \(\text { Limaçon: } r=3-5 \cos (\theta)\)

    

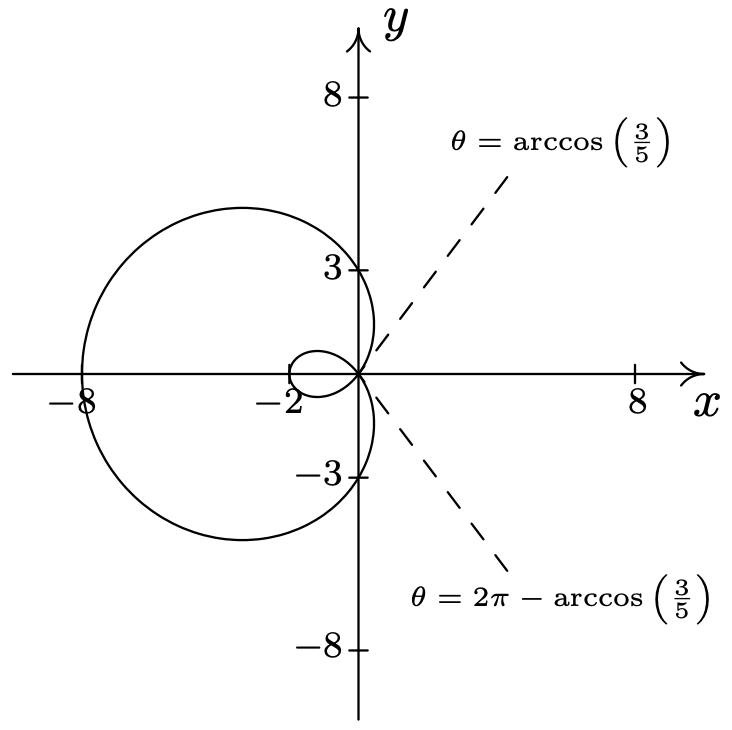
17. \(\text { Limaçon: } r=3-5 \sin (\theta)\)

    

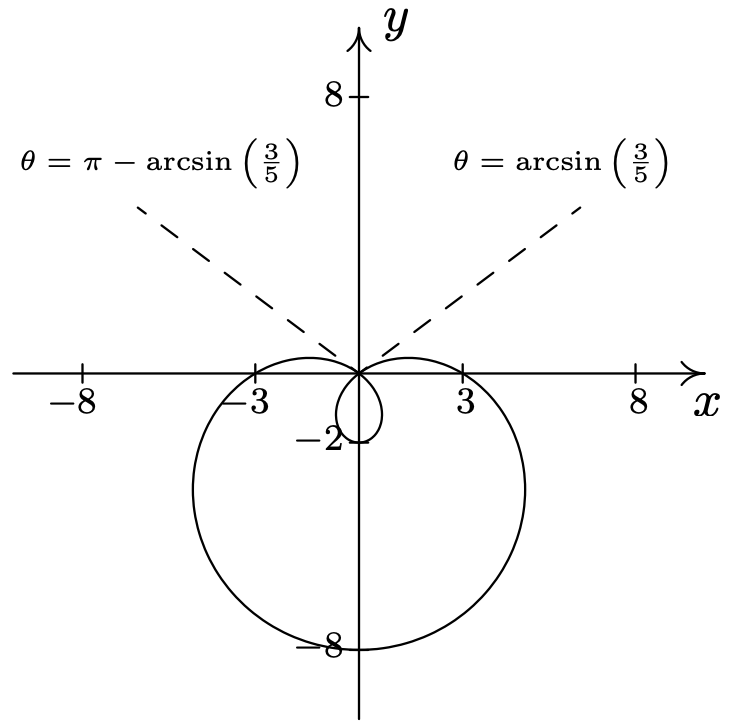
18. \(\text { Limaçon: } r=2+7 \sin (\theta)\)

    

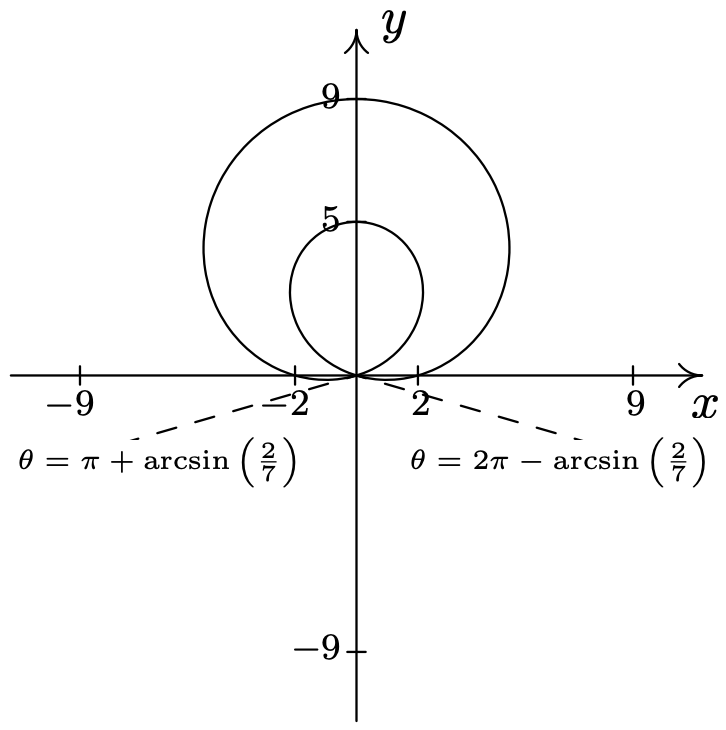
19. \(\text { Lemniscate: } r^{2}=\sin (2 \theta)\)

    

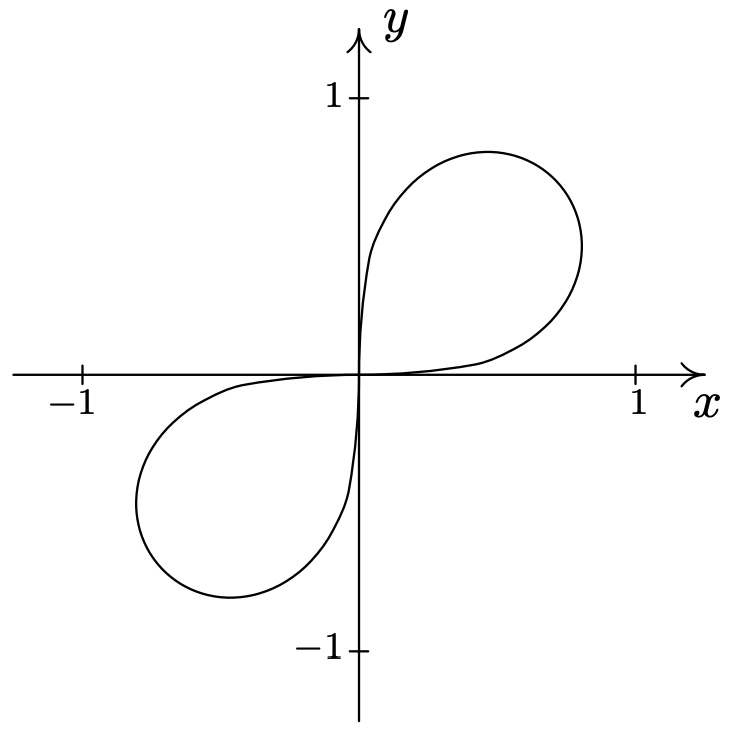
20. \(\text { Lemniscate: } r^{2}=4 \cos (2 \theta)\)

    

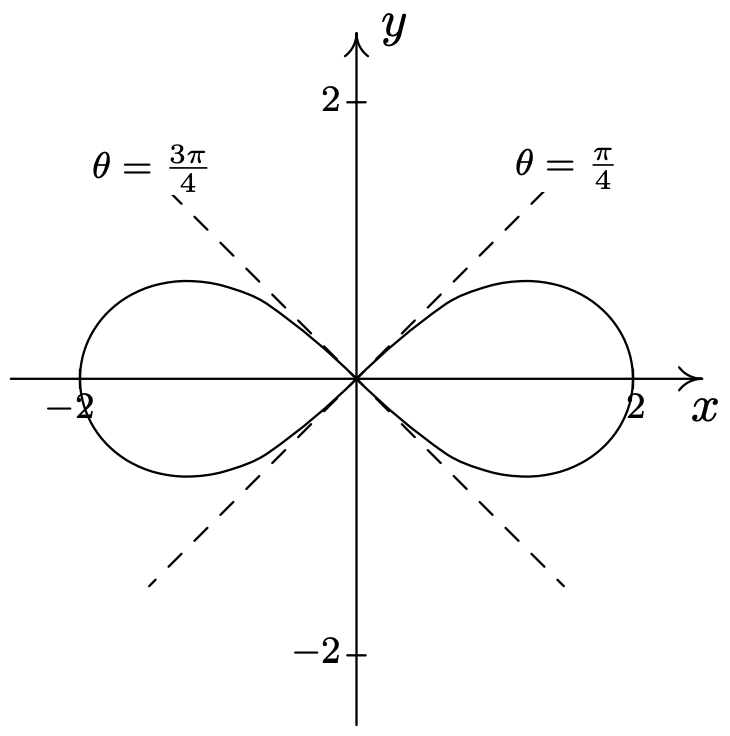
21. \(r=3 \cos (\theta) \text { and } r=1+\cos (\theta)\)\(\quad\quad\quad\quad\)\(\left(\frac{3}{2}, \frac{\pi}{3}\right),\left(\frac{3}{2}, \frac{5 \pi}{3}\right), \text { pole }\)

    

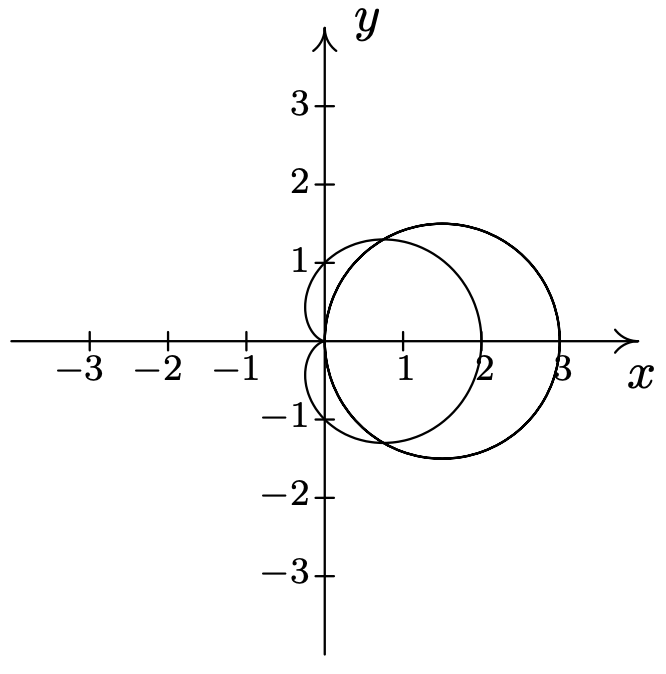
22. \(r=1+\sin (\theta) \text { and } r=1-\cos (\theta)\)\(\quad\quad\quad\quad\)\(\left(\frac{2+\sqrt{2}}{2}, \frac{3 \pi}{4}\right),\left(\frac{2-\sqrt{2}}{2}, \frac{7 \pi}{4}\right), \text { pole }\)

    

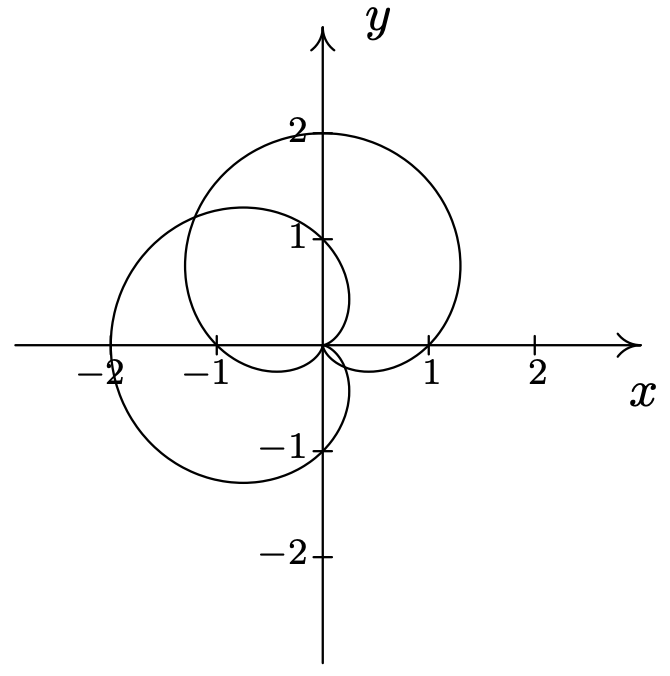
23. \(r=1-2 \sin (\theta) \text { and } r=2\)\(\quad\quad\quad\quad\)\(\left(2, \frac{7 \pi}{6}\right),\left(2, \frac{11 \pi}{6}\right)\)

    

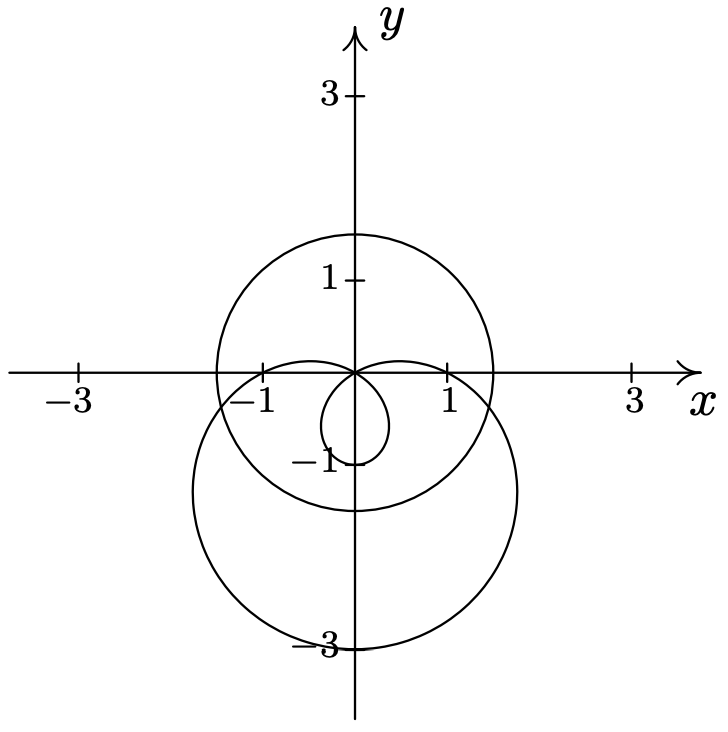
24. \(r=1-2 \cos (\theta) \text { and } r=1\)\(\quad\quad\quad\quad\)\(\left(1, \frac{\pi}{2}\right),\left(1, \frac{3 \pi}{2}\right),(-1,0)\)

    

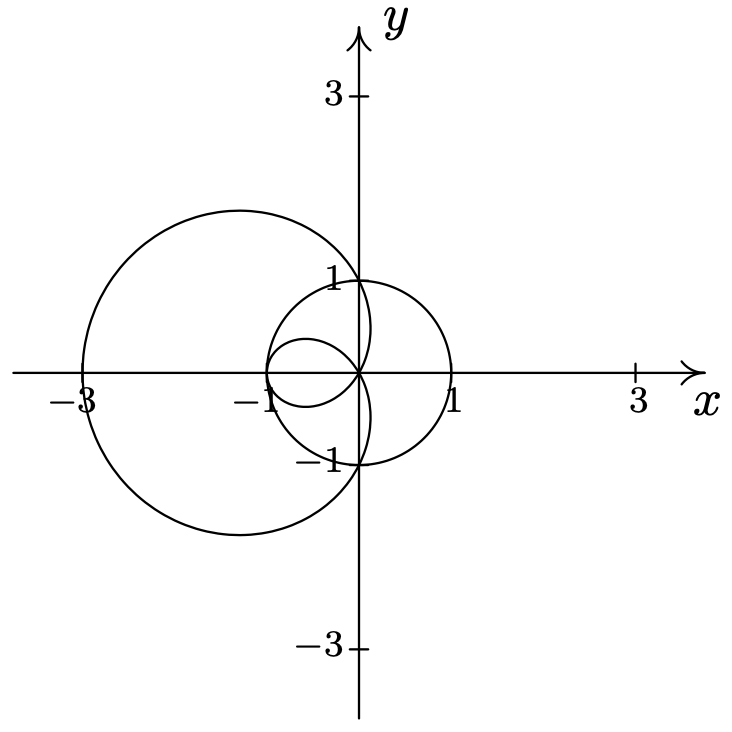
25. \(r=2 \cos (\theta) \text { and } r=2 \sqrt{3} \sin (\theta)\)\(\quad\quad\quad\quad\)\(\left(\sqrt{3}, \frac{\pi}{6}\right), \text { pole }\)

    

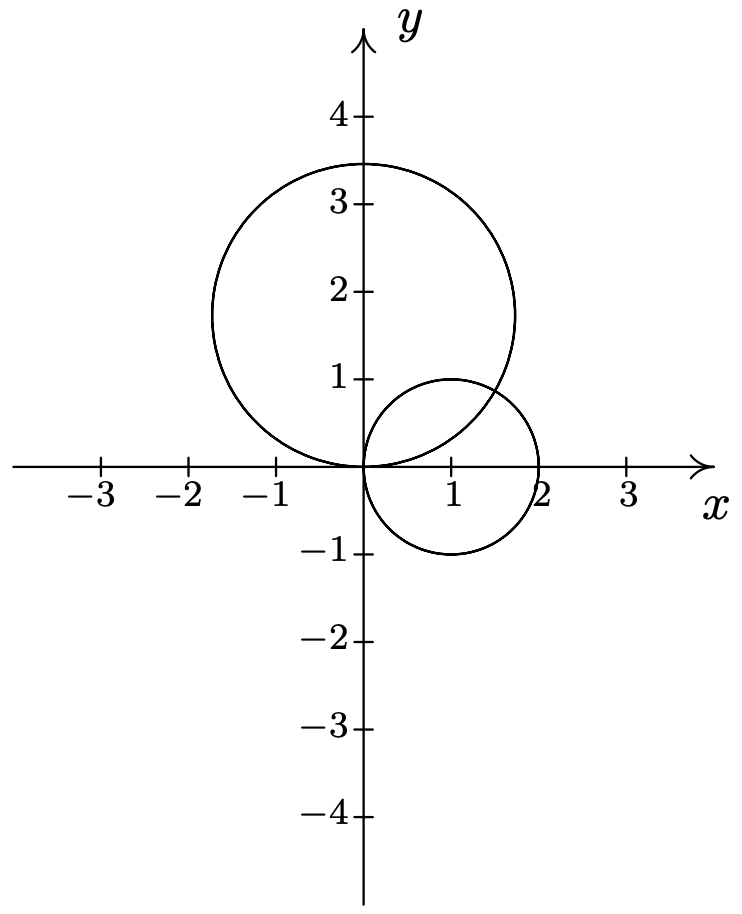
26. \(r=3 \cos (\theta) \text { and } r=\sin (\theta)\)\(\quad\quad\quad\quad\)\(\left(\frac{3 \sqrt{10}}{10}, \arctan (3)\right), \text { pole }\)

    

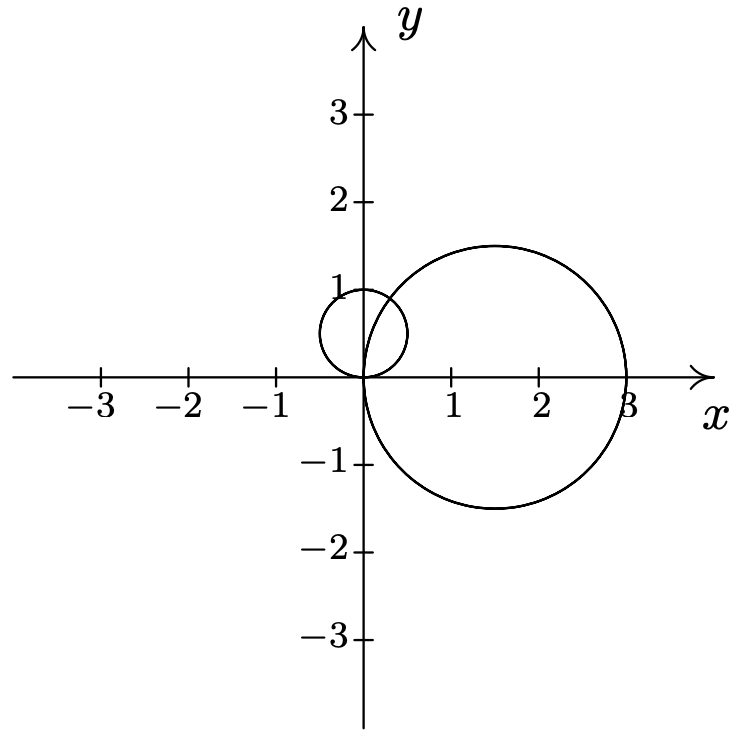
27. \(r^{2}=4 \cos (2 \theta) \text { and } r=\sqrt{2}\)\(\quad\quad\quad\quad\)\(\left(\sqrt{2}, \frac{\pi}{6}\right),\left(\sqrt{2}, \frac{5 \pi}{6}\right),\left(\sqrt{2}, \frac{7 \pi}{6}\right),\left(\sqrt{2}, \frac{11 \pi}{6}\right)\)

    

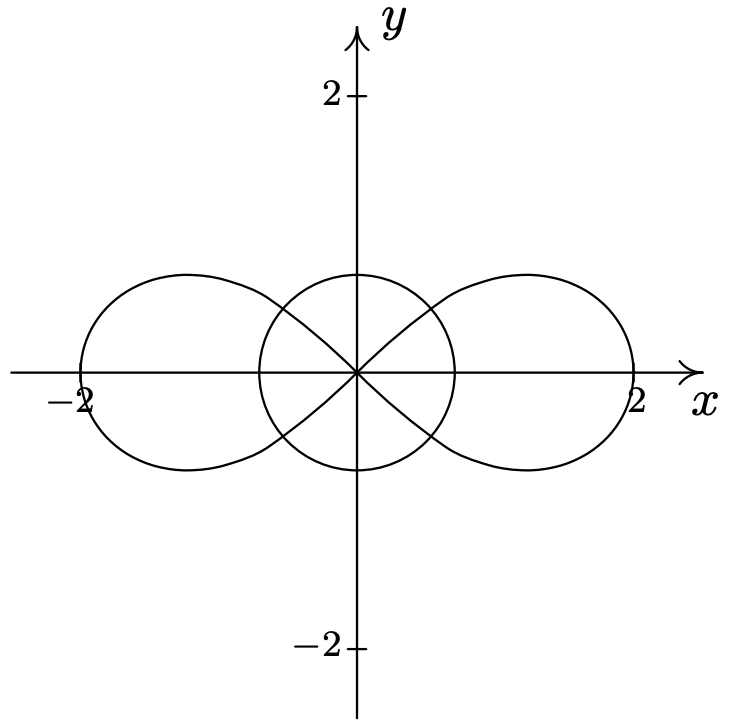
28. \(r^{2}=2 \sin (2 \theta) \text { and } r=1\)\(\quad\quad\quad\quad\)\(\left(1, \frac{\pi}{12}\right),\left(1, \frac{5 \pi}{12}\right),\left(1, \frac{13 \pi}{12}\right),\left(1, \frac{17 \pi}{12}\right)\)

    

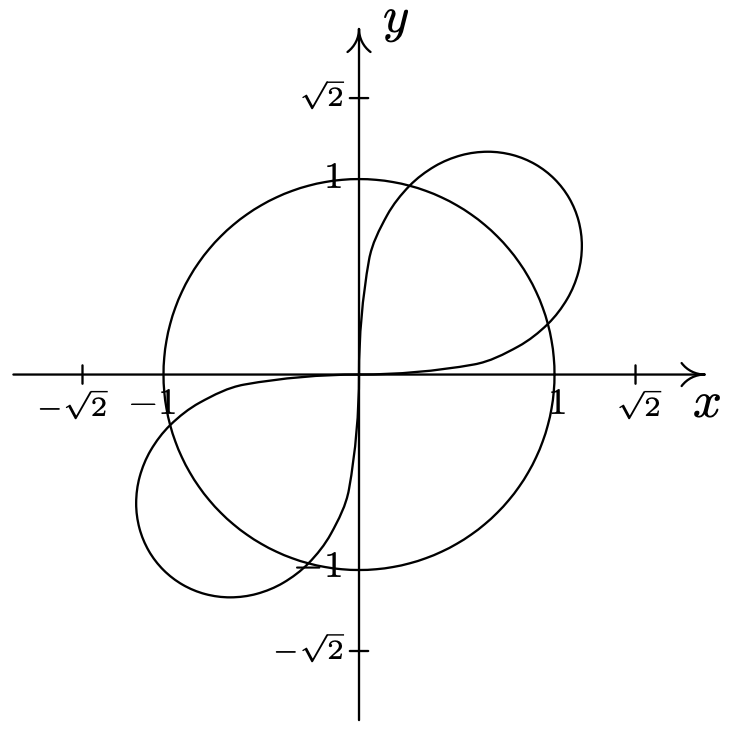
29. \(r=4 \cos (2 \theta) \text { and } r=2\)\(\quad\quad\quad\quad\)\ (\ begin {alineada}
    &\ izquierda (2,\ frac {\ pi} {6}\ derecha),\ izquierda (2,\ frac {5\ pi} {6}\ derecha),\ izquierda (2,\ frac {7\ pi} {6}\ derecha),\\
    &\ izquierda (2,\ frac {11\ pi} {6}\ derecha),\ izquierda (-2,\ frac {\ pi} {3}\ derecha),\ izquierda (-2,\ frac {2\ pi} {3}\ derecha),\\
    &\ izquierda (-2,\ frac {4\ pi} {3}\ derecha),\ izquierda (-2,\ frac {5\ pi} {3}\ derecha)\ end {alineado}\)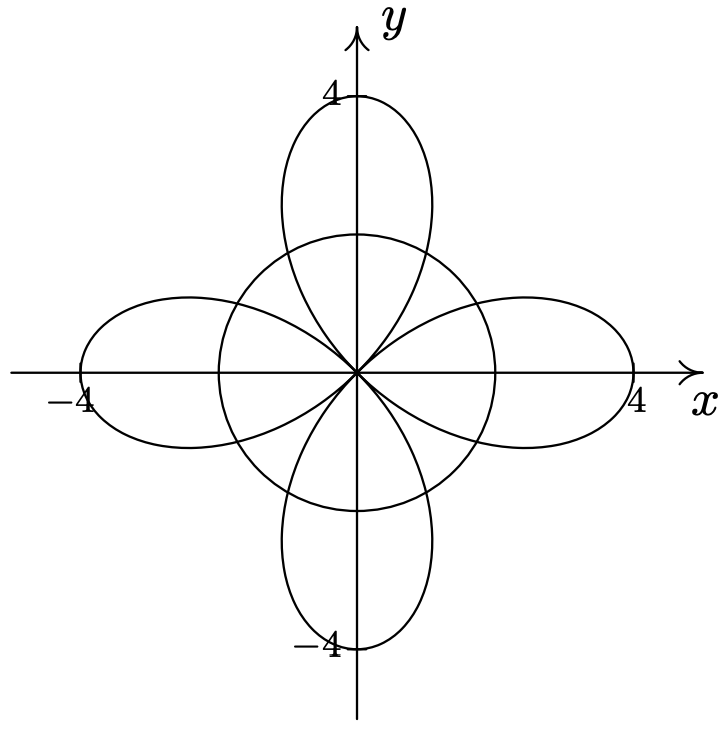

    

30. \(r=2 \sin (2 \theta) \text { and } r=1\)\(\quad\quad\quad\quad\)\ (\ begin {aligned}
    &\ left (1,\ frac {\ pi} {12}\ right),\ left (1,\ frac {5\ pi} {12}\ right),\ left (1,\ frac {13\ pi} {12}\ right),\\
    &\ left (1,\ frac {17\ pi} {12}\ right),\ left (-1,\ frac {7\ pi} {12}\ derecha),\ izquierda (-1,\ frac {11\ pi} {12}\ derecha),\\
    &\ izquierda (-1,\ frac {19\ pi} {12}\ derecha),\ izquierda (-1,\ frac {23\ pi} {12}\ derecha)\ end {alineado}\)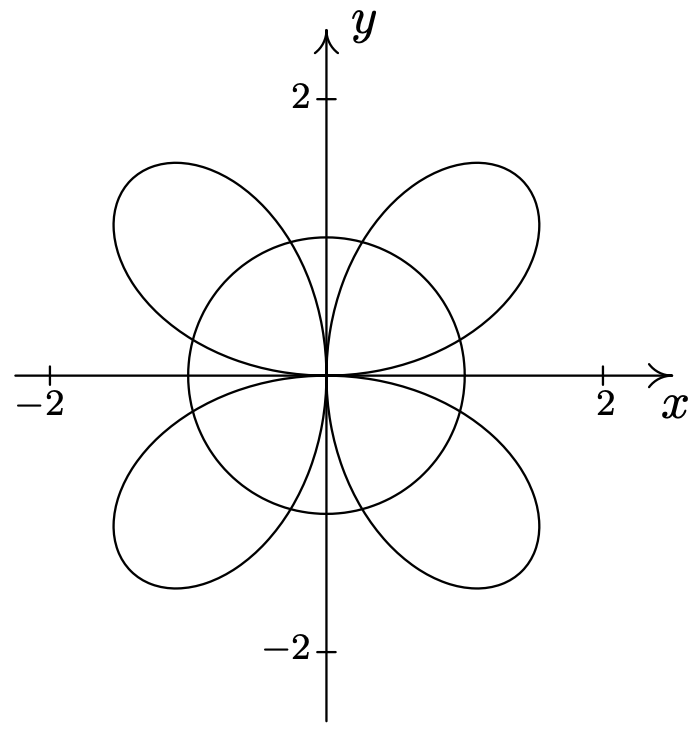

    

31. \(\{(r, \theta) \mid 0 \leq r \leq 3,0 \leq \theta \leq 2 \pi\}\)

    

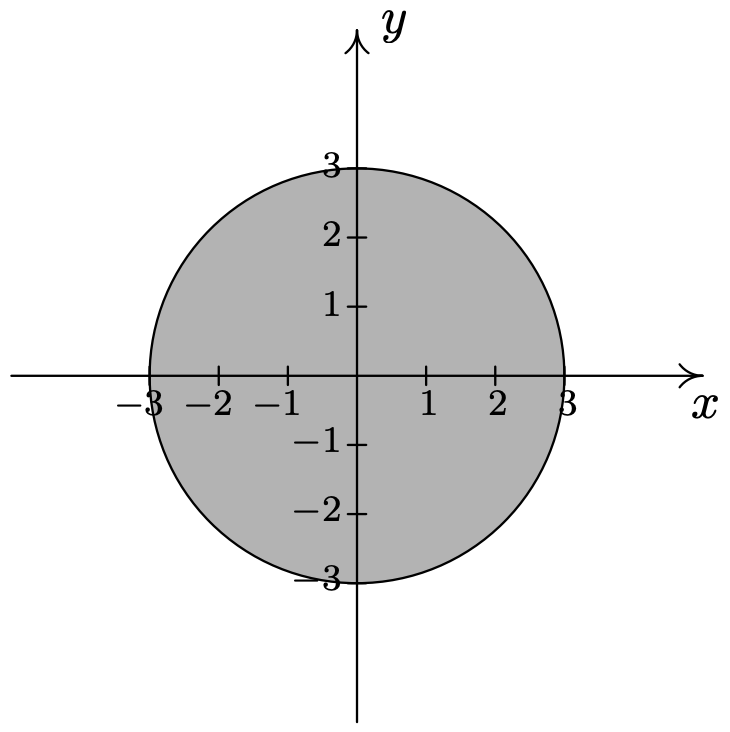
32. \(\{(r, \theta) \mid 0 \leq r \leq 4 \sin (\theta), 0 \leq \theta \leq \pi\}\)

    

33. \(\left\{(r, \theta) \mid 0 \leq r \leq 3 \cos (\theta),-\frac{\pi}{2} \leq \theta \leq \frac{\pi}{2}\right\}\)

    

34. \(\left\{(r, \theta) \mid 0 \leq r \leq 2 \sin (2 \theta), 0 \leq \theta \leq \frac{\pi}{2}\right\}\)

    

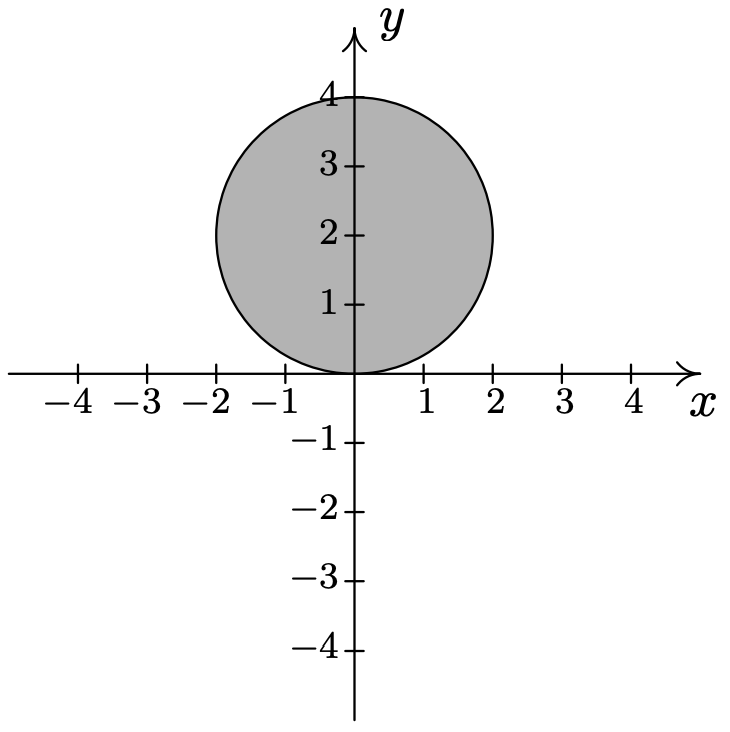
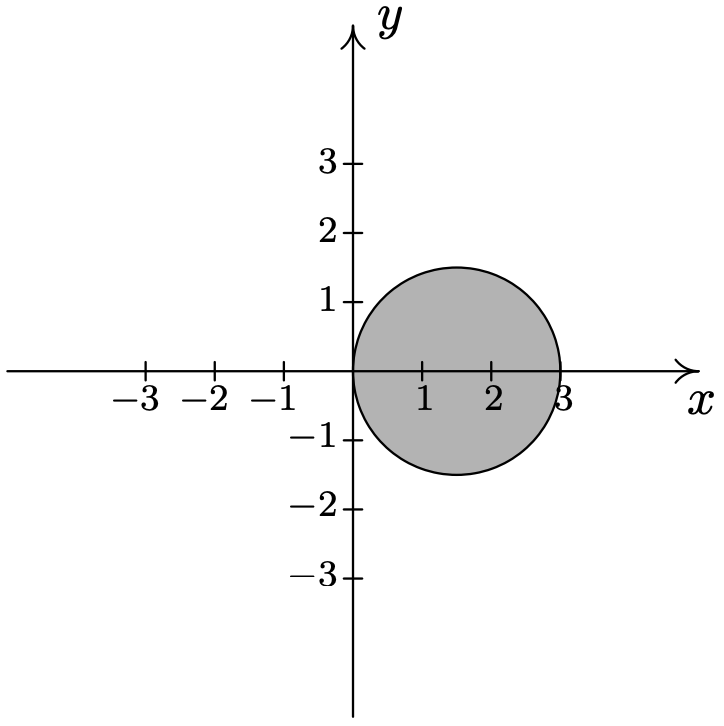
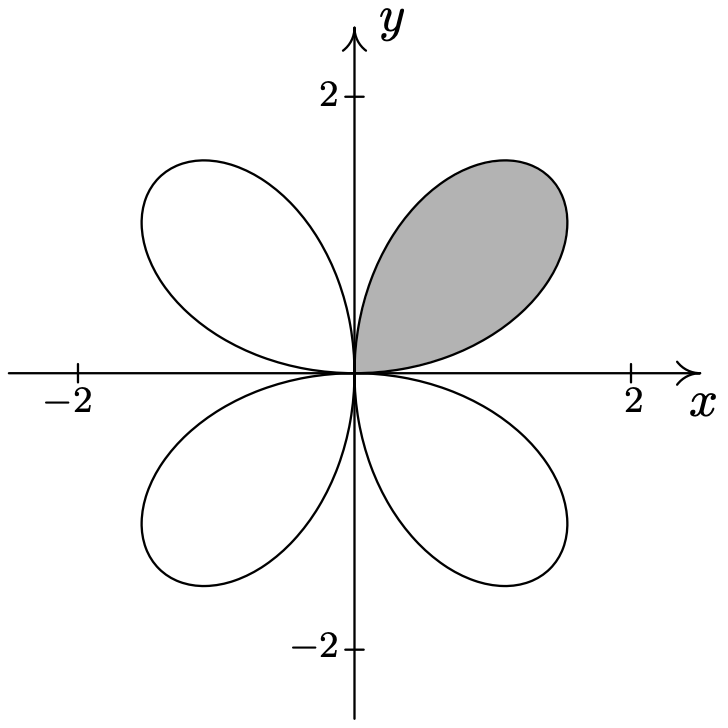
35. \(\left\{(r, \theta) \mid 0 \leq r \leq 4 \cos (2 \theta),-\frac{\pi}{4} \leq \theta \leq \frac{\pi}{4}\right\}\)

    

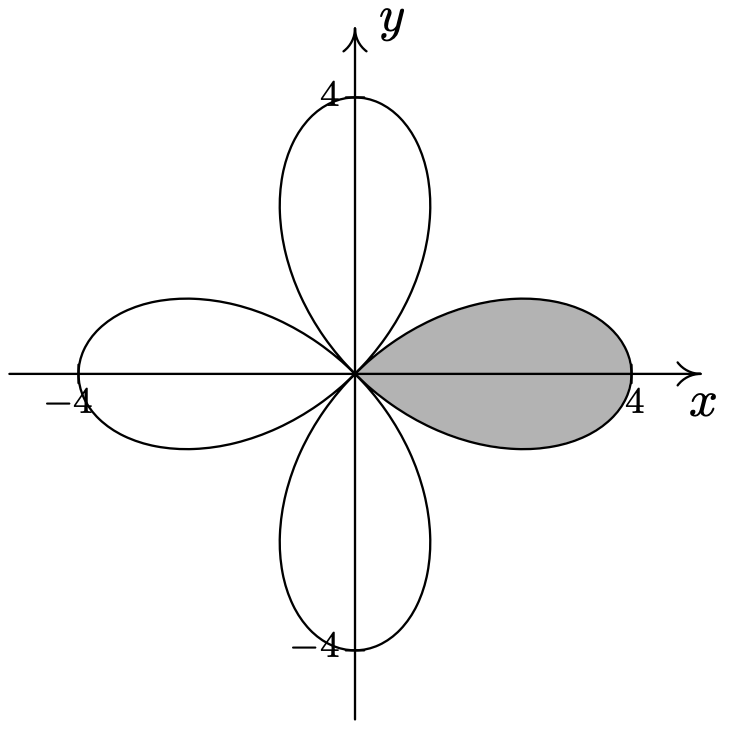
36. \(\left\{(r, \theta) \mid 1 \leq r \leq 1-2 \cos (\theta), \frac{\pi}{2} \leq \theta \leq \frac{3 \pi}{2}\right\}\)

    

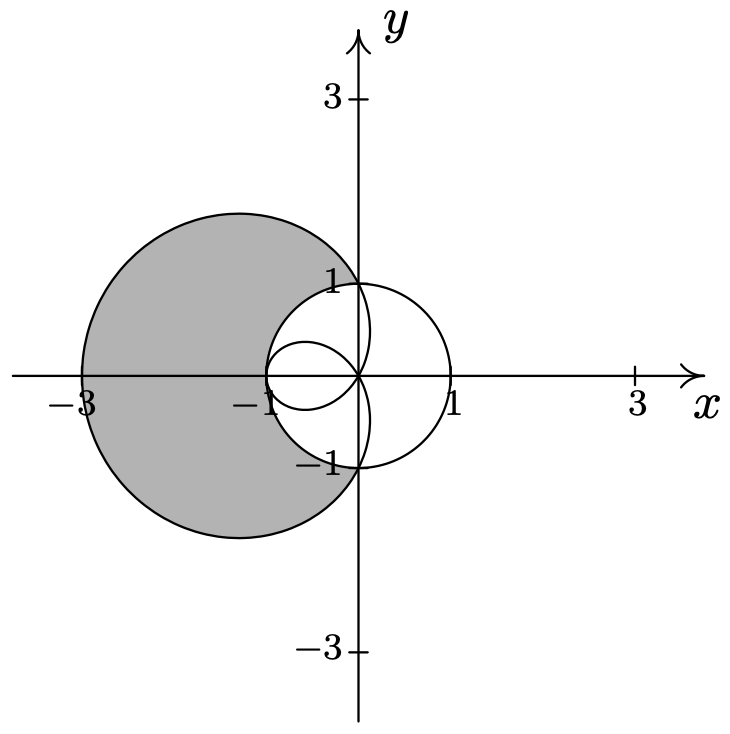
37. \(\left\{(r, \theta) \mid 1+\cos (\theta) \leq r \leq 3 \cos (\theta),-\frac{\pi}{3} \leq \theta \leq \frac{\pi}{3}\right\}\)

    

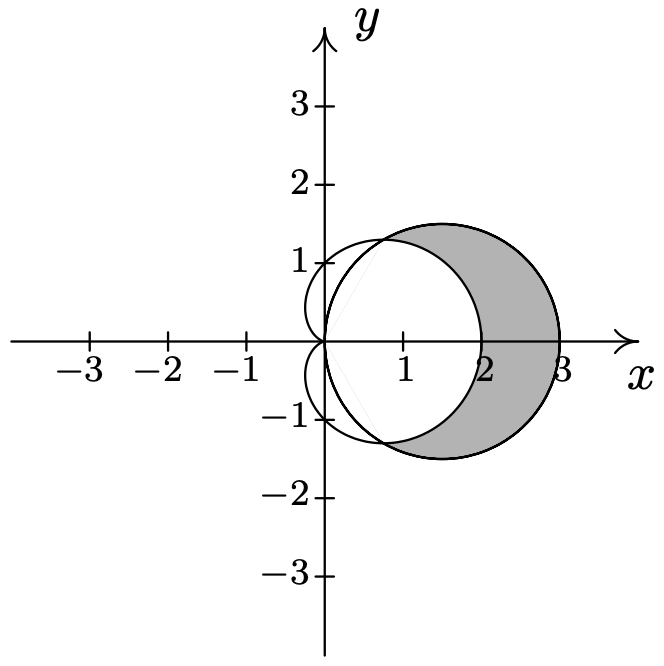
38. \(\left\{(r, \theta) \mid 1 \leq r \leq \sqrt{2 \sin (2 \theta)}, \frac{13 \pi}{12} \leq \theta \leq \frac{17 \pi}{12}\right\}\)

    

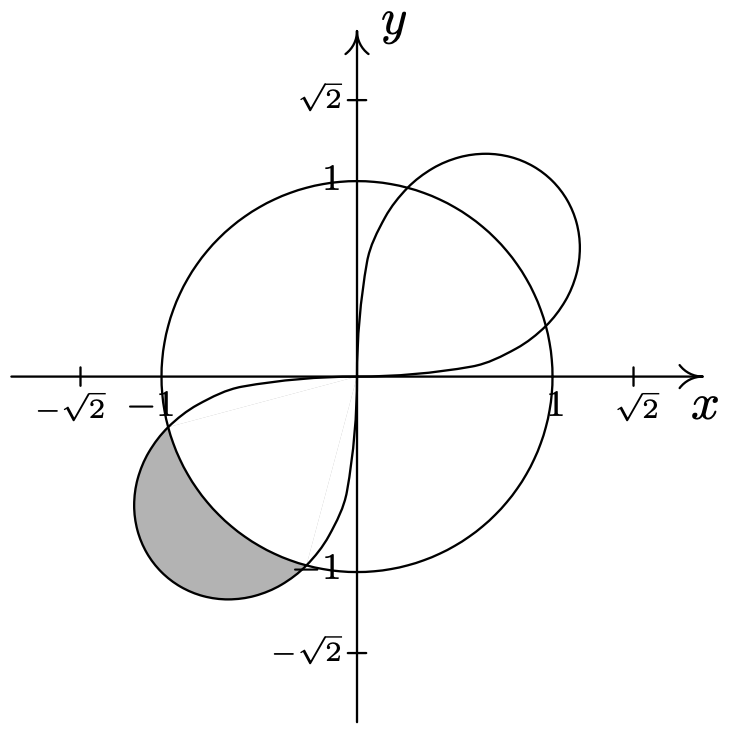
39. \(\left\{(r, \theta) \mid 0 \leq r \leq 2 \sqrt{3} \sin (\theta), 0 \leq \theta \leq \frac{\pi}{6}\right\} \cup\left\{(r, \theta) \mid 0 \leq r \leq 2 \cos (\theta), \frac{\pi}{6} \leq \theta \leq \frac{\pi}{2}\right\}\)

    

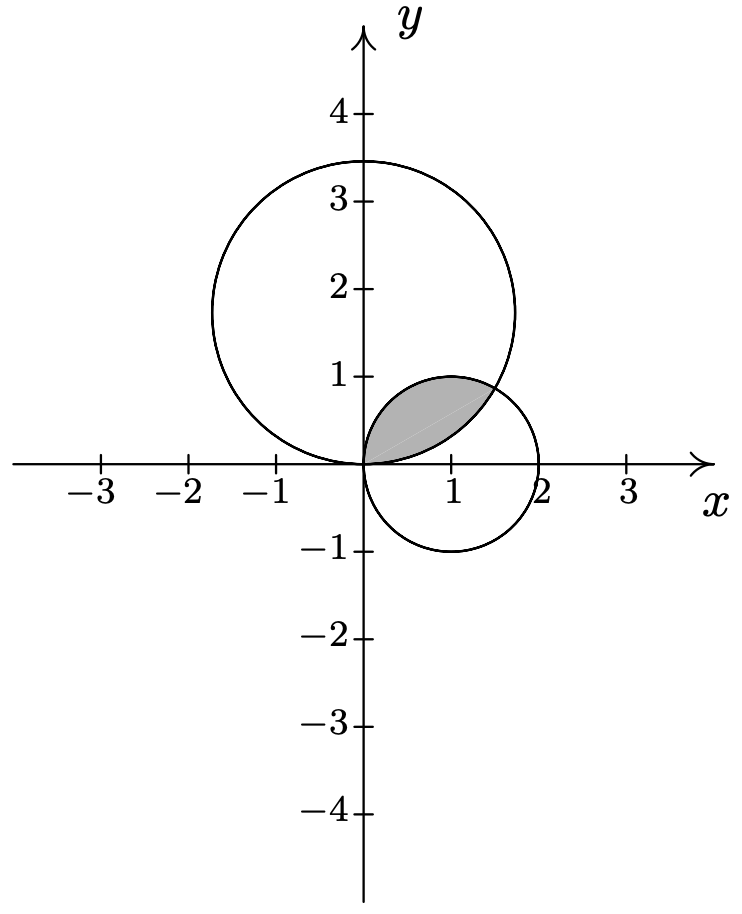
40. \(\left\{(r, \theta) \mid 0 \leq r \leq 2 \sin (2 \theta), 0 \leq \theta \leq \frac{\pi}{12}\right\} \cup\left\{(r, \theta) \mid 0 \leq r \leq 1, \frac{\pi}{12} \leq \theta \leq \frac{\pi}{4}\right\}\)

    

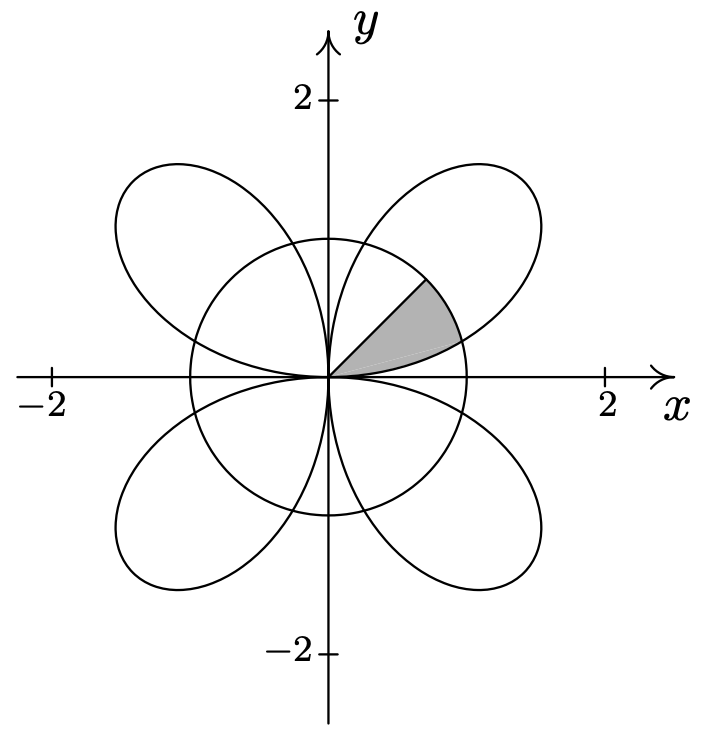
41. \(\{(r, \theta) \mid 0 \leq r \leq 5,0 \leq \theta \leq 2 \pi\}\)
42. \(\left\{(r, \theta) \mid 0 \leq r \leq 5, \pi \leq \theta \leq \frac{3 \pi}{2}\right\}\)
43. \(\left\{(r, \theta) \mid 0 \leq r \leq 6 \sin (\theta), \frac{\pi}{2} \leq \theta \leq \pi\right\}\)
44. \(\left\{(r, \theta) \mid 4 \cos (\theta) \leq r \leq 0, \frac{\pi}{2} \leq \theta \leq \pi\right\}\)
45. \(\{(r, \theta) \mid 0 \leq r \leq 3-3 \cos (\theta), 0 \leq \theta \leq \pi\}\)
46. \ (\ comenzar {alineado}
    &\ izquierda\ {(r,\ theta)\ mediados 0\ leq r\ leq 2-2\ sin (\ theta), 0\ leq\ theta\ leq\ frac {\ pi} {2}\ derecha\}\ copa\ izquierda\ {(r,\ theta)\ mediados 0\ leq r\ leq 2-2\ sin (\ theta),\ frac {3\ pi} {2}\ leq\ theta\ leq 2\ pi\ derecha\}\\
    &\ texto {o}\ izquierda\ {(r,\ theta)\ mediados 0\ leq r\ leq 2-2\ sin (\ theta),\ frac {3\ pi} {2}\ leq\ theta\ leq\ frac {5\ pi} {2}\ derecha\}
    \ final {alineado}\)
47. \ (\ comenzar {alineado}
    &\ izquierda\ {(r,\ theta)\ mediados 0\ leq r\ leq 3\ cos (4\ theta), 0\ leq\ theta\ leq\ frac {\ pi} {8}\ derecha\}\ copa\ izquierda\ {(r,\ theta)\ mediados 0\ leq r\ leq 3\ cos (4\ theta),\ frac {15\ pi} {8}\ leq\ theta\ leq 2\ pi\ derecha\}\\
    &\ texto {o}\ izquierda\ {(r,\ theta)\ mediados 0 \ leq r\ leq 3\ cos (4\ theta), -\ frac {\ pi} {8}\ leq\ theta\ leq\ frac {\ pi} {8}\ derecho\}
    \ final {alineado}\)
48. \(\{(r, \theta) \mid 3 \leq r \leq 5,0 \leq \theta \leq 2 \pi\}\)
49. \(\left\{(r, \theta) \mid 0 \leq r \leq 3 \cos (\theta),-\frac{\pi}{2} \leq \theta \leq 0\right\} \cup\{(r, \theta) \mid \sin (\theta) \leq r \leq 3 \cos (\theta), 0 \leq \theta \leq \arctan (3)\}\)
50. \ (\ comenzar {alineado}
    &\ izquierda\ {(r,\ theta)\ mediados 0\ leq r\ leq 6\ sin (2\ theta), 0\ leq\ theta\ leq\ frac {\ pi} {12}\ derecha\}\ copa\ izquierda\ {(r,\ theta)\ mediados 0\ leq r\ leq 3,\ frac {\ pi} {12}\ leq\ theta\ leq\ frac {5\ pi} {12}\ derecha\}\ copa\\
    &\ izquierda\ {(r,\ theta)\ mediados 0\ leq r\ leq 6 \ sin (2\ theta),\ frac {5\ pi} {12}\ leq\ theta\ leq\ frac {\ pi} {2}\ derecho\}
    \ final {alineado}\)

---

Referencia

¹ Ver la discusión en el Ejemplo 11.4.3 número 2a.

² Para una revisión de estos conceptos y de este proceso, véanse las Secciones 1.4 y 1.6.

³ La gráfica se ve exactamente igual que\(y=6 \cos (x)\) en el\(xy\) plano -y por una buena razón. En esta etapa, solo estamos graficando la relación entre\(r\) y\(\theta\) antes de interpretarlos como coordenadas polares\((r, \theta)\) en el\(xy\) plano.

⁴ La gráfica de\(r=6 \cos (\theta)\) se ve sospechosamente como un círculo, por una buena razón. Ver el número 1a en el Ejemplo 11.4.3.

⁵ El teorema de las 'tangentes en el polo' del Cálculo del segundo semestre.

⁶ Recordemos que una forma de visualizar trazando coordenadas polares\((r, \theta)\) con\(r < 0\) es iniciar la rotación desde el lado izquierdo del polo\(x\) -en este caso, el eje negativo-. Girar entre\(\frac{2 \pi}{3}\) y\(\pi\) radianes desde el\(x\) eje negativo en este caso determina la región entre la línea\(\theta=\frac{2 \pi}{3}\) y el\(x\) eje en el Cuadrante IV.

⁷ Debido a la relación entre\(y = x\) y\(y=\sqrt{x}\) sobre [0, 1], también conocemos\(\sqrt{\cos (2 \theta)} \geq \cos (2 \theta)\) donde se define el primero.

⁸ En este caso, podríamos haber generado toda la gráfica usando solo la gráfica\(r=4 \sqrt{\cos (2 \theta)}\), pero graficada a lo largo del intervalo\([0,2 \pi]\) en el\(\theta r \text {-plane }\). Dejamos los detalles al lector.

⁹ Los números 1 y 2 del Ejemplo 11.5.2 son ejemplos de 'limaçon', el número 3 es un ejemplo de una 'rosa polar', y el número 4 es el famoso 'Lemniscate de Bernoulli.'

¹⁰ Presumiblemente, el nombre se deriva de su parecido con un corazón humano estilizado.

¹¹ Realmente estamos usando la técnica de sustitución para resolver el sistema de ecuaciones\(\left\{\begin{array}{l} r=2 \sin (\theta) \\ r=2-2 \sin (\theta) \end{array}\right.\)

¹² Ver Ejemplo 11.5.2 número 3.

¹³ Los autores han elegido\(\theta\) con\(\theta+2 \pi k\) en la ecuación únicamente con\(r=6 \cos (2 \theta)\) fines ilustrativos. Podríamos haber elegido con la misma facilidad hacer esta sustitución en la ecuación\(r = 3\). Dado que no hay\(\theta\) en\(r=3\), sin embargo, este caso se reduciría al caso anterior instantáneamente. Se alienta al lector a seguir este último procedimiento en aras de la eficiencia.

¹⁴ Nuevamente, podríamos haber optado fácilmente por sustituir estos en\(r = 3\) los que darían\(−r = 3\), o\(r = −3\).

¹⁵ Obtenemos estas representaciones sustituyendo los valores por\(\theta\)\(r=6 \cos (2 \theta)\), una vez más, con fines ilustrativos. Nuevamente, en aras de la eficiencia, podríamos 'tapar' estos valores para\(\theta\) en\(r = 3\) (donde no hay\(\theta\)) y obtener la lista de puntos:\(\left(3, \frac{\pi}{3}\right),\left(3, \frac{2 \pi}{3}\right),\left(3, \frac{4 \pi}{3}\right) \text { and }\left(3, \frac{5 \pi}{3}\right)\). Blanco no es cierto que\(\left(3, \frac{\pi}{3}\right)\) representa el mismo punto que\(\left(-3, \frac{\pi}{3}\right)\), todavía obtenemos el conjunto de soluciones.

¹⁶ Un boceto rápido de\(r=3 \sin \left(\frac{\theta}{2}\right)\) y\(r=3 \cos \left(\frac{\theta}{2}\right)\) en el te\(\theta r \text {-plane }\) convencerá de que, visto como funciones de\(r\), estos son dos animales diferentes.

¹⁷ Recordemos que esto significa\(f(-\theta)=f(\theta)\) para\(\theta\) en el dominio de\(f\).

¹⁸ Recordemos que esto significa\(f(-\theta)=-f(\theta)\) para\(\theta\) en el dominio de\(f\).