11.8: Vectores

Última actualización
Guardar como PDF

Page ID: 119510

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

Como hemos visto numerosas veces en este libro, las matemáticas pueden ser utilizadas para modelar y resolver problemas del mundo real. Para muchas aplicaciones, los números reales son suficientes; es decir, los números reales con las unidades apropiadas adjuntas se pueden usar para responder preguntas como “¿Qué tan cerca está el nido Sasquatch más cercano?” Sin embargo, hay otras ocasiones, en las que este tipo de cantidades no bastan. Quizás sea importante saber, por ejemplo, qué tan cerca está el nido Sasquatch más cercano así como la dirección en la que se encuentra. (¿Prefigurando el uso de cojinetes en los ejercicios, quizás?) Para responder preguntas como estas que involucran tanto una respuesta cuantitativa, como magnitud, junto con una dirección, utilizamos los objetos matemáticos llamados vectores. ¹ Un vector se representa geométricamente como un segmento de línea dirigida donde la magnitud del vector se toma como la longitud del segmento de línea y la dirección se aclara con el uso de una flecha en un punto final del segmento. Al referirnos a vectores en este texto, adoptaremos ² la notación 'flecha', por lo que el símbolo$\vec{v}$ se lee como 'el vector$v^{\prime}$. A continuación se muestra un vector típico$\vec{v}$ con puntos finales$P$ (1, 2) y$Q$ (4, 6). El punto$P$ se llama el punto inicial o cola de$\vec{v}$ y el punto$Q$ se llama el punto terminal o cabeza de$\vec{v}$. Ya que podemos reconstruir$\vec{v}$ completamente desde$P$ y$Q$, escribimos$\vec{v}=\overrightarrow{P Q}$, donde es importante el orden de los puntos$P$ (punto inicial) y$Q$ (punto terminal). (Piensa en esto antes de seguir adelante.)

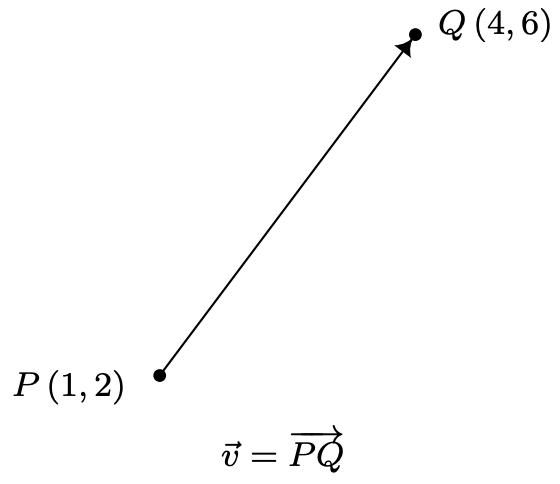
$Screen Shot 2022-06-09 a las 10.52.00 AM.png$

Si bien es cierto que$P$ y determinar$Q$ completamente$\vec{v}$, es importante señalar que dado que los vectores se definen en términos de sus dos características, magnitud y dirección, cualquier segmento de línea dirigido con la misma longitud y dirección que se considera que$\vec{v}$ es el mismo vector como$\vec{v}$, independientemente de su punto inicial. En el caso de nuestro vector$\vec{v}$ anterior, cualquier vector que mueva tres unidades hacia la derecha y cuatro hacia arriba ³ desde su punto inicial para llegar a su punto terminal se considera el mismo vector que$\vec{v}$. La notación que utilizamos para capturar esta idea es la forma componente del vector,$\vec{v}=\langle 3,4\rangle$, donde el primer número, 3, se llama el$x$ -componente de$\vec{v}$ y el segundo número, 4, se llama el$y$ -componente de$\vec{v}$. Si quisiéramos reconstruir$\vec{v}=\langle 3,4\rangle$ con punto inicial$P^{\prime}(-2,3)$, entonces encontraríamos el punto terminal de$\vec{v}$ sumando 3 a la$x$ coordenada -y sumando 4 a la$y$ coordenada -para obtener el punto terminal$Q^{\prime}(1,7)$, como se ve a continuación.

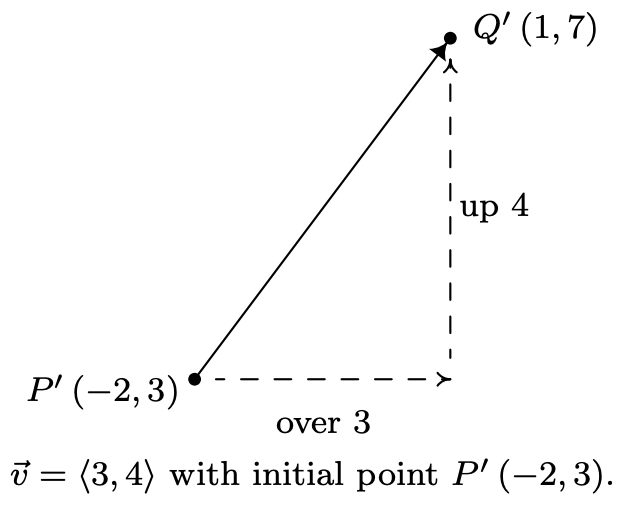
$Screen Shot 2022-06-09 en 5.33.36 PM.png$

La forma componente de un vector es lo que une estos objetos muy geométricos de nuevo al Álgebra y finalmente a la Trigonometría. Generalizamos nuestro ejemplo en nuestra definición a continuación.

Definición 11.5

Supongamos que$\vec{v}$ está representado por un segmento de línea dirigida con punto inicial$P\left(x_{0}, y_{0}\right)$ y punto terminal$Q\left(x_{1}, y_{1}\right)$. La forma componente de$\vec{v}$ viene dada por

\[\vec{v}=\overrightarrow{P Q}=\left\langle x_{1}-x_{0}, y_{1}-y_{0}\right\rangle\nonumber\]

Usando el lenguaje de componentes, tenemos que dos vectores son iguales si y solo si sus componentes correspondientes son iguales. Es decir,$\left\langle v_{1}, v_{2}\right\rangle=\left\langle v_{1}^{\prime}, v_{2}^{\prime}\right\rangle$ si y sólo si$v_{1}=v_{1}^{\prime}$ y$v_{2}=v_{2}^{\prime}$. (Una vez más, piense en esto antes de seguir leyendo.) Ahora nos pusimos a definir operaciones en vectores. Supongamos que se nos dan dos vectores$\vec{v}$ y$\vec{w}$. La suma, o vector resultante$\vec{v}+\vec{w}$ se obtiene de la siguiente manera. Primero, parcela$\vec{v}$. A continuación, trazar$\vec{w}$ para que su punto inicial sea el punto terminal de$\vec{v}$. Para trazar el vector$\vec{v}+\vec{w}$ comenzamos en el punto inicial de$\vec{v}$ y terminamos en el punto terminal de$\vec{w}$. Es útil pensar en el vector$\vec{v}+\vec{w}$ como el 'resultado neto' de moverse a lo largo y$\vec{v}$ luego moverse a lo largo$\vec{w}$.

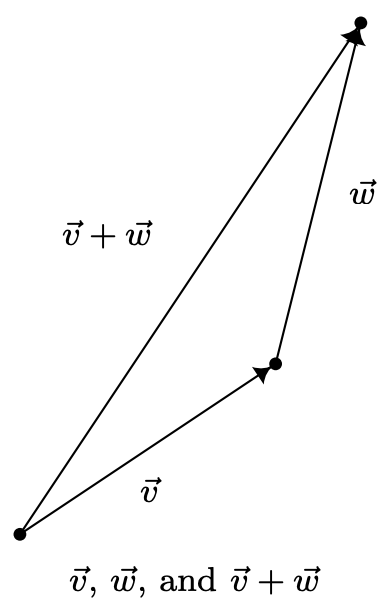
$Screen Shot 2022-06-09 en 5.46.10 PM.png$

Nuestro siguiente ejemplo hace un buen uso de los vectores resultantes y revisa los cojinetes y la Ley de Cosinos. ⁴

Ejemplo 11.8.1

Un avión sale de un aeropuerto con una velocidad aérea ⁵ de 175 millas por hora a una dirección de$\mathrm{N} 40^{\circ} \mathrm{E}$. Un viento de 35 millas por hora sopla a un rumbo de$\mathrm{S} 60^{\circ} \mathrm{E}$. Encuentra la verdadera velocidad del avión, redondeada a la milla por hora más cercana, y el rumbo verdadero del avión, redondeado al grado más cercano.

Solución

Tanto para el avión como para el viento, se nos dan sus velocidades y sus direcciones. La velocidad de acoplamiento (como magnitud) con dirección es el concepto de velocidad que hemos visto algunas veces antes en este libro de texto. ⁶ Dejamos$\vec{v}$ denotar la velocidad del avión y$\vec{w}$ denotar la velocidad del viento en el siguiente diagrama. La velocidad “verdadera” y rumbo se encuentra analizando el vector resultante,$\vec{v}+\vec{w}$. Del diagrama vectorial, obtenemos un triángulo, cuyas longitudes de lados son la magnitud de$\vec{v}$, que es 175, la magnitud de$\vec{w}$, que es 35, y la magnitud de$\vec{v}+\vec{w}$, que llamaremos$c$. A partir de la información de rodamiento dada, pasamos por la geometría habitual para determinar que el ángulo entre los lados de longitud 35 y 175 mide$100^{\circ}$.

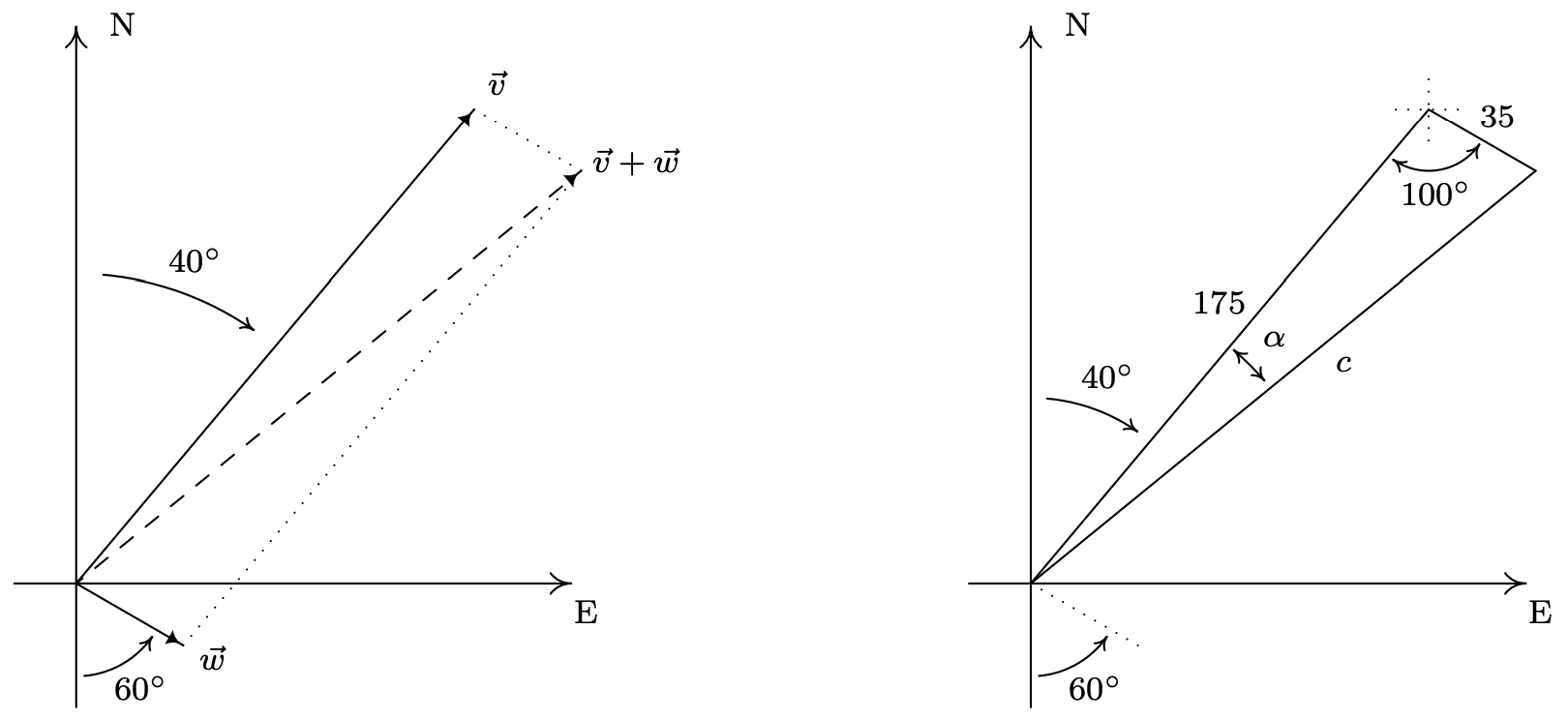
$Screen Shot 2022-06-09 en 5.56.34 PM.png$

De la Ley de Cosines, determinamos$c=\sqrt{31850-12250 \cos \left(100^{\circ}\right)} \approx 184$, lo que significa que la verdadera velocidad del avión es (aproximadamente) 184 millas por hora. Para determinar el verdadero rumbo del plano, necesitamos determinar el ángulo$\alpha$. Usando una vez más la Ley de los Cosinos, ⁷ nos encontramos$\cos (\alpha)=\frac{c^{2}+29400}{350 c}$ así que$\alpha \approx 11^{\circ}$. Dada la geometría de la situación, sumamos$\alpha$ a lo dado$40^{\circ}$ y encontramos el verdadero rumbo del plano para ser (aproximadamente)$\mathrm{N} 51^{\circ} \mathrm{E}$.

Nuestro siguiente paso es definir la adición de vectores por componentes para que coincidan con la acción geométrica. ⁸

Definición 11.6

Supongamos$\vec{v}=\left\langle v_{1}, v_{2}\right\rangle$ y$\vec{w}=\left\langle w_{1}, w_{2}\right\rangle$. El vector$\vec{v}+\vec{w}$ se define por

$\vec{v}+\vec{w}=\left\langle v_{1}+w_{1}, v_{2}+w_{2}\right\rangle$

Ejemplo 11.8.2

Vamos$\vec{v}=\langle 3,4\rangle$ y supongamos$\vec{w}=\overrightarrow{P Q}$ dónde$P(−3, 7)$ y$Q(−2, 5)$. Encuentra$\vec{v}+\vec{w}$ e interpreta esta suma geométricamente.

Solución

Antes podemos agregar los vectores usando la Definición 11.6, necesitamos escribir$\vec{w}$ en forma de componente. Usando la Definición 11.5, obtenemos$\vec{w}=\langle-2-(-3), 5-7\rangle=\langle 1,-2\rangle$. Así

\ [\ begin {alineado}
\ vec {v} +\ vec {w} &=\ langle 3,4\ rangle+\ langle 1, -2\ rangle\\
&=\ langle 3+1,4+ (-2)\ rangle\\
&=\ langle 4,2\ rangle
\ end {alineado}\ nonumber\]

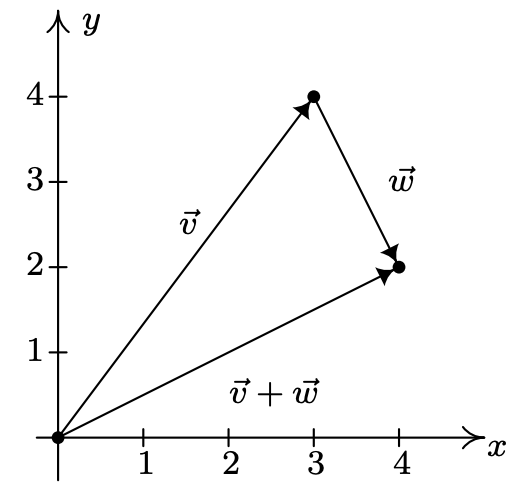
Para visualizar esta suma, dibujamos$\vec{v}$ con su punto inicial en (0, 0) (por conveniencia) para que su punto terminal sea (3, 4). A continuación, graficamos$\vec{w}$ con su punto inicial en (3, 4). Al mover uno a la derecha y dos hacia abajo, encontramos el punto terminal de$\vec{w}$ ser (4, 2). Vemos que el vector$\vec{v}+\vec{w}$ tiene punto inicial (0, 0) y punto terminal (4, 2) por lo que su forma componente es$\langle 4,2\rangle$, según se requiera.

$Screen Shot 2022-06-09 a las 6.17.22 PM.png$

Para que la adición de vectores disfrute de los mismos tipos de propiedades que la adición de números reales, es necesario ampliar nuestra definición de vectores para incluir un 'vector cero',$\overrightarrow{0}=\langle 0,0\rangle$. Geométricamente,$\overrightarrow{0}$ representa un punto, que podemos pensar como un segmento de línea dirigido con los mismos puntos inicial y terminal. El lector bien puede objetar la inclusión de$\overrightarrow{0}$, ya que después de todo, se supone que los vectores tienen tanto una magnitud (longitud) como una dirección. Si bien parece claro que la magnitud de$\overrightarrow{0}$ debería ser 0, no está claro cuál es su dirección. Como veremos, la dirección de$\overrightarrow{0}$ es de hecho indefinida, pero este pequeño hipo en el flujo natural de las cosas merece los beneficios que cosechamos al incluir$\overrightarrow{0}$ en nuestras discusiones. Tenemos el siguiente teorema.

Teorema 11.18. Propiedades de la adición de vectores

Propiedad Conmutativa: Para todos los vectores$\vec{v}$ y$\vec{w}, \vec{v}+\vec{w}=\vec{w}+\vec{v}$.
Propiedad Asociativa: Para todos los vectores$\vec{u}, \vec{v} \text { and } \vec{w},(\vec{u}+\vec{v})+\vec{w}=\vec{u}+(\vec{v}+\vec{w})$.
Propiedad de Identidad: El vector$\overrightarrow{0}$ actúa como la identidad aditiva para la adición del vector. Es decir, para todos los vectores$\vec{v}$,\[\vec{v}+\overrightarrow{0}=\overrightarrow{0}+\vec{v}=\vec{v}.\nonumber\]
Propiedad inversa: Cada vector$\vec{v}$ tiene una inversa aditiva única, denotada$-\vec{v}$. Es decir, por cada vector$\vec{v}$, hay un vector$-\vec{v}$ para que\[\vec{v}+(-\vec{v})=(-\vec{v})+\vec{v}=\overrightarrow{0}\nonumber\]

Las propiedades en el Teorema 11.18 se verifican fácilmente usando la definición de adición de vector. ⁹ Para la propiedad conmutativa, observamos que si$\vec{v}=\left\langle v_{1}, v_{2}\right\rangle$ y$\vec{w}=\left\langle w_{1}, w_{2}\right\rangle$ entonces

$\begin{aligned} \vec{v}+\vec{w} &=\left\langle v_{1}, v_{2}\right\rangle+\left\langle w_{1}, w_{2}\right\rangle \\ &=\left\langle v_{1}+w_{1}, v_{2}+w_{2}\right\rangle \\ &=\left\langle w_{1}+v_{1}, w_{2}+v_{2}\right\rangle \\ &=\vec{w}+\vec{v} \end{aligned}$

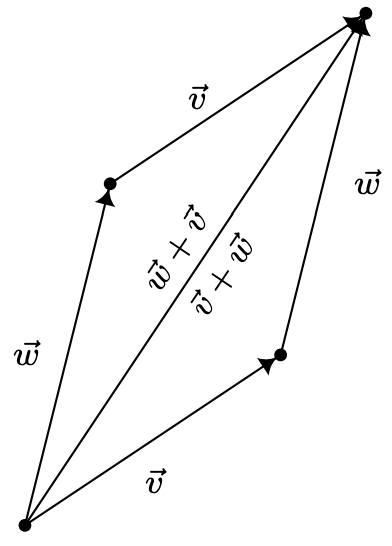
Geométricamente, podemos 'ver' la propiedad conmutativa al darnos cuenta de que las sumas$\vec{v}+\vec{w}$ y$\vec{w}+\vec{v}$ son la misma diagonal dirigida determinada por el paralelogramo de abajo.

Screen Shot 2022-06-09 a las 6.35.17 PM.png

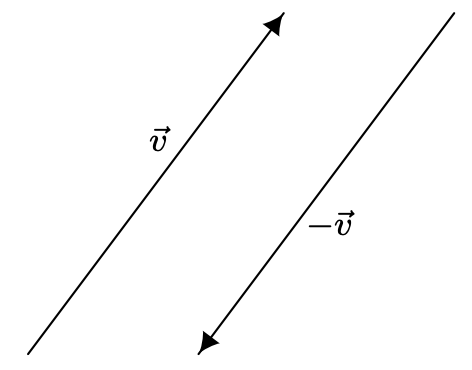
Las pruebas de las propiedades asociativas e identitarias proceden de manera similar, y se alienta al lector a verificarlas y proporcionar diagramas acompañantes. La existencia y singularidad del inverso aditivo es otra propiedad heredada de los números reales. Dado un vector$\vec{v}=\left\langle v_{1}, v_{2}\right\rangle$, supongamos que deseamos encontrar un vector$\vec{w}=\left\langle w_{1}, w_{2}\right\rangle$ para que$\vec{v}+\vec{w}=\overrightarrow{0}$. Por la definición de adición de vectores, tenemos$\left\langle v_{1}+w_{1}, v_{2}+w_{2}\right\rangle=\langle 0,0\rangle$, y por lo tanto,$v_{1}+w_{1}=0$ y$v_{2}+w_{2}=0$. Lo conseguimos$w_{1}=-v_{1}$ y$w_{2}=-v_{2}$ para eso$\vec{w}=\left\langle-v_{1},-v_{2}\right\rangle$. De ahí$\vec{v}$ que tenga una inversa aditiva, y además, es única y se puede obtener por la fórmula$-\vec{v}=\left\langle-v_{1},-v_{2}\right\rangle$. Geométricamente, los vectores$\vec{v}=\left\langle v_{1}, v_{2}\right\rangle$ y$-\vec{v}=\left\langle-v_{1},-v_{2}\right\rangle$ tienen la misma longitud, pero direcciones opuestas. Como resultado, al sumar los vectores geométricamente, la suma$\vec{v}+(-\vec{v})$ da como resultado comenzar en el punto inicial de$\vec{v}$ y terminar de nuevo en el punto inicial de$\vec{v}$, o en otras palabras, el resultado neto de mover$\vec{v}$ entonces no$-\vec{v}$ se mueve en absoluto.

$Screen Shot 2022-06-09 en 6.49.35 PM.png$

Usando la inversa aditiva de un vector, podemos definir la diferencia de dos vectores,$\vec{v}-\vec{w}=\vec{v}+(-\vec{w})$. Si$\vec{v}=\left\langle v_{1}, v_{2}\right\rangle$ y$\vec{w}=\left\langle w_{1}, w_{2}\right\rangle$ entonces

$\begin{aligned} \vec{v}-\vec{w} &=\vec{v}+(-\vec{w}) \\ &=\left\langle v_{1}, v_{2}\right\rangle+\left\langle-w_{1},-w_{2}\right\rangle \\ &=\left\langle v_{1}+\left(-w_{1}\right), v_{2}+\left(-w_{2}\right)\right\rangle \\ &=\left\langle v_{1}-w_{1}, v_{2}-w_{2}\right\rangle \end{aligned}$

En otras palabras, al igual que la suma de vectores, la resta vectorial funciona en cuanto a componentes. Para interpretar el vector$\vec{v}-\vec{w}$ geométricamente, observamos

$\begin{array}{l} \vec{w}+(\vec{v}-\vec{w}) &=\vec{w}+(\vec{v}+(-\vec{w})) & \text { Definition of Vector Subtraction } \\ &=\vec{w}+((-\vec{w})+\vec{v}) & \text { Commutativity of Vector Addition } \\ &=(\vec{w}+(-\vec{w}))+\vec{v} & \text { Associativity of Vector Addition } \\ &=\overrightarrow{0}+\vec{v} & \text { Definition of Additive Inverse } \\ &=\vec{v} & \text { Definition of Additive Identity } \end{array}$

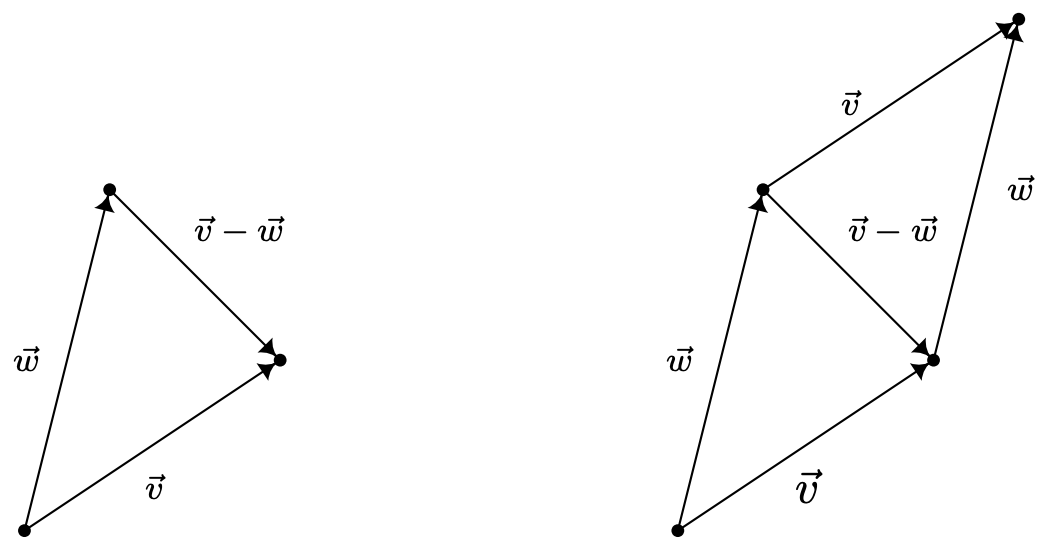
Esto significa que el 'resultado neto' de moverse a lo largo y$\vec{w}$ luego moverse a lo largo$\vec{v}-\vec{w}$ es solo$\vec{v}$ en sí mismo. A partir del diagrama siguiente, vemos que$\vec{v}-\vec{w}$ puede interpretarse como el vector cuyo punto inicial es el punto terminal de$\vec{w}$ y cuyo punto terminal es el punto terminal de$\vec{v}$ como se representa a continuación. También cabe mencionar que en el paralelogramo determinado por los vectores$\vec{v}$ y$\vec{w}$, el vector$\vec{v}-\vec{w}$ es una de las diagonales —siendo la otra$\vec{v}+\vec{w}$.

$Screen Shot 2022-06-09 en 7.05.49 PM.png$

A continuación, discutimos la multiplicación escalar —es decir, tomar un número real por un vector. Definimos la multiplicación escalar para vectores de la misma manera que la definimos para matrices en la Sección 8.3.

Definición 11.7

Si$k$ es un número real y$\vec{v}=\left\langle v_{1}, v_{2}\right\rangle$, definimos$k \vec{v}$ por\[k \vec{v}=k\left\langle v_{1}, v_{2}\right\rangle=\left\langle k v_{1}, k v_{2}\right\rangle\nonumber\]

La multiplicación escalar por$k$ vectores puede entenderse geométricamente como escalar el vector (if$k > 0$) o escalar el vector e invertir su dirección (if$k < 0$) como se demuestra a continuación.

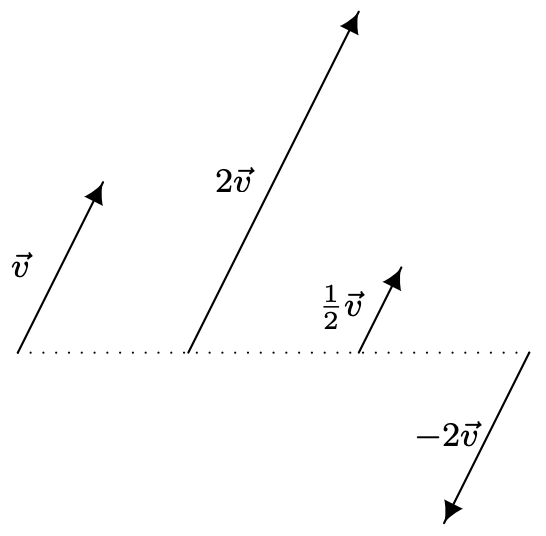
$Screen Shot 2022-06-09 a las 7.15.07 PM.png$

Obsérvese que, por definición 11.7,$(-1) \vec{v}=(-1)\left\langle v_{1}, v_{2}\right\rangle=\left\langle(-1) v_{1},(-1) v_{2}\right\rangle=\left\langle-v_{1},-v_{2}\right\rangle=-\vec{v}$. Esta y otras propiedades de la multiplicación escalar se resumen a continuación.

Teorema 11.19. Propiedades de la Multiplicación Escalar

Propiedad asociativa: Por cada vector$\vec{v}$ y escalares$k$ y$r$,$(k r) \vec{v}=k(r \vec{v})$.
Propiedad de Identidad: Para todos los vectores$\vec{v}, 1 \vec{v}=\vec{v}$.
Propiedad inversa aditiva: Para todos los vectores$\vec{v},-\vec{v}=(-1) \vec{v}$.
Propiedad Distributiva de Multiplicación Escalar sobre Adición Escalar: Para cada vector$\vec{v}$ y escalar$k$ y$r$,\[(k+r) \vec{v}=k \vec{v}+r \vec{v}\nonumber\]
Propiedad Distributiva de Multiplicación Escalar sobre Vector Adición: Para todos los vectores$\vec{v}$ y$\vec{w}$ y escalares$k$,\[k(\vec{v}+\vec{w})=k \vec{v}+k \vec{w}\nonumber\]
Zero Product Property: Si$\vec{v}$ es vector y$k$ es un escalar, entonces\[k \vec{v}=\overrightarrow{0} \quad \text { if and only if } \quad k=0 \quad \text { or } \quad \vec{v}=\overrightarrow{0}\nonumber\]

La prueba del Teorema 11.19, al igual que la prueba del Teorema 11.18, finalmente se reduce a la definición de multiplicación escalar y propiedades de los números reales. Por ejemplo, para probar la propiedad asociativa, dejamos$\vec{v}=\left\langle v_{1}, v_{2}\right\rangle$. Si$k$ y$r$ son escalares entonces

$\begin{aligned} (k r) \vec{v} &=(k r)\left\langle v_{1}, v_{2}\right\rangle & & \\ &=\left\langle(k r) v_{1},(k r) v_{2}\right\rangle & & \text { Definition of Scalar Multiplication } \\ &=\left\langle k\left(r v_{1}\right), k\left(r v_{2}\right)\right\rangle & & \text { Associative Property of Real Number Multiplication } \\ &=k\left\langle r v_{1}, r v_{2}\right\rangle & & \text { Definition of Scalar Multiplication } \\ &=k\left(r\left\langle v_{1}, v_{2}\right\rangle\right) & & \text { Definition of Scalar Multiplication } \\ &=k(r \vec{v}) & & \end{aligned}$

Las propiedades restantes se prueban de manera similar y se dejan como ejercicios.

Nuestro siguiente ejemplo demuestra cómo el Teorema 11.19 nos permite hacer el mismo tipo de manipulaciones algebraicas con vectores que lo hacemos con variables — a pesar de la multiplicación y división de vectores. Si la pedantería le parece familiar, debería. Este es el mismo tratamiento que dimos Ejemplo 8.3.1 en la Sección 8.3. Al igual que en ese ejemplo, detallamos la solución con insoportable detalle para animar al lector a pensar detenidamente por qué se justifica cada paso.

Ejemplo 11.8.3

Resolver$5 \vec{v}-2(\vec{v}+\langle 1,-2\rangle)=\overrightarrow{0} \text { for } \vec{v}$.

Solución

\ (\ begin {alineado}
5\ vec {v} -2 (\ vec {v} +\ langle 1, -2\ rangle) &=\ overrightarrow {0}\\
5\ vec {v} + (-1) [2 (\ vec {v} +\ langle 1, -2\ rangle)] &=\ overrightarrow {0}\\
5\ vec {vec {v} + [(-1) (2)] (\ vec {v} +\ langle 1, -2\ rangle) &=\ overrightarrow {0}\\
5\ vec {v} + (-2) ( \ vec {v} +\ langle 1, -2\ rangle) &=\ overrightarrow {0}\\
5\ vec {v} + [(-2)\ vec {v} + (-2)\ langle 1, -2\ rangle] &=\ overrightarrow {0}\\
5\ vec {v} + [(-2)\ vec {v} +\ angle (-2) (1), (-2) (-2)\ rangle] &=\ overrightarrow {0}\\
{[5\ vec {v} + (-2)\ vec {v}] +\ langle-2,4\ rangle} & ; =\ overrightarrow {0}\\
(5+ (-2))\ vec {v} +\ langle-2,4\ rangle &=\ overrightarrow {0}\\
3\ vec {v} +\ langle-2,4\ rangle &=\ overrightarrow {0}\
(3\ vec {v} +\ langle-2,4\ rangle) + (-\ langle-2,4\ rangle) &=\ overrightarrow {0} + (-\ langle-2,4\ rangle)\\
3\ vec {v} + [\ langle-2,4\ rangle+ (-\ langle-2,4\ rangle)] &=\ overrightarrow {0} + (-1)\ langle-2,4\ rangle\\
3\ vec {v} +\ overrightarrow {0} &=\ overrightarrow {0} +\ langle (-1) (-2), (-1) (4)\ rangle\\
3\ vec {v} &=\ langle 2, -4\ rangle\
\ frac {1} {3} (3\ vec {v}) &=\ frac {1} { 3} (\ langle 2, -4\ rangle)\\
{\ izquierda [\ izquierda (\ frac {1} {3}\ derecha) (3)\ derecha]\ vec {v}} &=\ izquierda\ langle\ izquierda (\ frac {1} {3}\ derecha) (2),\ izquierda (\ frac {1} {3}\ derecha) (-4\ derecha\ rangle\\
1\ vec {v} &=\ izquierda\ langle\ frac {2} {3}, -\ frac {4} {3}\ derecha\ rangle\
\ vec {v} &=\ izquierda\ langle\ frac {2} {3}, -\ frac {4} {3}\ derecha\ rangle
\ final {alineado}\)

Se dice que un vector cuyo punto inicial es (0, 0) está en posición estándar. Si$\vec{v}=\left\langle v_{1}, v_{2}\right\rangle$ se traza en posición estándar, entonces su punto terminal es necesario$\left(v_{1}, v_{2}\right)$. (Una vez más, piense en esto antes de seguir leyendo.)

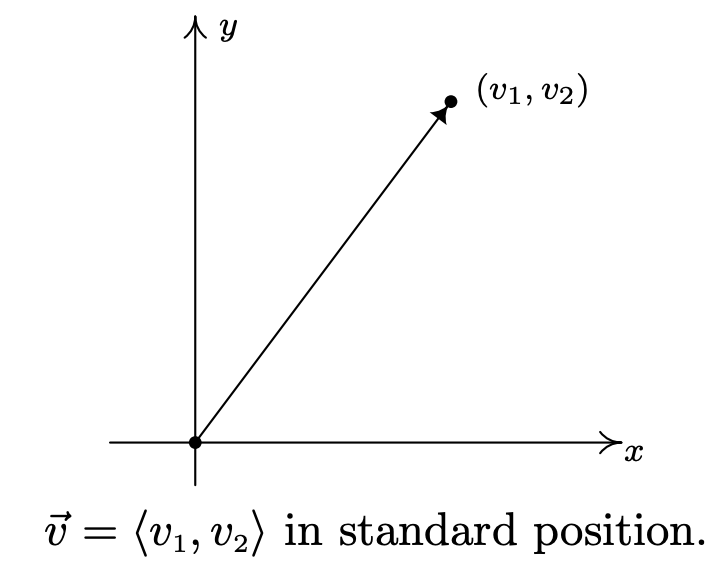
$Screen Shot 2022-06-11 a las 12.30.22 AM.png$

Trazar un vector en posición estándar nos permite cuantificar más fácilmente los conceptos de magnitud y dirección del vector. Podemos convertir el punto$\left(v_{1}, v_{2}\right)$ en coordenadas rectangulares a un par$(r, \theta)$ en coordenadas polares donde$r \geq 0$. La magnitud de$\vec{v}$, que dijimos antes era la longitud del segmento de línea dirigida, es$r=\sqrt{v_{1}^{2}+v_{2}^{2}}$ y se denota por$\|\vec{v}\|$. De la Sección 11.4, sabemos$v_{1}=r \cos (\theta)=\|\vec{v}\| \cos (\theta)$ y$v_{2}=r \sin (\theta)=\|\vec{v}\| \sin (\theta)$. De la definición de multiplicación escalar e igualdad vectorial, obtenemos

$\begin{aligned} \vec{v} &=\left\langle v_{1}, v_{2}\right\rangle \\ &=\langle\|\vec{v}\| \cos (\theta),\|\vec{v}\| \sin (\theta)\rangle \\ &=\|\vec{v}\|\langle\cos (\theta), \sin (\theta)\rangle \end{aligned}$

Esto motiva la siguiente definición.

Definición 11.8

Supongamos que$\vec{v}$ es un vector con forma de componente$\vec{v}=\left\langle v_{1}, v_{2}\right\rangle$. Dejar$(r, \theta)$ ser una representación polar del punto con coordenadas rectangulares$\left(v_{1}, v_{2}\right)$ con$r \geq 0$.

La magnitud de$\vec{v}$, denotada$\|\vec{v}\|$, viene dada por$\|\vec{v}\|=r=\sqrt{v_{1}^{2}+v_{2}^{2}}$
Si$\vec{v} \neq \overrightarrow{0}$, la dirección (vector) de$\vec{v}$, denotada$\hat{v}$ viene dada por$\hat{v}=\langle\cos (\theta), \sin (\theta)\rangle$

Tomados en conjunto, obtenemos$\vec{v}=\langle\|\vec{v}\| \cos (\theta),\|\vec{v}\| \sin (\theta)\rangle$.

Algunas observaciones están en orden. Primero, observamos que si$\vec{v} \neq 0$ entonces, aunque hay infinitamente muchos ángulos$\theta$ que satisfacen la Definición 11.8, la estipulación$r > 0$ significa que todos los ángulos son coterminales. De ahí que si$\theta$ y$\theta^{\prime}$ ambos satisfacen las condiciones de la Definición 11.8, entonces$\cos (\theta)=\cos \left(\theta^{\prime}\right)$ y$\sin (\theta)=\sin \left(\theta^{\prime}\right)$, y como tal,$\langle\cos (\theta), \sin (\theta)\rangle=\left\langle\cos \left(\theta^{\prime}\right), \sin \left(\theta^{\prime}\right)\right\rangle$ hacer$\hat{v}$ está bien definido. ¹⁰ Si$\vec{v}=\overrightarrow{0}$, entonces$\vec{v}=\langle 0,0\rangle$, y sabemos por la Sección 11.4 que$(0, \theta)$ es una representación polar para el origen para cualquier ángulo$\theta$. Por ello,$\hat{0}$ es indefinido. El siguiente teorema resume los hechos importantes sobre la magnitud y dirección de un vector.

Teorema 11.20. Propiedades de Magnitud y Dirección

Supongamos que$\vec{v}$ es un vector.

$\|\vec{v}\| \geq 0$y$\|\vec{v}\|=0$ si y solo si$\vec{v}=\overrightarrow{0}$
Para todos los escalares$k$,$\|k \vec{v}\|=|k|\|\vec{v}\|$.
Si$\vec{v} \neq \overrightarrow{0}$ entonces$\vec{v}=\|\vec{v}\| \hat{v}$, así que$\hat{v}=\left(\frac{1}{\|\vec{v}\|}\right) \vec{v}$.

El comprobante del primer inmueble en el Teorema 11.20 es consecuencia directa de la definición de$\|\vec{v}\|$. Si$\vec{v}=\left\langle v_{1}, v_{2}\right\rangle$, entonces$\|\vec{v}\|=\sqrt{v_{1}^{2}+v_{2}^{2}}$ que es por definición mayor o igual a 0. Además,$\sqrt{v_{1}^{2}+v_{2}^{2}}=0$ si y sólo de$v_{1}^{2}+v_{2}^{2}=0$ si y sólo si$v_{1}=v_{2}=0$. De ahí,$\|\vec{v}\|=0$ si y sólo si$\vec{v}=\langle 0,0\rangle=\overrightarrow{0}$, según se requiera.

La segunda propiedad es el resultado de la definición de magnitud y multiplicación escalar junto con una propiedad de radicales. Si$\vec{v}=\left\langle v_{1}, v_{2}\right\rangle$ y$k$ es un escalar entonces

$\begin{aligned} \|k \vec{v}\| &=\left\|k\left\langle v_{1}, v_{2}\right\rangle\right\| & & \\ &=\left\|\left\langle k v_{1}, k v_{2}\right\rangle\right\| & & \text { Definition of scalar multiplication } \\ &=\sqrt{\left(k v_{1}\right)^{2}+\left(k v_{2}\right)^{2}} & & \text { Definition of magnitude } \\ &=\sqrt{k^{2} v_{1}^{2}+k^{2} v_{2}^{2}} & & \\ &=\sqrt{k^{2}\left(v_{1}^{2}+v_{2}^{2}\right)} & & \\ &=\sqrt{k^{2}} \sqrt{v_{1}^{2}+v_{2}^{2}} & & \text { Product Rule for Radicals } \\ &=|k| \sqrt{v_{1}^{2}+v_{2}^{2}} & & \text { Since } \sqrt{k^{2}}=|k| \\ &=|k|\|\vec{v}\| & & \end{aligned}$

La ecuación$\vec{v}=\|\vec{v}\| \hat{v}$ en el Teorema 11.20 es consecuencia de las definiciones de$\|\vec{v}\|$$\hat{v}$ y se elaboró en la discusión justo antes de la Definición 11.8 en la página 1020. En palabras, la ecuación$\vec{v}=\|\vec{v}\| \hat{v}$ dice que cualquier vector dado es producto de su magnitud y su dirección —un concepto importante a tener en cuenta a la hora de estudiar y utilizar vectores. La ecuación$\hat{v}=\left(\frac{1}{\|\vec{v}\|}\right) \vec{v}$ es el resultado de resolver$\vec{v}=\|\vec{v}\| \hat{v}$ para$\hat{v}$ multiplicando ¹¹ ambos lados de la ecuación por$\frac{1}{\|\vec{v}\|}$ y usando las propiedades del Teorema 11.19. Estamos atrasados por un ejemplo.

Ejemplo 11.8.4

Encuentra la forma componente del vector$\vec{v}$ con$\|\vec{v}\|=5$ para que cuando$\vec{v}$ se traza en posición estándar, se encuentre en el Cuadrante II y forme un$60^{\circ}$ ángulo ¹² con el eje x negativo.
Para$\vec{v}=\langle 3,-3 \sqrt{3}\rangle$, encontrar$\|\vec{v}\|$ y$\theta$,$0 \leq \theta<2 \pi$ para que$\vec{v}=\|\vec{v}\|\langle\cos (\theta), \sin (\theta)\rangle$.
Para los vectores$\vec{v}=\langle 3,4\rangle$ y$\vec{w}=\langle 1,-2\rangle$, encuentra lo siguiente.
1. $\hat{v}$
2. $\|\vec{v}\|-2\|\vec{w}\|$
3. $\|\vec{v}-2 \vec{w}\|$
4. $\|\hat{w}\|$

Solución

Se nos dice eso$\|\vec{v}\|=5$ y se nos da información sobre su dirección, por lo que podemos usar la fórmula$\vec{v}=\|\vec{v}\| \hat{v}$ para obtener la forma componente de$\vec{v}$. Para determinar$\hat{v}$, apelamos a la Definición 11.8. Se nos dice que$\vec{v}$ se encuentra en el Cuadrante II y hace un$60^{\circ}$ ángulo con el$x$ eje negativo, por lo que la forma polar del punto terminal de$\vec{v}$, cuando se traza en posición estándar es$\left(5,120^{\circ}\right)$. (Consulte el diagrama a continuación.) Así$\hat{v}=\left\langle\cos \left(120^{\circ}\right), \sin \left(120^{\circ}\right)\right\rangle=\left\langle-\frac{1}{2}, \frac{\sqrt{3}}{2}\right\rangle, \text { so } \vec{v}=\|\vec{v}\| \hat{v}=5\left\langle-\frac{1}{2}, \frac{\sqrt{3}}{2}\right\rangle=\left\langle-\frac{5}{2}, \frac{5 \sqrt{3}}{2}\right\rangle$.
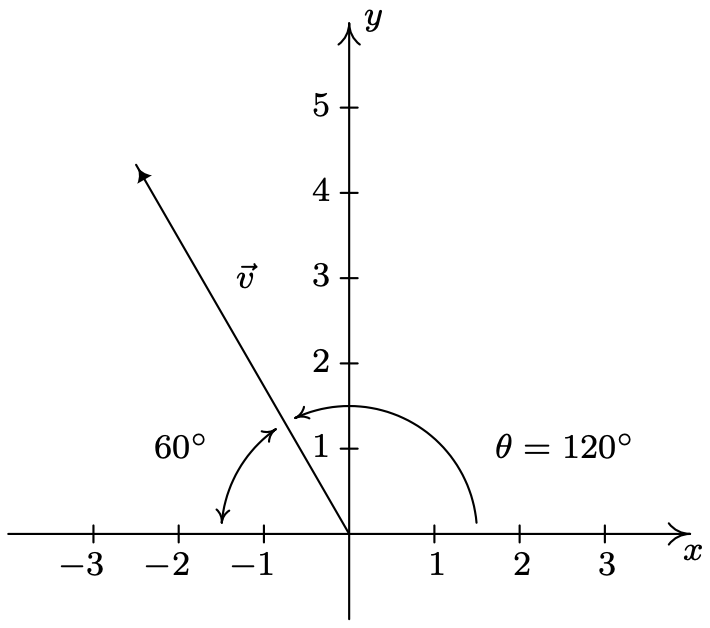
$Screen Shot 2022-06-11 en 1.52.19 AM.png$
Para$\vec{v}=\langle 3,-3 \sqrt{3}\rangle$, obtenemos$\|\vec{v}\|=\sqrt{(3)^{2}+(-3 \sqrt{3})^{2}}=6$. A la luz de la Definición 11.8,$\theta$ podemos encontrar el que buscamos convirtiendo el punto con coordenadas$(3,-3 \sqrt{3})$ rectangulares en forma polar$(r, \theta)$ donde$r=\|\vec{v}\|>0$. De la Sección 11.4, tenemos$\tan (\theta)=\frac{-3 \sqrt{3}}{3}=-\sqrt{3}$. Ya que$(3,-3 \sqrt{3})$ es un punto en el Cuadrante IV,$\theta$ es un ángulo del Cuadrante IV. De ahí que escojamos$\theta=\frac{5 \pi}{3}$. Podemos verificar nuestra respuesta verificando$\vec{v}=\langle 3,-3 \sqrt{3}\rangle=6\left\langle\cos \left(\frac{5 \pi}{3}\right), \sin \left(\frac{5 \pi}{3}\right)\right\rangle$.
1. Como se nos da la forma componente de$\vec{v}$, usaremos la fórmula$\hat{v}=\left(\frac{1}{\|\vec{v}\|}\right) \vec{v}$. Para$\vec{v}=\langle 3,4\rangle$, tenemos$\|\vec{v}\|=\sqrt{3^{2}+4^{2}}=\sqrt{25}=5$. De ahí,$\hat{v}=\frac{1}{5}\langle 3,4\rangle=\left\langle\frac{3}{5}, \frac{4}{5}\right\rangle$.
2. Sabemos por nuestro trabajo anterior que$\|\vec{v}\|=5$, así que para encontrar$\|\vec{v}\|-2\|\vec{w}\|$, sólo necesitamos encontrar$\|\vec{w}\|$. Ya que$\vec{w}=\langle 1,-2\rangle$, obtenemos$\|\vec{w}\|=\sqrt{1^{2}+(-2)^{2}}=\sqrt{5}$. De ahí,$\|\vec{v}\|-2\|\vec{w}\|=5-2 \sqrt{5}$.
3. En la expresión$\|\vec{v}-2 \vec{w}\|$, observe que la aritmética sobre los vectores viene primero, luego la magnitud. De ahí que nuestro primer paso sea encontrar la forma componente del vector$\vec{v}-2 \vec{w}$. Obtenemos$\vec{v}-2 \vec{w}=\langle 3,4\rangle-2\langle 1,-2\rangle=\langle 1,8\rangle$. De ahí,$\|\vec{v}-2 \vec{w}\|=\|\langle 1,8\rangle\|=\sqrt{1^{2}+8^{2}}=\sqrt{65}$.
4. Para encontrar$\|\hat{w}\|$, primero necesitamos$\hat{w}$. Usando la fórmula$\hat{w}=\left(\frac{1}{\|\vec{w}\|}\right) \vec{w}$ junto con$\|\vec{w}\|=\sqrt{5}$, que encontramos la en el problema anterior, obtenemos$\hat{w}=\frac{1}{\sqrt{5}}\langle 1,-2\rangle=\left\langle\frac{1}{\sqrt{5}},-\frac{2}{\sqrt{5}}\right\rangle=\left\langle\frac{\sqrt{5}}{5},-\frac{2 \sqrt{5}}{5}\right\rangle$. De ahí,$\|\hat{w}\|=\sqrt{\left(\frac{\sqrt{5}}{5}\right)^{2}+\left(-\frac{2 \sqrt{5}}{5}\right)^{2}}=\sqrt{\frac{5}{25}+\frac{20}{25}}=\sqrt{1}=1$.

El proceso ejemplificado por el número 1 en el Ejemplo 11.8.4 anterior mediante el cual tomamos información sobre la magnitud y dirección de un vector y encontramos la forma componente de un vector se llama resolver un vector en sus componentes. Como aplicación de este proceso, revisamos el Ejemplo 11.8.1 a continuación.

Ejemplo 11.8.5

Un avión sale de un aeropuerto con una velocidad aérea de 175 millas por hora con rumbo$\mathrm{N} 40^{\circ} \mathrm{E}$. Un viento de 35 millas por hora sopla a un rumbo de$\mathrm{S} 60^{\circ} \mathrm{E}$. Encuentra la verdadera velocidad del avión, redondeada a la milla por hora más cercana, y el rumbo verdadero del avión, redondeado al grado más cercano.

Solución

Procedemos como hicimos en el Ejemplo 11.8.1 y dejamos$\vec{v}$ denotar la velocidad del avión y$\vec{w}$ denotar la velocidad del viento, y nos fijamos sobre la determinación$\vec{v}+\vec{w}$. Si consideramos que el aeropuerto está en el origen, el$y$ eje positivo que actúa como debido norte y el$x$ eje positivo que actúa como debido este, vemos que los vectores$\vec{v}$ y$\vec{w}$ están en posición estándar y sus direcciones corresponden a los ángulos$50^{\circ}$ y$-30^{\circ}$, respectivamente. Por lo tanto, la forma componente de$\vec{v}=175\left\langle\cos \left(50^{\circ}\right), \sin \left(50^{\circ}\right)\right\rangle=\left\langle 175 \cos \left(50^{\circ}\right), 175 \sin \left(50^{\circ}\right)\right\rangle$ y la forma componente de$\vec{w}=\left\langle 35 \cos \left(-30^{\circ}\right), 35 \sin \left(-30^{\circ}\right)\right\rangle$. Como no tenemos una manera conveniente de expresar los valores exactos de coseno y seno de$50^{\circ}$, dejamos ambos vectores en términos de cosenos y senos. ¹³ Añadiendo los componentes correspondientes, encontramos el vector resultante$\vec{v}+\vec{w}=\left\langle 175 \cos \left(50^{\circ}\right)+35 \cos \left(-30^{\circ}\right), 175 \sin \left(50^{\circ}\right)+35 \sin \left(-30^{\circ}\right)\right\rangle$. Para encontrar la velocidad 'verdadera' del avión, calculamos la magnitud de este vector resultante\[\|\vec{v}+\vec{w}\|=\sqrt{\left(175 \cos \left(50^{\circ}\right)+35 \cos \left(-30^{\circ}\right)\right)^{2}+\left(175 \sin \left(50^{\circ}\right)+35 \sin \left(-30^{\circ}\right)\right)^{2}} \approx 184\nonumber\] Por lo tanto, la velocidad 'verdadera' del avión es de aproximadamente 184 millas por hora. Para encontrar el verdadero rumbo, necesitamos encontrar el ángulo$\theta$ que corresponde a la forma polar$(r, \theta), r>0$, del punto$(x, y)=\left(175 \cos \left(50^{\circ}\right)+35 \cos \left(-30^{\circ}\right), 175 \sin \left(50^{\circ}\right)+35 \sin \left(-30^{\circ}\right)\right)$. Dado que ambas coordenadas son positivas, ¹⁴ sabemos que$\theta$ es un ángulo del Cuadrante I, como se muestra a continuación. Además,\[\tan (\theta)=\frac{y}{x}=\frac{175 \sin \left(50^{\circ}\right)+35 \sin \left(-30^{\circ}\right)}{175 \cos \left(50^{\circ}\right)+35 \cos \left(-30^{\circ}\right)},\nonumber\] por lo que usando la función arctangente, obtenemos$\theta \approx 39^{\circ}$. Dado que, para los fines de rodamiento, necesitamos el ángulo entre$\vec{v}+\vec{w}$ y el$y$ eje positivo, tomamos el complemento$\theta$ y encontramos que el rumbo 'verdadero' del plano sea aproximadamente$\mathrm{N} 51^{\circ} \mathrm{E}$.

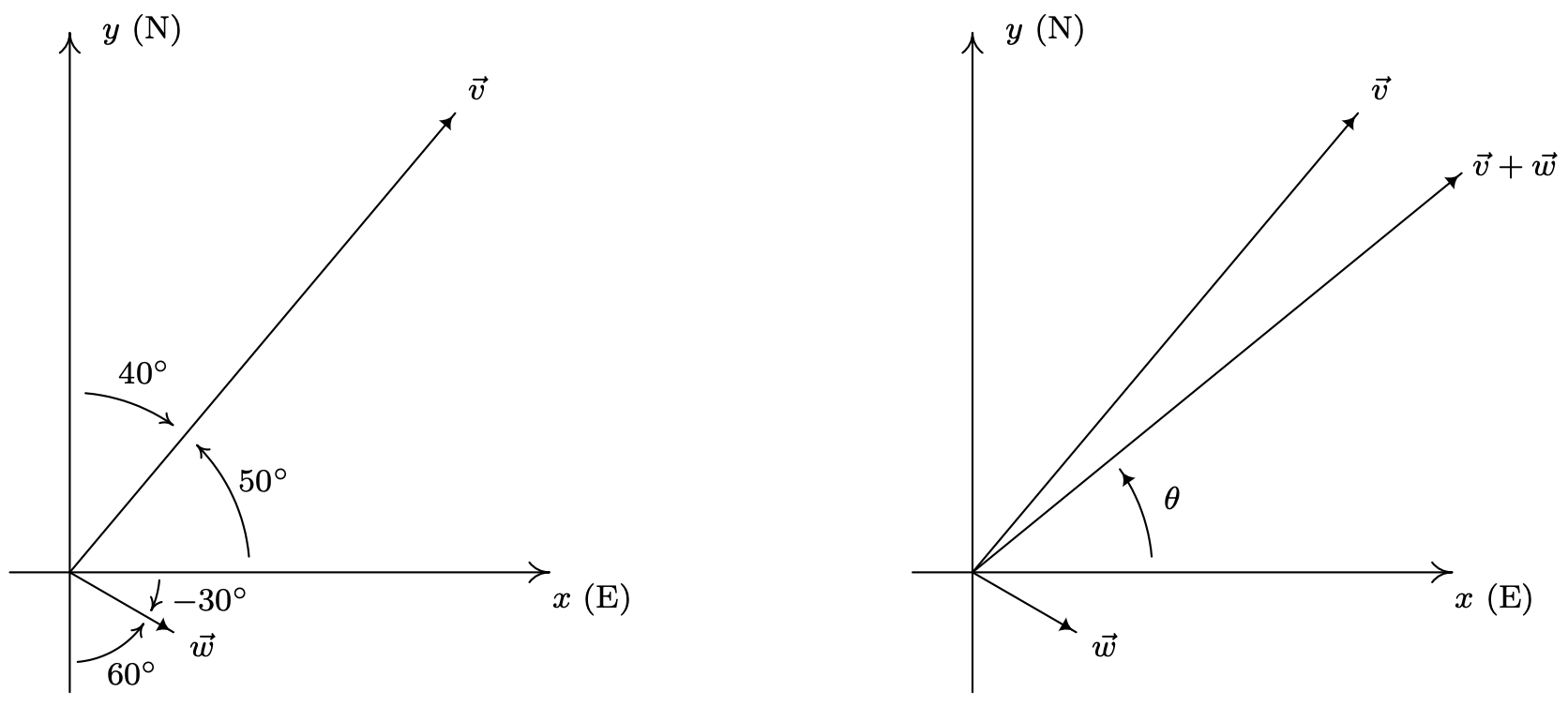
$Screen Shot 2022-06-11 en 3.10.05 AM.png$

En la parte 3d del Ejemplo 11.8.4, lo vimos$\|\hat{w}\|=1$. Los vectores con longitud 1 tienen un nombre especial y son importantes en nuestro estudio posterior de vectores.

Definición 11.9

Vectores de Unidad: Let$\vec{v}$ Ser un vector. Si$\|\vec{v}\|=1$, decimos que$\vec{v}$ es un vector unitario.

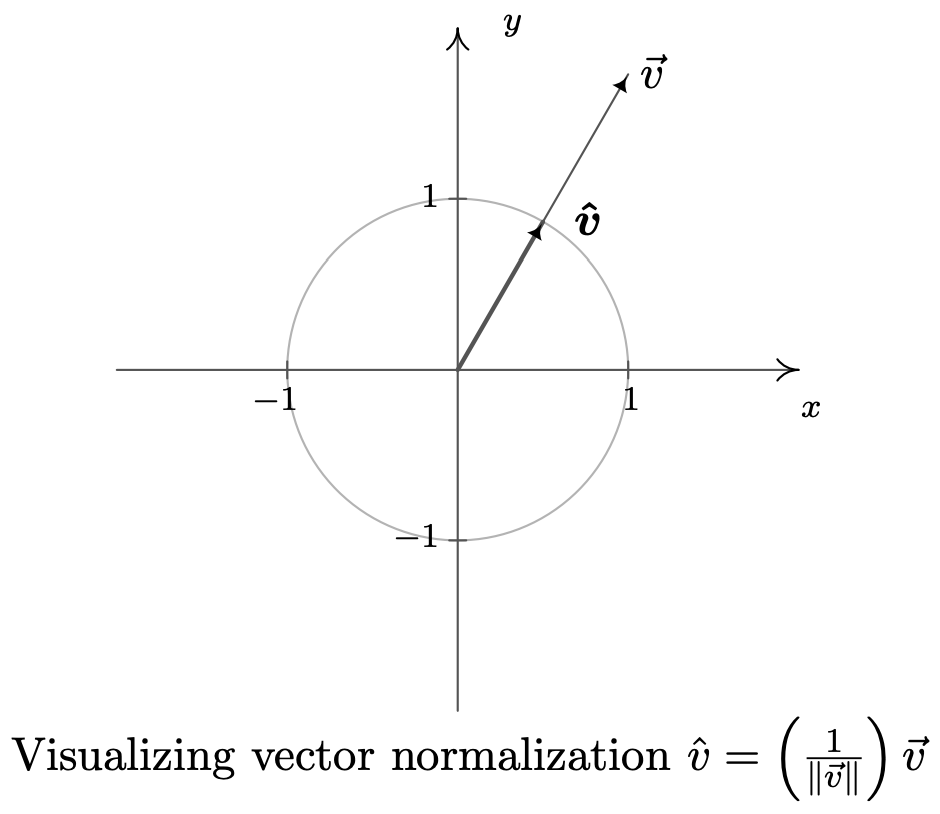
Si$\vec{v}$ es un vector unitario, entonces necesariamente,$\vec{v}=\|\vec{v}\| \hat{v}=1 \cdot \hat{v}=\hat{v}$. Por el contrario, lo dejamos como un ejercicio ¹⁵ para mostrar que$\hat{v}=\left(\frac{1}{\|\vec{v}\|}\right) \vec{v}$ es un vector unitario para cualquier vector distinto de cero$\vec{v}$. En la práctica, si$\vec{v}$ es un vector unitario lo escribimos en$\vec{v}$ contraposición a$\vec{v}$ porque hemos reservado la notación '\' para vectores unitarios. El proceso de multiplicar un vector distinto de cero por el factor$\frac{1}{\|\vec{v}\|}$ para producir un vector unitario se llama 'normalizar el vector', y el vector resultante$\vec{v}$ se llama 'vector unitario en la dirección de$\vec{v^{\prime}}$. Los puntos terminales de los vectores unitarios, cuando se trazan en posición estándar, se encuentran en el Círculo de Unidad. (Deberías tomarte el tiempo para mostrar esto.) Como resultado, visualizamos la normalización de un vector distinto de cero$\vec{v}$ como encogiendo ¹⁶ su punto terminal, cuando se traza en posición estándar, de vuelta al Círculo de Unidad.

$Screen Shot 2022-06-11 en 3.25.43 AM.png$

De todos los vectores unitarios, dos merecen mención especial.

Definición 11.10. Los vectores de la unidad principal

El vector$\hat{\imath}$ se define por$\hat{\imath}=\langle 1,0\rangle$
El vector$\hat{\jmath}$ se define por$\hat{\imath}=\langle 0,1\rangle$

Podemos pensar que el vector$\hat{\imath}$ representa la$x$ dirección positiva, mientras que$\hat{\jmath}$ representa la$y$ dirección positiva. Tenemos el siguiente teorema de 'descomposición'. ¹⁷

Teorema 11.21. Teorema de descomposición de vectores principales

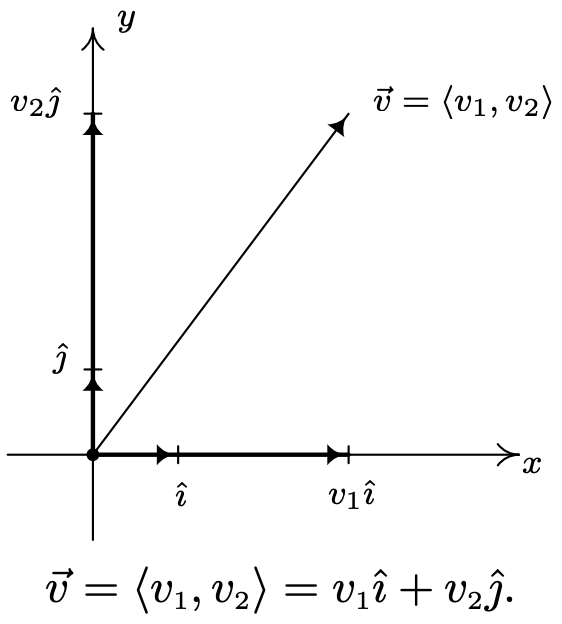
Let$\vec{v}$ Ser un vector con forma de componente$\vec{v}=\left\langle v_{1}, v_{2}\right\rangle$. Entonces$\vec{v}=v_{1} \hat{\imath}+v_{2} \hat{\jmath}$.

La prueba del Teorema 11.21 es sencilla. Desde$\hat{\imath}=\langle 1,0\rangle$ y$\hat{\jmath}=\langle 0,1\rangle$, tenemos a partir de la definición de multiplicación escalar y adición vectorial que

$v_{1} \hat{\imath}+v_{2} \hat{\jmath}=v_{1}\langle 1,0\rangle+v_{2}\langle 0,1\rangle=\left\langle v_{1}, 0\right\rangle+\left\langle 0, v_{2}\right\rangle=\left\langle v_{1}, v_{2}\right\rangle=\vec{v}$

Geométricamente, la situación se ve así:

$Screen Shot 2022-06-11 en 3.40.06 AM.png$

Concluimos esta sección con un ejemplo clásico que demuestra cómo se utilizan los vectores para modelar fuerzas. Una 'fuerza' se define como un 'empuje' o un 'tirón'. La intensidad del empuje o tracción es la magnitud de la fuerza, y se mide en Netwons (N) en el sistema SI o libras (lbs.) en el sistema inglés. ¹⁸ El siguiente ejemplo utiliza todos los conceptos de esta sección, y debe estudiarse con gran detalle.

Ejemplo 11.8.6

Un altavoz de 50 libras está suspendido del techo por dos tirantes de soporte. Si uno de ellos hace un$60^{\circ}$ ángulo con el techo y el otro hace un$30^{\circ}$ ángulo con el techo, ¿cuáles son las tensiones en cada uno de los soportes?

Solución

Representamos el problema esquemáticamente a continuación y luego proporcionamos el diagrama vectorial correspondiente.

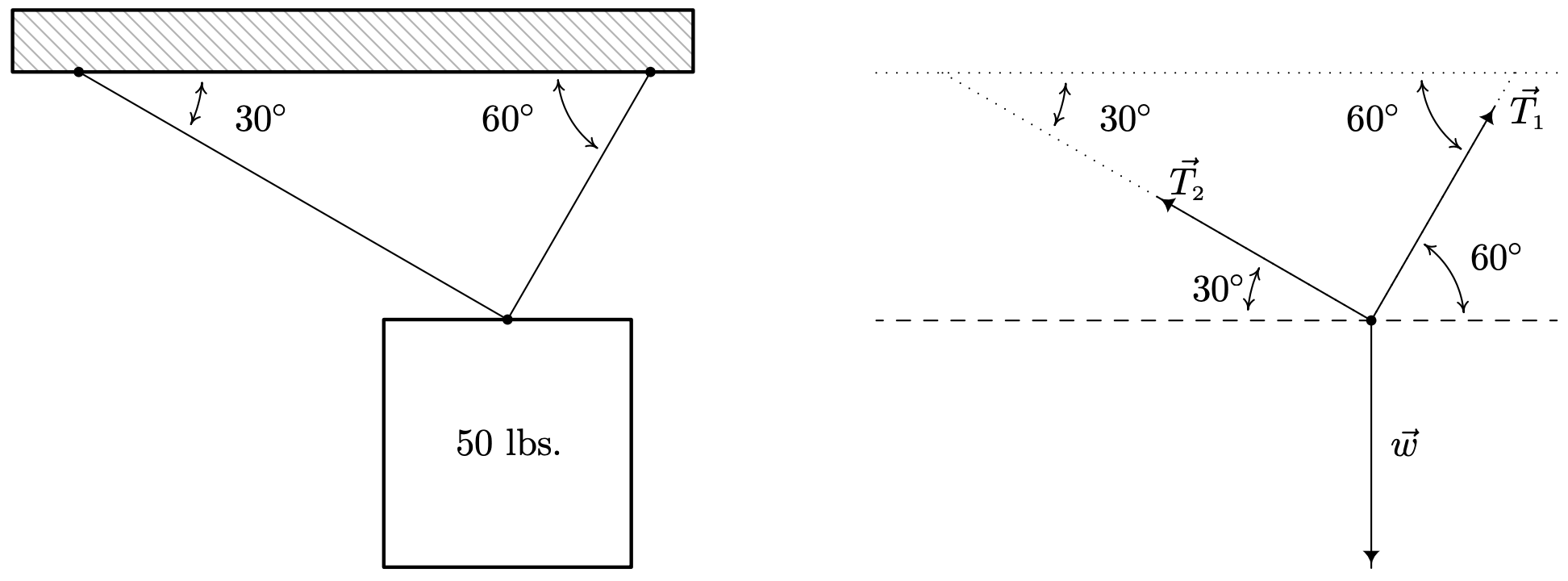
$Screen Shot 2022-06-11 en 3.42.05 AM.png$

Tenemos tres fuerzas que actúan sobre el altavoz: el peso del altavoz, al que llamaremos$\vec{w}$, tirando del altavoz directamente hacia abajo, y las fuerzas sobre las varillas de soporte, a las que llamaremos$\vec{T}_{1}$ y$\vec{T}_{2}$ (para 'tensiones') actuando hacia arriba en ángulos$60^{\circ}$ y$30^{\circ}$, respectivamente. Estamos buscando las tensiones sobre el soporte, que son las magnitudes$\left\|\vec{T}_{1}\right\|$ y$\left\|\vec{T}_{2}\right\|$. Para que el altavoz permanezca estacionario, ¹⁹ requerimos$\vec{w}+\overrightarrow{T_{1}}+\overrightarrow{T_{2}}=\overrightarrow{0}$. Viendo el punto inicial común de estos vectores como el origen y la línea discontinua como el$x$ eje -eje, utilizamos el Teorema 11.20 para obtener representaciones de componentes para los tres vectores involucrados. Podemos modelar el peso del altavoz como un vector apuntando directamente hacia abajo con una magnitud de 50 libras. Es decir,$\|\vec{w}\|=50$ y$\hat{w}=-\hat{\jmath}=\langle 0,-1\rangle$. De ahí,$\vec{w}=50\langle 0,-1\rangle=\langle 0,-50\rangle$. Para la fuerza en el primer soporte, obtenemos\ [\ begin {aligned}
\ vec {T} _ {1} &=\ left\ |\ vec {T} _ {1}\ right\ |\ left\ langle\ cos\ left (60^ {\ circ}\ right),\ sin\ left (60^ {\ circ}\ right)\ right\ rangle\\ &= left\\ langle\ frac {\ izquierda\ |\ vec {T} _ {1}\ derecha\ |} {2},\ frac {\ izquierda\ |\ vec {T} _ {1}\ derecha\ |\ sqrt {3}} {2}\ right\ rangle\ end {aligned}\ nonumber\] Para el segundo soporte, observamos que el ángulo$30^{\circ}$ se mide desde el$x$ eje negativo, por lo que el ángulo necesario para escribir$\overrightarrow{T_{2}}$ en forma de componente es$150^{\circ}$. De ahí\ [\ begin {alineado}\ vec {T} _ {2} &=\ izquierda\ |\ vec {T} _ {2}\ derecha\ |\ izquierda\ langle\ cos\ izquierda (150^ {\ circ}\ derecha),\ sin\ izquierda (150^ {\ circ}\ derecha)\ derecha\ rangle\\ &=\ izquierda\ langle-\ frac\ izquierda\ |\ vec {T} _ {2}\ derecha\ |\ sqrt {3}} {2},\ frac {\ izquierda\ |\ vec {T} _ {2}\ derecha\ |} {2}\ derecha\ rangle
\ end {alineada}\] La requisito nos$\vec{w}+\vec{T}_{1}+\vec{T}_{2}=\overrightarrow{0}$ da esta ecuación vectorial. \ [\ begin {array} {rrl}
&\ vec {w} +\ vec {T} _ {1} +\ vec {T} _ {2} &=&\ overrightarrow {0}\\ &\ langle 0, -50\ rangle+\ izquierda\ langle\ frac {\ izquierda\ |\ vec {T} _ {1}\ derecha\ |} 2},\ frac {\ izquierda\ |\ vec {T} _ {1}\ derecha\ |\ sqrt {3}} {2}\ derecha\ rangle+\ izquierda\ langle-\ frac {\ izquierda\ |\ vec {T} _ {2}\ derecha\ |\ sqrt {3}} {2},\ frac {\ izquierda\ |\ vec {T} _ {2}\ derecha\ |} {2}\ derecha\ rangle&=&\ langle 0,0\ rangle\\ &\ izquierda\ langle\ frac {\ izquierda\ |\ vec {T} _ {1}\ derecha\ |} {2} -\ frac {\ izquierda\ |\ vec {T} _ {2}\ derecha\ |\ sqrt {3}} {2},\ frac {\ izquierda\ |\ vec {T} _ {1}\ derecha\ |\ sqrt {3}} {2} +\ frac {\ izquierda\ |\ vec {T} _ {2}\ derecha\ |} {2} -50\ derecha\ rangle&=&\ langle 0,0\ rangle\ end {array}\ nonumber\] Igualando los componentes correspondientes de los vectores en cada lado, obtenemos un sistema de ecuaciones lineales en las variables$\left\|\overrightarrow{T_{1}}\right\|$ y$\left\|\vec{T}_{2}\right\|$. \[\left\{\begin{array}{l} (E 1) \quad \frac{\left\|\vec{T}_{1}\right\|}{2}-\frac{\left\|\vec{T}_{2}\right\| \sqrt{3}}{2}&=0 \\ (E 2) \frac{\left\|\vec{T}_{1}\right\| \sqrt{3}}{2}+\frac{\left\|\vec{T}_{2}\right\|}{2}-50&=0 \end{array}\right.\nonumber\]De$(E 1)$, obtenemos$\left\|\vec{T}_{1}\right\|=\left\|\vec{T}_{2}\right\| \sqrt{3}$. Sustituyendo eso en$(E 2)$ da$\frac{\left(\left\|\overrightarrow{T_{2}}\right\| \sqrt{3}\right) \sqrt{3}}{2}+\frac{\left\|\vec{T}_{2}\right\|}{2}-50=0$ que rinde$2\left\|\vec{T}_{2}\right\|-50=0$. De ahí,$\left\|\vec{T}_{2}\right\|=25$ libras y$\left\|\vec{T}_{1}\right\|=\left\|\vec{T}_{2}\right\| \sqrt{3}=25 \sqrt{3}$ libras.

11.8.1 Ejercicios

En los Ejercicios 1 - 10, utilice el par de vectores dado$\vec{v}$ y$\vec{w}$ para encontrar las siguientes cantidades. Indique si el resultado es un vector o un escalar.

$\vec{v}+\vec{w}$
$\vec{w}-2 \vec{v}$
$\|\vec{v}+\vec{w}\|$
$\|\vec{v}\|+\|\vec{w}\|$
$\|\vec{v}\| \vec{w}-\|\vec{w}\| \vec{v}$
$\|\vec{w}\| \hat{v}$

Finalmente, verificar que los vectores cumplan con la Ley de Paralelogramo

$\|\vec{v}\|^{2}+\|\vec{w}\|^{2}=\frac{1}{2}\left[\|\vec{v}+\vec{w}\|^{2}+\|\vec{v}-\vec{w}\|^{2}\right]$

$\vec{v}=\langle 12,-5\rangle, \vec{w}=\langle 3,4\rangle$
$\vec{v}=\langle-7,24\rangle, \vec{w}=\langle-5,-12\rangle$
$\vec{v}=\langle 2,-1\rangle, \vec{w}=\langle-2,4\rangle$
$\vec{v}=\langle 10,4\rangle, \vec{w}=\langle-2,5\rangle$
$\vec{v}=\langle-\sqrt{3}, 1\rangle, \vec{w}=\langle 2 \sqrt{3}, 2\rangle$
$\vec{v}=\left\langle\frac{3}{5}, \frac{4}{5}\right\rangle, \vec{w}=\left\langle-\frac{4}{5}, \frac{3}{5}\right\rangle$
$\vec{v}=\left\langle\frac{\sqrt{2}}{2},-\frac{\sqrt{2}}{2}\right\rangle, \vec{w}=\left\langle-\frac{\sqrt{2}}{2}, \frac{\sqrt{2}}{2}\right\rangle$
$\vec{v}=\left\langle\frac{1}{2}, \frac{\sqrt{3}}{2}\right\rangle, \vec{w}=\langle-1,-\sqrt{3}\rangle$
$\vec{v}=3 \hat{\imath}+4 \hat{\jmath}, \vec{w}=-2 \hat{\jmath}$
$\vec{v}=\frac{1}{2}(\hat{\imath}+\hat{\jmath}), \vec{w}=\frac{1}{2}(\hat{\imath}-\hat{\jmath})$

En los Ejercicios 11 - 25, encuentra la forma componente del vector$\vec{v}$ utilizando la información dada sobre su magnitud y dirección. Dar valores exactos.

$\|\vec{v}\|=6$; cuando se dibuja en posición estándar$\vec{v}$ se encuentra en el Cuadrante I y$60^{\circ}$ forma un ángulo con el$x$ eje positivo
$\|\vec{v}\|=3$; cuando se dibuja en posición estándar$\vec{v}$ se encuentra en el Cuadrante I y$45^{\circ}$ forma un ángulo con el$x$ eje positivo
$\|\vec{v}\|=\frac{2}{3}$; cuando se dibuja en posición estándar$\vec{v}$ se encuentra en el Cuadrante I y$60^{\circ}$ forma un ángulo con el$y$ eje positivo
$\|\vec{v}\|=12$; cuando se dibuja en posición estándar$\vec{v}$ se encuentra a lo largo del$y$ eje positivo
$\|\vec{v}\|=4$; cuando se dibuja en posición estándar$\vec{v}$ se encuentra en el Cuadrante II y$30^{\circ}$ forma un ángulo con el$x$ eje negativo
$\|\vec{v}\|=2 \sqrt{3}$; cuando se dibuja en posición estándar$\vec{v}$ se encuentra en el Cuadrante II y$30^{\circ}$ forma un ángulo con el$y$ eje positivo
$\|\vec{v}\|=\frac{7}{2}$; cuando se dibuja en posición estándar$\vec{v}$ se encuentra a lo largo del$x$ eje negativo
$\|\vec{v}\|=5 \sqrt{6}$; cuando se dibuja en posición estándar$\vec{v}$ se encuentra en el Cuadrante III y$45^{\circ}$ forma un ángulo con el$x$ eje negativo
$\|\vec{v}\|=6.25$; cuando se dibuja en posición estándar$\vec{v}$ se encuentra a lo largo del$y$ eje negativo
$\|\vec{v}\|=4 \sqrt{3}$; cuando se dibuja en posición estándar$\vec{v}$ se encuentra en el cuadrante IV y$30^{\circ}$ forma un ángulo con el$x$ eje positivo
$\|\vec{v}\|=5 \sqrt{2}$; cuando se dibuja en posición estándar$\vec{v}$ se encuentra en el cuadrante IV y$45^{\circ}$ forma un ángulo con el$y$ eje negativo
$\|\vec{v}\|=2 \sqrt{5}$; cuando se dibuja en posición estándar$\vec{v}$ se encuentra en el Cuadrante I y hace un ángulo que mide arctan (2) con el$x$ eje positivo
$\|\vec{v}\|=\sqrt{10}$; cuando se dibuja en posición estándar$\vec{v}$ se encuentra en el Cuadrante II y hace un ángulo que mide arctan (3) con el$x$ eje negativo
$\|\vec{v}\|=5$; cuando se dibuja en posición estándar$\vec{v}$ se encuentra en el Cuadrante III y hace un ángulo que mide$\arctan \left(\frac{4}{3}\right)$ con el$x$ eje negativo
$\|\vec{v}\|=26$; cuando se dibuja en posición estándar$\vec{v}$ se encuentra en el cuadrante IV y hace un ángulo que mide$\arctan \left(\frac{5}{12}\right)$ con el$x$ eje positivo

En los Ejercicios 26 - 31, aproximar la forma componente del vector$\vec{v}$ utilizando la información dada sobre su magnitud y dirección. Redondee sus aproximaciones a dos decimales.

$\|\vec{v}\|=392$; cuando se dibuja en posición estándar$\vec{v}$ hace un$117^{\circ}$ ángulo con el$x$ eje positivo
$\|\vec{v}\|=63.92$; cuando se dibuja en posición estándar$\vec{v}$ hace un$78.3^{\circ}$ ángulo con el$x$ eje positivo
$\|\vec{v}\|=5280$; cuando se dibuja en posición estándar$\vec{v}$ hace un$12^{\circ}$ ángulo con el$x$ eje positivo
$\|\vec{v}\|=450$; cuando se dibuja en posición estándar$\vec{v}$ hace un$210.75^{\circ}$ ángulo con el$x$ eje positivo
$\|\vec{v}\|=168.7$; cuando se dibuja en posición estándar$\vec{v}$ hace un$252^{\circ}$ ángulo con el$x$ eje positivo
$\|\vec{v}\|=26$; cuando se dibuja en posición estándar$\vec{v}$ enmascara un$304.5^{\circ}$ ángulo con el$x$ eje positivo

En los Ejercicios 32 - 52, para el vector dado$\vec{v}$, encuentra la magnitud$\|\vec{v}\|$ y un ángulo$\theta$ con$0 \leq \theta<360^{\circ}$ para que$\vec{v}=\|\vec{v}\|\langle\cos (\theta), \sin (\theta)\rangle$ (Ver Definición 11.8.) Redondear aproximaciones a dos decimales.

$\vec{v}=\langle 1, \sqrt{3}\rangle$
$\vec{v}=\langle 5,5\rangle$
$\vec{v}=\langle-2 \sqrt{3}, 2\rangle$
$\vec{v}=\langle-\sqrt{2}, \sqrt{2}\rangle$
$\vec{v}=\left\langle-\frac{\sqrt{2}}{2},-\frac{\sqrt{2}}{2}\right\rangle$
$\vec{v}=\left\langle-\frac{1}{2},-\frac{\sqrt{3}}{2}\right\rangle$
$\vec{v}=\langle 6,0\rangle$
$\vec{v}=\langle-2.5,0\rangle$
$\vec{v}=\langle 0, \sqrt{7}\rangle$
$\vec{v}=-10 \hat{\jmath}$
$\vec{v}=\langle 3,4\rangle$
$\vec{v}=\langle 12,5\rangle$
$\vec{v}=\langle-4,3\rangle$
$\vec{v}=\langle-7,24\rangle$
$\vec{v}=\langle-2,-1\rangle$
$\vec{v}=\langle-2,-6\rangle$
$\vec{v}=\hat{\imath}+\hat{\jmath}$
$\vec{v}=\hat{\imath}-4 \hat{\jmath}$
$\vec{v}=\langle 123.4,-77.05\rangle$
$\vec{v}=\langle 965.15,831.6\rangle$
$\vec{v}=\langle-114.1,42.3\rangle$
Un pequeño bote sale del muelle en Camp DunuThin y cruza el río Nessie a 17 millas por hora (es decir, con respecto al agua) en una dirección de S68° O El río fluye hacia el este a 8 millas por hora. ¿Cuál es la verdadera velocidad y rumbo del barco? Redondea la velocidad a la milla por hora más cercana y expresa el rumbo como rumbo, redondeado a la décima de grado más cercana.
El HMS Sasquatch sale de puerto con rumbo$\mathrm{S} 20^{\circ} \mathrm{E}$ manteniendo una velocidad de 42 millas por hora (es decir, con respecto al agua). Si la corriente oceánica es de 5 millas por hora con un rumbo de$\mathrm{N} 60^{\circ} \mathrm{E}$, encuentre la verdadera velocidad y rumbo del HMS Sasquatch. Redondea la velocidad a la milla por hora más cercana y expresa el rumbo como rumbo, redondeado a la décima de grado más cercana.
Si el capitán del HMS Sasquatch en el Ejercicio 54 desea llegar a la Cala Chupacabras, una isla a 100 millas de distancia a una dirección$\mathrm{S} 20^{\circ} \mathrm{E}$ de puerto, en tres horas, ¿qué velocidad y rumbo debe establecer para tomar en cuenta la corriente oceánica? Redondea la velocidad a la milla por hora más cercana y expresa el rumbo como rumbo, redondeado a la décima de grado más cercana.
SUGERENCIA: Si$\vec{v}$ denota la velocidad del Sasquatch del HMS y$\vec{w}$ denota la velocidad de la corriente, ¿qué$\vec{v}+\vec{w}$ necesita ser para llegar a Cala Chupacabras en tres horas?
En un aire tranquilo, un avión que vuela desde el Aeropuerto Internacional Pedimaxus puede llegar a Cliffs of Insanity Point en dos horas siguiendo una dirección de$\mathrm{N} 8.2^{\circ} \mathrm{E}$ a 96 millas por hora. (La distancia entre el aeropuerto y los acantilados es de 192 millas.) Si el viento sopla desde el sureste a 25 millas por hora, ¿qué velocidad y rumbo debe tomar la piloto para que haga el viaje en dos horas por el rumbo original? Redondee la velocidad a la centésima de milla por hora más cercana y su ángulo a la décima de grado más cercana.
El SS Bigfoot sale de Yeti Bay en un curso de$\mathrm{N} 37^{\circ} \mathrm{W}$ a una velocidad de 50 millas por hora. Después de viajar media hora, el capitán determina que está a 30 millas de la bahía y su rumbo de regreso a la bahía es$\mathrm{S} 40^{\circ} \mathrm{E}$. ¿Cuál es la velocidad y rumbo de la corriente oceánica? Redondea la velocidad a la milla por hora más cercana y expresa el rumbo como rumbo, redondeado a la décima de grado más cercana.
Una estatua de Sasquatch de 600 libras está suspendida por dos cables del techo de un gimnasio. Si cada cable hace un$60^{\circ}$ ángulo con el techo, encuentre la tensión en cada cable. Redondee su respuesta a la libra más cercana.
Dos cables son para soportar un objeto colgado de un techo. Si los cables son cada uno para hacer un$42^{\circ}$ ángulo con el techo, y cada cable está clasificado para soportar una tensión máxima de 100 libras, ¿cuál es el objeto más pesado que se puede soportar? Redondee su respuesta a la libra más cercana.
Una estrella metálica de 300 libras está colgada de dos cables que están unidos al techo. El cable de la izquierda hace un$72^{\circ}$ ángulo con el techo mientras que el cable de la derecha hace un$18^{\circ}$ ángulo con el techo. ¿Cuál es la tensión en cada uno de los cables? Redondee sus respuestas a tres decimales.
Dos universitarios borrachos han llenado con piedras un barril de cerveza vacío y le han atado cuerdas para arrastrarlo por la calle en mitad de la noche. El más fuerte de los dos alumnos tira con una fuerza de 100 libras a un rumbo de$\mathrm{N} 77^{\circ} \mathrm{E}$ y el otro tira a un rumbo de$\mathrm{S} 68^{\circ} \mathrm{E}$. ¿Qué fuerza debe aplicar el estudiante más débil a su cuerda para que el barril de rocas se dirija hacia el este? ¿Qué fuerza resultante se aplica al barril? Redondee su respuesta a la libra más cercana.
Envalentonados por el éxito de su tirón nocturno de barril en el Ejercicio 61 anterior, nuestros intrépidos jóvenes estudiosos han decidido rendir homenaje a la escena de la carrera de carros de la película 'Ben-Hur' atando tres cuerdas a un sofá, cargando el sofá con todos menos uno de sus amigos y tirando de él hacia el oeste por la calle. La primera cuerda apunta$\mathrm{N} 80^{\circ} \mathrm{W}$, los segundos puntos con destino al oeste y los terceros puntos$\mathrm{S} 80^{\circ} \mathrm{W}$. La fuerza aplicada a la primera cuerda es de 100 libras, la fuerza aplicada a la segunda cuerda es de 40 libras y la fuerza aplicada (por el amigo que no monta) a la tercera cuerda es de 160 libras. Necesitan que la fuerza resultante sea de al menos 300 libras de lo contrario el sofá no se moverá. ¿Se mueve? Si es así, ¿se dirige hacia el oeste?
Dejar$\vec{v}=\left\langle v_{1}, v_{2}\right\rangle$ ser cualquier vector distinto de cero. Demostrar que$\frac{1}{\|\vec{v}\|} \vec{v}$ tiene longitud 1.
Decimos que dos vectores distintos de cero$\vec{v}$ y$\vec{w}$ son paralelos si tienen direcciones iguales u opuestas. Es decir,$\vec{v} \neq \overrightarrow{0}$ y$\vec{w} \neq \overrightarrow{0}$ son paralelos si cualquiera$\hat{v}=\hat{w}$ o$\hat{v}=-\hat{w}$. Mostrar que esto significa$\vec{v}=k \vec{w}$ para algún escalar distinto de cero$k$ y que$k > 0$ si los vectores tienen la misma dirección y$k < 0$ si apuntan en direcciones opuestas.
El objetivo de este ejercicio es utilizar vectores para describir líneas no verticales en el plano. Para ello, considera la línea$y=2 x-4$. Dejar$\vec{v}_{0}=\langle 0,-4\rangle$ y dejar$\vec{s}=\langle 1,2\rangle$. $t$Sea cualquier número real. Mostrar que el vector definido por$\vec{v}=\vec{v}_{0}+t \vec{s}$, cuando se dibuja en posición estándar, tiene su punto terminal en la línea$y = 2x − 4$. (Pista:$\vec{v}_{0}+t \vec{s}=\langle t, 2 t-4\rangle$ Muéstralo para cualquier número real$t$.) Ahora considere la línea no vertical$y = mx+b$. Repita el análisis previo con$\vec{v}_{0}=\langle 0, b\rangle$ y deje$\vec{s}=\langle 1, m\rangle$. Así, cualquier línea no vertical puede considerarse como una colección de puntos terminales de la suma vectorial de$\langle 0, b\rangle$ (el vector de posición$y$ de la intersección) y un múltiplo escalar del vector de pendiente$\vec{s}=\langle 1, m\rangle$.
Demostrar las propiedades asociativas y de identidad de la adición de vectores en el Teorema 11.18.
Demostrar las propiedades de la multiplicación escalar en el Teorema 11.19.

11.8.2 Respuestas

- $\vec{v}+\vec{w}=\langle 15,-1\rangle, \text { vector }$
- $\vec{w}-2 \vec{v}=\langle-21,14\rangle, \text { vector }$
- $\|\vec{v}+\vec{w}\|=\sqrt{226}, \text { scalar }$
- $\|\vec{v}\|+\|\vec{w}\|=18, \text { scalar }$
- $\|\vec{v}\| \vec{w}-\|\vec{w}\| \vec{v}=\langle-21,77\rangle, \text { vector }$
- $\|w\| \hat{v}=\left\langle\frac{60}{13},-\frac{25}{13}\right\rangle, \text { vector }$
- $\vec{v}+\vec{w}=\langle-12,12\rangle, \text { vector }$
- $\vec{w}-2 \vec{v}=\langle 9,-60\rangle, \text { vector }$
- $\|\vec{v}+\vec{w}\|=12 \sqrt{2}, \text { scalar }$
- $\|\vec{v}\|+\|\vec{w}\|=38, \text { scalar }$
- $\|\vec{v}\| \vec{w}-\|\vec{w}\| \vec{v}=\langle-34,-612\rangle, \text { vector }$
- $\|w\| \hat{v}=\left\langle-\frac{91}{25}, \frac{312}{25}\right\rangle, \text { vector }$
- $\vec{v}+\vec{w}=\langle 0,3\rangle, \text { vector }$
- $\vec{w}-2 \vec{v}=\langle-6,6\rangle, \text { vector }$
- $\|\vec{v}+\vec{w}\|=3, \text { scalar }$
- $\|\vec{v}\|+\|\vec{w}\|=3 \sqrt{5}, \text { scalar }$
- $\|\vec{v}\| \vec{w}-\|\vec{w}\| \vec{v}=\langle-6 \sqrt{5}, 6 \sqrt{5}\rangle, \text { vector }$
- $\|w\| \hat{v}=\langle 4,-2\rangle, \text { vector }$
- $\vec{v}+\vec{w}=\langle 8,9\rangle, \text { vector }$
- $\vec{w}-2 \vec{v}=\langle-22,-3\rangle, \text { vector }$
- $\|\vec{v}+\vec{w}\|=\sqrt{145}, \text { scalar }$
- $\|\vec{v}\|+\|\vec{w}\|=3 \sqrt{29}, \text { scalar }$
- $\|\vec{v}\| \vec{w}-\|\vec{w}\| \vec{v}=\langle-14 \sqrt{29}, 6 \sqrt{29}\rangle, \text { vector }$
- $\|w\| \hat{v}=\langle 5,2\rangle, \text { vector }$
- $\vec{v}+\vec{w}=\langle\sqrt{3}, 3\rangle, \text { vector }$
- $\vec{w}-2 \vec{v}=\langle 4 \sqrt{3}, 0\rangle, \text { vector }$
- $\|\vec{v}+\vec{w}\|=2 \sqrt{3}, \text { scalar }$
- $\|\vec{v}\|+\|\vec{w}\|=6, \text { scalar }$
- $\|\vec{v}\| \vec{w}-\|\vec{w}\| \vec{v}=\langle 8 \sqrt{3}, 0\rangle, \text { vector }$
- $\|w\| \hat{v}=\langle-2 \sqrt{3}, 2\rangle, \text { vector }$
- $\vec{v}+\vec{w}=\left\langle-\frac{1}{5}, \frac{7}{5}\right\rangle, \text { vector }$
- $\vec{w}-2 \vec{v}=\langle-2,-1\rangle, \text { vector }$
- $\|\vec{v}+\vec{w}\|=\sqrt{2} \text {, scalar }$
- $\|\vec{v}\|+\|\vec{w}\|=2, \text { scalar }$
- $\|\vec{v}\| \vec{w}-\|\vec{w}\| \vec{v}=\left\langle-\frac{7}{5},-\frac{1}{5}\right\rangle, \text { vector }$
- $\|w\| \hat{v}=\left\langle\frac{3}{5}, \frac{4}{5}\right\rangle, \text { vector }$
- $\vec{v}+\vec{w}=\langle 0,0\rangle, \text { vector }$
- $\vec{w}-2 \vec{v}=\left\langle-\frac{3 \sqrt{2}}{2}, \frac{3 \sqrt{2}}{2}\right\rangle, \text { vector }$
- $\|\vec{v}+\vec{w}\|=0, \text { scalar }$
- $\|\vec{v}\|+\|\vec{w}\|=2, \text { scalar }$
- $\|\vec{v}\| \vec{w}-\|\vec{w}\| \vec{v}=\langle-\sqrt{2}, \sqrt{2}\rangle, \text { vector }$
- $\|w\| \hat{v}=\left\langle\frac{\sqrt{2}}{2},-\frac{\sqrt{2}}{2}\right\rangle, \text { vector }$
- $\vec{v}+\vec{w}=\left\langle-\frac{1}{2},-\frac{\sqrt{3}}{2}\right\rangle, \text { vector }$
- $\vec{w}-2 \vec{v}=\langle-2,-2 \sqrt{3}\rangle, \text { vector }$
- $\|\vec{v}+\vec{w}\|=1, \text { scalar }$
- $\|\vec{v}\|+\|\vec{w}\|=3, \text { scalar }$
- $\|\vec{v}\| \vec{w}-\|\vec{w}\| \vec{v}=\langle-2,-2 \sqrt{3}\rangle, \text { vector }$
- $\|w\| \hat{v}=\langle 1, \sqrt{3}\rangle, \text { vector }$
- $\vec{v}+\vec{w}=\langle 3,2\rangle, \text { vector }$
- $\vec{w}-2 \vec{v}=\langle-6,-10\rangle, \text { vector }$
- $\|\vec{v}+\vec{w}\|=\sqrt{13}, \text { scalar }$
- $\|\vec{v}\|+\|\vec{w}\|=7, \text { scalar }$
- $\|\vec{v}\| \vec{w}-\|\vec{w}\| \vec{v}=\langle-6,-18\rangle, \text { vector }$
- $\|w\| \hat{v}=\left\langle\frac{6}{5}, \frac{8}{5}\right\rangle, \text { vector }$
- $\vec{v}+\vec{w}=\langle 1,0\rangle, \text { vector }$
- $\vec{w}-2 \vec{v}=\left\langle-\frac{1}{2},-\frac{3}{2}\right\rangle, \text { vector }$
- $\|\vec{v}+\vec{w}\|=1, \text { scalar }$
- $\|\vec{v}\|+\|\vec{w}\|=\sqrt{2}, \text { scalar }$
- $\|\vec{v}\| \vec{w}-\|\vec{w}\| \vec{v}=\left\langle 0,-\frac{\sqrt{2}}{2}\right\rangle, \text { vector }$
- $\|w\| \hat{v}=\left\langle\frac{1}{2}, \frac{1}{2}\right\rangle, \text { vector }$
$\vec{v}=\langle 3,3 \sqrt{3}\rangle$
$\vec{v}=\left\langle\frac{3 \sqrt{2}}{2}, \frac{3 \sqrt{2}}{2}\right\rangle$
$\vec{v}=\left\langle\frac{\sqrt{3}}{3}, \frac{1}{3}\right\rangle$
$\vec{v}=\langle 0,12\rangle$
$\vec{v}=\langle-2 \sqrt{3}, 2\rangle$
$\vec{v}=\langle-\sqrt{3}, 3\rangle$
$\vec{v}=\left\langle-\frac{7}{2}, 0\right\rangle$
$\vec{v}=\langle-5 \sqrt{3},-5 \sqrt{3}\rangle$
$\vec{v}=\langle 0,-6.25\rangle$
$\vec{v}=\langle 6,-2 \sqrt{3}\rangle$
$\vec{v}=\langle 5,-5\rangle$
$\vec{v}=\langle 2,4\rangle$
$\vec{v}=\langle-1,3\rangle$
$\vec{v}=\langle-3,-4\rangle$
$\vec{v}=\langle 24,-10\rangle$
$\vec{v} \approx\langle-177.96,349.27\rangle$
$\vec{v} \approx\langle 12.96,62.59\rangle$
$\vec{v} \approx\langle 5164.62,1097.77\rangle$
$\vec{v} \approx\langle-386.73,-230.08\rangle$
$\vec{v} \approx\langle-52.13,-160.44\rangle$
$\vec{v} \approx\langle 14.73,-21.43\rangle$
$\|\vec{v}\|=2, \theta=60^{\circ}$
$\|\vec{v}\|=5 \sqrt{2}, \theta=45^{\circ}$
$\|\vec{v}\|=4, \theta=150^{\circ}$
$\|\vec{v}\|=2, \theta=135^{\circ}$
$\|\vec{v}\|=1, \theta=225^{\circ}$
$\|\vec{v}\|=1, \theta=240^{\circ}$
$\|\vec{v}\|=6, \theta=0^{\circ}$
$\|\vec{v}\|=2.5, \theta=180^{\circ}$
$\|\vec{v}\|=\sqrt{7}, \theta=90^{\circ}$
$\|\vec{v}\|=10, \theta=270^{\circ}$
$\|\vec{v}\|=5, \theta \approx 53.13^{\circ}$
$\|\vec{v}\|=13, \theta \approx 22.62^{\circ}$
$\|\vec{v}\|=5, \theta \approx 143.13^{\circ}$
$\|\vec{v}\|=25, \theta \approx 106.26^{\circ}$
$\|\vec{v}\|=\sqrt{5}, \theta \approx 206.57^{\circ}$
$\|\vec{v}\|=2 \sqrt{10}, \theta \approx 251.57^{\circ}$
$\|\vec{v}\|=\sqrt{2}, \theta \approx 45^{\circ}$
$\|\vec{v}\|=\sqrt{17}, \theta \approx 284.04^{\circ}$
$\|\vec{v}\| \approx 145.48, \theta \approx 328.02^{\circ}$
$\|\vec{v}\| \approx 1274.00, \theta \approx 40.75^{\circ}$
$\|\vec{v}\| \approx 121.69, \theta \approx 159.66^{\circ}$
La verdadera velocidad del barco es de aproximadamente 10 millas por hora a una dirección de$\mathrm{S} 50.6^{\circ} \mathrm{W}$.
La verdadera velocidad del HMS Sasquatch es de aproximadamente 41 millas por hora a una dirección de$\mathrm{S} 26.8^{\circ} \mathrm{E}$.
Ella debe mantener una velocidad de aproximadamente 35 millas por hora a un rumbo de$\mathrm{S} 11.8^{\circ} \mathrm{E}$.
Debería volar a 83.46 millas por hora con un rumbo de$\mathrm{N} 22.1^{\circ} \mathrm{E}$
La corriente se mueve a unas 10 millas por hora rumbo$\mathrm{N} 54.6^{\circ} \mathrm{W}$.
La tensión en cada uno de los cables es de aproximadamente 346 libras.
El peso máximo que pueden sostener los cables en esa configuración es de aproximadamente 133 libras.
La tensión en el cable de la izquierda es de 285.317 lbs. y en el cable de la derecha es de 92.705 lbs.
El estudiante más débil debería tirar alrededor de 60 libras. La fuerza neta sobre el barril es de unas 153 libras.
La fuerza resultante es de sólo unas 296 libras por lo que el sofá no se mueve. Incluso si se moviera, la fuerza más fuerte sobre la tercera cuerda habría hecho que el sofá se desplazara ligeramente hacia el sur mientras viajaba por la calle.

Referencia

¹ La palabra 'vector' viene del latín vehere que significa 'transportar' o 'llevar'.

² Otros autores de libros de texto utilizan vectores en negrita como$\boldsymbol{v}$. Encontramos que escribir en negrita en la pizarra es inconveniente en el mejor de los casos, por lo que hemos elegido la notación 'flecha'.

³ Si esta idea de 'encima' y 'arriba' parece familiar, debería. La pendiente del segmento de línea que contiene$\vec{v}$ es$\frac{4}{3}$.

⁴ Si es necesario, revise la página 905 y la Sección 11.3.

⁵ Es decir, la velocidad del avión en relación con el aire que lo rodea. Si no hubiera viento, la velocidad aérea del avión sería la misma que su velocidad observada desde el suelo. ¿Cómo afecta esto el viento? ¡Sigue leyendo!

⁶ Véase la Sección 10.1.1, por ejemplo.

⁷ O, como nuestro ángulo dado,$100^{\circ}$, es obtuso, podríamos usar aquí la Ley de los Senos sin ambigüedad alguna.

⁸ Agregar vectores 'en cuanto a componentes' debería parecer angustiosamente familiar. Compare esto con cómo se definió la adición de matriz en la sección 8.3. De hecho, en cursos más avanzados como Álgebra Lineal, los vectores se definen como$1 \times n$ o$n \times 1$ matrices, dependiendo de la situación.

⁹ Se anima al lector interesado a comparar el Teorema 11.18 y la discusión subsiguiente con el Teorema 8.3 en la Sección 8.3 y la discusión ahí.

¹⁰ Si todo esto le resulta familiar, debería. Se invita al lector interesado a comparar la Definición 11.8 con la Definición 11.2 en la Sección 11.7.

¹¹ Por supuesto, para pasar de$\vec{v}=\|\vec{v}\| \hat{v}$ a$\hat{v}=\left(\frac{1}{\|\vec{v}\|}\right) \vec{v}$, estamos esencialmente 'dividiendo ambos lados' de la ecuación por el escalar$\|\vec{v}\|$. Los autores animan al lector, sin embargo, a elaborar los detalles cuidadosamente para obtener una apreciación de las propiedades en juego.

¹² Debido a la utilidad de los vectores en aplicaciones del “mundo real”, generalmente usaremos la medida de grado para el ángulo al dar la dirección del vector. Sin embargo, como Carl no quiere que te olvides de los radianes, se ha asegurado de que haya ejemplos y ejercicios que los usen.

¹³ ¡Mantener las cosas 'calculadora' amigables, por una vez!

¹⁴ Sí, una aproximación de calculadora es la forma más rápida de ver esto, pero también puedes usar buenas desigualdades anticuadas y el hecho de que$45^{\circ} \leq 50^{\circ} \leq 60^{\circ}$.

¹⁵ Una prueba utiliza las propiedades de multiplicación escalar y magnitud. Si$\vec{v} \neq \overrightarrow{0}$, considere$\|\hat{v}\|=\left\|\left(\frac{1}{\|\vec{v}\|}\right) \vec{v}\right\|$. Usa el hecho de que$\|\vec{v}\| \geq 0$ es un escalar y considerar factorizar.

^16.. si$\|\vec{v}\|>1$..

¹⁷ Veremos una generalización del Teorema 11.21 en la Sección 11.9. ¡Estén atentos!

¹⁸ Véase también la Sección 11.1.1.

¹⁹ Este es el criterio para el 'equilbrio estático'.