11.9: El Producto Dot y Proyección

Última actualización
Guardar como PDF

Page ID: 119497

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

En la Sección 11.8 aprendimos cómo sumar y restar vectores y cómo multiplicar vectores por escalares. En esta sección, definimos un producto de vectores. Comenzamos con la siguiente definición.

Definición 11.11

Supongamos$\vec{v}$ y$\vec{w}$ son vectores cuyas formas componentes son$\vec{v}=\left\langle v_{1}, v_{2}\right\rangle$ y$\vec{w}=\left\langle w_{1}, w_{2}\right\rangle$. El producto puntual de$\vec{v}$ y$\vec{w}$ viene dado por\[\vec{v} \cdot \vec{w}=\left\langle v_{1}, v_{2}\right\rangle \cdot\left\langle w_{1}, w_{2}\right\rangle=v_{1} w_{1}+v_{2} w_{2}\nonumber\]

Por ejemplo, vamos$\vec{v}=\langle 3,4\rangle$ y$\vec{w}=\langle 1,-2\rangle$. Entonces$\vec{v} \cdot \vec{w}=\langle 3,4\rangle \cdot\langle 1,-2\rangle=(3)(1)+(4)(-2)=-5$. Tenga en cuenta que el producto punto toma dos vectores y produce un escalar. Por esa razón, a la cantidad$\vec{v} \cdot \vec{w}$ se le suele llamar el producto escalar de$\vec{v}$ y$\vec{w}$. El producto dot goza de las siguientes propiedades.

Teorema 11.22. Propiedades del Producto Dot

Propiedad Conmutativa: Para todos los vectores$\vec{v}$ y$\vec{w}$,$\vec{v} \cdot \vec{w}=\vec{w} \cdot \vec{v}$.
Propiedad Distributiva: Para todos los vectores$\vec{u}, \vec{v} \text { and } \vec{w}$,$\vec{u} \cdot(\vec{v}+\vec{w})=\vec{u} \cdot \vec{v}+\vec{u} \cdot \vec{w}$.
Propiedad escalar: Para todos los vectores$\vec{v}$ y$\vec{w}$ y escalares$k$,$(k \vec{v}) \cdot \vec{w}=k(\vec{v} \cdot \vec{w})=\vec{v} \cdot(k \vec{w})$.
Relación con Magnitud: Para todos los vectores$\vec{v}, \vec{v} \cdot \vec{v}=\|\vec{v}\|^{2}$.

Como la mayoría de los teoremas que involucran vectores, la prueba del Teorema 11.22 equivale a usar la definición del producto punto y las propiedades de la aritmética de números reales. Para mostrar la propiedad conmutativa por ejemplo, let$\vec{v}=\left\langle v_{1}, v_{2}\right\rangle$ y$\vec{w}=\left\langle w_{1}, w_{2}\right\rangle$. Entonces\ [\ begin {array} {l}
&\ vec {v}\ cdot\ vec {w} =\ izquierda\ langle v_ {1}, v_ {2}\ derecha\ rangle\ cdot\ izquierda\ langle w_ {1}, w_ {2}\ derecha\ rangle\\ &=v_ {1} w_ {1} +v_ {2} _ {2} &\ text {Definición de producto de punto}\\ &=w_ {1} v_ {1} +w_ {2} v_ {2} &\ text {Conmutatividad de la multiplicación de números reales} \\ &=\ izquierda\ langle w_ {1}, w_ {2}\ derecha\ rangle\ cdot\ izquierda\ langle v_ {1}, v_ {2}\ derecha\ rangle &\ texto {Definición de producto de punto}\\ &=\ vec {w}\ cdot\ vec {v}\ end {array}\ nonumber\]

La propiedad distributiva se prueba de manera similar y se deja como ejercicio.

Para la propiedad escalar, asumir que$\vec{v}=\left\langle v_{1}, v_{2}\right\rangle$ y$\vec{w}=\left\langle w_{1}, w_{2}\right\rangle$ y$k$ es un escalar. Entonces

\[\begin{aligned} (k \vec{v}) \cdot \vec{w} &=\left(k\left\langle v_{1}, v_{2}\right\rangle\right) \cdot\left\langle w_{1}, w_{2}\right\rangle & & \\ &=\left\langle k v_{1}, k v_{2}\right\rangle \cdot\left\langle w_{1}, w_{2}\right\rangle & & \text { Definition of Scalar Multiplication } \\ &=\left(k v_{1}\right)\left(w_{1}\right)+\left(k v_{2}\right)\left(w_{2}\right) & & \text { Definition of Dot Product } \\ &=k\left(v_{1} w_{1}\right)+k\left(v_{2} w_{2}\right) & & \text { Associativity of Real Number Multiplication } \\ &=k\left(v_{1} w_{1}+v_{2} w_{2}\right) & & \text { Distributive Law of Real Numbers } \\ &=k\left\langle v_{1}, v_{2}\right\rangle \cdot\left\langle w_{1}, w_{2}\right\rangle & & \text { Definition of Dot Product } \\ &=k(\vec{v} \cdot \vec{w}) & & \end{aligned}\nonumber\]

Dejamos la prueba de$k(\vec{v} \cdot \vec{w})=\vec{v} \cdot(k \vec{w})$ como ejercicio.

Para el último inmueble, observamos que si$\vec{v}=\left\langle v_{1}, v_{2}\right\rangle$, entonces$\vec{v} \cdot \vec{v}=\left\langle v_{1}, v_{2}\right\rangle \cdot\left\langle v_{1}, v_{2}\right\rangle=v_{1}^{2}+v_{2}^{2}=\|\vec{v}\|^{2}$, donde viene la última igualdad cortesía de la Definición 11.8.

El siguiente ejemplo le da buen uso al Teorema 11.22. Al igual que en el Ejemplo 11.8.3, resolvemos el problema con gran detalle y animamos al lector a aportar la justificación de cada paso.

Ejemplo 11.9.1

Demostrar la identidad:$\|\vec{v}-\vec{w}\|^{2}=\|\vec{v}\|^{2}-2(\vec{v} \cdot \vec{w})+\|\vec{w}\|^{2}$.

Solución

Comenzamos por reescribir$\|\vec{v}-\vec{w}\|^{2}$ en términos del producto punto usando el Teorema 11.22. \[\begin{aligned} \|\vec{v}-\vec{w}\|^{2} &=(\vec{v}-\vec{w}) \cdot(\vec{v}-\vec{w}) \\ &=(\vec{v}+[-\vec{w}]) \cdot(\vec{v}+[-\vec{w}]) \\ &=(\vec{v}+[-\vec{w}]) \cdot \vec{v}+(\vec{v}+[-\vec{w}]) \cdot[-\vec{w}] \\ &=\vec{v} \cdot(\vec{v}+[-\vec{w}])+[-\vec{w}] \cdot(\vec{v}+[-\vec{w}]) \\ &=\vec{v} \cdot \vec{v}+\vec{v} \cdot[-\vec{w}]+[-\vec{w}] \cdot \vec{v}+[-\vec{w}] \cdot[-\vec{w}] \\ &=\vec{v} \cdot \vec{v}+\vec{v} \cdot[(-1) \vec{w}]+[(-1) \vec{w}] \cdot \vec{v}+[(-1) \vec{w}] \cdot[(-1) \vec{w}] \\ &=\vec{v} \cdot \vec{v}+(-1)(\vec{v} \cdot \vec{w})+(-1)(\vec{w} \cdot \vec{v})+[(-1)(-1)](\vec{w} \cdot \vec{w}) \\ &=\vec{v} \cdot \vec{v}+(-1)(\vec{v} \cdot \vec{w})+(-1)(\vec{v} \cdot \vec{w})+\vec{w} \cdot \vec{w} \\ &=\vec{v} \cdot \vec{v}-2(\vec{v} \cdot \vec{w})+\vec{w} \cdot \vec{w} \\ &=\|\vec{v}\|^{2}-2(\vec{v} \cdot \vec{w})+\|\vec{w}\|^{2} \end{aligned}\nonumber\]De ahí,$\|\vec{v}-\vec{w}\|^{2}=\|\vec{v}\|^{2}-2(\vec{v} \cdot \vec{w})+\|\vec{w}\|^{2}$ según se requiera.

Si damos un paso atrás de la pedantería en el Ejemplo 11.9.1, vemos que se necesita la mayor parte de la obra para demostrarlo$(\vec{v}-\vec{w}) \cdot(\vec{v}-\vec{w})=\vec{v} \cdot \vec{v}-2(\vec{v} \cdot \vec{w})+\vec{w} \cdot \vec{w}$. Si esto le resulta familiar, debería. Dado que el producto dot disfruta de muchas de las mismas propiedades que disfrutan los números reales, las maquinaciones requeridas para expandirse$(\vec{v}-\vec{w}) \cdot(\vec{v}-\vec{w})$ para vectores$\vec{v}$ y$\vec{w}$ coincidir con las requeridas$(v-w)(v-w)$ para expandirse para números reales$v$ y$w$, y por lo tanto obtenemos resultados similares. La identidad verificada en el Ejemplo 11.9.1 juega un papel importante en el desarrollo de las propiedades geométricas del producto punto, que ahora exploramos.

Supongamos$\vec{v}$ y$\vec{w}$ son dos vectores distintos de cero. Si dibujamos$\vec{v}$ y$\vec{w}$ con el mismo punto inicial, definimos el ángulo entre$\vec{v}$ y$\vec{w}$ para ser el ángulo$\theta$ determinado por los rayos que contienen los vectores$\vec{v}$ y$\vec{w}$, como se ilustra a continuación. Requerimos$0 \leq \theta \leq \pi$. (Piense en por qué esto es necesario en la definición.)

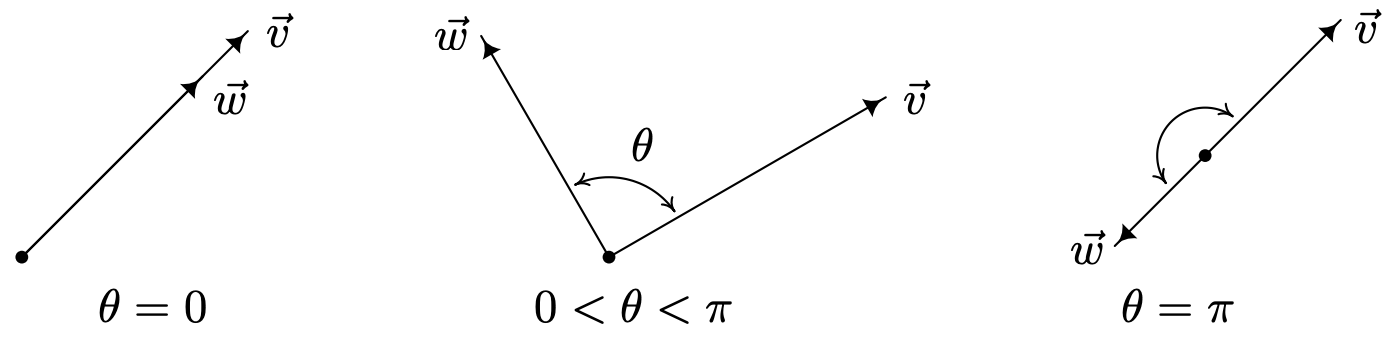
$Screen Shot 2022-06-11 a las 4.24.30 PM.png$

El siguiente teorema nos da una idea del papel geométrico que juega el producto punto.

Teorema 11.23. Interpretación Geométrica del Producto Dot

Si$\vec{v}$ y$\vec{w}$ son vectores distintos de cero entonces$\vec{v} \cdot \vec{w}=\|\vec{v}\|\|\vec{w}\| \cos (\theta)$, ¿dónde$\theta$ está el ángulo entre$\vec{v}$ y$\vec{w}$.

Demostramos el Teorema 11.23 en los casos. Si$\theta=0$, entonces$\vec{v}$ y$\vec{w}$ tener la misma dirección. De ello se deduce ¹ que hay un número real$k > 0$ así que eso$\vec{w}=k \vec{v}$. De ahí,$\vec{v} \cdot \vec{w}=\vec{v} \cdot(k \vec{v})=k(\vec{v} \cdot \vec{v})=k\|\vec{v}\|^{2}=k\|\vec{v}\|\|\vec{v}\|$. Desde$k>0, k=|k| \text {, so } k\|\vec{v}\|=|k|\|\vec{v}\|=\|k \vec{v}\|$ por Teorema 11.20. De ahí,$k\|\vec{v}\|\|\vec{v}\|=\|\vec{v}\|(k\|\vec{v}\|)=\|\vec{v}\|\|k \vec{v}\|=\|\vec{v}\|\|\vec{w}\|$. Ya que$\cos (0)=1$, obtenemos$\vec{v} \cdot \vec{w}=k\|\vec{v}\|\|\vec{v}\|=\|\vec{v}\|\|\vec{w}\|=\|\vec{v}\|\|\vec{w}\| \cos (0)$, demostrando que la fórmula se mantiene para$\theta=0$. Si$\theta=\pi$, repetimos el argumento con la diferencia siendo$\vec{w}=k \vec{v}$ donde$k < 0$. En este caso,$|k|=-k$, entonces$k\|\vec{v}\|=-|k|\|\vec{v}\|=-\|k \vec{v}\|=-\|\vec{w}\|$. Ya que$\cos (\pi)=-1$, obtenemos$\vec{v} \cdot \vec{w}=-\|\vec{v}\|\|\vec{w}\|=\|\vec{v}\|\|\vec{w}\| \cos (\pi)$, según sea necesario. A continuación, si$0<\theta<\pi$, los vectores$\vec{v}, \vec{w}$ y$\vec{v}-\vec{w}$ determinan un triángulo con longitudes laterales$\|\vec{v}\|,\|\vec{w}\|$ y$\|\vec{v}-\vec{w}\|$, respectivamente, como se ve a continuación.

$Screen Shot 2022-06-11 en 5.08.03 PM.png$

La Ley de Cosinos rinde$\|\vec{v}-\vec{w}\|^{2}=\|\vec{v}\|^{2}+\|\vec{w}\|^{2}-2\|\vec{v}\|\|\vec{w}\| \cos (\theta)$. Del Ejemplo 11.9.1, sabemos$\|\vec{v}-\vec{w}\|^{2}=\|\vec{v}\|^{2}-2(\vec{v} \cdot \vec{w})+\|\vec{w}\|^{2}$. Equiparando estas dos expresiones para$\|\vec{v}-\vec{w}\|^{2}$ da$\|\vec{v}\|^{2}+\|\vec{w}\|^{2}-2\|\vec{v}\|\|\vec{w}\| \cos (\theta)=\|\vec{v}\|^{2}-2(\vec{v} \cdot \vec{w})+\|\vec{w}\|^{2}$ que reduce a$-2\|\vec{v}\|\|\vec{w}\| \cos (\theta)=-2(\vec{v} \cdot \vec{w})$, o$\vec{v} \cdot \vec{w}=\|\vec{v}\|\|\vec{w}\| \cos (\theta)$, según se requiera. Una consecuencia inmediata del Teorema 11.23 es la siguiente.

Teorema 11.24

Dejar$\vec{v}$ y$\vec{w}$ ser vectores distintos de cero y dejar que$\theta$ el ángulo entre$\vec{v}$ y$\vec{w}$. Entonces\[\theta=\arccos \left(\frac{\vec{v} \cdot \vec{w}}{\|\vec{v}\|\|\vec{w}\|}\right)=\arccos (\hat{v} \cdot \hat{w})\nonumber\]

Obtenemos la fórmula en el Teorema 11.24 resolviendo la ecuación dada en el Teorema 11.23 para$\theta$. Ya que$\vec{v}$ y$\vec{w}$ son distintos de cero, también lo son$\|\vec{v}\| \text { and }\|\vec{w}\|$. De ahí que podamos dividir ambos lados de$\vec{v} \cdot \vec{w}=\|\vec{v}\|\|\vec{w}\| \cos (\theta)$ por$\|\vec{v}\|\|\vec{w}\|$ para conseguir$\cos (\theta)=\frac{\vec{v} \cdot \vec{w}}{\|\vec{v}\|\|\vec{w}\|}$. Ya que$0 \leq \theta \leq \pi$ por definición, los valores de coinciden$\theta$ exactamente con el rango de la función arccosine. De ahí,$\theta=\arccos \left(\frac{\vec{v} \cdot \vec{w}}{\|\vec{v}\|\|\vec{w}\|}\right)$. Usando el Teorema 11.22, podemos reescribir$\frac{\vec{v} \cdot \vec{w}}{\|\vec{v}\|\|\vec{w}\|}=\left(\frac{1}{\|\vec{v}\|} \vec{v}\right) \cdot\left(\frac{1}{\|\vec{w}\|} \vec{w}\right)=\hat{v} \cdot \hat{w}$, dándonos la fórmula alternativa$\theta=\arccos (\hat{v} \cdot \hat{w})$.

Estamos atrasados por un ejemplo.

Ejemplo 11.9.2

Encuentra el ángulo entre los siguientes pares de vectores.

$\vec{v}=\langle 3,-3 \sqrt{3}\rangle, \text { and } \vec{w}=\langle-\sqrt{3}, 1\rangle$
$\vec{v}=\langle 2,2\rangle, \text { and } \vec{w}=\langle 5,-5\rangle$
$\vec{v}=\langle 3,-4\rangle, \text { and } \vec{w}=\langle 2,1\rangle$

Solución

Utilizamos la fórmula$\theta=\arccos \left(\frac{\vec{v} \cdot \vec{w}}{\|\vec{v}\|\|\vec{w}\|}\right)$ del Teorema 11.24 en cada caso a continuación.

Nosotros tenemos$\vec{v} \cdot \vec{w}=\langle 3,-3 \sqrt{3}\rangle \cdot\langle-\sqrt{3}, 1\rangle=-3 \sqrt{3}-3 \sqrt{3}=-6 \sqrt{3}$. Desde$\|\vec{v}\|=\sqrt{3^{2}+(-3 \sqrt{3})^{2}}=\sqrt{36}=6$ y$\|\vec{w}\|=\sqrt{(-\sqrt{3})^{2}+1^{2}}=\sqrt{4}=2, \theta=\arccos \left(\frac{-6 \sqrt{3}}{12}\right)=\arccos \left(-\frac{\sqrt{3}}{2}\right)=\frac{5 \pi}{6}$.
Para$\vec{v}=\langle 2,2\rangle$ y$\vec{w}=\langle 5,-5\rangle$, nos encontramos$\vec{v} \cdot \vec{w}=\langle 2,2\rangle \cdot\langle 5,-5\rangle=10-10=0$. De ahí que no importa qué$\|\vec{v}\|$ y$\|\vec{w}\|$ sean, ²$\theta=\arccos \left(\frac{\vec{v} \cdot \vec{w}}{\|\vec{v}\|\|\vec{w}\|}\right)=\arccos (0)=\frac{\pi}{2}$.
Nos encontramos$\vec{v} \cdot \vec{w}=\langle 3,-4\rangle \cdot\langle 2,1\rangle=6-4=2$. También$\|\vec{v}\|=\sqrt{3^{2}+(-4)^{2}}=\sqrt{25}=5$ y$\vec{w}=\sqrt{2^{2}+1^{2}}=\sqrt{5}$, entonces$\theta=\arccos \left(\frac{2}{5 \sqrt{5}}\right)=\arccos \left(\frac{2 \sqrt{5}}{25}\right)$. Ya que$\frac{2 \sqrt{5}}{25}$ no es el coseno de uno de los ángulos comunes, dejamos nuestra respuesta como$\theta=\arccos \left(\frac{2 \sqrt{5}}{25}\right)$.

Los vectores$\vec{v}=\langle 2,2\rangle$, y$\vec{w}=\langle 5,-5\rangle$ en el Ejemplo 11.9.2 se llaman ortogonales y escribimos$\vec{v} \perp \vec{w}$, porque el ángulo entre ellos es$\frac{\pi}{2} \text { radians }=90^{\circ}$. Geométricamente, cuando los vectores ortogonales se esbozan con el mismo punto inicial, las líneas que contienen los vectores son perpendiculares.

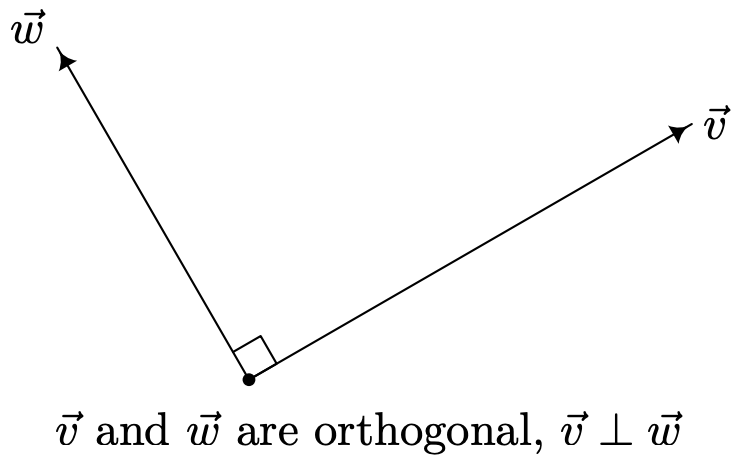
$Screen Shot 2022-06-11 en 5.39.16 PM.png$

Se expone la relación entre los vectores ortogonales y su producto puntual en el siguiente teorema.

Teorema 11.25. El producto Dot detecta ortogonalidad

Dejar$\vec{v}$ y$\vec{w}$ ser vectores distintos de cero. Entonces$\vec{v} \perp \vec{w}$ si y sólo si$\vec{v} \cdot \vec{w}=0$.

Para probar el Teorema 11.25, primero asumimos$\vec{v}$ y$\vec{w}$ son vectores distintos de cero con$\vec{v} \perp \vec{w}$. Por definición, el ángulo entre$\vec{v}$ y$\vec{w}$ es$\frac{\pi}{2}$. Por Teorema 11.23,$\vec{v} \cdot \vec{w}=\|\vec{v}\|\|\vec{w}\| \cos \left(\frac{\pi}{2}\right)=0$. Por el contrario, si$\vec{v}$ y$\vec{w}$ son vectores distintos de cero y$\vec{v} \cdot \vec{w}=0$. entonces el Teorema 11.24 da$\theta=\arccos \left(\frac{\vec{v} \cdot \vec{w}}{\|\vec{v}\|\|\vec{w}\|}\right)=\arccos \left(\frac{0}{\|\vec{v}\|\|\vec{w}\|}\right)=\arccos (0)=\frac{\pi}{2}$, así$\vec{v} \perp \vec{w}$. Podemos utilizar el Teorema 11.25 en el siguiente ejemplo para proporcionar una prueba diferente sobre la relación entre las pendientes de las líneas perpendiculares. ³

Ejemplo 11.9.3

Deja$L_{1}$ ser la línea$y=m_{1} x+b_{1}$ y deja$L_{2}$ ser la línea$y=m_{2} x+b_{2}$. Demostrar que$L_{1}$ es perpendicular a$L_{2}$ si y solo si$m_{1} \cdot m_{2}=-1$.

Solución

Nuestra estrategia es encontrar dos vectores:$\overrightarrow{v_{1}}$, que tiene la misma dirección que$L_{1}$, y$\overrightarrow{v_{2}}$, que tiene la misma dirección que$L_{2}$ y mostrar$\overrightarrow{v_{1}} \perp \overrightarrow{v_{2}}$ si y solo si$m_{1} m_{2}=-1$. Para ello, sustituimos$x = 0$ y$x = 1$ en$y=m_{1} x+b_{1}$ encontrar dos puntos en los que se encuentran$L_{1}$, a saber,$P\left(0, b_{1}\right)$ y$Q\left(1, m_{1}+b_{1}\right)$. Dejamos$\overrightarrow{v_{1}}=\overrightarrow{P Q}=\left\langle 1-0,\left(m_{1}+b_{1}\right)-b_{1}\right\rangle=\left\langle 1, m_{1}\right\rangle$, y notamos que dado que$\overrightarrow{v_{1}}$ está determinado por dos puntos sobre$L_{1}$, puede ser visto como acostado$L_{1}$. De ahí que tenga la misma dirección que$L_{1}$. Del mismo modo, obtenemos el vector$\overrightarrow{v_{2}}=\left\langle 1, m_{2}\right\rangle$ que tiene la misma dirección que la línea$L_{2}$. De ahí,$L_{1}$ y$L_{2}$ son perpendiculares si y solo si$\overrightarrow{v_{1}} \perp \overrightarrow{v_{2}}$. Según el Teorema 11.25,$\overrightarrow{v_{1}} \perp \overrightarrow{v_{2}}$ si y sólo si$\overrightarrow{v_{1}} \cdot \overrightarrow{v_{2}}=0$. Observe eso$\overrightarrow{v_{1}} \cdot \overrightarrow{v_{2}}=\left\langle 1, m_{1}\right\rangle \cdot\left\langle 1, m_{2}\right\rangle=1+m_{1} m_{2}$. De ahí,$\overrightarrow{v_{1}} \cdot \overrightarrow{v_{2}}=0$ si y sólo si$1+m_{1} m_{2}=0$, que es cierto si y sólo si$m_{1} m_{2}=-1$, según se requiera.

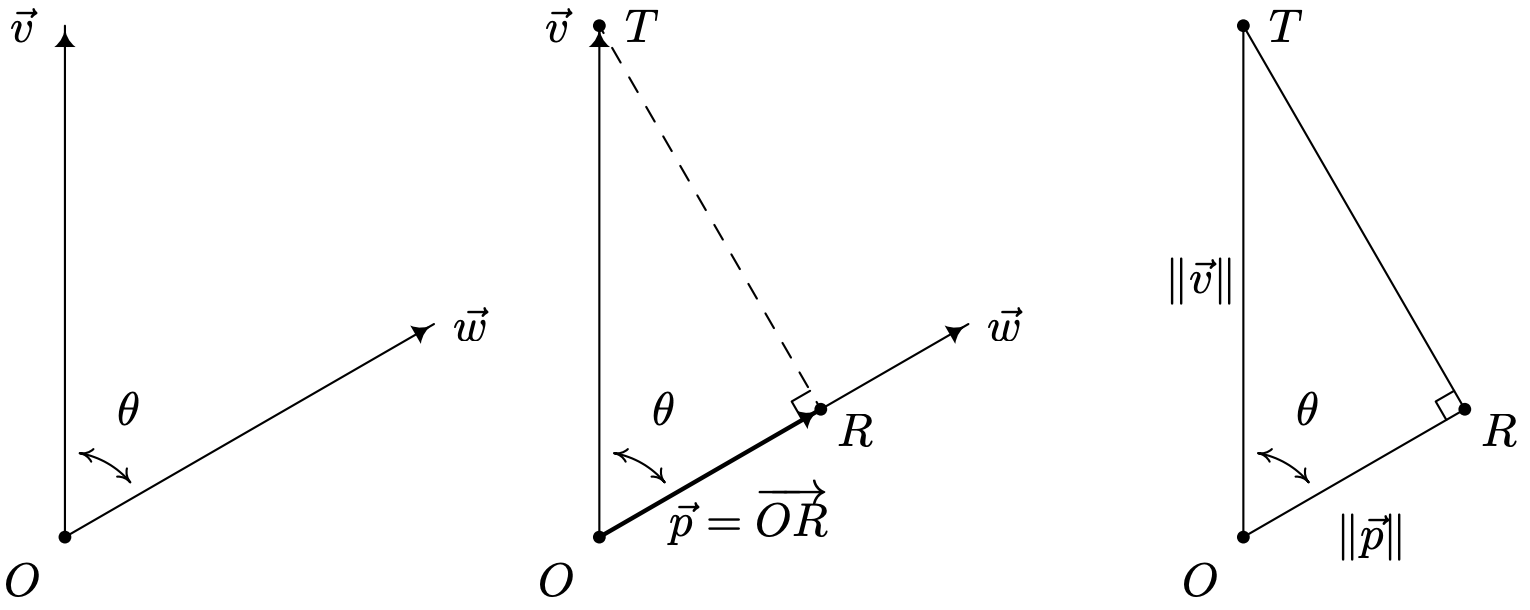
Si bien el Teorema 11.25 ciertamente nos da una idea de lo que el producto punto significa geométricamente, hay más en la historia del producto punto. Considere los dos vectores distintos de cero$\vec{v}$ y$\vec{w}$ dibujados con un punto inicial común$O$ a continuación. Por el momento, supongamos que el ángulo entre$\vec{v}$ y$\vec{w}$, que vamos a denotar$\theta$, es agudo. Deseamos desarrollar una fórmula para el vector$\vec{p}$, que se indica a continuación, que se denomina proyección ortogonal de$\vec{v}$ onto$\vec{w}$. El vector$\vec{p}$ se obtiene geométricamente de la siguiente manera: soltar una perpendicular desde el punto$T$ terminal del vector$\vec{w}$ y llamar al punto de intersección$R$.$\vec{v}$ El vector (\ vec {p}\) se define entonces como$\vec{p}=\overrightarrow{O R}$. Como cualquier vector,$\vec{p}$ está determinado por su magnitud$\|\vec{p}\|$ y su dirección$\hat{p}$ según la fórmula$\vec{p}=\|\vec{p}\| \hat{p}$. Ya que queremos$\hat{p}$ tener la misma dirección que (\ vec {w}\), tenemos$\hat{p}=\hat{w}$. Para determinar$\|\vec{p}\|$, hacemos uso del Teorema 10.4 tal como se aplica al triángulo rectángulo$\triangle O R T$. Nos encontramos$\cos (\theta)=\frac{\|\vec{p}\|}{\|\vec{v}\|}$, o$\|\vec{p}\|=\|\vec{v}\| \cos (\theta)$. Para obtener las cosas en términos de lo justo$\vec{v}$ y$\vec{w}$, utilizamos el Teorema 11.23 para obtener$\|\vec{p}\|=\|\vec{v}\| \cos (\theta)=\frac{\|\vec{v}\|\|\vec{w}\| \cos (\theta)}{\|\vec{w}\|}=\frac{\vec{v} \cdot \vec{w}}{\|\vec{w}\|}$. Usando el Teorema 11.22, reescribimos$\frac{\vec{v} \cdot \vec{w}}{\|\vec{w}\|}=\vec{v} \cdot\left(\frac{1}{\|\vec{w}\|} \vec{w}\right)=\vec{v} \cdot \hat{w}$. De ahí$\|\vec{p}\|=\vec{v} \cdot \hat{w}$,, y desde entonces$\hat{p}=\hat{w}$, ahora tenemos una fórmula para$\vec{p}$ completamente en términos de$\vec{v}$ y$\vec{w}$, a saber$\vec{p}=\|\vec{p}\| \hat{p}=(\vec{v} \cdot \hat{w}) \hat{w}$.

$Screen Shot 2022-06-11 a las 6.19.25 PM.png$

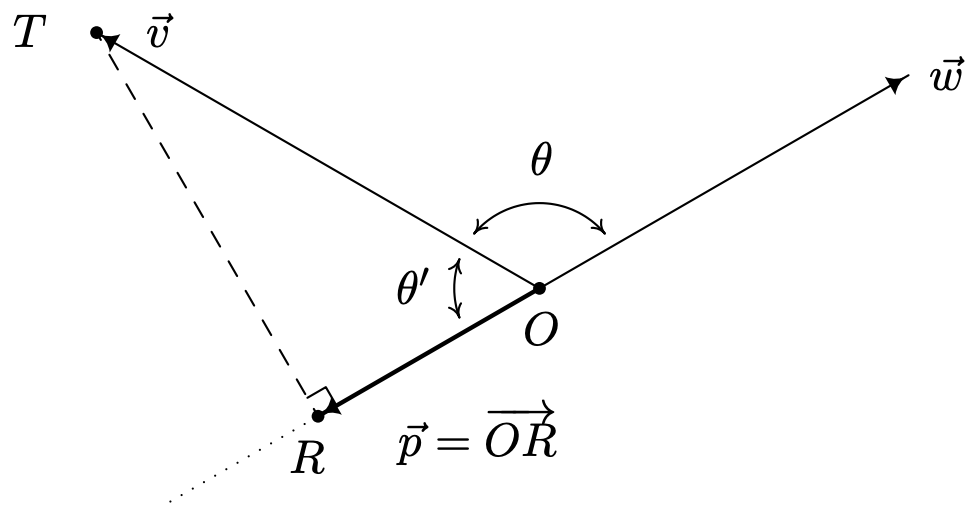
Ahora supongamos que el ángulo$\theta$ entre$\vec{v}$ y$\vec{w}$ es obtuso, y considera el diagrama a continuación. En este caso, vemos eso$\hat{p}=-\hat{w}$ y usando el triángulo$\triangle O R T$, nos encontramos$\|\vec{p}\|=\|\vec{v}\| \cos \left(\theta^{\prime}\right)$. Ya que$\theta+\theta^{\prime}=\pi$, se deduce que$\cos \left(\theta^{\prime}\right)=-\cos (\theta)$, lo que significa$\|\vec{p}\|=\|\vec{v}\| \cos \left(\theta^{\prime}\right)=-\|\vec{v}\| \cos (\theta)$. Reescribiendo esta última ecuación en términos de$\vec{v}$ y$\vec{w}$ como antes, obtenemos$\|\vec{p}\|=-(\vec{v} \cdot \hat{w})$. Armando esto con$\hat{p}=-\hat{w}$, obtenemos$\vec{p}=\|\vec{p}\| \hat{p}=-(\vec{v} \cdot \hat{w})(-\hat{w})=(\vec{v} \cdot \hat{w}) \hat{w}$ en este caso también.

$Screen Shot 2022-06-11 en 6.31.14 PM.png$

Si el ángulo entre$\vec{v}$ y$\vec{w}$ es$\frac{\pi}{2}$ entonces es fácil mostrar ⁴ eso$\vec{p}=\overrightarrow{0}$. Ya que$\vec{v} \perp \vec{w}$ en este caso,$\vec{v} \cdot \vec{w}=0$. De ello se deduce que$\vec{v} \cdot \hat{w}=0 \text { and } \vec{p}=\overrightarrow{0}=0 \hat{w}=(\vec{v} \cdot \hat{w}) \hat{w}$ en este caso, también. Esto nos da

Definición 11.12

Dejar$\vec{v}$ y$\vec{w}$ ser vectores distintos de cero. La proyección ortogonal de$\vec{v}$ en$\vec{w}$, denotada$\operatorname{proj}_{\vec{w}}(\vec{v})$ viene dada por$\operatorname{proj}_{\vec{w}}(\vec{v})=(\vec{v} \cdot \hat{w}) \hat{w}$.

La definición 11.12 nos da una buena idea de lo que hace el producto dot. El escalar$\vec{v} \cdot \hat{w}$ es una medida de cuánto del vector$\vec{v}$ está en la dirección del vector$\vec{w}$ y así se llama la proyección escalar de$\vec{v}$ y$\vec{w}$. Si bien la fórmula dada en la Definición 11.12 es teóricamente atractiva, debido a la presencia del vector unitario normalizado$\vec{w}$, calcular la proyección usando la fórmula$\operatorname{proj}_{\vec{w}}(\vec{v})=(\vec{v} \cdot \hat{w}) \hat{w}$ puede ser desordenado. Presentamos otras dos fórmulas que a menudo se utilizan en la práctica.

Teorema 11.26. Fórmulas alternativas para proyecciones vectoriales

Si$\vec{v}$ y$\vec{w}$ son vectores distintos de cero entonces\[\operatorname{proj}_{\vec{w}}(\vec{v})=(\vec{v} \cdot \hat{w}) \hat{w}=\left(\frac{\vec{v} \cdot \vec{w}}{\|\vec{w}\|^{2}}\right) \vec{w}=\left(\frac{\vec{v} \cdot \vec{w}}{\vec{w} \cdot \vec{w}}\right) \vec{w}\nonumber\]

La prueba del Teorema 11.26, que dejamos al lector como ejercicio, equivale a usar la fórmula$\hat{w}=\left(\frac{1}{\|\vec{w}\|}\right) \vec{w}$ y propiedades del producto punto. Es hora de dar un ejemplo.

Ejemplo 11.9.4

Dejar$\vec{v}=\langle 1,8\rangle$ y$\vec{w}=\langle-1,2\rangle$. Encuentra$\vec{p}=\operatorname{proj}_{\vec{w}}(\vec{v})$, y parcela$\vec{v}$,$\vec{w}$ y$\vec{p}$ en posición estándar.

Solución

Nos encontramos$\vec{v} \cdot \vec{w}=\langle 1,8\rangle \cdot\langle-1,2\rangle=(-1)+16=15$ y$\vec{w} \cdot \vec{w}=\langle-1,2\rangle \cdot\langle-1,2\rangle=1+4=5$. De ahí,$\vec{p}=\frac{\vec{v} \cdot \vec{w}}{\vec{w} \cdot \vec{w}} \vec{w}=\frac{15}{5}\langle-1,2\rangle=\langle-3,6\rangle$. Tramamos$\vec{v}$,$\vec{w}$ y$\vec{p}$ abajo.

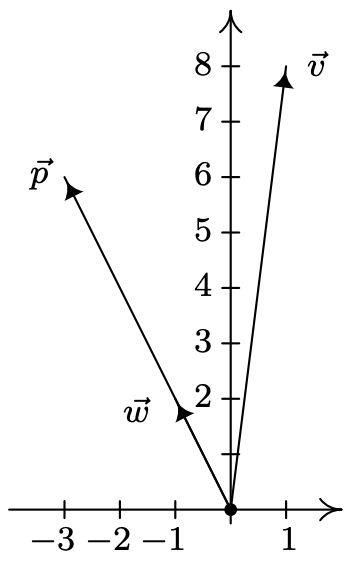
$Screen Shot 2022-06-11 a las 7.00.46 PM.png$

Supongamos que quisiéramos verificar que nuestra respuesta$\vec{p}$ en el Ejemplo 11.9.4 es de hecho la proyección ortogonal de$\vec{v}$ onto$\vec{w}$. Primero notamos que dado que$\vec{p}$ es un múltiplo escalar de$\vec{w}$, tiene la dirección correcta, entonces lo que queda por verificar es la condición de ortogonalidad. Considere el vector$\vec{q}$ cuyo punto inicial es el punto terminal de$\vec{p}$ y cuyo punto terminal es el punto terminal de$\vec{v}$.

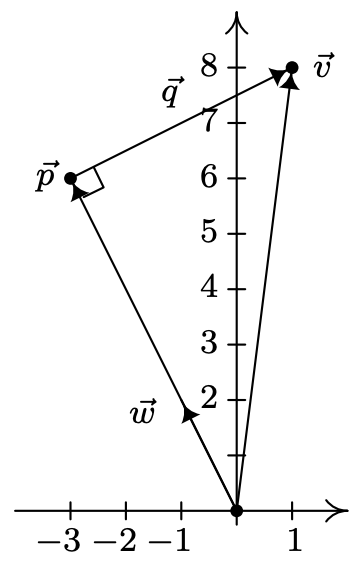
$Screen Shot 2022-06-11 en 7.04.10 PM.png$

A partir de la definición de aritmética vectorial$\vec{p}+\vec{q}=\vec{v}$,, así que$\vec{q}=\vec{v}-\vec{p}$. En el caso del Ejemplo 11.9.4,$\vec{v}=\langle 1,8\rangle$ y$\vec{p}=\langle-3,6\rangle$, así$\vec{q}=\langle 1,8\rangle-\langle-3,6\rangle=\langle 4,2\rangle$. Entonces$\vec{q} \cdot \vec{w}=\langle 4,2\rangle \cdot\langle-1,2\rangle=(-4)+4=0$, lo que muestra$\vec{q} \perp \vec{w}$, según se requiera. Este resultado se generaliza en el siguiente teorema.

Teorema 11.27. Teorema de descomposición generalizada

Dejar$\vec{q}$ y$\vec{w}$ ser vectores distintos de cero. Hay vectores únicos$\vec{p}$ y$\vec{q}$ tal que$\vec{v}=\vec{p}+\vec{q}$ donde$\vec{p}=k \vec{w}$ para algunos escalar$k$, y$\vec{q} \cdot \vec{w}=0$.

Obsérvese que si los vectores$\vec{p}$ y$\vec{q}$ en el Teorema 11.27 son distintos de cero, entonces podemos decir que$\vec{p}$ es paralelo ⁵ a$\vec{w}$ y$\vec{q}$ es ortogonal a$\vec{w}$. En este caso, el vector a veces$\vec{p}$ se llama el 'componente vectorial de$\vec{v}$ paralelo a$\vec{w}$ 'y$\vec{q}$ se llama el 'componente vectorial de$\vec{v}$ ortogonal a$\vec{w}$.' Para probar el Teorema 11.27, tomamos$\vec{p}=\operatorname{proj}_{\vec{w}}(\vec{v})$ y$\vec{q}=\vec{v}-\vec{p}$. Entonces$\vec{p}$ es, por definición, un múltiplo escalar de$\vec{w}$. A continuación, calculamos$\vec{q} \cdot \vec{w}$.

\ [\ begin {alineado}
\ vec {q}\ cdot\ vec {w} & =(\ vec {v} -\ vec {p})\ cdot\ vec {w} &\ text {Definición de}\ vec {q}.\\ &=\ vec {v}\ cdot\ vec {w} -\ vec {p}\ cdot\ c {w} & &\ text {Propiedades del producto Dot}\\ &=\ vec {v}\ cdot\ vec {w} -\ left (\ frac {\ vec {v}\ cdot\ vec {w}} {\ vec {w} \ cdot\ vec {w}}\ vec {w}\ derecha)\ cdot\ vec {w} &\ text {Desde}\ vec {p} =\ nombreoperador {proj} _ {\ vec {w}} (\ vec {v}).\\ &=\ vec {v}\ cdot\ vec {w} -\ izquierda (\ frac {\ vec {v}\ cdot\ vec {w}} {\ vec {w}\ cdot\ vec {w}}\ derecha) (\ vec {w}\ cdot\ vec {w}) &\ text {Propiedades del producto Dot.}\\ &=\ vec {v}\ cdot\ vec {w} -\ vec {v}\ cdot\ vec {w} & &\\ &=0 & &\ end {alineado}\ nonumber\]

De ahí,$\vec{q} \cdot \vec{w}=0$, según se requiera. En este punto, hemos demostrado que los vectores$\vec{p}$ y$\vec{q}$ garantizados por el Teorema 11.27 existen. Ahora necesitamos demostrar que son únicos. Supongamos$\vec{v}=\vec{p}+\vec{q}=\vec{p}^{\prime}+\vec{q}^{\prime}$ donde los vectores$\vec{p}^{\prime}$ y$\vec{q}^{\prime}$ satisfacen las mismas propiedades descritas en el Teorema 11.27 como$\vec{p}$ y$\vec{q}$. Entonces$\vec{p}-\vec{p}^{\prime}=\vec{q}^{\prime}-\vec{q}$, entonces$\vec{w} \cdot\left(\vec{p}-\vec{p}^{\prime}\right)=\vec{w} \cdot\left(\vec{q}^{\prime}-\vec{q}\right)=\vec{w} \cdot \vec{q}^{\prime}-\vec{w} \cdot \vec{q}=0-0=0$. De ahí,$\vec{w} \cdot\left(\vec{p}-\vec{p}^{\prime}\right)=0$. Ahora hay escalares$k$ y$k^{\prime}$ así que$\vec{p}=k \vec{w}$ y$\vec{p}^{\prime}=k^{\prime} \vec{w}$. Esto significa$\vec{w} \cdot\left(\vec{p}-\vec{p}^{\prime}\right)=\vec{w} \cdot\left(k \vec{w}-k^{\prime} \vec{w}\right)=\vec{w} \cdot\left(\left[k-k^{\prime}\right] \vec{w}\right)=\left(k-k^{\prime}\right)(\vec{w} \cdot \vec{w})=\left(k-k^{\prime}\right)\|\vec{w}\|^{2}$. Ya que$\vec{w} \neq \overrightarrow{0}$,$\|\vec{w}\|^{2} \neq 0$, lo que significa que la única forma$\vec{w} \cdot\left(\vec{p}-\vec{p}^{\prime}\right)=\left(k-k^{\prime}\right)\|\vec{w}\|^{2}=0$ es para$k-k^{\prime}=0$, o$k=k^{\prime}$. Esto significa$\vec{p}=k \vec{w}=k^{\prime} \vec{w}=\vec{p}^{\prime}$. Con$\vec{q}^{\prime}-\vec{q}=\vec{p}-\vec{p}^{\prime}=\vec{p}-\vec{p}=\overrightarrow{0}$, debe ser eso$\vec{q}^{\prime}=\vec{q}$ también. De ahí que hayamos demostrado que sólo hay una manera de escribir$\vec{v}$ como suma de vectores como se describe en el Teorema 11.27.

Cerramos esta sección con una aplicación del producto punto. En Física, si$F$ se ejerce una fuerza constante sobre una distancia$d$, el trabajo$W$ realizado por la fuerza viene dado por$W = F d$. Aquí, asumimos que la fuerza se está aplicando en la dirección del movimiento. Si la fuerza aplicada no está en la dirección del movimiento, podemos usar el producto punto para encontrar el trabajo realizado. Considera el escenario a continuación donde$\vec{F}$ se aplica la fuerza constante para mover un objeto del punto$P$ al punto$Q$.

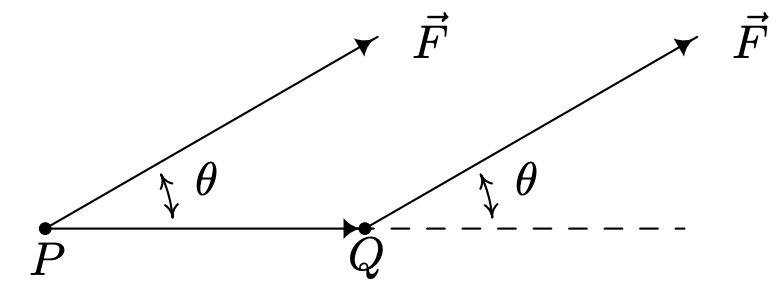
$Screen Shot 2022-06-12 en 2.39.05 PM.png$

Para encontrar el trabajo$W$ realizado en este escenario, necesitamos encontrar cuánta fuerza$\vec{F}$ está en la dirección del movimiento$\overrightarrow{P Q}$. Esto es precisamente lo que$\vec{F} \cdot \widehat{P Q}$ representa el producto punto. Ya que la distancia que recorre el objeto es$\|\overrightarrow{P Q}\|$, obtenemos$W=(\vec{F} \cdot \widehat{P Q})\|\overrightarrow{P Q}\|$. Ya que$\overrightarrow{P Q}=\|\overrightarrow{P Q}\| \widehat{P Q}$$W=(\vec{F} \cdot \widehat{P Q})\|\overrightarrow{P Q}\|=\vec{F} \cdot(\|\overrightarrow{P Q}\| \widehat{P Q})=\vec{F} \cdot \overrightarrow{P Q}=\|\vec{F}\|\|\overrightarrow{P Q}\| \cos (\theta)$,, donde$\theta$ está el ángulo entre la fuerza aplicada$\vec{F}$ y la trayectoria del movimiento$\overrightarrow{P Q}$. Hemos demostrado lo siguiente.

Teorema 11.28. Trabajar como un producto Dot

Supongamos que$\vec{F}$ se aplica una fuerza constante a lo largo del vector$\overrightarrow{P Q}$. El trabajo$W$ realizado por$\vec{F}$ viene dado por\[W=\vec{F} \cdot \overrightarrow{P Q}=\|\vec{F}\|\|\overrightarrow{P Q}\| \cos (\theta),\nonumber\] dónde$\theta$ está el ángulo entre$\vec{F}$ y$\overrightarrow{P Q}$.

Ejemplo 11.9.5

Taylor ejerce una fuerza de 10 libras para tirar de su vagón a una distancia de 50 pies sobre terreno nivelado. Si el asa del vagón hace un$30^{\circ}$ ángulo con la horizontal, ¿cuánto trabajo hizo Taylor tirando del vagón? Supongamos que Taylor ejerce la fuerza de 10 libras en$30^{\circ}$ ángulo durante la duración de los 50 pies.

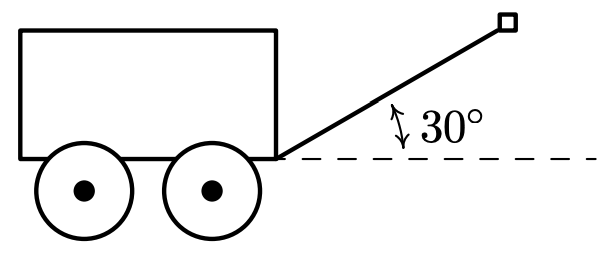
$Screen Shot 2022-06-12 en 2.52.45 PM.png$

Solución

Hay dos formas de atacar este problema. Una manera es encontrar los vectores$\vec{F}$ y$\overrightarrow{P Q}$ mencionados en el Teorema 11.28 y computar$W=\vec{F} \cdot \overrightarrow{P Q}$. Para ello, asumimos que el origen es en el punto donde el asa del vagón se encuentra con el vagón y el$x$ eje positivo se encuentra a lo largo de la línea discontinua en la figura anterior. Ya que la fuerza aplicada es de una constante de 10 libras, tenemos$\|\vec{F}\|=10$. Ya que se está aplicando en un ángulo constante de$\theta=30^{\circ}$ con respecto al$x$ eje positivo, la Definición 11.8 nos da$\vec{F}=10\left\langle\cos \left(30^{\circ}, \sin \left(30^{\circ}\right)\right\rangle=\langle 5 \sqrt{3}, 5\rangle\right.$. Dado que el vagón está siendo arrastrado a lo largo de 50 pies en la dirección positiva, el vector de desplazamiento es$\overrightarrow{P Q}=50 \hat{\imath}=50\langle 1,0\rangle=\langle 50,0\rangle$. Obtenemos$W=\vec{F} \cdot \overrightarrow{P Q}=\langle 5 \sqrt{3}, 5\rangle \cdot\langle 50,0\rangle=250 \sqrt{3}$. Dado que la fuerza se mide en libras y la distancia se mide en pies, obtenemos$W=250 \sqrt{3}$ pie-libras. Alternativamente, podemos usar la formulación$W=\|\vec{F}\|\|\overrightarrow{P Q}\| \cos (\theta)$ para obtener$W=(10 \text { pounds })(50 \text { feet }) \cos \left(30^{\circ}\right)=250 \sqrt{3}$ pie-libras de trabajo.

11.9.1 Ejercicios

En Ejercicios 1 - 20, usa el par de vectores$\vec{v}$ y$\vec{w}$ para encontrar las siguientes cantidades.

$\vec{v} \cdot \vec{w}$
$\operatorname{proj}_{\vec{w}}(\vec{v})$
El ángulo θ (en grados) entre$\vec{v}$ y$\vec{w}$
$\vec{q}=\vec{v}-\operatorname{proj}_{\vec{w}}(\vec{v})$($\vec{q} \cdot \vec{w}=0$Demuéstralo.)

$\vec{v}=\langle-2,-7\rangle \text { and } \vec{w}=\langle 5,-9\rangle$
$\vec{v}=\langle-6,-5\rangle \text { and } \vec{w}=\langle 10,-12\rangle$
$\vec{v}=\langle 1, \sqrt{3}\rangle \text { and } \vec{w}=\langle 1,-\sqrt{3}\rangle$
$\vec{v}=\langle 3,4\rangle \text { and } \vec{w}=\langle-6,-8\rangle$
$\vec{v}=\langle-2,1\rangle \text { and } \vec{w}=\langle 3,6\rangle$
$\vec{v}=\langle-3 \sqrt{3}, 3\rangle \text { and } \vec{w}=\langle-\sqrt{3},-1\rangle$
$\vec{v}=\langle 1,17\rangle \text { and } \vec{w}=\langle-1,0\rangle$
$\vec{v}=\langle 3,4\rangle \text { and } \vec{w}=\langle 5,12\rangle$
$\vec{v}=\langle-4,-2\rangle \text { and } \vec{w}=\langle 1,-5\rangle$
$\vec{v}=\langle-5,6\rangle \text { and } \vec{w}=\langle 4,-7\rangle$
$\vec{v}=\langle-8,3\rangle \text { and } \vec{w}=\langle 2,6\rangle$
$\vec{v}=\langle 34,-91\rangle \text { and } \vec{w}=\langle 0,1\rangle$
$\vec{v}=3 \hat{\imath}-\hat{\jmath} \text { and } \vec{w}=4 \hat{\jmath}$
$\vec{v}=-24 \hat{\imath}+7 \hat{\jmath} \text { and } \vec{w}=2 \hat{\imath}$
$\vec{v}=\frac{3}{2} \hat{\imath}+\frac{3}{2} \hat{\jmath} \text { and } \vec{w}=\hat{\imath}-\hat{\jmath}$
$\vec{v}=5 \hat{\imath}+12 \hat{\jmath} \text { and } \vec{w}=-3 \hat{\imath}+4 \hat{\jmath}$
$\vec{v}=\left\langle\frac{1}{2}, \frac{\sqrt{3}}{2}\right\rangle \text { and } \vec{w}=\left\langle-\frac{\sqrt{2}}{2}, \frac{\sqrt{2}}{2}\right\rangle$
$\vec{v}=\left\langle\frac{\sqrt{2}}{2}, \frac{\sqrt{2}}{2}\right\rangle \text { and } \vec{w}=\left\langle\frac{1}{2},-\frac{\sqrt{3}}{2}\right\rangle$
$\vec{v}=\left\langle\frac{\sqrt{3}}{2}, \frac{1}{2}\right\rangle \text { and } \vec{w}=\left\langle-\frac{\sqrt{2}}{2},-\frac{\sqrt{2}}{2}\right\rangle$
$\vec{v}=\left\langle\frac{1}{2},-\frac{\sqrt{3}}{2}\right\rangle \text { and } \vec{w}=\left\langle\frac{\sqrt{2}}{2},-\frac{\sqrt{2}}{2}\right\rangle$
Se requiere una fuerza de 1500 libras para remolcar un remolque. Encuentra el trabajo realizado remolcando el tráiler a lo largo de un tramo plano de carretera de 300 pies. Supongamos que la fuerza se aplica en la dirección del movimiento.
Encuentra el trabajo realizado levantando un libro de 10 libras 3 pies recto hacia arriba en el aire. Supongamos que la fuerza de la gravedad está actuando recto hacia abajo.
Supongamos que Taylor llena su vagón de rocas y debe ejercer una fuerza de 13 libras para tirar de su vagón por el patio. Si mantiene un$15^{\circ}$ ángulo entre el asa del vagón y la horizontal, computa cuánto trabajo hace Taylor tirando de su vagón 25 pies. Redondee su respuesta a dos decimales.
En el Ejercicio 61 de la Sección 11.8, dos universitarios borrachos han llenado un barril de cerveza vacío con rocas que arrastran por la calle tirando de dos cuerdas adheridas. El más fuerte de los dos alumnos tira con una fuerza de 100 libras sobre una cuerda que hace un$13^{\circ}$ ángulo con la dirección del movimiento. (En este caso, el barril estaba siendo jalado hacia el este y el rumbo del estudiante estaba$\mathrm{N} 77^{\circ} \mathrm{E}$.) Encuentra el trabajo realizado por este alumno si el barril es arrastrado 42 pies.
Encuentra el trabajo realizado empujando un barril de 200 libras 10 pies hacia arriba por una$12.5^{\circ}$ pendiente. Ignorar todas las fuerzas que actúan sobre el cañón excepto la gravedad, que actúa hacia abajo. Redondee su respuesta a dos decimales.
CONSEJO: Como se está trabajando solo para superar la gravedad, la fuerza que se aplica actúa directamente hacia arriba. Esto significa que el ángulo entre la fuerza aplicada en este caso y el movimiento del objeto no es el$12.5^{\circ}$ de la inclinación!
Demostrar la propiedad distributiva del producto punto en el Teorema 11.22.
Terminar el comprobante de la propiedad escalar del producto punto en el Teorema 11.22.
Usar la identidad en el Ejemplo 11.9.1 para probar la Ley de Paralelogramo\[\|\vec{v}\|^{2}+\|\vec{w}\|^{2}=\frac{1}{2}\left[\|\vec{v}+\vec{w}\|^{2}+\|\vec{v}-\vec{w}\|^{2}\right]\nonumber\]
Sabemos que$|x+y| \leq|x|+|y|$ para todos los números reales$x$ y$y$ por el Triángulo Desigualdad establecido en el Ejercicio 36 en la Sección 2.2. Ahora podemos establecer un Triángulo Desigualdad para vectores. En este ejercicio, demostramos que$\|\vec{u}+\vec{v}\| \leq\|\vec{u}\|+\|\vec{v}\|$ para todos los pares de vectores$\vec{u}$ y$\vec{v}$.
1. (Paso 1) Demuéstralo$\|\vec{u}+\vec{v}\|^{2}=\|\vec{u}\|^{2}+2 \vec{u} \cdot \vec{v}+\|\vec{v}\|^{2}$.
2. (Paso 2) Demuéstralo$|\vec{u} \cdot \vec{v}| \leq\|\vec{u}\|\|\vec{v}\|$. Se trata de la célebre Desigualdad Cauchy-Schwarz. ⁶ (Pista: Para mostrar esta desigualdad, comience con el hecho de que$|\vec{u} \cdot \vec{v}|=|\|\vec{u}\|\|\vec{v}\| \cos (\theta)|$ y use el hecho de que$|\cos (\theta)| \leq 1$ para todos θ.)
3. (Paso 3) Demuéstralo$\|\vec{u}+\vec{v}\|^{2}=\|\vec{u}\|^{2}+2 \vec{u} \cdot \vec{v}+\|\vec{v}\|^{2} \leq\|\vec{u}\|^{2}+2|\vec{u} \cdot \vec{v}|+\|\vec{v}\|^{2} \leq\|\vec{u}\|^{2}+2\|\vec{u}\|\|\vec{v}\|+\|\vec{v}\|^{2}=(\|\vec{u}\|+\|\vec{v}\|)^{2}$.
4. (Paso 4) Utilice el Paso 3 para mostrar que$\|\vec{u}+\vec{v}\| \leq\|\vec{u}\|+\|\vec{v}\|$ para todos los pares de vectores$\vec{u}$ y$\vec{v}$.
5. Como bono agregado, ahora podemos demostrar que la Desigualdad del Triángulo se$|z+w| \leq|z|+|w|$ mantiene para todos los números complejos$z$ y$w$ también. Identifica el número complejo$z=a+b i$ con el vector$u=\langle a, b\rangle$ e identifica el número complejo$w = c + di$ con el vector$v = hc$, di y ¡solo sigue tu nariz!

11.9.2 Respuestas

\ (\ begin {alineado}
&\ vec {v} =\ langle-2, -7\ rangle\ texto {y}\ vec {w} =\ langle 5, -9\ rangle\\
&\ vec {v}\ cdot\ vec {w} =53\
&\ theta=45^ {\ circ}\\
&\ nombreoperador {proj} _\ vec {w}} (\ vec {v}) =\ izquierda\ langle\ frac {5} {2}, -\ frac {9} {2}\ derecha\ rangle\\
&\ vec {q} =\ izquierda\ langle-\ frac {9} {2}, -\ frac {5} {2}\ derecha\ rangle
\ final {alineado}\)
\ (\ begin {alineado}
&\ vec {v} =\ langle-6, -5\ rangle\ texto {y}\ vec {w} =\ langle 10, -12\ rangle\\
&\ vec {v}\ cdot\ vec {w} =0\\
&\ theta=90^ {\ circ}\\
&\ nombreoperador {proj} _ {vec {w}} (\ vec {v}) =\ langle 0,0\ rangle\\
&\ vec {q} =\ langle-6, -5\ rangle
\ end {alineado}\)
\ (\ begin {alineado}
&\ vec {v} =\ langle 1,\ sqrt {3}\ rangle\ texto {y}\ vec {w} =\ langle 1, -\ sqrt {3}\ rangle\\
&\ vec {v}\ cdot\ vec {w} =-2\
&\ theta=120^ {\ circ}\
&\ nombreoperador {proj} _ {\ vec {w}} (\ vec {v}) =\ izquierda\ langle-\ frac {1} {2} ,\ frac {\ sqrt {3}} {2}\ derecha\ rangle\\
&\ vec {q} =\ izquierda\ langle\ frac {3} {2},\ frac {\ sqrt {3}} {2}\ derecha\ rangle
\ final {alineado}\)
\ (\ begin {alineado}
&\ vec {v} =\ langle 3,4\ rangle\ texto {y}\ vec {w} =\ langle-6, -8\ rangle\\
&\ vec {v}\ cdot\ vec {w} =-50\
&\ theta=180^ {\ circ}\\
&\ nombreoperador {proj} _ {\ vec c {w}} (\ vec {v}) =\ langle 3,4\ rangle\\
&\ vec {q} =\ langle 0,0\ rangle
\ end {alineado}\)
\ (\ begin {alineado}
&\ vec {v} =\ langle-2,1\ rangle\ texto {y}\ vec {w} =\ langle 3,6\ rangle\\
&\ vec {v}\ cdot\ vec {w} =0\\
&\ theta=90^ {\ circ}\\
&\ nombreoperador {proj} _ {\ vec {w}} (\ vec {v}) =\ langle 0,0\ rangle\\
& amp;\ vec {q} =\ langle-2,1\ rangle
\ end {alineado}\)
\ (\ begin {alineado}
&\ vec {v} =\ langle-3\ sqrt {3}, 3\ rangle\ texto {y}\ vec {w} =\ langle-\ sqrt {3}, -1\ rangle\\
&\ vec {v}\ cdot\ vec {w} =6\
&\ theta=60^ {\ circ}\
&\ nombreoperador {proj} _ {\ vec {w}} (\ vec {v}) =\ izquierda\ langle-\ frac {3\ sqrt {3}} {2}, -\ frac {3} {2}\ derecha\ rangle\\
&\ vec {q} =\ izquierda\ langle-\ frac {3\ sqrt {3}} {2},\ frac {9} {2}\ derecha\ rangle
\ final {alineado}\)
\ (\ begin {alineado}
&\ vec {v} =\ langle 1,17\ rangle\ texto {y}\ vec {w} =\ langle-1,0\ rangle\\
&\ vec {v}\ cdot\ vec {w} =-1\
&\ theta\ aproximadamente 93.37^ {\ circ}\\
&\ nombreoperador {proj} _ {\ vec {w}} (\ vec {v}) =\ langle 1,0\ rangle\\
&\ vec {q} =\ langle 0,17\ rangle
\ end {alineado}\)
\ (\ begin {alineado}
&\ vec {v} =\ langle 3,4\ rangle\ texto {y}\ vec {w} =\ langle 5,12\ rangle\\
&\ vec {v}\ cdot\ vec {w} =63\
&\ theta\ aproximadamente 14.25^ {\ circ}\\
&\ nombreoperador {proj} _ {\ vec {w}} (\ vec {v}) =\ izquierda\ langle\ frac {315} {169}, \ frac {756} {169}\ derecha\ rangle\\
&\ vec {q} =\ izquierda\ langle\ frac {192} {169}, -\ frac {80} {169}\ derecha\ rangle
\ final {alineado}\)
\ (\ begin {alineado}
&\ vec {v} =\ langle-4, -2\ rangle\ texto {y}\ vec {w} =\ langle 1, -5\ rangle\\
&\ vec {v}\ cdot\ vec {w} =6\
&\ theta\ aproximadamente 74.74^ {\ circ}\\
&\ nombreoperador {proj} _\ vec {w}} (\ vec {v}) =\ izquierda\ langle\ frac {3} {13}, -\ frac {15} {13}\ derecha\ rangle\\
&\ vec {q} =\ izquierda\ langle-\ frac {55} {13}, -\ frac {11} {13}\ derecha\ rangle
\ final {alineado}\)
\ (\ begin {alineado}
&\ vec {v} =\ langle-5,6\ rangle\ texto {y}\ vec {w} =\ langle 4, -7\ rangle\\
&\ vec {v}\ cdot\ vec {w} =-62\
&\ theta\ aproximadamente 169.94^ {\ circ}\\
&\ nombreoperador {proj} _ {\ vec {w}} (\ vec {v}) =\ izquierda\ langle-\ frac {248} {65} ,\ frac {434} {65}\ derecha\ rangle\\
&\ vec {q} =\ izquierda\ langle-\ frac {77} {65}, -\ frac {44} {65}\ derecha\ rangle
\ final {alineado}\)
\ (\ begin {alineado}
&\ vec {v} =\ langle-8,3\ rangle\ texto {y}\ vec {w} =\ langle 2,6\ rangle\\
&\ vec {v}\ cdot\ vec {w} =2\
&\ theta\ aproximadamente 87.88^ {\ circ}\\
&\ nombreoperador {proj} _ {\ vec {w}} (\ vec {v}) =\ izquierda\ langle\ frac {1} {10},\ frac {3} {10}\ derecha\ rangle\\
&\ vec {q} =\ izquierda\ langle-\ frac {81} {10},\ frac {27} {10}\ derecha\ rangle
\ final {alineado}\)
\ (\ begin {alineado}
&\ vec {v} =\ langle 34, -91\ rangle\ texto {y}\ vec {w} =\ langle 0,1\ rangle\\
&\ vec {v}\ cdot\ vec {w} =-91\
&\ theta\ aprox 159.51^ {\ circ}\\
&\ nombreoperador {proj} _ {\ vec {w}} (\ vec {v}) =\ langle 0, -91\ rangle\\
&\ vec {q} =\ langle 34,0\ rangle
\ end {alineado}\)
\ (\ begin {alineado}
&\ vec {v} =3\ hat {\ imath} -\ hat {\ jmath}\ text {y}\ vec {w} =4\ hat {\ jmath}\\
&\ vec {v}\ cdot\ vec {w} =-4\
&\ thatoreta\ aprox 108.43^ {\ circ}\\
&\ operopernombre {proj} _ {\ vec {w}} (\ vec {v}) =\ langle 0, -1\ rangle\\
&\ vec {q} =\ langle 3,0\ rangle
\ end {alineado}\)
\ (\ begin {alineado}
&\ vec {v} =-24\ hat {\ imath} +7\ hat {\ jmath}\ text {y}\ vec {w} =2\ hat {\ imath}\\
&\ vec {v}\ cdot\ vec {w} =-48\
&\ theta\ aprox 163.74^ {\ circ}\
&\ nombreoperador {proj} _ {\ vec {w}} (\ vec {v}) =\ langle-24,0\ rangle \\
&\ vec {q} =\ langle 0,7\ rangle
\ end {alineado}\)
\ (\ begin {alineado}
&\ vec {v} =\ frac {3} {2}\ hat {\ imath} +\ frac {3} {2}\ hat {\ jmath}\ text {y}\ vec {w} =\ hat {\ imath} -\ hat {\ jmath}\\
&\ vec {v}\ cdot\ vec {w} =0\\
&\ theta=90^ {\ circ}\\
&\ nombreoperador {proj} _ {\ vec {w}} (\ vec {v}) =\ langle 0,0\ rangle\\
&\ vec {q} =\ izquierda\ langle\ frac {3} {2},\ frac {3} {2}\ derecha\ rangle
\ final {alineado}\)
\ (\ begin {alineado}
&\ vec {v} =5\ hat {\ imath} +12\ hat {\ jmath}\ text {y}\ vec {w} =-3\ hat {\ imath} +4\ hat {\ jmath}\\
&\ vec {v}\ cdot\ vec {w} =33\
&\ theta\ aproximadamente 59.49^ {\ c}\\
&\ nombreoperador {proj} _ {\ vec {w}} (\ vec {v}) =\ izquierda\ langle-\ frac {99} {25},\ frac {132} {25}\ derecha\ rangle\\
&\ vec {q} =\ izquierda\ langle\ frac {224} {25},\ frac {168} {25}\ derecha\ rangle
\ final {alineado}\)
\ (\ begin {alineado}
&\ vec {v} =\ izquierda\ langle\ frac {1} {2},\ frac {\ sqrt {3}} {2}\ derecha\ rangle\ texto {y}\ vec {w} =\ izquierda\ langle-\ frac {\ sqrt {2}} {2},\ frac {\ sqrt {2}} 2}\ derecha\ rangle\\
&\ vec {v}\ cdot\ vec {w} =\ frac {\ sqrt {6} -\ sqrt {2}} {4}\\
&\ theta=75^ {\ circ }\\
&\ nombreoperador {proj} _ {\ vec {w}} (\ vec {v}) =\ izquierda\ langle\ frac {1-\ sqrt {3}} {4},\ frac {\ sqrt {3} -1} {4}\ derecha\ rangle\
&\ vec {q} =\ izquierda\ langle\ frac {1+\ sqrt {3}} {4},\ frac {1+\ sqrt {3}} {4}\ derecha\ rangle
\ final {alineado}\)
\ (\ begin {alineado}
&\ vec {v} =\ izquierda\ langle\ frac {\ sqrt {2}} {2},\ frac {\ sqrt {2}} {2}\ derecha\ rangle\ texto {y}\ vec {w} =\ izquierda\ langle\ frac {1} {2}, -\ frac {\ sqrt {3}} 2}\ derecha\ rangle\\
&\ vec {v}\ cdot\ vec {w} =\ frac {\ sqrt {2} -\ sqrt {6}} {4}\\
&\ theta=105^ {\ circ }\\
&\ nombreoperador {proj} _ {\ vec {w}} (\ vec {v}) =\ izquierda\ langle\ frac {\ sqrt {2} -\ sqrt {6}} {8},\ frac {3\ sqrt {2} -\ sqrt {6}} {8}\ derecha\ rangle\\
&\ vec {q}\ izquierda\ langle\ frac {3\ sqrt {2} +\ sqrt {6}} {8},\ frac {\ sqrt {2} +\ sqrt {6}} {8}\ derecha\ rangle
\ final {alineado}\)
\ (\ begin {alineado}
&\ vec {v} =\ izquierda\ langle\ frac {\ sqrt {3}} {2},\ frac {1} {2}\ derecha\ rangle\ texto {y}\ vec {w} =\ izquierda\ langle-\ frac {\ sqrt {2}} {2}, -\ frac {\ sqrt {2} {2}\ derecha\ rangle\\
&\ vec {v}\ cdot\ vec {w} =-\ frac {\ sqrt {6} +\ sqrt {2}} {4}\\
&\ theta=165^ {\ circ}\\
&\ nombreoperador {proj} _ {\ vec {w}} (\ vec {v}) =\ izquierda\ langle\ frac {\ sqrt {3} +1} {4},\ frac {\ sqrt {3} +1} {4}\ derecha\ rangle\
&\ vec {q} =\ izquierda\ langle\ frac {sqac\ rt {3} -1} {4},\ frac {1-\ sqrt {3}} {4}\ derecha\ rangle
\ final {alineado}\)
\ (\ begin {alineado}
&\ vec {v} =\ izquierda\ langle\ frac {1} {2}, -\ frac {\ sqrt {3}} {2}\ derecha\ rangle\ texto {y}\ vec {w} =\ izquierda\ langle\ frac {\ sqrt {2}} {2}, -\ frac {\ sqrt {2} {2}\ derecha\ rangle\\
&\ vec {v}\ cdot\ vec {w} =\ frac {\ sqrt {6} +\ sqrt {2}} {4}\\
&\ theta=15^ {\ circ} \\
&\ nombreoperador {proj} _ {\ vec {w}} (\ vec {v}) =\ izquierda\ langle\ frac {\ sqrt {3} +1} {4}, -\ frac {\ sqrt {3} +1} {4}\ derecha\ rangle\
&\ vec {q} =\ izquierda\ langle\ frac {1-\ sqr rt {3}} {4},\ frac {1-\ sqrt {3}} {4}\ derecha\ rangle
\ final {alineado}\)
$(1500 \text { pounds }) \text { ( } 300 \text { feet) } \cos \left(0^{\circ}\right)=450,000 \text { foot-pounds }$
$(10 \text { pounds })(3 \text { feet }) \cos \left(0^{\circ}\right)=30 \text { foot-pounds }$
$\text { (13 pounds })(25 \text { feet }) \cos \left(15^{\circ}\right) \approx 313.92 \text { foot-pounds }$
$\text { (100 pounds })\left(42 \text { feet) } \cos \left(13^{\circ}\right) \approx 4092.35\right. \text { foot-pounds }$
$\text { (200 pounds })(10 \text { feet }) \cos \left(77.5^{\circ}\right) \approx 432.88 \text { foot-pounds }$

Referencia

¹ Desde$\vec{v}=\|\vec{v}\| \hat{v} \text { and } \vec{w}=\|\vec{w}\| \hat{w}, \text { if } \hat{v}=\hat{w} \text { then } \vec{w}=\|\vec{w}\| \hat{v}=\frac{\|\vec{w}\|}{\|\vec{v}\|}(\|\vec{v}\| \hat{v})=\frac{\|\vec{w}\|}{\|\vec{v}\|} \vec{v}$. En este caso,$k=\frac{\|\vec{w}\|}{\|\vec{v}\|}>0$.

² Tenga en cuenta que no hay 'propiedad cero del producto' para el producto punto ya que ninguno$\vec{v}$ y lo$\vec{w}$ es$\overrightarrow{0}$, todavía$\vec{v} \cdot \vec{w}=0$.

³ Véase Ejercicio 2.1.1 en la Sección 2.1.

⁴ En este caso, el punto$R$ coincide con el punto$O$, así$\vec{p}=\overrightarrow{O R}=\overrightarrow{O O}=\overrightarrow{0}$.

⁵ Ver Ejercicio 64 en la Sección 11.8.

⁶ También se le conoce con otros nombres. Echa un vistazo a este sitio para más detalles.