1.3: Tasas de Cambio y Comportamiento de las Gráficas
- Page ID
- 121392
Objetivos de aprendizaje
- Encuentra la tasa promedio de cambio de una función.
- Utilice una gráfica para determinar dónde una función está aumentando, disminuyendo o siendo constante.
- Utilice una gráfica para localizar máximos locales y mínimos locales.
- Utilice una gráfica para localizar el máximo absoluto y el mínimo absoluto.
Los costos de la gasolina han experimentado algunas fluctuaciones salvajes en las últimas décadas. En la tabla se\(\PageIndex{1}\) enumera el costo promedio, en dólares, de un galón de gasolina para los años 2005-2012. El costo de la gasolina puede considerarse como una función del año.
| \(y\) | 2005 | 2006 | 2007 | 2008 | 2009 | 2010 | 2011 | 2012 |
|---|---|---|---|---|---|---|---|---|
| \(C(y)\) | 2.31 | 2.62 | 2.84 | 3.30 | 2.41 | 2.84 | 3.58 | 3.68 |
Si solo nos interesara cómo cambiaron los precios de la gasolina entre 2005 y 2012, podríamos calcular que el costo por galón había aumentado de $2.31 a $3.68, un incremento de $1.37. Si bien esto es interesante, podría ser más útil observar cuánto cambió el precio por año. En esta sección, investigaremos cambios como estos.
Encontrar la tasa promedio de cambio de una función
El cambio de precio por año es una tasa de cambio porque describe cómo cambia una cantidad de salida en relación con el cambio en la cantidad de entrada. Podemos ver que el precio de la gasolina en la Tabla\(\PageIndex{1}\) no cambiaba por la misma cantidad cada año, por lo que la tasa de cambio no fue constante. Si usamos solo los datos de inicio y finalización, estaríamos encontrando la tasa promedio de cambio durante el período de tiempo especificado. Para encontrar la tasa promedio de cambio, dividimos el cambio en el valor de salida por el cambio en el valor de entrada.
\[\begin{align*} \text{Average rate of change}&=\dfrac{\text{Change in output}}{\text{Change in input}} \\[4pt] &=\dfrac{\Delta y}{\Delta x}\\[4pt] &=\dfrac{y_2-y_1}{x_2-x_1}\\[4pt] &=\dfrac{f(x_2)-f(x_1)}{x_2-x_1}\end{align*} \label{1.3.1}\]
La letra griega\(\Delta\) (delta) significa el cambio en una cantidad; leemos la relación como “delta-\(y\) sobre delta-\(x\)” o “el cambio en\(y\) dividido por el cambio en”\(x\). Ocasionalmente escribimos\(\Delta f\) en lugar de\(\Delta y\), lo que todavía representa el cambio en el valor de salida de la función resultante de un cambio en su valor de entrada. No significa que estemos cambiando la función en alguna otra función.
En nuestro ejemplo, el precio de la gasolina aumentó $1.37 de 2005 a 2012. A lo largo de 7 años, la tasa promedio de cambio fue
\[\dfrac{\Delta y}{\Delta x}=\dfrac{$1.37}{7 \text{years}}\approx \text{0.196 dollars per year.} \label{1.3.2}\]
En promedio, el precio del gas aumentó aproximadamente 19.6¢ cada año. Otros ejemplos de tasas de cambio incluyen:
- Una población de ratas que aumenta en 40 ratas por semana
- Un automóvil que viaja 68 millas por hora (la distancia recorrida cambia 68 millas cada hora a medida que pasa el tiempo)
- Un automóvil manejando 27 millas por galón (la distancia recorrida cambia en 27 millas por cada galón)
- La corriente a través de un circuito eléctrico aumenta en 0.125 amperios por cada voltio de voltaje aumentado
- La cantidad de dinero en una cuenta universitaria disminuye en $4,000 por trimestre
Definición: Tasa de cambio
Una tasa de cambio describe cómo cambia una cantidad de salida en relación con el cambio en la cantidad de entrada. Las unidades en una tasa de cambio son “unidades de salida por unidades de entrada”.
La tasa promedio de cambio entre dos valores de entrada es el cambio total de los valores de función (valores de salida) dividido por el cambio en los valores de entrada.
\[\dfrac{\Delta y}{\Delta x}=\dfrac{f(x_2)-f(x_1)}{x_2-x_1}\]
Cómo...
Dado el valor de una función en diferentes puntos, calcular la tasa promedio de cambio de una función para el intervalo entre dos valores\(x_1\) y\(x_2\).
- Calcular la diferencia\(y_2−y_1=\Delta y\).
- Calcular la diferencia\(x_2−x_1=\Delta x\).
- Encuentra la proporción\(\dfrac{\Delta y}{\Delta x}\).
Ejemplo\(\PageIndex{1}\): Computing an Average Rate of Change
Utilizando los datos de la Tabla\(\PageIndex{1}\), encuentra la tasa promedio de cambio del precio de la gasolina entre 2007 y 2009.
Solución
En 2007, el precio de la gasolina era de $2.84. En 2009, el costo fue de $2.41. La tasa promedio de cambio es
\[\begin{align*} \dfrac{\Delta y}{\Delta x}&=\dfrac{y_2−y_1}{x_2−x_1} \\[4pt] &=\dfrac{$2.41−$2.84}{2009−2007} \\[4pt] &=\dfrac{−$0.43}{2 \text{ years}} \\[4pt] &=−$0.22 \text{ per year} \end{align*}\]
Análisis
Tenga en cuenta que una disminución se expresa por un cambio negativo o “aumento negativo”. Una tasa de cambio es negativa cuando la salida disminuye a medida que aumenta la entrada o cuando la salida aumenta a medida que disminuye la entrada.
Ejercicio\(\PageIndex{1}\)
Utilizando los datos de la Tabla\(\PageIndex{1}\), encuentra la tasa promedio de cambio entre 2005 y 2010.
- Solución
-
\(\dfrac{$2.84−$2.315}{5 \text{ years}} =\dfrac{$0.535}{5 \text{ years}} =$0.106 \text{per year.}\)
Ejemplo\(\PageIndex{2}\): Computing Average Rate of Change from a Graph
Dada la función que\(g(t)\) se muestra en la Figura\(\PageIndex{1}\), encuentre la tasa promedio de cambio en el intervalo\([−1,2]\).
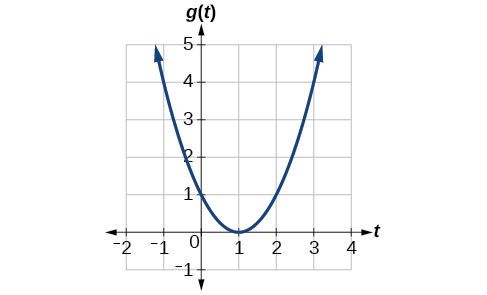
Solución
En\(t=−1\), La figura\(\PageIndex{2}\) muestra\(g(−1)=4\). En\(t=2\), la gráfica muestra\(g(2)=1\).
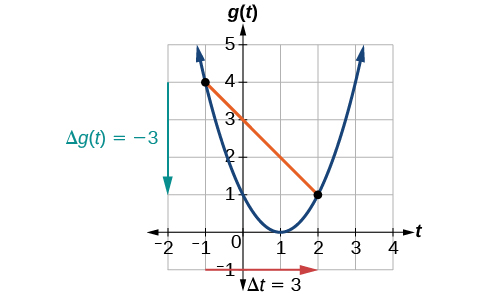
El cambio horizontal\(\Delta t=3\) se muestra por la flecha roja, y el cambio vertical\(\Delta g(t)=−3\) se muestra por la flecha turquesa. La salida cambia en —3 mientras que la entrada cambia en 3, dando una tasa promedio de cambio de
\[\dfrac{1−4}{2−(−1)}=\dfrac{−3}{3}=−1\]
Análisis
Tenga en cuenta que el orden que elegimos es muy importante. Si, por ejemplo, usamos\(\dfrac{y_2−y_1}{x_1−x_2}\), no obtendremos la respuesta correcta. Decidir qué punto será 1 y qué punto será 2, y mantener las coordenadas fijas como\((x_1,y_1)\) y\((x_2,y_2)\).
Ejemplo\(\PageIndex{3}\): Computing Average Rate of Change from a Table
Después de recoger a una amiga que vive a 10 millas de distancia, Anna registra su distancia de casa a lo largo del tiempo. Los valores se muestran en la Tabla\(\PageIndex{2}\). Encuentra su velocidad promedio durante las primeras 6 horas.
| \(t\)(horas) | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
|---|---|---|---|---|---|---|---|---|
| \(D(t)\)(millas) | 10 | 55 | 90 | 153 | 214 | 240 | 292 | 300 |
Solución
Aquí, la velocidad promedio es la tasa promedio de cambio. Viajó 292 millas en 6 horas, para una velocidad promedio de
\[\begin{align*}\dfrac{292−10}{6−0}&=\dfrac{282}{6}\\[4pt] &= 47\end{align*}\]
La velocidad promedio es de unas 47 millas por hora.
Análisis
Debido a que la velocidad no es constante, la velocidad promedio depende del intervalo elegido. Para el intervalo\([2,3]\), la velocidad promedio es de 63 millas por hora.
Ejemplo\(\PageIndex{4}\): Computing Average Rate of Change for a Function Expressed as a Formula
Calcular la tasa promedio de cambio de\(f(x)=x^2−\frac{1}{x}\) en el intervalo\([2, 4]\).
Solución
Podemos comenzar calculando los valores de las funciones en cada punto final del intervalo.
\[\begin{align*}f(2)&=2^2−\frac{1}{2} f(4)&=4^2−\frac{1}{4} \\[4pt] &=4−\frac{1}{2} &=16−\frac{1}{4} \\[4pt] &=72 &=\frac{63}{4}\end{align*}\]
Ahora calculamos la tasa promedio de cambio.
\[\begin{align*}\text{Average rate of change} &=\dfrac{f(4)−f(2)}{4−2} \\[4pt] &=\dfrac{\frac{63}{4}-\frac{7}{2}}{4-2} \\[4pt] &=\dfrac{\frac{49}{4}}{2} \\[4pt] &= \dfrac{49}{8}\end{align*}\]
Ejercicio\(\PageIndex{2}\)
Encuentra la tasa promedio de cambio de\(f(x)=x−2\sqrt{x}\) en el intervalo\([1, 9]\).
- Solución
-
\(\frac{1}{2}\)
Ejemplo\(\PageIndex{5}\): Finding the Average Rate of Change of a Force
La fuerza electrostática\(F\), medida en newtons, entre dos partículas cargadas puede estar relacionada con la distancia entre las partículas\(d\), en centímetros, por la fórmula\(F(d)=\frac{2}{d^2}\). Encuentra la tasa promedio de cambio de fuerza si la distancia entre las partículas se incrementa de 2 cm a 6 cm.
Solución
Estamos calculando la tasa promedio de cambio de\(F(d)=\dfrac{2}{d^2}\) en el intervalo\([2,6]\).
\[\begin{align*}\text{Average rate of change }&=\dfrac{F(6)−F(2)}{6−2} \\[4pt] &=\dfrac{\frac{2}{6^2}-\frac{2}{2^2}}{6-2} & \text{Simplify} \\[4pt] &=\dfrac{\frac{2}{36}-\frac{2}{4}}{4} \\[4pt] &=\dfrac{-\frac{16}{36}}{4} & \text{Combine numerator terms.} \\[4pt] &=−\dfrac{1}{9} & \text{Simplify}\end{align*}\]
La tasa promedio de cambio es\(−\frac{1}{9}\) newton por centímetro.
Ejemplo\(\PageIndex{6}\): Finding an Average Rate of Change as an Expression
Encuentra la tasa promedio de cambio de\(g(t)=t^2+3t+1\) en el intervalo\([0, a]\). La respuesta será una expresión que involucre\(a\).
Solución
Utilizamos la fórmula promedio de tasa de cambio.
\(\begin{align*}\text{Average rate of change} &=\dfrac{g(a)−g(0)}{a−0} & \text{Evaluate.} \\[4pt] &=\dfrac{(a^2+3a+1)−(0^2+3(0)+1)}{a−0} & \text{Simplify.} \\[4pt] &=\dfrac{a^2+3a+1−1}{a} & \text{Simplify and factor.}\\[4pt] &= \dfrac{a(a+3)}{a} & \text{Divide by the common factor a.}\\[4pt] &= a+3 \end{align*}\)
Este resultado nos indica la tasa promedio de cambio en términos de un punto entre\(t=0\) y cualquier otro punto\(t=a\). Por ejemplo, en el intervalo\([0,5]\), la tasa promedio de cambio sería\(5+3=8\).Ejercicio\(\PageIndex{3}\)
Encuentra la tasa promedio de cambio de\(f(x)=x^2+2x−8\) en el intervalo\([5, a]\).
- Solución
-
\(a+7\)
Uso de una Gráfica para Determinar Dónde una Función está Aumentando, Disminuyendo o Constante
Como parte de explorar cómo cambian las funciones, podemos identificar intervalos sobre los cuales la función está cambiando de maneras específicas. Decimos que una función está aumentando en un intervalo si los valores de la función aumentan a medida que los valores de entrada aumentan dentro de ese intervalo. Del mismo modo, una función disminuye en un intervalo si los valores de la función disminuyen a medida que los valores de entrada aumentan a lo largo de ese intervalo. La tasa promedio de cambio de una función creciente es positiva, y la tasa promedio de cambio de una función decreciente es negativa. La figura\(\PageIndex{3}\) muestra ejemplos de intervalos crecientes y decrecientes en una función.
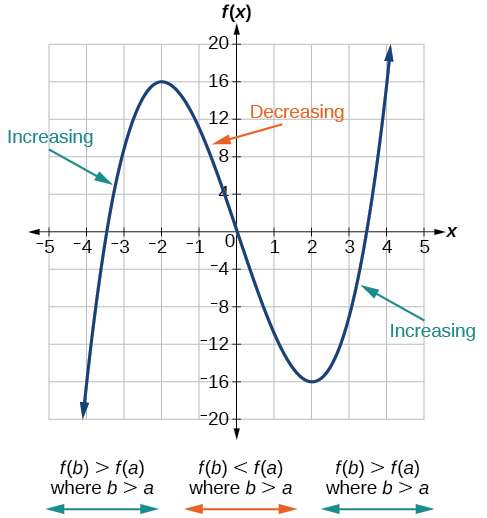
Si bien algunas funciones están aumentando (o disminuyendo) en todo su dominio, muchas otras no lo son. Un valor de la entrada donde una función cambia de aumentar a disminuir (a medida que vamos de izquierda a derecha, es decir, a medida que aumenta la variable de entrada) se denomina máximo local. Si una función tiene más de una, decimos que tiene máximos locales. De manera similar, un valor de la entrada donde una función cambia de disminuir a aumentar a medida que aumenta la variable de entrada se denomina mínimo local. La forma plural es “mínimos locales”. En conjunto, los máximos y mínimos locales se denominan extremos locales, o valores extremos locales, de la función. (La forma singular es “extrema”.) A menudo, el término local se sustituye por el término relativo. En este texto, utilizaremos el término local.
Claramente, una función no aumenta ni disminuye en un intervalo donde es constante. Una función tampoco está aumentando ni disminuyendo en los extremos. Tenga en cuenta que tenemos que hablar de extremos locales, porque cualquier extremo local dado como se define aquí no es necesariamente el máximo más alto o el mínimo más bajo en todo el dominio de la función.
Para la función cuya gráfica se muestra en la Figura\(\PageIndex{4}\), el máximo local es 16, y ocurre en\(x=−2\). El mínimo local es −16 y ocurre en\(x=2\).
![Gráfica de un polinomio que muestra los intervalos crecientes y decrecientes y el máximo local.] Definición de un máximo local](https://math.libretexts.org/@api/deki/files/916/CNX_Precalc_Figure_01_03_014.jpg)
Para ubicar los máximos y mínimos locales a partir de una gráfica, necesitamos observar la gráfica para determinar dónde la gráfica alcanza sus puntos más altos y más bajos, respectivamente, dentro de un intervalo abierto. Al igual que la cima de una montaña rusa, la gráfica de una función es mayor en un máximo local que en puntos cercanos de ambos lados. La gráfica también será menor en un mínimo local que en los puntos vecinos. La figura\(\PageIndex{5}\) ilustra estas ideas para un máximo local.
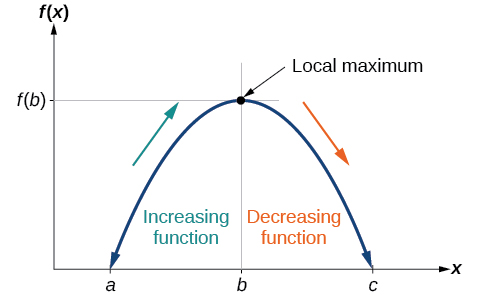
Estas observaciones nos llevan a una definición formal de extrema local.
Minima Local y Maxima Local
- Una función\(f\) es una función creciente en un intervalo abierto si\(f(b)>f(a)\) para cada\(a\),\(b\) intervalo donde\(b>a\).
- Una función\(f\) es una función decreciente en un intervalo abierto si\(f(b)<f(a)\) para cada\(a\),\(b\) intervalo donde\(b>a\).
Una función\(f\) tiene un máximo local en un punto\(b\) en un intervalo abierto\((a,c)\) si\(f(b)\) es mayor o igual a\(f(x)\) para cada punto\(x\) (\(x\)no es igual\(b\)) en el intervalo. De igual manera,\(f\) tiene un mínimo local\(b\) en un punto en\((a,c)\) si\(f(b)\) es menor o igual a\(f(x)\) para cada\(x\) (\(x\)no es igual\(b\)) en el intervalo.
Ejemplo\(\PageIndex{7}\) Finding Increasing and Decreasing Intervals on a Graph
Dada la función\(p(t)\) en la Figura\(\PageIndex{6}\), identificar los intervalos en los que la función parece estar aumentando.
![[Gráfica de un polinomio.]](https://math.libretexts.org/@api/deki/files/920/CNX_Precalc_Figure_01_03_006.jpg)
Solución
Vemos que la función no es constante en ningún intervalo. La función es aumentar donde se inclina hacia arriba a medida que nos movemos hacia la derecha y disminuyendo donde se inclina hacia abajo a medida que nos movemos hacia la derecha. La función parece estar aumentando de\(t=1\) a\(t=3\) y de\(t=4\) en adelante.
En la notación de intervalos, diríamos que la función parece estar aumentando en el intervalo\((1,3)\) y el intervalo\((4,\infty)\).
Análisis
Observe en este ejemplo que usamos intervalos abiertos (intervalos que no incluyen los puntos finales), porque la función no está aumentando ni disminuyendo a\(t=1\),\(t=3\), y\(t=4\). Estos puntos son los extremos locales (dos mínimos y un máximo).
Ejemplo\(\PageIndex{8}\): Finding Local Extrema from a Graph
Grafica la función\(f(x)=\frac{2}{x}+\frac{x}{3}\). A continuación, utilice la gráfica para estimar los extremos locales de la función y determinar los intervalos en los que la función está aumentando.
Solución
Usando la tecnología, encontramos que la gráfica de la función se ve así en la Figura\(\PageIndex{7}\). Parece que hay un punto bajo, o mínimo local, entre\(x=2\) y\(x=3\), y un punto alto de imagen especular, o máximo local, en algún lugar entre\(x=−3\) y\(x=−2\)
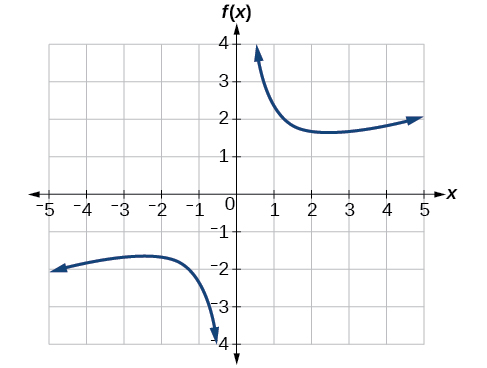 .
.
Análisis
La mayoría de las calculadoras gráficas y las utilidades gráficas pueden estimar la ubicación de máximos y mínimos. La figura\(\PageIndex{8}\) proporciona imágenes en pantalla de dos tecnologías diferentes, mostrando la estimación para el máximo y mínimo local.
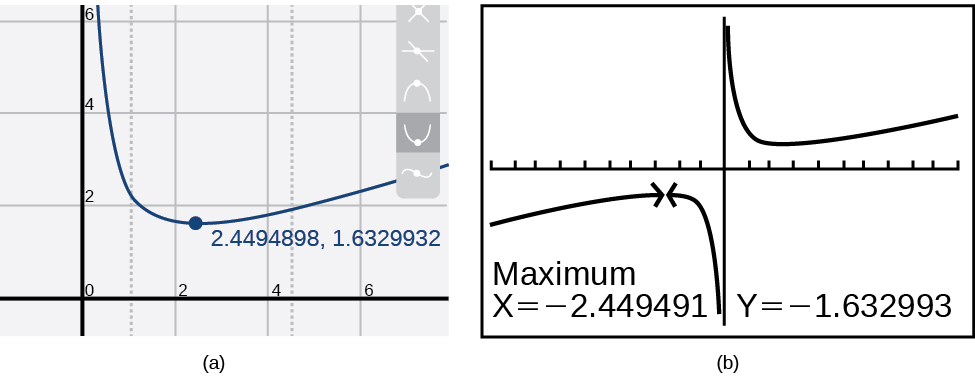
Con base en estas estimaciones, la función está aumentando en el intervalo\((−\infty,−2.449)\) y\((2.449,\infty)\). Observe que, si bien esperamos que los extremos sean simétricos, las dos tecnologías diferentes coinciden solo hasta cuatro decimales debido a los diferentes algoritmos de aproximación utilizados por cada una. (La ubicación exacta de los extremos está en\(\pm\sqrt{6}\), pero determinar esto requiere cálculo).
Ejercicio\(\PageIndex{8}\)
Grafica la función\(f(x)=x^3−6x^2−15x+20\) para estimar los extremos locales de la función. Úselos para determinar los intervalos en los que la función está aumentando y disminuyendo.
- Solución
-
El máximo local parece ocurrir en\((−1,28)\), y el mínimo local ocurre en\((5,−80)\). La función está aumentando\((−\infty,−1)\cup(5,\infty)\) y disminuyendo en\((−1,5)\).
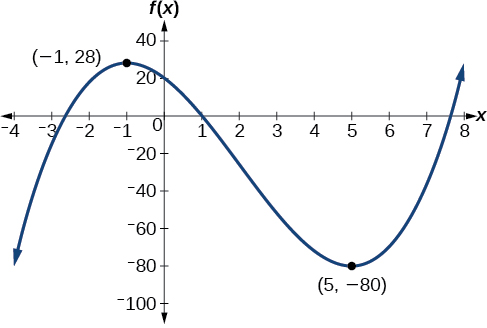
Gráfica de un polinomio con un máximo local en (-1, 28) y mínimo local en (5, -80).
Ejemplo\(\PageIndex{9}\): Finding Local Maxima and Minima from a Graph
Para la función f cuya gráfica se muestra en la Figura\(\PageIndex{9}\), busque todos los máximos y mínimos locales.
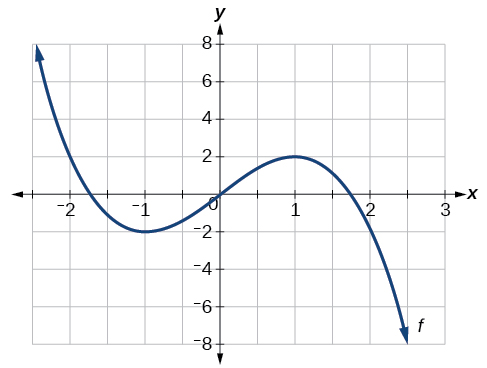
Solución
Observe la gráfica de\(f\). La gráfica alcanza un máximo local en\(x=1\) porque es el punto más alto en un intervalo abierto\(x=1\) alrededor.El máximo local es la coordenada y en\(x=1\), que es 2.
La gráfica alcanza un mínimo local en\(x=−1\) porque es el punto más bajo en un intervalo abierto alrededor\(x=−1\). El mínimo local es la coordenada y en\(x=−1\), que es −2.
Análisis de las funciones del kit de herramientas para aumentar o disminuir intervalos
Ahora volveremos a nuestras funciones del kit de herramientas y discutiremos su comportamiento gráfico en Figura\(\PageIndex{10}\)\(\PageIndex{11}\), Figura y Figura\(\PageIndex{12}\).

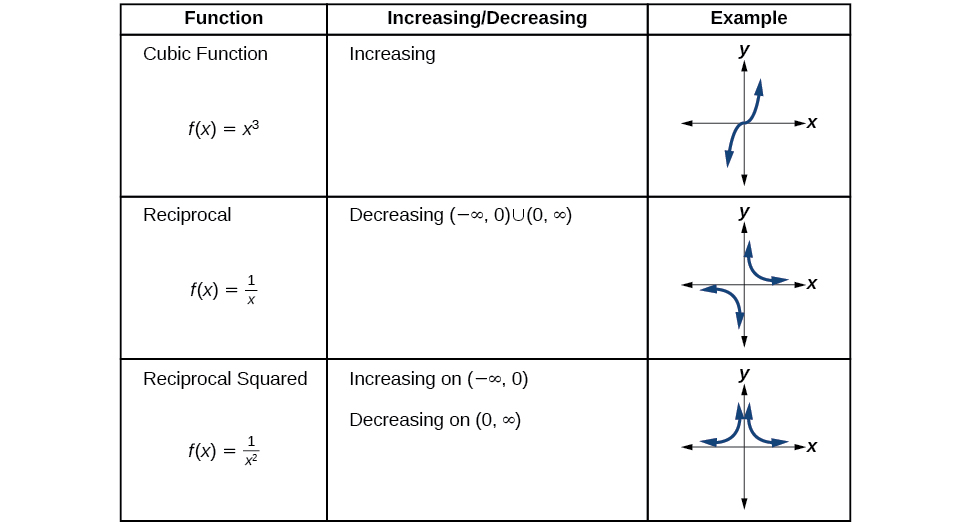 .
.
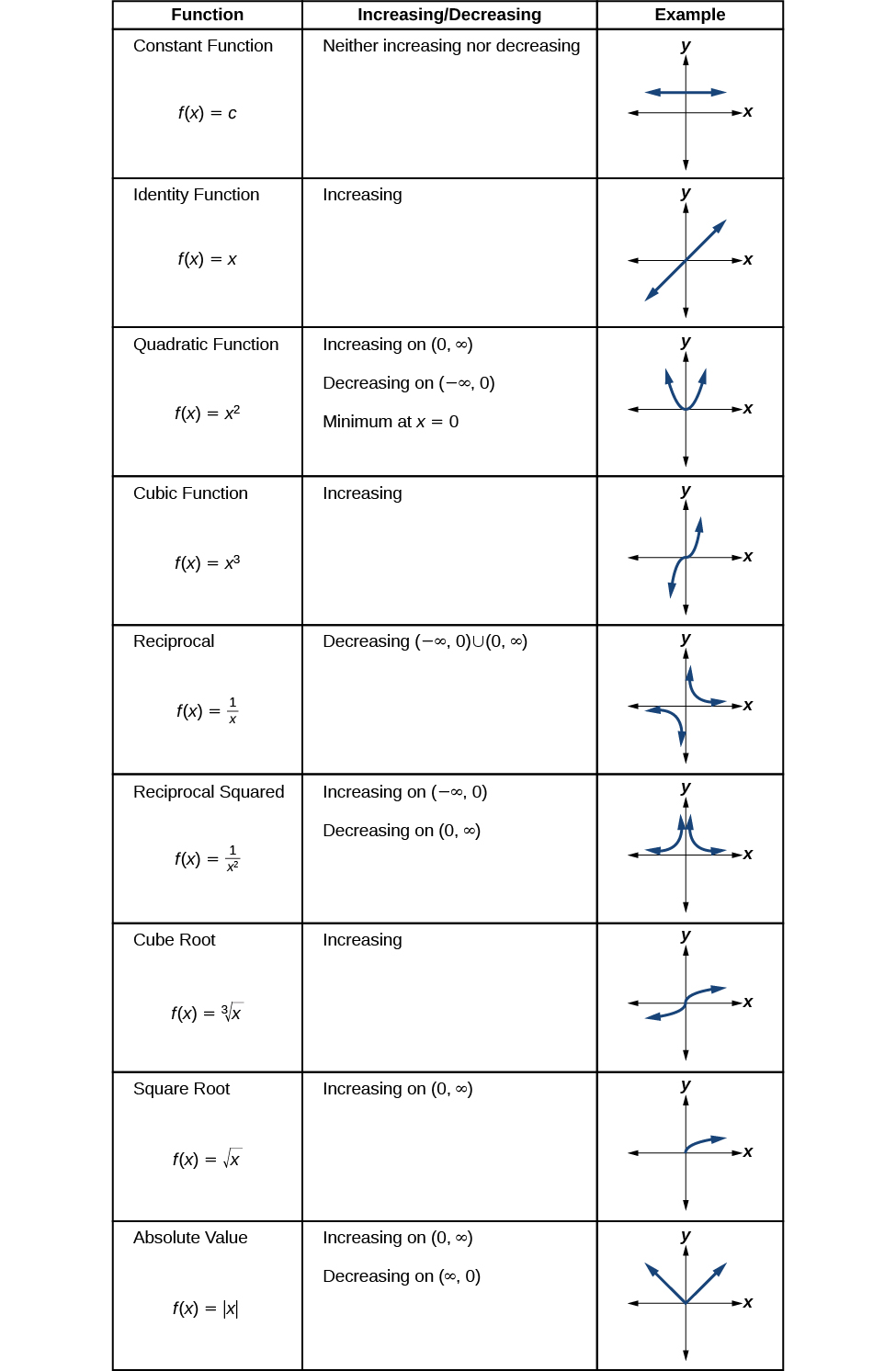
Figura\(\PageIndex{12}\)
Utilice una gráfica para localizar el máximo absoluto y el mínimo absoluto
Existe una diferencia entre ubicar los puntos más altos y más bajos en una gráfica en una región alrededor de un intervalo abierto (localmente) y ubicar los puntos más altos y más bajos en la gráfica para todo el dominio. Las coordenadas y (salida) en los puntos más altos y más bajos se denominan máximo absoluto y mínimo absoluto, respectivamente. Para ubicar máximos y mínimos absolutos a partir de una gráfica, necesitamos observar la gráfica para determinar dónde la gráfica alcanza los puntos más altos y más bajos en el dominio de la función (Figura\(\PageIndex{13}\)).
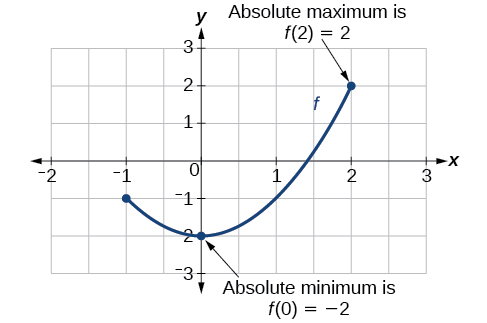
No todas las funciones tienen un valor máximo o mínimo absoluto. La función del kit de herramientas\(f(x)=x^3\) es una de esas funciones.
Máximo y Mínimo Absoluto
- El máximo absoluto de\(f\) at\(x=c\) es\(f(c)\) donde\(f(c)≥f(x)\) para todos\(x\) en el dominio de\(f\).
- El mínimo absoluto de\(f\) at\(x=d\) es\(f(d)\) donde\(f(d)≤f(x)\) para todos\(x\) en el dominio de\(f\).
Ejemplo\(\PageIndex{10}\): Finding Absolute Maxima and Minima from a Graph
Para la función f que se muestra en la Figura\(\PageIndex{14}\), encuentre todos los máximos y mínimos absolutos.
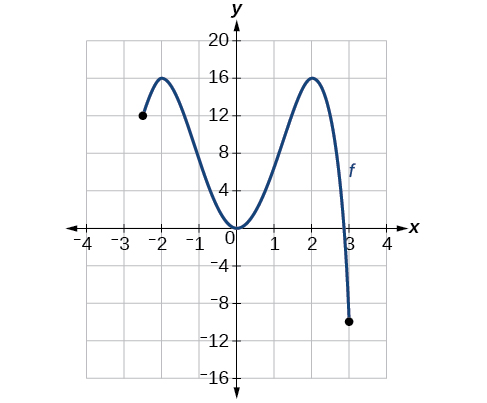
Solución
Observe la gráfica de\(f\). La gráfica alcanza un máximo absoluto en dos ubicaciones,\(x=−2\) y\(x=2\), debido a que en estas ubicaciones, la gráfica alcanza su punto más alto en el dominio de la función. El máximo absoluto es la coordenada\(x=−2\) y en y\(x=2\), que es 16.
La gráfica alcanza un mínimo absoluto en x=3, ya que es el punto más bajo en el dominio de la gráfica de la función. El mínimo absoluto es la coordenada y en x=3, que es −10.
Ecuaciones Clave
- Tasa promedio de cambio:\(\dfrac{\Delta y}{\Delta x}=\dfrac{f(x_2)-f(x_1)}{x_2-x_1}\)
Conceptos clave
- Una tasa de cambio relaciona un cambio en una cantidad de salida con un cambio en una cantidad de entrada. La tasa promedio de cambio se determina utilizando únicamente los datos de inicio y finalización. Ver Ejemplo.
- Identificar los puntos que marcan el intervalo en una gráfica se puede utilizar para encontrar la tasa promedio de cambio. Ver Ejemplo.
- La comparación de pares de valores de entrada y salida en una tabla también se puede utilizar para encontrar la tasa de cambio promedio. Ver Ejemplo.
- También se puede calcular una tasa de cambio promedio determinando los valores de función en los puntos finales de un intervalo descrito por una fórmula. Ver Ejemplo y Ejemplo.
- La tasa promedio de cambio a veces se puede determinar como una expresión. Ver Ejemplo.
- Una función está aumentando donde su tasa de cambio es positiva y decreciente donde su tasa de cambio es negativa. Ver Ejemplo.
- Un máximo local es donde una función cambia de aumentar a disminuir y tiene un valor de salida mayor (más positivo o menos negativo) que los valores de salida en valores de entrada vecinos.
- Un mínimo local es donde la función cambia de decreciente a creciente (a medida que aumenta la entrada) y tiene un valor de salida menor (más negativo o menos positivo) que los valores de salida en valores de entrada vecinos.
- Los mínimos y máximos también se llaman extremos.
- Podemos encontrar extremos locales a partir de una gráfica. Ver Ejemplo y Ejemplo.
- Los puntos más altos y más bajos de una gráfica indican los máximos y mínimos. Ver Ejemplo.


