3.E: Funciones polinómicas y racionales (Ejercicios)

3.1 Números Complejos

Verbal

1) Explicar cómo agregar números complejos.

Contestar

Suma las partes reales juntas y las partes imaginarias juntas.

2) ¿Cuál es el principio básico en la multiplicación de números complejos?

3) Dar un ejemplo para mostrar el producto de dos números imaginarios no siempre es imaginario.

Contestar

\(i\)veces\(i\) es igual\(-1\), que no es imaginario (las respuestas varían)

4) ¿Cuál es una característica de la trama de un número real en el plano complejo?

Algebraico

Para los ejercicios 5-10, evaluar las expresiones algebraicas.

5) Si\(f(x)=x^2+x−4\), evaluar\(f(2i)\).

Contestar

\(−8+2i\)

6) Si\(f(x)=x^3−2\), evaluar\(f(i)\).

7) Si\(f(x)=x^2+3x+5\), evaluar\(f(2+i)\).

Contestar

\(14+7i\)

8) Si\(f(x)=2x^2+x−3\), evaluar\(f(2−3i)\).

9) Si\(f(x)=\dfrac{x+1}{2−x}\), evaluar\(f(5i)\).

Responder

\(−\dfrac{23}{29}+\dfrac{15}{29}i\)

10) Si\(f(x)=\dfrac{1+2x}{x+3}\), evaluar\(f(4i)\).

Gráfica

Para los ejercicios 11-12, determinar el número de soluciones reales y no reales para cada función cuadrática mostrada.

11)

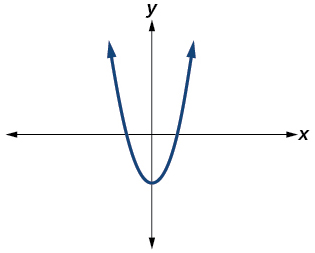
Responder

\(2\)real e\(0\) irreal

12)

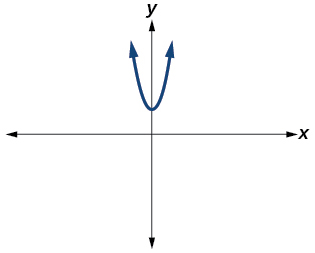
Para los ejercicios 13-16, trazar los números complejos en el plano complejo.

13)\(1−2i\)

Responder

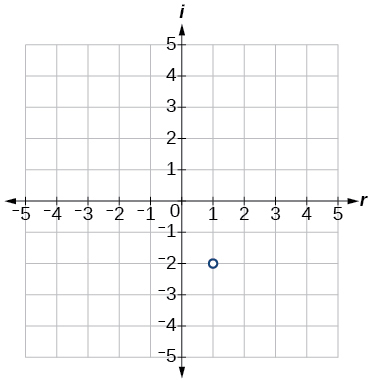
14)\(−2+3i\)

15)\(i\)

Responder

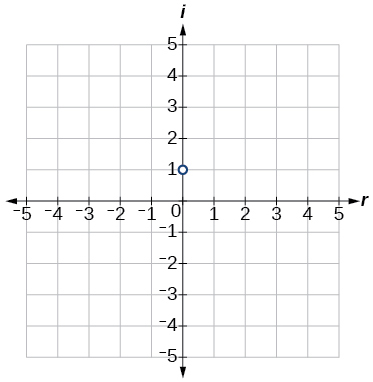
16)\(−3−4i\)

Numérico

Para los ejercicios 17-43, realizar la operación indicada y expresar el resultado como un número complejo simplificado.

17)\((3+2i)+(5−3i)\)

Responder

\(8−i\)

18)\((−2−4i)+(1+6i)\)

19)\((−5+3i)−(6−i)\)

Responder

\(−11+4i\)

20)\((2−3i)−(3+2i)\)

21)\((−4+4i)−(−6+9i)\)

Responder

\(2−5i\)

22)\((2+3i)(4i)\)

23)\((5−2i)(3i)\)

Responder

\(6+15i\)

24)\((6−2i)(5)\)

25)\((−2+4i)(8)\)

Responder

\(−16+32i\)

26)\((2+3i)(4−i)\)

27)\((−1+2i)(−2+3i)\)

Responder

\(−4−7i\)

28)\((4−2i)(4+2i)\)

29)\((3+4i)(3−4i)\)

Responder

\(25\)

30)\(\dfrac{3+4i}{2}\)

31)\(\dfrac{6−2i}{3}\)

Responder

\(2−\dfrac{2}{3}i\)

32)\(\dfrac{−5+3i}{2i}\)

33)\(\dfrac{6+4i}{i}\)

Responder

\(4−6i\)

34)\(\dfrac{2−3i}{4+3i}\)

35)\(\dfrac{3+4i}{2−i}\)

Responder

\(\dfrac{2}{5}+\dfrac{11}{5}i\)

36)\(\dfrac{2+3i}{2−3i}\)

37)\(\sqrt{−9}+3\sqrt{−16}\)

Responder

\(15i\)

38)\(−\sqrt{−4}−4\sqrt{−25}\)

39)\(\dfrac{2+\sqrt{−12}}{2}\)

Responder

\(1+i\sqrt{3}\)

40)\(\dfrac{4+\sqrt{−20}}{2}\)

41)\(i^8\)

Responder

\(1\)

42)\(i^{15}\)

43)\(i^{22}\)

Responder

\(−1\)

Tecnología

Para los ejercicios 44-48, usa una calculadora para ayudar a responder las preguntas.

44) Evaluar\((1+i)^k\) para\(k=4, 8, \) y\(12\) .Predecir el valor si\(k=16\).

45) Evaluar\((1−i)^k\) para\(k=2, 6,\) y\(10\) .Predecir el valor si\(k=14\).

Responder

\(128i\)

46) Evaluar\((1+i)^k-(1-i)^k\) para\(k=4\),\(8\), y\(12\). Predecir el valor para\(k=16\).

47) Demostrar que una solución de\(x^6+1=0\) es\(\dfrac{\sqrt{3}}{2}+\dfrac{1}{2}i\).

Responder

\((\dfrac{\sqrt{3}}{2}+\dfrac{1}{2}i)^6=−1\)

48) Demostrar que una solución de\(x^8−1=0\) es\(\dfrac{\sqrt{2}}{2}+\dfrac{\sqrt{2}}{2}i\).

Extensiones

Para los ejercicios 49-58, evaluar las expresiones, escribiendo el resultado como un número complejo simplificado.

49)\(\dfrac{1}{i}+\dfrac{4}{i^3}\)

Responder

\(3i\)

50)\(\dfrac{1}{i^{11}}−\dfrac{1}{i^{21}}\)

51)\(i^7(1+i^2)\)

Responder

\(0\)

52)\(i^{−3}+5i^7\)

53)\(\dfrac{(2+i)(4−2i)}{(1+i)}\)

Responder

\(5 – 5i\)

54)\(\dfrac{(1+3i)(2−4i)}{(1+2i)}\)

55)\(\dfrac{(3+i)^2}{(1+2i)^2}\)

Responder

\(−2i\)

56)\(\dfrac{3+2i}{2+i}+(4+3i)\)

57)\(\dfrac{4+i}{i}+\dfrac{3−4i}{1−i}\)

Responder

\(\dfrac{9}{2}−\dfrac{9}{2}i\)

58)\(\dfrac{3+2i}{1+2i}−\dfrac{2−3i}{3+i}\)

3.2 Funciones cuadráticas

Verbal

1) Explicar la ventaja de escribir una función cuadrática en forma estándar.

Responder

Cuando se escribe en esa forma, el vértice se puede identificar fácilmente.

2) ¿Cómo se puede utilizar el vértice de una parábola para resolver problemas del mundo real?

3) Explicar por qué\(a≠0\) se impone la condición de en la definición de la función cuadrática.

Responder

Si\(a=0\) entonces la función se convierte en una función lineal.

4) ¿Cuál es otro nombre para la forma estándar de una función cuadrática?

5) ¿Qué dos métodos algebraicos se pueden utilizar para encontrar las intercepciones horizontales de una función cuadrática?

Responder

Si es posible, podemos usar factoring. De lo contrario, podemos usar la fórmula cuadrática.

Algebraico

Para los ejercicios 6-13, reescribir las funciones cuadráticas en forma estándar y dar el vértice.

6)\(f(x)=x^2−12x+32\)

7)\(g(x)=x^2+2x−3\)

Responder

\(g(x)=(x+1)^2−4\), Vértice\((−1,−4)\)

8)\(f(x)=x^2−x\)

9)\(f(x)=x^2+5x−2\)

Responder

\(f(x)=\left(x+\dfrac{5}{2}\right)^2−\dfrac{33}{4}\), Vértice\(\left(−\dfrac{5}{2},−\dfrac{33}{4}\right)\)

10)\(h(x)=2x^2+8x−10\)

11)\(k(x)=3x^2−6x−9\)

Responder

\(k(x)=3(x−1)^2−12\), Vértice\((1,−12)\)

12)\(f(x)=2x^2−6x\)

13)\(f(x)=3x^2−5x−1\)

Responder

\(f(x)=3\left(x−\dfrac{5}{6}\right)^2−\dfrac{37}{12}\), Vértice\(\left(\dfrac{5}{6},−\dfrac{37}{12}\right)\)

Para los ejercicios 14-20, determinar si hay un valor mínimo o máximo para cada función cuadrática. Encuentra el valor y el eje de simetría.

14)\(y(x)=2x^2+10x+12\)

15)\(f(x)=2x^2−10x+4\)

Responder

El mínimo es\(−\dfrac{17}{2}\) y ocurre en\(\dfrac{5}{2}\). Eje de simetría es\(x=\dfrac{5}{2}\).

16)\(f(x)=−x^2+4x+3\)

17)\(f(x)=4x^2+x−1\)

Responder

El mínimo es\(−\dfrac{17}{16}\) y ocurre en\(−\dfrac{1}{8}\). Eje de simetría es\(x=−\dfrac{1}{8}\).

18)\(h(t)=−4t^2+6t−1\)

19)\(f(x)=\dfrac{1}{2}x^2+3x+1\)

Responder

El mínimo es\(−\dfrac{7}{2}\) y ocurre en\(−3\). Eje de simetría es\(x=−3\).

20)\(f(x)=−\dfrac{1}{3}x^2−2x+3\)

Para los ejercicios 21-25, determinar el dominio y el rango de la función cuadrática.

21)\(f(x)=(x−3)^2+2\)

Responder

El dominio es\((−∞,∞)\). El alcance es\([2,∞)\).

22)\(f(x)=−2(x+3)^2−6\)

23)\(f(x)=x^2+6x+4\)

Responder

El dominio es\((−∞,∞)\). El alcance es\([−5,∞)\).

24)\(f(x)=2x^2−4x+2\)

25)\(k(x)=3x^2−6x−9\)

Responder

El dominio es\((−∞,∞)\). El alcance es\([−12,∞)\).

Para los ejercicios 26-44, resolver las ecuaciones sobre los números complejos.

26)\(x^2=−25\)

27)\(x^2=−8\)

Responder

\({2i \sqrt{2},−2i \sqrt{2}}\)

28)\(x^2+36=0\)

29)\(x^2+27=0\)

Responder

\({3i \sqrt{3},−3i\sqrt{3}}\)

30)\(x^2+2x+5=0\)

31)\(x^2−4x+5=0\)

Responder

\({2+i,2−i}\)

32)\(x^2+8x+25=0\)

33)\(x^2−4x+13=0\)

Responder

\({2+3i,2−3i}\)

34)\(x^2+6x+25=0\)

35)\(x^2−10x+26=0\)

Responder

\({5+i,5−i}\)

36)\(x^2−6x+10=0\)

37)\(x(x−4)=20\)

Responder

\({2+2 \sqrt{6}, 2−2\sqrt{6}}\)

38)\(x(x−2)=10\)

39)\(2x^2+2x+5=0\)

Responder

\(\left\{−\dfrac{1}{2}+\dfrac{3}{2}i, −\dfrac{1}{2}−\dfrac{3}{2}i\right\}\)

40)\(5x^2−8x+5=0\)

41)\(5x^2+6x+2=0\)

Responder

\(\left\{−\dfrac{3}{5}+\dfrac{1}{5}i, −\dfrac{3}{5}−\dfrac{1}{5}i\right\}\)

42)\(2x^2−6x+5=0\)

43)\(x^2+x+2=0\)

Responder

\(\left\{−\dfrac{1}{2}+\dfrac{1}{2}i\sqrt{7}, −\dfrac{1}{2}−\dfrac{1}{2}i\sqrt{7}\right\}\)

44)\(x^2−2x+4=0\)

Para los ejercicios 45-52, usa el vértice\((h,k)\) y un punto en la gráfica\((x,y)\) para encontrar la forma general de la ecuación de la función cuadrática.

45)\((h,k)=(2,0),(x,y)=(4,4)\)

Responder

\(f(x)=x^2−4x+4\)

46)\((h,k)=(−2,−1),(x,y)=(−4,3)\)

47)\((h,k)=(0,1),(x,y)=(2,5)\)

Responder

\(f(x)=x^2+1\)

48)\((h,k)=(2,3),(x,y)=(5,12)\)

49)\((h,k)=(−5,3),(x,y)=(2,9)\)

Responder

\(f(x)=\dfrac{6}{49}x^2+\dfrac{60}{49}x+\dfrac{297}{49}\)

50)\((h,k)=(3,2),(x,y)=(10,1)\)

51)\((h,k)=(0,1),(x,y)=(1,0)\)

Responder

\(f(x)=−x^2+1\)

52)\((h,k)=(1,0),(x,y)=(0,1)\)

Gráfica

Para los ejercicios 53-58, esbozar una gráfica de la función cuadrática y dar el vértice, eje de simetría e intercepciones.

53)\(f(x)=x^2−2x\)

Responder

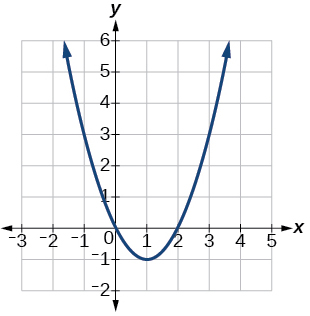
Vértice\((1, −1)\), Eje de simetría es\(x=1\). Las intercepciones son\((0,0), (2,0)\).

54)\(f(x)=x^2−6x−1\)

55)\(f(x)=x^2−5x−6\)

Responder

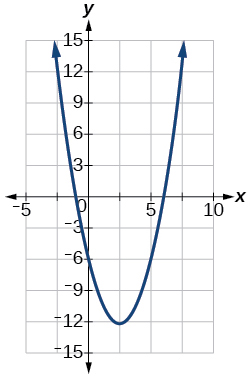
Vértice\(\left(\dfrac{5}{2},\dfrac{−49}{4}\right)\), Eje de simetría es\(x=\dfrac{5}{2}\). Las intercepciones son\((0,−6),(−1,0),(6,0)\).

56)\(f(x)=x^2−7x+3\)

57)\(f(x)=−2x^2+5x−8\)

Responder

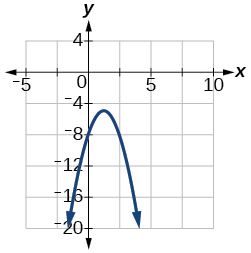
Vértice\(\left(\dfrac{5}{4}, −\dfrac{39}{8}\right)\), Eje de simetría es\(x=\dfrac{5}{4}\). Las intercepciones son\((0, −8)\).

58)\(f(x)=4x^2−12x−3\)

Responder

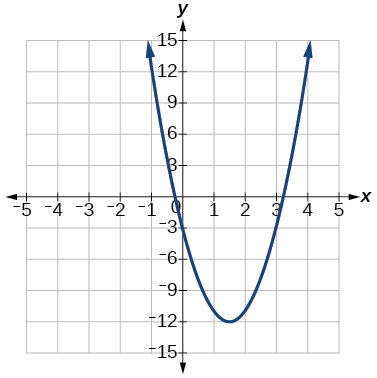
Para los ejercicios 59-64, escriba la ecuación para la función gráfica.

59)

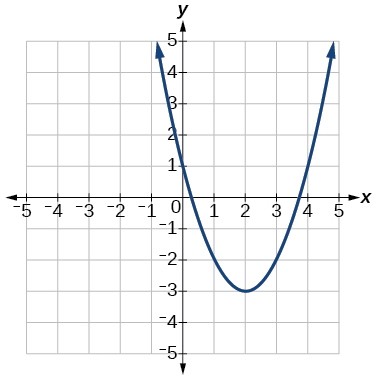
Responder

\(f(x)=x^2−4x+1\)

60)

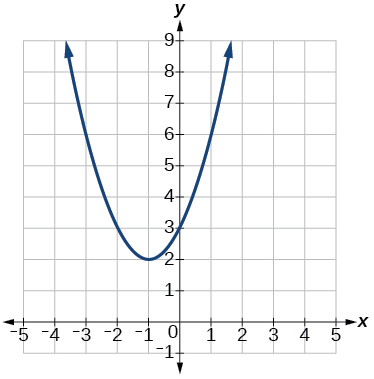
61)

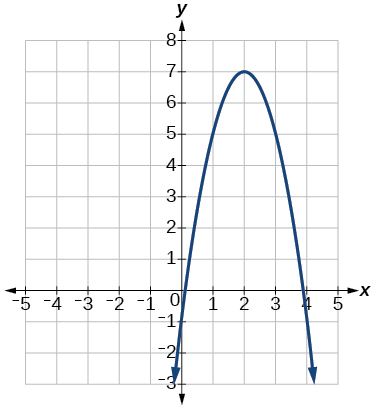
Responder

\(f(x)=−2x^2+8x−1\)

62)

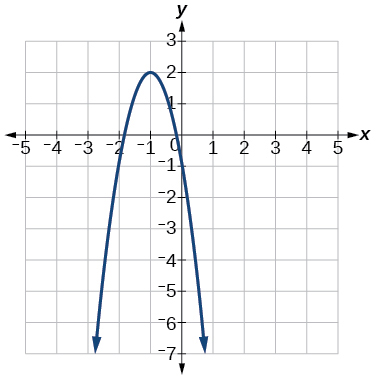
63)

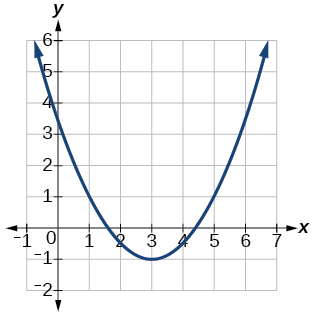
Responder

\(f(x)=\dfrac{1}{2}x^2−3x+\dfrac{7}{2}\)

64)

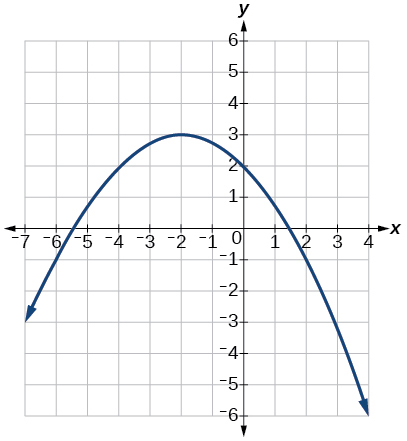
Numérico

Para los ejercicios 65-69, utilice la tabla de valores que representan puntos en la gráfica de una función cuadrática. Al determinar el vértice y el eje de simetría, encontrar la forma general de la ecuación de la función cuadrática.

65)

\(x\)	—2	—1	0	1	2
\(y\)	5	2	1	2	5

Responder

\(f(x)=x^2+1\)

66)

\(x\)	—2	—1	0	1	2
\(y\)	1	0	1	4	9

67)

\(x\)	—2	—1	0	1	2
\(y\)	—2	1	2	1	—2

Responder

\(f(x)=2−x^2\)

68)

\(x\)	—2	—1	0	1	2
\(y\)	—8	—3	0	1	0

69)

\(x\)	—2	—1	0	1	2
\(y\)	8	2	0	2	8

Responder

\(f(x)=2x^2\)

Tecnología

Para los ejercicios 70-74, usa una calculadora para encontrar la respuesta.

70) Gráfica sobre el mismo conjunto de ejes las funciones\(f(x)=x^2,f(x)=2x^2,\) y\(f(x)=\dfrac{1}{3}x^2\). ¿Cuál parece ser el efecto de cambiar el coeficiente?

71) Gráfica sobre el mismo conjunto de ejes\(f(x)=x^2,f(x)=x^2+2\) y\(f(x)=x^2,f(x)=x^2+5\) y\(f(x)=x^2−3\). ¿Cuál parece ser el efecto de agregar una constante?

Responder

El gráfico se desplaza hacia arriba o hacia abajo (un desplazamiento vertical).

72) Gráfica sobre el mismo conjunto de ejes\(f(x)=x^2,f(x)=(x−2)^2,f(x−3)2,\) y\(f(x)=(x+4)^2\). ¿Cuál parece ser el efecto de sumar o restar esos números?

73) La trayectoria de un objeto proyectado en ángulo de\(45\) grado con velocidad inicial de\(80\) pies por segundo viene dada por la función\(h(x)=−\dfrac{32}{(80)^2}x^2+x\) donde\(x\) está la distancia horizontal recorrida y\(h(x)\) es la altura en pies. Utilice la función TRACE de su calculadora para determinar la altura del objeto cuando se haya recorrido\(100\) pies de distancia horizontalmente.

Responder

\(50\)pies

74) Un puente colgante puede ser modelado por la función cuadrática\(h(x)=.0001x^2\) con\(−2000≤x≤2000\) donde\(|x|\) está el número de pies del centro y\(h(x)\) es la altura en pies. Use la función TRACE de su calculadora para estimar qué tan lejos del centro tiene el puente una altura de\(100\) pies.

Extensiones

Para los ejercicios 75-78, usa el vértice de la gráfica de la función cuadrática y la dirección en la que se abre la gráfica para encontrar el dominio y el rango de la función.

75) Vértice\((1,−2)\), se abre.

Responder

El dominio es\((−∞,∞)\). El alcance es\([−2,∞)\).

76) El vértice\((−1,2)\) se abre hacia abajo.

77) Vértice\((−5,11)\), se abre hacia abajo.

Responder

Dominio es\((−∞,∞)\) Rango es\((−∞,11]\).

78) Vértice\((−100,100)\), se abre.

Para los ejercicios 79-84, escribe la ecuación de la función cuadrática que contiene el punto dado y tiene la misma forma que la función dada.

79) Contiene\((1,1)\) y tiene forma de\(f(x)=2x^2\). El vértice está en el\(y\) eje.

Responder

\(f(x)=2x^2−1\)

80) Contiene\((−1,4)\) y tiene la forma de\(f(x)=2x^2\). El vértice está en el\(y\) eje.

81) Contiene\((2,3)\) y tiene la forma de\(f(x)=3x^2\). El vértice está en el\(y\) eje.

Responder

\(f(x)=3x^2−9\)

82) Contiene\((1,−3)\) y tiene la forma de\(f(x)=−x^2\). El vértice está en el\(y\) eje.

83) Contiene\((4,3)\) y tiene la forma de\(f(x)=5x^2\). El vértice está en el\(y\) eje.

Responder

\(f(x)=5x^2−77\)

84) Contiene\((1,−6)\) tiene la forma de\(f(x)=3x^2\). Vértice tiene\(x\) -coordenada de\(-1\).

Aplicaciones del mundo real

85) Encontrar las dimensiones del corral rectangular produciendo el mayor área cerrada dada\(200\) los pies de cercado.

Responder

\(50\)pies a\(50\) pies. Maximizar\(f(x)=−x^2+100x\).

86) Encontrar las dimensiones del corral rectangular dividido en\(2\) corrales del mismo tamaño produciendo el mayor área cerrada posible dados\(300\) los pies de cercado.

87) Encuentra las dimensiones del corral rectangular produciendo el mayor área cerrada dividida en\(3\) corrales del mismo tamaño dados\(500\) los pies de esgrima.

Responder

\(125\)pies a\(62.5\) pies. Maximizar\(f(x)=−2x^2+250x\).

88) Entre todos los pares de números cuya suma es\(6\), encuentra el par con el producto más grande. ¿Cuál es el producto?

89) Entre todos los pares de números cuya diferencia es\(12\), encuentra el par con el producto más pequeño. ¿Cuál es el producto?

Responder

\(6\)y\(-\) 6; producto es\(-36\); maximizar\(f(x)=x^2+12x\).

90) Supongamos que el precio por unidad en dólares de una producción de celulares está modelado por\(p=$45−0.0125x\), donde\(x\) se produce en miles de teléfonos, y los ingresos representados por miles de dólares lo son\(R=x⋅p\). Encuentra el nivel de producción que maximizará los ingresos.

91) Se lanza un cohete en el aire. Su altura, en metros sobre el nivel del mar, en función del tiempo, en segundos, viene dada por\(h(t)=−4.9t^2+229t+234\). Encuentra la altura máxima que alcanza el cohete.

Responder

\(2909.56\)metros

92) Se lanza una pelota al aire desde lo alto de un edificio. Su altura, en metros sobre el suelo, en función del tiempo, en segundos, viene dada por\(h(t)=−4.9t^2+24t+8\). ¿Cuánto tiempo se tarda en alcanzar la altura máxima?

93) Un estadio de futbol retiene\(62,000\) espectadores. Con un precio de entrada de\(\$11\), la asistencia promedio ha sido\(26,000\). Cuando el precio bajó a\(\$9\), la asistencia promedio subió a\(31,000\). Suponiendo que la asistencia está linealmente relacionada con el precio del boleto, ¿qué precio de boleto maximizaría los ingresos?

Responder

\(\$10.70\)

94) Una agricultora encuentra que si planta\(75\) árboles por acre, cada árbol dará\(20\) fanegas de fruto. Estima que por cada árbol adicional plantado por acre, el rendimiento de cada árbol disminuirá\(3\) en bushels. ¿Cuántos árboles debe plantar por acre para maximizar su cosecha?

3.3 Funciones de Potencia y Funciones Polinómicas

Verbal

1) Explicar la diferencia entre el coeficiente de una función de potencia y su grado.

Responder

El coeficiente de la función power es el número real que se multiplica por la variable elevada a una potencia. El grado es el mayor poder que aparece en la función.

2) Si una función polinómica está en forma factorizada, ¿cuál sería un buen primer paso para determinar el grado de la función?

3) En general, explicar el comportamiento final de una función de potencia con grado impar si el coeficiente principal es positivo.

Responder

Como\(x\) disminuye sin ataduras, también lo hace\(f(x)\). A medida que\(x\) aumenta sin ataduras, también lo hace\(f(x)\).

4) ¿Cuál es la relación entre el grado de una función polinómica y el número máximo de puntos de inflexión en su gráfica?

5) ¿Qué podemos concluir si, en general, la gráfica de una función polinómica exhibe el siguiente comportamiento final? Como\(x \rightarrow-\infty, f(x) \rightarrow-\infty\) y como\(x \rightarrow \infty, f(x) \rightarrow-\infty\).

Responder

La función polinómica es de grado par y el coeficiente principal es negativo.

Algebraico

Para los ejercicios 6-11, identificar la función como una función de poder, una función polinómica, o ninguna.

6)\(f(x)=x^5\)

7)\(f(x)=(x^2)^3\)

Responder

Función de alimentación

8)\(f(x)=x−x^4\)

9)\(f(x)=\dfrac{x^2}{x^2−1}\)

Responder

Tampoco

10)\(f(x)=2x(x+2)(x−1)^2\)

11)\(f(x)=3^{x+1}\)

Responder

Tampoco

Para los ejercicios 12-16, encuentra el grado y el coeficiente principal para el polinomio dado.

12)\(−3x^4\)

13)\(7−2x^2\)

Responder

Grado =\(2\), Coeficiente =\(-2\)

14)\(−2x^2− 3x^5+ x−6\)

15)\(x(4−x^2)(2x+1)\)

Responder

Grado =\(4\), Coeficiente =\(-2\)

16)\(x^2(2x−3)^2\)

Para los ejercicios 17-24, determinar el comportamiento final de las funciones.

17)\(f(x)=x^4\)

Responder

Como\(x→∞\)\(f(x)→∞\), como\(x→−∞\),\(f(x)→∞\)

18)\(f(x)=x^3\)

19)\(f(x)=−x^4\)

Responder

Como\(x→−∞\)\(f(x)→−∞\), como\(x→∞\),\(f(x)→−∞\)

20)\(f(x)=−x^9\)

21)\(f(x)=−2x^4− 3x^2+ x−1\)

Responder

Como\(x→−∞\)\(f(x)→−∞\), como\(x→∞\),\(f(x)→−∞\)

22)\(f(x)=3x^2+ x−2\)

23)\(f(x)=x^2(2x^3−x+1)\)

Responder

Como\(x→∞\)\(f(x)→∞\), como\(x→−∞\),\(f(x)→−∞\)

24)\(f(x)=(2−x)^7\)

Para los ejercicios 25-30, encuentra las intercepciones de las funciones.

25)\(f(t)=2(t−1)(t+2)(t−3)\)

Responder

\(y\)-interceptar es\((0,12)\),\(t\) -intercepciones son\((1,0);(–2,0); \) y\((3,0)\).

26)\(g(n)=−2(3n−1)(2n+1)\)

27)\(f(x)=x^4−16\)

Responder

\(y\)-interceptar es\((0,−16)\),\(x\) -intercepciones son\((2,0)\) y\((−2,0)\).

28)\(f(x)=x^3+27\)

29)\(f(x)=x(x^2−2x−8)\)

Responder

\(y\)-interceptar es\((0,0)\),\(x\) -intercepciones son\((0,0),(4,0),\) y\((−2, 0)\).

30)\(f(x)=(x+3)(4x^2−1)\)

Gráfica

Para los ejercicios 31-38, determinar el menor grado posible de la función polinómica mostrada.

31)

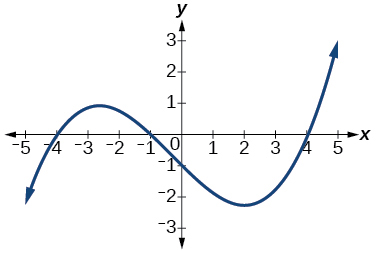
Responder

\(3\)

32)

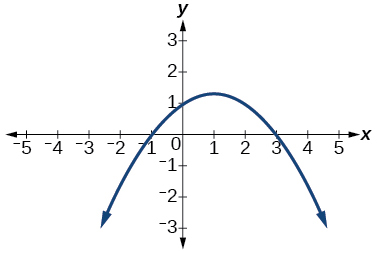
33)

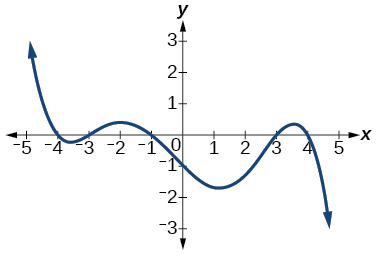
Responder

\(5\)

34)

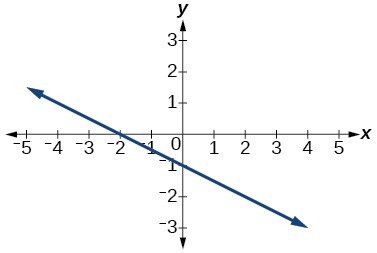
35)

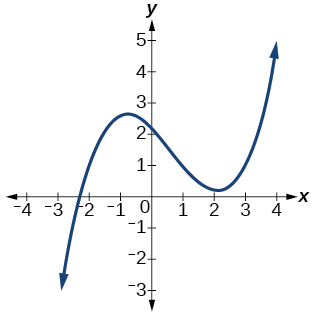
Responder

\(3\)

36)

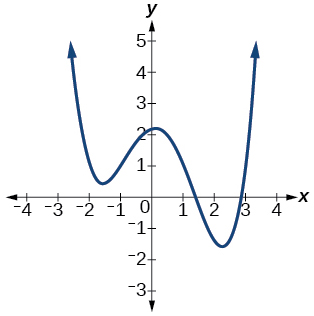
37)

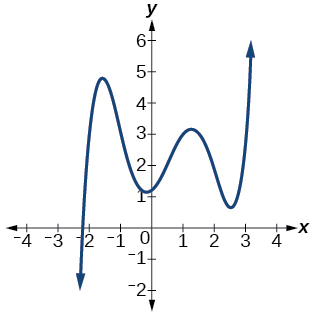
Responder

\(5\)

38)

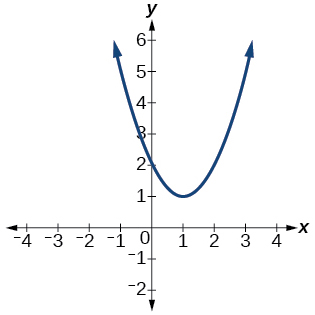
Para los ejercicios 39-45, determinar si la gráfica de la función proporcionada es una gráfica de una función polinómica. Si es así, determinar el número de puntos de inflexión y el menor grado posible para la función.

39)

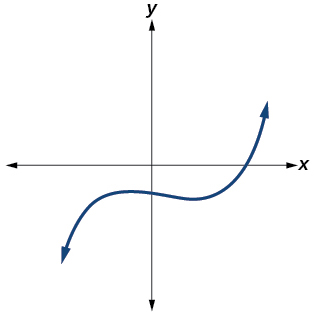
Responder

Sí. Número de puntos de inflexión es\(2\). El menor grado posible es\(3\).

40)

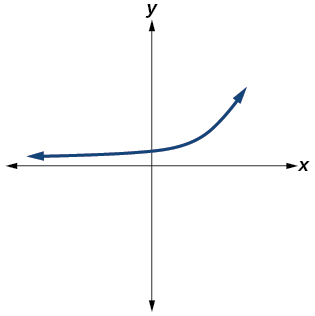
41)

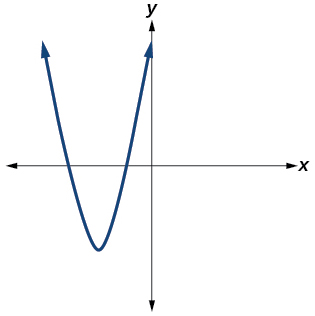
Responder

Sí. Número de puntos de inflexión es\(1\). El menor grado posible es\(2\).

42)

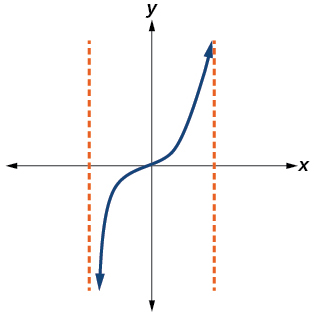
43)

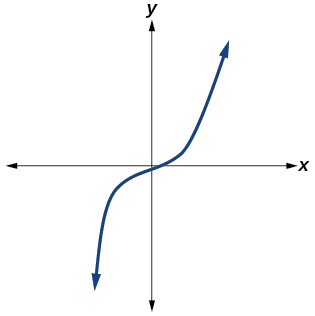
Responder

Sí. Número de puntos de inflexión es\(0\). El menor grado posible es\(1\).

44)

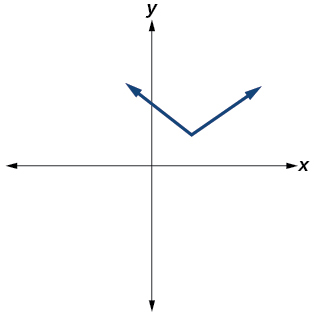
Responder

No.

45)

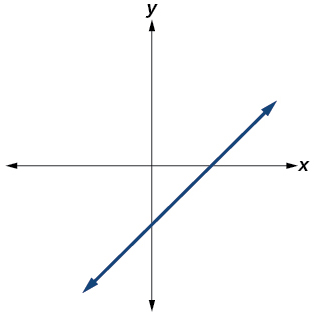
Responder

Sí. Número de puntos de inflexión es\(0\). El menor grado posible es\(1\).

Numérico

Para los ejercicios 46-50, hacer una tabla para confirmar el comportamiento final de la función.

46)\(f(x)=−x^3\)

47)\(f(x)=x^4−5x^2\)

Responder

\(x\)	\(f(x)\)
\ (x\) ">10	\ (f (x)\) ">9.500
\ (x\) ">100	\ (f (x)\) ">99.950.000
\ (x\) ">—10	\ (f (x)\) ">9.500
\ (x\) ">—100	\ (f (x)\) ">99.950.000

como\(x→−∞,\)\(f(x)→∞\), como\(x→∞,\)\(f(x)→∞\)

48)\(f(x)=x^2(1−x)^2\)

49)\(f(x)=(x−1)(x−2)(3−x)\)

Responder

\(x\)	\(f(x)\)
\ (x\) ">10	\ (f (x)\) ">—504
\ (x\) ">100	\ (f (x)\) ">—941.094
\ (x\) ">—10	\ (f (x)\) ">1,716
\ (x\) ">—100	\ (f (x)\) ">1,061,106

como\(x→−∞,\)\(f(x)→∞\), como\(x→∞,\)\(f(x)→−∞\)

50)\(f(x)=\dfrac{x^5}{10}−x^4\)

Tecnología

Para los ejercicios 51-60, grafica las funciones polinómicas usando una calculadora. Con base en la gráfica, determinar las intercepciones y el comportamiento final.

51)\(f(x)=x^3(x−2)\)

Responder

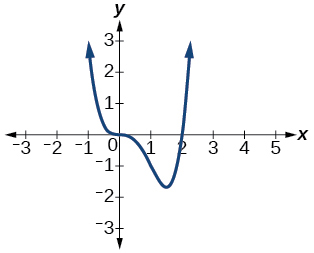
El\(y\) -intercepto es\((0, 0)\). Las intercepciones x son\((0, 0), (2, 0).\) As\(x→−∞,\)\(f(x)→∞\), como\(x→∞,\)\(f(x)→∞\)

52)\(f(x)=x(x−3)(x+3)\)

53)\(f(x)=x(14−2x)(10−2x)\)

Responder

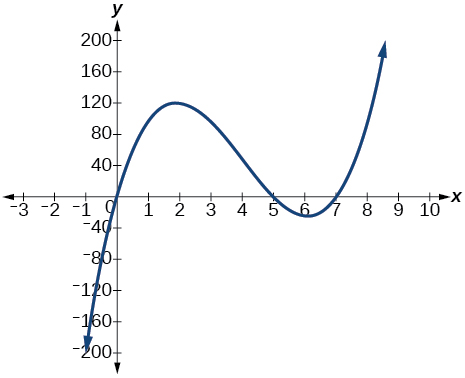
El\(y\) -intercepto es\((0,0)\). Las intercepciones x son\((0, 0), (5, 0), (7, 0)\). Como\(x→−∞\),\(f(x)→−∞\), como\(x→∞,\)\(f(x)→∞\)

54)\(f(x)=x(14−2x)(10−2x)^2\)

55)\(f(x)=x^3−16x\)

Responder

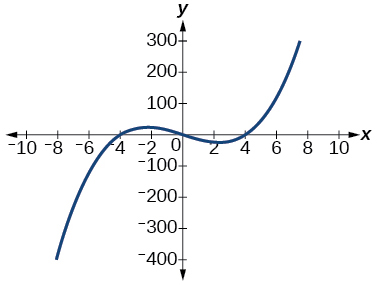
El\(y\) -intercepto es\((0, 0)\). La intercepción x es\((−4, 0), (0, 0), (4, 0)\). Como\(x→−∞\),\(f(x)→−∞\), como\(x→∞,\)\(f(x)→∞\)

56)\(f(x)=x^3−27\)

57)\(f(x)=x^4−81\)

Responder

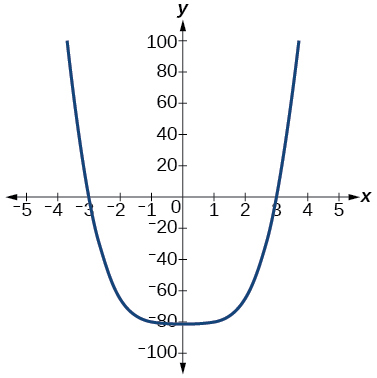
El\(y\) -intercepto es\((0, -81)\). Los\(x\) -intercepción son\((3, 0), (−3, 0)\). Como\(x→−∞,\)\(f(x)→∞\), como\(x→∞,\)\(f(x)→∞\)

58)\(f(x)=−x^3+x^2+2x\)

59)\(f(x)=x^3−2x^2−15x\)

Responder

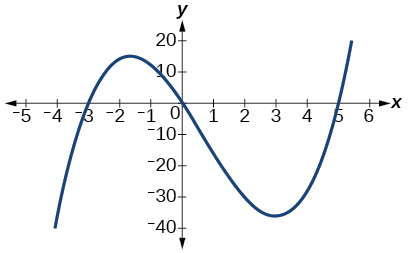
El\(y\) -intercepto es\((0, 0)\). Las intercepciones x son\((−3, 0), (0, 0), (5, 0).\) As\(x→−∞\),\(f(x)→−∞\), as\(x→∞,\)\(f(x)→∞\)

60)\(f(x)=x^3−0.01x\)

Extensiones

Para los ejercicios 61-65, utilice la información sobre la gráfica de una función polinómica para determinar la función. Supongamos que el coeficiente principal es\(1\) o\(-1\). Puede haber más de una respuesta correcta.

61) El\(y\) -intercepto es\((0,−4)\). Los\(x\) -interceptos son\((−2,0), (2,0)\). El grado es\(2\).

Comportamiento final: como\(x→−∞,\)\(f(x)→∞\), como\(x→∞,\)\(f(x)→∞\).

Responder

\(f(x)=x^2−4\)

62) El\(y\) -intercepto es\((0,9)\). Los\(x\) -interceptos son\((−3,0), (3,0)\). El grado es\(2\).

Comportamiento final: como\(x→−∞,\)\(f(x)→−∞\), como\(x→∞,\)\(f(x)→−∞\).

63) El\(y\) -intercepto es\((0,0)\). Los\(x\) -interceptos son\((0,0), (2,0)\). El grado es\(3\).

Comportamiento final: como\(x→−∞,\)\(f(x)→−∞\), como\(x→∞,\)\(f(x)→∞\).

Responder

\(f(x)=x^3−4x^2+4x\)

64) El\(y\) -intercepto es\((0,1)\). La intercepción x es\((1,0)\). El grado es\(3\).

Comportamiento final: como\(x→−∞\),\(f(x)→∞\), as\(x→∞\),\(f(x)→−∞\).

65) El\(y\) -intercepto es\((0,1)\). No hay\(x\) -intercepción. El grado es\(4\).

Comportamiento final: como\(x→−∞,\)\(f(x)→∞\), como\(x→∞,\)\(f(x)→∞\).

Responder

\(f(x)=x^4+1\)

Aplicaciones del mundo real

Para los ejercicios 66-70, utilice las declaraciones escritas para construir una función polinómica que represente la información requerida.

66) Una marea de petróleo se está expandiendo como un círculo. El radio del círculo está aumentando a razón de\(20\) metros por día. Expresar el área del círculo en función de\(d\), el número de días transcurridos.

67) Un cubo tiene un borde de\(3\) pies. El borde está aumentando a razón de\(2\) pies por minuto. Exprese el volumen del cubo en función de\(m\), el número de minutos transcurridos.

Responder

\(V(m)=8m^3+36m^2+54m+27\)

68) Un rectángulo tiene una longitud de\(10\) pulgadas y un ancho de\(6\) pulgadas. Si la longitud se incrementa en\(x\) pulgadas y la anchura aumenta el doble de esa cantidad, exprese el área del rectángulo en función de\(x\).

69) Una caja abierta debe construirse cortando esquinas cuadradas de lados\(x\) de pulgadas de un trozo de cartón\(8\) pulgadas por\(8\) pulgadas y luego doblando los lados. Expresar el volumen de la caja en función de\(x\).

Responder

\(V(x)=4x^3−32x^2+64x\)

70) Un rectángulo es el doble de largo que ancho. Se recortan cuadrados de\(2\) pies laterales de cada esquina. Después los lados se pliegan hacia arriba para hacer una caja abierta. Exprese el volumen de la caja en función del ancho (\(x\)).

3.4 Gráficas de Funciones Polinómicas

Verbal

1) ¿Cuál es la diferencia entre una\(x\) -intercepción y un cero de una función polinómica\(f\)?

Responder

El\(x\) -intercept es donde la gráfica de la función cruza el\(x\) -eje, y el cero de la función es el valor de entrada para el cual\(f(x)=0\).

2) Si una función polinómica de grado\(n\) tiene ceros\(n\) distintos, ¿qué sabe de la gráfica de la función?

3) Explicar cómo el Teorema del Valor Intermedio puede ayudarnos a encontrar un cero de una función.

Responder

Si evaluamos la función at\(a\) y at\(b\) y el signo del valor de la función cambia, entonces sabemos que existe un cero entre\(a\) y\(b\).

4) Explicar cómo la forma factorizada del polinomio nos ayuda a graficarlo.

5) Si la gráfica de un polinomio apenas toca el\(x\) eje -y luego cambia de dirección, ¿qué podemos concluir sobre la forma factorizada del polinomio?

Responder

Habrá un factor elevado a una potencia parejo.

Algebraico

Para los ejercicios 6-23, encuentra las\(x\)\(t\) -o -intercepciones de las funciones polinómicas.

6)\(C(t)=2(t−4)(t+1)(t−6)\)

7)\(C(t)=3(t+2)(t−3)(t+5)\)

Responder

\((−2,0),(3,0),(−5,0)\)

8)\(C(t)=4t(t−2)^2(t+1)\)

9)\(C(t)=2t(t−3)(t+1)^2\)

Responder

\((3,0),(−1,0),(0,0)\)

10)\(C(t)=2t^4−8t^3+6t^2\)

11)\(C(t)=4t^4+12t^3−40t^2\)

Responder

\((0,0), (−5,0), (2,0)\)

12)\(f(x)=x^4−x^2\)

13)\(f(x)=x^3+x^2−20x\)

Responder

\((0,0), (−5,0), (4,0)\)

14)\(f(x)=x^3+6x^2−7x\)

15)\(f(x)=x^3+x^2−4x−4\)

Responder

\((2,0), (−2,0), (−1,0)\)

16)\(f(x)=x^3+2x^2−9x−18\)

17)\(f(x)=2x^3−x^2−8x+4\)

Responder

\((−2,0),(2,0),\left(\dfrac{1}{2},0\right)\)

18)\(f(x)=x^6−7x^3−8\)

19)\(f(x)=2x^4+6x^2−8\)

Responder

\((1,0), (−1,0)\)

20)\(f(x)=x^3−3x^2−x+3\)

21)\(f(x)=x^6−2x^4−3x^2\)

Responder

\((0,0),(\sqrt{3},0),(−\sqrt{3},0)\)

22)\(f(x)=x^6−3x^4−4x^2\)

23)\(f(x)=x^5−5x^3+4x\)

Responder

\((0,0), (1,0), (−1,0), (2,0), (−2,0)\)

Para los ejercicios 24-29, utilice el Teorema del Valor Intermedio para confirmar que el polinomio dado tiene al menos un cero dentro del intervalo dado.

24)\(f(x)=x^3−9x\), entre\(x=−4\) y\(x=−2\).

25)\(f(x)=x^3−9x\), entre\(x=2\) y\(x=4\).

Responder

\(f(2)=–10\)y\(f(4)=28\). Cambio de señal confirma.

26)\(f(x)=x^5−2x\), entre\(x=1\) y\(x=2\).

27)\(f(x)=−x^4+4\), entre\(x=1\) y\(x=3\).

Responder

\(f(1)=3\)y\(f(3)=–77.\) Firma de cambio confirma.

28)\(f(x)=−2x^3−x\), entre\(x=–1\) y\(x=1\).

29)\(f(x)=x^3−100x+2\), entre\(x=0.01\) y\(x=0.1\)

Responder

\(f(0.01)=1.000001 \)y\(f(0.1)=–7.999\). Cambio de señal confirma.

Para los ejercicios 30-41, encuentra los ceros y da la multiplicidad de cada uno.

30)\(f(x)=(x+2)^3(x−3)^2\)

31)\(f(x)=x^2(2x+3)^5(x−4)^2\)

Responder

\(0\)con multiplicidad\(2\),\(−\dfrac{3}{2}\) con multiplicidad\(5\),\(4\) con multiplicidad\(2\)

32)\(f(x)=x^3(x−1)^3(x+2)\)

33)\(f(x)=x^2(x^2+4x+4)\)

Responder

\(0\)con multiplicidad\(2\),\(-2\) con multiplicidad\(2\)

34)\(f(x)=(2x+1)^3(9x^2−6x+1)\)

35)\(f(x)=(3x+2)^5(x^2−10x+25)\)

Responder

\(−\dfrac{2}{3}\)con multiplicidad\(5\),\(5\) con multiplicidad\(2\)

36)\(f(x)=x(4x^2−12x+9)(x^2+8x+16)\)

37)\(f(x)=x^6−x^5−2x^4\)

Responder

\(0\)con multiplicidad\(4\),\(2\) con multiplicidad\(1\),\(-1\) con multiplicidad\(1\)

38)\(f(x)=3x^4+6x^3+3x^2\)

39)\(f(x)=4x^5−12x^4+9x^3\)

Responder

\(\dfrac{3}{2}\)con multiplicidad\(2\),\(0\) con multiplicidad\(3\)

40)\(f(x)=2x^4(x^3−4x^2+4x)\)

41)\(f(x)=4x^4(9x^4−12x^3+4x^2)\)

Responder

\(0\)con multiplicidad\(6\),\(\dfrac{2}{3}\) con multiplicidad\(2\)

Gráfica

Para los ejercicios 42-47, graficar las funciones polinómicas. Nota\(x\) - y\(y\) - intercepciones, multiplicidad y comportamiento final.

42)\(f(x)=(x+3)^2(x−2)\)

43)\(g(x)=(x+4)(x−1)^2\)

Responder

\(x\)-intercepta,\((1, 0)\) con multiplicidad\(2\),\((–4, 0)\) con multiplicidad\(1\),\(y\) - interceptar\((0, 4)\). Como\(x→−∞\),\(f(x)→−∞\), como\(x→∞,\)\(f(x)→∞\).

44)\(h(x)=(x−1)^3(x+3)^2\)

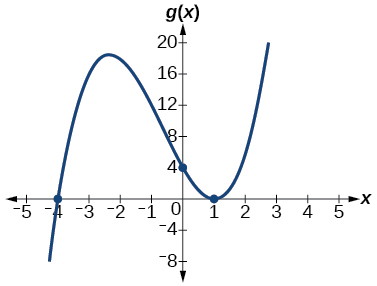
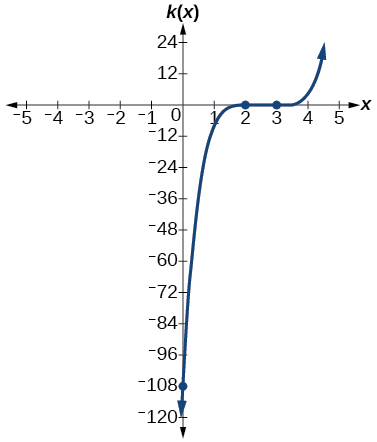
45)\(k(x)=(x−3)^3(x−2)^2\)

Responder

\(x\)-intercepta\((3,0)\) con multiplicidad\(3\),\((2,0)\) con multiplicidad\(2\),\(y\) - interceptar\((0,–108).\) As\(x→−∞,\)\(f(x)→−∞\), as\(x→∞,\)\(f(x)→∞\).

46)\(m(x)=−2x(x−1)(x+3)\)

47)\(n(x)=−3x(x+2)(x−4)\)

Responder

\(x\)-intercepta\((0, 0),(–2, 0),(4, 0)\) con multiplicidad\(1\),\(y\) -interceptar (0, 0). Como\(x→−∞,\)\(f(x)→∞\), como\(x→∞,\)\(f(x)→−∞\).

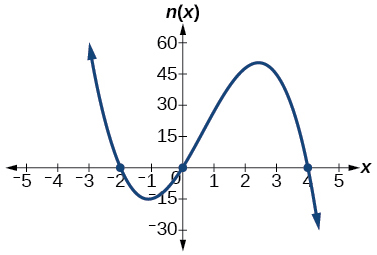
Para los ejercicios 48-52, utilice las gráficas para escribir la fórmula para una función polinómica de menor grado.

48)

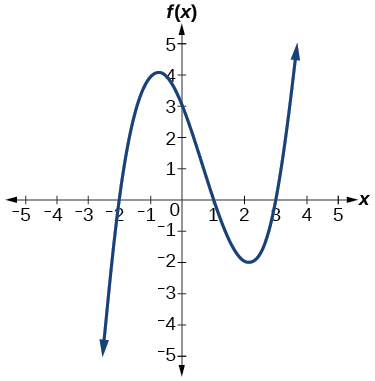
49)

Responder

\(f(x)=−\dfrac{2}{9}(x−3)(x+1)(x+3)\)

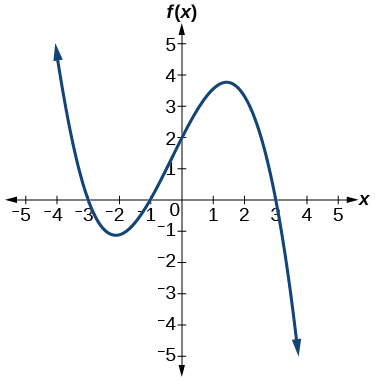
50)

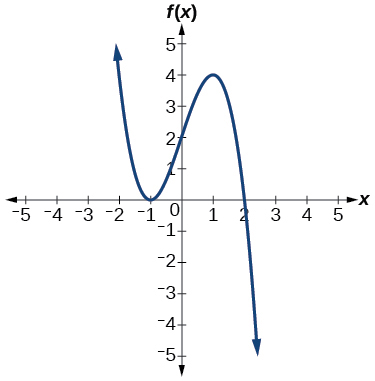
51)

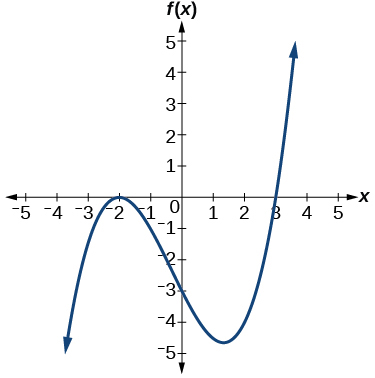
Responder

\(f(x)=\dfrac{1}{4}(x+2)^2(x−3)\)

52)

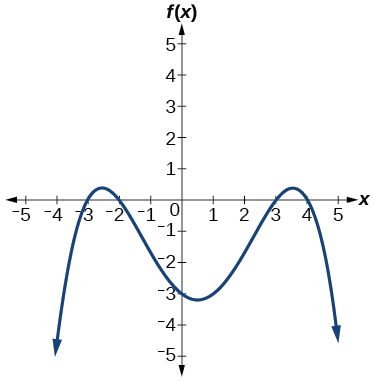
Para los ejercicios 53-56, utilice la gráfica para identificar ceros y multiplicidad.

53)

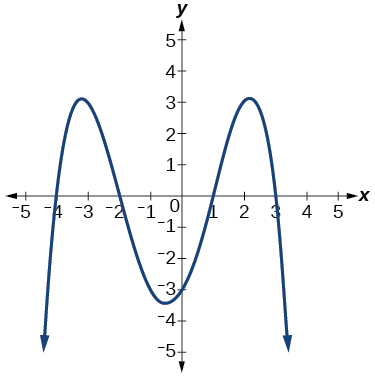
Responder

\(–4, –2, 1, 3\)con multiplicidad\(1\)

54)

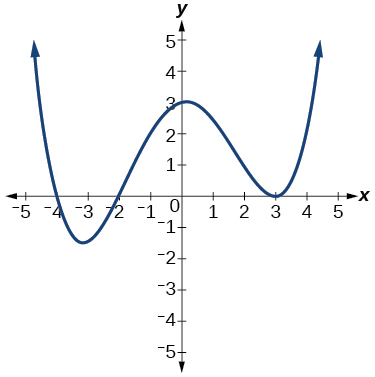
55)

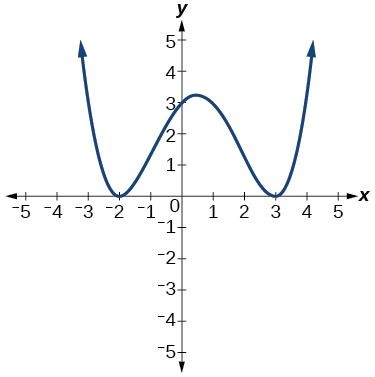
Responder

\(–2, 3\)cada uno con multiplicidad\(2\)

56)

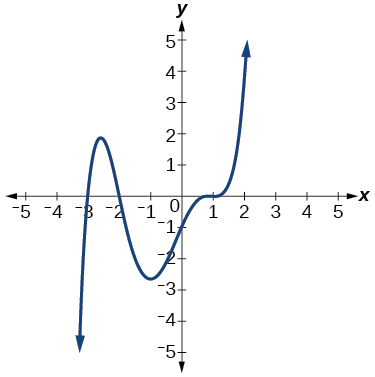
Para los ejercicios 57-66, utilice la información dada sobre la gráfica polinómica para escribir la ecuación.

57) Titulación\(3\). Ceros en\(x=–2\),\(x=1\), y\(x=3\). \(y\)-interceptar en\((0,–4)\)

Responder

\(f(x)=−\dfrac{2}{3}(x+2)(x−1)(x−3)\)

58) Titulación\(3\). Ceros en\(x=–5\),\(x=–2\), y\(x=1\). \(y\)-interceptar en\((0,6)\)

59) Titulación\(5\). Raíces de multiplicidad\(2\) en\(x=3\) y\(x=1\), y una raíz de multiplicidad\(1\) en\(x=–3\). \(y\)-interceptar en\((0,9)\)

Responder

\(f(x)=\dfrac{1}{3}(x−3)^2(x−1)^2(x+3)\)

60) Titulación\(4\). Raíz de multiplicidad\(2\) en\(x=4\), y raíces de multiplicidad\(1\) en\(x=1\) y\(x=–2\). \(y\)-interceptar en\((0,–3)\)

61) Titulación\(5\). Doble cero a\(x=1\), y triple cero a\(x=3\). Pasa por el punto\((2,15)\)

Responder

\(f(x)=−15(x−1)^2(x−3)^3\)

62) Titulación\(3\). Ceros en\(x=4\),\(x=3\), y\(x=2\). \(y\)-interceptar en\((0,−24)\)

63) Titulación\(3\). Ceros en\(x=−3\),\(x=−2\) y\(x=1\). \(y\)-interceptar en\((0,12)\)

Responder

\(f(x)=−2(x+3)(x+2)(x−1)\)

64) Titulación\(5\). Raíces de multiplicidad\(2\) en\(x=−3\) y\(x=2\) y una raíz de multiplicidad\(1\) en\(x=−2\). \(y\)-interceptar en\((0, 4)\).

65) Titulación\(4\). Raíces de multiplicidad\(2\) en\(x=\dfrac{1}{2}\) y raíces de multiplicidad\(1\) en\(x=6 \) y\(x=−2\). \(y\)-interceptar en\((0,18)\)

Responder

\(f(x)=−\dfrac{3}{2}(2x−1)^2(x−6)(x+2)\)

66) Doble cero at\(x=−3\) y triple cero at\(x=0\). Pasa por el punto\((1,32)\).

Tecnología

Para los ejercicios 67-71, utilice una calculadora para aproximar mínimos y máximos locales o los mínimos y máximos globales.

67)\(f(x)=x^3−x−1\)

Responder

local max\((–.58, –.62)\), local min\((.58, –1.38)\)

68)\(f(x)=2x^3−3x−1\)

69)\(f(x)=x^4+x\)

Responder

global min\((–.63, –.47)\)

70)\(f(x)=−x^4+3x−2\)

71)\(f(x)=x^4−x^3+1\)

Responder

global min\((.75, .89)\)

Extensiones

Para los ejercicios 72-74, utilice las gráficas para escribir una función polinómica de menor grado.

72)

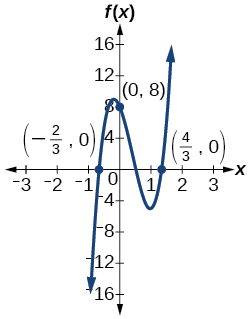
73)

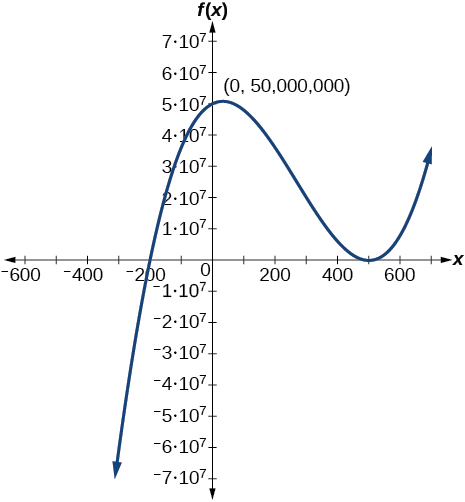
Responder

\(f(x)=(x−500)^2(x+200)\)

74)

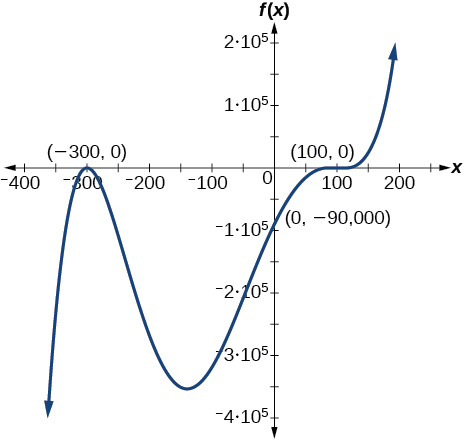
Aplicaciones del mundo real

Para los ejercicios 75-, escriba la función polinómica que modela la situación dada.

75) Un rectángulo tiene una longitud de\(10\) unidades y un ancho de 8 unidades. Los cuadrados de\(x\) por\(x\) unidades se cortan de cada esquina, y luego los lados se pliegan hacia arriba para crear una caja abierta. Expresar el volumen de la caja como una función polinómica en términos de\(x\).

Responder

\(f(x)=4x^3−36x^2+80x\)

76) Considerar el mismo rectángulo del problema anterior. Se recortan cuadrados de\(2x\) por\(2x\) unidades de cada esquina. Expresar el volumen de la caja como polinomio en términos de\(x\).

77) Un cuadrado tiene lados de\(12\) unidades. Los cuadrados\(x +1\) por\(x +1\) unidades se cortan de cada esquina, y luego los lados se pliegan hacia arriba para crear una caja abierta. Expresar el volumen de la caja como una función en términos de\(x\).

Responder

\(f(x)=4x^3−36x^2+60x+100\)

78) Un cilindro tiene un radio de\(x+2\) unidades y una altura de\(3\) unidades mayor. Expresar el volumen del cilindro como una función polinómica.

79) Un cono circular derecho tiene un radio de\(3x+6\) y unas\(3\) unidades de altura menores. Expresar el volumen del cono como una función polinómica. El volumen de un cono es\(V=\dfrac{1}{3}πr^2h\) para radio\(r\) y altura\(h\).

Responder

\(f(x)=π(9x^3+45x^2+72x+36)\)

3.5 Dividir polinomios

Verbal

1) Si la división de un polinomio por un binomio da como resultado un resto de cero, ¿qué se puede concluir?

Responder

El binomio es un factor del polinomio.

2) Si un polinomio de grado\(n\) se divide por un binomio de grado\(1\), ¿cuál es el grado del cociente?

Algebraico

Para los ejercicios 3-13, usa división larga para dividir. Especificar el cociente y el resto.

3)\((x^2+5x−1)÷(x−1)\)

Responder

\(\mathrm{x+6+\dfrac{5}{x−1}, quotient: x+6, remainder: 5}\)

4)\((2x^2−9x−5)÷(x−5)\)

5)\((3x^2+23x+14)÷(x+7)\)

Responder

\(\mathrm{3x+2, quotient: 3x+2, remainder: 0}\)

6)\((4x^2−10x+6)÷(4x+2)\)

7)\((6x^2−25x−25)÷(6x+5)\)

Responder

\(\mathrm{x−5, quotient: x−5, remainder: 0}\)

8)\((−x^2−1)÷(x+1)\)

9)\((2x^2−3x+2)÷(x+2)\)

Responder

\(\mathrm{2x−7+\dfrac{16}{x+2}, quotient: 2x−7, remainder: 16}\)

10)\((x^3−126)÷(x−5)\)

11)\((3x^2−5x+4)÷(3x+1)\)

Responder

\(\mathrm{x−2+\dfrac{6}{3x+1}, quotient: x−2, remainder: 6}\)

12)\((x^3−3x^2+5x−6)÷(x−2)\)

13)\((2x^3+3x^2−4x+15)÷(x+3)\)

Responder

\(\mathrm{2x^2−3x+5, quotient: 2x^2−3x+5, remainder: 0}\)

Para los ejercicios 14-37, usa la división sintética para encontrar el cociente.

14)\((3x^3−2x^2+x−4)÷(x+3)\)

15)\((2x^3−6x^2−7x+6)÷(x−4)\)

Responder

\(2x^2+2x+1+\dfrac{10}{x−4}\)

16)\((6x^3−10x^2−7x−15)÷(x+1)\)

17)\((4x^3−12x^2−5x−1)÷(2x+1)\)

Responder

\(2x^2−7x+1−\dfrac{2}{2x+1}\)

18)\((9x^3−9x^2+18x+5)÷(3x−1)\)

19)\((3x^3−2x^2+x−4)÷(x+3)\)

Responder

\(3x^2−11x+34−\dfrac{106}{x+3}\)

20)\((−6x^3+x^2−4)÷(2x−3)\)

21)\((2x^3+7x^2−13x−3)÷(2x−3)\)

Responder

\(x^2+5x+1\)

22)\((3x^3−5x^2+2x+3)÷(x+2)\)

23)\((4x^3−5x^2+13)÷(x+4)\)

Responder

\(4x^2−21x+84−\dfrac{323}{x+4}\)

24)\((x^3−3x+2)÷(x+2)\)

25)\((x^3−21x^2+147x−343)÷(x−7)\)

Responder

\(x^2−14x+49\)

26)\((x^3−15x^2+75x−125)÷(x−5)\)

27)\((9x^3−x+2)÷(3x−1)\)

Responder

\(3x^2+x+\dfrac{2}{3x−1}\)

28)\((6x^3−x^2+5x+2)÷(3x+1)\)

29)\((x^4+x^3−3x^2−2x+1)÷(x+1)\)

Responder

\(x^3−3x+1\)

30)\((x^4−3x^2+1)÷(x−1)\)

31)\((x^4+2x^3−3x^2+2x+6)÷(x+3)\)

Responder

\(x^3−x^2+2\)

32)\((x^4−10x^3+37x^2−60x+36)÷(x−2)\)

33)\((x^4−8x^3+24x^2−32x+16)÷(x−2)\)

Responder

\(x^3−6x^2+12x−8\)

34)\((x^4+5x^3−3x^2−13x+10)÷(x+5)\)

35)\((x^4−12x^3+54x^2−108x+81)÷(x−3)\)

Responder

\(x^3−9x^2+27x−27\)

36)\((4x^4−2x^3−4x+2)÷(2x−1)\)

37)\((4x^4+2x^3−4x^2+2x+2)÷(2x+1)\)

Responder

\(2x^3−2x+2\)

Para los ejercicios 38-43, utilice la división sintética para determinar si la primera expresión es un factor de la segunda. Si es así, indicar la factorización.

38)\(x−2, 4x^3−3x^2−8x+4\)

39)\(x−2, 3x^4−6x^3−5x+10\)

Responder

Sí\((x−2)(3x^3−5)\)

40)\(x+3, −4x^3+5x^2+8\)

41)\(x−2, 4x^4−15x^2−4\)

Responder

Sí\((x−2)(4x^3+8x^2+x+2)\)

42)\(x−\dfrac{1}{2}, 2x^4−x^3+2x−1\)

43)\(x+\dfrac{1}{3}, 3x^4+x^3−3x+1\)

Responder

No

Gráfica

Para los ejercicios 44-48, utilice la gráfica del polinomio de tercer grado y un factor para escribir la forma factorizada del polinomio sugerida por la gráfica. El coeficiente principal es uno.

44) El factor es\(x^2−x+3\)

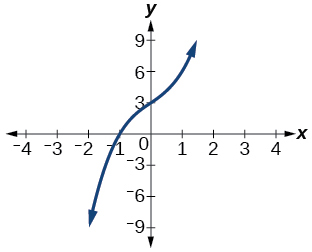
45) El factor es\((x^2+2x+4)\)

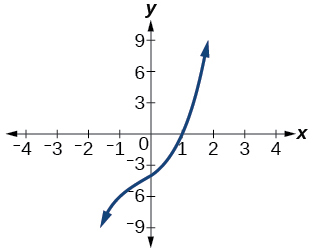
Responder

\((x−1)(x^2+2x+4)\)

46) El factor es\(x^2+2x+5\)

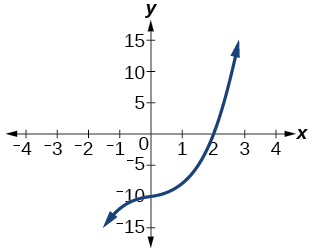
47) El factor es\(x^2+x+1\)

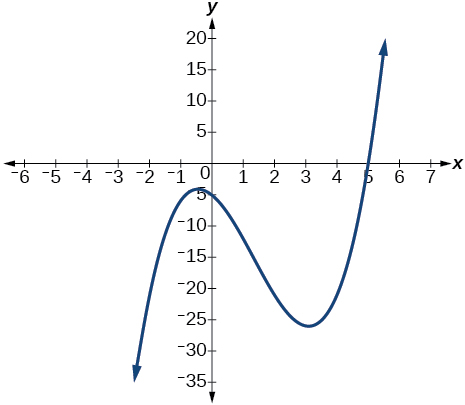
Responder

\((x−5)(x^2+x+1)\)

48) El factor es\(x^2+2x+2\)

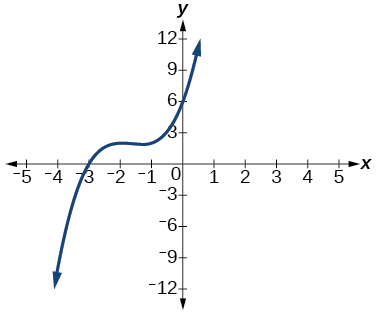
Para los ejercicios 49-53, usa la división sintética para encontrar el cociente y el resto.

49)\(\dfrac{4x^3−33}{x−2}\)

Responder

\(\mathrm{Quotient: 4x^2+8x+16, remainder: −1}\)

50)\(\dfrac{2x^3+25}{x+3}\)

51)\(\dfrac{3x^3+2x−5}{x−1}\)

Responder

\(\mathrm{Quotient: 3x^2+3x+5, remainder: 0}\)

52)\(\dfrac{−4x^3−x^2−12}{x+4}\)

53)\(\dfrac{x^4−22}{x+2}\)

Responder

\(\mathrm{Quotient: x^3−2x^2+4x−8, remainder: −6}\)

Tecnología

Para los ejercicios 54-58, usa una calculadora con CAS para responder a las preguntas.

54) Considerar\(\dfrac{x^k−1}{x−1}\) con\(k=1, 2, 3\). ¿Cuál esperas que sea el resultado si\(k=4\)?

55) Considerar\(\dfrac{x^k+1}{x+1}\) para\(k=1, 3, 5\). ¿Cuál esperas que sea el resultado si\(k=7\)?

Responder

\(x^6−x^5+x^4−x^3+x^2−x+1\)

56) Considerar\(\dfrac{x^4−k^4}{x−k}\) para\(k=1, 2, 3\). ¿Cuál esperas que sea el resultado si\(k=4\)?

57) Considerar\(\dfrac{x^k}{x+1}\) con\(k=1, 2, 3\). ¿Cuál esperas que sea el resultado si\(k=4\)?

Responder

\(x^3−x^2+x−1+\dfrac{1}{x+1}\)

58) Considerar\(\dfrac{x^k}{x−1}\) con\(k=1, 2, 3\). ¿Cuál esperas que sea el resultado si\(k=4\)?

Extensiones

Para los ejercicios 59-63, utilice la división sintética para determinar el cociente que involucra un número complejo.

59)\(\dfrac{x+1}{x−i}\)

Responder

\(1+\dfrac{1+i}{x−i}\)

60)\(\dfrac{x^2+1}{x−i}\)

61)\(\dfrac{x+1}{x+i}\)

Responder

\(1+\dfrac{1−i}{x+i}\)

62)\(\dfrac{x^2+1}{x+i}\)

63)\(\dfrac{x^3+1}{x−i}\)

Responder

\(x^2−ix−1+\dfrac{1−i}{x−i}\)

Aplicaciones del mundo real

Para los ejercicios 64-66, use la longitud y el área dados de un rectángulo para expresar el ancho algebraicamente.

64) La longitud es\(x+5\), el área es\(2x^2+9x−5\).

65) La longitud es\(2x + 5\), el área es\(4x^3+10x^2+6x+15\).

Responder

\(2x^2+3\)

66) La longitud es\(3x–4\), el área es\(6x^4−8x^3+9x^2−9x−4\).

Para los ejercicios 67-70, utilice el volumen dado de una caja y su longitud y anchura para expresar algebraicamente la altura de la caja.

67) El volumen es\(12x^3+20x^2−21x−36\), el largo es\(2x+3\), el ancho es\(3x−4\).

Responder

\(2x+3\)

68) El volumen es\(18x^3−21x^2−40x+48\), el largo es\(3x–4\), el ancho es\(3x–4\).

69) El volumen es\(10x^3+27x^2+2x−24\), el largo es\(5x–4\), el ancho es\(2x+3\).

Responder

\(x+2\)

70) El volumen es\(10x^3+30x^2−8x−24\), el largo es\(2\), el ancho es\(x+3\).

Para los ejercicios 71-73, utilice el volumen y radio dados de un cilindro para expresar algebraicamente la altura del cilindro.

71) El volumen es\(π(25x^3−65x^2−29x−3)\), el radio es\(5x+1\).

Responder

\(x−3\)

72) El volumen es\(π(4x^3+12x^2−15x−50)\), el radio es\(2x+5\).

73) El volumen es\(π(3x^4+24x^3+46x^2−16x−32)\), el radio es\(x+4\).

Responder

\(3x^2−2\)

3.6 Ceros de Funciones Polinómicas

Verbal

1) Describir un uso para el Teorema del Resto.

Responder

El teorema puede ser utilizado para evaluar un polinomio.

2) Explicar por qué el Teorema Racional del Cero no garantiza la búsqueda de ceros de una función polinómica.

3) ¿Cuál es la diferencia entre ceros racionales y reales?

Responder

Los ceros racionales se pueden expresar como fracciones, mientras que los ceros reales incluyen números irracionales.

4) Si la Regla de Signos de Descartes revela un no cambio de signos o un signo de cambios, ¿qué conclusión específica se puede sacar?

5) Si la división sintética revela un cero, ¿por qué deberíamos volver a intentar ese valor como posible solución?

Responder

Las funciones polinómicas pueden tener ceros repetidos, por lo que el hecho de que el número sea un cero no excluye que vuelva a ser un cero.

Algebraico

Para los ejercicios 6-13, usa el Teorema del Resto para encontrar el resto.

6)\((x^4−9x^2+14)÷(x−2)\)

7)\((3x^3−2x^2+x−4)÷(x+3)\)

Responder

\(−106\)

8)\((x^4+5x^3−4x−17)÷(x+1)\)

9)\((−3x^2+6x+24)÷(x−4)\)

Responder

\(0\)

10)\((5x^5−4x^4+3x^3−2x^2+x−1)÷(x+6)\)

11)\((x^4−1)÷(x−4)\)

Responder

\(255\)

12)\((3x^3+4x^2−8x+2)÷(x−3)\)

13)\((4x^3+5x^2−2x+7)÷(x+2)\)

Responder

\(−1\)

Para los ejercicios 14-21, utilice el Teorema de Factores para encontrar todos los ceros reales para la función polinómica dada y un factor.

14)\(f(x)=2x^3−9x^2+13x−6; x−1\)

15)\(f(x)=2x^3+x^2−5x+2; x+2 \)

Responder

\(−2, 1, \dfrac{1}{2}\)

16)\(f(x)=3x^3+x^2−20x+12; x+3\)

17)\(f(x)=2x^3+3x^2+x+6;x+2\)

Responder

\(−2\)

18)\(f(x)=−5x^3+16x^2−9;x−3\)

19)\(x^3+3x^2+4x+12;x+3\)

Responder

\(−3\)

20)\(4x^3−7x+3;x−1\)

21)\(2x^3+5x^2−12x−30,2x+5\)

Responder

\(−\dfrac{5}{2}, \sqrt{6}, −\sqrt{6}\)

Para los ejercicios 22-39, usa el Teorema Racional del Cero para encontrar todos los ceros reales.

22)\(x^3−3x^2−10x+24=0\)

23)\(2x^3+7x^2−10x−24=0\)

Responder

\(2, −4, −\dfrac{3}{2}\)

24)\(x^3+2x^2−9x−18=0\)

25)\(x^3+5x^2−16x−80=0\)

Responder

\(4, −4, −5\)

26)\(x^3−3x^2−25x+75=0\)

27)\(2x^3−3x^2−32x−15=0\)

Responder

\(5, −3, −\dfrac{1}{2} \)

28)\(2x^3+x^2−7x−6=0\)

29)\(2x^3−3x^2−x+1=0\)

Responder

\(\dfrac{1}{2}, \dfrac{1+\sqrt{5}}{2}, \dfrac{1−\sqrt{5}}{2}\)

30)\(3x^3−x^2−11x−6=0\)

31)\(2x^3−5x^2+9x−9=0\)

Responder

\(\dfrac{3}{2}\)

32)\(2x^3−3x^2+4x+3=0\)

33)\(x^4−2x^3−7x^2+8x+12=0\)

Responder

\(2, 3, −1, −2\)

34)\(x^4+2x^3−9x^2−2x+8=0\)

35)\(4x^4+4x^3−25x^2−x+6=0\)

Responder

\(\dfrac{1}{2}, −\dfrac{1}{2}, 2, −3\)

36)\(2x^4−3x^3−15x^2+32x−12=0\)

37)\(x^4+2x^3−4x^2−10x−5=0\)

Responder

\(−1, −1, \sqrt{5}, −\sqrt{5}\)

38)\(4x^3−3x+1=0\)

39)\(8x^4+26x^3+39x^2+26x+6\)

Responder

\(−\dfrac{3}{4}, −\dfrac{1}{2}\)

Para los ejercicios 40-45, encuentra todas las soluciones complejas (reales y no reales).

40)\(x^3+x^2+x+1=0\)

41)\(x^3−8x^2+25x−26=0\)

Responder

\(2, 3+2i, 3−2i\)

42)\(x^3+13x^2+57x+85=0\)

43)\(3x^3−4x^2+11x+10=0\)

Responder

\(−\dfrac{2}{3}, 1+2i, 1−2i\)

44)\(x^4+2x^3+22x^2+50x−75=0\)

45)\(2x^3−3x^2+32x+17=0\)

Responder

\(−\dfrac{1}{2}, 1+4i, 1−4i\)

Gráfica

Para los ejercicios 46-55, utilice la Regla de Descartes para determinar el posible número de soluciones positivas y negativas. Confirme con la gráfica dada.

46)\(f(x)=x^3−1\)

47)\(f(x)=x^4−x^2−1\)

Responder

\(1\)positivo,\(1\) negativo

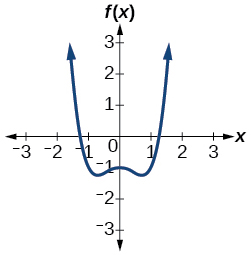
48)\(f(x)=x^3−2x^2−5x+6\)

49)\(f(x)=x^3−2x^2+x−1\)

Responder

\(3\)o\(1\) positivo,\(0\) negativo

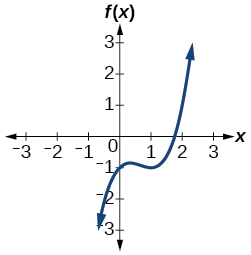
50)\(f(x)=x^4+2x^3−12x^2+14x−5\)

51)\(f(x)=2x^3+37x^2+200x+300\)

Responder

\(0\)positivo\(3\) o\(1\) negativo

52)\(f(x)=x^3−2x^2−16x+32\)

53)\(f(x)=2x^4−5x^3−5x^2+5x+3\)

Responder

\(2\)o\(0\) positivo,\(2\) o\(0\) negativo

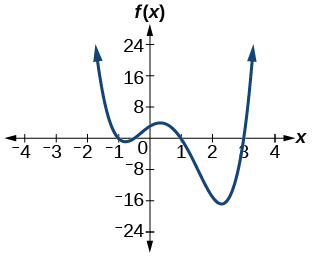
54)\(f(x)=2x^4−5x^3−14x^2+20x+8\)

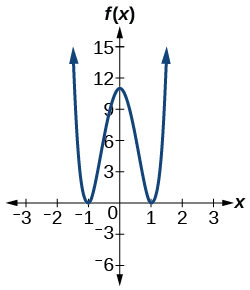
55)\(f(x)=10x^4−21x^2+11\)

Responder

\(2\)o\(0\) positivo,\(2\) o\(0\) negativo

Numérico

Para los ejercicios 56-60, enumere todos los ceros racionales posibles para las funciones.

56)\(f(x)=x^4+3x^3−4x+4\)

57)\(f(x)=2x^3+3x^2−8x+5\)

Responder

\(±5, ±1, ± \dfrac{5}{2}\)

58)\(f(x)=3x^3+5x^2−5x+4\)

59)\(f(x)=6x^4−10x^2+13x+1\)

Responder

\(±1, ±\dfrac{1}{2}, ±\dfrac{1}{3}, ±\dfrac{1}{6}\)

60)\(f(x)=4x^5−10x^4+8x^3+x^2−8\)

Tecnología

Para los ejercicios 61-65, usa tu calculadora para graficar la función polinómica. A partir de la gráfica, encuentra los ceros racionales. Todas las soluciones reales son racionales.

61)\(f(x)=6x^3−7x^2+1\)

Responder

\(1, \dfrac{1}{2}, −\dfrac{1}{3}\)

62)\(f(x)=4x^3−4x^2−13x−5\)

63)\(f(x)=8x^3−6x^2−23x+6\)

Responder

\(2, \dfrac{1}{4}, −\dfrac{3}{2}\)

64)\(f(x)=12x^4+55x^3+12x^2−117x+54\)

65)\(f(x)=16x^4−24x^3+x^2−15x+25\)

Responder

\(\dfrac{5}{4}\)

Extensiones

Para los ejercicios 66-70, construir una función polinómica del menor grado posible utilizando la información dada.

66) Raíces reales:\(–1, 1, 3\) y\((2,f(2))=(2,4)\)

67) Raíces reales:\(–1\) (con multiplicidad\(2\) y\(1\)) y\((2,f(2))=(2,4)\)

Responder

\(f(x)=\dfrac{4}{9}(x^3+x^2−x−1)\)

68) Raíces reales:\(–2, \dfrac{1}{2}\) (con multiplicidad\(2\)) y\((−3,f(−3))=(−3,5)\)

69) Raíces reales:\(−\dfrac{1}{2}, 0,\dfrac{1}{2}\) y\((−2,f(−2))=(−2,6)\)

Responder

\(f(x)=−\dfrac{1}{5}(4x^3−x)\)

70) Raíces reales:\(–4, –1, 1, 4\) y\((−2,f(−2))=(−2,10)\)

Aplicaciones del mundo real

Para los ejercicios 71-75, encuentra las dimensiones de la caja descrita.

71) La longitud es dos veces más larga que la anchura. La altura es\(2\) pulgadas mayor que la anchura. El volumen es de pulgadas\(192\) cúbicas.

Responder

\(8\)\(4\)por\(6\) pulgadas

72) La longitud, anchura y altura son números enteros consecutivos. El volumen es de pulgadas\(120 \) cúbicas.

73) La longitud es una pulgada más que la anchura, que es una pulgada más que la altura. El volumen es de pulgadas\(86.625\) cúbicas.

Responder

\(5.5\)\(4.5\)por\(3.5\) pulgadas

74) La longitud es tres veces la altura y la altura es una pulgada menos que la anchura. El volumen es de pulgadas\(108\) cúbicas.

75) El largo es\(3\) pulgadas más que el ancho. El ancho es\(2\) pulgadas más que la altura. El volumen es de pulgadas\(120\) cúbicas.

Responder

\(8\)\(5\)por\(3\) pulgadas

Para los ejercicios 76-80, encuentra las dimensiones del cilindro circular derecho descritas.

76) El radio es\(3\) pulgadas más que la altura. El volumen es de metros\(16π\) cúbicos.

77) La altura es una menos de la mitad del radio. El volumen es de metros\(72π\) cúbicos.

Responder

Radio =\(6\) metros, Altura =\(2\) metros

78) El radio y la altura difieren en un metro. El radio es mayor y el volumen es de metros\(48π\) cúbicos.

79) El radio y la altura difieren en dos metros. La altura es mayor y el volumen es de metros\(28.125π\) cúbicos.

Responder

Radio =\(2.5\) metros, Altura =\(4.5\) metros

80) El radio es\(\dfrac{1}{3}\) metro mayor que la altura. El volumen es de metros\(\dfrac{98}{9}π\) cúbicos.

3.7 Funciones racionales

Verbal

1) ¿Cuál es la diferencia fundamental en la representación algebraica de una función polinómica y una función racional?

Responder

La función racional estará representada por un cociente de funciones polinómicas.

2) ¿Cuál es la diferencia fundamental en las gráficas de funciones polinómicas y funciones racionales?

3) Si la gráfica de una función racional tiene una discontinuidad removible, ¿qué debe ser cierto de la regla funcional?

Responder

El numerador y denominador deben tener un factor común.

4) ¿Puede una gráfica de una función racional no tener asíntota vertical? Si es así, ¿cómo?

5) ¿Puede una gráfica de una función racional no tener intercepciones x? Si es así, ¿cómo?

Responder

Sí. El numerador de la fórmula de las funciones tendría solo raíces complejas y/o factores comunes tanto al numerador como al denominador.

Algebraico

Para los ejercicios 6-9, encuentra el dominio de las funciones racionales.

6)\(f(x)=\dfrac{x-1}{x+2}\)

7)\(f(x)=\dfrac{x+1}{x^{2}-1}\)

Responder

Todos los reales\(x \neq -1,1\)

8)\(f(x)=\dfrac{x^{2}+4}{x^{2}-2 x-8}\)

9)\(f(x)=\dfrac{x^{2}+4 x-3}{x^{4}-5 x^{2}+4}\)

Responder

Todos los reales\(x \neq-1,-2,1,2\)

Para los ejercicios 10-19, encontrar el dominio, asíntotas verticales y asíntotas horizontales de las funciones.

10)\(f(x)=\dfrac{4}{x-1}\)

11)\(f(x)=\dfrac{2}{5 x+2}\)

Responder

V.A. en\(x=-\dfrac{2}{5}\); H.A. en\(y=0\); Dominio es todo real\(x \neq-\dfrac{2}{5}\)

12)\(f(x)=\dfrac{x}{x^{2}-9}\)

13)\(f(x)=\dfrac{x}{x^{2}+5 x-36}\)

Responder

V.A. en\(x=4,-9\); H.A. en\(y=0\); Dominio es todo real\(x \neq 4,-9\)

14)\(f(x)=\dfrac{3+x}{x^{3}-27}\)

15)\(f(x)=\dfrac{3x-4}{x^{3}-16x}\)

Responder

V.A. en\(x=0,4,-4\); H.A. en\(y=0\); Dominio es todo real\(x \neq 0,4,-4\)

16)\(f(x)=\dfrac{x^{2}-1}{x^{3}+9 x^{2}+14 x}\)

17)\(f(x)=\dfrac{x+5}{x^{2}-25}\)

Responder

V.A. en\(x=-5\); H.A. en\(y=0\); Dominio es todo real\(x \neq 5,-5\)

18)\(f(x)=\dfrac{x-4}{x-6}\)

19)\(f(x)=\dfrac{4-2x}{3 x-1}\)

Responder

V.A. en\(x=\dfrac{1}{3}\); H.A. en\(y=-\dfrac{2}{3}\); Dominio es todo real\(x \neq \dfrac{1}{3}\)

Para los ejercicios 20-24, encuentra las\(x\) - y\(y\) -intercepciones para las funciones.

20)\(f(x)=\dfrac{x+5}{x^{2}+4}\)

21)\(f(x)=\dfrac{x}{x^{2}-x}\)

Responder

ninguno

22)\(f(x)=\dfrac{x^{2}+8 x+7}{x^{2}+11 x+30}\)

23)\(f(x)=\dfrac{x^{2}+x+6}{x^{2}-10 x+24}\)

Responder

\(x\)-intercepta ninguno,\(y\) -intercepta\(\left(0, \dfrac{1}{4}\right)\)

24)\(f(x)=\dfrac{94-2 x^{2}}{3 x^{2}-12}\)

Para los ejercicios 25-29, describa el comportamiento local y final de las funciones.

25)\(f(x)=\dfrac{x}{2 x+1}\)

Responder

Comportamiento local:\(x \rightarrow-\dfrac{1}{2}^{+}, f(x) \rightarrow-\infty, x \rightarrow-\dfrac{1}{2}^{-}, f(x) \rightarrow \infty\)

Comportamiento final:\(x \rightarrow \pm \infty, f(x) \rightarrow \dfrac{1}{2}\)

26)\(f(x)=\dfrac{2x}{x-6}\)

27)\(f(x)=\dfrac{-2x}{x-6}\)

Responder

Comportamiento local:\(x \rightarrow 6^{+}, f(x) \rightarrow-\infty, x \rightarrow 6^{-}, f(x) \rightarrow \infty \)

Comportamiento final:\(x \rightarrow \pm \infty, f(x) \rightarrow-2\)

28)\(f(x)=\dfrac{x^{2}-4 x+3}{x^{2}-4x-5}\)

29)\(f(x)=\dfrac{2 x^{2}-32}{6 x^{2}+13x-5}\)

Responder

Comportamiento local:\(x \rightarrow-\dfrac{1}{3}, f(x) \rightarrow \infty, x \rightarrow-\dfrac{1}{3}, f(x) \rightarrow-\infty, x \rightarrow \dfrac{5}{2}, f(x) \rightarrow \infty, x \rightarrow \dfrac{5}{2}+f(x) \rightarrow-\infty\)

Comportamiento final:\(x \rightarrow \pm \infty, f(x) \rightarrow \dfrac{1}{3}\)

Para los ejercicios 30-34, encuentra la asíntota inclinada de las funciones.

30)\(f(x)=\dfrac{24 x^{2}+6 x}{2 x+1}\)

31)\(f(x)=\dfrac{4 x^{2}-10}{2 x-4}\)

Responder

\(y=2 x+4\)

32)\(f(x)=\dfrac{81 x^{2}-18}{3 x-2}\)

33)\(f(x)=\dfrac{6 x^{3}-5 x}{3 x^{2}+4}\)

Responder

\(y=2 x\)

34)\(f(x)=\dfrac{x^{2}+5x+4}{x-1}\)

Gráfica

Para los ejercicios 35-38, utilice la transformación dada para graficar la función. Anote las asíntotas verticales y horizontales.

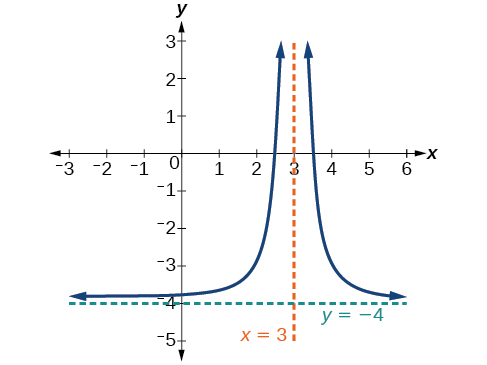
35) La función recíproca desplazó hacia arriba dos unidades.

Responder

V.A.\(x=0\), H.A.\(y=2\)

36) La función recíproca desplazó hacia abajo una unidad y dejó tres unidades.

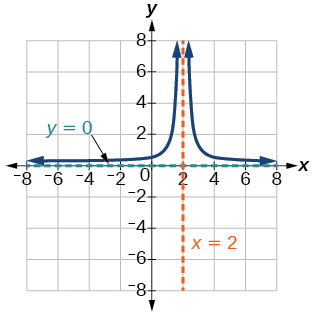
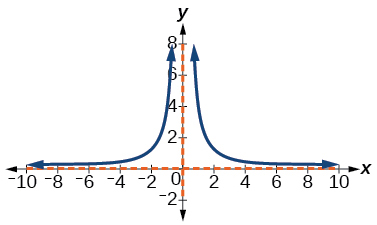
37) La función cuadrada recíproca se desplazó a las\(2\) unidades de la derecha.

Responder

V.A.\(x=2\), H.A.\(y=0\)

38) La función cuadrada recíproca desplazó hacia abajo\(2\) las unidades y la\(1\) unidad derecha.

Para los ejercicios 39-50, se encuentran las intercepciones horizontales, la intercepción vertical, las asíntotas verticales y la asíntota horizontal o inclinada de las funciones. Usa esa información para bosquejar una gráfica.

39)\(p(x)=\dfrac{2x-3}{x+4}\)

Responder

V.A.\(x=-4\), H.A.\(y=2\)\(\left(\dfrac{3}{2}, 0\right)\);\(\left(0,-\dfrac{3}{4}\right)\)

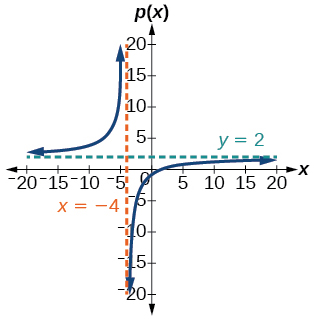
40)\(q(x)=\dfrac{x-5}{3 x-1}\)

41)\(s(x)=\dfrac{4}{(x-2)^{2}}\)

Responder

V.A.\(x=2\), H.A.\(y=0\),\((0,1)\)

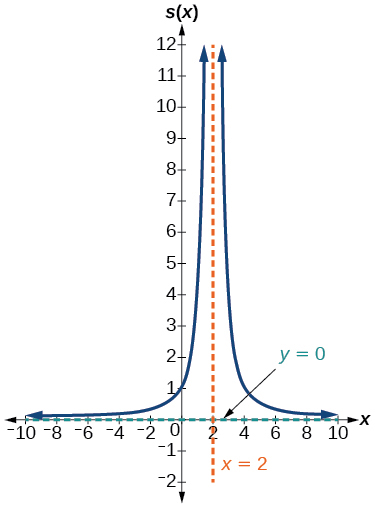
42)\(r(x)=\dfrac{5}{(x+1)^{2}}\)

43)\(f(x)=\dfrac{3 x^{2}-14 x-5}{3 x^{2}+8 x-16}\)

Responder

V.A.\(x=-4\)\(x=\dfrac{4}{3}\), H.A.\(y=1\)\((5,0)\);\(\left(-\dfrac{1}{3}, 0\right)\);\(\left(0, \dfrac{5}{16}\right)\)

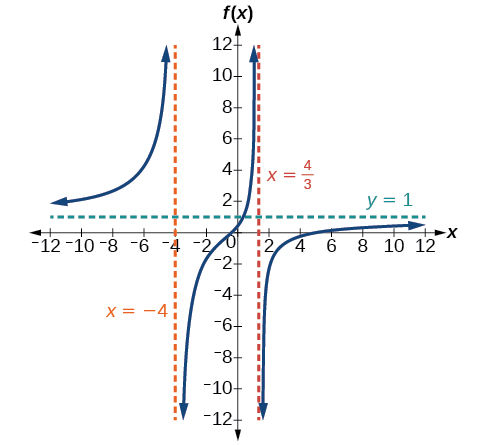
44)\(g(x)=\dfrac{2 x^{2}+7 x-15}{3 x^{2}-14+15}\)

45)\(a(x)=\dfrac{x^{2}+2 x-3}{x^{2}-1}\)

Responder

V.A.\(x=−1\), H.A.\(y=1\)\((−3,0)\);\((0,3)\)

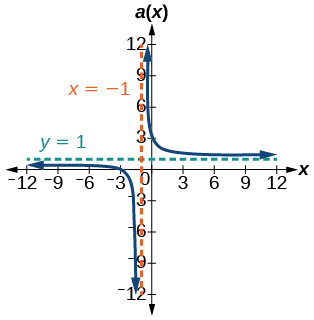
46)\(b(x)=\dfrac{x^{2}-x-6}{x^{2}-4}\)

47)\(h(x)=\dfrac{2 x^{2}+x-1}{x-4}\)

Responder

V.A.\(x=4\), S.A.\(y=2x+9\);\((-1,0)\);\(\left(\dfrac{1}{2}, 0\right)\);\(\left(0, \dfrac{1}{4}\right)\)

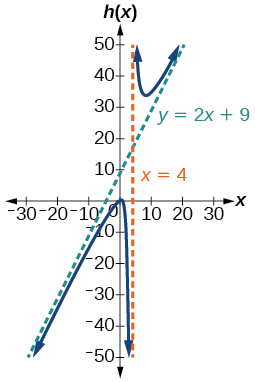
48)\(k(x)=\dfrac{2 x^{2}-3 x-20}{x-5}\)

49)\(w(x)=\dfrac{(x-1)(x+3)(x-5)}{(x+2)^{2}(x-4)}\)

Contestar

V.A.\(x=-2\),\(x=4\), H.A.\(y=1\),\((1,0)\);\((5,0)\);\((-3,0)\);\(\left(0,-\dfrac{15}{16}\right)\)

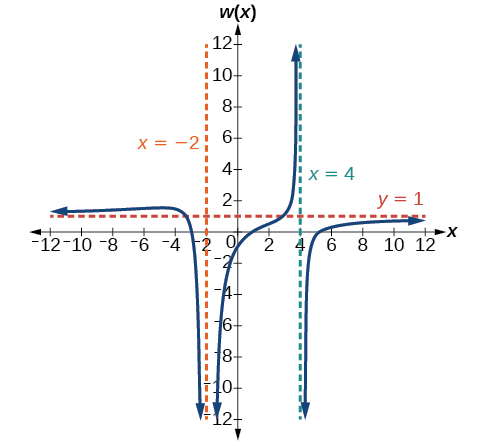
50)\(z(x)=\dfrac{(x+2)^{2}(x-5)}{(x-3)(x+1)(x+4)}\)

Para los ejercicios 51-56, escribir una ecuación para una función racional con las características dadas.

51) Asíntotas verticales en\(x=5\),\(x\) -intercepta\((2,0)\) e\((-1,0), y\) intercepta en\((0,4)\)

Contestar

\(y=50 \dfrac{x^{2}-x-2}{x^{2}-25}\)

52) Asíntotas verticales en\(x=-4\) e\(x=-1, x\) -intercepta en\((1,0)\) e\((5,0), y\) interceptar en\((0,7)\)

53) Asíntotas verticales en\(x=-4\) e\(x=-5, x\) -intercepta en\((4,0)\) y asíntota\((-6,0),\) horizontal en\(y=7\)

Contestar

\(y=7 \dfrac{x^{2}+2 x-24}{x^{2}+9 x+20}\)

54) Asíntotas verticales en\(x=-3\) e\(x=6, x\) -intercepta en\((-2,0)\) y asíntota\((1,0),\) horizontal en\(y=-2\)

55) Asíntota vertical en\(x=-1,\) Doble cero en\(x=2, y\) -intercepción en\((0,2)\)

Contestar

\(y=\dfrac{1}{2} \dfrac{x^{2}-4 x+4}{x+1}\)

56) Asíntota vertical en\(x=3,\) Doble cero en\(x=1, y\) -intercepción en\((0,4)\)

Para los ejercicios 57-,64 usa las gráficas para escribir una ecuación para la función.

57)

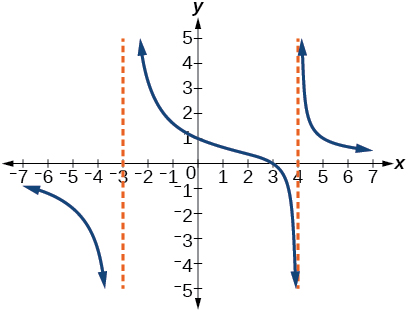
Contestar

\(y=4 \dfrac{x-3}{x^{2}-x-12}\)

58)

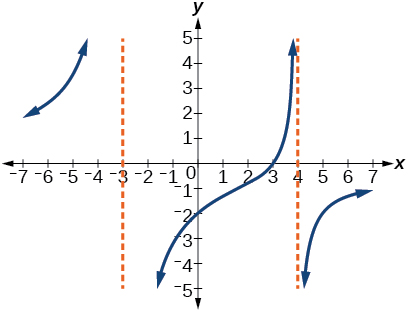
59)

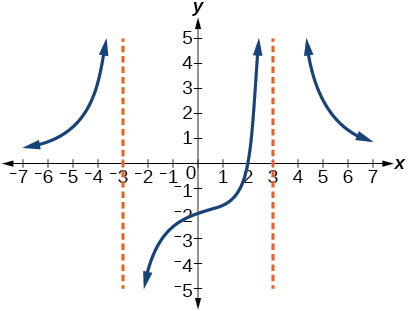
Contestar

\(y=-9 \dfrac{x-2}{x^{2}-9}\)

60)

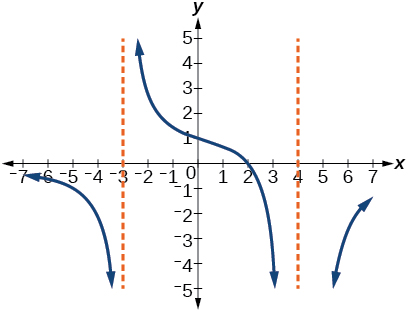
61)

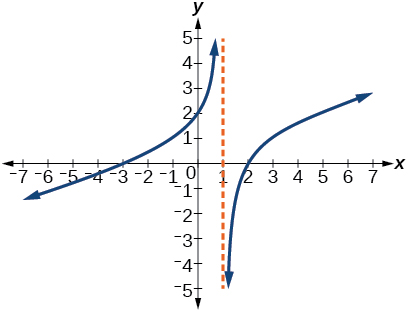
Contestar

\(y=\dfrac{1}{3} \dfrac{x^{2}+x-6}{x-1}\)

62)

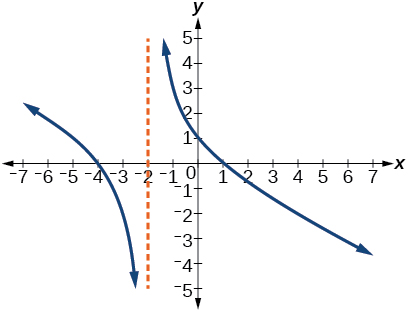
63)

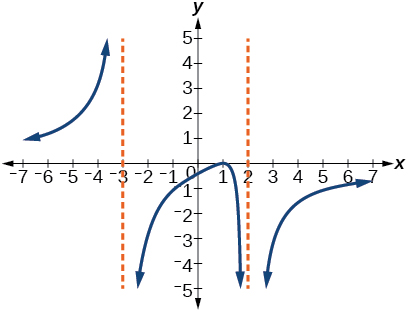
Contestar

\(y=-6 \dfrac{(x-1)^{2}}{(x+3)(x-2)^{2}}\)

64)

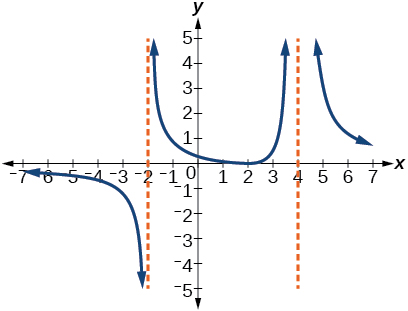
Numérico

Para los ejercicios 65-69, hacer tablas para mostrar el comportamiento de la función cerca de la asíntota vertical y reflejando la asíntota horizontal

65)\(f(x)=\dfrac{1}{x-2}\)

Contestar

\(x\)	2.01	2.001	2.0001	1.99	1.999
\ (x\) ">\(y\)	100	1,000	10,000	—100	—1,000

\(x\)	10	100	1,000	10,000	100,000
\ (x\) ">\(y\)	.125	.0102	.001	.0001	.00001

Asíntota vertical\(x=2\), asíntota horizontal\(y=0\)

66)\(f(x)=\dfrac{x}{x-3}\)

67)\(f(x)=\dfrac{2x}{x+4}\)

Contestar

\(x\)	—4.1	—4.01	—4.001	—3.99	—3.999
\ (x\) ">\(y\)	82	802	8,002	—798	—7998

\(x\)	10	100	1,000	10,000	100,000
\ (x\) ">\(y\)	1.4286	1.9331	1.992	1.9992	1.999992

Asíntota vertical\(x=-4\), asíntota horizontal\(y=2\)

68)\(f(x)=\dfrac{2 x}{(x-3)^{2}}\)

69)\(f(x)=\dfrac{x^{2}}{x^{2}+2 x+1}\)

Contestar

\(x\)	—.9	—.99	—.999	—1.1	—1.01
\ (x\) ">\(y\)	81	9,801	998,001	121	10,201

\(x\)	10	100	1,000	10,000	100,000
\ (x\) ">\(y\)	.82645	.9803	.998	.9998

Aíntota vertical\(x=-1\), Asíntota horizontal\(y=1\)

Tecnología

Para los ejercicios 70-74, utilice una calculadora para graficar\(f(x)\). Usa la gráfica para resolver \(f(x)>0\).

70)\(f(x)=\dfrac{2}{x+1}\)

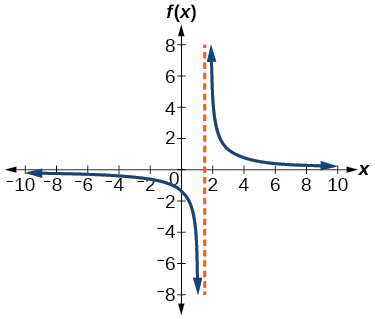
71)\(f(x)=\dfrac{4}{2x-3}\)

Contestar

\(\left(\dfrac{3}{2}, \infty\right)\)

72)\(f(x)=\dfrac{2}{(x-1)(x+2)}\)

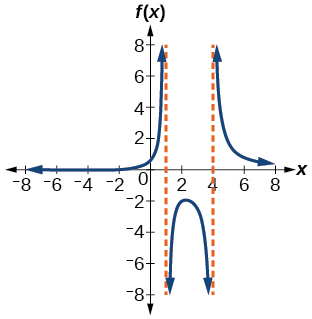
73)\(f(x)=\dfrac{x+2}{(x-1)(x-4)}\)

Contestar

\((-2,1) \cup(4, \infty)\)

74)\(f(x)=\dfrac{(x+3)^{2}}{(x-1)^{2}(x+1)}\)

Extensiones

Para los ejercicios 75-79, identificar la discontinuidad removible.

75)\(f(x)=\dfrac{x^{2}-4}{x-2}\)

Contestar

\((2,4)\)

76)\(f(x)=\dfrac{x^{3}+1}{x+1}\)

77)\(f(x)=\dfrac{x^{2}+x-6}{x-2}\)

Contestar

\((2,5)\)

78)\(f(x)=\dfrac{2 x^{2}+5 x-3}{x+3}\)

79)\(f(x)=\dfrac{x^{3}+x^{2}}{x+1}\)

Contestar

\((-1,1)\)

Aplicaciones del mundo real

Para los ejercicios 80-81, expresar una función racional que describa la situación.

80) Un gran tanque de mezcla contiene actualmente\(200\) galones de agua, en los que se han mezclado\(10\) libras de azúcar. Se abrirá un grifo, vertiendo\(10\) galones de agua por minuto en el tanque al mismo tiempo que se vierte azúcar en el tanque a razón de\(3\) libras por minuto. Encuentra la concentración (libras por galón) de azúcar en el tanque después\(t\) minutos.

81) Un gran tanque de mezcla contiene actualmente\(300\) galones de agua, en los que se han mezclado\(8\) libras de azúcar. Se abrirá un grifo, vertiendo\(20\) galones de agua por minuto en el tanque al mismo tiempo que se vierte azúcar en el tanque a razón de\(2\) libras por minuto. Encuentra la concentración (libras por galón) de azúcar en el tanque después de\(t\) minutos.

Contestar

\(C(t)=\dfrac{8+2t}{300+20t}\)

Para los ejercicios 82-83, utilizar la función racional dada para responder a la pregunta.

82) La concentración\(C\) de un fármaco en el torrente sanguíneo de un paciente\(t\) horas después de la inyección en dado por\(C(t)=\dfrac{2t}{3+t^{2}}\). ¿Qué sucede con la concentración de la droga a medida que\(t\) aumenta?

83) La concentración\(C\) de un fármaco en el torrente sanguíneo de un paciente, horas después de la inyección es dada por\(C(t)=\dfrac{100t}{2 t^{2}+75}\). Use una calculadora para aproximar el tiempo en que la concentración es mayor.

Contestar

Después de aproximadamente\(6.12\) horas.

Para los ejercicios 84-88, construir una función racional que ayude a resolver el problema. Entonces, usa una calculadora para responder a la pregunta.

84) Una caja abierta con base cuadrada es tener un volumen de pulgadas\(108\) cúbicas. Encuentra las dimensiones de la caja que tendrán una superficie mínima. Let\(x\) = longitud del lado de la base.

85) Una caja rectangular con base cuadrada es tener un volumen de pies\(20\) cúbicos. El material para la base cuesta\(30\) centas/ pie cuadrado. El material para los lados cuesta\(10\) centros/pie cuadrado. El material para los costos superiores\(20\) centros/pie cuadrado. Determinar las dimensiones que producirán el costo mínimo. Let\(x\) = longitud del lado de la base.

Contestar

\(A(x)=50 x^{2}+\dfrac{800}{x} \cdot 2\)\(2\)por los\(5\) pies.

86) Un cilindro circular derecho tiene volumen de pulgadas\(100\) cúbicas. Encuentre el radio y la altura que producirá el área de superficie mínima. Let\(x\) = radio.

87) Un cilindro circular derecho sin tapa tiene un volumen de metros\(50\) cúbicos. Encuentra el radio que producirá un área de superficie mínima. Let\(x\) = radio.

Contestar

\(A(x)=\pi x^{2}+\dfrac{100}{x}\). Radio =\(2.52\) metros.

88) Un cilindro circular derecho es tener un volumen de pulgadas\(40\) cúbicas. Cuesta\(4\) centavos/pulgada cuadrada construir la parte superior e inferior y\(1\) cent/pulgada cuadrada para construir el resto del cilindro. Encuentra el radio para obtener el costo mínimo. Let\(x\) = radio.

3.8 Funciones inversas y radicales

Verbal

1) Explicar por qué no podemos encontrar funciones inversas para todas las funciones polinómicas.

Contestar

Puede ser demasiado difícil o imposible de resolver para en términos de\(y\).

2) ¿Por qué debemos restringir el dominio de una función cuadrática al encontrar su inversa?

3) Al encontrar la inversa de una función radical, ¿qué restricción necesitaremos hacer?

Contestar

Necesitaremos una restricción en el dominio de la respuesta.

4) ¿La inversa de una función cuadrática siempre tomará qué forma?

Algebraico

Para los ejercicios 5-12, encuentra la inversa de la función en el dominio dado.

5)\(f(x)=(x-4)^{2},[4, \infty)\)

Contestar

\(f^{-1}(x)=\sqrt{x}+4\)

6)\(f(x)=(x+2)^{2},[-2, \infty)\)

7)\(f(x)=(x+1)^{2}-3,[-1, \infty)\)

Contestar

\(f^{-1}(x)=\sqrt{x+3}-1\)

8)\(f(x)=2-\sqrt{3+x}\)

9)\(f(x)=3 x^{2}+5,(-\infty, 0]\)

Contestar

\(f^{-1}(x)=-\sqrt{\dfrac{x-5}{3}}\)

10)\(f(x)=12-x^{2},[0, \infty)\)

11)\(f(x)=9-x^{2},[0, \infty)\)

Contestar

\(f(x)=\sqrt{9-x}\)

12)\(f(x)=2 x^{2}+4,[0, \infty)\)

Para los ejercicios 13-16, encuentra la inversa de las funciones.

13)\(f(x)=x^{3}+5\)

Contestar

\(f^{-1}(x)=\sqrt[3]{x-5}\)

14)\(f(x)=3 x^{3}+1\)

15)\(f(x)=4-x^{3}\)

Contestar

\(f^{-1}(x)=\sqrt[3]{4-x}\)

16)\(f(x)=4-2 x^{3}\)

Para los ejercicios 17-31, encuentra la inversa de las funciones.

17)\(f(x)=\sqrt{2x+1}\)

Contestar

\(f^{-1}(x)=\dfrac{x^{2}-1}{2},[0, \infty)\)

18)\(f(x)=\sqrt{3-4x}\)

19)\(f(x)=9+\sqrt{4x-4}\)

Contestar

\(f^{-1}(x)=\dfrac{(x-9)^{2}+4}{4},[9, \infty)\)

20)\(f(x)=\sqrt{6x-8}+5\)

21)\(f(x)=9+2 \sqrt[3]{x}\)

Contestar

\(f^{-1}(x)=\left(\dfrac{x-9}{2}\right)^{3}\)

22)\(f(x)=3-\sqrt[3]{x}\)

23)\(f(x)=\dfrac{2}{x+8}\)

Contestar

\(f^{-1}(x)=\dfrac{2-8x}{x}\)

24)\(f(x)=\dfrac{3}{x-4}\)

25)\(f(x)=\dfrac{x+3}{x+7}\)

Contestar

\(f^{-1}(x)=\dfrac{7x-3}{1-x}\)

26)\(f(x)=\dfrac{x-2}{x+7}\)

27)\(f(x)=\dfrac{3x+4}{5}\)

Contestar

\(f^{-1}(x)=\dfrac{5x-4}{4x+3}\)

28)\(f(x)=\dfrac{5x+1}{2-5x}\)

29)\(f(x)=x^{2}+2 x,[-1, \infty)\)

Contestar

\(f^{-1}(x)=\sqrt{x+1}-1\)

30)\(f(x)=x^{2}+4 x+1,[-2, \infty)\)

31)\(f(x)=x^{2}-6 x+3,[3, \infty)\)

Contestar

\(f^{-1}(x)=\sqrt{x+6}+3\)

Gráfica

Para los ejercicios 32-41, encuentra la inversa de la función y grafica tanto la función como su inversa.

32)\(f(x)=x^{2}+2, x \geq 0\)

33)\(f(x)=4-x^{2}, x \geq 0\)

Contestar

\(f^{-1}(x)=\sqrt{4-x}\)

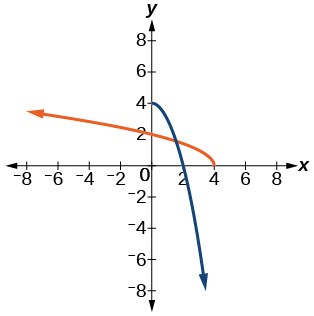
34)\(f(x)=(x+3)^{2}, x \geq-3\)

35)\(f(x)=(x-4)^{2}, x \geq 4\)

Contestar

\(f^{-1}(x)=\sqrt{x}+4\)

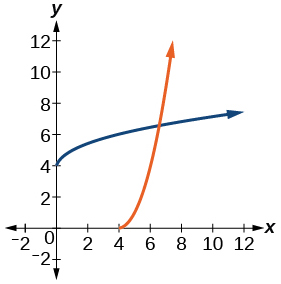
36)\(f(x)=x^{3}+3\)

37)\(f(x)=1-x^{3}\)

Contestar

\(f^{-1}(x)=\sqrt[3]{1-x}\)

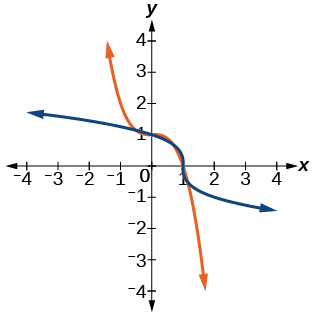
38)\(f(x)=x^{2}+4 x, x \geq-2\)

39)\(f(x)=x^{2}-6 x+1, x \geq 3\)

Contestar

\(f^{-1}(x)=\sqrt{x+8}+3\)

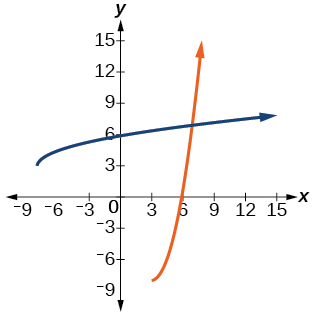
40)\(f(x)=\dfrac{2}{x}\)

41)\(f(x)=\dfrac{1}{x^{2}}, x \geq 0\)

Contestar

\(f^{-1}(x)=\sqrt{\dfrac{1}{x}}\)

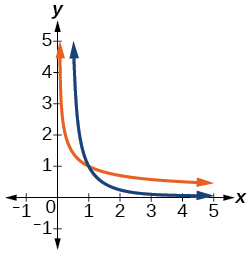
Para los ejercicios 42-46, utilice una gráfica que ayude a determinar el dominio de las funciones.

42)\(f(x)=\sqrt{\dfrac{(x+1)(x-1)}{x}}\)

43)\(f(x)=\sqrt{\dfrac{(x+2)(x-3)}{x-1}}\)

Contestar

\([-2,1) \cup[3, \infty)\)

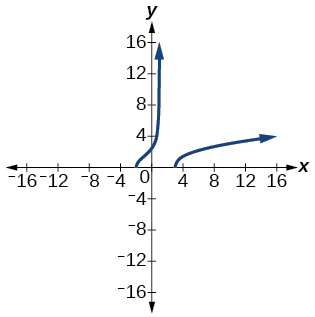
44)\(f(x)=\sqrt{\dfrac{x(x+3)}{x-4}}\)

45)\(f(x)=\sqrt{\dfrac{x^{2}-x-20}{x-2}}\)

Contestar

\([-4,2) \cup[5, \infty)\)

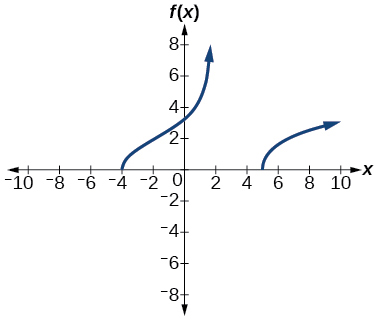
46)\(f(x)=\sqrt{\dfrac{9 x^{2}}{x+4}}\)

Tecnología

Para los ejercicios 47-51, utilice una calculadora para graficar la función. Después, usando la gráfica, dar tres puntos en la gráfica de la inversa con\(y\) -coordenadas dadas.

47)\(f(x)=x^{3}-x-2, y=1,2,3\)

Contestar

\((-2,0) ;(4,2) ;(22,3)\)

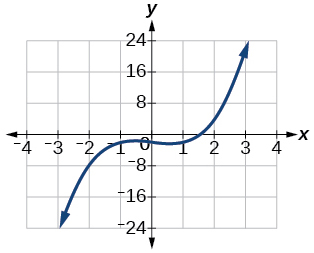
48)\(f(x)=x^{3}+x-2, y=0,1,2\)

49)\(f(x)=x^{3}+3 x-4, y=0,1,2\)

Contestar

\((-4,0) ;(0,1) ;(10,2)\)

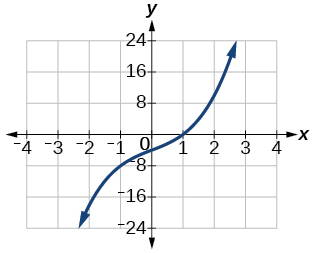
50)\(f(x)=x^{3}+8 x-4, y=-1,0,1\)

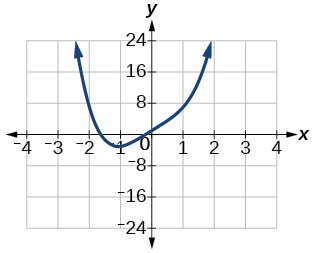
51)\(f(x)=x^{4}+5 x+1, y=-1,0,1\)

Contestar

\((-3,-1) ;(1,0) ;(7,1)\)

Extensiones

Para los ejercicios 52-56, encuentra la inversa de las funciones con números reales\(a, b, c\) positivos.

52)\(f(x)=ax^{3}+b\)

53)\(f(x)=x^{2}+bx\)

Contestar

\(f^{-1}(x)=\sqrt{x+\dfrac{b^{2}}{4}}-\dfrac{b}{2}\)

54)\(f(x)=\sqrt{a x^{2}+b}\)

55)\(f(x)=\sqrt[3]{a x+b}\)

Contestar

\(f^{-1}(x)=\dfrac{x^{2}-b}{a}\)

56)\(f(x)=\dfrac{ax+b}{x+c}\)

Aplicaciones del mundo real

Para los ejercicios 57-66, determine la función descrita y luego utilízala para responder a la pregunta.

57) Un objeto caído desde una altura de\(200\) metros tiene una altura,\(h(t)\), en metros después de que hayan transcurrido\(t\) segundos, tal que\(h(t)=200-4.9 t^{2}\). \(t\)Exprese en función de la altura\(h\),, y encuentre el tiempo para alcanzar una altura de\(50\) metros.

Contestar

\(t(h)=\sqrt{\dfrac{200-h}{4.9}}\),\(5.53\) segundos

58) Un objeto caído desde una altura de\(600\) pies tiene una altura,\(h(t),\) en pies después de que hayan transcurrido\(t\) segundos, tal que\(h(t)=600-16 t^{2}\). \(t\)Exprese en función de la altura\(h\), y encuentre el tiempo para alcanzar una altura de\(400\) pies.

59) El volumen,\(V\), de una esfera en cuanto a su radio,\(r\), viene dado por\(V(r)=\frac{4}{3} \pi r^{3}\). Expresar\(r\) en función de\(V\), y encontrar el radio de una esfera con volumen de pies\(200\) cúbicos.

Contestar

\(r(V)=\sqrt[3]{\dfrac{3 V}{4 \pi}}\),\(3.63\) pies

60) La superficie,\(A\), de una esfera en cuanto a su radio,\(r\), viene dada por\(A(r)=4 \pi r^{2}\). Expresar\(r\) en función de\(V\), y encontrar el radio de una esfera con una superficie de pulgadas\(1000\) cuadradas.

61) Un recipiente contiene\(100\) ml de una solución que es\(25\) ml de ácido. Si se agregan\(n\) ml de una solución que es\(60\%\) ácida, la función\(C(n)=\dfrac{25+.6 n}{100+n}\) da la concentración\(C\),, en función del número de ml añadidos,\(n\). Expresar\(n\) en función de\(C\) y determinar el número de mL que se necesitan agregar para tener una solución que sea\(50\%\) ácida.

Contestar

\(n(C)=\dfrac{100 C-25}{6-C}, 250 \mathrm{mL}\)

62) El periodo\(T\), en segundos, de un simple péndulo en función de su longitud\(l\), en pies, viene dado por\(T(l)=2 \pi \sqrt{\dfrac{l}{322}}\). Expresar\(l\) en función\(T\) y determinar la longitud de un péndulo con periodo de\(2\) segundos.

63) El volumen de un cilindro\(V\), en términos de radio,\(r\), y altura\(h\), viene dado por\(V=\pi r^{2} h\). Si un cilindro tiene una altura de\(6\) metros, exprese el radio en función de\(V\) y encuentre el radio de un cilindro con volumen de metros\(300\) cúbicos.

Contestar

\(r(V)=\sqrt{\dfrac{V}{6 \pi}}, 3.99\)metros

64) La superficie,\(A\), de un cilindro en términos de su radio,\(r\), y altura,\(h\), viene dada por\(A=2 \pi r^{2}+2 \pi r h\). Si la altura del cilindro es\(4\) pies, exprese el radio en función de\(V\) y encuentre el radio si el área de superficie es de pies\(200\) cuadrados.

65) El volumen de un cono circular derecho\(V\), en términos de su radio,\(r\), y su altura,\(h\), viene dado por\(V=\frac{1}{3} \pi r^{2} h\). Exprese\(r\) en términos de\(V\) si la altura del cono es\(12\) pies y encuentra el radio de un cono con volumen de pulgadas\(50\) cúbicas.

Contestar

\(r(V)=\sqrt{\dfrac{V}{4 \pi}}, 1.99\)pulgadas

66) Considera un cono con altura de\(30\) pies. Expresar el radio,\(r\), en términos del volumen,\(V\), y encontrar el radio de un cono con volumen de pies\(1000\) cúbicos.

3.9 Modelado con Variación

Verbal

1) ¿Qué es cierto de la aparición de gráficas que reflejan una variación directa entre dos variables?

Contestar

La gráfica tendrá la apariencia de una función de potencia.

2) Si dos variables varían inversamente, ¿cómo será una ecuación que represente su relación?

3) ¿Existe un límite en el número de variables que pueden variar conjuntamente? Explique.

Contestar

No. Múltiples variables pueden variar conjuntamente.

Algebraico

Para los ejercicios 4-23, escribir una ecuación que describa la relación de las variables dadas.

4)\(y\) varía directamente según\(x\) y cuando\(x=6, y=12\)

5)\(y\) varía directamente como el cuadrado de\(x\) y cuando\(x=4, y=80\)

Contestar

\(y=5 x^{2}\)

6)\(y\) varía directamente como la raíz cuadrada de\(x\) y cuando\(x=36, y=24\)

7)\(y\) varía directamente como el cubo de\(x\) y cuando\(x=36, y=24\)

Contestar

\(y=10 x^{3}\)

8)\(y\) varía directamente como la raíz cúbica de\(x\) y cuando\(x=27, y=15\)

9)\(y\) varía directamente como el cuarto poder de\(x\) y cuando\(x=1, y=6\)

Contestar

\(y=6 x^{4}\)

10)\(y\) varía inversamente como\(x\) y cuando\(x=4, y=2\)

11)\(y\) varía inversamente como el cuadrado de\(x\) y cuando\(x=3, y=2\)

Contestar

\(y=\dfrac{18}{x^{2}}\)

12)\(y\) varía inversamente como el cubo de\(x\) y cuando\(x=2, y=5\)

13)\(y\) varía inversamente como el cuarto poder de\(x\) y cuando\(x=3, y=1\)

Contestar

\(y=\dfrac{81}{x^{4}}\)

14)\(y\) varía inversamente como la raíz cuadrada de\(x\) y cuando\(x=25, y=3\)

15)\(y\) varía inversamente como la raíz cúbica de\(x\) y cuando\(x=64, y=5\)

Contestar

\(y=\dfrac{20}{\sqrt[3]{x}}\)

16)\(y\) varía conjuntamente con\(x\) y\(z\) y cuándo\(x=2\) y\(z=3, y=36\)

17)\(y\) varía conjuntamente como\(x, z,\)\(w\) y cuándo\(x=1, z=2, w=5\), entonces\(y=100\)

Contestar

\(y=10 x z w\)

18)\(y\) varía conjuntamente como el cuadrado de\(x\) y el cuadrado de\(z\) y cuándo\(x=3\) y\(z=4\), entonces\(y=72\)

19)\(y\) varía conjuntamente como\(x\) y la raíz cuadrada de\(z\) y cuándo\(x=2\) y\(z=25\), entonces\(y=100\)

Contestar

\(y=10 x \sqrt{z}\)

20)\(y\) varía conjuntamente como el cuadrado\(x\) del cubo de\(z\) y la raíz cuadrada de\(w .\) Cuando\(x=1, z=2,\) y\(w=36,\) luego\(y=48\)

21)\(y\) varía conjuntamente como\(x\)\(z\) e inversamente como\(w\). Cuándo\(x=3, z=5,\) y\(w=6,\) luego\(y=10\)

Contestar

\(y=4 \dfrac{x z}{w}\)

22)\(y\) varía conjuntamente como el cuadrado de\(x\) y la raíz cuadrada de\(z\) e inversamente como el cubo de\(w\). Cuando\(x=3, z=4\), y\(w=3\), entonces\(y=6\)

23)\(y\) varía conjuntamente como\(x\)\(z\) e inversamente como la raíz cuadrada de varita el cuadrado de\(t\). Cuando\(x=3, z=1, w=25\), y\(t=2\), entonces\(y=6\)

Contestar

\(y=40 \dfrac{x z}{\sqrt{w} t^{2}}\)

Numérico

Para los ejercicios 24-40, utilice la información dada para encontrar el valor desconocido.

24)\(y\) varía directamente como\(x\). Cuando\(x=3,\) entonces\(y=12\). Encuentra\(y\) cuándo\(x=20\).

25)\(y\) varía directamente como el cuadrado de\(x\). Cuando\(x=2\), entonces\(y=16\). Encuentra\(y\) cuándo\(x=8\).

Contestar

\(y=256\)

26)\(y\) varía directamente como el cubo de\(x\). Cuando\(x=3\), entonces\(y=5\). Encuentra\(y\) cuándo\(x=4\).

27)\(y\) varía directamente como la raíz cuadrada de\(x\). Cuando\(x=16\), entonces\(y=4\). Encuentra\(y\) cuándo\(x=36\).

Contestar

\(y=6\)

28)\(y\) varía directamente como la raíz cúbica de\(x\). Cuando\(x=125\), entonces\(y=15\). Encuentra\(y\) cuándo\(x=1,000\).

29)\(y\) varía inversamente con\(x\). Cuando\(x=3\), entonces\(y=2\). Encuentra\(y\) cuándo\(x=1\).

Contestar

\(y=6\)

30)\(y\) varía inversamente con el cuadrado de\(x\). Cuando\(x=4\), entonces\(y=3\). Encuentra\(y\) cuándo\(x=2\).

31)\(y\) varía inversamente con el cubo de\(x\). Cuando\(x=3\), entonces\(y=1\). Encuentra\(y\) cuándo\(x=1\).

Contestar

\(y=27\)

32)\(y\) varía inversamente con la raíz cuadrada de\(x\). Cuando\(x=64\), entonces\(y=12\). Encuentra\(y\) cuándo\(x=36\).

33)\(y\) varía inversamente con la raíz cúbica de\(x\). Cuando\(x=27\), entonces\(y=5\). Encuentra\(y\) cuándo\(x=125\).

Contestar

\(y=3\)

34)\(y\) varía conjuntamente como\(x\) y\(z\). Cuando\(x=4\) y\(z=2\), entonces\(y=16\). Encuentra\(y\) cuándo\(x=3\) y\(z=3\).

35)\(y\) varía conjuntamente como\(x, z\), y\(w\). Cuando\(x=2, z=1\), y\(w=12\), entonces\(y=72\). Encuentra\(y\) cuándo\(x=1, z=2\), y\(w=3\).

Contestar

\(y=18\)

36)\(y\) varía conjuntamente como\(x\) y el cuadrado de\(z\). Cuando\(x=2\) y\(z=4\), entonces\(y=144\). Encuentra\(y\) cuándo\(x=4\) y\(z=5\).

37)\(y\) varía conjuntamente como el cuadrado de\(x\) y la raíz cuadrada de\(z\). Cuando\(x=9\), entonces\(y=24\). Encuentra\(y\) cuándo\(x=3\) y\(z=25\).

Contestar

\(y=90\)

38)\(y\) varía conjuntamente como\(x\) e inversamente como\(w\). Cuando\(x=5, z=2\), y\(w=20\), entonces\(y=4\). Encuentra\(y\) cuándo\(x=3\) y\(z=8\) y\(w=48\).

39)\(y\) varía conjuntamente como el cuadrado de\(x\) y el cubo de\(z\) e inversamente como la raíz cuadrada de\(w\). Cuando\(x=2, z=2\), y\(w=64\) luego\(y=12\). Encuentra\(y\) cuándo\(x=1, z=3\), y\(w=4\).

Contestar

\(y=\dfrac{81}{2}\)

40)\(y\) varía conjuntamente como el cuadrado de\(x\) y de\(z\) e inversamente como la raíz cuadrada de varita de\(t\). Cuando\(x=2, z=3, w=16\), y\(t=3\), entonces\(y=1\). Encuentra\(y\) cuándo\(x=3, z=2, w=36\), y\(t=5\).

Tecnología

Para los ejercicios 41-45, utilice una calculadora para graficar la ecuación implícita por la variación dada.

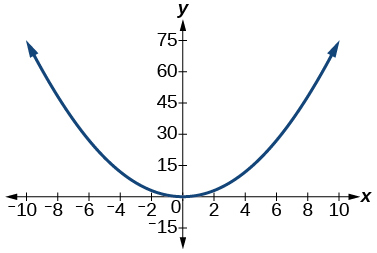
41)\(y\) varía directamente con el cuadrado de\(x\) y cuando\(x=2, y=3\)

Contestar

\(y=\dfrac{3}{4} x^{2}\)

42)\(y\) varía directamente como el cubo de\(x\) y cuándo\(x=2, y=4\).

43)\(y\) varía directamente como la raíz cuadrada de\(x\) y cuándo\(x=36, y=2\).

Contestar

\(y=\dfrac{1}{3} \sqrt{x}\)

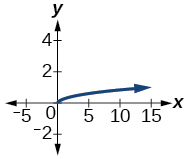
44)\(y\) varía inversamente con\(x\) y cuándo\(x=6, y=2\).

45)\(y\) varía inversamente como el cuadrado de\(x\) y cuándo\(x=1, y=4\).

Contestar

\(y=\dfrac{4}{x^{2}}\)

Extensiones

Para los ejercicios 46-50, use la Ley de Kepler, que establece que el cuadrado del tiempo,\(T\), requerido para que un planeta orbita el Sol varía directamente con el cubo de la distancia media\(a\),, que el planeta es del Sol.

46) Utilizando la época del\(1\) año de la Tierra y la distancia media de 93 millones de millas, encontrar la ecuación relativa\(T\) y\(a\).

47) Utilizar el resultado del ejercicio anterior para determinar el tiempo requerido para que Marte orbita el Sol si su distancia media es de\(142\) millones de millas.

Contestar

\(1.89\)años

48) Utilizando la distancia terrestre de\(150\) millones de kilómetros, encontrar la ecuación relativa\(T\) y\(a\).

49) Utilizar el resultado del ejercicio anterior para determinar el tiempo requerido para que Venus orbita el Sol si su distancia media es de\(108\) millones de kilómetros.

Contestar

\(0.61\)años

50) Utilizando la distancia terrestre de la unidad\(1\) astronómica (A.U.), determinar el tiempo para que Saturno orbita el Sol si su distancia media es\(9.54\) A.U.

Aplicaciones del mundo real

Para los ejercicios 51-60, utilice la información dada para responder a las preguntas.

51) La distancia\(s\) que cae un objeto varía directamente con el cuadrado del tiempo,\(t\), de la caída. Si un objeto cae\(16\) pies en un segundo, ¿cuánto tiempo para que caiga\(144\) pies?

Contestar

\(3\)segundos

52) La velocidad\(v\) de un objeto que cae varía directamente al tiempo,\(t\), de la caída. Si después de\(2\) segundos, la velocidad del objeto es\(64\) pies por segundo, ¿cuál es la velocidad después de\(5\) segundos?

53) La velocidad de vibración de una cuerda bajo tensión constante varía inversamente con la longitud de la cuerda. Si una cuerda mide\(24\) pulgadas de largo y vibra\(128\) veces por segundo, ¿cuál es la longitud de una cuerda que vibra\(64\) veces por segundo?

Contestar

\(48\)pulgadas

54) El volumen de un gas mantenido a temperatura constante varía indirectamente según la presión del gas. Si el volumen de un gas es de centímetros\(1200\) cúbicos cuando la presión es\(200\) milímetros de mercurio, ¿cuál es el volumen cuando la presión es\(300\) milímetros de mercurio?

55) El peso de un objeto sobre la superficie de la Tierra varía inversamente con el cuadrado de la distancia desde el centro de la Tierra. Si un cuerpo pesa\(50\) libras cuando está\(3960\) a millas del centro de la Tierra, ¿qué pesaría serían\(3970\) millas del centro de la Tierra?

Contestar

\(49.75\)libras

56) La intensidad de la luz medida en velas de pie varía inversamente con el cuadrado de la distancia desde la fuente de luz. Supongamos que la intensidad de una bombilla es\(0.08\) pie-velas a una distancia de\(3\) metros. Encuentra el nivel de intensidad en\(8\) metros.

57) La corriente en un circuito varía inversamente con su resistencia medida en ohmios. Cuando la corriente en un circuito es de\(40\) amperios, la resistencia es\(10\) ohmios. Encuentra la corriente si la resistencia es\(12\) ohmios.

Contestar

\(33.33\)amperios

58) La fuerza ejercida por el viento sobre una superficie plana varía conjuntamente con el cuadrado de la velocidad del viento y con el área de la superficie plana. Si el área de la superficie es de pies\(40\) cuadrados de superficie y la velocidad del viento es\(20\) millas por hora, la fuerza resultante es\(15\) libras. Encuentra la fuerza en una superficie de pies\(65\) cuadrados con una velocidad de\(30\) millas por hora.

59) Los caballos de fuerza (hp) que un eje puede transmitir de manera segura varían conjuntamente con su velocidad (en revoluciones por minuto (rpm)) y el cubo del diámetro. Si el eje de un determinado material\(3\) pulgadas de diámetro puede transmitir\(45\) hp a\(100\) rpm, ¿cuál debe ser el diámetro para transmitir\(60\) hp a\(150\) rpm?

Contestar

\(2.88\)pulgadas

60) La energía cinética\(K\) de un objeto en movimiento varía conjuntamente con su masa\(m\) y el cuadrado de su velocidad\(v\). Si un objeto que pesa\(40\) kilogramos con una velocidad de\(15\) metros por segundo tiene una energía cinética de\(1000\) julios, encuentre la energía cinética si la velocidad se incrementa a\(20\) metros por segundo.