3.R: Funciones polinómicas y racionales (Revisión)

Última actualización
Guardar como PDF

Page ID: 121451

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

3.1 Números Complejos

Realizar la operación indicada con números complejos.

1)$(4+3 i)+(-2-5 i)$

Contestar: $2-2 i$

2)$(6-5 i)-(10+3 i)$

3)$(2-3 i)(3+6 i)$

Contestar: $24+3 i$

4)$\dfrac{2-i}{2+i}$

Resolver las siguientes ecuaciones sobre el complejo sistema numérico.

5)$x^{2}-4 x+5=0$

Contestar: $\{2+i, 2-i\}$

6)$x^{2}+2 x+10=0$

3.2 Funciones cuadráticas

Para los ejercicios 1-2, escriba la función cuadrática en forma estándar. Entonces, dale las intercepciones del vértice y los ejes. Por último, graficar la función.

1)$f(x)=x^{2}-4 x-5$

Contestar

$f(x)=(x-2)^{2}-9$vértice$(2,-9)$, intercepta$(5,0); (-1,0); (0,-5)$

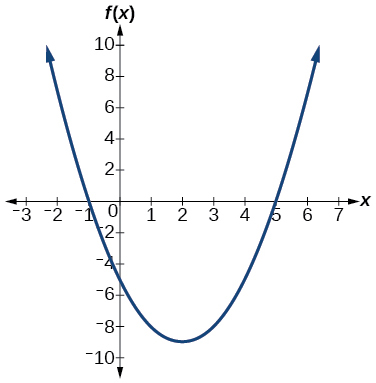
$CNX_Precalc_Figure_03_09_206.jpg$

2)$f(x)=-2 x^{2}-4 x$

Para los problemas 3-4, encuentre la ecuación de la función cuadrática utilizando la información dada.

3) El vértice es$(-2,3)$ y un punto en la gráfica es$(3,6)$.

Contestar: $f(x)=\dfrac{3}{25}(x+2)^{2}+3$

4) El vértice es$(-3,6.5)$ y un punto en la gráfica es$(2,6)$.

Contesta las siguientes preguntas.

5) Un terreno rectangular debe ser encerrado por cercas. Un lado está a lo largo de un río y por lo tanto no necesita barda. Si el cercado total disponible es de$600$ metros, encuentra las dimensiones de la parcela para tener área máxima.

Contestar: $300$metros por$150$ metros, el lado más largo paralelo al río.

6) Un objeto proyectado desde el suelo en un ángulo de$45$ grado con velocidad inicial de$120$ pies por segundo tiene altura,$h$, en términos de distancia horizontal recorrida,$x$, dado por$h(x)=\dfrac{-32}{(120)^{2}} x^{2}+x$. Encuentra la altura máxima que alcanza el objeto.

3.3 Funciones de Potencia y Funciones Polinómicas

Para los ejercicios 1-3, determinar si la función es una función polinómica y, de ser así, dar el grado y el coeficiente principal.

1)$f(x)=4 x^{5}-3 x^{3}+2 x-1$

Contestar: Sí,$\text{degree} = 5$,$\text{leading coefficient} = 4$

2)$f(x)=5^{x+1}-x^{2}$

3)$f(x)=x^{2}\left(3-6 x+x^{2}\right)$

Contestar: Sí,$\text{degree} = 4$,$\text{leading coefficient} = 1$

Para los ejercicios 4-6, determinar el comportamiento final de la función polinómica.

4)$f(x)=2 x^{4}+3 x^{3}-5 x^{2}+7$

5)$f(x)=4 x^{3}-6 x^{2}+2$

Contestar: Como$x \rightarrow-\infty, f(x) \rightarrow-\infty $, como$x \rightarrow \infty, f(x) \rightarrow \infty$

6)$f(x)=2 x^{2}\left(1+3 x-x^{2}\right)$

3.4 Gráficas de Funciones Polinómicas

Para los ejercicios 1-3, encuentra todos los ceros de la función polinómica, señalando multiplicidades.

1)$f(x)=(x+3)^{2}(2 x-1)(x+1)^{3}$

Contestar: $-3$con multiplicidad$2$,$-\dfrac{1}{2}$ con multiplicidad$1$,$-1$ con multiplicidad$3$

2)$f(x)=x^{5}+4 x^{4}+4 x^{3}$

3)$f(x)=x^{3}-4 x^{2}+x-4$

Contestar: $4$con multiplicidad$1$

Para los ejercicios 4-5, con base en la gráfica dada, determinar los ceros de la función y anotar multiplicidad.

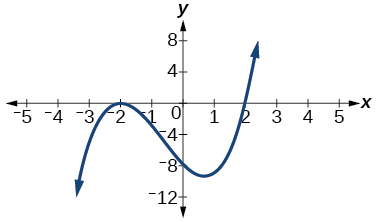
$CNX_Precalc_Figure_03_09_208.jpg$

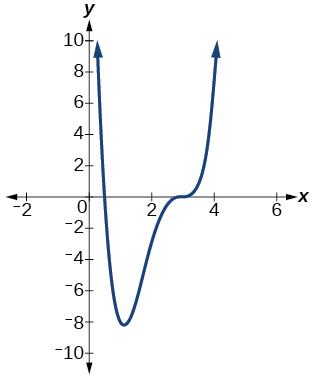
$CNX_Precalc_Figure_03_09_209.jpg$

Contestar: $\dfrac{1}{2}$con multiplicidad$1$,$3$ con multiplicidad$3$

6) Utilice el Teorema del Valor Intermedio para mostrar que al menos un cero se encuentra entre$2$ y$3$ para la función$f(x)=x^{3}-5 x+1$

3.5 Dividir polinomios

Para los ejercicios 1-2, usa división larga para encontrar el cociente y el resto.

1)$\dfrac{x^{3}-2 x^{2}+4 x+4}{x-2}$

Contestar: $x^{2}+4$con resto$12$

2)$\dfrac{3 x^{4}-4 x^{2}+4 x+8}{x+1}$

Para los ejercicios 3-6, usa la división sintética para encontrar el cociente. Si el divisor es un factor, entonces escriba la forma factorizada.

3)$\dfrac{x^{2}-2 x^{2}+5 x-1}{x+3}$

Contestar: $x^{2}-5 x+20-\dfrac{61}{x+3}$

4)$\dfrac{x^{2}+4 x+10}{x-3}$

5)$\dfrac{2 x^{3}+6 x^{2}-11 x-12}{x+4}$

Contestar: $2 x^{2}-2x-3$, por lo que la forma factorizada es$(x+4)\left(2 x^{2}-2x-3\right)$

6)$\dfrac{3 x^{4}+3 x^{3}+2 x+2}{x+1}$

3.6 Ceros de funciones polinómicas

Para los ejercicios 1-4, usa el Teorema Racional del Cero para ayudarte a resolver la ecuación polinómica.

1)$2 x^{3}-3 x^{2}-18 x-8=0$

Contestar: $\left\{-2,4,-\dfrac{1}{2}\right\}$

2)$3x^{3}+11 x^{2}+8 x-4=0$

3)$2 x^{4}-17 x^{3}+46 x^{2}-43 x+12=0$

Contestar: $\left\{1,3,4, \dfrac{1}{2}\right\}$

4)$4 x^{4}+8 x^{3}+19 x^{2}+32 x+12=0$

Para los ejercicios 5-6, usa la Regla de Signos de Descartes para encontrar el posible número de soluciones positivas y negativas.

5)$x^{3}-3 x^{2}-2 x+4=0$

Contestar: $0$o$2$ positivo,$1$ negativo

6)$2 x^{4}-x^{3}+4 x^{2}-5 x+1=0$

3.7 Funciones racionales

Para las siguientes funciones racionales 1-4, busque las intercepciones y las asíntotas verticales y horizontales, y luego utilícelas para esbozar una gráfica.

1)$f(x)=\dfrac{x+2}{x-5}$

Contestar

Intercepta$(-2,0)$ y$\left(0,-\dfrac{2}{5}\right)$, Asíntotas$x=5$ y$y=1$

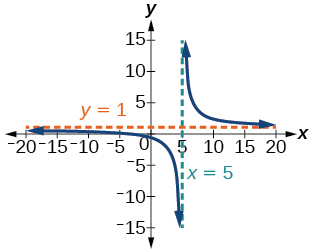
$CNX_Precalc_Figure_03_09_210.jpg$

2)$f(x)=\dfrac{x^{2}+1}{x^{2}-4}$

3)$f(x)=\dfrac{3 x^{2}-27}{x^{2}-9}$

Contestar

$(3,0),(-3,0)$Interceptos y$\left(0, \dfrac{27}{2}\right)$ asíntotas$x=1, x=-2, y=3$

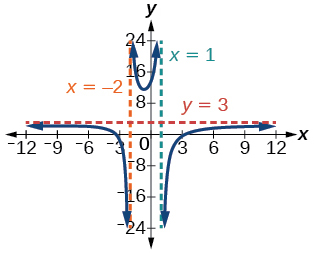
$CNX_Precalc_Figure_03_09_212.jpg$

4)$f(x)=\dfrac{x+2}{x^{2}-9}$

Para los ejercicios 5-6, encuentra la asíntota inclinada.

5)$f(x)=\dfrac{x^{2}-1}{x+2}$

Contestar: $y=x-2$

6)$f(x)=\dfrac{2 x^{3}-x^{2}+4}{x^{2}+1}$

3.8 Funciones inversas y radicales

Para los ejercicios 1-6, encuentra la inversa de la función con el dominio dado.

1)$f(x)=(x-2)^{2}, x \geq 2$

Contestar: $f^{-1}(x)=\sqrt{x}+2$

2)$f(x)=(x+4)^{2}-3, x \geq-4$

3)$f(x)=x^{2}+6 x-2, x \geq-3$

Contestar: $f^{-1}(x)=\sqrt{x+11}-3$

4)$f(x)=2 x^{3}-3$

5)$f(x)=\sqrt{4 x+5}-3$

Contestar: $f^{-1}(x)=\dfrac{(x+3)^{2}-5}{4}, x \geq-3$

6)$f(x)=\dfrac{x-3}{2 x+1}$

3.9 Modelado con Variación

Para los ejercicios 1-4, encuentra el valor desconocido.

1)$y$ varía directamente como el cuadrado de$x$. Si cuando$x=3, y=36$, encuentra$y$ si$x=4$.

Contestar: $y=64$

2)$y$ varía inversamente como la raíz cuadrada de$x$. Si cuando$x=25, y=2$, encuentra$y$ si$x=4$.

3)$y$ varía conjuntamente como el cubo de$x$ y como$z$. Si cuando$x=1$ y$z=2, y=6$, encontrar$y$ si$x=2$ y$z=3$.

Contestar: $y=72$

4)$y$ varía conjuntamente como$x$ y el cuadrado de$z$ e inversamente como el cubo de$w$. Si cuando$x=3, z=4$, y$w=2, y=48$, ind$y$ si$x=4, z=5$, y$w=3$.

Para los ejercicios 5-6, resolver el problema de la aplicación.

5) El peso de un objeto sobre la superficie de la tierra varía inversamente con la distancia desde el centro de la tierra. Si una persona pesa$150$ libras cuando está en la superficie de la tierra ($3,960$millas del centro), encuentra el peso de la persona si está$20$ a millas por encima de la superficie.

Contestar: $148.5$libras

6) El volumen$V$ de un gas ideal varía directamente con la temperatura$T$ e inversamente con la presión$P$. Un cilindro contiene oxígeno a una temperatura de$310$ grados K y una presión de$18$ atmósferas en un volumen de$120$ litros. Encuentra la presión si el volumen se disminuye a$100$ litros y la temperatura se incrementa a$320$ grados K.

Prueba de práctica

Realizar la operación indicada o resolver la ecuación.

1)$(3-4 i)(4+2 i)$

Contestar: $20-10 i$

2)$\dfrac{1-4 i}{3+4 i}$

3)$x^{2}-4 x+13=0$

Contestar: $\{2+3 i, 2-3 i\}$

4) Dar el grado y coeficiente principal de la siguiente función polinómica. \[f(x)=x^{3}\left(3-6 x^{2}-2 x^{2}\right) \nonumber \]

Determinar el comportamiento final de la función polinómica.

5)$f(x)=8 x^{3}-3 x^{2}+2 x-4$

Contestar: Como$x \rightarrow-\infty, f(x) \rightarrow-\infty$, como$x \rightarrow \infty, f(x) \rightarrow \infty$

6)$f(x)=-2 x^{2}\left(4-3 x-5 x^{2}\right)$

7) Escribir la función cuadrática en forma estándar. Determinar las intercepciones de vértice y ejes y graficar la función. \[f(x)=x^{2}+2 x-8 \nonumber \]

Contestar

$f(x)=(x+1)^{2}-9,$$(-1,-9),$intercepta vértice$(2,0); (-4,0); (0,-8)$

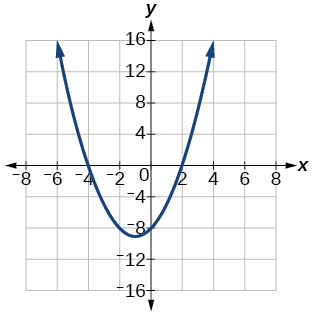
$CNX_Precalc_Figure_03_09_214.jpg$

8) Dada la información sobre la gráfica de una función cuadrática, encuentra su ecuación: Vértice$(2,0)$ y punto sobre gráfico$(4,12)$

Resolver el siguiente problema de aplicación.

9) Un campo rectangular debe ser encerrado por cercas. Además de la barda de cerramiento, otra barda es dividir el campo en dos partes, corriendo paralelas a dos lados. Si hay$1,200$ pies de cercado disponibles, encuentre el área máxima que se pueda encerrar.

Contestar: $60,000$pies cuadrados

Encuentra todos los ceros de las siguientes funciones polinómicas, señalando multiplicidades.

10)$f(x)=(x-3)^{3}(3 x-1)(x-1)^{2}$

11)$f(x)=2 x^{6}-12 x^{5}+18 x^{4}$

Contestar: $0$con multiplicidad$4$,$3$ con multiplicidad$2$

12) Con base en la gráfica, determinar los ceros de la función y multiplicidades.

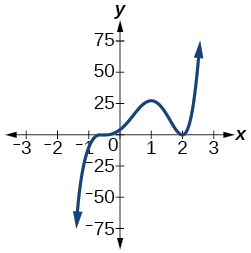
$CNX_Precalc_Figure_03_09_215.jpg$

13) Utilice la división larga para encontrar el cociente:\[\dfrac{2 x^{2}+3 x-4}{x+2} \nonumber \]

Contestar: $2 x^{2}-4 x+11-\dfrac{26}{x+2}$

Usa la división sintética para encontrar el cociente. Si el divisor es un factor, escriba la forma factorizada.

14)$\dfrac{x^{4}+3 x^{2}-4}{x-2}$

15)$\dfrac{2 x^{3}+5 x^{2}-7 x-12}{x+3}$

Contestar: $2 x^{2}-x-4$. Así que la forma factorizada es$(x+3)\left(2 x^{2}-x-4\right)$

Usa el Teorema Racional del Cero para ayudarte a encontrar los ceros de las funciones polinómicas.

16)$f(x)=2 x^{3}+5 x^{2}-6 x-9$

17)$f(x)=4 x^{4}+8 x^{3}+21 x^{2}+17 x+4$

Contestar: $-\dfrac{1}{2}$(tiene multiplicidad$2$),$\dfrac{-1+i \sqrt{15}}{2}$

18)$f(x)=4 x^{4}+16 x^{3}+13 x^{2}-15 x-18$

19)$f(x)=x^{5}+6 x^{4}+13 x^{3}+14 x^{2}+12 x+8$

Contestar: $-2$(tiene multiplicidad$3$),$\pm i$

Dada la siguiente información acerca de una función polinómica, busque la función.

20) Tiene un doble cero at$x=3$ y ceros en$x=1$ y$x=-2$. Su$y$ -intercepción es$(0,12)$.

21) Tiene un cero de multiplicidad$3$ a$x=\dfrac{1}{2}$ y otro cero a$x=-3$. Contiene el punto$(1,8)$.

Contestar: $f(x)=2(2 x-1)^{3}(x+3)$

22) Utilizar la Regla de Signos de Descartes para determinar el posible número de soluciones positivas y negativas. \[8 x^{3}-21 x^{2}+6=0 \nonumber \]

Para las siguientes funciones racionales, encontrar las intercepciones y asíntotas horizontales y verticales, y esbozar una gráfica.

23)$f(x)=\dfrac{x+4}{x^{2}-2 x-3}$

Contestar

Interceptos$(-4,0)$$\left(0,-\dfrac{4}{3}\right)$,, Asíntotas$x=3, x=-1, y=0$

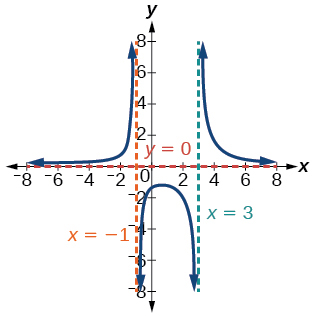
$CNX_Precalc_Figure_03_09_216.jpg$

24)$f(x)=\dfrac{x^{2}+2 x-3}{x^{2}-4}$

25) Encontrar la asíntota inclinada de la función racional. \[f(x)=\dfrac{x^{2}+3 x-3}{x-1} \nonumber \]

Contestar: $y=x+4$

Encuentra la inversa de la función.

26)$f(x)=\sqrt{x-2}+4$

27)$f(x)=3 x^{3}-4$

Contestar: $f^{-1}(x)=\sqrt[3]{\dfrac{x+4}{3}}$

28)$f(x)=\dfrac{2 x+3}{3 x-1}$

Encuentra el valor desconocido.

29)$y$ varía inversamente como el cuadrado de$x$ y cuándo$x=3, y=2$. Encuentra$y$ si$x=1$.

Contestar: $y=18$

30)$y$ varía conjuntamente con$x$ y la raíz cubo de$z$. Si cuando$x=27, y=12$, encuentra$y$ si$x=5$ y$z=8$.

Resolver el siguiente problema de aplicación.

31) La distancia que cae un cuerpo varía directamente según el cuadrado del tiempo que cae. Si un objeto cae$64$ pies en$2$ segundos, ¿cuánto tiempo tardará en caer$256$ pies?

Contestar: $4$segundos