4.2: Gráficas de Funciones Exponenciales
- Page ID
- 121455
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)- Graficar funciones exponenciales.
- Graficar funciones exponenciales usando transformaciones.
Como discutimos en la sección anterior, las funciones exponenciales se utilizan para muchas aplicaciones del mundo real como finanzas, forense, ciencias de la computación y la mayoría de las ciencias de la vida. Trabajar con una ecuación que describe una situación del mundo real nos da un método para hacer predicciones. La mayoría de las veces, sin embargo, la ecuación en sí no es suficiente. Aprendemos mucho de las cosas al ver sus representaciones pictóricas, y es exactamente por eso que graficar ecuaciones exponenciales es una herramienta poderosa. Nos da otra capa de conocimiento para predecir eventos futuros.
Graficando Funciones Exponenciales
Antes de comenzar a graficar, es útil revisar el comportamiento del crecimiento exponencial. Recordemos la tabla de valores para una función de la forma\(f(x)=b^x\) cuya base es mayor que uno. Vamos a usar la función\(f(x)=2^x\). Observe cómo\(\PageIndex{1}\) cambian los valores de salida en Table a medida que la entrada aumenta en\(1\).
| \(x\) | \(−3\) | \(−2\) | \(−1\) | \(0\) | \(1\) | \(2\) | \(3\) |
|---|---|---|---|---|---|---|---|
| \(f(x)=2^x\) | \(\dfrac{1}{8}\) | \(\dfrac{1}{4}\) | \(\dfrac{1}{2}\) | \(1\) | \(2\) | \(4\) | \(8\) |
Cada valor de salida es el producto de la salida anterior y la base,\(2\). Llamamos a la base\(2\) la relación constante. De hecho, para cualquier función exponencial con la forma\(f(x)=ab^x\),\(b\) es la relación constante de la función. Esto significa que a medida que aumenta la entrada\(1\), el valor de salida será el producto de la base y la salida anterior, independientemente del valor de\(a\).
Observe de la mesa que
- los valores de salida son positivos para todos los valores de\(x\);
- a\(x\) medida que aumenta, los valores de salida aumentan sin límite; y
- como\(x\) disminuye, los valores de salida crecen más pequeños, acercándose a cero.
La figura\(\PageIndex{1}\) muestra la función de crecimiento exponencial\(f(x)=2^x\).
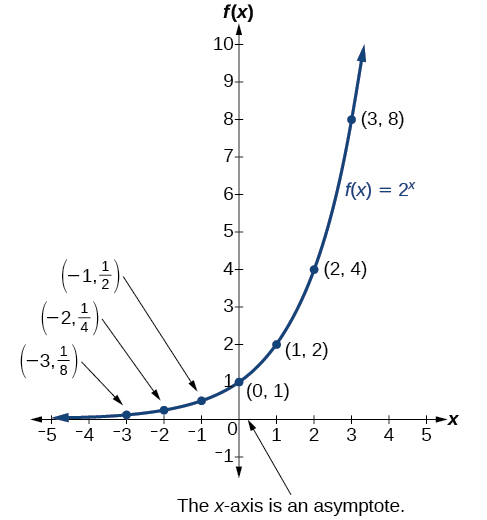
El dominio de\(f(x)=2^x\) es todos los números reales, el rango es\((0,\infty)\), y la asíntota horizontal es\(y=0\).
Para tener una idea del comportamiento de decaimiento exponencial, podemos crear una tabla de valores para una función de la forma\(f(x)=b^x\) cuya base está entre cero y uno. Vamos a usar la función\(g(x)={\left(\dfrac{1}{2}\right)}^x\). Observe cómo\(\PageIndex{2}\) cambian los valores de salida en Table a medida que la entrada aumenta en\(1\).
| \(x\) | \(-3\) | \(-2\) | \(-1\) | \(0\) | \(1\) | \(2\) | \(3\) |
|---|---|---|---|---|---|---|---|
| \(g(x)={\left(\dfrac{1}{2}\right)}^x\) | \(8\) | \(4\) | \(2\) | \(1\) | \(\dfrac{1}{2}\) | \(\dfrac{1}{4}\) | \(\dfrac{1}{8}\) |
Nuevamente, debido a que la entrada está aumentando en\(1\), cada valor de salida es el producto de la salida anterior y la base, o relación constante\(\dfrac{1}{2}\).
Observe de la mesa que
- los valores de salida son positivos para todos los valores de\(x\);
- a medida que\(x\) aumenta, los valores de salida crecen más pequeños, acercándose a cero;
- a\(x\) medida que disminuye, los valores de salida crecen sin límite.
La figura\(\PageIndex{2}\) muestra la función de decaimiento exponencial,\(g(x)={\left(\dfrac{1}{2}\right)}^x\).
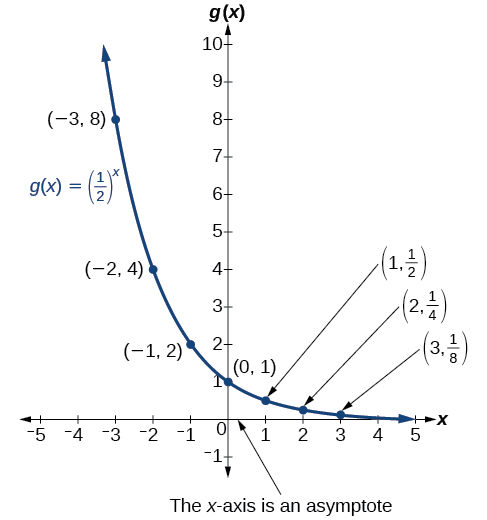
El dominio de\(g(x)={(\dfrac{1}{2})}^x\) es todos los números reales, el rango es\((0,\infty)\), y la asíntota horizontal es\(y=0\).
Una función exponencial con la forma\(f(x)=b^x\)\(b>0\),\(b≠1\), tiene estas características:
- función uno-a-uno
- asíntota horizontal:\(y=0\)
- dominio:\((–\infty, \infty)\)
- rango:\((0,\infty)\)
- x- intercepción: ninguna
- y- interceptar:\((0,1)\)
- aumentando si\(b>1\)
- decreciente si\(b<1\)
La figura\(\PageIndex{3}\) compara las gráficas de crecimiento exponencial y funciones de decaimiento.
- Crear una tabla de puntos.
- Trazar al menos\(3\) punto de la tabla, incluyendo la intersección y\((0,1)\).
- Dibuja una curva suave a través de los puntos.
- Indicar el dominio\((−\infty,\infty)\),, el rango\((0,\infty)\), y la asíntota horizontal,\(y=0\).
Esbozar una gráfica de\(f(x)=0.25^x\). Indicar el dominio, el rango y la asíntota.
Solución
Antes de graficar, identifique el comportamiento y cree una tabla de puntos para la gráfica.
| \(x\) | \(−3\) | \(−2\) | \(−1\) | \(0\) | \(1\) | \(2\) | \(3\) |
|---|---|---|---|---|---|---|---|
| \(f(x)={0.25}^x\) | \(64\) | \(16\) | \(4\) | \(1\) | \(0.25\) | \ (0.0625\ 0 | \(0.015625\) |
- Ya que\(b=0.25\) está entre cero y uno, sabemos que la función está disminuyendo. La cola izquierda de la gráfica aumentará sin encuadernación, y la cola derecha se acercará a la asíntota\(y=0\).
- Crear una tabla de puntos como en Tabla\(\PageIndex{3}\).
- Trazar la intersección y\((0,1)\), junto con otros dos puntos. Podemos usar\((−1,4)\) y\((1,0.25)\).
Dibuja una curva suave conectando los puntos como en la Figura\(\PageIndex{4}\).
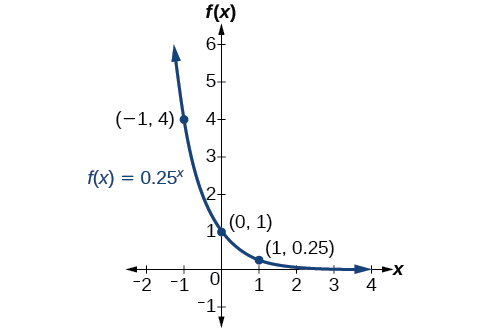
El dominio es\((−\infty,\infty)\); el rango es\((0,\infty)\); la asíntota horizontal es\(y=0\).
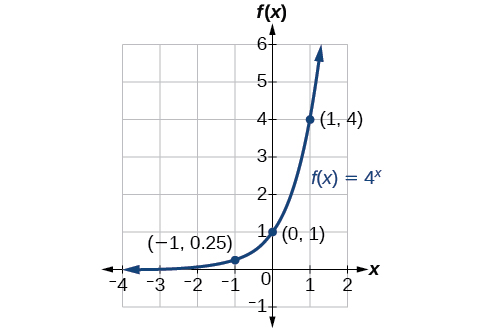
Esbozar la gráfica de\(f(x)=4^x\). Indicar el dominio, el rango y la asíntota.
- Contestar
-
El dominio es\((−\infty,\infty)\); el rango es\((0,\infty)\); la asíntota horizontal es\(y=0\).
Graficando transformaciones de funciones exponenciales
Las transformaciones de las gráficas exponenciales se comportan de manera similar a las de otras funciones. Al igual que con otras funciones padre, podemos aplicar los cuatro tipos de transformaciones (desplazamientos, reflexiones, estiramientos y compresiones) a la función padre\(f(x)=b^x\) sin pérdida de forma. Por ejemplo, así como la función cuadrática mantiene su forma parabólica cuando se desplaza, refleja, estira o comprime, la función exponencial también mantiene su forma general independientemente de las transformaciones aplicadas.
Graficando un Desplazamiento Vertical
La primera transformación ocurre cuando agregamos una constante\(d\) a la función padre\(f(x)=b^x\), dándonos un shift vertical d unidades en la misma dirección que el signo. Por ejemplo, si comenzamos por graficar una función padre,\(f(x)=2^x\), entonces podemos graficar dos desplazamientos verticales a su lado, usando\(d=3\): el desplazamiento hacia arriba,\(g(x)=2^x+3\) y el desplazamiento hacia abajo,\(h(x)=2^x−3\). Ambos desplazamientos verticales se muestran en la Figura\(\PageIndex{5}\).
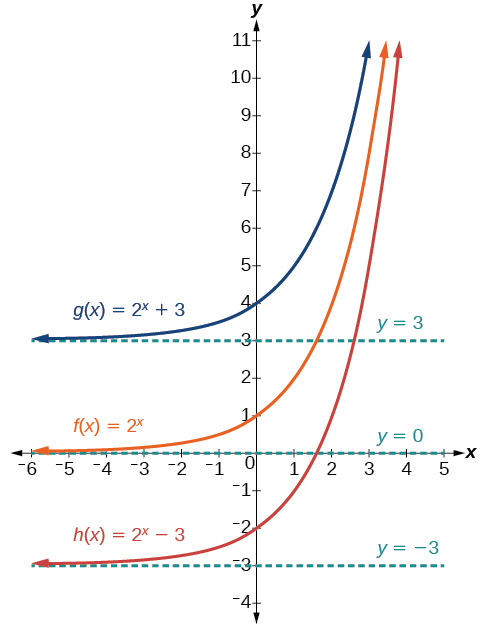
Observe los resultados del desplazamiento\(f(x)=2^x\) vertical:
- El dominio,\((−\infty,\infty)\) permanece sin cambios.
- Cuando la función se desplaza hacia arriba\(3\) unidades a\(g(x)=2^x+3\):
- La intercepción y desplaza\(3\) unidades hacia arriba a\((0,4)\).
- La asíntota sube\(3\) unidades a\(y=3\).
- El rango se convierte\((3,\infty)\).
- Cuando la función se desplaza hacia abajo\(3\) unidades a\(h(x)=2^x−3\):
- La intercepción y desplaza hacia abajo\(3\) las unidades a\((0,−2)\).
- La asíntota también desplaza\(3\) unidades hacia abajo a\(y=−3\).
- El rango se convierte\((−3,\infty)\).
Graficando un Desplazamiento Horizontal
La siguiente transformación ocurre cuando agregamos una constante\(c\) a la entrada de la función padre\(f(x)=b^x\), dándonos un desplazamiento horizontal de\(c\) unidades en la dirección opuesta al signo. Por ejemplo, si comenzamos graficando la función padre\(f(x)=2^x\), entonces podemos graficar dos desplazamientos horizontales a su lado, usando\(c=3\): el shift left,\(g(x)=2^{x+3}\), y el shift right,\(h(x)=2^{x−3}\). \(h(x)=2^{x−3}\). Ambos desplazamientos horizontales se muestran en la Figura\(\PageIndex{6}\).
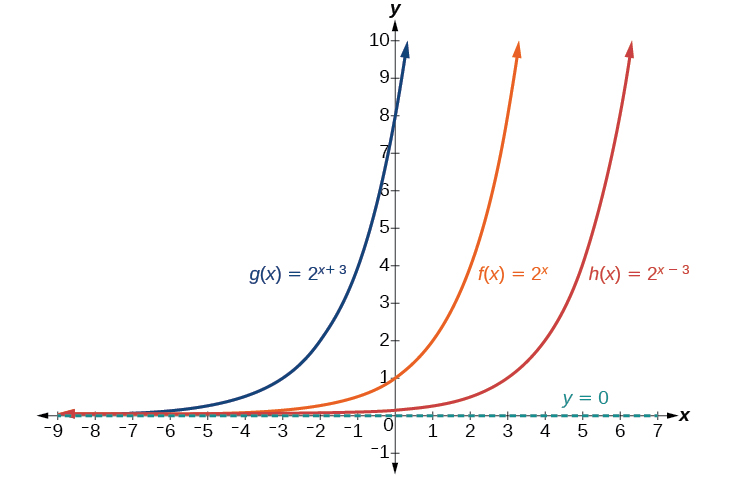
Observe los resultados del desplazamiento\(f(x)=2^x\) horizontal:
- El dominio,\((−\infty,\infty)\), permanece sin cambios.
- La asíntota,\(y=0\), permanece sin cambios.
- El y- interceptar turnos de tal manera que:
- Cuando la función se desplaza a\(3\) las unidades de la izquierda a\(g(x)=2^{x+3}\), la intersección y se convierte en\((0,8)\). Esto se debe a que\(2^{x+3}=(8)2^x\), por lo que el valor inicial de la función es\(8\).
- Cuando la función se desplaza a\(3\) las unidades de la derecha a\(h(x)=2^{x−3}\), la intersección y se convierte en\((0,\dfrac{1}{8})\). Nuevamente, vea eso\(2^{x−3}=(\dfrac{1}{8})2^x\), así que el valor inicial de la función es\(\dfrac{1}{8}\).
Para cualquier constante\(c\) y\(d\), la función\(f(x)=b^{x+c}+d\) desplaza la función padre\(f(x)=b^x\)
- \(d\)unidades verticalmente, en la misma dirección del signo de\(d\).
- horizontalmente\(c\) unidades, en la dirección opuesta al signo de\(c\).
- La y -intercepción se convierte\((0,b^c+d)\).
- La asíntota horizontal se convierte\(y=d\).
- El rango se convierte\((d,\infty)\).
- El dominio,\((−\infty,\infty)\), permanece sin cambios.
- Dibuja la asíntota horizontal\(y=d\).
- Identificar el turno como\((−c,d)\). Desplace la gráfica de\(c\) unidades\(f(x)=b^x\) izquierdas si\(c\) es positiva, y\(c\) las unidades derechas si\(c\) es negativa.
- Desplazar la gráfica de\(d\) unidades hacia\(f(x)=b^x\) arriba si\(d\) es positivo, y\(d\) las unidades descendentes si\(d\) es negativo.
- Indicar el dominio\((−\infty,\infty)\), el rango y la asíntota horizontal\(y=d\).\((d,\infty)\)
Gráfica\(f(x)=2^{x+1}−3\). Indicar el dominio, el rango y la asíntota.
Solución
Tenemos una ecuación exponencial de la forma\(f(x)=b^{x+c}+d\), con\(b=2\)\(c=1\), y\(d=−3\).
Dibuja la asíntota horizontal\(y=d\), así dibuja\(y=−3\).
Identificar el turno como\((−c,d)\), así es el turno\((−1,−3)\).
Desplazar la gráfica de\(1\) unidades\(f(x)=b^x\) izquierdas y\(3\) unidades hacia abajo.
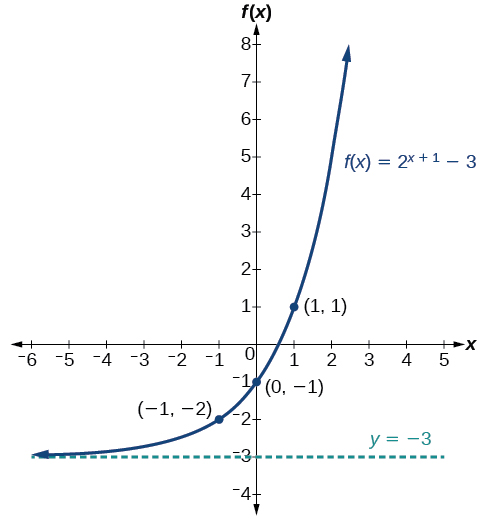
El dominio es\((−\infty,\infty)\); el rango es\((−3,\infty)\); la asíntota horizontal es\(y=−3\).
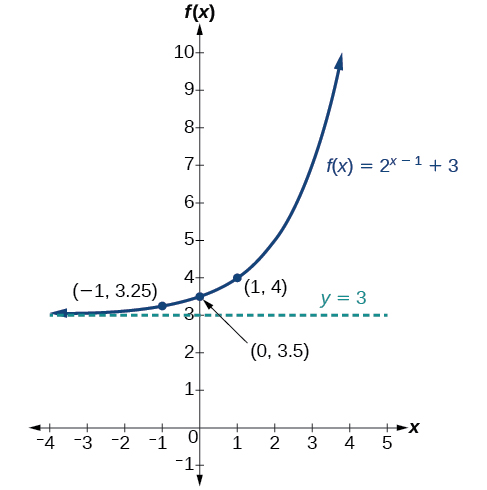
Gráfica\(f(x)=2^{x−1}+3\). Dominio estatal, rango y asíntota.
- Contestar
-
El dominio es\((−\infty,\infty)\); el rango es\((3,\infty)\); la asíntota horizontal es\(y=3\).
- Presione [Y=]. Ingrese la ecuación exponencial dada en la línea encabezada “Y 1 =”.
- Ingresa el valor dado forf (x) f (x) en la línea encabezada “Y 2 =”.
- Pulse [VENTANA]. Ajustar el eje y para que incluya el valor ingresado para “Y 2 =”.
- Pulse [GRAPH] para observar la gráfica de la función exponencial junto con la línea para el valor especificado off (x). f (x).
- Para encontrar el valor ofx, x, calculamos el punto de intersección. Presione [2ND] y luego [CALC]. Seleccione “intersectar” y pulse [ENTRAR] tres veces. El punto de intersección da el valor de x para el valor indicado de la función.
Resuelve\(42=1.2{(5)}^x+2.8\) gráficamente. Redondear a la milésima más cercana.
Solución
Presione [Y=] e ingrese\(1.2{(5)}^x+2.8\) junto a Y 1 =. Después ingresa\(42\) junto a Y2=. Para una ventana, use los valores\(–3\) a\(3\) for\(x\) y\(–5\) to\(55\) for\(y\). Pulse [GRÁFICO]. Las gráficas deben cruzarse en algún lugar cercano\(x=2\).
Para una mejor aproximación, presione [2ND] luego [CALC]. Seleccione [5: intersectar] y pulse [ENTRAR] tres veces. La coordenada x del punto de intersección se muestra como\(2.1661943\). (Tu respuesta puede ser diferente si usas una ventana diferente o usas un valor diferente para Guess? ) A la milésima más cercana,\(x≈2.166\).
Resuelve\(4=7.85{(1.15)}^x−2.27\) gráficamente. Redondear a la milésima más cercana.
- Contestar
-
\(x≈−1.608\)
Graficando un Estiramiento o Compresión
Mientras que los desplazamientos horizontales y verticales implican agregar constantes a la entrada o a la función misma, se produce un estiramiento o compresión cuando multiplicamos la función padre\(f(x)=b^x\) por una constante\(|a|>0\). Por ejemplo, si comenzamos por graficar la función padre\(f(x)=2^x\), entonces podemos graficar el stretch, usando\(a=3\), para obtener\(g(x)=3{(2)}^x\) como se muestra a la izquierda en la Figura\(\PageIndex{8}\), y la compresión, usando\(a=\dfrac{1}{3}\), para obtener\(h(x)=\dfrac{1}{3}{(2)}^x\) como se muestra a la derecha en la Figura\(\PageIndex{8}\).
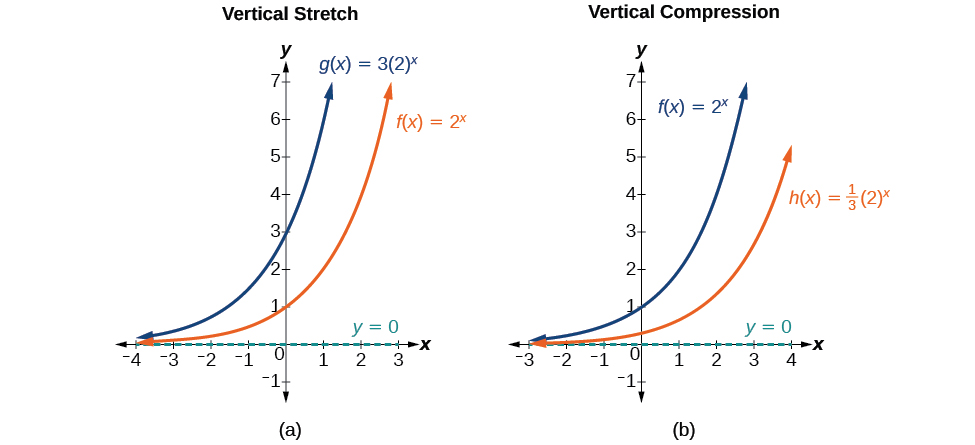
Para cualquier factor\(a>0\), la función\(f(x)=a{(b)}^x\)
- se estira verticalmente por un factor de\(a\) si\(|a|>1\).
- se comprime verticalmente por un factor de\(a\) if\(|a|<1\).
- tiene una intercepción y de\((0,a)\).
- tiene una asíntota horizontal en\(y=0\), un rango de\((0,\infty)\), y un dominio de\((−\infty,\infty)\), que no cambian de la función padre.
Esbozar una gráfica de\(f(x)=4{(\dfrac{1}{2})}^x\). Indicar el dominio, el rango y la asíntota.
Solución
Antes de graficar, identificar el comportamiento y los puntos clave en la gráfica.
- Dado que\(b=\dfrac{1}{2}\) está entre cero y uno, la cola izquierda de la gráfica aumentará sin límite a medida que\(x\) disminuya, y la cola derecha se acercará al eje x a medida que\(x\) aumente.
- Ya que\(a=4\), la gráfica de se\(f(x)={(\dfrac{1}{2})}^x\) estirará por un factor de\(4\).
- Crear una tabla de puntos como se muestra en Tabla\(\PageIndex{4}\).
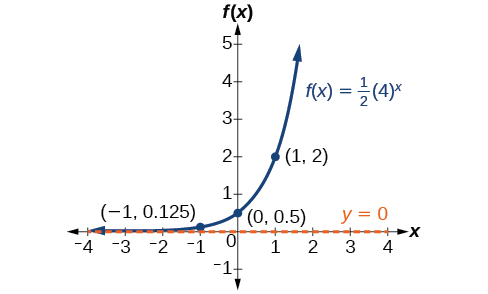
Mesa\(\PageIndex{4}\) \(x\) \(−3\) \(−2\) \(−1\) \(0\) \(1\) \(2\) \(3\) \(f(x)=4{(\dfrac{1}{2})}^x\) \(32\) \(16\) \(8\) \(4\) \(2\) \(1\) \(0.5\) - Trazar la intersección y\((0,4)\), junto con otros dos puntos. Podemos usar\((−1,8)\) y\((1,2)\).
Dibuja una curva suave conectando los puntos, como se muestra en la Figura\(\PageIndex{9}\).
El dominio es\((−\infty,\infty)\); el rango es\((0,\infty)\); la asíntota horizontal es\(y=0\).
Esbozar la gráfica de\(f(x)=\dfrac{1}{2}{(4)}^x\). Indicar el dominio, el rango y la asíntota.
- Contestar
-
El dominio es\((−\infty,\infty)\); el rango es\((0,\infty)\); la asíntota horizontal es\(y=0\).
Graficando Reflexiones
Además de desplazar, comprimir y estirar una gráfica, también podemos reflejarla alrededor del eje x o del eje y. Cuando multiplicamos la función padre\(f(x)=b^x\) por\(−1\), obtenemos una reflexión sobre el eje x. Cuando multiplicamos la entrada por\(−1\), obtenemos una reflexión sobre el eje y. Por ejemplo, si comenzamos por graficar la función padre\(f(x)=2^x\), entonces podemos graficar las dos reflexiones a su lado. La reflexión alrededor del eje x,\(g(x)=−2^x\), se muestra en el lado izquierdo de la Figura\(\PageIndex{10}\), y la reflexión alrededor del eje y\(h(x)=2^{−x}\), se muestra en el lado derecho de la Figura\(\PageIndex{10}\).
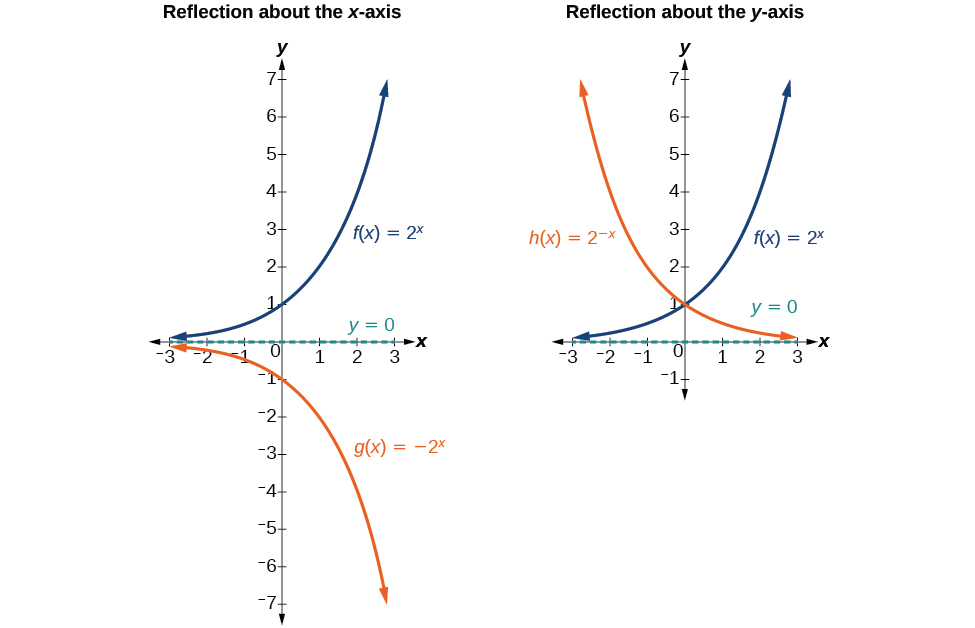
La función\(f(x)=−b^x\)
- refleja la función padre\(f(x)=b^x\) sobre el eje x.
- tiene una intercepción y de\((0,−1)\).
- tiene una gama de\((−\infty,0)\)
- tiene una asíntota horizontal en\(y=0\) y dominio de\((−\infty,\infty)\), que no cambian de la función padre.
La función\(f(x)=b^{−x}\)
- refleja la función padre\(f(x)=b^x\) sobre el eje y.
- tiene una intercepción y de\((0,1)\), una asíntota horizontal en\(y=0\), un rango de\((0,\infty)\), y un dominio de\((−\infty,\infty)\), que no cambian de la función padre.
Encuentra y grafica la ecuación para una función\(g(x)\),, que refleja\(f(x)={(\dfrac{1}{4})}^x\) alrededor del eje x. Indicar su dominio, rango y asíntota.
Solución
Ya que queremos reflejar la función padre\(f(x)={(\dfrac{1}{4})}^x\) sobre el eje x, multiplicamos\(f(x)\) por\(−1\) para obtener,\(g(x)=−{(\dfrac{1}{4})}^x\). A continuación creamos una tabla de puntos como en Tabla\(\PageIndex{5}\).
| \(x\) | \(−3\) | \(−2\) | \(−1\) | \(0\) | \(1\) | \(2\) | \(3\) |
|---|---|---|---|---|---|---|---|
| \(g(x)=−{(\dfrac{1}{4})}^x\) | \(−64\) | \(−16\) | \(−4\) | \(−1\) | \(−0.25\) | \(−0.0625\) | \(−0.0156\) |
Trazar la intersección y\((0,−1)\), junto con otros dos puntos. Podemos usar\((−1,−4)\) y\((1,−0.25)\).
Dibuja una curva suave conectando los puntos:
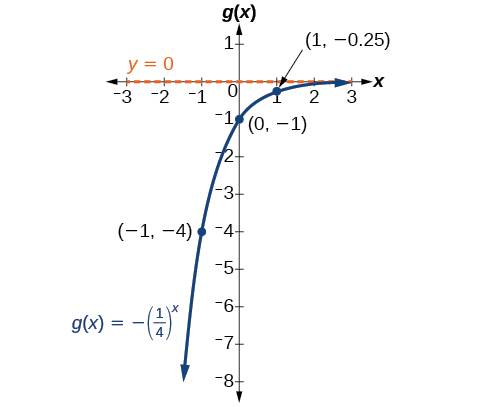
El dominio es\((−\infty,\infty)\); el rango es\((−\infty,0)\); la asíntota horizontal es\(y=0\).
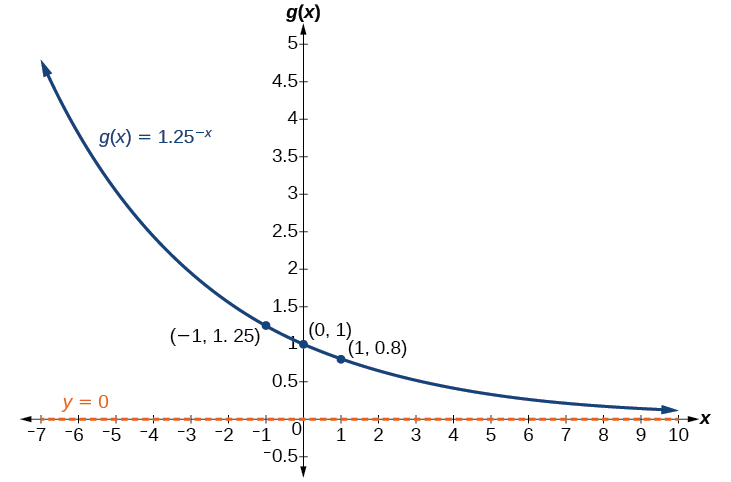
Encuentra y grafica la ecuación para una función\(g(x)\),, que refleja\(f(x)={1.25}^x\) alrededor del eje y. Indicar su dominio, rango y asíntota.
- Contestar
-
El dominio es\((−\infty,\infty)\); el rango es\((0,\infty)\); la asíntota horizontal es\(y=0\).
Resumiendo Traducciones de la Función Exponencial
Ahora que hemos trabajado con cada tipo de traducción para la función exponencial, podemos resumirlos en Tabla\(\PageIndex{6}\) para llegar a la ecuación general para traducir funciones exponenciales.
Una traducción de una función exponencial tiene la forma
\(f(x)=ab^{x+c}+d\)
Donde la función padre,\(y=b^x\),\(b>1\), es
- desplazó horizontalmente\(c\) las unidades hacia la izquierda.
- estirado verticalmente por un factor de\(|a|\) si\(|a|>0\).
- comprimido verticalmente por un factor de\(|a|\) if\(0<|a|<1\).
- \(d\)unidades desplazadas verticalmente.
- reflejado alrededor del eje x cuando\(a<0\).
Obsérvese el orden de los turnos, transformaciones y reflexiones siguiendo el orden de las operaciones.
Escribe la ecuación para la función que se describe a continuación. Dar la asíntota horizontal, el dominio y el rango.
\(f(x)=e^x\)se estira verticalmente por un factor de\(2\), se refleja a través del eje y, y luego se desplaza hacia arriba\(4\) unidades.
Solución
Queremos encontrar una ecuación de la forma general f (x) =abx+c+d. f (x) =abx+c+d. Utilizamos la descripción proporcionada para finda, a, b, b, c, c y d. d.
- Se nos da la función padre\(f(x)=e^x\), entonces\(b=e\).
- La función se estira por un factor de\(2\), entonces\(a=2\).
- La función se refleja alrededor del eje y. Reemplazamos\(x\) con\(−x\) para obtener:\(e^{−x}\).
- El gráfico se desplaza verticalmente 4 unidades, entonces\(d=4\).
Sustituyendo en la forma general que obtenemos,
\(f(x)=ab^{x+c}+d\)
\(=2e^{−x+0}+4\)
\(=2e^{−x}+4\)
El dominio es\((−\infty,\infty)\); el rango es\((4,\infty)\); la asíntota horizontal es\(y=4\).
Escribe la ecuación para la función que se describe a continuación. Dar la asíntota horizontal, el dominio y el rango.
\(f(x)=e^x\)se comprime verticalmente por un factor de\(\dfrac{1}{3}\), se refleja a través del eje x y luego se desplaza hacia abajo\(2\) unidades.
- Contestar
-
\(f(x)=−\dfrac{1}{3}e^{x}−2\); el dominio es\((−\infty,\infty)\); el rango es\((−\infty,2)\); la asíntota horizontal es\(y=2\).
Acceda a este recurso en línea para obtener instrucción y práctica adicionales con funciones exponenciales gráficas.
- Funciones Exponenciales Gráficas
Ecuaciones Clave
| Formulario General para la Traducción de la Función Padre\(f(x)=b^x\) | \(f(x)=ab^{x+c}+d\) |
Conceptos clave
- La gráfica de la función\(f(x)=b^x\) tiene una intersección y en\((0, 1)\), dominio\((−\infty, \infty)\)\((0, \infty)\), rango y asíntota horizontal\(y=0\). Ver Ejemplo.
- Si\(b>1\), la función va en aumento. La cola izquierda de la gráfica se acercará a la asíntota\(y=0\), y la cola derecha aumentará sin ataduras.
- Si\(0<b<1\), la función es decreciente. La cola izquierda de la gráfica aumentará sin encuadernación, y la cola derecha se acercará a la asíntota\(y=0\).
- La ecuación\(f(x)=b^x+d\) representa un desplazamiento vertical de la función padre\(f(x)=b^x\).
- La ecuación\(f(x)=b^{x+c}\) representa un desplazamiento horizontal de la función padre\(f(x)=b^x\). Ver Ejemplo.
- Las soluciones aproximadas de la ecuación se\(f(x)=b^{x+c}+d\) pueden encontrar usando una calculadora gráfica. Ver Ejemplo.
- La ecuación\(f(x)=ab^x\), donde\(a>0\), representa un estiramiento vertical si\(|a|>1\) o compresión if\(0<|a|<1\) de la función padre\(f(x)=b^x\). Ver Ejemplo.
- Cuando la función padre\(f(x)=b^x\) se multiplica por\(−1\), el resultado\(f(x)=−b^x\),, es una reflexión alrededor del eje x. Cuando la entrada se multiplica por\(−1\), el resultado\(f(x)=b^{−x}\),, es un reflejo alrededor del eje y. Ver Ejemplo.
- Todas las traducciones de la función exponencial se pueden resumir mediante la ecuación general\(f(x)=ab^{x+c}+d\). Ver Tabla.
- Usando la ecuación general\(f(x)=ab^{x+c}+d\), podemos escribir la ecuación de una función dada su descripción. Ver Ejemplo.