4.6: Ecuaciones Exponenciales y Logarítmicas
- Page ID
- 121417
- Usa como bases para resolver ecuaciones exponenciales.
- Usa logaritmos para resolver ecuaciones exponenciales.
- Utilice la definición de un logaritmo para resolver ecuaciones logarítmicas.
- Utilice la propiedad uno a uno de logaritmos para resolver ecuaciones logarítmicas.
- Resolver problemas aplicados que involucran ecuaciones exponenciales y logarítmicas.
En 1859, un terrateniente australiano llamado Thomas Austin liberó\(24\) conejos en la naturaleza para cazar. Debido a que Australia tenía pocos depredadores y abundante comida, la población de conejos explotó. En menos de diez años, la población de conejos contaba en millones.

El crecimiento descontrolado de la población, como en los conejos salvajes en Australia, se puede modelar con funciones exponenciales. Las ecuaciones resultantes de esas funciones exponenciales se pueden resolver para analizar y hacer predicciones sobre el crecimiento exponencial. En esta sección, aprenderemos técnicas para resolver funciones exponenciales.
Uso de bases similares para resolver ecuaciones exponenciales
La primera técnica implica dos funciones con bases similares. Recordemos que la propiedad uno-a-uno de las funciones exponenciales nos dice que, para cualquier número real\(b\)\(S\),, y\(T\), dónde\(b>0\),\(b≠1\),\(b^S=b^T\) si y sólo si\(S=T\).
Es decir, cuando una ecuación exponencial tiene la misma base en cada lado, los exponentes deben ser iguales. Esto también se aplica cuando los exponentes son expresiones algebraicas. Por lo tanto, podemos resolver muchas ecuaciones exponenciales mediante el uso de las reglas de exponentes para reescribir cada lado como una potencia con la misma base. Entonces, usamos el hecho de que las funciones exponenciales son uno a uno para establecer los exponentes iguales entre sí, y resolver para lo desconocido.
Por ejemplo, considere la ecuación\(3^{4x−7}=\dfrac{3^{2x}}{3}\). Para resolver por\(x\), utilizamos la propiedad de división de exponentes para reescribir el lado derecho para que ambos lados tengan la base común,\(3\). Luego aplicamos la propiedad uno a uno de los exponentes estableciendo los exponentes iguales entre sí y resolviendo para\(x\):
\[\begin{align*} 3^{4x-7}&= \dfrac{3^{2x}}{3}\\ 3^{4x-7}&= \dfrac{3^{2x}}{3^1} \qquad &&\text{Rewrite 3 as } 3^1\\ 3^{4x-7}&= 3^{2x-1} \qquad &&\text{Use the division property of exponents}\\ 4x-7&= 2x-1 \qquad &&\text{Apply the one-to-one property of exponents}\\ 2x&= 6 \qquad &&\text{Subtract 2x and add 7 to both sides}\\ x&= 3 \qquad &&\text{Divide by 3} \end{align*}\]
Para cualquier expresión algebraica\(S\) y\(T\), y cualquier número real positivo\(b≠1\),
\[\begin{align} b^S=b^T\text{ if and only if } S=T \end{align}\]
- Usa las reglas de exponentes para simplificar, si es necesario, para que la ecuación resultante tenga la forma\(b^S=b^T\).
- Utilice la propiedad uno a uno para establecer los exponentes iguales.
- Resolver la ecuación resultante\(S=T\),, para lo desconocido.
Resolver\(2^{x−1}=2^{2x−4}\).
Solución
\[\begin{align*} 2^{x-1}&= 2^{2x-4} \qquad &&\text{The common base is 2}\\ x-1&= 2x-4 \qquad &&\text{By the one-to-one property the exponents must be equal}\\ x&= 3 \qquad &&\text{Solve for x} \end{align*}\]
Resolver\(5^{2x}=5^{3x+2}\).
- Contestar
-
\(x=−2\)
Reescribe ecuaciones para que todos los poderes tengan la misma base
A veces no se muestra explícitamente la base común para una ecuación exponencial. En estos casos, simplemente reescribimos los términos de la ecuación como potencias con una base común, y resolvemos usando la propiedad uno a uno.
Por ejemplo, considere la ecuación\(256=4^{x−5}\). Podemos reescribir ambos lados de esta ecuación como un poder de\(2\). Luego aplicamos las reglas de los exponentes, junto con la propiedad uno-a-uno, para resolver para\(x\):
\[\begin{align*} 256&= 4^{x-5}\\ 2^8&= {(2^2)}^{x-5} \qquad &&\text{Rewrite each side as a power with base 2}\\ 2^8&= 2^{2x-10} \qquad &&\text{Use the one-to-one property of exponents}\\ 8&= 2x-10 \qquad &&\text{Apply the one-to-one property of exponents}\\ 18&= 2x \qquad &&\text{Add 10 to both sides}\\ x&= 9 \qquad &&\text{Divide by 2} \end{align*}\]
- Reescribe cada lado de la ecuación como una potencia con una base común.
- Usa las reglas de exponentes para simplificar, si es necesario, para que la ecuación resultante tenga la forma\(b^S=b^T\).
- Utilice la propiedad uno a uno para establecer los exponentes iguales.
- Resolver la ecuación resultante\(S=T\),, para lo desconocido.
Resolver\(8^{x+2}={16}^{x+1}\).
Solución
\[\begin{align*} 8^{x+2}&= {16}^{x+1}\\ {(2^3)}^{x+2}&= {(2^4)}^{x+1} \qquad &&\text{Write 8 and 16 as powers of 2}\\ 2^{3x+6}&= 2^{4x+4} \qquad &&\text{To take a power of a power, multiply exponents}\\ 3x+6&= 4x+4 \qquad &&\text{Use the one-to-one property to set the exponents equal}\\ x&= 2 \qquad &&\text{Solve for x} \end{align*}\]
Resolver\(5^{2x}={25}^{3x+2}\).
- Contestar
-
\(x=−1\)
Resolver\(2^{5x}=\sqrt{2}\).
Solución
\[\begin{align*} 2^{5x}&= 2^{\frac{1}{2}} \qquad &&\text{Write the square root of 2 as a power of 2}\\ 5x&= \dfrac{1}{2} \qquad &&\text{Use the one-to-one property}\\ x&= \dfrac{1}{10} \qquad &&\text{Solve for x} \end{align*}\]
Resolver\(5^x=\sqrt{5}\).
- Contestar
-
\(x=\dfrac{1}{2}\)
No. Recordemos que el rango de una función exponencial es siempre positivo. Mientras resolvemos la ecuación, podemos obtener una expresión que no está definida.
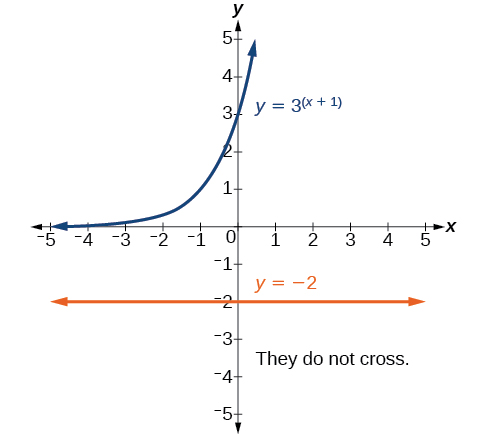
Resolver\(3^{x+1}=−2\).
Solución
Esta ecuación no tiene solución. No hay un valor real de\(x\) eso hará de la ecuación una declaración verdadera porque cualquier potencia de un número positivo es positiva.
Análisis
La figura\(\PageIndex{2}\) muestra que las dos gráficas no se cruzan por lo que el lado izquierdo nunca es igual al lado derecho. Por lo tanto, la ecuación no tiene solución.
Resolver\(2^x=−100\).
- Contestar
-
La ecuación no tiene solución.
Resolver ecuaciones exponenciales usando logaritmos
A veces los términos de una ecuación exponencial no se pueden reescribir con una base común. En estos casos, resolvemos tomando el logaritmo de cada lado. Recordemos, ya que\(\log(a)=\log(b)\) es equivalente a\(a=b\), podemos aplicar logaritmos con la misma base en ambos lados de una ecuación exponencial.
- Aplicar el logaritmo de ambos lados de la ecuación.
- Si uno de los términos de la ecuación tiene base 10, utilice el logaritmo común.
- Si ninguno de los términos de la ecuación tiene base 10, utilice el logaritmo natural.
- Utilizar las reglas de logaritmos para resolver por lo desconocido.
Resolver\(5^{x+2}=4^x\).
Solución
\ [\ begin {align*}
5^ {x+2} &= 4^x\ qquad &&\ text {No hay manera fácil de conseguir que los poderes tengan la misma base}\\
\ ln5^ {x+2} &=\ ln4^x\ qquad &&\ text {Toma ln de ambos lados}\\
(x+2)\ ln5&= x\ ln4\ qquad &&\ text {Leyes de uso de registros}\\
x\ ln5+2\ ln5&= x\ ln4\ qquad &&\ text {Usa la ley distributiva}\\
x\ ln5-x\ ln4&= -2\ ln5\ qquad &&\ text {Obtener términos que contengan x en un lado, términos sin x en el otro}\\
x (\ ln5-\ ln4) &= -2\ ln5\ qquad &&\ text On el lado izquierdo, factorizar una x} \\
x\ ln\ izquierda (\ dfrac {5} {4}\ derecha) &=\ ln\ izquierda (\ dfrac {1} {25}\ derecha)\ qquad &&\ text {Usa las leyes de los registros}\\
x&=\ dfrac {\ ln\ izquierda (\ dfrac {1} {25}\ derecha)} {\ ln\ izquierda (\ dfrac {1} {25}\ derecha)} {\ ln\ izquierda (\ dfrac {5} {4}\ derecha)}\ qquad &&\ text {Dividir por el coeficiente de x}
\ end { alinear*}\]
Resolver\(2^x=3^{x+1}\).
- Contestar
-
\(x=\dfrac{\ln3}{\ln \left (\dfrac{2}{3} \right )}\)
Sí. La solución es\(0\).
Ecuaciones que contienen\(e\)
Un tipo común de ecuaciones exponenciales son las que tienen base\(e\). Esta constante ocurre una y otra vez en la naturaleza, en las matemáticas, en las ciencias, en la ingeniería y en las finanzas. Cuando tenemos una ecuación con una base a cada\(e\) lado, podemos usar el logaritmo natural para resolverla.
- Dividir ambos lados de la ecuación por\(A\).
- Aplicar el logaritmo natural de ambos lados de la ecuación.
- Dividir ambos lados de la ecuación por\(k\).
Resolver\(100=20e^{2t}\).
Solución
\[\begin{align*} 100&= 20e^{2t}\\ 5&= e^{2t} \qquad &&\text{Divide by the coefficient of the power}\\ \ln5&= 2t \qquad &&\text{Take ln of both sides. Use the fact that } ln(x) \text{ and } e^x \text{ are inverse functions}\\ t&= \dfrac{\ln5}{2} \qquad &&\text{Divide by the coefficient of t} \end{align*}\]
Análisis
Usando leyes de registros, también podemos escribir esta respuesta en el formulario\(t=\ln\sqrt{5}\). Si queremos una aproximación decimal de la respuesta, utilizamos una calculadora.
Resolver\(3e^{0.5t}=11\).
- Contestar
-
\(t=2\ln \left (\dfrac{11}{3} \right )\)o\(\ln{ \left (\dfrac{11}{3} \right )}^2\)
No. Hay una solución cuando\(k≠0\), y cuando\(y\) y\(A\) son ambos 0 o ninguno 0, y tienen el mismo signo. Un ejemplo de una ecuación con esta forma que no tiene solución es\(2=−3e^t\).
Resolver\(4e^{2x}+5=12\).
Solución
\[\begin{align*} 4e^{2x}+5&= 12\\ 4e^{2x}&= 7 \qquad &&\text{Combine like terms}\\ e^{2x}&= \dfrac{7}{4} \qquad &&\text{Divide by the coefficient of the power}\\ 2x&= \ln \left (\dfrac{7}{4} \right ) \qquad &&\text{Take ln of both sides}\\ x&= \dfrac{1}{2}\ln \left (\dfrac{7}{4} \right ) \qquad &&\text{Solve for x} \end{align*}\]
Resolver\(3+e^{2t}=7e^{2t}\).
- Contestar
-
\(t=\ln \left (\dfrac{1}{\sqrt{2}} \right )=−\dfrac{1}{2}\ln(2)\)
Soluciones Extranas
En ocasiones los métodos utilizados para resolver una ecuación introducen una solución extraña, que es una solución que es correcta algebraicamente pero que no satisface las condiciones de la ecuación original. Una de esas situaciones surge al resolver cuando el logaritmo se toma en ambos lados de la ecuación. En tales casos, recuerde que el argumento del logaritmo debe ser positivo. Si el número que estamos evaluando en una función logaritmo es negativo, no hay salida.
Resolver\(e^{2x}−e^x=56\).
Solución
\[\begin{align*} e^{2x}-e^x&= 56\\ e^{2x}-e^x-56&= 0 \qquad &&\text{Get one side of the equation equal to zero}\\ (e^x+7)(e^x-8)&= 0 \qquad &&\text{Factor by the FOIL method}\\ e^x+7&= 0 \qquad &&\text{or} \\ e^x-8&= 0 \qquad &&\text{If a product is zero, then one factor must be zero}\\ e^x&= -7 \qquad &&\text{or} \\ e^x&= 8 \qquad &&\text{Isolate the exponentials}\\ e^x&= 8 \qquad &&\text{Reject the equation in which the power equals a negative number}\\ x&= \ln8 \qquad &&\text{Solve the equation in which the power equals a positive number} \end{align*}\]
Análisis
Cuando planeamos usar el factoring para resolver un problema, siempre obtenemos cero en un lado de la ecuación, porque cero tiene la propiedad única de que cuando un producto es cero, uno o ambos factores deben ser cero. Rechazamos la ecuación\(e^x=−7\) porque un número positivo nunca equivale a un número negativo. La solución no\(\ln(−7)\) es un número real, y en el sistema de números reales esta solución es rechazada como una solución extraña.
Resolver\(e^{2x}=e^x+2\).
- Contestar
-
\(x=\ln2\)
No. Tenga en cuenta que sólo podemos aplicar el logaritmo a un número positivo. Siempre verifique si hay soluciones extrañas.
Uso de la definición de un logaritmo para resolver ecuaciones logarítmicas
Ya hemos visto que cada ecuación logarítmica\({\log}_b(x)=y\) es equivalente a la ecuación exponencial\(b^y=x\). Podemos utilizar este hecho, junto con las reglas de logaritmos, para resolver ecuaciones logarítmicas donde el argumento es una expresión algebraica.
Por ejemplo, considere la ecuación\({\log}_2(2)+{\log}_2(3x−5)=3\). Para resolver esta ecuación, podemos usar reglas de logaritmos para reescribir el lado izquierdo en forma compacta y luego aplicar la definición de registros a resolver para\(x\):
\[\begin{align*} {\log}_2(2)+{\log}_2(3x-5)&= 3\\ {\log}_2(2(3x-5))&= 3 \qquad \text{Apply the product rule of logarithms}\\ {\log}_2(6x-10)&= 3 \qquad \text{Distribute}\\ 2^3&= 6x-10 \qquad \text{Apply the definition of a logarithm}\\ 8&= 6x-10 \qquad \text{Calculate } 2^3\\ 18&= 6x \qquad \text{Add 10 to both sides}\\ x&= 3 \qquad \text{Divide by 6} \end{align*}\]
Para cualquier expresión algebraica\(S\) y números reales\(b\) y\(c\), donde\(b>0\)\(b≠1\),
\[\begin{align} {\log}_b(S)=c \text{ if and only if } b^c=S \end{align}\]
Resolver\(2\ln x+3=7\).
Solución
\[\begin{align*} 2\ln x+3&= 7\\ 2\ln x&= 4 \qquad \text{Subtract 3}\\ \ln x&= 2 \qquad \text{Divide by 2}\\ x&= e^2 \qquad \text{Rewrite in exponential form} \end{align*}\]
Resolver\(6+\ln x=10\).
- Contestar
-
\(x=e^4\)
Resolver\(2\ln(6x)=7\).
Solución
\[\begin{align*} 2\ln(6x)&= 7\\ \ln(6x)&= \dfrac{7}{2} \qquad \text{Divide by 2}\\ 6x&= e^{\left (\dfrac{7}{2} \right )} \qquad \text{Use the definition of }\ln \\ x&= \dfrac{1}{6}e^{\left (\dfrac{7}{2} \right )} \qquad \text{Divide by 6} \end{align*}\]
Resolver\(2\ln(x+1)=10\).
- Contestar
-
\(x=e^5−1\)
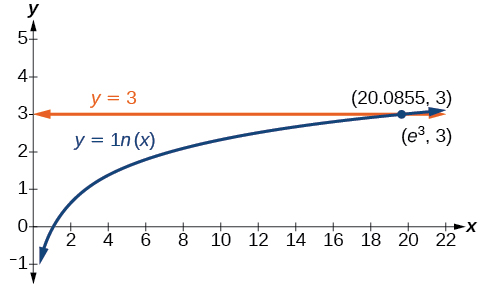
Resolver\(\ln x=3\).
Solución
\[\begin{align*} \ln x&= 3\\ x&= e^3 \qquad \text{Use the definition of the natural logarithm} \end{align*}\]
La figura\(\PageIndex{3}\) representa la gráfica de la ecuación. En la gráfica, la coordenada x del punto en el que se cruzan las dos gráficas está cerca\(20\). En otras palabras\(e^3≈20\). Una calculadora da una mejor aproximación:\(e^3≈20.0855\).
Utilice una calculadora gráfica para estimar la solución aproximada a la ecuación logarítmica\(2^x=1000\) a lugares\(2\) decimales.
- Contestar
-
\(x≈9.97\)
Uso de la propiedad uno a uno de logaritmos para resolver ecuaciones logarítmicas
Al igual que con las ecuaciones exponenciales, podemos usar la propiedad uno a uno para resolver ecuaciones logarítmicas. La propiedad uno a uno de las funciones logarítmicas nos dice que, para cualquier número real\(x>0\)\(S>0\),\(T>0\) y cualquier número real positivo\(b\), donde\(b≠1\),
\({\log}_bS={\log}_bT\)si y sólo si\(S=T\).
Por ejemplo,
Si\({\log}_2(x−1)={\log}_2(8)\), entonces\(x−1=8\).
Entonces, si\(x−1=8\), entonces podemos resolver para\(x\), y obtenemos\(x=9\). Para verificar, podemos sustituir\(x=9\) en la ecuación original:\({\log}_2(9−1)={\log}_2(8)=3\). Es decir, cuando una ecuación logarítmica tiene la misma base en cada lado, los argumentos deben ser iguales. Esto también se aplica cuando los argumentos son expresiones algebraicas. Por lo tanto, cuando se le da una ecuación con logs de la misma base en cada lado, podemos usar reglas de logaritmos para reescribir cada lado como un solo logaritmo. Entonces usamos el hecho de que las funciones logarítmicas son uno a uno para establecer los argumentos iguales entre sí y resolver para lo desconocido.
Por ejemplo, considere la ecuación\(\log(3x−2)−\log(2)=\log(x+4)\). Para resolver esta ecuación, podemos usar las reglas de logaritmos para reescribir el lado izquierdo como un logaritmo único, y luego aplicar la propiedad uno a uno para resolver para\(x\):
\[\begin{align*} \log(3x-2)-\log(2)&= \log(x+4)\\ \log \left (\dfrac{3x-2}{2} \right )&= \log(x+4) \qquad \text{Apply the quotient rule of logarithms}\\ \dfrac{3x-2}{2}&= x+4 \qquad \text{Apply the one to one property of a logarithm}\\ 3x-2&= 2x+8 \qquad \text{Multiply both sides of the equation by 2}\\ x&= 10 \qquad \text{Subtract 2x and add 2} \end{align*}\]
Para verificar el resultado, sustituya\(x=10\) en\(\log(3x−2)−\log(2)=\log(x+4)\).
\[\begin{align*} \log(3(10)-2)-\log(2)&= \log((10)+4) \\ \log(28)-\log(2)&= \log(14)\\ \log \left (\dfrac{28}{2} \right )&= \log(14) \qquad \text{The solution checks} \end{align*}\]
Para cualquier expresión algebraica\(S\) y\(T\) y cualquier número real positivo\(b\), donde\(b≠1\),
\[\begin{align} b^S=b^T\text{ if and only if } S=T \end{align}\]
Tenga en cuenta, al resolver una ecuación que involucre logaritmos, siempre verifique si la respuesta es correcta o si es una solución extraña.
- Usa las reglas de logaritmos para combinar términos similares, si es necesario, para que la ecuación resultante tenga la forma\({\log}_bS={\log}_bT\).
- Utilice la propiedad uno a uno para establecer los argumentos iguales.
- Resolver la ecuación resultante\(S=T\),, para lo desconocido.
Resolver\(\ln(x^2)=\ln(2x+3)\).
Solución
\[\begin{align*} \ln(x^2)&= \ln(2x+3)\\ x^2&= 2x+3 \qquad \text{Use the one-to-one property of the logarithm}\\ x^2-2x-3&= 0 \qquad \text{Get zero on one side before factoring}\\ (x-3)(x+1)&= 0 \qquad \text{Factor using FOIL}\\ x-3&= 0 \qquad \text{or } x+1=0 \text{ If a product is zero, one of the factors must be zero}\\ x=3 \qquad \text{or} \\ x&= -11 \qquad \text{Solve for x} \end{align*}\]
Análisis
Hay dos soluciones:\(3\) o\(−1\). La solución\(−1\) es negativa, pero comprueba cuando se sustituye en la ecuación original porque el argumento de las funciones logarítmicas sigue siendo positivo.
Resolver\(\ln(x^2)=\ln1\).
- Contestar
-
\(x=1\)o\(x=−1\)
Resolución de problemas aplicados mediante ecuaciones exponenciales y logarítmicas
En secciones anteriores aprendimos las propiedades y reglas tanto para funciones exponenciales como logarítmicas. Hemos visto que cualquier función exponencial puede escribirse como una función logarítmica y viceversa. Hemos utilizado exponentes para resolver ecuaciones logarítmicas y logaritmos para resolver ecuaciones exponenciales. Ahora estamos listos para combinar nuestras habilidades para resolver ecuaciones que modelan situaciones del mundo real, ya sea que lo desconocido esté en un exponente o en el argumento de un logaritmo.
Una de esas aplicaciones está en la ciencia, al calcular el tiempo que tarda la mitad del material inestable en una muestra de una sustancia radiactiva en desintegrarse, llamado su vida media. La tabla\(\PageIndex{1}\) enumera la vida media de varias de las sustancias radiactivas más comunes.
| Sustancia | Uso | Vida media |
|---|---|---|
| galio-67 | medicina nuclear | 80 horas |
| cobalto-60 | manufactura | 5.3 años |
| tecnecio-99m | medicina nuclear | 6 horas |
| americio-241 | construcción | 432 años |
| carbono-14 | datación arqueológica | 5,715 años |
| uranio-235 | poder atómico | 703,800,000 años |
Podemos ver cuán ampliamente varían las vidas medias de estas sustancias. Conocer la vida media de una sustancia nos permite calcular la cantidad restante después de un tiempo determinado. Podemos usar la fórmula para la desintegración radiactiva:
\[\begin{align} A(t)&= A_0e^{\tfrac{\ln(0.5)}{T}t}\\ A(t)&= A_0e^{\tfrac{\ln(0.5)t}{T}}\\ A(t)&= A_0{(e^{\ln(0.5)})}^{\tfrac{t}{T}}\\ A(t)&= A_0{\left (\dfrac{1}{2}\right )}^{\tfrac{t}{T}}\\ \end{align}\]
donde
- \(A_0\)es la cantidad inicialmente presente
- \(T\)es la vida media de la sustancia
- \(t\)es el periodo de tiempo durante el cual se estudia la sustancia
- \(y\)es la cantidad de la sustancia presente después del tiempo\(t\)
¿Cuánto tiempo tardará en decairse el diez por ciento de una muestra de\(1000\) -gramo de uranio-235?
Solución
\[\begin{align*} y&= 1000e^{\tfrac{\ln(0.5)}{703,800,000}t}\\ 900&= 1000e^{\tfrac{\ln(0.5)}{703,800,000}t} \qquad \text{After } 10\% \text{ decays, 900 grams are left}\\ 0.9&= e^{\tfrac{\ln(0.5)}{703,800,000}t} \qquad \text{Divide by 1000}\\ \ln(0.9)&= \ln \left (e^{\tfrac{\ln(0.5)}{703,800,000}t} \right ) \qquad \text{Take ln of both sides}\\ \ln(0.9)&= \dfrac{\ln(0.5)}{703,800,000}t \qquad \ln(e^M)=M\\ t&= 703,800,000\times \dfrac{\ln(0.9)}{\ln(0.5)} \qquad \text{years Solve for t}\\ t&\approx 106,979,777 \qquad \text{years} \end {align*} \]
Análisis
El diez por ciento de\(1000\) gramos son\(100\) gramos. Si los\(100\) gramos se descomponen, la cantidad de uranio-235 restante son\(900\) gramos.
¿Cuánto tiempo tardará antes de que el veinte por ciento de nuestra muestra de 1000 gramos de uranio-235 se haya descompuesto?
- Contestar
-
\(t=703,800,000×\dfrac{\ln(0.8)}{\ln(0.5)}\)años ≈ 226,572,993 años.
Acceda a estos recursos en línea para obtener instrucción y práctica adicionales con ecuaciones exponenciales y logarítmicas.
- Resolver ecuaciones logarítmicas
- Resolver ecuaciones exponenciales con logaritmos
Ecuaciones Clave
| Propiedad uno a uno para funciones exponenciales | Para cualquier expresión algebraica\(S\) y\(T\) y cualquier número real positivo\(b\), donde\(b^S=b^T\) si y solo si\(S=T\). |
| Definición de un logaritmo | Para cualquier expresión algebraica S y números reales positivos\(b\) y\(c\), donde\(b≠1\),\({\log}_b(S)=c\) si y solo si\(b^c=S\). |
| Propiedad uno a uno para funciones logarítmicas | Para cualquier expresión algebraica\(S\) y\(T\) y cualquier número real positivo\(b\), donde\(b≠1\), \({\log}_bS={\log}_bT\) si y solo si\(S=T\). |
Conceptos clave
- Podemos resolver muchas ecuaciones exponenciales usando las reglas de exponentes para reescribir cada lado como una potencia con la misma base. Entonces usamos el hecho de que las funciones exponenciales son uno a uno para establecer los exponentes iguales entre sí y resolver para lo desconocido.
- Cuando se nos da una ecuación exponencial donde las bases se muestran explícitamente como iguales, establecer los exponentes iguales entre sí y resolver para lo desconocido. Ver Ejemplo\(\PageIndex{1}\).
- Cuando se nos da una ecuación exponencial donde las bases no se muestran explícitamente como iguales, reescribe cada lado de la ecuación como potencias de la misma base, luego establece los exponentes iguales entre sí y resuelve para lo desconocido. Ver Ejemplo\(\PageIndex{2}\)\(\PageIndex{3}\), Ejemplo y Ejemplo\(\PageIndex{4}\).
- Cuando una ecuación exponencial no puede ser reescrita con una base común, resuelva tomando el logaritmo de cada lado. Ver Ejemplo\(\PageIndex{5}\).
- Podemos resolver ecuaciones exponenciales con base\(e\), aplicando el logaritmo natural de ambos lados porque las funciones exponenciales y logarítmicas son inversas unas de otras. Ver Ejemplo\(\PageIndex{6}\) y Ejemplo\(\PageIndex{7}\).
- Después de resolver una ecuación exponencial, verifique cada solución en la ecuación original para encontrar y eliminar cualquier solución extraña. Ver Ejemplo\(\PageIndex{8}\).
- Cuando se le da una ecuación de la forma\({\log}_b(S)=c\), donde\(S\) es una expresión algebraica, podemos usar la definición de un logaritmo para reescribir la ecuación como la ecuación exponencial equivalente\(b^c=S\), y resolver para lo desconocido. Ver Ejemplo\(\PageIndex{9}\) y Ejemplo\(\PageIndex{10}\).
- También podemos usar la gráfica para resolver ecuaciones con la forma\({\log}_b(S)=c\). Gráficamos ambas ecuaciones\(y={\log}_b(S)\) y\(y=c\) en el mismo plano de coordenadas e identificamos la solución como el valor x del punto de intersección. Ver Ejemplo\(\PageIndex{11}\).
- Cuando se le da una ecuación de la forma\({\log}_bS={\log}_bT\), donde\(S\) y\(T\) son expresiones algebraicas, podemos usar la propiedad uno-a-uno de logaritmos para resolver la ecuación\(S=T\) para lo desconocido. Ver Ejemplo\(\PageIndex{12}\).
- Combinando las habilidades aprendidas en esta y en las secciones anteriores, podemos resolver ecuaciones que modelan situaciones del mundo real, ya sea que lo desconocido esté en un exponente o en el argumento de un logaritmo. Ver Ejemplo\(\PageIndex{13}\).


