7.2: Identidades de suma y diferencia
- Page ID
- 121575
- Utilice fórmulas de suma y diferencia para coseno.
- Usa fórmulas de suma y diferencia para seno.
- Utilice fórmulas de suma y diferencia para tangente.
- Utilice fórmulas de suma y diferencia para las cofunciones.
- Utilice fórmulas de suma y diferencia para verificar identidades.
¿Cómo se puede medir la altura de una montaña? ¿Y la distancia de la Tierra al Sol? Como muchos problemas aparentemente imposibles, confiamos en fórmulas matemáticas para encontrar las respuestas. Las identidades trigonométricas, comúnmente utilizadas en pruebas matemáticas, han tenido aplicaciones en el mundo real durante siglos, incluyendo su uso en el cálculo de largas distancias.
Las identidades trigonométricas que examinaremos en esta sección se pueden rastrear hasta un astrónomo persa que vivió alrededor del 950 d.C., pero los antiguos griegos descubrieron estas mismas fórmulas mucho antes y las declararon en términos de acordes. Se trata de ecuaciones o postulados especiales, verdaderos para todos los valores ingresados a las ecuaciones, y con innumerables aplicaciones.

En esta sección, aprenderemos técnicas que nos permitirán resolver problemas como los presentados anteriormente. Las fórmulas que siguen simplificarán muchas expresiones y ecuaciones trigonométricas. Tenga en cuenta que, a lo largo de este apartado, el término fórmula se utiliza como sinónimo de la palabra identidad.
Uso de las fórmulas de suma y diferencia para coseno
Encontrar el valor exacto del seno, coseno o tangente de un ángulo suele ser más fácil si podemos reescribir el ángulo dado en términos de dos ángulos que tienen valores trigonométricos conocidos. Podemos usar los ángulos especiales, que podemos revisar en el círculo unitario que se muestra en la Figura\(\PageIndex{2}\).
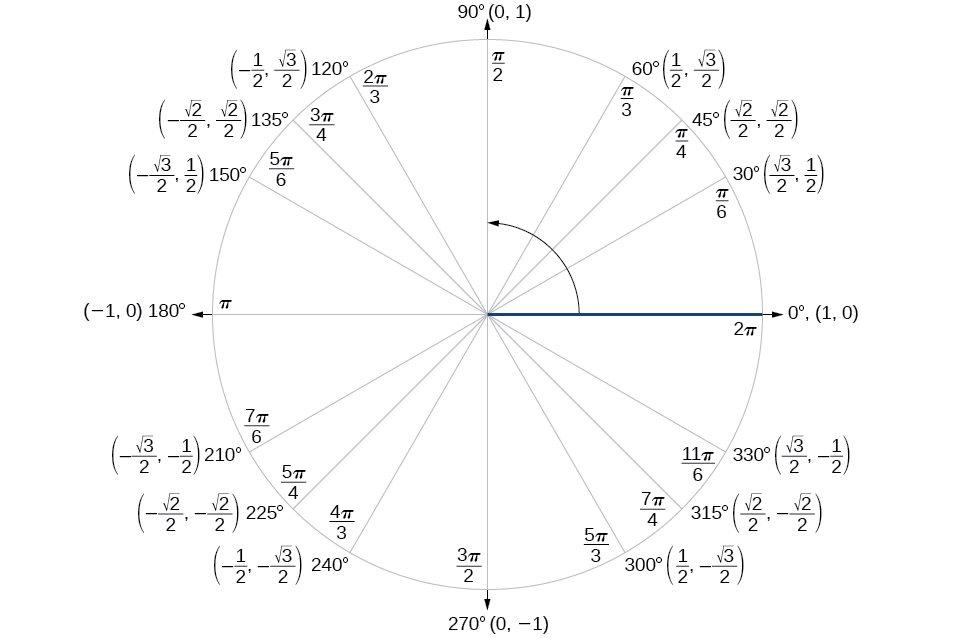
Comenzaremos con las fórmulas suma y diferencia para coseno, para que podamos encontrar el coseno de un ángulo dado si podemos dividirlo en la suma o diferencia de dos de los ángulos especiales (Tabla\(\PageIndex{1}\)).
| Fórmula de suma para coseno | \(\cos(\alpha+\beta)=\cos \alpha \cos \beta−\sin \alpha \sin \beta\) |
| Fórmula de diferencia para coseno | \(\cos(\alpha−\beta)=\cos \alpha \cos \beta+\sin \alpha \sin \beta\) |
Primero, probaremos la fórmula de diferencia para los cosenos. Consideremos dos puntos en el círculo unitario (Figura\(\PageIndex{3}\)). \(P\)El punto está en un ángulo\(\alpha\) desde el eje positivo\(x\) con coordenadas\((\cos \alpha,\sin \alpha)\) y el punto\(Q\) está en un ángulo\(\beta\) del eje positivo\(x\) con coordenadas\((\cos \beta,\sin \beta)\). Tenga en cuenta que la medida del ángulo\(POQ\) es\(\alpha−\beta\).
Etiquete dos puntos más:\(A\) en ángulo\((\alpha−\beta)\) desde el eje positivo\(x\) con coordenadas\((\cos(\alpha−\beta),\sin(\alpha−\beta))\); y punto\(B\) con coordenadas\((1,0)\). Triángulo\(POQ\) es una rotación de triángulo\(AOB\) y por lo tanto la distancia de\(P\) a\(Q\) es la misma que la distancia de\(A\) a\(B\).
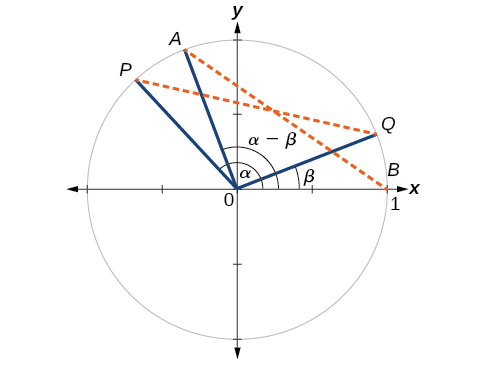
Podemos encontrar la distancia desde\(P\) hasta\(Q\) usando la fórmula de distancia.
\ [\ begin {alinear*}
d_ {PQ} &=\ sqrt {{(\ cos\ alfa -\ cos\ beta)} ^2+ {(sin\ alfa - sin\ beta)} ^2}\\ [4pt]
&=\ sqrt {{\ cos} ^2\ alfa-2\ cos\ alfa\ cos\ beta+ {\ cos} ^2\ beta+ {\ sin} ^2\ alpha-2\ sin\ alpha\ sin\ beta+ {\ sin} ^2\ beta} &\ text {Aplicar identidad pitagórica y simplificar.}\\ [4pt]
&=\ sqrt {({\ cos} ^2\ alfa+ {\ sin} ^2\ alfa) + ({\ cos} ^2\ beta+ {\ sin} ^2\ beta) -2\ cos\ alfa\ cos\ beta-2\ sin\ alfa\ sin\ beta}\\ [4pt]
&=\ sqrt {1+1-2\ cos\ alfa\ cos\ beta-2\ sin\ alfa\ sin\ beta}\\ [4pt]
&=\ sqrt {2-2\ cos\ alfa\ cos\ alfa\ cos\ beta-2\ sin\ alfa\ sin\ beta}\ fin {alinear*}\]
De igual manera, usando la fórmula de distancia podemos encontrar la distancia desde\(A\) hasta\(B\).
\ [\ begin {alinear*}
d_ {AB} &=\ sqrt {{(\ cos (\ alfa-\ beta) -1)} ^2+ {(\ sin (\ alfa-\ beta) -0)} ^2}\\ [4pt]
&=\ sqrt {{\ cos} ^2 (\ alfa-\ beta) -2\ cos (\ alfa-\ beta) +1+ {\ sin} ^2 (\ alpha-\ beta)} & &\ text {Aplicar identidad pitagórica y simplificar}\\ [4pt]
&=\ sqrt {({\ cos} ^2 (\ alpha-\ beta) + {\ sin} ^2 (\ alpha-\ beta)) -2\ cos (\ alpha-\ beta) +1}\\ [4pt]
&=\ sqrt {1-2\ cos (\ alpha-\ beta) +1}\\ [4pt]
&=\ sqrt {2-2\ cos (\ alpha-\ beta)} &\ text {Restar 2 de ambos lados y dividir ambos lados por −2.}\\ [4pt]
\ cos\ alfa\ cos\ beta+\ sin\ alfa\ sin\ beta&=\ cos (\ alfa-\ beta)
\ fin {alinear*}\]
Así, tenemos la fórmula de diferencia para el coseno. Podemos usar métodos similares para derivar el coseno de la suma de dos ángulos.
Estas fórmulas se pueden utilizar para calcular el coseno de sumas y diferencias de ángulos.
\[\cos(\alpha+\beta)=\cos \alpha \cos \beta−\sin \alpha \sin \beta\]
\[\cos(\alpha−\beta)=\cos \alpha \cos \beta+\sin \alpha \sin \beta\]
- Escribe la fórmula de diferencia para coseno.
- Sustituir los valores de los ángulos dados en la fórmula.
- Simplificar.
Usando la fórmula para el coseno de la diferencia de dos ángulos, encuentra el valor exacto de\(\cos\left(\dfrac{5\pi}{4}−\dfrac{\pi}{6}\right)\).
Solución
Comience por escribir la fórmula para el coseno de la diferencia de dos ángulos. Después sustituya los valores dados.
\[\begin{align*} \cos(\alpha-\beta)&= \cos \alpha \cos \beta+\sin \alpha \sin \beta\\[4pt] \cos\left(\dfrac{5\pi}{4}-\dfrac{\pi}{6}\right)&= \cos\left(\dfrac{5\pi}{4}\right)\cos\left(\dfrac{\pi}{6}\right)+\sin\left(\dfrac{5\pi}{4}\right)\sin\left(\dfrac{\pi}{6}\right)\\[4pt] &= \left(-\dfrac{\sqrt{2}}{2}\right)\left(\dfrac{\sqrt{3}}{2}\right)-\left(\dfrac{\sqrt{2}}{2}\right )\left(\dfrac{1}{2}\right)\\[4pt] &= -\dfrac{\sqrt{6}}{4}-\dfrac{\sqrt{2}}{4}\\[4pt] &= \dfrac{-\sqrt{6}-\sqrt{2}}{4} \end{align*}\]
Ten en cuenta que siempre podemos verificar la respuesta usando una calculadora gráfica en modo radián.
Encuentra el valor exacto de\(\cos\left(\dfrac{\pi}{3}−\dfrac{\pi}{4}\right)\).
- Contestar
-
\(\dfrac{\sqrt{2}+\sqrt{6}}{4}\)
Encuentra el valor exacto de\(\cos(75°)\).
Solución
Como\(75°=45°+30°\), podemos evaluar\(\cos(75°)\) como\(\cos(45°+30°)\).
\[\begin{align*} \cos(\alpha+\beta)&= \cos \alpha \cos \beta -\sin \alpha \sin \beta\\[4pt] \cos(45^{\circ}+30^{\circ})&= \cos(45^{\circ})\cos(30^{\circ})-\sin(45^{\circ})\sin(30^{\circ})\\[4pt] &= \dfrac{\sqrt{2}}{2}\left(\dfrac{\sqrt{3}}{2}\right)-\dfrac{\sqrt{2}}{2}\left(\dfrac{1}{2}\right)\\[4pt] &= \dfrac{\sqrt{6}}{4}-\dfrac{\sqrt{2}}{4}\\[4pt] &= \dfrac{\sqrt{6}-\sqrt{2}}{4} \end{align*}\]
Ten en cuenta que siempre podemos verificar la respuesta usando una calculadora gráfica en modo grados.
Análisis
Tenga en cuenta que también podríamos haber resuelto este problema usando el hecho de que\( 75°=135°−60°\).
\[\begin{align*} \cos(\alpha-\beta)&= \cos \alpha \cos \beta+\sin \alpha \sin \beta\\[4pt] \cos(135^{\circ}-60^{\circ})&= \cos(135^{\circ})\cos(60^{\circ})+\sin(135^{\circ})\sin(60^{\circ})\\[4pt] &= \left(-\dfrac{\sqrt{2}}{2}\right)\left(\dfrac{1}{2}\right)+\left(\dfrac{\sqrt{2}}{2}\right )\left(\dfrac{\sqrt{3}}{2}\right)\\[4pt] &= -\dfrac{\sqrt{2}}{4}+\dfrac{\sqrt{6}}{4}\\[4pt] &= \dfrac{\sqrt{6}-\sqrt{2}}{4} \end{align*}\]
Encuentra el valor exacto de\(\cos(105°)\).
- Contestar
-
\(\dfrac{\sqrt{2}-\sqrt{6}}{4}\)
Uso de las fórmulas de suma y diferencia para seno
Las fórmulas de suma y diferencia para seno se pueden derivar de la misma manera que las del coseno, y se asemejan a las fórmulas coseno.
Estas fórmulas se pueden utilizar para calcular los senos de las sumas y las diferencias de ángulos.
\[\sin(\alpha+\beta)=\sin \alpha \cos \beta+\cos \alpha \sin \beta\]
\[\sin(\alpha−\beta)=\sin \alpha \cos \beta−\cos \alpha \sin \beta\]
- Escribe la fórmula de diferencia para seno.
- Sustituir los ángulos dados en la fórmula.
- Simplificar.
Utilice las identidades de suma y diferencia para evaluar la diferencia de los ángulos y mostrar que la parte a es igual a la parte b.
- \(\sin(45°−30°)\)
- \(\sin(135°−120°)\)
Solución
- Empecemos por escribir la fórmula y sustituir los ángulos dados.
\[\begin{align*} \sin(\alpha-\beta)&= \sin \alpha \cos \beta-\cos \alpha \sin \beta\\[4pt] \sin(45^{\circ}-30^{\circ})&= \sin(45^{\circ})\cos(30^{\circ})-\cos(45^{\circ})\sin(30^{\circ}) \end{align*}\]
A continuación, necesitamos encontrar los valores de las expresiones trigonométricas.
\(\sin(45°)=\frac{\sqrt{2}}{2}, \qquad \cos(30°)=\frac{\sqrt{3}}{2}, \qquad \cos(45°)=\frac{\sqrt{2}}{2}, \qquad \sin(30°)=\frac{1}{2}\)
Ahora podemos sustituir estos valores en la ecuación y simplificar.
\[\begin{align*} \sin(45°-30°)&= \dfrac{\sqrt{2}}{2}\left(\dfrac{\sqrt{3}}{2}\right)-\dfrac{\sqrt{2}}{2}\left(\dfrac{1}{2}\right)\\[4pt] &= \dfrac{\sqrt{6}-\sqrt{2}}{4} \end{align*}\]
- Nuevamente, escribimos la fórmula y sustituimos los ángulos dados.
\[\begin{align*} \sin(\alpha-\beta)&= \sin \alpha \cos \beta-\cos \alpha \sin \beta\\[4pt] \sin(135^{\circ}-120^{\circ})&= \sin(135^{\circ})\cos(120^{\circ})-\cos(135^{\circ})\sin(120^{\circ}) \end{align*}\]
A continuación, encontramos los valores de las expresiones trigonométricas.
\(\sin(135°)=\frac{\sqrt{2}}{2}, \qquad \cos(120°)=-\frac{1}{2}, \qquad \cos(135°)=\frac{\sqrt{2}}{2}, \qquad \sin(120°)=\frac{\sqrt{3}}{2}\)
Ahora podemos sustituir estos valores en la ecuación y simplificar.
\[\begin{align*} \sin(135^{\circ}-120^{\circ})&= \dfrac{\sqrt{2}}{2}\left(-\dfrac{1}{2}\right)-\left(-\dfrac{\sqrt{2}}{2}\right)\left (\dfrac{\sqrt{3}}{2}\right)\\[4pt] &= \dfrac{\sqrt{6}-\sqrt{2}}{4} \end{align*}\]
Encuentra el valor exacto de\(\sin\left ({\cos}^{−1}\frac{1}{2}+{\sin}^{−1}\frac{3}{5}\right)\). Después revisa la respuesta con una calculadora gráfica.
Solución
El patrón que se muestra en este problema es\(\sin(\alpha+\beta)\). Dejar\(\alpha={\cos}^{−1}\frac{1}{2}\) y\(\beta={\sin}^{−1}\frac{3}{5}\). Entonces podemos escribir
\ [\ begin {align*}
\ cos\ alpha&=\ dfrac {1} {2},\ quad 0\ leq\ alfa\ leq\ pi\ [4pt]
\ sin\ beta&=\ dfrac {3} {5},\ quad -\ dfrac {\ pi} {2}\ leq\ beta\ leq\ dfrac {\ pi} {2}}\\[4pt]\end{align*}\]
Usaremos las identidades pitagóricas para encontrar\(\sin \alpha\) y\(\cos \beta\)
\ [\ begin {align*}
\ sin\ alpha&=\ sqrt {1- {\ cos} ^2\ alfa}\\ [4pt]
&=\ sqrt {1-\ dfrac {1} {4}}\\ [4pt]
&=\ sqrt {\ dfrac {3} {4}}\ [4pt]
&=\ dfrac {\ sqrt 3}} {2}\\ [4pt]
\ cos\ beta&=\ sqrt {1- {\ sin} ^2\ beta}\\ [4pt]
& =\ sqrt {1-\ dfrac {9} {25}}\\ [4pt]
&=\ sqrt {\ dfrac {16} {25}}\\ [4pt]
&=\ dfrac {4} {5}
\ end {align*}\]
Usando la fórmula de suma para seno,
\[\begin{align*} \sin \left({\cos}^{-1}\tfrac{1}{2}+{\sin}^{-1}\tfrac{3}{5}\right)&= \sin(\alpha+\beta)\\[4pt] &= \sin \alpha \cos \beta+\cos \alpha \sin \beta\\[4pt] &= \dfrac{\sqrt{3}}{2}\cdot \dfrac{4}{5}+\dfrac{1}{2}\cdot \dfrac{3}{5}\\[4pt] &= \dfrac{4\sqrt{3}+3}{10} \end{align*}\]
Uso de las fórmulas de suma y diferencia para tangente
Encontrar valores exactos para la tangente de la suma o diferencia de dos ángulos es un poco más complicado, pero nuevamente, se trata de reconocer el patrón.
Encontrar la fórmula de suma de dos ángulos para tangente implica tomar cociente de las fórmulas de suma para seno y coseno y simplificar. Recordemos,\(\tan x=\dfrac{\sin x}{\cos x}\), cuándo\(\cos x≠0\).
Derivamos la fórmula de suma para tangente.
\ [\ begin {align*}
\ tan\ left (\ alpha+\ beta\ right) &=\ dfrac {\ sin\ left (\ alpha+\ beta\ right)} {\ cos (\ alpha+\ beta)}\\ [6pt]
&=\ dfrac {\ sin\ alpha\ cos\ beta+\ cos\ alpha\ sin\ beta} {\ cos\ alpha\ cos\ beta-\ sin\ alfa\ sin\ beta}\\ [6pt]
&=\ dfrac {\ dfrac {\ dfrac {\ sin\ alfa \ cos\ beta+\ cos\ alfa\ sin\ beta} {\ cos\ alfa\ cos\ beta}} {\ dfrac {\ cos\ alfa\ cos\ alfa\ cos\ beta-\ sin\ alfa\ sin\ beta} {\ cos\ alfa\ cos\ beta}}\\ [6pt]
&=\ dfrac {\ dfrac {\ sin\ alfa\ cos\ beta} {\ cos\ alfa\ cos\ alfa\ cos\\ beta} +\ dfrac {\ cos\ alfa\ sin\ beta} {\ cos\ alfa\ cos\ beta}} {\ dfrac {\ cos\ alfa\ cos\ beta} {\ cos\ alfa\ cos\ beta} -\ dfrac {\ sin\ alfa\ sin\ beta} {\ cos\ alfa\ cos\ beta}}\\ [6pt]
&=\ dfrac {\ dfrac {\ sin\ alfa} {\ cos\ alfa} +\ dfrac {\ sin\ beta} {\ cos\ beta} {1-\ dfrac\ sin\ alfa\ sin\ beta} {\ cos\ alfa\ cos\ beta}}\\ [6pt]
&=\ dfrac {\ tan\ alpha+\ tan\ beta} {1-\ tan\ alfa\ tan\ beta}
\ final {alinear*}\]
Podemos derivar la fórmula de diferencia para tangente de manera similar.
Las fórmulas de suma y diferencia para tangente son:
\[\tan(\alpha+\beta)=\dfrac{\tan \alpha+\tan \beta}{1−\tan \alpha \tan \beta}\]
\[\tan(\alpha-\beta)=\dfrac{\tan \alpha-\tan \beta}{1+\tan \alpha \tan \beta}\]
- Escribe la fórmula de suma para tangente.
- Sustituir los ángulos dados en la fórmula.
- Simplificar.
Encuentra el valor exacto de\(\tan\left(\dfrac{\pi}{6}+\dfrac{\pi}{4}\right)\).
Solución
Primero escribamos la fórmula de suma para tangente y luego sustituyamos los ángulos dados en la fórmula.
\ [\ begin {alinear*}
\ tan (\ alpha+\ beta) &=\ dfrac {\ tan\ alpha+\ tan\ beta} {1-\ tan\ alfa\ tan\ beta}\ [4pt]
\ tan\ izquierda (\ dfrac {\ pi} {6} +\ dfrac {\ pi} {4}\ derecha) &=\ dfrac {\ tan izquierda\ (\ dfrac {\ pi} {6}\ derecha) +\ tan\ izquierda (\ dfrac {\ pi} {4}\ derecha)} {1-\ izquierda (\ tan\ izquierda (\ dfrac {\ pi} {6}\ derecha)\ derecha)\ derecha )\ izquierda (\ tan\ izquierda (\ dfrac {\ pi} {4}\ derecha)\ derecha)}\ end {alinear*}\]
A continuación, determinamos los valores de función individuales dentro de la fórmula:
\[\tan\left (\dfrac{\pi}{6}\right )= \dfrac{1}{\sqrt{3}}, \quad \text{and} \quad \tan\left (\dfrac{\pi}{4}\right) = 1\]
Así tenemos,
\ [\ begin {align*}\ tan\ left (\ dfrac {\ pi} {6} +\ dfrac {\ pi} {4}\ right) &=\ dfrac {\ dfrac {\ dfrac {1} {\ sqrt {3}} +1} {1-\ left (\ dfrac {1} {\ sqrt {3}}\ right) (1)}\\ [6pt]
&=\ dfrac {\ dfrac {1+\ sqrt {3}} {\ sqrt {3}}} {\ dfrac {\ sqrt {3} -1} {\ sqrt {3}}}\\ [6pt]
& amp; =\ dfrac {1+\ sqrt {3}} {\ sqrt {3}}\ cdot\ dfrac {\ sqrt {3}} {\ sqrt {3} -1}\\ [6pt]
&=\ dfrac {\ sqrt {3} +1} {\ sqrt {3} -1}
\ end {align*}\]
Encuentra el valor exacto de\(\tan\left (\dfrac{2\pi}{3}+\dfrac{\pi}{4}\right )\).
- Contestar
-
\(\dfrac{1-\sqrt{3}}{1+\sqrt{3}}\)
Dado\(\sin \alpha=\frac{3}{5}, \quad 0<\alpha<\frac{\pi}{2},\) y\(\cos \beta=−\frac{5}{13}, \quad \pi<\beta<\frac{3\pi}{2}\),
encontrar
- \(\sin(\alpha+\beta)\)
- \(\cos(\alpha+\beta)\)
- \(\tan(\alpha+\beta)\)
- \(\tan(\alpha−\beta)\)
Solución
Podemos usar las fórmulas suma y diferencia para identificar la suma o diferencia de ángulos cuando se proporciona la relación de seno, coseno o tangente para cada uno de los ángulos individuales. Para ello, construimos lo que se llama un triángulo de referencia para ayudar a encontrar cada componente de las fórmulas suma y diferencia.
- Para encontrar\(\sin(\alpha+\beta)\), comenzamos con\(\sin \alpha=\dfrac{3}{5}\) y\(0<\alpha<\dfrac{\pi}{2}\). El lado opuesto\(\alpha\) tiene longitud 3, la hipotenusa tiene longitud 5, y\(\alpha\) está en el primer cuadrante. Ver Figura\(\PageIndex{4}\). Usando el Teorema de Pitágoras, podemos encontrar la longitud del lado\(a\):
\[\begin{align*} a^2+3^2&= 5^2\\[4pt] a^2&= 16\\[4pt] a&= 4 \end{align*}\]
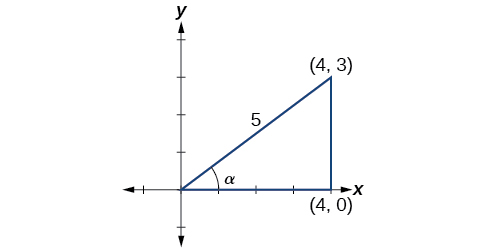
Desde\(\cos \beta=−\dfrac{5}{13}\) y\(\pi<\beta<\dfrac{3\pi}{2}\), el lado adyacente a\(\beta\) es\(−5\), la hipotenusa está\(13\), y\(\beta\) está en el tercer cuadrante. Ver Figura\(\PageIndex{5}\). Nuevamente, usando el Teorema de Pitágoras, tenemos
\[\begin{align*} {(-5)}^2+a^2&= {13}^2\\[4pt] 25+a^2&= 169\\[4pt] a^2&= 144\\[4pt] a&= \pm 12 \end{align*}\]
Ya que\(\beta\) está en el tercer cuadrante,\(a=–12\).
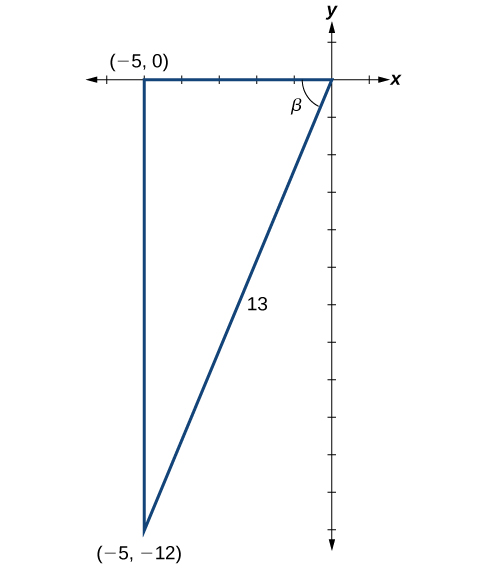
El siguiente paso es encontrar el coseno de\(\alpha\) y el seno de\(\beta\). El coseno de α α es el lado adyacente sobre la hipotenusa. Lo podemos encontrar desde el triángulo en la Figura\(\PageIndex{5}\):\(\cos \alpha=\dfrac{4}{5}\). También podemos encontrar el seno\(\beta\) del triángulo en la Figura\(\PageIndex{5}\), como lado opuesto sobre la hipotenusa:\(\sin \beta=−\dfrac{12}{13}\). Ahora estamos listos para evaluar\(\sin(\alpha+\beta)\).
\[\begin{align*} \sin(\alpha+\beta)&= \sin \alpha \cos \beta+\cos \alpha \sin \beta\\[4pt] &= \left(\dfrac{3}{5}\right)\left(-\dfrac{5}{13}\right )+\left (\dfrac{4}{5}\right )\left(-\dfrac{12}{13}\right )\\[4pt] &= -\dfrac{15}{65}-\dfrac{48}{65}\\[4pt] &= -\dfrac{63}{65} \end{align*}\]
- Podemos encontrar\(\cos(\alpha+\beta)\) de manera similar. Sustituimos los valores según la fórmula.
\[\begin{align*} \cos(\alpha+\beta)&= \cos \alpha \cos \beta-\sin \alpha \sin \beta\\[4pt] &= \left(\dfrac{4}{5}\right)\left(-\dfrac{5}{13}\right)-\left(\dfrac{3}{5}\right )\left(-\dfrac{12}{13}\right)\\[4pt] &= -\dfrac{20}{65}+\dfrac{36}{65}\\[4pt] &= \dfrac{16}{65} \end{align*}\]
- Para\(\tan(\alpha+\beta)\), si\(\sin \alpha=\dfrac{3}{5}\) y\(\cos \alpha=\dfrac{4}{5}\), entonces
\(\tan \alpha=\dfrac{\dfrac{3}{5}}{\dfrac{4}{5}}=\dfrac{3}{4}\)
Si\(\sin \beta=−\dfrac{12}{13}\) y\(\cos \beta=−\dfrac{5}{13}\), entonces
\(\tan \beta=\dfrac{−\dfrac{12}{13}}{−\dfrac{5}{13}}=\dfrac{12}{5}\)
Entonces,
\ [\ begin {align*}
\ tan (\ alpha+\ beta) &=\ dfrac {\ tan\ alpha+\ tan\ beta} {1-\ tan\ alfa\ tan\ beta}\\ [6pt]
&=\ dfrac {\ dfrac {3} {4} +\ dfrac {12} {5}} {1-\ dfrac {3} {4}\ izquierda (\ dfrac {12} {5}\ derecha)}\\ [6pt]
&=\ dfrac {\ dfrac {63} {20}} {-\ dfrac {16} {20}}\\ [6pt]
& amp; = -\ dfrac {63} {16}
\ final {alinear*}\]
- Para encontrar\(\tan(\alpha−\beta)\), tenemos los valores que necesitamos. Podemos sustituirlos y evaluarlos.
\ [\ begin {alinear*}
\ tan (\ alpha-\ beta) &=\ dfrac {\ tan\ alfa-\ tan\ beta} {1+\ tan\ alfa\ tan\ beta}\\ [6pt]
&=\ dfrac {\ dfrac {3} {4} -\ dfrac {12} {5}} {1+\ dfrac {3} {4} izquierda\ (\ dfrac {12} {5}\ derecha)}\\ [6pt]
&=\ dfrac {-\ dfrac {33} {20}} {\ dfrac {56} {20}}\\ [6pt]
& amp; = -\ dfrac {33} {56}
\ final {alinear*}\]
Análisis
Un error común a la hora de abordar problemas como éste es que podemos tener la tentación de pensar eso\(\alpha\) y\(\beta\) son ángulos en un mismo triángulo, que por supuesto, no lo son. También tenga en cuenta que
\(\tan(\alpha+\beta)=\sin(\alpha+\beta)\cos(\alpha+\beta)\)
Uso de fórmulas de suma y diferencia para cofunciones
Ahora que podemos encontrar las funciones seno, coseno y tangente para las sumas y diferencias de ángulos, podemos utilizarlas para hacer lo mismo con sus cofunciones. Se puede recordar de Trigonometría de Triángulo Recto que, si la suma de dos ángulos positivos es\(\frac{\pi}{2}\), esos dos ángulos son complementos, y la suma de los dos ángulos agudos en un triángulo rectángulo es\(\frac{\pi}{2}\), por lo que también son complementos. En la Figura\(\PageIndex{6}\), observe que si uno de los ángulos agudos está etiquetado como\(\theta\), entonces el otro ángulo agudo debe ser etiquetado\(\frac{\pi}{2}−\theta\).
Observe también eso\(\sin \theta=\cos\left(\frac{\pi}{2}−\theta\right)\), que es opuesto sobre la hipotenusa. Así, cuando dos ángulos son complementarios, podemos decir que el seno de\(\theta\) es igual a la cofunción del complemento de\(\theta\). Del mismo modo, tangente y cotangente son cofunciones, y secante y cosecante son cofunciones.
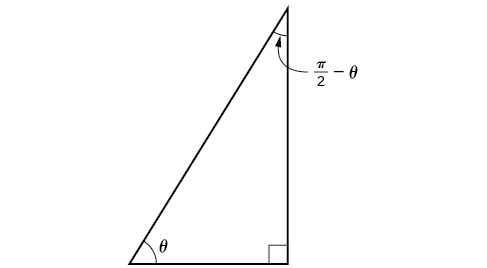
A partir de estas relaciones, se forman las identidades de cofunción. Recuerda que por primera vez encontraste estas identidades en El círculo unitario: funciones sinusoidales y cosenales.
Las identidades de cofunción se resumen en la Tabla\(\PageIndex{2}\).
| \(\sin \theta=\cos\left(\dfrac{\pi}{2}−\theta\right)\) | \(\cos \theta=\sin\left(\dfrac{\pi}{2}−\theta\right)\) |
| \(\tan \theta=\cot\left(\dfrac{\pi}{2}−\theta\right)\) | \(\cot \theta=\tan\left(\dfrac{\pi}{2}−\theta\right )\) |
| \(\sec \theta=\csc\left (\dfrac{\pi}{2}−\theta\right )\) | \(\csc \theta=\sec\left (\dfrac{\pi}{2}−\theta\right )\) |
Observe que las fórmulas en la tabla también pueden justificarse algebraicamente usando las fórmulas suma y diferencia. Por ejemplo, usando
\(\cos(\alpha-\beta)=\cos \alpha \cos \beta+\sin \alpha \sin \beta\)
Podemos escribir
\[\begin{align*} \cos\left (\dfrac{\pi}{2}-\theta \right )&= \cos \dfrac{\pi}{2} \cos \theta+\sin \dfrac{\pi}{2} \sin \theta \\[4pt] &=(0)\cos \theta+(1)\sin \theta \\[4pt] &=\sin \theta \end{align*}\]
Escribir\(\tan \dfrac{\pi}{9}\) en términos de su cofunción.
Solución
La cofunción de\(\tan \theta=\cot\left (\dfrac{\pi}{2}−\theta\right )\). Por lo tanto,
\[\begin{align*} \tan\left (\dfrac{\pi}{9}\right )&= \cot\left (\dfrac{\pi}{2}-\dfrac{\pi}{9}\right )\\[4pt] &= \cot\left (\dfrac{9\pi}{18}-\dfrac{2\pi}{18}\right )\\[4pt] &= \cot\left (\dfrac{7\pi}{18}\right ) \end{align*}\]
Escribir\(\sin \dfrac{\pi}{7}\) in terms of its cofunción.
- Responder
-
\(\cos\left (\dfrac{5\pi}{14}\right )\)
Uso de las fórmulas de suma y diferencia para verificar identidades
Verificar una identidad significa demostrar que la ecuación se mantiene para todos los valores de la variable. Ayuda estar muy familiarizado con las identidades o tener una lista de ellas accesible mientras se trabaja los problemas. Revisar las reglas generales presentadas anteriormente puede ayudar a simplificar el proceso de verificación de una identidad.
- Comienza con la expresión en el lado del signo igual que aparece más complejo. Reescribe esa expresión hasta que coincida con el otro lado del signo igual. Ocasionalmente, tal vez tengamos que alterar ambos lados, pero trabajar en un solo lado es lo más eficiente.
- Busque oportunidades para usar las fórmulas de suma y diferencia.
- Reescribir sumas o diferencias de cocientes como cocientes simples.
- Si el proceso se vuelve engorroso, reescribe la expresión en términos de senos y cosenos.
Verificar la identidad\(\sin(\alpha+\beta)+\sin(\alpha−\beta)=2\sin \alpha \cos \beta\).
Solución
Vemos que el lado izquierdo de la ecuación incluye los senos de la suma y la diferencia de ángulos.
\(\sin(\alpha+\beta)=\sin \alpha \cos \beta+\cos \alpha \sin \beta\)
\(\sin(\alpha-\beta)=\sin \alpha \cos \beta-\cos \alpha \sin \beta\)
Podemos reescribir cada uno usando las fórmulas de suma y diferencia.
\[\begin{align*} \sin(\alpha+\beta)+\sin(\alpha-\beta)&= \sin \alpha \cos \beta+\cos \alpha \sin \beta+\sin \alpha \cos \beta-\cos \alpha \sin \beta\\[4pt] &= 2\sin \alpha \cos \beta \end{align*}\]
Vemos que se verifica la identidad.
Verificar la siguiente identidad.
\(\dfrac{\sin(\alpha−\beta)}{\cos \alpha \cos \beta}=\tan \alpha−\tan \beta\)
Solución
Podemos comenzar reescribiendo el numerador en el lado izquierdo de la ecuación.
\[\begin{align*} \dfrac{\sin(\alpha-\beta)}{\cos \alpha \cos \beta}&= \dfrac{\sin \alpha \cos \beta-\cos \alpha \sin \beta}{\cos \alpha \cos \beta}\\[4pt] &= \dfrac{\sin \alpha \cos \beta}{\cos \alpha \cos \beta}-\dfrac{\cos \alpha \sin \beta}{\cos \alpha \cos \beta} & & \text{Rewrite using a common denominator}\\[4pt] &= \dfrac{\sin \alpha}{\cos \alpha}-\dfrac{\sin \beta}{\cos \beta} & & \text{Cancel}\\[4pt] &= \tan \alpha-\tan \beta & & \text{Rewrite in terms of tangent} \end{align*}\]
Verificar la identidad:\(\tan(\pi−\theta)=−\tan \theta\).
- Contestar
-
\[\begin{align*} \tan(\pi-\theta)&= \dfrac{\tan(\pi)-\tan \theta}{1+\tan(\pi)\tan \theta}\\[4pt] &= \dfrac{0-\tan \theta}{1+0\cdot \tan \theta}\\[4pt] &= -\tan \theta \end{align*}\]
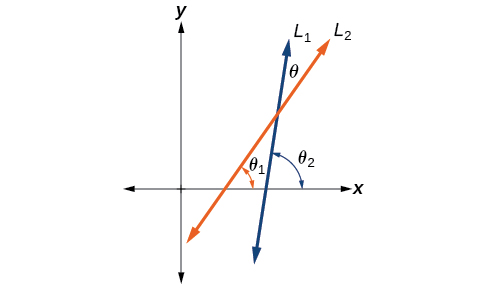
Dejar\(L_1\) y\(L_2\) denotar dos líneas de intersección no verticales, y dejar\(θ\) denotar el ángulo agudo entre\(L_1\) y\(L_2\). Ver Figura\(\PageIndex{7}\). Demostrar que
\(\tan \theta=\dfrac{m_2-m_1}{1+m_1m_2}\)
donde\(m_1\) y\(m_2\) son las laderas de\(L_1\) y\(L_2\) respectivamente. (Pista: Utilice el hecho de que\(\tan \theta_1=m_1\) y\(\tan \theta_2=m_2\).)
Solución
Usando la fórmula de diferencia para tangente, este problema no parece tan desalentador como podría ser.
\[\begin{align*} \tan \theta&= \tan(\theta_2-\theta_1)\\[4pt] &= \dfrac{\tan \theta_2-\tan \theta_1}{1+\tan \theta_1 \tan \theta_2}\\[4pt] &= \dfrac{m_2-m_1}{1+m_1m_2} \end{align*}\]
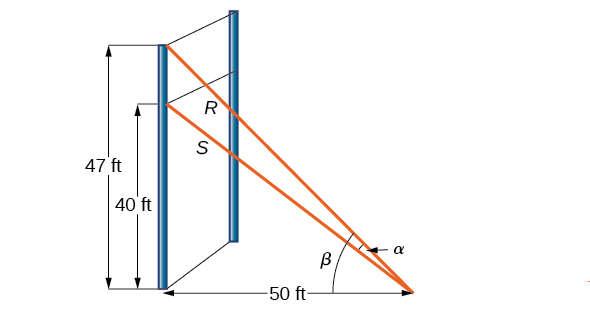
Para un muro de escalada, un cable para chicos\(R\) está unido con\(47\) pies de altura en un poste vertical. El soporte adicional es proporcionado por otros\(40\) pies\(S\) unidos por cable de tipo sobre el suelo en el mismo poste. Si los cables están unidos a los\(50\) pies de tierra desde el poste, encuentre el ángulo\(\alpha\) entre los cables. Ver Figura\(\PageIndex{8}\).
Solución
Resumamos primero la información que podemos recopilar del diagrama. Como solo se conocen los lados adyacentes al ángulo recto, podemos usar la función tangente. Observe eso\(\tan \beta=\frac{47}{50}\), y\(\tan(\beta−\alpha)=\frac{40}{50}=\frac{4}{5}\). Entonces podemos usar la fórmula de diferencia para tangente.
\[\tan(\beta-\alpha) = \dfrac{\tan \beta-\tan \alpha}{1+\tan \beta \tan \alpha}\]
Ahora, sustituyendo los valores que conocemos en la fórmula, tenemos,
\ [\ begin {align*}\ dfrac {4} {5} &=\ dfrac {\ tfrac {\ tfrac {47} {50} -\ tan\ alpha} {1+\ tfrac {47} {50}\ tan\ alpha}\\ [4pt]
4\ left (1+\ tfrac {47} {50}\ tan\ alfa\ derecha) &= 5\ izquierda (\ tfrac {47} {50} -\ tan\ alfa\ right)\ end {align*}\]
Usa la propiedad distributiva, y luego simplifica las funciones.
\ [\ begin {alinear*} 4 (1) +4\ izquierda (\ tfrac {47} {50}\ derecha)\ tan\ alfa &= 5\ izquierda (\ tfrac {47} {50}\ derecha) -5\ tan\ alfa\\ [4pt]
4+3.76\ tan\ alpha&= 4.7-5\ tan\ alpha\ [4pt]
5\ tan\ alfa\ 3.76\ tan\ alfa&= 0.7\\ [4pt]
8.76\ tan\ alpha&= 0.7\\ [4pt]
\ tan\ alpha&\ approx 0.07991\\ [4pt]
\ tan^ {-1} (0.07991) &\ approx .079741\ end {align*}\]
Ahora podemos calcular el ángulo en grados.
\ [\ comenzar {alinear*}\ alfa &\ aprox 0.079741\ izquierda (\ dfrac {180} {\ pi}\ derecha)\\ [4pt]
&\ aprox 4.57^ {\ circ}
\ final {alinear*}\]
Análisis
Ocasionalmente, cuando aparece una aplicación que incluye un triángulo rectángulo, podemos pensar que resolver es cuestión de aplicar el Teorema de Pitágoras. Eso puede ser parcialmente cierto, pero depende de lo que se pregunte el problema y de qué información se dé.
Acceda a estos recursos en línea para obtener instrucción y práctica adicionales con identidades de suma y diferencia.
- Identidades de suma y diferencia para coseno
- Identidades de suma y diferencia para seno
- Identidades de suma y diferencia para tangente
Ecuaciones Clave
| Fórmula de suma para coseno | \(\cos(\alpha+\beta)=\cos \alpha \cos \beta−\sin \alpha \sin \beta\) |
| Fórmula de diferencia para coseno | \(\cos(\alpha-\beta)=\cos \alpha \cos \beta+\sin \alpha \sin \beta\) |
| Fórmula de suma para seno | \(\sin(\alpha+\beta)=\sin \alpha \cos \beta+\cos \alpha \sin \beta\) |
| Fórmula de diferencia para seno | \(\sin(\alpha-\beta)=\sin \alpha \cos \beta-\cos \alpha \sin \beta\) |
| Fórmula de suma para tangente | \(\tan(\alpha+\beta)=\dfrac{\tan \alpha+\tan \beta}{1-\tan \alpha \tan \beta}\) |
| Fórmula de diferencia para tangente | \(\cos(\alpha−\beta)=\cos \alpha \cos \beta+\sin \alpha \sin \beta\) |
| Identidades de cofunción |
\(\sin \theta=\cos\left(\dfrac{\pi}{2}-\theta\right)\) \(\cos \theta=\sin\left(\dfrac{\pi}{2}-\theta\right)\) \(\tan \theta=\cot\left(\dfrac{\pi}{2}-\theta\right)\) \(\cot \theta=\tan\left(\dfrac{\pi}{2}-\theta\right)\) \(\sec \theta=\csc\left(\dfrac{\pi}{2}-\theta\right)\) \(\csc \theta=\sec\left(\dfrac{\pi}{2}-\theta\right)\) |
Conceptos clave
- La fórmula de suma para cosenos establece que el coseno de la suma de dos ángulos es igual al producto de los cosenos de los ángulos menos el producto de los senos de los ángulos. La fórmula de diferencia para cosenos establece que el coseno de la diferencia de dos ángulos es igual al producto de los cosenos de los ángulos más el producto de los senos de los ángulos.
- Las fórmulas de suma y diferencia se pueden usar para encontrar los valores exactos del seno, coseno o tangente de un ángulo. Ver Ejemplo\(\PageIndex{1}\) y Ejemplo\(\PageIndex{2}\).
- La fórmula de suma para senos establece que el seno de la suma de dos ángulos es igual al producto del seno del primer ángulo y coseno del segundo ángulo más el producto del coseno del primer ángulo y el seno del segundo ángulo. La fórmula de diferencia para senos establece que el seno de la diferencia de dos ángulos es igual al producto del seno del primer ángulo y coseno del segundo ángulo menos el producto del coseno del primer ángulo y el seno del segundo ángulo. Ver Ejemplo\(\PageIndex{3}\).
- Las fórmulas de suma y diferencia para seno y coseno también se pueden utilizar para funciones trigonométricas inversas. Ver Ejemplo\(\PageIndex{4}\).
- La fórmula de suma para tangente establece que la tangente de la suma de dos ángulos es igual a la suma de las tangentes de los ángulos divididos por\(1\) menos el producto de las tangentes de los ángulos. La fórmula de diferencia para tangente establece que la tangente de la diferencia de dos ángulos es igual a la diferencia de las tangentes de los ángulos divididos por\(1\) más el producto de las tangentes de los ángulos. Ver Ejemplo\(\PageIndex{5}\).
- El Teorema de Pitágoras junto con las fórmulas suma y diferencia se pueden utilizar para encontrar múltiples sumas y diferencias de ángulos. Ver Ejemplo\(\PageIndex{6}\).
- Las identidades de cofunción se aplican a ángulos complementarios y pares de funciones recíprocas. Ver Ejemplo\(\PageIndex{7}\).
- Las fórmulas de suma y diferencia son útiles para verificar identidades. Ver Ejemplo\(\PageIndex{8}\) y Ejemplo\(\PageIndex{9}\).
- Los problemas de aplicación suelen ser más fáciles de resolver mediante el uso de fórmulas de suma y diferencia. Ver Ejemplo\(\PageIndex{10}\) y Ejemplo\(\PageIndex{11}\).


