8.4: Coordenadas polares - Gráficas
- Page ID
- 121235
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)- Prueba de ecuaciones polares para simetría.
- Graficar ecuaciones polares trazando puntos.
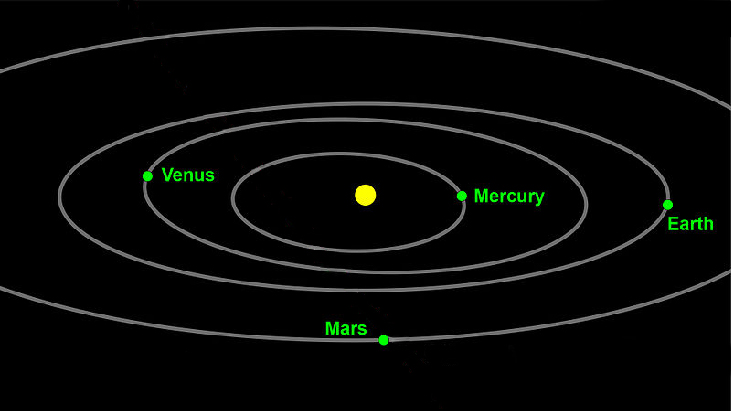
La Primera Ley de Movimiento Planetario de Keplar sostiene que los planetas se mueven a través del espacio en órbitas elípticas y periódicas alrededor del sol, como se muestra en la Figura\(\PageIndex{1}\). Están en constante movimiento, por lo que fijar una posición exacta de cualquier planeta es válido sólo por un momento. En otras palabras, solo podemos fijar la posición instantánea de un planeta. Esta es una aplicación de coordenadas polares, representadas como\((r,\theta)\). Interpretamos\(r\) como la distancia del sol y\(\theta\) como el rumbo angular del planeta, o su dirección desde un punto fijo sobre el sol. En esta sección, nos centraremos en el sistema polar y las gráficas que se generan directamente a partir de coordenadas polares.
Prueba de ecuaciones polares para simetría
Así como una ecuación rectangular como\(y=x^2\) describe la relación entre\(x\) y\(y\) sobre una cuadrícula cartesiana, una ecuación polar describe una relación entre\(r\) y\(\theta\) sobre una cuadrícula polar. Recordemos que el par de coordenadas\((r,\theta)\) indica que nos movemos en sentido antihorario desde el eje polar (\(x\)eje positivo) por un ángulo de\(\theta\), y extendemos un rayo desde las\(r\) unidades polares (origen) en la dirección de\(\theta\). Todos los puntos que satisfacen la ecuación polar están en la gráfica.
La simetría es una propiedad que nos ayuda a reconocer y trazar la gráfica de cualquier ecuación. Si una ecuación tiene una gráfica que es simétrica con respecto a un eje, significa que si doblamos la gráfica por la mitad sobre ese eje, la porción de la gráfica en un lado coincidiría con la porción del otro lado. Al realizar tres pruebas, veremos cómo aplicar las propiedades de la simetría a las ecuaciones polares. Además, utilizaremos simetría (además de trazar puntos clave, ceros y máximos de\(r\)) para determinar la gráfica de una ecuación polar.
En la primera prueba, consideramos la simetría con respecto a la línea\(\theta=\dfrac{\pi}{2}\) (\(y\)-eje). \((r,\theta)\)Reemplazamos\((−r,−\theta)\) por para determinar si la nueva ecuación es equivalente a la ecuación original. Por ejemplo, supongamos que se nos da la ecuación\(r=2 \sin \theta\);
\[\begin{align*} r&= 2 \sin \theta \\ -r&= 2 \sin -\theta \qquad \text{Replace } (r,\theta) \text{ with }(-r,-\theta). \\ -r&= -2 \sin \theta \qquad \text{Identity: }\sin(-\theta)=-\sin \theta. \\ r&= 2 \sin \theta \qquad \text{Multiply both sides by }-1 \end{align*}\]
Esta ecuación exhibe simetría con respecto a la línea\(\theta=\dfrac{\pi}{2}\).
En la segunda prueba, consideramos la simetría con respecto al eje polar (\(x\)-eje). Reemplazamos por\((r,\theta)\)\((r,−\theta)\) o\((−r,\pi−\theta)\) para determinar la equivalencia entre la ecuación probada y la original. Por ejemplo, supongamos que se nos da la ecuación\(r=1−2 \cos \theta\).
\[\begin{align*} r&= 1-2 \cos \theta \\ r&= 1-2 \cos(-\theta)\qquad \text{Replace }(r,\theta) \text{ with }(r,-\theta). \\ r&= 1-2 \cos \theta \qquad \text{Even/Odd identity} \end{align*}\]
La gráfica de esta ecuación exhibe simetría con respecto al eje polar.
En la tercera prueba, consideramos la simetría con respecto al polo (origen). \((r,\theta)\)Reemplazamos\((−r,\theta)\) por para determinar si la ecuación probada es equivalente a la ecuación original. Por ejemplo, supongamos que se nos da la ecuación\(r=2 \sin(3\theta)\).
\(r=2 \sin(3\theta)\)
\(−r=2 \sin(3\theta)\)
La ecuación ha fallado la prueba de simetría, pero eso no quiere decir que no sea simétrica con respecto al polo. Al pasar una o más de las pruebas de simetría se verifica que la simetría se exhibirá en una gráfica. Sin embargo, fallar las pruebas de simetría no necesariamente indica que una gráfica no será simétrica alrededor de la línea\(\theta=\dfrac{\pi}{2}\), el eje polar o el polo. En estos casos, podemos confirmar que la simetría existe trazando puntos reflectantes a través del eje aparente de simetría o el polo. La prueba de simetría es una técnica que simplifica la representación gráfica de ecuaciones polares, pero su aplicación no es perfecta.
Una ecuación polar describe una curva en la cuadrícula polar. La gráfica de una ecuación polar se puede evaluar para tres tipos de simetría, como se muestra en la Figura\(\PageIndex{2}\).
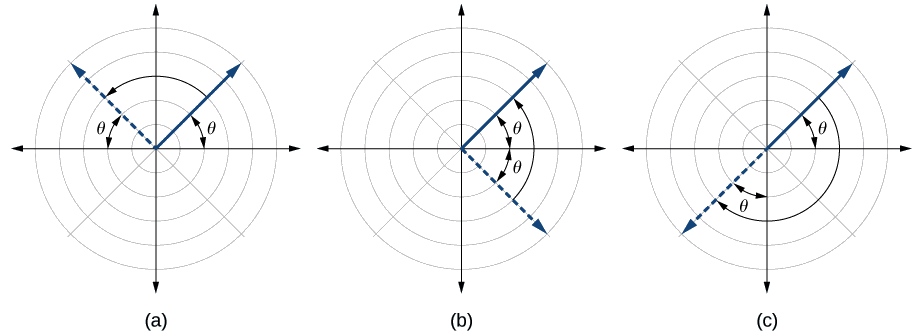
- Sustituir la combinación apropiada de componentes por\((r,\theta)\):\((−r,−\theta)\) para\(\theta=\dfrac{\pi}{2}\) simetría;\((r,−\theta)\) para simetría de eje polar; y\((−r,\theta)\) para simetría con respecto al polo.
- Si las ecuaciones resultantes son equivalentes en una o más de las pruebas, la gráfica produce la simetría esperada.
Probar la ecuación\(r=2 \sin \theta\) para la simetría.
Solución
Prueba para cada uno de los tres tipos de simetría.
| 1) Sustituir\((r,\theta)\) con\((−r,−\theta)\) rinde el mismo resultado. Así, la gráfica es simétrica con respecto a la línea\(\theta=\dfrac{\pi}{2}\). |
\(−r=2 \sin(−\theta)\) \(−r=−2 \sin \theta\)Identidad par e impar \(r=2 \sin \theta\)Multiplicar por\(−1\) Aprobado |
| 2) Reemplazar\(\theta\) con\(−\theta\) no arroja la misma ecuación. Por lo tanto, la gráfica falla en la prueba y puede ser o no simétrica con respecto al eje polar. |
\(r=2 \sin(−\theta)\) \(r=−2 \sin \theta\)Identidad par e impar \(r=−2 \sin \theta ≠ 2 \sin \theta\) Falló |
| 3) Reemplazar\(r\) con\(–r\) cambios la ecuación y falla la prueba. La gráfica puede o no ser simétrica con respecto al polo. |
\(−r=2 \sin \theta\) \(r=−2 \sin \theta ≠2 \sin \theta\) Falló |
Análisis
Usando una calculadora gráfica, podemos ver que la ecuación\(r=2 \sin \theta\) es un círculo centrado en\((0,1)\) con radio\(r=1\) y de hecho es simétrico a la línea\(\theta=\dfrac{\pi}{2}\). También podemos ver que la gráfica no es simétrica con el eje polar o con el polo. Ver Figura\(\PageIndex{3}\).
Pruebe la ecuación para simetría:\(r=−2 \cos \theta\).
- Contestar
-
La ecuación falla la prueba de simetría con respecto a la línea\(\theta=\dfrac{\pi}{2}\) y con respecto al polo. Pasa la prueba de simetría del eje polar.
Graficar Ecuaciones Polares Trazando Puntos
Para graficar en el sistema de coordenadas rectangulares construimos una tabla de\(x\) y\(y\) valores. Para graficar en el sistema de coordenadas polares construimos una tabla de\(\theta\) y\(r\) valores. Ingresamos valores de\(\theta\) en una ecuación polar y calculamos\(r\). Sin embargo, usar las propiedades de simetría y encontrar valores clave de\(\theta\) y\(r\) significa que se necesitarán menos cálculos.
Encontrar ceros y Maxima
Para encontrar los ceros de una ecuación polar, resolvemos para los valores de\(\theta\) ese resultado en\(r=0\). Recordemos que, para encontrar los ceros de las funciones polinómicas, establecemos la ecuación igual a cero y luego resolvemos para\(x\). Utilizamos el mismo proceso para ecuaciones polares. Establecer\(r=0\), y resolver para\(\theta\).
Para muchas de las formas que encontraremos, el valor máximo de una ecuación polar se encuentra sustituyendo aquellos valores de\(\theta\) en la ecuación que dan como resultado el valor máximo de las funciones trigonométricas. Considera\(r=5 \cos \theta\); la distancia máxima entre la curva y el polo es\(5\) unidades. El valor máximo de la función coseno es\(1\) cuándo\(\theta=0\), así es nuestra ecuación polar\(5 \cos \theta\), y el valor\(\theta=0\) producirá el máximo\(| r |\).
De igual manera, el valor máximo de la función sinusoidal es\(1\) cuándo\(\theta=\dfrac{\pi}{2}\), y si nuestra ecuación polar es\(r=5 \sin \theta\), el valor\(\theta=\dfrac{\pi}{2}\) producirá el máximo\(| r |\). Podemos encontrar información adicional calculando los valores de\(r\) cuándo\(\theta=0\). Estos puntos serían intercepciones de ejes polares, lo que puede ser útil para dibujar la gráfica e identificar la curva de una ecuación polar.
Usando la ecuación en Ejemplo\(\PageIndex{1}\), encuentra los ceros y el máximo\(| r |\) y, si es necesario, el eje polar intercepta de\(r=2 \sin \theta\).
Solución
Para encontrar los ceros, establecer\(r\) igual a cero y resolver para\(\theta\).
\[\begin{align*} 2 \sin \theta &= 0 \\ \sin \theta &= 0 \\ \theta &= {\sin}^{-1} 0 \\ \theta &= n\pi \qquad \text{where n is an integer} \end{align*}\]
Sustituir cualquiera de los\(\theta\) valores en la ecuación. Vamos a utilizar\(0\).
\[\begin{align*} r&= 2 \sin(0) \\ r&= 0 \end{align*}\]
Los puntos\((0,0)\) y\((0,\pm n\pi)\) son los ceros de la ecuación. Todos coinciden, por lo que solo un punto es visible en la gráfica. Este punto es también la única intercepción del eje polar.
Para encontrar el valor máximo de la ecuación, observe el valor máximo de la función trigonométrica\(\sin \theta\), que se produce al dar\(\theta=\dfrac{\pi}{2}\pm 2k\pi\) como resultado\(\sin\left(\dfrac{\pi}{2}\right)=1\). Sustituto\(\dfrac{\pi}{2}\) de\(\theta\).
\[\begin{align*} r&= 2 \sin\left(\dfrac{\pi}{2}\right) \\ r&= 2(1) \\ r&= 2 \end{align*}\]
Análisis
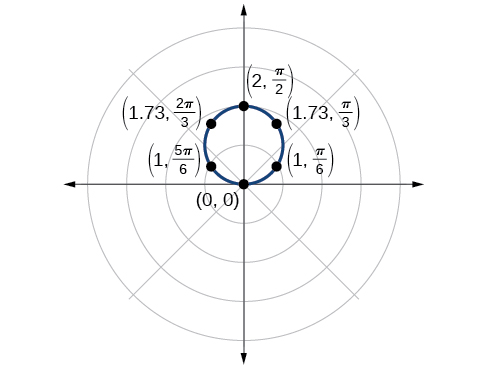
El punto\(\left(2,\dfrac{\pi}{2}\right)\) será el valor máximo en la gráfica. Trazemos algunos puntos más para verificar la gráfica de un círculo. Ver Tabla\(\PageIndex{1}\) y Figura\(\PageIndex{4}\).
| \(\theta\) | \(r=2 \sin \theta\) | \(r\) |
|---|---|---|
| \ (\ theta\) ">\(0\) | \ (r=2\ sin\ theta\) ">\(r=2 \sin(0)=0\) | \ (r\) ">\(0\) |
| \ (\ theta\) ">\(\dfrac{\pi}{6}\) | \ (r=2\ sin\ theta\) ">\(r=2 \sin\left(\dfrac{\pi}{6}\right)=1\) | \ (r\) ">\(1\) |
| \ (\ theta\) ">\(\dfrac{\pi}{3}\) | \ (r=2\ sin\ theta\) ">\(r=2 \sin\left(\dfrac{\pi}{3}\right)≈1.73\) | \ (r\) ">\(1.73\) |
| \ (\ theta\) ">\(\dfrac{pi}{2}\) | \ (r=2\ sin\ theta\) ">\(r=2 \sin\left(\dfrac{\pi}{2}\right)=2\) | \ (r\) ">\(2\) |
| \ (\ theta\) ">\(\dfrac{2\pi}{3}\) | \ (r=2\ sin\ theta\) ">\(r=2 \sin\left(\dfrac{2\pi}{3}\right)≈1.73\) | \ (r\) ">\(1.73\) |
| \ (\ theta\) ">\(\dfrac{5\pi}{6}\) | \ (r=2\ sin\ theta\) ">\(r=2 \sin\left(\dfrac{5\pi}{6}\right)=1\) | \ (r\) ">\(1\) |
| \ (\ theta\) ">\(\pi\) | \ (r=2\ sin\ theta\) ">\(r=2 \sin(\pi)=0\) | \ (r\) ">\(0\) |
Sin convertir a coordenadas cartesianas, pruebe la ecuación dada para la simetría y encuentre los ceros y los valores máximos de\(| r |\):\(r=3 \cos \theta\).
- Contestar
-
Las pruebas revelarán simetría alrededor del eje polar. El cero es\(\left(0,\dfrac{\pi}{2}\right)\), y el valor máximo es\((3,0)\).
Círculos Investigadores
Ahora hemos visto la ecuación de un círculo en el sistema de coordenadas polares. En los dos últimos ejemplos, se utilizó la misma ecuación para ilustrar las propiedades de simetría y demostrar cómo encontrar los ceros, los valores máximos y los puntos trazados que produjeron las gráficas. Sin embargo, el círculo es solo una de las muchas formas en el conjunto de curvas polares.
Hay cinco curvas polares clásicas: cardioides, limaons, lemniscados, curvas de rosas y espirales de Arquímedes. Tocaremos brevemente las fórmulas polares para el círculo antes de pasar a las curvas clásicas y sus variaciones.
Algunas de las fórmulas que producen la gráfica de un círculo en coordenadas polares vienen dadas por\(r=a \cos \theta\) y\(r=a \sin \theta\), donde a es el diámetro del círculo o la distancia desde el polo hasta el punto más alejado de la circunferencia. El radio es\(\dfrac{|a|}{2}\), o la mitad del diámetro. Para\(r=a \cos \theta\), el centro es\(\left(\dfrac{a}{2},0\right)\). Para\(r=a \sin \theta\), el centro es\(\left(\dfrac{a}{2},\pi\right)\). En la\(\PageIndex{5}\) figura se muestran las gráficas de estos cuatro círculos.
Esbozar la gráfica de\(r=4 \cos \theta\).
Solución
Primero, probando la ecuación de simetría, encontramos que la gráfica es simétrica alrededor del eje polar. A continuación, encontramos los ceros y el máximo\(| r |\) para\(r=4 \cos \theta\). Primero, establecer\(r=0\), y resolver para\(\theta\). Por lo tanto, se produce un cero en\(\theta=\dfrac{\pi}{2}\pm k\pi\). Un punto clave para trazar es\(\left(0,\dfrac{\pi}{2}\right)\).
Para encontrar el valor máximo de\(r\), tenga en cuenta que el valor máximo de la función coseno es\(1\) cuándo\(\theta=0\pm 2k\pi\). Sustituir\(\theta=0\) en la ecuación:
\[\begin{align*} r&= 4 \cos \theta\\ r&= 4 \cos(0)\\ r&= 4(1)\\ &= 4 \end{align*}\]
El valor máximo de la ecuación es\(4\). Un punto clave para trazar es\((4, 0)\).
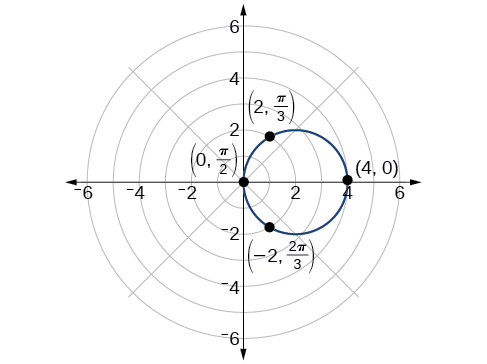
Como\(r=4 \cos \theta\) es simétrico con respecto al eje polar, solo necesitamos calcular\(r\) -valores para\(θ\) sobre el intervalo\([0, \pi]\). Los puntos en el cuadrante superior pueden reflejarse entonces hacia el cuadrante inferior. Hacer una tabla de valores similar a Tabla\(\PageIndex{2}\). La gráfica se muestra en la Figura\(\PageIndex{6}\).
| \(\theta\) | \(0\) | \(\dfrac{\pi}{6}\) | \(\dfrac{\pi}{4}\) | \(\dfrac{\pi}{3}\) | \(\dfrac{\pi}{2}\) | \(\dfrac{2\pi}{3}\) | \(\dfrac{3\pi}{4}\) | \(\dfrac{5\pi}{6}\) | \(\pi\) |
|---|---|---|---|---|---|---|---|---|---|
| \(r\) | \(4\) | \(3.46\) | \(2.83\) | \(2\) | \(0\) | \(−2\) | \(−2.83\) | \(−3.46\) | \(4\) |
Investigando Cardioides
Si bien la traducción de coordenadas polares a coordenadas cartesianas puede parecer más simple en algunos casos, graficar las curvas clásicas es en realidad menos complicado en el sistema polar. La siguiente curva se llama cardioide, ya que se asemeja a un corazón. Esta forma a menudo se incluye con la familia de curvas llamadas limaçons, pero aquí discutiremos el cardioide por sí solo.
Las fórmulas que producen las gráficas de un cardioide vienen dadas por\(r=a\pm b \cos \theta\) y\(r=a\pm b \sin \theta\) dónde\(a>0\),\(b>0\), y\(\dfrac{a}{b}=1\). El gráfico cardioide pasa por el polo, como podemos ver en la Figura\(\PageIndex{7}\).
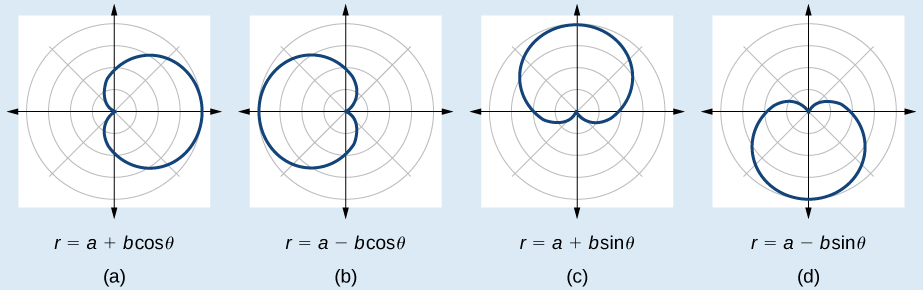
- Compruebe la ecuación para los tres tipos de simetría.
- Encuentra los ceros. Set\(r=0\).
- Encuentra el valor máximo de la ecuación de acuerdo con el valor máximo de la expresión trigonométrica.
- Hacer una tabla de valores para\(r\) y\(\theta\).
- Trazar los puntos y bosquejar la gráfica.
Esbozar la gráfica de\(r=2+2 \cos \theta\).
Solución
Primero, probando la ecuación de simetría, encontramos que la gráfica de esta ecuación será simétrica alrededor del eje polar. A continuación, encontramos los ceros y máximos. \(r=0\)Emplazamiento, tenemos\(\theta=\pi+2k\pi\). El cero de la ecuación se ubica en\((0,\pi)\). La gráfica pasa por este punto.
El valor máximo de\(r=2+2 \cos \theta\) ocurre cuando\(\cos \theta\) es un máximo, que es cuándo\(\cos \theta=1\) o cuándo\(\theta=0\). Sustituir\(\theta=0\) en la ecuación, y resolver para\(r\).
\[\begin{align*} r&= 2+2 \cos(0)\\ r&= 2+2(1)\\ &= 4 \end{align*}\]
El punto\((4,0)\) es el valor máximo en la gráfica.
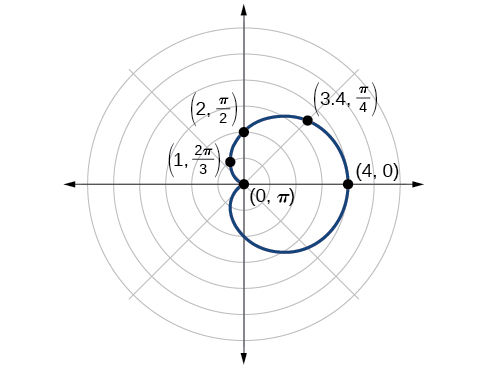
Encontramos que la ecuación polar es simétrica con respecto al eje polar, pero a medida que se extiende a los cuatro cuadrantes, necesitamos trazar valores a lo largo del intervalo\([0, \pi]\). La parte superior de la gráfica se refleja entonces sobre el eje polar. A continuación, hacemos una tabla de valores, como en Tabla\(\PageIndex{3}\), y luego trazamos los puntos y dibujamos la gráfica. Ver Figura\(\PageIndex{8}\).
| θ | 0 | \(\dfrac{π}{4}\) | \(\dfrac{π}{2}\) | \(\dfrac{2π}{3}\) | \(π\) |
|---|---|---|---|---|---|
| r | 4 | 3.41 | 2 | 1 | 0 |
Investigando Limaçons
La palabra limaçon es francés antiguo para “caracol”, un nombre que describe la forma de la gráfica. Como se mencionó anteriormente, el cardioide es miembro de la familia limaçon, y podemos ver las similitudes en las gráficas. Las otras imágenes de esta categoría incluyen el limaçon de un bucle y el limaçon de dos bucles (o bucle interno). Los limaçons de un bucle a veces se conocen como limaçons hoyuelos cuando\(1<\dfrac{a}{b}<2\) y limaçons convexos cuando\(\dfrac{a}{b}≥2\).
Las fórmulas que producen la gráfica de un limaçon de un bucle con hoyuelos vienen dadas por\(r=a\pm b \cos \theta\) y\(r=a\pm b \sin \theta\) dónde\(a>0\),\(b>0\), y\(1<ab<2\). Las cuatro gráficas se muestran en la Figura\(\PageIndex{9}\).
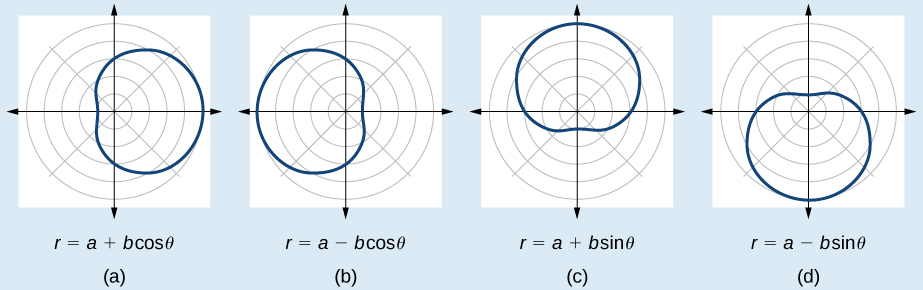
- Probar la ecuación para la simetría. Recuerde que fallar en una prueba de simetría no significa que la forma no exhiba simetría. A menudo, la simetría puede revelarse cuando se trazan los puntos.
- Encuentra los ceros.
- Encuentra los valores máximos de acuerdo a la expresión trigonométrica.
- Hacer una mesa.
- Trazar los puntos y bosquejar la gráfica.
Grafica la ecuación\(r=4−3 \sin \theta\).
Solución
Primero, probando la ecuación de simetría, encontramos que falla las tres pruebas de simetría, lo que significa que la gráfica puede o no exhibir simetría, por lo que no podemos usar la simetría para ayudarnos a graficarla. Sin embargo, esta ecuación tiene una gráfica que muestra claramente la simetría con respecto a la línea\(\theta=\dfrac{\pi}{2}\), sin embargo, falla las tres pruebas de simetría. Una calculadora gráfica ilustrará inmediatamente la calidad reflectante de la gráfica.
A continuación, encontramos los ceros y el máximo, y trazamos los puntos reflectantes para verificar cualquier simetría. Establecer\(r=0\) resultados en\(\theta\) ser indefinido. ¿Qué significa esto? ¿Cómo podría\(\theta\) ser indefinido? El ángulo no\(\theta\) está definido para cualquier valor de\(\sin \theta>1\). Por lo tanto,\(\theta\) es indefinido porque no hay valor de\(\theta\) para el cual\(\sin \theta>1\). En consecuencia, la gráfica no pasa por el polo. Quizás la gráfica sí cruza el eje polar, pero no en el polo. Podemos investigar otras intercepciones calculando\(r\) cuándo\(\theta=0\).
\[\begin{align*} r(0)&= 4-3 \sin(0)\\ r&= 4-3\cdot 0\\ &= 4 \end{align*}\]
Entonces, hay al menos una intercepción de eje polar en\((4,0)\).
A continuación, como el valor máximo de la función sinusoidal es\(1\) cuándo\(\theta=\dfrac{\pi}{2}\), sustituiremos\(\theta=\dfrac{\pi}{2}\) en la ecuación y resolveremos por\(r\). Así,\(r=1\).
Hacer una tabla de las coordenadas similar a Tabla\(\PageIndex{4}\).
| \(\theta\) | \(0\) | \(\dfrac{\pi}{6}\) | \(\dfrac{\pi}{3}\) | \(\dfrac{\pi}{2}\) | \(\dfrac{2\pi}{3}\) | \(\dfrac{5\pi}{6}\) | \(\pi\) | \(\dfrac{7\pi}{6}\) | \(\dfrac{4\pi}{3}\) | \(\dfrac{3\pi}{2}\) | \(\dfrac{5\pi}{3}\) | \(\dfrac{11\pi}{6}\) | \(2\pi\) |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| \(r\) | \(4\) | \(2.5\) | \(1.4\) | \(1\) | \(1.4\) | \(2.5\) | \(4\) | \(5.5\) | \(6.6\) | \(7\) | \(6.6\) | \(5.5\) | \(4\) |
La gráfica se muestra en la Figura\(\PageIndex{10}\).
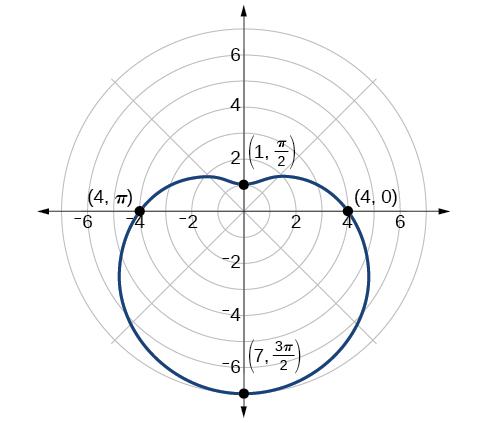
Análisis
Este es un ejemplo de una curva para la cual hacer una tabla de valores es fundamental para producir una gráfica precisa. Las pruebas de simetría fallan; el cero es indefinido. Si bien puede ser evidente que una ecuación que implica\(\sin \theta\) es probablemente simétrica con respecto a la línea\(\theta=\dfrac{\pi}{2}\), evaluar más puntos ayuda a verificar que la gráfica es correcta.
Esbozar la gráfica de\(r=3−2 \cos \theta\).
- Contestar
-
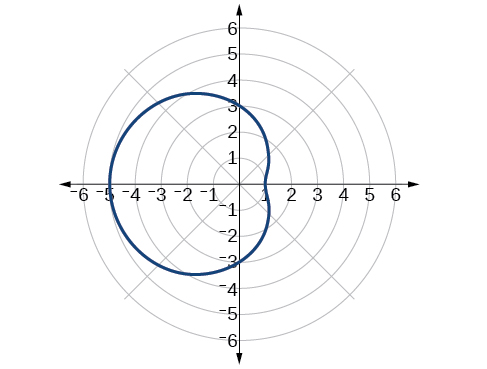
Figura\(\PageIndex{11}\)
Otro tipo de limaçon, el limaçon de bucle interno, se llama así por el bucle formado dentro de la forma general de limaçon. Fue descubierto por el artista alemán Alberto Durero (1471-1528), quien reveló un método para dibujar la limaçon de bucle interno en su libro de 1525 Underweysung der Messing. Un siglo después, el padre del matemático Blaise Pascal, Étienne Pascal (1588-1651), la redescubrió.
Las fórmulas que generan las limaçons de bucle interno vienen dadas por\(r=a\pm b\cos \theta\) y\(r=a\pm b \sin \theta\) dónde\(a>0\),\(b>0\), y\(a<b\). La gráfica del limaçon de bucle interno pasa a través del polo dos veces: una para el bucle externo y otra para el bucle interno. Consulte la Figura 10.5.12 para las gráficas.
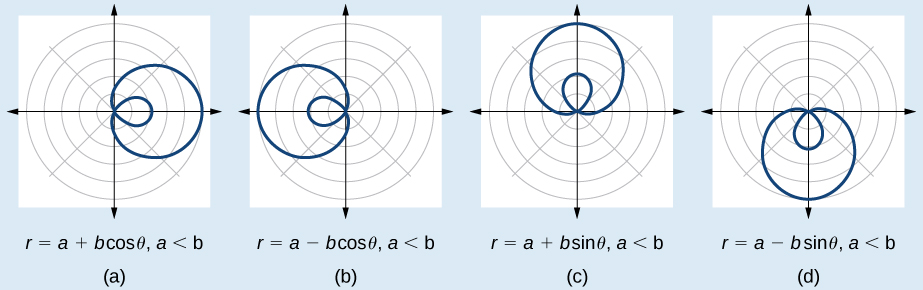
Esbozar la gráfica de\(r=2+5 \cos \theta\).
Solución
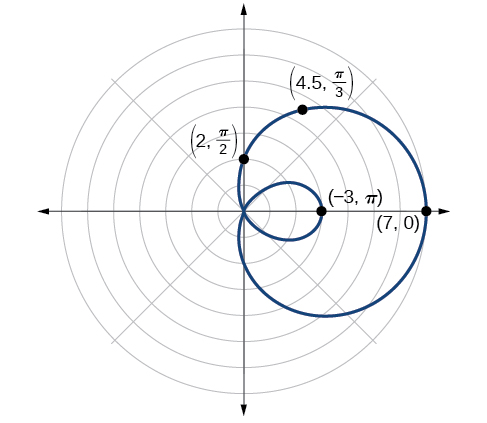
Al probar la simetría, encontramos que la gráfica de la ecuación es simétrica alrededor del eje polar. A continuación, encontrar los ceros revela que cuando\(r=0\),\(\theta=1.98\). El máximo\(| r |\) se encuentra cuando\(\cos \theta=1\) o cuando\(\theta=0\). Así, el máximo se encuentra en el punto\((7, 0)\).
A pesar de que hemos encontrado simetría, el cero, y el máximo, trazar más puntos ayudará a definir la forma, y luego emergerá un patrón. Ver Tabla\(\PageIndex{5}\).
| \(\theta\) | \(0\) | \(\dfrac{\pi}{6}\) | \(\dfrac{\pi}{3}\) | \(\dfrac{\pi}{2}\) | \(\dfrac{2\pi}{3}\) | \(\dfrac{5\pi}{6}\) | \(\pi\) | \(\dfrac{7\pi}{6}\) | \(\dfrac{4\pi}{3}\) | \(\dfrac{3\pi}{2}\) | \(\dfrac{5\pi}{3}\) | \(\dfrac{11\pi}{6}\) | \(2\pi\) |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| \(r\) | \(7\) | \(6.3\) | \(4.5\) | \(2\) | \(−0.5\) | \(−2.3\) | \(−3\) | \(−2.3\) | \(−0.5\) | \(2\) | \(4.5\) | \(6.3\) | \(7\) |
Como era de esperar, los valores comienzan a repetirse después\(\theta=\pi\). La gráfica se muestra en la Figura\(\PageIndex{13}\).
Investigando Lemniscates
El lemniscado es una curva polar que se asemeja al símbolo del infinito\(\infty\) o una figura\(8\). Centrado en el polo, un lemniscado es simétrico por definición.
Las fórmulas que generan la gráfica de un lemniscado están dadas por\(r^2=a^2 \cos 2\theta\) y\(r^2=a^2 \sin 2\theta\) dónde\(a≠0\). La fórmula\(r^2=a^2 \sin 2\theta\) es simétrica con respecto al polo. La fórmula\(r^2=a^2 \cos 2\theta\) es simétrica con respecto al polo, la línea\(\theta=\dfrac{\pi}{2}\) y el eje polar. Ver Figura\(\PageIndex{14}\) para las gráficas.
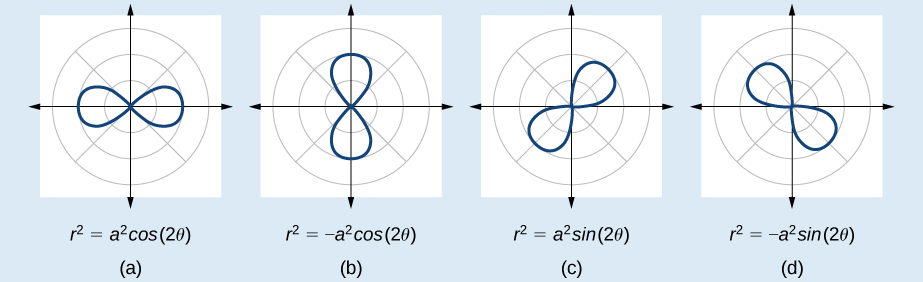
Esbozar la gráfica de\(r^2=4 \cos 2\theta\).
Solución
La ecuación exhibe simetría con respecto a la línea\(\theta=\dfrac{\pi}{2}\), el eje polar y el polo.
Encontremos los ceros. Ya debería ser rutinario, pero abordaremos esta ecuación de manera un poco diferente haciendo la sustitución\(u=2\theta\).
\[\begin{align*} 0 &= 4 \cos 2\theta \\ 0 &= 4 \cos u \\ 0 &= \cos u \\ {\cos}^{-1} 0 &= \dfrac{\pi}{2} \\ u &= \dfrac{\pi}{2} \qquad \text{Substitute } 2\theta \text{ back in for } u. \\ 2\theta &= \dfrac{\pi}{2} \\ \theta &= \dfrac{\pi}{4} \end{align*}\]
Entonces, el punto\(\left(0,\dfrac{\pi}{4}\right)\) es un cero de la ecuación.
Ahora encontremos el valor máximo. Desde el máximo de\(\cos u=1\) cuándo\(u=0\), el máximo\(\cos 2\theta=1\) cuándo\(2\theta=0\). Por lo tanto,
\[\begin{align*} r^2 &= 4 \cos(0) \\ r^2 &= 4(1)\\ r^2&= 4 \\ r&= \pm 4\\ &=2 \end{align*}\]
Tenemos un máximo en\((2, 0)\). Dado que esta gráfica es simétrica con respecto al polo, la línea\(\theta=\dfrac{\pi}{2}\) y el eje polar, solo necesitamos trazar puntos en el primer cuadrante.
Hacer una mesa similar a Mesa\(\PageIndex{6}\).
| \(\theta\) | \(0\) | \(\dfrac{\pi}{6}\) | \(\dfrac{\pi}{4}\) | \(\dfrac{\pi}{3}\) | \(\dfrac{\pi}{2}\) |
|---|---|---|---|---|---|
| \(r\) | \(2\) | \(\sqrt{2}\) | \(0\) | \(\sqrt{2}\) | \(0\) |
Trazar los puntos en la gráfica, como el que se muestra en la Figura\(\PageIndex{15}\).
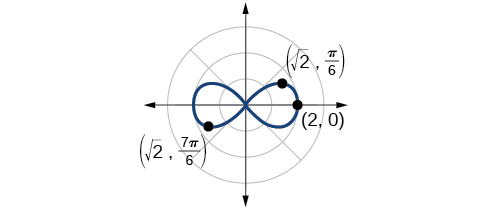
Análisis
Hacer una sustitución como\(u=2\theta\) es una práctica común en matemáticas porque puede simplificar los cálculos. No obstante, no debemos olvidar sustituir el término de sustitución por el término original al final, para luego resolver por lo desconocido.
Algunos de los puntos en esta gráfica pueden no aparecer usando la función Trace en la calculadora gráfica TI-84, y la tabla de la calculadora puede mostrar un error para estos mismos puntos de\(r\). Esto se debe a que no hay raíces cuadradas reales para estos valores de\(θ\). En otras palabras, los\(r\) valores correspondientes de\(\sqrt{4 \cos(2\theta)}\) son números complejos porque hay un número negativo debajo del radical.
Investigando Curvas de Rosa
El siguiente tipo de ecuación polar produce una forma similar a un pétalos llamada curva de rosa. Aunque las gráficas parecen complejas, una simple ecuación polar genera el patrón.
Las fórmulas que generan la gráfica de una curva de rosa vienen dadas por\(r=a \cos n\theta\) y\(r=a \sin n\theta\) dónde\(a≠0\). Si\(n\) es par, la curva tiene\(2n\) pétalos. Si\(n\) es impar, la curva tiene\(n\) pétalos. Ver Figura\(\PageIndex{16}\).
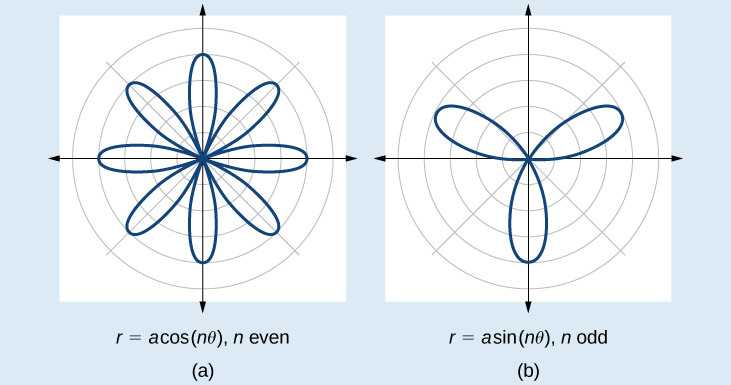
Esbozar la gráfica de\(r=2 \cos 4\theta\).
Solución
Al probar la simetría, encontramos de nuevo que las pruebas de simetría no cuentan toda la historia. La gráfica no sólo es simétrica con respecto al eje polar, sino también con respecto a la línea\(\theta=\dfrac{\pi}{2}\) y al polo.
Ahora encontraremos los ceros. Primero haz la sustitución\(u=4\theta\).
\[\begin{align*} 0 &= 2 \cos 4\theta \\ 0 &= \cos 4\theta \\ 0 &= \cos u \\ {\cos}^{-1} 0 &=u \\ u &= \dfrac{\pi}{2} \\ 4\theta &= \dfrac{\pi}{2} \\ \theta &=\dfrac{\pi}{8} \end{align*}\]
El cero es\(\theta=\dfrac{\pi}{8}\). El punto\(\left(0,\dfrac{\pi}{8}\right)\) está en la curva.
A continuación, encontramos el máximo\(| r |\). Sabemos que el valor máximo de\(\cos u=1\) cuándo\(\theta=0\). Por lo tanto,
\[\begin{align*} r &=2 \cos(4\cdot 0) \\ r &=2 \cos(0) \\ r &=2(1)\\ &= 2 \end{align*}\]
El punto\((2,0)\) está en la curva.
La gráfica de la curva de la rosa tiene propiedades únicas, las cuales se revelan en la Tabla\(\PageIndex{7}\).
| \(\theta\) | \(0\) | \(\dfrac{\pi}{8}\) | \(\dfrac{\pi}{4}\) | \(\dfrac{3\pi}{8}\) | \(\dfrac{\pi}{2}\) | \(5π8\) | \(3π4\) |
|---|---|---|---|---|---|---|---|
| \(r\) | \(2\) | \(0\) | \(−2\) | \(0\) | \(2\) | \(0\) | \(−2\) |
Como\(r=0\) cuando\(\theta=\dfrac{\pi}{8}\), tiene sentido dividir los valores en la tabla por\(\dfrac{\pi}{8}\) unidades. Surge un patrón definido. Mira el rango de\(r\) -valores:\(2, 0, −2, 0\) y así sucesivamente. Esto representa el desarrollo de la curva de un pétalo a la vez. A partir de\(r=0\), cada pétalo se extiende una distancia de\(r=2\), y luego vuelve a cero\(2n\) veces para un total de ocho pétalos. Ver la gráfica en la Figura\(\PageIndex{17}\).
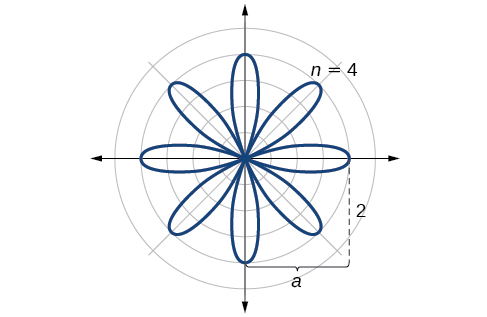
Análisis
Cuando se dibujan estas curvas, lo mejor es trazar los puntos en orden, como en la Tabla\(\PageIndex{7}\). Esto nos permite ver cómo la gráfica golpea un máximo (la punta de un pétalo), bucles hacia atrás cruzando el polo, golpea el máximo opuesto y vuelve al polo. La acción es continua hasta que se dibujan todos los pétalos.
Esbozar la gráfica de\(r=4 \sin(2\theta)\).
- Contestar
-
La gráfica es una curva de rosa,\(n\) incluso
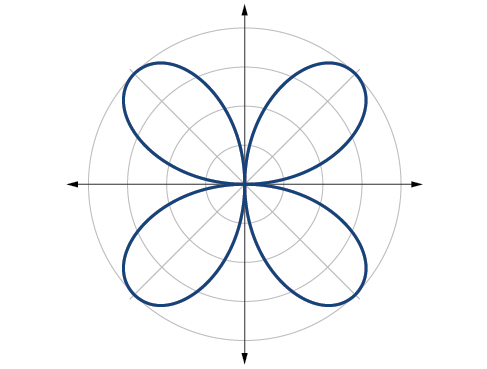
Figura\(\PageIndex{18}\)
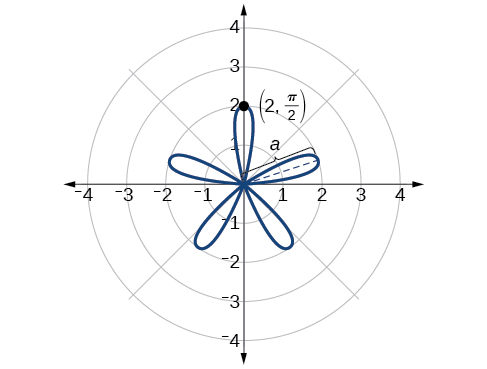
Esbozar la gráfica de\(r=2 \sin(5\theta)\).
Solución
La gráfica de la ecuación muestra simetría con respecto a la línea\(\theta=\dfrac{\pi}{2}\). A continuación, encuentra los ceros y el máximo. Vamos a querer hacer la sustitución\(u=5\theta\).
\[\begin{align*} 0 &=2 \sin(5\theta) \\ 0 &=\sin u \\ {\sin}^{-1} 0 &=0 \\ u &=0 \\ 5\theta &=0 \\ \theta &=0 \end{align*}\]
El valor máximo se calcula en el ángulo donde\(\sin \theta\) es un máximo. Por lo tanto,
\[\begin{align*} r&= 2 \sin\left(5\cdot \dfrac{\pi}{2}\right) \\ r&= 2(1)\\ &= 2 \end{align*}\]
Así, el valor máximo de la ecuación polar es\(2\). Esta es la longitud de cada pétalo. Como la curva para\(n\) impar arroja el mismo número de pétalos que\(n\), habrá cinco pétalos en la gráfica. Ver Figura\(\PageIndex{19}\).
Crear una tabla de valores similar a Tabla\(\PageIndex{8}\).
| \(\theta\) | \(0\) | \(\dfrac{\pi}{6}\) | \(\dfrac{\pi}{3}\) | \(\dfrac{\pi}{2}\) | \(\dfrac{2\pi}{3}\) | \(\dfrac{5\pi}{6}\) | \(\pi\) |
|---|---|---|---|---|---|---|---|
| \(r\) | \ (0\ 0 | \(1\) | \(−1.73\) | \(2\) | \(−1.73\) | \(1\) | \(0\) |
Esbozar la gráfica de\(r=3 \cos(3\theta)\).
- Contestar
-
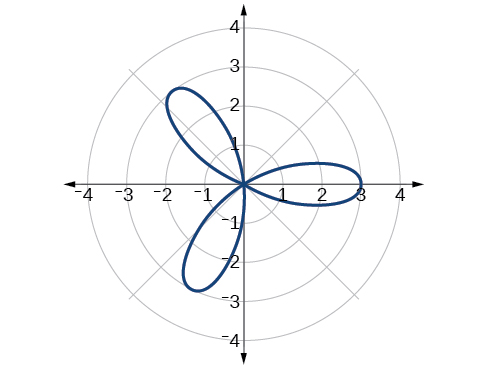
Figura\(\PageIndex{20}\) Curva de rosa,\(n\) impar
Investigando la Espiral de Arquímedes
La ecuación polar final que discutiremos es la espiral de Arquímedes, llamada así por su descubridor, el matemático griego Arquímedes (c. 287 a. C. - c. 212 a. C.), a quien se le atribuyen numerosos descubrimientos en los campos de la geometría y la mecánica.
La fórmula que genera la gráfica de la espiral de Arquímedes viene dada por\(r=\theta\) for\(\theta≥0\). A\(\theta\) medida que\(r\) aumenta, aumenta a un ritmo constante en un camino cada vez mayor, interminable y en espiral. Ver Figura\(\PageIndex{21}\).
![Dos gráficas lado a lado de la espiral de Arquímedes. (A) es r= theta, [0, 2pi]. (B) es r=theta, [0, 4pi]. Ambos comienzan en origen y salen en espiral en sentido antihorario. El segundo tiene dos espirales hacia fuera mientras que el primero tiene uno.](https://math.libretexts.org/@api/deki/files/7445/CNX_Precalc_Figure_08_04_020new.jpg)
- Hacer una tabla de valores para\(r\) y\(\theta\) sobre el dominio dado.
- Trazar los puntos y bosquejar la gráfica.
Esbozar la gráfica de\(r=\theta\) más\([0,2\pi]\).
Solución
Como\(r\) es igual a\(\theta\), la trama de la espiral de Arquímedes comienza en el polo en el punto\((0, 0)\). Si bien la gráfica insinúa simetría, no hay simetría formal con respecto a pasar las pruebas de simetría. Además, no hay valor máximo, a menos que el dominio esté restringido.
Crear una tabla como Tabla\(\PageIndex{9}\).
| \(\theta\) | \(\dfrac{\pi}{4}\) | \(\dfrac{\pi}{2}\) | \(\pi\) | \(\dfrac{3\pi}{2}\) | \(\dfrac{7\pi}{4}\) | \(2\pi\) |
|---|---|---|---|---|---|---|
| \(r\) | \(0.785\) | \(1.57\) | \(3.14\) | \(4.71\) | \(5.50\) | \(6.28\) |
Observe que los valores r son solo la forma decimal del ángulo medido en radianes. Los podemos ver en una gráfica en la Figura\(\PageIndex{22}\).
![Gráfica de la espiral de Arquímedes r=theta sobre [0,2pi]. Comienza en el origen y sale en espiral en un bucle en sentido antihorario. Se marcan los puntos (pi/4, pi/4), (pi/2, pi/2), (pi, pi), (5pi/4, 5pi/4), (7pi/4, pi/4) y (2pi, 2pi).](https://math.libretexts.org/@api/deki/files/7446/CNX_Precalc_Figure_08_04_021F.jpg)
Análisis
El dominio de esta curva polar es\([ 0,2\pi ]\). En general, sin embargo, el dominio de esta función lo es\((−\infty,\infty)\). Graficar la ecuación de la espiral de Arquímedes es bastante simple, aunque la imagen la hace parecer compleja.
Dibuje la gráfica de\(r=−\theta\) sobre el intervalo\([ 0,4\pi ]\).
- Contestar
-
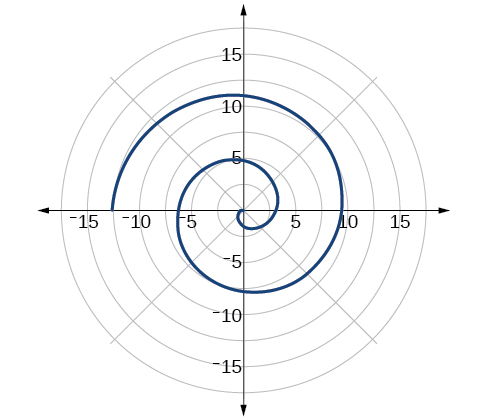
Figura\(\PageIndex{23}\)
Resumen de Curves
Hemos explorado una serie de curvas polares aparentemente complejas en esta sección. Figura\(\PageIndex{24}\) y Figura\(\PageIndex{25}\) resumen las gráficas y ecuaciones para cada una de estas curvas.
Acceda a estos recursos en línea para obtener instrucción adicional y práctica con gráficos de coordenadas polares.
- Graficando Ecuaciones Polares Parte 1
- Graficando Ecuaciones Polares Parte 2
- Animación: Las gráficas de las ecuaciones polares
- Graficando ecuaciones polares en el TI-84
Conceptos clave
- Es más fácil graficar ecuaciones polares si podemos probar la simetría de las ecuaciones con respecto a la línea\(\theta=\dfrac{\pi}{2}\), el eje polar o el polo.
- Existen tres pruebas de simetría que indican si la gráfica de una ecuación polar exhibirá simetría. Si una ecuación falla en una prueba de simetría, la gráfica puede o no exhibir simetría. Ver Ejemplo\(\PageIndex{1}\).
- Las ecuaciones polares se pueden graficar haciendo una tabla de valores para\(\theta\) y\(r\).
- El valor máximo de una ecuación polar se encuentra sustituyendo el valor\(\theta\) que conduce al valor máximo de la expresión trigonométrica.
- Los ceros de una ecuación polar se encuentran estableciendo\(r=0\) y resolviendo para\(\theta\). Ver Ejemplo\(\PageIndex{2}\).
- Algunas fórmulas que producen la gráfica de un círculo en coordenadas polares vienen dadas por\(r=a \cos \theta\) y\(r=a \sin \theta\). Ver Ejemplo\(\PageIndex{3}\).
- Las fórmulas que producen las gráficas de un cardioide vienen dadas por\(r=a\pm b \cos \theta\) y\(r=a\pm b \sin \theta\), para\(a>0\)\(b>0\), y\(ab=1\). Ver Ejemplo\(\PageIndex{4}\).
- Las fórmulas que producen las gráficas de un limaçon de un bucle están dadas por\(r=a\pm b \cos \theta\) y\(r=a\pm b \sin \theta\) para\(1<ab<2\). Ver Ejemplo\(\PageIndex{5}\).
- Las fórmulas que producen las gráficas de un limaçon de bucle interno vienen dadas por\(r=a\pm b \cos \theta\) y\(r=a\pm b \sin \theta\) para\(a>0\),\(b>0\), y\(a<b\). Ver Ejemplo\(\PageIndex{6}\).
- Las fórmulas que producen las gráficas de un lemniscates vienen dadas por\(r^2=a^2 \cos 2\theta\) y\(r^2=a^2 \sin 2\theta\), donde\(a≠0\) .Ver Ejemplo\(\PageIndex{7}\).
- Las fórmulas que producen las gráficas de las curvas de rosas vienen dadas por\(r=a \cos n\theta\) y\(r=a \sin n\theta\), donde\(a≠0\); si\(n\) es par, hay\(2n\) pétalos, y si\(n\) es impar, hay n pétalos. Ver Ejemplo\(\PageIndex{8}\) y Ejemplo\(\PageIndex{9}\).
- La fórmula que produce la gráfica de una espiral de Arquímedes viene dada por\(r=\theta\),\(\theta≥0\). Ver Ejemplo\(\PageIndex{10}\).