9.2: Sistemas de Ecuaciones Lineales - Tres Variables
- Page ID
- 121236
- Resolver sistemas de tres ecuaciones en tres variables.
- Identificar sistemas inconsistentes de ecuaciones que contengan tres variables.
- Expresar la solución de un sistema de ecuaciones dependientes que contenga tres variables.
John recibió una herencia de la\($12,000\) que dividió en tres partes e invirtió de tres maneras: en un fondo del mercado monetario que pagaba intereses\(3\%\) anuales; en bonos municipales que pagaban intereses\(4\%\) anuales; y en fondos mutuos que\(7\%\) pagaban intereses anuales. John invirtió\($4,000\) más en fondos municipales que en bonos municipales. Ganó\($670\) en intereses el primer año. ¿Cuánto invirtió John en cada tipo de fondo?

Figura\(\PageIndex{1}\): (crédito: “Elembis”, Wikimedia Commons)
Comprender el enfoque correcto para establecer problemas como éste hace que encontrar una solución sea cuestión de seguir un patrón. Resolveremos este y otros problemas similares que involucran tres ecuaciones y tres variables en esta sección. Al hacerlo, se utilizan técnicas similares a las utilizadas para resolver sistemas de dos ecuaciones en dos variables. Sin embargo, encontrar soluciones a sistemas de tres ecuaciones requiere un poco más de organización y un toque de gimnasia visual.
Resolver sistemas de tres ecuaciones en tres variables
Para resolver sistemas de ecuaciones en tres variables, conocidas como sistemas de tres por tres, la herramienta primaria que usaremos se llama eliminación gaussiana, llamada así por el prolífico matemático alemán Karl Friedrich Gauss. Si bien no existe un orden definitivo en el que se van a realizar las operaciones, existen pautas específicas en cuanto a qué tipo de movimientos se pueden realizar. Podemos numerar las ecuaciones para realizar un seguimiento de los pasos que aplicamos. El objetivo es eliminar una variable a la vez para lograr la forma triangular superior, la forma ideal para un sistema de tres por tres porque permite una sustitución directa hacia atrás para encontrar una solución\((x,y,z)\), que llamamos triple ordenado. Un sistema en forma triangular superior tiene el siguiente aspecto:
\[\begin{align*} Ax+By+Cz &= D \nonumber \\[4pt] Ey+Fz &= G \nonumber \\[4pt] Hz &= K \nonumber \end{align*} \nonumber\]
La tercera ecuación se puede resolver para\(z\), y luego volvemos a sustituir para encontrar\(y\) y\(x\). Para escribir el sistema en forma triangular superior, podemos realizar las siguientes operaciones:
- Intercambiar el orden de cualquiera de las dos ecuaciones.
- Multiplique ambos lados de una ecuación por una constante distinta de cero.
- Agregue un múltiplo distinto de cero de una ecuación a otra ecuación.
La solución establecida en un sistema de tres por tres es un triple ordenado\({(x,y,z)}\). Gráficamente, el triple ordenado define el punto que es la intersección de tres planos en el espacio. Se puede visualizar tal intersección imaginando cualquier rincón en una habitación rectangular. Una esquina se define por tres planos: dos muros contiguos y el piso (o techo). Cualquier punto donde dos muros y el piso se encuentran representa la intersección de tres planos.
La figura\(\PageIndex{2}\) y la figura\(\PageIndex{3}\) ilustran posibles escenarios de solución para sistemas de tres por tres.
- Los sistemas que tienen una sola solución son aquellos que, después de la eliminación, dan como resultado un conjunto de soluciones consistente en un triple ordenado\({(x,y,z)}\). Gráficamente, el triple ordenado define un punto que es la intersección de tres planos en el espacio.
- Los sistemas que tienen un número infinito de soluciones son aquellos que, después de la eliminación, dan como resultado una expresión que siempre es cierta, como\(0=0\). Gráficamente, un número infinito de soluciones representa una línea o plano coincidente que sirve como intersección de tres planos en el espacio.
- Los sistemas que no tienen solución son aquellos que, después de la eliminación, resultan en una afirmación que es una contradicción, como\(3=0\). Gráficamente, un sistema sin solución está representado por tres planos sin punto en común.

Figura\(\PageIndex{2}\): (a) Tres planos se cruzan en un solo punto, representando un sistema de tres por tres con una sola solución. b) Tres planos se cruzan en una línea, representando un sistema de tres por tres con infinitas soluciones.

Figura\(\PageIndex{3}\): Las tres figuras representan tres por tres sistemas sin solución. a) Los tres planos se cruzan entre sí, pero no en un punto común. b) Dos de los planos son paralelos y se cruzan con el tercer plano, pero no entre sí. (c) Los tres planos son paralelos, por lo que no hay punto de intersección.
Determinar si el triple ordenado\((3,−2,1)\) es una solución al sistema.
\[\begin{align*} x+y+z &= 2 \nonumber \\[4pt] 6x−4y+5z &= 31 \nonumber \\[4pt] 5x+2y+2z &= 13 \nonumber \end{align*} \nonumber\]
Solución
Comprobaremos cada ecuación sustituyendo en los valores del triple ordenado por\( x,y\), y\(z\).
\[\begin{array}{rrr} { \text{} \nonumber \\[4pt] x+y+z=2 \nonumber \\[4pt] (3)+(−2)+(1)=2 \nonumber \\[4pt] \text{True}} & {6x−4y+5z=31 \nonumber \\[4pt] 6(3)−4(−2)+5(1)=31 \nonumber \\[4pt] 18+8+5=31 \nonumber \\[4pt] \text{True} } & { 5x+2y+2z = 13 \nonumber \\[4pt] 5(3)+2(−2)+2(1)=13 \nonumber \\[4pt] 15−4+2=13 \nonumber \\[4pt] \text{True}} \end{array}\]
El triple ordenado\((3,−2,1)\) es de hecho una solución al sistema.
- Elija cualquier par de ecuaciones y resuelva para una variable.
- Escoge otro par de ecuaciones y resuelve para la misma variable.
- Se ha creado un sistema de dos ecuaciones en dos incógnitas. Resuelve el sistema resultante de dos por dos.
- Vuelva a sustituir las variables conocidas en cualquiera de las ecuaciones originales y resolver la variable faltante.
Encuentre una solución al siguiente sistema:
\[\begin{align} x−2y+3z=9 \; &(1) \nonumber \\[4pt] −x+3y−z=−6 \; &(2) \nonumber \\[4pt] 2x−5y+5z=17 \; &(3) \nonumber \end{align} \nonumber\]
Solución
Siempre habrá varias opciones en cuanto a por dónde empezar, pero el primer paso más obvio aquí es eliminar\(x\) sumando las ecuaciones (1) y (2).
\[\begin{align} x−2y+3z=9 \; \; &(1) \nonumber \\[4pt] \underline{−x+3y−z=−6 }\; \; &(2) \nonumber \\[4pt] y+2z=3 \;\; &(3) \nonumber \end{align} \nonumber\]
El segundo paso es multiplicar la ecuación (1) por\(−2\) y sumar el resultado a la ecuación (3). Estos dos pasos eliminarán la variable\(x\).
\[\begin{align} −2x+4y−6z=−18\; &(1) \;\;\;\; \text{ multiplied by }−2 \nonumber \\[4pt] \underline{2x−5y+5z=17} \; & (3) \nonumber \\[4pt]−y−z=−1 \; &(5) \nonumber \end{align} \nonumber\]
En las ecuaciones (4) y (5), hemos creado un nuevo sistema de dos por dos. Podemos resolver\(z\) por sumando las dos ecuaciones.
\[\begin{align} y+2z=3 \; &(4) \nonumber \\[4pt] \underline{−y−z=−1} \; & (5) \nonumber \\[4pt] z=2 \; & (6) \nonumber \end{align} \nonumber\]
Al elegir una ecuación de cada nuevo sistema, obtenemos la forma triangular superior:
\[\begin{align} x−2y+3z=9 \; &(1) \nonumber \\[4pt] y+2z =3 \; &(4) \nonumber \\[4pt] z=2 \; &(6) \nonumber \end{align} \nonumber\]
A continuación, volvemos\(z=2\) a sustituir en la ecuación (4) y resolver para\(y\).
\[\begin{align} y+2(2) &=3 \nonumber \\[4pt] y+4 &= 3 \nonumber \\[4pt] y &= −1 \nonumber \end{align} \nonumber\]
Finalmente, podemos volver a sustituir\(z=2\) y\(y=−1\) en la ecuación (1). Esto dará como resultado la solución para\(x\).
\[\begin{align} x−2(−1)+3(2) &= 9 \nonumber \\[4pt] x+2+6 &=9 \nonumber \\[4pt] x &= 1 \nonumber \end{align} \nonumber\]
La solución es el triple ordenado\((1,−1,2)\). Ver Figura\(\PageIndex{4}\).
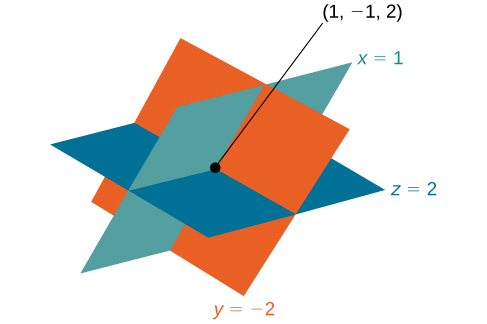
Figura\(\PageIndex{4}\)
En el problema planteado al inicio de la sección, John invirtió su herencia de\($12,000\) en tres fondos diferentes: parte en un fondo del mercado monetario que paga\(3\%\) intereses anualmente; parte en bonos municipales que pagan\(4\%\) anualmente; y el resto en fondos mutuos que pagan\(7\%\) anualmente. John invirtió\($4,000\) más en fondos mutuos de lo que invirtió en bonos municipales. El interés total ganado en un año fue\($670\). ¿Cuánto invirtió en cada tipo de fondo?
Solución
Para resolver este problema, utilizamos toda la información proporcionada y configuramos tres ecuaciones. Primero, asignamos una variable a cada uno de los tres montos de inversión:
\[\begin{align} x &= \text{amount invested in money-market fund} \nonumber \\[4pt] y &= \text{amount invested in municipal bonds} \nonumber \\[4pt] z &= \text{amount invested in mutual funds} \nonumber \end{align} \nonumber\]
La primera ecuación indica que la suma de los tres montos principales es\($12,000\).
\[x+y+z=12,000 \nonumber\]
Formamos la segunda ecuación de acuerdo a la información de que John invirtió\($4,000\) más en fondos mutuos que en bonos municipales.
\[z=y+4,000 \nonumber\]
La tercera ecuación muestra que el monto total de los intereses devengados de cada fondo es igual\($670\).
\[0.03x+0.04y+0.07z=670 \nonumber\]
Entonces, escribimos las tres ecuaciones como un sistema.
\[\begin{align} x+y+z &=12,000 \nonumber \\[4pt] −y+z &= 4,000 \nonumber \\[4pt] 0.03x+0.04y+0.07z &= 670 \nonumber \end{align} \nonumber\]
Para hacer los cálculos más simples, podemos multiplicar la tercera ecuación por\(100\). Por lo tanto,
\[\begin{align} x+y+z &=12,000 \; &(1) \nonumber \\[4pt] −y+z &= 4,000 \; &(2) \nonumber \\[4pt] 3x+4y+7z &= 67,000 \; &(3) \nonumber \end{align} \nonumber\]
Paso 1. Intercambia la ecuación (2) y la ecuación (3) para que las dos ecuaciones con tres variables se alineen.
\[\begin{align} x+y+z &= 12,000 \nonumber \\[4pt] 3x+4y+7z &= 67,000 \nonumber \\[4pt] −y+z &= 4,000 \nonumber \end{align} \nonumber\]
Paso 2. Multiplica la ecuación (1) por\(−3\) y suma a la ecuación (2). Escribe el resultado como fila 2.
\[\begin{align} x+y+z &= 12,000 \nonumber \\[4pt] y+4z &= 31,000 \nonumber \\[4pt] −y+z &= 4,000 \nonumber \end{align} \nonumber\]
Paso 3. Agregue la ecuación (2) a la ecuación (3) y escriba el resultado como la ecuación (3).
\[\begin{align} x+y+z &= 12,000 \nonumber \\[4pt] y+4z &= 31,000 \nonumber \\[4pt] 5z &= 35,000 \nonumber \end{align} \nonumber\]
Paso 4. Resolver para\(z\) en la ecuación (3). Volver a sustituir ese valor en la ecuación (2) y resolver para\(y\). Luego, vuelva a sustituir los valores para\(z\) y\(y\) en la ecuación (1) y resuelva para\(x\).
\[\begin{align} 5z &= 35,000 \nonumber \\[4pt] z &= 7,000 \nonumber \\[4pt] \nonumber \\[4pt] y+4(7,000) &= 31,000 \nonumber \\[4pt] y &=3,000 \nonumber \\[4pt] \nonumber \\[4pt] x+3,000+7,000 &= 12,000 \nonumber \\[4pt] x &= 2,000 \nonumber \end{align} \nonumber\]
John invirtió\($2,000\) en un fondo del mercado monetario,\($3,000\) en bonos municipales y\($7,000\) en fondos mutuos.
Resolver el sistema de ecuaciones en tres variables.
\[\begin{align} 2x+y−2z &= −1 \nonumber \\[4pt] 3x−3y−z &= 5 \nonumber \\[4pt] x−2y+3z &= 6 \nonumber \end{align} \nonumber\]
- Contestar
-
\((1,−1,1)\)
Identificación de sistemas inconsistentes de ecuaciones que contienen tres variables
Al igual que con los sistemas de ecuaciones en dos variables, podemos encontrarnos con un sistema inconsistente de ecuaciones en tres variables, lo que significa que no tiene una solución que satisfaga las tres ecuaciones. Las ecuaciones podrían representar tres planos paralelos, dos planos paralelos y un plano de intersección, o tres planos que intersectan los otros dos pero no en la misma ubicación. El proceso de eliminación resultará en una declaración falsa, como\(3=7\) o alguna otra contradicción.
Resuelve el siguiente sistema.
\[\begin{align} x−3y+z &=4 \label{4.1}\\[4pt] −x+2y−5z &=3 \label{4.2} \\[4pt] 5x−13y+13z &=8 \label{4.3} \end{align} \nonumber\]
Solución
Mirando los coeficientes de\(x\), podemos ver que podemos eliminar\(x\) sumando la Ecuación\ ref {4.1} a la Ecuación\ ref {4.2}.
\[\begin{align} x−3y+z = 4 &(1) \nonumber \\[4pt] \underline{−x+2y−5z=3} & (2) \nonumber \\[4pt] −y−4z =7 & (4) \nonumber \end{align} \nonumber\]
A continuación, multiplicamos la ecuación (1) por\(−5\) y la agregamos a la ecuación (3).
\[\begin{align} −5x+15y−5z =−20 & (1) \;\;\;\;\; \text{multiplied by }−5 \nonumber \\[4pt] \underline{5x−13y+13z=8} &(3) \nonumber \\[4pt] 2y+8z=−12 &(5) \nonumber \end{align} \nonumber\]
Entonces, multiplicamos la ecuación (4) por 2 y la agregamos a la ecuación (5).
\[\begin{align} −2y−8z=14 & (4) \;\;\;\;\; \text{multiplied by }2 \nonumber \\[4pt] \underline{2y+8z=−12} & (5) \nonumber \\[4pt] 0=2 & \nonumber \end{align} \nonumber\]
La ecuación final\(0=2\) es una contradicción, por lo que concluimos que el sistema de ecuaciones es inconsistente y, por lo tanto, no tiene solución.
Análisis
En este sistema, cada plano se cruza con los otros dos, pero no en la misma ubicación. Por lo tanto, el sistema es inconsistente.
Resolver el sistema de tres ecuaciones en tres variables.
\[\begin{align} x+y+z &= 2 \nonumber \\[4pt] y−3z &=1 \nonumber \\[4pt] 2x+y+5z &=0 \nonumber \end{align} \nonumber\]
- Contestar
-
Sin solución.
Expresando la Solución de un Sistema de Ecuaciones Dependientes que Contiene Tres Variables
Sabemos por trabajar con sistemas de ecuaciones en dos variables que un sistema dependiente de ecuaciones tiene un número infinito de soluciones. Lo mismo es cierto para los sistemas dependientes de ecuaciones en tres variables. Un número infinito de soluciones puede resultar de varias situaciones. Los tres planos podrían ser iguales, de manera que una solución a una ecuación será la solución a las otras dos ecuaciones. Las tres ecuaciones podrían ser diferentes pero se cruzan en una línea, que tiene infinitas soluciones. O dos de las ecuaciones podrían ser iguales e intersectar la tercera en una línea.
Encontrar la solución al sistema dado de tres ecuaciones en tres variables.
\[\begin{align} 2x+y−3z &= 0 &(1) \nonumber \\[4pt] 4x+2y−6z &=0 &(2) \nonumber \\[4pt] x−y+z &= 0 &(3) \nonumber \end{align} \nonumber\]
Solución
Primero, podemos multiplicar la ecuación (1) por\(−2\) y agregarla a la ecuación (2).
\[\begin{align} −4x−2y+6z =0 & (1) \;\;\;\;\; \text{multiplied by }−2 \nonumber \\[4pt] \underline{4x+2y−6z=0} & (2) \nonumber \\[4pt] 0=0& \nonumber \end{align} \nonumber\]
No es necesario que sigamos adelante. El resultado que obtenemos es una identidad,\(0=0\), que nos dice que este sistema tiene un número infinito de soluciones. Hay otras formas de comenzar a resolver este sistema, como multiplicar la ecuación (3) por\(−2\), y agregarla a la ecuación (1). Luego realizamos los mismos pasos que arriba y encontramos el mismo resultado,\(0=0\).
Cuando un sistema es dependiente, podemos encontrar expresiones generales para las soluciones. Sumando ecuaciones (1) y (3), tenemos
\[\begin{align} 2x+y−3z &= 0 \nonumber \\[4pt]x−y+z &= 0 \nonumber \\[4pt] 3x−2z &= 0 \nonumber \end{align} \nonumber\]
Luego resolvemos la ecuación resultante para\(z\).
\[\begin{align} 3x−2z &= 0 \nonumber \\[4pt] z &= \dfrac{3}{2}x \nonumber \end{align} \nonumber\]
Volvemos a sustituir la expresión\(z\) en una de las ecuaciones y resolvemos para\(y\).
\[\begin{align} 2x+y−3 (\dfrac{3}{2}x) &= 0 \nonumber \\[4pt] 2x+y−\dfrac{9}{2}x &= 0 \nonumber \\[4pt] y &= \dfrac{9}{2}x−2x \nonumber \\[4pt] y &=\dfrac{5}{2}x \nonumber \end{align} \nonumber\]
Entonces la solución general es\(\left(x,\dfrac{5}{2}x,\dfrac{3}{2}x\right)\). En esta solución,\(x\) puede ser cualquier número real. Los valores de\(y\) y\(z\) dependen del valor seleccionado para\(x\).
Análisis
Como se muestra en la Figura\(\PageIndex{5}\), dos de los planos son iguales y se cruzan con el tercer plano en una línea. El conjunto de soluciones es infinito, ya que todos los puntos a lo largo de la línea de intersección satisfarán las tres ecuaciones.

Figura\(\PageIndex{5}\)
No, se puede escribir la solución genérica en términos de cualquiera de las variables, pero es común escribirla en términos de\(x\) y si es necesario\(x\) y\(y\).
Resuelve el siguiente sistema.
\[\begin{align} x+y+z &= 7 \nonumber \\[4pt] 3x−2y−z &= 4 \nonumber \\[4pt] x+6y+5z &= 24 \nonumber \end{align} \nonumber\]
- Contestar
-
Infinito número de soluciones de la forma\((x,4x−11,−5x+18)\).
Acceda a estos recursos en línea para una instrucción adicional y práctica con sistemas de ecuaciones en tres variables.
Conceptos clave
- Un conjunto de soluciones es un triple ordenado {(x, y, z)} que representa la intersección de tres planos en el espacio. Ver Ejemplo\(\PageIndex{1}\).
- Un sistema de tres ecuaciones en tres variables se puede resolver usando una serie de pasos que fuerzan a una variable a ser eliminada. Los pasos incluyen intercambiar el orden de las ecuaciones, multiplicar ambos lados de una ecuación por una constante distinta de cero y agregar un múltiplo distinto de cero de una ecuación a otra ecuación. Ver Ejemplo\(\PageIndex{2}\).
- Los sistemas de tres ecuaciones en tres variables son útiles para resolver muchos tipos diferentes de problemas del mundo real. Ver Ejemplo\(\PageIndex{3}\).
- Un sistema de ecuaciones en tres variables es inconsistente si no existe solución. Después de realizar operaciones de eliminación, el resultado es una contradicción. Ver Ejemplo\(\PageIndex{4}\).
- Los sistemas de ecuaciones en tres variables que son inconsistentes podrían resultar de tres planos paralelos, dos planos paralelos y un plano de intersección, o tres planos que intersectan los otros dos pero no en la misma ubicación.
- Un sistema de ecuaciones en tres variables depende si tiene un número infinito de soluciones. Después de realizar operaciones de eliminación, el resultado es una identidad. Ver Ejemplo\(\PageIndex{5}\).
- Los sistemas de ecuaciones en tres variables que son dependientes podrían resultar de tres planos idénticos, tres planos que se cruzan en una línea o dos planos idénticos que intersectan el tercero en una línea.


