9.E: Sistemas de Ecuaciones y Desigualdades (Ejercicios)

Última actualización
Guardar como PDF

Page ID: 121234

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

9.1: Sistemas de Ecuaciones Lineales: Dos Variables

Verbal

1) ¿Un sistema de ecuaciones lineales puede tener exactamente dos soluciones? Explique por qué o por qué no.

Contestar: No, puedes tener cero, uno, o infinitamente muchos. Examine las gráficas.

2) Si estás realizando un análisis de equilibrio para un negocio y sus ecuaciones de costos e ingresos son dependientes, explica qué significa esto para los márgenes de ganancia de la compañía.

3) Si estás resolviendo un análisis de equilibrio y obtienes un punto de equilibrio negativo, ¿explica qué significa esto para la empresa?

Contestar: Esto significa que no hay un punto de equilibrio realista. Para cuando la compañía produce una unidad ya están obteniendo ganancias.

4) Si estás resolviendo un análisis de equilibrio y no hay punto de equilibrio, explica lo que esto significa para la empresa. ¿Cómo deben asegurarse de que haya un punto de equilibrio?

5) Dado un sistema de ecuaciones, explicar al menos dos métodos diferentes para resolver ese sistema.

Contestar: Se puede resolver por sustitución (aislamiento$x$ o$y$), gráficamente, o por adición.

Algebraico

Para los ejercicios 6-10, determinar si el par ordenado dado es una solución al sistema de ecuaciones.

6)$\begin{align*} 5x-y &= 4\\ x+6y &= 2 \end{align*}\; \text{ and } (4,0)$

7)$\begin{align*} -3x-5y &= 13\\ -x+4y &= 10 \end{align*}\; \text{ and } (-6,1)$

Contestar: Sí

8)$\begin{align*} 3x+7y &= 1\\ 2x+4y &= 0 \end{align*}\; \text{ and } (2,3)$

9)$\begin{align*} -2x+5y &= 7\\ 2x+9y &= 7 \end{align*}\; \text{ and } (-1,1)$

Contestar: Sí

10)$\begin{align*} x+8y &= 43\\ 3x-2y &= -1 \end{align*}\; \text{ and } (3,5)$

Para los ejercicios 11-20, resolver cada sistema por sustitución.

11)$\begin{align*} x+5y &= 5\\ 2x+3y &= 4 \end{align*}$

Contestar: $(-1,2)$

12)$\begin{align*} 3x-2y &= 18\\ 5x+10y &= -10 \end{align*}$

13)$\begin{align*} 4x+2y &= -10\\ 3x+9y &= 0 \end{align*}$

Contestar: $(-3,1)$

14)$\begin{align*} 2x+4y &= -3.8\\ 9x-5y &= 1.3 \end{align*}$

15)$\begin{align*} -2x+3y &= 1.2\\ -3x-6y &= 1.8 \end{align*}$

Contestar: $\left ( -\dfrac{3}{5},0 \right )$

16)$\begin{align*} x-0.2y &= 1\\ -10x+2y &= 5 \end{align*}$

17)$\begin{align*} 3x+5y &= 9\\ 30x+50y &= -90 \end{align*}$

Contestar: No existen soluciones

18)$\begin{align*} -3x+y &= 2\\ 12x-4y &= -8 \end{align*}$

19)$\begin{align*} \dfrac{1}{2}x+\dfrac{1}{3}y &= 16\\ \dfrac{1}{6}x+\dfrac{1}{4}y &= 9 \end{align*}$

Contestar: $\left ( \dfrac{72}{5},\dfrac{132}{5} \right )$

20)$\begin{align*} -\dfrac{1}{4}x+\dfrac{3}{2}y &= 11\\ -\dfrac{1}{8}x+\dfrac{1}{3}y &= 3 \end{align*}$

Para los ejercicios 21-30, resuelve cada sistema por suma.

21)$\begin{align*} -2x+5y &= -42\\ 7x+2y &= 30 \end{align*}$

Contestar: $(6,-6)$

22)$\begin{align*} 6x-5y &= -34\\ 2x+6y &= 4 \end{align*}$

23)$\begin{align*} 5x-y &= -2.6\\ -4x-6y &= 1.4 \end{align*}$

Contestar: $\left ( -\dfrac{1}{2},\dfrac{1}{10} \right )$

24)$\begin{align*} 7x-2y &= 3\\ 4x+5y &= 3.25 \end{align*}$

25)$\begin{align*} -x+2y &= -1\\ 5x-10y &= 6 \end{align*}$

Contestar: No existen soluciones

26)$\begin{align*} 7x+6y &= 2\\ -28x-24y &= -8 \end{align*}$

27)$\begin{align*} \dfrac{5}{6}x+\dfrac{1}{4}y &= 0\\ \dfrac{1}{8}x-\dfrac{1}{2}y &= -\dfrac{43}{120} \end{align*}$

Contestar: $\left ( -\dfrac{1}{5},\dfrac{2}{3} \right )$

28)$\begin{align*} \dfrac{1}{3}x+\dfrac{1}{9}y &= \dfrac{2}{9}\\ -\dfrac{1}{2}x+\dfrac{4}{5}y &= -\dfrac{1}{3} \end{align*}$

29)$\begin{align*} -0.2x+0.4y &= 0.6\\ x-2y &= -3 \end{align*}$

Contestar: $\left ( x,\dfrac{x+3}{2} \right )$

30)$\begin{align*} -0.1x+0.2y &= 0.6\\ 5x-10y &= 1 \end{align*}$

Para los ejercicios 31-40, resuelve cada sistema por cualquier método.

31)$\begin{align*} 5x+9y &= 16\\ x+2y &= 4 \end{align*}$

Contestar: $(-4,4)$

32)$\begin{align*} 6x-8y &= -0.6\\ 3x+2y &= 0.9 \end{align*}$

33)$\begin{align*} 5x-2y &= 2.25\\ 7x-4y &= 3 \end{align*}$

Contestar: $\left ( \dfrac{1}{2},\dfrac{1}{8} \right )$

34)$\begin{align*} x-\dfrac{5}{12}y &= -\dfrac{55}{12}\\ -6x+\dfrac{5}{2}y &= \dfrac{55}{2} \end{align*}$

35)$\begin{align*} 7x-4y &= \dfrac{7}{6}\\ 2x+4y &= \dfrac{1}{3} \end{align*}$

Contestar: $\left ( \dfrac{1}{6},0 \right )$

36)$\begin{align*} 3x+6y &= 11\\ 2x+4y &= 9 \end{align*}$

37)$\begin{align*} \dfrac{7}{3}x-\dfrac{1}{6}y &= 2\\ -\dfrac{21}{6}x+\dfrac{3}{12}y &= -3 \end{align*}$

Contestar: $(x,2(7x-6))$

38)$\begin{align*} \dfrac{1}{2}x+\dfrac{1}{3}y &= \dfrac{1}{3}\\ \dfrac{3}{2}x+\dfrac{1}{4}y &= -\dfrac{1}{8} \end{align*}$

39)$\begin{align*} 2.2x+1.3y &= -0.1\\ 4.2x+4.2y &= 2.1 \end{align*}$

Contestar: $\left ( -\dfrac{5}{6},\dfrac{4}{3} \right )$

40)$\begin{align*} 0.1x+0.2y &= 2\\ 0.35x-0.3y &= 0 \end{align*}$

Gráfica

Para los ejercicios 41-45, grafica el sistema de ecuaciones y establece si el sistema es consistente, inconsistente o dependiente y si el sistema tiene una solución, ninguna solución o soluciones infinitas.

41)$\begin{align*} 3x-y &= 0.6\\ x-2y &= 1.3 \end{align*}$

Contestar: Consistente con una solución

42)$\begin{align*} -x+2y &= 4\\ 2x-4y &= 1 \end{align*}$

43)$\begin{align*} x+2y &= 7\\ 2x+6y &= 12 \end{align*}$

Contestar: Consistente con una solución

44)$\begin{align*} 3x-5y &= 7\\ x-2y &= 3 \end{align*}$

45)$\begin{align*} 3x-2y &= 5\\ -9x+6y &= -15 \end{align*}$

Contestar: Dependiente con infinitamente muchas soluciones

Tecnología

Para los ejercicios 46-50, utilice la función de intersección en un dispositivo gráfico para resolver cada sistema. Redondea todas las respuestas a la centésima más cercana.

46)$\begin{align*} 0.1x+0.2y &= 0.3\\ -0.3x+0.5y &= 1 \end{align*}$

47)$\begin{align*} -0.01x+0.12y &= 0.62\\ 0.15x+0.20y &= 0.52 \end{align*}$

Contestar: $(-3.08,4.91)$

48)$\begin{align*} 0.5x+0.3y &= 4\\ 0.25x-0.9y &= 0.46 \end{align*}$

49)$\begin{align*} 0.15x+0.27y &= 0.39\\ -0.34x+0.56y &= 1.8 \end{align*}$

Contestar: $(-1.52,2.29)$

50)$\begin{align*} -0.71x+0.92y &= 0.13\\ 0.83x+0.05y &= 2.1 \end{align*}$

Extensiones

Para los ejercicios 51-55, resuelve cada sistema en términos de$A, B, C, D,$ y$F$ dónde$A-F$ están números distintos de cero. Tenga en cuenta que$A\neq B$ y$AE\neq BD$.

51)$\begin{align*} x+y &= A\\ x-y &= B \end{align*}$

Contestar: $\left ( \dfrac{A+B}{2},\dfrac{A-B}{2} \right )$

52)$\begin{align*} x+Ay &= 1\\ x+By &= 1 \end{align*}$

53)$\begin{align*} Ax+y &= 0\\ Bx+y &= 1 \end{align*}$

Contestar: $\left ( \dfrac{-1}{A-B},\dfrac{A}{A-B} \right )$

54)$\begin{align*} Ax+By &= C\\ x+y &= 1 \end{align*}$

55)$\begin{align*} Ax+By &= C\\ Dx+Ey &= F \end{align*}$

Contestar: $\left ( \dfrac{CE-BF}{BD-AE},\dfrac{AF-CD}{BD-AE} \right )$

Aplicaciones del mundo real

Para los ejercicios 56-60, resuelva por la cantidad deseada.

56) Un negocio de animales de peluche tiene un costo total de producción$C=12x+30$ y una función de ingresos$R=20x$. Encuentra el punto de equilibrio.

57) Un restaurante de comida rápida tiene un costo de producción$C(x)=11x+120$ y una función de ingresos$R(x)=5x$. ¿Cuándo comienza la empresa a obtener ganancias?

Contestar: Nunca obtienen ganancias.

58) Una fábrica de teléfonos celulares tiene un costo de productiona$C(x)=150x+10,000$ y una función de ingresos$R(x)=200x$. ¿Cuál es el punto de equilibrio?

59) Un músico cobra$C(x)=64x+20,000$, donde$x$ está el número total de asistentes al concierto. El lugar cobra$\$80$ por boleto. Después de cuántas personas compran boletos, el lugar se equipara, y ¿cuál es el valor del total de boletos vendidos en ese momento?

Contestar: $(1,250, 100,000)$

60) Una fábrica de guitarras tiene un costo de producción$C(x)=75x+50,000$. Si la empresa necesita romper el equilibrio después de$150$ las unidades vendidas, ¿a qué precio deberían vender cada guitarra? Redondear al dólar más cercano y escribir la función de ingresos.

Para los ejercicios 61-77, utilizar un sistema de ecuaciones lineales con dos variables y dos ecuaciones para resolver.

61) Encuentra dos números cuya suma es$28$ y la diferencia es$13$.

Contestar: Los números son$7.5$ y$20.5$

62) Un número es$9$ más que otro número. Dos veces la suma de los dos números es$10$. Encuentra los dos números.

63) El costo inicial de un restaurante es$\$120,000$, y cada comida cuesta$\$10$ para que el restaurante haga. Si entonces se vende por cada comida$\$15$, ¿después de cuántas comidas se equivoca el restaurante?

Contestar: $24,000$

64) Una empresa de mudanzas cobra una tarifa plana de$\$150$, y un adicional$\$5$ por cada caja. Si un servicio de taxi cobrara$\$20$ por cada caja, ¿cuántas cajas necesitarías para que sea más económico usar la compañía de mudanzas, y cuál sería el costo total?

65) Un total de estudiantes universitarios de$1,595$ primer y segundo año se reunieron en un mitin de pep. El número de estudiantes de primer año superó al número de estudiantes de segundo año por$15$. ¿Cuántos estudiantes de primer y segundo año estuvieron presentes?

Contestar: $790$estudiantes de segundo$805$ año, estudiante de primer año

66)$276$ estudiantes matriculados en una clase de química de primer nivel. Al final del semestre,$5$ veces el número de alumnos que pasaron como fracasados. Encuentra el número de alumnos que aprobaron, y el número de alumnos que fallaron.

67) Había$130$ profesores en una conferencia. Si asistieron$18$ más mujeres que hombres, ¿cuántas de cada género asistieron a la conferencia?

Contestar: $56$hombres,$74$ mujeres

68) Un jeep y BMW ingresan a una autopista que corre de este-oeste en la misma salida con dirección opuesta. El jeep entró a la autopista$30$ minutos antes que lo hiciera el BMW, y viajó$7$ mph más lento que el BMW. Después de$2$ horas desde que el BMW ingresó a la autopista, los autos estaban$306.5$ a kilómetros de distancia. Encuentra la velocidad de cada auto, asumiendo que fueron conducidos con control de crucero.

69) Si un científico mezcló solución$10\%$ salina con solución$60\%$ salina para obtener$25$ galones de solución$40\%$ salina, ¿cuántos galones de$10\%$ y$60\%$ soluciones se mezclaron?

Contestar: $10$galones de$10\%$ solución,$15$ galones de$60\%$ solución

70) Una inversionista obtuvo el triple de ganancias de lo que obtuvo el año pasado. Si hizo$\$500,000.48$ total por ambos años, ¿cuánto ganaba en ganancias cada año?

71) Un inversionista que incursiona en bienes raíces invirtió$1.1$ millones de dólares en dos inversiones de tierra. En la primera inversión, Swan Peak, su retorno fue un$110\%$ incremento en el dinero que invirtió. En la segunda inversión, Riverside Community, ganó$50\%$ sobre lo que invirtió. Si ganaba$\$1$ millones en ganancias, ¿cuánto invirtió en cada uno de los tratos de tierras?

Contestar: Pico del cisne:$\$750,000$, Orilla:$\$350,000$

72) Si un inversionista invierte un total de$\$25,000$ dos bonos, uno que paga intereses$3\%$ simples, y el otro que paga$2\dfrac{7}{8}\%$ intereses, y el inversionista gana intereses$\$737.50$ anuales, ¿cuánto se invirtió en cada cuenta?

73) Si un inversionista invierte$\$23,000$ en dos bonos, uno que paga$4\%$ con intereses simples, y el otro pagando intereses$2\%$ simples, y el inversionista gana intereses$\$710.00$ anuales, ¿cuánto se invirtió en cada cuenta?

Contestar: $\$12,500$en la primera cuenta,$\$10,500$ en la segunda cuenta.

74) Los CD cuestan$\$5.96$ más que los DVD en All Bets Are Off Electronics. ¿Cuánto costarían los$6$ CD y$2$ DVDs si los$5$ CDs y$2$ DVDs costarían$\$127.73$?

75) Un empleado de tienda vendía$60$ pares de zapatillas deportivas. Los altos se venden por$\$98.99$ y los tops bajos se venden para$\$129.99$. Si los recibos de los dos tipos de ventas sumaron$\$6,404.40$, ¿cuántos de cada tipo de zapatilla se vendieron?

Contestar: Tops altos:$45$, Tops bajos:$15$

76) Un director de conciertos contó los recibos de$350$ entradas al día siguiente de un concierto. El precio de un boleto de estudiante era$\$12.50$, y el precio de un boleto de adulto era$\$16.00$. El registro confirma que$\$5,075$ fue acogido. ¿Cuántos boletos de estudiante y boletos de adultos se vendieron?

77) La entrada a un parque de diversiones para$4$ niños y$2$ adultos es$\$116.90$. Para$6$ niños y$3$ adultos, la admisión es$\$175.35$. Asumiendo un precio diferente para niños y adultos, ¿cuál es el precio del boleto infantil y el precio del boleto de adulto?

Contestar: Infinitamente muchas soluciones. Necesitamos más información.

9.2: Sistemas de Ecuaciones Lineales: Tres Variables

Verbal

1) ¿Un sistema lineal de tres ecuaciones puede tener exactamente dos soluciones? Explicar por qué o por qué no

Contestar: No, solo puede haber una, cero o infinitamente muchas soluciones.

2) Si un triple ordenado determinado resuelve el sistema de ecuaciones, ¿esa solución es única? Si es así, explique por qué. Si no, da un ejemplo donde no sea único.

3) Si un triple ordenado dado no resuelve el sistema de ecuaciones, ¿no hay solución? Si es así, explique por qué. Si no, da un ejemplo.

Contestar

No necesariamente. Podría haber cero, una, o infinitamente muchas soluciones. Por ejemplo, no$(0,0,0)$ es una solución al sistema de abajo, pero eso no quiere decir que no tenga solución.

$\begin{align*} 2x+3y-6z &= 1\\ -4x-6y+12z &= -2\\ x+2y+5z &= 10 \end{align*}$

4) Utilizando el método de adición, ¿hay una sola manera de resolver el sistema?

5) ¿Se puede explicar si sólo puede haber un método para resolver un sistema lineal de ecuaciones? En caso afirmativo, dar un ejemplo de tal sistema de ecuaciones. Si no, explica por qué no.

Contestar: Cada sistema de ecuaciones se puede resolver gráficamente, por sustitución y por adición. Sin embargo, los sistemas de tres ecuaciones se vuelven muy complejos de resolver gráficamente por lo que otros métodos suelen ser preferibles.

Algebraico

Para los ejercicios 6-10, determinar si el triple ordenado dado es la solución al sistema de ecuaciones.

6)$\begin{align*} 2x-6y+6z &= -12\\ x+4y+5z &= -1\\ -x+2y+3z &= -1 \end{align*}\; \; \text{ and }\; (0,1,-1)$

7)$\begin{align*} 6x-y+3z &= 6\\ 3x+5y+2z &= 0\\ x+y &= 0 \end{align*}\; \; \text{ and }\; (3,-3,-5)$

Contestar: No

8)$\begin{align*} 6x-7y+z &= 2\\ -x-y+3z &= 4\\ 2x+y-z &= 1 \end{align*}\; \; \text{ and }\; (4,2,-6)$

9)$\begin{align*} x-y &= 0\\ x-z &= 5\\ x-y+z &= -1 \end{align*}\; \; \text{ and }\; (4,4,-1)$

Contestar: Sí

10)$\begin{align*} -x-y+2z &= 3\\ 5x+8y-3z &= 4\\ -x+3y-5z &= -5 \end{align*}\; \; \text{ and }\; (4,1,-7)$

Para los ejercicios 11-16, resolver cada sistema por sustitución.

11)$\begin{align*} 3x-4y+2z &= -15\\ 2x+4y+z &= 16\\ 2x+3y+5z &= 20 \end{align*}$

Contestar: $(-1,4,2)$

12)$\begin{align*} 5x-2y+3z &= 20\\ 2x-4y-3z &= -9\\ x+6y-8z &= 21 \end{align*}$

13)$\begin{align*} 5x+2y+4z &= 9\\ -3x+2y+z &= 10\\ 4x-3y+5z &= -3 \end{align*}$

Contestar: $\left ( -\dfrac{85}{107},\dfrac{312}{107},\dfrac{191}{107} \right )$

14)$\begin{align*} 4x-3y+5z &= 31\\ -x+2y+4z &= 20\\ x+5y-2z &= -29 \end{align*}$

15)$\begin{align*} 5x-2y+3z &= 4\\ -4x+6y-7z &= -1\\ 3x+2y-z &= 4 \end{align*}$

Contestar: $\left ( 1,\dfrac{1}{2},0 \right )$

16)$\begin{align*} 4x+6y+9z &= 4\\ -5x+2y-6z &= 3\\ 7x-4y+3z &= -3 \end{align*}$

Para los ejercicios 17-45, resuelve cada sistema por eliminación gaussiana.

17)$\begin{align*} 2x-y+3z &= 17\\ -5x+4y-2z &= -46\\ 2y+5z &= -7 \end{align*}$

Contestar: $(4,-6,1)$

18)$\begin{align*} 5x-6y+3z &= 50\\ -x+4y &= 10\\ 2x-z &= 10 \end{align*}$

19)$\begin{align*} 2x+3y-6z &= 1\\ -4x-6y+12z &= -2\\ x+2y+5z &= 10 \end{align*}$

Contestar: $\left ( x,\dfrac{1}{27}(65-16x),\dfrac{x+28}{27} \right )$

20)$\begin{align*} 4x+6y-2z &= 8\\ 6x+9y-3z &= 12\\ -2x-3y+z &= -4 \end{align*}$

21)$\begin{align*} 2x+3y-4z &= 5\\ -3x+2y+z &= 11\\ -x+5y+3z &= 4 \end{align*}$

Contestar: $\left ( -\dfrac{45}{13},\dfrac{17}{13},-2 \right )$

22)$\begin{align*} 10x+2y-14z &= 8\\ -x-2y-4z &= -1\\ -12x-6y+6z &= -12 \end{align*}$

23)$\begin{align*} x+y+z &= 14\\ 2y+3z &= -14\\ -16y-24z &= -112 \end{align*}$

Contestar: No existen soluciones

24)$\begin{align*} 5x-3y+4z &= -1\\ -4x+2y-3z &= 0\\ -x+5y+7z &= -11 \end{align*}$

25)$\begin{align*} x+y+z &= 0\\ 2x-y+3z &= 0\\ x-z &= 0 \end{align*}$

Responder: $(0,0,0)$

26)$\begin{align*} 3x+2y-5z &= 6\\ 5x-4y+3z &= -12\\ 4x+5y-2z &= 15 \end{align*}$

27)$\begin{align*} x+y+z &= 0\\ 2x-y+3z &= 0\\ x-z &= 1 \end{align*}$

Responder: $\left ( \dfrac{4}{7},-\dfrac{1}{7},-\dfrac{3}{7} \right )$

28)$\begin{align*} 3x-\dfrac{1}{2}y-z &= -\dfrac{1}{2}\\ 4x+z &= 3\\ -x+\dfrac{3}{2}y &= \dfrac{5}{2} \end{align*}$

29)$\begin{align*} 6x-5y+6z &= 38\\ \dfrac{1}{5}x-\dfrac{1}{2}y+\dfrac{3}{5}z &= 1\\ -4x-\dfrac{3}{2}y-z &= -74 \end{align*}$

Responder: $(7,20,16)$

30)$\begin{align*} \dfrac{1}{2}x-\dfrac{1}{5}y+\dfrac{2}{5}z &= -\dfrac{13}{10}\\ \dfrac{1}{4}x-\dfrac{2}{5}y-\dfrac{1}{5}z &= -\dfrac{7}{20}\\ -\dfrac{1}{2}x-\dfrac{3}{4}y-\dfrac{1}{2}z &= -\dfrac{5}{4} \end{align*}$

31)$\begin{align*} -\dfrac{1}{3}x-\dfrac{1}{2}y-\dfrac{1}{4}z &= \dfrac{3}{4}\\ -\dfrac{1}{2}x-\dfrac{1}{4}y-\dfrac{1}{2}z &= 2\\ -\dfrac{1}{4}x-\dfrac{3}{4}y-\dfrac{1}{2}z &= -\dfrac{1}{2} \end{align*}$

Responder: $(-6,2,1)$

32)$\begin{align*} \dfrac{1}{2}x-\dfrac{1}{4}y+\dfrac{3}{4}z &= 0\\ \dfrac{1}{4}x-\dfrac{1}{10}y+\dfrac{2}{5}z &= -2\\ \dfrac{1}{8}x+\dfrac{1}{5}y-\dfrac{1}{8}z &= 2 \end{align*}$

33)$\begin{align*} \dfrac{4}{5}x-\dfrac{7}{8}y+\dfrac{1}{2}z &= 1\\ -\dfrac{4}{5}x-\dfrac{3}{4}y+\dfrac{1}{3}z &= -8\\ -\dfrac{2}{5}x-\dfrac{7}{8}y+\dfrac{1}{2}z &= -5 \end{align*}$

Responder: $(5,12,15)$

34)$\begin{align*} -\dfrac{1}{3}x-\dfrac{1}{8}y+\dfrac{1}{6}z &= -\dfrac{4}{3}\\ -\dfrac{2}{3}x-\dfrac{7}{8}y+\dfrac{1}{3}z &= -\dfrac{23}{3}\\ -\dfrac{1}{3}x-\dfrac{5}{8}y+\dfrac{5}{6}z &= 0 \end{align*}$

35)$\begin{align*} -\dfrac{1}{4}x-\dfrac{5}{4}y+\dfrac{5}{2}z &= -5\\ -\dfrac{1}{2}x-\dfrac{5}{3}y+\dfrac{5}{4}z &= \dfrac{55}{12}\\ -\dfrac{1}{3}x-\dfrac{1}{3}y+\dfrac{1}{3}z &= \dfrac{5}{3} \end{align*}$

Responder: $(-5,-5,-5)$

36)$\begin{align*} \dfrac{1}{40}x+\dfrac{1}{60}y+\dfrac{1}{80}z &= \dfrac{1}{100}\\ -\dfrac{1}{2}x-\dfrac{1}{3}y-\dfrac{1}{4}z &= -\dfrac{1}{5}\\ \dfrac{3}{8}x+\dfrac{3}{12}y+\dfrac{3}{16}z &= \dfrac{3}{20} \end{align*}$

37)$\begin{align*} 0.1x-0.2y+0.3z &= 2\\ 0.5x-0.1y+0.4z &= 8\\ 0.7x-0.2y+0.3z &= 8 \end{align*}$

Responder: $(10,10,10)$

38)$\begin{align*} 0.2x+0.1y-0.3z &= 0.2\\ 0.8x+0.4y-1.2z &= 0.1\\ 1.6x+0.8y-2.4z &= 0.2 \end{align*}$

39)$\begin{align*} 1.1x+0.7y-3.1z &= -1.79\\ 2.1x+0.5y-1.6z &= -0.13\\ 0.5x+0.4y-0.5z &= -0.07 \end{align*}$

Responder: $\left ( \dfrac{1}{2},\dfrac{1}{5},\dfrac{4}{5} \right )$

40)$\begin{align*} 0.5x-0.5y+0.5z &= 10\\ 0.2x-0.2y+0.2z &= 4\\ 0.1x-0.1y+0.1z &= 2 \end{align*}$

41)$\begin{align*} 0.1x+0.2y+0.3z &= 0.37\\ 0.1x-0.2y-0.3z &= -0.27\\ 0.5x-0.1y-0.3z &= -0.03 \end{align*}$

Responder: $\left ( \dfrac{1}{2},\dfrac{2}{5},\dfrac{4}{5} \right )$

42)$\begin{align*} 0.5x-0.5y-0.3z &= 0.13\\ 0.4x-0.1y-0.3z &= 0.11\\ 0.2x-0.8y-0.9z &= -0.32 \end{align*}$

43)$\begin{align*} 0.5x+0.2y-0.3z &= 1\\ 0.4x-0.6y+0.7z &= 0.8\\ 0.3x-0.1y-0.9z &= 0.6 \end{align*}$

Responder: $(2,0,0)$

44)$\begin{align*} 0.3x+0.3y+0.5z &= 0.6\\ 0.4x+0.4y+0.4z &= 1.8\\ 0.4x+0.2y+0.1z &= 1.6 \end{align*}$

45)$\begin{align*} 0.8x+0.8y+0.8z &= 2.4\\ 0.3x-0.5y+0.2z &= 0\\ 0.1x+0.2y+0.3z &= 0.6 \end{align*}$

Responder: $(1,1,1)$

Extensiones

Para los ejercicios 46-50, resolver el sistema para$x,y,$ y$z$.

46)$\begin{align*} x+y+z &= 3\\ \dfrac{x-1}{2}+\dfrac{y-3}{2}+\dfrac{z+1}{2} &= 0\\ \dfrac{x-2}{3}+\dfrac{y+4}{3}+\dfrac{z-3}{3} &= \dfrac{2}{3} \end{align*}$

47)$\begin{align*} 5x-3y-\dfrac{z+1}{2} &= \dfrac{1}{2}\\ 6x+\dfrac{y-9}{2}+2z &= -3\\ \dfrac{x+8}{2}-4y+z &= 4\end{align*}$

Responder: $\left ( \dfrac{128}{557},\dfrac{23}{557},\dfrac{428}{557} \right )$

48)$\begin{align*} \dfrac{x+4}{7}-\dfrac{y-1}{6}+\dfrac{z+2}{3} &= 1\\ \dfrac{x-2}{4}+\dfrac{y+1}{8}-\dfrac{z+8}{2} &= 0\\ \dfrac{x+6}{3}-\dfrac{y+2}{3}+\dfrac{z+4}{2} &= 3 \end{align*}$

49)$\begin{align*} \dfrac{x-3}{6}+\dfrac{y+2}{2}-\dfrac{z-3}{3} &= 2\\ \dfrac{x+2}{4}+\dfrac{y-5}{2}+\dfrac{z+4}{2} &= 1\\ \dfrac{x+6}{2}-\dfrac{y-3}{3}+z+1 &= 9 \end{align*}$

Responder: $(6,-1,0)$

50)$\begin{align*} \dfrac{x-1}{3}+\dfrac{y+3}{4}+\dfrac{z+2}{6} &= 1\\ 4x+3y-2z &= 11\\ 0.02x+0.015y-0.01z &= 0.065 \end{align*}$

Aplicaciones del mundo real

51) Tres números pares suman hasta$108$. Cuanto más pequeño es la mitad más grande y el número medio es$\dfrac{3}{4}$ el mayor. ¿Cuáles son los tres números?

Responder: $24, 36, 48$

52) Tres números suman hasta$147$. El número más pequeño es la mitad del número medio, que es la mitad del número más grande. ¿Cuáles son los tres números?

53) En una reunión familiar, sólo había familiares consanguíneos, consistentes en hijos, padres y abuelos, presentes. Había$400$ personas en total. Había el doble de padres que abuelos, y 50 hijos más que padres. ¿Cuántos hijos, padres y abuelos estuvieron presentes?

Responder: $70$abuelos,$140$ padres,$190$ hijos

54) Un refugio de animales tiene un total de$350$ animales compuestos por gatos, perros y conejos. Si el número de conejos es$5$ inferior a la mitad del número de gatos, y hay$20$ más gatos que perros, ¿cuántos de cada animal hay en el refugio?

55) Tu compañera de cuarto, Sarah, se ofreció a comprar comestibles para ti y tu otra compañera de cuarto. El total de la factura fue$\$82$. Se olvidó de guardar los recibos individuales pero recordó que tus abarrotes eran$\$0.05$ más baratos que la mitad de sus abarrotes, y que los comestibles de tu otra compañera de cuarto eran$\$2.10$ más que tus abarrotes. ¿Cuánto costó cada uno de su parte de los abarrotes?

Responder: Tu parte era$\$19.95$, la parte de Sarah era$\$40$, y la de tu otro compañero de cuarto lo era$\$22.05$.

56) Tu compañero de cuarto, John, se ofreció a comprar artículos para el hogar para ti y tu otro compañero de cuarto. Vives cerca de la frontera de tres estados, cada uno de los cuales tiene un impuesto sobre las ventas diferente. El monto total de dinero gastado fue$\$100.75$. Tus suministros fueron comprados con$5\%$ impuestos, John's con$8\%$ impuestos y tu tercer compañero de cuarto con impuesto a$9\%$ las ventas. El monto total de dinero gastado sin impuestos es$\$93.50$. Si sus suministros antes de impuestos eran$\$1$ más de la mitad de lo que eran los suministros de su tercer compañero de cuarto antes de impuestos, ¿cuánto gastó cada uno de ustedes? Da tu respuesta tanto con como sin impuestos.

57) Tres compañeros de trabajo trabajan para el mismo patrón. Sus trabajos son gerente de almacén, gerente de oficina y chofer de camión. La suma de los salarios anuales del encargado de almacén y del encargado de oficina es$\$82,000$. El encargado de oficina gana$\$4,000$ más que el camionero anualmente. Los salarios anuales del encargado de almacén y del chofer del camión suman$\$78,000$. ¿Cuál es el salario anual de cada uno de los compañeros de trabajo?

Responder: Hay infinitamente muchas soluciones; necesitamos más información

58) En un carnaval,$\$2,914.25$ en recibos se tomaron al final del día. El costo del boleto de un niño era$\$20.50$, un boleto de adulto era$\$29.75$, y un boleto para la tercera edad lo era$\$15.25$. Había el doble de personas mayores que adultos presentes, y$20$ más niños que personas mayores. ¿Cuántos boletos para niños, adultos y adultos mayores se vendieron?

59) Una banda local se agota para su concierto. Venden todos los$1,175$ boletos por un monedero total de$\$28,112.50$. Los boletos tenían un precio$\$20$ para boletos de estudiantes,$\$22.50$ para niños y$\$29$ para adultos. Si la banda vendió el doble de boletos para adultos que para niños, ¿cuántos de cada tipo se vendieron?

Responder: $500$estudiantes,$225$ niños y$450$ adultos

60) En una bolsa, un niño tiene$325$ monedas que valen$\$19.50$. Había tres tipos de monedas: centavos, monedas de cinco centavos y monedas de diez centavos. Si la bolsa contenía la misma cantidad de monedas de cinco centavos que las monedas de diez centavos, ¿cuántas de cada tipo de moneda había en la bolsa?

61) El año pasado, en el concesionario de autos Haven Pond, para un modelo particular de BMW, Jeep, y Toyota, uno podría comprar los tres autos por un total de$\$140,000$. Este año, debido a la inflación, los mismos autos costarían$\$151,830$. El costo del BMW aumentó en$8\%$, el Jeep por$5\%$, y el Toyota por$12\%$. Si el precio del Jeep del año pasado era$\$7,000$ menor que el precio del BMW del año pasado, ¿cuál fue el precio de cada uno de los tres autos del año pasado?

Responder: El BMW era$\$49,636$, el Jeep estaba$\$42,636$, y el Toyota lo estaba$\$47,727$.

62) Un recién graduado universitario aprovechó su educación empresarial e invirtió en tres inversiones inmediatamente después de graduarse. $\$80,500$Invirtió en tres cuentas, una que pagaba intereses$4\%$ simples, otra que pagaba intereses$3\dfrac{1}{8}\%$ simples y otra que pagaba intereses$2\dfrac{1}{2}\%$ simples. Ganó$\$2,670$ intereses al término de un año. Si el monto del dinero invertido en la segunda cuenta era cuatro veces el monto invertido en la tercera cuenta, ¿cuánto se invirtió en cada cuenta?

63) Heredas un millón de dólares. Lo inviertes todo en tres cuentas por un año. La primera cuenta paga$3\%$ compuesta anualmente, la segunda cuenta paga$4\%$ compuesta anualmente y la tercera cuenta paga$2\%$ compuesta anualmente. Después de un año, ganas$\$34,000$ en intereses. Si inviertes cuatro veces el dinero en la cuenta que paga en$3\%$ comparación con$2\%$, ¿cuánto invirtiste en cada cuenta?

Responder: $\$400,000$en la cuenta que paga$3\%$ intereses,$\$500,000$ en la cuenta que paga$4\%$ intereses y$\$100,000$ en la cuenta que paga$2\%$ intereses.

64) Heredas cien mil dólares. Lo inviertes todo en tres cuentas por un año. La primera cuenta paga$4\%$ compuesta anualmente, la segunda cuenta paga$3\%$ compuesta anualmente y la tercera cuenta paga$2\%$ compuesta anualmente. Después de un año, ganas$\$3,650$ en intereses. Si inviertes cinco veces el dinero en la cuenta que paga en$4\%$ comparación con$3\%$, ¿cuánto invirtiste en cada cuenta?

65) Los tres principales países en consumo de petróleo en un año determinado son los siguientes: Estados Unidos, Japón y China. En millones de barriles diarios, los tres principales países consumieron$39.8\%$ del petróleo consumido en el mundo. Estados Unidos consumió$0.7\%$ más de cuatro veces el consumo de China. Estados Unidos consumió$5\%$ más del triple del consumo de Japón. ¿Qué porcentaje del consumo mundial de petróleo consumieron Estados Unidos, Japón y China?

Responder: Estados Unidos consumió$26.3\%$$7.1\%$, Japón y China$6.4\%$ del petróleo mundial.

66) Los tres principales países en producción de petróleo en el mismo año son Arabia Saudita, Estados Unidos y Rusia. En millones de barriles diarios, los tres principales países producen$31.4\%$ del petróleo producido en el mundo. Arabia Saudita y Estados Unidos combinaron para$22.1\%$ de la producción mundial, y Arabia Saudita produjo$2\%$ más petróleo que Rusia. ¿Qué porcentaje de la producción mundial de petróleo produjo Arabia Saudita, Estados Unidos y Rusia?

67) Las tres principales fuentes de importaciones de petróleo para Estados Unidos en el mismo año fueron Arabia Saudita, México y Canadá. Los tres principales países contabilizaron las importaciones$47\%$ de petróleo. Estados Unidos importaba$1.8\%$ más de Arabia Saudita que de México, y$1.7\%$ más de Arabia Saudita que de Canadá. ¿Qué porcentaje de las importaciones de petróleo de Estados Unidos procedían de estos tres países?

Responder: Arabia Saudita importada$16.8\%$, Canadá$15.1\%$ importada y México$15.0\%$

68) Los tres principales productores de petróleo en Estados Unidos en un año determinado son el Golfo de México, Texas y Alaska. Las tres regiones fueron responsables$64\%$ de la producción petrolera de Estados Unidos. El Golfo de México y Texas se combinaron para$47\%$ la producción de petróleo. Texas produjo$3\%$ más que Alaska. ¿Qué porcentaje de la producción petrolera de Estados Unidos provino de estas regiones?

69) En un momento, en Estados Unidos, las$398$ especies de animales estaban en la lista de especies en peligro de extinción. Los grupos principales fueron mamíferos, aves y peces, los cuales comprendían las especies en peligro$55\%$ de extinción. Las aves representaban$0.7\%$ más que los peces, y los peces representaban$1.5\%$ más que los mamíferos. ¿Qué porcentaje de las especies en peligro de extinción provino de mamíferos, aves y peces?

Responder: Las aves eran$19.3\%$, los peces y los$18.6\%$ mamíferos eran$17.1\%$ de especies en peligro de extinción

70) El consumo de carne en Estados Unidos puede dividirse en tres categorías: carne roja, aves de corral y pescado. Si el pescado representa$4\%$ menos de una cuarta parte del consumo de aves de corral y el consumo de carne roja es$18.2\%$ mayor que el consumo de aves de corral, ¿cuáles son los porcentajes de consumo de carne?

9.3: Sistemas de Ecuaciones No Lineales y Desigualdades: Dos Variables

Verbal

1) Explicar si un sistema de dos ecuaciones no lineales puede tener exactamente dos soluciones. ¿Y exactamente tres? Si no, explica por qué no. Si es así, dé un ejemplo de dicho sistema, en forma de gráfico, y explique por qué su elección da dos o tres respuestas.

Responder: Un sistema no lineal podría ser representativo de dos círculos que se superponen y se cruzan en dos ubicaciones, de ahí dos soluciones. Un sistema no lineal podría ser representativo de una parábola y un círculo, donde el vértice de la parábola se encuentra con el círculo y las ramas también se cruzan con el círculo, de ahí tres soluciones.

2) Al graficar una desigualdad, ¿explicar por qué solo necesitamos probar un punto para determinar si una región entera es la solución?

3) Cuando graficas un sistema de desigualdades, ¿siempre habrá una región factible? Si es así, explique por qué. De no ser así, dar un ejemplo de una gráfica de desigualdades que no tenga una región factible. ¿Por qué no tiene una región factible?

Responder: No. No hace falta que haya una región factible. Considera un sistema que está delimitado por dos líneas paralelas. Una desigualdad representa la región por encima de la línea superior; la otra representa la región debajo de la línea inferior. En este caso, no se localizan puntos en el plano en ambas regiones; de ahí que no haya región factible.

4) Si graficas una función de ingresos y costos, explica cómo determinar en qué regiones hay ganancia.

5) Si realiza su análisis de equilibrio y hay más de una solución, explique cómo determinaría qué valores x son ganancias y cuáles no.

Responder: Elija cualquier número entre cada solución y conéctelo a$C(x)$ y$R(x)$. Si$C(x)<r(x)$>< span="">, then there is profit./span>

Algebraico

Para los ejercicios 6-10, resolver el sistema de ecuaciones no lineales mediante sustitución.

6)$\begin{align*} x+y &= 4\\ x^2 + y^2 &= 9 \end{align*}$

7)$\begin{align*} y &= x-3\\ x^2 + y^2 &= 9 \end{align*}$

Responder: $(0,-3)$,$(3,0)$

8)$\begin{align*} y &= x\\ x^2 + y^2 &= 9 \end{align*}$

9)$\begin{align*} y &= -x\\ x^2 + y^2 &= 9 \end{align*}$

Responder: $\left ( -\dfrac{3\sqrt{2}}{2},\dfrac{3\sqrt{2}}{2} \right )$,$\left ( \dfrac{3\sqrt{2}}{2},-\dfrac{3\sqrt{2}}{2} \right )$

10)$\begin{align*} x &= 2\\ x^2 - y^2 &= 9 \end{align*}$

Para los ejercicios 11-15, resolver el sistema de ecuaciones no lineales utilizando la eliminación.

11)$\begin{align*} 4x^2 - 9y^2 &= 36\\ 4x^2 + 9y^2 &= 36 \end{align*}$

Responder: $(-3,0)$,$(3,0)$

12)$\begin{align*} x^2 + y^2 &= 25\\ x^2 - y^2 &= 1 \end{align*}$

13)$\begin{align*} 2x^2 + 4y^2 &= 4\\ 2x^2 - 4y^2 &= 25x-10 \end{align*}$

Responder: $\left ( \dfrac{1}{4},-\dfrac{\sqrt{62}}{8} \right )$,$\left ( \dfrac{1}{4},\dfrac{\sqrt{62}}{8} \right )$

14)$\begin{align*} y^2 - x^2 &= 9\\ 3x^2 + 2y^2 &= 8 \end{align*}$

15)$\begin{align*} x^2 + y^2+\dfrac{1}{16} &= 2500\\ y &= 2x^2 \end{align*}$

Responder: $\left ( -\dfrac{\sqrt{398}}{4},\dfrac{199}{4} \right )$,$\left ( \dfrac{\sqrt{398}}{4},\dfrac{199}{4} \right )$

Para los ejercicios 16-23, utilizar cualquier método para resolver el sistema de ecuaciones no lineales.

16)$\begin{align*} -2x^2+y &= -5\\ 6x-y &= 9 \end{align*}$

17)$\begin{align*} -x^2+y &= 2\\ -x+y &= 2 \end{align*}$

Responder: $(0,2)$,$(1,3)$

18)$\begin{align*} x^2+y^2 &= 1\\ y &= 20x^2-1 \end{align*}$

19)$\begin{align*} x^2+y^2 &= 1\\ y &= -x^2 \end{align*}$

Responder: $\left ( -\sqrt{\dfrac{1}{2}(\sqrt{5}-1)},\dfrac{1}{2}\left (1-\sqrt{5} \right ) \right )$,$\left ( \sqrt{\dfrac{1}{2}(\sqrt{5}-1)},\dfrac{1}{2}\left (1-\sqrt{5} \right ) \right )$

20)$\begin{align*} 2x^3-x^2 &= y\\ y &= \dfrac{1}{2} -x \end{align*}$

21)$\begin{align*} 9x^2+25y^2 &= 225\\ (x-6)^2+y^2 &= 1 \end{align*}$

Responder: $(5,0)$

22)$\begin{align*} x^4-x^2 &= y\\ x^2+y &= 0 \end{align*}$

23)$\begin{align*} 2x^3-x^2 &= y\\ x^2+y &= 0 \end{align*}$

Responder: $(0,0)$

Para los ejercicios 24-38, utilice cualquier método para resolver el sistema no lineal.

24)$\begin{align*} x^2+y^2 &= 9\\ y &= 3-x^2 \end{align*}$

25)$\begin{align*} x^2-y^2 &= 9\\ x &= 3 \end{align*}$

Responder: $(3,0)$

26)$\begin{align*} x^2-y^2 &= 9\\ y &= 3 \end{align*}$

27)$\begin{align*} x^2-y^2 &= 9\\ x-y &= 0 \end{align*}$

Responder: No existen soluciones

28)$\begin{align*} -x^2+y &= 2\\ -4x+y &= -1 \end{align*}$

29)$\begin{align*} -x^2+y &= 2\\ 2y &= -x \end{align*}$

Responder: No existen soluciones

30)$\begin{align*} x^2+y^2 &= 25\\ x^2-y^2 &= 36 \end{align*}$

31)$\begin{align*} x^2+y^2 &= 1\\ y^2 &= x^2 \end{align*}$

Responder: $\left ( -\dfrac{\sqrt{2}}{2},-\dfrac{\sqrt{2}}{2} \right )$,$\left ( -\dfrac{\sqrt{2}}{2},\dfrac{\sqrt{2}}{2} \right )$,$\left ( \dfrac{\sqrt{2}}{2},-\dfrac{\sqrt{2}}{2} \right )$,$\left ( \dfrac{\sqrt{2}}{2},\dfrac{\sqrt{2}}{2} \right )$

32)$\begin{align*} 16x^2-9y^2+144 &= 0\\ y^2 + x^2 &= 16 \end{align*}$

33)$\begin{align*} 3x^2-y^2 &= 12\\ (x-1)^2 + y^2 &= 1 \end{align*}$

Responder: $(2,0)$

34)$\begin{align*} 3x^2-y^2 &= 12\\ (x-1)^2 + y^2 &= 4 \end{align*}$

35)$\begin{align*} 3x^2-y^2 &= 12\\ x^2 + y^2 &= 16 \end{align*}$

Responder: $(-\sqrt{7},-3)$,$(-\sqrt{7},3)$,$(\sqrt{7},-3)$,$(\sqrt{7},3)$

36)$\begin{align*} x^2-y^2-6x-4y-11 &= 0\\ -x^2 + y^2 &= 5 \end{align*}$

37)$\begin{align*} x^2+y^2-6y &= 7\\ x^2 + y &= 1 \end{align*}$

Responder: $\left ( -\sqrt{\dfrac{1}{2}(\sqrt{73}-5)},\dfrac{1}{2}\left (7-\sqrt{73} \right ) \right )$,$\left ( \sqrt{\dfrac{1}{2}(\sqrt{73}-5)},\dfrac{1}{2}\left (7-\sqrt{73} \right ) \right )$

38)$\begin{align*} x^2+y^2 &= 6\\ xy &= 1 \end{align*}$

Gráfica

Para los ejercicios 39-40, grafica la desigualdad.

39)$x^2+y<9$

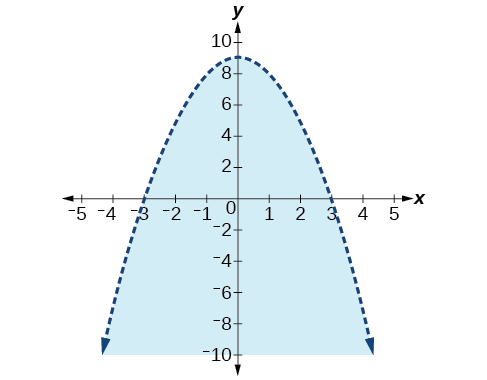
Responder: $CNX_Precalc_Figure_09_03_201.jpg$

40)$x^2+y^2<4$

Para los ejercicios 41-45, graficar el sistema de desigualdades. Etiquetar todos los puntos de intersección.

41)$\begin{align*} x^2 + y &<1 \\ y &>2x \end{align*}$

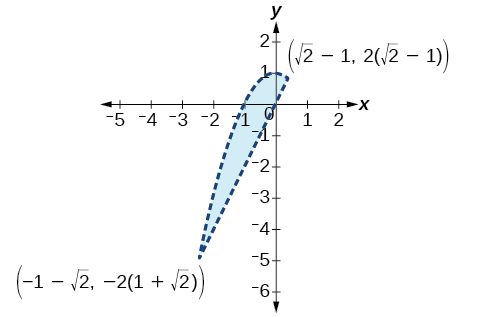
Responder: $CNX_Precalc_Figure_09_03_204.jpg$

42)$\begin{align*} x^2 + y &<-5 \\ y &>5x+10 \end{align*}$

43)$\begin{align*} x^2 + y^2 &<25 \\ 3x^2 - y^2 &>12 \end{align*}$

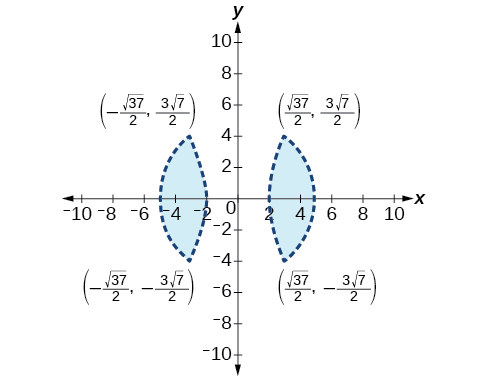
Responder: $CNX_Precalc_Figure_09_03_207.jpg$

44)$\begin{align*} x^2 - y^2 &>-4 \\ x^2 + y^2 &<12 \end{align*}$

45)$\begin{align*} x^2 + 3y^2 &>16 \\ 3x^2 - y^2 &<1 \end{align*}$

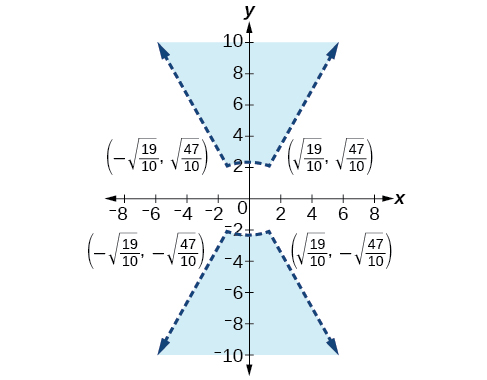
Responder: $CNX_Precalc_Figure_09_03_209.jpg$

Extensiones

Para los ejercicios 46-47, grafica la desigualdad.

46)$\begin{align*} y &\geq e^x \\ y &\leq \ln (x)+5 \end{align*}$

47)$\begin{align*} y &\leq -\log (x)\\ y &\leq e^x \end{align*}$

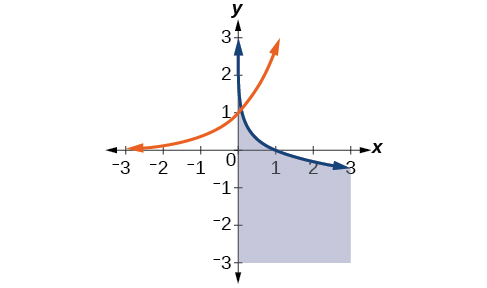
Responder: $CNX_Precalc_Figure_09_03_210.jpg$

Para los ejercicios 48-52, encuentra las soluciones a las ecuaciones no lineales con dos variables.

48)$\begin{align*} \dfrac{4}{x^2} + \dfrac{1}{y^2} &= 24\\ \dfrac{5}{x^2} - \dfrac{2}{y^2} + 4 &= 0 \end{align*}$

49)$\begin{align*} \dfrac{6}{x^2} - \dfrac{1}{y^2} &= 8\\ \dfrac{1}{x^2} - \dfrac{6}{y^2} &= \dfrac{1}{8} \end{align*}$

Responder: $\left ( -2\sqrt{\dfrac{70}{383}},-2\sqrt{\dfrac{35}{29}} \right )$,$\left ( -2\sqrt{\dfrac{70}{383}},2\sqrt{\dfrac{35}{29}} \right )$,$\left ( 2\sqrt{\dfrac{70}{383}},-2\sqrt{\dfrac{35}{29}} \right )$,$\left ( 2\sqrt{\dfrac{70}{383}},2\sqrt{\dfrac{35}{29}} \right )$

50)$\begin{align*} x^2 - xy + y^2 - 2 &= 0\\ x+3y &= 4 \end{align*}$

51)$\begin{align*} x^2 - xy - 2y^2 - 6 &= 0\\ x^2 + y^2 &= 1 \end{align*}$

Responder: No existe ninguna solución

52)$\begin{align*} x^2 + 4xy - 2y^2 - 6 &= 0\\ x &= y+2 \end{align*}$

Tecnología

Para los ejercicios 53-54, resolver el sistema de desigualdades. Use una calculadora para graficar el sistema para confirmar la respuesta.

53)$\begin{align*} xy &< 1\\ y &> \sqrt{x} \end{align*}$

Responder: $x=0$,$y>0$ y$0<1$>< span="">, $\sqrt{x} < y < \dfrac{1}{x}$/span>

54)$\begin{align*} x^2 + y &< 3\\ y &> 2x \end{align*}$

Aplicaciones del mundo real

Para los ejercicios 55-, construir un sistema de ecuaciones no lineales para describir el comportamiento dado, luego resolver para las soluciones solicitadas.

55) Dos números suman$300$. Un número es el doble del cuadrado del otro número. ¿Cuáles son los números?

Responder: $12,288$

56) Los cuadrados de dos números se suman a$360$. El segundo número es la mitad del valor del primer número al cuadrado. ¿Cuáles son los números?

57) Una empresa de computadoras portátiles ha descubierto sus funciones de costo e ingresos para cada día:$C(x)=3x^2-10x+200$ y$R(x)=-2x^2+100x+50$. Si quieren obtener ganancias, ¿cuál es la gama de laptops por día que deben producir? Redondear al número más cercano que generaría ganancias.

Responder: $2$-$20$ computadoras

58) Una compañía de telefonía celular tiene las siguientes funciones de costo e ingresos:$C(x)=8x^2-600x+21,500$ y$R(x)=-3x^2+480x$. ¿Cuál es la gama de celulares que deben producir cada día para que haya ganancias? Redondear al número más cercano que genere ganancias.

9.4: Fracciones Parciales

Verbal

1) ¿Se puede descomponer algún cociente de polinomios en al menos dos fracciones parciales? Si es así, explique por qué, y si no, dé un ejemplo de tal fracción.

Responder: No, un cociente de polinomios sólo puede descomponerse si se puede factorizar el denominador. Por ejemplo,$\dfrac{1}{x^2+1}$ no se puede descomponer porque no se puede factorizar el denominador.

2) ¿Puede explicar por qué una descomposición parcial de una fracción es única? (Pista: Piense en ello como un sistema de ecuaciones.)

3) ¿Se puede explicar cómo verificar gráficamente una descomposición parcial de una fracción?

Responder: Grafica ambos lados y asegúrate de que sean iguales.

4) No está seguro si descompuso correctamente la fracción parcial correctamente. Explica cómo podrías volver a verificar tu respuesta.

5) Una vez que se tiene un sistema de ecuaciones generado por la descomposición parcial de la fracción, ¿puede explicar otro método para resolverlo? Por ejemplo si lo tuvieras finalmente$\dfrac{7x+13}{3x^2+8x+15}=\dfrac{A}{x+1}+\dfrac{B}{3x+5}$ simplificamos a$7x+13=A(3x+5)+B(x+1)$. Explica cómo podrías elegir inteligentemente un$x$ -valor que eliminará cualquiera$A$ o$B$ y resolverá por$A$ y$B$.

Responder: Si elegimos$x=-1$, entonces el$B$ -término desaparece, haciéndonos saber de inmediato eso$A=3$. Alternativamente, podríamos enchufar$x=-\dfrac{5}{3}$, dándonos un$B$ -valor de$-2$.

Algebraico

Para los ejercicios 6-19, encontrar la descomposición de la fracción parcial para los factores lineales no repetitivos.

6)$\dfrac{5x+16}{x^2+10x+24}$

7)$\dfrac{3x-79}{x^2-5x-24}$

Responder: $\dfrac{8}{x+3}-\dfrac{5}{x-8}$

8)$\dfrac{-x-24}{x^2-2x-24}$

9)$\dfrac{10x+47}{x^2+7x+10}$

Responder: $\dfrac{1}{x+5}+\dfrac{9}{x+2}$

10)$\dfrac{x}{6x^2+25x+25}$

11)$\dfrac{32x-11}{20x^2-13x+2}$

Responder: $\dfrac{3}{5x-2}+\dfrac{4}{4x-1}$

12)$\dfrac{x+1}{x^2+7x+10}$

13)$\dfrac{5x}{x^2-9}$

Responder: $\dfrac{5}{2(x+3)}+\dfrac{5}{2(x-3)}$

14)$\dfrac{10x}{x^2-25}$

15)$\dfrac{6x}{x^2-4}$

Responder: $\dfrac{3}{x+2}+\dfrac{3}{x-2}$

16)$\dfrac{2x-3}{x^2-6x+5}$

17)$\dfrac{4x-1}{x^2-x-6}$

Responder: $\dfrac{9}{5(x+2)}+\dfrac{11}{5(x-3)}$

18)$\dfrac{4x+3}{x^2+8x+15}$

19)$\dfrac{3x-1}{x^2-5x+6}$

Responder: $\dfrac{8}{x-3}-\dfrac{5}{x-2}$

Para los ejercicios 20-30, encontrar la descomposición de la fracción parcial para los factores lineales repetitivos.

20)$\dfrac{-5x-19}{(x+4)^2}$

21)$\dfrac{x}{(x-2)^2}$

Responder: $\dfrac{1}{x-2}-\dfrac{2}{(x-2)^2}$

22)$\dfrac{7x+14}{(x+3)^2}$

23)$\dfrac{-24x-27}{(4x+5)^2}$

Responder: $-\dfrac{6}{4x+5}+\dfrac{3}{(4x+5)^2}$

24)$\dfrac{-24x-27}{(6x-7)^2}$

25)$\dfrac{5-x}{(x-7)^2}$

Responder: $-\dfrac{1}{x-7}-\dfrac{2}{(x-7)^2}$

26)$\dfrac{5x+14}{2x^2+12x+18}$

27)$\dfrac{5x^2+20x+8}{2x(x+1)^2}$

Responder: $\dfrac{4}{x}-\dfrac{3}{2(x+1)}+\dfrac{7}{2(x+1)^2}$

28)$\dfrac{4x^2+55x+25}{5x(3x+5)^2}$

29)$\dfrac{54x^3+127x^2+80x+16}{2x^2(3x+2)^2}$

Responder: $\dfrac{4}{x}+\dfrac{2}{x^2}-\dfrac{3}{3x+2}+\dfrac{7}{2(3x+2)^2}$

30)$\dfrac{x^3-5x^2+12x+144}{x^2(x^2+12x+36)}$

Para los ejercicios 31-43, encontrar la descomposición de la fracción parcial para el factor cuadrático irreducible no repetitivo.

31)$\dfrac{4x^2+6x+11}{(x+2)(x^2+x+3)}$

Responder: $\dfrac{x+1}{x^2+x+3}+\dfrac{3}{(x+2)}$

32)$\dfrac{4x^2+9x+23}{(x-1)(x^2+6x+11)}$

33)$\dfrac{-2x^2+10x+4}{(x-1)(x^2+3x+8)}$

Responder: $\dfrac{4-3x}{x^2+3x+8}+\dfrac{1}{(x-1)}$

34)$\dfrac{x^2+3x+1}{(x+1)(x^2+5x-2)}$

35)$\dfrac{4x^2+17x-1}{(x+3)(x^2+6x+1)}$

Responder: $\dfrac{2x-1}{x^2+6x+1}+\dfrac{2}{(x+3)}$

36)$\dfrac{4x^2}{(x+5)(x^2+7x-5)}$

37)$\dfrac{4x^2+x+3}{x^3 - 1}$

Responder: $\dfrac{1}{x^2+x+1}+\dfrac{4}{(x-1)}$

38)$\dfrac{-5x^2+18x-4}{x^3 + 8}$

39)$\dfrac{3x^2-7x+33}{x^3 + 27}$

Responder: $\dfrac{2}{x^2-3x+9}+\dfrac{3}{(x+3)}$

40)$\dfrac{x^2+2x+40}{x^3 - 125}$

41)$\dfrac{4x^2+4x+12}{8x^3 - 27}$

Responder: $-\dfrac{1}{4x^2+6x+9}+\dfrac{1}{(2x-3)}$

42)$\dfrac{-50x^2+5x-3}{125x^3 - 1}$

43)$\dfrac{-2x^3-30x^2+36x+216}{x^4 + 216x}$

Responder: $\dfrac{1}{x}+\dfrac{1}{x+6}-\dfrac{4x}{x^2-6x+36}$

Para los ejercicios 44-54, encontrar la descomposición de la fracción parcial para el factor cuadrático repetitivo irreducible.

44)$\dfrac{3x^3+2x^2+14x+15}{(x^2 + 4)^2}$

45)$\dfrac{x^3+6x^2+5x+9}{(x^2 + 1)^2}$

Responder: $\dfrac{x+6}{x^2+1}+\dfrac{4x+3}{(x^2+1)^2}$

46)$\dfrac{x^3-x^2+x-1}{(x^2 - 3)^2}$

47)$\dfrac{x^2+5x+5}{(x+2)^2}$

Responder: $\dfrac{x+1}{x+2}+\dfrac{2x+3}{(x+2)^2}$

48)$\dfrac{x^3+2x^2+4x}{(x^2+2x+9)^2}$

49)$\dfrac{x^2+25}{(x^2+3x+25)^2}$

Responder: $\dfrac{1}{x^2+3x+25}-\dfrac{3x}{(x^2+3x+25)^2}$

50)$\dfrac{2x^3+11x+7x+70}{(2x^2+x+14)^2}$

51)$\dfrac{5x+2}{x(x^2+4)^2}$

Responder: $\dfrac{1}{8x}-\dfrac{x}{8(x^2+4)}+\dfrac{10-x}{8(x^2+4)^2}$

52)$\dfrac{x^4+x^3+8x^2+6x+36}{x(x^2+6)^2}$

53)$\dfrac{2x-9}{(x^2-x)^2}$

Responder: $-\dfrac{16}{x}-\dfrac{9}{x^2}+\dfrac{16}{x-1}-\dfrac{7}{(x-1)^2}$

54)$\dfrac{5x^3-2x+1}{(x^2+2x)^2}$

Extensiones

Para los ejercicios 55-56, encuentra la expansión parcial de la fracción.

55)$\dfrac{x^2+4}{(x+1)^3}$

Responder: $\dfrac{1}{x+1}-\dfrac{2}{(x+1)^2}+\dfrac{5}{(x+1)^3}$

56)$\dfrac{x^3-4x^2+5x+4}{(x-2)^3}$

Para los ejercicios 57-59, realiza la operación y luego encuentra la descomposición parcial de la fracción.

57)$\dfrac{7}{x+8}+\dfrac{5}{x-2}-\dfrac{x-1}{x^2-6x-16}$

Responder: $\dfrac{5}{x-2}-\dfrac{3}{10(x+2)}+\dfrac{7}{x+8}-\dfrac{7}{10(x-8)}$

58)$\dfrac{1}{x-4}-\dfrac{3}{x+6}-\dfrac{2x+7}{x^2+2x-24}$

59)$\dfrac{2x}{x^2-16}-\dfrac{1-2x}{x^2+6x+8}-\dfrac{x-5}{x^2-4x}$

Responder: $-\dfrac{5}{4x}-\dfrac{5}{2(x+2)}+\dfrac{11}{2(x+4)}+\dfrac{5}{4(x+4)}$

9.5: Matrices y Operaciones Matriciales

Verbal

1) ¿Podemos agregar dos matrices cualesquiera juntas? Si es así, explique por qué; si no, explique por qué no y dé un ejemplo de dos matrices que no se pueden sumar.

Responder: No, deben tener las mismas dimensiones. Un ejemplo incluiría dos matrices de diferentes dimensiones. No se pueden agregar las dos matrices siguientes porque la primera es una$2\times 2$ matriz y la segunda es una$2\times 3$. $\begin{bmatrix} 1 & 2\\ 3 & 4 \end{bmatrix} + \begin{bmatrix} 6 & 5 & 4\\ 3 & 2 & 1 \end{bmatrix}$no tiene suma.

2) ¿Podemos multiplicar cualquier matriz de columna por cualquier matriz de filas? Explique por qué o por qué no.

3) ¿Se$BA$ pueden definir tanto$AB$ los productos como? Si es así, explique cómo; si no, explique por qué.

Responder: Sí, si se definirán las dimensiones de$A$$B$ son$m\times n$ y las dimensiones de son$n\times m$ ambos productos.

4) ¿Se pueden multiplicar dos matrices del mismo tamaño? Si es así, explique por qué, y si no, explique por qué no y dé un ejemplo de dos matrices del mismo tamaño que no se puedan multiplicar juntas.

5) ¿La multiplicación matricial conmuta? Es decir, ¿no$AB=BA$? Si es así, demuestre por qué lo hace. Si no, explica por qué no lo hace.

Responder: No necesariamente. Para encontrar$AB$, multiplicamos la primera fila de$A$ por la primera columna de$B$ para obtener la primera entrada de$AB$. Para encontrar$BA$, multiplicamos la primera fila de$B$ por la primera columna de$A$ para obtener la primera entrada de$BA$. Así, si esos son desiguales, entonces la multiplicación matricial no conmuta.

Algebraico

Para los ejercicios 6-11, use las matrices a continuación y realice la suma o resta de la matriz. Indicar si la operación es indefinida.

\[A=\begin{bmatrix} 1 & 3\\ 0 & 7 \end{bmatrix}, B=\begin{bmatrix} 2 & 14\\ 22 & 6 \end{bmatrix}, C=\begin{bmatrix} 1 & 5\\ 8 & 92\\ 12 & 6 \end{bmatrix}, D=\begin{bmatrix} 10 & 14\\ 7 & 2\\ 5 & 61 \end{bmatrix}, E=\begin{bmatrix} 6 & 12\\ 14 & 5 \end{bmatrix}, F=\begin{bmatrix} 0 & 9\\ 78 & 17\\ 15 & 4 \end{bmatrix} \nonumber\]

6)$A+B$

7)$C+D$

Responder: $\begin{bmatrix} 11 & 19\\ 15 & 94\\ 17 & 67 \end{bmatrix}$

8)$A+C$

9)$B-E$

Responder: $\begin{bmatrix} -4 & 2\\ 8 & 1 \end{bmatrix}$

10)$C+F$

11)$D-B$

Responder: Indefinido; las dimensiones no coinciden

Para los ejercicios 12-17, utilice las matrices a continuación para realizar la multiplicación escalar.

\[A=\begin{bmatrix} 4 & 6\\ 13 & 12 \end{bmatrix}, B=\begin{bmatrix} 3 & 9\\ 21 & 12\\ 0 & 64 \end{bmatrix}, C=\begin{bmatrix} 16 & 3 & 7 & 18\\ 90 & 5 & 3 & 29 \end{bmatrix}, D=\begin{bmatrix} 18 & 12 & 13\\ 8 & 14 & 6\\ 7 & 4 & 21 \end{bmatrix} \nonumber\]

12)$5A$

13)$3B$

Responder: $\begin{bmatrix} 9 & 27\\ 63 & 36\\ 0 & 192 \end{bmatrix}$

14)$-2B$

15)$-4C$

Responder: $\begin{bmatrix} -64 & -12 & -28 & -72\\ -360 & -20 & -12 & -116 \end{bmatrix}$

16)$\dfrac{1}{2}C$

17)$100D$

Responder: $\begin{bmatrix} 1,800 & 1,200 & 1,300\\ 800 & 1,400 & 600\\ 700 & 400 & 2,100 \end{bmatrix}$

Para los ejercicios 18-23, utilice las matrices a continuación para realizar la multiplicación de matrices.

\[A=\begin{bmatrix} -1 & 5\\ 3 & 2 \end{bmatrix}, B=\begin{bmatrix} 3 & 6 & 4\\ -8 & 0 & 12 \end{bmatrix}, C=\begin{bmatrix} 4 & 10\\ -2 & 6\\ 5 & 9 \end{bmatrix}, D=\begin{bmatrix} 2 & -3 & 12\\ 9 & 3 & 1\\ 0 & 8 & -10 \end{bmatrix} \nonumber\]

18)$AB$

19)$BC$

Responder: $\begin{bmatrix} 20 & 102\\ 28 & 28 \end{bmatrix}$

20)$CA$

21)$BD$

Responder: $\begin{bmatrix} 60 & 41 & 2\\ -16 & 120 & -216 \end{bmatrix}$

22)$DC$

23)$CB$

Responder: $\begin{bmatrix} -68 & 24 & 136\\ -54 & -12 & 64\\ -57 & 30 & 128 \end{bmatrix}$

Para los ejercicios 24-29, utilice las matrices a continuación para realizar la operación indicada si es posible. Si no es posible, explique por qué no se puede realizar la operación.

\[A=\begin{bmatrix} 2 & -5\\ 6 & 7 \end{bmatrix}, B=\begin{bmatrix} -9 & 6\\ -4 & 2 \end{bmatrix}, C=\begin{bmatrix} 0 & 9\\ 7 & 1 \end{bmatrix}, D=\begin{bmatrix} -8 & 7 & -5\\ 4 & 3 & 2\\ 0 & 9 & 2 \end{bmatrix}, E=\begin{bmatrix} 4 & 5 & 3\\ 7 & -6 & -5\\ 1 & 0 & 9 \end{bmatrix} \nonumber\]

24)$A+B-C$

25)$4A+5D$

Responder: Indefinido; las dimensiones no coinciden.

26)$2C+B$

27)$3D+4E$

Responder: $\begin{bmatrix} -8 & 41 & -3\\ 40 & -15 & -14\\ 4 & 27 & 42 \end{bmatrix}$

28)$C-0.5D$

29)$100D-10E$

Responder: $\begin{bmatrix} -840 & 650 & -530\\ 330 & 360 & 250\\ -10 & 900 & 110 \end{bmatrix}$

Para los ejercicios 30-40, utilice las matrices a continuación para realizar la operación indicada si es posible. Si no es posible, explique por qué no se puede realizar la operación. (Pista:$A^2=A\cdot A$)

\[A=\begin{bmatrix} -10 & 20\\ 5 & 25 \end{bmatrix}, B=\begin{bmatrix} 40 & 10\\ -20 & 30 \end{bmatrix}, C=\begin{bmatrix} -1 & 0\\ 0 & -1\\ 1 & 0 \end{bmatrix} \nonumber\]

30)$AB$

31)$BA$

Responder: $\begin{bmatrix} -350 & 1,050\\ 350 & 350 \end{bmatrix}$

32)$CA$

33)$BC$

Responder: Indefinido; las dimensiones internas no coinciden.

34)$A^2$

35)$B^2$

Responder: $\begin{bmatrix} 1,400 & 700\\ -1,400 & 700 \end{bmatrix}$

36)$C^2$

37)$B^2A^2$

Responder: $\begin{bmatrix} 332,500 & 927,500\\ -227,500 & 87,500 \end{bmatrix}$

38)$A^2B^2$

39)$(AB)^2$

Responder: $\begin{bmatrix} 490,000 & 0\\ 0 & 490,000 \end{bmatrix}$

40)$(BA)^2$

Para los ejercicios 41-49, utilice las matrices a continuación para realizar la operación indicada si es posible. Si no es posible, explique por qué no se puede realizar la operación. (Pista:$A^2=A\cdot A$)

\[A=\begin{bmatrix} 1 & 0\\ 2 & 3 \end{bmatrix}, B=\begin{bmatrix} -2 & 3 & 4\\ -1 & 1 & -5 \end{bmatrix}, C=\begin{bmatrix} 0.5 & 0.1\\ 1 & 0.2\\ -0.5 & 0.3 \end{bmatrix}, D=\begin{bmatrix} 1 & 0 & -1\\ -6 & 7 & 5\\ 4 & 2 & 1 \end{bmatrix} \nonumber\]

41)$AB$

Responder: $\begin{bmatrix} -2 & 3 & 4\\ -7 & 9 & -7 \end{bmatrix} \nonumber$

42)$BA$

43)$BD$

Responder: $\begin{bmatrix} -4 & 29 & 21\\ -27 & -3 & 1 \end{bmatrix} \nonumber$

44)$DC$

45)$D^2$

Responder: $\begin{bmatrix} -3 & -2 & -2\\ -28 & 59 & 46\\ -4 & 16 & 7 \end{bmatrix} \nonumber$

46)$A^2$

47)$D^3$

Responder: $\begin{bmatrix} 1 & -18 & -9\\ -198 & 505 & 369\\ -72 & 126 & 91 \end{bmatrix} \nonumber$

48)$(AB)C$

49)$A(BC)$

Responder: $\begin{bmatrix} 0 & 1.6\\ 9 & -1 \end{bmatrix} \nonumber$

Tecnología

Para los ejercicios 50-54, utilice las matrices a continuación para realizar la operación indicada si es posible. Si no es posible, explique por qué no se puede realizar la operación. Usa una calculadora para verificar tu solución.

\[A=\begin{bmatrix} -2 & 0 & 9\\ 1 & 8 & -3\\ 0.5 & 4 & 5 \end{bmatrix}, B=\begin{bmatrix} 0.5 & 3 & 0\\ -4 & 1 & 6\\ 8 & 7 & 2 \end{bmatrix}, C=\begin{bmatrix} 1 & 0 & 1\\ 0 & 1 & 0\\ 1 & 0 & 1 \end{bmatrix} \nonumber\]

50)$AB$

51)$BA$

Responder: $\begin{bmatrix} 2 & 24 & -4.5\\ 12 & 32 & -9\\ -8 & 64 & 61 \end{bmatrix} \nonumber$

52)$CA$

53)$BC$

Responder: $\begin{bmatrix} 0.5 & 3 & 0.5\\ 2 & 1 & 2\\ 10 & 7 & 10 \end{bmatrix} \nonumber$

54)$ABC$

Extensiones

Para los ejercicios 55-, utilice la matriz a continuación para realizar la operación indicada en la matriz dada.

\[B=\begin{bmatrix} 1 & 0 & 0\\ 0 & 0 & 1\\ 0 & 1 & 0 \end{bmatrix} \nonumber\]

55)$B^2$

Responder: $\begin{bmatrix} 1 & 0 & 0\\ 0 & 1 & 0\\ 0 & 0 & 1 \end{bmatrix} \nonumber$

56)$B^3$

57)$B^4$

Responder: $\begin{bmatrix} 1 & 0 & 0\\ 0 & 1 & 0\\ 0 & 0 & 1 \end{bmatrix} \nonumber$

58)$B^5$

59) Usando las preguntas anteriores, encuentre una fórmula para$B^n$. Pruebe la fórmula para$B^{201}$ y$B^{202}$, usando una calculadora.

Responder: $B^n=\begin{cases} \begin{bmatrix} 1 & 0 & 0\\ 0 & 1 & 0\\ 0 & 0 & 1 \end{bmatrix}, & n\text{ even }\\ \\ \begin{bmatrix} 1 & 0 & 0\\ 0 & 0 & 1\\ 0 & 1 & 0 \end{bmatrix}, & n\text{ odd } \end{cases}$

9.6: Resolviendo sistemas con eliminación gaussiana

Verbal

1) ¿Se puede escribir algún sistema de ecuaciones lineales como una matriz aumentada? Explique por qué o por qué no. Explique cómo escribir esa matriz aumentada.

Responder: Sí. Para cada fila, los coeficientes de las variables se escriben a través de la fila correspondiente, y se coloca una barra vertical; luego las constantes se colocan a la derecha de la barra vertical.

2) ¿Se puede escribir alguna matriz como un sistema de ecuaciones lineales? Explique por qué o por qué no. Explique cómo escribir ese sistema de ecuaciones.

3) ¿Existe solo un método correcto para usar operaciones de fila en una matriz? Trate de explicar dos operaciones de fila diferentes posibles para resolver la matriz aumentada$\left [ \begin{array}{cc|c} 9 & 3 & 0\\ 1 & -2 & 6\\ \end{array} \right ]$.

Responder

No, existen numerosos métodos correctos para usar operaciones de fila en una matriz. Dos formas posibles son las siguientes:

Intercambia las filas 1 y 2. Entonces$R_2=R_2-9R_1$.
$R_2=R_1-9R_2$. Luego divide la fila 1 por$9$.

4) ¿Se puede resolver una matriz cuya entrada está$0$ en la diagonal? Explique por qué o por qué no. ¿Qué harías para remediar la situación?

5) ¿Puede una matriz que tenga$0$ entradas para una fila completa tener una solución? Explique por qué o por qué no.

Responder: No. Una matriz con$0$ entradas para una fila entera tendría cero o infinitamente muchas soluciones.

Algebraico

Para los ejercicios 6-10, escriba la matriz aumentada para el sistema lineal.

6)$\begin{align*} 8x-37y &= 8\\ 2x+12y &= 3 \end{align*}$

7)$\begin{align*} 16y &= 4\\ 9x-y &= 2 \end{align*}$

Responder: $\left [ \begin{array}{cc|c} 0 & 16 & 4\\ 9 & -1 & 2\\ \end{array} \right ]$

8)$\begin{align*} 3x+2y+10z &= 3\\ -6x+2y+5z &= 13\\ 4x+z &= 18 \end{align*}$

9)$\begin{align*} x+5y+8z &= 19\\ 12x+3y &= 4\\ 3x+4y+9z &= -7 \end{align*}$

Responder: $\left [ \begin{array}{ccc|c} 1 & 5 & 8 & 16\\ 12 & 3 & 0 & 4\\ 3 & 4 & 9 & -7\end{array} \right ]$

10)$\begin{align*} 6x+12y+16z &= 4\\ 19x-5y+3z &= -9\\ x+2y &= -8 \end{align*}$

Para los ejercicios 11-15, escriba el sistema lineal a partir de la matriz aumentada.

11)$\left [ \begin{array}{cc|c} -2 & 5 & 5\\ 6 & -18 & 26\\ \end{array} \right ]$

Responder: $\begin{align*} -2x+5y &= 5\\ 6x-18y &= 26 \end{align*}$

12)$\left [ \begin{array}{cc|c} 3 & 4 & 10\\ 10 & 17 & 439\\ \end{array} \right ]$

13)$\left [ \begin{array}{ccc|c} 3 & 2 & 0 & 3\\ -1 & -9 & 4& -1\\ 8 & 5 & 7 & 8\\ \end{array} \right ]$

Responder: $\begin{align*} 3x+2y &= 13\\ -x-9y+4z &= 53\\ 8x+5y+7z &= 80 \end{align*}$

14)$\left [ \begin{array}{ccc|c} 8 & 29 & 1 & 43\\ -1 & 7 & 5 & 38\\ 0 & 0 & 3 & 10\\ \end{array} \right ]$

15)$\left [ \begin{array}{ccc|c} 4 & 5 & -2 & 12\\ 0 & 1 & 58 & 2\\ 8 & 7 & -3 & -5\\ \end{array} \right ]$

Responder: $\begin{align*} 4x+5y-2z &= 12\\ y+58z &= 2\\ 8x+7y-3z &= -5 \end{align*}$

Para los ejercicios 16-46, resolver el sistema por eliminación gaussiana.

16)$\left [ \begin{array}{cc|c} 1 & 0 & 3\\ 0 & 0 & 0\\ \end{array} \right ]$

17)$\left [ \begin{array}{cc|c} 1 & 0 & 1\\ 1 & 0 & 2\\ \end{array} \right ]$

Responder: Sin soluciones

18)$\left [ \begin{array}{cc|c} 1 & 2 & 3\\ 4 & 5 & 6\\ \end{array} \right ]$

19)$\left [ \begin{array}{cc|c} -1 & 2 & -3\\ 4 & -5 & 6\\ \end{array} \right ]$

Responder: $(-1,-2)$

20)$\left [ \begin{array}{cc|c} -2 & 0 & 1\\ 0 & 2 & -1\\ \end{array} \right ]$

21)$\begin{align*} 2x-3y &= -9\\ 5x+4y &= 58 \end{align*}$

Responder: $(6,7)$

22)$\begin{align*} 6x+2y &= -4\\ 3x+4y &= -17 \end{align*}$

23)$\begin{align*} 2x+3y &= 12\\ 4x+y &= 14 \end{align*}$

Responder: $(3,2)$

24)$\begin{align*} -4x-3y &= -2\\ 3x-5y &= -13 \end{align*}$

25)$\begin{align*} -5x+8y &= 3\\ 10x+6y &= 5 \end{align*}$

Responder: $\left (\dfrac{1}{5}, \dfrac{1}{2} \right )$

26)$\begin{align*} 3x+4y &= 12\\ -6x-8y &= -24 \end{align*}$

27)$\begin{align*} -60x+45y &= 12\\ 20x-15y &= -4 \end{align*}$

Responder: $\left (x, \dfrac{4}{15}(5x+1) \right )$

28)$\begin{align*} 11x+10y &= 43\\ 15x+20y &= 65 \end{align*}$

29)$\begin{align*} 2x-y &= 2\\ 3x+2y &= 17 \end{align*}$

Responder: $(3,4)$

30)$\begin{align*} -1.06x-2.25y &= 5.51\\ -5.03x-1.08y &= 5.40 \end{align*}$

31)$\begin{align*} \dfrac{3}{4}x-\dfrac{3}{5}y &= 4\\ \dfrac{1}{4}x+\dfrac{2}{3}y &= 1 \end{align*}$

Responder: $\left (\dfrac{196}{39}, -\dfrac{5}{13} \right )$

32)$\begin{align*} \dfrac{1}{4}x-\dfrac{2}{3}y &= -1\\ \dfrac{1}{2}x+\dfrac{1}{3}y &= 3 \end{align*}$

33)$\left [ \begin{array}{ccc|c} 1 & 0 & 0 & 31\\ 0 & 1 & 1 & 45\\ 0 & 0 & 1 & 87\\ \end{array} \right ]$

Responder: $(31,-42,87)$

34)$\left [ \begin{array}{ccc|c} 1 & 0 & 1 & 50\\ 1 & 1 & 0 & 20\\ 0 & 1 & 1 & -90\\ \end{array} \right ]$

35)$\left [ \begin{array}{ccc|c} 1 & 2 & 3 & 4\\ 0 & 5 & 6 & 7\\ 0 & 0 & 8 & 9\\ \end{array} \right ]$

Responder: $\left (\dfrac{21}{40}, \dfrac{1}{20}, \dfrac{9}{8} \right )$

36)$\left [ \begin{array}{ccc|c} -0.1 & 0.3 & -0.1 & 0.2\\ -0.4 & 0.2 & 0.1 & 0.8\\ 0.6 & 0.1 & 0.7 & -0.8\\ \end{array} \right ]$

37)$\begin{align*} -2x+3y-2z &= 3\\ 4x+2y-z &= 9\\ 4x-8y+2z &= -6 \end{align*}$

Responder: $\left (\dfrac{18}{13}, \dfrac{15}{13}, -\dfrac{15}{13} \right )$

38)$\begin{align*} x+y-4z &= -4\\ 5x-3y-2z &= 0\\ 2x+6y+7z &= 30 \end{align*}$

39)$\begin{align*} 2x+3y+2z &= 1\\ -4x-6y-4z &= -2\\ 10x+15y+10z &= 5 \end{align*}$

Responder: $\left (x, y, \dfrac{1}{2}(1-2x-3y) \right )$

40)$\begin{align*} x+2y-z &= 1\\ -x-2y+2z &= -2\\ 3x+6y-3z &= 5 \end{align*}$

41)$\begin{align*} x+2y-z &= 1\\ -x-2y+2z &= -2\\ 3x+6y-3z &= 3 \end{align*}$

Responder: $\left (x, -\dfrac{x}{2}, -1 \right )$

42)$\begin{align*} x+y &= 2\\ x+z &= 1\\ -y-z &= -3 \end{align*}$

43)$\begin{align*} x+y+z &= 100\\ x+2z &= 125\\ -y+2z &= 25 \end{align*}$

Responder: $(125,-25,0)$

44)$\begin{align*} \dfrac{1}{4}x-\dfrac{2}{3}z &= -\dfrac{1}{2}\\ \dfrac{1}{5}x+\dfrac{1}{3}y &= \dfrac{4}{7}\\ \dfrac{1}{5}y-\dfrac{1}{3}z &= \dfrac{2}{9} \end{align*}$

45)$\begin{align*} -\dfrac{1}{2}x+\dfrac{1}{2}y+\dfrac{1}{7}z &= -\dfrac{53}{14}\\ \dfrac{1}{2}x-\dfrac{1}{2}y+\dfrac{1}{4}z &= 3\\ \dfrac{1}{4}x+\dfrac{1}{5}y+\dfrac{1}{3}z &= \dfrac{23}{15} \end{align*}$

Responder: $(8,1,-2)$

46)$\begin{align*} -\dfrac{1}{2}x-\dfrac{1}{3}y+\dfrac{1}{4}z &= -\dfrac{29}{6}\\ \dfrac{1}{5}x+\dfrac{1}{6}y-\dfrac{1}{7}z &= \dfrac{431}{210}\\ -\dfrac{1}{8}x+\dfrac{1}{9}y+\dfrac{1}{10}z &= -\dfrac{49}{45} \end{align*}$

Extensiones

Para los ejercicios 47-51, usa la eliminación gaussiana para resolver el sistema.

47)$\begin{align*} \dfrac{x-1}{7}+\dfrac{y-2}{8}+\dfrac{z-3}{4} &= 0\\ x+y+z &= 6\\ \dfrac{x+2}{3}+2y+\dfrac{z-3}{3} &= 5 \end{align*}$

Responder: $(1,2,3)$

48)$\begin{align*} \dfrac{x-1}{4}-\dfrac{y+1}{4}+3z &= -1\\ \dfrac{x+5}{2}+\dfrac{y+7}{4}-z &= 4\\ x+y-\dfrac{z-2}{2} &= 1 \end{align*}$

49)$\begin{align*} \dfrac{x-3}{4}-\dfrac{y-1}{3}+2z &= -1\\ \dfrac{x+5}{2}+\dfrac{y+5}{2}+\dfrac{z+5}{2} &= 8\\ x+y+z &= 1 \end{align*}$

Responder: $\left (x, \dfrac{31}{28}-\dfrac{3x}{4}, \dfrac{1}{28}(-7x-3) \right )$

50)$\begin{align*} \dfrac{x-3}{10}+\dfrac{y+3}{2}-2z &= 3\\ \dfrac{x+5}{4}-\dfrac{y-1}{8}+z &= \dfrac{3}{2}\\ \dfrac{x-1}{4}+\dfrac{y+4}{2}+3z &= \dfrac{3}{2} \end{align*}$

51)$\begin{align*} \dfrac{x-3}{4}-\dfrac{y-1}{3}+2z &= -1\\ \dfrac{x+5}{2}+\dfrac{y+5}{2}+\dfrac{z+5}{2} &= 7\\ x+y+z &= 1 \end{align*}$

Responder: No existen soluciones.

Aplicaciones del mundo real

Para los ejercicios 52-61, configurar la matriz aumentada que describa la situación, y resuelva para la solución deseada.

52) Todos los días, una tienda de$5,000$ magdalenas vende magdalenas en sabores de chocolate y vainilla. Si el sabor a chocolate es$3$ veces tan popular como el sabor a vainilla, ¿cuántos de cada cupcake venden al día?

53) En una tienda de magdalenas competidora,$\$4,520$ por valor de cupcakes se venden diariamente. Los cupcakes de chocolate cuestan$\$2.25$ y los cupcakes de terciopelo rojo cuestan$\$1.75$. Si el número total de cupcakes vendidos por día es$2,200$, ¿cuántos de cada sabor se venden cada día?

Responder: $860$terciopelo rojo,$1,340$ chocolate

54) Invirtió$\$10,000$ en dos cuentas: una que tiene$3\%$ interés simple y la otra con$2.5\%$ intereses. Si su pago total de intereses después de un año era$\$283.50$, ¿cuánto había en cada cuenta después del año pasado?

55) Invirtió$\$2,300$ en la cuenta 1, y$\$2,700$ en la cuenta 2. Si el monto total de intereses después de un año es$\$254$, y la cuenta 2 tiene$1.5$ veces la tasa de interés de la cuenta 1, ¿cuáles son las tasas de interés? Asumir tasas de interés simples.

Responder: $4\%$para la cuenta 1,$6\%$ para la cuenta 2

56) Bikes'R'Us fabrica bicicletas, que se venden para$\$250$. Cuesta al fabricante$\$180$ por bicicleta, más una tarifa de inicio de$\$3,500$. ¿Después de cuántas bicicletas vendidas se romperá el fabricante?

57) Una importante tienda de electrodomésticos está considerando comprar aspiradoras de un pequeño fabricante. La tienda podría adquirir las aspiradoras para$\$86$ cada una, con una tarifa de entrega de$\$9,200$, independientemente de cuántas aspiradoras se vendan. Si la tienda necesita comenzar a ver una ganancia después de que se vendan$230$ las unidades, ¿cuánto deben cobrar por las aspiradoras?

Responder: $\$126$

58) Los tres sabores de helado más populares son el chocolate, la fresa y la vainilla, que comprenden$83\%$ los sabores que se venden en una heladería. Si la vainilla vende$1\%$ más del doble de fresa, y el chocolate vende$11\%$ más que la vainilla, ¿cuánto del consumo total de helado son los sabores de vainilla, chocolate y fresa?

59) En una heladería, tres sabores están aumentando en la demanda. El año pasado, helado de plátano, calabaza y rocoso camino compuesto por ventas totales$12\%$ de helados. Este año, los mismos tres helados conformados por ventas$16.9\%$ de helados. Las ventas rocosas de carreteras se duplicaron, las ventas de banano aumentaron en$50\%$, y las ventas de calabaza aumentaron en$20\%$. Si el helado rocoso del camino tenía uno por ciento menos de las ventas que el helado de plátano, averigua el porcentaje de ventas de helados que cada helado individual hizo el año pasado.

Responder: El plátano era$3\%$, la calabaza era$7\%$, y el camino rocoso estaba$2\%$

60) Una bolsa de nueces mixtas contiene anacardos, pistachos y almendras. Hay nueces$1,000$ totales en la bolsa, y hay$100$ menos almendras que pistachos. Los anacardo pesan$3$ g, los pistachos pesan$4$ g y las almendras pesan$5$ g. Si la bolsa pesa$3.7$ kg, averigua cuántos de cada tipo de nuez hay en la bolsa.

61) Una bolsa de nueces mixtas contiene anacardos, pistachos y almendras. Originalmente había$900$ nueces en la bolsa. $30\%$de las almendras,$20\%$ de los anacardos, y$10\%$ de los pistachos se comieron, y ahora quedan$770$ frutos secos en la bolsa. Originalmente, había$100$ más anacardos que almendras. Averigua cuántos de cada tipo de tuerca había en la bolsa para empezar.

Responder: $100$almendras,$200$ anacardos,$600$ pistachos

9.7: Resolver sistemas con inversos

Verbal

1) En una sección anterior, mostramos que la multiplicación matricial no es conmutativa, es decir,$AB\neq BA$ en la mayoría de los casos. ¿Puede explicar por qué la multiplicación matricial es conmutativa para inversiones matriciales, es decir,$A^{-1}A=AA^{-1}$?

Responder: Si$A^{-1}$ es la inversa de$A$, entonces$AA^{-1}=I$, la matriz de identidad. Dado que también$A$ es la inversa de$A^{-1}$,$A^{-1}A=I$. También se puede verificar demostrando esto para una$2\times 2$ matriz.

2) ¿Cada$2\times 2$ matriz tiene una inversa? Explique por qué o por qué no. Explique qué condición es necesaria para que exista una inversa.

3) ¿Puedes explicar si una$2\times 2$ matriz con una fila entera de ceros puede tener una inversa?

Responder: No, porque$ad$ y$bc$ son las dos$0$, así$ad-bc=0$, lo que nos obliga a dividirnos por$0$ en la fórmula.

4) ¿Puede una matriz con una columna entera de ceros tener una inversa? Explique por qué o por qué no.

5) ¿Puede una matriz con ceros en la diagonal tener una inversa? Si es así, encuentra un ejemplo. Si no, prueba por qué no. Por simplicidad, asumir una$2\times 2$ matriz.

Responder

Sí. Considera la matriz$\begin{bmatrix} 0 & 1\\ 1 & 0 \end{bmatrix}$. La inversa se encuentra con el siguiente cálculo:

$A^{-1} = \dfrac{1}{0(0)-1(1)} \begin{bmatrix} 0 & -1\\ -1 & 0 \end{bmatrix} = \begin{bmatrix} 0 & 1\\ 1 & 0 \end{bmatrix}$

Algebraico

En los ejercicios 6-12, muestran que la matriz$A$ es la inversa de la matriz$B$.

6)$A = \begin{bmatrix} 1 & 0\\ -1 & 1 \end{bmatrix}, B = \begin{bmatrix} 1 & 0\\ 1 & 1 \end{bmatrix}$

7)$A = \begin{bmatrix} 1 & 2\\ 3 & 4 \end{bmatrix}, B = \begin{bmatrix} -2 & 1\\ \frac{3}{2} & -\frac{1}{2} \end{bmatrix}$

Responder: $AB = BA = \begin{bmatrix} 1 & 0\\ 0 & 1 \end{bmatrix} = I$

8)$A = \begin{bmatrix} 4 & 5\\ 7 & 0 \end{bmatrix}, B = \begin{bmatrix} 0 & \frac{1}{7}\\ \frac{1}{5} & -\frac{4}{35} \end{bmatrix}$

9)$A = \begin{bmatrix} -2 & \frac{1}{2}\\ 3 & -1 \end{bmatrix}, B = \begin{bmatrix} -2 & -1\\ -6 & -4 \end{bmatrix}$

Responder: $AB = BA = \begin{bmatrix} 1 & 0\\ 0 & 1 \end{bmatrix} = I$

10)$A = \begin{bmatrix} 1 & 0 & 1\\ 0 & 1 & -1\\ 0 & 1 & 1 \end{bmatrix}, B = \dfrac{1}{2}\begin{bmatrix} 2 & 1 & -1\\ 0 & 1 & 1\\ 0 & -1 & 1 \end{bmatrix}$

11)$A = \begin{bmatrix} 1 & 0 & 1\\ 0 & 1 & -1\\ 0 & 1 & 1 \end{bmatrix}, B = \dfrac{1}{2}\begin{bmatrix} 2 & 1 & -1\\ 0 & 1 & 1\\ 0 & -1 & 1 \end{bmatrix}$

Responder: $AB = BA = \begin{bmatrix} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{bmatrix} = I$

12)$A = \begin{bmatrix} 3 & 8 & 2\\ 1 & 1 & 1\\ 5 & 6 & 12 \end{bmatrix}, B = \dfrac{1}{36}\begin{bmatrix} -6 & 84 & -6\\ 7 & -26 & 1\\ -1 & -22 & 5 \end{bmatrix}$

Para los ejercicios 13-26, encuentra el inverso multiplicativo de cada matriz, si existe.

13)$\begin{bmatrix} 3 & -2\\ 1 & 9 \end{bmatrix}$

Responder: $\dfrac{1}{29}\begin{bmatrix} 9 & 2\\ -1 & 3 \end{bmatrix}$

14)$\begin{bmatrix} -2 & 2\\ 3 & 1 \end{bmatrix}$

15)$\begin{bmatrix} -3 & 7\\ 9 & 2 \end{bmatrix}$

Responder: $\dfrac{1}{69}\begin{bmatrix} -2 & 7\\ 9 & 3 \end{bmatrix}$

16)$\begin{bmatrix} -4 & -3\\ -5 & 8 \end{bmatrix}$

17)$\begin{bmatrix} 1 & 1\\ 2 & 2 \end{bmatrix}$

Responder: No hay inversa

18)$\begin{bmatrix} 0 & 1\\ 1 & 0 \end{bmatrix}$

19)$\begin{bmatrix} 0.5 & 1.5\\ 1 & -0.5 \end{bmatrix}$

Responder: $\dfrac{4}{7}\begin{bmatrix} 0.5 & 1.5\\ 1 & -0.5 \end{bmatrix}$

20)$\begin{bmatrix} 1 & 0 & 6\\ -2 & 1 & 7\\ 3 & 0 & 2 \end{bmatrix}$

21)$\begin{bmatrix} 0 & 1 & -3\\ 4 & 1 & 0\\ 1 & 0 & 5 \end{bmatrix}$

Responder: $\dfrac{1}{17}\begin{bmatrix} -5 & 5 & -3\\ 20 & -3 & 12\\ 1 & -1 & 4 \end{bmatrix}$

22)$\begin{bmatrix} 1 & 2 & -1\\ -3 & 4 & 1\\ -2 & -4 & -5 \end{bmatrix}$

23)$\begin{bmatrix} 1 & 9 & -3\\ 2 & 5 & 6\\ 4 & -2 & -7 \end{bmatrix}$

Responder: $\dfrac{1}{209}\begin{bmatrix} 47 & -57 & 69\\ 10 & 19 & -12\\ -24 & 38 & -13 \end{bmatrix}$

24)$\begin{bmatrix} 1 & -2 & 3\\ -4 & 8 & -12\\ 1 & 4 & 2 \end{bmatrix}$

25)$\begin{bmatrix} \frac{1}{2} & \frac{1}{2} & \frac{1}{2}\\ \frac{1}{3} & \frac{1}{4} & \frac{1}{5}\\ \frac{1}{6} & \frac{1}{7} & \frac{1}{8} \end{bmatrix}$

Responder: $\begin{bmatrix} 18 & 60 & -168\\ -56 & -140 & 448\\ 40 & 80 & -280 \end{bmatrix}$

26)$\begin{bmatrix} 1 & 2 & 3\\ 4 & 5 & 6\\ 7 & 8 & 9 \end{bmatrix}$

Para los ejercicios 27-34, resolver el sistema utilizando la inversa de una$2\times 2$ matriz.

27)$\begin{align*} 5x-6y &= -61\\ 4x+3y &= -2 \end{align*}$

Responder: $(-5,6)$

28)$\begin{align*} 8x+4y &= -100\\ 3x-4y &= 1 \end{align*}$

29)$\begin{align*} 3x-2y &= 6\\ -x+5y &= -2 \end{align*}$

Responder: $(2,0)$

30)$\begin{align*} 5x-4y &= -5\\ 4x+y &= 2.3 \end{align*}$

31)$\begin{align*} -3x-4y &= 9\\ 12x+4y &= -6 \end{align*}$

Responder: $\left (\dfrac{1}{3}, -\dfrac{5}{2} \right )$

32)$\begin{align*} -2x+3y &= \dfrac{3}{10}\\ -x+5y &= \dfrac{1}{2} \end{align*}$

33)$\begin{align*} \dfrac{8}{5}x-\dfrac{4}{5}y &= \dfrac{2}{5}\\ -\dfrac{8}{5}x+\dfrac{1}{5}y &= \dfrac{7}{10} \end{align*}$

Responder: $\left (-\dfrac{2}{3}, -\dfrac{11}{6} \right )$

34)$\begin{align*} \dfrac{1}{2}x+\dfrac{1}{5}y &= -\dfrac{1}{4}\\ \dfrac{1}{2}x-\dfrac{3}{5}y &= -\dfrac{9}{4} \end{align*}$

Para los ejercicios 35-42, resolver un sistema utilizando la inversa de una$3\times 3$ matriz.

35)$\begin{align*} 3x-2y+5z &= 21\\ 5x+4y &= 37\\ x-2y-5z &= 5 \end{align*}$

Responder: $\left (7, \dfrac{1}{2}, \dfrac{1}{5} \right )$

36)$\begin{align*} 4x+4y+4z &= 40\\ 2x-3y+4z &= -12\\ -x+3y+4z &= 9 \end{align*}$

37)$\begin{align*} 6x-5y-z &= 31\\ -x+2y+z &= -6\\ 3x+3y+2z &= 13 \end{align*}$

Responder: $(5,0,-1)$

38)$\begin{align*} 6x-5y+2z &= -4\\ 2x+5y-z &= 12\\ 2x+5y+z &= 12 \end{align*}$

39)$\begin{align*} 4x-2y+3z &= -12\\ 2x+2y-9z &= 33\\ 6y-4z &= 1 \end{align*}$

Responder: $\dfrac{1}{34} \left(-35, -97, -154 \right)$

40)$\begin{align*} \dfrac{1}{10}x-\dfrac{1}{5}y+4z &= \dfrac{-41}{2}\\ \dfrac{1}{5}x-20y+\dfrac{2}{5}z &= -101\\ \dfrac{3}{10}x+4y-\dfrac{3}{10}z &= 23 \end{align*}$

41)$\begin{align*} \dfrac{1}{2}x-\dfrac{1}{5}y+\dfrac{1}{5}z &= \dfrac{31}{100}\\ -\dfrac{3}{4}x-\dfrac{1}{4}y+\dfrac{1}{2}z &= \dfrac{7}{40}\\ -\dfrac{4}{5}x-\dfrac{1}{2}y+\dfrac{3}{2}z &= \dfrac{1}{4} \end{align*}$

Responder: $\dfrac{1}{690} \left(65, -1136, -229 \right)$

42)$\begin{align*} 0.1x+0.2y+0.3z &= -1.4\\ 0.1x-0.2y+0.3z &= 0.6\\ 0.4y+0.9z &= -2 \end{align*}$

Tecnología

Para los ejercicios 43-46, utilice una calculadora para resolver el sistema de ecuaciones con inversión matricial.

43)$\begin{align*} 2x-y &= -3\\ -x+2y &= 2.3\\ \end{align*}$

Responder: $\left (-\dfrac{37}{30}, \dfrac{8}{15} \right )$

44)$\begin{align*} -\dfrac{1}{2}x-\dfrac{3}{2}y &= -\dfrac{43}{20}\\ \dfrac{5}{2}x+\dfrac{11}{5}y &= \dfrac{31}{4}\\ \end{align*}$

45)$\begin{align*} 12.3x-2y-2.5z &= 2\\ 36.9x+7y-7.5z &= -7\\ 8y-5z &= -10 \end{align*}$

Responder: $\left (\dfrac{10}{123}, -1, \dfrac{2}{5} \right )$

46)$\begin{align*} 0.5x-3y+6z &= -0.8\\ 0.7x-2y &= -0.06\\ 0.5x+4y+5z &= 0 \end{align*}$

Extensiones

Para los ejercicios 47-51, encuentra la inversa de la matriz dada.

47)$\begin{bmatrix} 1 & 0 & 1 & 0\\ 0 & 1 & 0 & 1\\ 0 & 1 & 1 & 0\\ 0 & 0 & 1 & 1 \end{bmatrix}$

Responder: $\dfrac{1}{2}\begin{bmatrix} 2 & 1 & -1 & -1\\ 0 & 1 & 1 & -1\\ 0 & -1 & 1 & 1\\ 0 & 1 & -1 & 1 \end{bmatrix}$

48)$\begin{bmatrix} -1 & 0 & 2 & 5\\ 0 & 0 & 0 & 2\\ 0 & 2 & -1 & 0\\ 1 & -3 & 0 & 1 \end{bmatrix}$

49)$\begin{bmatrix} 1 & -2 & 3 & 0\\ 0 & 1 & 0 & 2\\ 1 & 4 & -2 & 3\\ -5 & 0 & 1 & 1 \end{bmatrix}$

Responder: $\dfrac{1}{39}\begin{bmatrix} 3 & 2 & 1 & -7\\ 18 & -53 & 32 & 10\\ 24 & -36 & 21 & 9\\ -9 & 46 & -16 & -5 \end{bmatrix}$

50)$\begin{bmatrix} 1 & 2 & 0 & 2 & 3\\ 0 & 2 & 1 & 0 & 0\\ 0 & 0 & 3 & 0 & 1\\ 0 & 2 & 0 & 0 & 1\\ 0 & 0 & 1 & 2 & 0 \end{bmatrix}$

51)$\begin{bmatrix} 1 & 0 & 0 & 0 & 0 & 0\\ 0 & 1 & 0 & 0 & 0 & 0\\ 0 & 0 & 1 & 0 & 0 & 0\\ 0 & 0 & 0 & 1 & 0 & 0\\ 0 & 0 & 0 & 0 & 1 & 0\\ 1 & 1 & 1 & 1 & 1 & 1 \end{bmatrix}$

Responder: $\begin{bmatrix} 1 & 0 & 0 & 0 & 0 & 0\\ 0 & 1 & 0 & 0 & 0 & 0\\ 0 & 0 & 1 & 0 & 0 & 0\\ 0 & 0 & 0 & 1 & 0 & 0\\ 0 & 0 & 0 & 0 & 1 & 0\\ -1 & -1 & -1 & -1 & -1 & 1 \end{bmatrix}$

Aplicaciones del mundo real

Para los ejercicios 52-61, escribir un sistema de ecuaciones que represente la situación. Después, resuelve el sistema usando la inversa de una matriz.

52) se vendieron$2,400$ boletos para un partido de basquetbol. Si los precios para el piso 1 y el piso 2 eran diferentes, y la cantidad total de dinero traída es$\$64,000$, ¿cuánto fue el precio de cada boleto?

53) En el ejercicio anterior, si te dijeron que había$400$ más boletos vendidos para el piso 2 que para el piso 1, ¿cuánto era el precio de cada boleto?

Responder: Soluciones infinitas.

54) Una campaña de alimentos recolectó dos tipos diferentes de productos enlatados, judías verdes y frijoles. El número total de latas recolectadas fue$350$ y el peso total de todos los alimentos donados fue$348$ lb,$12$ oz Si las latas de frijol verde pesan$2$ oz menos que las latas de frijol renal, ¿cuántas de cada lata se donaron?

55) Se pidió a los alumnos que llevaran su fruta favorita a clase. $95\%$de los frutos consistieron en plátano, manzana y naranjas. Si las naranjas eran dos veces más populares que los plátanos, y las manzanas eran$5\%$ menos populares que los plátanos, ¿cuáles son los porcentajes de cada fruta individual?

Responder: $50\%$naranjas,$25\%$ plátanos,$20\%$ manzanas

56) Una hermandad realizó una venta de pasteles para recaudar dinero y vendió brownies y galletas con chispas de chocolate. Le dieron un precio a los brownies$\$1$ y a las galletas con chispas de chocolate en$\$0.75$. Levantaron$\$700$ y vendieron$850$ artículos. ¿Cuántos brownies y cuántas galletas se vendieron?

57) Una tienda de ropa necesita ordenar nuevo inventario. Cuenta con tres tipos diferentes de sombreros a la venta: sombreros de paja, gorros y sombreros de vaquero. El sombrero de paja tiene un precio en$\$13.99$, el gorro en$\$7.99$, y el sombrero vaquero en$\$14.49$. Si los$100$ sombreros se vendieron este último trimestre,$\$1,119$ fue absorbido por las ventas, y la cantidad de gorros vendidos era$10$ más que sombreros de vaquero, ¿cuántos de cada uno debería ordenar la tienda de ropa para reemplazar los ya vendidos?

Responder: $10$sombreros de paja,$50$ gorros, sombreros de$40$ vaquero

58) Anna, Ashley y Andrea pesan una$370$ libra combinada Si Andrea pesa$20$ lb más que Ashley, y Anna pesa$1.5$ veces más que Ashley, ¿cuánto pesa cada chica?

59) Tres compañeros de cuarto compartieron un paquete de barras de$12$ helado, pero nadie recuerda quién comió cuántos. Si Tom comió el doble de barras de helado que Joe, y Albert comió tres menos que Tom, ¿cuántas barras de helado comió cada compañero de cuarto?

Responder: Tom comió$6$, Joe comió$3$ y Albert comió$3$.

60) Un granjero construyó un gallinero con alambre de pollo, madera y madera contrachapada. El alambre de pollo cuesta$\$2$ por pie cuadrado, la madera$\$10$ por pie cuadrado y la madera contrachapada$\$5$ por pie cuadrado. El agricultor gastó un total de$\$51$, y la cantidad total de materiales utilizados fue$14$ ft ². Usó$3$ ft ² más alambre de pollo que contrachapado. ¿Cuánto de cada material en usó el agricultor?

61) Jay tiene limoneros, naranjos y granados en su patio trasero. Una naranja pesa$8$ oz, una$5$ oz de limón y una$11$ oz de granada. Jay recogió$142$ trozos de fruta que pesaban un total de$70$ lb,$10$ oz. Recogió$15.5$ veces más naranjas que granadas. ¿Cuántas de cada fruta escogió Jay?

Responder: $124$naranjas,$10$ limones,$8$ granadas

9.8: Resolviendo sistemas con la regla de Cramer

Verbal

1) Explicar por qué siempre podemos evaluar el determinante de una matriz cuadrada.

Responder: Un determinante es la suma y los productos de las entradas en la matriz, por lo que siempre puedes evaluar ese producto, aunque termine siendo$0$.

2) Examinando la regla de Cramer, explica por qué no hay una solución única para el sistema cuando el determinante de tu matriz es$0$. Para simplificar, use una$2\times 2$ matriz.

3) Explicar lo que significa en términos de una inversa que una matriz tenga un$0$ determinante.

Responder: El inverso no existe.

4) El determinante de la$2\times 2$ matriz$A$ es$3$. Si cambia las filas y multiplica la primera fila por$6$ y la segunda fila por$2$, explique cómo encontrar el determinante y proporcionar la respuesta.

Algebraico

Para los ejercicios 5-24, encuentra el determinante.

5)$\begin{vmatrix} 1 & 2\\ 3 & 4 \end{vmatrix}$

Responder: $-2$

6)$\begin{vmatrix} -1 & 2\\ 3 & -4 \end{vmatrix}$

7)$\begin{vmatrix} 2 & -5\\ -1 & 6 \end{vmatrix}$

Responder: $7$

8)$\begin{vmatrix} -8 & 4\\ -1 & 5 \end{vmatrix}$

9)$\begin{vmatrix} 1 & 0\\ 3 & -4 \end{vmatrix}$

Responder: $-4$

10)$\begin{vmatrix} 10 & 20\\ 0 & -10 \end{vmatrix}$

11)$\begin{vmatrix} 10 & 0.2\\ 5 & 0.1 \end{vmatrix}$

Responder: $0$

12)$\begin{vmatrix} 6 & -3\\ 8 & 4 \end{vmatrix}$

13)$\begin{vmatrix} -2 & -3\\ 3.1 & 4,000 \end{vmatrix}$

Responder: $-7,990.7$

14)$\begin{vmatrix} -1.1 & 0.6\\ 7.2 & -0.5 \end{vmatrix}$

15)$\begin{vmatrix} -1 & 0 & 0\\ 0 & 1 & 0\\ 0 & 0 & -3 \end{vmatrix}$

Responder: $3$

16)$\begin{vmatrix} -1 & 4 & 0\\ 0 & 2 & 3\\ 0 & 0 & -3 \end{vmatrix}$

17)$\begin{vmatrix} 1 & 0 & 1\\ 0 & 1 & 0\\ 1 & 0 & 0 \end{vmatrix}$

Responder: $-1$

18)$\begin{vmatrix} 2 & -3 & 1\\ 3 & -4 & 1\\ -5 & 6 & 1 \end{vmatrix}$

19)$\begin{vmatrix} -2 & 1 & 4\\ -4 & 2 & -8\\ 2 & -8 & -3 \end{vmatrix}$

Responder: $224$

20)$\begin{vmatrix} 6 & -1 & 2\\ -4 & -3 & 5\\ 1 & 9 & -1 \end{vmatrix}$

21)$\begin{vmatrix} 5 & 1 & -1\\ 2 & 3 & 1\\ 3 & -6 & -3 \end{vmatrix}$

Responder: $15$

22)$\begin{vmatrix} 1.1 & 2 & -1\\ -4 & 0 & 0\\ 4.1 & -0.4 & 2.5 \end{vmatrix}$

23)$\begin{vmatrix} 2 & -1.6 & 3.1\\ 1.1 & 3 & -8\\ -9.3 & 0 & 2 \end{vmatrix}$

Responder: $-17.03$

24)$\begin{vmatrix} -\frac{1}{2} & \frac{1}{3} & \frac{1}{4}\\ \frac{1}{5} & -\frac{1}{6} & \frac{1}{7}\\ 0 & 0 & \frac{1}{8} \end{vmatrix}$

Para los ejercicios 25-34, resuelve el sistema de ecuaciones lineales usando la Regla de Cramer.

25)$\begin{align*} 2x-3y &= -1\\ 4x+5y &= 9 \end{align*}$

Contestar: $(1,1)$

26)$\begin{align*} 5x-4y &= 2\\ -4x+7y &= 6 \end{align*}$

27)$\begin{align*} 6x-3y &= 2\\ -8x+9y &= -1 \end{align*}$

Contestar: $\left (\dfrac{1}{2}, \dfrac{1}{3} \right )$

28)$\begin{align*} 2x+6y &= 12\\ 5x-2y &= 13 \end{align*}$

29)$\begin{align*} 4x+3y &= 23\\ 2x-y &= -1 \end{align*}$

Contestar: $(2,5)$

30)$\begin{align*} 10x-6y &= 2\\ -5x+8y &= -1 \end{align*}$

31)$\begin{align*} 4x-3y &= -3\\ 2x+6y &= -4 \end{align*}$

Contestar: $\left (-1, -\dfrac{1}{3} \right )$

32)$\begin{align*} 4x-5y &= 7\\ -3x+9y &= 0 \end{align*}$

33)$\begin{align*} 4x+10y &= 180\\ -3x-5y &= -105 \end{align*}$

Contestar: $(15,12)$

34)$\begin{align*} 8x-2y &= -3\\ -4x+6y &= 4 \end{align*}$

Para los ejercicios 35-44, resolver el sistema de ecuaciones lineales utilizando la Regla de Cramer.

35)$\begin{align*} x+2y-4z &= -1\\ 7x+3y+5z &= 26\\ -2x-6y+7z &= -6 \end{align*}$

Contestar: $(1,3,2)$

36)$\begin{align*} -5x+2y-4z &= -47\\ 4x-3y-z &= -94\\ 3x-3y+2z &= 94 \end{align*}$

37)$\begin{align*} 4x+5y-z &= -7\\ -2x-9y+2z &= 8\\ 5y+7z &= 21 \end{align*}$

Contestar: $(-1,0,3)$

38)$\begin{align*} 4x-3y+4z &= 10\\ 5x-2z &= -2\\ 3x+2y-5z &= -9 \end{align*}$

39)$\begin{align*} 4x-2y+3z &= 6\\ -6x+y &= -2\\ 2x+7y+8z &= 24 \end{align*}$

Contestar: $\left (\dfrac{1}{2}, 1, 2 \right )$

40)$\begin{align*} 5x+2y-z &= 1\\ -7x-8y+3z &= 1.5\\ 6x-12y+z &= 7 \end{align*}$

41)$\begin{align*} 13x-17y+16z &= 73\\ -11x+15y+17z &= 61\\ 46x+10y-30z &= -18 \end{align*}$

Contestar: $(2,1,4)$

42)$\begin{align*} -4x-3y-8z &= -7\\ 2x-9y+5z &= 0.5\\ 5x-6y-5z &= -2 \end{align*}$

43)$\begin{align*} 4x-6y+8z &= 10\\ -2x+3y-4z &= -5\\ x+y+z &= 1 \end{align*}$

Contestar: Soluciones infinitas

44)$\begin{align*} 4x-6y+8z &= 10\\ -2x+3y-4z &= -5\\ 12x+18y-24z &= -30 \end{align*}$

Tecnología

Para los ejercicios 45-48, utilice la función determinante en una utilidad gráfica.

45)$\begin{vmatrix} 1 & 0 & 8 & 9\\ 0 & 2 & 1 & 0\\ 1 & 0 & 3 & 0\\ 0 & 2 & 4 & 3 \end{vmatrix}$

Contestar: $24$

46)$\begin{vmatrix} 1 & 0 & 2 & 1\\ 0 & -9 & 1 & 3\\ 3 & 0 & -2 & -1\\ 0 & 1 & 1 & -2 \end{vmatrix}$

47)$\begin{vmatrix} \frac{1}{2} & 1 & 7 & 4\\ 0 & \frac{1}{2} & 100 & 5\\ 0 & 0 & 2 & 2,000\\ 0 & 0 & 0 & 2 \end{vmatrix}$

Contestar: $1$

48)$\begin{vmatrix} 1 & 0 & 0 & 0\\ 2 & 3 & 0 & 0\\ 4 & 5 & 6 & 0\\ 7 & 8 & 9 & 0 \end{vmatrix}$

Aplicaciones del mundo real

Para los ejercicios 49-52, crear un sistema de ecuaciones lineales para describir el comportamiento. Después, calcula el determinante. ¿Habrá una solución única? Si es así, encuentra la solución única.

49) Dos números suman$56$. Un número es$20$ menor que el otro.

Contestar: Sí;$18$,$38$

50) Dos números suman$104$. Si agregas dos veces el primer número más dos veces el segundo número, tu total es$208$

51) Tres números suman$106$. El primer número es$3$ menor que el segundo número. El tercer número es$4$ más que el primer número.

Contestar: Sí;$33$,$36$,$37$

52) Tres números se suman a$216$. La suma de los dos primeros números es$112$. El tercer número es 8 menos que los dos primeros números combinados.

Para los ejercicios 53-65, crear un sistema de ecuaciones lineales para describir el comportamiento. Entonces, resuelve el sistema para todas las soluciones usando la Regla de Cramer.

53)$\$10,000$ Invierte en dos cuentas, las cuales reciben$8\%$ intereses e$5\%$ intereses. Al final de un año, tenías$\$10,710$ en tus cuentas combinadas. ¿Cuánto se invirtió en cada cuenta?

Contestar: $\$7,000$en primera cuenta,$\$3,000$ en segunda cuenta.

54)$\$80,000$ Invierte en dos cuentas,$\$22,000$ en una cuenta y$\$58,000$ en la otra. Al término de un año, asumiendo intereses simples, has ganado$\$2,470$ en intereses. La segunda cuenta recibe medio por ciento menos del doble de los intereses de la primera cuenta. ¿Cuáles son las tasas de interés para tus cuentas?

55) Una sala de cine necesita saber cuántos boletos para adultos y boletos para niños se agotaron del$1,200$ total de boletos. Si los boletos para niños son$\$5.95$, los boletos para adultos son$\$11.15$, y el monto total de ingresos fue$\$12,756$, ¿cuántos boletos infantiles y boletos para adultos se vendieron?

Contestar: $120$niños,$1,080$ adultos

56) Una sala de conciertos vende boletos individuales para$\$40$ cada uno y boletos de pareja para$\$65$. Si los ingresos totales eran$\$18,090$ y se vendieron los$321$ boletos, ¿cuántos boletos individuales y cuántos boletos de pareja se vendieron?

57) Tú decides pintar tu cocina de verde. Se crea el color de la pintura mezclando pinturas amarillas y azules. No puedes recordar cuántos galones de cada color entraron en tu mezcla, pero sabes que había$10$ gal total. Adicionalmente, guardó su recibo, y sabe que la cantidad total gastada fue$\$29.50$. Si cada galón de amarillo cuesta$\$2.59$, y cada galón de azul cuesta$\$3.19$, ¿cuántos galones de cada color van a tu mezcla verde?

Contestar: $4$Gal Amarillo,$6$ Gal Azul

58) Vendiste dos tipos de bufandas en un mercado de agricultores y te gustaría saber cuál era más popular. El número total de bufandas vendidas fue$56$, el costo de la bufanda amarilla y el costo$\$10$ de la bufanda morada$\$11$. Si tuviste ingresos totales de$\$583$, ¿cuántas bufandas amarillas y cuántas bufandas moradas se vendieron?

59) Su jardín produjo dos tipos de tomates, uno verde y otro rojo. El rojo pesa$10$ oz, y el verde pesa$4$ oz. Tienes$30$ tomates, y un peso total de$13$ lb,$14$ oz. ¿Cuántos de cada tipo de tomate tienes?

Contestar: $13$tomates verdes, tomates$17$ rojos

60) En un mercado, las tres verduras más populares conforman$53\%$ la venta de hortalizas. El maíz tiene$4\%$ mayores ventas que el brócoli, que tiene$5\%$ más ventas que las cebollas. ¿Qué porcentaje tiene cada verdura en la cuota de mercado?

61) En el mismo mercado, las tres frutas más populares conforman el total$37\%$ de fruta que se vende. Las fresas venden el doble que las naranjas, y los kiwis venden un punto porcentual más que las naranjas. Por cada fruto, encuentra el porcentaje de fruta total que se vende.

Contestar: Fresas$18\%$, naranjas$9\%$, kiwi$10\%$

62) Tres bandas actuaron en una sala de conciertos. La primera banda cobró$\$15$ por boleto, la segunda banda cobrada$\$45$ por boleto y la banda final cobrada$\$22$ por boleto. Se vendieron$510$ boletos, por un total de$\$12,700$. Si la primera banda tenía$40$ más miembros de audiencia que la segunda banda, ¿cuántos boletos se vendieron para cada banda?

63) Una sala de cine vendió boletos para tres películas. Los boletos para la primera película fueron$\$5$, los boletos para la segunda película fueron$\$11$, y la tercera película lo fue$\$12$. $100$se vendieron boletos para la primera película. El número total de boletos vendidos fue$642$, para un ingreso total de$\$6,774$. ¿Cuántos boletos por cada película se vendieron?

Contestar: $100$para película 1,$230$ para película 2,$312$ para película 3

64) Hombres de edad$20–29$,$30–39$, y$40–49$ conformados por$78\%$ la población en una prisión el año pasado. Este año, los mismos grupos de edad conformados por$82.08\%$ la población. El grupo de$20–29$ edad aumentó en$20%$, el grupo de$30–39$ edad aumentó en$2\%$, y el grupo de$40–49$ edad disminuyó a$\dfrac{3}{4}$ de su población anterior. Originalmente, el grupo de$30–39$ edad tenía$2\%$ más presos que el grupo de$20–29$ edad. Determinar el porcentaje de población carcelaria para cada grupo de edad el año pasado.

65) En un penal de mujeres en el camino, el total de internos de edad$20–49$ totalizó$5,525$. Este año, el grupo de$20–29$ edad aumentó en$10\%$, el grupo de$30–39$ edad disminuyó en$20\%$, y el grupo de$40–49$ edad se duplicó. Ahora hay$6,040$ presos. Originalmente, había$500$ más en el grupo de$30–39$ edad que en el grupo de$20–29$ edad. Determinar la población carcelaria para cada grupo de edad el año pasado.

Contestar: $20–29: 2,100$,$30–39: 2,600$,$40–49: 825$

Para los ejercicios 66-68, usa este escenario: Una compañía consciente de la salud decide hacer una mezcla de trail con almendras, arándanos secos y anacardo cubiertos de chocolate. La información nutricional de estos ítems se muestra en la Tabla siguiente.

	Grasa (g)	Proteína (g)	Carbohidratos (g)
Almendras (10)	6	2	3
Arándanos (10)	0.02	0	8
Anacardo (10)	7	3.5	5.5

66) Para la mezcla especial de trail “baja en carbohidratos”, hay$1,000$ trozos de mezcla. El número total de carbohidratos es$425$ g, y la cantidad total de grasa es$570.2$ g. Si hay$200$ más trozos de anacardo que arándanos, ¿cuántos de cada ítem hay en la mezcla de trail?

67) Para la mezcla “senderismo”, hay$1,000$ piezas en la mezcla, que contienen$390.8$ g de grasa, y$165$ g de proteína. Si hay la misma cantidad de almendras que los anacardos, ¿cuántos de cada artículo hay en la mezcla de trail?

Contestar: $300$almendras,$400$ arándanos,$300$ anacardos

68) Para la mezcla “potenciador de energía”, hay$1,000$ piezas en la mezcla, que contienen$145$ g de proteína y$625$ g de carbohidratos. Si el número de almendras y anacardos sumados es equivalente a la cantidad de arándanos, ¿cuántos de cada ítem hay en la mezcla de trail?

Colaboradores y Atribuciones

Template:OpenStaxPreCalc