9.R: Sistemas de Ecuaciones y Desigualdades (Revisión)

Última actualización
Guardar como PDF

Page ID: 121254

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

9.1: Sistemas de Ecuaciones Lineales: Dos Variables

Para los ejercicios 1-2, determinar si el par ordenado es una solución al sistema de ecuaciones.

1)$\begin{align*} 3x-y &= 4\\ x+4y &= -3 \end{align*}\; \; \text{ and }\; (-1,1)$

Contestar: No

2)$\begin{align*} 6x-2y &= 24\\ -3x+3y &= 18 \end{align*}\; \; \text{ and }\; (9,15)$

Para los ejercicios 3-5, utilice la sustitución para resolver el sistema de ecuaciones.

3)$\begin{align*} 10x+5y &= -5\\ 3x-2y &= -12 \end{align*}$

Contestar: $(-2,3)$

4)$\begin{align*} \dfrac{4}{7}x+\dfrac{1}{5}y &= \dfrac{43}{70}\\ \dfrac{5}{6}x-\dfrac{1}{3}y &= -\dfrac{2}{3} \end{align*}$

5)$\begin{align*} 5x+6y &= 14\\ 4x+8y &= 8 \end{align*}$

Contestar: $(4,-1)$

Para los ejercicios 6-8, use además para resolver el sistema de ecuaciones.

6)$\begin{align*} 3x+2y &= -7\\ 2x+4y &= 6 \end{align*}$

7)$\begin{align*} 3x+4y &= 2\\ 9x+12y &= 3 \end{align*}$

Contestar: No existen soluciones.

8)$\begin{align*} 8x+4y &= 2\\ 6x-5y &= 0.7 \end{align*}$

Para los ejercicios 9-10, escribir un sistema de ecuaciones para resolver cada problema. Resolver el sistema de ecuaciones.

9) Una fábrica tiene un costo de producción$C(x)=150x+15,000$ y una función de ingresos$R(x)=200x$. ¿Cuál es el punto de equilibrio?

Contestar: $(300,60,000)$

10) Un intérprete cobra$C(x)=50x+10,000$, donde$x$ es el número total de asistentes a un espectáculo. El lugar cobra$\$75$ por boleto. Después de cuántas personas compran boletos, el lugar se equipara, y ¿cuál es el valor del total de boletos vendidos en ese momento?

Contestar: $(400,30,000)$

9.2: Sistemas de Ecuaciones Lineales: Tres Variables

Para los ejercicios 1-8, resolver el sistema de tres ecuaciones mediante sustitución o suma.

1)$\begin{align*} 0.5x-0.5y &= 10\\ -0.2y+0.2x &= 4\\ 0.1x+0.1z &= 2 \end{align*}$

Contestar: $(10,-10,10)$

2)$\begin{align*} 5x+3y-z &= 5\\ 3x-2y+4z &= 13\\ 4x+3y+5z &= 22 \end{align*}$

3)$\begin{align*} x+y+z &= 1\\ 2x+2y+2z &= 1\\ 3x+3y &= 2 \end{align*}$

Contestar: No existen soluciones.

4)$\begin{align*} 2x-3y+z &= -1\\ x+y+z &= -4\\ 4x+2y-3z &= 33 \end{align*}$

5)$\begin{align*} 3x+2y-z &= -10\\ x-y+2z &= 7\\ -x+3y+z &= -2 \end{align*}$

Contestar: $(-1,-2,3)$

6)$\begin{align*} 3x+4z &= -11\\ x-2y &= 5\\ 4y-z &= -10 \end{align*}$

7)$\begin{align*} 2x-3y+z &= 0\\ 2x+4y-3z &= 0\\ 6x-2y-z &= 0 \end{align*}$

Contestar: $\left (x, \dfrac{8x}{5}, \dfrac{14x}{5} \right )$

8)$\begin{align*} 6x-4y-2z &= 2\\ 3x+2y-5z &= 4\\ 6y-7z &= 5 \end{align*}$

Para los ejercicios 9-10, escribir un sistema de ecuaciones para resolver cada problema. Resolver el sistema de ecuaciones.

9) Tres números impares suman hasta$61$. Cuanto más pequeño es un tercio más grande y el número medio es$16$ menor que el mayor. ¿Cuáles son los tres números?

Contestar: $11, 17, 33$

10) Un teatro local se agota para su espectáculo. Venden todos los$500$ boletos por un monedero total de$\$8,070.00$. Los boletos tenían un precio$\$15$ para estudiantes,$\$12$ para niños y$\$18$ para adultos. Si la banda vendió tres veces más boletos para adultos que boletos infantiles, ¿cuántos de cada tipo se vendieron?

9.3: Sistemas de ecuaciones no lineales y desigualdades: dos variables

Para los ejercicios 1-5, resolver el sistema de ecuaciones no lineales.

1)$\begin{align*} y &= x^2 - 7\\ y &= 5x-13 \end{align*}$

Contestar: $(2,−3),(3,2)$

2)$\begin{align*} y &= x^2 - 4\\ y &= 5x+10 \end{align*}$

3)$\begin{align*} x^2 + y^2 &= 16\\ y &= x-8 \end{align*}$

Contestar: Sin solución

4)$\begin{align*} x^2 + y^2 &= 25\\ y &= x^2 + 5 \end{align*}$

5)$\begin{align*} x^2 + y^2 &= 4\\ y - x^2 &= 3 \end{align*}$

Contestar: Sin solución

Para los ejercicios 6-7, grafica la desigualdad.

6)$y>x^2 - 1$

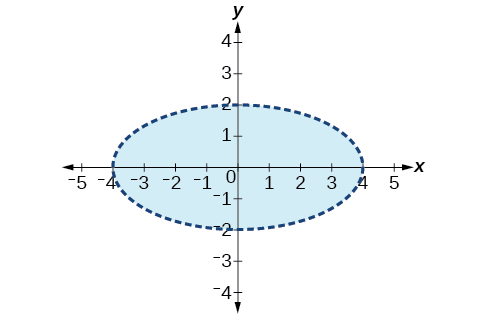
7)$\dfrac{1}{4}x^2 + y^2 < 4$

Contestar: $CNX_Precalc_Figure_09_08_202.jpg$

Para los ejercicios 8-10, graficar el sistema de desigualdades.

8)$\begin{align*} x^2 + y^2 +2x &<3 \\ y &>-x^2 - 3 \end{align*}$

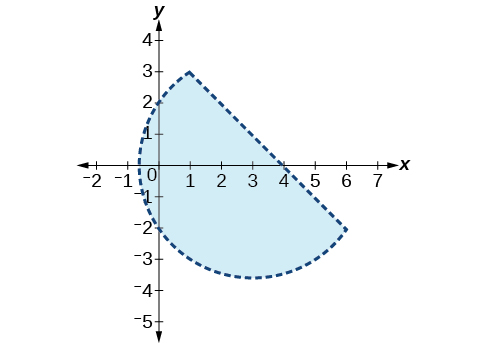
9)$\begin{align*} x^2 -2x + y^2 - 4x &< 4\\ y &<-x+4 \end{align*}$

Contestar: $CNX_Precalc_Figure_09_08_204.jpg$

10)$\begin{align*} x^2 + y^2 &< 1\\ y^2 &< x \end{align*}$

9.4: Fracciones Parciales

Para los ejercicios 1-8, descomponerse en fracciones parciales.

1)$\dfrac{-2x+6}{x^2 +3x+2}$

Contestar: $\dfrac{2}{x+2}, \dfrac{-4}{x+1}$

2)$\dfrac{10x+2}{4x^2 +4x+1}$

3)$\dfrac{7x+20}{x^2 +10x+25}$

Contestar: $\dfrac{7}{x+5}, \dfrac{-15}{(x+5)^2}$

4)$\dfrac{x-18}{x^2 -12x+36}$

5)$\dfrac{-x^2 +36x + 70}{x^3 -125}$

Contestar: $\dfrac{3}{x-5}, \dfrac{-4x+1}{x^2 +5x+25}$

6)$\dfrac{-5x^2 +6x-2}{x^3 +27}$

7)$\dfrac{x^3 -4x^2 +3x+11}{(x^2 -2)^2}$

Contestar: $\dfrac{x-4}{(x^2 -2)}, \dfrac{5x+3}{(x^2 -2)^2}$

8)$\dfrac{4x^4 -2x^3 +22x^2 -6x+48}{x(x^2 +4)^2}$

9.5: Matrices y Operaciones Matriciales

Para los ejercicios 1-12, realizar las operaciones solicitadas en las matrices dadas.

\[A=\begin{bmatrix} 4 & -2\\ 1 & 3 \end{bmatrix}, \begin{bmatrix} 6 & 7 & -3\\ 11 & -2 & 4 \end{bmatrix}, C=\begin{bmatrix} 6 & 7\\ 11 & -2\\ 14 & 0 \end{bmatrix} D=\begin{bmatrix} 1 & -4 & 9\\ 10 & 5 & -7\\ 2 & 8 & 5 \end{bmatrix} E=\begin{bmatrix} 7 & -14 & 3\\ 2 & -1 & 3\\ 0 & 1 & 9 \end{bmatrix} \nonumber\]

1)$-4A$

Contestar: $\begin{bmatrix} -16 & 8\\ -4 & -12 \end{bmatrix}$

2)$10D-6E$

3)$B+C$

Contestar: undefined; las dimensiones no coinciden

4)$AB$

5)$BA$

Contestar: undefined; las dimensiones internas no coinciden

6)$BC$

7)$CB$

Contestar: $\begin{bmatrix} 113 & 28 & 10\\ 44 & 81 & -41\\ 84 & 98 & -42 \end{bmatrix}$

8)$DE$

9)$ED$

Contestar: $\begin{bmatrix} -127 & -74 & 176\\ -2 & 11 & 40\\ 28 & 77 & 38 \end{bmatrix}$

10)$EC$

11)$CE$

Contestar: undefined; las dimensiones internas no coinciden

12)$A^3$

9.6: Resolviendo sistemas con eliminación gaussiana

Para los ejercicios 1-2, escriba el sistema de ecuaciones lineales a partir de la matriz aumentada. Indicar si habrá una solución única.

1)$\left [ \begin{array}{ccc|c} 1 & 0 & -3 & 7 \\ 0 & 1 & 2 & -5\\ 0 & 0 & 0 & 0\\ \end{array} \right ]$

Contestar: $\begin{align*} x-3z &= 7\\ y+2z &= -5 \end{align*}\; \; \text{with infinite solutions}$

2)$\left [ \begin{array}{ccc|c} 1 & 0 & 5 & -9 \\ 0 & 1 & -2 & 4\\ 0 & 0 & 0 & 3\\ \end{array} \right ]$

Para los ejercicios 3-5, escriba la matriz aumentada a partir del sistema de ecuaciones lineales.

3)$\begin{align*} -2x+2y+z &= 7\\ 2x-8y+5z &= 0\\ 19x-10y+22z &= 3 \end{align*}$

Contestar: $\left [ \begin{array}{ccc|c} -2 & 2 & 1 & 7 \\ 2 & -8 & 5 & 0\\ 19 & -10 & 22 & 3\\ \end{array} \right ]$

4)$\begin{align*} 4x+2y-3z &= 14\\ -12x+3y+z &= 100\\ 9x-6y+2z &= 31 \end{align*}$

5)$\begin{align*} x+3z &= 12\\ -x+4y &= 0\\ y+2z &= -7 \end{align*}$

Contestar: $\left [ \begin{array}{ccc|c} 1 & 0 & 3 & 12 \\ -1 & 4 & 0 & 0\\ 0 & 1 & 2 & -7\\ \end{array} \right ]$

Para los ejercicios 6-10, resolver el sistema de ecuaciones lineales utilizando la eliminación gaussiana.

6)$\begin{align*} 3x-4y &= -7\\ -6x+8y &= 14 \end{align*}$

7)$\begin{align*} 3x-4y &= 1\\ -6x+8y &= 6 \end{align*}$

Contestar: No existen soluciones.

8)$\begin{align*} -1.1x-2.3y &= 6.2\\ -5.2x-4.1y &= 4.3 \end{align*}$

9)$\begin{align*} 2x+3y+2z &= 1\\ -4x-6y-4z &= -2\\ 10x+15y+10z &= 0 \end{align*}$

Contestar: No existen soluciones.

10)$\begin{align*} -x+2y-4z &= 8\\ 3y+8z &= -4\\ -7x+y+2z &= 1 \end{align*}$

9.7: Resolver sistemas con inversos

Para los ejercicios 1-4, encuentra la inversa de la matriz.

1)$\begin{bmatrix} -0.2 & 1.4\\ 1.2 & -0.4 \end{bmatrix}$

Contestar: $\dfrac{1}{8}\begin{bmatrix} 2 & 7\\ 6 & 1 \end{bmatrix}$

2)$\begin{bmatrix} \frac{1}{2} & -\frac{1}{2}\\ -\frac{1}{4} & \frac{3}{4} \end{bmatrix}$

3)$\begin{bmatrix} 12 & 9 & -6\\ -1 & 3 & 2\\ -4 & -3 & 2 \end{bmatrix}$

Contestar: No existe inversa.

4)$\begin{bmatrix} 2 & 1 & 3\\ 1 & 2 & 3\\ 3 & 2 & 1 \end{bmatrix}$

Para los ejercicios 5-8, encuentra las soluciones calculando la inversa de la matriz.

5)$\begin{align*} 0.3x-0.1y &= -10\\ -0.1x+0.3y &= 14 \end{align*}$

Contestar: $(-20,40)$

6)$\begin{align*} 0.4x-0.2y &= -0.6\\ -0.1x+0.05y &= 0.3 \end{align*}$

7)$\begin{align*} 4x+3y-3z &= -4.3\\ 5x-4y-z &= -6.1\\ x+z &= -0.7 \end{align*}$

Contestar: $(-1, 0.2, 0.3)$

8)$\begin{align*} -2x-3y+2z &= 3\\ -x+2y+4z &= -5\\ -2y+5z &= -3 \end{align*}$

Para los ejercicios 9-10, escribir un sistema de ecuaciones para resolver cada problema. Resolver el sistema de ecuaciones.

9) Se pidió a los alumnos que llevaran su fruta favorita a clase. $90\%$de los frutos consistieron en plátano, manzana y naranjas. Si las naranjas fueran la mitad de populares que los plátanos y las manzanas fueran$5\%$ más populares que los plátanos, ¿cuáles son los porcentajes de cada fruta individual?

Contestar: $17\%$naranjas,$34\%$ plátanos,$39\%$ manzanas

10) Una hermandad realizó una venta de repostería para recaudar dinero y vendió brownies y galletas con chispas de chocolate. Le dieron un precio a los brownies$\$2$ y a las galletas con chispas de chocolate en$\$1$. Levantaron$\$250$ y vendieron$175$ artículos. ¿Cuántos brownies y cuántas galletas se vendieron?

9.8: Resolviendo sistemas con la regla de Cramer

Para los ejercicios 1-4, encuentra el determinante.

1)$\begin{vmatrix} 100 & 0\\ 0 & 0 \end{vmatrix}$

Contestar: $0$

2)$\begin{vmatrix} 0.2 & -0.6\\ 0.7 & -1.1 \end{vmatrix}$

3)$\begin{vmatrix} -1 & 4 & 3\\ 0 & 2 & 3\\ 0 & 0 & -3 \end{vmatrix}$

Contestar: $6$

4)$\begin{vmatrix} \sqrt{2} & 0 & 0\\ 0 & \sqrt{2} & 0\\ 0 & 0 & \sqrt{2} \end{vmatrix}$

Para los ejercicios 5-10, usa la Regla de Cramer para resolver los sistemas lineales de ecuaciones.

5)$\begin{align*} 4x-2y &= 23\\ -5x-10y &= -35 \end{align*}$

Contestar: $\left(6, \dfrac{1}{2} \right)$

6)$\begin{align*} 0.2x-0.1y &= 0\\ -0.3x+0.3y &= 2.5 \end{align*}$

7)$\begin{align*} -0.5x+0.1y &= 0.3\\ -0.25x+0.05y &= 0.15 \end{align*}$

Contestar: $x, 5x+3$

8)$\begin{align*} x+6y+3z &= 4\\ 2x+y+2z &= 3\\ 3x-2y+z &= 0 \end{align*}$

9)$\begin{align*} 4x-3y+5z &= -\dfrac{5}{2}\\ 7x-9y-3z &= \dfrac{3}{2}\\ x-5y-5z &= \dfrac{5}{2} \end{align*}$

Contestar: $\left(0, 0, -\dfrac{1}{2} \right)$

10)$\begin{align*} \dfrac{3}{10}x-\dfrac{1}{5}y-\dfrac{3}{10}z &= -\dfrac{1}{50}\\ \dfrac{1}{10}x-\dfrac{1}{10}y-\dfrac{1}{2}z &= -\dfrac{9}{50}\\ \dfrac{2}{5}x-\dfrac{1}{2}y-\dfrac{3}{5}z &= -\dfrac{1}{5} \end{align*}$

Prueba de práctica

1) ¿El siguiente par ordenado es una solución al sistema de ecuaciones? \[\begin{align*} -5x-y &= 12 \text{ with } (-3,3)\\ x+4y &= 9 \end{align*} \nonumber \]

Contestar: Sí

Para los ejercicios 2-9, resolver los sistemas de ecuaciones lineales y no lineales mediante sustitución o eliminación. Indicar si no existe solución.

2)$\begin{align*} \dfrac{1}{2}x-\dfrac{1}{3}y &= 4\\ \dfrac{3}{2}x-y &= 0 \end{align*}$

3)$\begin{align*} -\dfrac{1}{2}x-4y &= 4\\ 2x+16y &= 2 \end{align*}$

Contestar: No existen soluciones.

4)$\begin{align*} 5x-y &= 1\\ -10x+2y &= -2 \end{align*}$

5)$\begin{align*} 4x-6y-2z &= \dfrac{1}{10}\\ x-7y+5z &= -\dfrac{1}{4}\\ 3x+6y-9z &= \dfrac{6}{5} \end{align*}$

Contestar: $\dfrac{1}{20} (10, 5, 4)$

6)$\begin{align*} x+z &= 20\\ x+y+z &= 20\\ x+2y+z &= 10 \end{align*}$

7)$\begin{align*} 5x-4y-3z &= 0\\ 2x+y+2z &= 0\\ x-6y-7z &= 0 \end{align*}$

Contestar: $\left ( x, \dfrac{16x}{5} - \dfrac{13x}{5} \right )$

8)$\begin{align*} y &= x^2 +2x-3\\ y &= x-1 \end{align*}$

9)$\begin{align*} y^2 + x^2 &= 25\\ y^2 -2x^2 &= 1 \end{align*}$

Contestar: $(-2\sqrt{2}, -\sqrt{17}), (-2\sqrt{2}, \sqrt{17}), (2\sqrt{2}, -\sqrt{17}), (2\sqrt{2}, \sqrt{17})$

Para los ejercicios 10-11, grafica las siguientes desigualdades.

10)$y < x^2 + 9$

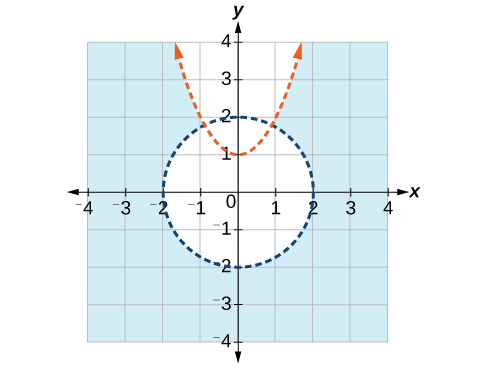
11)$\begin{align*} x^2 + y^2 &> 4 \\ y &< x^2 + 1 \end{align*}$

Contestar: $9PT11.png$

Para los ejercicios 12-14, escriba la descomposición parcial de la fracción.

12)$\dfrac{-8x-30}{x^2 + 10x+25}$

13)$\dfrac{13x+2}{(3x+1)^2}$

Contestar: $\dfrac{5}{3x+1}-\dfrac{2x+3}{(3x+1)^2}$

14)$\dfrac{x^4 - x^3 +2x-1}{x(x^2+1)^2}$

Para los ejercicios 15-21, realizar las operaciones matriciales dadas.

15)$5\begin{bmatrix} 4 & 9\\ -2 & 3 \end{bmatrix}+\dfrac{1}{2} \begin{bmatrix} -6 & 12\\ 4 & -8 \end{bmatrix}$

Contestar: $\begin{bmatrix} 17 & 51\\ -8 & 11 \end{bmatrix}$

16)$\begin{bmatrix} 1 & 4 & -7\\ -2 & 9 & 5\\ 12 & 0 & -4 \end{bmatrix} \begin{bmatrix} 3 & -4\\ 1 & 3\\ 5 & 10 \end{bmatrix}$

17)$\begin{bmatrix} \frac{1}{2} & \frac{1}{3}\\ \frac{1}{4} & \frac{1}{5} \end{bmatrix} ^{-1}$

Contestar: $\begin{bmatrix} 12 & -20\\ -15 & 30 \end{bmatrix}$

18)$\textbf{det}\begin{vmatrix} 0 & 0\\ 400 & 4,000 \end{vmatrix}$

19)$\textbf{det}\begin{vmatrix} \frac{1}{2} & -\frac{1}{2} & 0\\ -\frac{1}{2} & 0 & \frac{1}{2}\\ 0 & \frac{1}{2} & 0 \end{vmatrix}$

Contestar: $-\dfrac{1}{8}$

20) Si$\textbf{det}(A)=-6$, ¿cuál sería el determinante si cambiaras las filas 1 y 3, multiplicaras la segunda fila por$12$, y tomaras la inversa?

21) Reescribir el sistema de ecuaciones lineales como una matriz aumentada. \[\begin{align*} 14x-2y-13z &= 140\\ -2x+3y-6z &= -1\\ x-5y+12z &= 11 \end{align*} \nonumber\]

Contestar: $\left [ \begin{array}{ccc|c} 14 & -2 & 13 & 140 \\ -2 & 3 & -6 & -1\\ 1 & -5 & 12 & 11\\ \end{array} \right ]$

22) Reescribir la matriz aumentada como un sistema de ecuaciones lineales. \[\left [ \begin{array}{ccc|c} 1 & 0 & 3 & 12 \\ -2 & 4 & 9 & -5\\ -6 & 1 & 2 & 8\\ \end{array} \right ] \nonumber\]

Para los ejercicios 23-24, utilizar la eliminación gaussiana para resolver los sistemas de ecuaciones.

23)$\begin{align*} x-6y &= 4\\ 2x-12y &= 0 \end{align*}$

Contestar: No existen soluciones.

24)$\begin{align*} 2x+y+z &= -3\\ x-2y+3z &= 6\\ x-y-z &= 6 \end{align*}$

Para los ejercicios 25-26, utilizar la inversa de una matriz para resolver los sistemas de ecuaciones.

25)$\begin{align*} 4x-5y &= -50\\ -x+2y &= 80 \end{align*}$

Contestar: $(100, 90)$

26)$\begin{align*} \dfrac{1}{100}x-\dfrac{3}{100}y+\dfrac{1}{20}z &= -49\\ \dfrac{3}{100}x-\dfrac{7}{100}y-\dfrac{1}{100}z &= 13\\ \dfrac{9}{100}x-\dfrac{9}{100}y-\dfrac{9}{100}z &= 99 \end{align*}$

Para los ejercicios 27-28, usa la Regla de Cramer para resolver los sistemas de ecuaciones.

27)$\begin{align*} 200x-300y &= 2\\ 400x+715y &= 4 \end{align*}$

Contestar: $\left (\dfrac{1}{100}, 0 \right )$

28)$\begin{align*} 0.1x+0.1y-0.1z &= -1.2\\ 0.1x-0.2y+0.4z &= -1.2\\ 0.5x-0.3y+0.8z &= -5.9 \end{align*}$

Para los ejercicios 29-30, resolver utilizando un sistema de ecuaciones lineales.

29) Una fábrica que produce teléfonos celulares tiene las siguientes funciones de costo e ingresos:$C(x)=x^2+75x+2,688$ y$R(x)=x^2+160x$. ¿Cuál es la gama de celulares que deben producir cada día para que haya ganancias? Redondear al número más cercano que genere ganancias.

Contestar: $32$o más celulares por día

30) Un pequeño cobro justo$\$1.50$ para los estudiantes,$\$1$ para los niños y$\$2$ para los adultos. En un día, asistieron tres veces más niños que adultos. Se vendieron un total de$800$ boletos por un ingreso total de$\$1,050$. ¿Cuántos de cada tipo de boleto se vendió?

Colaboradores y Atribuciones

Template:OpenStaxPreCalc