10.5: Secciones cónicas en coordenadas polares
- Page ID
- 121582
- Identificar una cónica en forma polar.
- Grafica las ecuaciones polares de cónicas.
- Definir cónicas en términos de un enfoque y una directriz.
La mayoría de nosotros estamos familiarizados con el movimiento orbital, como el movimiento de un planeta alrededor del sol o un electrón alrededor de un núcleo atómico. Dentro del sistema planetario, las órbitas de planetas, asteroides y cometas alrededor de un cuerpo celeste más grande suelen ser elípticas. Los cometas, sin embargo, pueden tomar una órbita parabólica o hiperbólica en su lugar. Y, en realidad, las características de las órbitas de los planetas pueden variar con el tiempo. Cada órbita está ligada a la ubicación del cuerpo celeste orbitado y a la distancia y dirección del planeta u otro objeto desde ese cuerpo. Como resultado, tendemos a utilizar coordenadas polares para representar estas órbitas.
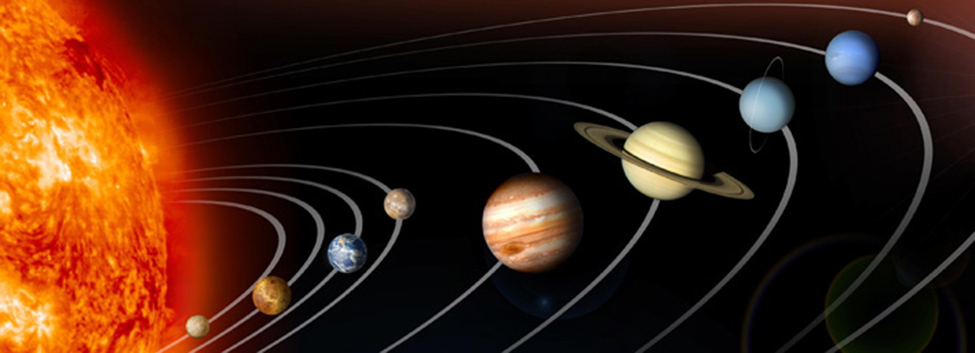
En una órbita elíptica, la periapsis es el punto en el que los dos objetos están más cerca, y la apoapsis es el punto en el que están más alejados. Generalmente, la velocidad del cuerpo en órbita tiende a aumentar a medida que se acerca a la periapsis y disminuir a medida que se acerca a la apoapsis. Algunos objetos alcanzan una velocidad de escape, lo que resulta en una órbita infinita. Estos cuerpos exhiben una órbita parabólica o hiperbólica alrededor de un cuerpo; el cuerpo en órbita se libera de la atracción gravitacional del cuerpo celeste y dispara hacia el espacio. Cada una de estas órbitas puede ser modelada por una sección cónica en el sistema de coordenadas polares.
Identificar una Cónica en Forma Polar
Cualquier cónica puede estar determinada por tres características: un solo foco, una línea fija llamada directriz, y la relación de las distancias de cada uno a un punto en la gráfica. Considera la parábola que\(x=2+y^2\) se muestra en la Figura\(\PageIndex{2}\).
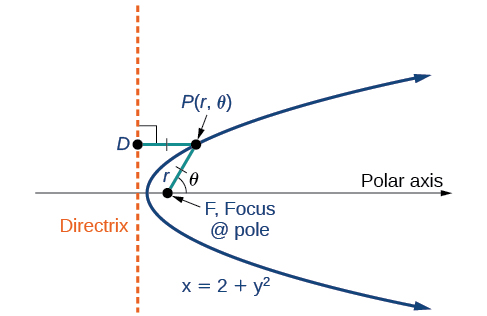
Anteriormente aprendimos cómo una parábola se define por el foco (un punto fijo) y la directrix (una línea fija). En esta sección, aprenderemos a definir cualquier cónica en el sistema de coordenadas polares en términos de un punto fijo, el foco\(P(r,\theta)\) en el polo, y una línea, la directriz, que es perpendicular al eje polar.
Si\(F\) es un punto fijo, el foco, y\(D\) es una línea fija, la directriz, entonces podemos dejar que\(e\) sea un número positivo fijo, llamado la excentricidad, que podemos definir como la relación de las distancias de un punto en la gráfica al foco y el punto en la gráfica a la directrix. Entonces el conjunto de todos los puntos\(P\) tal que\(e=\dfrac{PF}{PD}\) es una cónica. En otras palabras, podemos definir una cónica como el conjunto de todos los puntos\(P\) con la propiedad de que la relación de la distancia de\(P\) a\(F\) a la distancia de\(P\) a\(D\) es igual a la constante\(e\).
Para una cónica con excentricidad\(e\),
- si\(0≤e<1\), la cónica es una elipse
- si\(e=1\), la cónica es una parábola
- si\(e>1\), la cónica es una hipérbola
Con esta definición, ahora podemos definir una cónica en términos de la directriz\(x=\pm p\), la excentricidad\(e\) y el ángulo\(\theta\). Así, cada cónica puede escribirse como una ecuación polar, una ecuación escrita en términos de\(r\) y\(\theta\).
Para una cónica con un foco en el origen, si la directriz es\(x=\pm p\), donde\(p\) es un número real positivo, y la excentricidad es un número real positivo\(e\), la cónica tiene una ecuación polar
\[r=\dfrac{ep}{1\pm e \cos \theta}\]
Para una cónica con un foco en el origen, si la directriz es\(y=\pm p\), donde\(p\) es un número real positivo, y la excentricidad es un número real positivo\(e\), la cónica tiene una ecuación polar
\[r=\dfrac{ep}{1\pm e \sin \theta}\]
- Multiplique el numerador y el denominador por el recíproco de la constante en el denominador para reescribir la ecuación en forma estándar.
- Identificar la excentricidad\(e\) como el coeficiente de la función trigonométrica en el denominador.
- Comparar\(e\) con\(1\) para determinar la forma de la cónica.
- Determina la directrix como\(x=p\) si el coseno está en el denominador y\(y=p\) si el seno está en el denominador. Establecer\(ep\) igual al numerador en forma estándar para resolver para\(x\) o\(y\).
Para cada una de las siguientes ecuaciones, identifique la cónica con foco en el origen, la directrix y la excentricidad.
- \(r=\dfrac{6}{3+2 \sin \theta}\)
- \(r=\dfrac{12}{4+5 \cos \theta}\)
- \(r=\dfrac{7}{2−2 \sin \theta}\)
Solución
Para cada una de las tres cónicas, reescribiremos la ecuación en forma estándar. La forma estándar tiene a\(1\) como la constante en el denominador. Por lo tanto, en las tres partes, el primer paso será multiplicar el numerador y el denominador por el recíproco de la constante de la ecuación original,\(\dfrac{1}{c}\), donde\(c\) está esa constante.
- Multiplique el numerador y el denominador por\(\dfrac{1}{3}\).
\(r=\dfrac{6}{3+2\sin \theta}⋅\dfrac{\left(\dfrac{1}{3}\right)}{\left(\dfrac{1}{3}\right)}=\dfrac{6\left(\dfrac{1}{3}\right)}{3\left(\dfrac{1}{3}\right)+2\left(\dfrac{1}{3}\right)\sin \theta}=\dfrac{2}{1+\dfrac{2}{3} \sin \theta}\)
Porque\(\sin \theta\) está en el denominador, la directrix está\(y=p\). Comparando con la forma estándar, tenga en cuenta que\(e=\dfrac{2}{3}\) .Por lo tanto, del numerador,
\[\begin{align*} 2&=ep\\ 2&=\dfrac{2}{3}p\\ \left(\dfrac{3}{2}\right)2&=\left(\dfrac{3}{2}\right)\dfrac{2}{3}p\\ 3&=p \end{align*}\]
Ya que\(e<1\), la cónica es una elipse. La excentricidad es\(e=\dfrac{2}{3}\) y la directriz es\(y=3\).
- Multiplique el numerador y el denominador por\(\dfrac{1}{4}\).
\[\begin{align*} r&=\dfrac{12}{4+5 \cos \theta}\cdot \dfrac{\left(\dfrac{1}{4}\right)}{\left(\dfrac{1}{4}\right)}\\ r&=\dfrac{12\left(\dfrac{1}{4}\right)}{4\left(\dfrac{1}{4}\right)+5\left(\dfrac{1}{4}\right)\cos \theta}\\ r&=\dfrac{3}{1+\dfrac{5}{4} \cos \theta} \end{align*}\]
Porque\(\cos \theta\) está en el denominador, la directrix está\(x=p\). Comparando con la forma estándar,\(e=\dfrac{5}{4}\). Por lo tanto, desde el numerador,
\[\begin{align*} 3&=ep\\ 3&=\dfrac{5}{4}p\\ \left(\dfrac{4}{5}\right)3&=\left(\dfrac{4}{5}\right)\dfrac{5}{4}p\\ \dfrac{12}{5}&=p \end{align*}\]
Ya que\(e>1\), la cónica es una hipérbola. La excentricidad es\(e=\dfrac{5}{4}\) y la directriz es\(x=\dfrac{12}{5}=2.4\).
- Multiplique el numerador y el denominador por\(\dfrac{1}{2}\).
\[\begin{align*} r&=\dfrac{7}{2-2 \sin \theta}\cdot \dfrac{\left(\dfrac{1}{2}\right)}{\left(\dfrac{1}{2}\right)}\\ r&=\dfrac{7\left(\dfrac{1}{2}\right)}{2\left(\dfrac{1}{2}\right)-2\left(\dfrac{1}{2}\right) \sin \theta}\\ r&=\dfrac{\dfrac{7}{2}}{1-\sin \theta} \end{align*}\]
Debido a que el seno está en el denominador, la directriz está\(y=−p\). Comparando con la forma estándar,\(e=1\). Por lo tanto, desde el numerador,
\[\begin{align*} \dfrac{7}{2}&=ep\\ \dfrac{7}{2}&=(1)p\\ \dfrac{7}{2}&=p \end{align*}\]
Porque\(e=1\), la cónica es una parábola. La excentricidad es\(e=1\) y la directriz es\(y=−\dfrac{7}{2}=−3.5\).
Identificar la cónica con foco en el origen, la directrix, y la excentricidad para\(r=\dfrac{2}{3−\cos \theta}\).
- Contestar
-
elipse;\(e=\dfrac{1}{3}\);\(x=−2\)
Graficando las Ecuaciones Polares de Cónicas
Al graficar en coordenadas cartesianas, cada sección cónica tiene una ecuación única. Este no es el caso al graficar en coordenadas polares. Debemos utilizar la excentricidad de una sección cónica para determinar qué tipo de curva graficar, y luego determinar sus características específicas. El primer paso es reescribir la cónica en forma estándar como lo hemos hecho en el ejemplo anterior. En otras palabras, necesitamos reescribir la ecuación para que el denominador comience con\(1\). Esto nos permite determinar\(e\) y, por tanto, la forma de la curva. El siguiente paso es sustituir valores\(\theta\) y resolver\(r\) para trazar algunos puntos clave. Establecer\(\theta\) igual a\(0\),\(\dfrac{\pi}{2}\),\(\pi\), y\(\dfrac{3\pi}{2}\) proporciona los vértices para que podamos crear un boceto aproximado de la gráfica.
Gráfica\(r=\dfrac{5}{3+3 \cos \theta}\).
Solución
Primero, reescribimos la cónica en forma estándar multiplicando el numerador y denominador por el recíproco de\(3\), que es\(\dfrac{1}{3}\).
\[\begin{align*} r &= \dfrac{5}{3+3 \cos \theta}=\dfrac{5\left(\dfrac{1}{3}\right)}{3\left(\dfrac{1}{3}\right)+3\left(\dfrac{1}{3}\right)\cos \theta} \\ r &= \dfrac{\dfrac{5}{3}}{1+\cos \theta} \end{align*}\]
Porque\(e=1\), vamos a graficar una parábola con un enfoque en el origen. La función tiene a\(\cos \theta\), y hay un signo de suma en el denominador, por lo que la directrix es\(x=p\).
\[\begin{align*} \dfrac{5}{3}&=ep\\ \dfrac{5}{3}&=(1)p\\ \dfrac{5}{3}&=p \end{align*}\]
La directrix es\(x=\dfrac{5}{3}\).
Trazar algunos puntos clave como en Tabla nos\(\PageIndex{1}\) permitirá ver los vértices. Ver Figura\(\PageIndex{3}\).
| A | B | C | D | |
|---|---|---|---|---|
| \(\theta\) | \(0\) | \(\dfrac{\pi}{2}\) | \(\pi\) | \(\dfrac{3\pi}{2}\) |
| \(r=\dfrac{5}{3+3 \cos \theta}\) | \(\dfrac{5}{6}≈0.83\) | \(\dfrac{5}{3}≈1.67\) | undefined | \(\dfrac{5}{3}≈1.67\) |
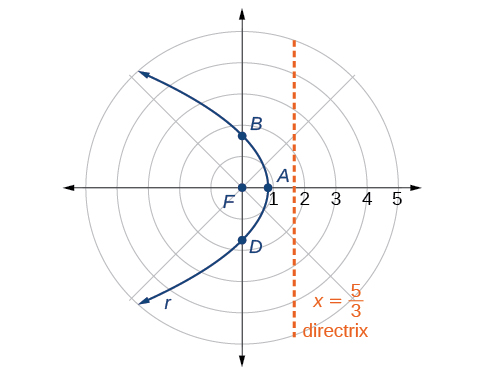
Podemos verificar nuestro resultado con una utilidad gráfica. Ver Figura\(\PageIndex{4}\).
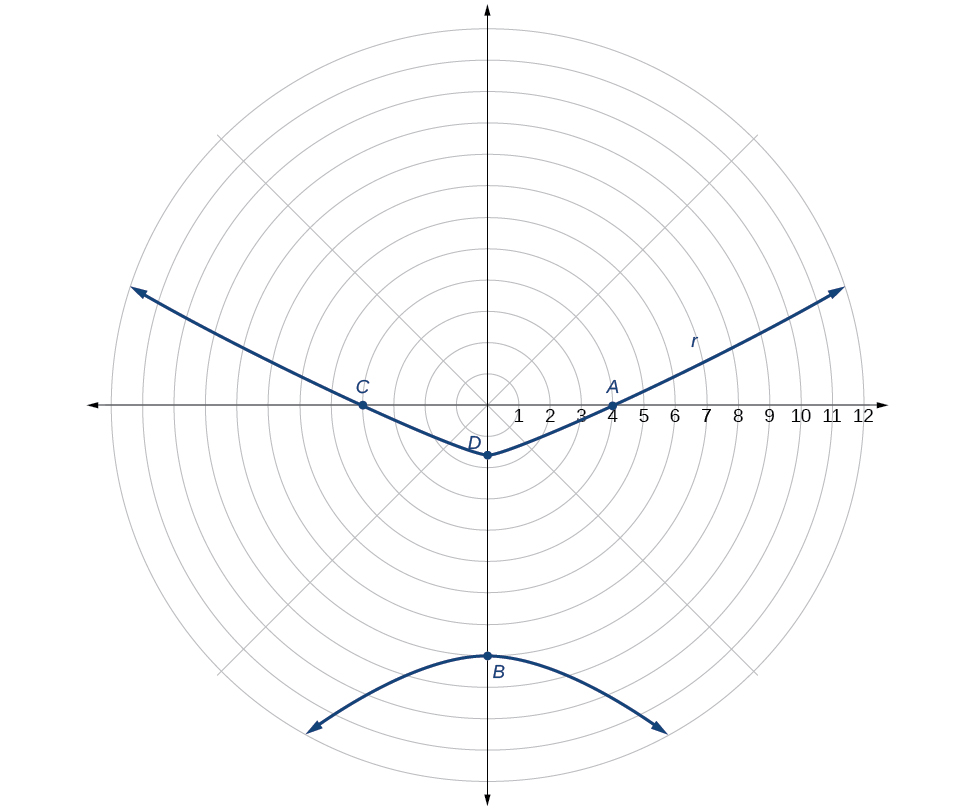
Gráfica\(r=\dfrac{8}{2−3 \sin \theta}\).
Solución
Primero, reescribimos la cónica en forma estándar multiplicando el numerador y denominador por el recíproco de\(2\), que es\(\dfrac{1}{2}\).
\[\begin{align*} r &=\dfrac{8}{2−3\sin \theta}=\dfrac{8\left(\dfrac{1}{2}\right)}{2\left(\dfrac{1}{2}\right)−3\left(\dfrac{1}{2}\right)\sin \theta} \\ r &= \dfrac{4}{1−\dfrac{3}{2} \sin \theta} \end{align*}\]
Porque\(e=\dfrac{3}{2}\),\(e>1\), así vamos a graficar una hipérbola con un enfoque en el origen. La función tiene un\(\sin \theta\) término y hay un signo de resta en el denominador, por lo que la directrix es\(y=−p\).
\[\begin{align*} 4&=ep\\ 4&=\left(\dfrac{3}{2}\right)p\\ 4\left(\dfrac{2}{3}\right)&=p\\ \dfrac{8}{3}&=p \end{align*}\]
La directrix es\(y=−\dfrac{8}{3}\).
Trazar algunos puntos clave como en Tabla nos\(\PageIndex{2}\) permitirá ver los vértices. Ver Figura\(\PageIndex{5}\).
| A | B | C | D | |
|---|---|---|---|---|
| \(\theta\) | \(0\) | \(\dfrac{\pi}{2}\) | \(\pi\) | \(\dfrac{3\pi}{2}\) |
| \(r=\dfrac{8}{2−3\sin \theta}\) | \(4\) | \(−8\) | \(4\) | \(\dfrac{8}{5}=1.6\) |
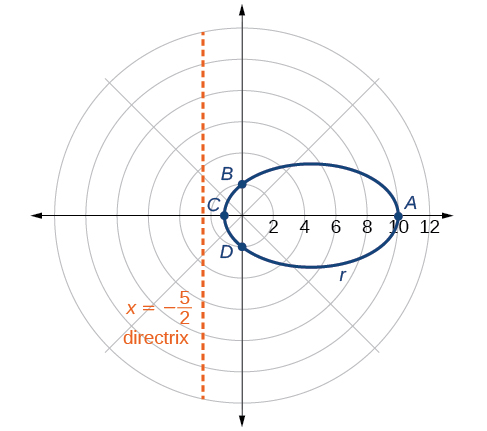
Gráfica\(r=\dfrac{10}{5−4 \cos \theta}\).
Solución
Primero, reescribimos la cónica en forma estándar multiplicando el numerador y denominador por el recíproco de 5, que es\(\dfrac{1}{5}\).
\[\begin{align*} r &= \dfrac{10}{5−4\cos \theta}=\dfrac{10\left(\dfrac{1}{5}\right)}{5\left(\dfrac{1}{5}\right)−4\left(\dfrac{1}{5}\right)\cos \theta} \\ r &= \dfrac{2}{1−\dfrac{4}{5} \cos \theta} \end{align*}\]
Porque\(e=\dfrac{4}{5}\),\(e<1\), así vamos a graficar una elipse con un foco en el origen. La función tiene a\(\cos \theta\), y hay un signo de resta en el denominador, por lo que la directriz es\(x=−p\).
\[\begin{align*} 2&=ep\\ 2&=\left(\dfrac{4}{5}\right)p\\ 2\left(\dfrac{5}{4}\right)&=p\\ \dfrac{5}{2}&=p \end{align*}\]
La directrix es\(x=−\dfrac{5}{2}\).
Trazar algunos puntos clave como en Tabla nos\(\PageIndex{3}\) permitirá ver los vértices. Ver Figura\(\PageIndex{6}\).
| A | B | C | D | |
|---|---|---|---|---|
| \(\theta\) | \(0\) | \(\dfrac{\pi}{2}\) | \(\pi\) | \(\dfrac{3\pi}{2}\) |
| \(r=\dfrac{10}{5−4 \cos \theta}\) | \(10\) | \(2\) | \(\dfrac{10}{9}≈1.1\) | \(2\) |
Análisis
Podemos verificar nuestro resultado usando una utilidad gráfica. Ver Figura\(\PageIndex{7}\).
Gráfica\(r=\dfrac{2}{4−\cos \theta}\).
- Contestar
-
Figura\(\PageIndex{7}\)
Definición de cónicas en términos de un enfoque y una directriz
Hasta el momento hemos estado usando ecuaciones polares de cónicas para describir y graficar la curva. Ahora trabajaremos a la inversa; usaremos información sobre el origen, la excentricidad y la directriz para determinar la ecuación polar.
- Determinar si la directriz es horizontal o vertical. Si la directrix se da en términos de\(y\), utilizamos la forma polar general en términos de seno. Si la directrix se da en términos de\(x\), utilizamos la forma polar general en términos de coseno.
- Determinar el signo en el denominador. Si\(p<0\), use resta. Si\(p>0\), use adición.
- Escribir el coeficiente de la función trigonométrica como la excentricidad dada.
- Escribe el valor absoluto de\(p\) en el numerador, y simplifica la ecuación.
Encuentra la forma polar de la cónica dada un foco en el origen,\(e=3\) y directrix\(y=−2\).
Solución
La directrix es\(y=−p\), entonces sabemos que la función trigonométrica en el denominador es seno.
Porque\(y=−2\),\(–2<0\), así sabemos que hay un signo de resta en el denominador. Utilizamos la forma estándar de
\(r=\dfrac{ep}{1−e \sin \theta}\)
y\(e=3\) y\(|−2|=2=p\).
Por lo tanto,
\[\begin{align*} r&=\dfrac{(3)(2)}{1-3 \sin \theta}\\ r&=\dfrac{6}{1-3 \sin \theta} \end{align*}\]
Encuentra la forma polar de una cónica dada un foco en el origen,\(e=\dfrac{3}{5}\), y directrix\(x=4\).
Solución
Porque la directrix es\(x=p\), sabemos que la función en el denominador es coseno. Porque\(x=4\),\(4>0\), así sabemos que hay un signo de suma en el denominador. Utilizamos la forma estándar de
\(r=\dfrac{ep}{1+e \cos \theta}\)
y\(e=\dfrac{3}{5}\) y\(|4|=4=p\).
Por lo tanto,
\[\begin{align*} r &= \dfrac{\left(\dfrac{3}{5}\right)(4)}{1+\dfrac{3}{5}\cos\theta} \\ r &= \dfrac{\dfrac{12}{5}}{1+\dfrac{3}{5}\cos\theta} \\ r &=\dfrac{\dfrac{12}{5}}{1\left(\dfrac{5}{5}\right)+\dfrac{3}{5}\cos\theta} \\ r &=\dfrac{\dfrac{12}{5}}{\dfrac{5}{5}+\dfrac{3}{5}\cos\theta} \\ r &= \dfrac{12}{5}⋅\dfrac{5}{5+3\cos\theta} \\ r &=\dfrac{12}{5+3\cos\theta} \end{align*}\]
Encuentra la forma polar de la cónica dada un foco en el origen,\(e=1\), y directrix\(x=−1\).
- Contestar
-
\(r=\dfrac{1}{1−\cos\theta}\)
Convierte la forma cónica\(r=\dfrac{1}{5−5\sin \theta}\) a rectangular.
Solución
Reorganizaremos la fórmula para usar las identidades\(r=\sqrt{x^2+y^2}\),\(x=r \cos \theta\), y\(y=r \sin \theta\).
\[\begin{align*} r&=\dfrac{1}{5-5 \sin \theta} \\ r\cdot (5-5 \sin \theta)&=\dfrac{1}{5-5 \sin \theta}\cdot (5-5 \sin \theta)\qquad \text{Eliminate the fraction.} \\ 5r-5r \sin \theta&=1 \qquad \text{Distribute.} \\ 5r&=1+5r \sin \theta \qquad \text{Isolate }5r. \\ 25r^2&={(1+5r \sin \theta)}^2 \qquad \text{Square both sides. } \\ 25(x^2+y^2)&={(1+5y)}^2 \qquad \text{Substitute } r=\sqrt{x^2+y^2} \text{ and }y=r \sin \theta. \\ 25x^2+25y^2&=1+10y+25y^2 \qquad \text{Distribute and use FOIL. } \\ 25x^2-10y&=1 \qquad \text{Rearrange terms and set equal to 1.} \end{align*}\]
Convierte la forma cónica\(r=\dfrac{2}{1+2 \cos \theta}\) a rectangular.
- Contestar
-
\(4−8x+3x^2−y^2=0\)
Acceda a estos recursos en línea para obtener instrucción adicional y práctica con cónicas en coordenadas polares.
- Ecuaciones polares de secciones cónicas
- Graficando Ecuaciones Polares de Cónicas - 1
- Graficando Ecuaciones Polares de Cónicas - 2
Visite este sitio web para obtener preguntas de práctica adicionales de Learningpod.
Conceptos clave
- Cualquier cónica puede ser determinada por un solo foco, la excentricidad correspondiente y la directrix. También podemos definir una cónica en términos de un punto fijo, el foco\(P(r,\theta)\) en el polo, y una línea, la directriz, que es perpendicular al eje polar.
- Una cónica es el conjunto de todos los puntos\(e=\dfrac{PF}{PD}\), donde la excentricidad\(e\) es un número real positivo. Cada cónica puede escribirse en términos de su ecuación polar. Ver Ejemplo\(\PageIndex{1}\).
- Se pueden graficar las ecuaciones polares de cónicas. Ver Ejemplo\(\PageIndex{2}\)\(\PageIndex{3}\), Ejemplo y Ejemplo\(\PageIndex{4}\).
- Las cónicas se pueden definir en términos de enfoque, directrix y excentricidad. Ver Ejemplo\(\PageIndex{5}\) y Ejemplo\(\PageIndex{6}\).
- Podemos usar las identidades\(r=\sqrt{x^2+y^2}\),\(x=r \cos \theta\), y\(y=r \sin \theta\) para convertir la ecuación para una cónica de forma polar a rectangular. Ver Ejemplo\(\PageIndex{7}\).


